Kinetics of the formation of β-casein/tannin mixed micelles
Wei
Ma
a,
Alain
Baron
b,
Sylvain
Guyot
b,
Saïd
Bouhallab
c and
Dražen
Zanchi
*a
aÉcole Normale Supérieure, Département de Chimie, UMR CNRS-ENS-UPMC 8640 PASTEUR, 24 rue Lhomond, F-75231 Paris Cedex 05, France. E-mail: zanchi@ens.fr
bINRA, UR117 Cidricoles et Biotransformation des Fruits et Légumes, F35653, Le Rheu, France
cINRA, Agrocampus Ouest, UMR1253 STLO, 65 rue de Saint Brieuc, F35042, Rennes, France
First published on 14th March 2012
Abstract
The complexation kinetics of β-casein with tannins were investigated by means of stopped flow and small-angle X-ray scattering (SAXS). Several small plant tannins have been considered: epigallocatechin-gallate (EGCG) from green tea and a set of oligomeric tannins from apples. We show that the kinetics are composed of two processes. The first process is a rapid uptake of tannins by the β-casein micelles over 40–100 ms and the second process is a slow reorganization of the tannin-dressed proteins into stable heavier micelles over a period of up to 200 s. In the first process, the protein segments in the cores of the micelles are rapidly coated by tannins. Detailed analysis of the SAXS profiles during the slow dynamics reveals that the system remains composed of micelles whose structural attributes evolve smoothly toward equilibrium values. The quantity of the bound tannins remains constant during the whole slow evolution of the system. We conclude that the dominant elementary events that drive the slow kinetics are the exchange processes of tannin-dressed proteins from one micelle to another.
Introduction
Mesoscopic assemblies and other soluble complexes between proteins and plant tannins attract attention because of the increasing evidence that the biological activity and potential therapeutic applications of tannins are based on their interaction with proteins. Several health benefits of plant tannins, such as their antioxidant activity, cancer prevention, cardiovascular disease prevention, antimicrobial and anti-viral activity and their action as neuro-protective agents, have been reported.1–3 Among the most perspective properties of tannins is the inhibition of protein aggregation, in particular of amyloid fibrilation. It has been shown that epigallocatechin-gallate (EGCG) inhibits prion amyloidogenesis in vitro and in vivo.4 A similar action of small polyphenol curcumin has also been reported.5 EGCG redirects the amyloid aggregation of α-synuclein and amyloid-β towards globular non-toxic assemblies6 and remodels mature fibrils, which reduces cellular toxicity.7 Redirection of the aggregation pathway and conversion of preformed amyloid fibrils to amorphous aggregates have also been reported for lysozyme in the presence of small polyphenols from tea, including EGCG.8 In all known examples the formation of tannin–protein nanometric clusters or micelles is observed whenever a natively unfolded or denatured protein (amyloidogenic or not) is put in contact with a small tannin.In recent works, several examples have been found where tannins and non-structured proteins form (meta-)stable mesoscopic structures, matching a universal theoretical model.9–11 On the other hand, the above mentioned findings indicate that the proposed tannin–protein clustering mechanisms are also relevant in the context of the tannin-driven inhibition of amyloidogenesis. Therefore, the present paper aims to gain insight into the mechanisms that govern the formation dynamics of finite assemblies between unfolded proteins and tannins.
Tannins in plants repel predators, whether an animal or a microbe.12 In either case, by a strong affinity for proteins and cell wall polysaccharides, the tannins render the tissues unacceptable as a food source for potential predators by precipitating surface glycoproteins or by immobilizing enzymes.1 Plant tannins are polyphenols with two or more phenolic groups, see Fig. 1. Plant tannins are divided into two categories: namely, hydrolysable tannins and condensed tannins. From a chemical point of view, condensed tannins are oligomeric and polymeric catechins. They exhibit greatly diverse structures on the basis of the number and position of the hydroxyl groups, the presence of the galloyl group and the nature, number and position of the interflavan linkages in a very large range of DP (degree of polymerization). For instance, apple varieties, and particularly cider varieties, contain homogeneous condensed tannins that are homo-polymers of (−)-epicatechin, varying from the dimeric forms (M = 578) to the highly polymerized forms, which are made of several dozens of catechin units reaching M values sometimes close to 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00013 (Fig. 1). In this work, we use the EGCG from green tea (M = 458), as well as tannins from apples with degrees of polymerization equal to DP = 2, DP = 6 and DP = 25 (named DP2, DP6 and DP25, respectively), with number average molecular weights of 578, 1730 and 7202, respectively.
00013 (Fig. 1). In this work, we use the EGCG from green tea (M = 458), as well as tannins from apples with degrees of polymerization equal to DP = 2, DP = 6 and DP = 25 (named DP2, DP6 and DP25, respectively), with number average molecular weights of 578, 1730 and 7202, respectively.
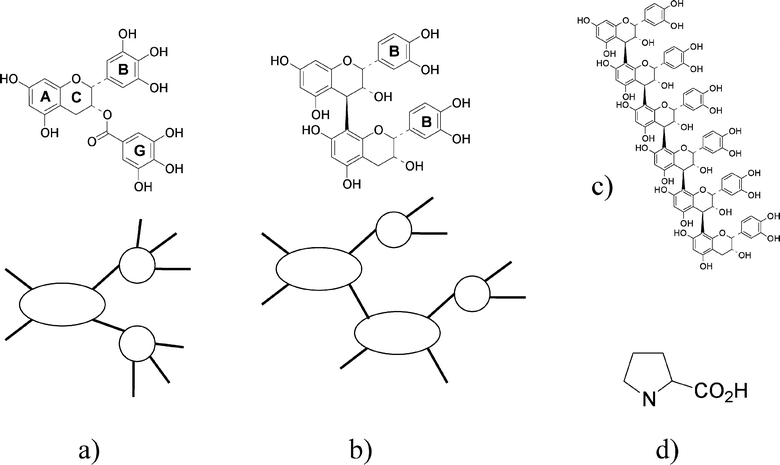 | ||
| Fig. 1 The chemical structures and schematic representations of the condensed tannins used in this study. a) Epigallocatechin-gallate (EGCG); the “B” and “G” rings are pyrogallols (three OH groups). b) Procyanidin dimer B2, the “B” rings are catechols (two OH groups). c) Procyanidin pentamer. Panel d) shows the amino acid, proline . The “active” tannin sites that bind to proline are the B ring and the G ring. | ||
In the present study, we focused on β-casein as a representative for the natural unfolded protein, whose structure, self-association and tannin-assisted aggregation are well known. β-casein is an intrinsically unstructured milk protein that contributes, together with α- and κ-caseins, to the structure of milk casein micelles. For its amphiphilic block structure, β-casein forms micelles in aqueous solutions containing between 5 and 30 proteins.14–16 With regards to the propensity of κ-casein to aggregate into amyloid fibers in milk, it is believed that β-casein performs a chaperone task to facilitate this.17
The micellization of β-casein can be described by the Kegeles Shell model.18,19 The theory calculates the aggregation number distribution for a cascade of association–dissociation processes given by:
A0 + Ai![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ↔ Ai. 1 ↔ Ai. | (1) |
The forward (association) and backward (dissociation) rates, respectively, can be written as:
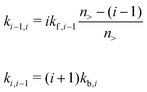 | (2) |
where n> is the aggregation number cutoff; kf,i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and kb,i are the forward and backward rates for the two-molecule processes. In principle, both are dependent of i because the free energy profile for adding or taking away depends on the size of the cluster. Within the shell model, the corresponding equilibrium constant, defined as Ki ≡ kf,i
1 and kb,i are the forward and backward rates for the two-molecule processes. In principle, both are dependent of i because the free energy profile for adding or taking away depends on the size of the cluster. Within the shell model, the corresponding equilibrium constant, defined as Ki ≡ kf,i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/kb,i, is assumed to be
1/kb,i, is assumed to be
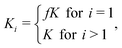 | (3) |
with K = exp(−ΔG/RT). For β-casein micelles, the parameters of the shell model have been found by Mikheeva et al.19 at 25 °C the a free energy of ΔG = G0 = −25 kJ mol−1 and a cooperativity parameter of f = 0.15, which corresponds to a difference of 4.7 kJ mol−1 between the work needed to make a dimer (i = 1) and the work required to add a monomer to the aggregate i > 1. The upper limit of the aggregation number, which fits the experimental value well, was found to be n> = 175.
In order to take into account the hydrophobic interaction between proteins and tannins and the resulting increase of the effective protein/protein binding tendencies, according to our previous study9 the free energy expression is:
| ΔG = G0 +γατa | (4) |
where G0 is the protein/protein association free energy, γ is the contribution to the free energy of protein/protein binding per bound tannin active site (B and G in Fig. 1), α is the fraction of tannins bound to proteins and τa is the number of tannin active sites per protein. The experimental data at pH = 6.5 are consistent with γ = −5 kJ mol−1, which is a typical value for hydrophobic and/or H–bond driven tannin–proline interactions.
The complexation of milk casein micelles (containing α-, β- and κ-casein) with the simplest tannin, EGCG extracted from green tea, has been studied recently by time-resolved SAXS using stopped flow.11 Analysis of the tannin uptake kinetics and consequential modification of the internal structure of the micelles revealed that the tannins penetrate the casein micelles over 180 ms and disintegrate calcium phosphate nanoparticles within the protein matrix, but do not change the micelle aggregation number. Namely, the casein micelles are sufficiently stable to keep their protein content unchanged, even when large amounts of tannin are absorbed by the micelles.
A clear difference between the way milk casein and β-casein micelles evolve after mixing with tannins is that β-casein micelles change their aggregation number9 by a factor of 10 or more, but the micelles keep their size unchanged. Consequently, the densities of the micelles increase. The process of this tannin-assisted micelle growth is a reorganization process of the proteins and tannins between the micelles: the tannins bind to the hydrophobic parts of the proteins (mostly in the micelle core) and bring more proteins into the micelles due to their supplementary “sticking” free energy of γ = −5 kJ mol−1 per bound tannin active site. The equilibrium state of tannin–protein micelles is thereby well understood within this modified Shell model. However, the question of whether the kinetics of this complexation are consistent with the one-protein processes, as given by eqn (1) and (2), is still an open issue. Moreover, in consideration of the applications of tannin–protein micelles, it is important to have control over the typical time scales and the corresponding driving mechanisms.
The present work aims to identify and quantitatively analyze the out-of-equilibrium processes which occur when pure β-casein micelles and tannins are rapidly mixed via a stopped flow device and then allowed to evolve an equilibrium. In particular, we want to investigate whether it is possible to separate in time the two processes: (i) the tannin uptake by micelles and (ii) the reorganization of micelles in order to reach a stable structure. Moreover, we aim to identify the elementary out-of-equilibrium association–dissociation events that govern the approach to equilibrium. In order to attain this objective, we analyzed the time evolution of the structure of the aggregates and of their size distribution using stopped flow coupled to SAXS.
Experimental
Materials
β-casein was prepared from whole casein as described by Pouliot et al.20 Almost monodisperse apple oligomeric procyanidin fractions from the monomer to the heptamer and polymer fraction DP25, with a mean degree of polymerization of 25, were obtained from cider apples (Kermerrien variety) using successive solvent extractions followed by fractionation on a semi-preparative normal phase HPLC as described by Guyot.13 In order to determine the percentage of procyanidin structures, the nature of the constitutive catechin units and the average degree of polymerization, all fractions were analyzed by thiolysis associated to reversed phase HPLC.13 All fractions contained close to 90% native procyanidins mainly consisting of (−)-epicatechin units (more than 95% of the total units). Oligomers DP2 and DP6 were almost monodispersed with regards to their molecular weight, whereas DP25 was somewhat polydispersed, with a polydispersity index (number over weight average) of Ip = 1.8. The tannin epigallocatechin-gallate (EGCG, a green tea extract) was purchased from Sigma–Aldrich and used without further purification. In this study, we used only the completely soluble tannin fractions, namely T2 in ref. 21. The ionic conditions of all the samples were adjusted with 5 mM NaCl and the pH was adjusted to 6.5 by adding HCl.SAXS measurement
Stopped flow SAXS experiments were performed at the beamline ID02 of the European Synchrotron Radiation Facility (ESRF, Grenoble, France) using a flow-through capillary cell. The X-ray wavelength was 0.1 nm and 2-dimensional SAXS patterns were recorded using a high resolution and low noise fiber-optically coupled CCD detector (FReLoN). The sample-to-detector distance was 1.5 m and the spectra covered a q range of 0.08 nm−1 < q < 4 nm−1. The measured SAXS intensities were normalized to an absolute scale and then azimuthally averaged to obtain the intensity profiles. The background-subtracted intensity is denoted by I(q). After rapid mixing of the tannin and protein by the stopped flow device, a set of 30 SAXS spectra were collected at evolution times with a time step that followed the geometrical progression from about 40 ms to 20 s over a typical period of 100 s. The acquisition time was 20 ms at each step, which allowed for a fair data precision of up to q = 2–3 nm−1. All the experiments were thermostated at 25 °C.Structural model
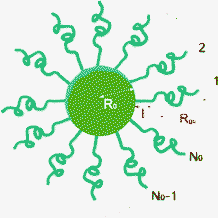
In order to capture the structure of the micelles, we used the Svaneborg–Pedersen model for core–crown micelles with partially rigid crown polymers.22 In this model it is supposed that the micelles consist of a core with the radius R0 to which the polymers are attached, see Fig. 2. The conformations of the polymers in the crown are not simple Gaussian coils because the polymers interact with each other via excluded volume or electrostatic repulsion. The corresponding stretching of the chains is included in the model by assuming that the chains are partially rigid over the length l starting from their end attached to the core. The remaining part of the chain is in the Gaussian random walk conformation. In the case of simple diblock copolymers with a hydrophilic block, α, and hydrophobic block, ρ = 1 − α, all the hydrophilic parts of the polymers constitute the crown and the remaining hydrophobic parts are in the core. In the β-casein molecule, the hydrophilic parts count for about 70% of the molecule.15 In our study we used this fraction as an approximate value for the fraction, α, of the polymer in the crown. Assuming that all the residues have the same scattering contrast, the Svaneborg–Pedersen form factor for micelles with a corona number N′ (number of polymer segments in the corona) gives: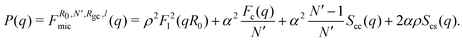 | (5) |
The first term comes from the scattering from the spherical core alone: F1(q) = 3(sin(qR0) − qR0cos(qR0))/(qR0)3. The term Fc(q) comes from individual chains in the crown and depends on Rgc and l, being respectively the gyration radius of the Gaussian part of the chain and the length of the rod part. The term Scc(q) is the inter-chain interference contribution and Scs(q) contains the core–crown interference. The analytical forms of the functions, Fc(q), Scc(q) and Scs(q), are given in ref. 22. In this work, the quantity of the tannins bound to the proteins in the micelles considerably contributes to the scattering intensity. Therefore, we modify the model (eqn (5)) by adding supplementary contrast into the cores of the micelles, by assuming
| ρ = 1 − α + φ | (6) |
where φ is the increment of the density of the micelle core per protein. This increment comes a priori from both tannins stuck to proteins and supplementary protein brought by the tannin into the core.
Protein micelles are polydispersed objects. We include polydispersity in our analysis by assuming that the scattering intensity is given by the following convolution integral:
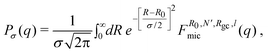 | (7) |
where σ is a distribution width. With this approach, the oscillations due to the spherical micelle core are averaged out. Polydispersity in the other parameters (N, Rgc and l) does not substantially change the scattering curves. Therefore, we simply used their average values to fit the data.
The resulting expression for the scattered intensity of protein–tannin micelles is:
| I(q) = pKpN′MpPσ(q) | (8) |
where p is the protein concentration in g l−1, Mp = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 is the molecular weight of the protein, N′ is the average number of the corona polymers and Kp = NA(VpΔρp/Mp)2 is the SAXS scattering constant for the protein expressed over the volume of the solvated protein Vp, which corresponds to the excess scattering length density, Δρp, and molecular weight Mp. For the X-ray contrast of the protein we use
000 g mol−1 is the molecular weight of the protein, N′ is the average number of the corona polymers and Kp = NA(VpΔρp/Mp)2 is the SAXS scattering constant for the protein expressed over the volume of the solvated protein Vp, which corresponds to the excess scattering length density, Δρp, and molecular weight Mp. For the X-ray contrast of the protein we use 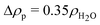 and for the tannin we have
and for the tannin we have 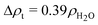 , where
, where 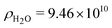 cm−2 is the SAXS scattering length density for water.23 Δρt was determined from the absolute forward intensity, It, of the monodispersed tannin dimer with a molecular weight of Mt = 2 × 289 g mol−1 at a concentration of c = 5 g L−1, using the following relationship:
cm−2 is the SAXS scattering length density for water.23 Δρt was determined from the absolute forward intensity, It, of the monodispersed tannin dimer with a molecular weight of Mt = 2 × 289 g mol−1 at a concentration of c = 5 g L−1, using the following relationship:
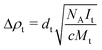 | (9) |
where the tannin relative density, dt = 1.55, was determined by a pycnometer. Excess electronic densities corresponding to the above contrasts are 118 electrons per nm3 for the protein and 132 electrons per nm3 for the tannin.
Results and discussion
The SAXS profiles of β-casein at a concentration of 2 g l−1 are shown in Fig. 3 (a), including the spectra of protein–EGCG mixtures at several evolution times after rapid mixture. Fig. 3 (b) shows the spectral evolution of the mixtures of β-casein with DP25, the longest tannin used in this study. In order to be sure that all parts of the scattering profile are dominated by the form factor of the micelles, we compared them with the form factor for a single protein and for a single tannin at the concentrations used. Both these spectra are, by at least a factor of 10, lower in intensity than the spectra of the micelles. This means that the excess electron density of a solution of tannins is always much lower than the excess electron density of any part of the micelle. Consequently, the scattering is dominated by the micelles. Let us first concentrate on β-casein alone before the mixing with tannins. Following a previously reported analysis,9 we fit the SAXS profile of β-casein to the calculated core–crown micelle model of Svaneborg and Pedersen, which is given by a formula.22 Best fits are obtained using the following parameters: a core radius of R0 = 5.5 nm, a corona composed of rigid segments with l = 0.4 nm, to which polymers with radius of gyration Rgc = 2.3 nm are grafted. The number of corona polymers is N′0 = 10. We assumed that the protein is composed of hydrophobic and hydrophilic segments, with all hydrophobic parts being in the core and all hydrophilic parts forming the corona. The hydrophobic-to-hydrophilic ratio is ρ = 30%. The molecular weight of the micelles is about 80 kDa. All quantities are in fair agreement with the results in the literature.9,15 The rather low value of the molar mass is due to the low ionic strength used in the present work and to an usual fluctuation in the protein quality from one batch to another.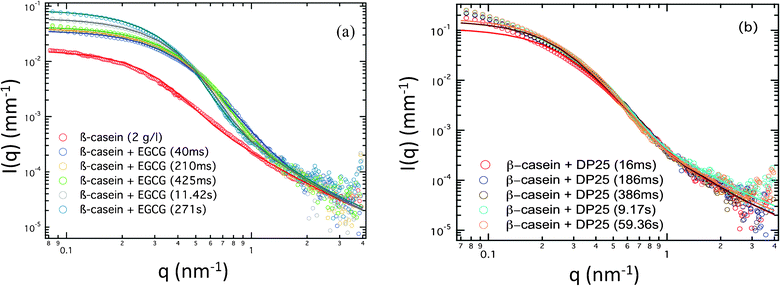 | ||
| Fig. 3 (a) SAXS profile for β-casein (2 g l−1) and the kinetics of β-casein/EGCG (0.4 g l−1 EGCG) at 40 ms, 210 ms, 425 ms, 11.42 s and 271 s. (b) SAXS profile for β-casein (2 g l−1) and the kinetics of β-casein/DP25 (0.4 g l−1 DP25) at 16 ms, 186 ms, 386 ms, 9.17 s and 59.36 s. | ||
After rapid mixing by the stopped flow device, the tannin–protein system evolves towards an equilibrium over about 1–2 min. The SAXS profile of the β-casein/EGCG sample, Fig. 3(a), shows a well defined Guinier regime at all evolution stages. Consequently, the sizes and masses of the micelles remain well defined during evolution. The radius of gyration, Rg, and the forward intensity, I0, can be determined by a simple fitting of the low-q part of the spectra to the Guinier formula as follows: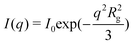 . The samples with the tannin dimers (DP2) and hexamers (DP6) have well defined Guinier regimes as well, which imply that the fitting by the Guinier formula is fully legitimate. Some caution is nevertheless necessary concerning samples with the tannin polymer DP25. Namely, some up-turn of the scattering intensity at low q values indicates that there exists a micelle–micelle attraction, as can be seen in Fig. 3(b). This is a signature of tannin-mediated micelle–micelle sticking, which becomes possible with tannins longer than two times the width of the corona (approximately 8 nm in this case). According to ref. 24, the end-to-end length of the tannin is approximately 0.34 nm × Dp. Thus, tannin DP25 is long enough to form a bridge between the micelles. The resulting sticking remains, however, rather low, as one can estimate by comparing the low-q up-turn of the protein + DP25 sample with the magnitude of the low-q up-turn for the protein + DP28 reported in ref. 9. We therefore fit the SAXS curves of samples with the DP25 tannin to ignore the lowest-q up-turn and concentrate on the curvature at the intermediate q values, which are associated to the geometry of the individual micelles and not to the inter-micelle attraction. Fig. 4 (a) and (b) show the radii of gyration and forward intensities resulting from the Guinier fits of the SAXS profiles for β-casein with the tannin “monomer” (EGCG), dimer (DP2), hexamer (DP6) and 25-mer (DP25) at tannin concentrations of 0.4 g l−1, 1 g l−1 and, for DP2, 2 g l−1. All the kinetics curves show a rapid variation at the time t < 1 s and a subsequent slow approach (over t ∼ 100 s) to the equilibrium values I∞ and R∞,shown in the inset image of Fig. 4. The intensity I∞ (which is related to the micelles' mass M) of the equilibrium tannin–protein micelles increases with tannin concentration, in agreement with ref. 9. We find here a plausible result that I∞ is an increasing function of Dp because the Dp range studied here is wider than the one used in ref. 9. By closer inspection of the curves, Rg(t) and I0(t), we see that while I0(t) varies over a factor ∼3 during the equilibration process, Rg(t) is modulated by less than 20%. These are indications that the micelles keep their core–crown structure and that the tannin brings material into the micelles without substantially changing their size. Another remarkable result is that I0(t) is a perpetually increasing function, while Rg(t) depends on the tannin used and can decrease or increase. Let us concentrate on the sample with the smallest tannin, EGCG. At times of t < 40 ms, Rg decreases by about 15% while I0 increases. This is an indication of the rapid arrival of a large number of EGCG molecules into the cores of the micelles. This induces a contraction of the scattering length toward the center of the micelle and a consequential drop in Rg. This extremely rapid uptake of EGCG by the micelles is in agreement with a similar phenomenon reported for milk caseins and EGCG in ref. 11. At later times, the individual proteins start to diffuse, implying a re-distribution of the tannin-coated protein within the micelles, producing a slow increase of both Rg(t) and I0(t). In the initial, rapid process, Rg(t) can either increase or decrease with time depending on the size of the tannin. Roughly speaking, longer tannins diffuse slower and, consequently, the time scales of the bare tannin intake become comparable to the most rapid protein diffusion processes. The time resolution and the experiment precision in the very first steps (less than 2 s) were, however, still insufficient to give quantitative information about the details of the tannin intake process, which obviously strongly depends on the tannin length. We can only be sure that the present set of Guinier analyses indicates clearly that we are dealing with complex kinetics that proceed at a minimum of two characteristic time scales. The first scale, τ0∼100 ms, is the tannin uptake process driven by tannin diffusion first through the solvent and then through the protein matrix of the micelle core. The time, τ0∼40 ms, which corresponds to the initial drop of Rg(t) in the case of EGCG, is comparable with the tannin uptake time of 180 ms reported by Shukla et al.11 for the milk casein + EGCG system. The reason for a surprising initial drop of Rg is that tannins diffuse very rapidly into the core of the micelles. This has two effects: (i) an increase in the core mass because of the extra tannin and (ii) the shrinking of the core because of the astringent effect of the tannin within the core. The result is that the density distribution is shifted towards the center, so that Rg (and also the core size) decrease. The remaining slow process over the times τ1 ∼ 100 s corresponds to the evolution of the out-of-equlibrium tannin–protein assemblies toward the stable micelles. It is plausible to assume that this process is driven by the extrication of proteins from the micelles, as well as micelle fragmentation, protein diffusion and micelle accretion and re-organization. We argue that the interpretation of the slow process in terms of a protein exchange and re-organization between micelles is the only possible explanation. Namely, if one supposes that upon addition of tannin the aggregation number remains the same, the observed increment of the forward SAXS intensity would be due to bound tannins only. We will show here that even if all the tannins were taken in by the micelles, the observed increase in the SAXS intensity is still too large. For that purpose, we started with the formula for the forward intensity, I0, of a micelle composed of N proteins at a concentration of p, dressed equally with bound tannins at a concentration of b.
. The samples with the tannin dimers (DP2) and hexamers (DP6) have well defined Guinier regimes as well, which imply that the fitting by the Guinier formula is fully legitimate. Some caution is nevertheless necessary concerning samples with the tannin polymer DP25. Namely, some up-turn of the scattering intensity at low q values indicates that there exists a micelle–micelle attraction, as can be seen in Fig. 3(b). This is a signature of tannin-mediated micelle–micelle sticking, which becomes possible with tannins longer than two times the width of the corona (approximately 8 nm in this case). According to ref. 24, the end-to-end length of the tannin is approximately 0.34 nm × Dp. Thus, tannin DP25 is long enough to form a bridge between the micelles. The resulting sticking remains, however, rather low, as one can estimate by comparing the low-q up-turn of the protein + DP25 sample with the magnitude of the low-q up-turn for the protein + DP28 reported in ref. 9. We therefore fit the SAXS curves of samples with the DP25 tannin to ignore the lowest-q up-turn and concentrate on the curvature at the intermediate q values, which are associated to the geometry of the individual micelles and not to the inter-micelle attraction. Fig. 4 (a) and (b) show the radii of gyration and forward intensities resulting from the Guinier fits of the SAXS profiles for β-casein with the tannin “monomer” (EGCG), dimer (DP2), hexamer (DP6) and 25-mer (DP25) at tannin concentrations of 0.4 g l−1, 1 g l−1 and, for DP2, 2 g l−1. All the kinetics curves show a rapid variation at the time t < 1 s and a subsequent slow approach (over t ∼ 100 s) to the equilibrium values I∞ and R∞,shown in the inset image of Fig. 4. The intensity I∞ (which is related to the micelles' mass M) of the equilibrium tannin–protein micelles increases with tannin concentration, in agreement with ref. 9. We find here a plausible result that I∞ is an increasing function of Dp because the Dp range studied here is wider than the one used in ref. 9. By closer inspection of the curves, Rg(t) and I0(t), we see that while I0(t) varies over a factor ∼3 during the equilibration process, Rg(t) is modulated by less than 20%. These are indications that the micelles keep their core–crown structure and that the tannin brings material into the micelles without substantially changing their size. Another remarkable result is that I0(t) is a perpetually increasing function, while Rg(t) depends on the tannin used and can decrease or increase. Let us concentrate on the sample with the smallest tannin, EGCG. At times of t < 40 ms, Rg decreases by about 15% while I0 increases. This is an indication of the rapid arrival of a large number of EGCG molecules into the cores of the micelles. This induces a contraction of the scattering length toward the center of the micelle and a consequential drop in Rg. This extremely rapid uptake of EGCG by the micelles is in agreement with a similar phenomenon reported for milk caseins and EGCG in ref. 11. At later times, the individual proteins start to diffuse, implying a re-distribution of the tannin-coated protein within the micelles, producing a slow increase of both Rg(t) and I0(t). In the initial, rapid process, Rg(t) can either increase or decrease with time depending on the size of the tannin. Roughly speaking, longer tannins diffuse slower and, consequently, the time scales of the bare tannin intake become comparable to the most rapid protein diffusion processes. The time resolution and the experiment precision in the very first steps (less than 2 s) were, however, still insufficient to give quantitative information about the details of the tannin intake process, which obviously strongly depends on the tannin length. We can only be sure that the present set of Guinier analyses indicates clearly that we are dealing with complex kinetics that proceed at a minimum of two characteristic time scales. The first scale, τ0∼100 ms, is the tannin uptake process driven by tannin diffusion first through the solvent and then through the protein matrix of the micelle core. The time, τ0∼40 ms, which corresponds to the initial drop of Rg(t) in the case of EGCG, is comparable with the tannin uptake time of 180 ms reported by Shukla et al.11 for the milk casein + EGCG system. The reason for a surprising initial drop of Rg is that tannins diffuse very rapidly into the core of the micelles. This has two effects: (i) an increase in the core mass because of the extra tannin and (ii) the shrinking of the core because of the astringent effect of the tannin within the core. The result is that the density distribution is shifted towards the center, so that Rg (and also the core size) decrease. The remaining slow process over the times τ1 ∼ 100 s corresponds to the evolution of the out-of-equlibrium tannin–protein assemblies toward the stable micelles. It is plausible to assume that this process is driven by the extrication of proteins from the micelles, as well as micelle fragmentation, protein diffusion and micelle accretion and re-organization. We argue that the interpretation of the slow process in terms of a protein exchange and re-organization between micelles is the only possible explanation. Namely, if one supposes that upon addition of tannin the aggregation number remains the same, the observed increment of the forward SAXS intensity would be due to bound tannins only. We will show here that even if all the tannins were taken in by the micelles, the observed increase in the SAXS intensity is still too large. For that purpose, we started with the formula for the forward intensity, I0, of a micelle composed of N proteins at a concentration of p, dressed equally with bound tannins at a concentration of b.
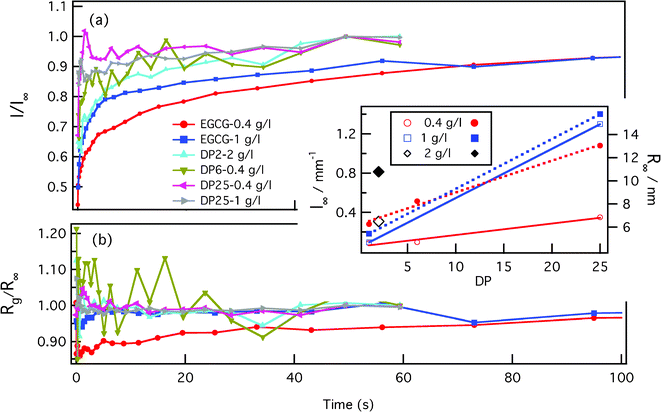 | ||
| Fig. 4 The time evolution of the forward scattering intensity I0 (a) and of the radii of gyration Rg (b) after stopped flow mixing of β-casein and tannins. Both results are obtained by fitting the series of SAXS spectra to the Guinier formula. Equilibrium values of I0 and Rg, called I∞ and R∞, are shown in the inset panel. | ||
| I 0 = NIp[1 + Γ1/2(b/p)]2 | (10) |
In order to investigate in more detail which are the most relevant processes and elementary events during the slow (τ1) micelle equilibration, a more detailed structural study was necessary. We fitted the SAXS spectra during τ1 using the modified Svaneborg and Pedersen model (ρ = 1 − α + φ), assuming that the quantity of the tannin fixed to the β-casein was constant with time and that it depends only on the tannin concentration and degree of polymerization. This way, we assume that the tannin–protein association process is completed after the time τ0 and that the slow equilibration involves the pre-formed tannin–protein molecular complexes with a constant number of bound tannins per protein. In addition to the parameter φ (an increase in the contrast in the micelle's core due to the tannins), the fitting parameters include the corona number N′, the core radius R0, the corona rod length l, the corona chain radius of gyration Rgc and a polydispersity parameter σ. The fits for two characteristic samples at several kinetic times are shown in Fig. 3. The fitting parameters resulting from the fits of all the samples are shown in Fig. 5. R0 evolves over less than 20% and N′ increases by a factor of 2 or 3, while the parameters describing the individual chains in the corona (l, and Rgc) remain essentially constant, as does the polydispersity parameter σ. In particular, this means that both the core and the corona densities increase. These results are consistent with the ones already found from the Guinier analysis. The added value of the present detailed analysis is that it reveals that the tannin–protein complex remains in the form of micelles throughout the slow kinetics. The micelles are composed of proteins coated with a constant number of tannins. The fact that the polydispersity remains constant and that R0(t) varies only weakly indicates that, at all times, the system contains just simple core–crown micelles and not other molecular assemblies that could result in conditions which destabilize the micelle system. The immediate conclusion is that the elementary processes which drive the system toward an equilibrium are not micelle–micelle aggregation, nor fragmentation processes N1 + N2 ↔ N with N1,N2 ≪ 1, but rather a one-protein exchange (emission–accretion) process. The one-polymer exchange is a complex process, studied recently for the case of almost monodispersed diblock copolymer micelles.25 According to that analysis, the process is rate limited by the extrication of the core block. The corresponding longest characteristic time is hypersensitive to the micellization number (or polydispersity) and to the Flory–Huggins interaction parameter. A detailed comparison of our data with theoretical expressions for the time evolution of micelles given in ref. 25 would necessarily involve estimations of relevant microscopic rheological constants and Flory–Huggins interactions between the protein segments coated randomly by tannins. We will not enter in to that analysis here.
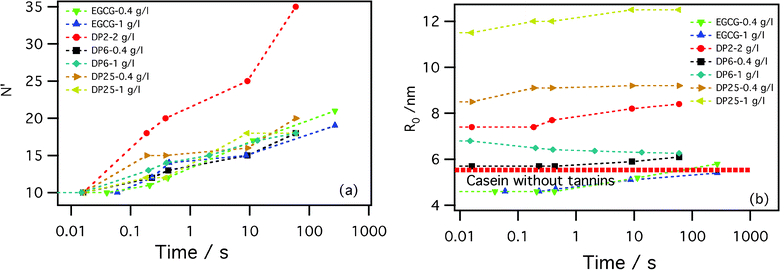 | ||
| Fig. 5 The results from fits of the SAXS data by the Svaneborg and Pedersen model, eqn (5) and ref. 22; the corona number, N′, (left panel) and the core radius, R0, (right panel) for β-casein at a concentration of 2 g l−1 with different tannins are shown. The thick broken line is the core radius of only β-casein at 2 g l−1. | ||
From our fitting, we get the parameter φ. It is constant throughout the slow kinetics. In other words, proteins that are being exchanged between micelles are all coated with tannin in the early moments after mixing. Simultaneously, intra-micelle re-organization brings some supplementary protein into the core. So far, we cannot distinguish between the contributions from the tannins and the proteins in φ: a detailed composition of the core in terms of the tannins and proteins is not possible with SAXS. However, from the quantity φ and the evolution of N′(t) and R0(t), we can find the time-dependence of the excess electron density in the core:
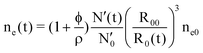 | (11) |
where N′ = 10, R00 = 5.6 nm and ne0 = 20 nm−3 are the number of protein chains in the corona, the core radius and the excess electron density of the core for micelles without tannins, respectively. Fig. 6 shows the slow evolution of the relative excess core density v ≡ ne(t)/ne0. It is interesting to note that the increment of the core density is the most important factor in the very first stages of the kinetics, while the subsequent micelle re-organization only moderately influences the core density. Another interesting piece of information given by this graph is that the strongest and the fastest core compaction is obtained with the smallest tannin, EGCG, while the lowest compaction is induced by the longest tannin, DP25. Namely, if we have in mind that tannins are rather rigid structures, then the longer the tannin, the more difficult it is to closely pack into a structure with protein segments in the core.
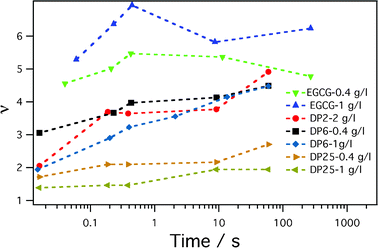 | ||
| Fig. 6 Evolution of the core density increment, v ≡ ne(t)/ne0 during the slow protein reorganization between micelles. | ||
The present analysis implies that the corona segments themselves are not affected by the presence of tannins. In the presence of tannins, only the number of corona segments increases because the aggregation number increases. These features are consistent with the fact that all (or a majority) of the tannin binding sites are in the core part of the protein, as has already been pointed out in ref. 9.
Conclusion
The kinetics of tannin/β-casein complexation after rapid mixing of a solution of tannins with a suspension of micelles was investigated by stopped flow/SAXS experiments. The micelles' average aggregation number increases from N0 towards a new equilibrium with N∞ > N0. Stable tannin/β-casein micelles contain tannins within a hydrophobic core. In order to identify the diffusion processes and elementary assemblies that govern the evolution of the system after rapid mixing, a series of SAXS spectra was monitored at time scales from 40 ms to 200 s after mixing. An analysis of the SAXS profiles shows that the kinetics are composed of two processes: (i) an initial rapid tannin uptake into the micelles with N = N0 and (ii) the slow exchange of tannin-dressed proteins between the micelles, leading to the equilibrium state with N = N∞.The tannin uptake process is extremely rapid, in the order of 100 ms. It is controlled by almost free diffusion of the tannins toward the cores of the micelles and a subsequent diffusion of the tannins into the micelle core through the protein matrix. Both these rapid processes were already identified in the case of EGCG uptake by milk casein micelles.11 This slow process is specific for β-casein and it has not been observed in the case of milk casein. In order to characterize the evolution of the micelles' structure during this slow equilibration process, SAXS data were fitted to a Svaneborg–Pedersen structural model (eqn(5)), which was modified in a way to add the contribution from the tannins to the micelle core scattering (eqn (6)). Our analysis shows that, at all the evolution steps, the system is composed of micelles, whose structural parameters evolve smoothly toward a final state. In particular, we found no sign of micelle–micelle aggregation at any of the intermediate steps. The quantity of bound tannin per protein is constant during the entire slow kinetics, implying that the tannin exchange processes are quenched after tannin uptake. We conclude that the elementary events that drive the tannin-induced micelle growth are a one-by-one exchange process of tannin-dressed proteins between the micelles. These intermediate micelles keep their core–crown structure throughout the evolution. These findings show that the kinetics of β-casein/tannin complexation can be well described by a series of accretion–erosion processes (eqn(1)) within a standard Shell model.
Acknowledgements
We thank Anuj Shukla and Theyencheri Narayanan for help at the SAXS beamline ID02 at ESRF, Grenoble. We also thank ESRF for beam time allocation.References
- A. Scalbert, Phytochemistry, 1991, 30, 3875 CrossRef CAS.
- C. Santos-Buelga and A. Scalbert, J. Sci. Food Agric., 2000, 80, 1094 CrossRef CAS.
- P. M. Aron and J. A. Kennedy, Mol. Nutr. Food Res., 2008, 52, 79 CAS.
- B. E. Roberts, M. L. Duennwald, H. Wang, C. Chung, N. P. Lopreiato, E. A. Sweeny, M. N. Knight and J. Shorter, Nat. Chem. Biol., 2009, 5, 936 CrossRef CAS.
- I. Hafner-Bratkovic, J. Gaspersic, L. M. Smid, M. Bresjanac and R. Jerala, J. Neurochem., 2008, 104, 1553 CrossRef CAS.
- D. E. Ehrnhoefer, J. Bieschke, A. Boeddrich, M. Herbst, L. Masino, R. Lurz, S. Engemann, A. Pastore and E. E. Wanker, Nat. Struct. Mol. Biol., 2008, 15, 558 CAS.
- J. Bieschke, J. Russ, R. P. Friedrich, D. E. Ehrnhoefer, H. Wobst, K. Neugebauer and E. E. Wanker, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7710 CrossRef CAS.
- J. He, Y. F. Xing, B. Huang, Y. Z. Zhang and C. M. Zeng, J. Agric. Food Chem., 2009, 57, 11391 CrossRef CAS.
- D. Zanchi, T. Narayanan, D. Hagenmuller, A. Baron, S. Guyot, B. Cabane and S. Bouhallab, Europhys. Lett., 2008, 82 Search PubMed.
- D. Zanchi, C. Poulain, P. Konarev, C. Tribet and D. I. Svergun, J. Phys.: Condens. Matter, 2008, 20, 494224 CrossRef.
- A. Shukla, T. Narayanan and D. Zanchi, Soft Matter, 2009, 5, 2884 RSC.
- E. Haslam, Phytochemistry, 2007, 68, 2713 CrossRef CAS.
- S. Guyot, N. Marnet and J.-F. Drilleau, J. Agric. Food Chem., 2001, 49, 14 CrossRef CAS.
- E. Leclerc and P. Calmettes, Physical Review Letters, 1997, 78 Search PubMed.
- E. Leclerc and P. Calmettes, Phys. B, 1997, 241–243, 1141 CrossRef CAS.
- J. E. O'Connell, V. Y. Grinberg and C. G. de Kruif, J. Colloid Interface Sci., 2003, 258, 33 CrossRef CAS.
- H. Ecroyd, T. Koudelka, D. C. Thorn, D. M. Williams, G. Devlin, P. Hoffmann and J. A. Carver, J. Biol. Chem., 2008, 283, 9012 CrossRef CAS.
- G. Kegeles, J. Phys. Chem., 1979, 83, 1728 CrossRef CAS.
- L. M. Mikheeva, N. V. Grinberg, V. Y. Grinberg, A. R. Khokhlov and C. G. de Kruif, Langmuir, 2003, 19, 2913 CrossRef CAS.
- M. Pouliot, Y. Pouliot, M. Britten, J. L. Maubois and J. Fauquant, Lait, 1994, 74, 325 CAS.
- D. Zanchi, A. Vernhet, C. Poncet-Legrand, D. Cartalade, C. Tribet, R. Schweins and B. Cabane, Langmuir, 2007, 23, 9949 CrossRef CAS.
- C. Svaneborg and J. S. Pedersen, J. Chem. Phys., 2000, 112, 9661 CrossRef CAS.
- P. Schurtenberger, in Neutrons, X-rays and Light: Scattering methods Applied to Soft Condensed Matter, ed. P. Lindner and T. Zemb, 2002, Elsevier, Amsterdam, 145–170 Search PubMed.
- D. Zanchi, P. V. Konarev, C. Tribet, A. Baron, D. I. Svergun and S. Guyot, J. Chem. Phys., 2009, 130, 245103 CrossRef.
- S.-H. Choi, T. P. Lodge and F. S. Bates, Phys. Rev. Lett., 2010, 104, 047802 CrossRef.
| This journal is © The Royal Society of Chemistry 2012 |