Proton-transfer paths in CH⋯O hydrogen bonds

Abstract

Potential energy surfaces for a series of intermolecular CH⋯O hydrogen bonds have been calculated in order to determine the Quantum Mechanical Reaction Coordinates (QMRCs). The results have shown that one QMRC curve is common for strong C–H⋯O hydrogen bonds, and another for very weak interactions. For intermediate hydrogen bonds the shape of the potential energy curve depends on the particular type of the C–H⋯O bond, which is related to the proton donor ability and geometry of the hydrogen bridge.

---

Introduction

The importance of hydrogen bonds in chemical, physical, biological and life processes,¹proton transfer reactions,² enzymatic catalysis,³ material sciences and crystal engineering⁴ is well known and the properties of the hydrogen bond have been intensively investigated for a long time. The strength of the hydrogen bonds is very variable. The OHO hydrogen bonds can vary from very weak to very strong and partially covalent.⁵ Similarly the OHN and NHN hydrogen bridges may be relatively strong.⁶ Increase of the hydrogen bond strength is connected with shifting of the proton from the donor towards the acceptor and for the strongest hydrogen bonds the proton may be located close to the hydrogen bridge centre. These strong hydrogen bonds influence the physical properties and can be investigated with many experimental methods, such as IR, NMR, UV-VIS, NQR spectroscopy and dipole moment measurement, in which the variable strength of the hydrogen bond is reflected.⁷

The CH⋯O hydrogen bond is considerably weaker than the OHO, OHN and NHN bonds, and the proton is always located closer to the carbon donor atom. Compared to typical hydrogen bonds the energy of C–H⋯O hydrogen bonds is significantly lower (less than 5 kcal mol⁻¹). A shift of the proton to the acceptor or location in the middle of the hydrogen bridge is not known for CH⋯O. However, the distance from the proton to the oxygen acceptor is shortened relatively to the sum of the Van der Waals radii and this is the most characteristic evidence for CH⋯O hydrogen-bond formation. Except for the strongest known CH⋯O bonds, for which there is a certain shift of the stretching CH vibration caused by the hydrogen bond,⁸ it is not possible to investigate this bond by spectroscopy or other physical methods. In several respects the CH⋯O bonds are more important than the strong hydrogen bonds. The reason for this importance is the common occurrence of CH⋯O hydrogen bonds in organic systems,⁹ such as sugars,^10,11carbohydrates¹¹and nucleic acids.¹² The common presence of C–H⋯O hydrogen bonds in organic systems is connected with their crucial role in biological processes. They are responsible for base pairing specificity,¹³ formation of general folding motifs¹⁴ interactions of nucleic acids with proteins,¹⁵drug binding¹⁶ and the structure of amino acids.¹⁷ Also the packing of the molecules in crystals can be determined by the C–H⋯O hydrogen bond.¹⁸ For this reason understanding of the main futures of the CH⋯O hydrogen bond is important in many areas of science.

One of the most general characteristic features of the hydrogen bond is connected with the valency of the proton. Applying Pauling's bond-order concept¹⁹ and the principle of conservation of bond order a Bond Order Reaction Curve (BORC) may be calculated which expresses a simple relation between the bond length and bond order: d(ρ) −d(1) = −a ln(ρ) where d(ρ) is the interatomic distance for a fractional bond with bond order ρ and d(1) is the corresponding single bond length. Before the hydrogen bond is formed d(ρ₁) = d(D–H, free) and d(ρ₂) = d(H–A, ∞), so ρ₁ = 1 and ρ₂ = 0; for the complete proton transferρ₁ = 0, ρ₂ = 1. In a proton transfer reaction D–H + A → D⋯H⋯A → D⁺ +H–A⁻ the sum (n) of the bond orders ρ₁ and ρ₂ for D–H and H–A, respectively, is assumed to remain constant along the reaction coordinate. When the proton moves from donor to acceptor the sum of the bond orders of D–H and H–A must be equal to 1, i.e. ρ₁ + ρ₂ = 1. Although the constant valency rule was proposed a very long time ago it is still used in discussions of hydrogen-bond systems.²⁰

To find the BORC relation linking the D–H and H–A distances it is sufficient to know d(1), the bond distance of the free D–H, and the shortest possible D⋯A bridge length²¹ (half of the D⋯A bridge length corresponds to ρ = 0.5). Using this method we have determined the BORC curves for different types of hydrogen bonds.²² It turns out that both D–H and H⋯A bond distances follow the Bond Order Reaction Coordinate (BORC), independent of the proton transfer degree for the stronger intermolecular hydrogen bonds.

Another description of the proton transfer process is connected with the assumption that the proton is shifted from donor to acceptor along the path passing through the lowest energy—the Quantum-Mechanically derived Reaction Coordinates (QMRCs). Calculation of the potential energy surfaces, determination of the QMRC curves and comparison with BORC have been performed for many systems and show that for the intermolecular OHO, OHN and NHN hydrogen bonds both curves are identical, whereas for the intramolecular hydrogen bonds they are different. The difference depends on the particular type of intramolecular hydrogen bond and can be significant.²²

The aim of this paper is the calculation of the QMRC curve for intermolecular C–H⋯O hydrogen bond, which may be expected to be identical with the BORC curve, similarly to the strong hydrogen bonds.²² The proton donor properties of C–H depend on the polarity of the C–H group: C≡C–H > C=CH₂ > –CH₃. As it is not clear if all these different proton donors will be described by one common curve, the QMRC curves for different types of C–H have been calculated.

Theoretical calculations

The crystal data used as starting structure in the potential energy surface calculations were taken from the CSD data base.²³ The structures of BEXMIA, TOYEW, WEQMAG, QQQAUG02 and SIXZOO have been determined by X-rays and the uncertainty in the C–H and H⋯O distance is therefore considerable (standard deviations around 0.05 Å). Other structures have been determined by neutron diffraction and the distances are determined more precisely. The CSD refcodes of the different compounds are used in the following. DFT calculations have been carried out at the B3LYP/6-31++G** level of theory with the Gaussian03 system.²⁴ The crystallographically determined coordinates for all atoms, except for the H atom involved in the hydrogen bond, have been kept fixed and the potential-energy surface been generated for carbon–hydrogen and oxygen–hydrogen distance successively changed in 0.04 Å steps. The C–H distance has been changed in the 0.9–1.8 Å range and the H⋯O distance 0.9–3.0 Å.

Results

As the acidity of the C–H group can change in a relatively broad range, several groups of compounds have been investigated. The strongest C–H⋯O hydrogen bonds can be formed with the C≡C–H proton donor in BETAXAZ01, BEXMIA, TOYJEW and WEQMAG. Protons linked to the aromatic ring in ACSALA12, HISTPA12, METHYM01 and QQQAUG02 should form weaker C–H⋯O hydrogen bonds but stronger than with the proton in aliphatic compounds. In FOMHAZ16, KHDFRM12 and TARTAC01 there is an aliphatic C–H bond, in AGLYSL01, CYACHZ01 and TGLYSU11 a CH₂ bond and in AJOHUC, MANMUJ and SIXZOO a methyl group. These compounds should cover the full range of C–H⋯O hydrogen bond strengths. The geometrical parameters of the investigated compounds are collected in Table 1. For certain compounds listed in Table 1, such as KHDFRM12, TARTAC01, AGLYSL01 and TGLYSU11, is it not clear if the interaction could be called a hydrogen bond due to the very low CHO angles. It is not easy to categorize the interaction without precise investigation of the charge shift between the atoms participating in the hydrogen bond, which is the main point of criteria of hydrogen bond formation. Independent of the type of interaction the potential energy surfaces have been calculated for all compounds in Table 1

Table 1 Geometrical parameters of investigated compounds (in Å and degrees)

Refcode	Compound name	Ref.	C–H	H⋯O	C⋯O	CHO
C≡C–H
BETXAZ01	2-ethynyl-2-adamantanol	25	1.070	2.255	3.183	171.2
BEXMIA	N-(p-methylphenyl)-N-prop-2-ynylurea	26	1.10	2.38	3.453	166
TOYJEW	3-phenylpenta-1,4-diyn-3-ol	27	0.94	2.50	3.377	155
WEQMAG	5β-hydroxy-5α-ethynyl-10β-methyl-Δ^1(9)-octalin-2-one	28	0.93	2.35	3.260	164
CH aromatic
ACSALA12	acetylsalicylic acid	29	1.054	2.542	3.120	120.8
HISTPA12	L-histidinium dihydrogen phosphate phosphoric acid	30	1.080	2.129	3.202	172.1
METHYM01	1-methylthymine	31	1.084	2.045	3.120	170.9
QQQAUG02	6-chloro-4H-1,2,4-benzathiadiazine-7-sulphonamide-1,1-dioxide	32	1.08	2.15	3.173	158
CH aliphatic
FOMHAZ16	N,N′-diformohydrazide	33	1.100	2.455	3.426	146.5
KHDFRM12	Potassium hydrogen diformate	34	1.099	2.713	3.146	103.0
TARTAC01	tartaric acid	35	1.105	2.592	3.107	107.4
CH2 aliphatic
AGLYSL01	Ammonium glycinium sulfate	36	1.085	2.631	3.190	111.4
CYACHZ01	α-cyanoacetohydrazide	37	1.095	2.412	3.161	124.3
TGLYSU11	triglycine sulfate	38	0.973	2.596	3.162	117.3
CH3 aliphatic
AJOHUC	1-dimethylamino-8-dimethylammonionaphthalene (o-benzoic sulfimide) dihydrate	39	1.084	2.434	3.400	147.7
AJOHUC		39	1.083	2.593	3.511	142.1
MANMUJ	betaine bis(imidazole picric acid)	40	1.090	2.334	3.338	152.4
SIXZOO	Methylammonium hydrogen succinate monohydrate	41	0.96	2.59	3.201	122

---

In Fig. 1 is shown the potential energy surface which is common for all the compounds with the C≡C–H proton donor. The elongated energy minimum is located along the QMRC curve and the experimental points for all the compounds are located within or close to the lowest energy level.

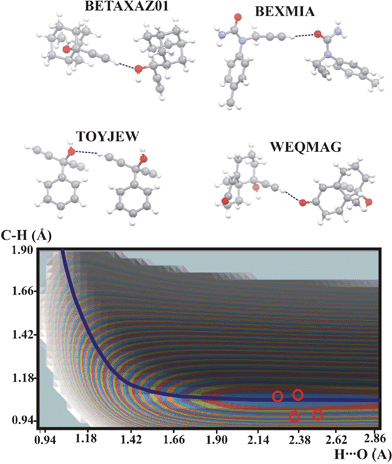Fig. 1 Potential energy surface for the compounds with C–H⋯O intermolecular hydrogen bond formed by C≡C–H proton donors. The QMRC curve is marked as a dark-blue line. The red circles represent experimental proton positions. Contour levels of the blue, red, green etc. curves, starting from the minimum energy contour: 1, 2, 3 kcal mol⁻¹. Color legend for the atoms in molecules: grey: carbon, white: hydrogen, red: oxygen, blue: nitrogen.

In Fig. 2 are shown the potential energy surfaces for the compounds with a C–H⋯O bond in which the proton is linked to the aromatic ring. For all compounds except ACSALA12 the potential energy surfaces are very similar and the QMRC curve can be common for all these compounds. The energy minima have different shapes and different locations on the QMRC curve. The shift of the minimum is correlated with the experimental C–H and H⋯O distances. The experimental points are always located within the energy minimum contour. The elongated shape of the minima is connected with the linearity of the hydrogen bond and for HISTPA12 the minimum is shortest. The different shape of the potential energy surface of ACSALA12 is probably connected with the low value of the CHO angle (120.8°) and long H⋯O distance. The very bent CHO bond leads to a short C⋯O distance and despite this short distance, the hydrogen bond in ACSALA12 is very weak and the hydrogen bond strength is reflected in the shape of potential energy surface.

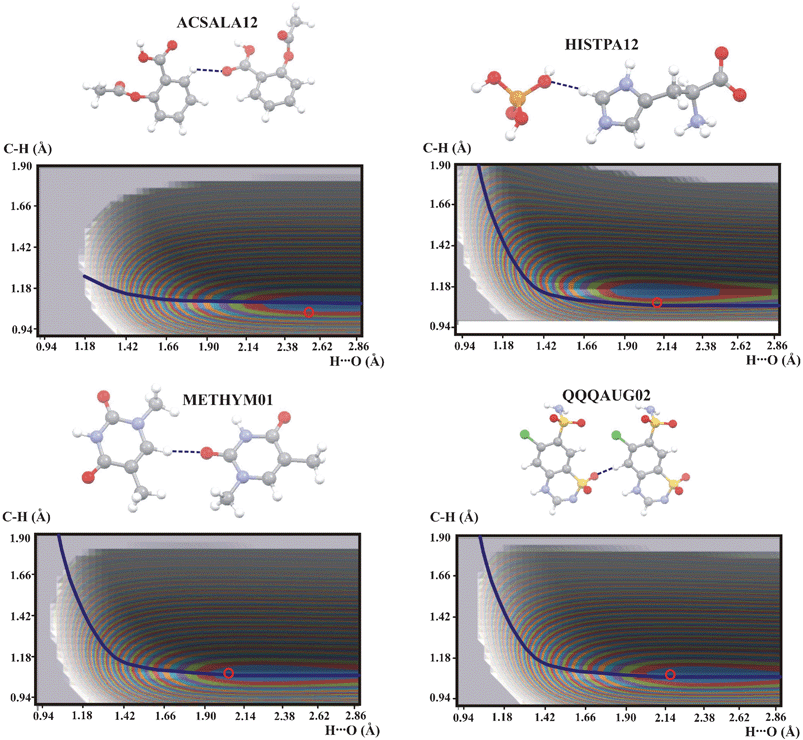Fig. 2 Potential energy surfaces for intermolecular C–H⋯O hydrogen bonds with the proton connected to aromatic ring. Contour levels and marks for experimental points as in Fig. 1. Color legend for the atoms in molecules: grey: carbon, white: hydrogen, red: oxygen, blue: nitrogen, yellow: sulfur, green: chlorine.

The potential energy surface is common for all the compounds presented in Fig. 3 and is similar to that of ACSALA12. The experimental points are located within the lowest energy contour. Taking into account the shape of the QMRC curve common for ACSALA12, FOMHAZ16, KHDFRM12 and TARTAC01 it can be concluded that the QMRC curve for these compounds is different compared to the strong C–H⋯O hydrogen bond in with C≡C–H proton donor.

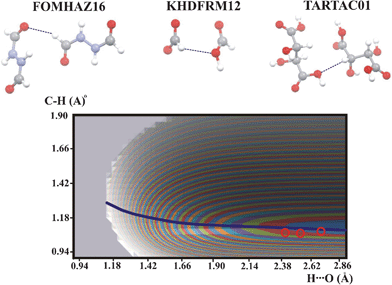Fig. 3 Potential energy surfaces for intermolecular C–H⋯O hydrogen bonds with aliphatic C–H proton donor. Contour levels, color legend and experimental points as in Fig. 1.

Another group of potential energy surfaces is shown in Fig. 4. It is characteristic that the QMRC curve for these hydrogen bonds is shifted to higher H⋯O values and its shape is different than for the hydrogen bonds with the C≡C–H proton donor. The energy minimum is located at long H⋯O but a second energy minimum is formed in the region of long C⋯H distances. The second energy minimum represents a chemical reaction but not proton transfer. As the QMRC curve is not connected with proton transfer it is not an equivalent to the QMRC curve for proton motion.

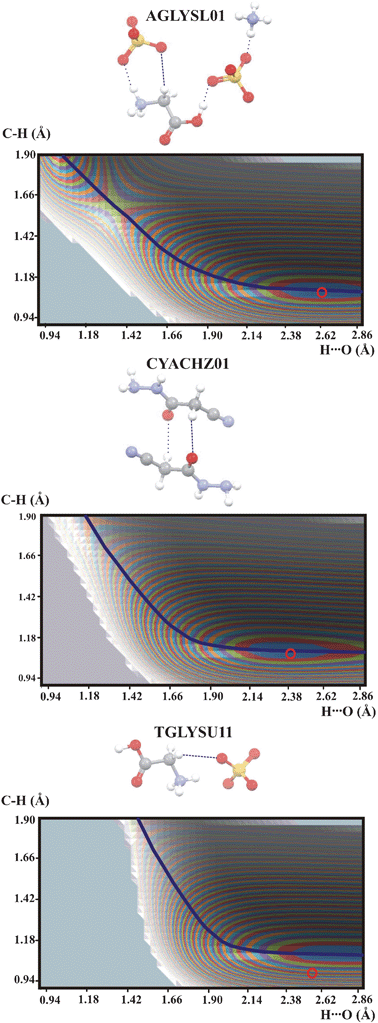Fig. 4 Potential energy surfaces for intermolecular C–H⋯O hydrogen bonds with the CH₂ proton donor. Contour levels as in Fig. 1. Additional interactions are marked as thin dotted lines. Color legend for the atoms as in Fig. 2.

The weakest C–H⋯O hydrogen bonds are expected for the methyl group as proton donor. In Fig. 5 are shown potential energy surfaces for hydrogen bonds in AJOHUC, MANMUJ and SIXZOO.

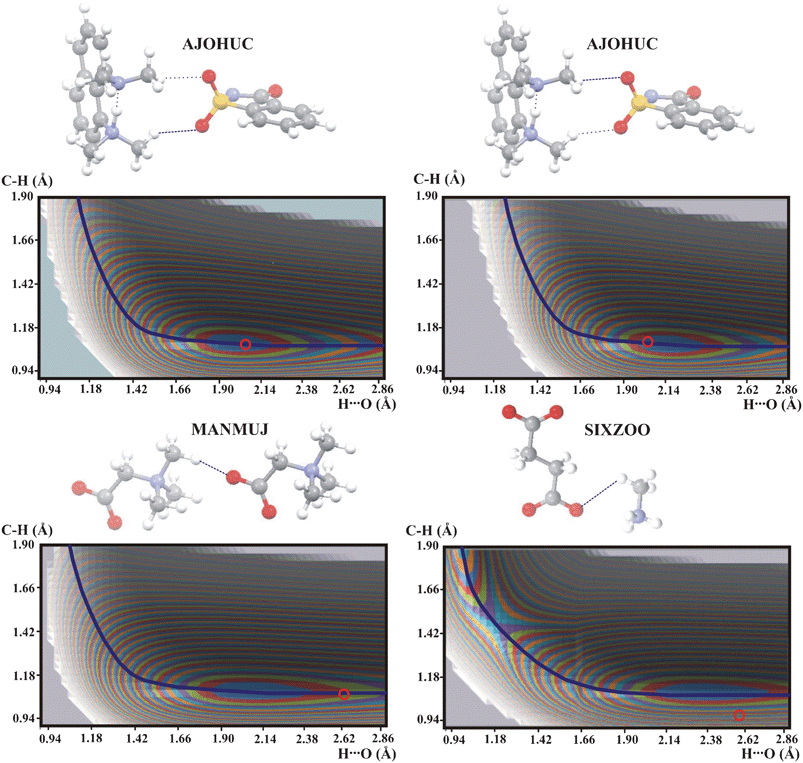Fig. 5 Potential energy surfaces for intermolecular C–H⋯O hydrogen bonds with the methyl group as proton donor. Contour levels as in Fig. 1. Color legend for the atoms as in Fig. 2.

The potential energy surfaces in Fig. 5 are different from each other. MANMUJ is typical for the strongest C–H⋯O hydrogen bonds. Potential energy surface of SIXZOO with the second energy minimum represents a chemical reaction but not proton transfer (cf.Fig. 4). Both hydrogen bonds in AJOHUC are different from the strong C–H⋯O hydrogen bonds shown in Fig. 1 or very weak interactions in Fig. 2. It is characteristic that the geometric parameters of both hydrogen bonds in AJOHUC are not very different but such a small difference is still sufficient to give QMRC curves which are very different. A study of the potential energy surface is clearly not sufficient to answer the question about the character of the interaction in AJOHUC and other investigations must be employed.

As mentioned earlier, the BORC curve coincides with the QMRC curve for the intermolecular OHO, OHN and NHN hydrogen bonds. An interesting question is now whether this is true also for the stronger intermolecular C–H⋯O hydrogen bonds, for which there is one common QMRC curve. The first step of looking for the BORC curve for the C–H⋯O hydrogen bond is elimination of interactions with the C–H group which do not correspond to hydrogen bonds. For SIXZOO, AJOHUC, AGLYSL01, CYACHZ01 and TGLYSU11 the QMRC curve does not correspond to a proton transfer process but a chemical reaction. For FOMHAZ16, KHDFRM12, TARTAC01 and ACSALA12 the QMRC curve represents a weak interaction which is typical for a very weak hydrogen bond. The curve which may be considered as the BORC curve typical for a C–H⋯O hydrogen bond is the QMRC curve for the C≡C–H⋯O hydrogen bonds. In the next step of estimation of the C–H⋯O BORC curve the parameters defining the BORC curve have been chosen to fit QMRC for the C≡C–H⋯O hydrogen bonds. An a_O parameter equal to 0.351 was used for the BORC curve for the OHO hydrogen bond. The free C–H bond length is 1.0870 Å.⁴² The length of the shortest C⋯O is not known. To estimate the shortest CHC hydrogen bond distance the non-bonded contact radius for carbon of 1.77 Å⁴³ can be used. To fit the QMRC curve for the C≡C–H⋯O hydrogen bonds the parameter a_C in the Pauling relation has to be set equal to 0.4. This value implies the shortest C⋯C contact of 2.87 Å, which is not in agreement with the non-bonded carbon contact radius suggested in ref. 43 to be equal to 1.77 Å. It is possible that the shortest CHC distance is not connected with the non-bonded carbon contact radius.⁴³ An open question is evidently whether the BORC curve actually coincides with the QMRC curve for the stronger intermolecular C–H⋯O hydrogen bonds. If not, this implies that the valency of the proton is not kept equal to one as the proton moves along the hydrogen bond.

Analysis of the QMRC curves for the proton motion in C–H⋯O hydrogen bonds shows how difficult is the determination of the BORC curve for this kind of hydrogen bond. Among the C–H⋯O hydrogen bonds there are interactions comparable with strong hydrogen bonds as well as with weak electrostatic interactions. In this situation estimation of the BORC curve common for all C–H⋯O hydrogen bonds is not possible. These results agree with other literature data on the untypical behaviour of C–H⋯O hydrogen bonds. This weak hydrogen bond is a balance between the attractive and repulsive interactions⁴⁴ and, depending on the dominating energy component, C–H⋯O can be red or blue shifted in the IR spectrum. Shift of the C–H stretching band as well as the elongation or contraction of the C–H bond can be correlated with the strength of the C–H⋯O hydrogen bond, so the spectroscopic properties can be used as a measure of the C–H⋯O hydrogen bond strength.⁴⁵ Theoretical methods used to investigate a very weak interaction such as the C–H⋯O hydrogen bond must be applied with caution, especially in the case of a nonlinear hydrogen bond.⁴⁶ Use of the MP2 method must be accompanied with a large basis set. A limited basis set with the MP2 method underestimates the potential energy surface if the hydrogen bond is not linear. The BLYP and B3LYP methods give a contrary behavior.

Summary

The QMRC curves of all the investigated compounds are compared in Fig. 6.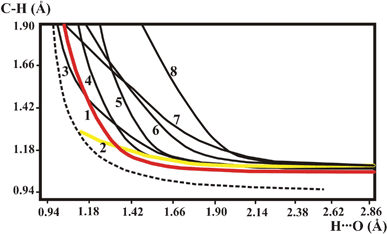

Fig. 6 QMRC curves of the investigated compounds: (1) BETXAZ01, BEXMIA, TOYJEW, WEQMAG, MANMUJ, HISTPA12, METHYM01, QQQAUG02; (2) FOMHAZ16, KHDFRM12, TARTAC01, ACSALA12; (3) SIXZOO, (4,5) AJOHUC; (6) AGLYSL01; (7) CYACHZ01; (8) TGLYSU11. Broken line is the BORC curve for the OHO hydrogen bond.

The different hydrogen bonds listed in Table 1 are represented by different QMRC curves. In the strongest C–H⋯O hydrogen bonds the QMRC curve has a similar shape as the QMRC for the OHO hydrogen bond and the present results allow a prediction which C–H⋯O can be relatively strong. The first condition is a high acidity of the proton, as it is for the C≡C–H group or aromatic ring proton. The second condition is linearity of the hydrogen bridge. If the CHO angle is 121° as for ACSALA, the hydrogen bond has features of a weak interaction represented by QMRC curve 2 in Fig. 6, without any possibility of proton transfer. The weak interaction is typical for an aliphatic CH proton donor for which a low CHO angle is also typical. A proton with low acidity can also form a typical C–H⋯O hydrogen bond if the CHO bond is sufficiently straight. The character of the hydrogen bond is different from strong and very weak C–H⋯O bonds for intermediate values of the CHO angle. The QMRC curves for AJOHUC are different from the BORC curve 1 in Fig. 6 but it is difficult to estimate the reason for their difference from BORC. The CHO angle about 145° should be sufficient to form a strong C–H⋯O bond, but simultaneously the C⋯O and H⋯O distances are too long to form a strong bond.

The potential energy surfaces and QMRC curves for present complexes with different hydrogen bond strengths illustrate the variability of this interaction. The proton motion in typical and very weak C–H⋯O hydrogen bonds is described by different QMRC curves. At the same time the geometry of the hydrogen bridge has even more important influence on the character of the interactions than the proton acidity.

Acknowledgements

This work has been supported by a grant from the Trygger Foundation for Scientific Research. We thank the Wroclaw Centre for Networking and Supercomputing for generous computer time.

References

1. (a) G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer, Berlin, 1991; (b) G. A. Jeffrey, An Introduction to Hydrogen Bonding; Oxford University Press: New York, 1997; (c) G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology; Oxford University Press Inc.: New York, 1999; (d) S. J Grabowski, Hydrogen Bonding—New Insights; In Series Challenges and Advances in Computational Chemistry and Physics, Ed. J. Leszczynski, Springer: New York, 2006; (e) J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304; (f) J.-M. Lehn, Supramolecular Chemistry, Verlag-Chemie: Weinheim, 1995; (g) L. F. Zacios, O. Gálvez and P. C. Gòmez, J. Chem. Phys., 2005, 122, 214307; (h) P. A. Frey, S. A. Whitt and J. B. Tobin, Science, 1994, 264, 1927; (i) P. A. Frey, J. Phys. Org. Chem., 2004, 17, 511; (j) W. W. Cleland and M. M. Kreevoy, Science, 1994, 264, 1887; (k) C. N. Fuhrmann, M. D. Daugherty and D. A. Agard, J. Am. Chem. Soc., 2006, 128, 9086; (l) Ł. Jaroszewski, B. Lessyng, J. J. Tanner and J. A. McCammon, Chem. Phys. Lett., 1990, 175, 282; (m) G. S. Li, B. Maigret, D. Rinaldi and M. F. Ruiz-Lopez, J. Comput. Chem., 1998, 19, 1675.
2. (a) G. Zundel, Hydrogen bonds with large proton polarizability and proton transfer processes in electrochemistry and biology, In Advances in Chemical Physics, 2000, 111, 1; (b) I. Prigogine, S. A. Rice, J. Wiley, New York , 2000, Vol. 111; (c) J. T. Hynes, J. P. Klinman, H.-H. Limbach and R. L. Schowen, Hydrogen-Transfer Reactions, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007.
3. (a) J. A. Gerlt, M. M. Kreevoy, W. W. Cleland and P. A. Frey, Chem. Biol., 1997, 4, 259; (b) C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511.
4. (a) L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 775; (b) G. R. Desiraju, Crystal Engineering. The Design of Organic Solids, Elsevier, Amsterdam, 1989; (c) J. Bernstein, M. C. Etter and L. Leiserowitz, The Role of Hydrogen Bonding in Molecular Assemblies, in Structure Correlation, Ed. H.-B. Bürgi and J. D. Dunitz, VCH, Weinheim, 1994; (d) M. C. Etter, Acc. Chem. Res., 1990, 23, 120; (e) M. C. Etter and G. M. Frankenbach, Materials, 1989, 1, 10; (f) F. Garcia-Tolledo, S. J. Geib, S. Goswani and A. D. Hamilton, J. Am. Chem. Soc., 1991, 113, 9265.
5. I. Majerz, Mol. Phys., 2007, 105, 2305.
6. (a) J. A. Cowan, J. A. K. Howard, G. J. McIntre, S. M.-F. Lo and J. D. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 724; (b) J. A. Cowan, J. A. K. Howard, G. J. McIntre, S. M.-F. Lo and J. D. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 794; (c) C. C. Wilson, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 435; (d) C. C. Wilson, K. Shankland and N. Z. Shankland, Z. Kristallogr., 2001, 216, 303; (e) E. C. Kostanek and W. R. Busing, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 2454; (f) B. L. Rodrigues, R. Tellgreen and N. G. Fernandes, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 353; (g) I. Olovsson, H. Ptasiewicz-Bąk, T. Gustafsson and I. Majerz, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 311; (h) T. Steiner, I. Majerz and C. C. Wilson, Angew. Chem., Int. Ed., 2001, 40, 2651.
7. (a) M. G. Barrow, J. Am. Chem. Soc., 1956, 78, 5802; (b) S. L. Johnson and K. A. Rumon, J. Phys. Chem., 1965, 69, 74; (c) H. Ratajczak and L. Sobczyk, J. Chem. Phys., 1969, 50, 556; (d) G. Debecker and P. Huyskens, J. Chim. Phys., 1971, 68, 287; (e) R. Nouven and P. Huyskens, J. Mol. Struct., 1973, 16, 459; (f) Z. Malarski, M. Rospenk, L. Sobczyk and E. Grech, J. Phys. Chem., 1985, 86, 401; (g) E. Grech, J. Kalenik and L. Sobczyk, J. Chem. Soc. Faraday Trans., 1979, 275, 1587; (h) J. Kalenik, I. Majerz, Z. Malarski and L. Sobczyk, Chem. Phys. Lett., 1990, 165, 15; (i) I. Majerz and L. Sobczyk, J. Chim. Phys., 1993, 90, 1657; (j) I. Majerz, Z. Malarski and L. Sobczyk, Chem. Phys. Lett., 1997, 274, 361; (k) Th. Zeegers-Huyskens, P. Huyskens, H. Ratajczak and W. J. Orville-Thomas, Molecular Interactions, vol. 2, J. Wiley & Sons, New York, 1980, p. 1; (l) B. Nogaj, J. Phys. Chem., 1987, 91, 5863; (m) B. Nogaj, E. Dulewicz, B. Brycki, A. Hrynio, P. Barczyński, Z. Dega-Szafran, M. Szafran, A. Kozioł and A. R. Katritzky, J. Phys. Chem., 1990, 94, 1279; (n) H. Ratajczak and L. Sobczyk, J. Chem. Phys., 1969, 50, 556; (o) R. Nouven and P. Huyskens, J. Mol. Struct., 1973, 16, 459; (p) P. Huyskens, W. Cleuren, M. Franz and M. A. Vuylstacke, J. Phys. Chem., 1980, 84, 2748; (q) Th. Zeegers-Huyskens, J. Mol. Liq., 1986, 32, 191; (r) Th. Zeegers-Huyskens, J. Mol. Struct., 1986, 135, 93; (s) J. Jadżyn and J. Małecki, Acta Phys. Polon., 1972, 41, 599; (t) G. M. Gale, G. Gallot, F. Hache, N. Lascoux, S. Bratos and J.-Cl. Leicknam, Phys. Rev. Lett., 1999, 82, 1068; (u) S. Bratos, J.-Cl. Leicknam, S. Pommeret and G. Gallot, J. Mol. Struct., 2004, 708, 197; (v) J. P. Hawranek and L. Sobczyk, Acta Phys. Pol. A, 1971, 39, 639; (w) R. Nouwen and P. Huyskens, J. Mol. Struct., 1973, 16, 459; (x) P. Huyskens, W. Cleuren, H. M. Van Brabant-Gevaerts and M. A. Vuylsteke, J. Phys. Chem., 1980, 84, 2740; (y) R. Wolny, A. Koll and L. Sobczyk, Bull. Soc. Chim. Belg., 1984, 93, 99; (z) P. Huyskens, W. Cleuren, M. Franz and M. A. Vuylsteke, J. Phys. Chem., 1980, 84, 2748; (a a) P. Huyskens, J. Mol. Struct., 1986, 135, 67; (a b) B. Nogaj, J. Phys. Chem., 1987, 91, 5863; (a c) E. Grech, J. Kalenik and L. Sobczyk, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 1587; (a d) E. Grech, J. Kalenik and L. Sobczyk, J. Chem. Soc. Faraday Trans., 1985, 81, 312; (a e) B. Nogaj, B. Brycki, Z. Dega-Szafran, M. Szafran and M. Mackowiak, J. Chem. Soc. Faraday Trans., 1987, 83, 2591; (a f) S. N. Smirnov, N. S. Golubev, G. S. Denisov, H. Benedict, P. Schah-Mohammedi and H.-H. Limbach, J. Am. Chem. Soc., 1996, 118, 4094; (a g) Z. Dega-Szafran, M. Szafran, L. Stefaniak, C. Brevard and M. Bourdonneau, Magn. Reson. Chem., 1986, 24, 424; (a h) B. Brycki, B. Brzezinski, G. Zundel and T. Keil, Magn. Reson. Chem., 1992, 30, 507; (a i) B. Brycki and M. Szafran, J. Chem. Soc. Perkin Trans. 2, 1982, 1833; (a j) B. Brycki and M. Szafran, J. Chem. Soc., Perkin Trans. 2, 1984, 223; (a k) M. Ilczyszyn, H. Ratajczak and K. Skowronek, Magn. Reson. Chem., 1988, 26, 445; (a l) J. Kalenik, I. Majerz, L. Sobczyk, E. Grech and M. M. M. Habeeb, Collect. Czech. Chem. Commun., 1990, 55, 80; (a m) S. E. Odinokov, A. A. Mashkovsky, V. P. Glazunov, A. V. Iogansen and B. V. Rassadin, Spectrochim. Acta, Part A, 1976, 32, 1355; (a n) J. Barczyński, Z. Dega-Szafran and M. Szafran, J. Chem. Soc., Perkin Trans. 2, 1985, 765; (a o) Z. Dega-Szafran and A. Hrynio, Spectrochim. Acta, Part A, 1987, 43, 1553; (a p) Th. Keil, B. Brzezinski and G. Zundel, J. Phys. Chem., 1992, 96, 4421; (a q) B. Nogaj, E. Dulewicz, B. Brycki, A. Hrynio, P. Barczyński, Z. Dega-Szafran, M. Szafran, P. Kozioł and A. R. Katritzky, J. Phys. Chem., 1990, 94, 1279; (a r) R. Langner and G. Zundel, J. Phys. Chem. A, 1998, 102, 6635; (a s) R. Langner and G. Zundel, J. Chem. Soc., Faraday Trans., 1998, 94, 1805; (a t) G. Albrecht and G. Zundel, J. Chem. Soc. Faraday Trans., 1984, 80, 553; (a u) J. P. Hawranek and A. S. Muszynski, J. Mol. Struct., 2000, 552, 205.
8. (a) T. Steiner, J. van der Maas and B. Lutz, J. Chem. Soc., Perkin Trans. 2, 1997, 1287; (b) M. G. Davidson, A. E. Goeta, J. A. K. Howard, S. Lamb and S. A. Mason, New J. Chem., 2000, 24, 477.
9. (a) W. Saenger, Angew. Chem., Int. Ed. Engl., 1973, 12, 591; (b) R. Taylor and O. Kennard, J. Am. Chem. Soc., 1982, 104, 5063.
10. R. Biswas and M. Sundaralingam, J. Mol. Biol., 1997, 270, 511.
11. T. Steiner and W. Saenger, J. Am. Chem. Soc., 1992, 114, 10146.
12. (a) G. A. Leonard, K. McAuley-Hecht, T. Brown and W. N. Hunter, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1995, 51, 136; (b) M. Brandl, K. Lindauer, M. Meyer and J. Sühnel, Theor. Chem. Acc., 1999, 101, 103.
13. M. C. Wahl, S. T. Rao and M. Sundaralingam, Nat. Struct. Biol., 1996, 3, 24.
14. I. Berger, M. Egli and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 12116.
15. (a) Y. Mandel-Gutfreund, H. Margalit, R. L. Jernigan and V. B. Zhurkin, J. Mol. Biol., 1998, 277, 1129; (b) N. S. Gray, L. Wodicka, A. W. H. Thunnissen, T. C. Norman, S. Kwon, F. H. Espinoza, D. O. Morgan, G. Barnes, S. LeClerc, L. Meijer, S.-H. Kim, D. J. Lockhart and P. G. Schultz, Science, 1998, 281, 533.
16. (a) J. P. Glusker, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1995, 51, 418; (b) C. Pascard, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1995, 51, 407; (c) P. M. Takahara, C. A. Frederick and S. J. Lippard, J. Am. Chem. Soc., 1996, 118, 12309.
17. (a) Z. Berkovitch-Yellin and L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 159; (b) K. T. Thomas, G. M. Smith, T. B. Thomas and R. J. Feldmann, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 4843; (c) P. Chakrabarti and S. Chakrabarti, J. Mol. Biol., 1998, 284, 867; (d) Z. S. Derewenda, U. Derewenda and P. M. Kobos, J. Mol. Biol., 1994, 241, 83; (e) E. L. Ash, J. L. Sudmeier, R. M. Day, M. Vincent, E. V. Torchilin, K. C. Haddad, E. M. Bradshaw, D. G. Sanford and W. W. Bachovchin, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 10371; (f) T. Steiner and W. Saenger, J. Am. Chem. Soc., 1993, 115, 4540.
18. (a) G. R. Desiraju, Chem. Commun., 2005, 2995; (b) V. S. Senthil Kumar, F. Christopher Pigge and Nigam P. Rath, New J. Chem., 2004, 28, 1192; (c) P. K. Thallapally, A. K. Katz, H. L. Carrell and G. R. Desiraju, CrystEngComm, 2003, 5, 87; (d) Ch. Dai, Z. Yuan, J. C. Collings, T. M. Fasina, R. L. Thomas, K. P. Roscoe, L. M. Stimson, D. S. Yufit, A. S. Batsanov, J. A. K. Howard and T. B. Marder, CrystEngComm, 2004, 6, 184.
19. L. Pauling, J. Am. Chem. Soc., 1947, 69, 542.
20. (a) S. J. Grabowski, J. Mol. Struct., 2000, 552, 153; (b) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48; (c) F. Mohri, J. Mol. Struct., 2005, 756, 25; (d) J. Olah, F. Blockhuis, T. Veszpremi and C. Van Alsenoy, Eur. J. Inorg. Chem., 2006, 69.
21. (a) I. Olovsson, Z. Phys. Chem., 2006, 220, 797; (b) J. D. Dunitz, X-Ray Analysis and the Structure of Organic Molecules; Cornell University Press: Ithaca, 1979; (c) H.-B. Bürgi, Angew. Chem., Int. Ed. Engl., 1975, 14, 460.
22. (a) I. Majerz and I. Olovsson, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 650; (b) I. Majerz and I. Olovsson, Phys. Chem. Chem. Phys., 2009, 11, 1297; (c) I. Majerz and I. Olovsson, Phys. Chem. Chem. Phys., 2010, 12, 5462; (d) I. Majerz and I. Olovsson, J. Mol. Struct., 2010, 968, 48.
23. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
24. Gaussian Inc. (2004), Gaussian03, Revision C.02, Gaussian, Inc., Wallingford, CT.
25. F. H. Allen, J. A. K. Howard, V. J. Hoy, G. R. Desiraju, D. S. Reddy and C. C. Wilson, J. Am. Chem. Soc., 1996, 118, 4081.
26. S. Kumar, K. Subramanian, R. Srinivasan, K. Rajagopalan, A. M. M. Schreurs, J. Kroon, G. Koellner and T. Steiner, J. Mol. Struct., 1998, 6, 51.
27. T. Steiner, M. Tamm, A. Grzegorzewski, N. Schulte, N. Veldman, A. M. M. Schreurs, J. A. Kanters, J. Kroon, J. van der Maas and B. Lutz, J. Chem. Soc., Perkin Trans. 2, 1996, 2441.
28. K. Subramanian, S. Lakshmi, K. Rajagopalan and T. Steiner, J. Chem. Crystallogr., 1999, 29, 735.
29. A. Harrison, R. Ibberson, G. Robb, G. Whittaker, C. Wilson and D. Youngson, Faraday Discuss., 2003, 122, 363.
30. I. Mata, E. Espinosa, E. Molins, S. Veintemillas, W. Maniukiewicz, C. Lecomte, A. Cousson and W. Paulus, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 365.
31. P. P. Sun, F. F. Jian and X. Wang, J. Chem. Crystallogr., 2010, 40, 4.
32. C. K. Leech, F. P. A. Fabbiani, K. Shankland, W. I. F. David and R. M. Ibberson, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 101.
33. G. A. Jeffrey, J. R. Ruble, R. K. McMullan, D. J. DeFrees and J. A. Pople, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1508.
34. K. Hermansson, R. Tellgren and M. S. Lehmann, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1507.
35. Y. Okaya, N. R. Stemple and M. I. Kay, Acta Crystallogr., 1966, 21, 237.
36. S. Vilminot, E. Philippot and M. Lehmann, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1817.
37. R. G. Nanni, J. R. Ruble, G. A. Jeffrey and R. K. McMullan, J. Mol. Struct., 1986, 147, 369.
38. M. I. Kay and R. Kleinberg, Ferroelectrics, 1973, 5, 45.
39. P. R. Mallinson, G. T. Smith, C. C. Wilson, E. Grech and K. Wozniak, J. Am. Chem. Soc., 2003, 125, 4259.
40. J. Overgaard, B. Schiøtt, F. K. Larsen, A. J. Schultz, J. C. MacDonald and B. B. Iversen, Angew. Chem., Int. Ed., 1999, 38, 1239.
41. N. Kalsbeek and S. Larsen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 1005.
42. G. Herzberg, Infrared and Raman Spectra of Polyatomic Molecules, New York, Van Nostrand, 1945.
43. R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384.
44. M. Hippler, J. Chem. Phys., 2005, 123, 204311 and references therein.
45. S. Scheiner, Int. J. Quantum Chem., 2010, 110, 2775.
46. J.-Z. Ramírez, R. Vargas and J. Garza, J. Mex. Chem. Soc., 2008, 52, 31.

---