Freezing and glass transition phenomena for 1,2-dichloroethane under high pressure as revealed by fluorescence spectroscopy

Abstract

The viscosity of 1,2-dichloroethane increases steadily with increasing pressure, as does the density, refractive index and polarizability of this solvent. The pressure dependence for each of these properties can be monitored by a combination of absorption and fluorescence spectroscopy carried out in the presence of a fluorescent molecular rotor that responds to changes in the local environment. At 20 °C, dichloroethane freezes under an applied pressure of ca. 370 MPa, causing sudden extinction of the fluorescence of the molecular rotor due to the opaque nature of the frozen solvent. However, this same emission is enhanced dramatically if a small amount of inert polymer is present in the solution. The behaviour is interpreted in terms of the polymeric solute promoting establishment of a glassy matrix with reasonably good optical transparency for emission spectroscopy.

---

Introduction

Most organic solvents are subjected to a marked increase in density under applied pressure, according to the degree of compressibility of the solvent.¹ Indirectly, this causes an increase in the polarizability of the solvent.² There is also an accompanying augmentation of the bulk viscosity³ as the pressure increases but this particular effect is usually nonlinear⁴ and rather difficult to express in a theoretical form,⁵ at least over a wide pressure variation. As a consequence of these pressure-induced phenomena, a dissolved dye molecule present at low concentration in a fluid solvent might be expected to undergo increased absorbance as the pressure rises, whilst both absorption and fluorescence peak maxima should evolve as the solvent polarizability is perturbed. Furthermore, if the dye functions as a molecular rotor,⁶ its fluorescence yield will increase progressively as the solvent viscosity is raised while also responding to any massive changes in solvent properties such as a pressure-induced phase change. Despite the significance of these multiple effects, there have been relatively few quantitative studies of how applied pressure perturbs the properties of dye solutions.⁷ We now report on an investigation aimed at establishing a better understanding of dye–solvent interactions for a fluorescent rotor dissolved in 1,2-dichloroethane (DCE) at 20 °C. Our main objective is to examine how pressure-induced perturbations of the DCE properties affect the optical properties of the dye. The research is extended to allow for the effects of a third component, namely an inert polymer, to the system.

There have been several earlier studies of pressure effects on the trans–gauche equilibrium for DCE in the neat liquid⁸ and in alkane solvents.⁹ Thus, using vibrational spectroscopy, it has been established⁹ that DCE undergoes a significant decrease in molar volume as the pressure is raised. This has been interpreted in terms of internal rotation from the trans form to the gauche conformer and accompanying overlap of the chlorine atoms as their mutual separation distance decreases. This equilibrium process is affected^8,9 by changes in solvent polarity, with the gauche form being somewhat stabilized by polar solvents. Since the gauche conformer is expected to exhibit a more significant dipole moment than the corresponding trans isomer, increased pressure should lead to a modest increase in the dielectric constant. The combined changes in refractive index and dielectric constant will influence the photophysical properties of any dissolved dye molecule.^10,11 It has also been shown^8,9 that the freezing point of DCE is elevated at higher pressures, at least in 2-methylpentane, causing precipitation at ambient temperature for applied pressures of around 1 GPa. This is an unusually large elevation of the freezing point, augmented by the strong decrease in molar volume, that pushes the freezing point from −35 °C at atmospheric pressure to >30 °C at 5 GPa. Most of these prior studies were aimed at evaluating the equilibrium step, rather than establishing bulk properties of DCE, and were carried out in the absence of a chemical probe.

Results and discussion

Properties of the bulk solvent

The molecular formula for the chemical sensor used in this study, ROBOD, is shown in Fig. 1. The chromophore is a boron dipyrromethene dye,¹² which absorbs strongly in the visible region, that is photostable and essentially non-polar. The latter feature means that the dye is relatively insensitive to changes in local polarity.¹³ It will be noted that ROBOD is a symmetrical intramolecular dimer but the two head-groups function independently and there is no indication for their self-association in fluid solution,¹⁴ even at low temperature or high pressure. The energy-minimized molecular conformation is shown as part of the ESI.†

Fig. 1 Molecular formula of the fluorescent rotor used in this work.

In the first instance, dilute solutions of ROBOD in DCE (typically in the order of 2–10 μM) were subjected to increasingly higher pressures and monitored by absorption spectroscopy at 20 °C. At moderate pressures (0 < P < 350 MPa), there is a progressive decrease in the baseline level, a small (i.e., 4 nm) red shift for the absorption maximum of the dye, and a significant (i.e., 25%) increase in absorbance at the peak maxima (Fig. 2). The change in the transmission level is due to a pressure-induced increase in the solvent refractive index (n) while the variation in the properties of the dye are due to the anticipated changes in polarisability (σ) and density (ρ) of DCE that accompany raising the pressure. Indeed, ρ and σ are related by way of the Lorentz–Lorenz expression.¹⁵ The original spectral profile is recovered on release of the applied pressure. The increased absorbance, this being due entirely to compression of the solvent, followed the same pattern for both the first-and second-allowed transitions found at 497 and 415 nm, respectively. These various effects are nonlinear with respect to applied pressure and tend towards saturation at high pressure (Fig. 3). Similar behaviour has been reported for certain other solvents¹⁶ and also for DCE,¹⁷ although data for this particular solvent are highly limited.

Fig. 2 Effect of applied pressure (0 < P < 370 MPa) on the absorption spectral profile recorded for ROBOD in DCE at 20 °C. The upper panel shows the absorbance at 500 nm over the full pressure range.

Fig. 3 Effect of applied pressure on some relevant properties of the system at 20 °C: (a) density of DCE, (b) wavenumber of the absorption peak recorded for ROBOD and (c) refractive index of DCE. In each case, the solid line drawn through the data points corresponds to a fit to the appropriate equation as discussed in the text.

The pressure-induced change in absorbance, analysed globally across the spectral window, can be used to compute the corresponding variation in ρ (Fig. 3). Thus, it was demonstrated that ROBOD follows the Beer–Lambert law in DCE at 20 °C, at least over the concentration range of interest, such that the increased absorbance can be assigned to the compressibility, k, of the solvent. This latter term is related to the molar volume, V_M, of DCE according to the Tait expression¹⁸ (eqn (1)). Here, the coefficients B and C are independent of pressure, P. Indeed, B is sensitive to the nature of the solvent and temperature while C is independent of temperature and remains closely comparable across series of similar solvents.¹⁹ Fitting the absorbance data to eqn (1) indicates that DCE undergoes a total decrease in V_M of ca. 14 cm³; at atmospheric pressure V_M⁰ = 73.3 cm³. Some of this reduced volume can be attributed^8a to the switch from trans to gauche conformers since quantum chemical calculations give an accompanying change in molar volume of 5 cm³. The main factor responsible for the fall in V_M, however, is closer packing of neighbouring DCE molecules in the fluid. Non-linear, least-squares analysis leads to estimates for B and C of 42.23 and 0.21, respectively (see ESI†). These values appear to be in line with estimates made for related solvents,²⁰ and allow calculation of the density at any applied pressure over the relevant range.

The molar density, ρ_M, can be related to the refractive index, n, according to the Lorentz–Lorenz expression¹⁵ (eqn (2)), where A is the molar refractivity. This latter term, in turn, is related to the molecular polarisability, α. On the basis that α is independent of pressure, the changes in absorbance can be used to calculate the pressure-induced effect on n. From this analysis, we find that n increases from 1.4421 at atmospheric pressure to a value of 1.5212 at an applied pressure of 330 MPa (see ESI†). Changes in refractive index also cause the red shift found for the absorption maximum of ROBOD (Fig. 3). Here, the shift given in terms of wavenumber, Δν, can be related to refractive index by way of the so-called Bayliss expression²¹ (eqn (3)), where R (= 7 ± 2 Å) is the radius of the cavity housing the chromophore, ν_ABS (= 20 120 cm⁻¹) is the absorption maximum in cm⁻¹, and μ_TD (= 5.8 D) is the transition dipole moment calculated²² from the absorption spectrum recorded for ROBOD in DCE at atmospheric pressure.

Curve-fitting analyses carried out for ROBOD in DCE indicate that the absorption spectral profile does not change with increasing pressure, other than the red shift. In particular, pressure has no effect on either the half-width (FWHM = 640 cm⁻¹) of the underlying vibronic bands or the Huang–Rhys²³ (S = 0.31) factor. This insensitivity towards pressure can be used to argue that the cavity holding the dye molecule does not change significantly during the pressure cycle. As such, the absorption spectral changes are likely to reflect the pressure effect on the refractive index. As above, n increases progressively but nonlinearly with pressure (see ESI†) and shows a net enhancement of ca. 10% over the available pressure range. Using this information together with eqn (2) it becomes possible to estimate a value of 0.127 for the molecular refractivity. An independent estimate of the pressure dependence for n was made using a Michelson-type interferometer with 632.8 nm illumination after calibration with pure toluene.²⁴ The two sets of data agree reasonably well and are compiled in the ESI.† We emphasize the pressure effect on n because this term is extremely important in many optical processes, including fluorescence and Förster-type electronic energy transfer.²⁵

The molecular rotor used for this study is a member of the unhindered boron dipyrromethene class of dyes¹⁴ and fluoresces strongly in viscous media. The emission quantum yield (Φ_F = 0.052) and excited-singlet state lifetime (τ_S = 0.39 ns) are set by the ease of rotation of the meso-phenylene ring, which itself is determined by frictional forces with the surrounding media. It has been shown¹⁴ that the rate constant (k_NR = (1 − Φ_F)/τ_S) for nonradiative decay of the first-excited singlet state of ROBOD follows eqn (4) where η is the bulk viscosity of DCE, χ is a limiting pressure (in the region of ca. 2 GPa) and E_A (being typically in the region of 2.5 kJ mol⁻¹) is the activation energy for internal rotation of the phenylene ring in that solvent. The dimensionless coefficient δ allows for the fact that ROBOD resides in a cavity within the solvent structure such that the full effect of viscosity is not observed. Over a wide range of solvents, linear log–log plots of k_NRvs. η have been observed¹⁴ with δ = 0.44. On this basis, ROBOD can be used to monitor changes in viscosity at applied pressures, provided there are no specific solvation effects.

Increasing pressure causes a small (i.e., 5 nm) red shift for the emission maximum and a steady increase in the emission quantum yield (Fig. 4). The red shift is comparable to that observed by absorption spectroscopy, and is a consequence of the change in polarisability of DCE under high pressure. The increase in emission yield, which amounts to a factor of ca. two-fold, can be assigned¹⁴ to a fall in k_NR and, after correction for changes in refractive index and absorbance, it can be concluded that the viscosity of DCE increases only slightly with increasing pressure over the range 0 < P < 370 MPa, despite the significant increase in density found over the same range (see ESI†). The magnitude of this pressure-induced increase in viscosity can be expressed in terms of a modified Tait equation²⁶ with B = 4320 and C = 0.63 (see ESI†). These derived parameters permit estimation of the viscosity of DCE at any reasonable pressure, although analysis is restricted to 20 °C.

Fig. 4 Effect of applied pressure on the fluorescence spectral profile recorded for ROBOD in DCE at 20 °C. The upper panel shows the integrated emission yield as a function of applied pressure.

Freezing of the solvent at elevated pressure

At an applied pressure of ca. 370 MPa, the absorption spectral transmission level is subjected to a dramatic decrease (Fig. 2). Further increases in applied pressure have no obvious effect, but on occasion the glass cell breaks. This effect occurs over a very narrow pressure range, the onset being 370 ± 5 MPa. Releasing the pressure restores the system to its original state within a few minutes. Separate experiments showed that identical baseline shifts were observed in the absence of ROBOD, thereby confirming that the effect is due to a pressure-induced phase transformation for DCE. Other solvents, such as the linear alcohols, show similar pressure-induced changes in both n and ρ but do not exhibit the phase change. The simplest explanation for this behaviour is that the solvent freezes at this pressure as a means by which to further reduce the molar volume.¹⁰ Indeed, V_M⁰ for frozen DCE at atmospheric pressure was measured to be ca. 11 cm³ less than that of the liquid at atmospheric pressure. The pressure effect on the isothermal freezing point⁸ of DCE is unusually large and is driven by the considerable decrease in molar volume available to this solvent.

At an applied pressure of 370 MPa, fluorescence from ROBOD suddenly decreases in intensity and falls to a value well below that recorded at atmospheric pressure (Fig. 4). Further increases in pressure have no effect on the fluorescence intensity but release of the pressure quickly restores the system to its original state. The pressure cycle can be repeated numerous times without change. Clearly, the switching of the fluorescence yield is associated with freezing of the solvent. Again, the effect occurs over a narrow pressure range.

Addition of an inert polymer

Adding a small quantity of poly(methylmethacrylate), PMMA (MW = 120 000 g mol⁻¹), to the DCE solution has no obvious effect on the absorption spectral profile of ROBOD; the polymer dissolves readily in DCE. There is, however, a change in density at atmospheric pressure that causes a small alteration of the absorbance due to ROBOD, which is in line with the law of additive volumes.²⁷ The pressure-induced changes in both n and ρ occur as noted above and the solvent freezes at high pressure. The equilibrium freezing pressure, P_F, defined as the pressure at which DCE freezes at 20 °C, increases very slightly with increasing concentration of PMMA. Indeed, P_F rises from 370 MPa in the absence of PMMA to ca. 380 MPa at high concentration (25% w/w) of dissolved polymer. The difference in P_F, ΔP_F, evolves in a non-linear manner with respect to PMMA concentration and can be traced to a combination of the colligative effect and the relative difference²⁸ in heat capacities for DCE and PMMA. Monitoring the solution by way of fluorescence spectroscopy shows that the presence of PMMA has no effect on the emission profile but leads to a modest increase in fluorescence yield at atmospheric pressure. This is because the polymer raises the viscosity of the solution.²⁹ This enhancement in the fluorescence yield is reasonably linear with respect to the concentration of PMMA. This finding indicates that the conformation of the polymer, expressed in terms of the hydrodynamic volume, is insensitive to concentration over the range of interest, at atmospheric pressure.

In the low pressure regime, at any given concentration of PMMA, there is an almost linear relationship between k_NR and the applied pressure (Fig. 5). The effective gradients of such plots, however, exhibit a clear dependence on the concentration of PMMA. This is an important finding, not least because it raises doubts about using fluorescent rotors to monitor the concentration of dissolved polymers. The implication here is that applied pressure alters the average conformation of PMMA dissolved in DCE. This is not the case, however, because the compressibility of the solution increases systematically with increasing concentration of PMMA. When the latter effect is taken into account, it is found that pressure has little effect on the intrinsic viscosity of the solution relative to that of DCE. In particular, there is no indication that the radius of gyration of the dissolved polymer is affected by pressure.

Fig. 5 Effect of applied pressure on the rate constant for nonradiative decay of the first-excited singlet state for ROBOD in DCE (○) and in the presence of 6% w/w PMMA (●).

In the presence of PMMA, there is a marked perturbation of the fluorescence yield at pressures where the solvent is expected to freeze. Thus, the presence of PMMA causes fluorescence from ROBOD to increase dramatically upon freezing (Fig. 6), in marked contrast to the virtual extinction of emission found in the absence of polymer. This effect on the fluorescence yield is fully reversible on releasing the pressure but causes no discernible shift of the peak maximum. The full impact of fluorescence enhancement is observed with quite low concentrations (i.e., 10% w/w) of PMMA (Fig. 7) and corresponds to an emission quantum yield of ca. 0.6. This is probably a lower limit because the optical transparency of the matrix is far from perfect but means that ROBOD must reside within a very high viscosity medium.¹⁴ The most likely explanation for this highly unusual effect is that the PMMA facilitates formation of glassy regions within the mixture that combine high viscosity with reasonable optical transparency. At all concentrations of PMMA, further increases in applied pressure cause a small but distinct loss of fluorescence (Fig. 3). We attribute this particular effect to restructuring of the glassy matrix with resultant degradation of the optical transparency. Although this effect loses fluorescence, the residual emission greatly exceeds that found in the absence of PMMA.

Fig. 6 Effect of increasing pressure on the fluorescence from ROBOD in DCE containing 12% w/w PMMA.

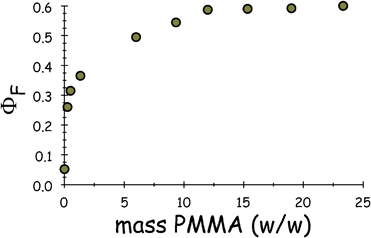Fig. 7 Effect of PMMA concentration on the fluorescence quantum yield for ROBOD in DCE as measured immediately after the sudden increase in fluorescence at the equilibrium freezing pressure.

Conclusions

A sensitive fluorescent rotor has been employed to measure how applied pressure affects certain properties inherent to DCE, most notably the molar density, refractive index and viscosity. Despite the involvement of a pressure-induced change in conformation¹⁴ and freezing^8,9,30 at ambient temperature, the rotor works well and allows facile collection of the experimental data. For this particular molecular rotor, the fluorescence yield and lifetime are insensitive to changes in solvent polarity and it is important to stress that pressure affects polarity as well as viscosity. There have been earlier reports of conformational relaxation in glassy media³¹ and under high pressure³² but the probe molecule utilised here is not susceptible to such effects and reports on the gross changes of the solvent. Introducing an inert polymer, namely PMMA, does not hinder data collection but allows properties of the solution to be determined. The experimental set-up provides quantitative output over a wide pressure range. Of particular interest are the following observations: (i) The pressure-induced enhancement of the viscosity is greatly amplified in the presence of dissolved polymer. (ii) There is a substantive decrease in V_M for DCE^8,9 under applied pressure but ambient temperature that causes a major perturbation of the freezing point; it might be noted that recent attention has been given to the crystal structure of DCE under isochoric conditions.³⁰ (iii) Under high pressure, the polymer provides a refuge for the rotor that protects it against the global effects of the solvent freezing. This is most evident by the enhanced fluorescence yield found at high pressure. This latter effect was completely unexpected and points towards the presence of unusual domains in the polymer solution at elevated pressure. It is possible that such regions could be exploited to provide new materials with interesting properties.

Experimental

Samples of the fluorescent rotor, ROBOD, were available from a previous study¹⁴ and were used after further purification by column chromatography and recrystallisation. 1,2-Dichloroethane was obtained from Aldrich Chemicals Ltd as Chromosolve HPLC grade and purified rigorously by washing with H₂SO₄, before drying and refluxing over P₄O₁₀. Poly(methylmethacrylate) (MW = 120 000 g mol⁻¹) was obtained from Aldrich Chemicals and used as received. No absorbing or fluorescing impurities could be detected. Absorption spectra were recorded with a Hitachi U3310 spectrophotometer while emission spectra were recorded with a Jobin-Yvon Fluorolog tau-3 spectrophotometer. The high-pressure rig was obtained from Stansted Fluids Ltd and operates via a series of interfaced pneumatic transducers. The sample chamber was connected to the spectrophotometers using optical light guides, each equipped with suitable filters. Fluorescence studies were made following excitation with a solid-state laser (λ = 406 nm) or using a 250 W xenon arc lamp fitted with a narrow bandpass filter. All spectroscopic experiments were repeated numerous times using fresh solutions.

Acknowledgements

We thank EPSRC (EP/E014062/1) and Newcastle University for financial support of this work. Drs J. P. Rostron and V. Autissier are acknowledged for help in setting up the high-pressure rig.

References

1. Y. Marcus and G. Heffer, J. Solution Chem., 1999, 28, 575.
2. I. Renge and E. Sild, J. Photochem. Photobiol., A, 2011, 218, 156.
3. L. Nikowa, D. Schwarzer, J. Troe and J. Schroeder, J. Chem. Phys., 1992, 97, 7827.
4. P. J. Daivis and D. J. Evans, J. Chem. Phys., 1994, 100, 541.
5. A. J. C. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191.
6. M. A. Haidekker, T. P. Brady, D. Lichlyter and E. A. Theodorakis, J. Am. Chem. Soc., 2006, 128, 398.
7. I. Renge, J. Phys. Chem. A, 2000, 104, 7452.
8. (a) R. J. Sabharwal, Y. Huang and Y. Song, J. Phys. Chem. B, 2007, 111, 7267; (b) M. Bujak, D. Bläser, A. Katrusiak and R. Boese, Chem. Commun., 2011, 47, 8769.
9. (a) S. Ikawa and E. Whalley, J. Chem. Phys., 1984, 81, 1620; (b) Y. Taniguchi, H. Takaya, P. T. T. Wong and E. Whalley, J. Chem. Phys., 1981, 75, 4815.
10. F. A. Bovey and S. S. Yanari, Nature, 1960, 186, 1042.
11. C. Reichardt, Chem. Soc. Rev., 1992, 21, 147.
12. G. Ulrich, R. Ziessel and A. Harriman, Angew. Chem., Int. Ed., 2008, 47, 1184.
13. A. Harriman and R. Ziessel, Photochem. Photobiol. Sci., 2010, 9, 960.
14. M. A. H. Alamiry, A. C. Benniston, G. Copley, K. J. Elliott, A. Harriman, B. Stewart and Y. G. Zhi, Chem. Mater., 2008, 20, 4024.
15. S. Y. Larsen, R. D. Mountain and R. Zwanzig, J. Chem. Phys., 1965, 42, 2187.
16. L. G. Schornack and C. A. Eckert, J. Phys. Chem., 1970, 74, 3014.
17. (a) M. Kato, I. Abe and Y. Taniguchi, J. Chem. Phys., 1999, 110, 11985; (b) M. Tono-oka, H. Nakayama and K. Ishii, Chem. Lett., 2007, 36, 1126.
18. E. Wilhelm, J. Chem. Phys., 1975, 63, 3379.
19. Y. Song, B. Caswell and E. A. Mason, Int. J. Thermophys., 1991, 12, 855.
20. M. E. Aldea, S. Martin, H. Artigas, M. C. Lopez and C. Lafuente, Thermochim. Acta, 2005, 429, 233.
21. B. Y. Okamoto and H. G. Drickamer, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 4757.
22. R. G. Alden, E. Johnson, V. Nagarajan, W. W. Parson, G. J. Law and R. G. Cogdell, J. Phys. Chem. B, 1997, 101, 4667.
23. Z. Shuai, J. L. Bredas and W. P. Su, Chem. Phys. Lett., 1994, 228, 301.
24. J. F. Skinner, E. L. Cussler and R. M. Fuoss, J. Phys. Chem., 1968, 72, 1057.
25. C. Curutchet, B. Mennucci, G. D. Scholes and D. Beljonne, J. Phys. Chem. B, 2008, 112, 3759.
26. A. Xuan, Y. Wu, C. Peng, P. Ma, C. Wang and L. Zhang, Chin. J. Chem. Eng., 2006, 14, 364.
27. G. Sivaramprasad, M. Venkateshwara Rao and D. H. L. Prasad, J. Chem. Eng. Data, 1990, 35, 122.
28. M. A. Masse, E. Kiran and A. L. Fricke, Polymer, 1986, 27, 619.
29. G. J. Singh and S. K. Gupta, J. Appl. Polym. Sci., 2008, 109, 2139.
30. M. Bujak, M. Podsiadlo and A. Katrusiak, J. Phys. Chem. B, 2008, 112, 1184.
31. D. S. Roy, K. Bhattacharyya, S. C. Bera and M. Chowdhury, Chem. Phys. Lett., 1980, 69, 134.
32. D. S. Bulgarevich, O. Kajimoto and K. Hara, J. Phys. Chem., 1994, 98, 2278.

---

Footnote

† Electronic supplementary information (ESI) available: Energy-minimised conformation of ROBOD, pressure effect on refractive index, viscosity and molar volume. See DOI: 10.1039/c2ra00848c

---