Cottonised flax fibres vs. cotton fibres: structural, textural and adsorption characteristics

Abstract

Structural (crystallinity), textural (pore volume, V_p, specific surface area, S_BET, pore size distribution, PSD) and adsorption characteristics of bleached flax fibres and cotton fibres have been determined using equilibrium adsorption of nitrogen, water, chlorhexidine diacetate (CHX) and methylene blue (MB), adsorption–desorption kinetics of MB and CHX, X-ray diffraction, infrared spectroscopy, thermogravimetry, differential scanning calorimetry (DSC) and DSC cryoporometry. Air-dry, degassed, wetted (RH ≈ 95%), swollen (24 h in water) and air-dried and heated (120 °C for 1 h) fibres were studied. Flax fibres have higher crystallinity, adsorption capacity (MB, CHX, water), and smaller MB desorption than cotton fibres. Cotton fibres have larger V_p value (nitrogen adsorption) and the S_BET,N2 similar to that of flax. Water vapour adsorption is higher on flax since the adsorbed water volume is V_p,w = 0.19 and 0.14 cm³ g⁻¹ for flax and cotton, respectively, at RH ≈ 95%. Wetted fibres are characterised by V_p,w larger by an order of magnitude than V_p,N2 for degassed samples because of swelling effect. However, nanopores at radius R < 1 nm are practically absent in all samples studied regardless of the characterisation technique. The adsorption of MB and CHX on flax fibres is much larger than that for cotton fibres. The specific surface area determined from MB adsorption is 51 m² g⁻¹ (close to S_BET,w estimated from water adsorption but larger than S_BET,N2) and 8 m² g⁻¹ (much smaller than S_BET,N2 and S_BET,w) for flax and cotton fibres, respectively.

---

Introduction

Cotton, flax and other natural plant fibres have a long history of industrial and health care applications^1–3 and have been a subject of numerous studies.^4–7 However, there is insufficient quantitative information regarding their structural, textural and adsorption characteristics. Plant fibres consist of elongated cells (of a cylindrical shape at 2–4 cm in average length for cotton and flax fibres) with a wall thickened by apposition of a so-called secondary cellulosic wall (CW-II).³ The main structural feature of the CW-II is a large content of crystalline cellulose. Nevertheless, there is a large morphological and structural difference between cotton and flax fibres. Cotton fibres originate from the seed capsules as elementary trichome cells, and mature in air over 2–3 weeks. The CW-II is mainly composed of cellulose. Its layers are integrated in the CW-II and the total CW-II thickness rarely exceeds 2 μm. Therefore, during the drying process, the cotton fibre cells adopt a kidney shape. Flax fibres developing in the stems between the cortex and the wood, within bundles, are linked together by their middle lamellae and tricellular junctions. They differentiate over several weeks, so that the cells are completely filled by CW-II and their shapes vary from slightly oval to hexagonal depending on the weather and the process of stem drying. The flax CW-II has some specific structural properties. Although its main component is cellulose (80–90%), it is actually a multilayer composite with cellulosic fibrils embedded in hemicellulose (up to 7%), pectins (up to 5%) and proteins (0–1.5%). A few phenolics (<1%), waxes and fats (0.5–1.0%), minerals (1%) are also present. In the main middle part of CW-II the orientation of cellulose microfibrils almost follows the longitudinal axis of fibres.^3–5 Therefore their textural (porosity, V_p, specific surface area, S, and pore size distribution, PSD) and structural (chemical composition, crystallinity, etc.) features are linked to cellulose fibrils. Fibrils have a high degree of polymerisation (∼10⁴, diameter ∼2 nm).^5–7 The main portion (65–85%) of fibres is crystalline with cellulose I having the lattice constants a = 0.835 nm, b = 1.03 nm, c = 0.79 nm.⁸ A smaller portion of fibres is amorphous. However, crystalline and amorphous contributions in fibres depend on their origin and treatment history. For instance, bleached fibres have a higher crystallinity because of removal of noncrystalline components during treatment. Cellulose fibrils aligned along the fibre length provide tensile and flexural strength and rigidity of fibres, that can be higher for flax than cotton fibres due to the difference in their structure.^6,9 Their structural and textural organisation creates certain inner porosity in fibres as voids between adjacent fibrils and other supramolecular structures.^5,10 This porosity is not fixed by covalent bonding of neighbour fibrils or other supramolecular structures. Their integrity is maintained by the hydrogen bonding, dispersion interactions and electrostatic forces. Therefore, the fibre porosity can significantly change due to interaction with water, especially during soaking and swelling for long time, and the water adsorption–desorption processes. The adsorption capacity of fibres can strongly differ for air-dry and swollen materials. Thus, adsorption of gases, vapours (air-dry fibres contain 4–8 wt% water adsorbed from air) or compounds dissolved in liquid media depends on the fibre origin, “history” of fibre interactions with water and media characteristics.

The efficiency of natural fibres in many applications depends on their nanoscale and microscale textural characteristics, chemical structure, crystallinity, amount and distribution of bound water.^5,6,11 The aim of this paper is to compare the crystalline, textural (at nano- and microscale levels) and adsorption characteristics of bleached flax and cotton fibres using a number of complementary physical and physicochemical methods described in the next section.

Experimental

Materials

Bleached cottonised flax fibres were prepared from waste products of flax scutching (Makarov Lenzavod, Kiev region, Ukraine). Short elementary flax fibres were separated from the technical fibres still linked by their tri-cellular junctions using a carding technique. This flax material is composed with fibres of a similar thickness to cotton fibres and further designated as cottonised flax fibres. Commercial absorbent cotton fibres were purchased from Fisher Scientific (Cotton Wool Absorb, 100% purity, BP quality, CTC-230-010S).

Methods

Nitrogen adsorption–desorption isotherms were recorded at 77.4 K using an Autosorb (Quantachome Instruments, USA) adsorption analyser. Pores in natural fibres have a complex shape.^5,10 Therefore, the pore size distributions (PSDs) were calculated using several models. First, a mixture of slit-shaped and cylindrical pores (SC-model) in carbon materials was used with non-local density functional theory (NLDFT) method (Quantachrome Instruments software, version 2.02, which does not include the parameters for polymer materials). Second, the model with cylindrical pores (C–model) was used. Third, a model with a mixture of slit-shaped and cylindrical pores and voids between spherical particles (SCV-model) in carbohydrate polymers was employed using a modified Nguyen-Do (MND) method with a self-consistent regularisation (SCR) procedure.^13,14 The differential PSDs f(R) ∼ dV/dR (∫f(R)dR ∼ V_p, where R is the radius or half-width of pores) were converted into incremental PSDs, IPSDs (ΣΦ (R_i) ∼ V_p). This was done for a better view of the PSDs over the total range of pore sizes, especially at large R values, where dV/dR typically has very low intensity. The integration of the dV/dR and dS/dR functions was used to estimate contributions of nanopores (R < 1 nm), mesopores (1 < R < 25 nm) and macropores (R > 25 nm) into total porosity (V_p) and specific surface area (S_BET). The S_BET values were determined from the nitrogen adsorption using the standard BET method.¹⁵ The total pore volume V_p was evaluated from the nitrogen adsorption at p/p₀ = 0.98–0.99 (p and p₀ denote the equilibrium and saturation pressures of nitrogen at 77.4 K, respectively).

The adsorption capacity of fibres was evaluated using methylene blue (MB) as an adsorptive. MB has been frequently used because of its chemical and spectroscopic characteristics to study the adsorption properties of different adsorbents including materials of biological origin.¹²

For equilibrium adsorption of methylene blue, a fibre sample (0.5 g), was soaked and stirred (by a glass rod) with 50 mL of distilled water for 5 min. Then 50 mL of an aqueous solution of MB was added (final MB concentration was in the 2.5–220 mg L⁻¹ range) and shaken at 180 rpm, 24 ± 1 °C for 24 h. The optical density (OD) of the equilibrium MB solution was measured at λ = 664 nm using a Shimadzu 2401 PC spectrophotometer. The amount a of MB adsorbed was calculated as a = (C₀ - C_eq)V/m, where C₀ and C_eq are the initial and equilibrium MB concentrations in the solution, respectively, V is the volume of the solution, and m is the weight of a dry fibre sample. Equilibrium adsorption of chlorhexidine (CHX) 2-[N'-[6-[[amino-[[amino-[(4-chlorophenyl)amino]methylidene]amino]methylidene]amino]hexyl]carbamimidoyl]-1-(4-chlorophenyl)guanidine diacetate, molecular formula C₂₂H₃₀Cl₂N₁₀·2(C₂H₄O₂) (Sigma) possessing antimicrobial properties was studied using solutions in a water–ethanol (0.65/0.35) mixture. The OD value was measured at 260 nm. Adsorption–desorption of CHX to/from different materials (silica, polymers, etc.) has been studied for medical applications.¹⁶

To study the adsorption kinetics of MB, a fibre sample (0.5 g) was soaked and stirred for 5 min with 50 mL of distilled water. Then 50 mL of the MB solution at a concentration of 20 mg L⁻¹ was added, shaken at 24 ± 1 °C and centrifuged at 7500 rpm for 5 min. The MB adsorption measurements were carried out at certain time (2, 3, 5 min, … 30 h, and 48 h, i.e. the fibre swelling was varied). The OD value of the control sample with the MB solution (10 mg L⁻¹) was measured after centrifugation at 7500 rpm for 5 min. The OD values of the MB solutions were measured using a 1 cm quartz cuvette. The adsorption kinetics of CHX was studied in a similar manner but from the water–ethanol (0.65/0.35) mixture. The OD value was measured at 260 nm.

The kinetics of MB or CHX desorption from fibres was studied by washing-off of fibres with pre-adsorbed MB or CHX in distilled water and then in phosphate buffered saline (PBS) using the same sample. Each sample (0.2 g fibres) was washed 2–6 times with 10 mL of water or PBS by shaking for 30 min. All adsorption–desorption experiments were carried out three times and the average values were calculated (average relative errors were smaller than ±3%). Calculations of the adsorption rate constant and energetic characteristics (adsorption energy, adsorption potential and adsorption free energy) from the equilibrium and kinetic data are described in detail in the ESI.†

Interactions of MB molecules with cellulose fragments were analysed using semiempirical quantum chemical PM6 method (MOPAC 2009, version 11.038L).¹⁷

The calorimetric measurements were performed using a differential scanning calorimeter (DSC 822e, Mettler Toledo) equipped with an intracooler. Air-dry and swollen fibre samples (5.0 ± 0.01 mg) were cooled at a cooling rate of 5 °C min⁻¹ from room temperature to −60 °C and then heated to 200 °C. Flax and cotton samples were swollen in distilled water for 24 h (as in the case of the equilibrium MB adsorption) and then excess water was removed with filter paper. Residual hydration was h = 0.52 g of water per gram of dry fibres. A set of initial and swollen samples were analysed in triplicate.

Freezing temperature of water in narrow pores is below normal freezing point (0 °C) as described by the Gibbs–Thomson eqn (1) for the freezing point depression for liquids confined in cylindrical pore of radius R_p¹⁸

where T_m and T_m0 are the melting temperatures of confined and bulk water, respectively. The pore size distribution, dV/dR can be calculated from water melting thermograms¹⁸

where dq/dt, ρ, β, m and ΔH(T) are the DSC heat flow, the water density, the heating rate, the sample mass and the melting enthalpy of water, respectively. The ΔH(T) function can be estimated as follows¹⁸

Water vapour sorption by fibres was studied at 25.0 ± 0.1 °C using an automated electronic microbalance (Cahn D200 with a mass resolution of 0.1 μg) with an automated gravimetric dynamic vapour sorption system DVS1 Advantage (Surface Measurement Systems Ltd). Water vapour adsorption isotherms were used to calculate the textural characteristics with the model of cylindrical pores using the corresponding Lennard-Jones potentials.¹⁵ Calculations of the adsorption energy distribution f(E) were carried out assuming clustered adsorption of water and using the corresponding integral equation (see ESI†).¹⁴

The X-ray diffraction (XRD) patterns of flax and cotton fibres were recorded at room temperature using a DRON-4-07 (Burevestnik, St. Petersburg) diffractometer with Cu Kα (λ= 0.154178 nm) radiation and a Ni filter in the 2θ range from 5 to 60 degrees with a step of 0.1 degree. The crystallinity was estimated using two methods (from integral and peak intensities) as described in detail elsewhere.^8,19 The XRD patterns were recorded for fibres air-dry, swollen for 24 h, blotted (∼27 wt% water according to thermogravimetric data), dried in air for 1–4 days, and heated at 120 °C for 1 h.

Infrared (IR) spectra (4000–300 cm⁻¹) were recorded using a Specord M80 (Karl Zeiss, Jena) spectrophotometer. Cut fibre samples (2–4 mg) were mixed with dry KBr (Merck) as 1 : 80 in a microbreaker for 10 min and then pressed into transparent thin pellets.

Results and discussion

Morphology and structural aspects (crystallinity) of fibres

Despite the difference in the shape (cylindrical, slightly oval or kidney-like) (Fig. 1), flax and cotton fibres studied are characterised by relatively similar distribution functions of the cross-section fibre diameter, f(d) in the range 3–50 μm (according to Fiji image processing package) or 5–52 μm (ImageJ) (Fig. 2).

Fig. 1 SEM images of (a, c) flax and (b, d) cotton fibres obtained with SEM JSM-6310 (Japan Electron Optics Ltd).

Fig. 2 Normalised distribution functions of cross-section fibre diameter for flax (curves 1 and 3) and cotton (curves 2 and 4) samples calculated from 26 SEM images using ImageJ (granulometry plugin, lower curves) and Fiji (local thickness plugin with a maximum entropy threshold).

The f(d) functions have been calculated from 26 different SEM images of samples using Fiji (local thickness plugin with a maximum entropy threshold)²⁰ and ImageJ (granulometry plugin)²¹ software. The f(d) functions show that flax fibres are slightly thinner than cotton fibres. For instance, their average diameter determined as the first moment of the f(d) distribution <d> = ∫df(d)dd/∫f(d)dd is equal to 21.4 and 26.2 μm (granulometry plugin) for flax and cotton fibres, respectively. However, f(d) at d < 7 μm (local thickness plugin) can be considered as an underestimation of the fibre diameter³ due to the image treatment software effects, e.g. one fibre can be considered as composed of two–three fibres because of its bending, the formation of helical structures and the presence of fibre cracks. Whatever the value, one can assume that thinner fibres would show a greater adsorption capacity, and faster adsorption kinetics, because of both a higher outer surface and faster penetration of adsorbed molecules into inner pores of thinner fibres under the same experimental conditions.

The XRD patterns of air-dry fibres (Fig. 3) are typical of cellulosic materials.^8,22

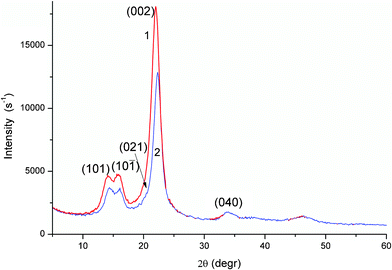Fig. 3 XRD patterns of air-dry flax (curve 1) and cotton (2) fibres.

A relative crystallinity of fibres estimated from integral intensity of three main XRD peaks and amorphous contribution¹⁹ in the range 2θ = 10–30° (Fig. 3 and Fig. S4 in ESI†) is higher for flax (73 ± 2%) than cotton (65 ± 2%). A simpler estimation of the crystallinity index CI(%) = 100×(I₀₀₂ − I_am)/I₀₀₂ from the intensity of the main peak (002) (Fig. 3) and the intensity of the amorphous part (I_am) in a minimum point at ∼18°,^8,19 also gives a higher crystallinity value for flax (86.5%) than cotton (84.1%). The difference between these values is smaller than that for the integral values. The difference in the crystallinity estimated using integral (65–73%) and peak (84–87%) XRD intensity is typical of natural cellulosic materials.²³ Additionally, the smaller values obtained from the integral intensity are similar to the CI values estimated from NMR measurements of cellulosic materials.²³ Low-intensity peaks at 2θ = 33.7° and 46.1° (Fig. 3) can be attributed to structures with hydrogen bonds. The length of these bonds was estimated for air-dry fibres as r_OH⋯O = 0.195 nm between H and O atoms and r_OO = 0.268 nm between oxygen atoms of neighbouring groups. These values are similar for flax and cotton samples because their XRD patterns are identical at 2θ = 25–60°. However, fibril packing appears to be more ordered in flax, which has a higher XRD intensity at 2θ = 10–25°.

Variations in the crystallinity of fibres can influence their textural characteristics, especially during interactions with water resulting in swelling. It should be noted that swelling (24 h, adsorbed 27 wt.% water), air-drying (1–4 days), and heating (120 °C for 1 h) all affect the fibre crystallinity (Fig. S5 in ESI†). These changes are more significant for cotton than flax fibres. For instance, r_OH⋯O = 0.196 and 0.197 nm, r_OO = 0.264 and 0.262 nm (swollen), r_OH⋯O = 0.197 and 0.194 nm, r_OO = 0.264 and 0.262 nm (heated at 120 °C) for flax and cotton fibres, respectively. Thus, the r_OH⋯O values increased but the r_OO values decreased during swelling and heating of fibres. These changes can be caused by changes in the hydrogen bond angles (∠O−H⋯O); i.e., the crystalline structure becomes slightly distorted during swelling–heating. This distortion results in a diminution or even disappearance of splitting of the (101) and (101̄) peaks, especially for cotton (Fig. S5 in ESI†). In other words, flax fibres are more stable during swelling–drying–heating than cotton fibres perhaps owing to a higher crystallinity, the difference in CW-II composition, and the presence of approximately 10% of non-cellulosic components encrusting fibrils and interacting with water load during swelling.

Infrared spectra of flax and cotton fibres (Fig. 4) are typical of natural cellulosic fibres and demonstrate OH (3600–3100 cm⁻¹), CH (2800–3000 cm⁻¹), C=O (∼1700 cm⁻¹), C–O–C, and C–O stretching vibrations, as well as other bands described in detail elsewhere.²⁴ There is no essential difference in the IR spectra of the studied fibres (Fig. 4). However, certain small differences are observed. For instance, CH₂ rocking vibrations at 710 cm⁻¹ characteristic for cellulose I_β²⁴ are more intensive for cotton fibres. Notice that estimation of the crystallinity as the intensity ratio of the IR bands 1371/2900 or 1371/665²⁴ gives 4–5% higher crystallinity index of cotton than flax fibres. The lateral order index, estimated as the ratio of the intensity of the bands at 1430 and 898 cm⁻¹ and giving contribution of cellulose I, is 15% higher for cotton fibres. This difference in the fibre properties, opposite to the XRD data for the crystallinity, is probably due to treatment of fibres with KBr in the microbreaker that can result in stronger diminution of the integrity (visually observed) and the crystallinity of flax compared to cotton fibres.

Fig. 4 Infrared spectra of flax and cotton fibres.

Textural and adsorption characteristics

For detailed and reliable analysis of the textural characteristics of fibres possessing pores of a complex shape, several models of pores (voids) (C–, SC– and SCV–models) and three different techniques (low-temperature nitrogen adsorption, water adsorption at room temperature and DSC cryoporometry of air-dry and swollen fibres at −60–0 °C) were applied (Table 1, Fig. 5 and 6c). The results based on the nitrogen adsorption show that flax and cotton fibres have practically the same S_BET (pore-shape independent parameter) and S_meso (pore-shape dependent) values (Table 1). The average S_BET values for eight flax and eight cotton samples are 26.4 ± 10.2 m² g⁻¹ and 27.0 ± 18.6 m² g⁻¹, respectively. However, there is some difference in the textural characteristics of fibres due to the difference in their partial swelling caused by water adsorption. Small water molecules can penetrate into polar carbohydrate supramolecular structures in fibres and incorporate into their hydrogen bond network.

Fig. 5 Pore size distributions: (a, b) incremental with the C-model (cyl) (MND method for polymers), SC-model (slit/cyl) with NLDFT method for carbons, and SCV-model (slit/cyl/void) (MND method for polymers); IPSD_V for (a) cotton and (b) flax and (c) PSD (DSC cryoporometry) for dry and swollen fibre samples.

Fig. 6 (a) Water adsorption isotherms and the distribution functions of (b) adsorption potential (eqn (S12)) for water and nitrogen; (c) pore sizes (IPSD_V) calculated from water adsorption isotherms using the C–model; (d) free energy (eqn (S9) in ESI†) and (e) energy of water adsorption (eqn (S11) in ESI†).

Table 1 Textural characteristics of flax and cotton fibres determined from nitrogen (SCV-model) and water (C-model) adsorption isotherms^a

Sample	S BET m^2 g^−1	S nano m^2 g^−1	S meso m^2 g^−1	S macro m^2 g^−1	V p cm^3 g^−1	V nano cm^3 g^−1	V meso cm^3 g^−1	V macro cm^3 g^−1	D	Adsorbate
a Note. The characteristics based on N2 adsorption were calculated for samples with the SBET values close to the average SBET values for eight samples of both materials. Nanopores (Snano and Vnano) are at pore radius R < 1 nm, mesopores (Smeso and Vmeso) at 1 < R < 25 nm, and macropores (Smacro and Vmacro) at 25 < R < 100 nm; D is the fractal dimension calculated with the Frenkel–Halsey–Hill equation.
Flax	27.6	0	26.8	0.8	0.018	0	0.013	0.005	2.609	N2
	46	0	46	0.1	0.194	0	0.192	0.002	2.670	H2O
Cotton	27.3	0	26.7	0.6	0.036	0	0.029	0.007	2.617	N2
	34	0	34	0	0.141	0	0.140	0.001	2.684	H2O

---

This causes swelling and changes in the textural (Fig. 5, Table 1) and crystalline (Fig. S5, ESI†) characteristics of fibres wetted by water vapour or swollen in the aqueous media. Many of the textural characteristics shown in Table 1 have larger values if determined from water vapour adsorption (because of partial swelling) than those determined from nitrogen adsorption (without swelling) (Table 1). A decrease in macroporosity (V_macro, S_macro) and a parallel increase in mesoporosity (V_meso, S_meso) determined from water adsorption can be explained by ‘mesopore swelling’ (V_meso,H2O > V_meso,N2) with contraction of macropores because the adsorption potential for water is higher in narrower pores.¹⁵ Additionally, this swelling of mesopores results in a decrease in the hydrogen bond lengths and a certain compaction of the crystalline lattice of fibrils (Fig. S5, ESI†). Water tends to be adsorbed in narrower pores, despite its clustered adsorption since these clusters can include only a few molecules. Both nitrogen and water (adsorbed from the gas or vapour phase) can fill macropores only partially because the adsorption potential there is very low (A < 0.5 kJ mol⁻¹ for both adsorbates, Fig. 6b) at large distances from the pore walls.

The PSD of flax obtained from mercury porosimetry data (Fig. S1 in ESI†) has the main maximum at R = 77 μm (with zero PSD intensity at R < 150 nm and marked intensity appearing only at R > 5 μm). These pores can be attributed to voids between neighbouring fibres (Fig. 1) in their beads because the fibre thickness is smaller than the size of these macropores. The mercury porosimetry gives the pore volume ∼0.2 cm³ g⁻¹ at R < 30 μm but at R < 5 μm it is very low (∼0.001 cm³ g⁻¹). In other words, during the intrusion phase, mercury, possessing very high surface tension, cannot practically penetrate into inner mesopores of fibres (in contrast to water or nitrogen) and remains between fibres in their beads. Thus, this measurement confirms a low inner macroporosity of flax fibres. The inner porosity of fibres at R > 25 nm is very low as estimated from the water or nitrogen adsorption (Table 1, V_macro, S_macro). This is in agreement with electron microscopy images (Fig. 1) showing relatively smooth surface of fibres without cracks. Thus, fibres have a smooth surface at a microscale level practically without visible macropores (Fig. 1c and 1d). The shape of the PSDs at 25 < R < 100 nm based on the nitrogen adsorption data (Fig. 5 shows only incremental PSD because the differential PSDdV/dR is low in this range) and at 25 < R < 35 nm based on water adsorption (Fig. 6c, IPSD) suggests that both water (RH < 95%) and nitrogen (p/p₀ ≤ 0.995) are mainly adsorbed in the inner mesopores of fibres.

The fibres studied have similar PSDs in respect to the pore volume (Fig. 5a, 5b and 6c). This is due to a certain similarity of both structural and textural features of natural fibres. Notice that nitrogen adsorption–desorption isotherms were recorded for samples degassed at 80 °C for 24 h (residual content of water < 1 wt%). In the case of air-dry fibres, water content was about 4 wt% (thermogravimetric measurements, Fig. S3, and sample weighting after DSC measurements).

The textural and structural characteristics of natural fibres can depend on the amounts of bound water adsorbed from air, vapour atmosphere (Table 1) or aqueous media resulting in increased swelling. Therefore, the textural characteristics of non-degassed air-dry and swollen (24 h in distilled water at room temperature) samples were estimated using the DSC cryoporometry (Fig. 5c). After swelling of fibres, the PSD becomes much broader and the peak shifts towards a larger pore size at R ∼ 5 nm (Fig. 5c). The DSC PSDs for air-dry samples have a maximum at R ∼ 2 nm (similar to that based on water adsorption, Fig. 6c) and a peak at smaller R values. However, the shape of these PSDs differs because of variations in the amounts of water (h ≈ 0.01, 0.05, 0.52 and 0.2 g g⁻¹, respectively) affecting the PSDs.

The fractality of fibres (Table 1, D) increases due to water adsorption. The surface becomes rougher and/or the pore shape becomes more complex but nanopores are absent (V_nano, S_nano). These results are in agreement with the nitrogen adsorption data. Enlarging mainly inter-fibrillar distances can occur during water adsorption. This results in partial swelling of fibres (mesopores broaden) without decomposition of the inner-fibrillar hydrogen bonds between adjacent cellulose chains (macropores decrease). It means that during water adsorption, the inner structure of fibres remains dense with tight contacts between cellulose chains in fibrils. The estimation of the specific surface area using a molecular model of cellulose gives about 3000 m² g⁻¹ for individual chains. Triple twisted cellulose coils can have an S value of approximately 1000 m² g⁻¹. However, strong interactions in supramolecular structures in fibres including strongly bound water result in denser packing (without nanopores) of cellulose macromolecules in microfibrils and other components in fibres that result in low S_BET < 50 m² g⁻¹ according to both nitrogen and water adsorption data (Table 1). These results can be interpreted so that strongly coiled and folded supramolecular structures with a continuous network of hydrogen bonds (with contributions of electrostatic and dispersion interactions) keep the fibre integrity during interaction with water vapour or aqueous medium.

As noted above, the similar shapes of water adsorption isotherms (Fig. 6a) for flax and cotton originate from the predominance of the cellulose network in the fibres. They are hydrophilic materials; therefore, the adsorption potential, A (affinity) and the distribution f(A) functions for water are much greater than those for nitrogen (Fig. 6b). The energetic characteristics of water adsorption expressed as changes in free energy (ΔG) (Fig. 6d) and adsorption energy (E) were calculated assuming that water is adsorbed in clusters of five water molecules (plus OH group of cellulose that give stable six-member rings) in the average cluster per an adsorption site (Fig. 6e) (see also ESI†). These calculations show that the water adsorption is characterised by relatively low energy since non-zero distribution functions are at −ΔG < 9 kJ mol⁻¹ and E < 30 kJ mol⁻¹, respectively. However, strong hydrogen bonds can give −ΔG > 20 kJ mol⁻¹ and E = 40–50 kJ mol⁻¹.^13–15 This result can be explained by the formation of the hydrogen bonds ≡CO−H⋯OH₂, ≡CO(H)⋯HOH, =CO(C−)⋯HOH and H₂O⋯HOH without significant contribution of charged structures providing much stronger hydrogen bonds. Additionally, very strongly bound water can remain in fibres during degassing of samples before the water adsorption measurements. The PSDs (Fig. 6c) calculated from water adsorption isotherms (Fig. 6a) give a more detailed picture of mesopores filled by water than the DSC PSDs of swollen fibres (Fig. 5c). This difference can be explained by a larger amount of water retained by fibres in DSC measurements of swollen samples (h = 0.52 g g⁻¹) than in water vapour adsorption (h < 0.2 g g⁻¹). Additionally, during heating of samples containing a relatively large amount of water (especially bulk water), the DSC method has relatively low sensitivity in respect to strongly bound water masked by bulk water. A significant portion of water in swollen fibres at h = 0.52 g g⁻¹ can be attributed to bulk or very weakly bound water since a very sharp exotherm of water crystallisation is observed at −10–−13 °C (Fig. 7a). This water reduces the resolving ability of the DSC cryoporometry (Fig. 5c, compare curves for air-dry and swollen samples). The main intensity of melting endotherm is at T > 0 °C (Fig. 7a) but the DSC cryoporometry can be applied to the DSC thermograms only at T < 0 °C. The DSC method has been successfully used for the analysis of the amount and state of absorbed water in polymers.²⁵ The DSC thermograms of swollen (Fig. 7a) or air-dry (Fig. 7b) samples are similar for flax and cotton fibres. However, there is some difference in an exotherm of water crystallisation (T_cr = −10.6 °C for cotton and −12.7 °C for flax) and an endotherm of water evaporation (98.8 °C for cotton and 94.6 °C for flax) despite the same amount of water in swollen fibres (Fig. 7a, h = 0.52 g g⁻¹). The difference in the T_cr value can be explained by larger S_BET, S_meso and V_meso values of flax (i.e. a larger number of narrower pores filled by water) than those of cotton for both degassed (nitrogen adsorption) and wetted (water adsorption) samples (Table 1).

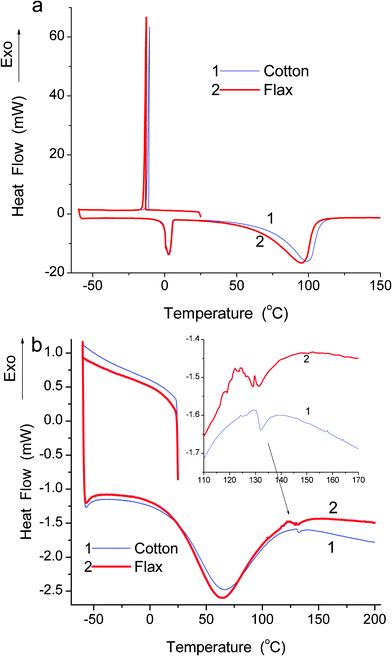Fig. 7 DSC thermograms for (a) wetted (h = 0.52 g g⁻¹) and (b) dry (h = 0.08 (1) and 0.04 (2) g g⁻¹) flax and cotton fibres.

For air-dry samples, the shape of DCS thermograms (Fig. 7b) strongly differs from that of swollen samples (Fig. 7a). Both a bulk water crystallisation exotherm and a melting endoterm are absent in air-dry samples. It means that bound water (∼4 wt%) does not form large structures capable of forming ice crystallites in air-dry samples. This water is strongly bound.^13,14 A broad endotherm at 64–66 °C (Fig. 7b) can be attributed to residual water evaporation, enthalpic relaxation and melting of some weak associates in fibres.²⁶ A very small endotherm at 131–132 °C (insert in Fig. 7b) can be attributed to the melting of some stronger water associates, since glass transition of dry cellulose is around 200 °C.^4,26 The results presented here for water adsorption and swelling of flax and cotton fibres are in good agreement with data published previously that showed greater water adsorption on flax than cotton fibres.²⁷

Adsorption/desorption of MB and CHX

Adsorptive properties of cotton, flax or hemp fibres are utilised in materials used for health care, wound dressings, and for removing organic pollutants from aqueous media.²⁸ For instance, cotton demonstrated a high adsorption capacity for such dyes as basic red 2 and acid blue 25.²⁸ In this paper, the adsorption of low molecular weight substances MB (as a model organic pollutant) and CHX (as a common antimicrobial agent) has been studied.

The flax fibres studied have much larger equilibrium adsorption capacity towards MB and CHX than cotton (Fig. 8 and 9). The specific surface area calculated from plateau adsorption of MB (Fig. 8) using the surface area of 1.19 nm² occupied by a MB molecule (Fig. S1 in ESI†) is 51 and 8 m² g⁻¹ for flax and cotton, respectively. For flax this value is close to S_BET,H2O and larger than S_BET,N2, but for cotton it is much lower than S_BET,H2O or S_BET,N2 (Table 1). The adsorption capacity of flax for MB is greater than that of cotton (Fig. 8).

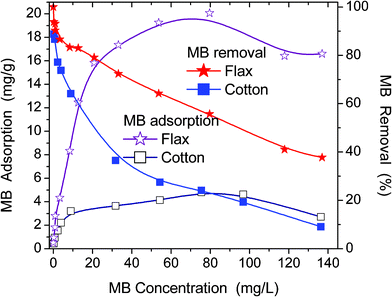Fig. 8 Adsorption isotherms and percentage removal of MB by flax and cotton fibres as a function of equilibrium MB concentration in solution.

Fig. 9 Adsorption isotherms of CHX on flax and cotton fibres from water–ethanol mixture.

The observed decrease in the MB adsorption at C_eq > 100 mg L⁻¹ (Fig. 8) is reproducible and cannot be explained by the experimental errors. It can be explained by several effects enhanced with increasing C_eq value, such as (i) faster MB adsorption and blocking of free adsorption sites, and (ii) formation of MB dimers, which have adsorption characteristics different from those of individual MB molecules. Natural fibres are texturally nonuniform (Fig. 2–6). Therefore, MB adsorption isotherms have a complex shape (Fig. 8) and correspond to broad (flax) or bimodal (cotton) distribution functions of the Gibbs free energy of adsorption, f(ΔG) (Fig. 10). MB adsorption is stronger on flax than cotton since the average value <−ΔG> for the former is greater. However, for both materials the <−ΔG> values are relatively small because of (i) desolvation effects accompanying the adsorption of MB possessing a polar structure (cation MB⁺ with Cl⁻ as a counterion), (ii) destabilising contribution of entropy changes to the adsorption onto hydrophilic adsorbents, (iii) the absence of nanopores accessible for MB. The adsorption of CHX has similar features (Fig. 9). However, the adsorption capacity for CHX of both flax and cotton fibres is much lower than that for MB because of the difference in their structures, Therefore, the f(ΔG) peaks for the CHX adsorption on both fibres are located at small −ΔG values (Fig. 10).

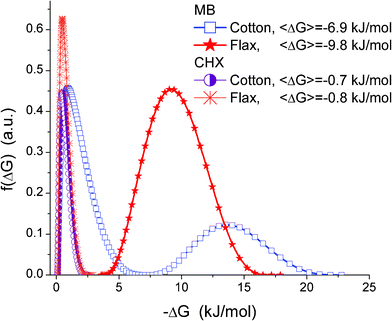Fig. 10 Distribution of Gibbs free energy of MB and CHX adsorption onto flax and cotton fibres from aqueous and water–alcohol mixtures.

The use of kinetic adsorption equations of pseudo-first order, eqn (S2) and pseudo-second order, eqn (S3) (in ESI†) gives k values (Table 2) greater for the MB adsorption on flax than cotton (Fig. S6). The calculations with eqn (S2) and (S3) give much worse fitting (Fig. 11a) than that with the integral eqn (S4) with appropriate weights w₁ and w₂ (Fig. 11b). However, the best fitting was obtained with a complex integral eqn (S5).

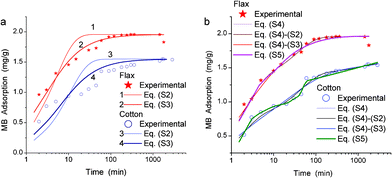Fig. 11 Adsorption kinetics of MB on cotton and flax fibres: experimental (symbols) and theoretical (lines) with (a) non-integral and (b) integral equations. Labels Eq. (S4)–(S2) or (S4)–(S3) correspond to calculations using eqn (S4) with the kernel corresponding to eqn (S2) or (S3), respectively.

Table 2 MB adsorption rate constant for flax and cotton fibres calculated with different equations (as a constant k with non-integral eqn (S2) and (S3) in the ESI or as the average <k> obtained from the f(k) distribution functions with integral eqn (S4) and (S5) in the ESI)^a

Sample	Equation	k or <k>
a Note. Labels eqn (S4)-(S2) or (S4)-(S3) correspond to calculations with eqn (S4) with the kernel corresponding to eqn (S2) (i.e. w1 = 1 and w2 = 0 in eqn (S4)) or (S3) (w1 = 0, w2 = 1), respectively.
Flax	(S2)	0.198
Cotton	(S2)	0.095
Flax	(S3)	0.175
Cotton	(S3)	0.104
Flax	(S2)-(S4)	1.563
Flax	(S3)-(S4)	0.541
Flax	(S4)	0.437
Cotton	(S2)-(S4)	0.288
Cotton	(S3)-(S4)	0.550
Cotton	(S4)	0.480
Flax	(S5)	0.176
Cotton	(S5)	0.038

---

Each MB⁺ cation can form several hydrogen bonds with OH– and O-containing groups in cellulose and bound water molecules (Fig. 12). The interaction energy is smaller (−41 kJ mol⁻¹ per MB⁺ with several hydrogen bonds with cellulose or water, method PM6) in the complex with a partial solvation shell (Fig. 12a) than without this shell, ΔE_t = −51 kJ mol⁻¹ (Fig. 12b). The interaction energy between MB⁺ and cellulose reduces in water as a polar solvent with high permittivity. The water permittivity reduces for water clusters and domains in confined space in narrow pores.¹⁴ Therefore, the diminution in the interaction energy of MB with fibres can be smaller in narrower pores where water is less active as a solvent. Therefore molecular MB and CHX ions can be more easily washed-off from broader pores due to strong hydration effects.

Fig. 12 Interaction of MB cations with cellulose (a) in the presence of water molecules (energy ΔE_t = −41.2 kJ mol⁻¹ per each MB, PM6 geometry) or (b) without water (ΔE_t = −51.0 kJ mol⁻¹) with different types of fields (FieldView 2.0.2²⁹) around a cellulose fragment and a MB molecular ion. The positive field (dark red) is around positively charged H atoms, the negative field (light blue) is due to negatively charged O, N, S and Cl atoms, and the hydrophobic field (yellow) is around hydrophobic CH groups.

These effects can explain the observed differences in the adsorption–desorption of MB (and CHX) on flax and cotton possessing different PSDs affected by swelling in water. The MB–cellulose–water interaction features (depending on the pore size where this adsorption occurs) can affect the k and ΔG values and the shape of the f(ΔG) distribution functions of the MB adsorption. Despite the difference in the equations used (S2)–(S5) (in ESI†), the k or <k> values (Table 2) are similar for flax and cotton fibres since these materials have relatively similar structural, textural and adsorption characteristics after interaction with water (Fig. 1–6, Table 1).

Flax fibres adsorb more and desorb less MB than cotton fibres (Fig. 13) as well as in the case of the CHX desorption (vide infra).

Fig. 13 Relative desorption of MB from (1, 2) cotton and (3, 4) flax in water (1, 3) water and then in PBS (2, 4) using the same samples after desorption in water.

Features and differences of the adsorption kinetics of CHX on flax and cotton fibres from the water–ethanol mixture (Fig. 14) are similar to those observed for MB (Fig. 11). The plateau of CHX adsorption is similar to that of MB and is reached at similar time (Fig. 11 and 14). Interaction of twice protonated CHX with the cellulose hydroxyls as a proton-donor is characterised by lower interaction energy than that of a monovalent MB cation (Fig. 10).

Fig. 14 Kinetic adsorption of CHX onto flax and cotton fibres from a water–ethanol mixture.

The lower CHX adsorption is also due to a strong negative field around CHX (Fig. 15), which forms a compacted charged structure in water to minimise interaction of hydrophobic fragments with water molecules. Therefore, the adsorption rate is larger for smaller and almost planar and less charged MB (Table 2). Relative desorption of CHX is much higher than that of MB, especially in PBS (Fig. 16). This can be explained by more shallow penetration of CHX into fibres (i.e. it locates in broader pores) than MB. Relative desorption of CHX is higher in PBS than water for both cotton and flax (Fig. 16 and S7). These results show that the ionic component of CHX interactions with fibres is predominant. In non-aqueous medium (e.g. in pure alcohol or without solvation) CHX can transform into the molecular form with less folded structure according to ab initio calculations (Fig. S8, ESI†).

Fig. 15 Structure of hydrated CHX in a compacted form (PM6 geometry, almost all water molecules were not shown in the left structure).

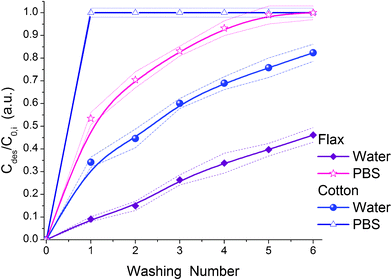Fig. 16 Relative desorption of CHX from flax and cotton fibres in water or PBS as a function of the washing number (dashed lines show the average error intervals).

Conclusions

Air-dry bleached flax and cotton fibres are characterised by a relatively high crystallinity (CI ≈ 85%) but a low specific surface area S ≈ 27 m² g⁻¹ (nitrogen adsorption). Wetted (RH ≈ 95%) or swollen in aqueous medium for 24 h fibres have larger S values. Degassed dry fibres have very low inner porosity V_p ≤ 0.04 cm³ g⁻¹ because of a high crystallinity, compacted supramolecular structures and a small amount of residual strongly bound water. For wetted fibres, the porosity V_p is larger for flax than cotton and it is larger than V_p, estimated from the nitrogen adsorption on degassed dry samples by an order of magnitude. Water-swollen fibres have increased mesoporosity and surface area. However, swelling does not generate nanopores and decreases macroporosity. The crystallinity is not affected by swelling (for 24 h), drying (for several days in air) or heating at 120 °C (for 1 h). This corresponds to structural stability of fibres in the aqueous media.

More strongly enlarged specific surface area and pore volume of flax during its interaction with water lead to a greater equilibrium adsorption and faster adsorption kinetics of methylene blue from an aqueous solution and CHX from a water–alcohol mixture than onto cotton. MB adsorption onto flax is characterised by more negative Gibbs free energy of the equilibrium adsorption and a higher adsorption rate constant than those on cotton. Relative desorption of MB from cotton is larger than from flax fibres. Thus, bleached flax is a more effective adsorbent than cotton for such polyaromatic organics as methylene blue and CHX.

Acknowledgements

The work was supported by the Interreg IVA (South) project 4044 Flax and the FP7-PEOPLE-IRSES project 230790 COMPOSITUM.

References

1. K. G. Satyanarayana, G. G. C. Arizaga and F. Wypych, Prog. Polym. Sci., 2009, 34, 982.
2. M. J. John and S. Thomas, Carbohydr. Polym., 2008, 71, 343.
3. (a) S. Alix, S. Marais, C. Morvan and L. Lebrun, Composites, Part A, 2008, 39, 1793; (b) S. Alix, E. Philippe, A. Bessadok, L. Lebrun, C. Morvan and S. Marais, Bioresour. Technol., 2009, 100, 4742; (c) C. Morvan, C. Andeme-Onzighi, R. Girault, D. S. Himmelsbach, A. Driouich and D. E. Akin, Plant Physiol. Biochem., 2003, 41, 935; (d) N. B. Brutch, O. Soret-Morvan, E. A. Porokhovinova, I. Y. Sharov and C. Morvan, J. Natur. Fibers, 2008, 5, 95.
4. (a) N. E. Zafeiropoulos, C. A. Baillie and F. L. Matthews, Composites, Part A, 2001, 32, 525; (b) T. T. Teeri, H. Brumer III, G. Daniel and P. Gatenholm, Trends Biotechnol., 2007, 25, 299; (c) J. Andersons, E. Spãrņiš, R. Joffe and L. Wallström, Compos. Sci. Technol., 2004, 65, 693; (d) G. Cantero, A. Arbelaiz, R. Llano-Ponte and I. Mondragon, Compos. Sci. Technol., 2003, 63, 1247; (e) K. Charlet, C. Baley, C. Morvan, J. P. Jernot, M. Gomina and J. Bréard, Composites, Part A, 2007, 38, 1912.
5. P. Zugenmaier, Crystalline Cellulose and Cellulose Derivatives. Characterization and Structures, Springer-Verlag, Berlin, 2008.
6. A. Bessadok, D. Langevin, F. Gouanve, C. Chappey, S. Roudesli and S. Marais, Carbohydr. Polym., 2009, 76, 74.
7. Y. Z. Zhang, X. L. Chen, J. Liu, P. J. Gao, D. X. Shi and S. J. Pang, J. Vac. Sci. Technol., B, 1997, 15, 1502.
8. D. V. Parikh, D. P. Thibodeaux and B. Condon, Text. Res. J., 2007, 77, 612.
9. V. Vadivelan and K. V. Kumar, J. Colloid Interface Sci., 2005, 286, 90.
10. M. R. Rowell, R. A. Young and J. K. Rowell (ed.)Paper and Composites from Agro-based Resources, CRC Lewis Publishers, New York, 1997.
11. (a) S. Alila and S. Boufi, Ind. Crops Prod., 2009, 30, 93; (b) N. M. Bikales and L. Segal (ed.)Cellulose and Cellulose Derivatives, Part V, Wiley Interscience, New York 1971.
12. (a) V. J. P. Vilar, C. M. S. Botelho and R. A. R. Boaventura, J. Hazard. Mater., 2007, 147, 120; (b) K. S. Low, C. K. Lee and K. K. Tan, Bioresour. Technol., 1995, 52, 79; (c) M. Ertaş, B. Acemioğlu, M. H. Alma and M. Usta, J. Hazard. Mater., 2010, 183, 421; (d) M. Rafatullah, O. Sulaiman, R. Hashim and A. Ahmad, J. Hazard. Mater., 2010, 177, 70.
13. (a) V. M. Gun'ko, V. V. Turov, V. M. Bogatyrev, V. I. Zarko, R. Leboda, E. V. Goncharuk, A. A. Novza, A. V. Turov and A. A. Chuiko, Adv. Colloid Interface Sci., 2005, 118, 125; (b) V. M. Gun'ko, R. Leboda, J. Skubiszewska-Zięba, B. Gawdzik and B. Charmas, Appl. Surf. Sci., 2005, 252, 612; (c) V. M. Gun'ko, Theor. Exp. Chem., 2007, 43, 139; (d) V. M. Gun'ko, V. V. Turov, R. Leboda, V. I. Zarko, J. Skubiszewska-Zięba and B. Charmas, Langmuir, 2007, 23, 3184.
14. (a) V. M. Gun'ko, V. V. Turov and P. P. Gorbik, Water at the Interfaces, Naukova Dumka, Kiev, 2009; (b) V. V. Turov and V. M. Gun'ko, Clustered Water and Ways of Its Applications, Naukova Dumka, Kiev, 2011.
15. A.W. Adamson and A.P. Gast, Physical Chemistry of Surface, sixth ed., Wiley, New York, 1997.
16. (a) D. S. Jones and N. J. Medlicott, Int. J. Pharm., 1995, 114, 257; (b) N. J. Medlicott, I. G. Tucker, M. J. Rathbone, D. W. Holborow and D. S. Jones, Int. J. Pharm., 1996, 143, 25; (c) N. J. Medlicott, D. W. Holborow, M. J. Rathbone, D. S. Jones and I. G. Tucker, J. Controlled Release, 1999, 61, 337; (d) K. J. Anusavice, N. Z. Zhang and C. Shen, J. Dent. Res., 2006, 85, 950; (e) A. Modesto and D. R. Drake, Curr. Microbiol., 2006, 52, 418; (f) R. O. Darouiche, Int. J. Artif. Organs, 2007, 340, 71; (g) E. Farkas, D. Kiss and R. Zelko, Int. J. Pharm., 2007, 340, 71; (h) E. Verraedt, M. Pendela, E. Adams, J. Hoogmartens and J. A. Martens, J. Controlled Release, 2010, 142, 47; (i) E. Verraedt, A. Braem, A. Chaudhari, K. Thevissen, E. Adams, L. Van Mellaert, B. P. A. Cammue, J. Duyck, J. Anne, J. Vleugels and J. A. Martens, Int. J. Pharm., 2011, 419, 28.
17. J. J. P. Stewart, MOPAC2009, Stewart Computational Chemistry, Colorado Springs, CO, USA, http://openmopac.net/,, 2008.
18. (a) M. R. Landry, Thermochim. Acta, 2005, 433, 27; (b) G. Rohman, F. Lauprêtre, S. Boileau, P. Guérin and D. Grande, Polymer, 2007, 48, 7017; (c) J. Weber and L. Bergström, Langmuir, 2010, 26, 10158.
19. (a) L. Segal, J. J. Creely, A. E. Martin and C. M. Conrad, Text. Res. J., 1959, 29, 786; (b) Yu. S. Lipatov, V. V. Shilov, Yu. P. Gomza and N. E. Kruglyak, Roentgenographic Methods of Study of Polymer Systems, Naukova Dumka, Kiev, 1982.
20. http://pacific.mpi-cbg.de/wiki/index.php .
21. http://rsbweb.nih.gov/ij/. http://rsb.info.nih.gov/ij/plugins/granulometry.html .
22. JCPDS (№ 50-2241) Database, International Center for Diffraction Data, PA, 2001..
23. S. Park, J. O. Baker, M. E. Himmel, P. A. Parilla and D. K. Johnson, Biotechnol. Biofuels, 2010, 3, 1.
24. (a) S. Y. Oh, D. I. Yoo, Y. Shin and H. C. Kim, Carbohydr. Res., 2005, 340, 2376; (b) M. Akerholm, B. Hinterstoisser and L. Salmen, Carbohydr. Res., 2004, 339, 569; (c) B. Focher, A. Naggi, G. Torri, A. Cosani and M. Terbojevich, Carbohyd. Res., 1992, 17, 97; (d) J. He, Y. Tang and S.-Y. Wang, Iran. Polym. J., 2007, 16, 807; (e) G. Nikolić, Fourier Transforms - New Analytical Approaches and FTIR Strategies, InTech, 2011 (http://www.intechopen.com/articles/show/title/applications-of-fourier-transform-infrared-spectroscopy-to-study-cotton-fibers.
25. (a) S. Rowland, Water in Polymers, Amer. Chem. Soc., Washington, D.C, 1980; (b) V.A. Bershtein and V.M. Egorov, Differential Scanning Calorimetry of Polymers. Physics, Chemistry, Analysis, Technology, Ellis Horwood, New York, 1994.
26. S. Paes, Sh. Sun, W. MacNaughtan, R. Ibbett, J. Ganster, T. Foster and J. Mitchell, Cellulose, 2010, 17, 693.
27. (a) B. M. Pejic, M. M. Kostic, P. D. Skundric and J. Z. Praskalo, Bioresour. Technol., 2008, 99, 7152; (b) C. A. S. Hill, A. Norton and G. Newman, J. Appl. Polym. Sci., 2009, 112, 1524; (c) F. Gouanvé, S. Marais, A. Bessadok, D. Langevin and M. Métayer, Eur. Polym. J., 2007, 43, 586.
28. (a) G. Crini, Bioresour. Technol., 2006, 97, 1061; (b) F. A. Pavan, A. C. Mazzocato and Y. Gushikem, Bioresour. Technol., 2008, 99, 3162; (c) N. Reddy and Y. Yang, Bioresour. Technol., 2009, 100, 3563; (d) K. T. Klasson, L. H. Wartelle, I. M. Lima, W. E. Marshall and D. E. Akin, Bioresour. Technol., 2009, 100, 5045; (e) K. S. Thangamani, M. Sathishkumar, Y. Sameena, N. Vennilamani, K. Kadirvelu, S. Pattabhi and S. E. Yun, Bioresour. Technol., 2007, 98, 1265.
29. FieldView 2.0.2, www.cresset-group.com. T. Cheeseright, M. Mackey, S. Rose and A. Vinter, J. Chem. Inf. Model., 2006, 46, 665.

---

Footnote

† Electronic Supplementary Information (ESI) available: See DOI: 10.1039/c2ra00725h/

---