Structure and complex magnetic behavior of disordered perovskite (Bi_0.5Sr_0.5)(Fe_0.5Mn_0.5)O₃

Abstract

(Bi_0.5Sr_0.5)(Fe_0.5Mn_0.5)O₃ crystallizes in a rhombohedral structure, with space group R3̄c, where the cations Bi³⁺/Sr²⁺ and Fe³⁺/Mn⁴⁺ occupy 6a and 6b sites respectively. Neutron diffraction, Mössbauer and magnetization measurements confirm long range antiferromagnetic ordering of the Fe³⁺ and Mn⁴⁺ moments at T_N (226 K). Below T_N, this oxide exhibits a cluster glass behavior and at low temperatures (∼30 K) a spin glass state is observed. The complex magnetic behavior is attributed to cation disorder in the system. Magnetic properties of this oxide are compared with those of the isostructural Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ where both Fe and Mn ions exist in trivalent state.

---

1. Introduction

Perovskite oxides (ABO₃) have been a subject of intense study for a few decades due to their exciting properties such as ferroelectricity, magnetism, multiferroicity, colossal magnetoresistance and superconductivity. For example, hole doped manganites show colossal magnetoresistance which forms the basis for magnetic read-head and related applications.¹Strontium doped (15–50%) LaMnO₃ is one such interesting system which shows ferromagnetic and metallic behavior arising from double exchange interaction between Mn³⁺ and Mn⁴⁺ ions.² Conversely, partial substitution of Mn by other transition metals in La_1-xSr_xMnO₃ (0.15 ≤ x ≤ 0.5) destroys ferromagnetism and metallic state due to suppression of double exchange (DE) interaction^3,4 and in many cases it results in a glassy behavior arising from competition between the DE and superexchange interactions.^4,5Substitution of Fe³⁺ for Mn³⁺ ions is particularly interesting to study as both the cations are of same ionic radii thus surpassing any structural change and only inducing a change in magnetic behavior.⁶ In the half-doped manganite when all the Mn³⁺ ions are replaced by Fe³⁺ ions, it is expected that the DE mediated ferromagnetism would disappear and the magnetic interaction is determined by the superexchange interactions among Fe³⁺ (d⁵) and Mn⁴⁺ (d³) . However, one may still expect ferromagnetic ordering based on Goodenough–Kanamori rule.^7,8

Another interesting aspect is that stoichiometric LaMnO₃ is an antiferromagnetic insulator (T_N∼143 K) with an orthorhombic structure,^2,9 while BiMnO₃ is ferromagnetic (T_C∼105 K),¹⁰ despite La³⁺ and Bi³⁺ ions have similar ionic radii (0.645 Å). The stereochemical activity of 6s² lone pair electrons of Bi³⁺ ions influences the structure and hence the physical properties.¹¹ For example, BiFeO₃ is antiferromagnetic (T_N = 643 K) and ferroelectric (T_C = 1103 K) at room temperature.¹² It may be mentioned here, except BiFeO₃, most of the other Bi based compounds are stabilized in the perovskite structure under high pressure and high temperature. The compound, BiFe_0.5Mn_0.5O₃, synthesized at high pressure and temperature, has an orthorhombic structure and exhibits a temperature-induced magnetization reversal below T_N = 240 K.¹³ However, it is possible to stabilize this compound at ambient pressure by partial substitution at the A or B sites.^14,15 For example, La or Sr substitutions at the Bi–site of the high pressure BiFe_0.5Mn_0.5O₃ phase stabilize it in the perovskite structure at ambient pressure. In La_0.5Bi_0.5Fe_0.5Mn_0.5O₃, Fe³⁺ and Mn³⁺ orders antiferromagnetically at 240 K and this compound is a multiferroic and exhibits a spin-glass state at low temperature.¹⁶ It is worthwhile to investigate and compare the physical properties of two close systems with 50% of La and Sr substituted at the Bi-site of BiFe_0.5Mn_0.5O₃, having d⁵–d⁴ (La doped) and d⁵–d³ (Sr doped) spin configuration respectively. Interestingly, both compounds have an identical crystal structure (R3̄c) but they differ in their magnetic properties. Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ (BLFMO) shows an antiferromagnetic ordering with spin canting below T_N∼220 K whereas Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ (BSFMO) exhibits a complex magnetic behavior. Below T_N (226 K), Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ exhibits a cluster glass state and at further low temperature 30 K a spin-glass state is observed.

2. Experimental

Polycrystalline samples of BSFMO and BLFMO have been prepared using solid state reaction route. Stoichiometric amounts of Bi₂O₃, SrCO₃, Fe₂O₃ and Mn₂O₃ were mixed and ground intimately and then heated between 1073 and 1273 K in air with several intermittent grindings. At the final stage, the powder was pelletized and sintered at 1373 K for 12 h and cooled slowly at the rate of 3 deg/min. The compound BLFMO was prepared using La₂O₃ preheated at 1223 K and final sintering was done at 1173 K for 12 h. Room temperature X-ray data were collected with a Bruker D8 Advance diffractometer. Neutron data were collected at various temperatures with the high resolution powder diffractometer D2B at ILL using wavelength of 1.594 Å. Rietveld refinements were carried out from the X-ray and neutron data using a software package Fullprof.¹⁷ Mössbauer spectra were recorded in transmission mode using ⁵⁷Coγ-ray source in a Rhodium matrix and multi-channel analyzer. The sample thickness was adjusted to obtain Fe content of ∼10 mg cm⁻². The calibrations for velocity and isomer shift were performed using iron (Fe) foil. Low temperature measurements were carried out using a helium closed-cycle cryo-cooler system attached to the sample chamber. The Mössbauer spectra were analyzed using SITE and DIST options in WinNormos-for-Igor software package. Magnetic studies were carried out by dc and ac susceptibility measurement in a physical property measurement system (PPMS, Quantum Design, USA).

3. Results and discussion

3.1 Crystal and magnetic structure

Indexing of room temperature powder X-ray data of BSFMO and BLFMO suggested a rhombohedral symmetry though earlier studies based on X-ray diffraction showed BLFMO to have an orthorhombic structure.¹⁶ We performed Rietveld refinements on the room temperature X-ray data with R3c and R3̄c space groups. A slightly better χ² and low values of estimated error in the refined parameters were obtained for the centrosymmetric space group R3̄c for both the compounds which is consistent with a previous report on BSFMO.¹⁸ The lattice parameters and the atomic positions obtained from X-ray data were used as initial parameters for the Rietveld refinement on the neutron data. The rhombohedral phase (R3̄c) in BSFMO persists over a wide temperature range (100 to 923 K) as confirmed from low and high temperature X-ray data (not shown).

The absence of super-lattice reflection in X-ray and neutron diffraction patterns suggests no A-site ordering between Bi and Sr cations or B-site ordering between Fe and Mn ions. A weak broad peak around 2θ∼20°, where there is no nuclear Bragg reflection, could be seen in neutron data at 300 K for both compounds which develops into a clear reflection with increased intensity at low temperatures as shown in Fig. 1 and 2. The presence of a broad peak at 300 K might be due to short range magnetic interactions of Fe³⁺/Mn⁴⁺ and Fe³⁺/Mn³⁺ ions in Sr and La substituted compounds, respectively. Our attempt to refine site occupancies of Bi³⁺ and Sr²⁺ ions gave unrealistic values with large errors which may be due to their close neutron scattering lengths. Further, Rietveld refinement on room temperature X-ray data showed site occupancies of Bi and Sr to be close to 1 : 1 ratio and therefore site occupancies of Bi and Sr (La) were fixed whereas the occupancies of Fe and Mn sites were refined and found to be stoichiometric. These facts are in accordance with energy-dispersive X-ray spectroscopy (EDX) data collected at various spots. Also, the refinement of oxygen occupancy does not deviate significantly from the stoichiometric value and therefore was kept fixed. Fig. 1b and 2b shows the Rietveld refinements on the neutron data for BSFMO and BLFMO collected at 90 K and 4 K, respectively. In Fig. 1b, the magnetic reflection near 2θ∼20° has been zoomed in for clarity. This reflection is rather weak which may be due to the fact that the data was collected at relatively higher temperature (90 K). The magnetic reflections in the low temperature neutron diffraction patterns (shown by arrows) were modelled by G-type antiferromagnetic coupling of disordered Fe/Mn moments aligned along the c-axis of the hexagonal lattice. Though the magnitudes of the magnetic moments associated with Fe³⁺ (S = 5/2) and Mn⁴⁺ or Mn³⁺ (S = 3/2 or S = 2) ions are different, due to the fact that these ions are distributed randomly, it is difficult to determine finite magnetization, if any, using thermal neutrons. The average magnetic moments of Fe/Mn in BSFMO (90 K) and BLFMO (4 K) are 1.11 (8) μ_B and 1.30 (3) μ_B respectively which are much lower than their respective theoretical values. Results from Rietveld refinement of neutron diffraction data have been summarized in Tables 1 and 2.

Fig. 1 Room temperature (a) and low temperature (90 K) (b) neutron diffraction pattern of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃. Closed symbols are the experimental points, solid line represents calculated pattern and the Bragg's positions are indicated by ticks. Solid line below the pattern shows the difference between the experimental and calculated patterns. Red arrow shows the magnetic reflection (1b). Magnetic reflection has been zoomed for clarity.

Fig. 2 Neutron diffraction pattern of Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ at (a) room temperature and (b) at 4 K.

Table 1 Lattice parameters, atomic positions and other parameters of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ and Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ obtained from Rietveld refinements of powder neutron (NPD) diffraction data at 300 K and low temperatures. Bi/Sr(La) occupy 6a (0,0,0.25) and Fe/Mn occupy 6b (0, 0, 0) positions whereas O takes the general position 18e (x, 0, 0.25)

Parameter		Bi0.5Sr0.5Fe0.5Mn0.5O3		Bi0.5La0.5Fe0.5Mn0.5O3
		300 K	90 K	300 K	4 K
a/Å		5.4817(2)	5.4810(1)	5.5275(1)	5.5206(1)
c/Å		13.4107(5)	13.4029(3)	13.5006(3)	13.4808(2)
O x		0.4693(2)	0.4652(2)	0.4537(3)	0.5462(2)
Biso	Bi/Sr(La)	2.05(5)	1.79(3)	2.27(5)	1.89(4)
	Fe/Mn	0.31(10)	0.10(70)	0.86(9)	0.20(6)
	O	1.59(3)	1.42(2)	2.19(4)	1.90(2)
χ2		3.99	6.80	8.36	9.61
Rp		25.4	16.4	24.4	21.7
Rwp		18.7	13.2	19.0	18.0
RB		7.01	5.06	11.0	9.90
Rf factor		6.76	4.69	9.50	7.49

---

Table 2 Selected bond lengths (Å) and bond angles (°) of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ and Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ at 300 K and low temperatures from neutron diffraction data

Parameter	Bi0.5Sr0.5Fe0.5Mn0.5O3		Bi0.5La0.5Fe0.5Mn0.5O3
	300 K	90 K	300 K	4 K
Bi/Sr(La)—O (Å)	2.909(1) × 3	2.931(1) × 3	2.508(2) × 3	2.506(1) × 3
	2.573(2) × 3	2.550(2) × 3	2.770(2) × 6	2.766(1) × 6
	2.744(8) × 6	2.744(1) × 6
Fe/Mn—O (Å)	1.945(1) × 6	1.946(2) × 6	1.969(1) × 6	1.966(1) × 6
Fe/Mn—O—Fe/Mn (°)	170.071(10) × 4	168.744(2) × 4	165.064(9) × 4	165.13(1) × 4

---

It is important to verify the valence state of the B-site cations as it plays a significant role in determining properties. In LaMnO₃, the valence state of the manganese ions depends on the synthesis conditions which determine stoichiometry of the compound.⁹ While the valence state of manganese in stoichiometric LaMnO₃ is +3, the cation and/or oxygen non-stoichiometry leads to a mixed valence of Mn³⁺/Mn⁴⁺.¹⁹ As discussed below, our Mössbauer study confirms that the Fe ions are present in trivalent state. The valence state of manganese in the present compound can indirectly be inferred from the inspection of average Fe/Mn–O bond lengths in BSFMO and BLFMO (Table 2). It can be noticed that the average Fe/Mn–O bond length in the former (1.945(1) Å) is smaller than that in the latter (1.969(1) Å). Since Fe ions are present in trivalent in both the compounds, the smaller average Fe/Mn–O bond length suggests that Mn ions are present in the tetravalent state in BSFMO and in the trivalent state in BLMFO.

To probe different magnetic interactions as well as to verify the iron valence in Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃, zero-field ⁵⁷Fe Mössbauer spectra were recorded at different temperatures as shown in Fig. 3(a)–(d). The spectrum at 300 K is fitted to a doublet and the obtained values of isomer shift, δ = 0.295 mm s⁻¹ and quadrupole shift, ε = 0.528 mm s⁻¹ confirms the presence of iron in Fe³⁺ state.²⁰ Low temperature spectra at 150, 80 and 10 K show six line patterns confirming the magnetic ordering. The hyperfine field is noticeably observed to increase for the spectra at and below 150 K. Due to the disorder of Fe³⁺ and Mn⁴⁺ ions at the B-site of the perovskite, the lines of Mössbauer spectra below the magnetic transition (T_N) become broader. This indicates the presence of several subspectra which can be ascribed to various environments around octahedral Fe³⁺ ions due to random distribution of Mn⁴⁺ ions. Since the hyperfine parameters, namely, hyperfine field B_hf, isomer shift δ and quadrupole shift ε of these subspectra are not known a priori, we have fitted the Mössbauer spectra to a model based on a random distribution of Fe and Mn ions on the octahedral sites. The probability of an octahedral site having n nearest-neighbour Mn atoms was calculated using the binomial formula,^21,22

where, x is the Mn concentration and n is the number of Mn ions among the nearest-neighbour Fe³⁺ ions that have a hyperfine field B_hf. The hyperfine fields for locally different magnetically ordered octahedral Fe sites are assumed to obey the relationship B_hf = B₀ – n ΔB_hf, where B₀ is the hyperfine field at Fe³⁺ ion that has no Mn⁴⁺ site neighbour and ΔB_hf is the decrease in the hyperfine field as a result of replacing Fe³⁺ by Mn⁴⁺. The relative intensity P(n, x) of the different hyperfine field patterns is fixed as decided by eqn 1. The P(n, x) values for x = 0.5 are found to be 0.015, 0.094, 0.234, 0.312, 0.234, 0.094 and 0.015 with (6–n) nearest Fe ions and n nearest Mn ion respectively. Typically the relative contributions more than 5% are considered during the analysis of the Mössbauer spectra.²² Very low value of the probability P(n, x) for n = 0 allows us to assume B₀ to be the hyperfine field at Fe³⁺ ion with 5 Fe and 1 Mn ions. As the spectra at 10 and 80 K are magnetically ordered relative to the spectrum at 150 K, the Mössbauer spectral lines could be constrained to fit in the ratio 3 : 2 : 1 : 1 : 2 : 3.²³ For each of the spectrum at 10 and 80 K, the values of isomer shift δ, quadrupole shift ε, hyperfine field B_hf and line width ω were first fitted for each subspectrum. In the final fits, the hyperfine field values are fixed by optimizing the B₀ and ΔB_hf to obey the above mentioned relation. In Fig. 3, the fits to the experimental data are plotted as lines over the open symbols whereas the different sub sextets corresponding to different environments around octahedral Fe site are also shown. The values of B₀ and ΔB_hf at 10 K are found to be 516 and 10 kOe respectively and obey the relation between B₀ and ΔB_hf whereas for 80 and 150 K these are found to deviate from this relation. In addition to the environmental effects around ferric ions, the broadening of the Mössbauer spectral lines at 80 and 150 K (more significant) may also arise due to the glassy behaviour as will be discussed in subsequent sections.²⁴

Fig. 3 (a)–(d) Mössbauer spectra of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ collected at 10, 80, 150 and 300 K. Solid lines over the open symbols are fits to the experimental data and sub sextets corresponding to different environments around octahedral Fe site are also shown as lines. (e) Distribution of hyperfine fields indicating the enhancement of Fe–Mn interactions with lowering the temperature.

To understand the behaviour of the magnetic interactions, the Mössbauer spectra at 10, 80 and 150 K were analyzed by a distribution of hyperfine field.²⁵ The hyperfine field was varied in a smooth way over a certain range of values to reproduce the observed Mössbauer spectra. In the present analysis, individual Mössbauer spectra (each consisting of six Lorentzian-shaped lines) were calculated at discrete B_hf values (10 kOe apart) along the abscissas of the P(B_hf)versus B_hf curves and added to form a resultant pattern for comparison with the experimental Mössbauer spectrum. Fig. 3(e) shows the temperature dependence of hyperfine field distribution P(B_hf). As the temperature is lowered, a decrease in the broadening of distribution pattern below the Néel temperature indicates enhancement in the strength of the exchange interactions between Fe and Mn ions.

3.2 Magnetic properties

DC magnetization data of the compound BSFMO were collected in zero field cooled (ZFC) and field cooled (FC) modes. In ZFC mode, the sample was cooled in absence of magnetic field whereas a field was applied while cooling in the FC mode and data were recorded while warming up in both the cases. The ZFC–FC data under a magnetic field of 100 Oe is shown in Fig. 4. Three anomalies are observed at 30, 114 and 226 K in the ZFC data. The antiferromagnetic ordering of Fe³⁺ and Mn⁴⁺ takes place below T_N = 226 K. In should be mentioned here that the magnetic properties are highly dependent on the sample preparation. In the present case, the cooling rate at the final stage of sintering was 3°/min and when this rate changed to higher or lower value, a short range magnetic ordering is observed above T_N similar to a previous report.¹⁸ As can be seen from the figure, ZFC–FC shows a large irreversibility which might indicate a glassy state below T_N. Moreover, as the field is increased, the anomalies below T_N shift towards lower temperature. At very high field (20 kOe), low temperature anomalies smear out and only the anomaly at T_N is observed (not shown). This is further indication of glassy state and when such a high field is applied, all the moments could orient along the field direction consistent with the disappearance of low temperature anomalies in the ZFC data. Above T_N, the magnetic susceptibility (100 Oe) follows the Curie–Weiss law and the fit resulted Weiss constant θ = 120 K and effective paramagnetic moment μ_eff = 4.68 μ_B. The positive Weiss constant reflects that the interaction between Fe³⁺ and Mn⁴⁺ is weakly ferromagnetic. The calculated magnetic moment is slightly higher than the theoretical spin only value of 4.42 μ_B for Fe³⁺–Mn⁴⁺ configuration. It is important to mention at this point is that the magnetic properties of BSFMO is highly dependent on the cooling rate at the final sintering. The samples cooled at the rate of 1 and 5 deg/min showed presence of short range ordering and does not follow Curie–Weiss behavior above T_N. The ZFC–FC curve at 100 Oe for Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ shows that the system orders antiferromagnetically at 220 K (inset in Fig. 4) which is consistent with an earlier report.¹⁶

Fig. 4 ZFC–FC curves under magnetic field of 100 Oe for Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ showing magnetic anomalies at 30, 114 and 226 K. Inset shows ZFC–FC curves for Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ at 50 Oe.

Magnetic isotherms of BSFMO recorded at different temperatures are shown in Fig. 5. At 5 K, the curve is slanted S-shaped with small coercive field of 400 Oe. At lower fields, the shape of the isotherm is related to the glassiness and is similar to that of observed similar compounds. At high fields, the curve shape changes to that of antiferromagnetic systems. This indicates that at high field the glassy feature disappears as all the frozen moments are forced to align towards the applied field. At 75 K, the isotherm shape changes with a higher coercive field value of 700 Oe which indicates a weak ferromagnetic behavior arising due to the canting of antiferromagnetic spins. The difference in the shape is related to the weak anomaly at 30 K in the ZFC data. At room temperature, a linear hysteresis curve is observed confirming the paramagnetic state. Magnetic isotherm (not shown) of Bi_0.5La_0.5Fe_0.5Mn_0.5O₃ at low temperature (at 5 K) shows weak ferromagnetic behavior which does not saturate but has a much higher coercive field (3100 Oe) than that of the Sr doped compound (400 Oe).

Fig. 5 Magnetic isotherms of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ at 5, 75, 150 and 300 K.

In order to understand the nature of magnetic interactions associated with three anomalies in BSFMO, we have performed ac susceptibility measurements and the results are shown in Fig. 6. Weak frequency dependence in the anomaly of real part of the ac susceptibility χ′ is observed in the vicinity of 40 and 105 K. The peak positions shift to higher temperature with increasing frequency. The imaginary part, χ′′ on the other hand, shows frequency dependent peaks near the magnetic anomalies. At the Néel temperature, χ′′ shows sharp peak which are frequency independent. These features along with the dc magnetization and Mössbauer data confirm the glassy nature of this system in which the competing magnetic interactions are present below a characteristic temperature. As the glassy state occurs below T_N, it can either be associated with a reentrant spin glass (RSG) or with a cluster glass (CG) behavior.^26,27 In a RSG, where the glassy nature persists into a long range ferromagnetic or antiferromagnetic order, the magnetic anomaly lies well below the paramagnetic to ferromagnetic/antiferromagnetic transition temperature. On the other hand, in a CG, where a set of clusters shows short range ordering below a characteristic temperature, a strong irreversibility in the ZFC–FC curves is observed below the magnetic ordering temperature. In the present case, the ZFC–FC in dc magnetization data shows a large irreversibility starting below the Néel temperature and also frequency dependent anomalies in χ′ lie closer to the Néel temperature which confirms the cluster glass phenomenon. The peak shift in the low temperature anomaly near 40 K is not very clear with frequency which is due to broad anomalies and existence of cluster glass state above this temperature. As both dc and ac magnetic measurements suggest that the anomaly near 40 K does not represent a long range magnetic ordering, this is assigned to a spin glass effect similar to that of Bi_0.5La_0.5Fe_0.5Mn_0.5O₃.¹⁶ Glassy features in a magnetic system results from the competing magnetic interactions due to disorder arrangement of magnetic ions or geometric frustration. In the present compound, three superexchange interactions between Fe and Mn ions exist, Fe³⁺–O–Fe³⁺, Fe³⁺–O–Mn⁴⁺ and Mn⁴⁺–O–Mn⁴⁺. According to the Goodenough–Kanamori rules, coupling of Fe–O–Fe and Mn–O–Mn superexchange interactions are antiferromagnetic whereas Fe–O–Mn is ferromagnetic. Thus the glassy nature might be arising due to the competing magnetic interactions due to the disordered magnetic ions in the same crystallographic site. It should be noted that, spin glass and/or cluster glass effect, induced by disorder is well known in doped manganites.^4,5,28 The glassy state in Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ is far more complex than in the La doped compound due to difference in sizes between the magnetic ions, Fe³⁺/Mn³⁺ and Fe³⁺/Mn⁴⁺ ions, which further increases disorder. Also, the possibility of oxygen non-stoichiometry in the compound though small, cannot be neglected which can lead to the presence of Mn³⁺ ions and contribute to the complex glassy nature. Thus our Mössbauer and magnetic studies suggest that the title compound BSFMO orders antiferromagnetically at 226 K and below the Néel temperature, the random and competing magnetic interactions lead to freezing of local magnetic moment of the clusters in random orientations which finally leads to a spin glass state at low temperature.

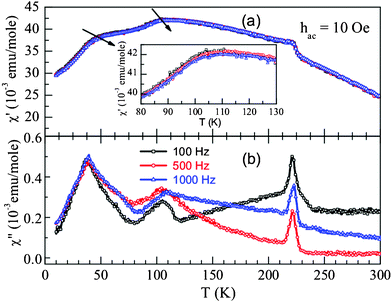Fig. 6 Ac susceptibility data of Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ plotted against temperature for different frequencies.

4. Conclusion

(Bi_0.5Sr_0.5)(Fe_0.5Mn_0.5)O₃ and (Bi_0.5La_0.5)(Fe_0.5Mn_0.5)O₃ crystallizes in the rhombohedral structure (space group R3̄c) where the cations are disordered at the A and B sites. Bi_0.5Sr_0.5Fe_0.5Mn_0.5O₃ shows an antiferromagnetic ordering of Fe³⁺ and Mn⁴⁺ below 226 K and a cluster glass and spin-glass states at low temperatures. The complex magnetic behavior in this compound is induced by the cation disorder.

Acknowledgements

Authors acknowledge Ms. N. R. Selvi for FESEM and EDAX measurements. Financial support from the DST-JST project under Indo-Japan exchange program is acknowledged.

References

1. Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides World Scientific, Singapore, 1998.
2. A. Urushibara, Y. Moritomo, T. Arima, A. Asamitsu, G. Kido and Y. Tokura, Phys. Rev. B: Condens. Matter, 1995, 51, 14103.
3. M. M. Xavier, F. A. O. Cabral, J. H. de Ara·jo, C. Chesman and T. Dumelow, Phys. Rev. B: Condens. Matter, 2000, 63, 012408.
4. J. Dho, W. S. Kim and N. H. Hur, Phys. Rev. Lett., 2002, 89, 027202.
5. J. W. Cai, C. Wang, B. G. Shen, J. G. Zhao and W. S. Zhan, Appl. Phys. Lett., 1997, 71, 1727.
6. R. D.Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
7. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
8. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87.
9. E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545.
10. A. Moreira dos Santos, A. K. Cheetham, T. Atou, Y. Syono, Y. Yamaguchi, K. Ohoyama, H. Chiba and C. N. R. Rao, Phys. Rev. B: Condens. Matter, 2002, 66, 064425.
11. R. Seshadri and N. A. Hill, Chem. Mater., 2001, 13, 2892.
12. G. A. Smolenskii and I. E. Chupis, Sov. Phys. Usp., 1982, 25, 475.
13. P. Mandal, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 100416.
14. L. Ortega-San Martin, A. J. Williams, A. Storer and J. P. Attfield, Chem. Mater., 2009, 21, 2436.
15. M. Hervieu, A. Maignan, C. Martin, N. Nguyen and B. Raveau, Chem. Mater., 2001, 13, 1356.
16. A. K. Kundu, R. Ranjith, B. Kundys, N. Nguyen, V. Caignaert, V. Pralong, W. Prellier and B. Raveau, Appl. Phys. Lett., 2008, 93, 052906.
17. J. Rodríguez-Carvajal, Abstracts of the Satellite Meeting on Powder Diffraction of the XV IUCr CongressToulouse, France, 1990, p. 127.
18. I. O. Troyanchuk, D. V. Karpinskii, M. V. Bushinskii, A. N. Chobot, N. V. Pushkarev, O. Prohnenko, M. Kopcewicz and R. Szymczak, Crystallogr. Rep., 2009, 54, 1172.
19. L. Ghivelder, I. Abrego Castillo, M. A. Gusmao, J. A. Alonso and L. F. Cohen, Phys. Rev. B: Condens. Matter, 1999, 60, 12184.
20. P. Gütlich, E. Bill and A. X. Trautwein, Mössbauer spectroscopy and transition metal chemistry: Fundamentals and Applications (Springer, Heidelberg, Germany, 2011).
21. W. C. Kim, S. I. Park, S. J. Kim, S. W. Lee and C. S. Kim, J. Appl. Phys., 2000, 87, 6241.
22. W. Kim, B. Kum and C. Kim, J. Supercond. Novel Magn., 2011, 24, 867.
23. V. R. Reddy, D. Kothari, A. Gupta and S. M. Gupta, Appl. Phys. Lett., 2009, 8, 082505.
24. S. Nakamura, M. Sato, S. Morimoto, S. Nasu and Y. Tsunoda, Hyperfine Interact., 2006, 169, 1235.
25. J. Hesse, J. B. Müller and B. Wiechmann, J. Phys. Colloq., 1979, 40, C2.
26. J. A. Mydosh, Spin glasses: an experimental introduction (Taylor & Francis, Washington, D.C., 1993).
27. S. Mukherjee, R. Ranganathan, P. S. Anilkumar and P. A. Joy, Phys. Rev. B: Condens. Matter, 1996, 54, 9267.
28. K. F. Wang, Y. Wang, L. F. Wang, S. Dong, D. Li, Z. D. Zhang, H. Yu, Q. C. Li and J. M. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 134411.

---