Adsorption of hazardous dyes indigo carmine and acid red on nanofiber membranes
Minxia
Li
abc,
Hongtao
Wang
abc,
Shengju
Wu
ab,
Fengting
Li
*abc and
Pengdan
Zhi
abc
aState Key Laboratory of Pollution Control and Resources Reuse, Tongji University, Shanghai, 200092, China
bCollege of Environmental Science and Engineering, Tongji University, Shanghai, 200092, China
cUNEP-Tongji Institute of Environment for Sustainable Development, Tongji University, Shanghai, China 200092. E-mail: fengting@tongji.edu.cn (F. Li); Tel: +86 21 65983302; Fax: +86 21 65983121
First published on 29th November 2011
Abstract
Through an electrospinning process, thiol-functionalized polyvinyl alcohol (PVA)/SiO2 composite nanofiber membranes were synthesized as adsorbents. The adsorption of indigo carmine and acid red onto the nanofiber membranes was investigated. The effect of contact time, initial concentration, pH, dosage, temperature, the adsorption equilibrium and thermodynamic parameters were studied. The adsorption equilibrium was reached within 20 min. The initial concentration, pH and the temperature played important roles on the adsorption capacity onto the nanofiber membranes. Increase of the initial concentration could effectively increase the adsorption capacity. The best adsorption pH was 2 for indigo carmine and acid red. Higher temperatures were favourable for the adsorption. The maximum indigo carmine adsorption capacity was 266.77 mg g−1 for 500 mg L−1 indigo carmine and 211.74 mg g−1 for 315 mg L−1 acid red at pH 2 and 25 °C. The adsorption isotherm studies showed that the adsorption of the two dyes fitted well with Langmuir, Freundlich, and Redlich–Peterson adsorption models, while the Redlich-Peterson model achieved the best results. The kinetic adsorption shows that the pseudo-second-order model fits the adsorption process of indigo carmine while the pseudo-first-order model fits the adsorption process of acid red.
Introduction
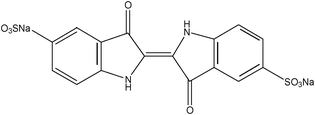
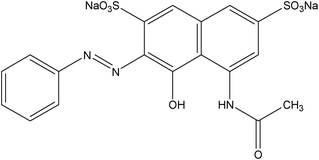
Dyes are widely used in many industries such as dyestuffs, textile, cosmetics, leather, plastic and paper. Very small amounts of dyes in water are highly visible, undesirable and even harmful to mankind.1–3 Indigo carmine is considered to be a highly toxic dye and the exposure can cause skin and eye irritations to human being.4 Acid red is a typical dye which contains nitrogen atoms with azo functional groups [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–] in its chemical structure.3
N–] in its chemical structure.3
With complex molecular structures, dyes are resistant to aerobic digestion and are stable to oxidizing agents, so they are very recalcitrant and difficult to be removed and degraded.1–5
Currently, there are many methods to remove these dyes from polluted water, such as sedimentation, coagulation, flocculation, chemical treatments, oxidation, electrochemical methodology, photodecomposition, biological treatments, adsorption, and membrane process.1–3 Adsorption techniques have found many practical applications for the separation and purification of liquid and gaseous mixtures in the chemical, biological, pharmaceutical, environmental, and electronics industries.6,7 Mesoporous nanofibers can remove different types of coloring materials, providing an attractive treatment5 and the functionalized mesoporous materials have been regarded as effective adsorbents6–15 because of their high surface area, large-diameter, large-volume of functionalized pore channels and their narrow pore size distribution. Our research group has successfully synthesized the thiol-functionalized PVA/SiO2 mesoporous composite nanofiber membranes and used them for the adsorption of heavy metal ions from water successfully.16–18 However, there is very little research on the use of thiol-functionalized PVA/SiO2 nanofibers membranes to remove dyes from water.
In this study, mercapto group functionalized PVA/SiO2 mesoporous composite nanofiber membranes were synthesized as an adsorbent. And then the adsorption performance of indigo carmine and acid red onto the membranes was systemically investigated for the effect of contact time, initial concentration, pH, the adsorption equilibrium, thermodynamic parameters, adsorption isotherms, kinetics, and the adsorption mechanisms. The results showed that the adsorption of indigo carmine and acid red onto PVA/SiO2 mesoporous composite nanofiber membranes has some advantages such as high adsorption capacity and short adsorption time.1,2,4,5
Materials and methods
Reagents and materials
Hydrochloric acid and tetraethyl orthosilicate silicate (TEOS) were purchased from Shanghai Chemical Reagent Factory; polyvinyl alcohol 1750 (PVA), cetyltrimethylammonium bromide (CTAB), nitric acid, potassium hydroxide and ethanol were purchased from Sinopharm Chemical Regent Co.Ltd., 3-mercaptopropyltrimethoxysilane (MPTMS,KH-590) was purchased from Jiangsu Jintan Organic Chemical Plants; distilled water was used throughout this work.The structure of indigo carmine and acid red is shown in Table 1.
Instruments
Electronic Analytical Balance (FA2004, Shanghai Jingke Balance Factory) was used to weigh chemicals; a temperature magnetic stirrer (85–2, Shanghai Siyue Instrument Factory) and electric-heated thermostatic water bath (HWS24, Shanghai Scientific Instrument Co., Ltd.) were adapted to mix solutions under different temperatures; a vacuum oven (DZF-6020, Test Equipment Co., Ltd. Shanghai Jing Hong) was used to dry fibers; FTIR spectra (Nicolet 7199, Nicolet Co., Ltd., U.S.A) , SEM (XL-30E, Philips Co., Ltd., Netherland), specific surface area and pore size distribution analyzer (Tristar 3000, Micromeritics Co., Ltd., U.S.A), TEM (JEM-2011, Japan Electronics Co., Ltd.) were used to characterize the PVA/SiO2 nanofiber membranes synthesized through electrospinning technology; precision pH meter (PHS-3C, Shanghai Lei Magnetic Co., Ltd.) was used to adjust the pH of solutions. A constant temperature shaker (DHZ-D, Experimental Equipment Factory, Jiangsu Taicang) was used to perform the adsorption experiment and a UV-Vis spectrophotometer (UV1700, Shimadzu Corporation, Japan) was used to measure the concentration of dyes before and after adsorption.Synthesis of the PVA/SiO2 mesoporous adsorbents
The PVA/SiO2 nanofibers were synthesized using electrospinning technology following the method in our previous study.16–18 First, 2.19 g cetyltrimethylammonium bromide (CTAB) was dissolved in 7.37 g ethanol and vigorously stirred for 0.5 h at 60 °C. Second, 8.64 g distilled water and 1.54 g 3-mercaptopropyltrimethoxysilane (MPTMS) were added, mixed and further stirred for 0.5 h at 60 °C. Then, 6.64 g tetraethyl orthosilicate silicate (TEOS) was slowly added into the solution mixture. Finally, 0.8 mL 2 mol L−1HCl was dropped into the mixture and a silica gel was obtained after reacting for 2 h at 60 °C. 10.0 g of 10 wt.% PVA solution was dropped slowly into the silica gel, and then the reaction proceeded in a water bath at 60 °C for another 4 h. Then the solution was added to a 50 mL syringe with a needle diameter of 1.2 mm, under a voltage of 15 kV and a speed of 0.3 ml h−1. The distance between the needle and the receiving polar was 20 cm and the temperature for the electrospinning was 25 °C. Thus the fibers were collected and dried initially for 12 h at 60 °C under vacuum. Then the electrospun PVA/SiO2 fibers were refluxed in ethanol/HCl (molar ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for 12 h at 70 °C to remove the template and dried for 6 h at 60 °C under vacuum.17,18,20
1) for 12 h at 70 °C to remove the template and dried for 6 h at 60 °C under vacuum.17,18,20
Adsorption study
Results and discussion
Characterization of adsorbents
The adsorbent was characterized by FTIR to ascertain the modification of –SH. The FTIR patterns present similar location and appearance of the major bands in Fig. 1. | ||
| Fig. 1 FTIR spectrum of PVA/SiO2 nanofibers. | ||
From Fig. 1, we can see that the characteristic bands for the mercapto group vibrational peak appear around 2560.0 cm−1, which means that the mercapto group has been successfully modified to the surface of PVA/SiO2 nano-fiber membranes through hydrolysis and condensation reactions.19,20 In Fig. 1, the peaks of VC–H (2920.8, 2847.2 cm−1), VC–OH (1617.1 and 591.3 cm−1), VSi–O–H (3420.3, 1637.5 and 955.0 cm−1) and VSi–O–Si (1069.4, 791.5 and 456.4 cm−1) are observed.19,20
SEM and TEM images of PVA/SiO2 nanofibers were depicted in Fig. 2a and Fig. 2b. From Fig. 2a, it is indicated that the diameter of the nanofibers is around 300 nm to 500 nm. The surface of the fiber was rough with a porous structure. Fig. 2b shows that the PVA/SiO2 nano-fiber surface has a mesoporous structure with smaller diameter and irregular pores.
The surface area and the average pore diameter of the nanofibers was 140.1 m2 g−1 and 6.34 nm, respectively, as mentioned in our previously published paper.18
Dyes adsorption
 | ||
| Fig. 3 Adsorption isothermal curve of indigo carmine (a) and acid red (b) onto PVA/SiO2 nanofibers. | ||
From Fig. 3, it can be seen that the equilibrium adsorption amount qe increased with increasing initial concentration of dye solutions. Some references7,21 indicated that when the test temperature was within 60 °C, the equilibrium adsorption amount qe increases with increasing temperature. The mesoporous nanofibers shows similar adsorbent behavior. The qe–ce curve ascends as temperature increased, indicating that the adsorption of indigo carmine and acid red was endothermic. It was also found that the qe of indigo carmine was higher than that of acid red.
Three adsorption models (Langmuir, Freundlich and Redlich–Peterson) were used to estimate the adsorption isotherm. Fig. 4 shows the non-line fitting adsorption isothermal curve of indigo carmine and acid red onto PVA/SiO2 nanofibers at 298.15 K.
 | ||
| Fig. 4 Non-linear fitting adsorption isothermal curve of indigo carmine (a) and acid red (b) onto PVA/SiO2 nanofibers at 298.15 K. | ||
Three nonlinear models (eqn (1) to eqn (5)) were used to estimate the adsorption capacity and its adsorption behavior.
(1) Langmuir equation22,23

| (1) |
In eqn (1),

| (2) |
The Langmuir equilibrium coefficient, RL, can be obtained by the following equation:

| (3) |
(2) Freundlich model:24,25

| (4) |
(3) Redlich–Peterson model:26
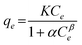 | (5) |
The isotherm equations and the fitting parameters of indigo carmine and acid red adsorption behavior onto adsorbent are depicted in Table 2–4.
| Dyes | T/K | Fitting parameters | |||
|---|---|---|---|---|---|
| b | Q | R 2 | RL | ||
| Indigo carmine | 288.15 | 258.581 | 0.67183 | 0.94962 | 0.00371 |
| 298.15 | 246.889 | 0.69845 | 0.94795 | 0.00418 | |
| 308.15 | 237.628 | 0.71236 | 0.94775 | 0.00438 | |
| 318.15 | 225.919 | 0.72925 | 0.94214 | 0.00512 | |
| Acid red | 288.15 | 86.7496 | 0.44597 | 0.92362 | 0.00288 |
| 298.15 | 81.7259 | 0.48198 | 0.92994 | 0.00311 | |
| 308.15 | 74.9700 | 0.52236 | 0.93802 | 0.00327 | |
| 318.15 | 71.8572 | 0.53537 | 0.94067 | 0.0033 | |
| Dyes | T/K | Fitting parameters | ||
|---|---|---|---|---|
| K | 1/n | R 2 | ||
| Indigo carmine | 288.15 | 1.05121 | 0.22499 | 0.95180 |
| 298.15 | 1.09825 | 0.22885 | 0.95212 | |
| 308.15 | 1.12523 | 0.23209 | 0.95664 | |
| 318.15 | 1.16031 | 0.23676 | 0.95952 | |
| Acid red | 288.15 | 0.60712 | 0.2737 | 0.89305 |
| 298.15 | 0.65712 | 0.27843 | 0.89783 | |
| 308.15 | 0.71407 | 0.28578 | 0.90372 | |
| 318.15 | 0.73184 | 0.28858 | 0.90573 | |
| Dyes | T/K | Fitting parameters | |||
|---|---|---|---|---|---|
| K | α | β | R 2 | ||
| Indigo carmine | 288.15 | 457.7047 | 508.2102 | 0.8568 | 0.98866 |
| 298.15 | 450.4240 | 478.8218 | 0.8539 | 0.98739 | |
| 308.15 | 461.4297 | 476.0791 | 0.8481 | 0.98936 | |
| 318.15 | 487.0656 | 482.3442 | 0.8384 | 0.98842 | |
| Acid red | 288.15 | 53.0577 | 104.8769 | 0.8998 | 0.9366 |
| 298.15 | 53.91888 | 98.90265 | 0.9006 | 0.94197 | |
| 308.15 | 53.41228 | 90.71756 | 0.9014 | 0.9489 | |
| 318.15 | 52.67624 | 87.43388 | 0.9013 | 0.95113 | |
As can be seen from Table 2 to Table 4, the fitting results of three isothermal models for the adsorption of indigo carmine are as follows: Redlich–Peterson > Freundlich > Langmuir, while the fitting results of the adsorption of acid red followed: Redlich–Peterson > Langmuir > Freundlich.
The Redlich–Peterson isotherm incorporates the features of the Langmuir and the Freundlich isotherms.26 The Redlich–Peterson model contains a description of the non-uniform adsorption, the R2 value is higher than the Langmuir model, indicating that the mesoporous adsorbent adsorption of indigo carmine and acid red were not ideal for monolayer adsorption. The adsorption sites and surface pores exhibit heterogeneity. From Table 4, the value of β was near to 1, indicating that the mesoporous adsorbent adsorption of indigo carmine and acid red is dominated by monolayer chemical adsorption. When the Freundlich adsorption model index 1/n is between 0.1–0.5 it means dyes were easily absorbed. If the value is above 2, it means that the adsorption was difficult to carry out. Here, 1/n for indigo carmine and acid red was between 0.1 to 0.5, indicating that the adsorption process occurred easily.
 | ||
| Fig. 5 Effect of pH on the adsorption of indigo carmine (a) and acid red (b) onto PVA/SiO2 nanofibers. | ||
It can be seen from Fig. 5 that the adsorption capacity of the mesoporous adsorbent is at its minimum near neutral conditions. From pH 2 to 6, the adsorption capacity decreased slightly for the two types of dyes.
There are many factors that may influence the adsorption of the dye such as surface charge and structure of the dye, adsorbent surface properties, hydrophobic and hydrophilic nature, hydrogen bonding, electrostatic interaction, steric effect, van der Waals forces, and so forth.27 Here, the mechanisms for indigo carmine and acid red adsorption include electrostatic interaction and the hydrophobic–hydrophobic interaction between dyes and the adsorbent. Through fitting three isothermal models, we can see that the adsorption was dominated by monolayer chemical adsorption. From Fig. 5 we can see that the adsorption capacity increases at lower pH (although not significantly), which indicated that the electrostatic interaction is not the dominant factor for adsorption. The main mechanism for adsorption was the hydrophobic–hydrophobic interaction between dyes and the adsorbent.
Under acidic conditions, the modified –SH and the –OH on the surface of the adsorbent can be protonated with H+ to produce –SH2+ and –OH2+. Meanwhile, the sulfonate groups of the dye (D–SO3Na) reacted with the H+, producing pigment acid (D–SO3H). The pigment acid and –SH2+ combined through chemical bonding. After reaction with –SH2+via chemical bonding, the sulfonic acid group becomes less hydrophilic, which results in decolorization. The protonated and pigment process were hindered at neutral conditions because of very low H+ concentration, so the value of qe was low. The electrostatic mechanism for the decolorization of indigo carmine and acid red onto the mesoporous adsorbents is shown in Fig. 6 (D in the dye molecular stands for the rest of the dye structure).
 | ||
| Fig. 6 Electrostatic mechanism of adsorption of dyes onto mercapto groups. | ||
Meanwhile, another important factor leading to the adsorption of dyes is the hydrogen bond interaction between dyes and the membrane. Hydrophobic–hydrophobic interactions exist between the hydrophobic part of the dye molecule and the hydrophobic regions of the adsorbent.28 The amine, imine, and hydroxyl groups of the adsorbent form hydrogen bonds with the azo, hydroxyl, and amine groups of dyes, as shown in Fig. 7.
 | ||
| Fig. 7 Hydrogen bonding mechanism of dye adsorption onto mercapto groups ((a) indigo carmine (b) acid red). | ||
 | ||
| Fig. 8 Effect of dosage on the adsorption of indigo carmine and acid red onto mesoporous adsorbent | ||
It can be seen from Fig. 8 that the adsorption capacity increased with increasing adsorbent dosage. For indigo carmine, the adsorption increased slightly in the range of 1 to 2 mg mL−1, and the increase of adsorption amount is almost the same with further increase in the adsorbent dosage. For acid red, the increase trend was great from 1 to 3 mg mL−1, but the increase trend was not obvious with further increase of the adsorbent dosage. The adsorbed amount increased with the increasing adsorbent dosage, due to the increased number of adsorption sites when increasing the adsorbent dosage. With a further increase in adsorbent dosage, the adsorbed amount was almost constant. This was due to a less commensurate increase in adsorption resulting from the lower adsorptive capacity utilization of the adsorbent with the increasing adsorbent;29–31 the increase of the adsorbent led to the overlap or accumulation of adsorption sites, resulting in the increase of diffusion path.32
In consideration of the long process for the synthesis of adsorbent, we choose 1 mg mL−1 as the optimum dosage of adsorbent in this study.
 | ||
| Fig. 9 Non-linear fitting adsorption kinetics curves of indigo carmine (a) and acid red (b) onto PVA/SiO2 nanofibers at different temperatures. | ||
Fig. 9 shows the adsorption process of indigo carmine and acid red under the temperatures of 288.15 K, 298.15 K, 308.15 K and 318.15 K. At the initial stage of the adsorption (0–20 min), the concentration of indigo carmine and acid red decreased quickly, and the decreasing rate of this phase was the maximum in the whole adsorption process; with the adsorption time going on (20–40 min), the adsorption amount was gradually increased. The concentration of indigo carmine and acid red decreased and the adsorption rate changed relatively slowly, while the adsorption reached equilibrium after 40 min. When the adsorption time was more than 60 min, the change of Ct/C0 was very small. The contact time of 60 min was determined as the ideal contact time for the adsorption of indigo carmine and acid red onto the mesoporous adsorbent.
The pseudo-first-order and pseudo-second-order kinetic models are commonly used to estimate the rate constants, initial adsorption rates and adsorption capacities of an adsorbent for some adsorbates.20
Pseudo-first-order model:33
 | (6) |

| (7) |
The fitting kinetic model parameters are listed in Table 5 and Table 6.
| Dyes | Temperature | Fitting parameters | q e | ||
|---|---|---|---|---|---|
| (K) | qe | k 1 | R 2 | Experimental data | |
| Indigo carmine | 288.15 | 0.59521 | 0.19621 | 0.98265 | 0.5755814 |
| 298.15 | 0.64867 | 0.19294 | 0.98947 | 0.5922176 | |
| 308.15 | 0.67649 | 0.18044 | 0.99119 | 0.6063276 | |
| 318.15 | 0.70626 | 0.20265 | 0.97813 | 0.6134442 | |
| Acid red | 288.15 | 0.37664 | 0.13497 | 0.993345 | 0.380523 |
| 298.15 | 0.39369 | 0.15254 | 0.99154 | 0.419616 | |
| 308.15 | 0.41405 | 0.19866 | 0.99108 | 0.450067 | |
| 318.15 | 0.4233 | 0.23929 | 0.99564 | 0.464963 | |
| Dyes | Temperature | Fitting parameters | qe | ||
|---|---|---|---|---|---|
| (K) | qe | k 2 | R 2 | Experimental data | |
| Indigo carmine | 288.15 | 0.63929 | 0.52823 | 0.99908 | 0.6894469 |
| 298.15 | 0.69563 | 0.48362 | 0.99832 | 0.7185602 | |
| 308.15 | 0.72618 | 0.4326 | 0.99746 | 0.7199108 | |
| 318.15 | 0.75548 | 0.47872 | 0.99737 | 0.7373222 | |
| Acid red | 288.15 | 0.40924 | 0.53189 | 0.97894 | 0.380523 |
| 298.15 | 0.42414 | 0.61432 | 0.98533 | 0.419616 | |
| 308.15 | 0.44137 | 0.82737 | 0.99647 | 0.450067 | |
| 318.15 | 0.44664 | 1.07529 | 0.99784 | 0.464963 | |
Table 5 and Table 6 indicate that the pseudo-second-order model fitted the adsorption process of indigo carmine and the pseudo-first-order model fitted the adsorption process of acid red. The value of qe and k showed that the adsorption amount of dyes increased with increasing temperature. The experimental data fitted well to the kinetic models. The value of qe obtained by the pseudo-first-order model was near the experimental qe of the same initial concentrations, while the qe obtained by the pseudo-second-order model better fitted to the experimental value of qe, slightly lower than the experimental value.
Conclusions
Based on this study, it can be concluded that the adsorption of indigo carmine and acid red onto the PVA/SiO2 nanofibers are affected by many factors such as the initial concentration of dyes, pH, dosage of the adsorbent, temperature and contact time. Increasing in the initial concentration could effectively promote the adsorption capacity. The lower the pH, the higher the adsorption capacity for indigo carmine and acid red. Increase in the temperature and the dosage of the adsorbent could effectively enhance the adsorption. The adsorption isotherm studies showed that the adsorption of the two dyes fitted well with Langmuir, Freundlich, and Redlich–Peterson adsorption models, while the Redlich–Peterson model achieved the best fitting. The result of kinetic adsorption shows that the pseudo-second-order model fits the adsorption process of indigo carmine while the pseudo-first-order model fits the adsorption process of acid red.Acknowledgements
This work was supported in part by the China International Science and Technology Cooperation Fund No.2010DFA92800, 2010DFA92820. The research was also partially supported by the National Natural Science Foundation of China No.51108328.References
- G. S. Prado Alexandre, D. Torres Jocilene, A. Faria Elaine and C.L. Dias Silvia, J. Colloid Interface Sci., 2004, 277, 43–47 CrossRef.
- Hasine Kasgoz, Colloids Surf., A, 2005, 266, 44–50 CrossRef.
- L. Donnaperna, L. Duclaux, R. Gadiou, M.-P. Hirn, C. Merli and L. Pietrelli, J. Colloid Interface Sci., 2009, 339, 275–284 CrossRef CAS.
- Alok Mittal, Jyoti Mittal and Lisha Kurup, J. Hazard. Mater., 2006, 137, 591–602 CrossRef CAS.
- Suzana Modesto de Oliveira Brito, Heloysa Martins Carvalho Andrade and Luciana FortaSoares, J. Hazard. Mater., 2010, 174, 84–92 CrossRef CAS.
- R. Cestari Antonio, F. S. Vieira Eunice, S. Vieira Glaucia and E. Almeida Luis, J. Colloid Interface Sci., 2007, 309, 402–411 CrossRef.
- S. Wang, Y. Boyjoo and A. Choueib, Water Res., 2005, 39, 129–138 CrossRef CAS.
- Kaili Lin, Jiayong Pan, Yiwei Chen, Rongming Cheng and Xuecheng Xu, J. Hazard. Mater., 2009, 161, 231–240 CrossRef CAS.
- Dongjiang Yang, Blain Paul and Wujun Xu, Water Res., 2010, 44, 741–750 CrossRef CAS.
- T. Asefa, M. J. Maclachlan and N. Coombs, Nature, 1999, 402, 867 CAS.
- K. Inumaru, J. Kiyoto and S. Yamanaka, Chem. Commun., 2000, 903–904 RSC.
- R. I. Nooney, M. Kalyanaraman, G. Kennedy and E. J. Maginn, Langmuir, 2001, 17, 528–533 CrossRef CAS.
- A. M. Liu, K. Hidajat, S. Kawi and D. Y. Zhao, Chem. Commun., 2000, 1145–1146 RSC.
- Zhijian Wu, Hyeonwoo Joo, Ik-Sung Ahn and Seungjoo Haam, Chem. Eng. J., 2004, 102, 277–282 CrossRef CAS.
- Gregorio Crini and Badot Pierre-Marie, Prog. Polym. Sci., 2008, 33, 399–447 CrossRef CAS.
- Shengju Wu, Fengting Li, Yinan Wu, Ran Xu and Guangtao Li, Chem. Commun., 2010, 46, 1694–1696 RSC.
- Shengju Wu, Fengting Li, Ran Xu, Shihui Wei and Guangtao Li, J. Nanopart. Res., 2009, 12, 2111–2124 CrossRef.
- Shengju Wu, Fengting Li, Ran Xu, Shihui Wei and Hongtao Wang, Mater. Lett., 2010, 64, 1295–1298 CrossRef CAS.
- L. X. Zhang, W. H. Zhang and J. L. Shi, Chem. Commun., 2003, 210–211 RSC.
- Hong Yang, Ran Xu and Xiaoming Xue, J. Hazard. Mater., 2008, 152, 690–698 CrossRef CAS.
- M. Al-Ghouti, M. A. M. Khraisheh and M. N. M. Ahmad, J. Colloid Interface Sci., 2005, 287, 6–13 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- B. C. Pan, Y. Xiong and A. M. Li, React. Funct. Polym., 2002, 53, 63–72 CrossRef CAS.
- Z. Reddad, C. Gerente and Y. Andres, Environ. Sci. Technol., 2002, 36, 2067–2073 CrossRef CAS.
- O. Redlich and D. L. Peterson, J. Phys. Chem., 1959, 63, 1024 CrossRef CAS.
- Rais Ahmad and Rajeev Kumar, J. Chem. Eng. Data, 2010, 55, 3489–3493 CrossRef CAS.
- K. Muller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–167 CrossRef.
- R. P. Han, W. H. Zou, Z. P. Zhang, J. Shi and J. J. Yang, J. Hazard. Mater., 2006, 137, 384–395 CrossRef CAS.
- Y. S. Ho and C. C. Chiang, Adsorption, 2001, 7, 139–147 CrossRef CAS.
- Y. C. Hsu, C. C. Chiang and M. F. Yu, Sep. Sci. Technol., 1997, 32, 2513–2534 CrossRef CAS.
- G. Crini and P. M. Badot, Prog. Polym. Sci., 2008, 33, 399–447 CrossRef CAS.
- V. K. Kumar, J. Hazard. Mater., 2006, 137, 1538–1544 CrossRef.
| This journal is © The Royal Society of Chemistry 2012 |