Dynamics, thermal behaviour and elastic properties of thin films of poly(vinyl alcohol) nanocomposites
Vladimir A.
Bershtein
a,
Vladimir M.
Gun'ko
bc,
Larisa M.
Egorova
a,
Zhaowei
Wang
b,
Matthew
Illsley
b,
Eugeny F.
Voronin
c,
Gennadiy P.
Prikhod'ko
c,
Pavel N.
Yakushev
a,
Roman
Leboda
d,
Jadwiga
Skubiszewska-Zięba
d and
Sergey V.
Mikhalovsky
*b
aIoffe Physical-Technical Institute RAS, 194021 St.-Petersburg, Russia. E-mail: vbersht.polmater@mail.ioffe.ru
bSchool of Pharmacy & Biomolecular Sciences, University of Brighton, Brighton, BN2 4GJ, UK. E-mail: s.mikhalovsky@brighton.ac.uk; Tel: 441273 642034
cChuiko Institute of Surface Chemistry, 17 General Naumov Str., Kiev, Ukraine. E-mail: vlad.gunko@ukr.net; Fax: 38044 4243567; Tel: 38044 4229627
dFaculty of Chemistry, Maria Curie-Skłodowska University, 20031, Lublin, Poland. E-mail: jskubisz@o2.pl
First published on 19th December 2011
Abstract
A combined differential scanning calorimetry (DSC), dynamic mechanical analysis (DMA), and laser-interferometric creep rate spectroscopy (CRS) approach has been utilised to study the dynamics, thermal behaviour and elastic properties of thin films (0.05–0.10 mm) with poly(vinyl alcohol) (PVA) based nanocomposites at temperatures ranging from 20 to 180–220 °C. 3D amorphous fumed silica (nanoparticles of ∼9 nm in average diameter, specific surface area SBET = 330 m2 g−1, bulk density ρb = 0.045 g cm−3) initial and compacted by mechanochemical activation to ρb = 0.32 g cm−3 (dense nanosilica with a small change in SBET), and exfoliated graphite (oxidised 2D sheets packed in stacks of approximately 200 nm in thickness) were used as nanofillers of the PVA films at content of 1, 10 or 20 wt%. The impact of nanofillers which significantly modified structure, dynamics and other properties of the PVA matrix due to constrained dynamics effects depends on the filler type and concentration. The most detailed, discrete pictures of the dynamics and pronounced dynamics heterogeneity in the glass transition of the composites were shown by the CRS method. At any temperature within the 20–180 °C range, the composite modules changed by an order of magnitude. Up to a 14 °C rise of the glass transition temperature was observed for the nanocomposites. The most dramatic enhancing effect of elastic and creep resistance properties was attained for a composite incorporating 10 wt% of exfoliated graphite.
Introduction
Semi-crystalline poly(vinyl alcohol) (PVA) possessing excellent biocompatibility and water solubility has been widely studied and employed in a variety of biomedical applications including hydrogels, bone tissue engineering, drug delivery and artificial articular cartilage, as well as in some modern technical applications.1 To improve mechanical and thermal properties of this polymer and to create functional biomedical and technical materials, PVA based nanocomposites with 1D, 2D or 3D nanofillers have recently been studied.2–14Carbon materials, such as carbon nanotubes,2graphite,3 oxidised graphite4 and graphene,5,6 have been employed for preparing PVA-based nanocomposites. Other fillers such as nanosilica,7 montmorillonite (MMT) nanolayers,8 hydroxyapatite,9titania,10tin oxide,11 CdS,12Ag13 and bacterial cellulose nanocrystals14 have also been used. In these works, a substantial improvement in mechanical strength2,3,5,6,10,11 and thermal stability3,11 has been observed for nanocomposites with optimal nanofiller loading, as compared to the properties of unmodified PVA or PVA microcomposites, under conditions of relatively homogeneous distribution of nanoparticles or their small clusters in the PVA matrix. For example, introducing 1.8 vol.% of graphene resulted in a 150% increase of PVA tensile strength.5 It has been demonstrated that the use of exfoliated graphite as a filler in polymer composites significantly alters many of the composite properties such as electrical and thermal conductivity, mechanical characteristics, etc.15Complex polymer systems including nanocomposites may have unusual molecular dynamic properties, such as an anomalous glass transition (see, e.g., reviews16,17). However, very scant information can be found in the literature concerning the PVA dynamic behaviour in nanocomposites. A small increase in glass transition temperature, Tg and even the disappearance of the glass transition was registered in PVA intercalated graphite oxide nanocomposites.4 An increase in the PVA dielectric relaxation time was observed in MMT–PVA composites.8 The double glass transition in a PVA–silica composite was shown by DMA.6 In this work, a combined differential scanning calorimetry (DSC), dynamic mechanical analysis (DMA), and laser-interferometric creep rate spectroscopy (CRS) approach has been applied to analyse the dynamics, dynamic heterogeneity, thermal behaviour and elastic properties of non-modified PVA and PVA-based nanocomposites with such fillers as nanosilica and exfoliated graphite over a wide temperature range.
Experimental
Materials
Poly(vinyl) alcohol, PVA (Kuraray Ltd, Germany, Mowiol® grade 13–88, viscosity 11.5–14.5 mPa s, hydrolysis 86.7–88.7 mol.%) was used for the preparation of thin films with PVA alone or PVA filled with fumed nanosilica (SiO2) or mechanochemically activated (MCA) nanosilica (dense silica, dSiO2), or exfoliated graphite (EG). Aqueous (10 wt.%) PVA solution was prepared by dissolving dry PVA pellets in deionised water and then refluxing at 80 °C. A filler was suspended in deionised water and added to the PVA solution with sonication at room temperature for 20 min. The filler content was 1, 10 or 20 wt.% of dry PVA. The solutions were poured onto a glass plate, and casting was achieved using a stainless steel bar with a fixed distance to the glass plate. The wet films of approximately 0.5 mm in thickness were dried at 70 °C for 30 min. The dried films were 0.05–0.10 mm in thickness.Nanosilica A-300 (Pilot plant of Chuiko Institute of Surface Chemistry, Kalush, Ukraine, specific surface area SBET = 330 m2 g−1) was used as the initial material. Nanosilica was heated at 450 °C for 4 h to remove residual HCl and adsorbed impurities.
Mechanochemically activated (MCA) nanosilica (dense nanosilica, dSiO2) was prepared from the initial fumed nanosilica treated in a ceramic ball-mill (volume 1 dm3, ⅔ filled by balls of 2–3 cm in diameter, 60 rpm) using wetted powders (0.5 g of water per gram of silica) for 4 h.18 This treatment strongly enhanced the bulk density (ρb) of nanosilica to 0.32 g cm−3 since the initial silica has ρb = 0.045 g cm−3. The textural characteristics and interactions with water and other adsorbates are changed for MCA silica. This material was described in detail elsewhere.18
Metamorphogenic natural graphite (from Zavalevskoe deposit, Ukraine) was used as the initial material to prepare exfoliated graphite (EG) using a procedure described elsewhere19,20 (Chuiko Institute of Surface Chemistry, Kiev, Ukraine). Graphite particles were intercalated with concentrated H2SO4 solution and then fast heated at 900–1000 °C. The vaporising intercalated substances force the graphite layers apart. Polar O-containing groups decorated the graphite surface (mostly at graphene sheet edges) during oxidation/heating.
Characterisation methods
Atomic force microscopic (AFM) images were obtained using a NanoScope III (Digital Instruments, USA, an AFM tip (VEECO, RTESP model) with a spring constant of 20–80 N m−1, resonance frequency of 300 kHz, curvature radius of 5 nm, software Nanoscope III version 5.12b) apparatus with the AFM tapping mode measurement technique.Scanning electron microscopy (SEM) images were obtained using a Tesla BS-301 (Tesla, Czech Republic) and Carl Zeiss SMT Ltd. (UK) apparatuses.
Raman spectra were recorded using a Raman microscope (inVia Reflex, Renishaw, UK, equipped with a DMLM Leica microscope).
A Perkin-Elmer DSC-2 apparatus was used for thermal characterisation of the materials studied. The following parameters were determined: PVA glass transition temperatures including Tg at the half-height of a heat capacity step ΔCp, the temperatures of transition onset, Tg′, and completion, Tg′′, the ΔCp values, and characteristics of melting phase transition including melting point Tm at the endothermic melting peak maximum, melting enthalpy ΔHm, and PVA crystallinity degree χcr.
The values of enthalpy relaxation ΔH, that is the enthalpy changes caused by heating samples to remove water, with simultaneous molecular rearrangement in the disordered regions, were determined using differential scanning calorimetry (DSC). The ΔH manifests itself as the endothermic peak on the DSC curve at temperatures just above the thermal treatment temperature (125 °C) and below the melting peak. The ΔH values characterise the ability of PVA for physical ageing.
The DSC measurements were performed in a nitrogen atmosphere over the temperature range from −20 to 220 °C. Sample mass was 17 mg, and amorphous quartz was used as a reference sample. To exclude the plasticising impact of absorbed water, the samples were first heated at a rate V = 20 °C min−1 to 125 °C and held there for 10 min; subsequent cooling to −20 °C was performed at V = 320 °C min−1. Then samples were heated at V = 20 °C min−1, and only these scans recorded in the second cycle were taken into consideration. The enthalpy characteristics ΔHm and ΔH were estimated by measuring the areas of endothermic peaks using the “triangle method” for ΔHm.21 The degree of PVA crystallinity was calculated from the ratio: χcr =(ΔHm/ΔHm0) × 100% where ΔHm0 = 138.6 J g−1 is the melting enthalpy for a perfect 100% PVA crystal.6
The original laser-interferometric CRS, which is a high-resolution method of relaxation spectrometry and thermal analysis, has allowed us to discretely characterise the dynamics, dynamic heterogeneity and creep resistance of materials over a broad temperature region; the CRS setups and experimental technique have been described in detail elsewhere.17 This technique allows precise measurements of the creep rate at a constant low stress, which is significantly lower than the yield stress, as a function of temperature (CR spectrum). For this purpose, a laser Doppler interferometer is used. The time evolution of deformation is registered as a sequence of low-frequency beats in an interferogram whose beat frequency ν yields a creep rate
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = λν/2I0 = λν/2I0 | (1) |
Here λ = 630 nm is the laser wavelength, and I0 is the initial length of the working part of a sample. Additionally, the elasticity modulus (E) versus temperature (T) plots could be obtained using the laser interferometer data on the value of deformation (ε) measured 1–2 s after loading a sample using the formula:
| ε = λn/2I0 | (2) |
The creep rate spectra and elasticity modulus versus temperature dependencies were measured over the temperature range from 20 to 140 °C at the tensile stress of 1 MPa. The stress was chosen in preliminary experiments as the force capable of inducing sufficient creep rates to allow measurements. The chosen stress maintained a high spectral resolution without smoothing out and distortion of a spectral contour and prevented premature rupture of the sample. At a heating rate of V = 1 °C min−1 a sample was loaded every 5 °C, and an interferogram was recorded at the moment of loading to estimate E and 10 s after loading to record the creep rate spectra; then the sample was unloaded, and the procedure repeated. In order to estimate the spectra and moduli for the PVA-based samples in both initial (hydrated) and thermally treated (water-free) states, two spectra were measured in each case: the first one was registered at temperatures up to 125 °C, at which it was held for 10 min (as in the DSC experiments, see above), and then cooled to room temperature during 0.5 h; the second series of measurements was performed for this annealed water-free sample up to 140 °C. The correlation frequency in the CRS experiments was νcorr = 10−3 to 10−2 Hz.
The dynamic viscoelasticity of the nanocomposites was analysed in tension mode at 1 Hz using a dynamic mechanical spectrometer (DMS6100, Seiko Instruments) at temperatures ranging from 20 to ∼180 °C. A sample was heated at a rate of 1 °C min−1. Thus the temperature dependence of tensile loss modulus (E′′), tensile storage modulus (dynamic modulus E′) and mechanical loss factor tanδ = E′′/E′ were measured. Two DMA spectra were measured in each case, for initial and annealed samples, under the same conditions as in the CRS experiments. DMA and CRS analyses were performed with film samples of ∼50 μm thickness, 8 mm width and 2 cm length.
The structure of two PVA molecules interacting with two stacks with two carbon sheets (with C–H and C–OH groups at the edges) was optimised using the AMBER force field using the Vega ZZ 2.4 package.22
Results and discussion
Structural features of fillers
The initial fumed nanosilica is composed of primary nanoparticles with an average diameter of ∼9 nm (from 5 to 16 nm), which form aggregates (bulk density ρb,a1 ≈ 0.3ρ0, whereas ρ0 = 2.2 g cm−3 is the true density of amorphous silica), agglomerates (ρb,a2 ≈ 0.07ρ0), and very loose visible particles. It has a bulk density of ρb,i = 0.045 g cm−3 and the specific surface area SBET = 330 m2 g−1 (estimated from the low-temperature nitrogen adsorption), the empty volume in the powder Vem = 1/ρb − 1/ρ0 = 21.8 cm3 g−1, and textural porosity φ = 100Vem/(Vem + 1/ρ0) = 98%.18 The MCA treatment did not affect the SBET value but strongly changed the textural porosity and some other characteristics of nanosilica.18 Dense nanosilica has a higher bulk density ρb,d = 0.32 g cm−3 due to rearrangement and better packing of nanoparticles (powder compaction) during the MCA treatment.The exfoliated graphite (EG) particles have an enormous c-direction expansion since its apparent volume increased more than 100-fold (Fig. 1a). EG has bulk density ρb,EG ≈ 0.01 g cm−3 and SBET = 21 m2 g−1. EG is composed of stacks of 2D sheet layers (Fig. 1) with the overall thickness of approximately 200 nm. AFM images of EG initial (Fig. 1b) and heated at 150 °C for 2 h (Fig. 1c) show that the carbon sheet surface includes some defects and small fragments which can increase EG interactions with PVA. The z-axis profile in AFM images includes 10–40 nm steps.
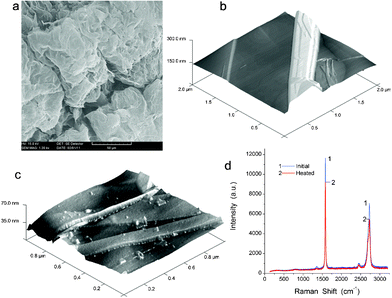 | ||
| Fig. 1 (a) SEM (scale bar 50 μm) and AFM images of (b) initial and (c) degassed (at 150 °C for 2 h) exfoliated graphite (2 × 2 × 0.3 and 1 × 1 × 0.07 μm, respectively), and (d) Raman spectra of initial (1) and degassed (2) EG. | ||
Raman spectra of initial and heated/degassed EG (Fig. 1d) show that the G-band at 1600 cm−1 (graphite sp2 structures)23 has the maximal intensity in the spectra. A weak D-band at 1352 cm−1 corresponds to the sp3 structures.23 The G and D bands, as well as the second order features at 2950 and 2700 cm−1,23 depend weakly on degassing/heating. There is no shift of the G-band. The D-band is very weak in both cases because EG retains a significant portion of the initial graphite sp2 structures in stacks of 2D sheets (Fig. 1a) and degassing at 150 °C does not affect its structure. Therefore, one can assume that EG and nanosilica fillers remain stable upon heating of PVA composites.18
Thus, all the temperature (20–220 °C) dependencies of the characteristics of composites studied can be attributed to the PVA component and possible influence of bound water. The latter is present only in small amount in the annealed samples. Insertion of polar PVA chains into EG can result in the formation of both exfoliated and intercalated composite structures. The presence of –OH and other polar groups at nanofiller surfaces causes strong interactions with PVA viahydrogen bonding and Coulomb and van der Waals forces.
Thermal and dynamic properties of nanocomposites
Fig. 2 shows examples of DSC thermograms for water-free unmodified PVA and four nanocomposites at T from 0 to 220 °C. The characteristics of the PVA glass transition, melting transition, crystallinity degree, and the ability for physical ageing are shown in Table 1. Filling of the PVA matrix results in changes in the thermal behaviour of PVA.
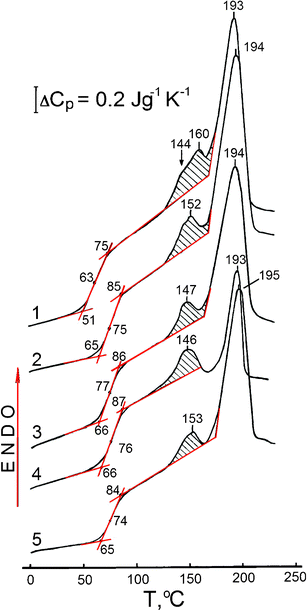 | ||
| Fig. 2 DSC curves obtained for unmodified PVA (curve 1), and PVA based nanocomposites with SiO2 (2) 10 and (3) 20 wt%, (4) 10 wt% EG, and (5) 20 wt% dSiO2 at a heating rate of V = 20 °C min−1. Scans II after heating samples at V = 20 °C min−1 to 125 °C, with holding for 10 min at this temperature and subsequent cooling to −20 °C at V = 320 °C min−1. | ||
| Sample | C PVA (wt.%) | C filler (wt%) | T g′ (°C) | T g (°C) | T g′′ (°C) | ΔCp (J gpol−1 K−1) | ΔH (J gpol−1) | T m (°C) | ΔHm (J gpol−1) | χ cr (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| PVA | 100 | 0 | 51 | 63 | 75 | 0.37 | 8.4 | 193 | 42.6 | 30.7 |
| PVA–SiO2 (99/1) | 99 | 1 | 52 | 64 | 82 | 0.34 | 7.0 | 191 | 34.9 | 25.2 |
| PVA–SiO2 (90/10) | 90 | 10 | 65 | 75 | 85 | 0.40 | 5.7 | 194 | 38.7 | 27.9 |
| PVA–SiO2 (80/20) | 80 | 20 | 66 | 77 | 86 | 0.35 | 4.5 | 194 | 38.5 | 27.7 |
| PVA–dSiO2 (99/1) | 99 | 1 | 57 | 67 | 79 | 0.28 | 5.3 | 193 | 28.4 | 20.5 |
| PVA–dSiO2 (90/10) | 90 | 10 | 62 | 75 | 83 | 0.45 | 8.3 | 195 | 40.6 | 29.3 |
| PVA–dSiO2 (80/20) | 80 | 20 | 65 | 74 | 84 | 0.39 | 3.5 | 195 | 41.4 | 29.9 |
| PVA–EG (99/1) | 99 | 1 | 50 | 62 | 77 | 0.39 | 7.0 | 193 | 31.4 | 22.6 |
| PVA–EG (90/10) | 90 | 10 | 66 | 76 | 87 | 0.37 | 4.4 | 193 | 12.6 | 9.1 |
These changes include an increasing glass transition temperature Tg; a decrease or increase in the ΔCp value as a characteristic of relaxation strength in the glass transition, transition width ΔTg = Tg′′ − Tg′; reduction of the PVA crystallinity degree χcr, and variation in the ability of PVA for physical ageing as estimated by the magnitude and temperature position of the endothermic peak close to the melting peak. The melting range starts at approximately 170 °C. The melting point is not practically affected by nanofillers since it remains practically unchanged for all samples (Tm =193 ± 2 °C).
DSC data reveal the three most important features in the thermal behaviour of the nanocomposites studied (Table 1, Fig. 2). First, a maximal Tg increase by 13 or 14 °C is observed for PVA–SiO2 (80/20) and PVA–EG (90/10) nanocomposites, although the latter exhibits an anomalously large, three-fold reduction of PVA crystallinity from 30.7 to 9.1%. Secondly, each nanofiller decreases the degree of PVA crystallinity. However, this reduction is negligible in the composites with a high content of dense nanosilica, PVA–dSiO2 (80/20 and 90/10) because dSiO2 remains aggregated in the PVA matrix resulting in a small surface area of the polymer-filler interface. Thirdly, enthalpy relaxation value, ΔH, as determined from the dashed areas of endothermic peaks located between the annealing temperature (125 °C) and 160–170 °C, is reduced in the studied nanocomposites compared to pure PVA. The ΔH value characterising the ability of PVA for physical ageing, tends to be reduced in nanocomposites. For example, adding 10% EG resulted in a two-fold decrease in the ΔH value (Table 1) and the doublet endotherm contour at temperatures of the peak maxima at 144 and 160 °C transformed into a single peak with the maximum at 146 °C (Fig. 2).
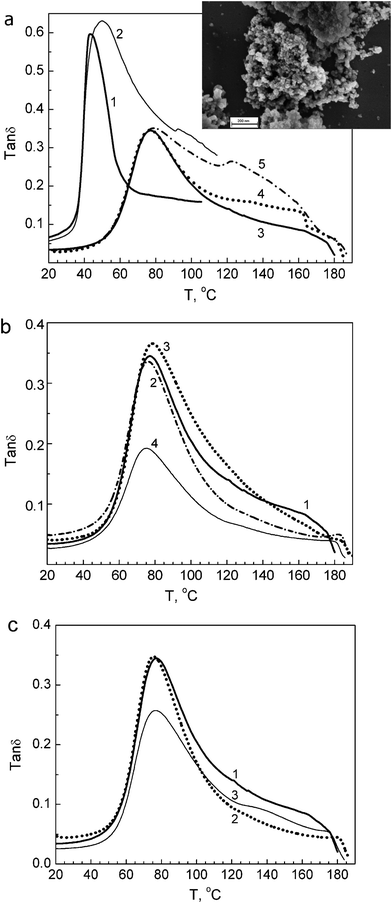 | ||
| Fig. 3 DMA spectra obtained at 1 Hz for unmodified PVA and PVA based nanocomposites: (a) unmodified PVA in initial hydrated (1) and annealed state (3); annealed composite with 1 wt% SiO2 (4), and composite with 10 wt% SiO2 in initial (2) and annealed state (5), insert: SEM image of aggregates of A-300 nanoparticles (scale bar 200 nm); (b) annealed films of unmodified PVA (1) and composites with 1 wt% (2), 10 wt% (3), or 20 wt% dSiO2 (4); (c) annealed films of unmodified PVA (1) and composites with 1 wt% (2) or 10 wt% EG (3). | ||
The DMA spectra obtained clearly demonstrate substantial changes in the segmental dynamics within the disordered, intercrystalline regions of PVA caused by the presence of silica nanoparticles or EG stacks.
Generally, PVA glass transition peak transforms in the mechanical spectra of nanocomposites in two ways: (i) as a decrease in the peak intensity without a substantial change in maximum temperature Tmax, and (ii) as an essential change in the higher-temperature wing of the glass transition peak.6
Both effects are associated with the suppression of segmental dynamics by nanoparticles.6,16,17 A small increase in a transition peak is registered only for the 10% dSiO2 nanocomposite (Fig. 3b). It should be noted that a large difference in the peak contour is observed for both annealed and initial hydrated films of unmodified PVA and nanocomposites (Fig. 3a).
The DMA characteristics obtained for all samples studied are shown in Table 2. Significant changes in the tanδmax and E′ (at 20 °C) values are observed, whereas Tmax varies within a narrow temperature range from 43 to 50 °C for hydrated films and from 73 to 79 °C for annealed samples.
| Sample | T max (°C) | tanδmax | E′ (GPa)a | |||
|---|---|---|---|---|---|---|
| Initial | Annealed | Initial | annealed | Initial | Annealed | |
| a E′ at 20 °C. | ||||||
| PVA | 43 | 77 | 0.60 | 0.35 | 1.7 | 1.3 |
| PVA–SiO2 (99/1) | 43 | 77 | 0.57 | 0.35 | 2.1 | 2.4 |
| PVA–SiO2 (90/10) | 50 | 79 | 0.63 | 0.35 | 1.2 | 0.9 |
| PVA–SiO2 (80/20) | 44 | 79 | 0.51 | 0.29 | — | 1.6 |
| PVA–dSiO2 (99/1) | 44 | 76 | 0.74 | 0.34 | 1.0 | 2.3 |
| PVA–dSiO2 (90/10) | 45 | 79 | 0.58 | 0.36 | 1.1 | 1.0 |
| PVA–dSiO2 (80/20) | 45 | 75 | 0.35 | 0.20 | 1.1 | 0.4 |
| PVA–EG (99/1) | 46 | 76 | 0.53 | 0.35 | 1.8 | 4.1 |
| PVA–EG (90/10) | 43 | 76 | 0.43 | 0.26 | 4.3 | 4.6 |
Fig. 3 shows that in nanocomposites changes in the glass transition peak depend on the type and content of the nanofiller used. For the PVA–SiO2 composites, a particularly intensive relaxation region arises over the 90–160 °C range, with a new maximum at 125 °C, at 10% nanofiller (Fig. 3a), whereas the intensity of the main peak remains constant. There are no such significant changes in the peak contour for PVA–dSiO2 nanocomposites but a decrease in the peak intensity is especially strong at 20% dSiO2 (Fig. 3b). Different dynamic behaviour is observed for EG-containing nanocomposites: introduction of 1% EG into PVA results in suppression of the higher-temperature wing of the glass transition peak whereas adding of 10% EG significantly decreases the main relaxation peak and simultaneously makes the relaxation at 120–160 °C more distinctive (Fig. 3c). On the whole, the nanofillers used cause an additional, along with the crystallites, “constrained dynamics” effect on the PVA matrix.
Fig. 4 shows the storage modulus (dynamic modulus) E′ as a DMA-measured function of temperature for annealed samples of PVA and six nanocomposites.
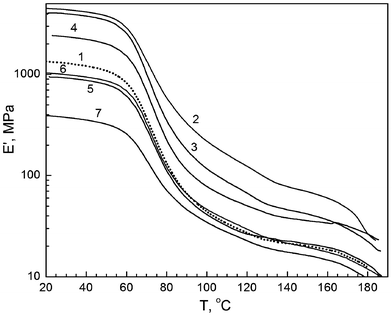 | ||
| Fig. 4 Tensile dynamic modulus (storage modulus) as a function of temperature obtained by DMA for annealed films of unmodified PVA (1), and PVA based nanocomposites with 10 wt% EG (2), 1 wt% EG (3), 1 wt% SiO2 (4), 10 wt% SiO2 (5), 10 wt% dSiO2 (6), and 20 wt% dSiO2 (7). | ||
There is a very large difference in the E′ values for the composites indicated: at any temperature within the range between 20 and 180 °C the storage modulus varies by an order of magnitude, e.g., from 400 MPa to 4.6 GPa at 20 °C or from 32 to 200 MPa at 100 °C. The effects observed depend on the nanofiller type and content. Thus, introducing 1% SiO2 results in about 80–100% increase of E′ at different temperatures, whereas introducing 10% SiO2 or dSiO2 does not change E′ at elevated temperatures and even reduces storage modulus at room and moderate temperatures. A three-fold drop in the E′ value is observed after adding 20% dSiO2 under the same conditions. This negative effect is associated with the enhanced aggregation of dSiO2 nanoparticles; in contrast to the initial nanosilica, dSiO2 remains in the composite mainly in a form of relatively large aggregates >1 μm.18
An extraordinarily large positive effect for E′ was attained in PVA–EG nanocomposites, particularly at 10% EG, with E′ increasing from 1.3 to 4.6 MPa at 20 °C and 5–7 times higher at elevated temperatures compared with the values characteristic of PVA alone (Fig. 4).
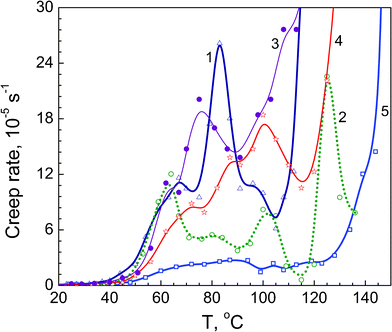 | ||
| Fig. 5 Creep rate spectra obtained at tensile stress 1 MPa for annealed films of neat PVA (1), and PVA based nanocomposites with 1 wt% SiO2 (2), 10 wt% dSiO2 (3), 10 wt% SiO2 (4), and 10 wt% EG (5). | ||
Judging by its temperature location, peak I can be assigned to the “normal”, undisturbed dynamic mode in the PVA glass transition, whereas peaks II–IV may be related to the segmental dynamics modes differently constrained by rigid structural elements, PVA crystallites or/and filler nanoparticles. Besides the chain conformation and the distance between the moving segment and crystallite/nano-particle surface, the constraining effect also depends on the interfacial interactions in a complex polymeric material. In the case of the nanofillers used in this work, these interactions are provided by the hydrogen bonds between PVA hydroxyls and surface O-containing functionalities of silica and oxidised graphite surface and dispersion interaction between nonpolar fragments.
Fig. 5 demonstrates very different constrained dynamics effects caused by adding nanoparticles. A rather large influence of 1% SiO2 on creep rate level and dynamic heterogeneity is obvious (curve 2); this effect is much less at 10% SiO2 (curve 4) and the smallest at 10% dSiO2 (curve 3). The latter may be explained by stronger aggregation of nanoparticles in MCA-nanosilica.18 These results are in accordance with the E′ data shown in Fig. 4 and E values presented below in Fig. 6a.
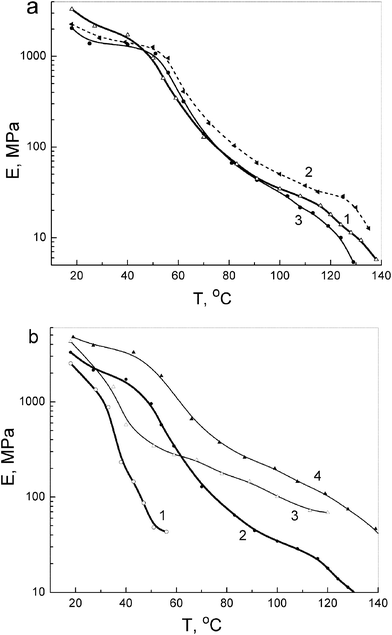 | ||
| Fig. 6 Modulus of elasticity as a function of temperature obtained at tensile stress 1 MPa using a laser interferometer for unmodified PVA and PVA-based nanocomposites: (a) annealed films of PVA (1), and PVA-based nanocomposites with 10 wt% SiO2 (2) and 10 wt% dSiO2 (3); (b) PVA (1, 2) and nanocomposite with 10 wt% EG (3, 4) in initial hydrated (1, 3) and annealed state (2, 4). | ||
The most pronounced effect on creep rate spectrum is seen with 10% EG, probably due to a mutually complementary impact of 2D nanoplates of exfoliated graphite (Figs. 1 and 7) and PVA crystallites: a strong suppression of relaxation peaks and a low level of creep rates up to 130 °C are observed in this case (Fig. 5, curve 5). Enhancing such an important property as creep resistance in this nanocomposite is noteworthy: a steep acceleration of creep at the tensile stress of 1 MPa is observed starting from ∼110 °C for unmodified PVA, from 130 °C for the nanocomposite with 10% SiO2 but only from ∼145 °C for the nanocomposite with 10% EG.
 | ||
| Fig. 7 Model of PVA intercalated EG (7710 atoms, with the geometry optimised using VEGA ZZ 2.4 with the AMBER force field22). | ||
The modulus of elasticity E versus temperature plots obtained at 1 MPa using a laser interferometer for unmodified PVA and several PVA-based nanocomposites shown in Fig. 6 are in a qualitative accordance with the experimental E′ (T) dependencies presented in Fig. 4. Fig. 6a shows that introducing 10% SiO2 or dSiO2 into PVA decreases the modulus at room temperature; adding SiO2 increases the E of the nanocomposite only at elevated temperatures between 50 and 130 °C, typically by 40–70%. Introducing 10% EG results in a strong increase in PVA rigidity over a broad temperature range: the E values are higher by 100–200% at moderate temperatures and 4–7 times higher at 60–120 °C compared with unmodified PVA (Fig. 6b). This effect can be explained by structural features of EG and the character of interactions between PVA and EG large sheets (Figs. 1 and 7) resulting in certain flattening of PVA molecules. Interactions PVA with silica nanoparticles do not lead to similar effects. For initial hydrated samples, the lesser modulus values and their sharp drop are already observed at ∼40 °C; however, a large, 2–6-fold difference between the rigidities of hydrated PVA and hydrated PVA nanocomposite with 10% EG is retained.
Thus, the dramatic effects of modifying structure, constraining dynamics, enhancing elastic properties and creep resistance were attained for poly(vinyl alcohol) doped by exfoliated graphite.
Conclusions
Characterisation of the glass transition dynamics, dynamic heterogeneity, structural state, thermal behaviour, elastic properties and creep resistance over a broad temperature range of thin films with PVA filled by initial and MCA-treated nanosilica or exfoliated graphite shows that silica and oxidised exfoliated graphite nanofillers have an effect on mechanical/relaxation and thermal properties and crystallinity of PVA. This effect depends on the filler type and content because of the different distribution of primary and secondary particles of the fillers in the PVA films. Generally, variations in the effect are caused by the constrained dynamics in the PVA matrix due to different fillers nanoparticles and PVA crystallites. The most detailed, discrete picture of the glass transition dynamics within the disordered regions of PVA in the nanocomposites was observed in the creep rate spectra manifesting at least four constituent dynamic modes at 60–70, 80–90, 100–105 and 125 °C.The most pronounced effects of modifying structure and behaviour of the PVA matrix were found in the nanocomposite with 10 wt% of exfoliated graphite as a 2D filler. In this case, a dramatic rise of creep resistance at small stress up to 140 °C and 2–7 times increase in static (CRS) and dynamic (DMA) moduli over the temperature range between 20 and 180 °C were observed. This is due to a large 2D size of the thin EG sheet stacks resulting in local strongly anisotropic behaviour (parallel and perpendicular to the EG sheets) in comparison with PVA–silica composites which comprise spherical SiO2 nanoparticles. These results show the possibility of strong changes in the characteristics of thin PVA films in two directions (along the film and perpendicularly to it) with such fillers as exfoliated graphite in contrast to nanosilica providing isotropic properties of the soft composites.
Acknowledgements
This work has been financially supported by FP7-PEOPLE-IAPP MONACO-EXTRA project No 218242, TSB (UK) project No TPBD410H and FP7-PEOPLE-IRSES COMPOSITUM project No 230790.References
- (a) A. S. Hoffman, Adv. Drug Delivery Rev., 2002, 54, 3–12 CrossRef CAS; (b) J. L. Drury and D. J. Mooney, Biomaterials, 2003, 24, 4337–4351 CrossRef CAS; (c) Y. H. Yu, C. Y. Lin, J. M. Yeh and W. H. Lin, Polymer, 2003, 44, 3553–3560 Search PubMed; (d) N. Barbani, F. Bertoni, G. Ciardelli, C. Cristallini, D. Silvestri, M. L. Coluccio and P. Giusti, Eur. Polym. J., 2005, 41, 3004–3010 CrossRef CAS; (e) G. Tzvetkov, G. Paradossi, M. Tortora, P. Fernandes, A. Fery, B. Graf-Zeiler and R. H. Fink, Mater. Sci. Eng., C, 2010, 30, 412–416 Search PubMed; (f) J. L. Holloway, K. L. Spiller, A. M. Lowman and G. R. Palmese, Acta Biomater., 2011, 7, 2477–2482 Search PubMed; (g) O. J. Cayre, N. Chagneux and S. Biggs, Soft Matter, 2011, 7, 2211–2234 RSC; (h) E. Otsuka, S. Sasaki, K. Koizumi, Y. Hirashima and A. Suzuki, Soft Matter, 2010, 6, 6155–6159 RSC.
- M. C. Paiva, B. Zhou, K. A. S. Fernando, Y. Lin, P. E. Lopes, W. T. Pennington, J. M. Kennedy and Y. P. Sun, Compos. Interfaces, 2005, 12, 757–768 Search PubMed.
- H. Hu and G. Chen, Polym. Compos., 2010, 31, 1770–1775 Search PubMed.
- J. Xu, Y. Hu, L. Song, Q. Wang, W. Fan, G. Liao and Z. Chen, Polym. Degrad. Stab., 2001, 73, 29–31 CrossRef CAS.
- X. Zhao, Q. Zhang, D. Chen and P. Lu, Macromolecules, 2010, 43, 2357–2363 CrossRef CAS.
- (a) L. Jiang, X. P. Shen, J. L. Wu and K. C. Shen, J. Appl. Polym. Sci., 2010, 118, 275–279 CAS; (b) X. Yang, L. Li, S. Shang and X. Tao, Polymer, 2010, 51, 3431–3435 CrossRef CAS; (c) J. Liang, Y. Huang, L. Zhang, Y. Wang, Y. Ma, T. Guo and Y. Chen, Adv. Funct. Mater., 2009, 19, 2297–2302 CrossRef CAS.
- (a) L. Chen, K. Zheng, X. Tian, K. Hu, R. Wang, C. Liu, Y. Li and P. Cui, Macromolecules, 2010, 43, 1076–1082 CrossRef CAS; (b) Z. Peng, L. X. Kong, S. D. Li and P. Spiridonov, J. Nanosci. Nanotechnol., 2006, 6, 3934–3938 Search PubMed; (c) A. Bandyopadhyay, M. DeSarkar and A. K. Bhowmick, J. Mater. Sci., 2006, 41, 5981–5993 Search PubMed.
- R. J. Sengwa, S. Choudhary and S. Sankhla, Compos. Sci. Technol., 2010, 70, 1621–1627 Search PubMed.
- (a) Y. Pan and D. Xiong, J. Mater. Sci., 2010, 45, 5495–5501 Search PubMed; (b) T. Mikołajczyk, S. Rabej, M. Bogun, G. Szparaga and Z. Draczynski, J. Appl. Polym. Sci., 2011, 120, 1234–1244 Search PubMed.
- Y. Lou, M. Liu, X. Miao, L. Zhang and X. Wang, Polymer Composites, 2010, 31, 1184–1193 Search PubMed.
- P. Wei, H. Xiaowei and C. Yan, Int. J. Polym. Mater., 2011, 60, 223–232 Search PubMed.
- (a) J. Kakati, P. K. Baruah and P. Datta, AIP Conf. Proc., 2010, 1276, 311–315 Search PubMed; (b) M. Pattah and A. B. Saraswathi, Compos. Interfaces, 2010, 17, 103–111 Search PubMed.
- W. Pan, H. Li and Y. Chen, Appl. Mech. Mater., 2010, 26–28, 127–130 Search PubMed.
- (a) J. George, A. S. Bawa and H. Siddaramaiah, Adv. Mater. Res., 2010, 123–125, 383–386 Search PubMed; (b) M. J. Cho and B. D. Park, J. Ind. Eng. Chem., 2011, 17, 36–40 Search PubMed.
- (a) S. Kim and L. T. Drzal, J. Adhes. Sci. Technol., 2009, 23, 1623–1638 Search PubMed; (b) X. Zhang, G. Lin, R. Abou-Hussein, W. Allen, I. Noda and J. Mark, J. Macromol. Sci., Part A: Pure Appl. Chem., 2008, 45, 431–439 Search PubMed; (c) D. G. Miloaga, A. Hosein Hazel-Ann, M. J. Rich, K. Kjoller and L. T. Drzal, J. Biobased Mater. Bioenergy, 2008, 2, 78–84 Search PubMed; (d) J. Li, Y. Xu, M. Li, C. Mi and J. Li, J. Low Temp. Phys., 2010, 160, 240–245 Search PubMed; (e) H. Fukushima, L. Drzal, B. Rook and M. Rich, J. Therm. Anal. Calorim., 2006, 85, 235–238 Search PubMed; (f) F. He, S. Lau, H. L. Chan and J. Fan, Adv. Mater., 2009, 21, 710–715 CrossRef CAS; (g) L. Wang, L. Zhang and Ming Tian, Polym. Adv. Technol., 2011 DOI:10.1002/pat.1940; (h) L. M. Veca, M. J. Meziani, W. Wang, X. Wang, F. Lu, P. Zhang, Y. Lin, R. Fee, J. W. Connell and Y.-P. Sun, Adv. Mater., 2009, 21, 2088–2092 CrossRef CAS; (i) V. Alzari, A. Mariani, O. Monticelli, L. Valentini, D. Nuvoli, M. Piccinini, S. Scognamillo, S. B. Bon and J. Illescas, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 5375–5381 CrossRef CAS; (j) B. Debelak and K. Lafdi, Carbon, 2007, 45, 1727–1734 CrossRef CAS.
- E. P. Giannelis, R. Krishnamoorti and E. Manias, Adv. Polym. Sci., 1999, 138, 107–148 CAS.
- V. A. Bershtein and P. N. Yakushev, Adv. Polym. Sci., 2010, 230, 73–219 Search PubMed.
- (a) V. M. Gun'ko, E. F. Voronin, L. V. Nosach, V. V. Turov, Z. Wang, A. P. Vasilenko, R. Leboda, J. Skubiszewska-Zięba, W. Janusz and S. V. Mikhalovsky, J. Colloid Interface Sci., 2011, 355, 300–311 Search PubMed; (b) V. M. Gun'ko, V. V. Turov and P. P. Gorbik, Water at the Interfaces.Naukova Dumka, Kiev, 2009 Search PubMed.
- (a) A. V. Melezhik, L. V. Makarova and A. A. Chuiko, Zh. Neorg. Khim. (Russ.), 1989, 34, 351–357 Search PubMed; (b) A. V. Melezhik, R. B. Rudyi, L. V. Makarova and A. A. Chuiko, Zh. Priklad. Khim. (Russ.), 1995, 68, 54–57 Search PubMed.
- (a) D. D. L. Chung, J. Mater. Sci., 1987, 22, 4190–4198 CAS; (b) I. M. Afanasov, O. N. Shornikova, D. A. Kirilenko, I. I. Vlasov, L. Zhang, J. Verbeeck, V. V. Avdeev and G. Van Tendeloo, Carbon, 2010, 48, 1858–1865 Search PubMed; (c) T. Enoki, M. Suzuki and M. Endo, Graphite Intercalation Compounds and Applications. University Press, Oxford, 2003 Search PubMed; (d) W. Gu, W. Zhang, X. Li, H. Zhu, J. Wei, Z. Li, Q. Shu, C. Wang, K. Wang, W. Shen, F. Kang and D. Wu, J. Mater. Chem., 2009, 19, 3367–3369 RSC.
- V. A. Bershtein and V. M. Egorov, Differential Scanning Calorimetry of Polymers. Physics, Chemistry, Analysis, Technology. Ellis Horwood, New York, 1994 Search PubMed.
- A. L. Pedretti, G. Villa and G. Vistoli, J. Comput.-Aided Mol. Des., 2004, 18, 167–173 CrossRef CAS VEGA ZZ, http://www.vegazz.net..
- (a) K. N. Kudin, B. Ozbas, H. C. Schniepp, R. K. Prud'homme, I. A. Aksay and R. Car, Nano Lett., 2008, 8, 36–41 CrossRef CAS; (b) A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter, 2000, 61, 14095–14107 CrossRef CAS; (c) M. Nakamizo, R. Kammereck and P. L. Walker, Jr., Carbon, 1974, 12, 259–267 CrossRef CAS; (d) P. L. Walker, Jr. and P. A. Thrower, editors, Chemistry and Physics of Carbon, Dekker, New York, 1981 Search PubMed; (e) A. Cuesta, P. Dhamelincourt, J. Laureyns, A. Martinez-Alonso and J. M. D. Tascon, Carbon, 1994, 32, 1523–1532 CAS; (f) Z.-M. Li, N. Zhang and F.-T. Li, Appl. Surf. Sci., 2006, 253, 2870–2874 CrossRef CAS; (g) R. Escribano, J. J. Sloan, N. Siddique, N. Sze and T. Dudev, Vib. Spectrosc., 2001, 26, 179–186 CrossRef CAS.
- B. Wunderlich, Prog. Polym. Sci., 2003, 28, 383–450 Search PubMed.
| This journal is © The Royal Society of Chemistry 2012 |
