Bragg extraction of light in 2D photonic Thue–Morse quasicrystals patterned in active CdSe/CdS nanorod–polymer nanocomposites

Abstract

In this paper two-dimensional (2D) photonic Thue–Morse quasicrystals (ThMo-PQCs) in active CdSe/CdS nanorod (NR) doped polymer nanocomposites are proposed and experimentally demonstrated. Active PQCs and undoped lattices have been prepared in a one-step fabrication process by an electron beam lithography technique (EBL) and the effects on light extraction and emission directionality are studied experimentally. Vertical extraction of light was found to be strongly dependent on both the geometric parameters of the ThMo-PQCs and the presence of NR dopants. By changing the geometrical parameters of the photonic structures, the resonance peak could be tuned from a narrow bluish green emission at 543 nm up to a red–NIR emission at 711 nm with a full width at half-maximum of 22 nm which is in good agreement with Bragg's diffraction theory and free photon band structure. Angular resolved measurements revealed a directional profile in the far-field distribution with guided mode extraction in both doped and undoped PQCs and an enhancement as high as 6.5-fold in light extraction was achieved in the doped photonic structures. These experimental results indicate the critical role of the CdSe/CdS NRs in improving the light extraction efficiency of 2D ThMo-PQCs for solid-state lighting and lasing.

---

Introduction

Photonic crystals¹ have traditionally emulated natural periodic structures such as gratings and square or triangular lattices which have 2, 4 and 6-fold symmetries respectively. The highest degree of symmetry found in nature is given by the triangular lattice which has 6-fold symmetry. As the level of symmetry increases the properties of the lattice become less directional and this is detrimental for some applications. Since photonic crystals are artificial photolithography defined structures, lattice patterns need not necessarily be constrained to designs found in nature and this could overcome the technological applicability of the natural structures. A completely different class of structures known as Photonic Quasi-Crystals (PQCs) are fascinating new photonic materials in which the lack of the translational symmetry is compensated by high rotational symmetries (such as octagonal or dodecagonal symmetry in two dimensions and icosahedral symmetry in three dimensions) not achievable by the conventional periodic crystals.^2–10 The existence of such high rotational symmetries and many unequivalent defective states¹¹ opens the possibility to realize versatile PQC based devices even for low dielectric contrast materials like polymeric ones. Different from random structures, PQCs are defined by the iteration of simple mathematical rules, rooted in symbolic dynamics and prime number theory, which possess very rich spectral features.⁴ The PQCs appear to exhibit some new kinds of bandgaps in addition to those of typical PCs. One dimensional (1D) aperiodic binary sequences based on specific substitution rules have been extensively studied in the field of mathematics, solid-state physics, and recently in photonics.^4,12 In the last few years, possible optical applications of light propagation in aperiodic media have deserved a major attention in order to understand the interplay between the optical properties and the underlying aperiodic arrangement. The spatial Fourier power spectrum of an infinitely long Thue–Morse (ThMo) structure is singular continuous,⁴ in contrast to the singular (δ function) Fourier spectra of periodic and quasiperiodic lattices. Consequently, photonic bandgaps (PBGs) and light transport in ThMo structures display unusual properties, e.g., fractal gaps.⁸ The scaling of the fractal bandgaps occurring in ThMo multilayers provides a large omnidirectional bandgap¹³ and a significant light-emission enhancement effect for multiple resonance states.⁷ Resonant transmission and frequency trifurcation have been reported in ThMo multistack layers.¹⁴

Recently the ThMo inflation method has been generalized from one dimension to two dimensions.^15,16 Such a structure is shown to support critical states that lie in between localized states and extended states.⁶ Experimental realization of photonic structures exhibiting large area 2D Thue–Morse arrangement has been recently reported by the authors.^17–19

Advances in 2D photonic structures can be achieved by the introduction of active media into a 2D photonic-crystal slab to realize extremely small active photonic devices. Semiconductor CdSe/CdS core–shell nanorods (NRs) are a very promising material as an active medium since they present the appealing characteristics of strong and tunable light emission from green to red, are highly fluorescent and show linearly polarized emission.^21–24

The fabrication of active nanocomposites based on CdSe/CdS core–shell NRs and polymers has already been demonstrated.^20,25–27 However, to the best of our knowledge, an investigation of the tuning properties of different designed ThMo structures to match the properties of the active photonic material to obtain enhanced performance of a device has not been reported so far.

In this paper, experimental and theoretical studies on the directional light extraction through Bragg diffraction of guided modes in doped and undoped ThMo-PQCs are addressed. We realized two-dimensional (2D) hybrid ThMo-PQCs composed of cylindrical air-holes etched in a nanocomposite prepared by incorporating CdSe/CdS core–shell NRs in a polymeric matrix of polymethylmethacrylate (PMMA). The active photonic structures were prepared in a one-step fabrication process. At the same time undoped 2D ThMo-PQCs were also prepared.

In this paper we show that, depending on the geometrical parameters of the photonic structures, the resonance peak can be tuned from a narrow bluish green emission at 543 nm up to a red emission at 711 nm with a full width at half-maximum of 22 nm. The measured resonance peaks are due to the QPC feedback effect and have been confirmed by both the measured angle resolution spectrum and by theoretical calculations. We focused on band-edge engineering approach²⁸ through which the formation of bandgaps is unnecessary and the use of weak PQCs is possible for realizing surface-emitting devices. The NR doped 2D ThMo-PQC enhanced the light extraction efficiency by 6.5 times compared to the undoped structure.

Results and discussion

The core–shell CdSe/CdS NRs employed in this study were prepared by a seeded growth approach, which yields highly uniform nanocrystals in terms of distribution of rod lengths and diameters. Two pictures of the stock solution of CdSe/CdS NRs dissolved in toluene are reported in Fig. 1a showing the same solution under visible and UV light irradiation, respectively.

A transmission electron microscopy (TEM) image of the sample is reported in Fig. 1b. The rods used for the fabrication of PQCs have a long axis size distribution ranging between 13 and 16.5 nm and their diameters range between 3 and 5.5 nm.

Fig. 1 (a) NRs in toluene under visible light (left) and UV light (right) showing photoluminescence. (b) A representative TEM image of CdSe/CdS core–shell NRs with average 4.5 nm diameter and 15 nm length, deposited by drop casting on a carbon-coated grid.

Generally, the inclusion of nanorods into an organic polymer matrix leads to the formation of a random structure, accompanied by phase separation, aggregation of nanoparticles, and loss of transparency.^26,29 In order to minimize these undesired effects in the film we fabricated a CdSe/CdS NR–polymer composite film by combining the CdSe/CdS NRs with an electron-sensitive polymer (PMMA) which was soluble in the same solvent of the nanorods.

After blending the nanoparticles with the polymer the 2D ThMo-PQC structures were fabricated by a single high-resolution lithographic step using an EBL technique. All fabrication details are reported in the sample fabrication section.

The Thue–Morse structure is generated by two symbols, A and B, following the inflation rule: A → AB and B → BA.⁶ The successive ThMo strings are A, AB, ABBA, ABBABAAB, etc. Recently the ThMo inflation method has been generalized from one-dimensional to two dimensional (2D) sequence, and .^6,17–19 A (or B) stands for the presence (or absence) of a dielectric scatterer on a 2D square lattice.

The 2D ThMo structures have been experimentally obtained by removing scatterers, namely A and B, from a regular square array with a lattice constant a by EBL following the ThMo inflation rule. This forms a pattern of air filled square rods whose centres are located at the vertices of a 2D ThMo lattice of order N = 10.

We designed and fabricated two 2D ThMo-PQCs with square rods of side size d = 480 nm and lattice constant a = 720 nm and with square rods of side size d = 750 nm and lattice constant a = 1080 (Fig. 2). The experimental hybrid ThMo-PQCs realized have been characterized in the direct space through SEM metrological measurements, whereas in the reciprocal space interesting properties of the aperiodic ThMo array can be studied through the experimental determination of the Fourier spectra of the sample. The inset of Fig. 2a shows the diffraction pattern produced by a 2D ThMo-PQC, orthogonally oriented with respect to a laser beam at a wavelength of 514.5 nm. Analysis of the far field diffraction pattern of the fabricated structure reveals a lot of diffuse scattering, namely, the singular continuous part³⁰ of the diffraction pattern. The theoretical Fourier spectrum of a two-dimensional Thue–Morse structure has been calculated elsewhere and it is compatible with our findings.^18–20

Fig. 2 SEM image of the 2D ThMo-PQCs obtained by arranging square air rods into the nanocomposite; (a) square rod of side size d = 480 nm and lattice constant a = 720 nm. The inset shows the corresponding far field diffraction pattern; (b) square rod of side size d = 750 nm and lattice constant a = 1080 nm.

Bragg extraction of light

Two main ways of improving light extraction by means of PQCs can be considered: one is the use of PQC bandgaps to prevent emission in guided modes (strong PQCs); the other makes use of PQCs to couple guided modes to radiative modes (weak PQCs).³¹ In this work we harness Bragg-diffraction effects to improve light extraction efficiency from the fabricated ThMo-PQC structures.

The vertical extraction of the light, by the coupling of the modes guided by the PQC slab to the free radiation via Bragg scattering, is ruled by a phase-matching condition, namely by the conservation of the in-plane component of the momentum at the air–dielectric interface.³²

When the period of a two-dimensional photonic crystal is equal to the cavity wavelength of the guided mode, the guided waves propagating to several in-plane directions are coupled to the radiation mode in the direction normal to the device surface since the Bragg diffraction condition is satisfied.^32–36

It turns out that the hybrid ThMo-PQC can be designed to match the properties of the active photonic material by changing the geometrical parameters of the structure to obtain, eventually, enhanced performances of the PQC device.

In Fig. 3 we report the spectrally integrated light intensity characteristics of the two hybrid ThMo-PQC structures measured from the surface normal using a multimode fiber, a CCD imaging telescope and a CCD-based spectroradiometer. For comparison we also show the emission profile of the active nanocomposite with its photoluminescence peak at 603 nm. Fig. 3a is the emission profile measured along the Γ–X direction of the ThMo-PQC composed of square rods of side size d = 480 nm and lattice constant a = 720 nm; Fig. 3c shows the emission spectrum of the ThMo-PQC composed of square rods of side size d = 750 nm and lattice constant a = 1080 nm.

Fig. 3 Emission spectra measured from the surface normal. A white light is introduced from an edge of the glass and propagates inside the glass. The emission profiles of the two ThMo-PQCs are measured along the Γ–X directions: (a) square rod of side size d = 480 nm and lattice constant a = 720 nm; (c) square rod of side size d = 750 nm and lattice constant a = 1080 nm. The main peaks in the emission spectra are at wavelengths 543 nm and 711 nm and they correspond to the resonant modes of the two hybrid ThMo-PQC structures; (b) the emission profile of the active nanocomposite with its photoluminescence peak at 603 nm.

The main features of the emission spectra are the presence of narrow peaks at wavelengths of 543 nm (yellowish green) and 711 nm (red), respectively, with an FWHM of 22 nm.

Fig. 3 shows impressively the tunability of the resonance in the photonic structure with the lattice constant and the dimensions of the cell elements. As underlined above the resonant points in the photonic structure are considered to originate from different transverse guiding modes with different modal indices, which are diffracted to the normal direction by the PQC effect.

Fig. 4 shows the emission spectra measured from the surface normal for the ThMo-PQCs composed of square rods of side size d = 480 nm and lattice constant a = 720 nm coming from the comparison between an undoped sample and a doped one. The contribution of the NRs affects the extraction of light which is remarkably enhanced by their presence: the NR doped 2D ThMo-PQC enhanced the light extraction efficiency by a factor of 6.5 compared to the undoped structure. The significant enhancement of the Bragg extracted light in an NR doped sample (black curve) compared to the undoped sample (red curve) is attributed to the strong light scattering due to the doping inclusions, resulting in the enhancement of the light escaping at the sample surface. The emission spectrum of the doped sample shows a main peak at 704 nm with some less intense peaks at smaller wavelengths.

Fig. 4 Emission spectra measured from the surface normal of two ThMo-PQCs, square rods of side size d = 480 nm and lattice constant a = 720 nm, in a doped structure (a) and an undoped one (b).

Theoretical band structure

Theoretical calculations have been performed to verify and confirm the resonance at 543 nm for the ThMo-PQC with lattice constant a = 1080 nm.

Fig. 5 shows the theoretical band structure calculated using the well known plane wave expansion (PWE) method for weakly interacting ThMo-PQCs along the edge of the Γ–X–M–Γ directions in the first Brillouin zone. The PWE method (frequency domain) solves the Maxwell's equations over a periodic geometry formulated as a linear eigenvalue problem (BandSOLVE, RSoft Design Group, Ossining, NY).³⁷ In this approximation, the guided-mode dispersion curves were calculated for a one-dimensional waveguide in which the PQC was treated as a homogeneous layer with a dielectric constant of 2.3 and band bending effects were neglected in favour of simple band folding according to in-plane Bragg diffraction.

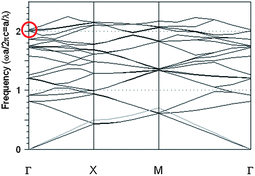Fig. 5 Dispersion relation of the 2D hybrid ThMo-PQC lattice composed of square air rods of side size 480 nm and lattice constant 1080 nm patterned in the active nanocomposite material with a dielectric constant of 2.3 for TM polarization. The circle marks the resonance point for the four bands at the singular point. The gray line in the band structure represents the light line. Modes above the light line are leaky and couple to free space.

From the curve in Fig. 5 we can say that the resonance point is found at the Γ point ωa/2πc = 2. Such a value is in agreement with the experimental value of the main resonant peak λ = 543 nm. The resulting four equivalent light waves combine at the band edge²⁸ causing a diffraction effect to take place simultaneously in a direction perpendicular to the surface.^28,37

It is worthwhile to underline that in the regime of strong PQCs band bending significantly alters the properties of light propagation and modifications of dispersion relation go beyond the pure band folding. In the case of a photonic crystal or quasi-crystal slabs in air nearly 100% extraction efficiency has been calculated, if the emission wavelength overlaps with the photonic bandgap. Since the emission into the guided modes is inhibited by the complete photonic bandgap (PBG), light can only radiate into the ambient medium resulting in high extraction efficiencies.³⁸

In our case we have no bandgaps as is evident from Fig. 5; therefore, instead of inhibition of spontaneous emission by a photonic bandgap we got an enhancement of extraction due to Bragg scattering and an increased density of photonic states.³⁹ In weak PQCs only Bragg's law of diffraction determines whether a guided mode gets folded above the light line. The lattice parameters, i.e. the lattice type, the lattice constant and the filling fraction have a strong impact on the diffraction process: they have to be chosen properly in order to obtain as much extraction as possible.

Far-field diffraction and angular spectra

An Ar⁺ laser operating on the fundamental Transverse Electromagnetic mode (TEM₀₀) at the wavelength λ = 514.5 nm with beam waist w₀ = 2 mm was used to measure the Fourier spectrum of the aperiodic hybrid ThMo-PQCs. After having spatially filtered the laser beam through a lens–pinhole–lens system, the source is incident on the sample. Through the spatial filter, the incident light is diffracted creating an Airy pattern: the central zero order has an excellent spatial coherence and represents a good approximation of a plane wave. Higher diffraction orders have highly divergent wave vectors with respect to the optical axis. The second pinhole filters only the central spot of the Airy pattern. An optical system consisting of two confocal lenses is placed between the two pinholes providing a magnification ratio of 3.47 that ensures a uniform illumination of the experimental sample having a square surface of ∼700 μm².

A CCD array coupled with a focusing lens system is finally used to acquire the far-field diffraction pattern of the structures.

The light propagating in the glass substrate, which is extracted by diffraction, was measured at room temperature using a multimode fiber, a CCD imaging telescope (OL610), and a CCD-based spectroradiometer (OL770-LED). Fig. 6 shows the angular plot of the far-field emission profiles of the ThMo-PQC slabs with a pitch of 720 nm, doped and undoped. The patterns show clearly an enhanced emission in the active ThMo-PCs, compared to the undoped ThMo lattice. The spectrally integrated emission profiles were analyzed through a polar angle dependent emission power measurement and the measurements were performed in the angular range of ±80°. The detector was moved along the Γ–X symmetric direction of the ThMo-PQC slabs.

Fig. 6 Measured angular dependence of the far-field emission profiles of ThMo-PQC slab square rods of side size d = 480 nm and lattice constant a = 720 nm doped (black curve) and undoped (red curve).

Sample fabrication

The CdSe/CdS core–shell NRs were prepared according to a procedure that was developed in a previously published work.⁴⁰ We fabricated the CdSe/CdS NR–polymer composite film by combining the CdSe/CdS NRs with PMMA of high optical transparency in the visible region and spin coating the composite solution on an ITO coated glass (1.5 cm × 2.5 cm). As an example of preparation of a typical nanocomposite solution, 0.45 ml of a polymer solution was mixed with 10 μl of the CdSe/CdS NR stock solution (4.5 nm diameter, 15 nm length, molar concentration of NRs equal to 6 × 10⁻⁶ M, in toluene). The final thickness of the nanocomposite film was about 600 nm.

The nanopatterning was impressed on the polymer film using electron beam lithography (Raith 150 system with current and area dosage of 27.8 pA at 20 KeV). PMMA was chosen as an embedding polymeric matrix for NRs since it is transparent in the visible spectral range and it is also an electron-sensitive material and can be patterned using EBL. The resist was developed in a 1 : 3 solution of MIBK (methyl isobutyl ketone) and IPA (isopropanol). The same procedure was applied to the fabrication of undoped ThMo-PQCs where the same design was imposed on PMMA.

Conclusions

In conclusion, we have presented and discussed the remarkable effect of the enhancement of light extraction in 2D photonic Thue–Morse quasicrystals in active core–shell CdSe/CdS NR–polymer nanocomposites. We proved that the tuning properties of different designed ThMo structures can match the properties of the active photonic material to obtain enhanced performance of a device. The vertical light extraction of the doped ThMo structure has been found to increase 6.5 times compared to that of the undoped structure and, depending on the geometrical parameters of the photonic structures, the resonance peak could be tuned from a narrow bluish green emission at 543 nm up to a red–NIR emission at 711 nm with a full width at half-maximum of 22 nm. We have demonstrated the possibility of employing a 2D ThMo photonic structure in active core–shell CdSe/CdS NR–polymer nanocomposites as a promising material in optoelectronic devices such as organic light-emitting diodes and solar cells in which high surface roughness is required to improve the quantum efficiency of the devices.

Notes and references

1. J. D. Joannopoulos, P. R. Velleneuve and S. Fan, Nature, 1997, 386, 143–149.
2. D. Levine and P. Steinhardt, Phys. Rev. Lett., 1984, 53, 2477–2480.
3. Z. M. Stadnik, Physical Properties of Quasicrystals, New York, Springer, 1999.
4. E. Macia, Rep. Prog. Phys., 2006, 69, 397–441.
5. M. Florescu, S. Torquato and P. Steinhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155112.
6. L. Moretti and V. Mocella, Opt. Express, 2007, 15, 15314.
7. L. Dal Negro, J. H. Yi, V. Nguyen, Y. Yi, J. Michel and L. C. Kimerling, Appl. Phys. Lett., 2005, 86, 261905.
8. X. Jiang, Y. Zhang, S. Feng, K. C. Huang, Y. Yi and J. D. Joannopoulos, Appl. Phys. Lett., 2005, 86, 201110.
9. W. Man, M. Megens, P. J. Steinhardt and P. M. Chaikin, Nature, 2005, 436, 993–996.
10. M. D. B. Charlton, M. E. Zoorob and T. Lee, Proc. SPIE, 2007, 6486, 64860R1.
11. C. Jin, B. Cheng, B. Man, Z. Li, D. Zhang, S. Ban and B. Sun, Appl. Phys. Lett., 1999, 75, 1848–1850.
12. W. Steurer and D. Sutter-Widmer, J. Phys. D: Appl. Phys., 2007, 40, R229.
13. L. Dal Negro, M. Stolfi, Y. Yi, J. Michel, X. Duan, L. C. Kimerling, J. Le Blanc and J. Haavisto, Appl. Phys. Lett., 2004, 84, 5186.
14. F. Qiu, R. W. Peng, X. Q. Huang, Y. M. Liu, M. Wang, A. Hu and S. S. Jiang, Europhys. Lett., 2003, 63, 853.
15. A. Barbé and F. Von Haeseler, Int. J. Bifurcation Chaos Appl. Sci. Eng., 2007, 17, 1265.
16. L. Dal Negro, N. N. Feng and A. Gopinath, J. Opt. A: Pure Appl. Opt., 2008, 10, 064013.
17. V. Matarazzo, S. De Nicola, G. Zito, P. Mormile, M. Rippa, G. Abbate, J. Zhou and L. Petti, J. Opt., 2011, 13, 015602.
18. Y. Ming-yang, J. Zhou, L. Petti, S. De Nicola and P. Mormile, Opto-electron. Lett., 2011, 7, 346–349.
19. J. Zhou, Y. Ming-yang, L. Petti and P. Mormile, Opt. Eng., 2011, 50, 11.
20. L. Petti, M. Rippa, J. Zhou, L. Manna, M. Zanella and P. Mormile, Nanoscale Res. Lett., 2011, 13, 015602.
21. R. Krahne, G. Morello, A. Figuerola, C. George, S. Deka and L. Manna, Phys. Rep., 2011, 501, 75–221.
22. P. D. Cozzoli, T. Pellegrino and L. Manna, Chem. Soc. Rev., 2006, 35, 1195.
23. M. Zavelani-Rossi, M. G. Lupo, R. Krahne, L. Manna and G. Lanzani, Nanoscale, 2010, 35, 931.
24. K. J. Wu, et al. , Nano Lett., 2007, 7, 1908–1913.
25. L. Petti, M. Rippa, J. Zhou, L. Manna and P. Mormile, Nanotechnology, 2011, 22, 285307.
26. J. Bomm, A. Buchtemann, A. Fiore, L. Manna, J. Nelson, D. Hill and W. G. J. H. M. Van Sark, Beilstein J. Nanotechnol., 2010, 1, 94–100.
27. I. Suarez, H. Gordillo, R. Abargues, S. Albert and J. Martınez-Pastor, Nanotechnology, 2011, 22, 435202.
28. S. Noda, J. Lightwave Technol., 2006, 24, 4554.
29. V. M. Rotello, Semiconductor Nanoparticles: Synthesis, Properties, and Integration into Polymers for the Generation of Novel Composite Materials, in Nanoparticles-Building Blocks for Nanotechnology, New York, Springer, 2004.
30. M. Rattier, H. Benisty, E. Schwoob, C. Weisbuch, T. F. Krauss, C. J. M. Smith, R. Houdre and U. Oesterle, Appl. Phys. Lett., 2003, 83(7), 21.
31. C. Wiesmann, K. Bergenek, N. Linder and U. T. Schwarz, Laser Photonics Rev., 2009, 3, 262–286.
32. S. Fan, P. R. Villeneuve, J. D. Joannopoulos and E. F. Schubert, Phys. Rev. Lett., 1997, 78, 3294.
33. M. Fujita, K. Ishihara, T. Ueno, T. Asano, S. Noda, H. Ohata, T. Tsuji, H. Nakada and N. Shimoji, Jpn. J. Appl. Phys., 2005, 44, 3669–3677.
34. C.-F. Lai, C.-H. Chao, H.-C. Kuo, H.-H. Yen, C.-E. Lee and W.-Y. Yeh, Appl. Phys. Lett., 2009, 94, 123106.
35. C.-F. Lai, H.-C. Kuo, P. Yu, T.-C. Lu, C.-H. Chao, H.-H. Yen and W.-Y. Yeh, Appl. Phys. Lett., 2010, 97, 013108.
36. Y.-J. Lee, S.-H. Kim, G.-H. Kim, Y.-C. Lee and Y. R. Do, Opt. Express, 2005, 13, 5864–5870.
37. Optical Properties of Photonic Crystals, ed. K. Sakoda, Springer, Berlin Heidelberg, 2005.
38. M. Fujita, S. Takahashi, Y. Tanaka, T. Asano and S. Noda, Science, 2005, 308, 1296.
39. M. Boroditsky, R. Vrijen, T. F. Krauss, R. Coccioli, R. Bhat and E. Yablonovitch, J. Lightwave Technol., 1999, 17, 2096.
40. L. Carbone, et al. , Nano Lett., 2007, 7, 2942.

---

Footnotes

† Authors would like to thank Dr George Chandramohan for helpful discussions.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c2nr31839c

---