Protein disorder in the centrosome correlates with complexity in cell types number

Abstract

Here we study the properties and the evolution of proteins that constitute the Centrosome, the complex molecular assembly that regulates the division and differentiation of animal cells. We found that centrosomal proteins are predicted to be significantly enriched in disordered and coiled-coil regions, more phosphorylated and longer than control proteins of the same organism. Interestingly, the ratio of these properties in centrosomal and control proteins tends to increase with the number of cell-types. We reconstructed indels evolution, finding that indels significantly increase disorder in both centrosomal and control proteins, at a rate that is typically larger along branches associated with a large growth in cell-types number, and larger for centrosomal than for control proteins. Substitutions show a similar trend for coiled-coil, but they contribute less to the evolution of disorder. Our results suggest that the increase in cell-types number in animal evolution is correlated with the gain of disordered and coiled-coil regions in centrosomal proteins, establishing a connection between organism and molecular complexity. We argue that the structural plasticity conferred to the Centrosome by disordered regions and phosphorylation plays an important role in its mechanical properties and its regulation in space and time.

---

Introduction

The centrosome is a dynamic molecular organelle that regulates microtubule nucleation and has an important role in the division and differentiation of animal cells,^2,3 in particular in asymmetric cell division, although it is not strictly necessary for development.⁴ The structure of the centrosome may be different in different cell types and organisms. It contains a pair of differentiated centrioles, highly structured macromolecular complexes that generally consist of nine microtubule (MT) triplet blades arranged in a cylinder, although exceptions are known. Centrioles also build the basal bodies required for the formation of cilia and flagella, and they were probably present in the common ancestor of all eukaryotes.⁶ In the centrosome, the centrioles are surrounded by a protein matrix called pericentriolar material (PCM) that lacks any discernible large scale structure and provides the main microtubule-nucleating activity of the centrosome. The relationship between abnormal number of centrioles and cancer has been proposed since long,⁷ and mutations in the centrosomes are related with several human diseases, most notably in brain development.^8–10

Recently, a large scale proteomic experiment has identified 114 proteins localized in the human centrosome.¹¹ Motivated by this study, Nogales-Cadenas et al.¹² retrieved from public databases such as Ensembl,¹³ the Human Protein Reference Database (HPRD)¹⁴ and MiCroKit¹⁵ a large number of genes annotated as centrosomal from previous literature evidence, collecting a total of 465 likely centrosomal human genes that constitute the CentrosomeDB http://centrosome.dacya.ucm.es. We take advantage of this knowledge in order to address some general aspects of the structural organization of the centrosome. Workers in the field know that proteins in the centrosome tend to be large, disordered and coiled-coil, and that phosphorylation plays a very important role in the dynamic organization of the centrosome. Here we quantify these properties, comparing them with analogous properties of non-centrosomal (control) proteins, and we investigate their evolutionary origin.

Disordered regions are protein fragments that do not take a well-defined three dimensional structure unless they form specific interactions. Experimental techniques to identify them include, among others, X-ray crystallography, where disordered regions are characterized as regions lacking electron density, nuclear magnetic resonance, using new methodologies that allow the assignment of resonances to unfolded and partially folded regions, circular dichroism, that allows to detect the lack of rigid structure of regions containing aromatic residues, and small-angle X-ray scattering (SAXS) and other techniques that allow to measure the hydrodynamic radius of a protein.¹⁶ Disordered regions are abundant in eukaryotic proteins,¹⁷ in particular in proteins that take part in cell regulation such as for instance transcription factors.¹⁶ This suitability of disordered proteins for regulatory functions is often attributed to the fact that disorder is thought to promote molecular interactions (either protein–protein or protein–DNA) with high specificity and low affinity, as needed in complex regulatory processes.¹⁶ Furthermore, disorder endows proteins with the structural plasticity necessary for multiple partner binding, so that it was proposed that it can provide the structural basis for the promiscuity of hubs in protein–protein interactions networks.¹⁸ Disorder is frequently found in interaction hubs, more in dynamic hubs forming transient interactions than in static hubs.¹⁹ Moreover, disordered proteins have a large propensity to interact between themselves.²⁰ These observations suggest that disordered proteins are frequently encountered in complex molecular machines such as the Centrosome.

Disordered regions are frequently phosphorylated,²¹ and their intrinsic structural flexibility amplifies the structural effect of the negatively charged phosphate, causing large conformation changes that control the capacity of the protein to recognize different partners. Protein kinases exert a coordinate control of cell physiology, in particular during the different phases of mitosis, using the centrosome as a scaffold that allows them to coordinate their action.²² These observations indicate a deep relationship between protein disorder, phosphorylation, and the centrosome.

Coiled-coil structures consist of homopolymeric or heteropolymeric bundles of long α-helical stretches formed by repeats of a typical heptameric hydrophylic/hydrophobic motif that are stabilized through hydrophobic or electrostatic interactions with their interactions partners.²³ Coiled-coil structures are very frequent in centrosomal proteins, and we found that they are frequently predicted to be disordered. This is consistent with previous observations that proteins with coiled-coil structure tend to be enriched of disordered regions.²⁴ A large scale proteomic experiment on thermostable proteins expressed in mouse fibroblast cells found that more than 2/3 of these proteins are predicted to be substantially disordered, and that disordered domains and coiled-coil domains occur together in a large number of expressed proteins.²⁵ Another study found that coiled-coils are often predicted to be unstructured, consistent with their obligate multimeric nature.²⁶ These predictions suggest that many coiled-coil proteins are disordered prior to molecular interaction, consistent with the finding that their sequence complexity is typically lower than for globular proteins.²⁴

Several recent experimental results are consistent with this view. For instance, the basic-helix-loop-helix-leucine-zipper domains of the c-Myc oncoprotein and its obligate partner Max are intrinsically disordered monomers that undergo coupled folding and binding upon heterodimerization forming a parallel coiled-coil.²⁷ Chibby, a small and highly conserved protein that plays an antagonistic role in Wnt signaling, has an N-terminal portion that is predominantly unstructured in solution, while its C-terminal half adopts a coiled-coil structure through self-association,²⁸ and the intrinsically disordered Thyroid cancer 1 protein interacts with Chibby via regions with high helical propensity, which strengthen their helical structure upon addition of Chibby.²⁹ Dynein light chain (LC) 8 interacts with the natively disordered N-terminal domain of the dynein intermediate chain (IC), promoting self-association of two IC chains at a region predicted to form a coiled-coil.³⁰ Prostate apoptosis response factor-4 (Par-4) is an intrinsically disordered protein that contains a highly conserved coiled-coil region that serves as the primary recognition domain for a large number of binding partners and self-associates via the C-terminal domain, forming a coiled-coil that is stabilized through an intramolecular association.³¹ The protein FIP2, which interacts with Rab11, a key regulator of plasma membrane recycling, has a C-terminal fragment that is disordered in the absence of Rab11, but acquires helical structure upon binding with it.³² The Huntingtin-interacting protein 1 (HIP1), obligate interaction partner of the protein that triggers Huntington's disease, was partly solved by X-rays and partly modeled as two coiled-coil domains linked by a disordered region that allows it to assume a U-shape upon interaction.³³ Even bacterial proteins present similar phenomena, for instance helical filaments of bacterial flagella are built up by a self-assembly process from thousands of flagellin subunits whose terminal regions are disordered. Removal of C-terminal segments or truncation at both ends result in the complete loss of binding ability, consistent with the coiled-coil model of filament formation, which assumes that the α-helical N- and C-terminal regions of axially adjacent subunits form an interlocking pattern of helical bundles upon polymerization.³⁴ Furthermore, bacterial gene clusters encoding type III secretion system (T3SS) code for small hydrophylic proteins whose amino acid sequences display a propensity for intrinsic disorder and coiled-coil formation. These properties were confirmed experimentally for the HrpO protein from the T3SS of Pseudomonas syringae, which exhibits high α-helical content with coiled-coil characteristics, low melting temperature, structural properties that are typical for disordered proteins, and a pronounced self-association propensity, most likely via coiled-coil interactions, suggesting that the flexibility and propensity for coiled-coil interactions of these proteins might play an important role for establishing the protein–protein interaction networks required for T3SS function.³⁵

We find here that regions that are both disordered and coiled-coil constitute the structural signature of centrosomal proteins.

Results

In this paper, we study centrosomal and control proteins from six animal species, two invertebrates (Caenorhabditis elegans and Drosophila melanogaster) and four vertebrates (Danio rerio, Xenopus tropicalis, Gallus gallus and Homo sapiens), and the yeast Saccharomyces cerevisiae as an out-group. These species cover a broad phylogenetic range, which allows us to investigate distant phylogenetic events in animal evolution. The choice of species was determined by the availability of orthologous proteins in the Compara database³⁶ of the Ensembl project,¹³ which mainly contains vertebrate genomes. The phylogenetic classification of C. elegans, D. melanogaster and vertebrates is currently subject of controversy about two competing hypothesis: the Ecdysozoa clade grouping Nematodes and Arthropods^37–39 and the traditional Coelomata clade grouping Arthropods and Vertebrates.^40–42 Despite our data strongly support the Coelomata clade, we verified that our results are robust with respect to both trees. As an order of magnitude estimate of divergence time, we quote in Fig. 1 divergence times obtained through a calibration of amino-acid substitution rates with the fossil record of vertebrates,⁴³ based on the Coelomata hypothesis. Besides being classified on a phylogenetic tree, the species that we consider can be ordered according to their estimated number of cell types¹ from less to more complex (see Fig. 1).

Fig. 1 Phylogenetic tree of the six model organisms used for this study. The number into brackets indicates the estimated number of cell types according to ref. 1. The approximate divergence estimated by ref. 43 is also shown. The tree is based on the Coelomata hypothesis according to which Arthropod is a sister group of vertebrates.

Centrosomal proteins for species other than humans were derived from the list of 465 human centrosomal proteins¹² by gathering orthologous proteins from the Compara database³⁶ of the Ensembl project,¹³http://www.ensembl.org. The set of control proteins was constructed with the same procedure starting with a randomly drawn set of 465 human genes. In this way, the unavoidable bias inherent in using the experimental information for human proteins and extending it to other species is present both in the centrosomal and in the control set, so that their comparison should be free from this bias.

Centrosome proteins tend to be disordered, coiled-coil, modular and heavily phosphorylated

We predicted disordered residues for all proteins in our data-sets using four publicly available algorithms: DISOPRED2,¹⁷ FoldIndex,⁴⁴ IUPred⁴⁵ and DisEMBL.⁴⁶ These algorithms use quite different methods and yield very consistent predictions and similar qualitative behaviors. DISOPRED2 and FoldIndex yield the most similar results and DisEMBL yields the most different results from the other predictors. We present in the main text results obtained with DISOPRED2, which was found to be the most accurate disorder predictor in a recent comparison.⁴⁷ Fig. S2 (ESI‡) shows that qualitative results are robust with respect to the predictor used.

A known feature of centrosomal proteins is the high incidence of coiled-coil structure. These structures can be reliably predicted from the protein sequence based on their characteristic heptameric pattern of hydrophobic and hydrophylic residues.²³ We used two algorithms, ncoil⁴⁸ and Pcoils,⁴⁹ to predict coiled-coils in the proteins of our data sets. These two algorithms yield very similar predictions: with a cut-off of⁴⁹ equal to 0.75, 61% of the predictions of either algorithm coincide. Moreover, they provide exactly the same qualitative picture (see Fig. S3, ESI‡). In the following, we present results obtained with the ncoil algorithm.

We computed the propensity of coiled-coil predictions and disorder prediction to occur at the same site through the formula p(x,y) = ln(P(x,y)/P(x,y)P(x,y)), where x and y represent the event that a given site is predicted as disordered and coiled-coil. Propensity is related to mutual information, and it also allows to detect the sign of the correlation: positive propensity means that x and y tend to co-occur more than at random (here this refers to co-occurrence of disorder and coiled-coil predictions).

Consistent with previous theoretical and experimental work,^24–35 we found that there is a positive propensity to predict a residue as coiled-coil if it is predicted to be disordered. This propensity is not a trivial consequence of overlapping training sets for the two predictors, since disordered regions lack any stable structure unless they interact with their binding partner, and they are characterized as regions that lack electron density in X-ray crystallography experiments, whereas coiled-coil regions are characterized as long α helices in the same experiments. Regions predicted both as disordered and coiled-coil may represent disordered regions that take coiled-coil structures upon binding with their proper binding partner. The view that coiled-coil proteins are often disordered prior to molecular interaction is consistent with previous theoretical and experimental work.^24–35 We found that propensities are significantly positive for all data-sets and all pairs of disordered and coiled-coil predictors, except for a few data-sets using the DisEMBL predictor. Using ncoil or Pcoils for coiled-coil predictions yields the same propensities within the statistical error. Therefore, the correlation between disorder and coiled-coil does not depend on the predictors used.

Interestingly, propensities are slightly but systematically larger for control than for centrosomal proteins and, for the latter, they tend to decrease with organism complexity, see Fig. S1 (ESI‡) consistent with the fact that in centrosomal proteins of more complex organisms there is a larger fraction of residues predicted to be disordered but not coiled-coil (see below).

We distinguish in Fig. 2 all four combinations of coiled-coil and disorder predictions, with the following results. (1) The fraction of residues predicted to be both disordered and coiled-coil is significantly larger in centrosomal than in control proteins for all organisms and it increases with the complexity (number of cell types) of the organism. The ratio of this fraction between centrosomal and control proteins also increases with the number of cell types (Fig. 2, top right). (2) The fraction of residues predicted to be disordered and not coiled-coil is significantly larger in centrosomal than in control proteins in vertebrates, but the difference is not significant in other organisms (Fig. 2, top left). Strikingly, whereas for control proteins the maximum amount of disorder is reached for D. melanogaster, the amount of disorder in centrosomal proteins tends to increase with the complexity (number of cell types) of the organism. (3) Finally, the fraction of residues predicted to be coiled-coil but not disordered is one order of magnitude smaller than those predicted to be both disordered and coiled-coil, it does not show significant differences between centrosomal and control proteins, and it does not vary significantly for different species (Fig. 2, bottom left). (4) As a consequence of these results, the fraction of globular residues (neither disordered nor coiled-coil) is significantly smaller in centrosomal than in control proteins and it decreases with the complexity of the organism, as shown in Fig. S4 (ESI‡). One can see that the fraction of disordered residues is larger for centrosomal than for control proteins for all model organisms, but the difference is only significant for vertebrates, and that disorder in centrosomal proteins tends to increase with the complexity of the organism. This behavior is robust with respect to the disorder predictor (Fig. S2, ESI‡). We obtained the same trend counting the fraction of proteins containing stretches with at least 40 consecutive disordered residues, which are likely to have functional relevance.

Fig. 2 Fraction of centrosomal and control residues predicted as disordered and not coiled-coil (top left), disordered and coiled-coil (top right, note the different scale), coiled-coil and not disordered (bottom left) and phosphorylated (bottom right, in this case the fraction is with respect to the number of serine, threonine and tyrosine residues). In each figure, solid lines refer to centrosomal proteins and dashed lines refer to control proteins. The insets show the ratio between centrosomal and control proteins.

We conclude that centrosomal proteins are enriched in disordered and coiled-coil regions in all organisms, with the enrichment correlated with the organism complexity, and they are enriched in disordered and not coiled-coil regions in vertebrates, whereas coiled-coil but not disordered regions are scarce and not significantly different from those in control proteins. As a consequence of these results, there is significant correlation between the amount of disorder and coiled-coil present in the same protein. Interestingly, these correlations are significantly stronger for centrosomal proteins than for control proteins, see Fig. 4.

We tested that the difference between centrosome and control proteins is not influenced by the fact that the control data-set contains extracellular proteins, whereas centrosomal proteins are intracellular. When we eliminated extracellular proteins from the control data-set using the Blast2GO suite,⁵⁰ we found that the differences between control and centrosome did not change at all concerning the coiled-coil fraction, and even increased concerning the disordered fraction. We also tested that the results were not a consequence of the fact that centrosomal proteins tend to be longer than control proteins, by taking a control data-set with the same length distribution of the centrosomal data-set, see Fig. S5 (ESI‡).

We then predicted phosphorylated residues using the GPS⁵¹ and NetPhos⁵² algorithms (see Methods). The fraction of serine, threonine and tyrosine (S, T, Y) residues predicted as phosphorylated is shown in Fig. 2, bottom right. We found that the fraction of phosphorylated residues is significantly larger in centrosomal than in control proteins for all vertebrates but not for invertebrates. There are two known factors that can contribute to enhanced predicted phosphorylation in the centrosome. First, centrosomal proteins tend to contain a larger number of S, T, Y residues, and therefore they tend to have a larger number of predicted phosphorylation sites. This possible artifact is eliminated with the normalization that we adopt. Secondly, disordered regions are enriched in Proline residues and basic residues that are frequently found in motifs recognized by kinases and used by phosphorylation predictors. This bias is very difficult to correct, and it can be a genuine phenomenon. In fact, disordered regions are more accessible to kinases and more plastic and they tend to be phosphorylated more often than other regions. This fact is used in a phosphorylation prediction algorithm,²¹ but not in the algorithms that we adopted, thus we believe that this correlation is not an artifact of the predictors but a genuine effect. Interestingly, the correlation between the predicted phosphorylation fraction of a protein and its fraction of predicted disordered residues is usually stronger in centrosomal than in control proteins, although the difference is small, see Fig. 4. We also compared phosphorylation predictions for kinases associated to the Centrosome, such as the families Polo, Aurora, Cdk and Nek2, with those for other kinases. Centrosomal kinases are more enriched than other kinases in the centrosomal set for all species except D. melanogaster, however the difference is only a few percents and it is hardly significant, since the same motif is very often predicted as being recognized by several kinases.

It is known that centrosomal proteins tend to be rather long. We found that they are on the average from 5 to almost 30% longer than control proteins for all of our model organisms, see Fig. 3 left inset. Neither the mean length of centrosomal proteins nor the mean length of control proteins are correlated with the complexity of the organism, but the ratio between them is significantly correlated with the number of cell types (correlation coefficient r = 0.76, student-t = 2.6, P < 0.05, not shown). This increased length of centrosomal proteins with respect to control proteins is achieved by different means in different organisms. We plot in Fig. 3 the mean number of exons per protein (left plot) and the mean exon length (right plot). Whereas for yeast the number of exons is essentially the same in centrosomal and control proteins but exons are substantially longer in the former, for worm and fly exons are both more numerous and longer for centrosomal proteins than for control proteins, and for vertebrates the number of exons is much larger in centrosomal than in control genes while exon length is slightly smaller. As a consequence, the mean number of exons per gene is significantly correlated with the number of cell types both for control proteins (r = 0.87, P < 0.01, not shown) and, more strongly, for centrosomal proteins (r = 0.94, P < 0.001, not shown), and the ratio between them is also significantly correlated (r = 0.81, P < 0.01, not shown). Exon length is negatively but not significantly correlated with the number of cell types both for control (r = −0.64, not shown) and for centrosomal proteins (r = −0.66, not shown). The ratio between them is strongly negatively correlated with the number of cell types (r = −0.99, P < 10⁻⁵, Fig. 3 right inset), i.e. centrosomal exons are shorter than control exons by a factor that is strongly correlated with the number of cell types. Summarizing, genes of more complex organisms tend to contain more modules and these modules tend to be shorter. Both trends are enhanced in the centrosome in a way that is quantitatively correlated with the number of cell types.

Fig. 3 Relationship between disorder content and gene length. Left: the number of exons per gene tend to be larger in centrosomal genes than in control genes, in particular for more complex organisms, and this number tends to increase with organism complexity. Left inset: Centrosomal proteins tend to be longer than control proteins. Right: exons tend to be larger in centrosomal than in control genes, in particular for simpler organisms. Right inset: the ratio between the length of centrosomal exons and the length of control exons tends to decrease with organism complexity.

For each organism, we measured the correlation between the length of a protein and its fraction of disordered and coiled-coil residues. Both correlations are almost always positive, see Fig. 4 and they are typically larger for centrosomal than for control proteins (except disorder-length correlation in fly and coil-length correlations in yeast). Our data sets contain from 85 to 465 proteins, so that correlation coefficients larger than 0.2 can be regarded as significant and this figure goes down to 0.10 for human proteins. For the set of centrosomal proteins the correlations between protein size on one hand and disorder or coiled-coil fraction on the other hand are significant for all species except C. elegans, whereas they are almost never significant for control proteins. This means that long centrosomal proteins tend to contain a larger fraction of disordered and coiled-coil residues. As we will see in the next section, this can be explained by the fact that highly disordered proteins evolve through the addition of long disordered stretches.

Fig. 4 Correlation coefficients between different properties of centrosomal and control proteins in model organisms are reported in colour code. The fraction of predicted disordered residues tend to be more correlated with the fraction of predicted coiled-coil residues in centrosomal than in control proteins, and both fractions tend to be more correlated with chain length (except for D. melanogaster and S. cerevisiae), so that longer centrosomal proteins tend to contain a larger fraction of disordered and coiled-coil residues. Disorder is also correlated with the predicted fraction of phosphorylation sites per S, T and Y residue. Both phosphorylation predictors GPS and NetPhos yield similar correlations, but systematically stronger for GPS. Here we use the intersection of the two predictions.

Evolutionary analysis of disorder and coiled-coil

The results reported above naturally raise the question of how the disorder content changed in evolution. To address this question, we performed multiple sequence alignments⁵³ of the protein sequences corresponding to the longest isoform of each putative orthologous gene in the Compara database.³⁶

Pairwise comparisons

First, we identified disorder gains between all pairs of model organisms. A disorder gain happens when a residue predicted to be disordered in organism a is absent or predicted to be ordered in organism b. We distinguish between five mutually exclusive mechanisms: (1) Np (new protein): the residue belongs to a gene that has no ortholog in organism b. If organism a has two paralogous genes corresponding to a single gene in organism b, one of the paralogs is considered a new protein and the other one is aligned with the protein in b. (2) Li (large indel): it belongs to a region that is aligned to a gap more than 20 residues long of the orthologous protein of organism b; (3) Si (short indel): same situation, but with a gap of fewer than 20 residues; (4) Su (substitution): it is aligned to an ordered residue in organism b that has undergone an amino acid substitution; (5) Co (conservation): it is aligned to a conserved residue in organism b, but this residue is ordered, which means that the change from disorder to order or the other way round has been produced by mutations at other positions. In this way, we measure which fraction of the disorder gain in the evolution between species b and a arises through each of the five mechanisms Np, Li, Si, Su and Co. Note that the expression “disorder gain” of organism a with respect to b refers to two distinct processes: either residues that were ordered in the common ancestor of a and b became disordered in a, or residues that were disordered in the common ancestor became ordered in b. Similarly, the Np mechanism refers either to proteins appeared in the branch leading to a or to proteins lost in the branch leading to b. Note that the way in which the data-sets are constructed may be biased. Disordered proteins tend to evolve faster than globular proteins, therefore it is difficult to identify their orthologs. This may partly explain the large incidence of disorder in the Np category. We face this unavoidable bias in two ways: first, we concentrate our analysis on large indels, which do not suffer of the problem of ortholog identification; second, we compare centrosomal proteins to a control data-set constructed exactly in the same way, which suffers of the same potential bias.

The way in which we constructed the data sets only allows us to examine the Np mechanism when species a is H. sapiens, because the human data-set always contains a protein in each family by construction, therefore we present this case in Fig. 5, where each point refers to the comparison of H. sapiens with another species. One can see that most of the disorder gain in H. sapiens arises either because of the Np or because of the Li mechanism. The sum of these mechanisms is at least 85% for all comparisons, but for species closely related to H. sapiens the percentage of disordered residues arising from new proteins (Np) decreases, as expected, and the percentage arising from long insertions (Li) increases. This trend is qualitatively similar for control proteins, but the contribution of large indels is much larger for centrosomal than for control proteins, in particular in the comparison between closely related species. A similar trend is also observed for coiled-coil residues. In this case, large indels contribute to coiled-coil gain much more in centrosomal than in control proteins. An important difference between disorder and coiled-coil is that the relative contribution of substitutions and residue conservation to coiled-coil gain is much larger than their contribution to disorder gain. Summarizing, new (loosely speaking) disordered and coiled-coil regions have a strong tendency to evolve modularly from large indels both in control proteins as well as in centrosomal proteins, but this tendency is much stronger in centrosomal proteins, which evolve much more modularly. The contribution due to substitutions is very weak for disorder gain, but it is relevant for coiled-coil gain.

Fig. 5 Origin of disordered residues in human centrosomal proteins. For all disordered residues that are disordered in human centrosomal proteins but not in proteins of other species we count how many of them are found in human proteins that do not have orthologs in the other species (black), how many of them correspond to gaps with more than 20 a.a. in the other species (red), to short gaps with fewer than 20 a.a. (green), to substituted amino acids (blue) and to conserved amino acids that change their nature from ordered to disordered (pink).

The above analysis of disorder gain was complemented by the analysis of the disorder flux from species a to species b, defined as the number of changes from residues that are ordered in species a and disordered in species b (gain) minus the number of changes from residues that are ordered in species b and disordered in species a (loss) for each kind of mechanism and each pair of species. These pairwise comparisons are presented in Fig. S6 (ESI‡). As expected from the fact that the proteins of organisms other than human are collected gathering orthologs of human proteins, we found that the disorder flux due to the New proteins mechanism always goes towards the more complex species or it is zero. The disorder flux due to large insertions is more interesting. This flux mostly goes towards the more complex species, but sometimes it goes towards the less complex species, notably Drosophila proteins gain disorder due to large insertions compared with vertebrate proteins. Substitutions contribute very little to the disorder flux: Typically, the net gain of disordered residues per protein in the human-worm and fly-worm comparison is 70 disordered residues through large insertions and only 5 residues through substitutions. This indicates that large indels and new proteins are quantitatively much more important than substitutions as a mechanism for the evolution of disorder. In contrast, the net gain of coiled-coil residues due to substitutions is large and positive in the comparisons from invertebrates to vertebrates, and it is much stronger for centrosomal than for control proteins, see Fig. S7 (ESI‡).

Nevertheless, pairwise comparisons do not give a very clear picture since they are not independent: for n = 7 species there are n(n − 1)/2 = 21 pairs of species, whereas the phylogenetic tree only contains 2n − 3 = 11 independent branches. We then tried to reconstruct the history of insertions and deletions leading to the current distribution of indels in multiple protein alignments.

Molecular clock for centrosomal proteins

Preliminary to the phylogenetic reconstruction, we tested that the multiple sequence alignments have sufficient quality for evolutionary inference. Specifically, for all pairs of species a and b we obtained the pairwise normalized sequence identity between all aligned residues of the two species, S_ab ∈ {0,1}, and we derived the Poisson's estimate of the divergence time as t_ab ≈ −log(1 − S_ab). We found that this estimated divergence time is approximately ultrametric, i.e. it is the same within the statistical error for all pairs of species with the same phylogenetic distance, such as for instance H. sapiens versus D. melanogaster and D. rerio versus D. melanogaster, so that it unambigously allows to reconstruct the phylogenetic tree. t_ab correlates almost perfectly with the divergence time estimated in ref. 43 from calibrated substitution rates, with intercept equal to zero within the error, see Fig. 6. The notable exception is the comparison between yeast and all animal species, in which case the divergence time is clearly underestimated. We speculate that this may be due to the large effective population size of yeast compared to animal populations, which is expected to slow down evolution on the branch with the larger population size.⁵⁴ Interestingly, centrosomal proteins evolve significantly more slowly than control proteins in the branch of yeast, which suggests that they are under stronger selective constraints than control proteins.

Fig. 6 Divergence time estimated from the fossil record (abscissa) and from multiple sequence alignments (ordinate) for all model species pairs. Black symbols refer to centrosomal proteins and red symbols refer to control proteins. The small panels represent control proteins divergences versus divergence times estimated in two competing hypothesis: Coelomata (the divergence between C. elegans and the clade constituted by D. melanogaster plus vertebrates happened ≈800 My ago, and the divergence between D. melanogaster and vertebrates happened ≈700 My ago) and Ecdysozoa (the divergence between vertebrates and the clade constituted by D. melanogaster plus C. elegans happened ≈800 My ago, and the divergence between D. melanogaster and C. elegans happened ≈700 My ago). One can see that data are consistent with the Coelomata hypothesis, on which the figure is based.

We note that our data strongly support the Coelomata hypothesis (grouping Arthropods and Vertebrates) with respect to the Ecdysozoa hypothesis (grouping Arthropods with Nematodes). In fact, the divergence between C. elegans and D. melanogaster, 1.029 ± 0.015, coincides within the statistical error with the divergences between C. elegans and the vertebrates (1.014 ± 0.018, 1.038 ± 0.016, 1.054 ± 0.016, 1.029 ± 0.017) and it is significantly larger than the divergence between D. melanogaster and the vertebrates (0.936 ± 0.013, 0.951 ± 0.014, 0.923 ± 0.016, 0.921 ± 0.016), see inset in Fig. 6. These data were obtained with control proteins, but the same qualitative results hold for centrosomal proteins. Note that these divergence estimates do not require any choice of an out-group and therefore they do not suffer from the artifact of long branch attraction that according to Philippe et al. produced the impression of the Coelomata clade.³⁷ Moreover, they are consistent with, but not dependent on the divergence time estimated by Feng et al.⁴³ using a different set of proteins. However, since the Coelomata versusEcdysozoa hypothesis is heavily debated, we tested that our results still hold without relying on it for our evolutionary reconstruction.

Reconstructing the evolution of disorder

We then applied a parsimonious algorithm, illustrated in Fig. 7 and described in the Methods section, to reconstruct on which branches of the phylogenetic tree insertions and deletions took place, and which disorder gain or loss they produced. We preferred parsimonious reconstruction since it does not require to choose a model of evolution and to fit its parameters, as maximum likelihood. For every branch of the phylogenetic tree sufficiently long to yield enough statistics, we counted the number of proteins and long insertions that appeared on that branch and we measured their disorder content. This is reported in Fig. 8. For insertions, we take as reference the insertion in human proteins, identified as described in Methods. One can see that proteins and insertions that appeared more recently in evolution are characterized by a significantly larger disorder content than more ancient ones, and that the disordered fraction is significantly larger in centrosomal than in control proteins.

Fig. 7 Example of the reconstruction of indels histories in the multiple alignment of extra spindle pole bodies homolog 1 (ESPL1) proteins. Gaps larger than 20 residues are clustered together (boxes). Insertions in the same gap region are separated if they do not satisfy a cut-off in sequence identity. Thus the first gap region contains two insertion clusters,one for vertebrates and the other for S. cerevisiae. The origin of these insertions are attributed by parsimony to the branch leading to vertebrates (cross in the figure) and the branch leading to S. cerevisiae. The disorder/order state of each site is represented by colour code (red = disordered).

Fig. 8 Disorder fraction of new proteins (left) and large insertions (right) appearing t million years ago. The leftmost points represents proteins and insertions present in the out-groupS. cerevisiae. Solid line: centrosome. Dashed line: control. The histograms represent the number of proteins and insertions per million years appearing along the branch of the phylogenetic tree that goes to the named species. Black bars: centrosome. Dotted bars: control.

Using this parsimonious reconstruction of insertion and deletion events, we then calculated the flux of disordered residues (number of disordered residues created by an insertion minus those eliminated by a deletion) along all branches of the phylogenetic trees. Since branches do not have the same length, we transformed these fluxes into rates dividing them by the branch lengths in million years estimated in ref. 43, which are in pretty good agreement with the Poisson distance computed from multiple alignments of centrosomal and control proteins (see Fig. 6) except for the branch that goes to yeast, for which we did not compute any flux, since we used yeast just as an out-group. The resulting rates are presented in Fig. 9. Each point represents a branch in the phylogenetic tree, labeled by the time of divergence in million years, so that the branches corresponding to 750 million years refer to the divergence between the fly and the vertebrates. For each pair of branches arising from the same node, we distinguish between the high complexity growth branch (HCG) where a larger growth in number of cell types took place and the low complexity growth (LCG) branch. For instance, of the two branches arising from the fly-vertebrate node, the one leading to the vertebrates is the HCG branch and the one leading to the fly is the LCG branch. Fig. 9 is based on the Coelomata hypothesis. To verify that our results do not depend on this hypothesis, we repeated our calculations eliminating either D. melanogaster or C. elegans, obtaining plots that almost look the same as if we eliminate from Fig. 9 the points at 750 and at 815 million years, respectively. These figures are presented in Fig. S8 (ESI‡).

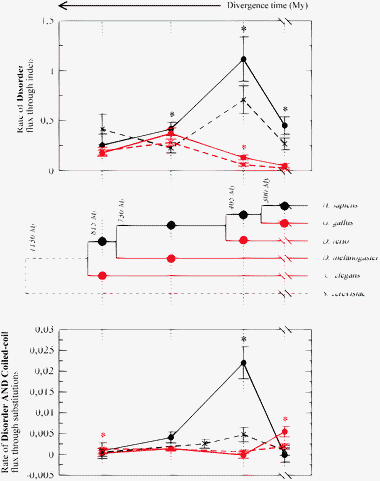Fig. 9 Rate of flux of disordered residues due to indels (top) and rate of flux of residues both coiled-coil and disordered due to substitutions (bottom) along branches of the phylogenetic tree. The abscissa shows the divergence time t in million years, for instance t = 730 My represents the splitting between vertebrates and fly. The tree is based on the Coelomata hypothesis. Not using this hypothesis gives similar results, reported in ESI.‡ For each node, we distinguish the HCG branch with larger increase in cell types (black) and the LCG branch with smaller increase in cell types (red). Centrosomal proteins are represented as solid line, control proteins as dashed lines. Disorder flux is normalized by the number of aligned proteins at each internal node. The panel below the tree represents the flux due to substitutions of residues that are both coiled-coil and disordered.

The HCG branch going from yeast to human is dissected into independent partial branches connecting bifurcation events, such as for instance the branch between the common ancestor of arthropods and vertebrates and the common ancestor of vertebrates, using 14 species (see Methods). All these species have been used to reconstruct insertion and deletion events, but we combined branches obtaining 4 HCG branches with sufficient length to give good statistics. Fig. 9 represents the rate per unit time of gain minus loss of disordered residues due to indels along HCG branches (black) and LCG branches (red), for centrosomal (circles) and control proteins (crosses). One can see that indels tend to increase the disorder along all branches both for control and for centrosomal proteins, except along the shortest LCG branch, for which the disorder flux is almost zero. The rate is always larger for centrosomal than for control proteins, except for the most ancient splitting between Nematodes and other animals where control proteins have a not-significantly larger rate both in the HCG and in the LCG branch. An asterisk in the plot means that the difference between centrosomal and control proteins is significant.

Strikingly, the disorder rate of centrosomal proteins is always larger along HCG branches than for the corresponding LCG branches, and the difference is significant for the two more recent splittings. This also holds for control proteins, but the difference between corresponding HCG and LCG branches tends to be larger for centrosomal than for control proteins, and the comparison is reversed at the splitting of Arthropods, where the LCG rate reaches its maximum. This is consistent with the pairwise comparisons, which show that D. melanogaster proteome is enriched of disordered residues both for centrosomal and for control proteins. Moreover, the difference between centrosome and control along a given branch is always larger along HCG branches than along LCG branches, and it is significant in 3 out of 4 cases for HCG branches and in 1 out of 4 cases for LCG branches. These results hold for the Coelomata hypothesis. In order not to rely on this hypothesis, we eliminated either C. elegans or D. melanogaster from the tree, finding the same qualitative results (see Fig. S8, ESI‡).

The evolution of coiled-coil through indels is qualitatively the same as the evolution of disorder both for centrosomal and for control proteins, and it is presented in Fig. S9 (ESI‡). For coiled-coils, the resulting picture is even more clear, since they do not present any exception: the coiled-coil rate is always larger for centrosomal than for control proteins, and it is always larger for the HCG branch than for the corresponding LCG branch. The evolutionary rate due to insertion is faster for disordered residues (the maximum rate is 1.1 residues per protein per million year) than for coiled-coil (the maximum rate is 0.27 residues per protein per million year) for centrosomal proteins, and it is much smaller for control proteins.

We finally examined the evolution of disordered and coiled-coil regions through substitutions, still adopting a parsimonious reconstruction of evolutionary events. The flux of disordered residues due to substitutions (gain minus loss, normalized by time) is zero within the error in most of the examined cases, and when it is significant it is much smaller than the flux due to indels, being positive five times and negative only for centrosomal proteins, along the two most ancient HCG branches, see Fig. S9 (ESI‡). The picture is more interesting for the flux of residues that are both disordered and coiled-coil (i.e. most of the coiled-coils residues). This is presented in the bottom panel in Fig. 9. The flux of coiled-coils due to substitutions is smaller by approximately a factor ten than the one due to large indels, but it is larger by a factor 3 than the corresponding flux of disordered residues. The coiled-coil flux due to substitutions is never negative, and it is significantly larger for centrosomal than for control proteins in two cases (the HCG branch at the splitting between fishes and terrestrial vertebrates, where the rate is maximum, and the LCG branch at the splitting between mammals and birds), whereas the opposite happens, but at a much smaller scale, for the LCG splitting of Nematodes. For centrosomal proteins, the rate is larger along HCG than along LCG branches in all cases except along the last HCG branch leading to mammals.

Discussion

Centrosomal proteins have a bad reputation among experimentalists for being very large and often coiled-coiled or disordered. We have quantified these trends using disorder and coiled-coil predictions. Interestingly, these predictions have a significant propensity to co-occur, i.e. the same region is predicted to be simultaneously disordered and coiled-coil, consistent with other computational studies^24–26 and with experiments that suggest that disordered regions can stabilize into a coiled-coil structure upon interaction,^2–35 which is how we also interpret these correlated predictions. This correlation exists for all organisms, and for the centrosomal and control data-sets. Nevertheless, we found that the fraction of residues that are coiled-coil and disordered is significantly larger in centrosomal than in control proteins of the same model organism, and this fraction is positively correlated with organism complexity (number of cell types) for centrosomal but not for control proteins. Furthermore, centrosomal proteins are also significantly enriched of residues that are disordered but not coiled-coil with respect to control proteins, and this enrichment is correlated with organism complexity.

Interestingly, centrosomal proteins also tend to be more phosphorylated than control proteins, and their predicted phosphorylated fraction also tends to be correlated with the number of cell types, although this is in part expected, since disordered regions and phosphorylation sites tend to have similar sequence features and kinases tend to exploit the exposure and the structural malleability of disordered regions.²¹

The main result of this work is the evolutionary analysis of disorder. We have shown that disordered regions are mainly gained in evolution through new proteins and through large insertions. Since the analysis of new proteins may be biased by the fact that it is more difficult to identify orthologs of disordered proteins, which tend to evolve faster than globular proteins, we focused our evolutionary analysis on insertions, and on the comparison between centrosome and control, which may suffer of the same bias. The disorder content of new proteins and large insertions is correlated with the time at which they appear, so that proteins and insertions that arose more recently contain a larger fraction of disordered residues. This holds true both for centrosomal and for control proteins but the effect is much stronger for centrosomal proteins. Substituted residues contribute very little to the evolution of disordered regions, and their contribution sometimes increases disorder, sometimes decreases it, most often it is neutral. In contrast, we found that the net effect of substitutions almost always tends to increase the size of coiled-coil regions, more strongly in centrosomal than in control proteins. This suggests that positive natural selection is involved in the growth of coiled-coil regions.

We then reconstructed the flux (gain minus loss) of disordered and coiled-coil residues due to long insertions along different branches of the phylogenetic tree. As a side result, we found that the simple evolutionary distance that we computed allows us to reconstruct the tree unambigously, and strongly supports the grouping of Arthropods and Vertebrates (Coelomata hypothesis) with respect to the grouping of Arthropods and Nematodes (Ecdysozoa hypothesis). Strikingly, we observed that disordered and coiled-coil regions evolved through insertion and deletion events at much faster rate along branches leading to a large growth in the number of cell types (HCG branches) than along branches leading to a small growth in cell type number (LGC branches). When it is significant, this difference is much larger for centrosomal than for control proteins, which means that, whatever the evolutionary force (mutation or selection) producing the bias between insertions and deletions and between HCG and LCG branches, this force acts more strongly on centrosomal than on control proteins.

Thus, the acceleration in the evolution of disorder and coiled-coil content along HGC branches is stronger for the centrosome, and it establishes a novel relationship between the molecular complexity of a proteome and the cellular complexity of the corresponding organism. Although complexity is a controversial concept with many possible definitions, complexity measured as the number of cell types is likely to be relevant for the evolution of the centrosome. The centrosome controls cell cycle and cell division, and it shows a remarkable plasticity in space and time. Unfortunately, order-of-magnitude estimates of cell-types numbers is only available for a few model organisms, which limited our analysis. From the molecular side, the relation between protein disorder and complexity naturally arises from the fact that disordered proteins can have a larger number of possible conformations and interaction partners, thus under this point of view they are more complex than globular proteins.

Interestingly, we found that indels tend to increase the disorder and coiled-coil content along all branches of the tree that we examined, both for centrosomal and for control proteins. This is consistent with the known fact that disordered proteins tend to evolve by repeat expansion,⁵⁵ and it can be attributed either to a mutational pattern or to positive selection. However, the fact that the rate is significantly accelerated for centrosomal proteins along the branches of high complexity growth with respect to control proteins suggests that positive selection is responsible for this acceleration. A relevant fraction (up to 1/3) of the predicted disordered residues in centrosomal proteins are also predicted to be coiled-coil. This fraction is much smaller in control proteins. Coiled-coil regions grow mainly through indels, but we also observed a significant bias to increase the content of coiled-coil residues through substitutions. When it is significant, this bias is much stronger for centrosomal proteins than for control proteins, which seems to be more consistent with positive selection than with a mutational pattern.

The fraction of predicted phosphorylated residues is much larger in centrosomal than in control proteins, even after taking into account the biased composition of centrosomal proteins that contain many more serine, threonine and tyrosine residues. The correlation between phosphorylation and disorder content is stronger in centrosomal than in control proteins, which suggests that the enhanced phosphorylation of centrosomal proteins cannot simply be explained by the known tendency of phosphorylation to take place in disordered regions. We speculate that phosphorylation and disorder are enhanced in the centrosome by an evolutionary force that favours the regulatory plasticity of centrosomal proteins. Experimental work will be needed to investigate the relationship between the increase of disorder and coiled-coil content and the biophysical properties of the centrosome. However, some hypothesis arise in a natural way. Disordered regions are frequently involved in molecular interactions, probably because they provide high specificity but low affinity interactions as those necessary for dynamically controlled processes.¹⁶ Thus, the plasticity conferred to the centrosomal proteome by disordered regions together with phosphorylation may be necessary for avoiding nonspecific interactions and may allow them to cope with the stringent requirements imposed by the very large number of interactions in the centrosome and their strict regulation in space and time.

Concerning the abundance of coiled-coil regions in centrosomal proteins, we would like to suggest two hypothesis. It is possible that the prevalence of coiled-coil regions is due to a principle of evolutionary economy, since coiled-coil are made of low complexity sequences²⁴ and combining coiled-coil interaction modules might be the simplest way to create a large super-molecular assembly,⁵⁶ which seems to be used even to assemble bacterial flagella³⁴ and secretion systems.³⁵ An alternative explanation involves natural selection. Coiled-coil residues seem to be favoured by natural selection, as suggested by the bias of substitutions to increase coiled-coil content, which is stronger in centrosomal than in control proteins. If this is the case, a possible explanation may lie in the mechanical properties of disordered coiled-coil residues that, upon folding, can change their shape from a flexible polymer with size scaling similar to a self-avoiding walk (L^0.6, where L is chain length) to a much longer stiff, rod-like molecule. This can have important consequences on the mechanical behavior of the centrosome. More precisely, we speculate that the prevalence of disordered residues in the centrosome might be due to their peculiar mechanical properties as entropic springs.⁵⁷ It has been recently found that charge interactions modulate the size of disordered proteins,⁶⁰ and that this modulation can be controlled through phosphorylation.⁵⁸ Interestingly, it has also been recently observed that the size of the centrosome varies with the pH.⁵⁹ These observations suggest that modulation of charge interactions in disordered centrosomal proteins through phosphorylation can have a physiological role in controlling the size and the mechanical properties of the centrosome as a whole, a possibility that is worth experimental evaluation.

Material and methods

Data sets

The centrosomal set was constructed starting with 465 human centrosomal genes.¹² In order to reconstruct the evolutionary history of genes, indels and substitutions, for each centrosomal gene we gathered orthologs from the Compara database of the Ensembl project,^13,36 release 55 (July 2009). This database allows to reliably identify orthologs, but unfortunately it only includes chordates and three non-vertebrate species included in this study. For each gene, we only considered the protein corresponding to the longest isoform.

We collected genes for 13 species with complete sequenced genome, chosen in such a way to divide the evolutionary distance between yeast and human in 13 independent branches. They are, in order of relatedness with respect to Human: Homo sapiens, Pan troglodytes (chimp), Macaca mulatta (macaque), Tarsius syrichta (primate), Rattus norvegicus (rat), Monodelphis domestica (opossum), Ornithorhynchus anatinus (platypus), Gallus gallus (chicken), Xenopus tropicalis (frog), Danio rerio (zebrafish), Ciona intestinalis (urochordate), Drosophila melanogaster (fruitfly), Caenorhabditis elegans (nematode worm), Saccharomyces cerevisiae (yeast). Out of these species, 7 model species for which the number of cell types is approximately known were chosen for mode detailed analysis, namely: G. gallus (370 proteins), X. tropicalis (370 proteins), D. rerio (392 proteins), D. melanogaster (241 proteins), C. elegans (206 proteins) and S. cerevisiae (104 proteins). The control set was constructed in the same way starting from 465 randomly drawn human genes, resulting in 297 proteins for G. gallus, 288 for X. tropicalis, 312 for D. rerio, 212 for D. melanogaster, 181 for C. elegans and 85 for S. cerevisiae.

Bioinformatics predictions

We used four disorder predictors: DISOPRED2,¹⁷ FoldIndex,⁴⁴ IUPred⁴⁵ and disEMBL,⁴⁶ all with the default parameters. Results in the paper are obtained with DISOPRED2, the other predictors have been used for robustness tests reported in ESI.‡

Coiled-coil structures have been predicted using the implementation by Rob Russell of the algorithm ncoil described by Lupas et al.,⁴⁸ and the more recent Pcoils algorithm.⁴⁹ Both algorithms yield the same fraction of coiled-coil residues and the same correlations between coiled-coil and disorder within the statistical error. Results presented in the paper are obtained with the ncoil algorithm.

Phosphorylation was predicted using NetPhos (portable version 3.1⁵²) and GPS 2.1.⁵¹ The significance of NetPhos predictions is given by a single score, being the default threshold (0.5) selected. GPS provides a specific threshold for each kind of kinase family and it allows to select different levels of stringency. The most stringent level has been selected in this case. Both predictors provide a similar number of significant phosphorylation sites although GPS predicts systematically a larger number of different kinases per site. In order to get a more reliable prediction, we have looked for all residues with a significant phosphorylation prediction for both algorithms. Since only serine, threonine and tyrosine residues can be phosphorylated and the fraction of such residues is different in the centrosomal and in the control set, we computed the fraction of predicted phosphorylated residues with respect to the total number of S, T or Y residues.

We estimated the statistical error as twice the standard deviation of the mean, , where p is the observed frequency of disordered (coiled-coil or phosphorylated) residues and n is the number of independent samples, estimated as n = L/30.

Multiple sequence alignments

For each human centrosomal or control protein, we gathered orthologs from 13 species using the Compara algorithm. When several paralogous genes and several isoforms of the same gene were present for the same organism, we aligned these proteins of the same organism and constructed a consensus sequence having as many positions as the multiple sequence alignment, each position containing the consensus (most frequent) amino acid. In this way also novelties in paralogous genes were counted as insertions. Then we constructed a multiple sequence alignment with one consensus proteins from each species with the program Muscle.⁵³

Pairwise comparisons

We analyzed the aligned proteins of all pairs of 7 model species, distinguishing five types of evolutionary transitions: new protein (no ortholog is found), large insertion, short insertion, amino acidic substitution or disorder change at a conserved residue (see text). Also in this case, the statistical error was estimated as twice the standard deviation of the mean. For this purpose, we considered each protein and each indel as an independent sample, whereas for aligned residues, we considered again L/30 as the number of independent samples.

Phylogenetic reconstruction of insertion/deletion events

Indels clustering. The first step of the phylogenetic reconstruction consists in clustering the insertions that are likely to be evolutionarily related. To this aim, we proceeded as follows: from the 465 alignments and for each of the model protein sequences, we gathered gaps longer than 20 positions and clustered them using as similarity measure the gap alignment overlap q, i.e. the number of shared gap positions in the alignment, divided by the length of the longest gap. We adopted single-linkage clustering and stopped the clustering when the threshold similarity falls below q = 0.8. Each of the resulting clusters represents a consensus indel region going from the first to the last alignment position of the gaps in the cluster. For each clusterm and each model species s present in the alignment, we assigned a binary variable G^m_s = 1 (insertion) if more than 50% of the cluster positions in the corresponding sequence contain amino-acids, and G^m_s = 0 otherwise (deletion).

Homology requirement. For all insertions (i.e. G^m_s = 1) in the same clusterm, we split insertions that are not homologous in different clusters. For this purpose, we computed pairwise sequence identities between insertions in the same cluster and further clustered them with single-linkage, until sequence identity fell below a length dependent threshold, t = s + (1 − s)4/L where L is the insertion length and s = 20%. In this way, the number of insertion clusters grew to 2562 for the centrosomal set and 1875 for the control set. We tested that qualitative results are robust if we vary the sequence identity parameter in the range from 0.15 to 0.25, see Fig. S10 (ESI‡).

Parsimony reconstruction. We then obtained the phylogenetic tree of the 14 species and reconstructed the evolutionary history of genes and indels. We took advantage of the simple topology of this tree, which is constituted by a main branch from which branches stem towards individual species (Coelomata hypothesis). In order not to rely on this hypothesis, we alternatively removed from the data set C. elegans and D. melanogaster, obtaining a tree with the same simple topology but one fewer species. For each clusterm we only considered model species for which the corresponding protein is present, and assigned the state of internal nodes based on parsimony, strictly forbidding horizontal transfer. Starting from the root, a protein or an insertion appears at the internal node corresponding to the first leave that bears it and disappears when no one of the descendant of the internal node bears it. State transitions between neighboring nodes where then mapped to insertion or deletion events along the corresponding branch.

Flux estimate. The disorder (coiled-coil) content of an insertion is estimated as the average number of predicted disordered residues of the daughter sequences. For each node s and gap clusterm, we define the variable D^m_s whose value is the disorder content of the insertion if G^m_s = 1, zero if G^m_s = 0, and −1 (undefined) if G^m_s = −1. In this way, indels induce a flux of disordered residues along the branches of the phylogenetic tree, defined as the difference between disorder gained through insertions and lost through deletions, summed over the gaps that are not undefined (G^m_s ≠ −1). We normalized the disorder flux dividing it by the number of proteins that are predicted to be present at the ancestral nods. Since branches have different lengths, we obtained rates dividing the flux by the length of the branch in million years estimated in ref. 43 combining molecular and fossil data. These estimates are in very good agreement with Poisson divergence times estimated from the present data. The statistical error of the estimated flux was estimated by 1000 bootstrap iterations.

Phylogenetic reconstruction of substitution events

In this case, each clusterm corresponds to a position in the alignment, only species where an amino-acid is present at that position are considered, and the state of each node may be either disordered (1) or ordered (0). The states of internal nodes are assigned by parsimony as follows. We assign to the ancestor node i the state of its sons if these states are equal, otherwise we assign it the state of the closest out-group. If there is no out-group, the state of the node is undefined, G^m_s = −1. Also in this case, the error was estimated by 1000 bootstrap iterations.

Acknowledgements

We thank the members of the Centrosome consortium, in particular Luis Serrano and Tano Gonzalez, for interesting discussions, the organizers of the workshop intrinsically disordered proteins in biomedicine, Keith Dunker for insightful comments and Manuel Irimia for drawing our attention on the Ecdysozoa hypothesis. This work was supported from the Spanish Science and Innovation Ministry through the Consolider grant CSD2006-00023, the grant BIO2008-04384, the Ramón y Cajal program (UB) and the FPI grant BES-2009-013072 to APG. Research at the CBMSO is facilitated by the Fundación Ramon Areces.

References

1. J. W. Valentine, A. G. Collins and D. P. Meyer, Morphological complexity increase in metazoans, Paleobiology, 1994, 20(2), 131–142.
2. Y. Ou, M. Zhang and J. B. Rattner, The centrosome: the centriole PCM coalition, Cell Motil. Cytoskeleton, 2004, 57, 1–7.
3. E. A. Nigg and J. W. Raff, Centrioles centrosomes, and cilia in health and disease, Cell (Cambridge, Mass.), 2009, 139, 663–678.
4. D. Gogendeaua and R. Basto, Centrioles in flies: The exception to the rule?, Semin. Cell Dev. Biol., 2010, 21(2), 163–173.
5. T. Cavalier-Smith, The phagotrophic origin of eukaryotes and phylogenetic classification of Protozoa, Int. J. Syst. Evol. Microbiol., 2002, 52(2), 297–354.
6. W. F. Marshall, Centriole evolution, Curr. Opin. Cell Biol., 2009, 21, 14–19.
7. T. Boveri (Translated and annotated by Henry Harris J) 2008. Zur frage der entstehung maligner tumoren, Gustav Fischer, Jena (1914). Concerning the origin of malignant tumours. Cell Sci., 121(1), 1–84.
8. M. Bettencourt-Dias and D. M. Glover, Centrosome biogenesis and function: centrosomics brings new understanding, Nat. Rev. Mol. Cell Biol., 2007, 8, 451–463.
9. J. Bond and C. G. Woods, Cytoskeletal genes regulating brain size, Curr. Opin. Cell Biol., 2006, 18, 95–101.
10. J. M. Gerdes, E. E. Davis and N. Katsanis, The vertebrate primary cilium in development, homeostasis, and disease, Cell (Cambridge, Mass.), 2009, 137, 32–45.
11. J. S. Andersen, C. J. Wilkinson, T. Mayor, P. Mortensen, E. A. Nigg and M. Mann, Proteomic characterization of the human centrosome by protein correlation profiling, Nature, 2003, 426, 570–574.
12. R. Nogales-Cadenas, F. Abascal, J. Díez-Pérez, J. M. Carazo and A. Pascual-Montano, CentrosomeDB: a human centrosomal proteins database, Nucleic Acids Res., 2009, 37, D175–D180.
13. P. Flicek, et al. Ensembl 2008, Nucleic Acids Res., 2008, 36(Database issue), D707–D714.
14. G. R. Mishra, et al. Human protein reference database—2006 update, Nucleic Acids Res., 2006, 34, D411–D414.
15. J. Ren, Z. Liu, X. Gao, C. Jin, M. Ye, H. Zou, L. Wen, Z. Zhang, Y. Xue and X. Yao, MiCroKit 3.0: an integrated database of midbody centrosome and kinetochore, Nucleic Acids Res., 2010, 38, D155–D160.
16. V. N. Uversky and A. K. Dunker, Understanding protein non-folding, Biochim. Biophys. Acta, 2010, 1804, 1231–1264.
17. J. J. Ward, J. S. Sodhi, L. J. McGuffin, B. F. Buxton and D. T. Jones, Prediction and functional analysis of native disorder in proteins from the three kingdoms of life, J. Mol. Biol., 2004, 337(3), 635–645.
18. A. K. Dunker, M. S. Cortese, P. Romero, L. M. Iakoucheva and V. N. Uversky, Flexible nets. The roles of intrinsic disorder in protein interaction networks, FEBS J., 2005, 272, 5129–5148.
19. D. Ekman, S. Light, A. K. Bjrklund and A. Elofsson, What properties characterize the hub proteins of the protein–protein interaction network of Saccharomyces cerevisiae?, Genome Biol., 2006, 7(6), R45.
20. K. Shimizu and H. Toh, Interaction between intrinsically disordered proteins frequently occurs in a human protein–protein interaction network, J. Mol. Biol., 2009, 392(5), 1253–1265.
21. L. M. Iakoucheva, P. Radivojac, C. J. Brown, T. R. O'Connor, J. G. Sikes, Z. Obradovic and A. K. Dunker, The importance of intrinsic disorder for protein phosphorylation, Nucleic Acids Res., 2004, 32, 1037–1049.
22. H. T. Ma and R. Y. Poon, How protein kinases co-ordinate mitosis in animal cells, Biochem. J., 2011, 435, 17–31.
23. A. N. Lupas and M. Gruber, The structure of alpha-helical coiled coils, Adv. Protein Chem., 2005, 70, 37–78.
24. P. Romero, Z. Obradovic and A. K. Dunker, Folding minimal sequences: the lower bound for sequence complexity of globular proteins, FEBS Lett., 1999, 462, 363–367.
25. C. A. Galea, A. A. High, J. C. Obenauer, A. Mishra, C. G. Park, M. Punta, A. Schlessinger, J. Ma, B. Rost, C. A. Slaughter and R. W. Kriwacki, Large-scale analysis of thermostable mammalian proteins provides insights into the intrinsically disordered proteome, J. Proteome Res., 2009, 8(1), 211–226.
26. B. Szappanos, D. Süveges, L. Nyitray, A. Perczel and Z. Gáspári, Folded-unfolded cross-predictions and protein evolution: the case study of coiled-coils, FEBS Lett., 2010, 584(8), 1623–1627.
27. A. V. Follis, D. I. Hammoudeh, H. B. Wang, E. V. Prochownik and S. J. Metallo, Structural rationale for the coupled binding and unfolding of the c-Myc oncoprotein by small molecules, Chem. Biol., 2008, 15, 1149–1155.
28. S. Mokhtarzada, C. Yu, A. Brickenden and W. Y. Choy, Structural characterization of partially disordered human Chibby: insights into its function in the Wnt-signaling pathway, Biochemistry, 2011, 50(5), 715–726.
29. C. Gall, H. Xu, A. Brickenden, X. Ai and W. Y. Choy, The intrinsically disordered TC-1 interacts with Chibby via regions with high helical propensity, Protein Sci., 16(11), 2510–2518.
30. A. Nyarko and E. Barbar, Light chain-dependent self-association of dynein intermediate chain, J. Biol. Chem., 2011, 286(2), 1556–1566.
31. D. S. Libich, M. Schwalbe, S. Kate, H. Venugopal, J. K. Claridge, P. J. Edwards, K. Dutta and S. M. Pascal, Intrinsic disorder and coiled-coil formation in prostate apoptosis response factor 4, FEBS J., 2009, 276(14), 3710–3728.
32. J. Wei, Y. Liu, K. Bose, G. D. Henry and J. D. Baleja, Disorder and structure in the Rab11 binding domain of Rab11 family interacting protein 2, Biochemistry, 2009, 48(3), 549–557.
33. Q. Niu and J. A. Ybe, Crystal structure at 2.8 A of Huntingtin-interacting protein 1 (HIP1) coiled-coil domain reveals a charged surface suitable for HIP1 protein interactor (HIPPI), J. Mol. Biol., 2008, 375(5), 1197–1205.
34. Z. Gugolya, A. Muskotl, A. Sebestyn, Z. Diszeghy and F. Vonderviszt, Interaction of the disordered terminal regions of flagellin upon flagellar filament formation, FEBS Lett., 2003, 535(1–3), 66–70.
35. A. D. Gazi, M. Bastaki, S. N. Charova, E. A. Gkougkoulia, E. A. Kapellios, N. J. Panopoulos and M. Kokkinidis, Evidence for a coiled-coil interaction mode of disordered proteins from bacterial type III secretion systems, J. Biol. Chem., 2008, 283(49), 34062–34068.
36. A. J. Vilella, J. Severin, A. Ureta-Vidal, L. Heng, R. Durbin and E. Birney, EnsemblCompara GeneTrees: Complete duplication-aware phylogenetic trees in vertebrates, Genome Res., 2009, 19(2), 327–335.
37. H. Philippe, N. Lartillot and H. Brinkmann, Multigene Analyses of Bilaterian Animals Corroborate the Monophyly of Ecdysozoa, Lophotrochozoa, and Protostomia, Mol. Biol. Evol., 2005, 22, 1246–1253.
38. H. Dopazo and J. Dopazo, Genome-scale evidence of the nematode-arthropod clade, Genome Biol., 2005, 6, R41.
39. C. W. Dunn, A. Hejnol, D. Q. Matus, K. Pang, W. E. Browne, S. A. Smith, E. Seaver, G. W. Rouse, M. Obst, G. D. Edgecombe, M. V. Soerensen, S. H. D. Haddock, A. Schmidt-Rhaesa, A. Okusu, R. Moebjerg Kristensen, W. C. Wheeler, M. Q. Martindale and G. Giribet, Broad phylogenomic sampling improves resolution of the animal tree of life, Nature, 2008, 452, 745–749.
40. G. W. Stuart and M. W. Berry, An SVD-based comparison of nine whole eukaryotic genomes supports a coelomate rather than ecdysozoan lineage, BMC Bioinf., 2004, 5, 204.
41. G. K. Philip, C. J. Creevey and J. O. McInerney, The Opisthokonta and the Ecdysozoa may not be clades: stronger support for the grouping of plant and animal than for animal and fungi and stronger support for the Coelomata than Ecdysozoa, Mol. Biol. Evol., 2005, 22, 1175–1184.
42. Igor B. Rogozin, Yuri I. Wolf, Liran Carmel and Eugene V. Koonin, Analysis of Rare Amino Acid Replacements Supports the Coelomata Clade, Mol. Biol. Evol., 2007, 24, 2594–2597.
43. D. Feng, G. Cho and R. F. Doolittle, Determining divergence times with a protein clock: Update and reevaluation, Proc. Natl. Acad. U. S. A., 1997, 94, 13028–13033.
44. J. Prilusky, C. E. Felder, T. Zeev-Ben-Mordehai, E. H. Rydberg, O. Man, J. S. Beckmann, I. Silman and J. L. Sussman, FoldIndex(C): a simple tool to predict whether a given protein sequence is intrinsically unfolded, Bioinformatics, 2005, 21(16), 3435–3438.
45. Z. Dosztanyi, V. Csizmok, P. Tompa and I. Simon, IUPred: web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content, Bioinformatics, 2005, 21, 3433–3434.
46. R. Linding, L. J. Jensen, F. Diella, P. Bork, T. J. Gibson and R. B. Russell, Protein disorder prediction: implications for structural proteomics, Structure, 2003, 11(11), 1453–1459.
47. F. L. Sirota, H. Ooi, T. Gattermayer, G. Schneider, F. Eisenhaber and S. Maurer-Stroh, Parametrization of disorder predictors for large-scale applications requiring high specificity by using an extended benchmark dataset, BMC Genomics, 2010, 11(Suppl 1), S15.
48. A. Lupas, M. Van Dyke and J. Stock, Predicting coiled coils from protein sequences, Science, 1991, 252, 1162–1164.
49. M. Gruber, J. Sding and A. N. Lupas, Comparative analysis of coiled-coil prediction methods, J. Struct. Biol., 2006, 155(2), 140–145.
50. S. Götz, J. M. García-Gómez, J. Terol, T. D. Williams, S. H. Nagaraj, M. J. Nueda, M. Robles, M. Talón, J. Dopazo and A. Conesa, High-throughput functional annotation and data mining with the Blast2GO suite, Nucleic Acids Res., 2008, 36(10), 3420–3435.
51. Y. Xue, J. Ren, X. Gao, C. Jin, L. Wen and X. Yao, GPS 2.0, a Tool to Predict Kinase-specific Phosphorylation Sites in Hierarchy, Mol. Cell. Proteomics, 2008, 7, 1598–1608.
52. N. Blom, S. Gammeltoft and S. Brunak, Sequence and structure-based prediction of eukaryotic protein phosphorylation sites, J. Mol. Biol., 1999, 294(5), 1351–1362.
53. R. C. Edgar, MUSCLE: multiple sequence alignment with high accuracy and high throughput, Nucleic Acids Res., 2004, 32(5), 1792–1797.
54. T. Ohta, Very slightly deleterious mutations and the molecular clock, J. Mol. Evol., 1987, 26, 1–6.
55. P. Tompa, Intrinsically unstructured proteins evolve by repeat expansion, BioEssays, 2003, 25, 847–855.
56. P. Burkhard, J. Stetefeld and S. V. Strelkov, Coiled coils: a highly versatile protein folding motif, Trends Cell Biol., 2001, 11, 82–88.
57. M. S. Kellermayer, S. B. Smith, H. L. Granzier and C. Bustamante, Folding–unfolding transitions in single titin molecules characterized with laser tweezers, Science, 1997, 276, 1112–1116.
58. T. Hegedus, A. W. Serohijos, N. V. Dokholyan, L. He and J. R. Riordan, Computational studies reveal phosphorylation-dependent changes in the unstructured R domain of CFTR, J. Mol. Biol., 2008, 378, 1052–1063.
59. S. Hormeño, B. Ibarra, F. J. Chichón, K. Habermann, B. M. Lange, J. M. Valpuesta, J. L. Carrascosa and J. R. Arias-Gonzalez, Single centrosome manipulation reveals its electric charge and associated dynamic structure, Biophys. J., 2009, 97(4), 1022–1030.
60. A. H. Mao, S. L. Crick, A. Vitalis, C. L. Chicoine and R. V. Pappu, Net charge per residue modulates conformational ensembles of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8183–8188.

---

Footnotes

† Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins: Guest Editor M. Madan Babu.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c1mb05199g

---