 Open Access Article
Open Access ArticleAn examination of the calcium and strontium site distribution in bioactive glasses through isomorphic neutron diffraction, X-ray diffraction, EXAFS and multinuclear solid state NMR
R. A.
Martin
*ab,
H. L.
Twyman
a,
G. J.
Rees
c,
E. R.
Barney
d,
R. M.
Moss
a,
J. M.
Smith
a,
R. G.
Hill
e,
G.
Cibin
f,
T.
Charpentier
g,
M. E.
Smith
c,
J. V.
Hanna
*c and
R. J.
Newport
*a
aSchool of Physical Sciences, University of Kent, Canterbury, Kent CT2 7NH, UK. E-mail: R.A.Martin@Aston.ac.uk
bSchool of Engineering & Applied Science and Aston Research Centre for Healthy Ageing, Aston University, Birmingham, B4 7ET, UK
cDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK
dFaculty of Engineering, University of Nottingham, Nottingham, NG7 2RD, UK
eInstitute of Dentistry, Queen Mary University of London, London, E1 4NS, UK
fDiamond Light Source, Rutherford Appleton Laboratory, Chilton, Didcot, OX11 0DE, UK
gCEA, IRAMIS, Service Interdisciplinaire sur les Systèmes Moléculaires et Matériaux, LSDRM, UMR CEA/CNRS 3299, F-91191 Gif-sur-Yvette cedex, France
First published on 11th September 2012
Abstract
Strontium has been substituted for calcium in the glass series (SiO2)49.46(Na2O)26.38(P2O5)1.07 (CaO)23.08−x(SrO)x (where x = 0, 11.54, 23.08) to elucidate their underlying atomic-scale structural characteristics as a basis for understanding features related to the bioactivity. These bioactive glasses have been investigated using isomorphic neutron and X-ray diffraction, Sr K-edge EXAFS and solid state 17O, 23Na, 29Si, 31P and 43Ca magic-angle-spinning (MAS) NMR. An effective isomorphic substitution first-order difference function has been applied to the neutron diffraction data, confirming that Ca and Sr behave in a similar manner within the glass network, with residual differences attributed to solely the variation in ionic radius between the two species. The diffraction data provides the first direct experimental evidence of split Ca–O nearest-neighbour correlations in these melt-quench bioactive glasses, together with an analogous splitting of the Sr–O correlations; the correlations are attributed to the metal ions correlated either to bridging or to non-bridging oxygen atoms. Triple quantum (3Q) 43Ca MAS NMR corroborates the split Ca–O correlations. Successful simplification of the 2 < r (Å) < 3 region via the difference method has also revealed two distinct Na environments. These environments are attributed to sodium correlated either to bridging or to non-bridging oxygen atoms. Complementary multinuclear MAS NMR, Sr K-edge EXAFS and X-ray diffraction data supports the structural model presented. The structural sites present will be intimately related to their release properties in physiological fluids such as plasma and saliva, and hence the bioactivity of the material. Detailed structural knowledge is therefore a prerequisite for optimising material design.
1. Introduction
Bioactive SiO2–Na2O–CaO–P2O5 glasses, including the original Bioglass®, have the ability to promote bone regeneration.1,2 Under physiological conditions these materials release essential elements such as Ca, P and Si, which promote the formation of hydroxyapatite (HA): the naturally occurring mineral present in both teeth and bones. Following the discovery of Bioglass, advances in biomedical research have yielded many materials for various applications including bone and tissue regeneration, drug delivery systems and dental treatments.3 The importance of Sr in biomaterials has become of increasing interest due to its radio-opacity, antibacterial properties and effects on new bone growth.4–6 Thus, the incorporation of Sr into bioactive glasses could provide scope for a number of new applications in dental and other medical fields.It is well established that cations with the same valence and a similar charge-to-size ratio can be substituted within a glass matrix. Sr and Ca have ionic radii of 1.18 and 1.00 Å, respectively,7 and this small difference allows Sr to be substituted for Ca in bioactive glasses and subsequently incorporated into HA. Indeed, Sr–Ca HA and pure Sr HA have both been reported to exist in mineral forms.8,9 Both Ca and Sr occur naturally in the body with >99% of the combined total localised in bone material.10 The concentration of Sr is typically between 0 and 3.5 mol% of the combined Ca + Sr content; however, Sr is preferentially sited in new bone structures where increases in Sr concentrations by factors of up to ∼3 to 3.5 have been observed.10 Thus, the importance of Sr has attracted an increasing research interest in recent years due to its beneficial properties: it is known to stimulate the bone-forming osteoblast cells (and inhibit the bone-resorbing osteoclasts) as well as reduce bone desorption, which consequently increases bone formation and mass without demonstrating an adverse effect on the bone mineralization process.11,12 These are all key attributes that are influential in the treatment of osteoporosis and other degenerative bone diseases. Further research has led to the therapeutic use of Sr salts in the forms of strontium ranelate and strontium chloride as treatments for osteoporosis,13–15 where their usage has led to a reduced risk in the occurrence of vertebral and non-vertebral fractures in post-menopausal osteoporosis.16,17
Strontium is also of interest in the field of dentistry. Some applications require the glasses and glass ceramics used to be relatively opaque to X-rays, in the context of post-treatment diagnostics, which can be achieved by incorporating Sr due to its greater radio-opacity compared to that of Ca.4 Strontium is also known to inhibit caries formation in teeth and promote apatite formation.18–22 In addition, Sr is used as an additive in toothpastes in the form of strontium chloride and strontium acetate to reduce tooth sensitivity. Hence, the incorporation of Sr into bioactive glasses that are currently used as remineralising additives in toothpaste is an attractive proposition. It is also worth noting that Sr has been shown to exhibit antibacterial properties6 which could be of benefit if a Sr-containing bioactive glass was to be used as an implant for bone or tissue regeneration, since it would reduce the risk of infection at the implant site and thus diminish the potential need for revision surgery.
Calcium, and in particular its release rate, is known to play a key role in the bioactivity of Bioglass, and the facile nature of Ca desorption is now reasonably well understood at the atomic scale following research on sol–gel synthesised analogues.23–25 However, the local environment that Ca adopts within melt-quench derived bioactive glasses is not as well understood. Calcium can adopt a wide range of environments in its crystalline phases; for example, the number of oxygen atoms surrounding calcium varies from 6.67 in wollastonite (CaO·SiO2) to 8 in pseudowollastonite (the high temperature phase of CaO·SiO2), whilst calcium oxide and HA have 6 and 8.4 oxygen atoms per Ca respectively.26 The corresponding Ca–O bond lengths also vary over the range 2.28–2.72 Å.26 It is anticipated therefore that Ca will have a complex local environment in amorphous bioactive glasses. In order to be able to model and predict the behaviour of such materials it is necessary to understand the local structure of the glass, particularly the local Ca environment, and secondly to monitor any differences that may arise with increasing Sr content. The dissolution of a bioresorbable glass will be determined partially by the connectivity of the glass-forming network27,28 and also in part by the local environment surrounding the active Ca2+ or Sr2+ ions.
We have therefore investigated the influence of substituting Sr for Ca in the glass series (SiO2)49.46(Na2O)26.38(P2O5)1.07(CaO)23.08−x(SrO)x (where x = 0, 11.54, 23.08) in terms of the glass' atomic-scale structural characteristics using neutron and X-ray diffraction, EXAFS and solid state 17O, 23Na, 29Si, 31P and 43Ca MAS NMR studies.
2. Experimental
2.1. Sample preparation
The melt-quenched glass samples were prepared using SiO2 (Alfa Aesar, 99.5%), Na2CO3 (Sigma-Aldrich, 99.5+%), P2O5 (Sigma-Aldrich, 98.5%), and CaCO3 (Alfa Aesar, 99.95–100.5%) and/or SrCO3 (Sigma-Aldrich, 99.9%). The precursors were heated in a platinum crucible to 1400 °C at 10 °C min−1 and held at temperature for 1.5 h. The molten glass was then poured into a pre-heated graphite mould (350 °C) and annealed at this temperature overnight before being allowed to cool slowly to room temperature.29 The composition of the three glasses prepared were (SiO2)49.46(Na2O)26.38(P2O5)1.07(CaO)23.08−x(SrO)x (where x = 0, 11.54 and 23.08) and they are labelled CaBio, CaSrBio and SrBio respectively. Isotopically enriched glasses were similarly prepared for the 17O and 43Ca NMR experiments. The 17O enriched samples were prepared using 40% enriched SiO2, the precursors were heated in an inert argon atmosphere to inhibit 17O exchange in air. 43Ca glasses were prepared using partially enriched 43Ca calcium carbonate to give ∼8% 43Ca enrichment.The macroscopic densities of the glass samples were determined by helium pycnometry using a Quantachrome Multipycnometer. Glass transition temperatures, Tg, were measured using a NETZSCH STA 409 PC differential scanning calorimeter.
2.2. Neutron diffraction
The neutron diffraction spectra were collected using the GEM diffractometer at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, UK.30 The samples were cast into 8 mm diameter rods, which eliminated the need for a container and therefore reduced the number of data corrections required. Interference patterns were collected for each of the samples, a vanadium rod of 8 mm diameter and the empty GEM instrument in order to perform the appropriate corrections. The data reduction and corrections were performed using the program GUDRUN.30 The corrections involve the removal of background scattering, normalization, correction for absorption, inelastic and multiple scattering effects and subtraction of the self-scattering term.30 Following these corrections, the resultant coherent scattering intensity, i(Q), is defined by31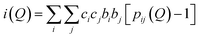 | (1) |
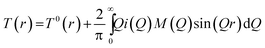 | (2) |
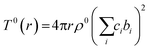 | (3) |
Structural information can be obtained by modelling the real-space correlation functions. Pair functions are generated in Q-space and Fourier transformed to allow comparison with the experimental data in real-space. The pair functions are given by:31
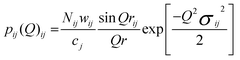 | (4) |
| wij = 2cicjbibj if i ≠ j | (5) |
| wij = ci2bi2 if i = j | (6) |
The method of isomorphic substitution was applied to the neutron diffraction data.32,33 If three total structure factors Sri(Q), CaSri(Q) and Cai(Q) are measured corresponding to scattering lengths bSr > bCaSr > bCa then those correlations not involving the calcium or strontium ion can be eliminated by subtracting two total structure factors to give a first order difference function such as Sr–CaΔi(Q) = Sri(Q) − Cai(Q). The addition of the third total structure factor enables three separate first order difference functions to determined, this can in turn be used check the reliability/mutual consistency of these difference functions. Full details on the method of isomorphic substitution are given by Martin et al.32 The assumption of isomorphism is valid over the short and medium range order, however due to the size difference between the Ca2+ and Sr2+ ions the extended range order is not assumed to be isomorphic. The diffraction data is therefore only modelled up to 3 Å.
2.3. Solid state NMR
One-dimensional 43Ca, 23Na, 31P, 29Si and 17O MAS NMR data were acquired using the set-up parameters given in Table 1. All data were collected under conditions to ensure quantitative reliability. Two-dimensional 43Ca 3QMAS NMR data were also acquired at a Larmor frequency of 57.22 MHz. These 3QMAS measurements employed a conventional Z-filter experiment,34 where initial (non-selective) 4.50 μs excitation and 1.25 μs conversion pulses were followed by two selective π/2 pulses each of ∼25.00 μs duration which comprised the Z-filter. In each experiment 96 transients were acquired for each of the 128 F1 dimension slices, with a recycle delay of 5 seconds being used. Two-dimensional 17O 3QMAS data were measured at a Larmor frequency of 81.25 MHz. The conventional Z-filter experiment used an excitation, conversion and Z-filter pulse durations of 4.2, 1.5 and 14.0 μs, respectively.| Field (T) | Frequency (MHz) | MAS (kHz) | Probe | Reference | |
|---|---|---|---|---|---|
| 43Ca | 20 | 57.22 | 10 | 4 mm Bruker | 0.1 M CaCl2 (aq.) |
| 43Ca | 14.1 | 40.34 | 10 | 4 mm Bruker | 0.1 M CaCl2 (aq.) |
| 43Ca | 9.4 | 26.89 | 10 | 4 mm Bruker | 0.1 M CaCl2 (aq.) |
| 23Na | 14.1 | 158.55 | 15 | 3.2 mm Bruker | 0.1 M NaCl (aq.) |
| 23Na | 9.4 | 105.65 | 15 | 3.2 mm Bruker | 0.1 M NaCl (aq.) |
| 31P | 9.4 | 161.92 | 10 | 4 mm Bruker | 85% H3PO4 |
| 29Si | 7.05 | 59.58 | 5 | 7 mm Bruker | Kaolinite |
| 17O | 14.1 | 81.25 | 20 | 3.2 mm Bruker | H2O |
2.4. Extended X-ray absorption fine spectra (EXAFS)
The Sr K-edge EXAFS were collected using B18 at the Diamond Light Source.35 The Sr-containing bioactive glasses were ground into a fine powder, mixed with cellulose and pressed into a pellet. The measurements were conducted at room temperature and in transmission mode. Ten scans were collected for each sample and the data averaged. The Sr K-edge is at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 eV. Spectra were collected with 5 eV steps in the pre-absorption edge region (15
105 eV. Spectra were collected with 5 eV steps in the pre-absorption edge region (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905–16
905–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 eV), 1 eV steps from 16
072 eV), 1 eV steps from 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 to 16
072 to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 eV, and 0.05 Å−1 steps up to a Q value of 16.95 Å−1. The Ifeffit software analysis suite was used for the background corrections and normalisation (Athena), and to model the local environment of Sr (Artemis).36,37
137 eV, and 0.05 Å−1 steps up to a Q value of 16.95 Å−1. The Ifeffit software analysis suite was used for the background corrections and normalisation (Athena), and to model the local environment of Sr (Artemis).36,37
2.5. X-ray diffraction
The X-ray diffraction data was measured using a Panalytical X'pert-Pro producing silver radiation (λ = 0.5638 Å) (ISIS, Rutherford Appleton Laboratory). The calcium-containing glasses were mounted in 1.0 mm diameter silica capillaries. Sr-containing glasses absorbed X-rays strongly, and there was a significant contribution from fluorescence in the measured data. To reduce the absorption corrections, the SrBio glass sample was mounted in a 0.5 mm thin-walled silica capillary.The data was reduced and corrected using the program GudrunX.38 The corrections applied follow the same procedure as Gudrun, detailed above, and also corrected for fluorescence and Bremsstrahlung effects. After the data corrections have been applied, the coherent scattering intensity, ix(Q), is obtained. As with neutron scattering, an X-ray total correlation function, Tx(r), can be calculated from a Fourier transform of ix(Q). However, X-ray scattering arises from interactions with the electron cloud around each atom, and as such the Tx(r) has relatively poor resolution due to the resultant form factor and to the limits imposed on the maximum attainable value of Q by the wavelength of the X-ray. To resolve this, GudrunX normalises the data by 〈f(Q)2〉, which has the effect of collapsing the scattering to that of an effective point scatterer. ix(Q) is calculated as:39
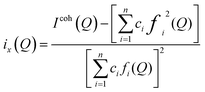 | (7) |
T x (r) is defined as:
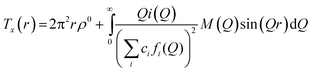 | (8) |
3. Results and discussion
The neutron diffraction interference functions (i(Q)) for the CaBio, CaSrBio and SrBio systems are shown in Fig. 1(a) and the first order difference functions (Δi(Q)) are shown in Fig. 1(b). Fig. 2(a) shows the corresponding real space total diffraction data, T(r), obtained by Fourier transforming the i(Q) functions given in Fig. 1(a) and 2(b) shows the real space pairwise correlation data ΔT(r) obtained by Fourier transforming the Δi(Q) functions given in Fig. 1(b). The weighting factors for each of the total structure factors and difference functions are given in Table 2. The first feature in T(r), Fig. 2(a), corresponds to P–O and Si–O correlations (∼1.6 Å), the second feature (∼2.1 to 2.9 Å) contains overlapping O–(P)–O, O–(Si)–O, Na–O and Ca–O and/or Sr–O correlations and it is therefore not usually possible to deconvolve these correlations from the real space total diffraction data. However, those correlations that do not contain Ca or Sr cancel during the formation of the first order difference functions (Table 2). This is confirmed by the notable absence of the P–O and Si–O peaks at ∼1.5 to 1.6 Å in the ΔT(r) functions, illustrated in Fig. 2(b). Similarly, the O–(P)–O, O–(Si)–O and Na–O correlations have been eliminated during the formation of the difference functions. Of the remaining correlations present, the first (shortest separation in r-space) correlations will correspond to nearest neighbours Ca–O and Sr–O. The second nearest neighbours such as Ca–(O)–Ca, Ca–(O)–Na, Ca–(O)–P and Ca–(O)–Si are not expected to occur until beyond 3 Å. The first order difference functions were therefore modelled exclusively using Ca–O and Sr–O correlations. The data was fitted using the NXFit program developed by Moss.40 Initially, the first order difference data was modelled over the region 2.1 < r (Å) < 2.9 using a single Ca–O correlation and a single Sr–O correlation. The single Ca–O/Sr–O fit was in reasonable agreement with the experimental data and the output parameters are given in Table 3. However, a small residual peak was present at high-r and the asymmetry in the ΔT(r) peaks suggested the data would be better modelled using two peaks for the Ca–O correlation and two peaks for the Sr–O correlation. The fit parameters for the three first order difference functions, modelled both with a single and with double peaks, and the goodness-of-fit parameter (F(X)) are given in Table 3. The NXFit program requires a nominal input for each correlation and a separate value to determine the range over which each individual correlation may vary. During the fitting the individual values were free to vary and none of these values were constrained. In particular, the coordination numbers for the second set of Ca–O/Sr–O correlations were allowed to vary to include zero values, thus effectively allowing a single peak fit if this resulted in a better goodness-of-fit. However, as shown, the F(X) values are significantly lower when fitting the data with two Ca–O and two Sr–O correlations. It is also apparent that the parameters for the first Ca–O and Sr–O parameter are largely unchanged whether fitting with a single or double peak model suggesting there is relatively little effective overlap between the first and second peaks, especially in the case of the Ca–O correlations. The negative peak in the 3–3.3 Å range consists of Ca–(O)–Ca, Ca–(O)–Na, Ca–(O)–P and Ca–(O)–Si correlations (the negative term arises solely due to the subtraction of Ca species from Sr as defined in Table 2), whilst the positive peak at ∼3.6 to 4 Å corresponds to next nearest neighbour Sr correlations. These second-neighbour correlations are not modelled due to the complexity of the overlapping pairwise correlations present at these larger separations. The Sr–CaΔT(r) has the highest signal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) noise ratio, being approximately twice that of the other first order difference functions. The average fit parameters given in Table 3 are therefore weighted 2
noise ratio, being approximately twice that of the other first order difference functions. The average fit parameters given in Table 3 are therefore weighted 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the Sr–CaΔT(r)
1 for the Sr–CaΔT(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sr–CaSrΔT(r)
Sr–CaSrΔT(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaSr–CaΔT(r) respectively.
CaSr–CaΔT(r) respectively.
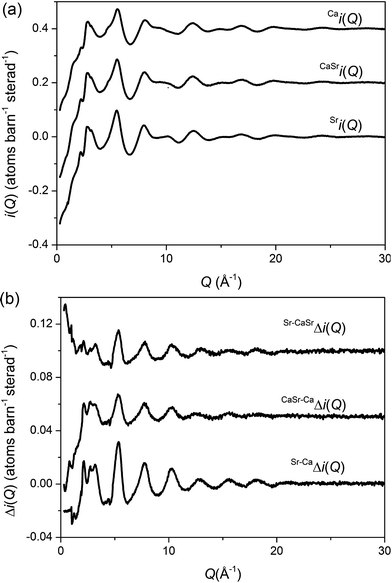 | ||
| Fig. 1 (a) Q-space interference functions, i(Q), for CaBio, CaSrBio and SrBio, (b) Q-space interference difference functions, Δi(Q), for Sr–CaΔi(Q), Sr–CaSrΔi(Q) and SrCa–CaΔi(Q). The datasets are offset for clarity. The Q-space data extends to 50 Å−1 but only 0 < Q (Å−1) < 30 is shown for clarity. | ||
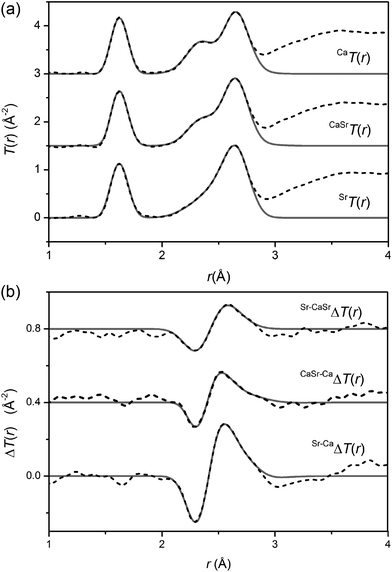 | ||
| Fig. 2 The real-space diffraction data for (a) the total diffraction patterns, T(r), and (b) the difference functions, ΔT(r). The broken curves represent the experimental data and the solid curves are the resultant fits. The datasets are offset for clarity. | ||
| Ca i(Q) | CaSr i(Q) | Sr i(Q) | Sr–CaΔi(Q) | Sr–CaSrΔi(Q) | CaSr–CaΔi(Q) | |
|---|---|---|---|---|---|---|
| p Ca–O(Q) | 24.48 | 12.24 | — | −24.48 | −12.24 | −12.24 |
| p Ca–Si(Q) | 5.63 | 2.82 | — | −5.63 | −2.82 | −2.82 |
| p Ca–Na(Q) | 5.26 | 2.63 | — | −5.26 | −2.63 | −2.63 |
| p Ca–P(Q) | 0.30 | 0.15 | — | −0.30 | −0.15 | −0.15 |
| p Ca–Ca(Q) | 1.49 | 0.37 | — | −1.49 | −0.37 | −1.12 |
| p Ca–Sr(Q) | — | 1.11 | — | — | −1.11 | 1.11 |
| p Sr–O(Q) | — | 18.28 | 36.57 | 36.57 | 18.28 | 18.28 |
| p Sr–Si(Q) | — | 4.21 | 8.41 | 8.41 | 4.21 | 4.21 |
| p Sr–Na(Q) | — | 3.93 | 7.85 | 7.85 | 3.93 | 3.93 |
| p Sr–P(Q) | — | 0.22 | 0.45 | 0.45 | 0.22 | 0.22 |
| p Sr–Sr(Q) | — | 0.83 | 3.32 | 3.32 | 2.49 | 0.83 |
| p Si–O(Q) | 46.31 | 46.31 | 46.31 | — | — | — |
| p P–O(Q) | 2.48 | 2.48 | 2.48 | — | — | — |
| p O–O(Q) | 100.67 | 100.67 | 100.67 | — | — | — |
| p Na–O(Q) | 43.22 | 43.22 | 43.22 | — | — | — |
| p Si–Na(Q) | 9.94 | 9.94 | 9.94 | — | — | — |
| p Si–P(Q) | 0.57 | 0.57 | 0.57 | — | — | — |
| p Si–Si(Q) | 5.33 | 5.33 | 5.33 | — | — | — |
| p Na–P(Q) | 0.53 | 0.53 | 0.53 | — | — | — |
| p Na–Na(Q) | 4.64 | 4.64 | 4.64 | — | — | — |
| p P–P(Q) | 0.02 | 0.02 | 0.02 | — | — | — |
| Single peak | Split peak | ||||||
|---|---|---|---|---|---|---|---|
| r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | ||
| Sr–CaΔT(r) | Ca–O | 2.33 | 5.21 | 0.10 | 2.33 | 5.42 | 0.09 |
| Sr–O | 2.52 | 4.85 | 0.14 | 2.49 | 4.70 | 0.14 | |
| Ca–O | 2.73 | 1.39 | 0.19 | ||||
| Sr–O | 2.75 | 1.23 | 0.12 | ||||
| F(X) = 0.006 | F(X) = 0.001 | ||||||
|---|---|---|---|---|---|---|---|
| r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | ||
| CaSr–CaΔT(r) | Ca–O | 2.33 | 5.67 | 0.11 | 2.33 | 5.34 | 0.08 |
| Sr–O | 2.52 | 4.64 | 0.15 | 2.46 | 4.73 | 0.14 | |
| Ca–O | 2.74 | 1.20 | 0.25 | ||||
| Sr–O | 2.75 | 1.85 | 0.18 | ||||
| F(X) = 0.0008 | F(X) = 0.0004 | ||||||
|---|---|---|---|---|---|---|---|
| r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | ||
| Sr–CaSrΔT(r) | Ca–O | 2.32 | 5.14 | 0.08 | 2.33 | 5.56 | 0.11 |
| Sr–O | 2.53 | 5.29 | 0.15 | 2.53 | 4.64 | 0.15 | |
| Ca–O | 2.72 | 1.27 | 0.17 | ||||
| Sr–O | 2.74 | 0.83 | 0.15 | ||||
| F(X) = 0.003 | F(X) = 0.0011 | ||||||
|---|---|---|---|---|---|---|---|
| r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | ||
| Average | Ca–O | 2.33 | 5.3 | 0.10 | 2.33 | 5.4 | 0.10 |
| Sr–O | 2.52 | 4.9 | 0.14 | 2.49 | 4.7 | 0.14 | |
| Ca–O | 2.73 | 1.3 | 0.20 | ||||
| Sr–O | 2.75 | 1.3 | 0.14 | ||||
The Ca–O values of ∼2.33 and ∼2.73 Å presented in Table 3 are consistent with crystalline Na2CaSi2O6 for which Ca–O values in the range 2.32–2.72 Å are reported.41 This compares with similar distances measured from sol–gel derived bioactive glasses where three distinct Ca–O correlations at ∼2.3, 2.5 and 2.75 Å have been assigned to Ca-non-bridging oxygen (Ca–ONB), Ca–OH and Ca-bridging oxygen (Ca–OB) bonds, respectively.23,42 Thus, the present results are in agreement with regard to the Ca bridging and Ca non-bridging oxygen species, whilst hydroxyl groups (and hence Ca–OH correlations) are absent, as reasonably expected for the melt-quench systems under study here. Furthermore, these results indicate that the addition of a second network modifier such as Na into the glass does not significantly change the Ca–ONB and Ca–OB correlations. This is an important observation since previous results have suggested that Na–Ca silicate glasses show a non-random distribution of cations, with a preference for Ca–O–Na bonds at the expense of Ca–O–Ca and Na–O–Na bonds.43 The Sr–O distances in strontium metasilicate, SrSiO3, range from 2.46 to 2.74 Å (ref. 44 and 45) whilst in sodium perovskite, Na2SrSi2O6, a shorter Sr–O distance of 2.46 Å dominates.46 Thus, the Sr–O distances measured in this study (see Table 3) of ∼2.50 and ∼2.75 Å are in good agreement with previously reported range of values from these crystalline systems.
In vitro studies of bioactive calcium silicate sol–gel glasses using isotopic substitution in neutron diffraction have shown that the gel preferentially loses the shortest length Ca–O correlation, which is attributed to Ca non-bridging oxygen species.23,42,47 It is anticipated that the Ca/Sr non-bridging oxygen species will be lost preferentially compared to bridging oxygen species in melt quench glasses. The presence of calcium associated with non-bridging oxygen correlations will therefore act as a driver for bioactivity being the first to leach under physiological conditions thereby releasing soluble Ca into the media. The calcium then precipitates to form a calcium phosphate layer which in turn crystallises into hydroxyapatite. The solid state 43Ca, 23Na, 31P and 29Si MAS NMR data acquired from the CaBio, CaSrBio and SrBio systems is shown in Fig. 3(a)–(d), respectively. All 43Ca MAS NMR data were acquired using a rotor-synchronised echo experiment and exhibit a single disorder-broadened resonance which exhibits a pronounced downfield movement of the apparent shift (δ) with increasing B0 field (see Fig. 3(a)). A graphical analysis of these data shown in Fig. 4(a) where the centre-of-gravity shift of the 43Ca resonance measured at each field is plotted against 1/υ02 (υ0 = Larmor frequency), the slope of this behaviour yields the mean value of the quadrupole interaction parameter PQ where:48,49
| PQ = CQ√(1 + ηQ2/3) | (9) |
| CQ = e2qQ/h | (10) |
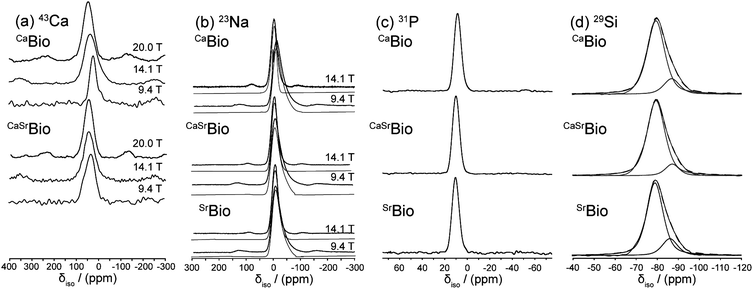 | ||
| Fig. 3 Solid state MAS NMR data for, (a) variable B043Ca study, (b) variable B023Na study (spectral simulations in grey), (c) 31P study and (d) 29Si study demonstrating the deconvolution into Q2 and Q3 components (spectral simulations in grey). | ||
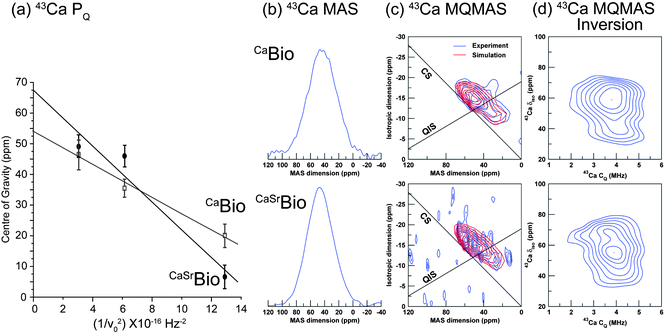 | ||
| Fig. 4 43Ca solid state MAS NMR data showing, (a) a plot of the resonance centre of gravity against the inverse square of the Larmor frequency υ0, (b) the 1D MAS spectra, (c) the 3QMAS data and corresponding spectral simulation, and (d) the numerical inversion of the simulated 3QMAS data. | ||
In PQ the quadrupole coupling constant (CQ) and asymmetry parameter (ηQ) are combined, however, the y intercept of this plot yields the mean value of the isotropic chemical shift (δiso). Fig. 4(a) suggests that this phenomenon is more evident for the CaSrBio system than for its CaBio counterpart, thus indicating that the average field gradient (eq) and the δiso characterising the Ca positions in the CaBio glass are larger. From Table 4 the PQ values for the CaBio and CaSrBio systems are 2.1 and 2.8 MHz, respectively; although ηQ values are not known explicitly, these PQ values approximate the characteristic CQ values for these systems to within a maximum error of ∼15%. Quadrupole coupling constants of this magnitude are typical of Ca in nearest-neighbour O–Ca–O environments,50 with the trend to larger CQ and δiso values upon Sr incorporation being attributed to next nearest neighbour effects whilst the nearest neighbour (Ca–O) effects are unperturbed, as shown in Table 3.
| Bioglass | δ iso (ppm) | P Q (MHz) | δ iso (ppm) | C Q centre | Width (MHz) | η Q | δ iso(MAS) (ppm) | δ iso (ppm) | Environment (%) | δ iso (ppm) | Environment (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nucleus | 43Ca | 43Ca | 23Na | 23Na | 23Na | 23Na | 31P | 29Si | 29Si | 29Si | 29Si |
| CaBio | 53.3 (4.2) | 2.1 (0.3) | 8.3 | 6.1 | 5.4 | 0.1 | 8.82 | −79.0 | Q 2/83 | −86.0 | Q 3/17 |
| CaSrBio | 67.5 (10.2) | 2.8 (0.5) | 10.0 | 7.3 | 6.7 | 0.1 | 9.71 | −79.0 | Q 2/89 | −86.0 | Q 3/11 |
| SrBio | — | — | 10.5 | 7.0 | 6.1 | 0.1 | 10.34 | −79.0 | Q 2/81 | −86.0 | Q 3/19 |
The 43Ca 3QMAS and numerical inversion data from the CaBio and CaSrBio systems are shown in Fig. 4(c) and (d). Each dataset suggests that more than one Ca species is present in the Bioglass. The two distinct Ca environments described in Fig. 4(c) for the CaBio system corroborate the neutron diffraction structural parameters described in Table 3. It is well established that Ca–O bond lengths profoundly influence the isotropic chemical shift position of each Ca resonance.51 Inversion of the 3QMAS data (see Fig. 4(d)) clearly exhibits two Ca populations with approximately the same CQ but with δiso values differing by ∼20 ppm. Previous work by Angeli et al. has demonstrated through a series of Ca-aluminosilicate glasses that a shift of up to ∼60 ppm has been observed as Ca changes from being solely coordinated by non-bridging oxygens (Ca–ONB) to being solely coordinated by bridging oxygens (Ca–OB).52 This change in shift correlates strongly with the average Ca–O bond distance. In the cases studied here, the downfield (or more shielded) resonance at δiso ∼ 41 ppm will be associated with Ca sites exhibiting (on average) longer Ca–O bonds, and hence corresponds to the feature in the neutron diffraction data identified at ∼2.73 Å (see Table 3), which represents an environment more influenced by Ca–OB linkages. Hence, the second more deshielded shift at δiso ∼ 60 ppm will be associated with the shorter bond length feature ∼2.33 Å (see Table 3), thus representing a Ca environment associated with more Ca–ONB moieties. The average of these shifts at ∼50 ppm agrees well with the average δiso determined from the graphical analysis of the variable B0 1D 43Ca MAS NMR data (δiso ∼ 53 ppm, see Table 4). Both 43Ca isotropic shifts of δiso ∼ 41 and ∼ 60 ppm are consistent with Ca occupying distorted octahedral positions, where mean Ca–O distances in the region of 2.35 to 2.41 Å have been reported, though this does not preclude the possibility of some seven fold Ca–O environments being present.50 A shift of δiso 59 ppm has been observed in pectolite (Ca2NaSi3O8(OH)) which has a distorted octahedral environment with mean Ca–O distances of 2.36–2.37 Å.50 However, a chemical shift of ∼41 ppm can also be associated with longer Ca–O distances ∼2.71 Å, as observed in perovskites.50 This demonstrates, therefore, that the 43Ca MAS NMR is in excellent agreement with the isomorphic neutron diffraction results. The introduction of Sr to this system shifts both resonances to lower field due to next nearest neighbour effects (Ca–O–Sr), however a minimal effect on the measured nearest neighbour (Ca–O) bond lengths is observed (see Table 3).
Fig. 5(a) presents the 17O MAS NMR data for the CaBio and SrBio bioglasses. These are generally featureless resonances that preclude any insight into the O speciation that characterises these systems. In contrast, the 17O 3QMAS and numerical inversion data of Fig. 5(b) and (c), respectively, evidently resolve this speciation and permit clear comparisons to be drawn. The left side of the 3QMAS numerically inverted data for both systems (see Fig. 5(c)) shows three distinct O environments in the 17O CQ region of ∼2 to 2.5 MHz; as δiso increases these are assigned to Si–O–Na, Si–O–(Na, M) and Si–O–M environments (where M represents Ca or Sr),53 providing strong evidence for the existence of a range of homo-bonds (Na–O–Na and M–O–M) and hetero-bonds (Na–O–M) within the glass structure. There is no significant variation in the Si–O–Na correlation at δiso ∼ 40 ppm observed for CaBio and SrBio, verifying that the substitution of Sr for Ca does not influence the local Na environment. This similarity is also reflected in the 23Na MAS NMR data shown in Fig. 3(b); the 23Na NMR parameters elucidated from the variable B0 simulation of these lineshapes which describe the structural disorder (using the QUADFIT simulation program)54 are summarised in Table 4. These data indicate that the 23Na isotropic shift values consistently reside in the δiso ∼ 8.3 to 10.5 ppm range, and the corresponding CQ values are ∼6.1 to 7.3 MHz. 2D inversion data for the SrBio Bioglass (Fig. 5(c)) shows that the δiso values of the Si–O–(Na, Sr) and Si–O–Sr moieties exhibit a marked downfield shift of ∼10 and ∼20 ppm, respectively, in comparison to its CaBio counterpart. This shift to increased deshielding is consistent with the longer Sr–O bond lengths, compared to Ca–O bond length, reported by the neutron diffraction measurements (see Table 3). Furthermore, the Si–O–(Na, Sr) and Si–O–Sr moieties for SrBio exhibit a greater distribution in their 17O δiso values as evidenced by the projection upon the CS axis in Fig. 5(b), and the elongated Si–O–(Na, Sr) and Si–O–Sr correlations in Fig. 5(c), suggesting a greater variation in the Sr–O distribution compared to the Ca–O distribution. This is consistent with the neutron diffraction data, where the structural disorder parameter of Sr–O is 0.14 for the dominant peak at 2.49 Å compared to 0.10 for the Ca–O distribution at 2.33 Å.
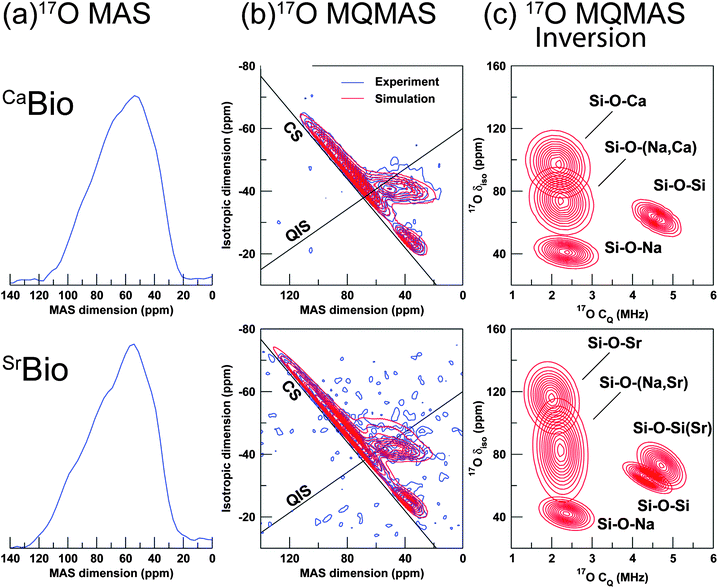 | ||
| Fig. 5 17O solid state MAS NMR data (υ0 = 20 kHz) showing, (a) 1D MAS spectra, (b) the 3QMAS data and corresponding spectral simulations, and (c) the numerical inversion of the simulated 3QMAS data with assignments. | ||
The Si–O–Si correlation at δiso ∼ 65 ppm, characterised by a larger CQ value of ∼4.5 MHz appears unperturbed by the substitution of Ca for Sr. However, a weak second correlation assigned to a Si–OB–Si(Sr) moiety is observed in SrBio at δiso ∼ 70 ppm and exhibits a slightly larger CQ value of ∼4.75 MHz. Previously reported 17O 3QMAS studies on Ca Bioglass have not resolved contributions from Si–OB–Si(Ca) and Si–OB–Si(Na).53
Sr K-edge EXAFS for the SrBio and the CaSrBio systems are shown in Fig. 6. The SrBio and CaSrBio EXAFS, represented by the broken and solid grey curves respectively, are almost indistinguishable and confirm that the local nearest neighbour environment surrounding Sr is unaffected by substituting half of the Sr by Ca. A model system, representing the first shell of Sr in an octahedral environment with a mean Sr–O distance of 2.51 Å (broken dark curve), is in reasonable agreement with the measured SrBio and CaSrBio datasets. The EXAFS data is therefore in good agreement with the neutron diffraction data (Table 3) where a distorted octahedral environment is reported where the main peak resides at 2.49(2) Å and a total Sr–O coordination number of 6.0 is reported.
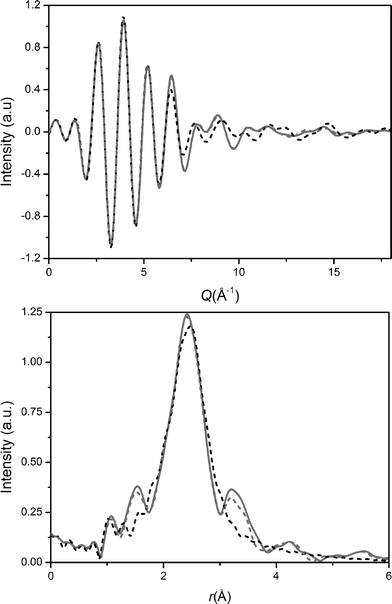 | ||
| Fig. 6 Sr K-edge EXAFS spectra (a) reciprocal space data and (b) real space data. The CaSrBio and SrBio data are represented by the grey dashed and solid curves respectively and the fit is given by the black dashed curve. | ||
As a result of the isomorphic substitution, and confirmation of the results through NMR and EXAFS, it is now possible to return to T(r), Fig. 2(a), and fit the complex overlapping correlations. The short-range order comprises ∼4 oxygens around Si at ∼1.62 Å and ∼4 oxygens around P at between 1.5–1.6 Å, depending on whether the P–O are bridging or non-bridging (also referred to as terminal).55 As discussed the intermediate range order between 2.1–2.9 Å consists of overlapping Ca–O (and/or Sr–O), Na–O, O–(P)–O and O–(Si)–O correlations and cannot usually be unambiguously deconvolved. However, by accurately determining the Ca–O (and Sr–O) correlations using the first order difference method, the remaining region is simplified and requires in addition only Na–O and O⋯O correlations to be fitted. Furthermore, it is possible to estimate a priori the most probable O⋯O correlations: the O–(P)–O and O–(Si)–O are both tetrahedrally coordinated, therefore the O–(X)–O separation is given by 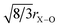 , where X represents P or Si. The concentration of Si is more than 20 times greater than the concentration of P; the O⋯O correlation can therefore be modelled using a single O⋯O correlation that is largely determined by the O–(Si)–O term.
, where X represents P or Si. The concentration of Si is more than 20 times greater than the concentration of P; the O⋯O correlation can therefore be modelled using a single O⋯O correlation that is largely determined by the O–(Si)–O term.
The O⋯O coordination number can be calculated using network connectivity models and confirmed using NMR data. For a silicate glass the network connectivity (NC) is given by
| NC = 4 − 2Z, | (11) |
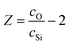 | (12) |
The addition of P complicates the connectivity slightly since P does not behave in an identical manner to Si and eqn (12) cannot therefore be modified simply by substituting cSi for cSi + cP. For a phosphate-based glass, NC = 3 − y, where y, the number of excess O per P2O5, is given by y = 2cO/cP − 5.56,57
31P MAS NMR data (see Fig. 3(c)) shows a single resonance at δiso ∼ 10 ppm representing Q0 species which are essentially isolated PO4 moieties present throughout the structure.53 There is no evidence of more covalent Si–O–P linkages as suggested by the absence of significant 31P MAS sideband structure that would invoke a substantial chemical shift anisotropy (CSA) expected from such environments. The 17O 3QMAS (Fig. 5(b) and (c)) also shows no signs of Si–O–P sites. This is consistent with results recently published by Pedone et al.53
Since each phosphorus atom is surrounded by 4 non-bridging oxygen atoms, the number of excess oxygen atoms per SiO2 is reduced accordingly and eqn (12) becomes
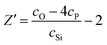 | (13) |
In this case, cO, cSi and cP are 0.603, 0.194 and 0.008 respectively. Therefore, Z′ = 0.935 and the network connectivity of the glass is equal to 2.13. This corresponds to 13% of the Si occupying Q3 connectivity and 87% occupying Q2 connectivity. The 29Si MAS NMR data (see Fig. 3(d)) show asymmetric resonances which can be deconvolved into two Gaussian components located at δ −79 and −86 ppm, which are assigned to be Q2 and Q3 units, respectively. The resultant fits give Q3 abundances of 17%, 11% and 19% for the CaBio, CaSrBio and SrBio respectively, with the balance of the Si speciation occupying a Q2 environment. The experimental data is therefore in good agreement with the calculated values (within experimental uncertainties). Knowledge of the Q speciation allows the average O⋯O coordination number to be calculated. A bridging O atom has six next nearest neighbour O atoms whilst a non-bridging O has only three next nearest neighbour O atoms. Thus, a Si atom having a Q speciation of Q2 or Q3 will have O⋯O coordination numbers of 4 and 4.8 respectively. It can therefore be calculated that the average O–(Si)–O coordination number associated with the samples discussed herein is 4.10. Taking the small concentration of P into account, which is in an orthophosphate environment with a corresponding average O–(P)–O coordination number of 3, and allowing for the relative concentrations, the overall average O⋯O coordination number of these glasses is therefore estimated to be 4.06. The O⋯O peak position is expected to occur at ∼2.66 Å, given that 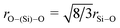 , where rSi–O is 1.63 Å. Thus, the complex region containing overlapping Ca–O, Na–O, O–(P)–O and O–(Si)–O correlations has effectively been further simplified and can now be modelled using the experimentally determined Ca–O input parameters and the O–(P)–O and O–(Si)–O parameters derived above, and confirmed using NMR. The only truly unknown feature remaining in this region of the total diffraction pattern (i.e. r < 3 Å) is the Na–O correlation.
, where rSi–O is 1.63 Å. Thus, the complex region containing overlapping Ca–O, Na–O, O–(P)–O and O–(Si)–O correlations has effectively been further simplified and can now be modelled using the experimentally determined Ca–O input parameters and the O–(P)–O and O–(Si)–O parameters derived above, and confirmed using NMR. The only truly unknown feature remaining in this region of the total diffraction pattern (i.e. r < 3 Å) is the Na–O correlation.
The O⋯O coordination number calculated above is larger than the coordination determined by previous Reverse Monte Carlo simulation, which estimated an O⋯O coordination number of ∼3.0.58 Given the significant weighting of the O⋯O term in the neutron diffraction studies modelled, this under-estimation of coordination number has a significant effect upon modelling the remaining overlapping correlations in the intermediate range order.
The total structure factors were modelled using the above input factors. An initial attempt to fit the T(r) functions using a single Na–O correlation resulted in a poor fit, and the data was thereafter modelled using two Na–O correlations. The fits are shown in Fig. 2(a) and the output parameters are given in Table 5.
| CaBio | CaSrBio | SrBio | |||||||
|---|---|---|---|---|---|---|---|---|---|
| r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | r (Å) | N | σ (Å) | |
| P–O | 1.55 | 3.95 | 0.01 | 1.58 | 3.99 | 0.01 | 1.56 | 3.98 | 0.02 |
| Si–O | 1.63 | 3.93 | 0.06 | 1.63 | 3.82 | 0.06 | 1.63 | 3.92 | 0.06 |
| Na–O | 2.34 | 3.08 | 0.14 | 2.36 | 3.02 | 0.14 | 2.33 | 3.08 | 0.15 |
| Na–O | 2.64 | 1.49 | 0.09 | 2.64 | 1.47 | 0.10 | 2.66 | 1.47 | 0.09 |
| Ca–O | 2.34 | 5.34 | 0.10 | 2.32 | 5.28 | 0.10 | — | — | — |
| Sr–O | — | — | — | 2.51 | 4.67 | 0.14 | 2.51 | 4.77 | 0.12 |
| O–O | 2.66 | 4.17 | 0.10 | 2.66 | 4.01 | 0.10 | 2.65 | 4.01 | 0.10 |
| Ca–O | 2.72 | 1.24 | 0.17 | 2.71 | 1.35 | 0.17 | — | — | — |
| Sr–O | — | — | — | 2.75 | 1.24 | 0.23 | 2.74 | 1.28 | 0.09 |
A split Na–O peak has been predicted in molecular dynamics (MD) simulations for sodium silicates and for Bioglass.59,60 However, published MD results for Bioglass are dependent upon the type of simulation employed. For example, classical MD simulations using Shell Models, Rigid Ion Models and Car–Parrinello simulations predicted Na–ONB distances of 2.33, 2.38 and 2.28 Å respectively with between 4.0 and 4.6 oxygen atoms surrounding each sodium atom, whilst Na–OB distances ranging between 2.45 and 2.52 Å were reported with Na–O coordination numbers between 1.0 and 1.6.60 In sodium silicates a lower Na–ONB coordination of ∼2.8 was reported.59 In crystalline Na2CaSi2O6 and Na2SrSi2O6 a wide range of Na–O distances are reported: 2.30–2.90 Å,41 and 2.38–2.75 Å (ref. 46) respectively. Recently a split Na–O peak in Bioglass has been confirmed by employing an effective isomorphic difference study.61 Thus, the decision to fit the Na–O correlation with two separate peaks corresponding to Na–ONB and Na–OB may be justified, and the values reported here (see Table 5) are within the expected values based on existing simulations, recent experimental data and on experimental data from crystalline analogues.
During the fitting process the nominal input values were allowed to vary in order to optimise the fit. Importantly, the parameters were not constrained during this fitting process, even the Ca–O/Sr–O parameters which had been previously measured. It is apparent from the fitting parameters returned that the model is fully self-consistent between the experimental values for the first order difference functions, the total diffraction data, the NMR data and theory.
The key assumption behind isomorphic substitution is that the pair correlations not containing the isomorphs, in this case Ca/Sr, are not significantly affected by the substitution and that these correlations therefore successfully cancel during the formation of the first order difference function. As shown in Table 5, the neutron diffraction correlations not containing Ca or Sr are consistent for each of the three total diffraction patterns. Further support is given by the 23Na NMR spectra (Fig. 3(b)) which confirms there is no variation in the sodium environment upon substituting Sr for Ca within these bioactive glasses, and the Sr K-edge EXAFS (Fig. 6) which confirms there is no variation in the strontium environment upon substituting half the Sr for Ca within these bioactive glasses.
X-ray diffraction measurements were undertaken to verify the above results. The X-ray diffraction weighting factors are significantly different to neutron diffraction weightings, as shown in Fig. 7. The neutron diffraction spectra are dominated by the O⋯O correlations whereas the X-ray diffraction data is relatively more sensitive to the Ca–O (and/or Sr–O) correlations. The X-ray interference function data is shown in Fig. 8(a) and the corresponding real space data is given in Fig. 8(b). The X-ray data was modelled using the output values from the neutron diffraction as given in Table 5. No attempts were made to optimise the X-ray fitting since the isomorphic neutron diffraction data presented is intrinsically more reliable. For example, the X-ray data has a maximum Q value of 17 Å−1, compared to 50 Å−1 for the neutron diffraction data, and is therefore relatively broadened in real-space. The neutron-derived fits are in good overall agreement with the total X-ray diffraction patterns. The small variations between the X-ray experimental data and the fit for the SrBio and CaSrBio may be attributed to fluorescence effects. The X-ray diffraction data and the NMR spectra therefore both support the results determined from the neutron diffraction experiments.
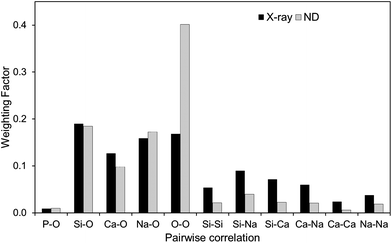 | ||
| Fig. 7 X-ray and neutron diffraction weighting factors. | ||
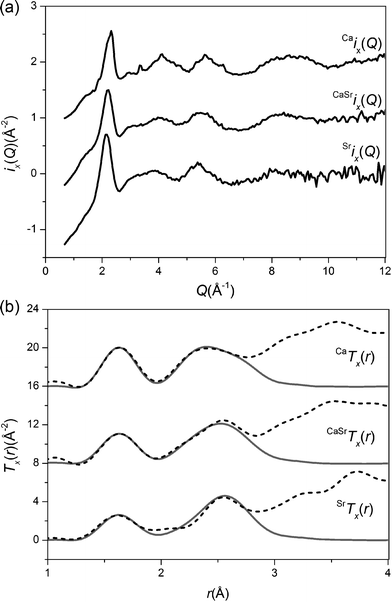 | ||
| Fig. 8 (a). X-ray diffraction Q-space functions, ix(Q), measured for CaBio, CaSrBio and SrBio. (b) The real-space data X-ray diffraction patterns, Tx(r), the dashed curve represents the experimental data and the solid curve represents the NXFIT data. The datasets are offset for clarity. | ||
Densities of 2.70, 2.83 and 3.03 g cm−3 (±0.01 g cm−3) were recorded for CaBio, CaSrBio and SrBio respectively via He pycnometry; the increase in density being directly attributed to the increased atomic weight of Sr compared to Ca. Glass transition temperatures, Tg, of 523, 480 and 462 °C (±1 °C) were recorded for CaBio, CaSrBio and SrBio respectively using DSC. The decrease in Tg is attributed to the expansion of the glass due to the increase in ionic radius of Sr compared to Ca.62,63 Based on the experimentally measured densities and the mean atomic weight, an expansion of the glass of the order 5.3% is calculated; using the nearest neighbour Ca–O and Sr–O distances an expansion of 5.1% is predicted for these glasses. This broad agreement provides assurance that the small differences in glass structure are due to the difference in ionic radius of Sr compared to Ca. The observed expansion of the glass network is thought to result in faster ion release and dissolution and increased bioactivity.64
4. Conclusions
Neutron diffraction data affords a detailed structural model of the local and intermediate range order in an important class of bioactive glasses wherein the study of the Ca site is made more tractable by substituting Sr for Ca within these systems. The conclusions drawn from these neutron diffraction studies are strongly supported by the complementary multinuclear solid state MAS NMR and X-ray diffraction data. The diffraction and NMR studies both suggest that Ca adopts two distinct environments within these glasses. The assumption that isomorphic substitution could be employed to determine the short and intermediate range order of Ca and Sr bioactive glasses was verified. The Ca–O environment for the present melt-quench glass was found to be very similar to those present in sol–gel derived bioactive glasses with significantly different compositions, with the exception of the Ca–OH correlation present in the sol–gel derived glasses being absent here. This indicates that the presence of sodium (and Ca–OH) does not significantly affect the coexisting Ca–OB and Ca–ONB correlations. Bioglass is a complex glass system, containing 5 separate elements and 15 overlapping correlation functions: the present study therefore represents one of the most detailed studies undertaken on any glassy system and has resulted in the characterisation of the short and intermediate range order. Through the detailed identification and characterisation of the sites, especially those associated with calcium and strontium, understanding the structural features that drive important bioactive properties becomes possible.Acknowledgements
This work was funded by EPSRC grants EP/E050611/1 and EP/E051669/1 and by the University of Kent. The authors wish to thank STFC-ISIS for the allocation of neutron diffraction beam-time and for access to the Ag tube X-ray diffractometer and the Diamond Light Source for X-ray beam-time. We wish to acknowledge the use of the Chemical Database Service at Daresbury. RAM acknowledges the Royal Society for the Research Grant RG100147. JVH and MES acknowledge the continued funding of the 300, 400 and 600 MHz instrumentation, and the UK National 850 MHz Solid State NMR Facility at Warwick used in this research was facilitated by EPSRC, BBSRC, the University of Warwick and partial funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (ERDF).References
- L. L. Hench, J. Mater. Sci.: Mater. Med., 2006, 17, 967 CrossRef CAS.
- L. L. Hench, R. J. Splinter, W. C. Allen and T. K. Greenlee, J. Biomed. Mater. Res. Symp., 1971, 5, 25 CrossRef.
- J. C. Knowles, J. Mater. Chem., 2003, 13, 2395 RSC.
- R. G. Hill, A. Stamboulis, R. V. Law, A. Clifford, M. R. Towler and C. Crowley, J. Non-Cryst. Solids, 2004, 336, 223 CrossRef CAS.
- E. Canalis, M. Hott, P. Deloffre, Y. Tsouderos and P. J. Marie, Bone, 1996, 18, 517 CrossRef CAS.
- A. Guida, M. R. Towler, J. G. Wall, R. G. Hill and S. Eramo, J. Mater. Sci. Lett., 2003, 22, 1401 CrossRef CAS.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- J. Terra, E. R. Dourado, J. G. Eon, D. E. Ellis, G. Gonzalez and A. Malta Rossi, Phys. Chem. Chem. Phys., 2009, 11, 568 RSC.
- S. Sugiyama, T. Moriga, M. Goda, H. Hayashi and J. B. Moffat, J. Chem. Soc., Faraday Trans., 1996, 92, 4305 RSC.
- S. G. Dahl, P. Allain, P. J. Marie, Y. Mauras, G. Boivin, P. Ammann, Y. Tsouderos, P. D. Delmas and C. Christiansen, Bone, 2001, 28, 446 CrossRef CAS.
- M. D. Grynpas and P. J. Marie, Bone, 1990, 11, 313 CrossRef CAS.
- P. J. Marie, M. T. Garba, M. Hott and L. Miravet, Miner. Electrolyte Metab., 1985, 11, 5 CAS.
- A. Barbara, P. Delannoy, B. G. Denis and P. J. Marie, Metab., Clin. Exp., 2004, 53, 532 CrossRef CAS.
- P. J. Marie, Bone, 2007, 40, S5 CrossRef CAS.
- P. J. Marie, Osteoporosis Int., 2005, 16(suppl. 1), S7 CrossRef CAS.
- P. J. Meunier, C. Roux, E. Seeman, S. Ortolani, J. E. Badurski, T. D. Spector, J. Cannata, A. Balogh, E. M. Lemmel, S. Pors-Nielsen, R. Rizzoli, H. K. Genant and J. Y. Reginster, N. Engl. J. Med., 2004, 350, 459 CrossRef CAS.
- J. Y. Reginster, E. Seeman, M. C. De Vernejoul, S. Adami, J. Compston, C. Phenekos, J. P. Devogelaer, M. D. Curiel, A. Sawicki, S. Goemaere, O. H. Sorensen, D. Felsenberg and P. J. Meunier, J. Clin. Endocrinol. Metab., 2005, 90, 2816 CrossRef CAS.
- M. G. Dedhiya, F. Young and W. I. Higuchi, J. Dent. Res., 1973, 52, 1097 CrossRef CAS.
- M. E. J. Curzon, J. Dent. Res., 1985, 64, 1386 CrossRef CAS.
- T. M. Athanassouli, D. S. Papastathopoulos and A. X. Apostolopoulos, J. Dent. Res., 1983, 62, 989 CrossRef CAS.
- T. T. Thuy, H. Nakagaki, K. Kato, P. A. Hung, J. Inukai, S. Tsuboi, H. Nakagaki, M. N. Hirose, S. Igarashi and C. Robinson, Arch. Oral Biol., 2008, 53, 1017 CrossRef CAS.
- J. D. B. Featherstone, C. P. Shields, B. Khademazad and M. D. Oldershaw, J. Dent. Res., 1983, 62, 1049 CrossRef CAS.
- L. J. Skipper, F. E. Sowrey, D. M. Pickup, K. O. Drake, M. E. Smith, P. Saravanapavan, L. L. Hench and R. J. Newport, J. Mater. Chem., 2005, 15, 2369 RSC.
- L. J. Skipper, F. E. Sowrey, R. Rashid, R. J. Newport, Z. Lin and M. E. Smith, Phys. Chem. Glasses, 2005, 46, 372 CAS.
- V. FitzGerald, R. A. Martin, J. R. Jones, D. Qiu, K. M. Wetherall, R. M. Moss and R. J. Newport, J. Biomed. Mater. Res., Part A, 2009, 91, 76 CrossRef CAS.
- Z. J. Lin, M. E. Smith, F. E. Sowrey and R. J. Newport, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 224107 CrossRef.
- R. Hill, J. Mater. Sci. Lett., 1996, 15, 1122 CrossRef CAS.
- I. Elgayar, A. E. Aliev, A. R. Boccaccini and R. G. Hill, J. Non-Cryst. Solids, 2005, 351, 173 CrossRef CAS.
- R. A. Martin, H. Twyman, D. Qiu, J. C. Knowles and R. J. Newport, J. Mater. Sci.: Mater. Med., 2009, 20, 883 CrossRef CAS.
- A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88 CrossRef CAS.
- P. H. Gaskell, Glasses and Amorphous Materials, Materials Science and Technology, 9th edn, 1991, p. 175 Search PubMed.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, J. Phys.: Condens. Matter, 2003, 15, 8235 CrossRef CAS.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, Phys. Rev. Lett., 2003, 90, 185501 CrossRef.
- J.-P. Amoureux, C. Fernandez and S. Steuernagel, J. Magn. Reson., Ser. A, 1996, 123, 116 CrossRef CAS.
- A. J. Dent, G. Cibin, S. Ramos, A. D. Smith, S. M. Scott, L. Varandas, M. R. Pearson, N. A. Krumpa, C. P. Jones and P. E. Robbins, B18: A Core XAS Spectroscopy Beamline for Diamond, 14th International Conference on X-Ray Absorption Fine Structure, ed. A. F. A. DiCicco, 2009, vol. 190 Search PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537 CrossRef CAS.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 322 CrossRef CAS.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714 CrossRef CAS.
- B. E. Warren, X-ray Diffraction, 1990 Search PubMed.
- R. M. Moss, PhD thesis, University of Kent, 2009.
- H. Ohsato, I. Maki and Y. Takeuchi, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 1575 CrossRef.
- R. J. Newport, L. J. Skipper, V. FitzGerald, D. M. Pickup, M. E. Smith and J. R. Jones, J. Non-Cryst. Solids, 2007, 353, 1854 CrossRef CAS.
- S. K. Lee and J. F. Stebbins, J. Phys. Chem. B, 2003, 107, 3141 CrossRef CAS.
- F. Nishi, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 534 Search PubMed.
- R. E. Marsh and F. H. Herbstein, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39, 280 CrossRef.
- V. Kahlenberg, J. Alloys Compd., 2004, 366, 132 CrossRef CAS.
- R. A. Martin, S. Yue, J. V. Hanna, P. D. Lee, R. J. Newport, M. E. Smith and J. R. Jones, Philos. Trans. R. Soc., A, 2012, 370, 1422 CrossRef CAS.
- A. Samoson, J. Magn. Reson., Ser. A, 1996, 121, 209 CrossRef CAS.
- A. P. M. Kentgens, Geoderma, 1997, 80, 271 CrossRef CAS.
- R. Dupree, A. P. Howes and S. C. Kohn, Chem. Phys. Lett., 1997, 276, 399 CrossRef CAS.
- C. Gervais, D. Laurencin, A. Wong, F. Pourpoint, J. Labram, B. Woodward, A. P. Howes, K. J. Pike, R. Dupree, F. Mauri, C. Bonhomme and M. E. Smith, Chem. Phys. Lett., 2008, 464, 42 CrossRef CAS.
- F. Angeli, M. Gaillard, P. Jollivet and T. Charpentier, Chem. Phys. Lett., 2007, 440, 324 CrossRef CAS.
- A. Pedone, T. Charpentier, G. Malavasi and M. C. Menziani, Chem. Mater., 2010, 22, 5644 CrossRef CAS.
- T. F. Kemp and M. E. Smith, Solid State Nucl. Magn. Reson., 2009, 35, 243 CrossRef CAS.
- U. Hoppe, G. Walter, A. Barz, D. Stachel and A. C. Hannon, J. Phys.: Condens. Matter, 1998, 10, 261 CrossRef CAS.
- R. A. Martin, P. S. Salmon, C. J. Benmore, H. E. Fischer and G. J. Cuello, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054203 CrossRef.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, J. Non-Cryst. Solids, 2004, 345–346, 208 CrossRef.
- V. FitzGerald, D. M. Pickup, D. Greenspan, G. Sarkar, J. J. Fitzgerald, K. M. Wetherall, R. M. Moss, J. R. Jones and R. J. Newport, Adv. Funct. Mater., 2007, 17, 3746 CrossRef CAS.
- A. N. Cormack and J. C. Du, J. Non-Cryst. Solids, 2001, 293, 283 CrossRef.
- A. Tilocca, J. Chem. Phys., 2008, 129, 084504 CrossRef.
- R. A. Martin, H. L. Twyman, G. J. Rees, J. M. Smith, E. R. Barney, M. E. Smith, J. V. Hanna and R. J. Newport, Phys. Chem. Chem. Phys., 2012, 14, 12105 RSC.
- Y. Xiang and J. Du, Chem. Mater., 2011, 23, 2703 CrossRef CAS.
- Y. C. Fredholm, N. Karpukhina, R. V. Law and R. G. Hill, J. Non-Cryst. Solids, 2010, 356, 2546 CrossRef CAS.
- Y. C. Fredholm, N. Karpukhina, D. S. Brauer, J. R. Jones, R. V. Law and R. G. Hill, J. R. Soc., Interface, 2011, 1742 Search PubMed.
| This journal is © The Royal Society of Chemistry 2012 |
