Chemically-mediated communication in self-oscillating, biomimetic cilia†
Pratyush
Dayal
,
Olga
Kuksenok
,
Amitabh
Bhattacharya
and
Anna C.
Balazs
*
Department of Chemical Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: balazs@pitt.edu
First published on 31st October 2011
Abstract
A single biological cilium can sense minute chemical variations and transmit this information to neighboring cilia to produce a global response to the local change. Herein, we undertake the first computational study of self-oscillating, artificial cilia and show that this system can “communicate” to undergo a biomimetic, collective response to small-scale chemical changes. The cilia are formed from chemo-responsive gels undergoing the oscillatory Belousov–Zhabotinsky (BZ) reaction. The activator for the reaction, u, is generated within these BZ cilia and diffuses between the neighboring gels. We find that the spatial arrangement of the BZ cilia affects the local distribution of u, which in turn affects the dynamic behavior of the system. Consequently, two closely spaced cilia bend away from each other and the chemo-mechanical traveling waves within the gels propagate top down. By increasing the inter-cilia spacing, we dramatically alter the behavior of the system and uncover a distinctive form of chemotaxis: the tethered gels bend towards higher concentrations of u and hence, towards each other. This chemotaxis is particularly pronounced in an array of five cilia, where we observe a “bunching” of the cilia towards the highest concentration in u, accompanied by the synchronization of the chemo-mechanical waves. We also show that the cilial oscillations can be controlled remotely and non-invasively by light. By selectively illuminating certain cilia, we could “play” the array like a keyboard, causing a rhythmic variation in the heights of the gels. These attributes could be exploited in a range of microfluidic applications, where the controllable communication among the BZ cilia and self-oscillating surface topology can be harnessed to transport microscopic objects within the devices.
Introduction
From bacteria to mammals, living organisms use arrays of hairs, or cilia, to sense local variations in the environment, amplify this local perturbation to a wide-spread “message” and consequently, promote a large-scale, collective action.1–3 Inspired by the versatility of biological cilia in extracting information from their surroundings, researchers have fabricated a range of artificial cilia4–9 in attempts to reproduce some of the sensory capabilities of the biological counterparts. Driven by a range of applied fields and forces, these synthetic filaments have revealed remarkable macroscopic dynamical behavior. The latter studies were primarily focused on creating biomimetic cilia that could be used as actuators for pumping or mixing fluids in microchannels. There have, however, been fewer studies focused on designing synthetic cilia that act as sensors, mimicking the chemo-sensitivity of biological cilia. Namely, an intriguing challenge is to devise filaments that can perform all of the following: (1) sense local chemical changes, (2) transmit information about these chemical changes to neighboring filaments and (3) respond to the changes by undergoing a coherent motion, much as the biological cilia.1–3 The creation of such motile, chemo-sensitive filaments can open new routes for controlling the self-organization and functionality of purely synthetic, biomimetic cilia, as well as provide insight into physicochemical processes that might be playing a role in the biological systems.To design biomimetic cilia that recognize and transmit chemical signals, it might be especially useful to focus on filaments formed from polymer gels undergoing the Belousov–Zhabotinsky (BZ) reaction.10 The BZ gels are unique because these materials undergo autonomous periodic oscillations; the system does not require an external stimulus to drive the periodic pulsations. The distinctive properties of BZ gels are due to a ruthenium catalyst that is grafted to the polymer chains;11,12 in a solution of reagents, the catalyst undergoes an oscillatory oxidization and reduction, which in turn drive the gel to undergo a periodic swelling and deswelling.11,12 In other words, the BZ gels autonomously transduce and amplify a chemical signal into mechanical pulsation. Due to this direct chemomechanical coupling, local variations in the concentration of reagents could affect the mechanical oscillation of a single cilium, and hence influence the interactions of multiple cilia.
Using a new computational model, we herein undertake the first studies of the chemical communication in systems of multiple BZ cilia. Our approach allows us to model the diffusion of the activator of the reaction (referred to as u) in the solution surrounding the cilia and thus, determine how the inter-cilia interactions are perturbed by variations in the activator concentration. Furthermore, we can capture the subtle interplay between the pulsations of the cilia and dispersion of u, where the motion of the cilia will affect the local distribution of u, which in turn will affect the movement of the cilia. Via this model, we show that these BZ “antenna” are highly sensitive to variations in u, which controls a distinctive chemotactic bending of the gels and the directionality of the traveling waves within the cilia. Notably, this responsive behavior is sensitive to the initial separation between the cilia and hence, variations in the distance between neighbors can be used to alter the behavior of the system.
There is another distinct advantage of focusing on BZ cilia: the gels are photosensitive.13 As detailed in the computational studies described below, by selectively illuminating specific cilia in an array, we can control the pattern of wave propagation within the system. In effect, the motion of the tops of the cilia resembles the movement of piano keys, with the light serving to control the “tune”. The process can be arrested by simply illuminating the entire array. The ability to utilize light to remotely and dynamically regulate motion within the system provides new opportunities for harnessing the BZ cilia to controllably transport particulates or fluids in specific directions within microfluidic devices.
We note that millimetre-sized pieces of BZ gels can oscillate autonomously for hours and the system can be refueled by adding more reagents to the solution.11 This autonomous functionality and inter-conversion of chemical and mechanical energy makes the system truly biomimetic. The findings described below provide valuable guidelines for experimentally realizing the versatility of these BZ cilia and reveal fundamental mechanisms that could be playing a central role in the sensing capabilities of biological cilia.
In what follows, we first describe our computational approach and then use this method to examine the factors that influence the dynamic behavior of the BZ cilia. We begin by considering the chemo-sensitivity of a single cilium. As we show below, even an isolated BZ filament is highly sensitive to local variations in u. In particular, we find that the oscillations originate from regions that border the highest concentration of u in the solution. Consequently, we show that the directionality of wave propagation within this cilium can be controlled by tailoring the distribution of the activator. To probe the mechanism of inter-cilial communication, we next consider the simplest multi-cilia system. Namely, we turn our attention to two cilia and show that the findings on the single cilium help rationalize the observed behavior in this system. In particular, we determine how the distribution of u affects the interactions between the two oscillating gels and demonstrate that the system again senses and responds to the highest concentration of u in the solution. Specifically, these studies reveal that when the arrangement of the cilia permits a build up of u between the gels, the cilia bend towards each other and effectively point to the highest concentration of u in the system. We then consider an array of five cilia and show how the complex, collective properties of these larger assemblies can be understood from our findings on the one and two cilia systems. Again we find that the dynamically generated distribution of u controls the oscillations among the five cilia, with the cilia nearest the highest u concentration controlling the directionality of wave propagation in the system. Having probed the behavior of the self-oscillating cilia in the absence of external stimuli, we finally show how an external light source can be used to access new dynamical behavior.
Methodology
Herein, we develop a computational approach that allows us to simulate the dynamics of a multi-component system containing several self-oscillating, chemo-responsive polymer gels immersed in solution. To describe the coupled elastodynamics and reaction-diffusion processes occurring within these BZ gels, we use our recently developed three-dimensional gel lattice spring model (gLSM).14Via this approach, we obtained qualitative agreement between our computational findings and various experimental results.14 For example, in agreement with the experiments, we observed the in-phase synchronization of the chemical and mechanical oscillations for relatively small sized samples.14,15 We also recover the decrease of the oscillation period with an increase in the concentration of one of the substrates.14,16 More recently, we showed qualitative agreement between the main features of shape- and size-dependent pattern formation observed in our gLSM simulations and in respective experimental studies.17 Our simulations also helped clarify recent experiments on gradient gels; namely, the computational studies were useful in explaining how gradients in crosslink density across the width of a BZ gel could drive long, thin BZ gels to both oscillate and bend, and thereby undergo concerted motion.18Here, we combine this gLSM technique with a finite difference approach that accounts for the diffusive exchange of reagents between the gels and fluid, and captures reaction-diffusion processes occurring in the solution. Hence, our system of multiple, self-oscillating gels can “communicate” via the diffusion of reagents in the surrounding fluid.
The chemo-responsive BZ gels exhibit mechanical oscillations in response to the periodic reduction and oxidation of ruthenium catalysts that are grafted to the polymer network.11,12 The kinetics of the gels undergoing the photosensitive BZ reaction is described by a modified version of the Oregonator model that explicitly takes into account the polymer volume fraction, ϕ. The governing equations for this system are:14,19
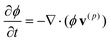 | (1) |
 | (2) |
 | (3) |
Here, v and u are the respective dimensionless concentrations of the oxidized catalyst and activator; v(p) and v(s) are the respective velocities of the polymer network and solvent. The dimensionless diffusive flux of the solvent j(u) through the gel in eqn (3) is calculated as:19j(u) = −(1 − ϕ)∇(u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1 − ϕ)−1). The terms G(u,v,ϕ) and F(u,v,ϕ), which describe the BZ reaction within the gel, are:
(1 − ϕ)−1). The terms G(u,v,ϕ) and F(u,v,ϕ), which describe the BZ reaction within the gel, are:
| G(u,v,ϕ) = (1 − ϕ)2u − (1 − ϕ)v | (4) |
 | (5) |
The parameters q, f and ε in the above equations have the same meaning as in the original Oregonator model.20 The dimensionless variable Φ accounts for the additional production of bromide ions due to illumination by light of a specific wavelength, and is proportional to the light intensity.21–23 By setting Φ = 0 in eqn (5), we recover our previous model for BZ gels in the absence of light.14,19
In the gLSM approach,19,24 the dynamics of the polymer network is treated according to the two-fluid model.25 Within the frame of this model,25 the forces acting on the deformed gel are assumed to be balanced by the frictional drag due to the motion of the solvent. Hence, the dynamics of the polymer network is assumed to be purely relaxational,25 and the corresponding force balance equation is written as:19,24
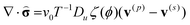 | (6) |
Here,  is the dimensionless stress tensor measured in units of v−10T, where v0 is the volume of a monomeric unit and T is temperature in energy units; ζ(ϕ) is the friction coefficient, and Du is the diffusion coefficient of the activator. We assume25 that the gel/solvent system satisfies the incompressibility condition, ∇·v = 0; in addition, we set the total velocity, v ≡ ϕ
is the dimensionless stress tensor measured in units of v−10T, where v0 is the volume of a monomeric unit and T is temperature in energy units; ζ(ϕ) is the friction coefficient, and Du is the diffusion coefficient of the activator. We assume25 that the gel/solvent system satisfies the incompressibility condition, ∇·v = 0; in addition, we set the total velocity, v ≡ ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v(p) + (1 − ϕ)v(s) = 0.19 In other words, it is solely the polymer-solvent inter-diffusion that contributes to the gel dynamics19,25 and, correspondingly, there is no net momentum exchange between the gel and the external fluid. Hence, by setting v = 0,19,25 we neglect the hydrodynamic interactions within the gels.26 The hydrodynamic effects in the gels are indeed small; in fact, neutral, non-responsive polymer gels were utilized as a medium for the BZ reaction to specifically suppress the hydrodynamics effects.27
v(p) + (1 − ϕ)v(s) = 0.19 In other words, it is solely the polymer-solvent inter-diffusion that contributes to the gel dynamics19,25 and, correspondingly, there is no net momentum exchange between the gel and the external fluid. Hence, by setting v = 0,19,25 we neglect the hydrodynamic interactions within the gels.26 The hydrodynamic effects in the gels are indeed small; in fact, neutral, non-responsive polymer gels were utilized as a medium for the BZ reaction to specifically suppress the hydrodynamics effects.27
Based on the above assumptions, we find the polymer velocity v(p), as:
 | (7) |
 | (8) |
 is the unit tensor and
is the unit tensor and  is a strain tensor. The pressure P(ϕ,v) is obtained as:28
is a strain tensor. The pressure P(ϕ,v) is obtained as:28| P(ϕ,v) = −[ϕ + ln(1 − ϕ) + χ(ϕ)ϕ2 − χ*vϕ] + c0v0ϕ(2ϕ0)−1 | (9) |
The osmotic term (in the square brackets) depends on χ(ϕ) = χ0 + χ1ϕ, which is derived from the Flory–Huggins parameter for the polymer–solvent interactions. The parameter χ* > 0 describes the hydrating effect of the metal-ion catalyst and captures the coupling between the gel dynamics and the BZ reaction. The last term on the right side of eqn (9) describes the pressure from the elasticity of the network; c0 represents the crosslink density of the gel, and ϕ0 is the polymer volume fraction in the undeformed state.
The evolution of the activator concentration, u, outside the gels and within the external fluid is given by
 | (10) |
The last term on the right hand side represents the decay of activator due to the dis-proportionation reaction.29 We focus only on reaction-diffusion processes in the outer fluid and neglect the effects of hydrodynamics. In the simulations presented below, the dimensionless velocity of the gel's expansion/contraction, v(p), is approximately 0.1, which corresponds to approximately 8 μm s−1 using the scaling provided below. If hydrodynamic effects were taken into account, one would expect the characteristic velocities created in the fluid by the cilial motion to be of the same order of magnitude, which in turn would correspond to low Reynolds numbers of Re∼10−2 (assuming the viscosity of the solution equals that of water). The hydrodynamic forces acting from the fluid on the gel surface would be negligibly small due to the low ratio of viscous to elastic forces; this ratio, the relevant capillary number,30 can be estimated as Ca ∼6 × 10−11, where the bulk elastic modulus of the poly(N-isopropylacrylamide) (NIPAAm) gel is taken to be 105 Pa.31 Hence, due to the slow dynamics of the gels and low viscous forces, we can neglect hydrodynamic effects. These effects could, however, be more important if, for example, the oscillations were of significantly higher frequency.
Eqn (1)–(3) are the governing equations for the polymer-solvent system and are solved solely inside the gel, on a Lagrangian grid. The deformable hexahedral elements of this grid are defined by gel nodes. Eqn (10) is solved solely in the fluid, on a fixed, regular, Eulerian grid. At every time step, the flux of activator from the fluid to the gel is interpolated from the Eulerian grid, while the flux of activator from the gel to the fluid is interpolated from the Lagrangian grid. For the surfaces of the Lagrangian grid that are attached to the wall, we impose no-flux boundary conditions for the activator. These boundary conditions allow for the exchange of activator between the fluid and gel only across the mobile gel–fluid interfaces. We use no-flux, Dirichlet or periodic boundary conditions for the external boundary on the fluid grid. We specify these boundary conditions in the text.
Where possible, the systems parameters are taken from known experimental data. In particular, for the BZ reaction parameters, we set18,19ε = 0.12, f = 0.9 and q = 9.52 × 10−5 and for the parameters characterizing the properties of the gel, we set ϕ0 = 0.139, and c0 = 1.3 × 10−3 (based on experimental data provided in ref. 11). For the interaction parameters in eqn (8), we use χ0 = 0.338 and χ1 = 0.518, which corresponds to the NIPAAm gel–solvent interaction parameters at 20 °C for a gel with the above values of ϕ0 and c0.31 We also set χ* = 0.105; χ* is an adjustable parameter of the model and is chosen to have the same value as in ref. 19, 23, 32, 33. For the initial conditions within the gels, we chose the concentrations of the oxidized catalyst and activator to be randomly distributed around their stationary solutions for the given reaction parameters,14vst = 0.18 and ust = 0.19, and we set the initial degree of swelling λ to its stationary value λst = 1.75. To determine the characteristic length and time scales of the system, we assume that the diffusion coefficient of the activator,19Du = 2 × 10−9 m2 s−1, remains the same in the gel and surrounding fluid.34 Using the above values, we find our dimensionless units of time and length correspond to the respective physical values of T0 = 0.31 s and  .
.
Results and discussion
Effect of u on oscillations on single BZ cilium
Before examining how the diffusion of the activator, u, in the fluid results in the communication among multiple oscillating cilia, it is useful to first consider the simpler case of an isolated BZ gel immersed in solution and determine how the concentration of u affects the chemo-mechanical oscillations of the gel. We focus on a sufficiently small sample that traveling waves are not generated within the material,14i.e., the gel swells and deswells essentially uniformly in all directions. This gel is placed in the center of the simulation box, with the initial separation between the walls and the gel surfaces being set to 5.5 lattice units. The diffusion of u takes place through all the gel surfaces and we set identical activator concentrations at all the six fluid boundaries (u = ub).Fig. 1a clearly shows that the frequency of the gel's oscillation, ω, increases monotonically with an increase in ub. In other words, the chemo-mechanical oscillations in the gel occur at a higher frequency when the concentration of the activator in the surrounding fluid has a higher value. The figure also shows that the frequency of oscillations is affected by the presence of light and ω for an illuminated sample remains lower than that for a non-illuminated one for a wide range of ub values. The value of the light intensity in Fig. 1a (represented by the dimensionless value Φ, see Methodology) is significantly greater than the critical value required to suppress the oscillations in an isolated sample,23,33 which does not experience an influx of u from the fluid boundaries.
 | ||
| Fig. 1 Effect of activator concentration on oscillations of a single gel placed in a surrounding fluid. (a) The dependence of frequency of the gel's oscillation,ω, on activator concentration at the fluid boundaries, ub (sample size is 8 × 8 × 8 nodes). The activator concentration is u = ub at all the six fluid boundaries. Two cases, with (Φ = 1.5 × 10−3) and without (Φ = 0) light, are shown. (b) Late time snapshot of BZ cilium (6 × 6 × 30 nodes) immersed in solution; the activator concentration is specified at the top boundary of the box (u = utop) and is maintained at u = 0 at all the other fluid boundaries. Here and below, the oxidized catalyst concentration (v) on the gel's surface and the activator concentration (u) across the central plane of the fluid box are mapped using the color-bar; the minimum values (in blue) are always set to zero, while we vary the maximum values (in red) as provided in each case. Here, we set umax = vmax = 0.3 for utop = 0.0 and 0.02 and vmax = 0.18 for utop = 0.10. Here and below, the black arrows represent the direction of traveling wave. | ||
The observed dependence of ω on u in the surrounding fluid provides significant insight into the effect of the activator concentration on the propagation of traveling chemo-mechanical waves in a single BZ cilium (see Fig. 1b). As we show further below, the results in Fig. 1a also allow us to predict the dynamic behavior of traveling chemo-mechanical waves in more complicated cases involving multiple, communicating cilia.
Each BZ cilium in Fig. 1b is immersed in solution and the activator concentration is specified at the top boundary of the box (u = utop) and is maintained at u = 0 at all the other fluid boundaries. The images in Fig. 1b represent three independent simulations. We observe that when the activator concentration is zero at the top fluid boundary (utop = 0, left image), the traveling wave propagates from the fixed to the free end. This phenomenon is consistent with experiments on a single, long rectangular BZ gel attached to a wall,12 and with earlier computer simulations on single, end-tethered BZ gels.18,19,35 When the activator concentration is increased to moderate values (utop = 0.02, central image), the traveling waves emerge simultaneously from both the ends of the sample. Notably, in each cycle, the waves travel towards the center of the gel, where they meet and annihilate each other. With a further increase in the activator concentration at the top boundary (utop = 0.1, right image), the traveling waves switch direction and emerge from the free tip and travel towards the fixed end.
The phenomena observed in Fig. 1b can be explained as follows. As the activator concentration at the top of the simulation box is increased, the frequency of the traveling waves emanating from the free end of the cilium increases (as can be rationalized by the data in Fig. 1a). In a system containing multiple oscillators, the region with the highest frequency determines the ultimate direction of wave propagation.36,37 In our BZ cilium, each element acts as an oscillator, and the effective intrinsic frequency38 of this oscillator depends on the boundary values of u in the outer fluid and neighboring elements. For utop = 0.0, the fixed end of the gel has the highest intrinsic frequency and hence, the traveling waves propagate bottom-up. In the case of utop = 0.1, the free end of the gel has the highest intrinsic frequency, and consequently, the waves travel top-down. Fig. 1b clearly shows that the local activator concentration in the fluid determines the directionality of wave propagation in the cilium.
Probing the behavior of two interacting cilia
Since our aim is to determine the factors that control the inter-cilial communication, we now focus on two BZ cilia immersed in fluid (Fig. 2) and examine how the separation between these gels, d, and the space between the cilia and the fluid boundary, b, affects the system's behavior. The size of each cilium is (5 × 5 × 29)λ, where λ denotes the gel's initial degree of swelling. The diffusive exchange of u between the gel and fluid occurs through all the gel's surfaces in contact with the solution. The parameters b, d and the size of the gel define the length of the simulation box in the x-direction; the length of the box in the y and z directions is fixed at 20 and 63 dimensionless units, respectively. The activator concentration at x = 0 and x = Lx is taken to be zero. Periodic boundary conditions are imposed in the y direction and no-flux boundary conditions are specified in the z direction. The use of periodic boundary conditions in the y direction removes the influence of edge effects in the lateral direction; the no-flux boundary conditions mimic the presence of impenetrable walls at the top and bottom of the simulation box. Based on the scaling provided in the Methodology, the initial size of the non-deformed gels corresponds to approximately 0.2 mm × 0.2 mm × 1.3 mm and the distance between the two cilia ranges from approximately 0.09 mm to 0.51 mm (i.e., from 3.5 to 20.5 dimensionless units). | ||
| Fig. 2 Effect of d and b on the dynamics of two cilia. (a) and (b) correspond to early (t = 8) and late (t = 486) time snapshots for b = d = 3.5, respectively. (c) and (d) correspond to early (t = 17) and late time (t = 684) snapshots for b = 5.5, d = 20.5, respectively. Panel (e) shows the late time configurations of the cilia with respect to their initial positions represented by vertical blue lines. Panel (f) shows the time evolution of β for values of d and b as given in legend. In (a–d), we set vmax = 0.12 and umax = 0.33. | ||
We observe that the u-mediated communication between the two cilia affects the following: (1) the direction of wave propagation within each cilium, (2) the relative bending of these filaments and hence, their effective separation. As discussed further below, we considered a range of b and d; the two exemplar cases in Fig. 2a and 2c capture the characteristic behavior of the two cilia system and hence, we primarily focus our discussion on these cases to illustrate the properties of this small array. The color of the points across the central plane of the simulation box indicates the activator concentration (see color bar in Fig. 1b). The colors on the gel represent the concentration of oxidized catalyst, v, at the surface elements, with red corresponding to the highest concentration.
At early times in the examples shown in Fig. 2a and 2c (also see movie ESI 1†), the chemo-mechanical waves generated by the BZ reaction within the gel travel bottom-up and the wave propagation in the neighboring cilia is synchronized. At late times, however, the behavior in these two examples becomes distinctly different. If the two cilia are placed relatively close together and close to the edges of the simulation box (b = d = 3.5), the waves travel from top to bottom at late times (Fig. 2b). In addition, these cilia bent away from each other (left image in Fig. 2e.)
In contrast, at late times for the two cilia that are placed relatively far apart and further from the boundary (b = 5.5, d = 20.5), the traveling waves are generated at the center of each cilium. The waves in the cilia oscillate out of phase with respect to each other (see Fig. 2d and movie ESI 2†). Furthermore, the free ends of these cilia are no longer bent towards the walls, but rather, are now tilted towards each other (right image in Fig. 2e.)
In the following discussion, we first isolate the phenomena that contribute to the relative bending of the cilia and then analyze the factors that control the directionality of the wave propagation. To characterize the effective bending of the gels and hence, the dynamics of separation between the two cilia, we define β(t) = α(t)/α(0) − 1, where  is a measure of the inter-cilia separation over the length of the cilium. xki(t) represents the abscissa of the kth gel node in ciliumi at time t, and the summation is over gel nodes. For β > 0, the two cilia are bent away from each other and for β <0, the cilia are bent towards each other.
is a measure of the inter-cilia separation over the length of the cilium. xki(t) represents the abscissa of the kth gel node in ciliumi at time t, and the summation is over gel nodes. For β > 0, the two cilia are bent away from each other and for β <0, the cilia are bent towards each other.
The plot in Fig. 2f of β versus time for various arrangements of two cilia reveals the effects of altering the spacing between the cilia, d, and the distance of the cilia to the boundaries, b. To generate the blue, green and red curves in Fig. 2f, we fixed d = 3.5 and varied b. When the gels are close to the fluid boundary (b = 3.5, blue curve), the entire length of each cilium bends towards the wall and away from each other (see Fig. 2e); hence β increases monotonically with time. As the distance from the x-boundary is increased (green and red curves), this effective bending becomes significantly less pronounced. To probe the effect of inter-cilia spacing, d, on the effective separation between the cilia, we fixed b = 5.5 and varied d (see red, cyan and magenta curves in Fig. 2f). Interestingly, at higher values of d, (7.5 and 20.5) the value of β is always negative, indicating that the cilia are effectively bent towards each other at all times.
To understand the change in the relative deflection of the cilia, we focus on the activator concentration in the fluid for the two different cases in Fig. 2. The plots in Fig. 3 reveal that the distribution of u is highly non-uniform and depends strongly on both d and b. (The distribution is calculated at a time t when the catalyst is predominantly in the reduced state.) Fig. 3 shows that in both these cases, the concentration of u is relatively higher along the inner than the outer surface of the cilia. (Recall that we set u = 0 at x = 0 and x = Lx.) Such gradients in u are expected to drive the cilia to bend away from each other. Recall that in the BZ reaction, the activator promotes the oxidation of the catalyst, which in turn promotes the swelling of the gel. Hence higher values of u close to the inner surfaces would produce higher concentrations of oxidized catalyst and thus, a greater swelling of the inner surface. The latter effect would promote the bending of the cilium towards the wall.
 | ||
| Fig. 3 The distribution of u across the central plane of the fluid box when the catalyst in the cilium is predominantly in the reduced state. Panels (a) and (b) correspond to b = d = 3.5 and b = 5.5, d = 20.5, respectively. The white lines at the bottom of each panel show the position of the bottom cilial surfaces. Here, we set umax = 0.02 in (a) and umax = 0.08 in (b). | ||
This is in fact the behavior seen in Fig. 2b, when the cilia are located relatively close to each other (d = b = 3.5). Notably, the highest concentration of u in the fluid is observed above the cilia (see Fig. 3a) rather than between the gels. The relatively low u values between the cilia at small d arises because the fraction of activator, which was produced during the oxidation phase and spread out from the cilia, diffuses back into the gels from the narrow inter-cilial spacing when the catalyst is in the reduced state.
For the case in Fig. 2d (d = 20.5, b = 5.5), the highest concentration of u is closer to the center of the box (see Fig. 3b). With the relatively large space between the cilia, the fraction of u that diffuses back to the gels during the reduction phase constitutes only a small fraction of the total amount of u that is located between the cilia. As noted above, such gradients in u are expected to cause the cilia to bend away from each other. Surprisingly, however, we find that at late times, these cilia's ends bend towards each other (see value of β in Fig. 2f).
To explain the seemingly anomalous bending in the case of the widely spaced cilia, we perform a more detailed analysis of the scenario where b = 5.5 and d = 20.5. The plot in Fig. 4a shows the temporal evolution of the activator concentration, u, at points P1, P2 and P3 within the fluid; the figure in the inset indicates the configuration of the cilia at early times, when the cilia are bent away from each other. Fig. 4b indicates the difference between the lengths of the left and right most surfaces of each cilium, < Ll–Lr >, as a function of time; the bottom curve is the data for the left cilium and the top curve is for the right cilium. The latter plots clearly highlight the existence of distinct early and late time regimes. During early times, the production of the activator inside the cilia and its subsequent diffusion through the cilial surfaces causes the concentration of u to rise sharply in the surrounding fluid (see Fig. 4a). The increase in u is quite dramatic at point P1 (center of the simulation box) compared to points P2 and P3 due to the u = 0 conditions at the lateral boundaries; consequently, at early times the value of < Ll–Lr > decreases sharply for the left cilium and increases for the right one (Fig. 4b). At later times, however, the average absolute values of < Ll–Lr > decrease for both cilia; this decrease corresponds to the tips of the cilia bending towards each other (see ESI 3).
 | ||
| Fig. 4 Analysis of interaction between two cilia (b = 5.5, d = 20.5. (a) Evolution of u at points P1, P2 and P3 within the fluid; the inset indicates the confirmation of the cilia at early times. (b) Evolution of < Ll–Lr > (see inset of (a)) for the left (blue) and right (green) cilium. (c) Temporal evolution for the distance between the bottom ends of the cilia (with respect to the initial distance between them) when these bottom surfaces are allowed to slide along the x-direction (see inset). | ||
Importantly, Fig. 4b highlights a non-uniform degree of swelling along the x-direction within each gel; furthermore, Fig. 3b indicates that the distribution of reagents is also non-uniform along x. These gradients across the sample indicate that there is a component of wave propagation in the x-direction. (Note that the wave propagates predominately along the length of the cilia due to the high aspect ratio of these filaments.) Since the concentration of u is higher for the inner than the outer surface, the inner surface has a higher intrinsic frequency and the lateral direction of wave propagation is from the inner to the outer surface of each cilium. The net process causes the “pumping” of some amount of solvent from the inner space between the two cilia to the outer regions. In previous studies on single BZ gel samples, we showed that the pumping of fluid in a given direction resulted in the net motion of BZ gels in the opposite direction. Here, however, the bottoms of the cilia are anchored to the substrate. Thus, the induced motion of the solvent (through the cilia) from the area between the cilia to the outer bath drives the cilia to bend in the opposite direction: namely, the tips of cilia bend inwards and thus, towards each other.
Notably, if the cilia were not attached to the bottom substrate, the above effect would cause a net motion of the two samples towards each other. To illustrate this phenomenon, we ran additional simulations where we considered the same cilia as in Fig. 2c and d, but allowed the bottom surface of cilia to slide in the x-direction. The samples are indeed observed to move towards each other, as indicated by the plots of distances between the bottom ends in Fig. 4c. It is noteworthy that the sliding cilia retain their initial mutually “bent away” structure, as seen in the inset. Such lateral excursions, however, cannot be executed by the tethered cilia; instead, these gels can only bend towards each other, as shown for example in Fig. 2e. The latter mutual bending gives rise to the negative values of β seen in Fig. 2f for both cases with relatively large inter-cilia separations.
Fig. 4c depicts a novel form of chemo-mechanical transduction in this synthetic system, where dynamically evolving chemical gradients in the solution induce a deflection of the cilia and an effective attraction between these anchored gels. These cilia display a distinct form of chemotaxis: the self-generated gradient in the activator for the chemical reaction ultimately draws the cilia towards the highest concentration of u (i.e., in the central region).
Finally, we return to the plots in Fig. 3 to explain the directionality of wave propagation in the two exemplar cases. For the case of the closely spaced cilia, the higher concentrations of u near the tops of the gels results in higher intrinsic oscillation frequencies close to the free ends (see Fig. 1a) and causes the observed top-to-bottom wave propagation (Fig. 2b), similar to the right most case of a single cilium in Fig. 1b. We observe a similar evolution in the distribution of u as in Fig. 3a for all three cases with d = 3.5 in Fig. 2f, which in turn explains the top-to-bottom wave propagation in all these cases.
In the case where the cilia lie further apart (d = 20.5, b = 5.5), the highest concentration of u and consequently, the highest intrinsic oscillation frequency corresponds to the center (in z-direction) of each cilium. The latter observation helps explain the observed late-time wave propagation in the example shown in Fig. 2d.
Investigating the communication among multiple BZ cilia
Having considered systems with one and two cilia, we now consider systems with many. In particular, we expand our system to encompass five cilia that are arranged along the x-direction with d = 3.5 and b = 5.5. The size of the simulation box is 69 × 20 × 63 in the respective x, y and z directions; the boundary conditions are the same as noted above. The early and late time snapshots in Fig. 5a and 5b–c indicate that the chemo-mechanical oscillations in the cilia are synchronized (see movies ESI 4–5†). Similar synchronization of five chemical oscillators has been observed for heterogeneous, two-dimensional BZ gel films.39 Here, however, we also observe a number of distinct features that are attributes of our three dimensional system. First, we observe that the traveling waves propagate from bottom-to-top during the early stages, when the activator concentration in the fluid is low, and then switch direction at late times. | ||
| Fig. 5 Dynamics of the five cilia system. The size of the simulation box is 69 × 20 × 63 (in x, y and z directions) with d = 3.5 and b = 5.5. (a) and (b–d) show respective early (t = 8) and late (t = 489, 485, 485, respectively) time snapshots in the absence of light (Φ = 0). (e) and (f–h) show respective early (t = 11) and late (t = 480,489,461, respectively) time snapshots when cilia 1, 2 and 3 (numbered from left to right) are illuminated by light (Φ = 1.5 × 10−3). Here, we set umax = 0.36, vmax = 0.26 in (a), umax = 0.32, vmax = 0.20 in (b), umax = 0.038 in (d), umax = 0.32, vmax = 0.30 in (e), umax = 0.30, vmax = 0.28 in (f), umax = 0.033 in (h). | ||
Second, due to the symmetric arrangement of the cilia and boundary conditions in the x-direction, which result in a relatively high average concentration of u in the central portion of the system (Fig. 5d), we observe that the central cilia leads the oscillations within the system (Fig. 5b and movies ESI 4–5†). Third, the cilia numbered 1,2 and 4,5 clearly bend towards the central cilium at late times (Fig. 5c). The middle cilium in Fig. 5b remains unbent due to the symmetric distribution of u in the surrounding fluid; however, the rest of the filaments, bend towards the high concentration of u at the center of the simulation box.
The “bunching” of the five cilia towards the center of the box is significantly more pronounced than the inward bending of the two cilia (Fig. 2). For the two cilia case with d = 3.5 and b = 5.5, the β values are significantly smaller (red curve in Fig. 2f) so that the bending is less pronounced (moreover, at late times, β > 0). The distinct clustering of cilia in Fig. 5b–c can be attributed to the maximum in u being located over the top of the middle cilium (Fig. 5d) rather than spread more uniformly over the tops of two cilia (much as in Fig. 3a). Importantly, the average values of u in the fluid are also significantly higher in Fig. 5d than for the examples involving two cilia (see scale bars for respective maximum values). These factors contribute to relatively large lateral gradients in u, which drives the outer cilia to cluster towards the central cilium.
Finally, the positions of the top surfaces of all the cilia (their heights, curvature, and the inter-cilia distance) change according to the observed synchronized oscillations. These dynamic changes can be visualized most dramatically by focusing on the vertical displacements of the tops of the cilia and watching as the surfaces move up and down in a complex dynamical pattern (see movie ESI 6†).
As noted above, the BZ gels are photosensitive; illuminating a sample with light of a specific wavelength gives rise to an additional flux of bromide ions, which inhibits the oscillatory behavior.13 By increasing the intensity of this light beyond a critical value, the oscillations can be completely suppressed (in the absence of the influx of u to the gels from the surrounding fluid).13 We now exploit these photo-responsive properties to control the interactions in our five cilia array, including regulating the rhythmic height variations in the oscillating array.
For the case shown in Fig. 5e, the geometric setup and boundary conditions are the same as in Fig. 5a, except that cilia 1, 2 and 3 (numbered from left to right) are illuminated by light. The effect of light is captured in our simulations by setting Φ = 1.5 × 10−3 (see eqn (5)), which represents the additional flux of bromide ions.21 This Φ value is greater than the critical value required to curb the production of u and suppress the oscillatory behavior23,33 and hence, under these conditions, an isolated cilium would not exhibit chemo-mechanical oscillations. (Notably, under different conditions, the peristaltic motion of BZ gels were suppressed at 6.45 mW for light of wavelength 436 nm.13) The oscillations in the five cilia array in Fig. 5e would also be suppressed if the entire array were illuminated with uniform light corresponding to this value of Φ. In Fig. 5e, however, the non-illuminated cilia (numbered 4 and 5) continue to produce the activator u, which diffuses through the fluid to cilia 1, 2 and 3. As the concentration waves travel from right to left (in the negative x direction), the local activator concentration increases sharply and thereby switches “on” each cilium (see Fig. 5e and movie ESI 7†). Correspondingly, the height of each cilium increases, reaches the maximum value and then decreases; we call this variation in height the “piano effect” since the cilia appear to move like the keys of a piano.
To illustrate this piano effect, in Fig. 6 we plot the temporal behavior of the top cilial surfaces (also see movie ESI 8†). Each cilium reaches its corresponding maximum height in a sequential manner. This piano effect is, however, a transient phenomenon that occurs while the activator concentration in the fluid remains relatively low (until about t ∼103, which corresponds to more than a dozen of oscillation cycles).
 | ||
| Fig. 6 The “piano” effect. Variation of the positions of the top cilial surfaces at early times (t = 150–152) when cilia 1, 2 and 3 (numbered from left to right) are illuminated by light (Φ = 1.5 × 10−3). Each cilium reaches its corresponding maximum height in a sequential manner and appears to move like the keys of a piano. | ||
Once the concentration of u builds ups in the system, the waves travel synchronously from top to bottom (see Fig. 5f and movie ESI 9†). Due to the light source, the leading wave front shifts towards the non-illuminated side; this is also reflected in the variations of heights of the cilia (see movies ESI 8, 10†). Here, all the cilia are effectively coming closer together, similar to the case in Fig. 5c. Unlike the case in Fig. 5c, however, the middle cilium in Fig. 5g is also somewhat tilted because now the distribution of u surrounding this central cilium is asymmetric, as seen in Fig. 5h.
The main features of the collective dynamics of the illuminated cilia (Fig. 5e–h) can be understood from the data in Fig.1a. On the one hand, the difference between ω for the non-illuminated and illuminated samples is rather small; hence, the change in the direction of wave propagation within the illuminated cilia with an increase in u near the free ends occurs in the same manner as for the cilium in the dark (Fig. 5b and 5f). On the other hand, ω in the presence of light remains lower than that in the absence of light for a wide range of ub. The latter observation explains both the shift in the position of the leading front towards the cilia in the dark (as in Fig. 5f and movie ESI 9†), as well as the asymmetric “bunching” of the cilia with respect to the center of the simulation box and closer to the non-illuminated region (see Fig. 5g).
Conclusions
In summary, through these studies, we demonstrated that the BZ cilia exhibit a remarkable chemo-sensing capability and can autonomously translate this chemo-sensitivity into a distinct mechanical response. These studies have allowed us to uncover a number of phenomena that are distinct to tethered, three-dimensional BZ filaments. By focusing on a single cilium, we showed that the gel is highly sensitive to the local distribution of the activator, as is evident by the changes in the directionality of the wave propagation with variations in the local distribution of u. Thus, the traveling waves in the cilium can be used as an indicator for the local chemical environment.The two cilia array revealed a novel means of controlling the deflection of the gels. By varying the inter-cilia separation, the filaments can be made to bend towards or away from each other, so that gels resemble the petals of a flower. This bending of the cilia is even more pronounced in the larger arrays; the five cilia highlighted the chemotactic behavior of the system, where the tethered gels bend towards higher concentration of u.
Finally, we showed how an external light source can be utilized to regulate the autonomous pulsations of the system. The light provides a useful means of modifying the intrinsic behavior of the system and thereby, tailoring the properties for specific applications.
These attributes could be usefully exploited in a range of microfluidic applications, where, for example, an external light source could be used to direct the movement of a soft “conveyor belt” 40–42 and thus, manage the transport of microscopic objects within the devices. As indicated above, the motion of the BZ cilia are relatively slow (on the order of 10 μm s−1) and hence, this conveyor belt would be most effective in scenarios that involve diagnostic studies or analyses of the species as they are transported through the microchannels. More generally, the findings provide guidelines for fashioning soft active materials to create useful components in fluidic environments. On a fundamental level, it is useful to recall that the BZ reaction is a classic example of non-linear chemical dynamics and hence, the results provide insight into factors that control the behavior of systems that are driven far from equilibrium.
Acknowledgements
The authors gratefully acknowledge funding from NSF (for partial support of P.D.) and the ARO (for partial support of O.K.).References
- A. S. Shah, Y. Ben-Shahar, T. O. Moninger, J. N. Kline and M. J. Welsh, Science, 2009, 325, 1131–1134 CrossRef CAS.
- S. T. Christensen, L. B. Pedersen, L. Schneider and P. Satir, Traffic, 2007, 8, 97–109 CrossRef CAS.
- R. A. Bloodgood, J. Cell Sci., 2010, 123, 505–509 CrossRef CAS.
- F. Liu, D. Ramachandran and M. W. Urban, Adv. Funct. Mater., 2010, 20, 3163–3167 CrossRef CAS.
- A. R. Shields, B. L. Fiser, B. A. Evans, M. R. Falvo, S. Washburn and R. Superfine, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15670–15675 CrossRef CAS.
- J. den Toonder, F. Bos, D. Broer, L. Filippini, M. Gillies, J. de Goede, T. Mol, M. Reijme, W. Talen, H. Wilderbeek, V. Khatavkar and P. Anderson, Lab Chip, 2008, 8, 533–541 RSC.
- M. Vilfan, A. Potocnik, B. Kavcic, N. Osterman, I. Poberaj, A. Vilfan and D. Babic, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1844–1847 CrossRef CAS.
- O. Tabata, H. Hirasawa, S. Aoki, R. Yoshida and E. Kokufuta, Sens. Actuators, A, 2002, 95, 234–238 CrossRef.
- J. Aizenberg, L. D. Zarzar and P. Kim, Adv. Mater., 2011, 23, 1442–1446 CrossRef.
- A. N. Zaikin and A. M. Zhabotinsky, Nature, 1970, 225, 535–537 CrossRef CAS.
- S. Sasaki, S. Koga, R. Yoshida and T. Yamaguchi, Langmuir, 2003, 19, 5595–5600 CrossRef CAS.
- R. Yoshida, E. Kokufuta and T. Yamaguchi, Chaos, 1999, 9, 260–266 CrossRef CAS.
- S. Shinohara, T. Seki, T. Sakai, R. Yoshida and Y. Takeoka, Angew. Chem., Int. Ed., 2008, 47, 9039–9043 CrossRef CAS.
- O. Kuksenok, V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041401–041416 CrossRef.
- R. Yoshida, M. Tanaka, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 2000, 104, 7549–7555 CrossRef CAS.
- R. Yoshida, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 1999, 103, 8573–8578 CrossRef CAS.
- I. C. Chen, O. Kuksenok, V. V. Yashin, R. M. Moslin, A. C. Balazs and K. J. Van Vliet, Soft Matter, 2011, 7, 3141–3146 RSC.
- O. Kuksenok, V. V. Yashin, M. Kinoshita, T. Sakai, R. Yoshida and A. C. Balazs, J. Mater. Chem., 2011, 21, 8360–8371 RSC.
- V. V. Yashin and A. C. Balazs, J. Chem. Phys., 2007, 126, 124707 CrossRef.
- J. J. Tyson and P. C. Fife, J. Chem. Phys., 1980, 73, 2224–2237 CrossRef CAS.
- H. J. Krug, L. Pohlmann and L. Kuhnert, J. Phys. Chem., 1990, 94, 4862–4866 CrossRef CAS.
- M. Hidaka and R. Yoshida, J. Controlled Release, 2011, 150, 171–176 CrossRef CAS.
- P. Dayal, O. Kuksenok and A. C. Balazs, Langmuir, 2009, 25, 4298–4301 CrossRef CAS.
- V. V. Yashin, O. Kuksenok and A. C. Balazs, Prog. Polym. Sci., 2010, 35, 155–173 CrossRef CAS.
- B. Barriere and L. Leibler, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 166–182 CrossRef CAS.
- To account for the hydrodynamic effects in gels, the condition of v = 0 should be lifted and, correspondingly, the above system of equations should be complemented with the respective Navier–Stokes equation.
- T. Yamaguchi, L. Kuhnert, Z. Nagy-Ungvarai, S. C. Mueller and B. Hess, J. Phys. Chem., 1991, 95, 5831–5837 CrossRef CAS.
- V. V. Yashin and A. C. Balazs, Macromolecules, 2006, 39, 2024–2026 CrossRef CAS.
- R. Aihara and K. Yoshikawa, J. Phys. Chem. A, 2001, 105, 8445–8448 CrossRef CAS.
- A. Bhattacharya and A. C. Balazs, J. Mater. Chem., 2010, 20, 10384–10396 RSC.
- S. Hirotsu, J. Chem. Phys., 1991, 94, 3949–3957 CrossRef CAS.
- V. V. Yashin and A. C. Balazs, Science, 2006, 314, 798–801 CrossRef CAS.
- P. Dayal, O. Kuksenok and A. C. Balazs, Soft Matter, 2010, 6, 768–773 RSC.
- R. Yoshida, G. Otoshi, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 2001, 105, 3667–3672 CrossRef CAS.
- O. Kuksenok, V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 056208 CrossRef.
- A. S. Mikhailov and A. Engel, Phys. Lett. A, 1986, 117, 257–260 CrossRef.
- O. U. Kheowan, E. Mihaliuk, B. Blasius, I. Sendina-Nadal and K. Showalter, Phys. Rev. Lett., 2007, 98, 074101 CrossRef.
- Here and below, by intrinsic frequency of the small region of the gel (with the given value of u in the outer fluid) we refer to the frequency the sample of the size of this region would oscillate in the fluid (with the same value of u set in the outer fluid, similarly to the sample in Fig. 1a).
- V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 046210 CrossRef.
- R. Yoshida, T. Sakai, Y. Hara, S. Maeda, S. Hashimoto, D. Suzuki and Y. Murase, J. Controlled Release, 2009, 140, 186–193 CrossRef CAS.
- Y. Murase, S. Maeda, S. Hashimoto and R. Yoshida, Langmuir, 2009, 25, 483–489 CrossRef CAS.
- Y. Murase, R. Takeshima and R. Yoshida, Macromol. Biosci., 2011 DOI:10.1002/mabi.201100184.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c1jm13787e |
| This journal is © The Royal Society of Chemistry 2012 |
