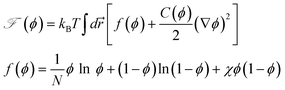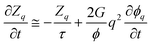Open Access Article
Open Access ArticleViscoelastic phase separation in soft matter and foods
Hajime
Tanaka
*
Institute of Industrial Science, University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153–8505, Japan. E-mail: tanaka@iis.u-tokyo.ac.jp; Fax: +81-3-5452-6126; Tel: +81-3-5452-6125
First published on 26th April 2012
Abstract
Phase separation is a fundamental phenomenon that produces spatially heterogeneous patterns in soft matter and foods. We argue that phase separation in these materials generally belongs to “viscoelastic phase separation”, where the morphology is determined by the mechanical balance of not only the thermodynamic force (interface tension) but also the viscoelastic force. The origin of the viscoelastic force is dynamic asymmetry between the components of a mixture, which can be caused by either a size disparity or a difference in the glass transition temperature between the components. Such dynamic asymmetry quite often exists in foods, which are typically mixtures of big molecules (polymers, proteins, etc.) and liquids (water, oil, etc.). We show examples of mechanically driven pattern formation in foods, in which dynamic asymmetry plays crucial roles, including the formation of network and cellular patterns in foods (e.g., breads, sponge cakes, butter, chocolates, etc.) and crack pattern formation (dried foods, cooked meat, etc.). Collapsing of these structures upon heating or moisture uptake is also discussed. We also argue that heterogeneous gels are in general formed as a consequence of dynamical arrest of the viscoelastic phase separation. Finally we mention an intimate link of viscoelastic phase separation, where deformation fields are spontaneously generated by phase separation itself, to mechanical instability and fracture induced by externally imposed strain fields. Such mechanical instability and nonlinear rheology may be relevant to food processing and also to separation and fracture of foods. We propose that all these phenomena can be understood as mechanically driven inhomogeneization with the concept of dynamic asymmetry in a unified manner.
1 Introduction
Phase-separation phenomena are commonly observed in various kinds of condensed matter including metals, semiconductors, simple liquids, soft materials such as polymers, surfactants, colloids, biological materials, and food materials. The phenomena play key roles in pattern evolution of immiscible multi-component mixtures of any materials. The resulting patterns are linked to optical, electrical, and mechanical properties of materials and also to taste, appearance, and sensory properties of foods. Thus, phase-separation dynamics has been intensively studied from both fundamental and applications viewpoints.1,2On the basis of the concept of dynamic universality of critical phenomena,3 phase separation were classified into a few groups. Phase separation in each group of condensed matter is described by a specific set of basic equations describing its dynamic process. For example, phase separation in solids is known as “solid model (model B)”, whereas phase separation in fluids as “fluid model (model H)”.1,3 For the former the local concentration can be changed only by material diffusion, whereas for the latter by both diffusion and flow. The universal nature of critical phenomena in each model and the scaling concept based on the self-similar nature of domain growth have been established.1,3 In all classical theories of critical phenomena and phase separation, however, the same dynamics for the two components of a binary mixture, which we call “dynamic symmetry”4,5 between the components, has been implicitly assumed. This assumption can always be justified very near a critical point, where the order parameter fluctuations are far slower than any other internal modes of a system (see Fig. 1). However, this is not the case far from a critical point, where most of practical phase separation takes place, for a mixture having strong dynamic asymmetry between the components. The presence of dynamic asymmetry means that there is also a large separation between the soft matter mode and the microscopic mode of a system. Furthermore, there is another gross variable of a system, the velocity field, whose relevance in dynamics comes from the momentum conservation law. Thus, dynamic asymmetry leads to complex couplings between the slow critical fluctuation mode, the slow soft matter mode, and the velocity field (see Fig. 1).
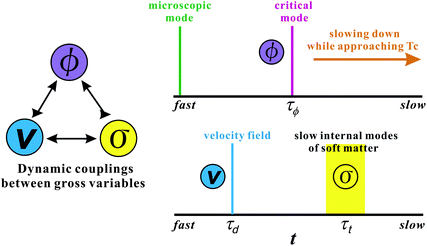 | ||
Fig. 1 Schematic figure showing dynamical couplings among the three gross variables, the composition ϕ, the velocity field ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) , and the stress field σ, The relation among these modes and the microscopic mode are also shown. When approaching the critical point Tc, the order parameter fluctuation mode τϕ should eventually become the slowest mode in principle. In this limit, the relaxation of σ does not play any role and thus the dynamic universality should hold. However, this situation may not be practically realized for a system of strong dynamic asymmetry. In phase separation, we should also consider the characteristic time of deformation τd. If the deformation rate τd is faster than the relaxation rate of the slow soft matter mode τt, the viscoelastic effects have a drastic influence on phase separation. , and the stress field σ, The relation among these modes and the microscopic mode are also shown. When approaching the critical point Tc, the order parameter fluctuation mode τϕ should eventually become the slowest mode in principle. In this limit, the relaxation of σ does not play any role and thus the dynamic universality should hold. However, this situation may not be practically realized for a system of strong dynamic asymmetry. In phase separation, we should also consider the characteristic time of deformation τd. If the deformation rate τd is faster than the relaxation rate of the slow soft matter mode τt, the viscoelastic effects have a drastic influence on phase separation. | ||
Nearly two decades ago we found unusual phase separation behaviour,4–8 which is markedly different from phase separation of a fluid mixture (model H).2,5–10 In the normal phase separation observed in dynamically symmetric mixtures (model H), the phase separation morphology is determined by the balance between the thermodynamic (interfacial) force and the viscous force, while satisfying the momentum conservation. In viscoelastic phase separation, on the other hand, the self-generated mechanical force also plays a crucial role in its pattern selection, in addition to the thermodynamic and viscous force. We named this type of phase separation “viscoelastic phase separation”. In addition to the solid and fluid model, thus, we need the third model for phase separation in condensed matter, i.e., the “viscoelastic model”.11,12 This model is actually a general model of phase separation, which includes the solid and fluid models as its special cases.12
Intuitively, viscoelastic phase separation can be explained as follows. When there is a large difference in the dynamics between the components of a mixture, phase separation tends to proceed in a speed between that of the fast and slow components. Then, the slow component cannot catch up with a deformation rate spontaneously generated by phase separation itself, τd, and thus starts to behave as an elastic body, which switches on the elastic mode of phase separation. Thus, this phenomenon can be regarded as “viscoelastic relaxation in pattern evolution”, which is the reason why we named it viscoelastic phase separation.6 Unlike ordinary mechanical relaxation experiments, the mechanical perturbation is characterized by the rate of deformation induced by phase separation, τd, and the relaxation rate is that of the slowest mechanical relaxation, τt, in a system (see Fig. 1). Without dynamic asymmetry, the deformation rate is always slower than the relaxation rate. Thus, phase separation in such a mixture can always be described by the fluid model, no matter how slow the dynamics of the components. For example, this is the case for a mixture of two polymers having similar molecular weights and glass transition temperatures. We emphasize that dynamic asymmetry, which is prerequisite to viscoelastic phase separation, often exists in materials, particularly in soft materials and food materials.
In this article, we review the basic physics of viscoelastic phase separation,11,13,14 including fracture phase separation,15 and discuss its importance in food science. We show that with an increase in the ratio of the deformation rate of phase separation to the slowest mechanical relaxation rate the type of phase separation switches from fluid phase separation, viscoelastic phase separation, to fracture phase separation. We point out that there is a physical analogy of this to the transition of the mechanical behaviour of materials under shear from liquid fracture, ductile fracture, to brittle fracture. This allows us to discuss phase separation and shear-induced instability of disordered materials,16,17 including soft matter10,18–23 and foods, on the same physical ground. As examples of mechanically driven pattern formation in foods, we also consider the formation of network and cellular patterns in foods (e.g., breads, sponge cakes, butter, chocolates, etc.) and crack pattern formation (dried foods, cooked meat, etc.) as well as collapsing of these structures upon heating or moisture uptake.
2 Importance of phase separation and rheological instability in foods
Processability, texture, flavour, taste, and stability of foods are controlled not only by chemical composition, but also by how the various ingredients are spatially organized, what is the topology, and what is the characteristic lengthscale. Food structures have rich varieties ranging from macroscopically homogeneous liquids to complex, multiphase solids containing water, salts, fats, proteins, and polysaccharides in the form of droplets, fibres, and networks and in the state of gases, liquids, liquid crystals, crystals, and glasses. Such a food structure is an important factor that affects visual impressions, sensory properties, product stability, and even digestion. These inhomogeneous structures are usually generated by nonequilibrium phenomena such as phase separation, emulsification, and crystallization. Such pattern formation has many features in common with that in soft matter. The common physics between pattern evolution in these two systems, soft matter and foods, have recently been addressed in a convincing manner.24–33 Along this line, we focus on the fact that in most cases there is strong dynamic asymmetry between the components of foods. We argue that the basic concept of viscoelastic phase separation that we established in soft matter is relevant to pattern evolution in food materials.There are also many situations where foods are in a strongly nonequilibrium state and exhibit nonlinear rheology such as shear thinning and thickening. For example, phase separation and emulsion stability are major issues for food structures and the effects of externally applied strain fields are also crucial for their processing. The strongest nonequilibrium situation for foods is seen in the processes of being violently mixed in cooking and being chewed in the mouth. In these processes, shear-induced instability and mechanical fracture of foods are key physical phenomena.
Here, we consider pattern formation in food materials and their mechanical instability under shear flow, on the basis of the knowledge of soft matter, putting a special emphasis on the concept of dynamic asymmetry.11
3 Theory
3.1 Two-fluid model of polymer solution and stress-diffusion coupling
Shear effects on complex fluids have attracted much attention because of their unusual nature known as “Reynolds effect”. For example, shear flow that intuitively helps the mixing of the components actually induces phase separation in polymer solutions.2,18 This is caused by couplings between the shear velocity fields and the elastic internal degrees of freedom of polymers. To explain this unique feature of polymer solution, there have been considerable theoretical efforts.18–22 Doi and Onuki10 established a basic set of coarse-grained equations describing critical polymeric mixtures, based on a two-fluid model whose original form was developed by de Gennes and Brochard34–36 for polymer solutions and by Tanaka and Filmore37 for chemical gels.Later, we proposed that an additional inclusion of the strong concentration dependence of the bulk stress, which is not important in shear-induced instability, is necessary for describing viscoelastic phase separation of dynamically asymmetric mixtures, more specifically, the volume shrinking behaviour of the slow-component-rich phase.12,38,39 We also argued its generality beyond polymer solutions to particle-like systems such as colloidal suspensions, emulsions, and protein solutions.23 That is, we showed that the internal degrees of polymer chains and entanglement effects peculiar to polymer systems are not necessary for viscoelastic phase separation to take place and strong dynamic asymmetry between the components of a mixture is the only necessary condition. A main difference between shear-induced phase separation and viscoelastic phase separation is that the velocity fields are induced by external shear fields in the former whereas they are self-induced by phase separation itself in the latter.
The dynamic equations for polymer solutions are given as follows:10
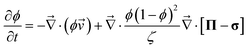 | (1) |
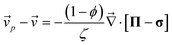 | (2) |
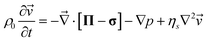 | (3) |
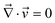 | (4) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p(
p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and
,t) and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) s(
s(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) are, respectively, the average velocities of polymer and solvent at point
,t) are, respectively, the average velocities of polymer and solvent at point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and time t, and then the average velocity of a mixture
and time t, and then the average velocity of a mixture ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) is given by
is given by ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = ϕ
= ϕ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p + (1 − ϕ)
p + (1 − ϕ)![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) s. ϕ(
s. ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is the composition of the polymer. Π is the osmotic stress tensor, which is related to the thermodynamic force
,t) is the composition of the polymer. Π is the osmotic stress tensor, which is related to the thermodynamic force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ϕ as shown in eqn (5):
ϕ as shown in eqn (5):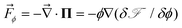 | (5) |
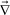 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0. The free energy
= 0. The free energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (ϕ) is given by the following Flory-Huggins-de Gennes form:
(ϕ) is given by the following Flory-Huggins-de Gennes form:where N is the degrees of polymerization of polymer and χ is the interaction parameter between polymer and solvent. The terms containing the mechanical stress tensor cause couplings between the composition and the stress fields via the velocity fields. The above equations clearly tell us that the relative velocity of polymers to the average velocity is determined not only by the thermodynamic osmotic force but also by the mechanical force. To close these equations, we need a constitutive equation, which describes the time evolution of σ.
Here it is worth noting that in eqn (3) the inertia term is not relevant for the description of viscoelastic phase separation in ordinary situations, since viscoelasicity suppresses the development of velocity fields. However, this is not necessarily the case for a shear problem, and even a nonlinear velocity term plays an important role for high Reynolds number flow. This, however, is out of the scope of this article.
In the above, we consider a case of polymer solution, where only polymers can support viscoelastic stress, for simplicity. However, for a more general case, where viscoelastic stress is not supported only by one of the components, we need a more general set of equations.12 In such a case, the constitutive relation may also become more complex.
For a later discussion, here we just note that effects of gravity can be included by replacing 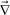 ·σ in eqn (1)–(3) by
·σ in eqn (1)–(3) by 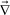 ·σ + Δρϕg
·σ + Δρϕg![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0069_20d1.gif) z, where Δρ is the density difference between the components of a mixture, g is the gravitational acceleration, and
z, where Δρ is the density difference between the components of a mixture, g is the gravitational acceleration, and ![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0069_20d1.gif) z is the unit vector along the gravitational direction.
z is the unit vector along the gravitational direction.
Finally, we mention a fundamental remaining problem of the two-fluid description. In the above derivation, the dissipation in a mixture is separated into the two contributions: one is viscous dissipation of the liquid component, and the other comes from the friction between the two components. This intuitively looks OK, however, the hydrodynamic couplings between the slow components are not considered in a systematic manner in the coarse-gaining procedure. This makes the validity of the above separation a bit obscure. Thus, we need theoretical justification for the treatment of dissipation, which remains a subject for future investigation.
3.2 What is the relevant form of the constitutive relation for a mixture of components having large size disparity?
We note that for mixtures composed of a large particle (or molecule) component, component 1, and a simple fluid (liquid or gas), component 2, the stress division becomes almost perfect (α1 ≅ 1 and α2 ≅ 0), reflecting the large size disparity and the resulting large difference in the friction constant. Stress is selectively supported almost by the large component 1 alone. This is the case for polymer solutions,10 and suspensions of colloids, proteins, and emulsions.23 So, the velocity relevant to the description of viscoelastic stress is the average velocity of component 1 (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p for a polymer solution).
p for a polymer solution).
As an example of this type of mixture, here we consider how the mechanical stress, σ, should be expressed in the case of a polymer solution. In principle, we can incorporate any constitutive equation into the above two-fluid model, depending upon materials. Doi and Onuki10 employed the upper-convective Maxwell equation as a constitutive relation describing its time evolution for polymer solution:40
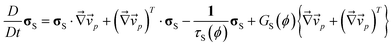 | (6) |
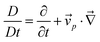 , and τS and GS are the relaxation time and the modulus of the shear stress, respectively. Note that (
, and τS and GS are the relaxation time and the modulus of the shear stress, respectively. Note that (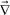
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p)ij = ∂ivpj. To make the shear stress a traceless tensor, σs was defined as
p)ij = ∂ivpj. To make the shear stress a traceless tensor, σs was defined as 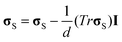 , where I is the unit tensor and d is the space dimensionality.
, where I is the unit tensor and d is the space dimensionality.
We proposed to introduce the bulk stress, to describe the volume shrinking behaviour of the viscoelastic phase separation.12,38,39 Since the bulk stress is isotropic, it can be expressed by a scalar variable, namely, 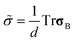 . Then, the bulk stress obeys the following equations:
. Then, the bulk stress obeys the following equations:
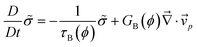 | (7) |
Here, we discuss the rheological functions in the above constitutive equations. In the case of polymer solutions, GS(t) was estimated10,19,20,22 on the basis of rheological theories of polymer solution including the reptation theory40,41 for good and θ solvents. The bulk stress related to GB(t) was not regarded to be important, since the longitudinal relaxation along a tube is much faster than the shear relaxation by reptation.40 This is true locally, however, even in a good solvent, there may be elasticity associated with entanglements for large scale volume deformation at a high concentration. The elastic modulus in such a case is scaled as34,35E ∼ kBT/ξ3e ∼ ϕ2.25, where ξe is the characteristic length of entanglement. Since such a modulus does not exist below the overlap concentration, ϕ*, there may be a steep concentration dependence of E on ϕ. Thus, the bulk modulus GB may be mimicked by a step-like function, Θ(x) (Θ(x) = 1 for x ≥ 1 and Θ(x) = 0 for x < 0),12,38,39 as GB(ϕ) = G0BΘ(ϕ − ϕ*). Furthermore, elastic effects associated with the volume deformation may be even more pronounced for polymer solutions under a poor solvent condition.12,38 It should be stressed that phase separation of polymer solutions always occurs in a poor-solvent condition. Thus, we cannot apply theories for polymers in good and θ solvents to our problem. In a poor solvent, there exist attractive interactions between polymer chains. Thus, we expect that there are temporal crosslinkings of energetic origin between the polymer chains, as schematically drawn in Fig. 2. The most natural model for polymer solutions under such a poor-solvent condition may be a transient gel model, in which the interpolymer attractive interactions produce temporal contact (crosslinking) points between polymer chains. If we assume that the lifetime of temporal contacts between chains is τx, we expect that the bulk relaxational modulus GB(t) has the relaxation time of the order of τx. Then, the deformation described by 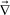 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p, which accompanies a change in the volume occupied by polymer chains, causes bulk stress if the characteristic time of the deformation, τd, is shorter than τx. However, since polymer dynamics in a poor solvent is far from being completely understood, we need further theoretical studies on this problem. We point out that this type of attractive interaction between molecules of the same component may commonly exist in the unstable region of a mixture, which may generally result in the formation of a transient gel in dynamically asymmetric mixtures.
p, which accompanies a change in the volume occupied by polymer chains, causes bulk stress if the characteristic time of the deformation, τd, is shorter than τx. However, since polymer dynamics in a poor solvent is far from being completely understood, we need further theoretical studies on this problem. We point out that this type of attractive interaction between molecules of the same component may commonly exist in the unstable region of a mixture, which may generally result in the formation of a transient gel in dynamically asymmetric mixtures.
 | ||
| Fig. 2 Schematic figure showing the topological and energetic entanglements between polymer chains in a poor solvent. Attractive interactions between polymer chains probably form temporal entanglement points between close segments, whose lifetime, τx, increases with a decrease in the temperature. Thus, the system behaves as a gel in a short time scale. We expect that, in addition to the shear relaxation modulus, GS(t), the system has the bulk mechanical relaxation modulus GB(t), which steeply depends upon the local concentration. | ||
We cannot estimate GB(t) and GS(t) on a quantitative level since we do not have any reliable theory for polymer dynamics in a poor solvent yet. However, we may use knowledge of gels to estimate their magnitudes. According to a standard theory of gels, the mechanical bulk and shear modulus, GB and GS, are given by the following relations:2
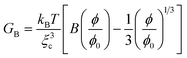 | (8) |
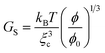 | (9) |
We argued23 that the same physics may be applied to particle-like systems, such as colloidal suspensions, emulsions, and protein solutions, on noting that under the action of attractive interactions particles tend to form a transient network with the help of hydrodynamic interactions.13,42,43 To include the effects of transient gel formation, and the resulting transient elasticity due to the gel-like connectivity, on an intuitive level, we introduced a steep ϕ-dependence of GB,12,29,38 as described above.
Besides the above origin, there is a possibility that for particle suspensions the slow bulk stress relaxation may originate from hydrodynamic interactions under the incompressible condition: hydrodynamic squeezing effects.23 The relative importance of the energetic and hydrodynamic origins in the bulk stress relaxation remains a problem for future investigation. This is related to the treatment of dissipation in the two-fluid description (see section 3.1).
3.3 Constitutive relation for a more general case
The above perfect stress division only applies to a mixture of large size disparity. In polymer blends10,44 or in a system where the glass transition has very different Tg's,12 stress is supported by both of the two components. In this case, the dynamical eqn (1)–(7) must be generalized.12Here, we briefly discuss a general rule of the stress division in such a case. First, we introduce the rheologically relevant velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r, which appears in the constitutive relation. It is defined as
r, which appears in the constitutive relation. It is defined as ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r = α1
r = α1![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 1 + α2
1 + α2![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 2, with α1 + α2 = 1.12,44 Here
2, with α1 + α2 = 1.12,44 Here ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) k is the relative motion of component k, which has the average velocity of
k is the relative motion of component k, which has the average velocity of ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) k, to the mean-field rheological environment, which has the velocity of
k, to the mean-field rheological environment, which has the velocity of ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r, and αk is the stress division parameter. For simplicity, we neglect the transport and rotation of the stress tensor, which does not affect the pattern evolution so much since the transport and rotation are very slow in viscoelastic phase separation. In a linear-response regime, then, the most general expression of σij is formally written by introducing the time dependence of bulk and shear moduli in the theory of elasticity,45 as shown in eqn (10):
r, and αk is the stress division parameter. For simplicity, we neglect the transport and rotation of the stress tensor, which does not affect the pattern evolution so much since the transport and rotation are very slow in viscoelastic phase separation. In a linear-response regime, then, the most general expression of σij is formally written by introducing the time dependence of bulk and shear moduli in the theory of elasticity,45 as shown in eqn (10):
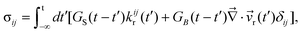 | (10) |
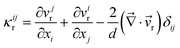 | (11) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r is the velocity relevant to rheological deformation and for polymer solutions
r is the velocity relevant to rheological deformation and for polymer solutions ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r =
r = ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p. GS(t) and GB(t) are material functions, which we call the shear and the bulk relaxation modulus, respectively. It should be noted that the rheological relaxation functions, GS(t) and GB(t), are functions of the local composition ϕ(
p. GS(t) and GB(t) are material functions, which we call the shear and the bulk relaxation modulus, respectively. It should be noted that the rheological relaxation functions, GS(t) and GB(t), are functions of the local composition ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). We note that GB(t) is a purely mechanical modulus and is different from the bulk osmotic modulus, Gos = ϕ2(∂2f/∂ϕ2). We have the relation η = ∫∞0G(t)dt, where η is the viscosity of a material.
). We note that GB(t) is a purely mechanical modulus and is different from the bulk osmotic modulus, Gos = ϕ2(∂2f/∂ϕ2). We have the relation η = ∫∞0G(t)dt, where η is the viscosity of a material.
The second term of eqn (10) was introduced to incorporate the effect of volume change into the stress tensor.12,39 In a two-component mixture, the mode associated with 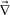 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r can exist as far as
r can exist as far as ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r ≠
r ≠ ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) , even if the system is incompressible,
, even if the system is incompressible, 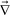 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0. We proposed that this term plays a crucial role in viscoelastic phase separation12,39 (see below), although it is not so important when we consider shear-induced demixing.10,19,20,22
= 0. We proposed that this term plays a crucial role in viscoelastic phase separation12,39 (see below), although it is not so important when we consider shear-induced demixing.10,19,20,22
Now we consider the stress division for the above general case. The friction force is given by ζk(![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r−
r−![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) k), where ζk is the average friction of component k and the mean-field rheological environment at point
k), where ζk is the average friction of component k and the mean-field rheological environment at point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , where the volume fraction of component k is ϕk(
, where the volume fraction of component k is ϕk(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). Here, ζk = ϕkζmk, and ζmk is proportional to the friction between an individual molecule of component k and the mean-field rheological environment, which we call the generalized friction parameter. Because of the physical definition of the mean-field rheological environment, the two friction forces should be balanced. This fact guarantees that the rheological properties can be described only by
). Here, ζk = ϕkζmk, and ζmk is proportional to the friction between an individual molecule of component k and the mean-field rheological environment, which we call the generalized friction parameter. Because of the physical definition of the mean-field rheological environment, the two friction forces should be balanced. This fact guarantees that the rheological properties can be described only by ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r. Thus, we have the following relation, in general:
r. Thus, we have the following relation, in general:
ζ1(![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r − r − ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 1) + ζ2( 1) + ζ2(![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) r − r − ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 2) = 0. 2) = 0. | (12) |
Then, the general expression of the stress division parameter, αk, is obtained as eqn (13).
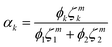 | (13) |
The above relation is consistent with a simple physical picture, where the friction only is the origin of the coupling between the motion of the component molecules and the rheological medium. We expect that this relation holds, irrespective of the microscopic details of rheological models, and, thus, we can apply it to a mixture of any material where the motion of both components is described by a common mechanism. However, for the theoretical estimation of friction coefficients, we need microscopic rheological theories, which are not generally available, unfortunately. More importantly, as mentioned in section 3.1, there is obscurity associated with the treatment of hydrodynamic couplings in the coarse-graining procedure of the two-fluid model.
3.4 Roles of dynamic asymmetry linked to glass transition in diffusion
Dynamic asymmetry affects not only the constitutive relation of a system, but also the kinetics of diffusion.8,12 This is particularly important in a mixture whose components have very different Tg, since there is drastic slowing down of the dynamics towards Tg. This gives rise to an extremely strong dependence of the diffusion coefficient, D, on the composition, ϕ, near Tg. Furthermore, the formation of a transient gel is not expected for a mixture that has little size disparity between its components. The formation of a transient gel may be specific to a mixture with large size disparity. Thus, for a mixture whose components have very different Tg, we do not expect a significant role of the bulk stress in suppressing the diffusion, unlike the case of a mixture of large size disparity (see above), since there may be no strong ϕ-dependence of GB. Even in this case, the strong ϕ dependence of D can cause an effect similar to the bulk stress, as shown below.The ϕ dependence of D near (colloid) glass transition can be expressed by the following empirical Vogel-Fulcher-Tammann (VFT) relation: D(ϕ) = D0exp(Aϕ/(ϕ0 − ϕ)), where ϕ0 is the VFT volume fraction and A is the fragility index. Thus, we have to take into account this ϕ-dependence of D, or the friction coefficient ζ. Effects of a steep ϕ-dependence of D(ϕ) were studied by numerical simulations.46 It should be noted that large bulk stress in the slow-component-rich phase (see above) and slow diffusion in the phase that is rich in the high Tg component play similar roles in phase separation: they both suppress the rapid growth of the composition fluctuations and slow down the composition change in the more viscoelastic phase. Accordingly, the rate of the material transport between the two phases is limited or controlled by that in the slower phase. In this manner, a disparity in the diffusion coefficient, D, between the two components of a mixture, i.e. a steep ϕ-dependence of D(ϕ), has similar effects on phase separation as that in the bulk relaxation modulus GB(ϕ).
Relevant examples of this type of dynamic asymmetry in foods can be found in many water soluble polymers and proteins,47–49 water/sugar mixtures,50 and meat proteins.51 It is widely known that glass transitions and water plasticization strongly affect food quality, safety, and stability.47 Water acts as a ubiquitous plasticizer of natural and fabricated amorphous food ingredients and products. Water-compatible food polymers include polysaccharides, starch, amylose, amylopectin, gluten, glutenin, gliadin, and gelatin. The strong composition (ϕ) dependence of the glass transition of water-soluble ingredients (polymers, proteins, sugars) leads to a steep ϕ-dependence of D(ϕ),50D(ϕ) = D0exp(AT0(ϕ)/(T − T0(ϕ))) and slow dynamics of the ingredients-rich phase, which are prerequisites for asymmetric stress division and the resulting viscoelastic phase separation.
Finally, we note that there is a decoupling between viscosity and translational diffusion in a supercooled liquid,52 which results in the violation of the Stokes–Einstein relation. Since the crystal growth rate is controlled by translational diffusion rather than viscosity, it is faster than that expected from the viscosity, which may solve the so-called Kauzmann paradox.53 This decoupling may even allow crystallization below Tg. This fact may be important when we want to keep amorphous foods while avoiding crystallization,54i.e. in food storage.
3.5 Roles of the steep ϕ dependence of bulk stress and/or diffusion in viscoelastic phase separation
Here we briefly discuss the roles of the steep ϕ dependence of bulk stress and diffusion. According to the continuity equation: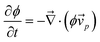 | (14) |
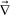 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p that causes the composition change. The bulk stress caused by the deformation type of
p that causes the composition change. The bulk stress caused by the deformation type of  ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p, thus, suppresses the growth of composition fluctuations if τd is shorter than τx. In this way, the bulk stress is directly coupled with the composition change and the volume shrinking.12,38 Note that the volume change of the polymer-rich (slow-component-rich) phase is directly associated with the deformation described by
p, thus, suppresses the growth of composition fluctuations if τd is shorter than τx. In this way, the bulk stress is directly coupled with the composition change and the volume shrinking.12,38 Note that the volume change of the polymer-rich (slow-component-rich) phase is directly associated with the deformation described by  ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p. So, the volume shrinking behaviour peculiar to viscoelastic phase separation is a consequence of (i) the slow bulk stress relaxation due to the connectivity of a transient gel formed by the large component and/or hydrodynamic squeezing effects, or (ii) a steep composition dependence of the diffusion constant D.
p. So, the volume shrinking behaviour peculiar to viscoelastic phase separation is a consequence of (i) the slow bulk stress relaxation due to the connectivity of a transient gel formed by the large component and/or hydrodynamic squeezing effects, or (ii) a steep composition dependence of the diffusion constant D.
3.6 Beyond the simple constitutive relation
As will be discussed later, viscoelastic phase separation accompanies mechanical fracture of the slow-component-rich phase and thus nonlinearity of rheology may also play an important role in the pattern evolution. In the above, we assume a simple Maxwell-type constitutive relation. However, in some cases, we need more complicated constitutive relations to describe the rheology of materials. For example, McLeish and Larson55 showed that strain hardening of branched polymers upon large deformation is related to the fact that the backbone can readily be stretched in an extensional flow since the branches are entangled with the surrounding molecules. Two key deformation types in viscoelastic phase separation are elongation (uniaxial stretching) and extension (biaxial extension). The former is important in a network-forming viscoelastic phase separation whereas the latter is important in a cellular one. The importance of strain hardening in the formation of cellular patterns has been recognized for both synthetic polymers56 and food polymers (e.g., breads).57,58 Qualitatively, strain hardening makes the more viscoelastic phase mechanically more resistive to fracture, or makes the morphological selection due to mechanical force balance more robust (see eqn (22)). It is highly desirable to incorporate these features into the constitutive relation for characterizing these nonlinear effects on a quantitative level.3.7 The early stage of viscoelastic phase separation
First we consider viscoelastic effects for a case of a shallow quench, where a transient gel is not formed and the characteristic deformation rate is slower than the viscoelastic relaxation rate (∼1/τ). This also applies to the early stage of viscoelastic phase separation.59,60 For simplicity, here we do not consider a difference in the relaxation time between shear and bulk stress and assume τB = τS = τ. Using the relation we obtain the linearized equation for zq = [
we obtain the linearized equation for zq = [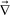 ·
·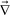 ·σp]q:
·σp]q:where
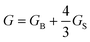 . Here, ϕq is the Fourier component of the deviation from the initial composition ϕ0, and it obeys, to linear order,10,59eqn (15).
. Here, ϕq is the Fourier component of the deviation from the initial composition ϕ0, and it obeys, to linear order,10,59eqn (15).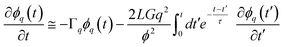 | (15) |
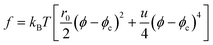 . This form of the free energy is reasonable as far as we concern only a shallow quench near a critical point. Then, Γq = Lq2(rϕ + cq2), where L = ϕ2(1 − ϕ)2/ζ(ϕ), is the decay rate in the absence of viscoelastic couplings. rϕ = r0 + 3u(ϕ0 − ϕc)2, where r0 = a(T − Tc) (a: a positive constant) and Tc and ϕc are the critical temperature and composition, respectively. The correlation length is given by
. This form of the free energy is reasonable as far as we concern only a shallow quench near a critical point. Then, Γq = Lq2(rϕ + cq2), where L = ϕ2(1 − ϕ)2/ζ(ϕ), is the decay rate in the absence of viscoelastic couplings. rϕ = r0 + 3u(ϕ0 − ϕc)2, where r0 = a(T − Tc) (a: a positive constant) and Tc and ϕc are the critical temperature and composition, respectively. The correlation length is given by 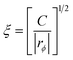 . For a case when the time scale of ϕq change is slower than τ, we can set
. For a case when the time scale of ϕq change is slower than τ, we can set 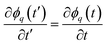 in eqn (15) and, thus, the growth rate of ϕq is given by:
in eqn (15) and, thus, the growth rate of ϕq is given by:| A(q)=L|rϕ|q2(1−ξ2q2)/(1 + ξ2veq2) | (16) |
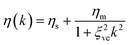 | (17) |
We emphasize that the early stage of phase separation in dynamically asymmetric mixtures, including soft matter and foods, should be analysed by this theory. Applications of the Cahn's theory without considering viscoelastic effects may not be appropriate in many cases since ξve can easily become mesoscopic in dynamically asymmetric mixtures. In relation to this, we note that the above relation [eqn (16)] well explains the unusual q-dependence of A(q) experimentally observed in colloid phase separation.23 This suggests the relevance of the viscoelastic model to phase separation not only in polymer solutions, but also in colloidal suspensions, emulsions, and protein solutions, which further indicates the importance of viscoelastic effects in any dynamically asymmetric mixtures, including food materials.11
3.8 The late stage of viscoelastic phase separation
In ordinary phase separation, the late stage phase separation is discussed on the basis of the scaling concept, which relies on the fact that there is only one characteristic length scale, i.e. the domain size, in a system. For viscoelastic phase separation, however, such a scaling concept is not valid because of the volume shrinking of the slow-component-rich phase during phase separation. Because of this difficulty, there has been no analytical theory on domain coarsening so far. In the following, thus, we describe pattern evolution in phase separation on a qualitative level.4 Pattern evolution in viscoelastic phase separation
4.1 Initiation of phase separation: quench
In ordinary physical experiments, phase separation is usually initiated by an almost instantaneous temperature change from the initial to the final target temperature. Depending upon the type of phase diagram, phase separation can be induced either by cooling or heating. However, phase separation in foods can also be induced by changes in pressure, pH, and salt concentrations, and also by polymerization, drying (removal of solvents), and mixing of an insoluble component. For example, gas-liquid phase transition can be initiated by a pressure drop: spontaneous cavitation of bubbles can be regarded as phase separation and if the growth of bubbles exceeds the relaxation rate of the slow-component-rich phase, the phase separation can be regarded as viscoelastic phase separation. Changes in pH, salt concentration, and mixing of insoluble components all modify the interaction potential of a system, which may result in phase separation. The polymerization reaction leads to the reduction of mixing entropy (note that mixing entropy is inversely proportional to the degree of polymerization, N, according to the Flory-Huggins theory). Removal of a solvent by drying may also lead to phase separation if a solvent is rather poor. All these changes in physical parameters may be very slow. Even for heating or cooling, the rate of the temperature change can be very slow as in the case of baking of breads. However, the key rate here is not the rate of the change of a physical variable, but the rate of deformation induced by phase separation itself. If this deformation rate is faster than the relaxation rate of the slow-component-rich phase, viscoelastic effects should play a crucial role in the resulting phase separation. We emphasize that the key is the Weissenberg number defined for the self-generated deformation rate (see below).Furthermore, in the pattern formation of foods, inhomogeneization is not necessarily induced by phase separation, but may involve much more complex nonequilibrium processes, such as crystallization of fats (fat crystal networks in butters, margarines, and chocolates), ice crystallization (freeze dry foods and ice creams). Some of these cases will also be discussed later.
4.2 General features
First we emphasize that pattern evolution in viscoelastic phase separation is essentially the same between the two types of dynamically asymmetric mixtures:11,13,14 one is a system like polymer solutions,5–7,64 colloidal suspensions,65 and protein solutions,66 where the strong dynamic asymmetry comes from a large difference in the molecular size and topology between the components, and the other is a system whose components have a large difference in the glass transition temperature.8In both cases, a mixture first becomes cloudy just after the temperature quench, then, after some incubation time, small solvent holes start to appear (see Fig. 3, left). We call this incubation period the “frozen period”, which is the initial stage of viscoelastic phase separation. The number and the size of solvent holes increase with time. The slow-component-rich matrix phase expels the fast liquid component and shrinks its volume and becomes networklike or sponge-like with the growth of holes made of the fast-component-rich phase (see Fig. 3, middle). In this volume-shrinking process, the bulk mechanical stress plays a crucial role.38,39 Thin parts of a networklike structure are elongated and eventually broken. In this network-forming process, the pattern is dominated by the mechanical shear force balance condition and thus the shear stress plays a major role.39 In the final stage, a networklike structure tends to relax to a structure of rounded shape and the domain shape starts to be dominated by the interface tension as in usual fluid-fluid phase separation (see Fig. 3, right). Domains finally become spherical. If the concentration of the slow-component-rich phase reaches the glass transition composition, a structure is eventually dynamically arrested. This may be regarded as the general scenario for formation of colloidal gels (see below).23,67,68 When the slow-component-rich phase is the minority phase, then there is a phase inversion during phase separation. This phase inversion is a unique feature specific to viscoelastic phase separation.
 | ||
| Fig. 3 The phase-separation process observed with phase contrast microscopy in a polymer solution of PS (molecular weight: 1.90 × 105) and diethyl malonate (8.53 wt% PS) at 0.0 °C, which is 11.6 K below the phase-separation temperature of 11.6 °C. Patterns are observed after 16 s, 103 s, and 2100 s after the quench from left to right. We can see a gradual transition in morphology from network to droplet, reflecting the crossover from the mechanical-stress-dominated to interface-tension-dominated regime. | ||
According to the common sense of ordinary phase separation, after the formation of a sharp interface between the coexisting phase (namely, in the so-called late stage) the concentration of each phase almost reaches the final equilibrium one and, thus, there should be no change in the volume and concentration of each phase.1,2 We pointed out11 that the volume decrease of the more viscoelastic phase with time, after the formation of a sharp interface, is essentially the same as the volume shrinking of gels during volume phase transition.69–71 The physical reason of this similarity to gels will be discussed later.
The scaling law, established in ordinary phase separation, is a direct consequence of the conservation of the volumes of the two phases after the formation of a sharp interface and the resulting self-similar growth of domains. The volume shrinking of the slow-component-rich phase inevitably leads to the absence of self-similarity during the viscoelastic phase separation and, thus, the absence of an extended scaling regime. Nevertheless, we observe a transient scaling law (the characteristic domain size R ∼ t1/2) in the intermediate coarsening stage for a few systems,65,66,72 although its physical mechanism remains elusive.
In sum, the whole pattern evolution process can be clearly divided into three regimes: the initial, intermediate, and late stages. The crossovers between these regimes can be explained by viscoelastic relaxation in pattern evolution and the resulting switching of the primary order parameter, as will be described below.
Besides the early stage, we do not have any reliable analytical predictions and thus numerical simulations based on the viscoelastic model play a crucial role in its understanding.13,39,72–77 We showed that a steep composition dependence of the bulk modulus or the diffusion constant is the key to volume shrinking and the resulting phase inversion and a rather smooth ϕ2-dependence of the shear modulus is responsible for the formation of a network-like structure.13,39,75
We also showed that the mechanical stress accumulated in a network structure leads to its coarsening by repeating the following sequence: stress concentration on a weak part of the network, its break up and the resulting stress relaxation, and structural rearrangements towards a lower interface energy structure.13,39,75 Such examples can be seen in 2D and 3D colloid simulations, as shown in Fig. 4. We stress that this process can proceed without any thermal activation. Actually, the simulations in Fig. 4 were performed without any thermal noises, namely, at T = 0. This indicates that the coarsening of network-type viscoelastic phase separation can proceed purely mechanically: mechanically driven coarsening. This is markedly different from a conventional picture based on the activation-type coarsening process. We emphasize that mechanically driven coarsening cannot be characterized by the strength of attractive interactions measured by the thermal energy kBT alone.
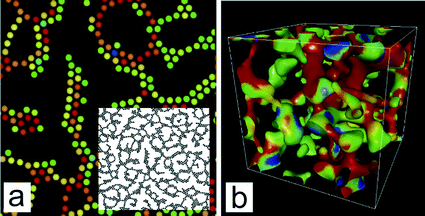 | ||
| Fig. 4 Phase separation processes of colloidal suspensions interacting with the Asakura-Oosawa potential, whose range is characterized by R = dp/Dp, where Dp is the particle diameter and dp is the range of the potential. (a) 2D pattern (the volume fraction is 0.248 and R = 0.7). The inset is the overall structure of the colloidal network. (b) 3D (coarse-grained) pattern evolution (the volume fraction is 0.100 and R = 0.6), where we coarse-grained structures by replacing a particle by a Gaussian field and extracting the interface by applying a black&white operation to the field. The details of the simulations are described in Ref. 72. In both (a) and (b), red particles are stretched and in a high energy state, whereas blue particles are in a low energy state. The most significantly stretched part, due to stress concentration, eventually breaks up, which allows the decrease in elastic energy and results in stress relaxation. This process, which is an elementary process of coarsening, is repeated. | ||
4.3 Examples of viscoelastic phase separation in foods
Phase separation in emulsions is also an important issue in food science. For example, sodium caseinate is widely used as an emulsifying agent in many dairy products, and it imparts stability to emulsions by a combination of steric and electrostatic mechanisms. However, despite excellent coalescence stability above a certain critical protein concentration, caseinate-based emulsions can exhibit pronounced creaming or serum separation due to depletion flocculation induced by excess unadsorbed proteins in the aqueous continuous phase. Upon destabilization, network-forming phase separation is observed and can be interpreted as viscoelastic phase separation.89 Similar behaviour is also observed in soy protein systems.90 This type of pattern formation is basically the same as the viscoelastic phase separation observed in polymer solutions6 and colloidal suspensions65 and protein solutions,66 which is supported by a striking similarity between the phase separation patterns observed.
Under a competition between phase separation and gelation, the final spatial pattern is determined by the stage at which the pattern is frozen by gelation. This is crucially dependent on the quenching condition: if phase separation can proceed sufficiently before gelation starts, a phase separation structure with large characteristic length scale can be formed. In the opposite case, a rather homogeneous pattern is formed. We also note that for the stability of a gel, the mechanical stress generated by viscoelastic phase separation has to be supported by the yield stress of the gel formed. On noting these points, we can say that slow quenching (slow temperature change, slow change in other external variables such as pH and salt concentration, or slow chemical reaction) generally leads to a phase separation structure with a large domain size, since phase separation can proceed before being arrested by glass transition or gelation.
Applying shear in the process of kneading94,95 may lead to the formation of complex phase-separation morphologies under dynamical couplings between stress and diffusion.96 The liquid phase acts as a lubricant and the composition heterogeneity further enhances viscoelastic heterogeneity. In this regime it was found that in a steady state the characteristic domain size is inversely proportional to the average shear stress for various shear rates. In the Newtonian liquid, it is known that the domain size R is determined by a balance between the surface energy density γ/R and the viscous shear stress η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In dynamically asymmetric mixtures, the stress is of elastic origin rather than viscous origin. During a mixing process, gluten particles deform and make crosslinkings via covalent di-sulphide bonds, which makes the process even more complicated. Later we will also discuss phenomena like shear-induced separation of starch and glutens.97
. In dynamically asymmetric mixtures, the stress is of elastic origin rather than viscous origin. During a mixing process, gluten particles deform and make crosslinkings via covalent di-sulphide bonds, which makes the process even more complicated. Later we will also discuss phenomena like shear-induced separation of starch and glutens.97
Here we note that the aggregation process must be affected by hydrodynamic interactions,42,43 as far as the viscosity of the surrounding liquid is not so high. Hydrodynamic interactions have significant effects on the formation of the network structure, such as its fractal dimension.23 The interplay between the shape of particles and the hydrodynamic interactions and their effects on the network morphology are also an interesting topic for future study. The stabilization of the network formed by microcrystallites might be induced by secondary crystallization, in addition to van der Waals attractions. This is related to the above mentioned degree of separation between the crystal growth and aggregation processes.
4.4 Collapsing of network or foam structures
As described above, in the final stage of viscoelastic phase separation, due to a dynamical crossover between the deformation rate induced by phase separation and the structural relaxation of the slow-component-rich phase, a network structure transforms into a droplet structure (see Fig. 3). This process is physically very similar to the collapsing of network or foam structures upon a loss of elasticity under gravity. We note that the collapsing behaviour in the absence of gravitational fields has successfully been simulated by the viscoelastic model.13,39,75 The essential behaviour should be captured by the viscoelastic model including the gravitational effects (see section 3.1). Here we mention a few examples in food products.Polymeric materials formed under these conditions were termed as cryogels, which we often see also in freeze-drying foods107–110 such as kori-tofu and dried vegetables and fruits. Similar phenomena are also observed for freezing colloidal suspensions,111,112 although there is a difference in the mechanism of exclusion between polymers and colloids. When the initial solution or colloidal sol is frozen non-deeply, i.e. not lower than several tens of degrees from the crystallization point of the pure solvent, the resulting system is composed of the crystallized solvent (ice in the case of aqueous systems) and the unfrozen liquid, where the gel-forming components are concentrated: cryoconcentration. Cryoconcentration is the consequence that the noncrystallizable component is expelled from crystals into the surrounding liquid. Although the physics behind the formation of spongy structures is very different, spongy patterns formed in this way have many similarities to those formed by foam-like structures that are formed in viscoelastic phase separation. The commonality comes from nucleation of solvent-rich holes or crystals and the continuous increase of the concentration of shrinking or expelled polymeric components during pattern evolution (phase separation or crystallization, respectively). Unlike viscoelastic phase separation, however, the mechanical force balance does not play any role in the formation of cryogels due to the solid nature of crystals, but after thawing the stress is divided quite asymmetrically between the polymer and solvent phase: the stress is supported exclusively by the spongy polymer structure.
Fruits and vegetables are cellular tissues containing gas-filled pores that tend to collapse upon dehydration.113 The collapsing in the drying process involves tissue shrinkage, cellular shrinkage, and then cell collapse. If the system size is small enough, the system may homogeneously shrink without the formation of pores. For a large enough system, however, the overall shrinkage of a system is very slow and thus internal mechanical instability spontaneously takes place inside the system, which leads to the formation of porous spongy structures. The physics of this phenomenon is the same as that of mechanical instability (solvent hole formation) upon volume shrinking of the slow-component-rich phase in viscoelastic phase separation (see Fig. 3) or in gels undergoing volume shrinking phase transition.64
As in the case of fat crystal networks, the reverse process, i.e., melting of spongy structures due to heating or absorption of solvents, should be essentially the same as the late stage break-up process of spongy or network structures into droplets in viscoelastic phase separation: the process is dominated by interface-tension driven flow (see Fig. 3). For example, when freeze-dried cake is heated to a certain temperature, a change in the structure called collapse generally takes place. The cause of this shrinkage has been attributed to a reduction in the elasticity and viscosity of the matrix, to a point where the viscosity is too low to support the matrix weight. This is essentially the same as the viscoelastic relaxation process of patterns in the final stage of viscoelastic phase separation (see Fig. 3). This may further be related to delayed sedimentation of gels under gravity (see, e.g., Ref. 23,65,114–116). Here transient gels formed by viscoelastic phase separation collapse under the gravitational field, when the gravitational force exceeds the yield stress of the gel network.
5 Pattern evolution in fracture phase separation
Here we show a special case of viscoelastic phase separation, where phase separation proceeds accompanying mechanical fracture of a mixture.5.1 Physical mechanism
The above-described mechanical nature of viscoelastic phase separation implies a close analogy to the mechanical response of materials. Indeed, we recently found novel phase-separation behaviour accompanying mechanical fracture (“fracture phase separation”) in polymer solutions15 (see Fig. 5(a)). Surprisingly, mechanical fracture becomes the dominant coarsening process in this phase separation. This type of phase separation is observed when the deformation rate of phase separation becomes much faster than the slowest mechanical relaxation time of a system. In this sense, the transition from viscoelastic to fracture phase separation corresponds to the “liquid-ductile-brittle transition” in the fracture of materials under shear deformation17 (see Fig. 5(b)). The only difference between fracture phase separation and material fracture is whether the deformation is induced internally by phase separation itself or externally by loading.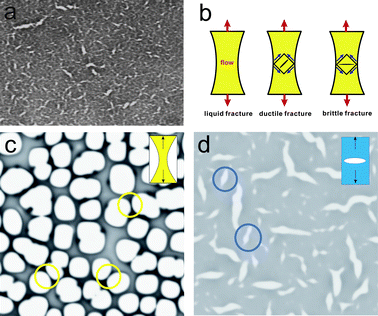 | ||
| Fig. 5 (a) Crack formation in the initial stage of fracture phase separation. Fracture phase separation observed for a polystyrene(PS)/diethylmalonate mixture (4 wt% PS) after a quench to 22 °C. Crack formation is clearly observed. Cracks are solvent-rich domains. The sample thickness is 5 μm. The width of the image corresponds to 0.5 mm. (b) Schematic figure showing liquid, ductile and brittle fracture of a material under elongational deformation. For ductile fracture a crack is formed along 45° from a stretching direction, whereas for brittle fracture it is formed perpendicular to a stretching direction. Brittle fracture is also characterized by crack formation just after the linear Hookian regime. On the other hand, liquid and ductile fracture occur after large nonlinear deformation. Viscoelastic phase separation accompanies liquid or ductile fracture for self-generated shear deformation, whereas fracture phase separation accompanies brittle fracture. (c) Viscoelastic phase separation and (d) fracture phase separation simulated on the basis of the viscoelastic model.15 We can see typical patterns of liquid and solid fracture in (c) and (d), respectively. | ||
We argue that fracture phase separation is the process of mechanical fracture of a transient gel against self-generated shear deformation, which is caused by volume shrinking of the slow-component-rich phase. For slow shear deformation, a transient gel behaves as viscoelastic matter and exhibits liquid fracture behaviour for shear deformation: viscoelastic phase separation. A network is stretched continuously under stress, elongated along the stretching direction, and eventually breaks up. This process resembles the process of liquid fracture of a material under a stretching force (see Fig. 5(c)).117–120 For fast shear deformation, a transient gel should behave in a solid-like manner, and exhibit brittle (or ductile) fracture behaviour: fracture phase separation (see Fig. 5(d)). At this moment, it is not so clear whether crack formation in fracture phase separation belongs to ductile or brittle fracture, since we are not able to visualize the deformation field in the coarse of phase separation. We speculate that cracks are formed perpendicular to the stretching direction (see Fig. 5(b)). This fracture behaviour is a manifestation of solid-like (or, elastic) behaviour119,120 of a transient gel.
The physical mechanism of this mechanical instability is basically the same as shear-induced fracture of a viscoelastic matter: self-amplification of density fluctuations under shear.16,17 In our view, a steep composition dependence of the bulk stress leads to instability of the interaction network for the volume deformation of type 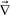 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p < 0, whereas that of the shear stress leads to its instability for shear-type deformation, which should be the origin of fracture-like behaviour. In fracture phase separation, elastic couplings between cracks also play a crucial role in pattern formation. We studied this problem by using a simple spring model,76 but further detailed studies are necessary to elucidate the roles of spatio-temporal elastic coupling.
p < 0, whereas that of the shear stress leads to its instability for shear-type deformation, which should be the origin of fracture-like behaviour. In fracture phase separation, elastic couplings between cracks also play a crucial role in pattern formation. We studied this problem by using a simple spring model,76 but further detailed studies are necessary to elucidate the roles of spatio-temporal elastic coupling.
For a situation of fracture phase separation, the break-up of bonds is required not only for volume deformation, but also for shear deformation of the network. To represent such a strongly nonlinear behaviour, we introduce a steep (actually, step-like) composition dependence also for the shear modulus:15GS(ϕ) = G0SΘ(ϕ − ϕS0), where ϕS0 is the threshold polymer composition for the shear modulus. ϕS0 may be material specific, reflecting its constitutive relation. We speculate that ϕS0 < ϕB0 since the instability occurs for volume deformation before it occurs for shear deformation. This is because only volume deformation can induce a composition change and shear deformation cannot. We confirmed that the introduction of a step-like ϕ dependence for the relaxation time τS has a similar effect.
Fracture phase separation also provides a mechanism for the formation of shrinkage crack patterns in both nature (tectonic plates, dried mud layers, and cracks on rocks) and materials (cracks in concretes and coatings and grazes on a ceramic mug). This mechanism may also be relevant to crack formation in foods upon shrinking, which we discuss below.
5.2 Examples of shrinkage crack formation in foods
Here we briefly discuss a few examples of fracture phase separation in foods. It is not easy to find such examples in the narrow meaning of fracture phase separation. However, pattern formation induced by mechanical fracture self-induced by volume shrinking can be found in many situations.The most obvious examples are surface crack formation upon drying of foods, i.e., evaporation of a liquid component (e.g. water) from them. Crack formation should occur when the deformation induced by evaporation exceeds the mechanical relaxation rate of a material. Thus, we propose that the control of the evaporation rate allows us to control surface crack formation or avoid it. We also note that in the process the mechanical boundary condition plays a crucial role. This issue will be discussed later in more detail.
An interesting example can also be seen in the structural change occurring post mortem in meats.121 This phenomenon is induced by slow fibre shrinkage, which leads to the formation of gaps between the fibre bundles. Lateral shrinkage of myofibrils, which is induced by pH drop after death, occurs while accompanying expelling water, which resembles viscoelastic phase separation or the volume shrinkage of gels. After the formation of gaps between fibre bundles, further shrinkage of fibres eventually leads to gap formation between fibres. Thus, gap formation occurs in a two step process, which leads to two-level gap patterns. This can be explained by two pre-existing boundaries, which have different strengths: weaker boundaries between fibre bundles and stronger boundaries between fibres. We note that even without such boundaries, mechanical instability generally takes place in a longer length scale and develops towards shorter length scale upon further shrinking. in this particular case, fracture takes place from weaker boundaries. In our viscoelastic model, we do not have any spatial heterogeneity in elastic and viscous properties in the initial state besides thermal fluctuations. However, if there is heterogeneity, fracture should first take place in a weak part due to stress concentration. This feature can be incorporated into the viscoelastic model by introducing the spatial dependence of the elastic modulus as an initial condition. After the detachment of fibre bundles, further shrinkage of the fibres creates mechanical stress. However, since at this stage each fibre bundle is already mechanically isolated, it has a free surface boundary condition. Since the transport of water from the surface of fibre bundles is limited, however, the mechanical stress is generated inside a fibre bundle, which leads to secondary fracture at boundaries between fibres. We note that the same mechanical instability also happens in cooking meats.122 When we heat meats in cooking, lateral shrinkage of fibres also takes place and leads to gap formation, which leads to the formation of a peculiar texture like surface crack patterns. The basic mechanism is the same as the above and may be classified into shrinkage-induced crack patterns.
In principle, similar cracking or porosity formation occurs when there is a significant volume shrinking in the drying process of foods such as vegetables and fruits.113,123,124 The basic physics should be the same. Whether volume shrinking leads to the formation of cracks or pores should depend upon the shrinking rate and the rheological relaxation rate of the matrix. If the relevant Weissenberg number is much larger than 1, fracture-type cracking should take place and otherwise a porous structure should be formed. Even in the fracture mode, significant shrinking may eventually lead to a porous structure (but without smooth interfaces).15 As in the above cases, the initial mechanical heterogeneity pre-existing in foods should significantly affect the spatial characteristics of initial mechanical instability. This feature is absent in ideal viscoelastic or fracture phase separation, besides very weak inhomogeneity due to thermal fluctuations, but can easily be incorporated into the model.
6 Switching of the order parameter during viscoelastic phase separation
6.1 Concept of order-parameter switching
Here we show that the dynamic behaviour of viscoelastic phase separation can be explained by the concept of “order-parameter switching”. Phase separation is usually driven by the thermodynamic force and the resulting ordering process can be described by the temporal evolution of the relevant order parameter associated with the thermodynamic driving force. The primary order parameter describing phase separation of a binary mixture of isotropic components is only the composition difference between the two phases in the solid or fluid model of phase separation. In the viscoelastic model, on the other hand, the phase-separation mode can be switched between “fluid mode” and “elastic gel mode”. This switching is caused by a change in the coupling between the stress and the velocity fields, which is described by eqn (10): eqn (10) tells us that these two ultimate cases, namely, (i) fluid model (κpij ∼ constant) and (ii) elastic gel model (GS(t) and GB(t) ∼constant), correspond to τts ≫ τd and τts ≪ τd, respectively. For τd ≫ τts the primary order parameter is the composition as in usual classical fluids, whereas for τd ≤ τts it is the deformation tensor as in elastic gels. The deformation tensor up is defined as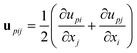 | (18) |
It is well known2,71 that the free energy of gel, f, can be expressed only by the local deformation tensor as f(up). Thus, we can say that the order-parameter switching is a result of the competition between two time scales characterizing the domain deformation τd and the rheological properties of domains τts. As mentioned above, thus, this can be regarded as viscoelastic relaxation in pattern evolution. Here it should be noted that the above two order parameters are related with each other in a gel state as2
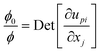 | (19) |
6.2 Crossovers between the characteristic timescales
We next consider how τts and τd change with time during phase separation. To simplify the problem, we estimate the temporal change of τd and τts, provided that they are independent of each other. Under this crude assumption, we can estimate the velocity field determining the deformation rate, neglecting the contribution of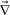 ·σ, from the relation
·σ, from the relation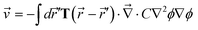 | (20) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the so-called Osceen tensor given by
) is the so-called Osceen tensor given by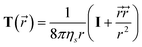 | (21) |
According to the above equation, in the initial stage the velocity fields should grow125 as |![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) | ∼ kBTC/3ηξΔϕ2, where Δϕ is the composition difference between the two phases, and ξ is the correlation length, or the interface thickness. Since Δϕ approaches to 2Δϕe (ϕe: the equilibrium composition) with time, this expression of |
| ∼ kBTC/3ηξΔϕ2, where Δϕ is the composition difference between the two phases, and ξ is the correlation length, or the interface thickness. Since Δϕ approaches to 2Δϕe (ϕe: the equilibrium composition) with time, this expression of |![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) | reduces to the well-known relation |
| reduces to the well-known relation |![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) | ∼ γ/η (γ: interface tension) in the late stage [note that γ ∼ kBTC(2ϕe)2/3ξ]. Thus, the characteristic deformation time τd changes with time as τd ∼ R(t)/V(t) ∼ R(t)/Δϕ(t)2. In the initial stage, the domain size does not grow so much with time whereas Δϕ rapidly increases with time; and, accordingly, τd decreases rapidly. On the other hand, τts increases steeply with an increase in Δϕ, reflecting the increase in the polymer concentration in the polymer-rich domain. Thus, τts becomes comparable to τd in this intermediate stage of phase separation. Once τd exceeds τts, the slower phase cannot follow a deformation speed and behaves as an elastic body: the mechanical force balance dominates a coarsening process in the intermediate stage. Next, we consider what happens in the late stage. Since Δϕ approaches the value of 2ϕe and becomes almost constant in the late stage, τd (∼Rη/γ) increases with an increase in R whereas τts becomes almost constant. Thus, τd becomes longer than τts again. This results in the fluid-like behaviour in the final stage of phase separation. We may regard Wi = τts/τd as the Weissenberg number for self-generated deformation rate. The viscoelastic effects become significant when this Wi significantly exceeds 1.
| ∼ γ/η (γ: interface tension) in the late stage [note that γ ∼ kBTC(2ϕe)2/3ξ]. Thus, the characteristic deformation time τd changes with time as τd ∼ R(t)/V(t) ∼ R(t)/Δϕ(t)2. In the initial stage, the domain size does not grow so much with time whereas Δϕ rapidly increases with time; and, accordingly, τd decreases rapidly. On the other hand, τts increases steeply with an increase in Δϕ, reflecting the increase in the polymer concentration in the polymer-rich domain. Thus, τts becomes comparable to τd in this intermediate stage of phase separation. Once τd exceeds τts, the slower phase cannot follow a deformation speed and behaves as an elastic body: the mechanical force balance dominates a coarsening process in the intermediate stage. Next, we consider what happens in the late stage. Since Δϕ approaches the value of 2ϕe and becomes almost constant in the late stage, τd (∼Rη/γ) increases with an increase in R whereas τts becomes almost constant. Thus, τd becomes longer than τts again. This results in the fluid-like behaviour in the final stage of phase separation. We may regard Wi = τts/τd as the Weissenberg number for self-generated deformation rate. The viscoelastic effects become significant when this Wi significantly exceeds 1.
In short, τd ≫ τts in the initial stage, τd ≤ τts in the intermediate stage, and τd ≫ τts in the late stage again. Accordingly, the order parameter switches from the composition to the deformation tensor, and then switches back to the composition again. When phase separation accompanies an ergodic-to-nonergodic transition such as glass transition, phase separation ends up with a dynamically arrested state, which can freeze network-like and sponge-like structures: gelation (see below).
Here we consider possible effects of a difference in the two types of origins of dynamic asymmetry on pattern evolution: size disparity and the difference in Tg between the two components. In the above, the domain deformation rate is related to the interfacial tension γ, or the coefficient c. It is known that γ is inversely proportional to ξ2, γ ∼ 0.1kBT/ξ2, according to the two scale-factor universality.2 Since the interfacial thickness, or the correlation length, ξ, is the size of a component, the interface tension, γ, is known to be extremely small for systems of macromolecules, emulsions, and colloids simply because of their large sizes.126–128 However, the large size of the slow component also results in the slow relaxation in proportion to ξ3. Thus, the above Weissenberg number, Wi, can become very large even for a system with size disparity.
7 Viscoelastic selection of phase-separation morphology
7.1 What physical factors determine the shape of pattern?
Since the deformation tensor up has an intrinsic coupling to the mechanical stress, a pattern in the elastic regime is essentially different from that of usual phase separation in fluid mixtures, which is dominated by the balance between the thermodynamic and the viscous force. The domain shape during viscoelastic phase separation is determined by which of the mechanical and interface force is more dominant in the momentum conservation equation. Roughly, the elastic energy is scaled as GSe2Rd (e: strain and d: spatial dimensionality) for a domain of size R, since it is the bulk energy. On the other hand, the interface energy is estimated as γRd−1. For macroscopic domains, thus, the elastic energy is much more important than the interface energy in the intermediate stage where τd ≤ τts.The momentum conservation tells us that the domain shape is generally determined by the mechanical shear force balance condition:11
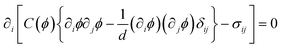 | (22) |
Here we note a possible difference between a system with size disparity and a system with disparity in Tg. As mentioned above, a system with large size disparity is characterized by ultra-low interface tension, γ. For such a system, the above force balance condition can approximately be given by ∂iσij = 0. For a system of disparity in Tg, on the other hand, the interface tension plays a more important role when the mechanical stress is about the same. In the final stage of viscoelastic phase separation, where the Weissenberg number, Wi, decreases and becomes smaller than 1, the interface tension leads to the breakage of a network structure, which transforms the morphology from network-like to droplet-like. This process may take place more slowly for a system with size disparity than for a system with disparity in Tg.
7.2 Crucial roles of the boundary condition for a system in viscoelastic and fracture phase separation
As described above, the mechanical force balance plays a crucial role in pattern selection in viscoelastic phase separation. A transient gel always tends to shrink to reduce the elastic energy, as a gel undergoing volume-shrinking transition does.69,70 This means that the entire network tends to shrink its volume. This stress leading to volume shrinking of a whole sample must be supported by the boundary to have only internal mechanical instability, leading to solvent-hole formation and crack formation. In simulations, the employment of a periodic boundary condition automatically allows us to avoid long-wavelength instabilities. The rate of volume shrinking is controlled by the rate of the transport of the fluid component under the stress fields. In many experimental situations, this elastic stress is supported by the boundary, which prevents the shrinking of the overall volume of a transient gel. This can be realized by wetting or adsorption of the slow-component-rich phase to walls confining a sample. In our experiments using a quasi two-dimensional sample for microscopic observation, or for an anisotropic confinement of a sample, the volume shrinking in the lateral direction is strongly suppressed by a large friction of the sample to the walls. This boundary effect is the very origin of the mechanical stress acting against concentration diffusion (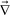 ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) p). Even if there is no fixed boundary condition, for a very large sample there is a clear separation between the time scale of the volume shrinking of the entire sample and that of the local development of the mechanical instability. For a small sample, however, the volume shrinking takes place rather rapidly and thus affects or interferes the internal mechanical instability. We reported such volume shrinking behaviour of the whole transient gel accompanying mechanical instability in a macroscopic length scale in Ref. 64.
p). Even if there is no fixed boundary condition, for a very large sample there is a clear separation between the time scale of the volume shrinking of the entire sample and that of the local development of the mechanical instability. For a small sample, however, the volume shrinking takes place rather rapidly and thus affects or interferes the internal mechanical instability. We reported such volume shrinking behaviour of the whole transient gel accompanying mechanical instability in a macroscopic length scale in Ref. 64.
This special role of the boundary condition in phase separation is a manifestation of the mechanical nature of phase separation, which is common to both viscoelastic and fracture phase separation. We note that surface crack formation is also affected by such a boundary condition. During evaporation of the liquid component, the volume shrinking of the surface part takes place much faster than the bulk part far from the surface. Thus, the bulk part plays the same role as a fixed boundary condition and supports the mechanical stress, which leads to the formation of surface crack patterns.
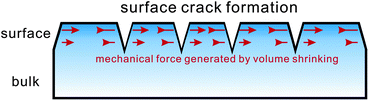 | ||
| Fig. 6 Schematic figure showing the localization of mechanical stress near the surface of drying soft matter and foods. The mechanical stress is a consequence of volume shrinking induced by solvent evaporation. | ||
Surface crack patterns can also be induced by bulk expansion: the slow (or solid-like) surface layer cannot catch up with the expansion of the bulk. This is, for example, the case of surface crack formation of chocolate loafs. Surface crack formation during freezing of foods may also share the same origin: volume expansion due to ice crystallization in the bulk may lead to surface crack patterns, if crystallization near the surface is more suppressed than bulk due to partial drying or any other reasons. We also note that surface crack formation can also be caused by cooling of a glassy material from its surface. This is because surface cooling leads to a larger volume shrinking near the surface. This causes the extensional mechanical stress on the surface, which may induce brittle fracture of the surface region that becomes solid-like near and below the glass transition upon cooling. This may be the case for formation of grazes on ceramic or glass mugs.
8 Arrest of viscoelastic phase separation
8.1 Gelation as dynamically arrested viscoelastic phase separation
Gels and glasses are important nonergodic states of condensed matter, both of which are dynamically arrested nonequilibrium states.129 Unlike crystals, their static elasticity does not come from translational order. These states are particularly important in soft matter and foods. In particular, a gel can sustain its shape under gravity, but is still soft enough to eat; because of these features, it is a major form of foods. Thus, we briefly consider the nature of gel and the mechanism of its formation.We show a schematic state diagram for colloidal suspensions in Fig. 7, which shows that a transient gel is a consequence of viscoelastic phase separation and a permanent gel is a consequence of viscoelastic phase separation dynamically arrested by glass transition.23 Recently, by combining careful experiments and simulations, Lu et al.68 showed evidence that colloidal gelation is spinodal decomposition dynamically arrested by glass transition. Here it is worth pointing out that spinodal decomposition is not the necessary condition, but phase separation including nucleation-growth type is enough to cause gelation if the slow-component-rich phase is the majority phase.23 In this scenario, there is an intimate relation between gels and glasses, since the source of dynamic arrest for these two nonergodic states is the same. However, there are many distinct differences in both structures and dynamics between them (see, e.g., Ref. 130). Locally the dynamic arrest is a consequence of glass transition. However, since gelation is a consequence of phase separation, it intrinsically has macroscopic spatial heterogeneity. This is always the case if a gel is formed by ordinary attractive interactions between particles.
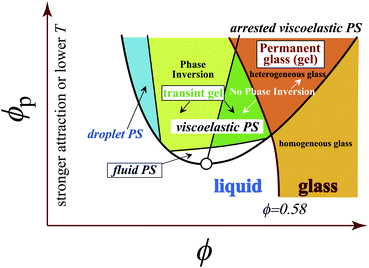 | ||
| Fig. 7 Schematic state diagram for colloidal suspensions, emulsions, and protein solutions. Whether phase inversion takes place or not is determined by the static symmetry line on which the two separated phases occupy the same volume. In the left-hand side of this line, a network pattern is formed, whereas in the right-hand side a sponge-like structure is formed. Whether viscoelastic phase separation is arrested or not is determined by the glass-transition line. The timing when viscoelastic phase separation is arrested by glass transition, or the degree of coarsening of a phase-separated structure, is dependent on the quenching condition (the composition, the effective temperature, and the quench speed). | ||
In some cases, however, gelation involves specific interactions such as strong hydrogen or covalent bonding and microcrystallite formation (e.g., gelatin gels and agarose gels). We note that the mechanism of gelation in these cases is different from the above scenario, reflecting the difference in the mechanism of local dynamic arrest. For example, in gelatin and agarose crosslinking points are formed by microcrystallites of polymers. In some biopolymers hydrogen bonding between polymers is responsible for gelation, whereas in gluten di-sulphide bonds are responsible. The difference in the physical interactions stabilizing a gel network leads to the difference in the stability and yield stress. Upon viscoelastic phase separation, mechanical stress is always generated in the polymer-rich phase but the formation of crosslinkings leads to an increase in the yield stress, which results in the stabilization of the gel under the mechanical stress. We emphasize that this mechanical stress is induced by many body effects (the sum of attractions between many molecules) and thus can well exceed the interaction strength per bond, which is often measured in the unit of kBT. Thus, even for strong attractions (≫kBT), coarsening can proceed upon phase separation accompanying gelation (see the discussion in section 4.2) if there is a strong driving force for volume shrinking, although stronger bonds of course tend to increase the yield stress and make a gel more stable. The level of coarsening can also crucially depend upon the stage at which gelation takes place upon phase separation (see the state diagram and the caption of Fig. 7).
8.2 Ageing of gels and glasses
The scenario that gelation is viscoelastic phase separation dynamically arrested by glass transition immediately tells us a crucial difference in the ageing mechanism between gelation and vitrification. In viscoelastic phase separation, the coarsening is driven by elastic stress associated with volume shrinking and interfacial tension. These features are absent in the ageing of glass transition, at least in colloidal suspensions, due to the conservation of the composition. In ordinary glass transition, which takes place under a condition of constant pressure, the volume of a sample decreases (or, the density increases) while ageing, since the ageing accompanies the densification due to attractive interactions. We can say that the ageing of gels proceeds under the momentum conservation while satisfying eqn (22).72 The intrinsic macroscopic heterogeneity of gels, which comes from its link to viscoelastic phase separation, leads to strong inhomogeneity of particle mobility, i.e., faster dynamics near the interface.131Whether viscoelastic phase separation is dynamically arrested or not may be determined by whether the connectivity of the slow-component-rich phase remains when the system reaches a nonergodic state or not. Once the volume shrinking stops, the driving force for domain coarsening becomes only the interfacial tension. If the yield stress of a gel is higher than the force exerted by this interfacial tension, the system is basically frozen and only exhibits slow ageing towards a lower free-energy configuration, which is basically the same as that of glasses.
8.3 Moving droplet phase
Here we mention another type of viscoelastic phase separation, which takes place in a mixture with a low volume fraction of the slow component. At such a low volume fraction, the slow-component-rich phase immediately forms droplets, which shrink their size by expelling a solvent. This shrinking process is finished rather quickly because of the small size of the droplets. Thus, the volume fraction inside droplets may rapidly reach a glassy state if the final volume fraction is higher than the glass transition volume fraction. If the collision timescale is shorter than the structural relaxation time, droplets behave as elastic glassy balls. This may also be expressed as follows. If the contact time during droplet collision due to Brownian motion is shorter than the material transport between droplets, droplets do not coalesce and stay without growing for a fairly long time. We refer to this interesting metastable state due to the elastic or glassy nature of droplets as “moving droplet phase”.4,5,7,11This phenomenon may be used to make rather monodisperse particles whose size is in the order of sub microns to microns. Recently, it has been shown that even random nonionic amphiphilic copolymers can form stable aggregates, a mesoglobular phase between individual collapsed single-chain globules and macroscopic precipitation.132 The monodisperse nature is a direct consequence of the formation of droplets due to the growth of concentration fluctuations with a characteristic wavenumber and little coarsening after that. So, this phenomenon may provide us with a new very simple and low cost method to make particles with a desired size, which may be useful in both soft materials and foods industries. For example, we speculate that the formation of elastic particle gels of proteins133 may share a common mechanism with the moving droplet phase.
We also note that if the droplet concentration becomes too high, droplets are no longer stable and tend to aggregate to form networks.65 After the formation of networks, the behaviour is similar to viscoelastic phase separation. This may be regarded as a two-step viscoelastic phase separation: the formation of elastic gel particle followed by network formation.
8.4 Arrest of viscoelastic phase separation by smectic order
So far we have considered only phase separation of a mixture of isotropic disordered materials. However, there is a possibility that viscoelastic phase separation accompanies other ordering phenomena. Here we show an interesting example in which viscoelastic phase separation is arrested by smectic ordering.134 We studied phase separation of an ordered phase (lamella) of a lyotropic liquid crystal (tri-ethyleneglycol mono n-decyl ether (C10E3)/water mixtures) into the coexistence of an ordered (lamella) and a disordered (sponge) phase upon heating. When phase separation cannot follow the heating rate, viscoelastic phase separation is observed. The slow lamella phase, which has internal smectic order and anisotropic elasticity, cannot catch up with the fast domain deformation, and thus it transiently behaves like an elastic body and supports most of the mechanical stress. On the other hand, the less viscous sponge phase, which is an isotropic Newtonian liquid, cannot support any stress. This dynamic asymmetry leads to the formation of a well-developed network structure of the lamella phase.If phase separation is slow enough to satisfy the quasi-equilibrium condition, then membranes can homeotropically align along the interface between the two phases while keeping their connectivity, to lower the elastic energy. This leads to the formation of a cellular structure (see Fig. 8). The lamellar films forming closed polyhedra cannot exchange material with layers in neighbouring polyhedra, except by permeation (i.e., diffusion of material normal to the layers). For slow permeation, which should be the case in our system, the lamellar films can exhibit dilational elasticity, which leads to a (quasi-)stable cellular structure. This is markedly different from a soap froth, where the stretching fluid film merely pulls in material from the others without any elastic cost. Thus, a high degree of smectic order in the cell walls and borders stabilises the cellular structure: any deformation of the smectic order increases elastic energy and thus the structure is selected by the elastic force balance condition.
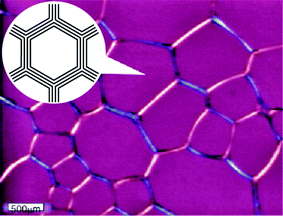 | ||
| Fig. 8 Cellular pattern formation in a lyotropic liquid crystal (a C10E3/water mixture of 19.9 wt% C10E3) observed at 42.15°with polarizing microscopy. The inset schematically shows how membranes are organized in a cellular structure. In a border region, there is a disclination line of strength −1/2. | ||
We also note that this is an interesting example showing that the heating rate can be used to control the type of phase separation, covering from droplet phase separation, to network phase separation, to foam-like phase separation. This may be relevant in pattern formation in foods, where the change in a physical variable, such as temperature, is not instantaneous (see also section 4.1).
This phenomenon may be applied to phase separation of systems with smectic order, such as lyotropic and thermotropic smectic liquid crystals and block copolymers.135 The basic physical strategy may also be used for various types of soft matter and foods, which have other internal order that can support elastic stress. Here it may be worth noting that similar stabilization of foam-like structures by introducing lamellar order in gels has been known as α-gels in food science.136–138 This phase is often thermodynamically unstable and further transforms into the coagel phase, where monoglycerides are crystallized into plate-like crystals. These states are applied to dressings, mayonnaises, sauces, processed cheese, meat products and fat spreads.136 The establishing lamellar order without crystallization would lead to extremely stable foam structures. We also note that the kinetics of phase separation is a key factor for attaining lamellar order in the cell wall.
9 General mechanism of the formation of cellular, foam-like, or sponge-like structures in materials
Next we discuss the universal nature of a spongelike morphology and its physical origin. It is known that gel undergoing volume-shrinking phase transition forms a bubble-like structure.69–71We argue that the physical origin of the appearance of a honeycomb structure in plastic foams (e.g. polystyrene and urethane foams) and breads is also similar to that of a network structure in viscoelastic phase separation. When we consider the mechanical force balance equation in the formation of network patterns, the pressure, p, plays only a minor role: p is determined to satisfy the incompressibility condition. However, the formation of foam structures is usually induced by the liquid-to-gas transformation of one of the components of a mixture (see below), which accompanies its large volume expansion. This expansion creates high internal pressure in gas bubbles, and thus the gas pressure, p, plays a key role in the morphological selection in the foam formation. To describe this phenomenon we need to use the dynamic equations for compressible liquids. The force balance can be satisfied only when a gas bubble is surrounded by the matrix phase: the internal gas pressure is balanced with the mechanical stress created by the stretched matrix phase surrounding the gas bubble. It is this feature that leads to the formation of cellular foam structures. As in the case of network formation in viscoelastic phase separation, we can say that the foam structure formation is a mechanically selected pattern formation, and thus can be regarded as a special case of viscoelastic phase separation.
Besides the above-mentioned difference in the morphological selection, all these processes have a common feature that holes of a less viscoelastic fluid phase (gas in plastic foams, water in gels, solvent in polymer solutions, and so on) are nucleated in a phase-separation process to balance the force associated with the formation of a heterogeneous structure in an elastic medium. Then, the more viscoelastic phase decreases its volume with time (only relatively in the case of foams). This volume shrinking process is dominated by the transfer (diffusion or flow) of the more mobile component under stress fields, from a more viscoelastic phase to the less viscoelastic phase. The limiting process of material transport between the two phases is that in the slower phase. The above picture suggests that a spongelike structure is the universal morphology for phase separation in systems in which one of the components asymmetrically has (visco)elasticity stemming from either topological connectivity or long-range interactions.
9.1 Selection principles of patterns for viscoelastic and elastic phase separation
It is worth noting that this pattern selection differs from phase separation of elastic solid mixtures (e.g. metal alloys). We note that elasticity, which is static, does not involve any time scales (or velocity fields). For elastic phase separation, thus, the momentum conservation, or force balance condition, is irrelevant for the selection of morphology and the pattern evolves solely to lower the elastic energy, while obeying the diffusion equation alone. We emphasize that the momentum conservation is relevant only when a mixture contains a fluid as its component.Elastic effects often originate from a lattice mismatch between the two atomic components in solid alloys. First of all, solid phase separation accompanies little volume change of each phase. Furthermore, the softer phase always forms a network-like continuous phase to minimize the total elastic energy,2 in contrast to our case. This is because it is energetically more favourable to deform the soft phase than the hard phase. In solid mixtures, the elastic energy minimization determines pattern formation, whereas in liquid mixtures the momentum conservation (or the force balance) determines the phase-separation morphology.
Concerning the momentum conservation, we note that hydrodynamic degrees of freedom play a significant role in the initial and final stage of phase separation. For example, network formation in colloid phase separation is significantly influenced by the hydrodynamic interactions between colloids.13,42,43 In the final stage, hydrodynamic effects are important to describe Rayleigh instability of tubes (or networks). In the intermediate stage, on the other hand, hydrodynamic effects are not so significant and only the force balance plays an important role in pattern evolution. To describe this regime, thus, we may use Langevin (Brownian) dynamics139–141 or Newton dynamics.
9.2 Pattern formation in plastic foam
A typical formation process of plastic foams is as follows (see, e.g., Ref. 142). First, a polymer matrix absorbing a low-boiling-point solvent is prepared. Then, its temperature is raised above the boiling point of the solvent, which induces bubble formation in the polymer matrix. These bubbles nucleate and grow as the result of evaporation of the solvent from the polymer matrix. The total volume of the sample expands as a result of the liquid-gas transformation of the solvent. In this process, a pattern is dominated by the mechanical force balance condition with the contribution of the gas pressure, p. This is caused by the strongly asymmetric stress division: gas bubbles cannot support any mechanical stress besides the hydrostatic pressure and only the polymeric phase can support it. In this way, a cellular pattern is formed. As mentioned above, it was pointed out that strain hardening plays an important role in the formation of cellular patterns.56 This may be because strain hardening prevents the liquid-type rupture of cell walls. Thus, it can be viewed as the enhancement of the importance of mechanical stress over interfacial tension in the force balance condition (see, e.g., eqn (22)). Finally, foam structures are stabilized by glass transition or crystallization.9.3 Foam structure formation in foods such as breads, cakes, snacks
Here we consider the formation mechanism of a foam structure of foods on the basis of the concept of viscoelastic phase separation. We note that a diverse range of foods are aerated, using a similarly varied assortment of processing methods. The physical mechanism is essentially the same as that for plastic foams.First we consider the foam structure formation in breads. A bread is basically comprised, at a macroscopic level, of the gas and the solid (cell wall material) phase. When viewing the final structure of a bread crumb, we can see that the solid wheat phase is connected and the gas cells are often isolated, but sometimes partially connected.143 The volume fraction of the phases and the nature of their connectivity and topology determines the structure, and consequently the mechanical properties of breads. Thus, it is crucial to understand how the two phases are formed in a bread-making process.31 First we prepare a dough, which is made from a mixture of wheat flour, yeast, and water. In the mixing processes, proteins are hydrated, small gas (CO2) bubbles are formed by yeast fermentation and then their sizes are reduced by kneading. In this process, gluten particles are crosslinked by di-sulfide bonding and a gluten network is formed. In the heating process, small CO2 bubbles may act as nucleation centres for water vapour droplets formation. This latter process creates a large mechanical stress upon their volume expansions and is responsible for the formation of a cellular structure. To maintain the vapour pressure, it is important that surface heating makes the dough surface dense enough to prevent transport of water vapour. Then the structure is frozen by glass transition48 or crystallization, namely, the transformation from a viscoelastic matter to a solid. An example of a cellular structure of a bread is shown in Fig. 9 (see also Ref. 144). Thus, this entire process is markedly similar to the above-explained formation process of plastic foams. As in plastic foams, the importance of strain hardening in the formation of cellular patterns are also pointed out for food polymers such as breads.57,58,145,146 We note that the formation of foam structures in other spongy foods such as cakes147,148 and baked starch foams149 is also basically the same as breads.
 | ||
| Fig. 9 A cellular pattern of a thin bread formed on a temperature-controlled hot stage. The pattern is observed with optical microscopy. Coexisting cellular and network-like structures are clearly observed. | ||
Here, we also mention the application of supercritical fluids for foaming of polymers and foods.150,151 A supercritical fluid, which is in a region above its critical temperature and pressure, exhibits interesting behaviour by combining the properties of conventional liquids and gases. Its liquid-like density allows for solvent power of orders of magnitude higher than gases, while gas-like viscosity leads to a high rate of diffusion. These facts combine to ensure rapid swelling of polymers by supercritical fluids to equilibrium values comparable to liquid solvents. In addition, supercooled fluids can readily plasticize glassy polymers. A pressure quench from supercritical conditions at constant temperature ensures that no vapour-liquid boundary is encountered during the process of solvent removal. This helps avoiding damaging the delicate cellular structure. Foam formation using supercritical liquid can be triggered simply by changing pressure. The mechanism of foam structure formation is essentially the same as the above plastic foams and breads.
10 Shear-induced composition fluctuations and demixing
10.1 Basic mechanism of shear-induced instability
Finally, we consider shear-induced composition fluctuations and demixing (or flocculation) in polymer solutions10,18–22,152–156 as well as in colloidal suspensions and emulsions.23 Shear-induced composition fluctuations are induced by a steep increase of η with ϕ. An intuitive explanation was given as follows.152,153 Shear-induced demixing is caused by a certain mechanism to store elastic energy under shear. This elastic energy effectively leads to a change in the free energy functional, which results in an effective shift of the phase diagram and destablizes a thermodynamically stable system. However, this picture has turned out to be too simplistic. It was shown by intensive theoretical studies10,18–22 that we need to treat dynamical couplings between the composition and stress fields properly to explain shear-induced demixing of polymer solutions. This phenomenon is now widely known as “shear-induced demixing” in polymer solutions under shear.18Some time ago we considered whether similar phenomena can be observed in colloidal suspensions, emulsions, and protein solutions or not.23 In polymers, the conformational degrees of freedom of chains and entanglement effects play a crucial role in shear-induced instability. Since such internal degrees of freedom are absent in suspensions of particle-like objects, the mechanism to store elastic energy under shear in colloidal suspensions should be essentially different from that in polymer solutions.23 At first sight, shear effects seem less pronounced for colloidal suspensions than for polymer solutions. Thus, this problem is far from being obvious.
In the following, we briefly discuss shear effects on colloidal suspensions on an intuitive level.23 Under thermal fluctuations, local shear stress is stored inhomogeneously due to a strong nonlinear and asymmetric dependence of GS(ϕ) and τS(ϕ) on ϕ. Note that the stress relevant to a shear problem is the “shear” stress, σSc. The linear stability analysis tells us that this enhances composition fluctuations along the extension axis of the flow, since this stress moves colloidal particles towards a more concentrated region. This positive feedback process results in shear induced instability in a self-catalytic manner.
In the linear Newtonian regime under the condition ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τS ≪ 1, where
τS ≪ 1, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, σc is given as
is the shear rate, σc is given as
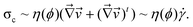 | (23) |
Then, one can straightforwardly obtain the following expression for the relaxation rate of the composition fluctuations convected by shear flow:18
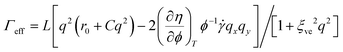 | (24) |
It is important to note that if (∂η/∂ϕ)T > 0, Γeff can be negative even for positive r0 for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) >
> ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, indicating the growth of composition fluctuations even in a thermodynamically stable region. Compare this equation for shear-induced instability with that for thermodynamic instability, eqn (16). The critical shear rate
c, indicating the growth of composition fluctuations even in a thermodynamically stable region. Compare this equation for shear-induced instability with that for thermodynamic instability, eqn (16). The critical shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is thus obtained, using rϕ defined in section 3.7, as
c is thus obtained, using rϕ defined in section 3.7, as
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ∼ rϕϕ/(∂η/∂ϕ)T. c ∼ rϕϕ/(∂η/∂ϕ)T. | (25) |
Recently it was demonstrated by Furukawa and Tanaka16 that this condition can be rewritten by using the osmotic pressure, Π, as follows:
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ∼ (∂η/∂Π)T−1. c ∼ (∂η/∂Π)T−1. | (26) |
For a general implication of this relation and its relevence to single-component glassy systems, please refer to Ref. 16 and 17.
10.2 Shear-induced instability and fracture in foods
Shear flow is often applied to foods in the processing. Because of intrinsic dynamic asymmetry between the components of foods, shear flow often enhances or induces phase separation.18 At the same time, shear gradient deforms and breaks up domains formed by phase separation.2,96 As mentioned above, such examples can be seen in dough formation by kneading.94 Unlike the formation of a rather narrow domain size distribution in simple shear, shear induced migration may lead to macroscopic phase separation under shear gradient or curve linear flow.157 Such migration phenomena may also been described in terms of the two fluid model similar to the viscoelastic model158 by considering effects of normal stress differences.159Furthermore, flow can generate anisotropic structures such as layered structures and fibrous structures, which provide anisotropic mechanical properties sometimes useful for food products known as anisotropic protein-rich foods.160 In polymer mixtures18,161 and colloidal suspensions,162 at a high shear rate string-like phase separated structures are formed. We note that string-like phase separation is observed for a system with rather weak dynamic asymmetry between the two phases. For strongly dynamically asymmetric cases, more chaotic and disordered structures are formed.96 This indicates that string-like domain formation is of hydrodynamic origin and the interplay between shear deformation and interface tension may play a primary role in the selection of the string structure. We also note that stringlike morphology, more precisely, leek-like structures, can also be formed along the flow direction by shear flow in a lyotropic lamellar phase.163
Lamella-like layered structures are often ascribed to so-called shear banding, which is a consequence of nonlinear rheology accompanying non-monotonic stress-strain rate relation.164,165 Such nonlinearity may come from a coupling between shear flow and internal degrees of freedom of slow components, e.g., orientation of polymer chains.166 A constitutive relation such as the nonlocal Johnson-Segalman (JS) model can describe rheological instability,164,165 which is very similar to the upper-convective Maxwell relation, besides additional inclusion of the slippage effects and the so-called stress diffusion term in the nonlocal JS model. Thus, the viscoelastic model may describe rich pattern evolution in a nonlinear flow regime at least on a phenomenological level. Unlike a single-component description, the two-fluid model provides a coupling between shear, stress, and concentration fields, which is crucial in multi-component systems such as foods. In relation to this, it is worth noting that in the two-fluid model, the nonlocal constitutive relation may not be required to have stable shear banding since similar nonlocal effects are expected to be produced by the concentration gradient and their couplings to stress and strain fields.18,96,167,168 For theoretical analysis, we need to treat nonlinear effects properly, including the spatial variation not only in the concentration field, but also the stress and strain fields, and their couplings. This is a difficult theoretical task. Whether we fix the total stress or strain rate applied is also crucial for the selection of nonequilibrium steady states, e.g., gradient and vorticity banding, if they exist.164,165,169 In previous studies of shear instability, the steep dependence of the transport coefficient, the structural relaxation time, and the elastic modulus on the order parameter such as the composition, ϕ, has not been considered carefully. However, as emphasized above, it may induce instability of a different mechanism and thus play a crucial role in shear-induced phenomena.10,16–23,152–156,170 This problem needs further study in the future.
11 General nature of viscoelastic phase separation and classifications of rheological behaviour of materials, phase separation, fracture
First we consider the general nature of the basic equations describing viscoelastic phase separation:12 (i) if we set GS(t − t′) = GS(ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)), where GS is the shear modulus, GB(t − t′) = GB(ϕ(
,t)), where GS is the shear modulus, GB(t − t′) = GB(ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)), where GB is the bulk modulus, and the absence of the velocity fields (
,t)), where GB is the bulk modulus, and the absence of the velocity fields (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0), a viscoelastic model reduces to the elastic solid model.171 (ii) If we further assume that GS and GB do not depend on the composition, ϕ, it reduces to the solid model (model B3). (iii) If we assume dynamic symmetry between the two components of a mixture in the viscoelastic model, it reduces to a new model of symmetric viscoelastic model.12 If we further assume slow enough deformation, then, it reduces to the fluid model (model H3). (iv) If we assume only GS(t) = GS and GB(t) = GB, the viscoelastic model reduces to the “elastic gel model”2,71 that describes phase separation in elastic gels. Note that the time integration of the velocity becomes the deformation
= 0), a viscoelastic model reduces to the elastic solid model.171 (ii) If we further assume that GS and GB do not depend on the composition, ϕ, it reduces to the solid model (model B3). (iii) If we assume dynamic symmetry between the two components of a mixture in the viscoelastic model, it reduces to a new model of symmetric viscoelastic model.12 If we further assume slow enough deformation, then, it reduces to the fluid model (model H3). (iv) If we assume only GS(t) = GS and GB(t) = GB, the viscoelastic model reduces to the “elastic gel model”2,71 that describes phase separation in elastic gels. Note that the time integration of the velocity becomes the deformation ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) p, and
p, and 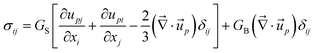 .
.
Thus, the viscoelastic model is the general model of phase separation that can describe any type of phase separation in mixtures of isotropic condensed matter, as its special cases.12
The viscoelastic model in the classification of isotropic phase separation corresponds to viscoelastic matter in the classification of isotropic condensed matter. Viscoelastic matter includes any condensed matter ranged from solid to fluid. The key factor for the classification of materials is the relation between the characteristic internal rheological time, τt, and the characteristic observation time, τo. Corresponding to this, the key physical factor for the classification of isotropic phase separation is the relation between the characteristic time of phase separation (domain deformation), τd, and the characteristic rheological time of the slower phase, τts. The above analogy is schematically summarized in Fig. 10.
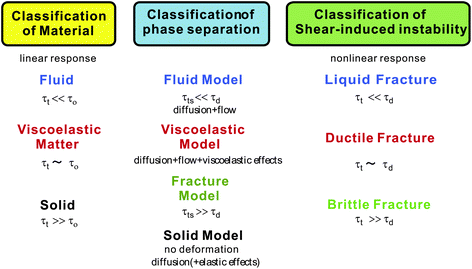 | ||
| Fig. 10 Schematic figure explaining the classification of phase separation of isotropic matter and its relation to the classification of materials and mechanical fracture. In the classification of materials (left), the ratio of the structural relaxation time, τt, to the observation time, τo, which is known as the Deborah number, is a key number. In the classification of phase separation (middle), the ratio of τts to τd, plays a crucial role, as discussed in section 6.2, and is regarded as the Weissenberg number for deformation self-induced by phase separation. On the classification of fracture (right), please refer to Ref. 17. | ||
Furthermore, this classification may also be common to that of mechanical fracture,17 which is determined by the relation between the time when instability set in, the mechanical relaxation rate, and the deformation rate (see Fig. 10). The only difference between the two is whether the deformation is induced by phase separation or externally imposed. See Ref. 17 on the details of mechanical fracture.
12 Summary
In summary, we show that viscoelastic phase separation and the concept of dynamic asymmetry are very useful for understanding not only phase separation and gelation in soft matter and food materials but also their mechanical instability under shear deformation. We demonstrated that the viscoelastic model including both bulk and shear stress contributions is a very general model that can universally describe phase separation of condensed matter.We also demonstrate that the formation of heterogeneous network or cellular structures in foods and their collapsing may be regarded as mechanically driven pattern evolution and can be understood in the framework of viscoelastic phase separation. Dynamic asymmetry may be a key to the physical understanding of not only phase separation but also mechanical instability of materials under deformation. These phenomena of mechanically driven inhomogeneization can be understood in a unified manner on the basis of the concept of dynamic asymmetry. Besides these direct applications, finally we mention another interesting possibility of applications of viscoelastic phase separation: recently it was shown that a spatially heterogeneous pattern formed by protein phase separation causes a Bragg reflection of light, which is an origin of a colour of bird feathers.172 We believe that this phase separation should also belong to viscoelastic phase separation. This phenomenon may be used to put beautiful colours to foods without using (toxic) dye molecules.
At this moment, viscoelastic phase separation and shear-induced mechanical instability can be studied analytically only in their linear regimes. Thus, numerical simulations play a major role in our understanding of these phenomena. Thus, simulations based on the phenomenological viscoelastic two-fluid model may be very useful in studying nonequilibrium and nonlinear dynamical behaviour of foods, including phase separation and flow-induced phenomena.
In relation to this, we finally mention some fundamental remaining problems of the current viscoelastic model.1 The dissipation in a dynamically asymmetric mixture may not be given by a simple sum of friction due to the relative motion of the components and hydrodynamic dissipation. Here the nonlocal nature of the transport, which is characterized by the viscoelastic length, ξve, should also be considered properly in the process of the coarse-graining.2 The phenomenological constitutive relation crucially depends on the composition dependence of the elastic moduli and the mechanical relaxation times. However, there is no firm basis for the physical description of these quantities. For more quantitative understanding of viscoelastic phase separation it is crucial to overcome these difficult problems.
We hope that this article will contribute to better understanding of pattern formation and mechanical instability of foods.
Acknowledgements
The author is indebted to the reviewer for his or her invaluable suggestions on possible connections between viscoelastic phase separation and many interesting phenomena in foods. He is also grateful to T. Araki, Y. Iwashita, T. Koyama, and Y. Nishikawa for their collaboration on viscoelastic phase separation and A. Furukawa for his collaboration on mechanical instability and fracture of materials. He also thanks M. Leocmach and K. Murata for their kind help in making experiments on cellular pattern formation in breads. This work was partly supported by a Grant-in-Aid from the Ministry of Education, Culture, Sports, Science and Technology, Japan and Aihara Project, the FIRST program from JSPS, initiated by CSTP.References
- J. D. Gunton, M. San Miguel and P. S. Sahni, Phase transitions and Critical phenomena, Vol. 8, Academic, London, 1983 Search PubMed.
- A. Onuki, Phase Transition Dynamics, Cambridge University Press, Cambridge, 2002 Search PubMed.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1976, 49, 435 CrossRef.
- H. Tanaka and T. Nishi, Jpn. J. Appl. Phys., 1988, 27, L1787 CrossRef CAS.
- H. Tanaka, Macromolecules, 1992, 25, 6377–6380 CrossRef CAS.
- H. Tanaka, Phys. Rev. Lett., 1993, 71, 3158–3161 CrossRef CAS.
- H. Tanaka, J. Chem. Phys., 1994, 100, 5323 CrossRef CAS.
- H. Tanaka, Phys. Rev. Lett., 1996, 76, 787–790 CrossRef CAS.
- H. Tanaka and T. Miura, Phys. Rev. Lett., 1993, 71, 2244–2247 CrossRef CAS.
- M. Doi and A. Onuki, J. Phys. (Paris) II, 1992, 2, 1631–1656 CrossRef CAS.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207 CrossRef CAS.
- H. Tanaka, Phys. Rev. E, 1997, 56, 4451 CrossRef CAS.
- H. Tanaka and T. Araki, Chem. Eng. Sci., 2006, 61, 2108–2141 CrossRef CAS.
- H. Tanaka, Adv. Mater., 2009, 21, 1872–1880 CrossRef CAS.
- T. Koyama, T. Araki and H. Tanaka, Phys. Rev. Lett., 2009, 102, 65701 CrossRef.
- A. Furukawa and H. Tanaka, Nature, 2006, 443, 434–438 CrossRef CAS.
- A. Furukawa and H. Tanaka, Nat. Mater., 2009, 8, 601–609 CrossRef CAS.
- A. Onuki, J. Phys.: Condens. Matter, 1997, 9, 6119 CrossRef CAS.
- A. Onuki, Phys. Rev. Lett., 1989, 62, 2472–2475 CrossRef CAS.
- E. Helfand and G. H. Fredrickson, Phys. Rev. Lett., 1989, 62, 2468–2471 CrossRef CAS.
- H. Ji and E. Helfand, Macromolecules, 1995, 28, 3869–3880 CrossRef CAS.
- S. T. Milner, Phys. Rev. E, 1993, 48, 3674–3691 CrossRef CAS.
- H. Tanaka, Phys. Rev. E, 1999, 59, 6842 CrossRef CAS.
- A. M. Donald, Rep. Prog. Phys., 1994, 57, 1081 CrossRef CAS.
- E. Dickinson, Colloids Surf., 1989, 42, 191–204 CrossRef CAS.
- E. Dickinson and M. Golding, Food Hydrocolloids, 1997, 11, 13–18 CrossRef CAS.
- E. Dickinson, Curr. Opin. Colloid & Interface Sci., 2010, 15, pp. 40–49 Search PubMed.
- R. Mezzenga, P. Schurtenberger, A. Burbidge and M. Michel, Nat. Mater., 2005, 4, 729–740 CrossRef CAS.
- R. Mezzenga, Food Hydrocolloids, 2007, 21, 674–682 CrossRef CAS.
- J. Ubbink, A. Burbidge and R. Mezzenga, Soft Matter, 2008, 4, 1569–1581 RSC.
- R. G. M. Van der Sman and A. J. Van der Goot, Soft Matter, 2009, 5, 501–510 RSC.
- S. Bhat, R. Tuinier and P. Schurtenberger, J. Phys.: Condens. Matter, 2006, 18, L339 CrossRef CAS.
- T. Gibaud and P. Schurtenberger, J. Phys.: Condens. Matter, 2009, 21, 322201 CrossRef.
- P. G. de Gennes, Macromolecules, 1976, 9, 587–593 CrossRef CAS.
- P. G. de Gennes, Macromolecules, 1976, 9, 594–598 CrossRef CAS.
- F. Brochard, J. Phys., 1983, 44, 39–43 CAS.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- H. Tanaka, Prog. Theor. Phys., Suppl., 1997, 126, 333–338 CrossRef CAS.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 1997, 78, 4966–4969 CrossRef CAS.
- M. Doi and S. Edwards, The Theory of Polymer Dynamics, Oxford University Press, USA, 1988, vol. 73 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS.
- A. Furukawa and H. Tanaka, Phys. Rev. Lett., 2010, 104, 245702 CrossRef.
- A. Onuki, J. Non-Cryst. Solids, 1994, 172–174, 1151–1157 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Butterworth-Heinenann, Oxford, 1975 Search PubMed.
- D. Sappelt and J. Jäckle, Europhys. Lett., 1997, 37, 13 CrossRef CAS.
- L. Slade and H. Levine, Adv. Food Nutr. Res., 1995, 38, 103–269 CrossRef CAS.
- B. Cuq, J. Abecassis and S. Guilbert, Int. J. Food Sci. Technol., 2003, 38, 759–766 CrossRef CAS.
- R. G. M. van der Sman and M. B. J. Meinders, Soft Matter, 2011, 7, 429–442 RSC.
- X. He, A. Fowler and M. Toner, J. Appl. Phys., 2006, 100, 074702 CrossRef.
- R. G. M. van der Sman, Food Hydrocolloids, 2011, 27, 529–535 CrossRef.
- M. D. Ediger, Annu. Rev. Phys. Chem., 2000, 51, 99–128 CrossRef CAS.
- H. Tanaka, Phys. Rev. E, 2003, 68, 011505 CrossRef.
- R. W. Hartel, R. Ergun and S. Vogel, Compr. Rev. Food Sci. Food Saf., 2011, 10, 17–32 CrossRef CAS.
- T. C. B. McLeish and R. G. Larson, J. Rheol., 1998, 42, 81 CrossRef CAS.
- P. Spitael and C. W. Macosko, Polym. Eng. Sci., 2004, 44, 2090–2100 CAS.
- B. Dobraszczyk, J. Non-Newtonian Fluid Mech., 2004, 124, 61–69 CrossRef CAS.
- B. J. Dobraszczyk and C. A. Roberts, J. Cereal Sci., 1994, 20, 265–274 CrossRef.
- A. Onuki and T. Taniguchi, J. Chem. Phys., 1997, 106, 5761–5770 CrossRef CAS.
- M. Takenaka, H. Takeno, T. Hashimoto and M. Nagao, J. Chem. Phys., 2006, 124, 104904 CrossRef.
- F. Brochard and P. de Gennes, Macromolecules, 1977, 10, 1157–1161 CrossRef CAS.
- A. Furukawa, J. Phys. Soc. Jpn., 2003, 72, 209–212 CrossRef CAS.
- A. Furukawa, J. Phys. Soc. Jpn., 2003, 72, 1436–1445 CrossRef CAS.
- T. Koyama and H. Tanaka, Europhys. Lett., 2007, 80, 68002 CrossRef.
- H. Tanaka, Y. Nishikawa and T. Koyama, J. Phys.: Condens. Matter, 2005, 17, L143 CrossRef CAS.
- H. Tanaka and Y. Nishikawa, Phys. Rev. Lett., 2005, 95, 78103 CrossRef.
- M. E. Cates, M. Fuchs, K. Kroy, W. C. K. Poon and A. M. Puertas, J. Phys.: Condens. Matter, 2004, 16, S4861 CrossRef CAS.
- P. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS.
- E. S. Matsuo and T. Tanaka, J. Chem. Phys., 1988, 89, 1695 CrossRef CAS.
- E. S. Matsuo and T. Tanaka, Nature, 1992, 358, 482–485 CrossRef CAS.
- K. Sekimoto, N. Suematsu and K. Kawasaki, Phys. Rev. A, 1989, 39, 4912–4914 CrossRef CAS.
- H. Tanaka and T. Araki, Europhys. Lett., 2007, 79, 58003 CrossRef.
- T. Taniguchi and A. Onuki, Phys. Rev. Lett., 1996, 77, 4910–4913 CrossRef CAS.
- A. Bhattacharya, S. D. Mahanti and A. Chakrabarti, Phys. Rev. Lett., 1998, 80, 333–336 CrossRef CAS.
- T. Araki and H. Tanaka, Macromolecules, 2001, 34, 1953–1963 CrossRef CAS.
- T. Araki and H. Tanaka, Phys. Rev. E, 2005, 72, 041509 CrossRef.
- J. Zhang, Z. Zhang, H. Zhang and Y. Yang, Phys. Rev. E, 2001, 64, 051510 CrossRef CAS.
- L. Donato, C. Garnier, B. Novales, S. Durand and J. L. Doublier, Biomacromolecules, 2005, 6, 374–385 CrossRef.
- R. Tuinier, J. K. G. Dhont and C. G. De Kruif, Langmuir, 2000, 16, 1497–1507 CrossRef CAS.
- P. W. de Bont, G. M. P. van Kempen and R. Vreeker, Food Hydrocolloids, 2002, 16, 127–138 CrossRef CAS.
- L. F. van Heijkamp, I. M. de Schepper, M. Strobl, R. H. Tromp, J. R. Heringa and W. G. Bouwman, J. Phys. Chem. A, 2010, 114, 2412–2426 CrossRef CAS.
- S. Bourriot, C. Garnier and J. Doublier, Food Hydrocolloids, 1999, 13, 43–49 CrossRef CAS.
- C. Sanchez, R. Zuniga-Lopez, C. Schmitt, S. Despond and J. Hardy, Int. Dairy J., 2000, 10, 199–212 CrossRef CAS.
- J. S. He, H. Yang, W. Zhu and T. H. Mu, J. Phys.: Conf. Ser., 2010, 215, 012169 CrossRef.
- C. Vega and H. D. Goff, Int. Dairy J., 2005, 15, 249–254 CrossRef.
- H. D. Goff, Curr. Opin. Colloid Interface Sci., 2002, 7, 432–437 CrossRef CAS.
- H. D. Goff, D. Ferdinando and C. Schorsch, Food Hydrocolloids, 1999, 13, 353–362 CrossRef CAS.
- P. Burey, B. R. Bhandari, R. P. G. Rutgers, P. J. Halley and P. J. Torley, Int. J. Food Prop., 2008, 12, 176–210 CrossRef.
- T. Moschakis, B. S. Murray and E. Dickinson, J. Colloid Interface Sci., 2005, 284, 714–728 CrossRef CAS.
- J. Renkema, Food Hydrocolloids, 2004, 18, 39–47 CrossRef CAS.
- V. Tolstoguzov, Food Hydrocolloids, 1997, 11, 181–193 CrossRef CAS.
- V. Tolstoguzov, Food Hydrocolloids, 2003, 17, 1–23 CrossRef CAS.
- C. G. De Kruif and R. Tuinier, Food Hydrocolloids, 2001, 15, 555–563 CrossRef CAS.
- D. Peressini, S. H. Peighambardoust, R. J. Hamer, A. Sensidoni and A. J. Van Der Goot, J. Cereal Sci., 2008, 48, 426–438 CrossRef CAS.
- S. H. Peighambardoust, A. J. Van der Goot, T. Van Vliet, R. J. Hamer and R. M. Boom, J. Cereal Sci., 2006, 43, 183–197 CrossRef CAS.
- T. Imaeda, A. Furukawa and A. Onuki, Phys. Rev. E, 2004, 70, 051503 CrossRef.
- E. E. J. van der Zalm, A. van der Goot and R. M. Boom, J. Food Eng., 2009, 95, 572–578 CrossRef CAS.
- J. M. Deman and A. M. Beers, J. Texture Stud., 1987, 18, 303–318 CrossRef.
- S. S. Narine and A. G. Marangoni, Food Res. Int., 1999, 32, 227–248 CrossRef CAS.
- S. S. Narine and A. G. Marangoni, Adv. Food Nutr. Res., 2002, 44, 33–145 CrossRef CAS.
- G. Alejandro and S. E. McGauley, Cryst. Growth Des., 2003, 3, 95–108 Search PubMed.
- S. S. Narine and A. G. Marangoni, Phys. Rev. E, 1999, 59, 1908 CrossRef CAS.
- V. I. Lozinsky, I. Y. Galaev, F. M. Plieva, I. N. Savina, H. Jungvid and B. Mattiasson, Trends Biotechnol., 2003, 21, 445–451 CrossRef CAS.
- V. I. Lozinsky, Russ. Chem. Bull., 2008, 57, 1015–1032 CrossRef CAS.
- F. M. Plieva, I. Y. Galaev and B. Mattiasson, J. Sep. Sci., 2007, 30, 1657–1671 CrossRef CAS.
- F. M. Plieva, H. Kirsebom and B. Mattiasson, J. Sep. Sci., 2011, 34, 2164–2172 CAS.
- M. C. Gutiérrez, M. L. Ferrer and F. Del Monte, Chem. Mater., 2008, 20, 634–648 CrossRef.
- G. Petzold and J. M. Aguilera, Food Biophys., 2009, 4, 378–396 CrossRef.
- L. Qian and H. Zhang, J. Chem. Technol. Biotechnol., 2011, 86, 172–184 CrossRef CAS.
- H. Kiani and D. W. Sun, Trends Food Sci. Technol., 2011, 22, 407–426 CrossRef CAS.
- H. Zhang, I. Hussain, M. Brust, M. Butler, S. P. Rannard and A. I. Cooper, Nat. Mater., 2005, 4, 787–793 CrossRef CAS.
- S. S. L. Peppin, M. G. Worster and J. S. Wettlaufer, Proc. R. Soc. London, Ser. A, 2007, 463, 723–733 CrossRef CAS.
- F. Prothon, L. Ahrne and I. Sjöholm, Crit. Rev. Food Sci. Nutr., 2003, 43, 447–479 CrossRef CAS.
- W. C. K. Poon, L. Starrs, S. P. Meeker, A. Moussaid, R. M. L. Evans, P. N. Pusey and M. M. Robins, Faraday Discuss., 1999, 112, 143–154 RSC.
- W. C. K. Poon, J. Phys.: Condens. Matter, 2002, 14, R859–R880 CrossRef CAS.
- P. Bartlett, L. J. Teece and M. A. Faers, Phys. Rev. E, 2012, 85, 021404 CrossRef.
- F. Spaepen, Acta Metall., 1977, 25, 407–415 CrossRef CAS.
- A. S. Argon, Acta Metall., 1979, 27, 47–58 CrossRef CAS.
- A. E. Carsson and E. R. Fuller Jr., Fracture: Instability Dynamics, Scaling, and Ductile/Brittle Behavior, Materials Research Society, Boston, 1996 Search PubMed.
- M. L. Falk and J. S. Langer, Phys. Rev. E, 1998, 57, 7192–7205 CrossRef CAS.
- G. Offer and T. Cousins, J. Sci. Food Agric., 1992, 58, 107–116 CrossRef.
- T. Astruc, P. Gatellier, R. Labas, V. S. Lhoutellier and P. Marinova, Meat Sci., 2010, 85, 743–751 CrossRef.
- M. S. Rahman, Drying Technol., 2001, 19, 1–13 CrossRef CAS.
- L. Mayor and A. M. Sereno, J. Food Eng., 2004, 61, 373–386 CrossRef.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 1998, 81, 389–392 CrossRef CAS.
- I. T. Norton and W. J. Frith, Food Hydrocolloids, 2001, 15, 543–553 CrossRef CAS.
- D. G. A. L. Aarts, M. Schmidt and H. N. W. Lekkerkerker, Science, 2004, 304, 847–850 CrossRef CAS.
- C. P. Royall, D. G. A. L. Aarts and H. Tanaka, Nat. Phys., 2007, 3, 636–640 CrossRef CAS.
- E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101 CrossRef.
- H. Tanaka, J. Meunier and D. Bonn, Phys. Rev. E, 2004, 69, 031404 CrossRef.
- T. Ohtsuka, C. P. Royall and H. Tanaka, Europhys. Lett., 2008, 84, 46002 CrossRef.
- C. Wu, W. Li and X. X. Zhu, Macromolecules, 2004, 37, 4989–4992 CrossRef CAS.
- L. E. van Riemsdijk, J. H. B. Sprakel, A. J. van der Goot and R. J. Hamer, Food Biophys., 2010, 5, 41–48 CrossRef.
- Y. Iwashita and H. Tanaka, Nat. Mater., 2006, 5, 147–152 CrossRef CAS.
- Y. L. Yan, X. G. Jia, M. Meng and C. T. Qu, Chem. Lett., 2011, 40, 261–263 CrossRef CAS.
- I. Heertje, E. C. Roijers and H. Hendrickx, LWT–Food Sci. Technol., 1998, 31, 387–396 CrossRef CAS.
- D. Van de Walle, P. Goossens and K. Dewettinck, Food Res. Int., 2008, 41, 1020–1025 CrossRef CAS.
- H. D. Batte, A. Wright, J. W. Rush, S. H. J. Idziak and A. G. Marangoni, Food Res. Int., 2007, 40, 982–988 CrossRef CAS.
- B. M. Whittle and E. Dickinson, Mol. Phys., 1997, 90, 739–758 CrossRef.
- M. T. A. Bos and J. H. J. van Opheusden, Phys. Rev. E, 1996, 53, 5044 CrossRef CAS.
- S. Babu, J. C. Gimel and T. Nicolai, J. Chem. Phys., 2006, 125, 184512 CrossRef.
- J. J. Crevecoeur, J. F. Coolegem, L. Nelissen and P. J. Lemstra, Polymer, 1999, 40, 3697–3702 CrossRef CAS.
- M. Scanlon and M. Zghal, Food Res. Int., 2001, 34, 841–864 CrossRef.
- P. M. Falcone, A. Baiano, F. Zanini, L. Mancini, G. Tromba, F. Montanari and M. A. D. Nobile, J. Food Sci., 2004, 69, FEP38–FEP43 CrossRef.
- L. E. van Riemsdijk, P. J. M. Pelgrom, A. J. van der Goot, R. M. Boom and R. J. Hamer, J. Cereal Sci., 2011, 53, 133–138 CrossRef CAS.
- L. E. van Riemsdijk, A. J. van der Goot, R. J. Hamer and R. M. Boom, J. Cereal Sci., 2011, 53, 355–361 CrossRef CAS.
- T. K. Berry, X. Yang and E. A. Foegeding, J. Food Sci., 2009, 74, E269–E277 CrossRef CAS.
- D. Kocer, Z. Hicsasmaz, A. Bayindirli and S. Katnas, J. Food Eng., 2007, 78, 953–964 CrossRef.
- R. L. Shogren, J. W. Lawton, W. M. Doane and K. F. Tiefenbacher, Polymer, 1998, 39, 6649–6655 CrossRef CAS.
- S. K. Goel and E. J. Beckman, Polym. Eng. Sci., 1994, 34, 1137–1147 CAS.
- M. Sauceau, J. Fages, A. Common, C. Nikitine and E. Rodier, Prog. Polym. Sci., 2010, 36, 749–766 CrossRef.
- B. A. Wolf and H. Krämer, J. Polym. Sci., Polym. Lett. Ed., 1980, 18, 789–794 CrossRef CAS.
- B. A. Wolf, Macromolecules, 1984, 17, 615–618 CrossRef CAS.
- X. L. Wu, D. J. Pine and P. K. Dixon, Phys. Rev. Lett., 1991, 66, 2408–2411 CrossRef CAS.
- T. Hashimoto and K. Fujioka, J. Phys. Soc. Jpn., 1991, 60, 356–359 CrossRef CAS.
- E. Moses, T. Kume and T. Hashimoto, Phys. Rev. Lett., 1994, 72, 2037–2040 CrossRef CAS.
- A. J. Van der Goot, S. H. Peighambardoust, C. Akkermans and J. M. van Oosten-Manski, Food Biophys., 2008, 3, 120–125 CrossRef.
- H. M. Vollebregt, R. G. M. van der Sman and R. M. Boom, Soft Matter, 2010, 6, 6052–6064 RSC.
- J. F. Morris, Rheol. Acta, 2009, 48, 909–923 CrossRef CAS.
- J. M. Manski, A. J. van der Goot and R. M. Boom, Trends Food Sci. Technol., 2007, 18, 546–557 CrossRef CAS.
- T. Hashimoto, K. Matsuzaka, E. Moses and A. Onuki, Phys. Rev. Lett., 1995, 74, 126–129 CrossRef CAS.
- D. Derks, D. G. A. L. Aarts, D. Bonn and A. Imhof, J. Phys.: Condens. Matter, 2008, 20, 404208 CrossRef.
- H. Miyazawa and H. Tanaka, Phys. Rev. E, 2007, 76, 011513 CrossRef.
- M. E. Cates and S. M. Fielding, Adv. Phys., 2006, 55, 799–879 CrossRef CAS.
- P. D. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS.
- H. Tanaka, J. Phys. Soc. Jpn., 2000, 69, 299–302 CrossRef CAS.
- L. Jupp, T. Kawakatsu and X. F. Yuan, J. Chem. Phys., 2003, 119, 6361 CrossRef CAS.
- L. Jupp and X. F. Yuan, J. Non-Newtonian Fluid Mech., 2004, 124, 93–101 CrossRef CAS.
- J. K. G. Dhont and W. J. Briels, Rheol. Acta, 2008, 47, 257–281 CrossRef CAS.
- R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2010, 105, 268301 CrossRef CAS.
- H. Nishimori and A. Onuki, Phys. Rev. B, 1990, 42, 980–983 CrossRef.
- E. R. Dufresne, H. Noh, V. Saranathan, S. G. J. Mochrie, H. Cao and R. O. Prum, Soft Matter, 2009, 5, 1792–1795 RSC.
| This journal is © The Royal Society of Chemistry 2012 |