Evaluating portable infrared spectrometers for measuring the silica content of coal dust

Abstract

Miners face a variety of respiratory hazards while on the job, including exposure to silica dust which can lead to silicosis, a potentially fatal lung disease. Currently, field-collected filter samples of silica are sent for laboratory analysis and the results take weeks to be reported. Since the mining workplace is constantly moving into new and often different geological strata with changing silica levels, more timely data on silica levels in mining workplaces could help reduce exposures. Improvements in infrared (IR) spectroscopy open the prospect for end-of-shift silica measurements at mine sites. Two field-portable IR spectrometers were evaluated for their ability to quantify the mass of silica on filter samples loaded with known amounts of either silica or silica-bearing coal dust (silica content ranging from 10–200 μg/filter). Analyses included a scheme to correct for the presence of kaolin, which is a confounder for IR analysis of silica. IR measurements of the samples were compared to parallel measurements derived using the laboratory-based U.S. Mine Safety and Health Administration P7 analytical method. Linear correlations between Fourier transform infrared (FTIR) and P7 data yielded slopes in the range of 0.90–0.97 with minimal bias. Data from a variable filter array spectrometer did not correlate as well, mainly due to poor wavelength resolution compared to the FTIR instrument. This work has shown that FTIR spectrometry has the potential to reasonably estimate the silica exposure of miners if employed in an end-of-shift method.

---

Environmental impact

This study focuses on the evaluation of human exposure to silica in working environments using an alternate field-portable method for quantifying silica. Current methods for workplace silica monitoring typically involve estimation of time-weighted average silica concentration using a traditional filter sampling system followed by laboratory analysis of the filter samples. However, since this entails a time lag of days to weeks before exposure data are received, the information is often of limited value for helping reduce exposures. The field portable infrared spectrometry method evaluated in this study is capable of on-site quantification of silica, thereby providing timely feedback to inform workplace modifications to reduce exposures to airborne silica dust.

Introduction

Inhalation of excessive amounts of dust that contains microscopic particles of crystalline silica can cause scar tissue to form in the lungs, which reduces their ability to extract oxygen from the air.¹ This condition is called silicosis, which is a disabling, irreversible, and sometimes fatal lung disease. National Institute for Occupational Safety and Health (NIOSH) studies have been important in documenting the extent of silicosis in industrial and occupational settings over the last 35 years.² Between the late 80s and mid-90s, silicosis, excluding carcinomas potentially caused by silica, prematurely shortened thousands of American miners' lives. Presently, more than 1 million U.S. workers are routinely exposed to crystalline silica, and each year more than 250 American workers die with silicosis. Between 1996 and 1999, a quarter of all silicosis-related deaths occurred in the mining industry.² Further, a study in 2003 suggested that mortality data may underestimate the incidence of silicosis, since only approximately 1 in 6 death certificates of people who died with silicosis made mention of it as a cause of death.³

Despite extensive knowledge of both causes and effective preventive actions, silica exposures in many occupational settings continue. Risks are particularly high in the mining industry, in both coal and non-coal miners.² Exposure to silica-bearing coal dust can lead to silicosis and coal workers' pneumoconiosis (CWP), both of which are a result of lung damage caused by fibrosis. Much research has been done to reduce CWP, but recently an increase in cases of CWP occurring in the U.S. has been identified⁴ and silica may be implicated in that resurgence.

To help reduce exposure to both dust and silica, NIOSH developed a direct reading monitor for measuring miners' exposure to coal dust.^5,6 This personal dust monitor (PDM) has been successfully used to aid miners in reducing their exposure to coal dust by making changes to their work activities based on the continuous reading of the device⁷ but does not provide information specific to silica exposure. Coal miners' exposure to silica is currently determined in the U.S. by collecting a filter sample and submitting it to the Mine Safety and Health Administration (MSHA) where it is analyzed by an ashing and Fourier transform infrared (FTIR) process known as the P7 analytical method.⁸ Since this method entails a time lag of weeks before exposure data are received, the information is often of little use to inform modifications to workplace conditions aimed at preventing overexposures. Based on the success of the PDM in reducing miners exposure to coal dust,⁷NIOSH is now taking a similar approach, specifically in regard to silica monitoring. The goal of this initial work is to evaluate spectrometers for end-of-shift (EOS) silica measurement on coal dust filter samples. Such EOS data would give miners timely feedback regarding whether silica-bearing strata had been encountered, preventing potentially prolonged periods of overexposure prior to receiving analytical results. This paper summarizes the evaluation of two field-portable infrared (IR) spectrometers with the potential for EOS quantification of silica on filter samples of coal dust.

Instrument considerations

The quantification of silica on filter samples has been studied extensively, with the goal of developing standard methods for determining worker exposures to airborne silica-bearing dusts. Historical work focused on developing methods for in-laboratory analysis of samples taken in the field.^9–11 It was found that IR techniques were amenable to quantification of filter samples if the samples were first ashed and a laboratory-grade FTIR spectrometer was used to analyze the ash. The current work expands on past efforts and aims at evaluating field-portable IR instruments for measuring silica directly on filter samples (a non-ashing approach). The idea is to take advantage of improvements such as instrumentation miniaturization and spectral interpretation software to enable the use of relatively sophisticated techniques in field settings.

The first challenge in applying field-portable spectrometry methods is that they are inherently less sensitive than their lab-based or benchtop counterparts. Respirable coal dust samples from mines are required to be below 5% quartz in a 2 mg full shift sample, which effectively limits the respirable quartz exposure to 100 μg per shift.¹² Any proposed silica quantification method must therefore be capable of accurately measuring small mass loadings of silica (down to about 25 μg/filter) on filter samples containing about 500–2000 μg/filter of coal dust. To simplify a potential EOS method, it is desired that this be done on the filters as collected, i.e. without treatment or redeposition as described previously.¹⁰

A second challenge is that in order to be of use, the portable method must be able to quantify silica in the presence of compounds that potentially interfere with quantification of the free silica on the filter. While more than a dozen minerals exist with IR-absorption bands that could potentially interfere with silica quantification,¹¹ it is expected that kaolin will be the primary interferent for coal dust samples based on MSHA's previous work.⁹ Kaolinite clay, or kaolin (Al₂Si₂O₅(OH)₄), is a layered silicate material that can be found in mines along with coal and silica. Since it contains silica as part of its composition, it has the potential to interfere with IR spectrometry methods and a correction must therefore be made to account for it. The kaolin correction scheme utilized in this study is described in the materials and methods section.

IR spectrometry is based on the principle that many different chemical compounds preferentially absorb IR radiation of a specific wavelength that is harmonic with the vibration frequency of their molecular bonding structure.¹³ The spectrometer measures which frequencies of radiation get absorbed by the sample and generates a unique absorption spectrum for that sample, which is used to identify compounds and thus to investigate sample composition. IR is well suited to measure the alpha quartz polymorph of silicon dioxide. Unlike elemental analyses, such as X-ray diffraction or laser-induced breakdown spectroscopy, IR measurement is based on the SiO₂ bond structure, enabling it to distinguish between amorphous and crystalline forms of silica.

The two spectrometers chosen for this study were an FTIR spectrometer and a variable filter array (VFA) spectrometer. FTIR is a spectrometry method whereby the sample is illuminated simultaneously with radiation of many wavelengths over a wide spectral range by using a blackbody IR emitting source and an interferometer, and the return signal analyzed using a Fourier transform algorithm.¹⁴ The number of different wavelengths generated by the interferometer determines the resolution of the spectra, which is inversely proportional to the mirror speed (scan time). Better resolution and wider spectral range are both benefits to using FTIR over VFA. Since the scan time is relatively short, the FTIR instrument typically conducts multiple sequential tests and the data from all tests are analyzed and averaged to reduce noise in the data.

VFA technology is based on the use of a linear variable filter (LVF). An LVF is a wedge-shaped filter that works similarly to a prism for visible light. An LVF typically covers approximately an octave in wavelength, and the proper octave is chosen to match that of the source beam used. The resolution is a function of the LVF and detector characteristics. Some VFA instruments employ a multi-pixel detector array, and in that case the maximum theoretical resolution is limited by the number of pixels in the array and by thermal and optical interference from pixel to pixel.¹⁵

It is notable that both FTIR and VFA-IR methods can be performed in two different modes: transmission mode or attenuated total reflection (ATR) mode. Since ATR requires physical contact with the sample and our analyses were required to be non-destructive to the filter samples, it was not used in this study.

It is preferable for IR spectrometers to work in an inert atmosphere, vacuum, or no atmosphere at all, because matter such as carbon dioxide and water vapor will absorb IR radiation.¹³ This issue can be avoided by filling the spectrometer with a noble gas during testing, by creating a vacuum inside, by leaving no open areas between the source and the detector, or by running a background scan to be subtracted from the sample scan. The latter approach accounts for any of the erroneous absorption as the beam passes through the sample chamber and filter media, and was therefore employed in this study.

The FTIR spectrometer (Bruker Alpha) and the VFA spectrometer (Wilks InfraSpec) chosen for this study were both designed for field portability and have the potential sensitivity to quantify small amounts of silica deposited on filters. The VFA has a fixed resolution of 25 cm⁻¹ while the FTIR can be adjusted by setting the mirror speed. For this study, the FTIR resolution was set to 4 cm⁻¹, which has been shown previously to eliminate unnecessary detail and thereby reduce noise¹⁶ while still providing adequate peak identification and maintaining a reasonably quick sampling time.

Both IR instruments are controlled by software that automatically generates an absorbance spectrum and sends it to the interface screen for viewing, post-processing, and archiving. Most modern spectrometers incorporate such software, designed to identify and quantify the relative amplitude of absorbance peaks. The software typically incorporates algorithms for baseline correction and peak integration, as well as routines for deconvolution of peak overlaps. Additionally, some software is capable of complex fitting schemes involving analysis of multiple spectra, using a variety of mathematical models and reference to stored libraries in order to discern commonalities of the spectra, which it then correlates with known information (mass) for the measurement of interest. For this work, while the manufacturer's software was used to integrate peak areas, additional libraries or fitting algorithms were not employed.

Both IR instruments in this study were calibrated using filter samples with known masses of a standard crystalline silica reference material. After calibration, a kaolin correction scheme was developed by analyzing multiple samples of well-characterized kaolin dust. Note that this laboratory-based method requires the deposition of known amounts of well-characterized material onto filters and using those samples to calibrate the method. Such empirical calibration has been shown to be repeatable if conducted carefully.¹

Materials and methods

Materials used

The four types of coal dust used to evaluate the spectrometers—Keystone Black, Pittsburgh 4, Pittsburgh 20, and Illinois 6—were characterized previously.¹⁷ Keystone Black is a commercially available pre-ground coal dust with a median particle diameter of 8 microns. Pittsburgh 4 and 20 are both derived from the Pittsburgh coal seam and were ground to target mean diameters of 4 and 20 microns, respectively. The coal dust from the Illinois 6 seam was the finest dust used in this study, with a target mean diameter of 3 microns.¹⁷

The Minusil reference material chosen for this study has a purity of 89%.¹⁸ The material chosen for developing the kaolin correction scheme was a well-characterized source of Georgia kaolin, similar to that chosen in previous research where the consistency of IR signals for various types of kaolin was investigated.¹⁹

Filter sample preparation

Filter samples with known amounts of coal dust, silica, and kaolin were made by aerosolizing each of these materials at ambient conditions (25 °C, 50% Rel. Humidity) in a Marple™ Aerosol chamber, using a TSI 3400A Fluidized Bed Aerosol Generator (TSI, Inc.). Samples were collected onto low ash, 37mm, 5.0 micron pore size, polyvinylchloride filters (SKC^® Corp., Inc.) that were pre-weighed by a gravimetric balance and placed in plastic cassettes. Each sample was preceded by a Dorr-Oliver cyclone. The samples were mounted in groups of six to ten samples, with each sampler connected to a critical orifice calibrated to 1.7 Lpm and each group connected to a flow manifold. A maximum of five manifolds were used per test run. The chamber concentration was monitored using two series 1400 TEOM (tapered element oscillating microbalance) particulate monitors (Thermo Scientific Model TEOM 1400ab Ambient Particulate Monitor) connected to Dorr-Oliver cyclones and operated at a flow rate of 1.7 Lpm. After collection, all filter samples were post-weighed to determine the mass of dust loaded onto each. For each group of filter samples collected during one run, three unused filters from the same lot were set aside as controls.

Sample analysis

The reference method used for comparison of the two IR instruments was the MSHA P7 method. This entails ashing the filters in a low-temperature radio-frequency asher to destroy any organics including coal dust and the PVC filter itself. Ashed samples are redeposited in a 9-mm-diameter circular area on a vinyl acrylic copolymer filter (VAC-DM450). The redeposited, ashed samples are then scanned by FTIR spectrometry between frequencies of 1,000 and 700 cm⁻¹ to determine the quartz and kaolin content. When the absorbance spectra data are graphed, silica appears as a set of doublet peaks at 780 and 800 cm⁻¹ as depicted in Fig. 1 for a pure quartz sample. In contrast, kaolin presents a spectrum with a large peak at 915 cm⁻¹ as well as a smaller peak at 790 cm⁻¹ that is in the same range as the silica doublet peaks (Fig. 1). Therefore, when analyzing coal samples, the silica doublet around 800 cm⁻¹ cannot simply be analyzed directly to determine the amount of silica because the peaks from kaolin and quartz will interfere (combine) and indicate a larger amount of free silica than is actually present.

Fig. 1 Idealized IR spectra for silica and kaolin showing locations of absorption peaks to highlight the region of overlap that interferes with silica quantification.

Since the larger kaolin peak at 915 cm⁻¹ is easily quantified on coal samples, while the smaller peak is “masked” by the silica present in the coal, MSHA developed a kaolin correction scheme that entails analyzing the kaolin peaks at 915 cm⁻¹ and 790 cm⁻¹ for a standard kaolin material and using a peak ratio calibration factor to estimate the size of the masked kaolin peak.⁸ This value is then subtracted from the doublet peak at 800 cm⁻¹, and the value of free silica in the sample is estimated.

The method used for analyzing filter samples with the portable IR instruments entailed mounting the filter in a stainless steel holder that was placed so that the filter was centered between the IR source and the detector. The IR beam was then turned on for the time required to complete 40 scans, determined by experimentation to be an adequate amount of sampling time to ensure both a dependable signal-to-noise ratio and shot-to-shot repeatability. Silica presented doublet peaks between 816 cm⁻¹ and 767 cm⁻¹ for FTIR and between 833 cm⁻¹ and 745 cm⁻¹ for VFA. Kaolin presented a main peak between 930 cm⁻¹ and 890 cm⁻¹ for FTIR and between 952 cm⁻¹ and 857 cm⁻¹ for VFA. Therefore, those integration regions were consistently used for all testing.

Prior to sampling the silica or coal filters, scans of the atmosphere and of the blank filter were run so that they could be subtracted from the resulting silica and coal spectra. This was done using the manufacturers' software, and was necessary to accurately quantify the silica peak. After the subtraction is performed, the remaining spectra relates only to the silica or coal that was on the filter.

Instrument calibration using standard silica material

To discern the sensitivity and accuracy of the two IR instruments for analyzing silica, both were first calibrated using samples of Minusil dust. As a guide to the selection of appropriate sample loadings, the NIOSH guidelines for air sampling and analytical method development and evaluation were followed, which calls for evaluating any new method in the range of 10–200% of the permissible exposure limit in question.²⁰ Using the current regulation for silica, which calls for less than 5% silica on a 2 mg sample, this translates into an evaluation range between 10 and 200 μg/filter. After samples were collected, one set was sent directly to MSHA for P7 analysis while a second (parallel) set was analyzed using the IR instruments. Calibration was based on comparing the IR generated spectra, more specifically the areas of the doublet absorbance peaks for silica, with the P7-derived mass of the parallel silica samples.

Kaolin correction scheme

In the MSHA P7 method, correction for kaolin is accomplished by running a set of kaolin standards of different loadings and calculating the average area ratio of the 915 cm⁻¹ and 790 cm⁻¹ peaks (Fig. 1). It has been shown that this number is fairly constant for each experimental setup using standard kaolin material.¹⁹ Using that approach, i.e. analyzing multiple samples of pure Georgia kaolin and taking the average ratio of the peak areas, the kaolin correction ratios for the FTIR and VFA instruments were found to be 3.8 and 12.4, respectively (Fig. 2). In analyzing all coal dust samples, those ratios were used to estimate the masked kaolin contribution, in order to subtract it from the silica peak. This was done by using the following equation:

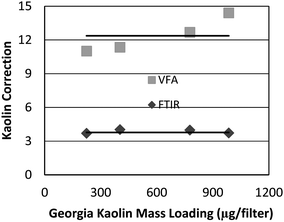Fig. 2 Ratios between the two main absorbance peaks for kaolin at 915 cm⁻¹ and 790 cm⁻¹vs. sample loading, with horizontal lines representing the average ratio for each instrument.

It is notable that this kaolin correction ratio for VFA varies with kaolin loading on the filters (Fig. 2). This outcome is related to the spectral resolution and its effect on the accuracy of peak integrations as will be discussed further in the Results and Discussion section. To verify our choice of a constant value for the correction ratio, we processed data using both the constant value (12.4) and a linear fit to the data of Fig. 2 and found that the effect on the resulting calibration curve was negligible.

Quantification of silica in coal dust

Once the silica calibration and kaolin correction were finalized, the IR instruments were used to quantify the silica content of challenge filters containing laboratory-generated coal dust, loaded in the range of 100–2000 μg/filter. The method used to derive quantitative values from the IR spectra were similar to the approach described in the P7 method.⁸ This entailed measuring the area of the silica absorbance doublet peak for the coal samples, correcting it for kaolin by subtracting the estimated kaolin contribution, and then using the silica calibration equation to derive silica mass. This process was used to measure silica on four different types of well-characterized coal dust and the results used to compare the performance of the two IR instruments.

The number of samples collected and analyzed varied slightly for the different cases. For each coal type, 12 total samples were analyzed with three samples at each of four target loadings. The three samples at each target loading were averaged for a total of four data points. For Minusil, the same pattern was followed, except there were 15 total samples and five target loadings. Because VFA was not sensitive enough to give a clear reading for the lowest Minusil samples, only 12 total samples at four target loadings are presented in that data set.

Each group or subset of data (measurements made on similarly loaded filters), were analyzed as follows, using guidelines developed by NIOSH.²¹ The data were averaged to give one value for each of at least three parallel samples and a standard deviation was calculated. The averaged values from all the data subsets were plotted using Microsoft Excel, with the P7 data on the x-axis and the corresponding data for the IR instruments on the y-axis. A linear regression curve was calculated in Excel for each set of data, with the equation for that curve describing the correlation between the averaged data and the P7 (reference) method. For the Minusil samples, this correlation was subsequently used as a calibration equation to calculate the estimated silica mass from the raw IR data. The estimated masses were then plotted against the reference masses provided by P7 analysis in order to assess the prediction ability of each IR method. The quality of correlation is reflected in the linear regression equation that was calculated for the plotted data, i.e. by how close the slope is to 1 and by the magnitude of the bias (constant) term in the equation.

Results and discussion

Instrument calibration using Minusil

For both instruments, the total area of the doublet silica peaks in the absorbance spectra were found to be linearly correlated with mass of the parallel P7 samples (Fig. 3). It is notable that the sample-to-sample measurements vary more at each loading for the VFA instrument, and that the variations result in a greater bias compared to the FTIR instrument. The vertical SD bars represent the variation in the IR data from triplicate filter samples at each level of silica loading, while the horizontal bars reflect the SDs of the parallel triplicate samples that were analyzed by the P7 method. While these SDs include potential errors due to sampling inaccuracies, such errors are assumed to be identical for both datasets. The relative variations in the SDs presented for the two methods therefore represent the differences in the performance and repeatability of the two instruments. One possible exception to that assumption is that there is the potential for non-uniform deposition of dust across the filter face.²² This can be addressed by taking multiple scans across the filter or by placing the sample at a location where the beam is diverged (to 37 mm). The former was not deemed practical for these instruments while the latter reduces instrument analytical sensitivity by an order of magnitude¹⁶ and therefore was not considered for these tests.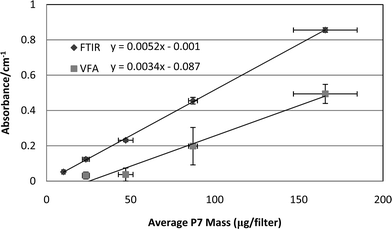

Fig. 3 Graph of P7-measured silica mass versus area of the silica doublet peaks for FTIR and VFA instruments.

Applying the calibration equations of Fig. 3 to IR data for a separate set of five unknown Minusil samples and plotting results against P7 data demonstrates the expected correlation between P7 and IR measurements for pure silica (Fig. 4). This correlation is the first step toward using the IR instruments for measuring silica on coal samples, and suggests that, barring interferences, either instrument could give reasonable estimates of silica mass. Note that the lowest loading of Minusil (10 μg) is missing from both the calibration and comparison graphs for VFA, since that instrument did not produce consistent or accurate results for the low loading condition. Also, Fig. 4 does not include error bars because only one filter sample was analyzed at each loading, i.e. to evaluate the calibration equations.

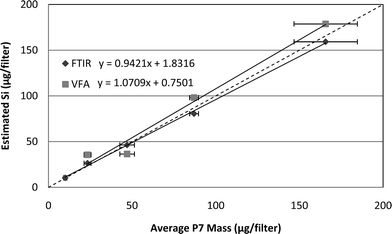Fig. 4 Method correlation for Minusil: P7 measured mass versusIR estimated mass for the FTIR and VFA instruments. The dashed diagonal line indicates a slope of one.

Estimation of (kaolin corrected) silica mass on coal samples

The FTIR and VFA instruments were next used to analyze four types of laboratory-generated coal samples for which the mass of coal had been measured gravimetrically and silica mass determined by P7 analysis, using sets of parallel samples. The areas of the kaolin-corrected silica peaks were used along with the calibration curves for each instrument (Fig. 3) to obtain estimated silica mass. That estimated mass was then compared to P7-derived silica mass of the parallel samples (Table 1). The Keystone Black coal dust samples contained only about 0.5% silica and, as expected, neither instrument was capable of quantifying the small mass of silica in the samples. Those data are therefore not included in Table 1 or in the discussion of the results. As expected, the P7 correlations for the other three coals were better for the FTIR instrument due to its better resolution compared to the VFA instrument (4 cm⁻¹versus 25 cm⁻¹). Smaller standard deviations in the sample-to-sample measurements of similarly loaded filters were observed for the FTIR instrument as well as a smaller percent difference, as shown in Table 1.

Table 1 Average results for each of the three coal types and the % difference between FTIR or VFA and P7

	Avg Loading, μg/filter	Avg P7, μg/filter	FTIR		VFA
			Avg Est Si, μg/filter	% Difference	Avg Est Si, μg/filter	% Difference
P4 Coal 1	107	4.3	9.2	110	42	880
P4 Coal 2	618	35	31.5	10	61.1	75
P4 Coal 3	1270	67	57.7	14	101	50.7
P4 Coal 4	1910	94	94.9	1.0	88.7	5.6
Ill6 Coal 1	258	11	14.2	29	80.4	630
Ill6 Coal 2	613	26	26.9	3.5	92.7	260
Ill6 Coal 3	1150	50	46.9	6.2	124	150
Ill6 Coal 4	1750	64	62.9	1.7	124	94
P20 Coal 1	219	14	16.1	15	54.7	290
P20 Coal 2	508	33	32.3	2.1	45.2	37
P20 Coal 3	1040	63	62.9	0.16	71.5	13
P20 Coal 4	2040	120	119	0.83	107	11

---

FTIR performance/results

The FTIR-estimated silica values for the three types of coal samples correlate linearly with the measurement of silica on parallel samples by the P7 method (Fig. 5), with slope very near unity (dashed diagonal line in the figure). There is an apparent lack of a trend in the sample-to-sample SD values, which derives mainly from inconsistencies in the collection of material onto the filters, as reflected in the rather high SDs for the triplicate samples analyzed by the P7 method.

Fig. 5 Correlation of P7 data and FTIR measurements of silica mass for three types of coal dust samples. The dashed diagonal line indicates a slope of one.

VFA performance/results

The VFA data for the coal samples does not correlate with the P7 method as well as the FTIR data (Fig. 6), and in particular the sample-to-sample SD values for the VFA data are higher. The higher SDs and poor correlation are not unexpected, since the lower resolution of this instrument affects the consistency of peak integrations as was reported previously²³ and is discussed in the next section of this paper. This in turn potentially affects the accuracy of the kaolin correction and that result is more pronounced at lower mass loadings, possibly contributing to the very high bias for this method.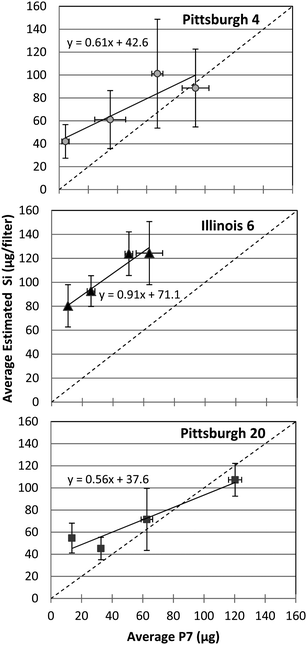

Fig. 6 Correlation of P7 data and VFA measurements of silica mass for three types of coal dust samples. The dashed diagonal line indicates a slope of one.

The wide variation in slope and bias for the three coals suggests that VFA is much less accurate at measuring silica on coal filters as opposed to pure silica samples. The deviations of the slopes from unity further support that deduction. These inconsistencies in the datasets led to further investigations of the role of instrument resolution and its effect on the peak quantification.

Since the FTIR instrument has the capability of resolution adjustment when the mirror positioning speed is changed, the approach was to re-run the Illinois 6 samples using the FTIR instrument set to a lower resolution and compare the results to the VFA data. For this investigation, the FTIR resolution was set to 25 cm⁻¹, identical to the VFA resolution. A new silica calibration curve and a new kaolin correction were then generated using the 25 cm⁻¹ setting and the Illinois 6 coal samples re-analyzed. It was observed that lowering the resolution changes the resulting spectra in two important ways that affect the accuracy of silica quantification. The first is that the coarseness of the resolution causes the silica doublet peak to morph into one larger peak. Comparing the doublet peak at 800 cm⁻¹ from the FTIR running at resolution of 25 cm⁻¹ with that for VFA (at fixed resolution of 25 cm⁻¹) showed that in both cases the doublet disappeared and became one peak, resulting in potential for inaccurate representation of that region during peak integration calculations by the software. A similar result has been described previously²³ and was shown to result in small or narrow peaks being masked or unrepresented due to dominance of larger neighboring peaks. The problem is compounded in our case by varying the mass loading of the filters, as the lower loadings tend to have slightly shorter and narrower spectral peaks while greater loadings have slightly taller and wider peaks. Due to this subtle change, an instrument with low resolution will not present consistently proportional spectral peaks over the range of mass loadings.

The second effect caused by lower resolution is the relative shifting of some peaks for certain samples, introducing variability into the peak-quantification process. This occurs when the absorbance from multiple neighboring peaks gets combined due to the coarseness of the resolution. For our case this is especially important in performing accurate and repeatable kaolin correction using the peak centered at 915 cm⁻¹ (Fig. 7). The data of that figure show that as resolution decreases, the relative position and magnitude of the original peaks affects the location of the resulting single peak. Furthermore, the variability in interferents among the different coals causes such peak shifts to be different for each coal type. This hinders the consistency of peak area integrations when using a consistent analytical method for multiple samples, which is necessary for a robust and dependable method.

Fig. 7 FTIR data from a single coal sample, showing the effect of decreasing instrument resolution on the shape and position of the kaolin peak at 915 cm⁻¹.

For the above reasons, when the Illinois 6 samples were analyzed by FTIR at resolution of 25 cm⁻¹, the results were also unacceptable, including a large bias and a slope much greater than unity (1.8). A plausible explanation for the steep slope is that when peak shifting occurs, as it does for the larger kaolin peak in the low resolution spectra of the Illinois 6 samples, the kaolin correction is no longer valid, since the correction factor is only applicable when the kaolin peak presents in the same region in both the pure kaolin samples and the coal samples. Because this issue does not arise for the FTIR analysis of Illinois 6 samples run at 4 cm⁻¹ resolution (Fig. 5), and because the only difference between the two FTIR results is resolution, the erroneous pattern across the board for VFA data appears to be mainly a result of the lower resolution of that instrument. The lack of resolution has the apparent effect of amplifying the interaction with interferents, resulting in inaccuracies in the data.

It is clear that reducing the resolution of the IR method has a significant effect on the quality of the results. Other factors that may affect the results include the possibility that some larger particles will have penetrated the cyclone²⁴ and deposited on the filter, potentially leading to a slight particle size dependence in the IR method as reported previously.²⁵ Additionally, an issue with this VFA instrument that is not related to resolution is the restriction to a certain band of IR radiation based on the LVF used. While the FTIR instrument uses wavelengths from 400 cm⁻¹ to 4000 cm⁻¹, the VFA instrument has a much narrower band (740 cm⁻¹–1260 cm⁻¹). The silica peak at 800 cm⁻¹ is therefore very close to the range limit of the LVF, where the LVF and detector array are not optimized and thus susceptible to higher noise levels.¹⁵ It is therefore possible that improved accuracy could be gained from an LVF with range centered on the peaks of interest.

The Keystone Black coal dust samples contained only about 0.5% silica and, as expected, neither instrument was capable of quantifying the small mass of silica in the samples. The data were therefore not included in the above discussion, but did serve to confirm that the kaolin-corrected peak areas were not influenced by the mass of coal on the filters, i.e. it is possible that the increasing spectral peak areas could correlate in part to the increasing mass of coal rather than (or in addition to) the mass of silica. That possibility was disproved for this case by observing the FTIR data from the Keystone Black coal samples, which have silica content approximately ten times lower than the other coals presented in this study. When the samples were analyzed using FTIR and kaolin corrected, the estimated amount of silica was approximately zero, which was consistent with the P7 data, while the coal mass loadings from filter to filter increased significantly, similar to the other samples. This confirmed that the peak area of the 800 cm⁻¹ doublet, after a kaolin correction, actually represents the amount of silica on the filter. If the correlation were linked to coal mass, the data would show falsely heightened values for the estimated silica, with a linear increase following the mass of coal on the filter. This was not the case, however, so it was concluded that the FTIR analysis of the 800 cm⁻¹ doublet, after a kaolin correction, represented only silica.

Conclusions

In summary, this study has provided data that demonstrate the efficacy of using field-portable IR spectrometry methods for measuring the mass of silica on filter samples of coal dust. The following findings are relevant:

• Both IR instruments evaluated are potentially usable for analysis of pure silica on filter media and yield linear correlations between estimated silica mass and actual silica mass, at the regulated respirable limit (100 μg).

• For quantifying silica on coal dust samples using a kaolin-correction scheme, the higher resolution of the FTIR instrument shows much promise, even when silica content is relatively low.

• For the two instruments evaluated, spectral resolution was the key factor affecting the difference in their ability to accurately quantify silica in coal dust samples.

The next step is to demonstrate the feasibility of using such a portable IR spectrometer to gather EOS data on a daily basis to estimate the exposure of miners to airborne silica. Such testing must also take into account other sources of error including those due to sample collection and handling, analytical errors due to sample overloading, and potential confounders including kaolin and possibly other silica-bearing minerals. An effective demonstration of an EOS method for quantifying silica on filter samples of coal dust will enable mine operators to obtain daily feedback about workplace silica levels. This knowledge will allow more timely modifications to equipment or processes by implementation of engineering or administrative controls to reduce worker exposure to silica and thus reduce silicosis in miners.

Disclaimer

Mention of any company or product does not constitute endorsement by the National Institute for Occupational Safety and Health (NIOSH). The findings and conclusions in this report are those of the authors and do not necessarily represent the views of NIOSH.

References

1. DHHS(NIOSH), Publ. No. 75-120, 1974, 130 pp.
2. K. Bang, M. Attfield, J. Wood and G. Syamlal, Am. J. Ind. Med., 2008, 51, 633–639.
3. K. D. Rosenman, M. J. Reilly and P. K. Henneberger, Am. J. Ind. Med., 2003, 44, 141–147.
4. V. C. Antao, E. L. Petsonk, L. Z. Sokolow, A. L. Wolfe, G. A. Pinheiro, J. M. Hals and M. D. Attfield, Occup. Environ. Med., 2005, 62, 670–674.
5. D. P. Tuchman, J. C. Volkwein and R. P. Vinson, J. Environ. Monit., 2008, 10, 671–678.
6. S. Page, J. Volkwein, R. Vinson, G. Joy, S. Mischler, D. Tuchman and L. McWilliams, J. Environ. Monit., 2008, 10, 96–101.
7. R. H. Peters, C. Vaught, E. E. Hall, J. C. Volkwein, DHHS (NIOSH), Publ. No. 2008-110, IC 9501, 2008, 47 pp.
8. US Dept of Labor (MSHA) Pittsburgh Safety and Health Technology Center, Method No. P-7, 2008.
9. S. M. Ainsworth, J. ASTM International, 2005, 2, 13.
10. R. W. Freedman, S. Z. Toma and H. W. Lang, AIHAJ, 1974, 35, 411–418.
11. J. Ojima, J. Occup. Health, 2003, 45, 94–103.
12. U.S. Code of Federal Regulations 30CFR70 Sub-part B 70.101, 1st July 2010, http://www.gpoaccess.gov/nara/index.html, 17th October 2011.
13. N. L. Alperti, W. E. Keiser and H. A. Szymanski, IR-theory and practice of infrared spectroscopy, Plenum/Rosetta, 1973.
14. P. R. Griffiths and J. A. de Haseth, ed., Fourier Transform Infrared Spectrometry, John Wiley & Sons, New York, 1986.
15. P. Wilks, Spectroscopy, 2005, 20(12), 2–4.
16. D. P. Tuchman, US Dept of Interior (BOM), IC 9309, 1992, 17 pp.
17. J. C. Volkwein, R. P. Vinson, L. J. McWilliams, D. P. Tuchman and S. E. Mischler, DHHS (NIOSH), Publ. No. 2004-151, RI 9663, 2004, 25 pp.
18. P. Stacy, E. Kauffer, J.-C. Moulut, C. Dion, M. Beauparlant, P. Fernandez, R. Key-Schwartz, B. Friede and D. Wake, Ann. Occup. Hyg., 2009, 53, 639–649.
19. C. C. Anderson, DHHS (NIOSH), Publ. No. 83-124, 1983, 157 pp.
20. E. R. Kennedy, T. J. Fischbach, R. Song, P. M. Eller and S. A. Shulman, Guidelines for Air Sampling and Analytical Method Development and Evaluation, NIOSH, Cincinnati, Ohio, 1995.
21. K. A. Bush and D. G. Taylor, Chemical Hazards in the Workplace - Measurement and Control, American Chemical Society, Washington, D.C., 1981.
22. R. D. Foster and R. F. Walker, Analyst, 1984, 109, 1117–1127.
23. Y. Li, D. L. Garcia-Gonzales, X. Yu and F. R. v. d. Voort, J. Am. Oil Chem. Soc., 2008, 85, 599–604.
24. T. Lee, S. W. Kim, W. P. Chisholm, J. Slaven and M. Harper, Ann. Occup. Hyg., 2010, 54, 697–709.
25. S. Page, J. ASTM Int, 2006, 3, 1–14.

---