Measurement of the proximity effect for indoor air pollutant sources in two homes

Abstract

Personal exposure to air pollutants can be substantially higher in close proximity to an active source due to non-instantaneous mixing of emissions. The research presented in this paper quantifies this proximity effect for a non-buoyant source in 2 naturally ventilated homes in Northern California (CA), assessing its spatial and temporal variation and the influence of factors such as ventilation rate on its magnitude. To quantify how proximity to residential sources of indoor air pollutants affects human exposure, we performed 16 separate monitoring experiments in the living rooms of two detached single-family homes. CO (as a tracer gas) was released from a point source in the center of the room at a controlled emission rate for 5–12 h per experiment, while an array of 30–37 real-time monitors simultaneously measured CO concentrations with 15 s time resolution at radial distances ranging from 0.25–5 m under a range of ventilation conditions. Concentrations measured in close proximity (within 1 m) to the source were highly variable, with 5 min averages that typically varied by >100-fold. This variability was due to short-duration (<1 min) pollutant concentration peaks (“microplumes”) that were frequently recorded in close proximity to the source. We decomposed the random microplume component from the total concentrations by subtracting predicted concentrations that assumed uniform, instantaneous mixing within the room and found that these microplumes can be modeled using a 3-parameter lognormal distribution. Average concentrations measured within 0.25 m of the source were 6–20 times as high as the predicted well-mixed concentrations.

---

Environmental impact

Peoples' daily activities often bring them into close contact with indoor sources such as cooking, candles, and cigarettes. However, modeling of exposure assessment to indoor air pollutants has traditionally assumed a well-mixed environment. To more accurately characterize exposure levels indoors, we have measured how pollutant concentrations vary with distance from an active indoor source. Our results show that concentrations in close proximity (less than 1 metre from a source) were as much as an order of magnitude above the levels predicted by a well-mixed indoor air pollution model. With these data, we develop quantitative relationships between concentration and distance from the source for different ventilation rates. Our results should allow more accurate predictions of human exposure to active air pollution sources in the indoor environment, which is needed to improve assessment of potential health effects.

Introduction

Americans spend about 90% of their time indoors, the greatest share of which is spent in their homes.¹ A number of studies have shown that pollutant concentrations measured using a personal exposure monitor worn by a person are consistently higher than those measured by a stationary monitor located in the person's home.^2–6 This phenomenon is called the personal cloud, but it has not been studied extensively.

In the EPA's Particle Total Exposure Assessment Methodology (PTEAM) study, 178 persons carried personal exposure monitors in Riverside, CA, and the results showed that 41% of their indoor PM₁₀ exposure was from outdoor air infiltrating into their homes, 30% was from indoor sources, and 29% was due to the personal cloud.^6–8 As part of the EPA's Total Exposure Assessment Methodology (TEAM) study, personal air, fixed site (indoor and outdoor) air, and breath samples were collected from 50 individuals in the Los Angeles, CA area and analyzed for 12 volatile organic compounds (VOCs). The median ratios of personal air concentrations to indoor (kitchen) air for these 12 VOCs ranged from 1.07 to 1.86.⁹

One possible cause of the personal cloud is a compartmental effect: closed or partially-closed doors between the rooms in a house cause higher concentrations in the room where both the person and a source are located, compared with a separate room where there is no source.^8,10,11 A second possible cause of the personal cloud is human activities: for particulate matter, particles from floors and surfaces are resuspended as people move about;⁵ for VOCs, the wearing of freshly dry-cleaned clothes can cause elevated tetrachloroethylene exposure.¹² Finally, a third important cause suggested for the personal cloud is the close proximity of the person wearing the monitor to an actively emitting source, called the proximity effect.^13,14 The proximity effect may occur if the person is in the same room as the source; for example, an individual in a kitchen cooking near a gas stove whose pilot light emits carbon monoxide, or a cook broiling meat with an open flame that emits particles, but it has not been studied as rigorously as the other two suggested causes.

When a point source is actively emitting a pollutant, concentrations measured close to the source are higher than those measured farther away. Mage and Ott¹⁵ describes the 3 periods of an indoor source as: t_α, the “alpha” or active source period, t_β the “beta” or poorly-mixed period after the source has ended, and t_γ, the “gamma” or well-mixed decay period. Fig. 1 illustrates these 3 periods. The proximity effect is associated with the active emission (t_α) period while the pollutants are being released into the imperfectly mixed surrounding air. For a cigarette, for example, the proximity effect occurs indoors near the cigarette while it is burning – typically 7–10 min – but concentrations in the room approach a uniform value over the entire room's volume shortly after the cigarette is extinguished, because it enters the gamma period.

Fig. 1 Time series plot showing how measured data compares with the well-mixed model's prediction for a brief (10 min) emission period in Home #1. The dotted line represents the hypothetical ambient CO concentration infiltrating from outdoors (very low), while the dashed line shows the well-mixed prediction for a given air change rate and emission rate. The solid line shows the CO concentration measured 0.25 m from the source. During the source emission period (t_α), the measured concentration can be much greater than the well-mixed predicted concentration and results in high concentration peaks, or microplumes. Occasionally, the measured concentration also dips below the predicted concentration (negative excursion) because of incomplete mixing during the alpha and beta periods. Our experiments consisted of longer source emission times (t_α), with alpha periods lasting 7.5–12 h.

Higher pollutant levels near an emitting source are caused by non-instantaneous mixing of the emissions released into the surrounding air. Due to the proximity effect, a person closer to an emitting pollution source receives a greater exposure than a person farther away. The main purpose of this paper is to gain a better understanding of the proximity effect by characterizing the complex relationship between concentrations and distance from the emitting source indoors. This relationship can be used in other studies to more accurately assess the relationship between exposure levels and health effects.

Current inhalation exposure models such as RISK¹⁶ and SHEDS-PM¹⁷ use the combination of human activity patterns and microenvironmental concentrations to describe this exposure: i.e. human exposure = Σ_iC_it_i, where C_i is the concentration in microenvironment i, and t_i is the time that a person spends in that microenvironment. The models differ in how activity patterns are chosen and in how to express C_i.¹⁸ Some models estimate C_i for indoor residential microenvironments using the mass balance model (e.g., SHEDS-PM as described in Burke et al.¹⁷). The mass balance model is useful and accurate for a long-term exposure to a short release of pollutant¹⁵ – specifically if the time scale over which exposure is estimated is much greater than the active source or alpha period (t_i ≫t_α). Conversely, if the exposure time of interest is comparable to the source emission period, then the non-instantaneous mixing of the pollutant becomes important to consider for human exposure modeling. Klepeis,¹⁹ in investigating appropriate time scales for neglecting mixing effects but not proximity effects in exposure modeling, found that averaging times of 12 min (alpha and beta periods) for a short source, e.g., a 6 min cigarette, and of up to 80 min for a continuous source (such as multiple smokers in a bar), were sufficient to reduce mixing-related errors to less than 10%.

McBride et al.¹³ and Ferro et al.⁵ have found that the source proximity effect plays an important role in the exposure of humans to indoor air pollution sources, but it has not received adequate study in very close proximity to the source. McBride et al.¹³ conducted CO tracer gas experiments measuring concentrations in 4 directions around the source, and at 3 different heights in the living room of a two-story detached home. They compared the measurements close to the source near the center of the room (C_0.25) with measurements at a Stationary Indoor Monitor (SIM, C_SIM) located at the edge of the room, and they found that the ratio of average concentrations measured at these two locations (C_0.25/C_SIM) ranged from 1.1 to 13.2.

This current study goes beyond McBride's research by measuring concentrations with greater spatial resolution – close to the source and in many horizontal directions around the source – to better predict average exposure as a function of distance from the source. Our major goals are: (1) to measure the proximity effect at distances of 0.25–5.0 m from an emitting point source; (2) to measure how important factors such as ventilation, source height, and source strength affect the proximity effect, and (3) to describe personal exposure close to a continuous point source as the sum of 3 components: the ambient concentration infiltrating from outdoors, the well-mixed (background) concentration from an indoor source component, and the proximity concentration component.

Methodology

Pure CO (99.99%) and SF₆ gases (Scott Specialty Gases, Plumsteadville, PA) were emitted from a point located roughly in the center of a room, surrounded by an array of 30–37 real-time monitors. Table 1 summarizes all study factors and key parameters for each experiment. In Home #1, 9 experiments (labeled C1…C9) were done over 9 days, each lasting 7.5–12 h. In Home #2, 7 experiments (labeled T1…T7) were done over 5 days, with 3 done overnight; each experiment lasted 5–11 h. These long alpha periods allowed us to measure the behavior of a continuously emitted pollutant in a room over many hours. Concentration data was collected every 15 s, yielding up to 2880 data points per monitor per experiment.

Table 1 Summary data from 16 proximity experiments performed in two residences

Experiment ID	Duration [h]	Emission rate [cc h^−1]	Source relative height [m]	Ventilation state^c	Air change ave^d [h^−1]	Well-mixed ave conc^e [ppm]
a Base Cases were C2, C9b, and T2. b HVAC was on during experiment C9a. c Windows states: CState 0 = all windows closed; CState 0H = all windows closed, HVAC On; CState 1 = 3 windows part way open, 4–6 in; CState 2 = 3 windows halfway open; CState 3 = 3 windows wide open; TState1 = 1 window partly open, 3 in, in living room; TState2 = 2 windows half open, 1 in living room, 1 in kitchen; TState3 = 3 windows half open, 2 in living room, 1 in kitchen; TState4 = 3 windows wide open, 2 in living room, 1 in kitchen. d Air change rates were determined from SF6 decay using two Brüel and Kjær real-time monitors. e Calculated from source emission rate, air change rate, and estimated mixing volume using eqn (2) for the first 6 h of each experiment, except for C9a and T1. f Experiments performed at night.
C1	11.50	1432	0	CState 0	0.17	6.9
C2^a	12.50	1415	0	CState 1	0.57	3.9
C3	7.50	1432	0	CState 2	0.79	3.2
C4	10.25	1419	0.25	CState 1	0.41	4.8
C5	12.00	1456	0	CState 3	1.25	2.2
C6	11.00	1441	−0.25	CState 1	0.33	5.4
C7	11.00	775	0	CState 1	0.5	2.3
C8	12.00	1418	−0.5	CState 1	0.4	4.8
C9a ^b	4.00	1423	0	CState 0H	0.35	4.3
C9b ^a	8.00	1423	0	CState 1	0.32	7.9
T1	5.17	1250	0	TState 0	0.37	11
T2^a	8.17	1137	0	TState 1	0.19	13.4
T3	8.50	1175	0	TState 3	2.1	2.8
T4^f	9.83	1178	0	TState 3	0.4	10.1
T5	8.50	1185	0	TState 4	5.4	1.2
T6^f	10.57	1218	0	TState 2	0.54	8.7
T7^f	10.75	1229	0.15	TState 2	1	5.6

---

Spatial array

The spatial array for these experiments expanded upon the array designed by McBride et al. for proximity measurements.¹³ We placed up to 37 continuous CO monitors (Model T5, Langan Products, Inc., San Francisco, CA) at radial distances ranging from 0.25 to 5 m from the source at 8–16 different angles (vs. 3 for McBride), each measuring CO concentrations every 15 s. Within the first metre from the source, monitors were grouped more closely together than McBride's array,¹³ because we expected the proximity effect to be more pronounced (see Fig. 2a and 2b for the floor plan and monitor array used in each home). At each radial distance, there were 2–12 monitors, with the highest number located at 1 and 2 m from the source.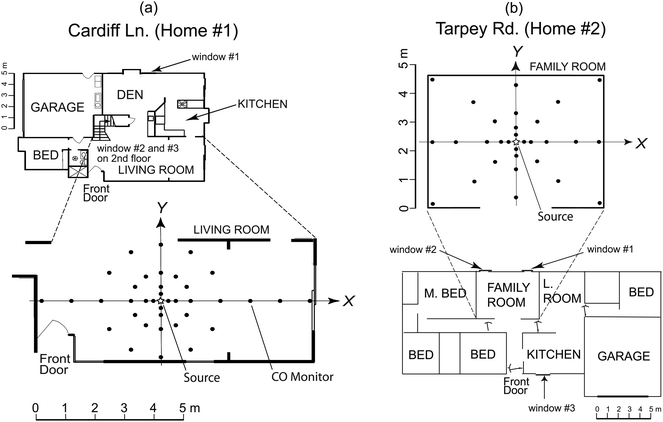

Fig. 2 Floor plan of the two homes in study with array of CO monitors used. The black dots represent CO monitor locations while an open star in the middle of the array represents the CO and SF₆ sources. Positive X and Y axes are shown on each array.

The array configuration was designed to fit the layout of the room. In the first house (a two-story detached home with a single-sloped vaulted ceiling in Redwood City, CA), the array extended 4 to 5 m from the source along the longer axis of the living room (9 m), but only 2 m from the source along the shorter axis (4 m), resulting in a total of 37 CO monitors (Fig. 2a). In the second house (a one-story ranch style home with a double-sloped vaulted ceiling in Watsonville, CA), the smaller square footage of the room (4.4 m by 5.6 m) allowed for only 30 monitors at radial distances of up to 2.8 m from the source (Fig. 2b). The mixing volumes of the two homes were 457 m³ and 183 m³. Most of the experiments were performed with the source and monitors at the same height (1 m above the floor, the typical breathing height of a sitting person); however, in a few experiments the source was above or below the base height of the monitors (see Table 1) to examine the vertical spread of the pollutant.

Measurements from 35 of the 41 monitors in Home #1 were used to examine changes in concentration with radial distance. For analysis of concentration versus radial distance from the source, data from the monitors at a radial distances of 1.5 m and 3 m were excluded, because the much lower monitor density (two monitors at 3 m, 4 monitors at 1.5 m versus 12 monitors at 1 m and 2 m) was not sufficient to capture the radial heterogeneity remaining at these distances.

Two SF₆ monitors (Brüel-Kjær Type 1302 Multigas™ monitor), placed at opposite ends of the room, measured SF₆ concentrations. The distance of the SF₆ monitors from the source was 4 m for Home #1, and 2.8 m for Home #2. A log-linear regression of SF₆ concentration vs. time, measured during the decay period, yielded an air change rate for every experiment, calculated as the average from the two monitors. The air change rate was measurable for the first 6–7 h of each experiment (until SF₆ concentrations dropped below detection level), and was fairly stable. The average air exchange rate for the first 6 h of each experiment is listed in Table 1.

Monitor calibration

We calibrated each CO monitor with a NIST-certified 50 or 60 ppm CO span gas (Scott Specialty Gases, Plumsteadville, PA) prior to starting experiments in each home. After calibration, the monitors were left in-place until the end of all experiments in a home. Calibration included “offset” concentrations of 1–2 ppm to maintain measurements in the positive range. Subsequently, in processing each data set, we subtracted the small background (ambient or offset) concentration measured during the first 10 min before gas release from the sources began.

Source emissions

Flow for both gases was controlled using an electronic mass flow controller (Model 5850E controller valve and Model 5896 electronic controller, Brooks Instrument Division, Emerson Electric Co., Hatfield, PA). Each flowrate was checked repeatedly during the first 10–15 min of each experiment using a primary flow calibrator (Gilibrator, Sensidyne, Inc. Clearwater, FL), ensuring stability. Pure CO gas was released from a point source at a flow rate of ∼20 cc min⁻¹ (exit velocity of 0.04 m s⁻¹) for 5–12 h per experiment. SF₆ was released from the same location at ∼200 cc min⁻¹ (exit velocity of 0.18 m s⁻¹) for 10–20 min at the beginning of each experiment, releasing enough gas so that its decay could be measured during the rest of the experiment, for calculating the air change rate. Both sources pointed vertically upwards.

Factorial design

During each of the 17 experiments, we varied one of 3 factors: window position, source height, or source strength. We viewed these factors as most likely to affect a person's exposure in a home. The factorial design used at each house is summarized in Table 1. For Home #1, we selected window positions based on previous work detailing the effect of window position on air change rates in this particular home.²⁰ In Home #2, we chose window positions expected to match closely the air change rates found in the first home. For all experiments we relied solely on natural ventilation, with the exception of one experiment in Home #1 in which we closed all windows and used the HVAC (heating, ventilation and air conditioning) fan for ventilation. We also ran experiments overnight in the second home to compare day vs. night.

Data analysis: Describing the proximity effect

Microplumes are short duration, high concentration peaks resulting randomly from imperfect mixing, and have been observed near active sources both indoors¹³ and outdoors.²¹ Our analysis of the proximity effect extends the superposition model of McBride et al.,²² which can be written generally as:

E = C_{DETERMINISTIC}{a,p,v,g,t,C_out(t)} + C_RANDOM{r,g,h,t} (1)

where E is a person's exposure concentration, C_{DETERMINISTIC} is the well-mixed concentration that depends on a (ventilation rate), p (outdoor-indoor penetration efficiency), v (room volume), g (indoor source emission rate), t (time), other removal or chemical processes, and the time-varying outdoor concentration C_out(t), and C_RANDOM is the random concentration that arises from microplumes and is theorized to depend in a complex, non-linear way on radial distance r from the source, source emission rate, source height h, time, and other variables related to dynamic air flow. The model posits that, as distance from the source increases, the contribution of microplumes to exposure decreases.

While the well-mixed indoor concentration can readily be predicted, little is known about how to predict the highly variable component occurring during the source emission period. We present two types of analysis: (1) decomposition of measurements into C_{DETERMINISTIC} and C_RANDOM , and (2) comparison of measurements to C_{DETERMINISTIC}via a dimensionless ratio. For homes with conditions similar to our study homes, the first analysis can be directly used in eqn (1) to predict magnitudes of human exposure, whereas the second analysis allows estimates of the magnitude of the proximity effect relative to the well-mixed component.

McBride et al.,²² modeled C_{DETERMINISTIC} using a lognormal tail-fitting algorithm. For both types of analysis, we find the well-mixed concentration via the mass balance model:²³

The initial (background) concentration is subtracted from our data, so eqn (2) assumes that initial concentrations are zero. C_RANDOM is then computed by subtracting the model-predicted C_{DETERMINISTIC} for each 5 min period from the average 5 min measured concentration.

Fig. 1 illustrates the superposition model, showing a hypothetical person's exposure during the active source period as the sum of: (1) well-mixed pollutant originating from outdoors (dotted line); (2) well-mixed concentration (eqn (2)) due to the indoor source (dashed line), and (3) a highly variable, random concentration due to imperfectly mixed emissions, which is realized as sharp peaks of short duration (solid line). During the source period (t_α), measurements show high excursions (microplumes) above, and small excursions below the well-mixed prediction. During the poorly-mixed period immediately after the source has stopped (t_β), the fluctuations become smaller in scale. Once the source emissions become well mixed in the room (t_γ), the measured concentration agrees consistently with the well-mixed prediction.

For the first type of analysis (decomposition), we present C_RANDOM (the microplume component) as either averages or plotted lognormal distributions as a function of radial distance from the source. We examine how C_RANDOM varies with different experimental factors (source strength, source height, ventilation state). These results can be used (viaeqn (1)) to predict point estimates or distributions of human exposure magnitudes near point sources for different circumstances, by selecting (or sampling from a log-probability distribution) an empirical C_RANDOM for a given proximity, ventilation state, source strength and source height.

For our second analysis, the measured data is normalized by dividing by the predicted C_{DETERMINISTIC}. A value of “1.0” indicates that the measured concentration matches the well-mixed prediction, while values above “1.0” reflect measurements exceeding the uniform mixing assumption. For both types of analysis we make comparisons between the two houses to see if similar conditions (e.g. air change rates) result in comparable proximity effects as a function of distance from the source.

Averaging time

The Langan CO monitor used in this study is a passive monitor that relies on diffusion of CO into the sensor, resulting in a finite response time that must be considered if the measured concentration is rapidly varying with time. For the Langan monitor, Cheng et al.²⁴ have shown that 1 min averages of rapidly varying microplumes are too short to be reliable without first applying a mathematical data reconstruction algorithm; however, with 5 min averages (>5 times the instrument response time), the error in the averaged concentrations is reduced to <15%. While further reductions in error would be achieved with even longer averaging times, a major drawback is that time resolution would be lost.

To select an appropriate averaging time, our second consideration involved an analysis of the variability as a function of averaging time. As expected, the variability of the data decreased as the averaging time increased. However, a very large decrease in standard deviation was seen between 1 min and 5 min averaging times, while the further decrease between averaging over 5 min versus 30 min was quite small. This finding suggested that there were two distinct sources of variability. The first, from the microplumes, occurred over times ranging from seconds to minutes. The second, due to changes in the airflow directions inside the room, occurred over times as long as an hour or more under natural ventilation. Based on this analysis of variability and the results of Cheng et al.,²⁴ a 5 min averaging time was chosen to minimize response time and synchronization issues (more visible at shorter averaging times) while retaining adequate real-time resolution.

The upper data logging limits of the CO instruments were between 128 ppm and 150 ppm, depending on the individual data logger and its signal processing board. At monitors closest to the source (0.25 and 0.5 m), the upper logging limit was often exceeded (see Fig. 3). Due to this upper limit, concentrations measured at these close-proximity monitors were often underestimates of the true exposure. Analysis of the effect of the upper logging limit on the frequency distribution²⁵ demonstrated that if more than 5 of the 20 (15 s) measurements that made up a 5 min average were off scale, the 5 min average was substantially underestimated. These data points were excluded in our analysis of the frequency distribution plots because they artificially skewed the distribution to level off at the value of the upper logging limit. However, these data were not excluded from the other results presented, since censoring these data would more greatly underestimate the normalized concentrations measured closest to the source.

Fig. 3 Time series plots of each monitor along the long axis of the array in Home #1, starting with the closest monitor and moving away from the source. This shows that clusters of microplumes that are biggest in duration and magnitude closest to the source diminish as they move farther away. This also shows that the preferred direction of motion changes throughout the day. Fig. 3a shows the time series plots for monitors along the negative X-axis, while 3b shows simultaneous monitors along the positive X-axis (refer to Fig. 2a).

Statistical analyses

Summary statistics, frequency distribution plots, and calculations were performed using SigmaPlot software Version 11.0 (Systat Software, Inc., San Jose, CA).

Results and discussion

Fig. 3a and 3b show simultaneous time-series plots for monitors placed at 0.25 to 5 m from the source along the long axis of the array inside Home #1 (Fig. 2a) for experiment C2 (base case). Fig. 3a shows measurements in one direction (negative X, as shown in Fig. 2a), while Fig. 3b shows the opposite direction (positive X). These illustrate that a “cluster” of microplumes (a group of microplumes bunched together) can be tracked as they move away from the source. For example, in the first time-series (Fig. 3a, 0.25 m from the source), there is a large cluster of microplumes near the beginning of the experiment. Moving farther away from the source (down to the next time-series plot), this cluster becomes smaller in magnitude and duration. These microplumes occurred with the greatest frequency and intensity closest to the source (within the first 0.5 m), resulting in higher average concentrations as well as higher variability.

Comparing the two sets of time-series graphs also illustrates how the preferred direction of motion varied throughout the day. During the first few hours of the experiment, Fig. 3a shows a large cluster of microplumes, while Fig. 3b shows almost no microplume activity. At nearly the same time that the microplumes diminish in Fig. 3a, they appear in Fig. 3b. Thus, when indoor exposure time scales are a few hours or less, this directionality, with short periods resembling plug flow conditions, can greatly affect a person's exposure at a specific location. Transient plug flow conditions could reduce the travel time between a source and receptor, making the highly-concentrated microplumes more likely to reach the receptor without substantial mixing/dilution. However, over the longer time periods of our experiments, no preferred direction in plume movement was observed.²⁶

Summary statistics

Table 2 contains mean background-adjusted CO concentrations grouped by combinations of the study factors (ventilation state, source emission rate and height, time of day) and the radial distance between the source and the receptor monitors for the first 6 h of each experiment (except for T1 which lasted 5 h). The values in Table 2 give the isolated proximity effect due to microplume activity (C_RANDOM of eqn (1)), removing the influence of the well-mixed accumulation of CO. Under similar conditions, these results can be used to predict the likely proximity effect in arbitrary locations for different pollutants, regardless of the background level.

Table 2 Grouped statistics for C_RANDOM (eqn (1)) vs. radial distance from source

Exp.	Air change rate (h^−1)	Source (relative)^a		Mean CO incremental conc. [ppm] vs. radial distance [m]
		Emission rate	Height	0.25	0.5	1	2	4	5
a Source emission rate relative to ∼1400 cc h^−1 and source height relative to monitors that are 1 m above the ground in Home #1. b Averaged over 4 h. C9b not included in this table because low SF6 concentrations during C9b insufficient to calculate predicted concentration. c Source emission rate relative to ∼1200 cc h^−1 and source height relative to monitors that are 1 m above the ground in Home #2. d Averaged over 5 h. e Experiments performed at night. f These incremental concentrations are lower–bound estimates. For these concentrations, 5–11% of the 5 min averages were underestimated.
C1	0.17	1	0	29 ^f	16	10	6	8	9
C9a ^b	0.35, HVAC	1	0	22	13	4	2	1	−1
C2	0.57	1	0	43 ^f	28	16	6	4	2
C3	0.79	1	0	43 ^f	29	16	6	5	3
C5	1.25	1	0	43 ^f	28	15	5	2	0
C7	0.50	0.5	0	39	23	10	3	1	1
C8	0.40	1	−0.5	3	2	0	−1	−1	−1
C6	0.33	1	−0.25	20 ^f	10	5	1	1	0
C4	0.41	1	0.25	13	10	8	3	3	−1
Exp.	Air change rate (h^−1)	Source (relative) ^c		Mean CO incremental conc. [ppm] vs. radial distance [m]
		Emission rate	Height	0.25	0.5	1	2	2.8	3.56
T2	0.19	1	0	38	47	30	18	11	11
T1^d	0.37	1	0	36	21	15	11	8	6
T3	2.1	1	0	24	13	10	7	6	6
T5	5.4	1	0	14	8	4	2	2	2
T4^e	0.40, night	1	0	48	38	23	6	4	4
T6^e	0.54, night	1	0	36	20	18	9	6	1
T7^e	1, night	1	0.15	1	1	2	2	2	3

---

To test the effects of ventilation, a heating ventilation and air conditioning (HVAC) system was compared with natural ventilation for one experiment (experiment C9a). The use of HVAC most noticeably lowered the incremental concentrations at 1–4 m away (compared with experiments C1 and C2), presumably due to increased mixing energy.^26,27 A single experiment was also performed in which the source strength was halved (C7 vs. C2). While this roughly halved the microplume component farther from the source, the changes in the incremental concentrations within 1 m of the source were quite small.

Several experiments involved moving the source above or below the monitoring plane, and consistently resulted in lowered incremental concentrations. As shown in Table 2, in Home #1, increasing or lowering by 0.25 m (C4 and C6) caused reductions of 50% or more (compared with C2) within the first 2 metres, while lowering the source by 0.5 m caused >90% reductions, and essentially eliminated the proximity effect. In Home #2, moving the source above the monitors just 0.15 m, at night, eliminated the proximity effect (T7 compared to T6).

As windows are opened more, and the air change rate increases, two possible effects should be considered: the directionality of airflow can increase, and mixing energy inside the home can increase. In the daytime, for Home #1, higher incremental concentrations were seen close to the source for the highest ventilation states (0.57–1.25 h⁻¹). This may be due to increased directional flow (that appears over a timescale comparable to our experiment duration) of concentrated emissions when windows were opened halfway or fully. However, in Home #2, where the range of air change rates was much greater, the highest air change rates (2.1 h⁻¹ and 5.4 h⁻¹) caused the lowest microplume components, suggesting that the higher mixing energy effect may be dominating for these experiments.

Going from day to night with the window positions kept constant (T3 vs. T4), the air change rate dropped from 2.1 h⁻¹ to 0.40 h⁻¹. The nighttime incremental concentrations doubled within the first metre, becoming roughly comparable to the values measured for the daytime experiment with a similar air change rate (T1). The drop in air change rate at night was likely due to the concurrent drop in wind speed outdoors.

Based on these results, the magnitude of the microplume component is most strongly a function of radial distance and relative height from the source. The incremental concentration near the source does not appear to scale linearly to the source strength, but more experiments at different source strengths are needed to fully investigate this finding. As noted in Table 2, several of the 0.25 m concentrations for Home #1 are lower-bound estimates, due to the upper logging limits of the CO monitors. The effect of the air change rate on microplume magnitude near the source is complex – it may depend on the relative influences of air directionality versusmixing energy.

Frequency distributions

Given the tremendous range of concentrations measured in close proximity to a point source, the best way to describe the entire exposure data set for a person close to the source is to use a frequency distribution plot. When the logarithm of the concentration is plotted versus the integral of the normal probability density function, a straight line indicates a lognormal distribution, a distribution commonly seen for environmental measurements involving the dilution of pollutants in air and water.²⁸ As an example of how to characterize the microplume concentrations for a data set, we plotted the frequency distributions of 5 min average incremental concentrations for experiment C7 on a lognormal graph (Fig. 4).

Fig. 4 Frequency distributions of the incremental exposure () plotted on a standard logarithmic-normal probability graph after subtracting the shift parameter θ. The lines are nearly straight, showing that the microplumes can be modeled as 3-parameter lognormal distributions. The parallel lines indicate that while the median and average values decrease as one moves farther away from the source, the variability (reflected by the slope) is similar within the first 2 m. The data for this typical example of our results were measured at base case air change rate (∼0.5 h⁻¹) and height conditions (1 m from ground), but at half the normal emission rate (∼700 cc h⁻¹).

A typical lognormal distribution relies on two parameters to describe the model fit to the data: the geometric mean and geometric standard deviation. The 3-parameter lognormal distribution is part of the family of lognormal distributions and has been shown to fit ambient air quality data well.^29,30 Unlike the two-parameter lognormal model, the 3-parameter lognormal model includes a shift parameter, θ, that is subtracted before the logarithm of the variable of interest is taken.³¹ Like the other parameters, the value of θ is determined empirically from the data. In Fig. 4, all 6 distributions fit the 3-parameter model well as indicated by their straightness on the graph, with the exception of some curvature at the high end of the 2 m distribution. Yet, the R² values based on fitting the distributions by linear regression were all still greater than 0.94.

Each separate line is the frequency distribution of a different radial distance from the source, ranging from 0.25–5 m. By focusing on incremental values, where the background (well-mixed) concentration is subtracted, the distribution reflects just the random component, or the microplumes. The CO concentration scale on this graph begins at 0.1 ppm, because the CO monitor has a lower sensitivity limit of 0.1 ppm. As discussed in the methodology section, some data points at the high end of the frequency distributions for 0.25 m, 0.5 m, and 1 m have been excluded due to the upper data logging limit of the instruments. For all 9 experiments in Home #1, experiments C3 and C5, which were performed at the highest ventilation states (CState 2 and CState 3, respectively) had the most 5 min averages (11–12% at 0.25 m) that met the criteria for exclusion – likely due to increased air flow. In Home #2, experiment T2 had the most 5 min averages that met the criteria for exclusion (4% at 0.5 m).

In Fig. 4, the horizontal axis (cumulative percentage) is the percentage of the 5 min average concentrations at a particular distance from the source that are less than the incremental concentration value shown on the vertical axis. To find the percentage of values above a specified incremental concentration, we read the concentration on the vertical axis; then we read the corresponding horizontal axis value and subtract that value from 100%. For example, 50% of 5 min incremental exposures are above 20 ppm at 0.25 m, while only 100% − 85% = 15% are above 20 ppm at 1 m (see dashed lines). The closest source proximity distances (up to 2 m from the source) show the greatest slopes in these plots, reflecting the largest variability seen in the real-time measurements due to the many large microplumes that occur close to the source. At 4 and 5 m from the source, the slopes are not as great, indicating less microplume activity and therefore less variability at these distances.

Table 3 shows the parameters that describe the fit of the incremental concentrations to the 3-parameter lognormal model for the experiment shown in Fig. 4. The first two parameters (geometric mean, μ_g , and geometric standard deviation, σ_g) are calculated from the slope and intercept of the model fit to the data after its third parameter, θ, has been subtracted from the logarithm of the incremental concentration. The third parameter, θ, for each distribution was found to be a value close to the highest negative value in the incremental concentrations.³² These negative values (see the negative excursions shown on Fig. 1) arise from measurements made during the buildup to equilibrium when imperfect mixing resulted in measurements occasionally below the predicted concentration. This shift parameter, θ, also appears to be associated with the lag time necessary for a parcel of pollutant to become well mixed within the room. The shift parameter θ was less than 2 ppm (0.6–1.88 ppm) at all distances, so it is very small compared to the microplume concentrations.

Table 3 3-parameter lognormal model fit to incremental CO concentration data plotted in Fig. 4

Distance (m)	μ g (ppm)	σ g	θ (ppm)	R ^2
0.25	15.6	9.0	−1.64	0.99
0.5	5.2	9.7	−1.41	0.99
1	2.2	7.4	−1.07	0.99
2	0.01	7.2	−0.60	0.99
4	1.7	1.8	−1.20	0.94
5	1.6	2.3	−1.88	0.96

---

The geometric means of this data set decrease from 15.6 ppm at 0.25 m to 0.01 ppm at 2 m, but with similar geometric standard deviations (ranging from 7.2 to 9.7). This indicates that within 2 m from the source, the frequency of the arrival of microplumes remains relatively constant, but the magnitude decreases as you move farther away from the source. At 4 and 5 m from the source, the geometric means (1.7 and 1.6, respectively) are higher than at 2 m, but the geometric standard deviations are lower (1.8 and 2.3, respectively). This result indicates that at 4 and 5 m from the source, there were fewer microplumes and therefore less variability in concentration. These frequency distributions can be used in the superposition model to simulate magnitudes of the microplumes for an exposure model. For example, given the conditions of the location of interest, C_RANDOM of eqn (1) can be sampled from a 3-parameter lognormal distribution at a given distance from an active source.

Proximity curves

The ratio of the measured concentration to the well-mixed model can be used to understand the relative proximity effect in similar kinds of homes with similar background levels. The ratios also serve as a rough estimate of the magnitude of the proximity effect. Fig. 5 shows proximity curves: the normalized CO concentration ratio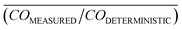 , with the ratios radially averaged as a function of distance from the emitting source for each of the experiments in both homes. These graphs show that the ratio is smallest (closest to unity, the well-mixed prediction) at the greatest distance from the source.

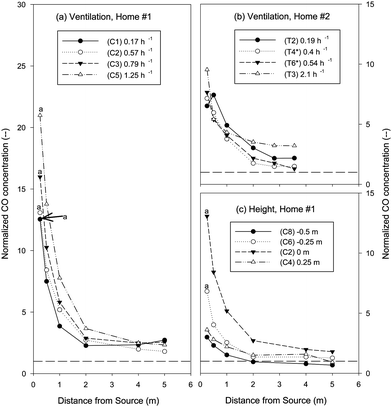Fig. 5 This shows the effect of ventilation conditions on concentration versus distance in Home #1 (a) and Home #2 (b), as well as the effect of source height relative to monitor height (c). The y-axis shows the normalized CO concentration (i.e.), and the x-axis shows horizontal distance from the source. As the air change rate increases, the proximity curve is more pronounced. “*” denotes experiments done at night. This graph shows that there is a maximum plane of exposure (in this case, at source height) and that the pollutant takes a long time to mix vertically. Data points marked by an “a” are lower-bound estimates due to the logging limit of the instruments.

The effect of increasing natural ventilation on the proximity curves is shown in Fig. 5a and 5b. For both homes, the proximity curve became more pronounced as the ventilation rate increased by opening windows. For the highest air change rate (C5) measured in the first home (Fig. 5a), an average 5 min exposure at 0.25 m from the source was 21 times higher than predicted, while a 5 min average exposure at 5 m was close to that predicted by the well-mixed model (eqn (2)). At the lowest air change rate (C1), the proximity curve was noticeably flattened. In Home #2 (Fig. 5b), a qualitatively similar trend was seen with ventilation rate – the highest ratio (12.8) at 0.25 m from the source occurred at the highest air change rate (T5), and the lowest ratio occurred at the lowest air change rate (T2). This effect was not seen for the isolated random component described in the summary statistics section. The trend here can be explained by the decreasing magnitude of the well-mixed model (denominator of ratio) as the air change rate increases.

Cheng et al. saw an opposite trend when averaging over just the first 30 min of the source.²⁶ As the source continues to emit, the background concentration (eqn (2)) contributes a larger portion to the total concentration, especially for the lower air change rate. Also, with a lower air change rate, there is less mixing, leading to higher concentrations near the source in the first 30 min. With a higher air change rate, there is less time for mixing to occur before ventilation removes the pollutant; therefore, concentrations are higher near the source.

Under comparable ventilation rates, the magnitude of the proximity effect closest to the source in the second home was only a little more than half of that seen in the first home (which had the single-sloped ceiling). However, the two homes differed in a few other ways, so it is not possible to attribute these differences in the proximity effect to specific home characteristics. One possibly important difference could be the opening of windows in the same room as the source and monitors in Home #2 to achieve the desired air change rates. In Home #1, the windows used to control air change rate were in adjacent rooms.

Results from Home #2 (Fig. 5b) also show that the proximity curve changed between day and night. The only difference between experiments T3 and T4 (shown as solid and open triangles) is that one was done during the day and one at night. The nighttime air change rate was one-fourth the daytime air change rate (associated with lower wind speeds measured outdoors), and the shape of the resulting proximity curve changed.

Our results are similar to those of Furtaw et al.,¹⁴ who found that, at arm's length distance from the source (0.4 m), the ratio of measured to predicted was, on average ∼2 : 1 (with the measured concentration ranging from nearly that predicted by eqn (2) to several times the predicted concentration). These experiments were conducted with SF₆ in a chamber at very high air change rates (10–49 air changes per hour) controlled using an HVAC system. While these rates are high, they are typical of industrial settings with mechanical ventilation. In our experiments with much smaller air change rates of 0.19–5.4 h⁻¹ (the range of typical air change rates in Californian homes³³ is 0.5–2.0 h⁻¹), we found at arm's length (0.5 m) ratios ranging from 5 : 1–14 : 1. Using both CO and SF₆, McBride¹³ measured up to 10 times as high a concentration 0.25 m from the source than at 5.4 m (the Stationary Indoor Monitor (SIM)), and up to 4.5 times higher at 0.5 m. A measurable proximity effect was still seen up to 2 m from the source, but no measurements were made between 2 and 5.4 m. Our results agree very well with these findings, with the addition that we found a proximity effect (relative to the predicted average) out to 5 m from the source.

The shape of the proximity curves were also affected by the height of the emissions relative to the heights of the sampling points. In Fig. 5c, the proximity curves for the different source heights are compared with the base case of a 1 m source height (C2, solid triangle). When the source was moved 0.25 m above the monitors (C4, open triangle), the proximity curve was greatly flattened, and a similar result was also observed when the source was moved 0.5 m below the source. This supports our finding that the spread of emissions is greater in the horizontal direction than in the vertical direction. Two temperature sensors, placed 2.4 m apart vertically, showed that both homes were stably stratified (+0.5 °C m⁻¹ in Home #1, and +0.05 °C m⁻¹ in Home #2), which would tend to inhibit vertical mixing. In an occupied home, people moving around the room could create some mixing, which might lead to an increase in the vertical spread of pollutants. Using the SF₆ measurements, the average horizontal rate of spread was 1.0 m min⁻¹ in Home #1 and 1.5 m min⁻¹ in Home #2. The vertical rate of spread was not measured.

For a source height 0.25 m below the monitors (open circle in Fig. 5c), the emissions still produced a pronounced proximity curve (although not as dramatic as C2, solid triangle). This result indicates that emissions of the tracer gas may initially spread vertically up to 0.25 m above the source release height, but further vertical spread (to 0.5 m above and 0.25 m below) is markedly inhibited. These findings are consistent with those of McBride et al.,¹³ who found the greatest proximity effect within 0.5 m above for the same source.

As was true in McBride's experiments, CO released from our single point source was not heated, the exit velocity was small (∼0.04 m s⁻¹), and the indoor temperature profile was stratified, so only a small amount of momentum-driven plume rise was expected. Thus, as would be expected for these types of experiments, the maximum plane of exposure was close to the height of the source. In contrast, a burning cigarette generates a buoyant (hot) plume, with a plume rise observed to be approximately 0.5 m in Home #1. For cigarette smoke emitted into a stratified environment, the maximum plane of exposure would be close to the effective plume height, which would include the buoyant plume rise.

With these data, it is also possible to explore the relationship between measured and predicted concentrations during those time periods when a “cluster” of microplumes is moving along a measurement axis. As was evident in Fig. 3, a cluster of microplumes moving along one axis of the array can be followed from the monitor closest to the source all the way out to the last monitor. In Fig. 6, we evaluated the proximity effect for the migrating clusters seen at the beginning of this experiment (between 10:30 and 13:53) in Fig. 3a (experiment C2), and in the middle of the day (between 14:05 and 15:50) in Fig. 3b. For the cluster evident in Fig. 3a, at 0.25 m from the source, a person's 5 min exposure would be almost 50 times as high as the well-mixed prediction, and about 4 times as high as the result found by radially averaging over all 4 monitors.

Fig. 6 This shows the proximity curves for 2 short (1–2 h) clusters of microplumes as shown in Fig. 3a and 3b (experiment C2). For a specific cluster of microplumes moving away from source, the concentration at 0.25 m from the source can be 4 times as high as when the results are averaged radially.

Conclusions

The major influential factors affecting the magnitude of the proximity effect were the ventilation rate, the relative height of the source, and the distance from the source. The bulk of this research project focused on naturally-ventilated homes; only one experiment was conducted using mechanical ventilation. In the future, it would be valuable to conduct more experiments involving mechanically-ventilated homes.

• For a source emission time scale t_α similar to the exposure time scale of interest, t_i in an indoor environment, the well-mixed mass balance model can underpredict the exposure of a person very close to the source (<1 m) by as much as 10-fold.

• The magnitudes of sporadic spikes in pollutant concentrations (“microplumes”) that occur close to indoor emission sources can be represented to a good approximation as 3-parameter lognormal distributions.

• Modeling exposure close to a continuous point source in a home is possible by summing 3 variables: (1) the indoor concentration caused by infiltration of outdoor air into the home; (2) the home's well-mixed (background) concentration due to the indoor source, evaluated deterministically from the mass balance model, and (3) the contribution of the concentrated fresh microplumes from the source, represented by a random variable sampled from a 3-parameter lognormal distribution.

• Vertical mixing of source emissions inside homes occurs on a much slower time scale than the horizontal dispersion, leading to a narrow range of heights near source release height with especially elevated concentrations.

Our method of characterizing the microplume (random) component of the proximity effect allows the prediction of close-proximity exposure to sources in naturally-ventilated homes using the superposition model (eqn (1)). Since we isolated the random component from the well-mixed time-varying behavior, our results can be used for predicting exposure to indoor pollutant releases of any duration, ranging from secondhand smoke (∼10 min) to long-term VOC emissions (∼hours).

Acknowledgements

The research presented in this paper was funded by the Tobacco-Related Disease Research Project (TRDRP, Oakland, CA). The authors would like to thank Lee Langan of Langan Products, Inc. for his advice on the operation and handling of the CO monitors, and Dr Frank Ludwig for helpful comments about indoor stratification.

References

1. N. E. Klepeis, W. C. Nelson, W. R. Ott, J. P. Robinson, A. M. Tsang, P. Switzer, J. V. Behar, S. C. Hern and W. H. Engelmann, J. Exposure Anal. Environ. Epidemiol., 2001, 11, 231–252.
2. C. E. Rodes, R. M. Kamens and R. W. Wiener, Indoor Air, 1991, 1, 123–145.
3. W. R. Ott, J. Exposure Anal. Environ. Epidemiol., 1995, 5, 449–472.
4. L. Wallace, J. Air Waste Manage. Assoc., 1996, 46, 98–126.
5. A. R. Ferro, R. J. Kopperud and L. M. Hildemann, J. Exposure Anal. Environ. Epidemiol., 2004, 14, S34–S40.
6. L. A. Wallace and K. R. Smith, in Exposure Analysis, ed. W. R. Ott, A. C. Steinemann and L. A. Wallace, CRC Press, Boca Raton, 2007, ch. 8, pp. 181–199.
7. H. Ozkaynak, J. Xue, J. Spengler, L. Wallace, E. Pellizzari and P. Jenkins, J. Exposure Anal. Environ. Epidemiol., 1996, 6, 57–78.
8. W. R. Ott, N. E. Klepeis and P. Switzer, J. Air Waste Manage. Assoc., 2003, 53, 918–936.
9. T. D. Hartwell, R. L. Perritt, E. D. Pellizzari and L. C. Michael, Atmos. Environ., Part A, 1992, 26, 1519–1527.
10. S. L. Miller, K. Leiserson and W. W. Nazaroff, Indoor Air-International Journal of Indoor Air Quality and Climate, 1997, 7, 64–75.
11. A. R. Ferro, N. E. Klepeis, W. R. Ott, W. W. Nazaroff, L. M. Hildemann and P. Switzer, Atmos. Environ., 2009, 43, 706–714.
12. L. A. Wallace and S. M. Gordon, in Exposure Analysis, ed. W. R. Ott, A. C. Steinemann and L. A. Wallace, CRC Press, Boca Raton, 2007, ch. 7, pp. 147–179.
13. S. J. McBride, A. R. Ferro, W. R. Ott, P. Switzer and L. M. Hildemann, J. Exposure Anal. Environ. Epidemiol., 1999, 9, 602–621.
14. E. J. Furtaw, M. D. Pandian, D. R. Nelson and J. V. Behar, J. Air Waste Manage. Assoc., 1996, 46, 861–868.
15. D. T. Mage and W. R. Ott, in Characterizing sources of indoor air pollution and related sink effects, ed. B. A. Tichenor, ASTM STP 1287, 1996, pp. 263–278.
16. L. E. Sparks, U.S. Environmental Protection Agency, Air and Energy Engineering Research Laboratory, Research Triangle Park, NC, 1991, EP 1.89/2:600/S 8-91/013.
17. J. M. Burke, M. J. Zufall and H. Ozkaynak, J. Exposure Anal. Environ. Epidemiol., 2001, 11, 470–489.
18. N. E. Klepeis, in Exposure Analysis, ed. W. R. Ott, A. C. Steinemann and L. A. Wallace, CRC Press, Boca Raton, 2007, ch.19, pp. 445–470.
19. N. E. Klepeis, Environ. Health Perspect., 1999, 107, 357–363.
20. C. Howard-Reed, L. A. Wallace and W. R. Ott, J. Air Waste Manage. Assoc., 2002, 52, 147–159.
21. N. E. Klepeis, E. B. Gabel, W. R. Ott and P. Switzer, Atmos. Environ., 2009, 43, 3155–3167.
22. S. J. McBride, J. Am. Stat. Assoc., 2002, 97, 683–691.
23. W. R. Ott, in Exposure Analysis, ed. W. R. Ott, A. C. Steinemann and L. A. Wallace, CRC Press, Boca Raton, 2007, ch. 18, pp. 411–444.
24. K.-C. Cheng, V. Acevedo-Bolton, R.-T. Jiang, N. E. Klepeis, W. R. Ott and L. M. Hildemann, J. Environ. Monit., 2010, 12, 846–853.
25. V. Acevedo-Bolton, Ph.D. Thesis, Stanford University, 2011.
26. K.-C. Cheng, V. Acevedo-Bolton, R.-T. Jiang, N. E. Klepeis, W. R. Ott, O. B. Fringer and L. M. Hildemann, Environ. Sci. Technol., 2011, 45, 4016–4022.
27. A. C. Drescher, C. Lobascio, A. J. Gadgil and W. W. Nazaroff, Indoor Air, 1995, 5, 204–214.
28. W. Ott, Environmental statistics and data analysis, Lewis Publishers, Boca Raton, 1995.
29. W. R. Ott and D. T. Mage, Comput. Oper. Res., 1976, 3, 209–216.
30. D. T. Mage and W. R. Ott, J. Air Pollut. Control Assoc., 1978, 28, 796–798.
31. P. Tobias, in NIST/SEMATECH e-handbook of statistical methods, http://www.itl.nist.gov/div898/handbook/apr/section1/apr164.htm.
32. D. T. Mage, personal communication with V. Acevedo-Bolton, 2010.
33. A. L. Wilson, S. D. Colome, Y. Tian, E. W. Becker, P. E. Baker, D. W. Behrens, I. H. Billick and C. A. Garrison, J. Exposure Anal. Environ. Epidemiol., 1996, 6, 311–326.

---