In situ redox functionalization of composite electrodes for high power–high energy electrochemical storage systems via a non-covalent approach

Abstract

The growing demand for new global resources of clean and sustainable energy emerges as the greatest challenge in today's society. For numerous applications such as hybrid vehicles, electrochemical storage systems simultaneously require high energy and high power. For this reason, intensive researches focus on proposing alternative devices to conventional Li battery and supercapacitors. Here, we report a proof of concept based on non-covalent redox functionalization of composite electrodes that may occur either during the calendar life or during the device functioning. The active material, a multi-redox pyrene derivative, is initially contained in the electrolyte. No additional benchmarking step is therefore required, and it can, in principle, be readily applied to any type of composite electrode (supercapacitors, battery, semi-solid flow celletc.). Accordingly, a practical carbon fiber electrode that is 10 mg cm⁻² loaded can deliver up to 130 kW kg_electrode⁻¹ and 130 Wh kg_electrode⁻¹ with negligible capacity loss over the first 60 000 charge/discharge cycles.

---

Broader context

In the context of urgent and increasing needs for intermittent renewable energy supply, power grid management, as well as low emission electrified vehicles, efficient and green electrochemical storage systems appear as priority targets. Among such devices, neither batteries nor supercapacitors can deliver both high power and high energy densities. In this work we propose a new strategy that allows not only approaching this double requirement but also simplifies benchmarking processes. It is based on non-covalent immobilization of organic redox material on carbon substrate that occurs spontaneously within the electrochemical device upon assembly. Remarkable cycle life is also achieved together with negligible side reactions.

1. Introduction

Storage systems designed for hybrid electric vehicles should be able to provide both high energy and power densities. Lithium (Li)-ion batteries are known to deliver relatively high energy densities (150–200 Wh kg⁻¹) in comparison to other electrochemical systems. This property is associated with faradic reactions that take place within the volume of active grains by simultaneous ion and electron uptake/removal. However, the amplitude of such reactions being large in regard to the amount of ions available in the porosity of electrodes, power performance (1–3 kW kg⁻¹) is usually frustrated by slow ionic “refuelling” from the electrolyte.^1,2 The opposite holds for electrochemical capacitors that provide relatively high power densities (10 kW kg⁻¹) at the expense of energy (5 Wh kg⁻¹) because storing reactions (capacitive ion adsorption and pseudocapacitive surface redox reactions) are confined to the surface.^3,4 Accordingly, a gap appears in the so-called Ragone Power/Energy plot because no system fulfils both power and energy requirements. In response to this considerable challenge, novel advances in materials chemistry and electrode engineering have been proposed.

Regarding lithium batteries, recent theoretical results along with modelling of electrode kinetics corroborate experimental works, and converge toward consistent conclusions. When low electronic and/or lithium motion materials are involved, high rates can be achieved upon reducing the transport length as in nanograins^5,6,7 or nanostructured materials.⁸ Recent calculations also point out that statistical crystal defects significantly reduces the 1D Li diffusion coefficient in LiFePO₄. Kinetics therefore depends on the Li diffusion length with microscopic crystals being much more impeded than nanoparticles.⁹ However, when fast Li motion is possible, such as for LiNi_0.5Mn_1.5O₄, micrometric grains were reported to outperform 50 nm particle size.¹⁰ Indeed, first principle calculations¹⁰ predict the lithium diffusion coefficient to be approximately 10⁻⁹ – 10⁻⁸ cm² s⁻¹ such that it takes less than 10 s for Li ions to cross a 3 μm particle. Therefore, ion and/or electron transport within the percolating networks of the whole electrode become critical aspects that hinder the use of nanoparticles. Accordingly researchers have focused considerable attention to the optimization of the composite electrodes through tailored porosity^2,11 and tortuosity,¹¹ efficient contacts between active material and conducting network,^12–18 3D architectures^19,20 and fast ion-conducting surface modification.²¹

In the case of electrochemical capacitors, additional energy compared to pure capacitive ones can be provided upon surface functionalization with redox molecules. For such electrodes, however, several key points need to be satisfied. From a power aspect, the electronic and ionic diffusion through the percolating networks should not be disrupted upon grafting whereas for improving the energy density, the number of exchanged electrons per surface and weight units should be maximized. Furthermore, the electrode benchmarking should remain as simple as possible while its loading should be kept to sufficient levels for practical applications. Interesting approaches to dealing with the energy increase of supercapacitors has been demonstrated by Pickup and Bélanger who functionalized carbon electrodes with redox molecules^22–27 therefore introducing a pseudocapacitive component in the charge storage process. Similarly Bélanger doubled the overall capacitance of an activated carbon-based electrode thanks to anthraquinone grafting.^25,26 Such an approach has led to the design of asymmetrical electrochemical supercapacitors using either two functionalized carbon electrodes with different electroactive molecules,²⁷ or a modified carbon negative electrode and a positive oxide-based electrode.²⁸Carbon functionalization has also allowed controlling the conductivity gradient within the electrolyte. A great step in this direction was taken by Bélanger who reported that anchored anionic species could avoid ionic depletion occurring within the electrolyte upon cycling, therefore maintaining a high level of conductivity.²⁹ More recently, Shao-Horn's group obtained impressive energy and power performance for grafted MWCNT-based electrodes of very high density.³⁰ They postulated these findings as being the result of Li reaction with grafted C=O groups in agreement with previous work from Poizot et al.³¹ Gaberscek and Dominko³² have also reported an elegant strategy that consists of grafting quinone derivatives onto carbon or silica substrates. Although all these reports are very promising, several limitations should be mentioned. First, reported power abilities must be taken in perspective of the electrode loading. Indeed, in case of ref. 30, power performance decreases by ca. 80%, from 500 kW kg⁻¹ to 100 kW kg⁻¹ as the electrode loading steps from one order of magnitude (25 to 250 μg cm⁻²).³⁰ Such critical dependence of performance with the electrode loading is ascribed to poor ionic “refuelling” within the porosity of dense electrodes. Second, all these works refer to covalent functionalization of carbon substrates. Such a strategy may not be, however, the most appropriate for power applications because of the potential adverse influence of covalent functionalization on the electrical properties of the conducting substrate. Indeed, covalent functionalizations or oxidation of carbon substrates results in formation of sp³ defects that lowers the electronic conductivity by one to several order of magnitudes.^33–37 This causes authors to resort to post-annealing treatments under reducing atmosphere.³⁰ Moreover, electronic and ionic percolating networks can be damaged by molecules blocking either electron transport in-between grafted carbon aggregates and/or ion diffusion within the resulting decreased porosity of the electrode.³⁸ Alternative approaches were also proposed by Nishide's group. Instead of using carbon powders as the substrates to be functionalized, polymer backbones were grafted with electroactive molecules such as nitroxyl radicals.³⁹

Moreover, from the industrial point of view, preparation of practical electrodes for electrochemical storage systems such as Li batteries or pseudo-capacitive electrochemical capacitors, result from several benchmarking processes including mixing steps (redox material with one or several polymers and one or several conductive agents) and electrode casting. Although being time consuming, these steps are essential for maximizing the storage performance because they allow for optimization of the charge and mass transports within the electrode.⁴⁰

Based on these considerations, it would be therefore of particular interest to propose new strategies according to which the redox material would not only self incorporate into the electrode but would also form optimized percolating electrical contacts without damaging the conduction properties of the substrate.

In this work we propose a new concept that aims at addressing these issues. It is based on self- and non-disruptive redox functionalization of carbon-containing composite electrodes during electrochemical cycling or during the calendar life by an organic redox-active material that is contained in the electrolyte. The latter is a pyrene derivative for which self adsorption on sp² domains of the electrode is thermodynamically driven⁴¹ and results in ideal electrical contacts. Indeed, molecular functionalization of carbon substrates by non-covalent interactions, typically π–π interactions, with aromatic ring units such as pyrene molecules, operates without detrimental effects to conduction properties.^41–43 The use of pyrene units for the anchoring of redox groups on a graphite substrate has been investigated for electroanalysis purposes.⁴⁴ Moreover, pyrene molecules have been reported to electro-oligomerize upon oxidation with the concomitant appearance of a redox-active oligomer.⁴⁵

Although electrodes of low surface area have been used (∼170 m² g_electrode⁻¹), we demonstrate that our strategy allows for simultaneously high energy and power performance using practical carbon fiber-containing electrodes of 10 mg cm⁻² without additional benchmarking steps. Moreover, although non-covalent interactions are involved, functionalized electrodes show an outstanding life cycle of at least 60 000 charge/discharge cycles with negligible capacity loss and side reactions.

2. Experimental

As a proof of concept we designed a model compound MM where two redox centers, a pyrene unit and a ferrocene⁴⁶ unit, were connected via a 1,2,3-triazole core which was generated by click chemistry.⁴⁷ The synthesis of compound MM is described in Scheme 1. Reaction between commercially available 4-(pyren-1-yl) butanoic acid with thionyl chloride led to the corresponding acyl chloride. This intermediate was rapidly engaged in an amidation reaction with 4-azidoaniline hydrochloride in the presence of triethylamine affording the compound 1 referred to as RN₃, in good yield (91%). Then, a Huisgen 1,3-dipolar cycloaddition between the azido derivative 1 and ethynylferrocene gave the target compound MM in 76% yield. Synthetic procedures and analytical characterizations of these molecules including ¹H NMR, mass spectrometry, IR and UV-Vis spectroscopy, are reported in the ESI.†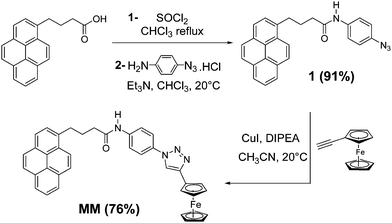

Scheme 1 Synthesis of MM (DIPEA stands for N,N-diisopropylethylamine). Compound 1 is referred to as RN₃.

2.1 Physical characterizations

Elemental analyses were performed by ICP at Service Central d'Analyse–CNRS, Vernaison, France.

¹H NMR spectra were recorded on a spectrometer operating at 500.13 MHz. Chemical shifts are given in ppm (relative to TMS) and coupling constants (J) in Hz.

Matrix Assisted Laser Desorption/Ionization was performed on a MALDI-TOF MS BIFLEX III Bruker Daltonics spectrometer using dithranol as matrix. Electrospray ionization (ESI) mass spectra were recorded on a JMS Jeol 700 spectrometer.

UV-Vis optical data were recorded with a Perkin Elmer Lambda 1050. Concentrations of MM in the electrolyte upon different immersion times of CF electrodes were deduced from the intensity of the absorption band at 343 nm (see ESI for corresponding spectra†).

Masses of immersed electrodes in the electrolyte were determined after rinsing with DMC and drying at room temperature under primary vacuum.

BET surface area analyses were performed with a Micromeritics ASAP 2010 apparatus using nitrogen gas.

Fourier transform infrared (FTIR) spectroscopy spectra were collected with a Brucker Vertex 70 in ATR mode.

X-ray photoelectron spectroscopy (XPS) data have been collected using a Kratos Axis Ultra spectrometer. The X-ray source is Al K working at 1486.6 eV and using a spot size of 0.7 × 0.3 mm². Semi-quantitative XPS analysis has been performed using a pseudo-Voigt function constrained by full width at half-maximum (FWHM) ranges typical of each element and all spectra are calibrated taking C(sp²) as a reference binding energy of 284.5 eV.

2.2 Electrochemical cell preparation and standard cycling protocol

Electrochemical tests were evaluated at 22 °C and monitored by a voltammetric potentiostat (VMP-Biologic SA, Claix, France) in voltammetric mode. All voltages given in the text are reported vs. Li⁺/Li⁰. According to a standard protocol, cycling was performed within a 2–4.4 V potential range in a three electrode cell. Counter and reference electrodes were Li⁰. Working electrodes were constituted of carbon fibers (VGCF-X from Showa Denko), which were hand mixed with 5% of PTFE and pressed at 6 tons cm⁻² on a stainless steel grid. Unless specified, the electrolyte was obtained upon dissolution of MM at 3.10⁻⁴ mol L⁻¹, in LiPF₆-EC/DMC 1M electrolyte (Novolyte, LP30). The obtained electrolyte is referred to as MM-electrolyte. For specific experiments however, RN₃ was substituted for MM in the electrolyte. The corresponding electrolyte is referred to as RN₃-electrolyte. Gravimetric capacity, energy and power performance were calculated per mass of the whole composite electrode. Gravimetric energy density was estimated by multiplying gravimetric capacity by the average potential whereas gravimetric power density was derived by dividing gravimetric energy density by the discharge time. A 1 C rate refers to discharge in 1 h.

3. Results

3.1 Quantification of the capacity enhancement resulting from redox grafting

The strategy that consists of grafting redox molecules onto the surface developed by a purely capacitive electrode leads to a theoretical gravimetric capacity that depends on the extent of such a surface, the number of exchanged electrons per molecular weight of the molecule and the molecular surface density. The gravimetric capacity recovered from such a composite electrode is:

Q_electrode (mAh g⁻¹) = x_SQ_dl (mAh g⁻¹) + x_MMQ_fara (mAh g⁻¹) (1)

where x_S is the weight ratio of the substrate, x_MM that of grafted molecules, Q_dl is the gravimetric capacity resulting from double layer ion adsorption on this substrate and Q_fara the faradic storage capacity associated with the redox centers of grafted molecules. x_S and x_MM equal:where S represents the electroactive surface for ion double layer adsorption, Γ the surface density of grafted molecules of molecular weight M_w. We note that the surface S is approximated as remaining constant during functionalization of the electrode. This hypothesis agrees with results discussed in the section 3.5.

Q _dl can be calculated from:

Q_dl = C_dl (F m⁻²) × ΔU (V) × S (m² g⁻¹) (4)

where C_dl is the double layer capacitance of the substrate and ΔU is the potential range. Therefore, taking a mean value for double layer capacitance of carbon black (C_dl ≈ 0.1 F m⁻²)³, eqn (4) can be written as:where n_e- is the number of electrons exchanged by a redox molecule.

Accordingly, the faradic contribution is enhanced by increasing S, Γ and n_e- and by decreasing M_w, with the most impactful parameter being n_e-. The dependence of Q_electrode on S and Γ is illustrated in Fig. 1a in a potential range ΔU = 2.4 V in the case of the model molecule MM used in this study (n_e- = 3.3 and M_w = 613.15 g mol⁻¹, n_e-/M_w = 1/185.8 mol g⁻¹). For S < 2000 m² g⁻¹, Q_electrode increases with Γ. Beyond 2000 m² g⁻¹ however, the strategy becomes inefficient as Q_electrode follows an opposite trend. Indeed, at this stage the molecular mass impacts the capacitive part of the gravimetric capacity as the substrate weight fraction decreases. This effect is postponed to higher S as the ratio n_e-/M_w increases. Calculations show that in this potential range, the minimum n_e-/M_w ratio from which redox functionalization of a substrate benefits to the overall capacity whatever S (0 < S < 2400) and Γ (0 < Γ< 10⁻⁹ mol cm⁻²) are, is n_e-/M_w = 1/166.6 mol g⁻¹. In the case of MM, the capacity gain (%) vs. the blank un-functionalized electrode shows a maximum as Γ increases in the vicinity of 400–500 m² g⁻¹ (Fig. 1b). This highlights what S value should be targeted in order for this strategy to be the most efficient.

Fig. 1 (a) Overall theoretical gravimetric capacity expected for an electrode constituted by 5 wt% of a binder and 95 wt% of a redox-functionalized substrate with n_e- = 3.3, M_w = 613.15 g mol⁻¹ cycling in a potential range ΔU = 2.4 V, and (b) corresponding capacity gain vs. the un-functionalized electrode.

3.2 Validation of the self activation process

Validation of carbon fiber (referred to as CF) self functionalization by RN₃ and MM were achieved upon immersion of CF for two days in RN₃- and MM-electrolyte respectively. The obtained products are referred to as CF-RN₃ and CF-MM respectively. Corresponding XPS spectra are shown in Fig. 2.

Fig. 2 XPS N 1s core spectra of (a) CF-RN₃, (b) CF-MM and (c) Fe 2p core spectrum of CF-MM, upon immersion for two days in the corresponding RN₃- or MM-electrolyte.

N 1s and Fe 2p core peaks clearly show that even though drastic washing using sonification has been applied to grafted samples, RN₃ and MM are strongly anchored onto the CF surface. Indeed, in the case of CF-RN₃, the azido group is detected at approx. 404 eV (0.09%) and 401 eV (0.17%) with a 1 : 2 atomic ratio respectively.⁴⁸ The latter are replaced by the triazole peak at approx. 400 eV (1.03%) for CF-MM.⁴⁹ Moreover, the Fe 2p core spectrum shows two additional peaks in the case of CF-MM, located at approx. 708 eV and 721 eV which correspond to 0.37% ferrocene unit,⁵⁰ and therefore to a Fe/N ratio of 0.36% that is close to the theoretical one for MM (0.33%).

3.3 CF-MM multi-redox activity, determination of n_e-

The structure of the model molecule MM has been designed to evaluate the possibility of increasing the n_e- parameter by multi-redox activity.⁵¹ Indeed, MM is derived from pyrene and ferrocene units both of which are electroactive. In addition, ferrocene is an excellent redox probe thanks to its well-known chemistry, high stability and standard monoelectronic activity (n_e- = 1). Comparison of CV curves obtained for CF-MM and CF-RN₃ are reported in Fig. 3 at 5 mV s⁻¹ in LP30 upon two days immersion in MM- and RN₃-electrolyte respectively, along with that of a blank electrode made of raw CF (referred to as CF-Raw). Three cycles were performed for each potential range but for the sake of clarity, only relevant cycles are shown. Faradic capacities over the whole potential range (referred to as Q_faraoverall) have been determined vs. the purely capacitive blank electrode, CF-Raw. Determination of the capacity associated with specific faradic peaks has been performed from peak fitting using the EC-lab software. Results are gathered in Table 1 for peak 1 (for peak 2 see ESI,† Table S1) along with the n_e− parameter and the structural unit (redox center) they are associated with.

Fig. 3 Voltammetry of CF-MM, CF-RN₃ and CF-Raw scanned at 5 mV s⁻¹. Cycle A between 2.8–3.8 V, cycle B between 2.8–4.4 V, cycle C between 2.8–3.8 V after three cycles between 2.0–3.8 V, and cycle D between 2.0–4.4 V.

Table 1 Faradic capacity of CF-MM along with involved redox centers vs. the potential range as obtained from CV at 5 mV s⁻¹. Fc stands for ferrocene/ferrocinium unit

	Capacity of peak 1 (mAh g^−1)	Q faraoverall (CF-MM) on discharge (mAh g^−1)	n e−	Redox center
Cycle A, 2.8–3.8 V	3.1	3.1	1	Fc
Cycle B, 2.8–4.4 V	3.1	7.2	2.3	Fc + oligopyrene
Cycle C, 2.8–3.8 V (after 2–3.8V)	2.8	3.0	1	Fc
Cycle D, 2.0–4.4 V	3.1	10.4	3.3	Fc + oligopyrene

---

Faradic activity only occurs for CF-MM during cycle A between 2.8 and 3.8 V (Fig. 3). The latter is therefore ascribed to the ferrocene/ferrocinium unit (Fc) (peak 1-1′) and shows a 3.1 mAh g⁻¹ capacity split into two 1/3–2/3 peaks. Although dedicated investigations are required to understand this splitting, it is worthwhile recalling that physical characterizations of MM (see ESI†) indicate a single isomer was obtained. Therefore we believe this effect to originate from the peculiar stacking arrangement of MM at the surface of CF. Increasing the potential range to 4.4 V (cycle B) results in a significant enhancement of the discharged capacity up to 7.2 mAh g⁻¹ along with concomitant modifications of CV profiles. This capacity corresponds to n_e- = 2.3. We note more particularly the fading anodic peak 2, above 4 V, which has been reported for pyrene oligomerization^45,52 through the occurrence of one-electron pyrene radicals [Pyr]^∘+. We note however, that in contrast to classical electropolymerization, there is no molecule in the electrolyte. This process is associated with already π-stacked species and is therefore 2D. It is ascribed to part of the redox activity of the resulting pyrene oligomer which is known to be associated with a two-electron exchange per dimer.⁵³ In comparison to the low and flat double layer current of the blank electrode (see CF-Raw cycle B, Fig. 3), the other part appears broadly distributed over the whole potential range. The reversible peak centred at 3.5 V on discharge (3.1 mAh g⁻¹) is ascribed to the ferrocene/ferrocinium (Fc) couple that shows as a single peak (no split) in this potential range. As a matter of fact, upon reducing the lower voltage limit to 2 V (2.0–3.8 V) for three cycles (not shown) and by cycling again between 2.8–3.8 V (cycle C), the initial split profile is retrieved along with nearly the same capacity (2.8 mAh g⁻¹) than initially (3.1 mAh g⁻¹). Interestingly, this result demonstrates that the ferrocene redox activity is not altered upon pyrene oligomerization. Finally the maximum faradic capacity is obtained during cycle D between 2 and 4.4 V (10.4 mAh g⁻¹), that corresponds to approx. 1.5 times that of the ferrocene/ferrocinium (Fc) redox probe (1e-) and oligopyrene (1e-) together. Although this point requires more experiments that are out of the scope of the present study, additional redox centers should therefore be considered. We note that the C=O amide bond is unlikely to participate to the redox activity because it can not be stabilized by delocalization.³¹ Nevertheless, results demonstrate the multi-redox capability of CF-MM along with n_e- close to 3.3 in the 2–4.4 V potential range. We note at this point that further increasing the potential range to 2–4.5 V or 1.5–4.4 V results in an increase of n_e- to 3.5 and 5 respectively but with a significant alteration of the cyclability of the system. Optimization of the cyclability within these two potential ranges was not investigated any further in this work.

3.4 Determination and tuning of molecular surface density, role of MM-electrolyte

As shown by eqn (5), for S < 2000 m² g⁻¹, capacity performance of the actual system increases with the extrinsic parameter Γ, which is a measure of the surface density of MM. Determination of Γ was first performed for different immersion times of the electrode in MM-electrolyte. Two complementary routes were investigated; from the extent of the purely faradic capacity, measured by voltammetry at 5 mV s⁻¹, and from the corresponding concentration variation of MM-electrolyte, by UV spectroscopy (see ESI for details and corresponding spectra†). Results are reported in Fig. 4. Error bars were evaluated by repeating each experiment twice. From both techniques, results show that during immersion in MM-electrolyte, surface saturation occurs for Γ_MM ∼ 8 × 10⁻¹¹ mol cm⁻² (6.8 wt% of MMvs. the overall electrode) within ∼120 h. All anchored molecules are therefore redox-active at a 5 mV s⁻¹ scanning rate. Final surface density of MM was also checked by determination of the weight variation of the dried electrode before and upon cycling (see experimental section 2.1 for details). The latter comes to Γ_MM ∼ 1 × 10⁻¹⁰ mol cm⁻² (8.8 wt%) which is in fair agreement with the previous value given the fact that electrolyte salt can be trapped in the molecular layer.

Fig. 4 Evolution of the molecular surface coverage, Γ, according to different immersion times of CF electrodes in MM-electrolyte. Data were obtained, either ex situ, (1) by UV spectroscopy and (2) by voltammetry at 5 mV s⁻¹ in LP30, during cycling in MM-electrolyte, by voltammetry at 5 mV s⁻¹, (3) between 2.8 V and 3.7 V and (4) between 2 V and 4.4 V.

Determination of Γ was also derived from the purely faradic activity obtained during cycling CF in MM-electrolyte at 5 mV s⁻¹ for different potential ranges. Results provided in Fig. 4 between 2.8 V and 3.7 V, show that saturation of the surface (Γ_MM ∼ 8 × 10⁻¹¹ mol cm⁻²) occurs similarly, although somewhat faster, to that happening upon simple immersion. The driving force for MM anchoring is associated with π–π interactions of the pyrene unit with CF. Surface saturation therefore presumably occurs due to steric hindrance between MM molecules with concomitant limitation of the faradic capacity. However, as inferred from Fig. 3, when the charge limit is shifted to 4.4 V, pyrene oligomerization is favored. The feasibility to tune Γ was therefore explored by cycling CF in MM-electrolyte within a 2.0–4.4 V range where both pyrene chemisorption and oligomerization processes are expected. Results provided in Fig. 4, show that in this condition, Γ can be more than doubled up to 1.7 × 10⁻¹⁰ mol cm⁻². We note that upon rinsing with LP30 and transferring the electrode in LP30, the same capacity was measured which demonstrates that additional capacity only comes from anchored molecules. We have therefore shown that owing to spontaneous functionalization of the electrode and possible electro-oligomerization, the use of MM-electrolyte allows a simple and controlled way to tune Γ at the surface of composite electrodes.

3.5 Electrochemical performance

Electrochemical performance was investigated on cycling electrodes of 10 mg cm⁻² loading in MM-electrolyte in the 2–4.4 V range.

Prior to cycling CF electrodes in MM-electrolyte, the pristine response of the electrode was evaluated in LP30 at 100 mV s⁻¹ in a 2.0–4.4 V range. In this case, the discharge capacity of the electrode corresponds to the double layer capacitance, referred to as Q_dl. It equals 12 mAh g_substrate⁻¹ (19 F g_substrate⁻¹) at 100 mV s⁻¹. Taking an average value of Q_dl = 10 μF cm⁻²,³ the active surface area of the electrode is approx. 170 m² g_electrode⁻¹ which is in fair agreement with that derived from the BET surface area of powder CF (245 m² g⁻¹) given the fact the electrode has been densified at 6 T cm⁻² (see experimental section for details) and that all pores measured from the BET method are not accessible to electrolyte ions. As soon as CF is transferred into MM-electrolyte, the capacity starts increasing and reaches 36 mAh g_substrate⁻¹ (57 F g_substrate⁻¹) after 3850 cycles at 100 mV s⁻¹ (150 C rate) (Fig. 5a). This increase of capacity is associated with the occurrence of two growing waves at 3.45 V and 3.55 V on discharge and charge respectively that corresponds to the faradic component of the capacity (Fig. 5b). The latter are much broader than those observed at 5 mV s⁻¹ in Fig. 3 due to kinetic effect. We note that the value of the capacitive current in the vicinity of 2.5 V on charge remains nearly unchanged (∼1.2 A g_substrate⁻¹) which indicates that the extent of the double layer adsorption mechanism is not decreased during MM anchoring. The same remark holds for the slope of I vs. E in this region that remains unchanged, indicating the electronic conductivity of the electrode is not significantly altered on grafting. Gravimetric energy and power performance have been evaluated by increasing the cycling rate from 5 mV s⁻¹ to 1 V s⁻¹. The mass of anchored molecules was derived from voltammetric cycles at 5 mV s⁻¹. At this stage Γ ∼ 1.6 × 10⁻¹⁰ mol cm⁻² and MM corresponds to 16 wt% of the whole electrode. The corresponding Ragone representation is reported in Fig. 6. Accordingly, self activated CF-MM electrodes of 10 mg cm⁻² can deliver up to 128 Wh kg_electrode⁻¹ at a power density of 1.9 kW kg⁻¹ and still 87 Wh kg⁻¹ at 130 kW kg_electrode⁻¹. These results represent very interesting performance considering the relatively high mass loading (10 mg m⁻²) of the electrode. It is clear that more efficient molecules with higher n_e-/M_w that are currently evaluated as well as substrates with higher S will benefit from this strategy.

Fig. 5 (a) Evolution of the capacity during cycling of a CF composite electrode in MM-electrolyte at 100 mV s⁻¹ within 2.0–4.4 V and (b) corresponding voltammograms. The inset of Fig. 5a relates to the cycling life of a CF-MM electrode obtained upon immersion in MM-electrolyte for 10 days. Oscillations correspond to periods of 12 h and are therefore associated with day/night temperature variations.

Fig. 6 Ragone plot obtained for CF-Raw in LP30 and CF-MM in MM-electrolyte at Γ ∼ 1.6 × 10⁻¹⁰ mol cm⁻².

Cycle life of CF-MM obtained upon immersion in MM-electrolyte for 10 days has been evaluated at 100 mV s⁻¹ in the 2.0–4.4 V range. The corresponding curve which is reported in the inset of Fig. 5a shows that 60 000 cycles can be reached with negligible capacity loss. Accordingly, despite the fact that MM is anchored by non-covalent interactions, this system is surprisingly robust. Moreover, we note that the coulombic efficiency remains very close to 100% all along the cycling test, which indicates irreversible side reactions are negligible.

Conclusions

A new concept that enhances the energy and/or power densities of electrochemical storage systems without a benchmarking requirement is shown. Demonstration is made in the present paper for supercapacitor electrodes. From a general perspective, our finding is based on a multi-redox molecule that can be dissolved in the electrolyte and that can self anchor, during charge/discharge cycling or during calendar life, onto sp² domains of a composite electrode without formation of impeding sp³ defects. Indeed, such a molecule is characterized by a pyrene chemical unit that can chemisorb at the surface of the substrate owing to thermodynamically driven π-stacking interactions.

Illustration of the concept is given for a model molecule constituted of an amide–pyrene unit that has been connected to a ferrocene group by Huisgen click chemistry. We demonstrate that when a composite electrode is cycled in presence of the corresponding electrolyte, its energy and power performance dramatically increases as pyrene π-stacks at the electrode surface. Moreover, based on rationalization of the gravimetric capacity of such systems, we showed that because electrochemical performance depends on the molecular coverage of the electrode, it was of the highest interest to be able to go beyond the thermodynamic saturation limit. This key issue was addressed by taking advantage of the possible additional electro-oligomerization of pyrene units. Indeed, although electrodes of low surface area have been used (∼170 m² g_electrode⁻¹), the use of MM-electrolyte allows reaching unprecedented simultaneous high energy, 85 Wh kg⁻¹ (0.5 mWh m⁻²_electrode), and high power, 130 kW kg⁻¹ (0.76 W m⁻²_electrode), although practical carbon fiber containing electrodes of high loading (10 mg cm⁻²) are used. Such an electrode can deliver up to 130 Wh kg_electrode⁻¹ (0.76 mWh m⁻²_electrode) at a low rate (discharge at 15 C).

Moreover, outstanding cycle life of 60 000 cycles can be obtained with negligible capacity loss, therefore highlighting the robustness of the systems despite the fact that non-covalent interactions are involved.

It is clear that better energy and power performance can easily be achieved by molecular engineering and upon increasing the surface extent of the electrode. This concept can be applied in principle to any type of electrode (supercap, battery, semi-solid flow cell, etc.). Our findings therefore open up new directions for future simultaneous high power and high energy practical rechargeable systems together with very simple benchmarking.

Acknowledgements

Financial funding from CNRS, Université de Nantes, and the ANR program n° ANR-09-STOCK-E-02-01 is acknowledged. JG is thankfull to M. Armand (LRCS, Amiens), P. Poizot (LRCS, Amiens) and P. Soudan (IMN, Nantes) for fruitful discussions.

References

1. P. A. Johns, M. R. Roberts, Y. Wakizaka, J. H. Sanders and J. R. Owen, Electrochem. Commun., 2009, 11, 2089.
2. C. Fongy, A. C. Gaillot, S. Jouanneau, D. Guyomard and B. Lestriez, J. Electrochem. Soc., 2010, 157, A885.
3. B. E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Kluwer, New York, 1999.
4. P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845.
5. C. Delacourt, P. Poizot, S. Levasseur and C. Masquelier, Electrochem. Solid-State Lett., 2006, 9, A352.
6. P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J.-M. Tarascon, Nature, 2000, 407, 496.
7. P. G. Bruce, B. Scrosati and J. M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930.
8. L. F. Nazar, G. Goward, F. Leroux, M. Duncan, H. Huang, T. Kerr and J. Gaubicher, Int. J. Inorg. Mater., 2001, 3, 191.
9. R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123.
10. G. Ceder, abstract KK.4.5, MRS fall meeting, 2010.
11. Y.-M. Chiang, abstract KK.4.10, MRS fall meeting, 2010.
12. X. L. Wu, L. Y. Jiang, F. F. Cao, Y. G. Guo and L. J. Wan, Adv. Mater., 2009, 21, 2710.
13. D. Guy, B. Lestriez and D. Guyomard, Adv. Mater., 2004, 16, 553.
14. S. D. Beattie, D. Larcher, M. Morcrette, B. Simon and J. M. Tarascon, J. Electrochem. Soc., 2008, 155, A158.
15. B. Lestriez, S. Bahri, I. Sandu, L. Roue and D. Guyomard, Electrochem. Commun., 2007, 9, 2801.
16. J. H. Lee, U. Paik, V. A. Hackley and Y. M. Choi, J. Electrochem. Soc., 2005, 152, A1763.
17. C. C. Li, J. T. Lee and X. W. Peng, J. Electrochem. Soc., 2006, 153, A809.
18. W. Porcher, B. Lestriez, S. Jouanneau and D. Guyomard, J. Electrochem. Soc., 2009, 156, A133.
19. R. Krishnan, T. M. Lu and N. Koratkar, Nano Lett., 2011, 11, 377.
20. L. Baggetto, R. Niessen, F. Roozeboom and P. Notten, Adv. Funct. Mater., 2008, 18, 1057.
21. B. Kang and G. Ceder, Nature, 2009, 458, 190.
22. K. Kalinathan, D. P. Desroches, X. Liu and P. G. Pickup, J. Power Sources, 2008, 181, 182.
23. R. D. L. Smith and P. G. Pickup, Electrochim. Acta, 2009, 54, 2305.
24. R. D. L. Smith and P.F G. Pickup, Electrochem. Commun., 2009, 11, 10.
25. G. Pognon, T. Brousse, L. Demarconnay and D. Bélanger, J. Power Sources, 2011, 196, 4117.
26. G. Pognon, T. Brousse and D. Bélanger, Carbon, 2011, 49, 1348.
27. Z. Algharaibeh and P. G. Pickup, Electrochem. Commun., 2011, 13, 147.
28. Z. Algharaibeh, X. Liu and P. G. Pickup, J. Power Sources, 2009, 187, 640.
29. D. Pech, D. Guay, T. Brousse and D. Bélanger, Electrochem. Solid-State Lett., 2008, 11, A202.
30. S. W. Lee, N. Yabuuchi, G. M. Gallant, S. Chen, B. S. Kim, P. T. Hammond and Y. Shao-Horn, Nat. Nanotechnol., 2010, 5, 531.
31. H. Chen, M. Armand, G. Demailly, F. Dolhem, P. Poizot and J. M. Tarascon, ChemSusChem, 2008, 1, 348.
32. B. Generio, K. Pirnat, R. Cerc-Korosec, R. Dominko and M. Gaberscek, Angew. Chem., Int. Ed, 2010, 49, 1.
33. C. Klinke, J. B. Hannon, A. Afzali and P. Avouris, Nano Lett., 2006, 6, 906.
34. L. S. Woo, B. S. Kim, S. Chen, Y. Shao-Horn and P. T. Hammond, J. Am. Chem. Soc., 2009, 131, 671.
35. D. Pantea, H. Darmstadt, S. Kaliaguine, L. Sümmchen and C. Roy, Carbon, 2001, 39, 1147.
36. K. Balasubramanian, M. Friedrich, C. Jiang, Y. Fan, M. Burghard and K. Kern, Adv. Mater., 2003, 15, 1515.
37. L. Cai, J. L. Bahr, Y. Yao and J. M. Tour, Chem. Mater., 2002, 14, 4235.
38. M. Toupin and D. Bélanger, Langmuir, 2008, 24, 1910.
39. K. Nakahara, K. Oyaizu and H. Nishide, Chem. Lett., 2011, 40, 222.
40. B. Lestriez, C. R. Chim., 2010, 13, 1341.
41. C. Ehli, G. M. A. Rahman, N. Jux, D. Balbinot, D. M. Guldi, F. Paolucci, M. Marcaccio, D. Paolucci, M. Melle-Franco, F. Zerbetto, S. Campidelli and M. Prato, J. Am. Chem. Soc., 2006, 128, 11222.
42. D. I. Schuster and J. D. Megiatto Jr, Nat. Chem., 2009, 1, 182.
43. C. Ehli, C. Oelsner, D. M. Guldi, A. Mateo-Alonso, M. Prato, C. Schmidt, C. Backes, F. Hauke and A. Hirsch, Nat. Chem., 2009, 1, 243.
44. H. Jaegfeldt, T. Kuwana and G. Johansson, J. Am. Chem. Soc., 1983, 105, 1805.
45. R. J. Waltman and J. Bargon, Can. J. Chem., 1986, 64, 76.
46. T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039.
47. C. W. Tornoe, C. Christensen and M. Meldal, J. Org. Chem., 2002, 67, 3057.
48. P. Cao, K. Xu and J. R. Heath, J. Am. Chem. Soc., 2008, 130, 14910.
49. A. Devadoss and C. E. D. Chidsey, J. Am. Chem. Soc., 2007, 129, 5370.
50. C. M. Woodbridge, D. L. Pugmire, R. C. Johnson, N. M. Boag and M. A. Langell, J. Phys. Chem. B, 2000, 104, 3085.
51. D. Canevet, A. P. del Pino, D. B. Amabilino and M. Sallé, J. Mater. Chem., 2011, 21, 1428.
52. S. Cosnier, R. S. Marks, J.-P. Lellouche, K. Perie, D. Fologea and S. Szunerits, Electroanalysis, 2000, 12, 1107.
53. K. C. Honeychurch, J. P. Hart and N. Kirsch, Electrochim. Acta, 2004, 49, 1141.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis of RN₃ and MM along with corresponding ¹H NMR spectra (Fig. S1–S6) and UV-Visible spectra of MM–electrolyte upon funtionalization of CF electrode for different periods of time (Fig. S7). See DOI: 10.1039/c1ee02490f

---