First-principles kinetic modeling in heterogeneous catalysis: an industrial perspective on best-practice, gaps and needs
Maarten K.
Sabbe
a,
Marie-Françoise
Reyniers
a and
Karsten
Reuter
*b
aLaboratory for Chemical Technology, Department of Chemical Engineering (EA12), Ghent University, Technologiepark 918 – 9052, Zwijnaarde, Belgium. E-mail: mariefrancoise.reyniers@ugent.be; Fax: +32 (0)9 264 4999; Tel: +32 (0)9 264 4516
bDepartment Chemie, Technische Universität München, Lichtenbergstr. 4, D-85747 Garching, Germany. E-mail: karsten.reuter@ch.tum.de; Fax: +49 89 289 13622; Tel: +49 89 289 13616
First published on 25th June 2012
Abstract
Electronic structure calculations have emerged as a key contributor in modern heterogeneous catalysis research, though their application in chemical reaction engineering remains largely limited to academia. This perspective aims at encouraging the judicious use of first-principles kinetic models in industrial settings based on a critical discussion of present-day best practices, identifying existing gaps, and defining where further progress is needed.
1 Introduction
Predictive-quality electronic structure calculations have emerged as a key contributor in modern heterogeneous catalysis research. Next to the dedicated computation of thermostability, spectroscopic signals and reactivity descriptors, they are increasingly used for detailed mechanistic studies that culminate in the formulation of entirely first-principles based microkinetic models,1–5 with often surprisingly good agreement to experimental rates and selectivities.6 While cherished by parts of the community, the application of quantum chemical calculations in chemical engineering and industry is unfortunately still far from optimal. Most likely, this has to do with a lack of awareness of what the current first-principles machinery can really do for “practical” or “real” technological catalysis. Intriguingly, this leads not only to profound skepticism, but also increasingly to unrealistic expectations. In the context of kinetic model development, a natural motivation is for instance the hope for improvement in the predictive capability and range of transferability to other mechanisms when substituting first-principles energetics into existing microkinetic formulations. However, here one must recognize that data fitting makes that many phenomenological models provide a good description of experimental data, even when based on an erroneous mechanism or unrealistic approximations.7 As first-principles kinetic parameters no longer allow for this fitting flexibility, it may well be that the “improvement” they bring first means deterioration in the performance of the model. Nourished by possibly existing resentments, this may then readily be blamed on an insufficient accuracy of the underlying quantum engine, e.g. the employed density-functional theory (DFT) exchange-correlation (xc) functional. Rather than realizing the potential of first-principles methods to allow identifying possible errors in the catalytic mechanism or model assumptions of the existing kinetic model,8 the deterioration of the model performance would only serve to confirm the preconceptions.Of course, one has to recognize that an insufficient accuracy of the quantum engine, or e.g. an inappropriate catalyst model, might indeed equally well be the reason for a disagreement to experimental data. Identifying which of the situations applies is admittedly not a simple task. The minimum it requires, however, is a critical understanding of the first-principles kinetic modeling methodology, of its present-day capabilities and challenges. This concerns not only electronic structure theory and microkinetic modeling techniques, for which many excellent accounts exist in the literature.9–12 Rather, it also concerns the specific implementation of the first-principles methodology in the context of heterogeneous catalytic reaction engineering.13,14 Here, next to the obvious accuracy issue, crucial aspects are (i) the modeling of the catalyst, including a proper representation of the reactive surface present in situ; (ii) the determination of accurate rate constants, (iii) the treatment of coverage effects (both at the electronic structure and mesoscopic level) to arrive at intrinsic reaction rates, and (iv) the integration of the first-principles kinetics into particle- or reactor-level models to arrive at effective reaction rates. These crucial aspects are rarely concisely covered in one text and in a style accessible to the practitioner. In this perspective, we therefore describe our views on the state-of-the-art and best practices in the field. Our motivation thereby is twofold. On the one hand the clear aim is to encourage the use of first-principles kinetic models in industrial settings. On the other hand, a critical discussion of present-day best practices inevitably identifies existing gaps and as such also provides a look forward to establish where further progress is needed.
2 Modeling the catalyst
Classical kinetic modeling of heterogeneous catalysis commonly assumes the existence of a single type of abstract “active sites”, uniformly distributed over the catalyst surface. Clearly, this is a profound approximation, far off from reality with its specific surface structure, site geometry, bonding pattern, dopants and additives, as well as edge and support effects. Furthermore often multiple reactive sites are in fact available, of which typically only the most dominant one is considered as the “active site”.15 It is exactly this straddle that causes much confusion and misunderstandings between experimental-based modelers and (quantitative) theory-based modelers: the former prefer to work at an abstract level, little interested in the exact nature of the site as long as the model fits the data, while the latter require a precise atomic-scale formulation of the active site structure, including all effects that contribute to its energetics.As illustrated in Fig. 1 there are currently three prevailing first-principles approaches to model the catalyst at the atomic level: (i) cluster approaches, (ii) embedded cluster approaches, and (iii) periodic models.16 They all have their merits and flaws, and the choice is mainly made depending on the catalyst in question – though in a practical, industrial context, a limited availability of computational resources is sometimes erroneously invoked to go for the computationally cheapest choice. Cluster approaches are fast, but critically depend in their accuracy on absolute size and the chosen bond saturation at the cluster periphery (e.g. saturation with H atoms). They are generally inadequate to model any kind of extended metal or ionic surface, but are useful for covalently bound surfaces (including amorphous structures) and obviously perfectly suited to describe finite atomic clusters of interest in nanocatalysis.17,18 Embedding the cluster into either arrays of mere point charges or atomistic potentials, often referred to as QM/MM, mitigates the edge effects and is a very efficient approach to ideal and defective ionic surfaces, as well as supported finite clusters.19 Periodic models computed in so-called supercell geometries, cf.Fig. 1, effectively mimic infinitely extended surfaces and are the only approach that reliably captures delocalized metallic bonding. They are thus the unparalleled best practice for metal surface calculations, properly representing a facet of a larger nanoparticle where facet edge effects become negligible. Due to the inherent periodic images (vide infra), modeling of lower adsorbate coverages, point defects or semi-crystalline materials requires larger surface unit-cells, i.e. increased lateral periodicities, which leads to further steep increases in the anyway comparatively large computational costs. Regardless of which approach is pursued though, it is essential to realize that each contains computational parameters that critically affect the results: the number of atoms in a cluster model, the number of slab layers or the vacuum thickness in periodic models etc. Just as much as with the computational settings (vide infra) it is thus imperative to rigorously check that the property of interest (imagine e.g. an energy difference for an activation energy) is converged with respect to these model parameters.
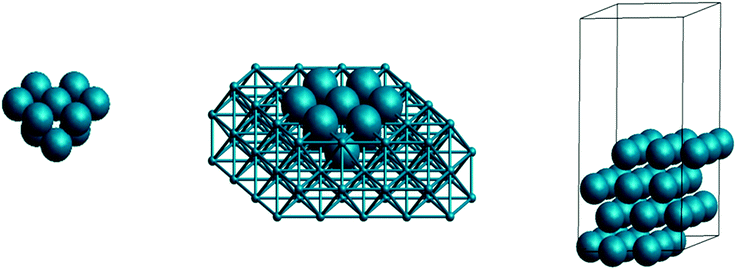 | ||
| Fig. 1 Different catalyst models for a fcc(111) surface: (left) cluster model, (middle) embedded cluster approach, and (right) periodic slab model with unit cell indicated. | ||
Applying these computational approaches it is straightforward to model ideal, ‘perfect’ systems: defect-free (low-index) surfaces, regular structures such as zeolites, or regularly formed nanoparticles with a mono-disperse particle size distribution. However, the actual catalyst under working conditions is often far from these idealizations. In order to properly describe the catalyst, the models should include (i) (point or extended) surface defects, (ii) multifaceted surfaces to include a possible structure sensitivity of the reaction, (iii) support effects on the catalytic phase, (iv) possible spillover effects and catalytically acting supports, and (v) the presence of dopant atoms and additives. Also surface restructuring to the extent of a morphological transition is an important phenomenon. Yet, this can be such a complex function of the reaction conditions that we discuss it separately in the following section. Generally speaking, there are computational approaches to each of these complications. They often require so much additional effort though, that current computational research typically incorporates at best only one of them, to merely illustrate the effects of the phenomenon that is expected to be most relevant for the system under study. As such, we are presently mostly still far away from routine quantitative calculations, which would instead require a model of the active site that mimics the realistic situation as faithfully as possible.
To better assess the current state of the art and the perspectives for future progress let us briefly review the various present-day approaches to address the individual complexities. In principle, the conceptually most straightforward to tackle, albeit at high computational cost, are multifaceted surfaces in the case of structure sensitivity.20 To first order this merely demands repetition of all calculations for differently indexed surfaces corresponding to the facets involved, and later on combining these data at the level of the microkinetic simulations as discussed in Section 7. What is not covered by this relates then already closely to the problem of modeling facet edges, steps or kinks, namely the processes occurring directly at the corresponding undercoordinated atoms or in their vicinity, such as B5 step-edge sites essential in many metal catalyzed processes.20 In cluster approaches both aspects are easily addressed by simply devising structural models that represent the edge, step or kink under study. In supercell geometries this is much harder to achieve and requires at brute force simply large enough lateral surface unit-cells and a zig-zag slab structure, cf.Fig. 2, this way simultaneously exposing the aspired edge, step or kink and complying with the periodic boundary conditions. Somewhat more efficient are calculations of high-index vicinal surfaces, which contain regular arrays of the desired step or kink, separated by terraces of specific width as illustrated in Fig. 2.16 The advantage of these surfaces is that they ideally only contain one defined type of step or kink in always the same local environment, which is not the case in most zig-zag realizations. The central disadvantage of both models is that the extracted properties may be masked by the inherent periodicity, e.g. step–step interactions at decreasing terrace width.21 Since one would precisely try to perform first-principles calculations by employing surface unit-cells that are as small as possible, in order to reduce the computational effort, this periodicity often profoundly affects the results. Exactly the same applies, of course, also to the modeling of individual point defects in periodic boundary models.
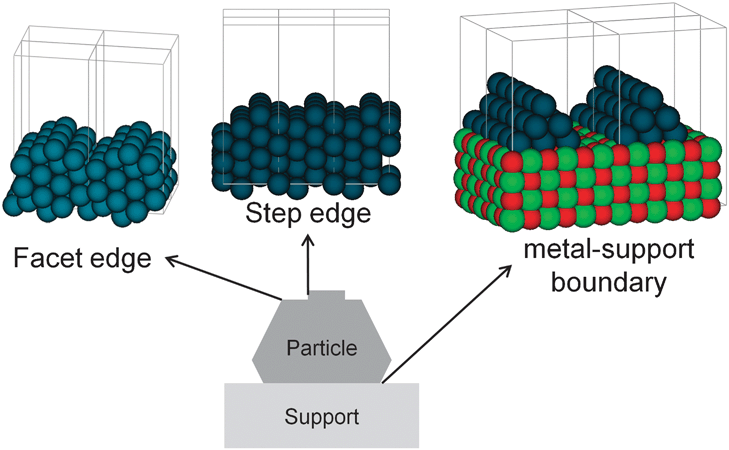 | ||
| Fig. 2 Modeling of more complex surfaces: facet edges, steps and three-phase boundary, shown for an fcc metal: (left) zig-zag slab structure; (middle) high-index surface, here the (211) surface; (right) modeling of the particle-support interface: infinite metal rod on support. | ||
Interaction with the support can strongly affect the bonding properties of catalyst particles due to e.g. charge transfer effects or strain effects in the case of epitaxial particles. The picture is further complicated by a possible coverage dependence of the metal–support interaction, in which the particle responds to molecular adsorption by adapting its geometry and changing its bonding with the underlying oxide support.22 Also spillover effects, i.e. adsorbate diffusion between the support and the particle, can have a significant contribution to the overall activity that surpasses the sum of the individual parts.23 While all this calls for a simultaneous modeling of the catalyst particle and the support (especially for smaller nanometer-scale particles), support effects are at present completely neglected in the vast majority of computational studies. Models that gradually start to integrate support effects rely typically either on fully periodic film formulations, in which several layers of the active phase are deposited on a periodically modeled support,24 or on approaches in which finite clusters are deposited on a periodically modeled support.25–29 The first approach is most interesting from a computational point of view, as it only requires relatively small unit cells. On the other hand, results obtained in this way may be severely affected by the (spurious) strain that is imposed by the lattice mismatch between the active phase and the support, or by a falsified charge transfer due to electrostatic effects between the periodic image cells. The cluster-on-periodic-support approach instead always allows for full relaxation of the catalyst structure, depending on the strength of the particle–support interaction, the adsorbate coverages, or the temperature. The exposure of the support to the fluid phase furthermore allows us to also study adsorption at the support, diffusion of adsorbates to and from it, as well as reactions at the support-cluster interphase. The corresponding DFT calculations on such models have e.g. been performed using static approaches,18 as well as molecular dynamics.30,31 On the down side, the necessity to include a sufficiently wide fringe of support to prevent spurious interactions between the cluster and its periodic images quickly leads to large surface-unit cell models. Out of computational constraints, typically only very small sub-nanometer metal clusters containing below ∼15 atoms were thus hitherto modeled using this approach. As such clusters often have surprisingly different catalytic properties compared to larger nanoparticles,18 an intermediate approach proposed by Hammer and co-workers appears particularly appealing.32,33 Here, the supported nanoparticle is described as an infinite rod, see Fig. 2, allowing to keep a small periodicity in one lateral direction (as in the film approach) and only using a large periodicity in the other lateral direction to explicitly model the finite nanoparticle, support and the support–particle–fluid boundary between the two. The Au rods on a MgO support, as modelled by Hammer and co-workers, result in an almost strainless metal rod, which however does not need to be the case for other oxide–metal combinations.34
Finally dopant materials, additives and remaining precursor material further complicate the picture; even modeling e.g. the traditional Lindlar's Pb-doped Pd hydrogenation catalyst requires a multistep procedure.35 Materials with extremely low dopant concentrations or very complex compositions can often simply not explicitly be modeled yet. This would require very large catalyst models that are currently computationally unfeasible. Notwithstanding, such explicit modeling might also in many cases not be required when considering what effects such dopants or compositional details might actually have on the surface reactions. If they e.g. merely induce elastic strain, then this can be captured by performing calculations at varying lattice constants. If their effect is to fine-tune the Fermi-level, and as such the electron availability, then ab initio thermodynamic approaches can provide a powerful alternative.36 Such approaches would concentrate on faithful representations of the local active site structure and consider e.g. the changing Fermi-level through appropriate electronic reservoirs with which the local site is in equilibrium. This is a very common procedure in semiconductor modeling,37,38 but has not yet been much appreciated in the catalyst modeling community.
This short overview illustrates that it is still a ‘cutting edge’ to include the many factors that may influence catalytic activity in the catalyst model. The key problem is that an effect is either included or neglected; there is no middle way in which an abstraction can be made of a certain effect as is common in parameter-fitting procedures. Therefore, it is of utmost importance to have as accurate an (experimental) view on the precise structure and composition of the catalyst during the reaction as possible. In situ spectroscopy methods are most helpful in this respect,39 explaining the many recent successes of experiment-and-theory-combined studies.40
3 Restructuring of the catalyst surface
In the attempt to minimize their surface energy, catalyst surfaces may restructure in many different ways to adapt to the reaction conditions. Most straightforwardly, this may simply be adsorbate/dopant/additive-induced changes in the top-layer structure of the catalyst. Examples are the hydrogen-induced lifting of the quasi-hexagonal overlayer of fcc(100) surfaces of some late transition metals,41 or the frequent hydroxylation of the surface of oxide catalysts (or oxidic supports).42,43 However, the structural changes may also extend further into the surface fringe. Adatoms on the surface, obtained either from adsorption or from decomposition of adsorbates, may diffuse into the bulk or eventually even induce a phase transition at sufficiently high concentrations. The resulting phase may lead to catalyst poisoning, e.g. sulfide formation on metal catalysts, or form an essential element in the catalyst activity, as e.g. the carbide formation that forms the active phase on Fe Fischer–Tropsch catalysts.44 For composite materials like oxides, hydrides and sulfides the on-going reactions may also (slowly) change the surface composition by consumption of lattice oxygen, hydrogen or sulfur, as e.g. in Mars–Van Krevelen oxidation mechanisms. During the oxidation, not only surface oxygen but also bulk oxygen may be consumed at low oxygen pressures due to the high mobility of lattice oxygen in e.g. CuO and CeO2 crystals.45,46 This may lead to complete phase changes at the surface (into totally or partially reduced states) or at least to significant (disordered) vacancy concentrations. The equivalent of this in metal alloys are (adsorbate-induced) surface segregation phenomena, in which the different types of metal atoms migrate preferentially to and from the surface, leading to substantially changed stoichiometries in the near-surface region.The crucial point in all of this is that the changes are intimately connected to the specific reaction conditions; the catalyst material adapts to them and as such knowledge of the nominal catalyst material and/or surface termination ex situ either before or after time on stream is often of very limited use, if not misleading. Obviously, rather than faithfully representing the nominal catalyst any first-principles catalyst model must instead aim at mimicking as closely as possible the actual structure and composition of the active surface in the reactive environment. This is a rather critical problem, the importance of which can hardly be overstated: Corresponding atomic-scale information about the detailed surface structure from experimental in situ characterization is rarely available, while performing first-principles kinetic calculations on the wrong surface model will simply not provide any adequate insight into the “real” system. Obtaining this information from comprehensive first-principles kinetic models that would explicitly account for the possibility of catalyst restructuring is at present also largely elusive. This would require knowledge of the detailed atomistic mechanism underlying the restructuring, which in particular for surface morphological transformations (even if known to happen) will typically involve an intractable number of elementary processes and correspondingly require first-principles kinetic parameters.
In this situation, next to whatever experimental guidance is available, ab initio thermodynamic considerations have become an invaluable tool to determine the best structural model to be used as basis for ensuing kinetic studies.36,47 The idea behind this approach is to compute the surface free energies of a range of candidate structures as a function of the gas-phase chemical potentials. Identifying the structure by minimizing the surface free energy as the most stable one then allows establishing surface phase diagrams covering the operational range of the catalyst as illustrated in Fig. 3. Hereby, the multi-component reactive environments of catalysis can be accounted for by suitably resorting to so-called “constrained equilibria”, in which the surface is considered in full equilibrium with all gas-phase chemical potentials, while the latter are treated as mutually independent of each other.49,50 The appealing feature of this approach is its computational efficiency. All that is required in a first step are total energies and vibrational free energies of the candidate structures. In many cases even rough estimates of the vibrational free energies may be sufficient,47 while routes for their detailed evaluation also exist.51 One has to clearly recognize though, that the approach is only approximate and may as such only provide rough guidance. Significant errors may arise from the typical neglect of configurational entropy, which above all precludes a reasonable description of phase coexistence,52 and from the neglect of kinetic effects, e.g. when the on-going reactions consume surface species faster than they can be replenished from the gas phase.53 However, probably the largest limitation of the approach arises from the selection of candidate structures itself, as the prevalent formulations of ab initio thermodynamics only allow comparing their relative stabilities. If an important structure is missing in this set of structures that are compared, it will also not show up in the surface phase diagram, potentially providing completely wrong guidance as to the selection of a useful catalyst model.
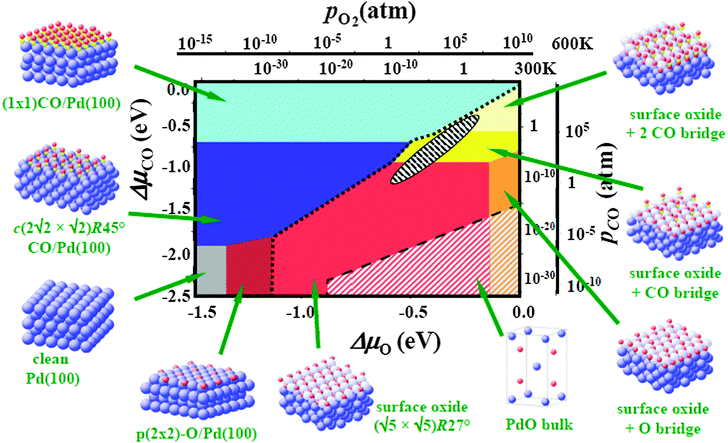 | ||
| Fig. 3 Surface phase diagram for the Pd(100) surface in ‘‘constrained thermodynamic equilibrium’’ with an environment consisting of O2 and CO. The atomic structures underlying the various stable (co-)adsorption phases on Pd(100) and the surface oxide, as well as a thick bulk-like oxide film (indicated by the bulk unit-cell), are also shown (Pd: large blue spheres, O: small red spheres, C: white spheres). Phases involving surface or bulk oxide are to the right bottom of the dotted and dashed line, respectively. The dependence on the chemical potentials of O2 and CO in the gas phase is translated into pressure scales at 300 and 600 K. The black hatched ellipse marks gas phase conditions representative of technological CO oxidation catalysis, i.e., partial pressures of 1 atm and temperatures between 300 and 600 K (adapted from Rogal, Reuter, Scheffler48). | ||
The ab initio thermodynamics approach has also been generalized to treat adsorbate-induced surface segregation in alloys.54–57 If the compositional segregation is restricted to the host lattice, it is even possible to combine this approach with cluster-expansion techniques common in bulk alloy modeling58,59 to explicitly address configurational disorder and entropy, i.e. a temperature-dependent non-uniform surface composition.60 In practice, however, most studies involving such or even more approximate theories completely neglect the effect of a surrounding gas-phase and evaluate the surface segregation profile under vacuum conditions.61 The focus in these works centered in the alloy/materials community is largely only the dependence of the segregation thermodynamics on the bulk alloy reservoir. As adsorbate-induced segregation can substantially change the surface composition in reactive environments, great caution is advised when aiming at transferring such vacuum results obtained for a clean surface to catalysts under working conditions.
In applied work, researchers resort mostly to even much less sophisticated (and accurate) treatments. The composition of alloy nanoparticles is often simply approximated by a core–shell structure, with enrichment of one type of metal atoms in the outer layers, and of the other type in the core. In periodic modeling this is then typically modeled as ‘skin’ or ‘monolayer’ surface alloys, with a uniform surface layer on top of a different substrate, cf.Fig. 4. However, this misses the frequent oscillatory pattern of surface segregation profiles, where the enrichment of one element in the top layer is compensated by a depletion of the same element in the second layer, while the third layer is already close to the bulk composition. Periodically formulated models for this type of segregation usually involve ‘surface sandwich’ structures with a subsurface layer of the minority compound in the alloy, and a homogeneous top and bulk composition, see Fig. 4. Such ‘skin’ or ‘sandwich’ models have the advantage of exposing only a few different types of adsorption sites, i.e. not more than a simple monometallic surface, in contrast to more realistic inhomogeneous structures that involve numerous inequivalent adsorption sites. On the other hand, of the effects that are commonly believed to have a strong influence on the catalytic properties of bimetallic systems,63 they thus completely miss out on any ensemble effects (e.g. blocking of reactions involving nearby ensembles of same active sites) and often also yield only a blurred view of ligand effects (i.e. modifications due to the electronic interaction between the system components). In principle, both ‘skin’ and ‘sandwich’ approaches could be extended to larger surface unit-cells, which would then allow mimicking local motifs involving surface atoms of different alloy species. The rapidly increasing number of inequivalent motifs to be studied makes this a rather tedious task though, which has to date been only rarely undertaken for bimetallics and simple adsorbates.56,57,64 Even less work covers the complex segregation behavior of ternary alloys, and if so it is typically not done at the full quantum mechanical level, but e.g. combines Monte Carlo models with DFT-based modified embedded atom methods.65
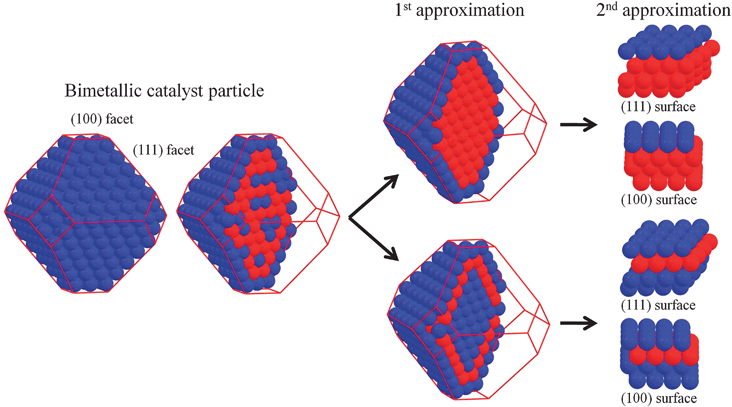 | ||
| Fig. 4 Common model assumptions for using approximated ‘skin’ (upper structures) and ‘surface sandwich’ (lower structure) monolayer bimetallic surfaces (after Menning and Chen62). | ||
4 Obtaining accurate electronic energies
At the core of all first-principles approaches is obviously the quantum mechanical determination of the electronic structure, usually a solution to the time-independent Schödinger equation for the electron–nuclei system. Direct wave-function based approaches, such as Hartree–Fock (HF) and post-HF methods, have a computational cost that grows very rapidly with the number of basis functions, and hence the number of electrons, in the system. The explosion of the computational cost with the size of the system has rendered it to date largely prohibitive to use such methods for heterogeneous catalytic systems. At present essentially all first-principles calculations in the area of heterogeneous catalysis are therefore done with DFT.9,10 DFT starts from a reformulation of the Schrödinger equation in terms of the three-dimensional electron density ρ(r) instead of the high-dimensional wave function without loss of relevant information. Within the DFT formalism, the energy E of the ground state can be expressed as a unique functional of the electron density. The key challenge with this functional is the exchange-correlation functional EXC[ρ(r)], the exact form of which remains unknown. Depending on the approximations made, this leads to the hierarchy of DFT functionals with increasing complexity and computational requirements as shown in the Jacob ladder classification scheme in Fig. 5.66 Constrained by the computational demands imposed in particular by the system sizes inherent to supercell geometries, many of the calculations in heterogeneous catalysis are in fact still performed with the semi-local xc functionals that represent the two lowest rungs in this scheme. While these local-density (LDA) and generalized gradient (GGA) approximation functionals often yield a surprisingly decent account of covalent bonds and geometric structure, they are generally plagued by two big problems: spurious electron delocalization and lack of van der Waals (vdW) interactions.67,68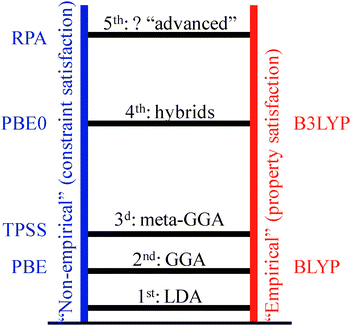 | ||
| Fig. 5 Jacob's ladder of density-functional approximations (after Perdew66). | ||
The former problem arises from an incomplete cancelation of repulsive Coulomb self-interaction contributions by the approximate exchange energy given by the employed functional. The resulting artificial delocalization of the electron density stands behind many of the well-known issues of semi-local DFT like the underestimation of band gaps and reaction barriers, or its inability to describe localized f-electron systems.69 For small gas-phase molecules this error can be substantial, with e.g. the popular PBE GGA-functional overestimating the binding energy of O2 by about 1 eV.70 When interested in the interaction of such molecules with solid surfaces, the best one can then hope for is a large degree of error cancelation. Intriguingly, this isn't as shaky a foundation though as one might think at first glance. With functionals often exhibiting rather systematic errors, for instance an on average always too strong binding of the mentioned PBE functional,71 it is primarily error cancelation that affords the often quoted ∼0.2–0.3 eV (20–30 kJ mol−1) generic uncertainty estimate for reaction energies.6 Nevertheless, infamous examples like the CO puzzle, where standard semi-local functionals even predict the wrong adsorption site at close-packed transition metal surfaces,72–75 underscore that uncritical use of semi-local energetics is ill-advised. This holds equally for the often uncritical mixing of experimental and semi-local data in kinetic models, which inevitably breaks the delicate balance of systematic errors and thus annihilates any hope for error cancelation.
The vdW problem of semi-local DFT arises from the mere fact that functionals that only consider the local density (or in the case of GGA functionals also the density at infinitesimally neighboring distances) can, by construction, not properly account for a fully non-local effect like dispersive interactions between distant fluctuating dipoles.76 For larger organic molecules with highly polarizable conjugated ring systems and molecules in porous media corresponding dispersive contributions to the adsorption energies become a crucial factor. This is e.g. nicely illustrated by benzene bonding to close-packed coinage metal surfaces, which prevalent GGA functionals underestimate by about 0.5 eV due to the lacking vdW interactions.77 For alkane, alkene and alcohol adsorption in zeolites these same functionals typically yield as low adsorption strengths as 0.1–0.2 eV per carbon atom, highlighting that it is in fact vdW interactions that are the dominant factor counteracting destabilization by steric constraints.78–80 Ironically, the large self-interaction error of the LDA functional sometimes mimics an artificial contribution of roughly the same size as the missing vdW component. Aware or unaware that this yields “the right answers for the wrong reason” this has led some applied works to resort to the doubtful approach of using LDA data as a pragmatic solution to the vdW problem.
Recent years have instead also brought considerable and proper fundamental progress to both problems of semi-local DFT. The admixture of exact HF exchange mitigates the self-interaction error in hybrid functionals like B3LYP, cf.Fig. 5.69,81 For molecular and band-gap systems such as organic molecules or simple metal oxides this indeed brings a qualitative improvement, such that corresponding fourth-rung functionals have already become the new standard there. This paradigm change has been particularly facilitated by the fact that the localized basis sets commonly applied for the corresponding finite catalyst models of such systems, cf. Section 2, allow for highly efficient evaluations of the Fock operator. The thus only moderately increased computational costs compared to semi-local DFT make hybrid functional level calculations especially appealing for practitioners. This stands in stark contrast to the situation for the plane wave basis sets traditionally employed in the context of periodic boundary supercell calculations. There, hybrid functional level calculations incur at present still roughly one order of magnitude higher computational costs, which is one of the reasons why even reference data for adsorption and reaction at metal surfaces are still rather scarce. Unfortunately, the few existing studies presently suggest that this class of functionals does not bring any significant improvement in the description of bonding in these systems.82,83
With respect to the vdW problem simple dispersion-correction approaches represent the biggest step forward for practical present-day calculations. In these semi-empirical, so-called DFT-D approaches the vdW interactions that are not described by the short-ranged xc functionals are approximately considered by adding a pairwise interatomic C6R−6 term to the DFT energy.84–86 At distances below a cut-off, motivated by the vdW radii of the atom pair, this long-range dispersion contribution is heuristically reduced to zero by multiplication with a short-range damping function. For molecular and band gap systems such simple corrections yield generally substantial improvements at essentially negligible costs compared to the semi-local or hybrid DFT calculations to which they are applied.84–88 On the down side, though their semi-empirical derivation has given rise to a manifold of suggested DFT-D schemes that all have the same conceptual structure, they differ in their material-specific parameters. While increasingly popular and widespread, also in the context of supercell packages,89 there is thus no particular scheme that would have emerged as a well-established standard. Also problematic is again the application to adsorption at metal surfaces. Due to the strictly pairwise evaluation of the dispersion interaction the strong electronic screening of the vdW interactions between the adsorbate and substrate atoms at such surfaces is difficult to account for. In prevalent DFT-D schemes bonding to metals is thus significantly overestimated,90 with only very recent schemes specifically aiming to overcome this limitation.91
Both with respect to the self-interaction error and the vdW problem it is thus catalytic processes at (supported) metals that represent a particular challenge to contemporary electronic structure theory. With no single approach beyond semi-local DFT established yet, there are several promising candidates which currently receive a great deal of attention. Among these are range-separated hybrids or advanced fifth-rung non-local functionals like the van der Waals functional92,93 or exact exchange with the Random Phase Approximation (RPA) to the correlation energy,94,95 where in particular the latter functionals offer the prospect to simultaneously tackle both the self-interaction and the vdW problem. Unfortunately, as a common feature all these exploratory functionals incur at present substantially increased computational costs, which is why only scattered applications to catalytic problems have been reported to date.96,97 Dedicated and extensive benchmark calculations for representative sets of reactions and adsorption problems are now urgently required to arrive at conclusive assessments as to the suitability of these functionals for technological applications.
Until then, the accuracy level accessible in production work will roughly remain at the one set by semi-local DFT. In this situation, only larger energy differences or trends are generally considered trustworthy.6,68 Notwithstanding, already at this level corresponding computational screening approaches provide for instance most valuable insight and popularize the use of first-principles calculations in the field.6,98 When aiming for more quantitative results for one specific system, repeating the calculations with different xc functionals represents a worthwhile, though not a fundamentally justified option. For a mindfully selected range of functionals this may at least provide some idea of the uncertainty in the computed energetics. Particularly in the context of kinetic models combining this with sensitivity analyses might then already provide conclusive answers if and how this uncertainty actually translates to the aspired catalytic function. Varying the kinetic parameters within the uncertainty range, corresponding sensitivity analyses allow identification of the rate-limiting steps99–102 and states103,104 in the reaction network. First applications in the context of first-principles microkinetic models show that only the uncertainty contained in these, typically few kinetic bottlenecks matters.105 This invalidates the traditional argument that first-principles based kinetic modeling is pointless, unless chemical accuracy is reached in all underlying energetics. On the other hand, it demonstrates that this accuracy is indeed needed for the few rate-limiting steps in order to reach a fully quantitative kinetic description. Fortunately, obtaining this accuracy for these few crucial steps e.g. with the computationally demanding exploratory functionals will be a much more feasible task than an unselective high-accuracy standard for all reaction steps.
While significant fundamental research efforts are thus necessary to reach fully quantitative first-principles energetics from the xc functional point of view, there is another source of (often at least as worrisome) uncertainty that requires no further research, but only best practice: the computational settings. This concerns both numerical convergence with respect to the employed basis set (or k-point sampling), and as already mentioned with respect to the employed surface model (cluster size, slab thickness). At the latest since the advent of hierarchical localized basis sets, there has been absolutely no excuse for not systematically testing numerical convergence anymore. One cannot overemphasize that just choosing e.g. a given plane wave cutoff without any further justification is a no-go that only brings harm to the field. Data computed this way contain an unspecified degree of error, and the corresponding literature should in fact be dismissed. Generic default values sometimes provided by DFT packages are also questionable, as they often refer to reference systems like bulk that must not necessarily meet the same demanding requirements as dedicated surface calculations. Instead, the best practice is undoubtedly to systematically check the effect of all parameters of the employed computational setting on the specifically targeted quantities for representative test systems that are as close as possible to those ultimately used in the production calculations. In order to minimize the computational burden this can e.g. be basis set tests for small surface unit-cell models corresponding to a high coverage limit, or single-point calculations for larger catalyst models that are derived from fully optimized smaller models by for instance adding further bulk-like layers at the bottom of the slab. The evaluation should also include the effects of parameters not directly related to the electronic structure calculation, such as geometry optimization parameters that can differ widely depending on the final purpose, e.g. preliminary geometry screening vs. frequency analyses.
5 From energies to rate constants
The central gateway to introduce the detailed first-principles electronic structure information into the microkinetic modeling level is via the rate constants of the individual elementary processes. These rate constants are inherently dynamical quantities that would correspondingly require dynamical simulations for their exact determination.106 Common practice in the area of surface chemistry and catalysis is instead to resort to approximate reaction rate theories that provide the rate constants exclusively from properties of the underlying potential energy surface and thus require only static total energy calculations.107 In fact, for the typically rather highly activated surface chemical processes even the lowest level reaction rate theory in the form of conventional transition state theory (TST) is generally deemed sufficient and, in turn, almost unanimously employed. However, despite its profound approximations and concomitant relative simplicity compared to more advanced reaction rate theories, even the application of conventional TST requires rather demanding first-principles calculations to properly determine the rate constants of surface chemical reactions. This concerns in particular the pre-exponential factor of the Arrhenius-type expression, which contains the entropy contributions and for which e.g. tedious (and numerically often severely impaired) surface vibrational frequency calculations are required to calculate the vibrational entropy.In this situation a vast majority of ‘kinetic’ studies in computational catalysis restrict themselves to merely reporting electronic reaction barriers and reaction energies. While this clearly provides a first idea of the reactivity of the elementary steps, it does generally not even allow us to safely conclude on typical mechanism reduction approaches such as the dominant path and rate determining steps,11,12 which instead follow from the interplay in the complex reaction network under the given reaction conditions. A widespread approach to hence get at least rough and minimal-effort rate constant estimates for explicit kinetic modeling resorts to the use of ‘generic’ prefactors like the kBT/h-motivated ∼1013 s−1 or of fixed pre-exponential factors depending on the degrees of freedom that are constrained or released during the reaction.108 In experimental-based microkinetic analysis this is very popular (and also largely justified), since parameter fitting (e.g. of the activation energies) can compensate for the errors introduced. In first-principles microkinetic studies there is instead a more conceptual argument to stay at the qualitative level, apart from simply dodging the large computational burden of more accurate prefactor determinations. This argument recognizes the much more pronounced influence of the energetic barrier in the exponential of the TST expression: As discussed in the previous section, a generic uncertainty estimate for reaction energies of semi-local DFT is 0.2–0.3 eV, implying an uncertainty in rate and equilibrium coefficients of 1 to 3 orders of magnitude in the 400–600 K range, which does not even include the additional uncertainty coming from the typically only approximately located transition states. At such uncertainty in the electronic energy, any improvement towards more elaborate prefactor calculations or even advanced reaction rate theories appears at the first glance of lower priority.
While the achievable accuracy of first-principles rate constants is admittedly a most central (and unresolved) issue in first-principles kinetic modeling, it is also clear that even perfectly quantitative reaction energetics would not help without adequate rate constant expressions. As such, the current best practice to improve beyond the qualitative rate constants as obtained with generic-prefactor TST is to perform harmonic vibrational analyses and use this information to explicitly compute (potentially tunneling-corrected) harmonic prefactors, as well as to correct for zero-point energy contributions. Both aspects can induce severe changes as compared to generic-prefactor TST, for instance already highlighted for methane steam reforming over Ni(111)109 or hydrogenation reactions over Pt(111).110 Exploiting e.g. the large mass difference between reacting species and transition metal catalysts, the computational burden of the corresponding vibrational analyses can often at least somewhat be reduced by focusing on the relevant adsorbate modes through Partial and Mobile Block Hessian approaches.111 Even less demanding is a somewhat intermediate approach, which avoids the explicit surface vibrational calculations and predicts the entropy of surface species by scaling that of the corresponding gas-phase molecule and subtracting the loss in translational entropy.112,113 This scaling factor is typically obtained from regression to experimental data, which clearly hampers the application of this method in a purely first-principles context.
Especially for kinetically insignificant steps, e.g. suitably identified through sensitivity analyses, maybe even less accurate rate constants than provided by generic-prefactor TST might also be of interest. Corresponding approaches have hitherto almost exclusively been used in the empirical/engineering context. However, they might also be of relevance for first-principles kinetic modeling, considering that the latter should ideally focus all its attention (and CPU time) on accurate rate constants for the critical rate-determining steps, while treating the other processes at more efficient and approximate levels.114 One route could be to use time-saving lower-level methods to get approximate reaction energetics for the TST exponential. Among these, Bond Order Conservation (BOC)/Unity Bond Index-Quadratic Exponential (UBI-QEP) potential methods115–117 and Brønsted–Evans–Polanyi relationships118–120 are most promising candidates that provide these energetics using only (measured or computed) thermochemical data. Basic BEP relationships sufficed e.g. for the computational screening to determine a Pareto optimal set of methanation catalysts.6 As another example, Benson-style group additive methods have e.g. been developed to predict the standard enthalpy of formation for adsorbate–metal surface interactions.121,122 While highly appealing in terms of their efficiency, key concerns in using these methods are, however, their parameterization procedures (in particular in hybrid theory–experiment procedures117), their unclear range of transferability (beyond what is covered by the parameterization), and their general reliability (how inaccurate may the energetics be to still yield useful rate constant estimates).
Another aspect of utmost importance both in general and in this mixing of calculations performed at different levels is to ensure overall thermodynamic consistency. An accurate surface thermochemistry is the heart and soul of any kinetic simulation, as no proper kinetic insight can be obtained from models that approach the wrong thermodynamic limits. This caveat is not limited to the classical picture of expressing a reverse rate coefficient as the ratio of the forward rate coefficient and the equilibrium coefficient for that reaction, as e.g. the use of different approaches to calculate the thermodynamics of the surface species may also infer incorrect relative stabilities. As a last point, let us also emphasize that all of the above TST-centered discussion only applies to processes with at least moderate activation energies. For barrierless processes or very low activation energies, TST is either inapplicable or exceedingly inaccurate as the actual rate constant is predominantly determined by entropic, not energetic bottlenecks. This applies e.g. prominently to adsorption processes which are often governed by the strong entropy reduction in going from the gas-phase to the bound state at the surface. The accurate determination of corresponding rate constants then necessarily needs to involve explicit dynamical simulations, in the context of adsorption processes presently often performed within efficient “divide & conquer” approaches.16 More approximate approaches typically rely, similar to the prefactor vs. exponential argument in TST, on the linear dependence of the rate constant on the sticking coefficient, and set the latter often simply to one.
6 From rate constants to intrinsic reaction rate
Surface coverages are non-uniform in many applications, with a heterogeneity that can range from the microscopic scale (concerning the occupation of immediately neighboring active sites) up to the mesoscopic scale (concerning the formation of different domains). In prevailing microkinetic modeling based on rate equation approaches any details of such heterogeneity are usually discarded in favor of an effective treatment in the form of average coverages, i.e. a mean field approximation is applied.123,124 It is well established in the academic literature that this approach has many flaws, with the microscopic spatial corrections often summarized under the header ‘strong site correlations’.7,125 However this has not at all impaired its popularity in practical catalysis research. Apart from the appealing simplicity, one reason for this is certainly that the errors incurred by the mean-field treatment can to some extent be fudged by the fitting power in prevailing phenomenological modeling, see Fig. 6. As pointed out before though, the latter does no longer apply when aiming for first-principles based descriptions.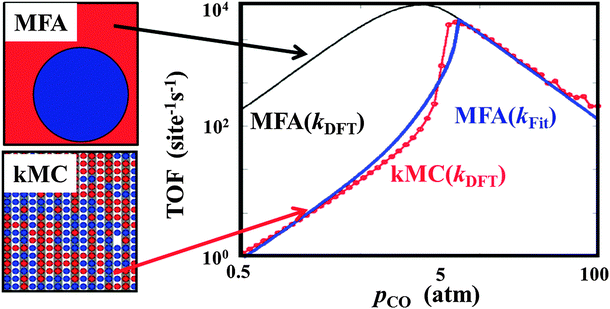 | ||
| Fig. 6 Dependence of the steady-state turnover frequency (TOF) for CO2 production as a function of the CO partial pressure at T = 600 K and p(O2) = 1 atm over a RuO2(110) model catalyst. The black line describes the TOFs obtained from standard mean-field (MFA) rate equations using the DFT rate coefficients. The red circles show the TOFs obtained using exactly the same rate coefficients and reaction mechanism, but using spatially resolved kinetic Monte Carlo (kMC) simulations. The blue line represents the TOFs given by the phenomenological microkinetic model when the reaction rate coefficients are adjusted to yield the best fit to the kMC data (adapted from Temel et al.7). | ||
At the microkinetic level this supports the recent rise of kinetic Monte Carlo (kMC) simulations to replace the traditional mean-field equations.126 Methodologically, both approaches tackle the solution of the same Markovian master equation that describes the time evolution of the reacting system, coarse-grained to the discrete rare events constituted by the elementary processes of the reaction cycle.127 In the catalytic context this master equation describes e.g. the change in time of the occupation of the active sites128
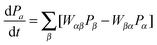 | (1) |
The down side of kMC simulations is to some extent the computational cost which is significantly increased as compared to solving the reaction network with rate equations. Notwithstanding, this increased cost is mostly still completely negligible compared to the cost of the first-principles calculations required to determine the rate constants. In this respect, a second disadvantage of the numerical nature of the solution is much more consequential. To one end, this renders the evaluation of partial derivatives as e.g. required for sensitivity analyses99–102 much more cumbersome than in rate equation theory, where such derivatives can be analytically derived and are thus easily available.105 For similar reasons, it is also much more involved to integrate numerical kMC-based microkinetic formulations into fluid dynamical simulations at the reactor level (vide infra). In consequence, application of kMC simulations in chemical engineering has to date been restricted to a few seminal works1,48,129–138 and significant efforts to provide these functionalities in easy-to-use program packages are required to popularize this technique.
While kMC simulations thus potentially provide a route to overcome present-day limitations in treating coverage effects at the mesoscopic level, one has to recognize that such effects are also omnipresent at the electronic structure level. The local spatial distribution, i.e. the species occupations in the immediate surroundings of an active site, determines not only possible elementary processes, namely events that involve neighboring sites, such as bimolecular reaction, diffusion, dissociative adsorption or associative desorption steps. It may also directly affect the kinetic parameter of each elementary process itself. Corresponding lateral interactions between species sitting in nearby surface sites may arise from through-space effects like dipole–dipole interactions between neighboring adsorbates, or through-surface-effects, e.g. due to bond competition arising from coordination of adsorbates to the same surface atoms, which in a more delocalized picture is often referred to as changes of the local metal density-of-states. With respect to the rate constant of an elementary process, such lateral interactions can change either the vibrational entropy in the prefactor and/or the activation energy in the exponential. Accounting for them in microkinetic formulations thus requires providing rate constants that are either coverage-dependent in mean field models or that even explicitly depend on the detailed local environment around an active site in kMC simulations.
Performing corresponding first-principles calculations that properly determine the vibrational properties and activation barriers as a function of the population of neighboring sites is to the least computationally very expensive – recall the discussion in Section 5 on the expense of determining the TST prefactor; now this would mean to perform such calculations for many different coverages/neighbor populations for every elementary process. Moreover, also technically it is not easy to realize. (Embedded) cluster models are typically chosen to have the actual active site of interest in their center to minimize possible edge effects due to the finite size of the (quantum-mechanically described) region. Neighboring active sites are then necessarily closer to the perimeter of the cluster model and their electronic structure description as such potentially more afflicted by edge effects. In contrast, in supercell calculations the problem is that periodic images of the adsorbates are inherently present, and lateral interactions with these images might in fact inadvertently mask the determined kinetic quantities. In this situation, it is common practice to perform the calculations in an aspired low-coverage limit, i.e. without any lateral interactions. This is naturally realized in (embedded) cluster calculations by considering only one adsorbate in the best described center site(s), and in supercell calculations by resorting to rather large surface unit-cell models to shift periodic images to large distances and thus suppress unwanted interactions. While this establishes a firm well-defined reference, it obviously incurs an error to use corresponding low-coverage rate constants later on in microkinetic simulations that need to describe a high local surface coverage.
Systematic approaches to properly extract lateral interactions from first-principles calculations exist and come under the name surface cluster-expansions or lattice-gas Hamiltonians,36,58,59,139cf. the discussion in Section 3 where these techniques are employed to describe surface segregation in alloys. The conceptual idea is to write the targeted quantity (typically the binding energy, but equally the activation energy or even a vibrational mode) as an algebraic sum of the low-coverage limit and all lateral interactions to first, second, third etc. neighbors. Here, not only pairwise interactions are considered, but also higher-order trio, quattro etc. interactions to describe many-body effects if e.g. the interaction with two simultaneously present nearby adsorbates is not just pairwise additive. Truncating this expansion at interaction terms that are deemed sufficiently small to become negligible, this gives rise to a finite set of interaction parameters that are systematically determined by first-principles calculations for different surface unit-cells and coverages. Being fairly expensive and requiring some methodical training of the modeler, the use of these rigorous approaches to include lateral interactions in kinetic models in heterogeneous catalysis is very limited. Somewhat more spread are more qualitative descriptions which consider a few leading lateral interactions, chosen to roughly reproduce the variation of activation barriers/vibrational modes observed in calculations at a small number of different coverages or local environments. In particular for more complex reaction networks and the concomitant need to further reduce the computational costs, alternative approaches even resort to either describing lateral interactions just effectively by consistently using first-principles data obtained at some fixed intermediate coverage (instead of the low-coverage limit). Or, interactions are described explicitly, but at a lower level. In the latter explicit first-principles data are then employed for the low-coverage limit, and selected lateral interactions to nearby neighbors are described semi-empirically or even just phenomenologically. One rather popular approach in this respect is again the UBI-QEP method,115 which allows coverage-dependent activation energies to be calculated by means of thermochemical data of the involved species.130,131,140,142 To date there have been very few to no detailed studies to assess how much the uncertainties inherited by any of these coarser approaches affect a given kinetic model. Singular works suggest on the positive side that an enhanced error cancelation could lead to particular accuracy in first-principles lateral interactions143 and on the negative side that particular care in mixing first-principles and experimental/semi-empirical data is again advised.117 At present this understanding is, however, too rudimentary to reach a recommendation on (tractable) best practice with respect to the treatment of lateral interactions in first-principles kinetic models.
7 From intrinsic reaction rate to effective reaction rate
Once established, a first-principles microkinetic model yields the intrinsic reaction rate, i.e. the catalytic conversions per unit area and time, as a function of the local composition and temperature of solid and fluid phase. Already at this level and despite their approximations, such first-principles calculations can offer mechanistic insights and structure–reactivity correlations that are invaluable for a rational design of novel catalysts. However, in an industrial context, assessment of the performance of novel catalysts at an industrial reactor scale is equally important since they potentially impact the plant economy. For large commodity plants, production costs are paramount and, given the high level of integration of processes, industry thus requires the novel catalyst technology to be reliably demonstrated since implementing a new catalyst technology for a given process engenders risks for all processes integrated in the chain.144 Also, catalyst deactivation phenomena – either by side reactions or by trace impurities in the feed – often determine the optimal process lay-out and operating conditions and, hence, establishing the factors that need to be controlled to ensure the desired lifetime of the catalyst is an important topic where first principles studies might contribute in the future.Scaling-up to the industrial process requires to account for heat and mass transfer effects in a given reactor geometry, i.e. the first-principles microkinetic description of the intrinsic catalyst function needs to be integrated into a modeling of the flow structures at the micro-scale, at the catalyst pellet size, and at the macro-scale, either through simplified heat and mass balance differential equations or detailed computational fluid dynamics (CFD) simulations. At the level of continuum heat and mass balances, the surface catalytic function merely appears as a boundary condition, albeit a dynamical one: the turnovers depend on local solid/fluid properties (temperature, gas-phase composition) at the boundary, which vice versa depend on the turnovers. This requires a self-consistent solution of both microkinetic and fluid-dynamical equations. For microkinetic formulations based on rate equations this is common practice, usually with closed-form expressions that can directly be incorporated in the continuum modeling or in CFD models, since most major CFD packages allow for versatile analytic expressions to be used as boundary conditions.145 As already pointed out in the previous section, integration of the only numerically available kMC solutions is much more involved. Seminal work attempted this through direct coupling, but found it potentially numerically unstable.146–148 This concept is furthermore difficult to extend to complex reactor geometries, as independent kMC simulations would be required for each spatially resolved cell at the surface. In this respect, a recent approach based on an instantaneous steady-state approximation appears much more promising. This approximation decouples the problem and allows presenting the boundary information for the CFD simulations in the form of pre-computed and interpolated kMC steady-state turnovers.149,150 Notwithstanding this progress, further work with respect to the integration of kMC-based microkinetics into reactor-level modeling is certainly still needed, keeping in mind that it is these models rather than traditional rate equation approaches that offer a proper account of the statistical interplay at the mesoscale and therewith the prospect of an error-controlled multiscale modeling.
Nevertheless, a much more crucial and hitherto barely tackled problem in the integration of first-principles kinetic models, which applies to both kMC and rate equation based approaches, concerns the resolution of the catalyst microstructure.145 Corresponding first-principles models are hitherto almost exclusively restricted to a dominant facet of the active particles. In contrast, reactor scale simulations, in particular in the industrial catalytic reaction engineering context, consider highly reduced dimensions, e.g. the one-dimensional plug-flow model. Furthermore, typical engineering models of catalyst pellets consider a homogeneous solid with simplified intraparticle mass and heat transfer, usually using effectiveness factors, Thiele and Weisz moduli etc.151 This discrepancy may again not be too consequential in phenomenological modeling, where effects not resolved in the fluid-dynamical model, e.g. explicit consideration of mass transport in the porous media, are at least to some degree fitted into the kinetic parameters. As pointed out several times already, this does no longer work when using first-principles kinetic parameters. A successful integration of first-principles kinetic models will therefore likely need to resolve the real catalyst structure in much more detail than in state-of-the-art engineering models. To which degree this will be necessary is presently largely unclear though and will require dedicated efforts bridging between the physicochemical and engineering modeling communities. Until then, the only thing we can hope for is that if a first principles based model can obtain quantitative agreement to intrinsic kinetics obtained from a lab-scale reactor experiment operated without mass transfer limitations, the traditional engineering scaling-up machinery will perform as good as for phenomenological kinetic models.
If the actual particle structure needs to be resolved, this would touch on another severe limitation of current first-principles based kinetic modeling, namely the accessible complexity. As mentioned, the high computational costs involved restrict present-day first-principles kinetic models almost exclusively to a single crystal surface as model for the dominant facet of nanoparticles. Extending this to full particles will require information about the crystal habit under reaction conditions (which can either come from experiment or theoretically from Wulff-constructions152) and will eventually mean having to build first-principles kinetic models not only for one facet, but for several ones, potentially even including reactions at facet edges or the particle/support perimeter. As discussed in Section 2 this is at present still as barely feasible a task as the description of extended defects like steps at individual facets, and has been to date only very rarely performed.153,154 Even for ideal facets, the same limitations arise when moving to more complex reaction networks. With the exploding number of possible elementary steps, the total amount of required first-principles data for a comprehensive kinetic modeling becomes intractable, let alone that it is not at all a trivial task to identify the elementary steps themselves. Full reaction networks including all possible pathways are therefore rarely studied, and kinetic models are often reduced to a dominant path with a rate determining step. This dominant path and/or rate determining step is thereby often not properly established, but instead simply postulated or at best only vaguely motivated. Obviously, this bears the risk that the model is based on an erroneous mechanism, invalidating the entire progress brought about by the first-principles kinetic parameters. Recent progress to overcome this dilemma relies as a central element on efficient sensitivity analyses to determine the rate determining steps.103,104 As it is only the latter which needs to be described with highest accuracy, this conceptually speaking would open up a treatment of more complex systems by focusing the modeling efforts to the really critical aspects. One potential approach in this philosophy would e.g. be an iterative refinement process, in which kinetic models based originally on less accurate kinetic parameters are subsequently improved by substituting the parameters of identified rate-limiting steps successively with first-principles ones. Clearly, such approaches are at present only in an exploratory stage though and significant research is still required to validate their practicability.
8 Conclusions
As initially stated, the objective of this paper was twofold. On the one hand, we briefly reviewed the current best practices and state-of-the-art of first-principles based kinetic modeling in order to promote its use in industrial heterogeneous catalytic reaction engineering. On the other hand, in doing so we attempted to localize existing gaps, identifying the ‘construction zones’ in which progress is needed. Particularly from the latter discussion it is clear that full-fledged, self-standing first-principles kinetic simulations remain out of reach to replace traditional experimental catalyst screening and testing in the foreseeable future. In contrast, first-principles modeling of idealized catalyst models and well-defined reaction sequences is rather straightforward nowadays. Already at this level, first-principles calculations can, despite their approximations, provide such invaluable mechanistic insights and structure–reactivity correlations that there is little doubt that missing out on emerging first-principles technology would be a fatal strategic decision. In fact, the two central general limitations presently preventing a further advancement of first-principles kinetic modeling in the engineering context have little to do with the methodological gaps reviewed in this paper, but instead concern (i) considerate use, including dedicated training and (ii) refined experiments. While breaking-edge method development and high-accuracy methods are for their complexity and computational demands always centered in the academic world, many problems in present-day industrial modeling arise mainly from uncritical use of the existing machinery and unawareness of tricks of the trade that are well established in leading academic groups but are not explicitly conveyed in journal papers. Closer collaborations, counseling, as well as hands-on training visits could provide miracles in this respect. As to (ii), it is generally not sufficiently appreciated how closely intertwined progress in first-principles catalyst modeling is with progress in refined characterization and kinetic experimentation. This so-called ‘dual-feedback loop’ allows e.g. first-principles aided interpretation of experimental data, while the experiments can be used as validation for the modeling. As became clear from the discussion on the choice of the catalyst model, the more atomic-scale information is available as input to the first principles modeling, the more detailed, reliable and relevant will be the insights it can provide. As such it finds a natural partner in novel in situ/in operando spectroscopy, providing data of unprecedented resolution and quality. However, this intimate relation should not be confused with “dependence”. After all, the one and foremost asset of first-principles quantitative modeling is the independent information it can provide. While traditional microkinetic modeling is often sufficient for reactor optimization and design, first-principles microkinetic modeling is not restricted to fitting of experimental data, but allows identifying mechanistic errors and inconsistencies and provides insights into kinetics not easily accessible otherwise. With time, this essential contribution of first-principles kinetic modeling in industrial heterogeneous catalytic reaction engineering will inevitably grow in relevance, until it will ultimately act as an equal partner to experiment and traditional modeling in the quest towards a rational design of novel catalysts with improved activity, selectivities and durability.Acknowledgements
Funding through the Eurokin Consortium is gratefully acknowledged.Notes and references
- K. Reuter, D. Frenkel and M. Scheffler, Phys. Rev. Lett., 2004, 93, 116105 CrossRef.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Norskov, Science, 2005, 307, 555–558 CrossRef CAS.
- M. Saeys, M. F. Reyniers, M. Neurock and G. B. Marin, J. Phys. Chem. B, 2005, 109, 2064–2073 CrossRef CAS.
- O. R. Inderwildi, S. J. Jenkins and D. A. King, J. Am. Chem. Soc., 2007, 129, 1751–1759 CrossRef CAS.
- A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402–1414 CrossRef CAS.
- J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef CAS.
- B. Temel, H. Meskine, K. Reuter, M. Scheffler and H. Metiu, J. Chem. Phys., 2007, 126, 204711 CrossRef.
- L. J. Broadbelt and R. Q. Snurr, Appl. Catal., A, 2000, 200, 23–46 CrossRef CAS.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Wiley, Chichester, 2nd edn, 2004 Search PubMed.
- R. M. Martin, Electronic-Structure: Basic Theory and Practical Methods, Cambridge University Press, Cambridge, 2004 Search PubMed.
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley, 2003 Search PubMed.
- G. B. Marin and G. S. Yablonsky, Kinetics of Chemical Reactions: Decoding Complexity, Wiley-VCH Verlag, Weinheim, 2011 Search PubMed.
- Computational methods in catalysis and Materials Science, ed. R. A. Van Santen and P. Sautet, Wiley-VCH Verlag, Weinheim, 2009 Search PubMed.
- F. J. Keil, Top. Curr. Chem., 2012, 307, 69–108 CrossRef CAS.
- J. K. Norskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- A. Gross, Theoretical Surface Science: A Microscopic Perspective, Springer, Berlin, 2nd edn, 2009 Search PubMed.
- Nanocatalysis, ed. U. Heiz and U. Landman, Springer, Berlin, 2006 Search PubMed.
- T. Gomez, E. Florez, J. A. Rodriguez and F. Illas, J. Phys. Chem. C, 2011, 115, 11666–11672 CAS.
- C. R. A. Catlow, S. A. French, A. A. Sokol and J. M. Thomas, Philos. Trans. R. Soc. London, Ser. A, 2005, 363, 913–936 CrossRef CAS.
- R. A. Van Santen, Acc. Chem. Res., 2008, 42, 57–66 CrossRef.
- Y. Zhang, J. Rogal and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 125414 CrossRef.
- M. C. Valero, P. Raybaud and P. Sautet, J. Catal., 2007, 247, 339–355 CrossRef CAS.
- S. T. Marshall and J. W. Medlin, Surf. Sci. Rep., 2011, 66, 173–184 CrossRef CAS.
- K. Alexopoulos, P. Hejduk, M. Witko, M. F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2010, 114, 3115–3130 CAS.
- C. H. Hu, C. Chizallet, C. Mager-Maury, M. Corral-Valero, P. Sautet, H. Toulhoat and P. Raybaud, J. Catal., 2010, 274, 99–110 CrossRef CAS.
- T. Fievez, P. Geerlings, B. M. Weckhuysen and F. De Proft, ChemPhysChem, 2011, 12, 3281–3290 CrossRef CAS.
- B. T. Teng, F. M. Wu, W. X. Huang, X. D. Wen, L. H. Zhao and M. F. Luo, ChemPhysChem, 2012, 13, 1261–1271 CrossRef CAS.
- R. Wanbayor and V. Ruangpornvisuti, Appl. Surf. Sci., 2012, 258, 3298–3301 CrossRef CAS.
- J. Yang, C. Q. Lv, Y. Guo and G. C. Wang, J. Chem. Phys., 2012, 136, 104107 CrossRef.
- C. Zaum, M. Rieger, K. Reuter and K. Morgenstern, Phys. Rev. Lett., 2011, 107, 046101 CrossRef.
- C. Mager-Maury, G. Bonnard, C. Chizallet, P. Sautet and P. Raybaud, ChemCatChem, 2011, 3, 200–207 CrossRef CAS.
- L. M. Molina and B. Hammer, Phys. Rev. Lett., 2003, 90, 206102 CrossRef CAS.
- L. M. Molina and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155424 CrossRef.
- B.-T. Teng, F.-M. Wu, W.-X. Huang, X.-D. Wen, L.-H. Zhao and M.-F. Luo, ChemPhysChem, 2012, 13, 1261–1271 CrossRef CAS.
- M. García-Mota, J. Gómez-Díaz, G. Novell-Leruth, C. Vargas-Fuentes, L. Bellarosa, B. Bridier, J. Pérez-Ramírez and N. López, Theor. Chem. Acc., 2011, 128, 663–673 CrossRef.
- K. Reuter, C. Stampfl and M. Scheffler, in Handbook of Materials Modeling, Part A: Methods, ed. S. Yip, Springer, Berlin, 2005, pp. 149–194 Search PubMed.
- H. Khang and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 214109 CrossRef.
- C. G. Van de Walle and J. Neugebauer, Annu. Rev. Mater. Res., 2006, 36, 179–198 CrossRef CAS.
- A. Stierle and A. M. Molenbroek, MRS Bull., 2007, 32, 1001–1005 CrossRef.
- G. A. Somorjai and Y. M. Li, Top. Catal., 2010, 53, 311–325 CrossRef CAS.
- X. Hu and Z. Lin, Phys. Rev. B: Condens. Matter, 1995, 52, 11467–11470 CrossRef CAS.
- Q. Sun, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter, 2003, 67, 205424 CrossRef.
- R. Wischert, C. Copéret, F. Delbecq and P. Sautet, Angew. Chem., Int. Ed., 2011, 50, 3202–3205 CrossRef CAS.
- P. J. Steynberg, J. A. van den Berg and W. Janse van Rensburg, J. Phys.: Condens. Matter, 2008, 20, 064238 CrossRef CAS.
- V. Balcaen, R. Roelant, H. Poelman, D. Poelman and G. B. Marin, Catal. Today, 2010, 157, 49–54 CrossRef CAS.
- A. P. Amrute, C. Mondelli, M. Moser, G. Novell-Leruth, N. Lopez, D. Rosenthal, R. Farra, M. E. Schuster, D. Teschner, T. Schmidt and J. Perez-Ramirez, J. Catal., 2012, 286, 287–297 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter, 2002, 65, 035406 CrossRef.
- J. Rogal, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2007, 98, 046101 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter, 2003, 68, 045407 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef.
- D. Loffreda, Surf. Sci., 2006, 600, 2103–2112 CrossRef CAS.
- J. Rogal and K. Reuter, in Experiment, Modeling and Simulation of Gas-Surface Interactions for Reactive Flows in Hypersonic Flights. Educational Notes RTO-EN-AVT-142., RTO, Neuilly-sur-Seine, 2007, p. 2-1–2-18 Search PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045433 CrossRef.
- E. Christoffersen, P. Stoltze and J. K. Norskov, Surf. Sci., 2002, 505, 200–214 CrossRef CAS.
- J. Greeley and M. Mavrikakis, Nat. Mater., 2004, 3, 810–815 CrossRef CAS.
- J. R. Kitchin, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075437 CrossRef.
- Y. G. Ma and P. B. Balbuena, Surf. Sci., 2009, 603, 349–353 CrossRef CAS.
- A. Zunger, in Statics and Dynamics of Alloy Phase Transformations, ed. P. E. A. Turchy and A. Gonis, NATO Advanced Studies Institute, Series B: Physics Plenum, New York, 1994 Search PubMed.
- S. Muller, J. Phys.: Condens. Matter, 2003, 15, R1429–R1500 CrossRef.
- B. C. Han, A. Van der Ven, G. Ceder and B. J. Hwang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205409 CrossRef.
- A. V. Ruban, H. L. Skriver and J. K. Norskov, Phys. Rev. B: Condens. Matter, 1999, 59, 15990–16000 CrossRef.
- C. A. Menning and J. G. G. Chen, J. Chem. Phys., 2009, 130, 174709 CrossRef.
- J. A. Rodriguez, Surf. Sci. Rep., 1996, 24, 225–287 CrossRef.
- S. Sakong, C. Mosch and A. Gross, Phys. Chem. Chem. Phys., 2007, 9, 2216–2225 RSC.
- J. Luyten and C. Creemers, Surf. Sci., 2008, 602, 2491–2495 CrossRef CAS.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1 CrossRef CAS.
- E. A. Carter, Science, 2008, 321, 800–803 CrossRef CAS.
- P. J. Feibelman, Top. Catal., 2010, 53, 417–422 CrossRef CAS.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Science, 2008, 321, 792–794 CrossRef CAS.
- A. Kiejna, G. Kresse, J. Rogal, A. De Sarkar, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035404 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter, 1999, 59, 7413–7421 CrossRef.
- P. J. Feibelman, B. Hammer, J. K. Norskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, J. Phys. Chem. B, 2001, 105, 4018–4025 CrossRef CAS.
- G. Kresse, A. Gil and P. Sautet, Phys. Rev. B: Condens. Matter, 2003, 68, 073401 CrossRef.
- M. Gajdos, A. Eichler and J. Hafner, J. Phys.: Condens. Matter, 2004, 16, 1141–1164 CrossRef CAS.
- Q. M. Hu, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2007, 98, 176103 CrossRef.
- S. Kristyan and P. Pulay, Chem. Phys. Lett., 1994, 229, 175–180 CrossRef CAS.
- E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414 CrossRef.
- B. A. De Moor, M. F. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, J. Phys. Chem. C, 2011, 115, 1204–1219 CAS.
- C. M. Nguyen, M. F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2010, 12, 9481–9493 RSC.
- C. M. Nguyen, M. F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2011, 115, 8658–8669 CAS.
- P. Mori-Sanchez, A. J. Cohen and W. T. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef.
- A. Stroppa and G. Kresse, New J. Phys., 2008, 10, 063020 CrossRef.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097 CrossRef CAS.
- A. Tkatchenko, L. Romaner, O. T. Hofmann, E. Zojer, C. Ambrosch-Draxl and M. Scheffler, MRS Bull., 2010, 35, 435–442 CrossRef CAS.
- K. Tonigold and A. Gross, J. Chem. Phys., 2010, 132, 224701 CrossRef.
- G. Mercurio, E. R. McNellis, I. Martin, S. Hagen, F. Leyssner, S. Soubatch, J. Meyer, M. Wolf, P. Tegeder, F. S. Tautz and K. Reuter, Phys. Rev. Lett., 2010, 104, 036102 CrossRef CAS.
- A. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 146103 CrossRef.
- H. Rydberg, M. Dion, N. Jacobson, E. Schroder, P. Hyldgaard, S. I. Simak, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2003, 91, 126402 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- P. Nozieres and D. Pines, Phys. Rev., 1958, 111, 442–454 CrossRef CAS.
- Y. M. Niquet, M. Fuchs and X. Gonze, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 032507 CrossRef , and references therein.
- X. G. Ren, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045402 CrossRef.
- L. Schimka, J. Harl, A. Stroppa, A. Gruneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Norskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS.
- M. Boudart and K. Tamaru, Catal. Lett., 1991, 9, 15–22 CrossRef CAS.
- C. T. Campbell, Top. Catal., 1994, 1, 353–366 CrossRef CAS.
- J. A. Dumesic, J. Catal., 1999, 185, 496–505 CrossRef CAS.
- A. Baranski, Solid State Ionics, 1999, 117, 123–128 CrossRef CAS.
- C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 13563–13563 CrossRef CAS.
- S. Kozuch and J. M. L. Martin, ChemPhysChem, 2011, 12, 1413–1418 CrossRef CAS.
- H. Meskine, S. Matera, M. Scheffler, K. Reuter and H. Metiu, Surf. Sci., 2009, 603, 1724–1730 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn. 2002 Search PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Treviño, The Microkinetics of Heterogeneous Catalysis, American Chemical Society, 1998 Search PubMed.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, J. Phys. Chem. C, 2009, 113, 4898–4908 CAS.
- X. M. Cao, R. Burch, C. Hardacre and P. Hu, Catal. Today, 2011, 165, 71–79 CrossRef CAS.
- B. A. De Moor, A. Ghysels, M. F. Reyniers, V. Van Speybroeck, M. Waroquier and G. B. Marin, J. Chem. Theory Comput., 2011, 7, 1090–1101 CrossRef CAS.
- M. A. N. Santiago, M. A. Sanchez-Castillo, R. D. Cortright and J. A. Dumesic, J. Catal., 2000, 193, 16–28 CrossRef CAS.
- S. Kandoi, J. Greeley, M. A. Sanchez-Castillo, S. T. Evans, A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, Top. Catal., 2006, 37, 17–28 CrossRef CAS.
- M. Maestri and K. Reuter, Chem. Eng. Sci., 2012, 74, 296–299 CrossRef CAS.
- E. Shustorovich and H. Sellers, Surf. Sci. Rep., 1998, 31, 5–119 CrossRef.
- E. Hansen and M. Neurock, Surf. Sci., 1999, 441, 410–424 CrossRef CAS.
- M. Maestri and K. Reuter, Angew. Chem., Int. Ed., 2011, 50, 1194–1197 CrossRef CAS.
- A. Logadottir, T. H. Rod, J. K. Norskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, J. Catal., 2001, 197, 229–231 CrossRef CAS.
- R. A. van Santen, M. Neurock and S. G. Shetty, Chem. Rev., 2010, 110, 2005–2048 CrossRef CAS.
- J. K. Norskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef CAS.
- J. Kua, F. Faglioni and W. A. Goddard, J. Am. Chem. Soc., 2000, 122, 2309–2321 CrossRef CAS.
- M. Salciccioli, Y. Chen and D. G. Vlachos, J. Phys. Chem. C, 2010, 114, 20155–20166 CAS.
- G. F. Froment, Catal. Rev. Sci. Eng., 2005, 47, 83–124 CAS.
- E. A. Kotomin and V. N. Kuzovkov, in Comprehensive Chemical Kinetics, ed. R. G. Compton and G. Hancock, Elsevier, Amsterdam, 1996, vol. 34, p. 1 Search PubMed.
- S. Matera, H. Meskine and K. Reuter, J. Chem. Phys., 2011, 134, 064713 CrossRef.
- K. Reuter, in Modeling and simulation of heterogeneous catalytic reactions: From the Molecular Process to the Technical System, ed. O. Deutschmann, Wiley-VCH, Weinheim, 2011, pp. 71–112 Search PubMed.
- C. W. Gardiner, Handbook of Stochastic Methods, Springer-Verlag, Berlin, 2003 Search PubMed.
- T. Jansen, in Computational methods in catalysis and materials science, ed. R. A. Van Santen and P. Sautet, Wiley, Weinheim, 2009 Search PubMed.
- S. Ovesson, A. Bogicevic and B. I. Lundqvist, Phys. Rev. Lett., 1999, 83, 2608–2611 CrossRef CAS.
- E. W. Hansen and M. Neurock, Surf. Sci., 2000, 464, 91–107 CrossRef CAS.
- E. W. Hansen and M. Neurock, J. Catal., 2000, 196, 241–252 CrossRef CAS.
- P. Kratzer and M. Scheffler, Phys. Rev. Lett., 2002, 88, 036102 CrossRef CAS.
- J. Rogal, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155410 CrossRef.
- L. J. Xu, D. H. Mei and G. Henkelman, J. Chem. Phys., 2009, 131, 244520 CrossRef.
- D. H. Mei, M. Neurock and C. M. Smith, J. Catal., 2009, 268, 181–195 CrossRef CAS.
- J. Jelic, K. Reuter and R. Meyer, ChemCatChem, 2010, 2, 658–660 CrossRef CAS.
- R. A. van Santen, M. M. Ghouri, S. Shetty and E. M. H. Hensen, Catal. Sci. Technol., 2011, 1, 891–911 CAS.
- H. A. Aleksandrov, L. V. Moskaleva, Z.-J. Zhao, D. Basaran, Z.-X. Chen, D. Mei and N. Rösch, J. Catal., 2012, 285, 187–195 CrossRef CAS.
- S. Yip, Handbook of Materials Modeling, Springer, Dordrecht, 2005 Search PubMed.
- P. Aghalayam, Y. K. Park and D. G. Vlachos, AIChE J., 2000, 46, 2017–2029 CrossRef CAS.
- E. Shustorovich, Russ. J. Phys. Chem. B, 2007, 1, 307–329 CrossRef.
- M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, J. Catal., 2008, 259, 211–222 CrossRef CAS.
- Y. S. Zhang, V. Blum and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235406 CrossRef.
- J. R. Rostrup-Nielsen, in Modeling and simulation of heterogeneous catalytic reactions: From the Molecular Process to the Technical System, ed. O. Deutschmann, Wiley, Weinheim, 2011 Search PubMed.
- Modeling and simulation of heterogeneous catalytic reactions – From the molecular process to the technical system, ed. O. Deutschmann, Wiley-VCH, Weinheim, 2012 Search PubMed.
- D. G. Vlachos, AIChE J., 1997, 43, 3031–3041 CrossRef CAS.
- R. Kissel-Osterrieder, F. Behrendt and J. Warnatz, Twenty-Seventh Symposium (International) on Combustion, 1998, vol. 1 and 2, pp. 2267–2274 Search PubMed.
- A. Chatterjee, M. A. Snyder and D. G. Vlachos, Chem. Eng. Sci., 2004, 59, 5559–5567 CrossRef CAS.
- S. Matera and K. Reuter, Catal. Lett., 2009, 133, 156–159 CrossRef CAS.
- S. Matera and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085446 CrossRef.
- G. F. Froment and K. B. Bischoff, Chemical reactor analysis and design, Wiley, New York, 2nd edn, 1990 Search PubMed.
- T. Bodineau, D. Ioffe and Y. Velenik, J. Math. Phys., 2000, 41, 1033–1098 CrossRef CAS.
- D. Blaylock, Y.-A. Zhu and W. Green, Top. Catal., 2011, 54, 828–844 CrossRef CAS.
- D. Teschner, R. Farra, L. D. Yao, R. Schlogl, H. Soerijanto, R. Schomacker, T. Schmidt, L. Szentmiklosi, A. P. Amrute, C. Mondelli, J. Perez-Ramirez, G. Novell-Leruth and N. Lopez, J. Catal., 2012, 285, 273–284 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
