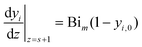Fischer–Tropsch reaction–diffusion in a cobalt catalyst particle: aspects of activity and selectivity for a variable chain growth probability
David
Vervloet
*a,
Freek
Kapteijn
b,
John
Nijenhuis
a and
J. Ruud
van Ommen
a
aProduct & Process Engineering, Delft University of Technology, Faculty of Applied Sciences, Julianalaan 136, 2628 BL Delft, The Netherlands. E-mail: d.vervloet@tudelft.nl
bCatalysis Engineering, Delft University of Technology, Faculty of Applied Sciences, Julianalaan 136, 2628 BL Delft, The Netherlands
First published on 28th February 2012
Abstract
The reaction–diffusion performance for the Fischer–Tropsch reaction in a single cobalt catalyst particle is analysed, comprising the Langmuir–Hinshelwood rate expression proposed by Yates and Satterfield and a variable chain growth parameter α, dependent on temperature and syngas composition (H2/CO ratio). The goal is to explore regions of favourable operating conditions for maximized C5+ productivity from the perspective of intra-particle diffusion limitations, which strongly affect the selectivity and activity. The results demonstrate the deteriorating effect of an increasing H2/CO ratio profile towards the centre of the catalyst particle on the local chain growth probability, arising from intrinsically unbalanced diffusivities and consumption ratios of H2 and CO. The C5+ space time yield, a combination of catalyst activity and selectivity, can be increased with a factor 3 (small catalyst particle, dcat = 50 μm) to 10 (large catalyst particle, dcat = 2.0 mm) by lowering the bulk H2/CO ratio from 2 to 1, and increasing temperature from 500 K to 530 K. For further maximization of the C5+ space time yield under these conditions (H2/CO = 1, T = 530 K) it seems more effective to focus catalyst development on improving the activity rather than selectivity. Furthermore, directions for optimal reactor operation conditions are indicated.
Introduction
Selecting an appropriate catalyst dimension for heterogeneous catalyzed reactions is crucial for realizing optimum catalyst utilization and selectivity, as expressed by the catalyst effectiveness factor (η). The Thiele modulus (ϕ) is the key parameter that defines the interplay between reaction rate(s) (Ri) in a porous catalyst (with characteristic length lcat) and mass transport by effective diffusion (Di,eff). The derivations and expressions for ϕ are well-known for numerous types of kinetics.1The heterogeneously catalyzed Fischer–Tropsch (FT) synthesis, in which syngas is converted into hydrocarbons and water, may be strongly affected by diffusion limitations.2,3 Therefore, an analysis of the Thiele moduli for the reactants (H2 and CO) is crucial for catalyst and reactor design purposes, irrespective of the reactor type in which the catalyst is applied. Furthermore, the selectivity towards desired hydrocarbon chain-lengths, typically C5+ in low-temperature Fischer–Tropsch synthesis (FTS), is a key factor. This is generally expressed by the chain growth probability parameter α, which depends on the local temperature (T) and reactant concentrations (ci).4
An analysis of the diffusivities of the reactants reveals that the ratio of diffusivities of H2 over CO in a typical liquid hydrocarbon product (e.g. C28n-paraffin, following the relations by Wang et al.5) at typical low temperature FT temperatures (e.g. 500 K) is approximately 2.7; this is similar to values reported by other authors, e.g. ref. 6. Not only is hydrogen diffusion faster than that of CO, but its concentration in the liquid phase is typically also higher. Although the CO solubility is approximately 1.3 times higher than that of H2 in a typical liquid product medium at 500 K (following the relations and parameter values for the Henry coefficients by Marano and Holder7), bulk syngas feed ratios of 2 (or slightly lower) are typically chosen for stoichiometric reasons, resulting in a liquid H2/CO concentration ratio of approximately 1.6.
The consumption ratio of H2 over CO on the other hand is a value between 2 (for production of infinitely long hydrocarbon chains) and 3 (for production of methane), so depending on α. It can be shown mathematically, analogous to,8 that the consumption ratio of H2 over CO follows the remarkably linear result (3 − α), given the assumption that α is independent of the chain length. For typical desired α values, between 0.9 and 0.95, the conclusion is that the diffusivity and concentration ratios do not match the consumption ratio of H2 and CO. Therefore, under typical reaction conditions, a syngas ratio (H2/CO) gradient is expected inside the catalyst particle for diffusion limited systems, having an impact on the catalyst performance in terms of reaction rate and selectivity. To avoid limitation in one of the reactants, the H2/CO consumption ratio (3 − α) inside a particle should preferably match its molar diffusion ratio, which is determined by the ratio of the diffusivities and the concentration gradients of H2 and CO. In a simple approximation with full conversion the latter suggests syngas compositions with H2/CO ratios below 1.0 as indicative feed composition, whereas generally values around 2.0 are used for stoichiometric reasons.
Objective and relevance
The key objective of this paper is to map the performance of a cobalt based FT catalyst particle as a function of a range of operating conditions (ϕCO, H2/CO, T, and p) by a numerical analysis. A numerical study on an FTS catalyst in itself is not new. Multiple examples of models can be found in the literature, many of which are directly coupled to some kind of reactor model,6,9–20 although several studies also report the performance of individual particles.3,5,21,22 However, all of the models are typically based on either simplified kinetics (mostly first order in hydrogen) and/or a limited parameter space (mostly at a single operating point for pressure, temperature, and/or syngas ratio). Furthermore, none of the previous studies takes into account that the selectivity inside the catalyst particle may change locally as a consequence of changing syngas ratio. These approaches have their limitations for several reasons:• Assuming a constant chain growth probability α may be too rudimentary.
• Investigation of a limited parameter space provides no insight into possible optimal conditions.
• Simplified FT kinetics based on H2 are not valid for cases that are CO diffusion limited (i.e. CO conversions above 0.6),23 which can easily occur in a single catalyst particle under typical conditions.
• Reporting only dimensionalized parameters, e.g. reaction rate in a catalyst particle of a certain size, does not give much generic insight in the catalyst performance.
This work combines the reaction–diffusion problem of the Langmuir–Hinshelwood FT kinetics as reported by Yates and Sattefield24 with a temperature- and H2/CO ratio dependent chain growth probability parameter (α), based on experimental data from the literature. The model results are presented for a broad range of several operating parameters to provide detailed insight in the catalyst performance. The performance of the catalyst is investigated for several criteria: the average chain growth probability (αave), catalyst effectiveness (η), total CO conversion rate per unit mass catalyst (![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total) and the C5+ space time yield (STYC5+).
CO,total) and the C5+ space time yield (STYC5+).
This work focuses on the evaluation of the catalyst performance from the perspective of a local reaction–diffusion process and selectivity in a reactor. External mass and heat transfer limitations are not considered. Reactor design aspects, such as pressure drop or cooling duty, are also left out of the analysis, as these take place on a different scale, although these may impose changing boundary conditions on the particle scale. The results are used as research motivation for the improvement of FT catalysts, and as explorative guidelines for optimum conditions for FTS, which can be used as a basis for reactor operating strategies.
Model derivation and approach
Reaction–diffusion equations
The dimensionless steady state reaction–diffusion mass balances in a catalyst particle with geometry indicated by s (0 for a slab, 1 for a cylinder, and 2 for a sphere) are captured by a second order differential equation (eqn (1)), where yi is the dimensionless concentration of species i (yi = ci/ci,0), z is the dimensionless length of the catalyst (z = x/lcat, where x denotes the location in the catalyst, and lcat represents the characteristic dimension of the catalyst, defined by lcat = Vcat/Scat, where Vcat is the catalyst particle volume and Scat is the external surface area), ϕi is the Thiele modulus and Ψi is the dimensionless reaction rate (Ψi = Ri/Ri,0, where Ri and Ri,0 are the local and surface reaction rates of species i). It is assumed that the catalyst is fully saturated with a liquid medium in which all reactants and products are dissolved. The effect of product flow leaving the catalyst is neglected (Appendix A) and therefore not included in the differential equation (eqn (1)) for the steady state reaction–diffusion problem. | (1) |
 | (2) |
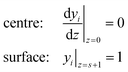 | (3) |
where Bim denotes the Biot number for mass transfer:
where kLS is the external liquid–solid mass transfer coefficient.
Langmuir–Hinshelwood kinetics for the FT reaction24 defines the reaction rate per catalyst volume:
 | (4) |
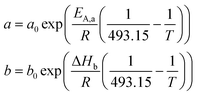 | (5) |
The partial pressures, pi, and the liquid phase concentrations, ci, of species i are coupled through Henry's law by pi = Hi × (ci/cl), where Hi represents temperature dependent Henry's constant and cl is the total molar liquid concentration.
The local dimensionless reaction rate for species i, defined as Ψi = Ri/Ri,0, can be derived from the rate equation (eqn (4)). Conveniently, the temperature inside the catalyst particle can be assumed constant as the internal Prater number is small (Appendix B).25,26 This was numerically verified, and agrees with conclusions by Wang et al.5 Additionally, we verified the absence of external interphase (liquid–solid) heat transport limitations by applying Mears' criterion27 (Appendix C). The absence of local temperature gradients inside the particle drastically reduces the complexity of the system. The temperature dependent reaction rate (a) and adsorption (b) parameters that appear in rate expression (eqn (4)) can now be assumed constant over the entire particle, as well as the Henry coefficients (Hi) for H2 and CO. The expression for the local dimensionless reaction rate Ψi becomes as (eqn (6)):
 | (6) |
Selectivity as a function of temperature and syngas ratio
To arrive at a suitable expression for the catalyst selectivity, the following assumptions are made:13,28• α is independent of chain length.
• α is a function of syngas ratio and temperature
• The selectivity can be described by the ratio of propagation and termination reactions at the active sites on the catalyst, following a standard Arrhenius dependency with temperature.
• The ratio of termination and propagation reactions scales with some power of the local syngas ratio.
The model for the chain growth probability that was derived is (Appendix D):
 | (7) |
We note that other proposals exist for the description of the product distribution, either based on a single chain growth probability α,29 a chain length dependent growth probability based on, for example, α1 and α2 for specific chain lengths,20,30,31 or more sophisticated models that rely on microkinetics to describe the product distribution,32 whether or not further extended by olefin readsorption models that are influenced by diffusion limitations.33 The suitability of all of these approaches is highly catalyst dependent and sometimes under debate, but may be included taking specific effects into account. Eqn (7), which has a sigmoidal shape, satisfies the general limiting trends observed in the literature: α approaches 1 with decreasing temperature and syngas ratio, and 0 with increasing temperature and syngas ratio.
Performance parameters
The performance of the full catalyst particle is evaluated on several criteria listed in Table 1. Eqn (8) is the classical definition of the effectiveness factor of a sphere based on the volume integral of the reaction rate divided by the total volume of the catalyst particle. Eqn (9) defines the average chain growth probability as volume integral over the catalyst particle, weighted with the local dimensionless reaction rate and corrected for effectiveness. Eqn (10) is the expression for the total CO conversion rate based on catalyst weight. Eqn (11) is the definition of C4− selectivity by weight34 (ch. 6, p. 403), which is used to calculate the C5+ selectivity by weight (eqn (12)), since both selectivities add up to unity. Eqn (13) expresses the C5+ space time yield on hourly basis as the product of total molar CO conversion rate, C5+ selectivity and molar weight of a CH2 building block in the hydrocarbon chains.| Performance parameter | Symbol (unit) | Equation | |
|---|---|---|---|
| a Using the molar mass of building block MCH2 = 14 g mol−1. | |||
| Catalyst effectiveness, sphere (s = 2) | η (—) |
 (8) (8) |
|
| Average chain growth probability, sphere (s = 2) | α ave (—) |
 (9) (9) |
|
| Total CO consumption rate per unit mass catalyst |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total (mol kgcat−1 s−1)
CO,total (mol kgcat−1 s−1) |
 (10) (10) |
|
| C4− selectivity | S C4− (—) |
 (11) (11) |
|
| C5+ selectivity | S C5+ (—) | S C5+ = 1 − SC4− (12) | |
| C5+ space time yielda | STYC5+ (g gcat−1 h−1) | STYC5+ = 3.6![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,totalSC5+MCH2 (13) CO,totalSC5+MCH2 (13) |
|
Numerical approach
The differential equation (eqn (1)) was solved numerically on a grid using a second order central difference scheme implemented in Fortran 95. For small ϕieqn (1) is solved over the entire domain (z = [0, s + 1]). For large ϕi (ϕCO > ∼1, depending on H2/CO surface conditions) the grid was scaled to the reactive (outer) shell of the catalyst particle (z = [zleft, s + 1]) to increase the numerical accuracy of the solution and the stability of the code, as well as speed to avoid wasting computational resources on the calculation of values in the centre of the catalyst particle that are essentially zero. In a coordinate scaling problem of a reaction–diffusion system the reactive shell thickness is typically inversely proportional to ϕi.35 However, due to the non-linear nature of the rate equation (eqn (4)) the conventional scaling approach35 of estimating the left (inner) boundary condition for a single-component first order reaction, zleft = max[0, (s + 1) × (1 − 1/ϕi)], was found inadequate. Instead, a satisfactory estimate of the location of the dimensionless left boundary condition (for the investigated range of parameters) was found, by trial and error, to be:For an appropriate range of analysis (ϕCO < 40), a number of 50 equidistant nodes were found sufficient to satisfy a relative and absolute tolerance of 10−3.
Results and discussion
The selectivity model
Numerous results are presented in the literature on the selectivity of different Co catalysts (promoted/unpromoted, various sizes in Co active sites, and several different support structures) under different process conditions (syngas ratio, temperature, pressure). Although the general trends in the data seem consistent, i.e. α decreases with increasing syngas ratio and temperature, the amount of scatter in the data points is too large to draw satisfactory conclusions about the trends. More than 220 reported chain growth parameters from various sources,2,11,36–61 mostly from the last decade, are given in Fig. 1A as a function of temperature and H2/CO ratio. The fit on the model equation (eqn (7)) is rather poor, judging from the R2 value. Remarkably, the reported α values are generally well below the commonly conjectured industrial range of 0.9–0.95. | ||
| Fig. 1 Fit of data on the chain growth parameter α on the model equation (eqn (7)). The grey intensity of the symbols represents the H2/CO ratio, as indicated by the grey scale bar. (A) Data from various sources. (B) Data from De Deugd et al.61α-Values obtained from methane selectivity: α = 1 − Smethane. Fitted model parameters (dependent), 95% confidence intervals and R2 values given in plot. | ||
A different approach to estimate α is to use the values for methane selectivity (α = 1 − Smethane). This approach leads to a conservative (lower) estimate for α, because it is generally observed that the methane selectivity is somewhat larger than (1 − α)34 (ch. 6). Using values for the methane selectivity reported by De Deugd et al. (ch. 4)46,61 for thin layer (30 μm) coated monolithic catalysts, which are assumed to be little affected by transport limitations,46 the fitting parameters for the model equation (eqn (7)) are obtained with a reasonably good fit (Fig. 1B). The α-values derived from methane selectivity follow the expected decreasing trends with increasing syngas ratio and temperature and, furthermore, the α-value for typical conditions is between 0.9–0.95, as conjectured for industrial application.
Model results of the reaction–diffusion equation: reference conditions
The parameter values that are used in the model and conditions explored are presented in Table 2. The results of the multidimensional reaction–diffusion problem are presented in the following paragraphs with an increasing number of variables, starting with a single experimental condition (Fig. 2).| Description | Symbol | Value | Motivation/reference |
|---|---|---|---|
| Temperature | T | 470–530 K | Varied range |
| Pressure | p | 12–36 bar | Varied range |
| Syngas ratio in the bulk | — | 0.1–3.0 | Varied range |
| Catalyst particle diameter | d cat | 10–5000 μm | Varied range |
| Catalyst intrinsic (skeleton) density | ρ cat | 2500 kg m−3 | Typical |
| Catalyst porosity | ε cat | 0.5 | Typical |
| Catalyst pore tortuosity | τ cat | 1.5 | Typical |
| Yates and Satterfield reaction rate constant | a(T) | T-dependent relation/mol s−1 kgcat−1 bar−2 | 24 |
| Yates and Satterfield adsorption constant | b(T) | T dependent relation/bar−1 | 24 |
| Catalyst activity multiplication factor | F | 1–10 | Estimated catalyst activity improvement15 |
| CO diffusion constant in product medium | D 0,CO | 5.584 × 10−7 m2 s−1 | 5 |
| CO diffusion activation energy | E D,CO | 14.85 × 103 J mol−1 | 5 |
| H2 diffusion constant in product medium | D 0,H2 | 1.085 × 10−6 m2 s−1 | 5 |
| H2 diffusion activation energy | E D,H2 | 13.51 × 103 J mol−1 | 5 |
| Henry coefficient | H i (T) | T dependent relation/bar | 7 |
| Chain growth probability | α | Model | This work (eqn (7)) |
| Selectivity constant | k α | 56.7 × 10−3 | This work (eqn (7)) |
| Selectivity exponential parameter | β | 1.76 | This work (eqn (7)) |
| Selectivity activation energy difference | ΔEα | 120.4 × 103 J mol−1 | This work (eqn (7)) |
 | ||
| Fig. 2 (A) Dimensionless concentration yi, reaction rate Ψi and α profiles in a spherical catalyst particle for a fixed α (dashed lines, α = 0.86) and for the variable α model (solid lines). Conditions: T = 490 K, p = 30 bar, syngas ratio at the catalyst surface = 2, dcat = 1.5 mm, F = 1; other parameters as in Table 2. z = 0 at the centre and z = 3 at the surface of the particle. Inset: the syngas (H2/CO) ratio profile in the catalyst. (B) Graphical representation of the dimensionless CO reaction rate profile in the catalyst sphere (variable α). An overview of other performance parameters is given in Table 3. | ||
Fig. 2 compares the results of two single calculations: one with a fixed α value of 0.86, which is the predicted value based on the bulk composition conditions (H2/CO = 2 and T = 490 K), and one with the variable α model. The profiles of the dimensionless concentrations, the dimensionless conversion rate of CO and the local chain growth probability parameter inside a spherical catalyst particle are given (conditions given in the caption). Table 3 contains a comparative overview of the performance parameters (ϕCO, η, αave, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total, SC5+, STYC5+).
CO,total, SC5+, STYC5+).
| Fixed α model | Variable α model | |
|---|---|---|
| ϕ CO (—) | 0.88 | 0.88 |
| η (—) | 1.37 | 1.28 |
| α ave (—) | 0.86 | 0.57 |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total (mmol kgcat−1 s−1)
CO,total (mmol kgcat−1 s−1) |
3.36 | 3.13 |
| S C5+ (—) | 0.86 | 0.29 |
| STYC5+ (g gcat−1 h−1) | 0.15 | 0.046 |
Both cases in Fig. 2 (fixed and variable α) are primarily CO diffusion limited. The dimensionless concentration of CO drops much faster than that of H2, as a result of the lower diffusion to consumption ratios. This is also visible in the top left inset in Fig. 2A, where the concentration ratio of H2 over CO varies over orders of magnitude towards the centre of the catalyst. The dimensionless CO conversion rate first increases towards the centre of the catalyst particle due to its negative reaction order, as a consequence of the higher order of the adsorption term in the rate expression, and then sharply drops to zero upon further decrease in CO concentration, whereby the reaction order of CO changes from negative to positive. Due to this phenomenon the catalyst effectiveness exceeds unity.
Comparing the two cases for the selectivity (dashed lines: α = 0.86, solid lines: α = variable) it is clear that the dimensionless concentration profiles for CO are not very different and that of H2 is somewhat lower for the variable α case. The H2/CO concentration ratio profile is lower for a variable α case (top left inset, Fig. 2A) due to the α-dependent consumption ratio. The catalyst effectiveness and overall CO consumption rates do not differ much (Table 3).
The major difference between the two cases is visible in the selectivity. In the variable α case the chain growth probability deteriorates as the H2/CO ratio increases in the region where the reaction rate is highest (z between 1.5 and 2.5). This causes significant differences in the overall selectivity of the catalyst particle, which results in a threefold reduction of the C5+ space time yield.
Model results for variable ϕCO and H2/CO ratio
The calculations with variable α have been performed for a wide range of conditions. In Fig. 3αave, η,![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total, SC5+, and STYC5+ are given as a function of ϕCO and the bulk syngas ratio at constant temperature and pressure using the variable α model. The corresponding particle diameters, dcat, are also given.
CO,total, SC5+, and STYC5+ are given as a function of ϕCO and the bulk syngas ratio at constant temperature and pressure using the variable α model. The corresponding particle diameters, dcat, are also given.
 | ||
Fig. 3 Catalyst performance for the variable α model as a function of ϕCO and the syngas ratio at the catalyst surface. Conditions: T = 490 K, p = 30 bar, F = 1 × Yates and Satterfield; other conditions as in Table 2. A: αave, B: η, C: ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total, D: SC5+ and E: STYC5+ and F: corresponding catalyst particle diameter dcat. CO,total, D: SC5+ and E: STYC5+ and F: corresponding catalyst particle diameter dcat. | ||
From the results follows that αave drops significantly in the region where ϕCO > 0.6 and bulk syngas ratio >1 (Fig. 3A). The catalyst effectiveness η shows a local maximum in the region where αave drops sharply, and decreases with increasing ϕCO for ϕCO > 1 (Fig. 3B). The total reaction rate in the catalyst particle, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total, increases with increasing H2/CO ratio due to less CO inhibition (Fig. 3C). Furthermore,
CO,total, increases with increasing H2/CO ratio due to less CO inhibition (Fig. 3C). Furthermore, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total (Fig. 3C) and the C5+ selectivity (Fig. 3D) are coupled to η and αave, respectively, and follow the same trends. The STYC5+ contour plot (Fig. 3E) shows that under these conditions (p = 30 bar, T = 490 K, F = 1 × Yates and Satterfield activity) the maximum C5+ productivity is obtained at H2/CO > 1.8 and ϕCO < 0.5. The contour lines of the corresponding particle diameters of the model results are given in Fig. 3F.
CO,total (Fig. 3C) and the C5+ selectivity (Fig. 3D) are coupled to η and αave, respectively, and follow the same trends. The STYC5+ contour plot (Fig. 3E) shows that under these conditions (p = 30 bar, T = 490 K, F = 1 × Yates and Satterfield activity) the maximum C5+ productivity is obtained at H2/CO > 1.8 and ϕCO < 0.5. The contour lines of the corresponding particle diameters of the model results are given in Fig. 3F.
The strength of this analysis is that (un-)favourable regions in the contour plots can be clearly distinguished, and directly compared to other (performance) parameters. Nevertheless, Fig. 3 is still only part of the full picture, since temperature, pressure, and catalyst activity are fixed, whereas in a reactor a broad range of conditions is covered.
Isolines at varying temperature, pressure and catalyst activity
Investigation of the same maps for other temperatures (T = 470–530 K), pressures (p = 12–36 bar) and catalyst activity (F = 1–10) shows that the general features of the contour plots remain the same, but that the values become different. Fig. 4 shows the changing position of some relevant contour lines depending on several performance parameters (column 1: αave = 0.9, column 2: η = 1, column 3:![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total = 3 mmol kgcat−1 s−1, column 4: STYC5+ = 0.1 or 0.2 g gcat−1 h−1) at varying temperature (top row), pressure (middle row) and catalyst activity factor F (bottom row).
CO,total = 3 mmol kgcat−1 s−1, column 4: STYC5+ = 0.1 or 0.2 g gcat−1 h−1) at varying temperature (top row), pressure (middle row) and catalyst activity factor F (bottom row).
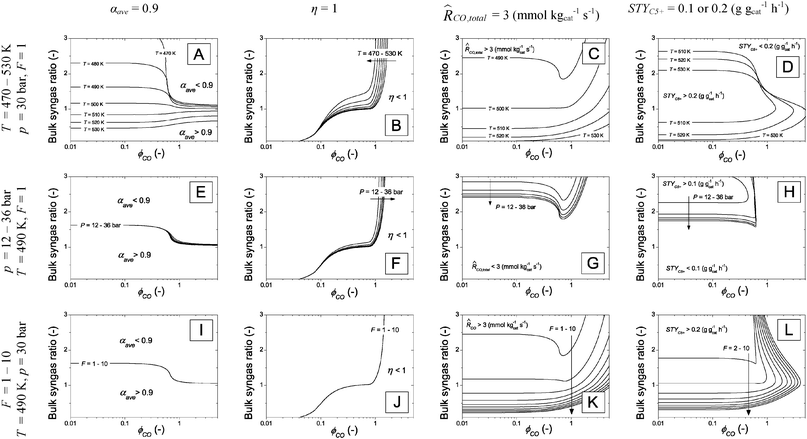 | ||
| Fig. 4 Matrix of selected isolines with conditions as in Table 2, unless specified. Top row (A–D): varying temperature from 470 to 530 K. Middle row (E–H): varying total pressure from 12–36 bar. Bottom row (I–L): varying catalyst activity multiplication factor from 1 to 10. The effects of the varied input parameters on the isolines of several performance indicators are shown. Column 1 (A, I and L): average chain growth parameter isolines of 0.9. Column 2 (B, F and J): catalyst effectiveness isolines of 1. Column 3 (C, G and K): total CO conversion rate isolines of 3 mmol kgcat−1 s−1. Column 4 (D, H and L): C5+ space time yield isolines of 0.1 (varying P) or 0.2 (varying T and F) g gcat−1 h−1. | ||
The most important observation in Fig. 4 is that the contour plots remain qualitatively similar to those of Fig. 3. Several isolines in the contour plots show even hardly any appreciable sensitivity to the varied parameters (Fig. 4B, E–G, I and J). The discussion is focused on the contour plots that do show sensitivity, i.e. the plots in which the isolines shift.
In Fig. 4A the influence of temperature on αave = 0.9 is shown for various ϕCO and H2/CO ratios at the catalyst surface. The negative impact of increased temperature on α can be compensated by decreasing the H2/CO ratio. For kinetically controlled conditions, ϕCO < 0.5, the unmatched diffusivity ratio of H2/CO in the catalyst particle does not play an important role, and a gradual shift of the isolines with temperature to smaller ratios is observed.
For diffusion controlled particles, ϕCO > 0.6, the contour lines are much closer to each other. In this situation the sensitivity between temperature and syngas ratio to maintain αave = 0.9 has changed tremendously, because of the unmatched diffusion and consumption ratios of H2 and CO. Increasing the H2/CO ratio slightly above 1 has a detrimental effect on the average selectivity of the catalyst.
In Fig. 4C and K the effect of varying temperature and catalyst activity factor F on the isolines of ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total = 3 mmol kgcat−1 s−1 can be observed. The trends in the two plots are quite comparable. The shift of the contour lines indicates that an increase in temperature or catalyst activity can be compensated by a reduction in the H2/CO ratio. The trend is approximately inversely proportional to the catalyst activity, which means that a doubling of the catalyst activity can be compensated by reducing the H2/CO ratio with 50%.
CO,total = 3 mmol kgcat−1 s−1 can be observed. The trends in the two plots are quite comparable. The shift of the contour lines indicates that an increase in temperature or catalyst activity can be compensated by a reduction in the H2/CO ratio. The trend is approximately inversely proportional to the catalyst activity, which means that a doubling of the catalyst activity can be compensated by reducing the H2/CO ratio with 50%.
This effect can be explained by simplifying the denominator of the kinetic expression (eqn (4)), obtaining a reaction rate that shows these proportionalities:
The combined influences of FT catalyst activity and selectivity are captured in Fig. 4D, H and L, where the effects of varying temperature, pressure and catalyst activity on the STYC5+ isolines are shown as a function of Thiele modulus and H2/CO ratio. In Fig. 4D the trade-off between activity, selectivity and catalyst effectiveness is clearly visible. The regions where STYC5+ > 0.2 for several temperatures are bound by the respective isolines at three sides. The north-boundaries of the regions exist as a consequence of selectivity loss with increasing H2/CO ratio. The east-boundaries are marked by a decreasing effectiveness with increasing ϕCO. And finally, south-boundaries exist, because of the decreasing reaction rate with decreasing H2/CO ratio. With increasing temperature, the optimum STYC5+ region moves south, and expands to the east. While the onset of selectivity loss occurs at lower H2/CO ratios with increasing temperature (the north-boundary), a decrease in H2/CO ratio also results in less CO diffusion limitation, allowing larger ϕCO (the east-boundary). The influence of pressure (Fig. 4H) is relatively small under the investigated conditions. When the catalyst activity factor F is increased (Fig. 4L) the region where STYC5+ > 0.2 expands to larger ϕCO and lower H2/CO ratios.
The presented contour plots in Fig. 4 are useful, both for giving direction to catalyst development studies as well as for explorative purposes for optimum conditions under which the FT catalyst may be operated. Both topics are addressed below.
Research directions for FT catalyst development
From Fig. 1 it is clear that α decreases with temperature. To better exploit the activity increase of catalysts at higher temperatures, improving the catalyst selectivity at higher temperatures is definitely a required objective. Fig. 2 shows that the increasing syngas H2/CO ratio profile in a CO diffusion limited system can have a detrimental effect on the overall selectivity of the catalyst, due to its coupled effects on the local α.Improving the chain growth parameter with the syngas ratio is therefore useful in systems where CO is the limiting species. The additional advantage of being able to operate at higher syngas ratios is that the reaction rate also increases (viz.Fig. 3C). Obviously, the benefits are smaller for systems that do not suffer from CO diffusion limitations, i.e. at low bulk syngas ratios. At bulk syngas ratios of approximately 1, and depending on the temperature, H2 becomes the limiting reactant. Obviously, under these conditions the advantage of improved α at higher syngas ratio has vanished.
Improving the catalyst activity seems, as always, an attractive objective to increase the space time yield. For reaction controlled systems this simply means higher mass-based production rates. In diffusion hindered systems the increased activity has to be exploited differently. One approach to tackle this problem is with geometrical solutions. Egg-shell catalysts33 or structured reactor internals that serve as catalyst support structure,62 such as monoliths,15,19,63,64 are used if the minimum particle diameter is constrained by the pressure drop in packed bed reactors. Egg-shell catalysts with thin active layers can be applied to reduce the diffusion length in the used catalyst, but at the same time increasing the inert catalyst core, thereby reducing the effective production per reactor volume.
However, additional opportunities for improved performance of diffusion controlled systems exist by optimizing the operating conditions. Lowering the syngas ratio in the bulk and/or the temperature leads to reduced CO diffusion limitations and improved selectivity, at the expense of a reduced total reaction rate. The combined effect can lead to improvements in C5+ productivity—for example, in Fig. 3E at ϕCO = 1, where a reduction in the bulk syngas ratio from 2 to 1 leads to an almost doubled STYC5+. Therefore, improving the catalyst activity is also an important objective, even for systems where diffusion limitations are present.
The question arises whether it is more interesting to improve the chain growth probability or the activity. We address this question by comparing improvements of Yates and Satterfield activity multiplication parameter F and the chain growth selectivity constant kα. The base case is represented by F = 1 and 1 × kα. Both parameters were independently improved 2, 5, and 10 times by multiplication or division, respectively. The latter implies a weaker dependency of the chain growth probability on the temperature and syngas ratio, viz.eqn (7). The effects of the improvements on the C5+ space time yield of a small particle (dcat = 50 μm) and a large particle (dcat = 1.5 mm, respectively) under typical conditions (p = 30 bar, bulk syngas ratio = 2.0 and T = 470–530 K) are shown in Fig. 5.
 | ||
| Fig. 5 Comparative analysis of improvement of the Yates and Satterfield activity parameter F (dashed lines) and the chain growth selectivity constant kα (solid lines). Conditions: p = 30 bar and H2/CO = 2. (A) STYC5+ of a small particle (dcat = 50 μm, ϕCO < 0.35). (B) STYC5+ of a large particle (dcat = 1.5 mm, ϕCO = 0.35–9.9). (C) STYC5+ sensitivity of a small particle (dcat = 50 μm) and (D) STYC5+ sensitivity of a large particle (dcat = 1.5 mm) with F and kα relative to the reference case. | ||
The C5+ space time yield of small particles benefits much more from improvements in catalyst activity (parameter F, dashed lines) than in selectivity at temperatures below approximately 520–530 K, depending on the improvement factor (Fig. 5A). Only at the high end of the investigated temperature range, where α is sufficiently negatively impacted by temperature, the improvements in kα (solid lines) are approximately equally effective compared to improvements in F. The data in Fig. 5A are also presented on a normalized scale with respect to the base case (F = 1 and 1 × kα). These normalized values are shown in Fig. 5C and D and represent the STYC5+ sensitivity with F and kα.
For large particles an increase in activity has a larger effect on the C5+ space time yield than improvements in selectivity at temperatures below 480–490 K (Fig. 5B), depending on the improvement factor. However, at higher temperatures, the effect of improved selectivity is much larger, as CO becomes more diffusion limited in the particle. The increase of STYC5+ with kα at high temperature is even more than proportional (Fig. 5D, solid lines)—e.g. a five-fold improvement of kα (blue solid line) at 530 K increases the C5+ productivity with a factor 14. Note that the kink in some of the curves in Fig. 5B and D (around 482 K) represents the onset of CO depletion in the centre of the particle.
Disregarding the research effort and complexity of improving either F or kα, it is clear that both developments are interesting for the improvement of the FT catalyst in general, but their impact depends on the catalyst design, reactor design and operating conditions. A priori, without additional design and operating considerations, one cannot be preferred over the other. In the next section we explore the effect of operating conditions on the performance of both small and large particles.
Exploration of favourable operating conditions
The catalyst particle size typically does not vary in reactors. This is exploited by converting the x-axes of Fig. 3 and 4 to dimensional units. One example is given in Fig. 6, where the contour-lines for αave = 0.9, which may be regarded as a boundary condition for industrial processes, are given as a function of particle radius and bulk syngas ratio. If we assume that the pressure effects are negligible for this map, which seems reasonable from Fig. 4E, it can be used to determine inlet and outlet conditions for reactor operation. For example, operating a fixed bed reactor with spherical catalyst particles of 1.5 mm diameter (particle radius rcat = 0.75 mm) and a substoichiometric syngas ratio of 1.8 at the inlet at a desired selectivity of αave = 0.9 shows that the temperature should be approximately 480 K at the reactor inlet. The syngas ratio will gradually decrease with reactor length, due to the chosen substoichiometric starting feed conditions. As the syngas ratio drops, the corresponding optimal operational temperature to maintain the desired αave = 0.9 can be found from the map (red arrow), in this case 505 K at a single-pass CO conversion of 73%. This information can be used to determine boundary conditions for the temperature profile in the reactor.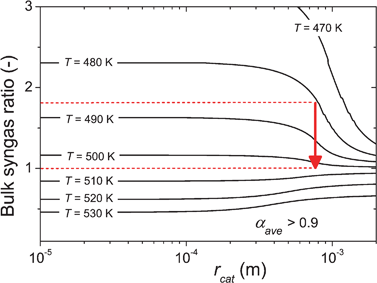 | ||
| Fig. 6 Contour-lines of αave = 0.9 vs. catalyst radius (rcat) and bulk syngas ratio at p = 30 bar and F = 1, other conditions as in Table 2. The desired temperature conditions can be estimated as a consequence of desired starting conditions and conversion levels. | ||
Another way of looking at the data is to plot the effect of varying temperature and bulk syngas ratio at constant particle diameter and pressure. In Fig. 7 the C5+ space time yield is given as a function of temperature and bulk syngas ratio for four particle diameters. Clearly, for all particle diameters, the optimum operating point for maximized STYC5+ is at a bulk syngas ratio just below 1, where both H2 and CO are approximately equally limiting, and the maximum presented temperature of 530 K. The figures also display the isocontour for αave = 0.9.
 | ||
| Fig. 7 C5+ space time yield (STYC5+ in g gcat−1 h−1) contour plots as a function of temperature and bulk syngas ratio at constant pressure (p = 30 bar) and particle diameter. (A) dcat = 0.5 mm, (B) dcat = 1.0 mm, (C) dcat = 1.5 mm, (D) dcat = 2.0 mm. Calculations performed with a catalyst activity multiplication factor F = 1. The dotted line indicates the isocontour for αave = 0.9. | ||
The most important observation from the contour plots in Fig. 7 is that the bulk syngas ratio and the temperature are strongly coupled. No single optimum value can be determined for either process parameter without specifying the other. The coupling between temperature and bulk syngas ratio takes place through the processes of diffusion, reaction and selectivity. Furthermore, this coupling is moderately dependent on the particle diameter. Finally, we observe that the operating conditions for maximum productivity are located in the regime where αave < 0.9.
Similarly, these types of maps can be used to, for example, estimate the productivity of various parts of a slurry bubble column, where the temperature remains fairly constant and the gas phase reactants can be considered to travel in plug flow. Fig. 8 is an overview of the results obtained at four different temperatures for a typical slurry catalyst particle diameter of 50 μm, effectively eliminating the influence of any internal diffusion limitations, at varying pressure and bulk syngas ratio. Again, the figures also display the isocontour for αave = 0.9, which is in this case not influenced by diffusion effects or pressure and is therefore horizontal.
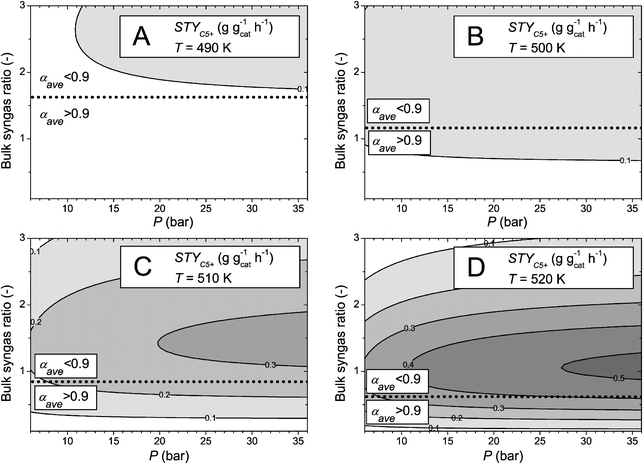 | ||
| Fig. 8 C5+ space time yield (STYC5+ in g gcat−1 h−1) contour plots as a function of total pressure and bulk syngas ratio at constant catalyst particle diameter (dcat = 50 μm) and various temperatures. (A) T = 490 K, (B) T = 500 K, (C) T = 510 K, (D) T = 520 K. Calculations performed with a catalyst activity parameter F = 1. The dotted line indicates the isocontour for αave = 0.9. | ||
Also the bulk syngas ratio and the pressure show some coupled behaviour, although for this example less complex than for larger particles (Fig. 7) due to the absence of diffusion effects. At temperatures of 490 K (Fig. 8A) and 500 K (Fig. 8B) the contour plots are rather flat (few contour lines) and show relatively little influence of the pressure. At temperatures of 510 K (Fig. 8C) and 520 K (Fig. 8D) the effect on α becomes apparent again and the C5+ productivity is optimal at high pressures (p > 30 bar) and a bulk syngas ratio of approximately 1. Similarly as for large particles, the optimum STYC5+ is found in the region where αave < 0.9,
Interestingly, both cases (large particle, Fig. 7, and small particle, Fig. 8) show significant potential to improve a single particle STYC5+ at high temperatures (>520 K), high pressures (p > 30 bar) and a bulk syngas ratio of approximately 1, in contrast to what is typically considered (T ≈ 500 K, and a bulk syngas ratio of approximately 2, much closer to the stoichiometric consumption ratio). Although the temperature has a negative impact on α, the lowered bulk syngas ratio and increased reaction rate with temperature more than compensate this, leading to a significant increase in STYC5+ values by a factor of 3 (small particles) to 10 (large particles). This modelling analysis corroborates the reasoning in the introduction that substoichiometric H2/CO feed ratios may be favourable in FTS.
This insight presents opportunities for reactor configurations that, for example, make use of staged feeding of H2 along the reactor coordinate to control the bulk syngas ratio around a value of 1 as the CO conversion increases. This can also be achieved by a catalytic water gas shift functionality in the reactor, whereby the relatively increasing CO is converted with the produced water to CO2 and H2, keeping up the proper desired H2/CO ratio. The indication to operate at low syngas ratios is especially interesting when the syngas is produced from coal or biomass, where typically low H2/CO ratios are found.65 Using a strict boundary condition for the chain growth parameter, for example αave = 0.9 (dotted line, Fig. 7 and 8) for carbon efficiency reasons, the conclusion is that the maximum STYC5+ for a single catalyst particle is achieved at even lower bulk syngas ratios (H2/CO = 0.5–0.8) and high temperature (T > 520 K).
Operating at low H2/CO ratios may lead to additional effects that are important for industrial application, such as the changed olefin/paraffin ratio in the product distribution,4 or the catalyst deactivation rate.66 These elements are not addressed in this modelling approach, and may be considered for further analysis and deeper insight in economical viability. Also, we note that the catalyst is an integral part of the reactor, in which gradients (T, H2/CO, P) are to be expected and must be taken into account. Reactor and overall process design—as other units, such as syngas manufacturing and product upgrading, roughly size with the amount of gas and liquid that needs to be processed—are ultimately a decision based on capital investment, operating cost and total productivity. These results aid in the exploration and selection of favourable operating conditions, whether or not under additional constraints, for maximum productivity.
As a final element, we readdress the earlier question on whether to focus catalyst development on improving the activity or the selectivity. The chosen operating conditions follow from our previous analysis at maximum STYC5+ (T = 530 K, p = 36 bar and H2/CO = 1). In Table 4 the results are presented for a base case calculation (F = 1 and 1 × kα) and a ten-fold improvement of the parameters for activity and selectivity, both for a small (dcat = 50 μm) and a large particle (dcat = 1.5 mm). Clearly, under these conditions, the STYC5+ improves more with catalyst activity than with selectivity. Improving both parameters at the same time increases the STYC5+, but without synergistic effects, as judged from the relative STYC5+ for the individual and combined parameter improvements.
| d cat = 50 μm | d cat = 1.5 mm | |||||||
|---|---|---|---|---|---|---|---|---|
| F (—) | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 |
| k α (—) | 1 | 1 | 0.1 | 0.1 | 1 | 1 | 0.1 | 0.1 |
| ϕ CO (—) | 4.0 × 10−3 | 4.0 × 10−2 | 4.0 × 10−3 | 4.0 × 10−2 | 3.6 | 35.8 | 3.6 | 35.8 |
| η (—) | 1.00 | 1.00 | 1.00 | 1.00 | 0.53 | 0.19 | 0.56 | 0.20 |
| α ave (—) | 0.70 | 0.70 | 0.96 | 0.96 | 0.72 | 0.73 | 0.93 | 0.93 |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total (mmol kgcat−1 s−1)
CO,total (mmol kgcat−1 s−1) |
29.1 | 289.6 | 29.1 | 290.4 | 15.9 | 57.9 | 16.8 | 61.1 |
| S C5+ (—) | 0.52 | 0.52 | 0.98 | 0.98 | 0.58 | 0.60 | 0.97 | 0.96 |
| STYC5+ (g gcat−1 h−1) | 0.76 | 7.60 | 1.44 | 14.39 | 0.47 | 1.75 | 0.82 | 2.95 |
| Relative STYC5+ (—) | 1.00 | 10.00 | 1.89 | 18.93 | 1.00 | 3.72 | 1.74 | 6.28 |
Validity of the results
The kinetic rate expression (eqn (4)) and parameters in the original paper by Yates and Satterfield24 were extensively validated on several data-sets that covered a temperature range of 454–523 K and a syngas ratio range of 0.2–8.3, although not varied independently over the entire range. Despite the broad range of conditions, diffusion limitations have been shown in this paper to cause situations where the H2/CO ratio approaches 0 or ∞, for which the validity of the equation was not proven. However, under the conditions outside the studied H2/CO range the reaction rate also rapidly decreases as one of the reactants becomes depleted, attenuating uncertainty issues.The data range used for the selectivity relation (eqn (7)) is narrower than that of the Yates and Satterfield rate expression (H2/CO = 1–3 and T = 450–500 K). Therefore, the interpretation of the exact numerical values of the analysis at some of the limits of the investigated domain (T = 530 K) should be taken with caution.
As a final consideration, we note that olefin formation is expected especially at low H2/CO ratios. Diffusion limitations of these molecules will result in further hydrogenation or reinsertion in the chain growth, just leading to more paraffinic products, but not essentially changing the chain length product distribution.46 Therefore, we remain confident that the displayed trends are a good indication of catalyst performance and present an incentive for future experimental and numerical studies.
Conclusions
The calculated H2 and CO concentration profiles inside a cobalt based Fischer–Tropsch catalyst particle under typical operating conditions (temperature = 490 K, pressure = 30 bar, bulk syngas ratio = 2, catalyst sphere diameter = 1.5 mm) demonstrate the severity of CO diffusion limitation that can occur. Incorporating a variable chain growth probability α shows the deteriorating effect of strong gradients in the syngas ratio over the catalyst particle on the local chain growth probability. These gradients are due to intrinsically unbalanced diffusivities and consumption ratios of H2 and CO, and cause significant reduction (a factor 3 in the presented example) of the desired C5+ space time yield.Analysis of the modelling results for a wide range of conditions (CO Thiele modulus ϕCO from 0.01–5, bulk syngas ratio from 0.1–3.0) at constant pressure (p = 30 bar) and temperature (T = 490 K) emphasizes the highly non-linear dynamics of the interplay between reaction, diffusion and selectivity. A common characteristic of all results is the critical conditions beyond which catalyst performance is impacted negatively: ϕCO > 0.6 and a bulk syngas ratio > 1. Analysis of an expanded parameter space (T = 470–530 K, p = 12–36 bar, and a catalyst activity multiplication factor F = 1–10) reveals the strong change in selectivity dependence between temperature and syngas ratio for reaction controlled particles and diffusion controlled particles.
The maximum space time yield of the desired C5+ products was found at high temperatures (T = 530 K), high pressures (p = 36 bar) and relatively low bulk syngas ratios (H2/CO = 1). Under these conditions the STYC5+ can be improved by a factor 3 (small particles, dcat = 50 μm) to 10 (large particles, dcat = 2.0 mm) compared to typical conditions (T = 500 K, p = 30 bar, and H2/CO = 2).
Under the proposed operating conditions for maximizing STYC5+ it is more effective—a factor 5 for a small catalyst particle (dcat = 50 μm) and a factor 2 for a large catalyst particle (dcat = 1.5 mm)—to focus catalyst research on improving the activity rather than the selectivity.
Appendix A—Péclet mass number in the catalyst particle
Differential eqn (1) does not include the effect of product flow leaving the completely liquid filled catalyst particle. This is justified by the result of estimating the Péclet number for mass:where product velocity vl is estimated (vl = 8 × 10−7 m s−1) by assuming a uniform (high) benchmark hydrocarbon productivity of 1 g gcat−1 h−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 (ch. 6, p. 432) of a liquid product with a density of 700 kg m−3 in a catalyst slab with thickness lcat = 1 mm, a density of 1000 kg m−3, a porosity of 0.5 and a pore tortuosity of 1.5, where the effective diffusion coefficient at a temperature of 500 K is 1.4 × 10−8 m2 s−1.
34 (ch. 6, p. 432) of a liquid product with a density of 700 kg m−3 in a catalyst slab with thickness lcat = 1 mm, a density of 1000 kg m−3, a porosity of 0.5 and a pore tortuosity of 1.5, where the effective diffusion coefficient at a temperature of 500 K is 1.4 × 10−8 m2 s−1.
Appendix B—absence of internal temperature gradients
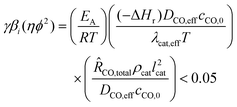
The temperature inside the catalyst particle can be assumed constant if the following criterion, depending on dimensionless activation energy γ, the internal Prater number βi and the Wheeler–Weisz modulus ηϕ2, is satisfied:The following values for the parameters are assumed or estimated: apparent activation energy EA = 100 kJ mol−1,34T = 500 K, a reaction enthalpy ΔHr = −165 kJ mol−1, a uniform large reaction rate of 0.02 mol CO/(kgcat s) is assumed, which is approximately 1 g hydrocarbon gcat−1 h−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 (ch. 6, p. 432), catalyst particle density ρcat = 1000 kg m−3, an effective diffusion coefficient of CO DCO,eff = 5.2 × 10−9 m2 s−1 (at 500 K, εcat = 0.5 and τcat = 1.5), the bulk concentration of CO cCO,0 = 300 mol m−3, the effective heat conductivity of the particle, corrected for a catalyst porosity εcat = 0.5, λcat,eff = 1 W m−1 K−1, and spherical catalyst particle with a diameter of 2 mm (lcat = 0.33 mm). This yields:
34 (ch. 6, p. 432), catalyst particle density ρcat = 1000 kg m−3, an effective diffusion coefficient of CO DCO,eff = 5.2 × 10−9 m2 s−1 (at 500 K, εcat = 0.5 and τcat = 1.5), the bulk concentration of CO cCO,0 = 300 mol m−3, the effective heat conductivity of the particle, corrected for a catalyst porosity εcat = 0.5, λcat,eff = 1 W m−1 K−1, and spherical catalyst particle with a diameter of 2 mm (lcat = 0.33 mm). This yields:| γβi(ηϕ2) = (24.1) × (0.51 × 10−3) × (1.4) = 0.017 < 0.05 |
Appendix C—Mears' criterion for external interphase (liquid–solid) heat transport limitations
According to Mears27 external interphase heat transport limitations can be safely neglected ifwhich was found satisfied (0.026) under the assumptions below. A spherical catalyst particle is assumed with a diameter of 2 mm (lcat = 0.33 mm, ρcat = 1000 kg m−3), large uniform hydrocarbon production of 1 g gcat−1 h−1,
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) CO,total = 0.02 mol kgcat−1 s−1, with an estimated apparent activation energy EA = 100 kJ mol−1,34 a reaction enthalpy ΔHr = −165 kJ mol−1 at T = 500 K. A typical value for the film heat transfer coefficient (h = 2 kW m−2 K−1) was found from the Nusselt number (Nu = h × lcat/λl, with liquid conductivity coefficient λl = 0.14 W m−1 K−1), where Nu was estimated with a packed bed correlation based on bed porosity (εbed = 0.35), Reynolds (Re = ρlvldcat/μl, with liquid density ρl = 700 kg m−3, liquid velocity vl = 0.02 m s−1, and liquid viscosity μl = 2.5 mPa s) and Prandtl (Pr = Cp,lμl/λl, with liquid heat capacity Cp,l = 2.2 kJ kg−1 K−1) number through Nu = 1.31Re1/3Pr1/3/εbed.
CO,total = 0.02 mol kgcat−1 s−1, with an estimated apparent activation energy EA = 100 kJ mol−1,34 a reaction enthalpy ΔHr = −165 kJ mol−1 at T = 500 K. A typical value for the film heat transfer coefficient (h = 2 kW m−2 K−1) was found from the Nusselt number (Nu = h × lcat/λl, with liquid conductivity coefficient λl = 0.14 W m−1 K−1), where Nu was estimated with a packed bed correlation based on bed porosity (εbed = 0.35), Reynolds (Re = ρlvldcat/μl, with liquid density ρl = 700 kg m−3, liquid velocity vl = 0.02 m s−1, and liquid viscosity μl = 2.5 mPa s) and Prandtl (Pr = Cp,lμl/λl, with liquid heat capacity Cp,l = 2.2 kJ kg−1 K−1) number through Nu = 1.31Re1/3Pr1/3/εbed.
Appendix D—selectivity model
The selectivity can be described by the ratio of propagation (p) and termination (t) reactions at the active sites on the catalyst, following a standard Arrhenius dependency with temperature, and the ratio of termination and propagation reactions scales with some power of the local syngas ratio.And:
Substitution and rearranging results in:
where kα = kt0/kp0 and ΔEα = Et − Ep.
Appendix E—list of symbols
| Roman | ||
| a | Yates and Satterfield reaction rate constant | mol s−1 kgcat−1 bar−2 |
| Bim | Biot mass number | — |
| b | Yates and Satterfield adsorption constant | bar−1 |
| C p | Specific heat | J kg−1 K−1 |
| c i | Concentration of species i | mol m−3 |
| D 0,i | Diffusion constant in product medium for species i | m2 s−1 |
| d cat | Catalyst particle diameter | m |
| E D,i | Diffusion activation energy for species i | J mol−1 |
| F | Catalyst activity multiplication factor | — |
| Hi | Henry coefficient for species i | bar |
| h | Film heat transfer coefficient | W m−2 K−1 |
| k α | Selectivity model fitting parameter | — |
| k LS | External liquid–solid mass transfer coefficient | m s−1 |
| l cat | Characteristic catalyst length | m |
| Nu | Nusselt number | — |
| p | Pressure | bar |
| Pem | Péclet mass number | — |
| Pr | Prandtl number | — |
| R | Gas constant | J mol−1 K−1 |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) i
i
|
Reaction rate of species i per unit mass catalyst | mol kgcat−1 s−1 |
| Ri | Reaction rate of species i per unit volume catalyst | mol mcat−3 s−1 |
| Re | Reynolds number | |
| r cat | Radius of a catalyst sphere | m |
| S C4− | C4− selectivity by weight | g g−1 |
| S C5+ | C5+ selectivity by weight | g g−1 |
| S cat | External catalyst surface area | m2 |
| STYC5+ | Space time yield of C5+ | g gcat−1 h−1 |
| s | Geometric parameter | |
| T | Temperature | K |
| V cat | Catalyst volume | m3 |
| v | Velocity | m s−1 |
| x | Location in the catalyst | m |
| yi | Dimensionless concentration of species i | — |
| z | Dimensionless length of the catalyst | — |
| Greek | ||
| α | Chain growth probability | — |
| β | Selectivity exponential fitting parameter | — |
| ΔHb | Heat of absorption | J mol−1 |
| ΔHr | Heat of reaction | J mol−1 |
| ΔEα | Selectivity activation energy difference | J mol−1 |
| ε | Porosity | — |
| ϕ | Thiele modulus | — |
| λ cat | Catalyst thermal conductivity | W m−1 K−1 |
| μ | Viscosity | mPa s |
| ρ | Density | kg m−3 |
| νi | Stoichiometric constant for species i | — |
| τ cat | Catalyst pore tortuosity | — |
| Ψ i | Dimensionless reaction rate | — |
| Subscripts | ||
| 0 | At the catalyst surface | |
| ave | Averaged over the catalyst particle | |
| bed | Packed bed | |
| C5+ | Hydrocarbon chains longer than 4 carbon atoms | |
| cat | Catalyst | |
| CO | Carbon monoxide | |
| eff | Effective | |
| H2 | Hydrogen | |
| i | Species i | |
| l | Liquid | |
| total | Summation over the entire catalyst particle | |
Acknowledgements
This research is supported by the Dutch Technology Foundation STW, which is the applied science division of NWO, and the Technology Program of the Ministry of Economic Affairs, Agriculture and Innovation.References
- P. Schneider, Catal. Rev., 1975, 12, 201–278 CAS.
- M. F. M. Post, A. C. van't Hoog, J. K. Minderhoud and S. T. Sie, AIChE J., 1989, 35, 1107–1114 CrossRef CAS.
- E. Iglesia, S. C. Reyes, R. J. Madon and S. L. Soled, Adv. Catal., 1993, 39, 221–302 CrossRef CAS.
- G. P. Van Der Laan and A. A. C. M. Beenackers, Catal. Rev. Sci. Eng., 1999, 41, 255–318 CAS.
- Y. N. Wang, Y. Y. Xu, H. W. Xiang, Y. W. Li and B. J. Zhang, Ind. Eng. Chem. Res., 2001, 40, 4324–4335 CrossRef CAS.
- C. Maretto and R. Krishna, Catal. Today, 1999, 52, 279–289 CrossRef CAS.
- J. J. Marano and G. D. Holder, Fluid Phase Equilib., 1997, 138, 1–21 CrossRef CAS.
- D. Stern, A. T. Bell and H. Heinemann, Chem. Eng. Sci., 1985, 40, 1665–1677 CrossRef CAS.
- J. W. A. De Swart and R. Krishna, Chem. Eng. Process., 2002, 41, 35–47 CrossRef CAS.
- R. M. de Deugd, R. B. Chougule, M. T. Kreutzer, F. M. Meeuse, J. Grievink, F. Kapteijn and J. A. Moulijn, Chem. Eng. Sci., 2003, 58, 583–591 CrossRef CAS.
- C. Cao, J. Hu, S. Li, W. Wilcox and Y. Wang, Catal. Today, 2009, 140, 149–156 CrossRef CAS.
- A. Jess and C. Kern, Chem. Eng. Technol., 2009, 32, 1164–1175 CrossRef CAS.
- K. Pangarkar, T. J. Schildhauer, J. R. van Ommen, J. Nijenhuis, J. A. Moulijn and F. Kapteijn, Catal. Today, 2009, 147, S2–S9 CrossRef CAS.
- R. Philippe, M. Lacroix, L. Dreibine, C. Pham-Huu, D. Edouard, S. Savin, F. Luck and D. Schweich, Catal. Today, 2009, 147, S305–S312 CrossRef CAS.
- R. Guettel and T. Turek, Chem. Eng. Sci., 2009, 64, 955–964 CrossRef CAS.
- A. Adl, H. A. Ebrahim and M. Sohrabi, J. Chem. Technol. Biotechnol., 2012, 87, 73–79 CrossRef CAS.
- M. H. Rafiq, H. A. Jakobsen, R. Schmid and J. E. Hustad, Fuel Process. Technol., 2011, 92, 893–907 CrossRef CAS.
- A. Sharma, R. Philippe, F. Luck and D. Schweich, Chem. Eng. Sci., 2011, 66, 6358–6366 CrossRef CAS.
- C. G. Visconti, E. Tronconi, G. Groppi, L. Lietti, M. Iovane, S. Rossini and R. Zennaro, Chem. Eng. J., 2011, 171, 1294–1307 CrossRef CAS.
- X. Zhan and B. H. Davis, Appl. Catal., A, 2002, 236, 149–161 CrossRef CAS.
- R. S. Dixit and L. L. Tavlarides, Chem. Eng. Sci., 1982, 37, 539–544 CrossRef CAS.
- H. Zarrin, M. T. Sadeghi and M. A. Marvast, Int. J. Chem. React. Eng., 2009, 7, 1–20 Search PubMed.
- R. Krishna and S. T. Sie, Fuel Process. Technol., 2000, 64, 73–105 CrossRef CAS.
- I. C. Yates and C. N. Satterfield, Energy Fuels, 1991, 5, 168–173 CrossRef CAS.
- J. A. Moulijn, A. Tarfaoui and F. Kapteijn, Catal. Today, 1991, 11, 1–12 CrossRef CAS.
- J. B. Pérez-Ramírez, R. J. Berger, G. Mul, F. Kapteijn and J. A. Moulijn, Catal. Today, 2000, 60, 93–109 CrossRef.
- D. E. Mears, J. Catal., 1971, 20, 127–131 CrossRef CAS.
- K. Pangarkar, in Applied Sciences, Delft University of Technology, Delft, 2010 Search PubMed.
- H. S. Song, D. Ramkrishn, S. Trinh and H. Wright, Korean J. Chem. Eng., 2004, 21, 308–317 CrossRef CAS.
- I. Puskas and R. S. Hurlbut, Catal. Today, 2003, 84, 99–109 CrossRef CAS.
- C. M. Masuku, D. Hildebrandt and D. Glasser, Chem. Eng. Sci., 2011, 66, 6254–6263 CrossRef CAS.
- C. G. Visconti, E. Tronconi, L. Lietti, P. Forzatti, S. Rossini and R. Zennaro, Top. Catal., 2011, 54, 786–800 CrossRef CAS.
- E. Iglesia, S. L. Soled, J. E. Baumgartner and S. C. Reyes, J. Catal., 1995, 153, 108–122 CrossRef CAS.
- C. H. Bartholomew and R. J. Farrauto, Fundamentals of Industrial Catalytic Processes, John Wiley & Sons, Inc, Hoboken, New Jersey, 2006 Search PubMed.
- W. M. Deen, Analysis of Transport Phenomena, Oxford University Press, Inc, New York, 1998, ch. 3 Search PubMed.
- J. Patzlaff, Y. Liu, C. Graffmann and J. Gaube, Appl. Catal., A, 1999, 186, 109–119 CrossRef CAS.
- N. Tsubaki, S. Sun and K. Fujimoto, J. Catal., 2001, 199, 236–246 CrossRef CAS.
- Y. Ohtsuka, Y. Takahashi, M. Noguchi, T. Arai, S. Takasaki, N. Tsubouchi and Y. Wang, Catal. Today, 2004, 89, 419–429 CrossRef CAS.
- A. Tavasoli, R. M. M. Abbaslou and A. K. Dalai, Appl. Catal., A, 2008, 346, 58–64 CrossRef CAS.
- G. Bian, T. Mochizuki, N. Fujishita, H. Nomoto and M. Yamada, Energy Fuels, 2003, 17, 799–803 CrossRef CAS.
- Y. Ohtsuka, T. Arai, S. Takasaki and N. Tsubouchi, Energy Fuels, 2003, 17, 804–809 CrossRef CAS.
- C. J. Bertole, G. Kiss and C. A. Mims, J. Catal., 2004, 223, 309–318 CrossRef CAS.
- C. J. Bertole, C. A. Mims and G. Kiss, J. Catal., 2004, 221, 191–203 CrossRef CAS.
- F. Bertoncini, M. C. Marion, N. Brodusch and S. Esnault, Oil Gas Sci. Technol., 2009, 64, 79–90 CrossRef CAS.
- O. Gonzalez, H. Perez, P. Navarro, L. C. Almeida, J. G. Pacheco and M. Montes, Catal. Today, 2009, 148, 140–147 CrossRef CAS.
- F. Kapteijn, R. M. De Deugd and J. A. Moulijn, Catal. Today, 2005, 105, 350–356 CrossRef CAS.
- Y. Liu, T. Hanaoka, T. Miyazawa, K. Murata, K. Okabe and K. Sakanishi, Fuel Process. Technol., 2009, 90, 901–908 CrossRef CAS.
- K. Okabe, M. Wei and H. Arakawa, Energy Fuels, 2003, 17, 822–828 CrossRef CAS.
- D. Pinna, E. Tronconi, L. Lietti, R. Zennaro and P. Forzatti, J. Catal., 2003, 214, 251–260 CrossRef CAS.
- E. Rytter, S. Eri, T. H. Skagseth, D. Schanke, E. Bergene, R. Myrstad and A. Lindvag, Ind. Eng. Chem. Res., 2007, 46, 9032–9036 CrossRef CAS.
- L. Spadaro, F. Arena, M. L. Granados, M. Ojeda, J. L. G. Fierro and F. Frusteri, J. Catal., 2005, 234, 451–462 CrossRef CAS.
- C. G. Visconti, L. Lietti, P. Forzatti and R. Zennaro, Appl. Catal., A, 2007, 330, 49–56 CrossRef CAS.
- S. Zheng, Y. Liu, J. Li and B. Shi, Appl. Catal., A, 2007, 330, 63–68 CrossRef CAS.
- M. C. J. Bradford, M. Te and A. Pollack, Appl. Catal., A, 2005, 283, 39–46 CrossRef CAS.
- H. Li, S. Wang, F. Ling and J. Li, J. Mol. Catal. A: Chem., 2006, 244, 33–40 CrossRef CAS.
- H. Xiong, Y. Zhang, K. Liew and J. Li, J. Mol. Catal. A: Chem., 2005, 231, 145–151 CrossRef CAS.
- D. Xu, W. Li, H. Duan, Q. Ge and H. Xu, Catal. Lett., 2005, 102, 229–235 CrossRef CAS.
- A. Tavasoli, A. N. Pour and M. G. Ahangari, J. Nat. Gas Chem., 2010, 19, 653–659 CrossRef CAS.
- F. Lu, H. Zhang, W. Ying and D. Fang, Pet. Sci. Technol., 2010, 28, 1834–1845 CrossRef CAS.
- S. Logdberg, M. Lualdi, S. Jars, J. C. Walmsley, E. A. Blekkan, E. Rytter and A. Holmen, J. Catal., 2010, 274, 84–98 CrossRef.
- R. M. De Deugd, PhD dissertation, Delft University of Technology, Delft, 2004 Search PubMed.
- K. Pangarkar, T. J. Schildhauer, J. R. Van Ommen, J. Nijenhuis, F. Kapteijn and J. A. Moulijn, Ind. Eng. Chem. Res., 2008, 47, 3720–3751 CrossRef CAS.
- R. Guettel, J. Knochen, U. Kunz, M. Kassing and T. Turek, Ind. Eng. Chem. Res., 2008, 47, 6589–6597 CrossRef CAS.
- C. G. Visconti, E. Tronconi, L. Lietti, G. Groppi, P. Forzatti, C. Cristiani, R. Zennaro and S. Rossini, Appl. Catal., A, 2009, 370, 93–101 CrossRef CAS.
- O. O. James, A. M. Mesubi, T. C. Ako and S. Maity, Fuel Process. Technol., 2010, 91, 136–144 CrossRef CAS.
- C. H. Bartholomew, Appl. Catal., A, 2001, 212, 17–60 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |