Received
12th September 2011
, Accepted 14th November 2011
First published on 1st December 2011
Abstract
The kinetics of L-arabinose selective oxidation over Au/Al2O3 catalysts was studied with simultaneous in situ catalyst electrical potential measurements. An oxidative dehydrogenation mechanism was proposed and a kinetic model taking into account the catalyst potential changes was developed. The kinetic model was implemented into the three-phase system and validated with the experimental observations. The agreement of the kinetic model to the experimental data, in line with the suggested reaction mechanism, was satisfactory.
1. Introduction
The intrinsic relationship between catalysis and electrocatalysis has given rise to the development and application of electrochemical methods for the investigation of elementary catalytic steps and for the study of the catalyst behavior.1 The interrelated phenomena on the surface of heterogeneous catalysts and electrodes have previously been demonstrated.2 Both heterogeneous catalysis and electrocatalysis are characterized with studies of the adsorption layer composition, surface reaction kinetics and mechanism, thus giving insights into the nature of catalytic sites responsible for the catalytic activity observed in various materials.3,4 Surface research methods which are commonly used in heterogeneous catalysis can essentially be complemented with respect to information obtained by electrochemical methods such as impedance and cyclic voltammetry.5
During the heterogeneously catalyzed aqueous phase oxidation, the metal surface in an aqueous solution may be considered as an electrochemical system. Both the oxidation and reduction processes take place on the same metal particle which is similar to a short-circuited electrochemical cell. If measured against the reference electrode immersed into the reaction mixture, the potential of this particle will represent the mixed potential characterizing the sum of all the redox processes taking place on the surface. Therefore, the catalyst potential measurement during the course of a three-phase catalytic process enables us to study the changing structure of the catalyst interface in situ, simultaneously with the catalytic processes.6,7
Liquid phase selective oxidation of alcohols and carbohydrates in an isolated reactor is accompanied with catalyst potential shift process due to the changes in the concentration of oxygen on the catalyst surface.8,9 The shift can be up to 850 mV, at constant pH values. According to Mallat and Baiker,10 noble metal catalyzed oxidations can be considered as electrochemical reactions. The oxidation takes place in two half reactions; the hydroxyl functional group dehydration producing electrons and protons; and oxygen reduction consuming electrons and protons.
The basis of catalytic reaction engineering is the study of the intrinsic reaction kinetics. The rate expressions used in the reaction kinetics are derived from the elementary reaction steps. The reaction rate expression then allows a quantitative description of the effect of the reaction conditions on the reaction rates, conversion, and the selectivities to the desired products. It is therefore important to derive the rate expressions that result in the best description of a full range of experimental data.
Supported gold nanoparticles have already demonstrated an exceptionally low temperature catalytic activity and high selectivity in the oxidation reactions in comparison to other noble metal catalysts such as palladium or platinum. Previous studies have demonstrated that gold supported on alumina has a high catalyst activity and selectivity in the selective oxidation of L-arabinose, D-galactose as well as lactose.11–14 The aim of this work was to study the kinetics of the selective oxidation of L-arabinose over gold catalysts with in situ catalyst electric potential measurements and to make a quantitative description of the reaction kinetics.
This work is in line with the concept of biorefineries, which is an integrated biomass processing entity producing multiple value-added products from a range of renewable feedstocks.15,16 Woody biomass is the essential part of the forest biorefineries. Noble metal catalyzed selective oxidation of carbohydrates in aqueous phase with an inexpensive oxidant such as air or oxygen has proved its potential illustrating a clean and elegant alternative because of the mild reaction conditions and the high selectivity which can be obtained. Moreover, it is an environmentally friendly process due to virtually non-existing by-products and no waste generated. During the selective oxidation of L-arabinose, the corresponding aldonic acid, arabinonic acid is obtained as the main product (Fig. 1). The sugar acid and its derivatives have many applications in the food, cosmetic and pharmaceutical industries.17,18
2. Results and discussion
The selective oxidation of L-arabinose to arabinonic acid over gold catalysts was conducted isothermally at atmospheric pressure, in the semi-batch mode. The pH, oxygen flow rate and temperature of the reaction medium were systematically varied. The pH of the reaction medium was regulated and kept constant during the course of the experiments. It has been previously verified that the kinetic experiments were performed under the reaction conditions at which external mass transfer at the phase boundaries does not limit the overall reaction rates.11
The catalyst electric potential reflects the processes taking place on the surface of the Au/Al2O3 catalysts. According to Mallat and Baiker, the catalyst potential is an indicator of the balance between reduction and oxidation processes taking place on the catalyst active sites.10 A noble metal catalyst stored in air has a potential close to its oxygen rest potential. The reduction of the oxidized catalyst surface is accompanied by a decrease in its potential. Fig. 2 depicts the potential of the Au/Al2O3 catalyst during the pre-reduction step with hydrogen and during the oxidation of L-arabinose with molecular oxygen.
The catalyst potential is determined by the composition of the adsorbed layer, which depends on the contents of the reaction mixture, i.e. concentration of oxygen and OH− species. The pre-reduction step with hydrogen is fast and complete. During the reaction, the catalyst potential increases continuously from the reduced state to the oxidized state, due to the consumption of the reactant and the accumulation and possibly saturation of the oxygen on the catalyst surface. In the case of other metal catalysts, such as palladium or platinum, a quick saturation of the catalyst surface by oxygen may result in catalyst over-oxidation or poisoning leading to a drop in the activity.13 Contrary to palladium or platinum, gold catalysts demonstrate high stability as they did not show any sign of decline in activity or decrease in selectivity to the main product. The catalyst electric potential as a function of L-arabinose conversion over 1 wt% Au/Al2O3 at 60 °C, pH 8 and gas flow rate 20 ml min−1 with 12.5 vol% oxygen is shown in Fig. 3. Under these conditions, L-arabinose was completely oxidized to the corresponding product, arabinonic acid within 200 min.
2.2. Influence of reaction conditions on kinetics
Aqueous phase selective oxidation of sugars is generally carried out in a weakly acidic or alkaline medium.19 Since the reaction results in the drop of pH due to the acid product formation, the pH of the reaction media was regulated and kept constant during the course of the experiment by an automatic pH controller. The influence of pH is complex as it can affect the reaction in several ways. To determine the impact of pH on the catalyst activity and product selectivity, it was varied in the range of 6 to 9. It was demonstrated that as the pH increases from 6 to 9, both the catalyst activity and L-arabinose conversion increased as shown in Fig. 4. In the acidic media, only a maximum conversion of 23% was reached after 200 min and the selectivity to arabinonic acid was 46%. The only other product detected was the intermediate species, arabinolactone. A pronounced increase in the rates of product formation was observed as the pH increases from 6 to 9. Under slightly alkaline conditions pH 8–9, a complete conversion of L-arabinose and a total selectivity to arabinonic acid were achieved after 200 min. Thus, by increasing the pH of the reaction media from slightly acidic conditions (pH 6) to slightly alkaline conditions (pH 9), the rates of oxidation can be accelerated to achieve from only a 23% conversion to a complete conversion within 200 min, respectively. The selectivity towards the main product was also increased from 46% at pH 6, to 100% at pH 9. Therefore, it can be stated that slightly alkaline conditions are favorable for selective oxidation of L-arabinose.
Under intrinsic kinetic regime, where only the true chemical kinetics plays a role and transport resistances are negligible, the amount of oxygen present in the liquid phase can greatly influence the catalytic activity. In our previous works,11,13 gold catalysts displayed the highest activity and selectivity in the oxidation of sugars compared to palladium catalysts. Moreover, a comparison of experiments was carried out under oxygen rich conditions, the palladium catalyst was more prone to deactivation due to over-oxidation. The product concentration profiles (arabinonic acid) plotted against Au mass proportional time at different oxygen flow rates are presented in Fig. 5. An increase in the oxygen flow rate resulted in the increase of the rate of oxidation. The amount of oxygen present in the lowest flow rates was only a slight excess to the formed moles of oxidation products. At the initial stages of the experiment, the oxidation reaction rate is proportional to the oxygen feed rate. A complete conversion of L-arabinose was achieved in all the cases. The selectivity to arabinonic acid over Au/Al2O3 at all the different oxygen flow rates was 99% and no catalyst deactivation or degradation products were observed.
The influence of reaction temperature on the oxidation of L-arabinose over Au/Al2O3 is depicted in Fig. 6. The reaction rates and conversion increased with increasing temperature. At a relatively low temperature of 50 °C, a maximum conversion of 88% was achieved after 200 min. A complete conversion and higher initials rates were observed at temperatures of 60 and 70 °C, respectively. The selectivity was, however, not affected by temperature under these conditions. Higher temperatures may nevertheless result in the formation of undesired by-products induced by the degradation of the sugars.
 |
| | Fig. 6 Influence of temperature on the selective oxidation of L-arabinose over Au/Al2O3 (O2 2.5 ml min−1, pH 8). | |
2.3. Mechanism and kinetic model
The mechanism widely proposed for the oxidative dehydrogenation suggests that the reaction proceeds via the dehydrogenation of the adsorbed hydroxyl functional group in the cyclic aldehydo-form, hemiacetal L-arabinose to the lactone, arabinolactone, followed by the oxidation of the adsorbed hydrogen atom with dissociatively adsorbed oxygen. In a pure dehydrogenation mechanism, the rate determining step is considered to be the dehydrogenation of the hydroxyl group to the lactone species with its subsequent saponification favored by alkaline pH into the acid product.10,20 It has also been observed that the aldehyde oxidation rate increases with increasing pH. Due to their high nucleophilic property at high pH, hydroxyl ions are believed to be involved in the aldehyde dehydrogenation rather than water.21 It has also been observed that slightly alkaline conditions are apparently necessary as the oxidation rate increases with an increase of the pH. Under such conditions, drastic catalyst deactivation can be avoided.13 However, such conditions may also be responsible for side reactions, such as isomerisation, that reduce the overall productivity.
There has been much debate concerning the nature of the active sites of supported gold nanoparticles in the literature. A model was proposed where Au atoms located at the interface between the Au particle and the oxide support are the active oxidation centers.22,23 Haruta and co-workers have reassessed the mechanism of CO oxidation on the basis of the same model.24,25 It was suggested that CO is activated by adsorption onto Au0 on the surface of the gold nanoparticles and that the dioxygen is activated by the atoms at the boundary between the support and the gold nanocrystals. The interface between the small gold particles and the support together with the availability of defect sites at this interface are probably the important features of the active centers. This effect is thought to be highly significant for gold particles with a diameter of around 2 nm, which coincides with a dramatic enhancement in activity in gas phase CO oxidation.
For the understanding of the roles of edges and faces in L-arabinose oxidation, it is necessary to consider the dependence of the reaction rate on the cluster size. It was demonstrated in ref. 26 that L-arabinose oxidation reaction is structure sensitive, i.e. activity depends on the size of gold nanoclusters. A volcano relationship of the activity as a function of the Au particle size was demonstrated and the mean particle size of 2.3 nm exhibited the highest activity. TOF increases with cluster size attaining a plateau. Such dependence, in essence, means that small clusters with a high ratio between edges and faces are less active, while large clusters consisting predominantly of faces display similar TOF values. It can therefore be suggested that the gold atoms at the faces are the probable active sites in L-arabinose oxidation.
After a short initial period, electrochemical potential reached a steady value, which was thereafter independent of conversion. These observations prompted to separate catalytic oxidation, occurring on the faces, from electron transfer, leading to electrochemical potential changes, which occur on the edges, vertices and perimeter of the cluster. It is thus reasonable to assume that oxygen adsorbs on the edges, and then migrates to the faces, where adsorption of L-arabinose occurs with subsequent reaction leading to arabinonic acid. Based on the dependence of the reaction rate on the oxygen partial pressure, it can be suggested that oxygen dissolved in the liquid participates in the oxidation reaction, rather than oxygen from hydroxyl ions.
A mechanistic model was used to describe the experimental data of L-arabinose oxidation over Au/Al2O3 catalyst with oxygen in the aqueous phase. The oxidative dehydrogenation mechanism was adopted in the oxidation of L-arabinose and the following sequence of stages was suggested showing the selective oxidation pathway:
| |
N(1) |
N(2) |
N(3) |
N(4) |
|
| A + * ≡ A* |
0 |
0 |
0 |
0 |
(1) |
| A + *′ ≡ A*′ |
2 |
0 |
0 |
0 |
(2) |
| O2 + 2* ≡ 2O* |
1 |
0 |
0 |
0 |
(3) |
| O* + *′ ≡ O*′ + * |
2 |
1 |
1 |
1 |
(4) |
| A*′ + O*′ → B*′ + H2O + *′ |
2 |
0 |
0 |
0 |
(5) |
| B*′ + OH−*′ → D*′ + *′ |
0 |
1 |
0 |
0 |
(6) |
| D*′ + H+ → (fast)C + *′ |
0 |
1 |
0 |
0 |
(6a) |
| O* + H2O + 2e− → 2OH− + * |
0 |
0 |
−1 |
1 |
(7) |
| OH− + *→ O* + H+ + 2e− |
0 |
1 |
0 |
2 |
(8) |
| O*′ + H2O + 2e− → 2OH− + *′ |
0 |
1 |
1 |
1 |
(9) |
| OH− + * ≡ OH−* |
0 |
0 |
0 |
0 |
(10) |
| OH− + *′ ≡ OH−*′ |
0 |
1 |
0 |
0 |
(11) |
| B*′ ≡ B + *′ |
2 |
−1 |
0 |
0 |
(12) |
| N(1): 2A + O2 = 2B + 2H2O, N(2): B + H2O = C, N(3): 0 = 0, N(4): 2H2O = 2OH− + 2H+. |
where *—is the active sites on the edges, *′—active sites on the faces, A—
L-arabinose, B—arabinolactone, C—
arabinonic acid. The elementary steps above can be described by 4 reaction routes,
i.e. sets of stoichiometric numbers of steps. Elementary reactions are grouped in steps, and chemical equations of steps contain reactants and intermediate products. A set of stoichiometric numbers of steps is defined as a reaction route. Routes must be essentially different, and it is impossible to obtain one route through multiplication of another route by a number, although their respective overall equations can be identical. The number of basic routes,
P, is determined by
P =
S +
W −
I, where
S is the number of steps,
W is the number of balance (link) equations, and
I is the number of intermediates. Such balance (link) equations can correspond to the total coverage of sites equal to unity or the balance between the electron consumption and production. In the right-hand side of equations for the steps stoichiometric numbers along the four routes N
(1)–N
(4) are given. These numbers are selected in a way that the overall chemical equations do not contain intermediates
2. One of the routes (
i.e. N
(3)) is a so-called empty route, which was discussed previously in the literature by Temkin
2 for example in relation to selective
oxidation of
ethylene.
It is assumed that L-arabinose can adsorb on both the faces and edges of the gold cluster (steps 1 and 2 respectively). Oxygen is adsorbed on the edges with dissociation (steps 3), thereafter migrating to faces (steps 4). The sugar oxidation involves dehydrogenation of the adsorbed L-arabinose to arabinolactone and oxygen reduction in step 5. The product, arabinonic acid, is formed in steps 6 and 6a via the intermediate species, while steps 7 and 8 account for electron transfer, which involves oxygen adsorbed on the edges. Finally, as the oxidation rate was found to be dependent on pH, adsorption of OH− on faces was also included in the model (step 11). Electron transfer involving adsorption of OH− on the edges was also included in the model (step 9). In addition, step 10 accounts for direct adsorption of OH− on the edges without electron transfer. The oxidative dehydrogenation of L-arabinose takes place in two steps (5 and 6) via the intermediate arabinolactone. The intermediate product, arabinolactone, has been found only in small amounts in the reaction mixture (step 12). It is assumed to react much faster than L-arabinose and as a reactive intermediate, it will have very low surface coverage.
The change in the catalyst potential during the course of the reaction is accounted for by the overall current balance. Thus, the catalyst potential is determined by balancing the rate of electrons produced in step 8, and the rate of electrons consumed in steps 7 and 9:
| |  | (13) |
where
R is the gas constant,
T is the absolute temperature,
F is Faraday's constant and the number of electrons
n = 2. The
catalyst potential equation can be rewritten as:
| |  | (14) |
where
k7,
k8 and
k9 are the rate constants,
θV is the coverage of the vacant sites,
θO is the
oxygen coverage of the active sites. Based on quasi-equilibrium
oxygen adsorption
| | 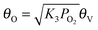 | (15) |
where
| |  | (16) |
The coverage of
oxygen on faces could be obtained from quasi-equilibria of step 4 and
eqn (15):
| |  | (17) |
where
K3 and
K4 are adsorption equilibrium constants of
oxygen on the edges and faces, respectively. From the balance equation of surface species, the fraction and coverage of vacant sites are given by
| |  | (18) |
And therefore
| |  | (19) |
where
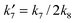
,

and

.
The oxidation reaction rate along the first route N(1) is defined in the following way:
| |  | (20) |
where
r is the reaction rate,
k5 is the rate constant,
K2 is the adsorption equilibrium constant of
L-arabinose on the faces,

is the adsorption equilibrium constant of
oxygen,
K11 is the adsorption equilibrium constant of the
hydroxide ions,
CA and
COH− are the relevant concentrations, and
PO2 is the
oxygen partial pressure.
The rate along the second route is given by
| |  | (21) |
Finally, the generation rates of compounds can be written as
| |  | (22) |
| | 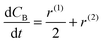 | (23) |
| |  | (24) |
The kinetic simulation used both the equations for potential and reaction rate, taking into account changes in the liquid phase volume due to addition of alkali and deduction of samples. The liquid phase concentration of
oxygen was calculated on the basis of its solubility.
27 The temperature dependence of only the rate constants
k5 and
k6 was assumed according to the Arrhenius equation
| | 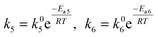 | (25) |
where
k5 and
k6 are the reaction rates,
k05 and
k06 are the pre-exponential factors,
Ea5 and
Ea6 the
activation energy,
R is the universal gas constant, and
T is the absolute reaction temperature. Temperature dependence for other constants was assumed to be negligible. Because of some variations of the values of the potential at the beginning of the experiments, these values of
catalyst potential were normalized.
For the calculation of parameters, a set of differential equations describing the changes in the concentration profiles of the reagents and products was solved by means of ModEst software.28 Using the Levenberg–Marquardt simplex method, the target function, which was defined as incompliance between the experimental and calculated values of concentrations and potential, was used to solve the system. The sum of the residual squares between the model and the experimental data was minimized using the following objective function:
| | 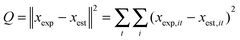 | (26) |
where
xexp is the experimental value and
xest denotes the predictions given by the model,
i is the component index and
t is the time value. The quality of the fit and accuracy of the model description was defined by the degree of explanation
R2| |  | (27) |
where
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) est
est is the mean value of all the data points.
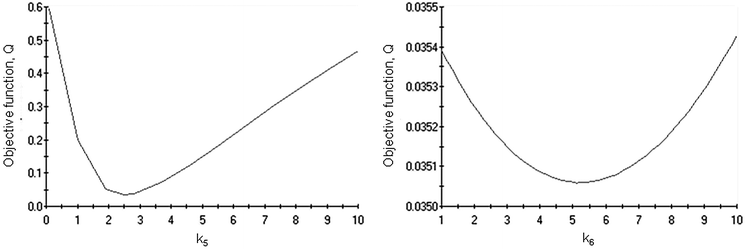
The results of the simulations are given in Table 1. The degree of explanation amounted to 98% evidencing a good compliance between the experimental data and the calculated values of the concentrations of the reagents and products and the catalyst potential. The fit of the kinetic model to the experimental data for the concentration profiles and normalized potential is shown in Fig. 7 and 8, respectively. Despite the relatively large number of parameters in the proposed mechanism and routes, the model was fitting the data with a good degree of accuracy. Sensitivity plots of two of the parameters, k5 and k6, the rate constants along the first and second routes, respectively, are presented in Fig. 9. The behaviour of most of the parameters was similar, obtaining a minimum of the objective function close to the estimated value. The model was able to rationalize the oxidative dehydrogenation mechanism taking into account the catalyst potential measured in situ. Some deviations observed in Fig. 7 and 8 could point out that the mechanism, especially steps involving transfer of electrons, could be even more complicated. The activation energy Ea for arabinonic acid was 23.9 kJ mol−1. The reliability of the determined values was verified by comparison to the apparent activation energy for the selective oxidation of L-arabinose to arabinonic acid, Ea 23.8 kJ mol−1 obtained by a different method11. The values obtained are in the same order of magnitude compared to other sugar oxidation reactions reported in the literature such as glucose to gluconic acid over Au/Al2O3 which was 27.0 kJ mol−1.29 By correlating the potential to the catalyst activity, it can be inferred that the common features characterizing both phenomena can be used for mechanistic analysis and elucidating reaction mechanisms.
| Parameter |
Value |
|
R
2 (%) |
98.7 |
|
K
1/l mol−1 |
Negligible |
|
K
2/l mol−1 |
0.120 × 102 |
|
K
3/bar−1 |
0.076 |
|
K
4/bar−1 |
0.956 × 10−2 |
|
k
5/l mol−1 s−1 |
2.521 |
|
k
6/l mol−1 s−1 |
5.074 |
|
k′7/l mol−1 |
0.609 × 10−10 |
|
k′9/l mol−1 |
0.462 × 10−16 |
|
K
10/l mol−1 |
Negligible |
|
K
11/l mol−1 |
0.493 × 10−3 |
|
K
12/l mol−1 |
0.390 |
|
E
a5/J mol−1 |
0.383 × 104 |
|
E
a6/J mol−1 |
0.239 × 105 |
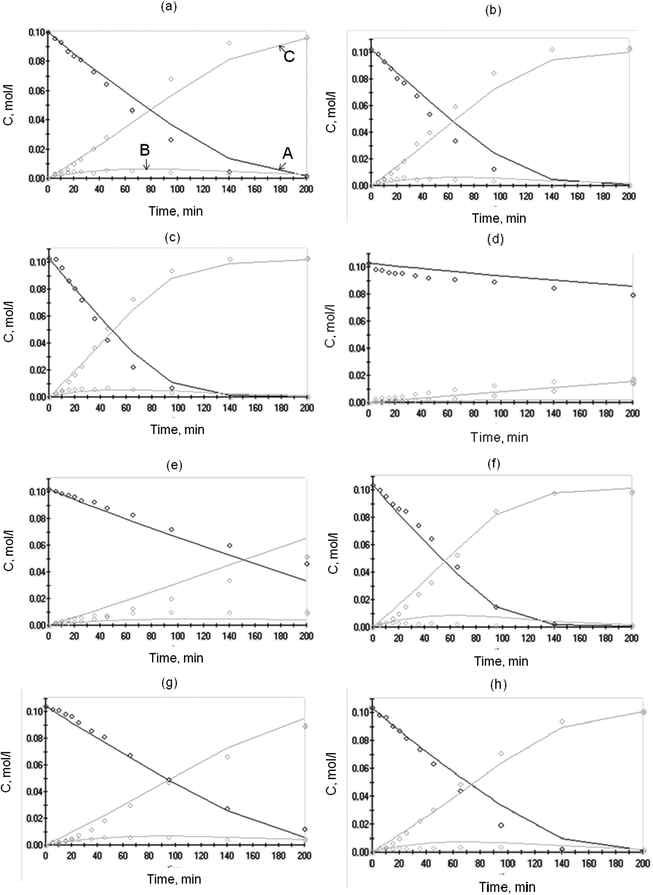 |
| | Fig. 7 Comparison of experimental (dots) and calculated (lines) concentration profiles (A—L-arabinose, B—arabinolactone, C—arabinonic acid) during L-arabinose oxidation over 1 wt% Au/Al2O3, m = 0.25 g at various temperatures, oxygen flow rates and pH: (a) 60 °C, 2.5 ml min−1, pH 8; (b) 60 °C, 3.5 ml min−1, pH 8; (c) 60 °C, 5.0 ml min−1, pH 8; (d) 60 °C, 2.5 ml min−1, pH 6; (e) 60 °C, 2.5 ml min−1, pH 7; (f) 60 °C, 2.5 ml min−1, pH 9; (g) 50 °C, 2.5 ml min−1, pH 8; (h) 70 °C, 2.5 ml min−1, pH 8. | |
 |
| | Fig. 8 Comparison of experimental (dots) and calculated (lines) for normalized potential during the selective oxidation of L-arabinose over 1 wt% Au/Al2O3 under the same conditions as in Fig. 7. | |
3. Experimental
3.1. Reactor setup
The oxidation of L-arabinose was performed in a tailor-made shaker reactor equipped with in situ catalyst potential measurements and a pH controller (Fig. 10). This reactor setup is convenient and well suited for such measurements due to a high shaking frequency (0.25 s−1) and at the same time, allowing the use of multiple electrodes and sensors all fitted into the reaction vessel. It also facilitates efficient mixing with the elimination of stagnant zones in the reaction mixture and improved gas-to-liquid mass transfer. Catalytic experiments were carried out in a semi-batch mode and a constant gas flow of oxygen in nitrogen was applied.
 |
| | Fig. 10 Tailor made shaker reactor setup for catalytic experiments with in situ catalyst potential measurements and pH controller. | |
After the introduction of 0.25 g catalyst with the particle size range below 63 μm to eliminate any internal diffusion limitations, which was suspended in water, the catalyst was exposed to hydrogen (AGA, 99.999%), at 60 °C for 10 min. Thereafter, the reactor was flushed with nitrogen. L-Arabinose (Danisco, 99%) was introduced into the reactor as an aqueous solution. At the beginning of each experiment, the overall mass of the reaction mixture was 100 g and the initial L-arabinose concentration in the reactor was 100 mmol l−1. The reaction was commenced by the introduction of oxygen into the nitrogen gas flow through mass flow controllers (Brooks 5850E) using the total gas flow of oxygen and nitrogen at 20 ml min−1. The pH of the reaction mixture was kept constant during the experiment by controlled addition of 2.5 M NaOH solution by an automatic titration device (Metrohm Titrino 751). The catalyst potential was measured in situ with an Ag/AgCl/3 M KCl reference electrode by using potential measurements from stainless steel wall, which acted as an electrode collector for the measurements of the catalyst potential.9,11
For the kinetic experiments, the reaction parameters, such as pH of the reaction medium, oxygen flow rate and temperature, were varied in a systematic manner. The pH range studied was 6–9. The oxygen flow rates of 2.5–5.0 ml min−1 and a temperature of 50–70 °C were applied.
3.2. Analysis of the reaction mixture
The samples (1 ml) were periodically withdrawn from the reactor for analysis. The concentration profiles of the reactants and the products were monitored by means of high precision liquid chromatography (HPLC, Hewlett Packard Inc.), equipped with a Bio-Rad Aminex HPX-87C carbohydrate column. The column temperature of 80 °C and 1.2 mM CaSO4 eluent flow rate of 0.4 ml min−1 were applied.9,11
3.3. Catalyst characterization
The catalyst, 1 wt% Au/Al2O3, was supplied by Mintek. The metal loading of the catalysts was determined by inductively coupled plasma optical emission spectrometry (ICP-OES) in a PerkinElmer, Optima 5300 DV spectrometer. The average metal particle size was determined by transmission electron microscopy (TEM). The histogram showing the size distribution for the gold nanoparticles is presented in Fig. 11. The gold nanoparticles supported on the metal oxide support were characterized by a uniform and narrow distribution of the metal particles. The average particle size obtained for Au/Al2O3 was 2.3 nm.
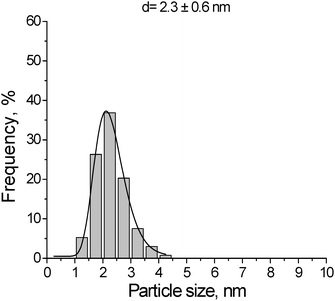 |
| | Fig. 11 Histogram showing gold particle size distribution for 1 wt% Au/Al2O3 catalyst, d = 2.3 ± 0.6 nm. | |
XPS analysis was conducted to investigate the electronic state of the gold catalyst. The XPS measurements were carried out in a PHI Quantum 2000 Scanning ESCA Microprobe spectrometer equipped with an AlKα (1486.6 eV) anode. The Au 4f region was deconvoluted considering three oxidation states: Au0, Au+ and Au3+ at 84.0, 84.6 and 85.9 eV, respectively.30–32 The deconvolution of the Au 4f spectrum of Au/Al2O3 showed the presence of gold in the metallic state Au0 with the peak shifted towards a lower binding energy of 84.0 eV.
4. Conclusions
The kinetics of aqueous-phase selective oxidation of L-arabinose over gold catalysts was studied in this work. The behavior of the catalyst potential under pH controlled conditions was correlated to the surface processes and catalyst activity. The shift of the potential during the course of the reaction expresses the situation of the catalyst surface with the adsorbed species. An oxidative dehydrogenation mechanism was proposed and the links between electrochemistry and catalysis were adopted for the interpretation of the phenomena occurring in the aqueous phase of this heterogeneous catalytic system. The influence of reaction conditions, i.e. pH of the reaction medium, oxygen partial pressure and temperature on the kinetics was demonstrated. The reaction was successfully described by the proposed oxidative dehydrogenation mechanism in the aqueous phase which was validated by the experimental observations. Based on the suggested mechanism and the experimental data, kinetic equations were derived and kinetic parameters were calculated by the model.
Acknowledgements
This work is part of the activities at the Åbo Akademi University Process Chemistry Centre (PCC) within the Finnish Centre of Excellence Programme (2000–2011) appointed by the Academy of Finland. Krisztián Kordás, Anne-Riikka Leino and Betiana Campo are gratefully acknowledged for their assistance in catalyst characterization, and Professor Johan Wärnå for his expertise in kinetic modelling.
References
- G. Horanyi, Catal. Today, 1994, 19, 285–312 CrossRef CAS.
- M. I. Temkin, Adv. Catal., 1979, 28, 173–281 CrossRef CAS.
-
J. O'M. Bockris and S. Srinivasan, Fuel Cells: Their Electrochemistry, McGraw-Hill, New York, 1969 Search PubMed.
- B. E. Conway and B. V. Tilak, Adv. Catal., 1992, 38, 1–147 CrossRef CAS.
- A. V. Tokarev, L. M. Kustov, A. Ivaska, D. Yu and Murzin, Appl. Catal., A, 2006, 309, 52–61 CrossRef CAS.
- S. Trasatti and R. Parsons, Pure Appl. Chem., 1986, 58, 437 CrossRef CAS.
- D. Yu. Murzin, E. V. Murzina, A. V. Tokarev and J.-P. Mikkola, Russ. J. Electrochem., 2009, 45, 1017–1026 CrossRef.
- V. R. Gangwal, B. G. M. van Wachem, B. F. M. Kuster and J. C. Schouten, Chem. Eng. Sci., 2002, 24, 5051–5063 CrossRef.
- A. V. Tokarev, E. V. Murzina, J. Kuusisto, J.-P. Mikkola, K. Eränen and D. Yu. Murzin, J. Mol. Catal. A: Chem., 2006, 255, 199–208 CrossRef CAS.
- T. Mallat and A. Baiker, Catal. Today, 1994, 19, 247–284 CrossRef CAS.
- B. T. Kusema, B. C. Campo, P. Mäki-Arvela, T. Salmi and D. Yu. Murzin, Appl. Catal., A, 2010, 386, 101–108 CrossRef CAS.
- B. T. Kusema, B. C. Campo, O. A. Simakova, A.-R. Leino, K. Kordás, P. Mäki-Arvela, T. Salmi and D. Yu. Murzin, ChemCatChem, 2011, 3, 1789–1798 CrossRef CAS.
- A. V. Tokarev, E. V. Murzina, J.-P. Mikkola, J. Kuusisto, L. M. Kustov and D. Yu. Murzin, Chem. Eng. J. (Amsterdam, Neth.), 2007, 134, 153–161 CAS.
- A. Mirescu and U. Pruße, Appl. Catal., B, 2007, 70, 644–652 CrossRef CAS.
- J. N. Chheda, G. W. Huber and J. A. Dumesic, Angew. Chem., Int. Ed., 2007, 46, 7164–7183 CrossRef CAS.
- P. Mäki-Arvela, B. Holmbom, T. Salmi and D. Yu. Murzin, Catal. Rev., 2007, 49, 197–340 Search PubMed.
-
F. W. Lichtenthaler, Ullmanns Encyclopedia of Industrial Chemistry, Carbohydrates, Electronic Release, Wiley–VCH, New York, 2002 Search PubMed.
- D. T. Sawyer, Chem. Rev., 1964, 64, 633–644 CrossRef CAS.
- U. Pruße, K. Heidkamp, N. Decker, M. Herrmann and K.-D. Vorlop, Chem.-Ing.-Tech., 2010, 8, 1231–1237 Search PubMed.
- K. Đ. Popović, A. V. Tripković and R. R. Adžić, J. Electroanal. Chem., 1992, 339, 227–245 CrossRef.
- V. R. Gangwal, J. van der Schaaf, B. F. M. Kuster and J. C. Schouten, J. Catal., 2004, 229, 389–403 CrossRef.
- G. C. Bond and D. T. Thompson, Gold Bull., 2000, 33, 41–52 CrossRef CAS.
- A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936 CrossRef.
- M. Haruta, Gold Bull., 2004, 37, 27–36 CrossRef CAS.
- K. Okazaki, S. Ichikawa, Y. Maeda, M. Haruta and M. Kohyama, Appl. Catal., A, 2005, 291, 45–54 CrossRef CAS.
- O. A. Simakova, B. T. Kusema, B. C. Campo, A.-R. Leino, K. Kordás, V. Pitchon, P. Mäki-Arvela and D. Yu. Murzin, J. Phys. Chem. C, 2011, 115, 1036–1043 CAS.
-
P. G. T. Fogg and W. Gerrard, Solubility of Gases in Liquids, Chichester, Wiley, 1991, p.293 Search PubMed.
-
H. Haario, ModEst User's Guide 6.1, ProfMath Oy, Helsinki, 2002 Search PubMed.
- T. Ishida, N. Kinoshita, H. Okatsu, T. Akita, T. Takei and M. Huruta, Angew. Chem., Int. Ed., 2008, 47, 9265–9268 CrossRef CAS.
- Q. Fu, H. Saltsburg and M. Flytzani-Stephanopoulos, Science, 2003, 301, 935–938 CrossRef CAS.
- Q. Fu, W. Deng, H. Saltsburg and M. Flytzani-Stephanopoulos, Appl. Catal., B, 2005, 56, 57–68 CrossRef CAS.
- A. M. Venezia, G. Pantaleo, A. Longo, G. Di Carlo, M. P. Casaletto, L. F. Liotta and G. Deganello, J. Phys. Chem. B, 2005, 109, 2821–2827 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 







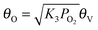




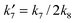 ,
,  and
and  .
.

 is the adsorption equilibrium constant of oxygen, K11 is the adsorption equilibrium constant of the hydroxide ions, CA and COH− are the relevant concentrations, and PO2 is the oxygen partial pressure.
is the adsorption equilibrium constant of oxygen, K11 is the adsorption equilibrium constant of the hydroxide ions, CA and COH− are the relevant concentrations, and PO2 is the oxygen partial pressure.


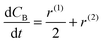

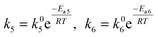
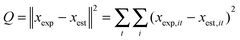

![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) est is the mean value of all the data points.
est is the mean value of all the data points.