Activation of C–Cl by ground-state aluminum atoms: an EPR and DFT investigation

Abstract

The reaction of ground-state Al atoms with dichloromethane (CH₂Cl₂) in an adamantane matrix at 77 K yielded two mononuclear Al species. The magnetic parameters, extracted from the axial EPR spectrum of Species A/A′ (g₁ = 2.0037, g₂ = g₃ = 2.0030, a_Al,1 = 1307 MHz, a_Al,2 = a_Al,3 = 1273 MHz, a_35Cl = 34 MHz and a_37Cl = 28 MHz) were assigned to the Al-atom insertion product, ClCH₂AlCl. Density functional theory (DFT) calculations of the values of the Al and Cl hyperfine interaction (hfi) of the Cl₁–Cl₂gauche conformer were in close agreement with the experimental values of ClCH₂AlCl. The second species, B/B′, had identical magnetic parameters to those of ClCH₂AlCl with the exception that the Al hfi was 15% smaller. Coordination of a ligand, possessing a lone pair of electrons, to the Al atom of the insertion product, [ClCH₂AlCl]:X, could cause the a_Al to decrease by 15%. Alternatively, it is possible that the Cl₁–Cl₂ anti conformer of ClCH₂AlCl is also isolated in the matrix. Support for the spectral assignments is given by calculation of the nuclear hfi of [ClCH₂AlCl]:H₂O and the Cl₁–Cl₂ anti conformer of ClCH₂AlCl using a DFT method. The potential energy hypersurface for an Al atom approaching CH₂Cl₂, calculated at the B3LYP level, suggests that Al atom abstraction of Cl forming AlCl and CH₂Cl is favoured in the gas phase. When produced in a matrix, the close proximity of AlCl and CH₂Cl could account for the formation of ClCH₂AlCl. EPR evidence was also found for the formation of the CHCl₂ radical.

---

Introduction

A strategy used to destroy man-made environmental pollutants, such as halogenated organic compounds, involves finding ways to activate the C–Cl or C–F bonds.^1,2 Ground-state Al (²P_1/2) atoms have been shown to activate a number of different types of bonds resulting in the formation of insertion products. Experiments involving NH₃,^3,4H₂O,⁵ H₂S, H₂Se,⁶CH₃OCH₃,^7,8 and CH₄⁹ yielded HAlNH₂, HAlOH, HAlSH, HAlSeH, CH₃AlOCH₃ and CH₃AlH, respectively, indicating that Al atoms can activate N–H, O–H, S–H, Se–H, C–O and C–H bonds. Al atoms have also been reported to activate the C–C bond of cyclohexanol,¹⁰1-methylcyclohexanol¹⁰ and diethyl ether.^8,11 With respect to halogenated compounds, co-condensation of Al atoms with HCl in an Ar matrix resulted in the formation of HAlCl^12,13 at low concentration while increasing the HCl concentration to ∼8% yielded AlCl₂. Finally, reaction of ground-state Al atoms with bromocyclopropane (CpBr) in adamantane at 77 K gave the two C–Br insertion products CpAl⁷⁹Br and CpAl⁸¹Br as well as the allyl radical.¹⁴

The above-mentioned Al-centered radicals were characterized by EPR spectroscopy. The magnitude of the isotropic Al hyperfine interactions (hfi) of the radicals is related to the nature of the ligands attached to Al, i.e., the Al hfi increases as the electron-withdrawing ability of the ligands increase.

Matrix-isolation infrared spectroscopy was used to study the reaction of Group 13 metal atoms (M) with halomethanes (CH₃X).^15,16 In the case of CH₃Br, a weak CH₃Br-M complex¹⁶ formed at low temperatures (<77 K) while higher temperatures favoured the formation of a “Grignard reagent”, CH₃MBr, via the oxidative addition^15,16 of CH₃Br to the metal. Insertion into the C–Br bond is the preferred reaction because of the low first ionization potentials (IP) of the Group 13 metal atoms and the large Group 13 metal–Br bond energies.¹⁶ In a recent study¹⁷ involving laser–ablated Pd atoms, Cho et al. found that only insertion complexes, HCX₂PdX formed in reactions with halomethanes containing H.

In the present study, the EPR investigation of the paramagnetic products resulting from the reaction of dichloromethane (CH₂Cl₂) with Al atoms, under matrix-isolation conditions, confirmed that C–Cl activation was possible. The spectral features are attributed to the Al-atom C–Cl insertion product, ClCH₂AlCl. Annealing the sample to higher temperatures led to the detection of a product with spectral features similar to those of ClCH₂AlCl with the exception of the magnitude of the Al hfi. The species is either ClCH₂AlCl in another conformation or [ClCH₂AlCl]:X where X is H₂O. A comparison of the experimental values of the Al and Cl hfi to those calculated for ClCH₂AlCl using density functional theory (DFT) supports the spectral assignments. A map of the potential energy hypersurface corresponding to the approach of an Al atom to CH₂Cl₂ indicated that in the gas phase formation of AlCl is barrierless. The combination of AlCl with CH₂Cl gives the observed insertion product. Finally, CHCl₂ dominates the center of the spectrum.

Experimental section

Preparation of Al atom–CH₂Cl₂ reaction mixtures

The CH₂Cl₂, CD₂Cl₂ and adamantane were the purest available commercial products (Aldrich) and were used as received after being subjected to a number of freeze-thaw cycles on a vacuum line.

The method used to prepare the reaction mixture of ground-state Al atoms with CH₂Cl₂ or CD₂Cl₂, has been described in detail elsewhere.¹⁸Aluminum wire, (Alpha Products) in a tungsten basket (No. 12070, Ernest F. Fullam, Inc., Schenectady, NY) suspended between the electrodes of a furnace, was resistively heated to produce Al atoms. The Al atoms, CH₂Cl₂ or CD₂Cl₂ and adamantane were co-condensed on the surface of the rotating liquid nitrogen-filled drum situated in the metal-atom reactor. During the experiment (ca. 10 to 12 min) the reactor was maintained at <10⁻⁵ Torr. A sample of the reaction mixture was scraped into a suprasil quartz tube and sealed under vacuum while maintaining a temperature of 77 K. EPR analysis was carried out between 77 and 298 K on a Varian E line spectrometer operating an X-band. A Varian gaussmeter and a Systron-Donner 6016 frequency counter were used in obtaining calibrated spectra. The magnetic parameters of the paramagnetic products were determined using the computer programs, ESRLSQ,¹⁹ EPRNMR²⁰ or ISOPLOT.¹⁹

Computational methods

(i) Geometry and nuclear hyperfine interaction (hfi)

The Gaussian 09²¹ suite of programs was used to calculate the values of the Al, H and ³⁵Cl hfi for ClCH₂AlCl. Full geometry optimization of ClCH₂AlCl was carried out at the correlated ab initio (QCISD method) and density functional levels of theory (B3LYP and B3P86). In the QCISD method²² the electron correlation was included through configuration interaction. The B3LYP²³ functional combines Becke's three parameter exchange functional²⁴ with Lee, Yang and Parr's²⁵ correlation functional which includes both local and non-local terms. B3P86 combines the exchange functional mentioned above with the non-local correlation introduced by Perdew.²⁶ The split valence 6-31G(df,p) basis set was used in the optimization of the insertion radical's geometry. In an exploratory investigation of the ClCH₂AlCl radical the 6-31G(df,p) basis set gave values for the Al hfi that agreed more closely with the experimental values than the basis set most often used in these types of calculations, namely the 6-31G(d,p).^10,13 The radical was characterized using frequency analysis. The Al, H and ³⁵Cl nuclear hfi values were determined from single point calculations using the following methods: B3LYP/6-311+G(2df,p), BHandHLYP/6-311+G(2df,p), BHandHLYP^25,27,28/6-311G(d,p), and mPWP86^26,29,30/IGLO-III.³¹

(ii) Born–Oppenheimer potential energy surface

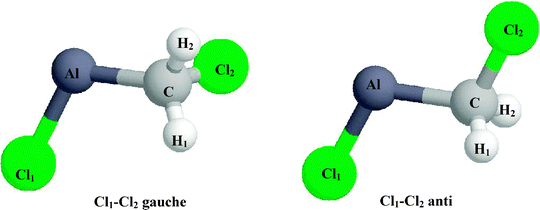
The Born–Oppenheimer potential energy surface for the lowest-energy doublet was calculated at the B3LYP level with a 6-31G(df,p) basis set by optimizing the geometry of the radical with fixed C–Cl₁ and C–Al distances. We chose to investigate the energy cross-section over the (C–Al, C–Cl₁) plane using geometries in which the dihedral angle defined by Cl₂, C, Al, and Cl₁ was approximately 90°. In calculations where no constraint was placed on the structures, the dihedral angle defined by Cl₂, C, Al, and Cl₁ for the most stable geometry was 91.1°. The B3LYP functional was used so that a comparison could be made with results previously reported for a similar system, namely, the reaction of Al atoms with CpBr.¹⁴

Results

EPR analysis of the products resulting from the reaction of Al atoms with CH₂Cl₂ revealed two overlapping sextets, labeled ³⁵A/³⁷A and ³⁵B/³⁷B (Fig. 1), in addition to a strong central feature (C). Five of the six transitions, characteristic of mononuclear Al (I = 5/2) radicals, are indicated for both ³⁵A/³⁷A and ³⁵B/³⁷B on the EPR spectrum recorded at 145 K. Close inspection of the Al transitions for each of ³⁵A/³⁷A and ³⁵B/³⁷B revealed superhfi consistent with the unpaired electron interacting with a nucleus with I = 3/2. Chlorine has two EPR active isotopes ³⁵Cl (I = 3/2, μ = +0.82181β_n, natural abundance = 75.53%)³² and ³⁷Cl (I = 3/2, μ = +0.68407 β_n, natural abundance = 24.47%).³² The high and low field features were simulated by assuming a mixture of ³⁵A/³⁷A, with the magnetic parameters g₁ = 2.0037 ± 0.0003, g₂ = g₃ = 2.0030 ± 0.0003, a₁(Al) = 1307 ± 1 MHz, a₂(Al) = a₃ (Al) = 1273 ± 1 MHz, a_35Cl = 34 ± 1 MHz and a_37Cl = 28 ± 1 MHz and ³⁵B/³⁷B with the magnetic parameters g₁ = g₂ = g₃ = 2.0030 ± 0.0003, a₁ (Al) = a₂(Al) = a₃ (Al) = 1086 ± 1 MHz, a_35Cl = 34 ± 1 MHz and a_37Cl = 28 ± 1 MHz. The a_35Cl/a_37Cl = μ_35Cl/μ_37Cl = 1.21 and the value of the ³⁵A/³⁷A and ³⁵B/³⁷B ratios used in the simulation was 3.09, i.e., the ratio of the natural abundance of ³⁵Cl to ³⁷Cl. The best simulation was obtained using a ratio of ³⁵A to ³⁵B of 13 to 1.

Fig. 1 (a) Five of the six Al EPR transitions for the paramagnetic species (³⁵A/³⁷A and ³⁵B/³⁷B) formed in the reaction of Al atoms with CH₂Cl₂ in an adamantane matrix. The low- and high-field regions of the EPR spectrum were recorded at 145 K (9120 MHz, microwave power [m.p. = 2 mW]); (b) Simulation of the low- and high-field regions of the EPR spectrum assuming the magnetic parameters for Species ³⁵A/³⁷A and for Species ³⁵B/³⁷B found in the text.

The EPR spectrum of the major product, Species C, recorded at 195 K, shown in Fig. 2, was simulated using the magnetic parameters g = 2.011, a_H(1) = 47.6 MHz and a_Cl(2) = 11.2 MHz.

Fig. 2 (a) The central region of the EPR spectrum of the Al–CH₂Cl₂ reaction mixture recorded at 195 K (9120 MHz, m.p. = 20 mW). (b) Simulation of the central feature assuming g = 2.011, a_H(1) = 47.6 MHz, and a_Cl(2) = 11.2 MHz.

Mononuclear Al radicals with magnetic parameters similar to those of Species ³⁵A/³⁷A and ³⁵B/³⁷B were found for the reaction of Al atoms with CD₂Cl₂. A comparison of the Al transitions of ³⁵A/³⁷A, Fig. 3a, and ³⁵B/³⁷B, Fig. 3c, with those obtained in the Al atom–CD₂Cl₂ reaction (Fig. 3b and d) did not show noticeable narrowing indicating that the unpaired electron on Al does not interact with H atoms in the CH₂Cl₂. The EPR spectrum of the central feature of the Al atom–CD₂Cl₂ reaction was simulated with the magnetic parameters g = 2.008, a_D(1) = 7.3 MHz and a_Cl(2) = 11.2 MHz, Fig. 4. It should be noted that the a_D was estimated by dividing the value of a_H by 6.5, i.e., the ratio of the magnetogyric ratios for the H and D nuclei.³²

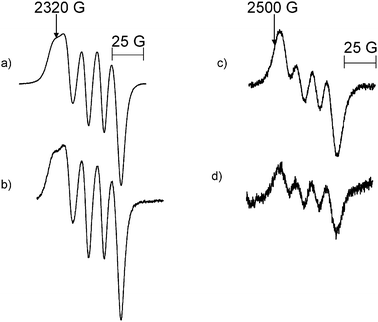Fig. 3 The M_I = 1/2 transition of species ³⁵A/³⁷A formed in (a) the reaction of Al atoms with CH₂Cl₂ (T = 115 K, m.p. = 20 mW and ν = 9120 MHz) (b) the reaction of Al atoms with CD₂Cl₂ (T = 115 K, m.p. = 20 mW and ν = 9121 MHz). The M_I = 1/2 transition of species ³⁵B/³⁷B formed in (c) the reaction of Al atoms with CH₂Cl₂ (T = 115 K, m.p. = 20 mW and ν = 9120 MHz) (d) the reaction of Al atoms with CD₂Cl₂ (T = 115 K, m.p. = 20 mW and ν = 9120 MHz).

Fig. 4 (a) The central region of the EPR spectrum of the Al- CD₂Cl₂ reaction mixture recorded at 195 K (9119 MHz, m.p. = 20 mW). (b) Simulation of the central feature assuming g = 2.008, a_D(1) = 7.3 MHz and a_Cl(2) = 11.2 MHz.

Computational results

We have been able to determine two stationary points for ClCH₂AlCl, namely, the Cl₁–Cl₂gauche and Cl₁–Cl₂ anti conformers. The geometry of these conformers was optimized using three different levels of theory, Table 1. The DFT calculations indicate that the Cl₁–Cl₂gauche conformer is slightly more stable than the anti conformer in the case of the B3LYP (0.7 kcal/mole) and the B3P86 (1.1 kcal/mole) calculations while the Cl₁–Cl₂ anti conformer is more stable in the QCISD calculations (0.8 kcal/mole). These small energy differences suggest that both of the two conformers are equally probable.

Table 1 Optimized geometries corresponding to the Cl₁–Cl₂gauche and anti conformers of ClCH₂AlCl. The interatomic distances, angles, dihedral angles and energy (hartrees) were obtained from QCISD/6-31G(df,p), B3LYP/6-31G(df,p), and B3P86/6-31G(df,p) calculations

	QCISD/6-31G(df,p)	B3LYP/6-31G(df,p)	B3P86/6-31G(df,p)	QCISD/6-31G(df,p)	B3LYP/6-31G(df,p)	B3P86/6-31G(df,p)
Cl1–Al (Å)	2.099	2.134	2.124	2.098	2.139	2.126
Al–C (Å)	1.962	1.990	1.973	1.985	2.005	1.993
C–Cl2 (Å)	1.845	1.847	1.844	1.788	1.815	1.799
C–H1 (Å)	1.085	1.090	1.088	1.091	1.093	1.093
C–H2 (Å)	1.086	1.089	1.089	1.091	1.093	1.093
∠AlCCl2 (°)	82.4	94.3	87.0	111.2	111.5	110.7
∠AlCH1 (°)	121.2	117.2	120.1	111.1	111.0	111.2
∠AlCH2 (°)	121.1	118.0	119.5	111.1	111.0	111.2
∠Cl1AlC (°)	117.7	116.9	116.7	115.9	114.2	114.5
D(Cl2CAlCl1) (°)	−93.0	−91.1	−91.9	180.0	180.0	180.0
D(H2CAlCl1) (°)	161.7	157.1	160.2	59.7	60.1	60.1
D(H1CAlCl1) (°)	12.5	20.8	16.2	−59.7	−60.1	−60.1
Energy (hartrees)	−1199.954657	−1202.177273	−1203.202415	−1199.955855	−1202.176135	−1203.200598

---

Single point calculations, using the computational methods listed in column 1 of Table 2 were used to determine the nuclear hfis of the gauche and anti conformers of ClCH₂AlCl. In the case of the Cl₁–Cl₂gauche conformer the variation in the Al and Cl hfi is ≈6–7% and ≈10–12%, respectively, for all four methods tested. Similarly, the variation in the Al and Cl hfi is ≈2–3% and ≈9–10%, respectively, for the Cl₁–Cl₂ anti conformer. This indicates that the effect on the value of the Al hfi of using different levels of theory to optimize the geometry of the conformers is relatively small. In comparing the results for the two conformers optimized at the same level of theory we note that the Al and Cl hfi are larger for the Cl₁–Cl₂gauche conformer in all cases. The increase in the value of the Al hfi in going from the anti to the gauche conformer is between 12–14%, 4–6% and 9–11% for the geometries optimized using the QCISD, B3LYP and B3P86 levels of theory, respectively, while the value of the Cl hfi increases by 8–13%, 7–12% and 8–14%, respectively. Although the variation in the H hfi is large for both conformers, it is interesting to note that (a) the hfi for H₁ and H₂ are approximately the same for the anti conformer while for the gauche conformer the H₁ hfi is larger than that of H₂; (b) the H₁ hfi of the anti conformer (1.3–5.6 MHz) is significantly smaller than that of the gauche conformer (10.5–16.1 MHz).

Table 2 The values of the Al, Cl and H hfi (in MHz) were calculated at the B3LYP/6-311+G(2df,p), BHandHLYP/6-311+G(2df,p), BHandHLYP/6-311G(d,p) and mPWP86/IGLO-III levels for the (a) Cl₁–Cl₂gauche conformer and (b) Cl₁–Cl₂ anti conformer optimized at the QCISD/6-31G(df,p), B3LYP/6-31G(df,p) and B3P86/6-31G(df,p) levels of theory, respectively

		Geometry
Method	Nuclei	QCISD/6-31G(df,p)	B3LYP/6-31G(df,p)	B3P86/6-31G(df,p)
(a) Cl1–Cl2gauche conformation
B3LYP/6-311+G(2df,p)	Al	1264.45	1182.53	1241.90
	Cl	37.42	33.30	34.66
	H1, H2	11.31, −5.80	14.43, −7.85	12.52, −6.76
BHandHLYP/6-311+G(2df,p)	Al	1298.68	1223.70	1280.22
	Cl	39.95	36.12	37.38
	H1, H2	10.51, −6.68	12.92, −9.22	11.43, −7.87
BHandHLYP/6-311G(d,p)	Al	1311.45	1234.80	1291.81
	Cl	39.45	35.64	36.84
	H1, H2	11.21, −6.61	13.55, −9.22	12.09, −7.84
mPWP86/IGLO-III	Al	1231.43	1145.07	1206.16
	Cl	34.15	30.22	31.53
	H1, H2	12.24, −4.80	16.10, −6.49	13.7, −5.59
(b) Cl1–Cl2 anti conformation
B3LYP/6-311+G(2df,p)	Al	1099.25	1124.90	1117.31
	Cl	33.57	30.24	30.91
	H1, H2	3.11, 3.10	3.58, 3.58	3.31, 3.32
BHandHLYP/6-311+G(2df,p)	Al	1146.41	1177.04	1168.04
	Cl	36.94	33.70	34.38
	H1, H2	1.31, 1.30	1.58, 1.58	1.41, 1.42
BHandHLYP/6-311G(d,p)	Al	1155.39	1186.72	1177.11
	Cl	36.47	33.18	33.84
	H1, H2	1.32, 1.31	1.60, 1.60	1.43, 1.43
mPWP86/IGLO-III	Al	1059.09	1079.14	1073.69
	Cl	29.69	26.58	27.2
	H1, H2	4.92, 4.92	5.55, 5.54	5.18, 5.19

---

Discussion

Spectrum ³⁵A/³⁷A

Spectrum ³⁵A/³⁷A can be described as two overlapping sextets of quartets corresponding to two mononuclear Al compounds containing ³⁵Cl and ³⁷Cl, respectively. The isotropic Al hfi, of ³⁵A/³⁷A, calculated from the equation (A_iso = (a₁+a₂+a₃)/3),³² is 1284 MHz. A comparison of this value to those reported in the literature for divalent Al radicals, Table 3, suggests that the C–Cl insertion products, ClCH₂Al³⁵Cl and ClCH₂Al³⁷Cl have generated Spectrum³⁵A/³⁷A. More specifically, the value of A_iso for ClCH₂AlCl falls between that of HAlCl and ClAlCl. This is consistent with the observation³³ that the magnitude of the Al hfi increases as the electronegativity (or the electron-withdrawing ability) of the ligands increases. This is obvious in comparing the A_iso for HAlH, HAlCl and ClAlCl. Replacing H by Cl in going from HAlH to HAlCl causes the Al hfi to increase by 25% and by 30% in going from HAlCl to ClAlCl. As the ligands become more electron-withdrawing the ionic character of the σ-bonds to Al increases. This is translated to sp_x hybrid orbitals with greater p-character and a semi-occupied molecular orbital (SOMO) with higher s character. Therefore we would expect A_iso for ClCH₂AlCl to be greater than that of HAlCl but less than that of ClAlCl because the electron-withdrawing ability of ClCH₂ is in between that of H and Cl.

Table 3 The values of the nuclear hfi (in MHz) and Al 3s unpaired spin population (ρ_3s) of several mononuclear Al insertion products

Radical	a Al	a H	a X	ρ 3s	Ref.
CH3AlH	772	152	—	0.20	9
HAlH	834	128	—	0.21	33
HAlOH	911	286	—	0.23	5, 6
HOAlOH	1220	—	—	0.31	33
HAlSH	984	210	—	0.25	6
HAlSeH	941	134	20 (H)	0.24	6
HAlCl	1115	279	31 (Cl)	0.29	12, 13
ClAlCl	1598	—	31 (Cl)	0.41	12, 13
ClCH2AlCl	1284	—	34 (Cl)	0.33	This work
HAlNH2	923	229	27 (N)	0.24	3
			27 (H)
CH3AlOCH3	1002	—	—	0.26	8
CpAl^79Br	1041	—	176 (^79Br)	0.27	14
CpAl^81Br	1042	—	190 (^81Br)	0.27	14

---

The Al 3s-spin contribution, ρ_3s, to the SOMO, estimated by dividing the A_iso values for the divalent Al radicals by the one-electron atomic parameter for an Al 3s (3911 MHz)³² orbital, has been included in Table 3. While the values range from 0.20–0.41, the ρ_3s for ClCH₂AlCl is 0.33 indicating that the σ-bonds involving Al are slightly more ionic than those of HAlCl.

DFT methods have been very useful in predicting the Al hfi of a number of divalent organoaluminium radicals.^14,34,35 Many different density functionals are available. It is not obvious which are the best suited for use in the DFT calculation of nuclear hfi. One of the main factors influencing the selection of a functional is its reported effectiveness in predicting the nuclear hfi of well-characterized systems.³⁶ We have had success in predicting the Al hfi of several divalent Al compounds by optimizing their geometries with the split valence 6-31(d,p) basis set and determining the nuclear hfi with the B3LYP functional and the 6-311+G(2df,p) basis set.³⁵ This method predicted values that deviated from the experimental values by no more that 8%. In a theoretical study carried out by Fängström et al.¹³ on the Al–atom insertion products of HCl and Cl₂, similar agreement was obtained between experiment and theory at the B3LYP/6-311+G(2df,p)//6-31G(d,p) and mPWP86/IGLO-III//QCISD/6-31G(d,p) levels. The Becke half and half functional (BHandH)^27,28 with the nonlocal correlation of Lee, Yang and Parr²⁵ (LYP) has been found to be effective in calculating the geometries and nuclear hfi of open shell systems.³⁷ Consequently, the nuclear hfi of the two conformers of ClCH₂AlCl were calculated at the B3LYP/6-311+G(2df,p), BHandHLYP/6-311+G(2df,p), BHandHLYP/6-311G(d,p) and mPWP86/IGLO-III levels of theory, Table 2.

In general, the deviation between the experimental Al (1284 MHz) and ³⁵Cl (34 MHz) hfi and the calculated values is smaller for the gauche conformer; the Al and ³⁵Cl hfi deviate from the experimental values by 0.2–11% and 1–18%, respectively for the gauche conformer and by 8–17% and 1–22% for the anti conformer. The Al and ³⁵Cl hfi values calculated at the B3LYP/6-311+G(2df,p)//B3P86/6-31G(df,p) level of theory for the gauche isomer agree the best with the experimental values; i.e., the deviation between the calculated and experimental values is 3% for the Al hfi and 2% for the Cl hfi. This is well within the expected error for these types of calculations.^14,34,35 At the same level of theory, the Al and Cl hfi calculated for the anti conformer differ from experiment by 13% and 9%, respectively. Experimentally the H hfi is too small to detect. The variation in the H hfi of the gauche conformer predicted by the different theoretical models is large making it difficult to draw any definitive conclusions.

Spectrum ³⁵B/³⁷B

The spectral pattern labeled ³⁵B/³⁷B in Fig. 1 is identical to that of ³⁵A/³⁷A, i.e., a sextet of quartets. As in the case of ³⁵A/³⁷A, one can deduce that the unpaired electron is interacting with an Al (I = 5/2) and a ^35/37Cl (I = 3/2) nucleus. The Al hfi (1086 MHz) extracted from the ³⁵B/³⁷B spectrum is 15% smaller than that of ClCH₂AlCl while the ³⁵Cl and ³⁷Cl hfi are identical, i.e., a_35Cl = 34 MHz and a_37Cl = 28 MHz.

As previously mentioned, the difference in the calculated energy for the Cl₁–Cl₂gauche versus the anti conformer is small suggesting that both conformers are equally possible. In addition, the theoretical methods predict a decrease of up to 14% in the Al hfi in going from the gauche to the anti conformer. This is close to the 15% difference in Al hfi found between the Al hfi of Species ³⁵A/³⁷A and ³⁵B/³⁷B. In a study involving the reaction of Al atoms with dimethyl ether, Kasai⁷ found that both the cis and trans conformers of CH₃OAlCH₃ were formed. In this case the Al hfi for the cis conformer was greater than that for the trans conformer by 14%. Although theory predicted only a marginal difference in stability, the trans conformer was more abundant indicating that it was in fact more stable. ³⁵B/³⁷B could therefore be the Cl₁–Cl₂ anti conformer of ClCH₂AlCl. The fact that both the gauche and anti conformers are observed on the EPR time scale would suggest that the barrier for the interconversion of the two conformers is relatively high.

Alternately, a decrease in the Al hfi could be due to the coordination of the Al atom of ClCH₂AlCl with a molecule containing a lone pair of electrons. For instance, in the reactions of Al atoms with NH₃ in Ar at 4 K,⁴cyclopropylamine in adamantane at 77 K,³⁵ and methoxymethane in Ar at 4 K⁷ radicals producing identical spectral patterns differing only in the magnitude of the values of the nuclear hfi were detected. This phenomenon was attributed to complexation of a vacant coordination site of the divalent Al insertion products by a molecule containing a lone pair of electrons, Table 4. Coordination of NH₃ to HAlNH₂ results in the 18% decrease in the Al hfi.⁴ The H hfi is estimated to decrease by 55% while the N hfi increases by about 4%. For [CpNH(AlH)]:CpNH₂, the Al, H and N hfi are 17, 38 and 28% smaller than that found for CpNH(AlH).³⁵ Kasai suggested that the radical with an Al hfi that was 4% smaller than that of CH₃AlOCH₃ was the complexed insertion product [CH₃AlOCH₃]:O(CH₃)₂. This suggests that ³⁵B /³⁷B could be a mixture of [ClCH₂Al³⁵Cl]:X and [ClCH₂Al³⁷Cl]:X where X is a molecule with a lone pair of electrons. X could be H₂O from adventitious water present in the cryostat. This possibility was tested by carrying out an exploratory DFT calculation. The geometry of the [ClCH₂AlCl]:OH₂ complex was optimized using the B3LYP and B3P86 functionals and the 6-31G(df,p) basis set, Table 5. The Al and Cl hfi were obtained from a single point calculation using the B3LYP/6-311+G(2df,p), BHandHLYP/6-311+G(2df,p) and BHandHLYP/6-311G(d,p) levels of theory, Table 6. The Al hfi and Cl hfi for [ClCH₂AlCl]:OH₂ differed from those of the gauche conformation of ClCH₂AlCl by 10–16% and 15–19%, respectively, at the same level of theory (Table 2 and 6). The calculation shows that complexation of a water molecule to the Al atom of ClCH₂AlCl causes the Al hfi to decrease by approximately the same amount as that observed between ³⁵A/³⁷A and ³⁵B/³⁷B.

Table 4 Isotropic nuclear hfis (MHz) for the uncomplexed and complexed Al–atom insertion products as well as the % difference (Δ) in nuclear hfi

Nucleus	HAlNH2^a	[HAlNH2]:NH3^a	%Δ in nuclear hfi
a Ref. 4. b Ref. 35. c Ref. 7. d This work.
Al	950	779	−18%
H1	213	95	−55%
H2	27	28	+4%
N	27	28	+4%
	CpNH(AlH) ^b	[CpNH(AlH)]:CpNH2^b	%Δ in nuclear hfi
Al	962	801	−17%
H	216	133	−38%
N	32	23	−28%
	CH3OAlCH3^c	[CH3OAlCH3]:O(CH3)2^c	%Δ in nuclear hfi
Al	873	838	−4%
	ClCH2AlCl ^d	[ClCH2AlCl]:X^d	%Δ in nuclear hfi
Al	1284	1086	−15%
^35Cl	34	34	0%

---

Table 5 The interatomic distances, angles, dihedral angles, and energy (hartrees) for the Cl₁–Cl₂gauche conformer of [ClCH₂AlCl]:OH₂ were optimized using B3LYP/6-31G(df,p), and B3P86/6-31G(df,p) levels of theory

	B3LYP/6-31G(df,p)	B3P86/6-31G(df,p)
Cl1–Al (Å)	2.185	2.174
Al–C (Å)	1.998	1.987
C–Cl2 (Å)	1.831	1.814
C–H1 (Å)	1.093	1.093
C–H2 (Å)	1.092	1.092
O–Al (Å)	2.065	2.050
∠AlCCl2 (°)	107.1	105.5
∠AlCH1 (°)	113.7	114.1
∠AlCH2 (°)	114.2	114.5
∠Cl1AlC (°)	114.2	113.9
∠OAlC (°)	102.2	103.1
D(Cl2CAlCl1) (°)	84.0	83.9
D(Cl2CAlO) (°)	−179.6	−179.3
D(H2CAlCl1) (°)	−158.6	−159.0
D(H1CAlCl1) (°)	−33.3	−33.1
Energy (hartrees)	−1278.630514	−1279.835873

---

Table 6 The values of the Al, Cl and H hfi (in MHz) were calculated at the B3LYP/6-311+G(2df,p), BHandHLYP/6-311+G(2df,p) and BHandHLYP/6-311G(d,p) levels for the Cl₁–Cl₂gauche conformer of [ClCH₂AlCl]:OH₂ optimized at the B3LYP/6-31G(df,p) and B3P86/6-31G(df,p) levels of theory

		Geometry
Method	Nuclei	B3LYP	B3P86
B3LYP/6-311+G(2df,p)	Al	1054.67	1044.43
	Cl	28.47	28.79
	H1	17.30	16.88
	H2	−5.90	−5.71
BHandHLYP/6-311+G(2df,p)	Al	1099.64	1087.93
	Cl	29.98	30.21
	H1	16.21	15.89
	H2	−6.70	−6.45
BHandHLYP/6-311G(d,p)	Al	1117.11	1104.95
	Cl	29.89	30.14
	H1	17.19	16.87
	H2	−6.81	−6.57

---

Spectrum C

The 8-lined spectrum, separated by 64 MHz, that dominates the central region at 77 K, disappears at temperatures >77 K leaving behind a doublet of septets with magnetic parameters, g = 2.011, a_H = 47.6 MHz and a_35Cl = 11.2 MHz, similar to those reported for CHCl₂ produced by exposing CH₂Cl₂ to ⁶⁰Co γ-rays, i.e., g = 2.007, a_H = 56 MHz and a_35Cl = 11 MHz.³⁸ The difference in the a_H may be due to the fact the spectra were recorded under different conditions. In fact, in another study³⁹ involving the γ-radiolysis of CH₂Cl₂, slightly different magnetic parameters were obtained for CHCl₂, i.e., g = 2.013, a_H = 56 MHz and a_35Cl = 18 MHz. The magnetic parameters are sensitive to the structure of the radical which can be distorted depending upon the nature of the matrix used in the experiment, i.e., adamantanevs.CH₂Cl₂.

There is some suggestion that the formation of Al-atom insertion products is a multistep process. Interaction of the Al atoms with the substrate promotes bond cleavage and the resulting radicals recombine with the lone pair of electrons on the Al atom to form the insertion product. In the case of CH₃AlOCH₃, Kasai⁷ proposed that Al atoms interact with a lone pair of electrons on the oxygen atom of dimethyl ether. Next, the C–O bond cleaves producing methyl radicals. The unpaired electron of the methyl radical interacts with the lone pair electrons of the Al atom to form the insertion product, CH₃AlOCH₃.

As in the case of the Al atom activation of the C–Br bond in CpBr we decided to carry out a theoretical investigation of the mechanism of the Al–CH₂Cl₂ insertion reaction. The Al atom was made to approach the CH₂Cl₂ molecule. We chose to investigate the energy cross-section over the (C–Al, C–Cl₁) plane using geometries in which the dihedral angle defined by Cl₂, C, Al, and Cl₁ was approximately 90°_. The geometry of structures with fixed Al–C and C–Cl₁ bond lengths were optimized at the B3LYP level with a 6-31G(d,p) basis set and a three dimensional plot of C–Al versus C–Cl₁versus energy was constructed, Fig. 5. As in the case of the interaction of Al atoms and CpBr, the Al atom–CH₂Cl₂ reaction favours the formation of AlCl and CH₂Cl. There is no low energy channel that leads directly to the gauche conformer. The energy profile suggests that its formation is barrierless. Similarly the decomposition of ClCH₂AlCl follows a barrierless channel that leads to AlCl and CH₂Cl. Presumably the recombination of AlCl and CH₂Cl trapped in an adamantane matrix could lead to the formation of the insertion product, ClCH₂AlCl.

Fig. 5 Born–Oppenheimer potential energy surface of the lowest energy doublet for the reaction of Al atoms with CH₂Cl₂. The contour lines represent the energy in kcal/mole and are spaced by +5 kcal/mole. The minimum energy point was set to 0 kcal/mole and is denoted by *. The other minima (for AlCl + ClCH₂ and Al + CH₂Cl₂) are asymptotic and hence not indicated on the diagram.

We did not detect the CH₂Cl radical; however this may have something to do with its stability. In the study³⁹ involving the γ-radiolysis of CH₂Cl₂ at 77 K, the resulting EPR spectrum was attributed to a mixture of CH₂Cl and CHCl₂ in the ratio of 1 : 3. From this we could speculate that the CH₂Cl may have formed in our case but in concentrations too low to detect.

Conclusions

Two main radicals were detected in the Al–CH₂Cl₂ reaction, namely, ClCH₂AlCl and CHCl₂. The large isotropic Al hfi for ClCH₂AlCl falls between those reported for HAlCl and ClAlCl supporting the hypothesis that the Al hfi increases as the electron-withdrawing ability of the ligands increases. At higher annealing temperatures, a weak spectrum, identical to that of ClCH₂AlCl, with the exception of the Al hfi, was observed. The smaller Al hfi led us to attribute the spectrum to either the anti conformer of ClCH₂AlCl or to ClCH₂AlCl:X where X possesses a lone pair of electrons, e.g., as in the case of H₂O. The nuclear hfi calculated using a DFT method support the assignments. Exploration of a cross section of the potential energy surface for the Al–CH₂Cl₂ reaction shows that AlCl and CH₂Cl are favoured. The recombination of AlCl and CH₂Cl, trapped in an adamantane matrix, could lead to the formation of the insertion product, ClCH₂AlCl.

Acknowledgements

The Natural Sciences and Engineering Research Council of Canada (NSERCC) and Laurentian University are gratefully acknowledged for financial support. We would like to thank Ms Julie Feola and Mr Jean Pierre Rank for their technical assistance. We express our gratitude to Drs Gustavo Arteca, Sabine Montaut and Tony Howard for helpful discussions. The authors also wish to thank the reviewers for comments as they helped improve the paper.

References

1. C. L. Geiger, K. Carvalho-Knighton, S. Novaes-Card, P. Maloney and R. DeVor, in Environmental Applications of Nanoscale and Microscale Reactive Metal Particles, ACS Symp. Ser., 2009, vol. 1027, p. 1.
2. C. Douvris, C. M. Nagaraja, C.-H. Chen, B. M. Foxman and O. V. Ozerov, J. Am. Chem. Soc., 2010, 132, 4946.
3. J. A. Howard, H. A. Joly, P. P. Edwards, R. J. Singer and D. E. Logan, J. Am. Chem. Soc., 1992, 114, 474.
4. P. H. Kasai and H.-J. Himmel, J. Phys. Chem. A, 2002, 106, 6765.
5. L. B. Knight, Jr., B. Gregory, J. Cleveland and C. A. Arrington, Chem. Phys. Lett., 1993, 204, 168.
6. H. A. Joly, J. A. Howard, M. Tomietto and J. S. Tse, J. Chem. Soc., Faraday Trans., 1994, 90, 3145.
7. P. H. Kasai, J. Phys. Chem. A, 2002, 106, 83.
8. J. H. B. Chenier, J. A. Howard, H. A. Joly, M. LeDuc and B. Mile, J. Chem. Soc., Faraday Trans., 1990, 86, 3321.
9. J. M. Parnis and G. A. Ozin, J. Phys. Chem., 1989, 93, 1204.
10. H. A. Joly, J. A. Howard and G. A. Arteca, Phys. Chem. Chem. Phys., 2001, 3, 760.
11. J. A. Howard, H. A. Joly and B. Mile, J. Chem. Soc., Faraday Trans., 1990, 86, 219.
12. R. Köppe and P. H. Kasai, J. Am. Chem. Soc., 1996, 118, 135.
13. T. Fängström, S. Lunell, P. H. Kasai and L. A. Eriksson, J. Phys. Chem. A, 1998, 102, 1005.
14. H. A. Joly, M. Y. Levesque, F. Koudra and J. P. Rank, Chem. Phys. Lett., 2006, 420, 140.
15. P. S. Skell and J. E. Girard, J. Am. Chem. Soc., 1972, 94, 5518.
16. B. S. Ault, J. Am. Chem. Soc., 1980, 102, 3480.
17. H.-G. Cho, L. Andrews, B. Vlaisavljevich and L. Gagliardi, Organometallics, 2009, 28, 6871.
18. A. J. Buck, B. Mile and J. A. Howard, J. Am. Chem. Soc., 1983, 105, 3381.
19. K. F. Preston and J. R. Morton, ISOPLOT and ESRLSQ, National Research Council of Canada, Ottawa.
20. J. A. Weils, EPR-NMR, University of Saskatchewan, Saskatoon.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.1), Gaussian, Inc., Wallingford, CT, 2009.
22. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968.
23. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
24. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
25. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
26. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822.
27. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
28. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
29. J. P. Perdew and W. Yue, Phys. Rev. B, 1986, 33, 8800.
30. J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
31. W. Kutzelnigg, U. Fleischer and M. Schindler, NMR: Basic principles and Progress, Springer-Verlag, 1990.
32. W. Weltner, Jr., Magnetic Atoms and Molecules, Dover, 1989.
33. L. B. Knight, Jr., J. R. Woodward, T. J. Kirk and C. A. Arrington, J. Phys. Chem., 1993, 97, 1304.
34. H. A. Joly, J. A. Howard and G. A. Arteca, Phys. Chem. Chem. Phys., 2001, 3, 750.
35. H. Joly, J. Ashley, M. Levesque and J. Rank, J. Phys. Chem. A, 2006, 110, 3911.
36. H. M. Tuononen, T. Chivers, A. Armstrong, C. Fedorchuk and R. T. Boeré, J. Organomet. Chem., 2007, 692, 2705.
37. J.-F. Xiao, Z.-S. Li, Y.-H. Ding, J.-Y. Liu, X.-R. Huang and C.-C. Sun, J. Phys. Chem. A, 2001, 106, 320.
38. S. P. Mishra, G. W. Neilson and M. C. R. Symons, J. Chem. Soc., Faraday Trans. 2, 1973, 69, 1425.
39. S. Truszkowski and W. Szymański, J. Radioanal. Nucl. Chem., 1994, 177, 415.

---

Footnote

† Present address: Gowlings, Ottawa, ON, K1P 1C3, Canada.

---