Self-assembly of supramolecular wires and cross-junctions and efficient electron tunnelling across them†
Josep
Puigmartí-Luis
ab,
Andrea
Minoia
c,
Shengbin
Lei
b,
Victor
Geskin
c,
Bing
Li
b,
Roberto
Lazzaroni
*c,
Steven
De Feyter
*b and
David B.
Amabilino
*a
aInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus Universitari de Bellaterra, 08193, Cerdanyola del Vallès, Catalonia, Spain. E-mail: amabilino@icmab.es
bKatholieke Universiteit Leuven, Laboratory of Photochemistry and Spectroscopy, and INPAC-Institute for Nanoscale Physics and Chemistry, Celestijnenlaan 200-F, 3001, Heverlee, Belgium. E-mail: steven.defeyter@chem.kuleuven.be
cService de Chimie des Matériaux Nouveaux, Université de Mons, 20, Place du Parc, B-7000, Mons, Belgium. E-mail: roberto.lazzaroni@umons.ac.be
First published on 21st July 2011
Abstract
The self-assembly of molecules incorporating π-electron rich units into supramolecular wires is shown by scanning tunnelling microscopy (STM) at a graphite–liquid interface. Hydrogen bonds between the side chains of these molecules ensure a face-to-face contact between the functional moieties, which would otherwise lie flat on the surface if the amide groups affording this effect were absent. The organisation in the wires also depends critically on the constitution of the molecule: The cis and trans isomers show ordered and disordered spacing between wires, respectively. The supramolecular wires formed by the cis isomer form crossed architectures, with multilayers of the linear structures being formed. Study of the junction points between the fibres by scanning tunnelling spectroscopy shows that tunnelling electrons are transported efficiently, practically with the same probability as through a single wire. Molecular modelling is used to determine how the π-electron rich units within two crossing wires organise at the crossing. Based on those structural data, the electron tunnelling probability between tip and substrate is then calculated; it shows that electron transmission can indeed take place at the crossing. This result implies that supramolecular fibres can be used as wires in order to build integrated circuits by bottom-up construction from the molecule scale.
Introduction
The self-assembly of purely molecular circuitry is a contemporary challenge which requires not only the preparation of molecular devices1 which can perform simple operations but also the cables which connect and link them into a system.2 By far and away the most common way to probe the properties of molecules between electrodes is to place them between traditional metals3—most usually noble ones—although carbon nanotubes are also interesting for this purpose.4 Although single molecule wires are potentially interesting, it is challenging to make very long wires showing significant charge transport, and formation of crossing points must be achieved. Supramolecular wires5 capable of self-assembling into crossed architectures are potentially interesting and more accessible in this respect. The fact that conducting supramolecular systems show bulk conductivity6 already indicates that significant charge transport is possible between stacked functional cores, and here we will probe this effect using tunnelling electrons.The technique used to study the self-assembled systems is scanning tunnelling microscopy (STM) at a graphite–solvent interface, a method which provides sub-molecular information concerning the structure of self-assembled monolayers.7 The tunnelling properties of the systems can be probed using scanning tunnelling spectroscopy (STS) which provides important information concerning the ability of molecule-containing systems to transport charge.8
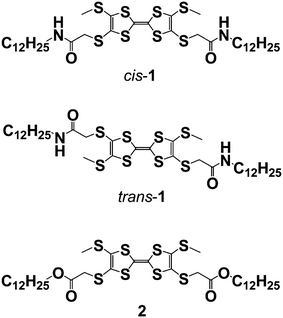
The functional component we chose was tetrathiafulvalene (TTF),9 whose π-electron rich units can be organised in a variety of ways in monolayers on the graphite surface.10 We have introduced amide groups in the structure to generate hydrogen bonded chains11,12 to modify the molecular orientation and create one-dimensional assemblies. The compounds we will discuss are the constitutional isomers cis-1 and trans-1 (which differ in the relative dispositions of the amide-containing substituents on the TTF core) and the bis-ester 2. The latter was studied in order to see the effect of the amide groups on the assembly of the monolayers. We show the self-assembly of crossed supramolecular wires and the formation of junctions between wires where tunnelling electrons are transported. This result implies that supramolecular fibres can be used as wires in order to build integrated circuits by bottom-up construction from the molecule scale.
Results and discussion
Imaging of the TTF derivatives at the graphite-liquid interface
The STM and STS experiments were performed at the interface between highly oriented pyrolytic graphite (HOPG) and 1-octanoic acid. The compounds used in this study were prepared according to the procedure described previously,11 and in order to perform the STM experiments they were dissolved in 1-octanoic acid and a drop of this solution was placed on the HOPG surface.When cis-1 is applied in a relatively concentrated solution in octanoic acid (see Experimental Section†) to the basal plane of HOPG, STM reveals strips of π–π stacked molecules, as before,12 but this time with clear evidence of wires which lay on top of the monolayer. This fact can be appreciated in the image shown in Fig. 1, in which bright lines—corresponding to the π–π stacked TTF moieties tilted quasi-perpendicularly to the HOPG surface—cross one another with no significant discontinuity in the brightness. The distances between the TTF derivatives in these strips appear to be identical to those formed in the purely monolayer system, as can be discerned in the fine detail in Fig. 1. Furthermore, the brightness of the two crossed wires is practically identical. This fact indicates that tunnelling is equally viable through either of them. In this area, the crossing point is clearly forming a minimum angle of 60 degrees, a value that is presumably determined by the HOPG substrate even onto the second layer. Also, atomic force microscopy (AFM) measurements confirm that cis-1 can easily assemble into lamellar structures on the HOPG surface (see ESI†). The distance measured between two lamellae is about 4.4 nm which is comparable with the value of 4.6 ± 0.2 nm obtained by STM. Besides ordered monolayers composed of lamellar structures, we frequently observed multilayers of supramolecular wires which lie on top of the monolayer, forming either co-parallel lamellae or crossing points. These observations are consistent with the STM study and further prove that the cis-1 supramolecular wires have the tendency to stack on top of each other. From these measurements, the height of a layer is approximately 0.33 nm.
 | ||
| Fig. 1 STM image of a physisorbed multilayer of cis-1 performed under atmospheric conditions at the 1-octanoic acid–HOPG interface. (a) Iset = 1.50 nA, Vbias = −0.32 V, constant height. | ||
In some cases it was possible to image parallel lines of TTF molecules on top of one another through the alkyl chains of an over-layer (Fig. 2), and to observe how one strip continues in one layer over a domain with a different orientation, while in the other layer the strip butts into the other domain. This observation gives proof that at these points the fibres cross and that the effect is not caused by abutting interdigitated domains (and given that sterically it is impossible for the TTF units to form such a tight packed two dimensional structure). This observation implies that, at least on the graphite substrate, the supramolecular wires have a tendency to stack on top of each other. The fibres can form the crossing points with the well-defined angles mentioned earlier, or can run co-parallel to each other (Fig. 2a and 2b, top part). There is no apparent distortion of the supramolecular wires which lie on top of the monolayer when compared with the former; they appear completely straight and with constant contrast in between crossing points. It is also important to consider that while we have observed supramolecular cross-wires in a similar system with just one amide unit,13 the present case forms much more well-defined fibres with no possibility of variation in the number of TTF units at the centre of the wire.
 | ||
| Fig. 2 STM image of a physisorbed multilayer of cis-1 performed under atmospheric conditions at the octanoic acid-HOPG interface. (a) Iset = 0.50 nA, Vbias = 1.04 V (constant current), an area showing parallel lamellae and crossing points, and (b) Iset = 0.50 nA, Vbias = 1.21 V. | ||
It is important to note that although STM images were recorded on different machines and at different tunnelling conditions and scanning mode (constant height or constant current, as noted in the Figure captions), all reveal strips of molecules overlaid on domains which are in contact with the substrate. As before, the virtually constant tunnelling current along the fibres indicates that the TTF moieties are aligned parallel to each other with their π-faces interacting strongly with each other. In between the stacks of TTF moieties, the alkyl chains do not contribute significantly to the STM contrast in the bilayer system.
In common with cis-1, the trans isomer forms strip-like aggregates at the octanoic acid–HOPG interface (Fig. 3(a) and (b)). This situation, along with the virtually identical distance between the units in these monolayers when compared with the cis isomer, implies that trans-1 is also arranged with the TTF unit oriented nearly perpendicular to the HOPG surface. The hydrogen bonds between the molecules maintain this arrangement. In addition, the molecules seem to have high affinity for each other, since well defined domains are observed next to bare HOPG, an infrequent feature in this kind of system and one not seen for the cis isomer. Given that the concentration is the same as that for the cis isomer, this observation may indicate a lower affinity of the trans isomer for the surface. Also, the spacing between the lines of molecules are not uniform, as can be appreciated in Fig. 3(a) and (b). In this situation two lamellar spacing distances exist, one established to be around 4.5 nm and the second around 6 nm. In contrast, cis-1 indicates regular spacing distances between lamellas of 4.6 ± 0.2 nm. This observation could be explained by the fact that in an edge-on orientation trans-1 has one alkyl chain in contact with the HOPG surface, while the other is away from the surface because of the constitution of the monolayer. Even at high concentrations (close to the saturation point) no multilayers were observed, possibly because of the irregularity in the packing of the layers.
 | ||
| Fig. 3 (a) and (b) STM images of physisorbed monolayers of trans-1 performed under atmospheric conditions at the octanoic acid-HOPG interface. (a) Iset = 1 nA, Vbias = −0.20 V, (b) Iset = 0.55 nA, Vbias = −0.39 V. In (b) the white lines indicate the orientation of the main symmetry axes of graphite. | ||
The bis-ester 2 has a completely different organization to the two amide derivatives: When it is deposited on the HOPG surface in n-octanol the compound (which is in principle a mixture of cis and trans isomers) forms lamellae in which the TTF moieties lie parallel to the surface (Fig. 4). This orientation is very similar to TTF compounds with simple alkyl chains at the extremes.10 The observation of this arrangement confirms the role that the hydrogen bonds between the carbonyl and NH groups have on the formation of the molecular wires in the case of these amide derivatives.
 | ||
| Fig. 4 STM image of a physisorbed monolayer of 2 performed under atmospheric conditions at the n-octanol-HOPG interface. (a) Iset = 0.95 nA, Vbias = −0.11 V, (b) Iset = 0.98 nA, Vbias = −0.11 V. | ||
Scanning tunnelling spectroscopy of crossed supramolecular wires
The scanning tunnelling spectroscopy (STS) of TTF derivatives at the solvent–graphite interface affords curves of tunnelling current versus potential which give an indication of the ease of current flow—determined by the density of electronic states—between STM tip and the surface mediated by the molecule between them. In systems where the TTF molecule lies parallel to the graphite, a relatively wide potential of low current flow (which we will refer to as the “experimentally observed gap”) is observed, although current is efficiently passed once a certain threshold is reached.14 In the case that the TTF units are stacked perpendicular to the surface by virtue of the amide bonds in cis-1 then the monolayer system shows an experimentally observed gap which was significantly smaller than the face-on-surface system.12 Theory confirmed that this effect was thanks to the stacking of the TTF moieties in the hydrogen bonded stacks on the surface.Here, STS was used to probe the electronic properties of the crossing junctions. The spectroscopic data was recorded with the STM tip located over the junctions in several different sites and different samples, and the layers were imaged before and after the current–voltage sweeps. All current–voltage (I/V) curves were measured in a short period after imaging in order to minimize the drift, and were achieved with quasi-constant measuring conditions to avoid large variations in the tip–sample distance.15 The averaged curves obtained from several measurements performed in different locations and samples of cis-1 at the octanoic acid–HOPG interface with setup conditions Iset = −0.50 nA, Vbias = 1.03 V are shown in Fig. 5.
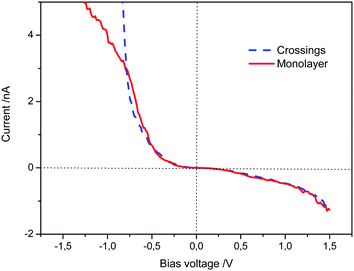 | ||
| Fig. 5 I–V curves obtained on the monolayer strips and crossings, setpoint: Iset = −0.50 nA, Vbias = 1.03 V. Each curve is the average of more than 100 curves obtained from different sites. | ||
Based on the above measurements we can state that the STS curves taken from the monolayer strips do not show a significant difference with respect to that from the crossing junctions in the bias range from −0.80 V to 1.50 V. Below −0.80 V the tunnelling current increase more sharply at the crossing junctions. These results demonstrate that the tunnelling probability across two edge-to-edge TTF stacks at the junctions is appreciable under the experimental conditions. Therefore, although at the crossing point the tunnelling electron must pass through more organic material, there is no apparent loss in tunnelling probability.
Modelling of structure and transport in crossed supramolecular wires
In order to understand the electronic properties of the assembly of TTFs effect, it is interesting to model the supramolecular structure of crossed stacks and to probe the electron transmission properties through them at the crossing point. To address this problem, a combined approach was used: first the molecular structure of the system at the crossing is modelled with Molecular Mechanics (MM) and Molecular Dynamics (MD) simulations; based on those structural data, the electron transmission spectrum between TTF molecules at the crossing is calculated with a Density Functional Theory (DFT) technique.The crossing has been modelled by considering two stacks of cis-1 molecules crossing each other (Fig. 6 a–c): the initial geometry of the stacks is taken from the results obtained for an assembly of TTF stacks forming a monolayer on graphite.12 One wire is directly adsorbed on the surface, while the second one is placed on top of the first one, so that its axis forms an angle of 30° with respect to the axis of the other wire. The system geometry is optimized with MM calculations, using the MM3 force field and the simulations are performed in “dry” conditions (i.e., without solvent molecules) to keep the computational effort to a tractable level. Despite these limitations, this simple model can be used to evaluate the distance between the two stacks at the crossing, which is the key parameter that governs the electron transmission at the crossing through the two overlaying wires.
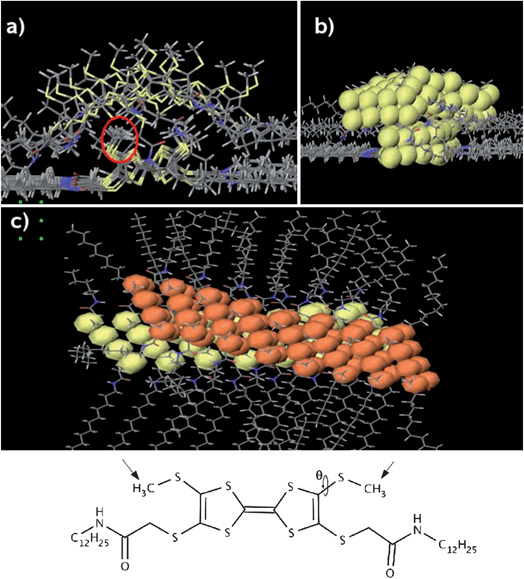 | ||
| Fig. 6 (a) Front view of the calculated crossing. The red circle shows the methyl groups that govern the inter-stack distance. (b) Front view with the van der Waals spheres for the sulphur atoms in yellow. (c) Top view of the crossing; the VdW spheres of the sulphur atoms in the upper wire are shown in orange. For the sake of clarity, the graphite surface is not shown. | ||
The distance between the wires depends mainly on the angle θ, which defines the orientation of the methyl groups attached to the sulphur atoms (see structure in Fig. 6). The largest separation between the wires is found when the methyl groups of the lower one are pointing away from the surface, towards the upper wire (this is the orientation they take in the monolayer12). In such a configuration, the average distance between the TTF cores at the crossing is about 5 Å. However, after allowing the structure to relax in a MD simulation, the interstack distance, defined as the shortest S–S contacts, is ranging from 3.5 Å to 5.5 Å, since the methyl group orientation varies along the crossing. Such a broad range of distances is related to the fact that the potential energy for the angle θ has a rather shallow energy minimum for a torsion of about 80° (i.e., the S–CH3 bond is almost perpendicular to the plane of the TTF core), which allows for substantial orientation variations of the methyl groups with respect to the TTF plane.
Based on that information, we calculated the electron transmission probabilities at the crossing for characteristic distances found in the model. The transmissions were calculated with TransiestaC 1.3 program16 implementing the non-equilibrium Green's function (NEGF) formalism.17 To calculate the transmission, we considered the dimer formed by two molecules (one in each wire) at the center of the crossing. The dimer was extracted from the force field model, reduced to a pair of TTF cores and placed in a unit cell between two 3-layer Al(111) clusters containing 12 atoms per layer (Fig. 7). The NEGF formalism serves to connect this central region to semi-infinite metal bulk at both ends and to calculate the probability for an electron arriving with a given energy from one side of the junction to be transmitted to the other side. The electron structure calculations were performed at the DFT Local Density Approximation (LDA) level, with a Single-Zeta numerical basis set and Monkhorst–Pack 3 × 3 × 100 k-sampling, at zero bias. The two metal clusters represent the STM tip and the surface; aluminium was chosen because it is a sp metal much simpler to model than platinum (a d metal) and graphite (a semi-metal). We focus here on the difference in electrical communication through a TTF dimer when changing the distance between the crossed wires, so the exact nature of the electrode is not a major issue.
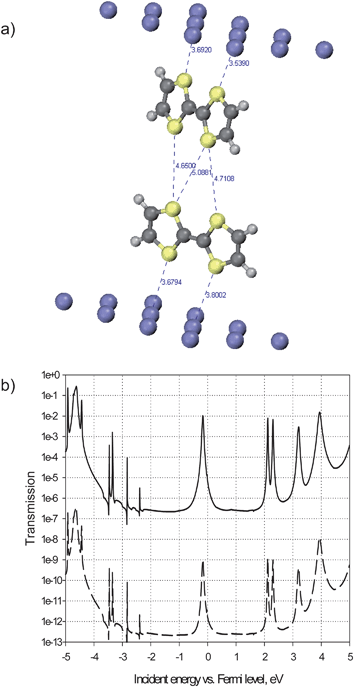 | ||
| Fig. 7 (a): Calculated structure of a unit cell containing a dimer composed by two TTF molecules (one from each wire) inserted between two Al(111) surfaces. The inter-TTF characteristic distances correspond to the “close” dimer; in the “distant” dimer these are 1 Å longer. (b): Calculated electron transmission spectra for the 5.5 Å- (bottom curve) and 4.5 Å- (top curve) separated TTF dimers. | ||
To interpret the transmission spectra, it should be first taken into account that, as the hybridization of the molecular orbitals (MOs) of TTF with the metal is negligible in the absence of specific chemisorption, the transmission peaks are due to the MOs, and the energy spacing between them remains very similar to that in the isolated molecule. This allows the assignment of the transmission peaks to specific MOs. Furthermore, electronic interactions in a dimer like that shown in Fig. 7 are weak enough, so that the splittings in MO energies are negligible. This makes the position of the peaks in the transmission spectrum of the dimer (Fig. 7 b) practically the same as in the monomer (not shown). Only the transmission peaks in the vicinity of the Fermi level (the zero-energy point on the x axis in Fig. 7 b) contribute to observable low-bias conductivity. In the case of TTF monomers and dimers, the peak just below the Fermi level arises from the molecular HOMO. Its close alignment to the Fermi level is indeed expected for a donor molecule and would certainly be conserved for other electrode materials, in particular for those with higher work functions than that of Al. The HOMO of TTF is a π orbital delocalized over the sulphur atoms and the double bond in the centre of the molecule. Its topology is therefore favourable for ensuring transmission between two electrodes when TTF unit is facing them with its sulphur atoms, while standing perpendicular to their surface. Indeed, the transmission peak through the HOMO of one TTF attains a maximum around 1 (that is, perfect transmission at resonance) and has appreciable width; the exact values are sensibly dependent on the molecule–electrode distance, but notably, not on the lateral position of the molecule with respect to the electrode, as the electron density at a few Å distance from the metal is quite uniform.
For the same reason, the HOMOs of two TTF molecules in the dimer geometry of Fig. 7 assure communication between two electrodes through both of them. However, the intensity of the transmission peaks crucially depends on the intermolecular distance. When the two molecules are ∼5.5 Å apart, the probability to transmit an electron through the HOMO is negligible, on the order of 10−9, as shown in the transmission spectrum in the bottom part of Fig. 7b: the two molecules are too far from each other and cannot interact. One should therefore not expect to have a high tunnelling current at the crossing when the distance between the stacked molecules is above 5 Å.
However, as mentioned above, the distance between the TTF units at the crossing can vary from 3.5 Å to 5.5 Å. By reducing the intermolecular distance from 5.5 Å to 4.5 Å the probability to have transmission through the HOMOs at the peak maximum increases to the order of 10−2, seven orders of magnitude higher than in the previous case. This spectacular increase can be attributed only to considerable overlap between the molecular orbitals of the partners that becomes effective at a certain intermolecular distance, as for tunnelling through vacuum, with a typical exponential decay coefficient of 2.8 Å−1, the gain per Å would be only 16-fold. At the same time, the full width at half maximum (FWHM) of the same peak attains 50 meV (as determined from the linear-scale plot of transmission), this dispersion of the transmission peak serving as evidence for the delocalization of the corresponding current-carrying MO throughout the system between the electrodes. These non-negligible intensity and width values are quite consistent with a tunnelling current that can be measured by STM/STS. These results clearly indicate that electron transmission can take place at the crossing, provided the intermolecular distance is sufficiently small. Such small separation can be reached when the methyl groups are arranged in a proper orientation, which can be readily accessed due to the easy rotation of those groups at the crossing.
Conclusions
We have provided evidence that supramolecular fibres based on organic donors are potentially useful as molecular wires for the creation of self-assembled circuits which include junctions. These unions reveal an electrical contact between layers. While different STM instruments provide quantitatively slightly different results, their qualitative similarity and the theoretical support for the hypothesis of efficient transport through junctions gives us confidence that very efficient electron transport is taking place between layers, and potentially might be propagated over relatively large distances.The magnitude of electron tunnelling in the overlayers observed in the STM experiments is apparently higher than expected, a result that could be a consequence of the tip–sample conditions, but in any case transport of electrons across the edges of TTF derived units is known in bulk systems. Indeed, this effect gives rise to bulk two dimensional organic conductors. Our experiments show that this effect can also take place between supramolecular wires formed by columns of TTF derivatives.
The spontaneous formation of overlaid supramolecular wires in equilibrium conditions and the efficient electron tunnelling through them augurs well for the conjecture that circuits may be self-assembled using suitably encoded components with the right electronic characteristics.
Acknowledgements
This work was supported by the European Union Marie Curie Research Training Network CHEXTAN (MRTN-CT-2004–512161), the MICINN (Spain, under the project CTQ2010-16339), and the Generalitat de Catalunya (2009 SGR 158). We thank Prof Concepció Rovira (ICMAB-CSIC) for helpful discussions. Research in Mons and Leuven is supported by the Interuniversity Attraction Pole program of the Belgian Federal Science Policy Office (PAI 6/27). The Mons group further acknowledges the Programme d’Excellence de la Region Wallonne (OPTI2MAT project) and FNRS-FRFC. The K.U.Leuven team acknowledges financial support via the Fund of Scientific Research - Flanders, and a ‘Geconcerteerde Onderzoeksactie (K.U.Leuven)-GOA'.References
- (a) R. L. Carroll and C. B. Gorman, Angew. Chem., Int. Ed., 2002, 41, 4378 CrossRef; (b) G. Maruccio, R. Cingolani and R. Rinaldi, J. Mater. Chem., 2004, 14, 542 RSC; (c) D. L. Long, E. Burkholder and L. Cronin, Chem. Soc. Rev., 2007, 36, 105–121 RSC; (d) Q. Shen, X. F. Guo, M. L. Steigerwald and C. Nuckolls, Chem. Asian J., 2010, 5, 1040–1057 CAS.
- (a) A. P. M. Mendes, A. H. Flood and J. F. Stoddart, Appl. Phys. A: Mater. Sci. Process., 2005, 80, 1197–1209 CrossRef; (b) Greiner, J. H. Wendorff, A. L. Yarin and E. Zussman, Appl. Microbiol. Biotechnol., 2006, 71, 387–393 CrossRef CAS; F. Patolsky, G. Zheng and C. M. Lieber, Nanomedicine, 2006, 1, 51–65 Search PubMed; (c) J. E. Green, J. W. Choi, A. Boukai, Y. Bunimovich, E. Johnston-Halperin, E. DeIonno, Y. Luo, B. A. Sheriff, K. Xu, Y. S. Shin, H. R. Tseng, J. F. Stoddart and J. R. Heath, Nature, 2007, 445, 414–417 CrossRef CAS; (d) D. M. Cardamone and G. Kirczenow, Nano Lett., 2010, 10, 1158–1162 CrossRef CAS; (e) G. Charron, A. Giusti, S. Mazerat, P. Mialane, A. Gloter, F. Miserque, B. Keita, L. Nadjo, A. Filoramo, E. Riviere, W. Wernsdorfer, V. Huc, J. P. Bourgoin and T. Mallah, Nanoscale, 2010, 2, 139–144 RSC.
- (a) A. Salomon, D. Cahen, S. Lindsay, J. Tomfohr, V. B. Engelkes and C. D. Frisbie, Adv. Mater., 2003, 15, 1881–1890 CrossRef CAS; (b) N. Weibel, S. Grunder and M. Mayor, Org. Biomol. Chem., 2007, 5, 2343–2353 CAS; (c) A. M. Moore, B. A. Mantooth, Z. J. Donhauser, Y. Yao, J. M. Tour and P. S. Weiss, J. Am. Chem. Soc., 2007, 129, 10352–10353 CrossRef CAS; (d) A. Kuhnle, Curr. Opin. Colloid Interface Sci., 2009, 14, 157–168 CrossRef; (e) J. R. Widawsky, M. Kamenetska, J. Klare, C. Nuckolls, M. L. Steigerwald, M. S. Hybertsen and L. Venkataraman, Nanotechnology, 2009, 20, 434009 CrossRef CAS; (f) C. Vericat, M. E. Vela, G. Benitez, P. Carro and R. C. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834 RSC; (g) T. Hines, I. Diez-Perez, J. Hihath, H. M. Liu, Z. S. Wang, J. W. Zhao, G. Zhou, K. Muellen and N. J. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664 CrossRef CAS.
- (a) A. K. Feldman, M. L. Steigerwald, X. Guo and C. Nuckolls, Acc. Chem. Res., 2008, 41, 1731–1741 CrossRef CAS; (b) L. He, J. Q. Lu and H. Q. Jiang, Small, 2009, 5, 2802–2806 CrossRef CAS; (c) X. F. Guo and C. Nuckolls, J. Mater. Chem., 2009, 19, 5470–5473 RSC.
- (a) F. S. Schoonbeek, J. H. van Esch, B. Wegewijs, D. B. A. Rep, M. P. de Haas, T. M. Klapwijk, R. M. Kellogg and B. L. Feringa, Angew. Chem., Int. Ed., 1999, 38, 1393 CrossRef CAS; (b) J. Sly, P. Kasák, E. Gomar-Nadal, C. Rovira, L. Górriz, P. Thordarson, D. B. Amabilino, A. E. Rowan and R. J. M. Nolte, Chem. Commun., 2005, 1255 RSC; (c) G. De Luca, A. Liscio, P. Maccagnani, F. Nolde, V. Palermo, K. Mullen and P. Samorì, Adv. Funct. Mater., 2007, 17, 3791 CrossRef CAS; (d) M. Iyoda, M. Hasegawa and H. Enozawa, Chem. Lett., 2007, 36, 1402–1407 CrossRef CAS; (e) W. Jin, Y. Yamamoto, T. Fukushima, N. Ishii, J. Kim, K. Kato, M. Takata and T. Aida, J. Am. Chem. Soc., 2008, 130, 9434 CrossRef CAS; (f) F. Fages, J. A. Wytko and J. Weiss, C. R. Chim., 2008, 11, 1241 CrossRef CAS; (g) Y. Geng, X. J. Wang, B. Chen, H. Xue, Y. P. Zhao, S. Lee, C. H. Tung and L. Z. Wu, Chem.–Eur. J., 2009, 15, 5124 CrossRef CAS; (h) J.-P. Hong, M.-C. Um, S.-R. Nam, J.-I. Hong and S. Lee, Chem. Commun., 2009, 300–312 Search PubMed; (i) S. Yagai, T. Kinoshita, Y. Kikkawa, T. Karatsu, A. Kitamura, Y. Honsho and S. Seki, Chem.–Eur. J., 2009, 15, 9320–9324 CrossRef CAS; (j) M. Hasegawa and M. Iyoda, Chem. Soc. Rev., 2010, 39, 2420–2427 RSC.
- (a) M. de Loos, J. van Esch, R. M. Kellogg and B. L. Feringa, Angew. Chem., Int. Ed., 2001, 40, 613–616 CrossRef CAS; (b) T. Kitamura, S. Nakaso, N. Mizoshita, Y. Tochigi, T. Shimomura, M. Moriyama, K. Ito and T. Kato, J. Am. Chem. Soc., 2005, 127, 14769–14775 CrossRef CAS; (c) J. Puigmartí-Luis, V. Laukhin, Á. Pérez del Pino, J. Vidal-Gancedo, C. Rovira, E. Laukhina and D. B. Amabilino, Angew. Chem., Int. Ed., 2007, 46, 238–241 CrossRef; (d) I. Danila, F. Riobé, J. Puigmartí-Luis, Á. Pérez del Pino, J. D. Wallis, D. B. Amabilino and N. Avarvari, J. Mater. Chem., 2009, 19, 4495–4504 RSC; (e) D. B. Amabilino and J. Puigmartí-Luis, Soft Matter, 2010, 6, 1605–1612 RSC.
- (a) S. Furukawa and S. De Feyter, Top. Curr. Chem., 2009, 287, 87–133 CrossRef CAS; (b) J. A. A. W. Elemans and S. De Feyter, Soft Matter, 2009, 5, 721–735 RSC.
- (a) P. Samorì, J. Mater. Chem., 2004, 14, 1353–1366 RSC; (b) H. J. Gao and L. Gao, Prog. Surf. Sci., 2010, 85, 28–91 CrossRef CAS; (c) C. E. Giusca, Y. Tison and S. R. P. Silva, Nano, 2008, 3, 65–73 CrossRef CAS; (d) S. B. Lei and S. De Feyter, Top. Curr. Chem., 2008, 285, 269–312 CrossRef CAS.
- (a) J.-L. Yamada, TTF Chemistry: Fundamentals and Applications of Tetrathiafulvalene, Springer-Verlag, Berlin and Heidelberg, 2004 Search PubMed; (b) E. Gomar-Nadal, J. Puigmartí-Luis and D. B. Amabilino, Chem. Soc. Rev., 2008, 37, 490–504 RSC; (c) D. Canevet, M. Sallé, G. X. Zhang, D. Q. Zhang and D. B. Zhu, Chem. Commun., 2009, 2245–2269 RSC.
- The TTF units lay flat on a graphite surface in absence of strong intermolecular interactions: (a) E. Gomar-Nadal, M. M. S. Abdel-Mottaleb, S. De Feyter, J. Veciana, C. Rovira, D. B. Amabilino and F. C. De Schryver, Chem. Commun., 2003, 906–907 RSC; (b) M. M. S. Abdel-Mottaleb, E. Gomar-Nadal, M. Surin, H. Uji-I, W. Mamdouh, J. Veciana, V. Lemaur, C. Rovira, J. Cornil, R. Lazzaroni, D. B. Amabilino, S. De Feyter and F. C. De Schryver, J. Mater. Chem., 2005, 15, 4601–4615 RSC.
- J. Puigmartí-Luis, A. Minoia, A. Pérez del Pino, G. Ujaque, C. Rovira, A. Lledós, R. Lazzaroni and D. B. Amabilino, Chem.–Eur. J., 2006, 12, 9161–9175 CrossRef.
- J. Puigmartí-Luis, A. Minoia, H. Uji-i, C. Rovira, J. Cornil, S. De Feyter, R. Lazzaroni and D. B. Amabilino, J. Am. Chem. Soc., 2006, 128, 12602–12603 CrossRef.
- S. Lei, J. Puigmartí-Luis, A. Minoia, M. Van der Auweraer, C. Rovira, R. Lazzaroni, D. B. Amabilino and S. De Feyter, Chem. Commun., 2008, 703–705 RSC.
- M. M. S. Abdel-Mottaleb, E. Gomar-Nadal, S. De Feyter, M. Zdanowska, J. Veciana, C. Rovira, D. B. Amabilino and F. C. De Schryver, Nano Lett., 2003, 3, 1375–1378 CrossRef CAS.
- K. Walzer, M. Sternberg and M. Hietschold, Surf. Sci., 1998, 415, 376–384 CrossRef CAS.
- TransistaC 1.3 ( 2004), Atomistix A/S, www.atomistix.com.
- M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of experimental and theoretical methods. See DOI: 10.1039/c1sc00330e |
| This journal is © The Royal Society of Chemistry 2011 |