Practical computation of electronic excitation in solution: vertical excitation model†
Aleksandr V.
Marenich
*a,
Christopher J.
Cramer
a,
Donald G.
Truhlar
a,
Ciro A.
Guido
b,
Benedetta
Mennucci
c,
Giovanni
Scalmani
d and
Michael J.
Frisch
d
aDepartment of Chemistry and Supercomputing Institute, University of Minnesota, 207 Pleasant Street S.E., Minneapolis, MN 55455-0431, USA. E-mail: marenich@comp.chem.umn.edu (AVM); cramer@umn.edu (CJC); truhlar@umn.edu (DGT)
bScuola Normale Superiore di Pisa, Piazza dei Cavalieri 7, 56100, Pisa, Italy
cDipartimento di Chimica e Chimica Industriale, Via Risorgimento 35, 56126, Pisa, Italy. E-mail: bene@dcci.unipi.it (BM)
dGaussian, Inc., 340 Quinnipiac Street, Building 40, Wallingford, Connecticut 06492, USA. E-mail: giovanni@gaussian.com (GS)
First published on 5th August 2011
Abstract
We present a unified treatment of solvatochromic shifts in liquid-phase absorption spectra, and we develop a self-consistent state-specific vertical excitation model (called VEM) for electronic excitation in solution. We discuss several other approaches to calculate vertical excitations in solution as an approximation to VEM. We illustrate these methods by presenting calculations of the solvatochromic shifts of the lowest excited states of several solutes (acetone, acrolein, coumarin 153, indolinedimethine-malononitrile, julolidine-malononitrile, methanal, methylenecyclopropene, and pyridine) in polar and nonpolar solvents (acetonitrile, cyclohexane, dimethyl sulfoxide, methanol, n-hexane, n-pentane, and water) using implicit solvation models combined with configuration interaction based on single excitations and with time-dependent density functional theory.
1. Introduction
Solvation effects on the electronic absorption spectra of chromophoric solutes have fascinated researchers for a very long time.1–22 A key concept of the modern viewpoint is the self-consistent reaction field, which appears in several of the historical treatments and in most modern treatments. The reaction field is the electrostatic field exerted on the solute by the polarization of the solvent due to the presence of the solute. Proper application of this concept to electronic excitation requires the recognition of time scales.23–29 Solute and solvent electronic distributions respond to each other and to the exciting photon much faster than nuclear motion responds; the response of nuclear motion is almost static on their time scale. From the point of view of the chromophoric solute, the relatively static character of the nuclear motion is called the Franck–Condon principle; from the point of view of the solvent it is associated with a slowly responding portion of the reaction field. But the solvent is static only during the absorption process itself; before fluorescence occurs and before many photochemical processes can occur, the solvent and excited-state solute typically have time to equilibrate not only their electronic distributions but also their nuclear geometry. The main purpose of the present article is to analyze various computational approaches for calculating the separate components of the solvent response and for calculating the self-consistent reorganizations on the fast time scale of vertical excitation. We build on this analysis to develop a new computational algorithm for accurate prediction of solvatochromic shifts on absorption in polar and nonpolar media.To illustrate the roles of the terms contributing on various time scales, we will consider several prototype transitions, namely, the lowest n → π* transitions of acetone, acrolein, methanal, and pyridine and the lowest π → π* transitions of coumarin 153 (C153), indolinedimethine-malononitrile (IM), julolidine-malononitrile (JM), and methylenecyclopropene (MCP) (see Fig. 1).
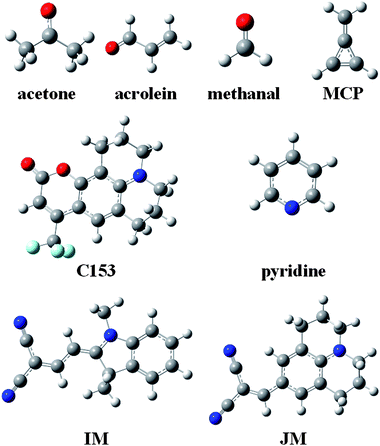 | ||
| Fig. 1 Molecular structures of solutes. Hydrogen atoms are white, carbon is grey, nitrogen is blue, fluorine is cyan, and oxygen is red. | ||
It is well known that there are several contributions to solvatochromic shifts, including solvent polarization, dispersion, exchange repulsion, charge transfer, and the partial covalent character of hydrogen bonding (the rest of hydrogen bonding is already included in contributions we have already mentioned). Note that the solvent polarization component can be modeled by treating the solvent as a dielectric continuum having the dielectric constant of the bulk solvent and is sometimes called the bulk electrostatic component.
Solvatochromic shifts of acetone, to pick an example, can be reasonably well accounted for by considering only dielectric polarization, dispersion, and hydrogen bonding,25,29 where the change in dispersion occurs on the fast time scale, but the dielectric polarization and the change in hydrogen bonding occur on both time scales. When only these three contributions are explicitly included, the hydrogen bonding term includes not only partial covalent character but also all other aspects of hydrogen bonding that are not included in the dielectric polarization and dispersion. For example, it must include the charge transfer that accompanies hydrogen bonding and the deviation of the local polarization from that predicted by the bulk dielectric model. Clearly then the partition into dielectric polarization and hydrogen bonding depends on the details of the dielectric polarization model. In particular, if the electrostatics is underestimated, one infers a greater contribution from hydrogen bonding. In the present study we center our attention on the dielectric polarization contribution to sort out the contributions from various time scales and the most consistent ways to treat them.
The main focus of the present study is on the use of various implicit solvation models combined with time-dependent density functional theory30–33 (TDDFT), which is a linear response (LR) theory that starts with a self-consistent-field (SCF) step for optimizing the orbitals of a reference state, i.e., the Kohn–Sham34 or generalized Kohn–Sham35 determinant that represents the ground-state density in density functional theory (DFT). In TDDFT, a one-electron time-dependent perturbation representing the interaction of the molecular electrons with the external electric field due to the incident light is applied to the density obtained from the ground-state Kohn–Sham or generalized Kohn–Sham SCF equations. The response is calculated to first order, yielding a generalized polarizability that has poles at energies that approximate the one-electron excitation energies. The excitation energies calculated this way are approximate because one must employ an approximate density functional and because of the linear response approximation. Linear response theory can be used not only with DFT but also with Hartree–Fock wave function theory, yielding time-dependent Hartree–Fock (TDHF) theory.36 The present article also considers the configuration interaction method of wave function theory. We will use the wave function language both for density functional theory and wave function theory, but one should keep in mind that in wave function theory, one is dealing with wave functions of the real system, but in density functional theory the wave functions are those of an auxiliary noninteracting system as introduced by Kohn and Sham.
In the polarized continuum method17 the reaction field exerted on the solute by the polarized solvent is represented by a set of surface charges on the assumed solute–solvent boundary surface (which is usually just called the solute surface). The combination of convenient TDDFT algorithms with the polarized continuum model17 (PCM) for dielectric polarization, as in the Gaussian computer package (Gaussian 0337 with significant updates in Gaussian 09,38 including those for solvation calculations39,40), opens the door to increased use of this kind of potentially very useful calculation for predicting and analyzing solvatochromic shifts. For example, it has been recently found that TDDFT with the M06 density functional41,42 combined with the integral equation formalism43–46 of PCM17,47,48 (IEF-PCM) with the SMD intrinsic Coulomb radii49 was useful for analyzing the solvatochromic shifts of the n → π* excitation of acetone in various solvents.29 (The intrinsic Coulomb radii are used in the determination of the solute surface.) The reader may consult two recent overview articles for other applications of TDDFT coupled to PCM to calculate excited state properties in solution.50,51 We will emphasize this combination for our analysis. We will also consider representing the reaction field by the generalized Born (GB) approximation.52–58 Any method that can be derived or defined in the context of PCM can be re-expressed in the GB approximation, and vice versa, as illustrated in more detail below.
In general the response of the medium depends on frequency and can be different for each kind of vibrational and orientational relaxation; however, in the present article we follow the usual convention of simply dividing the response into two time scales. Then the reaction field has two components, a fast one and a slow one. The fast reaction field is associated with polarizing the electronic structure of the solvent without changing the nuclear positions. This polarization occurs on the time scale of electronic excitation, but the polarization due to moving nuclei (re-orientation of solvent molecules, other solvent vibrational motions, and translation of solvent molecules) is much slower, as recognized in the Franck–Condon principle. The partition of the reaction field into fast and slow components is based on the refractive index n and the static dielectric constant ε0.17,23,25,59 The refractive index n is used to provide the dielectric constant at optical frequencies as εopt = n2. The reaction field can then be partitioned into fast and slow components in two different ways, often associated with the names of Pekar60 and Marcus,61 which are equivalent within the linear response approximation when correctly used.62 In both partitions, the total response is governed by the total dielectric constant εtotal, and the fast response is governed by its fast component εfast. In general, εtotal is set equal to ε0 which is essentially unity in a dilute gas but greater than εopt in a liquid. A convenient language that is used in the literature (and that will be useful here) is that a calculation in which εfast is set equal to εopt is labeled “nonequilibrium,” and a calculation in which εfast is set equal to ε0 (such that all the response is fast) is called “equilibrium.” Thus, equilibrium solvation can be considered as a special case of nonequilibrium solvation. Table 1 gives ε0 and εopt for the solvents considered in the present work, along with the solvents’ values of Abraham's hydrogen bond acidity parameters63–66 used by some of the solvation models in determining solvent-dependent intrinsic Coulomb radii.
| Solvent | ε 0 | ε opt | α H |
|---|---|---|---|
| a The hydrogen bond acidity parameters are used in the SM8, SM8AD, and SMD models to obtain intrinsic Coulomb radii for selected atoms in selected solvents (see Table 3). | |||
| Vacuum | 1 | 1 | 0 |
| n-Pentane | 1.8 | 1.8 | 0 |
| n-Hexane | 1.9 | 1.9 | 0 |
| Cyclohexane | 2.0 | 2.0 | 0 |
| Methanol | 32.6 | 1.8 | 0.43 |
| Acetonitrile | 35.7 | 1.8 | 0.07 |
| Dimethyl sulfoxide | 46.8 | 2.0 | 0 |
| Water | 78.4 | 1.8 | 0.82 |
This article proposes a self-consistent state-specific vertical excitation model for electronic excitation in solution which is called the vertical excitation model or VEM. The theoretical background for the proposed model is given in the next section, and in more detail in the Electronic Supplementary Information.† We also discuss several other approaches to calculate vertical excitations in solution as approximations to the VEM.
2. Theory
2.1 General considerations
A vertical (in general, nonequilibrium) excitation energy is calculated as follows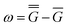 | (1) |
In eqn (1) and hereafter, the single bar refers to the ground electronic state of the solute molecule in solution, and the double bar refers to its excited state. The first term in eqn (1) denotes the nonequilibrium excited-state free energy,61 and the second term denotes the equilibrium ground-state free energy. The quantities G are defined as
| G = E0 + GP | (2) |
| E0 = 〈Ψ|H0|Ψ〉 | (3) |
In principle, the ground- and excited-state electronic wave functions Ψ in solution are eigenfunctions of effective Hamiltonians Heff defined as follows
| Heff = H0 + Φ | (4) |
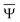 and
and 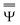 are approximations to these eigenfunctions, and our goal is to determine them. In addition, the reaction field Φ used in eqn (4) is self-consistently dependent on the solute electronic wave function Ψ, and it can be defined as
are approximations to these eigenfunctions, and our goal is to determine them. In addition, the reaction field Φ used in eqn (4) is self-consistently dependent on the solute electronic wave function Ψ, and it can be defined as 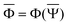 or
or 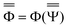 .
.
Within the polarized continuum model,17 one defines a discretized solute–solvent boundary, and the reaction field potential Φ(r) at an arbitrary position r in the cavity defined by the solute–solvent boundary is given by
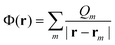 | (5) |
| Qm = σ(rm)ΔSm | (6) |
In contrast, the generalized Born (GB) approximation52–58 is equivalent to approximating the reaction field potential Φ(r) at the position rn as
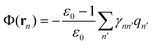 | (7) |
Note that in the recent PCM implementations39,40,67eqn (5) is replaced by the following equation:
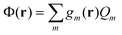 | (8) |
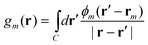 | (9) |
2.2 Description of the ground state
The ground state of the solute molecule in solution is described in terms of equilibrium solvation. Although the ground-state reaction field![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) can be defined by eqn (5), (7), or (8), we will develop the theory here by using eqn (5) with a set of ground-state total polarization charges. The latter are determined by solving the following equation17
can be defined by eqn (5), (7), or (8), we will develop the theory here by using eqn (5) with a set of ground-state total polarization charges. The latter are determined by solving the following equation17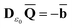 | (10) |
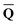 is a column vector of charges with components
is a column vector of charges with components ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) m, and Dε0 is a square matrix that depends on the static dielectric constant ε0 and on a particular PCM algorithm. The column vector
m, and Dε0 is a square matrix that depends on the static dielectric constant ε0 and on a particular PCM algorithm. The column vector ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) contains (at the reaction-field charge positions) the ground-state values of the solute normal electric field in the case of the dielectric version of PCM (DPCM) or the solute electrostatic potential on individual surface elements in the case of the conductor-like (CPCM) and integral-equation-formalism versions of PCM (IEF-PCM). In the present work we use the IEF model,43 and in this case the elements of the column vector
contains (at the reaction-field charge positions) the ground-state values of the solute normal electric field in the case of the dielectric version of PCM (DPCM) or the solute electrostatic potential on individual surface elements in the case of the conductor-like (CPCM) and integral-equation-formalism versions of PCM (IEF-PCM). In the present work we use the IEF model,43 and in this case the elements of the column vector ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) are defined using the following equation
are defined using the following equation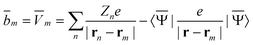 | (11) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) m is the ground-state electrostatic potential at the mth surface element due to the solute's nuclear and electronic charge density, and the sum over n runs over all solute nuclei; Zn is the atomic number of atom n, and e is the atomic unit of charge. Note that the recent PCM implementations39,40 define the apparent surface charge using eqn (9), and in this case eqn (11) becomes more complex, and it is not given here.
m is the ground-state electrostatic potential at the mth surface element due to the solute's nuclear and electronic charge density, and the sum over n runs over all solute nuclei; Zn is the atomic number of atom n, and e is the atomic unit of charge. Note that the recent PCM implementations39,40 define the apparent surface charge using eqn (9), and in this case eqn (11) becomes more complex, and it is not given here.
In practice, the column vector ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) in eqn (10) is considered to be an implicit function of the solvent's static dielectric constant ε0 because it is derived from the solute ground-state electronic density obtained in a self-consistent reaction field (SCRF) calculation, i.e., self-consistently with the ground-state reaction field
in eqn (10) is considered to be an implicit function of the solvent's static dielectric constant ε0 because it is derived from the solute ground-state electronic density obtained in a self-consistent reaction field (SCRF) calculation, i.e., self-consistently with the ground-state reaction field ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) that depends on the ground-state column vector
that depends on the ground-state column vector 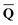 calculated by eqn (10) using
calculated by eqn (10) using ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) from the previous SCRF iteration. The resulting ground-state polarization free energy is defined as
from the previous SCRF iteration. The resulting ground-state polarization free energy is defined as
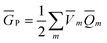 | (12) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) m is obtained from eqn (11) using the solute's electronic density obtained from the ground-state SCRF procedure.
m is obtained from eqn (11) using the solute's electronic density obtained from the ground-state SCRF procedure.
2.3 Description of the excited state
The excited state of the solute molecule in solution is described in terms of nonequilibrium solvation by incorporating two time scales (fast and slow) for solvent relaxation.There are two partition schemes that have been used in the literature17 to decompose the polarization response of a medium described by the frequency-dependent permittivity ε(ω) into fast and slow components. Here, we will call them Partition I and Partition II, according to the notation used in Ref. 17. Partition I is usually associated with the name of Marcus,61 and Partition II is associated with the name of Pekar.60 In terms of Partition I, the fast polarization response is assumed to be induced entirely by electronic degrees of freedom (we will use the index “el” to refer to the electronic polarization), and the slow polarization response is induced by nuclear or orientational motion (we will use the index “or” to refer to the orientational polarization). In contrast, Partition II does not specify physical degrees of freedom corresponding to electrons and nuclei, but instead it employs the concept of a dynamic (“dyn”) and an inertial (“in”) polarization response to define the fast and slow polarization, respectively. The fast and slow components of the polarization energy GP are determined differently within these schemes because in Partition I the part of the fast polarization that is in equilibrium with slow polarization is included in the fast response, but in Partition II that contribution is considered as part of the slow response.17,62 Nevertheless, the two partitions yield identical reaction fields, identical total GP polarization free energies, and identical solvatochromic shifts in the limit of linear response, which is assumed here. Next, we define the fast and slow components of the nonequilibrium excited-state reaction field Φ using both partitions, and we give expressions for the nonequilibrium excited-state polarization free energy GP in terms of both sets of partitioned reaction field potentials.
The total excited-state reaction field corresponding to nonequilibrium solvation is defined by eqn (5) in general or by eqn (8) in the most recent PCM implementations39,40 where Qm is replaced with the nonequilibrium (“neq”) polarization charge. The latter is partitioned in two ways. In Partition I, we have
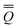 neqm = neqm = 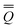 elm + elm + ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) orm orm | (13) |
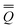 neqm = neqm = 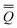 dynm + dynm + ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) inm inm | (14) |
First, we need to find a set of slow polarization charges (“or” or “in”). The column vector of orientational charges used in Partition I is expressed as [see, for example, eqn (30) in Ref. 59]
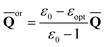 | (15) |
![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) is a set of the ground-state (equilibrium) total charges that satisfies eqn (10) using the column vector
is a set of the ground-state (equilibrium) total charges that satisfies eqn (10) using the column vector ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) obtained from the ground-state SCRF calculation with the equilibrium ground-state reaction field. The column vector of inertial charges used in Partition II is given as
obtained from the ground-state SCRF calculation with the equilibrium ground-state reaction field. The column vector of inertial charges used in Partition II is given as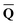 in = in =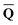 − − 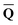 dyn dyn | (16) |
Dεopt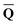 dyn = − dyn = −![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) | (17) |
![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) is the same as in eqn (11). Note that Partition II does not require a second ground-state SCRF calculation (using εopt) to obtain the ground-state dynamic polarization charge by eqn (17), and the column vector
is the same as in eqn (11). Note that Partition II does not require a second ground-state SCRF calculation (using εopt) to obtain the ground-state dynamic polarization charge by eqn (17), and the column vector ![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) used by eqn (17) is obtained from the original ground-state SCRF calculation based on ε0.
used by eqn (17) is obtained from the original ground-state SCRF calculation based on ε0.
Second, we need to find the fast excited-state polarization charges (“el” or “dyn”) while keeping the slow ground-state polarization charges (“or” or “in”) at the fixed values which are defined by the procedures described in the previous paragraph. The column vector of excited-state electronic polarization charges used in Partition I is determined by solving the following equation [see eqn (25) in Ref. 68]
Dεopt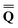 el = − el = −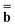 − Ω − Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 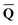 or or | (18) |
Dεopt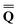 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dyn = − dyn = −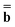 | (19) |
The matrix Dεopt used in both equations is the same as in eqn (17). The square matrix Ω used in eqn (18) does not depend on a dielectric constant, but it depends on a particular PCM algorithm [see eqn (22) in Ref. 59 and eqns (A7–A10) of the ESI† of the present article]. The column vector 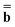 in both equations contains the excited-state values of the solute normal electric field in the case of DPCM or the solute electrostatic potential on individual surface elements in the case of CPCM or IEF-PCM. In the present work we use IEF-PCM, and the elements of this column vector are given by
in both equations contains the excited-state values of the solute normal electric field in the case of DPCM or the solute electrostatic potential on individual surface elements in the case of CPCM or IEF-PCM. In the present work we use IEF-PCM, and the elements of this column vector are given by
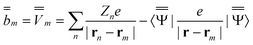 | (20) |
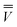 m is the excited-state electrostatic potential at the mth surface element due to the solute's nuclear and electronic charge density in the excited state. The column vector
m is the excited-state electrostatic potential at the mth surface element due to the solute's nuclear and electronic charge density in the excited state. The column vector 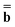 in eqn (19) is considered to be an implicit function of both εopt and ε0 because it is derived from the solute electronic density obtained self-consistently with the total nonequilibrium reaction field whose fast and slow components are defined using both εopt and ε0. The evaluation of the last term of eqn (20) in both the CIS and TDDFT schemes is discussed further in Section 2.8.
in eqn (19) is considered to be an implicit function of both εopt and ε0 because it is derived from the solute electronic density obtained self-consistently with the total nonequilibrium reaction field whose fast and slow components are defined using both εopt and ε0. The evaluation of the last term of eqn (20) in both the CIS and TDDFT schemes is discussed further in Section 2.8.
The difference between the electronic and the dynamic polarization charge is due to the second term on the right-hand side of eqn (18), which corresponds to the response of the solvent's electrons to the surface charge originated by the slow component of the total nonequilibrium reaction field.62 Since the given term does not depend on the change in the solute's charge distribution upon electronic excitation within the linear response limit which is applied here, its value is the same in the ground and excited states.62 The difference between the two partitions is that in Partition I, this term is a part of the fast response according to eqn (18) whereas, in Partition II, this term is included in the slow (inertial) component of the total nonequilibrium reaction field according to the following relation:
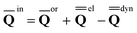 | (21) |
2.4 VEM method
In the VEM approach proposed in the present article, we evaluate the total nonequilibrium excited-state reaction field as follows. First, we evaluate the equilibrium ground-state reaction field and the slow (orientational or inertial) polarization charges using the procedure described above. Then, we evaluate the excited-state wave function with the effective Hamiltonian of eqn (4) using the ground-state reaction field as an initial approximation to the excited-state reaction field, which results in the zero-order approximation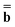 (0) to the solute's excited-state electrostatic potential
(0) to the solute's excited-state electrostatic potential 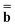 . The vector
. The vector 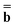 (0) is partition-independent by definition because it is defined by the excited-state wave function computed using the equilibrium ground-state reaction field
(0) is partition-independent by definition because it is defined by the excited-state wave function computed using the equilibrium ground-state reaction field ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) at this step, and the latter is not partitioned. Using the excited-state column vector
at this step, and the latter is not partitioned. Using the excited-state column vector 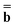 (0) and the fixed slow polarization charges saved earlier, and solving eqn (18) if Partition I is used or eqn (19) if Partition II is used, we can evaluate a new excited-state reaction field using eqn (13) or eqn (14). The resulting column vector of total nonequilibrium polarization charges satisfies the following equation within both Partition I and Partition II
(0) and the fixed slow polarization charges saved earlier, and solving eqn (18) if Partition I is used or eqn (19) if Partition II is used, we can evaluate a new excited-state reaction field using eqn (13) or eqn (14). The resulting column vector of total nonequilibrium polarization charges satisfies the following equation within both Partition I and Partition II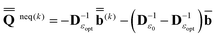 | (22) |
![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) and
and 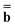 (k) in Partition I and in Partition II. Hence the excited-state column vector
(k) in Partition I and in Partition II. Hence the excited-state column vector 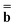 will continue to be independent of partition even at iterations after the first. Using the new total nonequilibrium excited-state reaction field, we evaluate new approximations to the excited-state electronic wave function of the solute molecule in solution and to the column vector
will continue to be independent of partition even at iterations after the first. Using the new total nonequilibrium excited-state reaction field, we evaluate new approximations to the excited-state electronic wave function of the solute molecule in solution and to the column vector 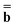 , until the procedure converges self-consistently with respect to these quantities. Note that during this procedure we change only the fast component of the total reaction field, which corresponds to the first term of eqn (22), at the fixed slow component corresponding to the second term of eqn (22). The total nonequilibrium excited-state reaction field at the last iteration will be the same in both partition schemes using the same initial approximation for this quantity. In practice, various initial approximations may lead to more than one solution (within the same partition) but this technicality is irrelevant to the choice of a particular partition scheme. See the ESI for more details on the derivation of eqn (22) and on the proof that the two partitions give the same total reaction field within the PCM formalism.† The latter conclusion is in agreement with Aguilar's proof using a less general model based on the Onsager reaction field.62 Note that eqn (22) defined here in terms of the PCM polarization surface charges corresponds to eqn (7) in Ref. 62 defined in terms of ground- and excited-state point dipoles.
, until the procedure converges self-consistently with respect to these quantities. Note that during this procedure we change only the fast component of the total reaction field, which corresponds to the first term of eqn (22), at the fixed slow component corresponding to the second term of eqn (22). The total nonequilibrium excited-state reaction field at the last iteration will be the same in both partition schemes using the same initial approximation for this quantity. In practice, various initial approximations may lead to more than one solution (within the same partition) but this technicality is irrelevant to the choice of a particular partition scheme. See the ESI for more details on the derivation of eqn (22) and on the proof that the two partitions give the same total reaction field within the PCM formalism.† The latter conclusion is in agreement with Aguilar's proof using a less general model based on the Onsager reaction field.62 Note that eqn (22) defined here in terms of the PCM polarization surface charges corresponds to eqn (7) in Ref. 62 defined in terms of ground- and excited-state point dipoles.
In Partition I, the resulting excited-state polarization free energy is defined as
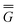 P = P = 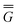 P, P,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) el + el + 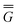 P, P,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or + or + 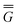 P, P,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) el-or el-or | (23) |
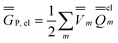 | (24) |
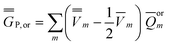 | (25) |
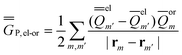 | (26) |
In the equations above, the indexes m and m′ run over all surface elements, and Vm is the electrostatic potential at the mth surface element due to the solute's nuclear and electronic charge density as given by eqn (11) and (20) for the ground state and for the excited state, respectively. Note that in the most recent PCM implementations39,40 the apparent surface charge is defined using eqn (9), and in this case eqn (26) is rewritten as
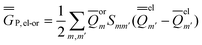 | (27) |
![[b with combining macron]](https://www.rsc.org/images/entities/b_char_0062_0304.gif) of eqn (10). However, it is more convenient to obtain this quantity by subtraction of the corresponding orientational polarization charge defined by eqn (15) from the total ground-state charge that satisfies eqn (10).
of eqn (10). However, it is more convenient to obtain this quantity by subtraction of the corresponding orientational polarization charge defined by eqn (15) from the total ground-state charge that satisfies eqn (10).
In Partition II, the excited-state polarization free energy is defined as
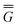 P = P = 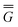 P,dyn + P,dyn + 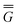 P,in P,in | (28) |
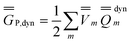 | (29) |
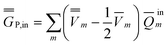 | (30) |
Note that Partition I's expression of 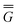 P contains the cross-term while Partition II's expression does not. This cross-term arises from the second term on the right-hand side of eqn (18). The latter corresponds to the response of the solvent's electrons to the surface charge originated by the slow component of the total nonequilibrium excited-state reaction field.62 Nevertheless, the two partitions should yield identical values of the total nonequilibrium polarization free energy when they are correctly applied, within the linear response approximation. Using eqn (2), (12) and (28), the excitation energy of eqn (1) can be expressed as
P contains the cross-term while Partition II's expression does not. This cross-term arises from the second term on the right-hand side of eqn (18). The latter corresponds to the response of the solvent's electrons to the surface charge originated by the slow component of the total nonequilibrium excited-state reaction field.62 Nevertheless, the two partitions should yield identical values of the total nonequilibrium polarization free energy when they are correctly applied, within the linear response approximation. Using eqn (2), (12) and (28), the excitation energy of eqn (1) can be expressed as
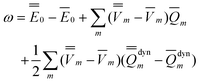 | (31) |
See the ESI for the proof of eqn (31).†
Within the classical framework used by Aguilar,62 the linear response approximation assumes that the solvent polarization response is linear with respect to the electric field induced by the solute unpolarized charge distribution (i.e., by the solute's charge density that remains the same in the gas phase and in solution), and the resulting equilibrium electrostatic free energy of solvation equals a half of the energy of the electrostatic interaction between the polarized solvent and the unpolarized solute.69 Within the quantum-mechanical framework used in the present work, the solute is polarized self-consistently with respect to the solvent's reaction field, and the mutual solute–solvent polarization can generally lead to the solvent polarization response that is no longer linear with respect to the electric field induced by the charge density of the unpolarized solute.69 However, the resulting polarization response remains linear with respect to the electric field induced by the charge distribution of the polarized solute, and the equilibrium electrostatic free energy of solvation equals a half of the energy of the electrostatic interaction between the mutually polarized solute and solvent, whereas the solute's polarization energy or, in other words, the solute's electronic distortion energy is accounted for in eqn (3). Thus, the present article shows the equivalence of Partitions I and II, independently of how the solute is treated (i.e., whether the solute is unpolarized or polarized self-consistently), and independently of how the solvent is treated (i.e., whether the solvent's reaction field is represented in terms of the continuous or the discrete charge density). In both respects this is a generalization of the results of Ref. 62, which was for unpolarized solute and the Onsager dipole approximation for solute–solvent interactions.
2.5 Definition of Φ and GP in the generalized Born approach
The ground-state reaction field and the ground-state polarization free energy can be expressed within the GB approximation in terms of partial atomic charges by using the following equations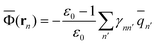 | (32) |
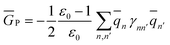 | (33) |
The GB expressions of the excited-state reaction field and the polarization free energy are given as
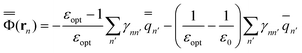 | (34) |
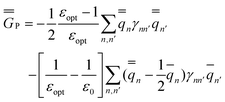 | (35) |
In the equations above, the index n or n′ runs over all nuclei situated at rn or rn′, γnn′ is a Coulomb integral, and qn or qn′ is a partial atomic charge in the ground state (single bar) or in the excited state (double bar). Note that eqn (34) and (35) correspond to nonequilibrium solvation either using Partition I or Partition II; the two partitions yield identical reaction fields and total polarization free energies. The first term of eqn (35) can be interpreted as the GB analog of eqn (29), whereas the second term is the GB analog of eqn (30). Using eqn (33) and (35), the excitation energy of eqn (1) can be expressed as
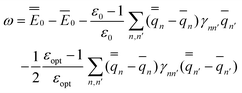 | (36) |
See the ESI for the proof of eqn (32)–(36).†
The Coulomb integral γnn′ is defined according to Still et al.57 in terms of the effective Born radius of atom n or n′. One can define the effective Born radius using an unshielded Coulomb field for the electric displacement field induced by the charge qn, as proposed originally by Still et al.57 The GB approximation that uses this approach will be called the generalized Born with symmetric descreening (GBSD) approximation hereafter. One can also define the effective Born radius using an alternative formula suggested by Grycuk.58 The GB approximation that uses Grycuk’s formulation will be called the GB with asymmetric descreening (GBAD) approximation. In the present paper we use both GBSD and GBAD approaches. More details on the model physics of these approximations are given in Ref. 70.
2.6 Computational protocols based on molecular orbitals determined in the ground-state reaction field
The reaction field Φ depends on the solute wave function. Therefore, the effective Hamiltonian in eqn (4) can differ for the ground and excited electronic states of the solute molecule in solution. In the present article we will consider solving electronic structure problems with the effective Hamiltonian of eqn (4) using several computational protocols summarized in Table 2.| Protocol | RF for MOs b | RF for CISc | Self-consistent | State-specific |
|---|---|---|---|---|
| a n/a means not applicable. The listed computational protocols are described in subsections 2.6 and 2.7. b This indicates whether the equilibrium ground-state (GS) or nonequilibrium excited-state (ES) reaction field is used in the ground-state SCRF calculation to get MOs. c This indicates whether the ground-state (GS) or excited-state (ES) reaction field is included either implicitly (i) or explicitly (e) in the CIS or TDDFT matrix and whether the linear response (LR) term is included. | ||||
| Gas | n/a | n/a | n/a | n/a |
| GSRF | GS | GS(i) | no | no |
| cGSRF | GS | GS(i) | no | yes |
| VEM | GS | ES(e) | yes | yes |
| LR | GS | GS(i)+LR(e) | no | no |
| cLR | GS | GS(i)+LR(e) | no | yes |
| IBSF | ES | ES(i) | yes | yes |
| IESRF | ES | ES(i) | yes | yes |
For some approximations considered here, the electronic excitation may be described by any electronic structure method, for example, configuration interaction with single excitations (CIS),71–74 the complete active space self-consistent field method (CASSCF),75,76 equation-of-motion coupled cluster theory with single and double excitations (EOM-CCSD),77 or TDDFT.30–33 However, in the present study we consider only the CIS and TDDFT implementations of the computational protocols described below.
The CIS calculations are carried out just like gas-phase CIS except that H0 is replaced by H0 + Φ, where the various approximation schemes correspond to different choices of Φ in the SCF step to obtain the molecular orbitals (MOs) and in forming the CIS matrix to be diagonalized. The TDDFT calculations can be discussed in the same way. In particular, we use eqn (9), (10), and (13) of Scalmani et al.78 with matrix elements of νPCM (in their notation) replaced by matrix elements of Φ, in the present notation. In that procedure, their eqn (13) is the matrix to be diagonalized, and, just as in CIS, it is built using singly excited configurations defined in terms of MOs obtained in a prior SCF step.
For the excited state calculations in the present section we always construct the CIS or TDDFT matrix using configurations built from the equilibrium SCRF ground-state orbitals, and we omit the ground-state configurations before diagonalizing the CIS or TDDFT matrix. This would not make a difference if the configurations were constructed from SCF orbitals obtained with the same Hamiltonian used to describe the excited state or if the excited state had a different symmetry than the ground state, but it does make a difference for some of the calculations carried out here (some examples are mentioned below). When it does make a difference because the SCF orbitals were obtained with a different Hamiltonian, our motivation for omitting the ground state is to ensure that the nonequilibrium excited state is orthogonal to the equilibrium ground state. Failure to enforce this can lead to spurious convergence of excited-state iterations to the ground-state solution or a solution with an unphysical admixture of the ground state.
The first computational protocol we use corresponds to a gas-phase calculation (gas) with no solvation effects included in the treatment of the ground or excited electronic state (Φ ≡ 0).
The second computational protocol is called the ground-state reaction field (GSRF) approximation. The GSRF method evaluates the excitation energy using an approximation that the excited-state reaction field is equal to the ground-state reaction field. A GSRF calculation involves two steps: (i) solve the SCF equations for the ground state in solution to obtain the ground-state molecular orbitals and the corresponding orbital energies as eigenfunctions and eigenvalues of the liquid-phase Fock operator, respectively; (ii) run a CIS or TDDFT calculation on these MOs and orbital energies by diagonalizing the corresponding CIS or TDDFT matrix. Considering only the CIS case for simplicity, we define a matrix to be diagonalized using the following equation
| HGSRFia,jb = δijδab[εa − εi] − (ja‖ib) | (37) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) |ψp〉 = εp|ψp〉 |ψp〉 = εp|ψp〉 | (38) |
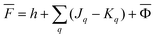 | (39) |
ωGSRF =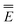 − Ē − Ē | (40) |
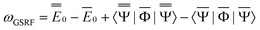 | (41) |
![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) , the quantities E0 are the corresponding ground- and excited-state expectation values of H0, and the last two terms in eqn (41) can be expressed using the solute's ground- and excited-state electrostatic potentials, yielding the following equation in terms of the PCM approach
, the quantities E0 are the corresponding ground- and excited-state expectation values of H0, and the last two terms in eqn (41) can be expressed using the solute's ground- and excited-state electrostatic potentials, yielding the following equation in terms of the PCM approach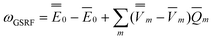 | (42) |
Note that the GSRF protocol need not involve an explicit calculation of the quantities E0, and they are not required for evaluation of ωGSRF. The quantity ωGSRF is associated in the literature with the notations ΔEGSK0, ΔE0, and ωK0.51,79,80
Comparing eqn (1) to eqn (42), and using eqn (12) to define the ground-state polarization free energy, one can readily obtain the GSRF definition of the excited-state polarization free energy as follows
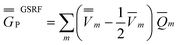 | (43) |
Comparing eqn (43) to eqn (23) or to eqn (28), one can see that eqn (43) yields the full excited-state polarization free energy only if εopt = 1, i.e., when all the charges are slow. In the case of εopt > 1, the GSRF approach does not account for the state-specific relaxation of the reaction field (specific to the excited state) because eqn (43) does not involve the fast excited-state polarization charges.
The third computational protocol is called the corrected ground-state reaction field (cGSRF) approximation. Using Partition II, the cGSRF excitation energy is defined by
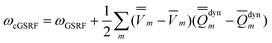 | (44) |
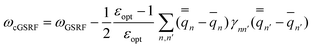 | (45) |
The fourth computational protocol is the vertical excitation model or VEM that can be understood as a self-consistent state-specific extension of the GSRF method. In other words, the cGSRF calculation can be considered the first iteration of the VEM method. The VEM iterative procedure itself is described in detail earlier in Section 2.4. The VEM method is the first method considered in which the Hamiltonian used to construct the CIS matrix is not the same as the Hamiltonian used to obtain the molecular orbitals because of using different reaction fields in the two Hamiltonians. See Table 2 for a summary of the methods in this section and the next that emphasizes this distinction.
The CIS matrix at the kth iteration is defined by
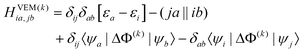 | (46) |
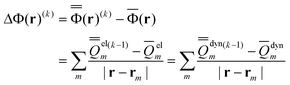 | (47) |
Note that when eqn (8) is used, the quantity |r–rm|−1 in eqn (47) is substituted with gm(r) defined by eqn (9). The quantities given in eqn (46) and (47) without the superscript (k) or (k−1) remain unchanged during the VEM iterations, and they are the same as those used in the GSRF and cGSRF protocols.
Using Partition II, the VEM excitation energy at the kth iteration (k > 1) is defined by
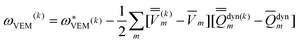 | (48) |
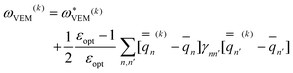 | (49) |
The VEM scheme has been implemented using CIS both with the GB approximation25 (in particular, GBSD) and with PCM,79 and the first VEM implementation for TDDFT is presented in this article. Note that in the original implementation25 of the VEM, we did not remove the ground state from the CIS matrix. This had no effect on the results because the excited state of the system treated in Ref. 25 (acetone) has a different symmetry than the ground state. Among the molecules considered here, however, there are three cases where it would matter, namely C153, IM, and JM. Thus, we emphasize that VEM is defined such that, when it matters, the ground state should be removed from the matrix to be diagonalized.
The literature has two additional PCM TDDFT schemes based on ground-state MOs in the ground-state reaction field, and both of these have been tested in the present study: namely, the solvent-induced linear response (LR) method24,26,51,78 and the corrected linear response (cLR) method.51,80 Contrary to eqn (46) used in the VEM calculation, the TDDFT A and B matrices used in the LR calculation do not contain the excited-state reaction field operator [see, for instance, eqn (10)–(12) in Ref. 51]. Instead, they include the νPCMia,jb perturbation term or, in other words, linear response term defined by eqn (13) in Ref. 51 using the ground-state molecular orbitals in solution ψp (p = a, b, i or j) from eqn (38) in the present paper (as usual, the indices i and j run over all occupied molecular orbitals and the indices a and b run over all virtual orbitals). The matrix element νPCMia,jb accounts for a dispersion-like interaction12 between the charge distribution ψa*ψi and the dynamic contribution to the solvent reaction potential due to the charge distribution ψb*ψj. The LR CIS matrix is the same as the GSRF matrix defined by eqn (37), except that the former includes νPCMia,jb. Therefore, the difference between the excitation energy ωLR and ωGSRF is solely due to the term νPCMia,jb included in the LR scheme.
The LR scheme has been widely used because it was the default in Gaussian 0337 and in Gaussian 0938 through revision B.01. We emphasize this point because many solvated excited-state calculations in the literature fail to indicate the protocol used to determine the excited-state energy.
The cLR method involves two independent CIS or TDDFT calculations.51,80 The first one is the GSRF calculation to obtain ωGSRF. The second one is the LR calculation to obtain the LR excited-state electron density. Then, the excitation energy ωcLR is calculated by eqn (44) where the second term is computed using the LR excited-state electron density. Therefore, the difference between the excitation energy ωcLR and ωcGSRF is solely due to the term νPCMia,jb included in the second CIS or TDDFT calculation to evaluate the second term of eqn (44) within the cLR scheme. The excitation energy ωLR is not used in the ωcLR calculation.
The methods in Table 2 that evaluate the excited-state electron density iteratively in the nonequilibrium excited-state reaction field will be called self-consistent in the present article. The methods that explicitly compute the fast polarization contribution to the excited-state polarization free energy using the electron density of the specific excited state will be called state-specific. There are three self-consistent methods in Table 2, namely, VEM, IBSF, and IESRF (the latter two are discussed in the next section). There are five state-specific methods, namely, cGSRF, VEM, cLR, IBSF, and IESRF. Note that VEM, IBSF, and IESRF are both self-consistent and state-specific, whereas GSRF and LR are neither self-consistent nor state-specific.
We also note that, among the methods in Table 2, only GSRF and LR are variational in the sense that the total energy in solution is explicitly required to be stationary with respect to both the MO coefficients and the CIS or TDDFT amplitudes. All the other methods in Table 2 are characterized by a coupling between MO coefficients and the CIS or TDDFT amplitudes that is introduced by the solvent reaction field and prevents a straightforward variational formulation of the method.
The excitation energies computed in the present study by the above protocols are all calculated at the solute ground-state molecular geometries in solution, which is appropriate for describing absorption (vertical electronic excitation). We do not consider here adiabatic solvation when one optimizes the geometry to minimize the energy of the adiabatically solvated excited state. In the latter case, it would correspond to a case when an excited state is equilibrated with the solvent, and this would be an initial state for fluorescence.
2.7 Computational protocols based on molecular orbitals determined in the excited-state reaction field
The next method we discuss is a method originally developed by Improta, Barone, Scalmani, and Frisch within the PCM framework,81 and we call it the IBSF scheme after the names of the authors. In the present work, this scheme has been extended to the GB approach.Similar to the VEM approach, the IBSF scheme can be considered a self-consistent state-specific extension of the GSRF method. According to the IBSF method, one runs an equilibrium ground-state SCRF calculation first to obtain a set of the slow polarization charges by solving eqn (15) or eqn (16) (depending on a particular partition scheme). These equilibrium ground-state charges will remain fixed during the whole IBSF procedure. Next, one runs a GSRF calculation that involves a diagonalization of the CIS or TDDFT matrix constructed using the quantities εp and ψp defined by eqn (38), resulting in the excited-state wave function which is used to obtain the column vector 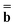 by eqn (20) and then to obtain a set of the excited-state fast polarization charges by solving eqn (18) or eqn (19) with the column vector
by eqn (20) and then to obtain a set of the excited-state fast polarization charges by solving eqn (18) or eqn (19) with the column vector 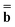 . These excited-state fast polarization charges along with the fixed slow charges are used to construct the nonequilibrium excited-state reaction field using eqn (13) or eqn (14). Then, a new ground-state SCRF calculation is done using this new reaction field to obtain a new set of ground-state MOs and orbital energies (which no longer correspond to the original ground state). Then, one repeats the CIS or TDDFT calculation using the new set of εp and ψp to evaluate the excited-state fast polarization charges again in order to update the nonequilibrium reaction field for the use in the next IBSF iteration which includes a new ground-state SCRF calculation followed by a CIS or TDDFT calculation. The IBSF CIS matrix at the kth iteration is defined by eqn (37) in which one replaces the quantities εp and ψp defined by eqn (38) with their counterparts εp(k) and ψp(k) defined as the corresponding eigenenergies and eigenfunctions of the following Fock operator:
. These excited-state fast polarization charges along with the fixed slow charges are used to construct the nonequilibrium excited-state reaction field using eqn (13) or eqn (14). Then, a new ground-state SCRF calculation is done using this new reaction field to obtain a new set of ground-state MOs and orbital energies (which no longer correspond to the original ground state). Then, one repeats the CIS or TDDFT calculation using the new set of εp and ψp to evaluate the excited-state fast polarization charges again in order to update the nonequilibrium reaction field for the use in the next IBSF iteration which includes a new ground-state SCRF calculation followed by a CIS or TDDFT calculation. The IBSF CIS matrix at the kth iteration is defined by eqn (37) in which one replaces the quantities εp and ψp defined by eqn (38) with their counterparts εp(k) and ψp(k) defined as the corresponding eigenenergies and eigenfunctions of the following Fock operator:
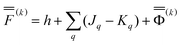 | (50) |
The IBSF excitation energy is calculated using the nonequilibrium excited-state polarization free energy defined by eqn (12) in the work of Improta et al.,81 which is equivalent to eqn (23) here given in terms of Partition I. We can define the IBSF excitation energy at the kth iteration (k > 1) using Partition II as
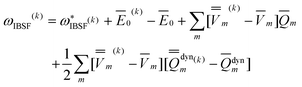 | (51) |
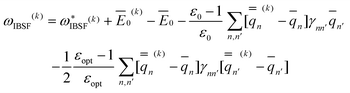 | (52) |
The quantities with a double bar in eqn (51) and (52) are calculated explicitly using the excited-state electron density after diagonalization of the corresponding CIS or TDDFT matrix at the current iteration. Note that in the GB implementation of the IBSF method the first IBSF iteration (k = 1) is equivalent to the GSRF calculation whereas in the original PCM/IBSF implementation81 the first IBSF iteration is simply a gas-phase calculation with no solvation effects included in the treatment of the ground or excited electronic state (Φ ≡ 0).
Eqn (51) for the IBSF protocol differs from eqn (31) for the VEM protocol, in particular, because the first term of eqn (51) by definition is not the same as 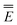 0 − Ē0 in eqn (31). Therefore, the IBSF protocol cannot be treated as an approximation to VEM. To make the comparison of VEM and IBSF meaningful, we have modified eqn (52), which is the GB analog of eqn (51), as follows
0 − Ē0 in eqn (31). Therefore, the IBSF protocol cannot be treated as an approximation to VEM. To make the comparison of VEM and IBSF meaningful, we have modified eqn (52), which is the GB analog of eqn (51), as follows
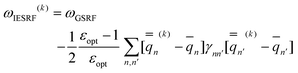 | (53) |
2.8 Additional computational details
The electronic excitation in all the systems studied in the present work is described using two electronic structure methods: (i) the CIS wave function method based on intermediate-neglect-of-differential-overlap molecular orbital (INDO) theory82,83 (in particular, INDO/S284 where S2 refers to spectroscopy-parameterization 2); (ii) TDDFT with the M0641,42 density functional and the MG3S basis set85,86 (the latter is identical to 6-311+G(2df,2p)87–89 for elements with atomic numbers 14 or lower).The excitation energies were calculated at the gas-phase ground-state molecular geometries in the case of gas-phase excitation energy calculations and at the corresponding liquid-phase ground-state molecular geometries in the case of liquid-phase excitation energy calculations. Molecular geometries were optimized using M06-2X/MG3S in the case of acetone, acrolein, methanal, methylenecyclopropene and pyridine, and using the M06-2X density functional41,42 with the 6-311G(d,p) basis set87 in the case of coumarin 153, indolinedimethine-malononitrile and julolidine-malononitrile. The optimizations in solution were carried out using the SMD solvation model49 of Gaussian 09.38
The CIS/INDO/S2 calculations were carried out using the following computational protocols: gas, GSRF/GBSD, cGSRF/GBSD, VEM/GBSD, IBSF/GBSD, and IESRF/GBSD. For liquid-phase CIS/INDO/S2 calculations, we employed the SM5.42 values90,91 of intrinsic Coulomb radii (see Table 3). All the CIS/INDO/S2 calculations in the present work were performed using a locally modified version of the ZINDO program.92 All the liquid-phase CIS/INDO/S2 calculations use the GBSD approximation based on CM2 class IV partial atomic charges.93,94
| Atom | Z | SM8AD | SMD | SM5.42 | 1.1 × UFF | ||
|---|---|---|---|---|---|---|---|
| α H ≥ 0.43 b | α H = 0 c | α H ≥ 0.43 b | α H = 0 c | ||||
| a Radii are given only for the elements in the studied molecules (Fig. 1). The SM8AD radii for H and O and the SMD radius for O are defined as functions of Abraham's hydrogen bond acidity parameter (αH) for a given solvent (Table 1). The remaining radii do not depend on solvent descriptors. b In methanol and water. c In cyclohexane, dimethyl sulfoxide, n-hexane, and n-pentane. | |||||||
| H | 1 | 1.02 | 0.80 | 1.20 | 1.20 | 0.91 | 1.5873 |
| C | 6 | 1.75 | 1.75 | 1.85 | 1.85 | 1.78 | 2.1186 |
| N | 7 | 1.94 | 1.94 | 1.89 | 1.89 | 1.92 | 2.013 |
| O | 8 | 1.52 | 2.29 | 1.52 | 2.29 | 1.60 | 1.925 |
| F | 9 | 1.68 | 1.68 | 1.73 | 1.73 | 1.50 | 1.8502 |
The TDDFT/M06/MG3S calculations were carried out using the following protocols: gas, GSRF/GBAD, GSRF/PCM, cGSRF/PCM, VEM/GBAD, VEM/PCM, LR/PCM, cLR/PCM, IBSF/GBAD, IBSF/PCM, and IESRF/GBAD. For the GBAD and PCM calculations, we employ the SM8AD70 and SMD49 values of intrinsic atomic Coulomb radii, respectively, and we also tested the universal force field (UFF) radii95 scaled by 1.1 (Gaussian 09's default) in selected liquid-phase TDDFT calculations. The GB calculations with TDDFT use the GB approximation based on the CHELPG partial atomic charges where CHELPG stands for Charges from Electrostatic Potentials using a Grid-based method.96 We used locally modified (Minnesota) versions of Gaussian 0337 and Gaussian 0938 along with the original version of Gaussian 0938 to carry out all the GB calculations with TDDFT, we used a locally modified (Pisa) version of Gaussian 0938 to carry out the cGSRF/PCM and VEM/PCM calculations, and we used the original version of Gaussian 0938 to carry out all other TDDFT computations (namely, gas, GSRF/PCM, LR/PCM, cLR/PCM, and IBSF/PCM). The GBSD/TDDFT calculations are also possible but we present here only the GBAD/TDDFT results because they are more closely related to the PCM/TDDFT ones. Indeed, as measured against (ground-state) electrostatic energies calculated by solving the nonhomogeneous Poisson equation, the GBAD approach is more accurate than the GBSD method.70
All the TDDFT calculations are based on the full TDDFT matrix equations, as given by Casida.31 Solvent-response TDDFT in the Tamm-Dancoff approximation97 to TDDFT may be an interesting subject for future consideration.
The VEM/GB protocol used here is identical to the VEM42 model developed in Ref. 25 and implemented in a local version of the ZINDO program (ZINDOMN version 1.2),98 except for two modifications. First, the last term (“cross-term”) of eqn (20) in Ref. 25 has been removed. This term was the result of an inconsistent partition within the original VEM42 formulation and is therefore not present in the VEM method presented here. Second, the version98 of the ZINDO code used in the VEM42 calculations by default calculated the CIS matrix that includes the H0n elements where “0” refers to the Slater determinant of the ground state in solution and “n” refers to the nth excited-state determinant generated by single excitations from orbitals occupied in the ground-state Slater determinant to virtual orbitals. In the present study, we do the CIS in the basis of singly excited basis states rather than in the basis of the ground state plus singly excited states, forcing the resulting vertically excited state of interest in solution to be orthogonal to the initial ground state. One can do this by working in the orbital basis of the ground-state SCRF calculation and deleting the first row and column of the CIS matrix corresponding to the H0n elements even though the matrix need not be block diagonal. As noted above, VEM is now defined to always involve the removal of the liquid-phase ground state from the expansion of the liquid-phase excited-state wave function.
The VEM/PCM algorithm implemented in Gaussian 09 employs eqn (48) and not eqn (31) because the latter requires a computation of the excited-state expectation energy E0 of the gas-phase Hamiltonian, and this is not available within the current VEM/PCM implementation. The VEM/GB algorithm implemented in ZINDOMN employs eqn (36), which is the GB analog of eqn (31), according to the original VEM42 formulation,25 but it can also use eqn (49) which is the GB analog of eqn (48). Note that both equations yield identical VEM excitation energies upon convergence of the VEM procedure. The GSRF/GB and PCM calculations with Gaussian always employ eqn (40). The GSRF/GB calculations with ZINDOMN can use either eqn (40) or the GB analog of eqn (42). Both of these yield identical excitation energies.
There are two schemes in Gaussian 0938 to calculate excited-state molecular properties such as electrostatic potentials when one employs CIS or TDDFT. The first scheme calculates excited-state molecular properties using only the CIS wave function or its TDDFT analog; these correspond to the so-called unrelaxed excited-state density (UD) (keyword density = rhoci). Another option is to use the Z-vector or relaxed-density (RD) approach.74,78,99 The latter is the preferred (and default), although computationally more expensive, method to calculate excited-state properties within CIS or TDDFT in Gaussian 09 because using the excited-state RD matrix partially accounts for orbital relaxation effects in response to electronic excitation while such effects are not accounted for when one uses the excited-state UD which is simply based on the single-excitation amplitudes. The difference between the UD and RD approaches is described in more detail elsewhere.74,78,99
In implementing the VEM/PCM method in Gaussian 0938 we considered two variants: the first is a “full” perturbation approach VEM(f) which corresponds to eqn (46), while in the second version we considered only the “diagonal” elements of the ΔΦ(k) state-specific reaction field operator. We call this approach VEM(d) and it corresponds to a modification of eqn (46) whereby we include the last two terms on the right hand side only for b = a and j = i. Our motivation to explore the behavior of VEM(d) with respect to VEM(f) lies in the fact that the “full” state-specific reaction field operator may lead to an undesirable and unphysical coupling. In fact, both in the solution of the CIS or TDDFT equations and the solution of the Z-vector equations, the reaction field operator ΔΦ(k) introduces additional couplings in the occupied-occupied, virtual-virtual, and occupied-virtual manifolds that effectively represent a mixing between the ground and excited states. Those couplings are not introduced by VEM(d). Note that both types of VEM/PCM calculations can be carried out either with the UD or the RD approach leading to the four variants VEM(f,RD), VEM(f,UD), VEM(d,RD) and VEM(d,UD). We have also developed the GB analog of VEM(d,RD) for CIS or TDDFT calculations using Gaussian 09. See the ESI for more details on the VEM(d,RD)/GB protocol.† This is the only VEM/GB protocol used in the TDDFT/M06/MG3S calculations in the present study.
In all TDDFT calculations with Gaussian 09 that require explicit evaluation of the excited-state electrostatic potential or polarization charges we use the RD approach. Namely, we use the RD approach to compute the second term of eqn (44) for cGSRF/PCM and cLR/PCM, the second term of eqn (48) for VEM(f,RD)/PCM and VEM(d,RD)/PCM, the last two terms of eqn (51) for IBSF/PCM, the last two terms of eqn (52) for IBSF/GBAD, and the second term of eqn (53) in the case of IESRF/GBAD. We used the UD approach to compute the second term of eqn (48) for VEM(d,UD). Note that the ZINDOMN calculations presented in this paper correspond to VEM(f,UD), and they were carried out using the unrelaxed CIS density because this is the only option in ZINDO.
A few qualitative remarks should be made about our choice of a partition scheme in the present study. Partition I and Partition II yield the same expressions for the nonequilibrium excited-state reaction field and polarization free energy (see the ESI for the proof of this†). Historically, the preference of one partition over another has been motivated only by the requirements of a specific computational code.17 Thus, the cGSRF/PCM, VEM/PCM, and cLR/PCM calculations here were performed using Partition II whereas the IBSF/PCM calculations were performed using Partition I. Within the GB approach we can use any partition. However, to analyze the fast and slow components of the nonequilibrium excited-state polarization free energy or the corresponding solvatochromic shift, we will use Partition II. Note that the GSRF and LR calculations do not use any partition scheme because these methods are not state-specific, and they do not involve the explicit evaluation of fast and slow polarization charges.
3. Reference data
Calculated excitation energies ω and solvatochromic shifts Δω of the lowest excited states of acetone, acrolein, C153, IM, JM, methanal, MCP, and pyridine in polar and nonpolar solvents will be compared with available reference data100–111 and the rest of this section is devoted to explaining the sources of this data.We use reference data for acetone and acrolein obtained from experimental UV absorption spectra. The reference excitation energies of the n → π* transition of acetone in the gas phase, n-hexane, and water are 35975, 35940, and 37760 cm−1, respectively.111 The reference excitation energies of the n → π* transition of acrolein in gas, n-hexane, and water are 29762,103 29895,102 and 31746 cm−1,100 respectively.
The reference excitation energy of the n → π* transition of methanal in the gas phase (31294 cm−1) was obtained from a CC3/aug-cc-pVQZ calculation.109 The corresponding excitation energy of methanal in water (33079 cm−1) was evaluated by using the gas-phase reference excitation energy and assuming that the gas–water solvatochromic shift of methanal is identical to that of acetone as suggested in Ref. 110 (the latter was taken from Ref. 111). The reference excitation energy of methanal in n-hexane (31259 cm−1) was evaluated by assuming that the corresponding gas–hexane shift of methanal equals that of acetone.111
The reference excitation energy for the n → π* transition of pyridine in cyclohexane (37000 cm−1) is obtained from the UV absorption spectrum.101 The reference value of ω in the gas phase (37323 cm−1) is evaluated in the present work by using the reference excitation energy of pyridine in cyclohexane and assuming that the gas–cyclohexane solvatochromic shift of pyridine is the average of the corresponding shifts of pyrimidine and pyrazine measured in Ref. 101. The reference value of ω in water (39813 cm−1) is evaluated by using the reference excitation energies of pyridine in cyclohexane and assuming that the cyclohexane–water solvatochromic shift of pyridine is the average of the corresponding experimental shifts of pyrimidine and pyrazine.101
The UV absorption excitation energy of C153 in the gas phase, cyclohexane, and dimethyl sulfoxide are 27600, 25980, and 23740 cm−1, respectively.106 There are no gas-phase reference excitation energies for the remaining three solutes. We have the values of ω from the UV absorption spectra of IM in cyclohexane (23392 cm−1) and acetonitrile (22989 cm−1),108JM in cyclohexane (22936 cm−1) and acetonitrile (21930 cm−1),107 and MCP in n-pentane (32362 cm−1) and methanol (36232 cm−1).105
4. Results
Table 4 presents vertical excitation energies of all solute molecules calculated in the gas phase (ωgas) using CIS/INDO/S2 and TDDFT/M06/MG3S. Results of CIS/INDO/S2 liquid-phase calculations with the GBSD model are presented in Tables 5 and 6. In particular, Table 5 shows vertical excitation energies of acetone, acrolein, C153, methanal, and pyridine in one polar and in one nonpolar solvent (ωsol), and the corresponding solvatochromic shifts calculated as ωgas − ωsol. Table 6 shows vertical excitation energies of IM, JM, and MCP in one polar and in one nonpolar solvent. Since the reference values of ωgas are not available for these three solutes, we define the corresponding shifts as a shift in a polar solvent relative to a nonpolar solvent, i.e., as ωsol(1) − ωsol(2) where ωsol(1) refers to the nonpolar solvent and ωsol(2) refers to the corresponding polar solvent.| Solute | CIS/INDO/S2 | TDDFT/M06/MG3S | Reference |
|---|---|---|---|
| a Reference data are described in Section 3; n/a means not available. | |||
| Acetone | 33055 | 36067 | 35975 |
| Acrolein | 30386 | 29617 | 29762 |
| C153 | 29241 | 27606 | 27600 |
| IM | 25805 | 27634 | n/a |
| JM | 26610 | 26553 | n/a |
| Methanal | 33346 | 31952 | 31294 |
| MCP | 35568 | 32981 | n/a |
| Pyridine | 34828 | 37856 | 37323 |
| Protocol | Nonpolar solvent | Polar solvent | ||
|---|---|---|---|---|
| ω sol | Δω | ω sol | Δω | |
| a Theoretical and reference values of Δω are defined as ωgas − ωsol where the corresponding values of ωgas are given in Table 4. Reference data are described in Section 3. | ||||
| Acetone, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 33638 | −583 | 34306 | −1251 |
| cGSRF | 33277 | −222 | 33947 | −892 |
| VEM(f,UD) | 33266 | −211 | 33936 | −881 |
| IBSF | 33754 | −699 | 35904 | −2849 |
| IESRF | 33229 | −174 | 33899 | −844 |
| Reference | 35940 | 35 | 37760 | −1785 |
| Acrolein, n → π* (1A′′) | ||||
| n-Hexane | Water | |||
| GSRF | 31129 | −743 | 32095 | −1709 |
| cGSRF | 30620 | −234 | 31641 | −1255 |
| VEM(f,UD) | 30552 | −166 | 31596 | −1210 |
| IBSF | 30915 | −529 | 33952 | −3566 |
| IESRF | 30410 | −25 | 31492 | −1106 |
| Reference | 29895 | −133 | 31746 | −1984 |
| Coumarin 153, π → π* (1A) | ||||
| Cyclohexane | Dimethyl sulfoxide | |||
| GSRF | 28873 | 368 | 28130 | 1111 |
| cGSRF | 28504 | 736 | 27594 | 1647 |
| VEM(f,UD) | 28251 | 990 | 27231 | 2010 |
| IBSF | 26928 | 2313 | 24623 | 4618 |
| IESRF | 28023 | 1218 | 26943 | 2298 |
| Reference | 25980 | 1620 | 23740 | 3860 |
| Methanal, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 33695 | −350 | 34035 | −690 |
| cGSRF | 33427 | −82 | 33773 | −427 |
| VEM(f,UD) | 33419 | −74 | 33764 | −419 |
| IBSF | 33739 | −394 | 35078 | −1733 |
| IESRF | 33395 | −50 | 33741 | −396 |
| Reference | 31259 | 35 | 33079 | −1785 |
| Pyridine, n → π* (1B1) | ||||
| Cyclohexane | Water | |||
| GSRF | 34978 | −151 | 35503 | −675 |
| cGSRF | 34669 | 159 | 35240 | −412 |
| VEM(f,UD) | 34640 | 188 | 35219 | −392 |
| IBSF | 34850 | −22 | 36270 | −1443 |
| IESRF | 34545 | 282 | 35153 | −326 |
| Reference | 37000 | 323 | 39813 | −2490 |
| Protocol | Nonpolar solvent | Polar solvent | |
|---|---|---|---|
| ω sol | ω sol | Δω | |
| a Theoretical and reference values of Δω are defined as ωsol(1) − ωsol(2) where ωsol(1) and ωsol(2) refer to the value of ωsol in the nonpolar and in the polar solvent, respectively. Reference data are described in Section 3. | |||
| Indolinedimethine-malononitrile, π → π* (1A′) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 25116 | 24191 | 925 |
| cGSRF | 24896 | 24057 | 839 |
| VEM(f,UD) | 24837 | 24041 | 796 |
| IBSF | 24305 | 24044 | 261 |
| IESRF | 24778 | 24007 | 771 |
| Reference | 23392 | 22989 | 403 |
| Julolidine-malononitrile, π → π* (1A) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 25824 | 24530 | 1294 |
| cGSRF | 25104 | 23915 | 1189 |
| VEM(f,UD) | 24722 | 23669 | 1053 |
| IBSF | 22977 | 21827 | 1151 |
| IESRF | 24474 | 23535 | 939 |
| Reference | 22936 | 21930 | 1006 |
| Methylenecyclopropene, π → π* (1B2) | |||
| n-Pentane | Methanol | ||
| GSRF | 36355 | 37882 | −1527 |
| cGSRF | 33668 | 35177 | −1509 |
| VEM(f,UD) | 33370 | 34855 | −1485 |
| IBSF | 31329 | 36299 | −4970 |
| IESRF | 32463 | 33934 | −1472 |
| Reference | 32362 | 36232 | −3870 |
Tables 7 and 8 show results of TDDFT/M06/MG3S liquid-phase calculations with the GBAD model for acetone, acrolein, C153, methanal, and pyridine, and for IM, JM, and MCP, respectively. Tables 9 and 10 show results of the corresponding liquid-phase calculations with the PCM model.
| Protocol | Nonpolar solvent | Polar solvent | ||
|---|---|---|---|---|
| ω sol | Δω | ω sol | Δω | |
| a See footnote a in Table 5. | ||||
| Acetone, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 36330 | −263 | 37304 | −1237 |
| VEM(d,RD) | 36111 | −44 | 36880 | −813 |
| IBSF | 36518 | −451 | 39162 | −3095 |
| IESRF | 36175 | −108 | 37041 | −974 |
| Reference | 35940 | 35 | 37760 | −1785 |
| Acrolein, n → π* (1A′′) | ||||
| n-Hexane | Water | |||
| GSRF | 30105 | −488 | 31567 | −1950 |
| VEM(d,RD) | 29268 | 349 | 30690 | −1073 |
| IBSF | 29301 | 316 | 32905 | −3288 |
| IESRF | 29448 | 169 | 30922 | −1305 |
| Reference | 29895 | −133 | 31746 | −1984 |
| Coumarin 153, π → π* (1A) | ||||
| Cyclohexane | Dimethyl sulfoxide | |||
| GSRF | 26861 | 745 | 25763 | 1843 |
| VEM(d,RD) | 25875 | 1731 | 24752 | 2854 |
| IBSF | 24507 | 3099 | 22274 | 5332 |
| IESRF | 26198 | 1408 | 25094 | 2512 |
| Reference | 25980 | 1620 | 23740 | 3860 |
| Methanal, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 32056 | −104 | 32466 | −514 |
| VEM(d,RD) | 31984 | −32 | 32218 | −266 |
| IBSF | 32062 | −110 | 33663 | −1711 |
| IESRF | 31956 | −4 | 32157 | −205 |
| Reference | 31259 | 35 | 33079 | −1785 |
| Pyridine, n → π* (1B1) | ||||
| Cyclohexane | Water | |||
| GSRF | 38114 | −258 | 38537 | −681 |
| VEM(d,RD) | 37479 | 377 | 38018 | −162 |
| IBSF | 37822 | 34 | 39334 | −1478 |
| IESRF | 37501 | 355 | 38042 | −186 |
| Reference | 37000 | 323 | 39813 | −2490 |
| Protocol | Nonpolar solvent | Polar solvent | |
|---|---|---|---|
| ω sol | ω sol | Δω | |
| a See footnote a in Table 6. | |||
| Indolinedimethine-malononitrile, π → π* (1A′) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 27367 | 27085 | 282 |
| VEM(d,RD) | 27174 | 26951 | 223 |
| IBSF | 26636 | 26362 | 274 |
| IESRF | 27192 | 26972 | 220 |
| Reference | 23392 | 22989 | 403 |
| Julolidine-malononitrile, π → π* (1A) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 26065 | 25416 | 649 |
| VEM(d,RD) | 25581 | 25086 | 495 |
| IBSF | 24977 | 23985 | 992 |
| IESRF | 25803 | 25253 | 550 |
| Reference | 22936 | 21930 | 1006 |
| Methylenecyclopropene, π → π* (1B2) | |||
| n-Pentane | Methanol | ||
| GSRF | 34089 | 35877 | −1788 |
| VEM(d,RD) | 32306 | 34014 | −1708 |
| IBSF | 31542 | 35912 | −4370 |
| IESRF | 32403 | 34223 | −1820 |
| Reference | 32362 | 36232 | −3870 |
| Protocol | Nonpolar solvent | Polar solvent | ||
|---|---|---|---|---|
| ω sol | Δω | ω sol | Δω | |
| a See footnote a in Table 5. b This calculation was carried out using the UFF Coulomb radii scaled by the factor of 1.1; all the other PCM calculations were carried out using the SMD radii. | ||||
| Acetone, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 36380 | −313 | 37922 | −1855 |
| cGSRF | 36263 | −196 | 37694 | −1627 |
| VEM(f,RD) | 36059 | 8 | 37270 | −1203 |
| VEM(d,RD) | 36043 | 24 | 37258 | −1191 |
| VEM(d,UD) | 35930 | 137 | 37163 | −1096 |
| LR | 36347 | −280 | 37857 | −1790 |
| cLR | 36253 | −186 | 37569 | −1502 |
| IBSF | 36449 | −382 | 39653 | −3586 |
| IBSF b | 36460 | −393 | 37862 | −1795 |
| Reference | 35940 | 35 | 37760 | −1785 |
| Acrolein, n → π* (1A′′) | ||||
| n-Hexane | Water | |||
| GSRF | 30008 | −391 | 31730 | −2113 |
| cGSRF | 29658 | −41 | 31277 | −1660 |
| VEM(f,RD) | 28962 | 655 | 30126 | −509 |
| VEM(d,RD) | 28779 | 838 | 30006 | −389 |
| VEM(d,UD) | 28366 | 1251 | 29741 | −124 |
| LR | 29979 | −362 | 31673 | −2056 |
| cLR | 29599 | 18 | 30943 | −1326 |
| IBSF | 29354 | 263 | 32911 | −3294 |
| IBSF b | 29593 | 24 | 31498 | −1881 |
| Reference | 29895 | −133 | 31746 | −1984 |
| Coumarin 153, π → π* (1A) | ||||
| Cyclohexane | Dimethyl sulfoxide | |||
| GSRF | 26849 | 757 | 25804 | 1802 |
| cGSRF | 26490 | 1116 | 25477 | 2129 |
| VEM(f,RD) | 24721 | 2885 | 23241 | 4365 |
| VEM(d,RD) | 25308 | 2298 | 23996 | 3610 |
| VEM(d,UD) | 24630 | 2976 | 23549 | 4057 |
| LR | 26131 | 1475 | 25065 | 2541 |
| cLR | 26381 | 1225 | 25056 | 2550 |
| IBSF | 24933 | 2673 | 23000 | 4606 |
| IBSF b | 25205 | 2401 | 23259 | 4347 |
| Reference | 25980 | 1620 | 23740 | 3860 |
| Methanal, n → π* (1A2) | ||||
| n-Hexane | Water | |||
| GSRF | 32164 | −212 | 33231 | −1279 |
| cGSRF | 31941 | 11 | 32914 | −962 |
| VEM(f,RD) | 31749 | 203 | 32543 | −591 |
| VEM(d,RD) | 31746 | 206 | 32548 | −596 |
| VEM(d,UD) | 31685 | 267 | 32465 | −513 |
| LR | 32081 | −129 | 33114 | −1162 |
| cLR | 31932 | 20 | 32824 | −872 |
| IBSF | 31776 | 176 | 33993 | −2041 |
| IBSF b | 32012 | −60 | 33124 | −1172 |
| Reference | 31259 | 35 | 33079 | −1785 |
| Pyridine, n → π* (1B1) | ||||
| Cyclohexane | Water | |||
| GSRF | 38377 | −521 | 39481 | −1625 |
| cGSRF | 37958 | −102 | 39140 | −1284 |
| VEM(f,RD) | 36989 | 867 | 38253 | −397 |
| VEM(d,RD) | 36992 | 864 | 38254 | −398 |
| VEM(d,UD) | 36530 | 1326 | 38055 | −199 |
| LR | 38292 | −436 | 39406 | −1550 |
| cLR | 37862 | −6 | 38873 | −1017 |
| IBSF | 37610 | 246 | 40058 | −2202 |
| IBSF b | 37666 | 190 | 39701 | −1845 |
| Reference | 37000 | 323 | 39813 | −2490 |
| Protocol | Nonpolar solvent | Polar solvent | |
|---|---|---|---|
| ω sol | ω sol | Δω | |
| a See footnote a in Table 6. b See footnote b in Table 9. | |||
| Indolinedimethine-malononitrile, π → π* (1A′) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 27352 | 27165 | 187 |
| cGSRF | 27253 | 27098 | 155 |
| VEM(f,RD) | 26720 | 26636 | 84 |
| VEM(d,RD) | 27052 | 26927 | 125 |
| VEM(d,UD) | 26981 | 26887 | 94 |
| LR | 25966 | 25940 | 26 |
| cLR | 27238 | 27047 | 191 |
| IBSF | 26680 | 26572 | 108 |
| IBSF b | 26765 | 26359 | 406 |
| Reference | 23392 | 22989 | 403 |
| Julolidine-malononitrile, π → π* (1A) | |||
| Cyclohexane | Acetonitrile | ||
| GSRF | 26002 | 25396 | 606 |
| cGSRF | 25860 | 25321 | 539 |
| VEM(f,RD) | 24949 | 24572 | 377 |
| VEM(d,RD) | 25194 | 24744 | 450 |
| VEM(d,UD) | 24629 | 24405 | 224 |
| LR | 24716 | 24184 | 532 |
| cLR | 25792 | 25191 | 601 |
| IBSF | 25057 | 24227 | 830 |
| IBSF b | 25247 | 24390 | 857 |
| Reference | 22936 | 21930 | 1006 |
| Methylenecyclopropene, π → π* (1B2) | |||
| n-Pentane | Methanol | ||
| GSRF | 33880 | 35825 | −1945 |
| cGSRF | 32842 | 34805 | −1963 |
| VEM(f,RD) | 30693 | 32382 | −1689 |
| VEM(d,RD) | 31258 | 33073 | −1815 |
| VEM(d,UD) | 30890 | 32965 | −2074 |
| LR | 33654 | 35595 | −1941 |
| cLR | 32585 | 33875 | −1290 |
| IBSF | 31532 | 35876 | −4344 |
| IBSF b | 31872 | 34753 | −2881 |
| Reference | 32362 | 36232 | −3870 |
Table 11 provides, as an example, a breakdown of the nonequilibrium components of the vertical excitation energy for the molecules of interest. Table 12 shows ground- and excited-state values of the dipole moment and selected partial atomic charges in the studied molecules in the gas phase and in solution.
| Solute | ω 0 | Ḡ P |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dyn dyn
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) in in
|
|
ω sol |
|---|---|---|---|---|---|---|
a These are obtained from the calculations of vertical excitation energies for given compounds in the corresponding polar solvent using the IESRF/GBAD/TDDFT/M06/MG3S protocol (see Tables 7 and 8). The quantity ω0 =  0 − Ē0 is evaluated by subtracting 0 − Ē0 is evaluated by subtracting 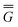 P − ḠP from ωsol where ωsol is the excitation energy calculated by eqn (53) at the last IESRF iteration, and P − ḠP from ωsol where ωsol is the excitation energy calculated by eqn (53) at the last IESRF iteration, and 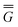 P and its dynamic and inertial components are calculated using eqn (35) with the corresponding double-bar quantities evaluated using the relaxed excited-state electron density. P and its dynamic and inertial components are calculated using eqn (35) with the corresponding double-bar quantities evaluated using the relaxed excited-state electron density.
|
||||||
| Acetone | 34627 | −3751 | −747 | −590 | −1337 | 37041 |
| Acrolein | 28356 | −3526 | −787 | −173 | −960 | 30922 |
| C153 | 28155 | −2923 | −3385 | −2599 | −5984 | 25094 |
| IM | 27613 | −7594 | −3827 | −4408 | −8235 | 26972 |
| JM | 26749 | −6020 | −3526 | −3991 | −7517 | 25253 |
| Methanal | 30597 | −2474 | −582 | −333 | −914 | 32157 |
| MCP | 31074 | −1767 | −263 | 1644 | 1381 | 34223 |
| Pyridine | 36702 | −1316 | −262 | 285 | 24 | 38042 |
| Property | Gas | Nonpolar solvent | Polar solvent | |||
|---|---|---|---|---|---|---|
| Ground | Excited | Ground | Excited | Ground | Excited | |
| a Absolute values of the dipole moment (μ) and nonzero values of its Cartesian components (μX, μY, μZ) corresponding to Gaussian 09' standard orientation are given in debyes, and partial charges (q) are given in atomic units of charge. The ground- and excited-state dipole moments were obtained from the ground- and excited-state electronic density calculated by M06 and TDDFT/M06, respectively; the basis set was MG3S. The excited-state electronic density in solution was calculated using the LR/PCM method with the SMD Coulomb radii. The partial atomic charges were obtained within the CHELPG electrostatic potential fitting scheme. The names of polar and nonpolar solvents used in these calculations are listed in Tables 5–10 for each solute. All the calculations were carried out at the ground-state molecular geometry optimized in the gas phase or in the corresponding solvent. b In the carbonyl group. c In the ring. d The carbon atom in the C3 cycle bonded to the CH2 group. e The carbon atom in the CH2 group. f The carbon atom in the para position with respect to N. | ||||||
| Acetone, n → π* (1A2) | ||||||
| μZ | −3.13 | −1.80 | −3.47 | −2.02 | −4.68 | −2.75 |
| μ | 3.13 | 1.80 | 3.47 | 2.02 | 4.68 | 2.75 |
| q(C) b | 0.73 | 0.30 | 0.74 | 0.31 | 0.81 | 0.35 |
| q(O) b | −0.57 | −0.31 | −0.60 | −0.33 | −0.71 | −0.40 |
| Acrolein, n → π* (1A′′) | ||||||
| μX | 2.60 | 0.89 | 2.93 | 1.01 | 4.05 | 1.43 |
| μY | 2.19 | −0.21 | 2.42 | −0.17 | 3.11 | 0.07 |
| μ | 3.40 | 0.92 | 3.80 | 1.03 | 5.11 | 1.44 |
| q(C) b | 0.56 | 0.14 | 0.57 | 0.13 | 0.62 | 0.11 |
| q(O) b | −0.50 | −0.21 | −0.53 | −0.22 | −0.64 | −0.26 |
| Coumarin 153, π → π* (1A) | ||||||
| μX | 6.39 | 11.94 | 7.52 | 14.18 | 9.28 | 17.70 |
| μY | −3.13 | −4.10 | −3.64 | −4.85 | −4.52 | −6.08 |
| μZ | −0.22 | −0.31 | −0.26 | −0.38 | −0.42 | −0.64 |
| μ | 7.11 | 12.63 | 8.36 | 15.00 | 10.33 | 18.72 |
| q(N) | −0.22 | −0.10 | −0.20 | −0.08 | −0.17 | −0.04 |
| Indolinedimethine-malononitrile, π → π* (1A′) | ||||||
| μX | 10.12 | 13.00 | 12.09 | 15.04 | 15.26 | 18.32 |
| μY | 2.06 | 3.15 | 2.53 | 3.71 | 3.20 | 4.48 |
| μ | 10.33 | 13.37 | 12.35 | 15.49 | 15.59 | 18.86 |
| q(N) c | −0.20 | −0.19 | −0.18 | −0.17 | −0.15 | −0.15 |
| Julolidine-malononitrile, π → π* (1A) | ||||||
| μX | −11.29 | −15.06 | −13.54 | −17.98 | −17.45 | −22.08 |
| μY | −1.55 | −1.56 | −1.83 | −1.80 | −2.41 | −2.44 |
| μZ | −0.28 | −0.28 | −0.25 | −0.29 | −0.41 | −0.50 |
| μ | 11.40 | 15.15 | 13.67 | 18.07 | 17.62 | 22.22 |
| q(N) c | −0.18 | −0.13 | −0.14 | −0.09 | −0.07 | −0.03 |
| Methanal, n → π* (1A2) | ||||||
| μZ | −2.43 | −1.48 | −2.65 | −1.65 | −3.40 | −2.14 |
| μ | 2.43 | 1.48 | 2.65 | 1.65 | 3.40 | 2.14 |
| q(C) b | 0.50 | −0.28 | 0.51 | −0.28 | 0.58 | −0.27 |
| q(O)b | −0.45 | −0.08 | −0.48 | −0.10 | −0.58 | −0.16 |
| Methylenecyclopropene, π → π* (1B2) | ||||||
| μZ | −2.16 | 2.34 | −2.51 | 2.69 | −3.26 | 3.40 |
| μ | 2.16 | 2.34 | 2.51 | 2.69 | 3.26 | 3.40 |
| q(C*) d | 0.32 | −0.06 | 0.32 | −0.08 | 0.33 | −0.12 |
| q(C) e | −0.74 | 0.17 | −0.78 | 0.19 | −0.85 | 0.23 |
| Pyridine, n → π* (1B1) | ||||||
| μZ | −2.29 | 0.40 | −2.65 | 0.40 | −3.36 | 0.32 |
| μ | 2.29 | 0.40 | 2.65 | 0.40 | 3.36 | 0.32 |
| q(C) f | 0.24 | −0.03 | 0.25 | −0.04 | 0.26 | −0.07 |
| q(N) | −0.65 | 0.02 | −0.70 | 0.02 | −0.79 | 0.02 |
5. Discussion
Before beginning the discussion of specific results, we should make several qualitative remarks. All computed solvatochromic shifts in this article are bulk-electrostatic contributions due to the polarization of bulk solvent modeled by treating the solvent as a dielectric continuum, and we do not treat explicitly other possible contributions to solvatochromic shifts (for example, due to dispersion, exchange repulsion, or charge transfer). We will focus our discussion mainly on solvatochromic shifts in polar solvents because the bulk-electrostatic contribution to the corresponding vertical energy there is likely to dominate the dispersion and shorter-range repulsion contributions which are undetermined in our calculations.We will use here the established sign convention for solvatochromic shifts,6 by which a “positive” shift (corresponding to a decrease in frequency and increase in wavelength) is called red (bathochromic), and a “negative” shift (with an increase in frequency and decrease in wavelength) is called blue (hypsochromic). All calculations of vertical excitation energies in polar solvents (ε0 > εopt) correspond to the regime of nonequilibrium solvation. All calculations in nonpolar solvents are carried out using ε0 = εopt (see Table 1). In this case, eqn (23) and (28) retain only the first term (all the solvent response is fast) which becomes identical in the two equations. Such calculations nominally correspond to the regime of equilibrium solvation at the solute's ground-state geometry, i.e., without the solute's nuclear relaxation.
First, we discuss qualitative trends in the GBSD/CIS/INDO/S2 results presented in Tables 5 and 6. One can expect significant blue shifts (especially in polar solvents) corresponding to the lowest n → π* electronic transition of acetone, acrolein, methanal, and pyridine because the dipole moments in these molecules decrease by factors of 1.6–5.7 upon the electronic excitation (Table 12), and, therefore, the excited electronic state is solvated less favorably than the ground state. An even larger blue shift is expected for the π → π* electronic transition in the MCP molecule, which presents an interesting challenge for theory because in this charge-transfer system the absolute value of the dipole moment (∼2.5 D) does not change substantially between the ground and excited electronic states but its Z component changes sign (Table 12). Tables 5 and 6 indicate that all the tested protocols yield qualitatively correct predictions of these blue shifts in polar solvents. The lowest π → π* electronic transition of C153, IM, and JM is accompanied by a red shift in part due to increase of the dipole moment upon excitation, which makes the excited state more favorably solvated than the ground state. All the methods in Tables 5 and 6 yield qualitatively correct predictions of the red shift.
The TDDFT results are presented in Tables 7–10. All the protocols yield qualitatively correct predictions of the blue shifts for the transitions of acetone, acrolein, methanal, MCP, and pyridine in polar solvents and the red shifts for the corresponding transitions of C153, IM, and JM.
Table 11 gives a breakdown of the excited-state total polarization energy into fast (dynamic) and slow (inertial) components. The slow components dominate in the case of IM, JM, MCP, and pyridine, with MCP (1644 cm−1) exhibiting the largest blue shift due to the slow polarization. Note that the inertial component is a nonequilibrium contribution that need not be negative or zero, unlike the dynamic component that is always negative in Table 11 because the latter is an equilibrium contribution to the nonequilibrium excited-state total polarization energy. Relaxation of the fast component of the excited-state reaction field (for example, during the VEM iterations) for the case of εopt > 1 always leads to the excited-state polarization free energy computed by eqn (23) or (28) that is more negative or less positive than the GSRF free energy computed by eqn (43) because the last term of eqn (31), which accounts for such a relaxation, is negative. Recall that the GSRF protocol neglects the last term of eqn (31). However, the VEM total excited-state energy of eqn (2) and the resulting excitation energy of eqn (1) need not be more negative or less positive than their GSRF counterparts. Indeed, the total excited-state energy in solution can be expressed as
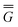 = Ēgas + ωgas + Δ = Ēgas + ωgas + Δ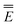 0 + 0 + 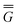 P P | (54) |
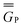 term can decrease, resulting in ωVEM > ωGSRF. However, among the excitations considered in this paper, there is no example of such behavior and we consistently observe ωVEM < ωGSRF.
term can decrease, resulting in ωVEM > ωGSRF. However, among the excitations considered in this paper, there is no example of such behavior and we consistently observe ωVEM < ωGSRF.
In the case of TDDFT calculations, all four versions of the VEM/PCM method described in Section 2.8 were tested, but we omit to report the results from VEM(f,UD) which seems to provide a strongly unbalanced description of the state-specific reaction field operator ΔΦ(k) in eqn (46), probably because it introduces coupling within the occupied and the virtual spaces, but not between them. In particular, in the case of indolinedimethine-malononitrile, VEM(f,UD) gives an unphysical red shift between cyclohexane and acetonitrile in the PCM/TDDFT calculations. Moreover, the difference between the VEM(d,RD) and VEM(d,UD) is typically less than 0.1 eV. Therefore, VEM(d,UD) appears to be a computationally affordable and viable method.
Next we compare theory quantitatively to experiment. Table 13 shows errors in theoretical solvatochromic shifts relative to available reference data described in Section 3. Note that both predicted and reference solvatochromic shifts used in Table 13 were defined for each solute in a polar solvent with respect to the excitation energy in the corresponding nonpolar solvent, and not in the gas phase, because the reference gas-phase excitation energies were not available for three out of eight solutes.
| Protocol | Without ΔωHb | With ΔωHc | ||
|---|---|---|---|---|
| MSE | MUE | MSE | MUE | |
| a Mean signed (MSE) and mean unsigned (MUE) errors are defined as Δω(calc) − Δω(ref) and |Δω(calc) − Δω(ref)|, respectively, averaged over eight solutes for each listed model. The theoretical values Δω(calc) and the reference values Δω(ref) are defined for each solute as ωsol(1) − ωsol(2) where ωsol(1) and ωsol(2) refer to the excitation energy ωsol in the nonpolar and in the polar solvent, respectively. b Based on theoretical and reference values of ωsol listed in Tables 5–10. c Based on theoretical and reference values of ωsol from Tables 5–10, the theoretical ones being augmented with the ΔωH correction (see the text and the ESI†). d See footnote b in Table 9. | ||||
| CIS/INDO/S2 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| GSRF/GBSD | 933 | 1307 | 203 | 751 |
| cGSRF/GBSD | 918 | 1251 | 188 | 709 |
| VEM(f,UD)/GBSD | 909 | 1214 | 179 | 678 |
| IBSF/GBSD | −84 | 605 | −815 | 867 |
| IESRF/GBSD | 892 | 1199 | 162 | 673 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| TDDFT/M06 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| GSRF/GBAD | 687 | 1092 | −43 | 737 |
| VEM(d,RD)/GBAD | 712 | 1164 | −18 | 747 |
| IBSF/GBAD | −213 | 593 | −944 | 944 |
| IESRF/GBAD | 687 | 1131 | −43 | 752 |
| GSRF/PCM | 373 | 826 | −357 | 839 |
| cGSRF/PCM | 383 | 869 | −347 | 824 |
| VEM(f,RD)/PCM | 543 | 970 | −187 | 732 |
| VEM(d,RD)/PCM | 511 | 952 | −219 | 732 |
| VEM(d,UD)/PCM | 367 | 930 | −363 | 812 |
| LR/PCM | 357 | 863 | −373 | 855 |
| cLR/PCM | 599 | 982 | −132 | 792 |
| IBSF/PCM | −547 | 638 | −1277 | 1277 |
| IBSF/PCMd | 300 | 424 | −430 | 678 |
The first set of MSEs and MUEs in Table 13 (the first two numerical columns) are the errors obtained using the excitation energies of Tables 5–10. The second set of MSEs and MUEs (the last two numerical columns) are the errors obtained using the theoretical excitation energies of Tables 5–10 adjusted by adding a state-specific hydrogen-bonding correction (ΔωH). The value of ΔωH was assumed to be zero for all tested solutes in any polar and nonpolar solvent, except for acetone, acrolein, methanal, and pyridine in water. These four solutes can form strong hydrogen bonds with water molecules, yielding the hydrogen-bonding contribution to the corresponding excitation energies that may not be fully accounted for by using an implicit continuum model only rather than using mixed discrete-continuum models (when one or a few solvent molecules are added explicitly to the solute molecule). Since we do not use the mixed discrete-continuum approach in the present study, we have simply corrected the excitation energies calculated for acetone, acrolein, methanal, and pyridine in water by adding the empirical hydrogen-bonding correction ΔωH which is evaluated as follows. For acetone, the value of ΔωH = 1367 cm−1 is evaluated as the difference between the experimental excitation energy of acetone in water (37760 cm−1) and that in propylene carbonate (36393 cm−1).111 Similar to water, propylene carbonate has a relatively high dielectric constant (62.9).111 However, it does not likely form hydrogen bonds with the acetone molecule. For acrolein and methanal, we assume that the hydrogen-bonding contribution is the same as for acetone (i.e., ΔωH = 1367 cm−1). The hydrogen-bonding correction to the theoretical excitation energy of pyridine in water is estimated as 1740 cm−1 by averaging the water–acetonitrile solvatochromic shifts of pyrimidine and pyrazine measured in Ref. 104. The excitation energies of acetone, acrolein, methanal, and pyridine in water computed with the use of ΔωH are given in the ESI.† A more detailed analysis of the hydrogen-bonding contributions to the solvatochromic shifts in the studied compounds is beyond the scope of the present article.
Note that quantitative agreement between the theoretical results and reference numbers across all investigated compounds may not be possible not only because of the approximations we use (for example, we do not treat solute–solvent dispersion explicitly) but also because of potentially large uncertainties in the available experimental excitation energies and solvatochromic shifts due to poorly defined maxima of broad spectral envelopes (see Renge's analysis111 of experimental inconsistencies in locating the maxima of broad spectra in the literature). Besides, the available UV spectrum of MCP in n-pentane and methanol105 was measured at 195 K whereas we do not model the solvent's behavior at this temperature, and our calculations nominally correspond to the solvent at 298 K. This may be an additional source of disagreement between theory and experiment.
In the rest of this section we will discuss only the errors obtained using the theoretical excitation energies corrected with ΔωH (i.e., using the second set of MSEs and MUEs in Table 13).
The cGSRF protocol, which is state-specific, is generally more accurate than the GSRF one because the former accounts for relaxation of the excited-state reaction field through the last term of eqn (44). Since this term is neglected in the GSRF scheme, this scheme may overestimate theoretical blue shifts (relative to gas phase), yielding the excitation energies that are higher than ωcGSRF by 673 and 386 cm−1 on average over all solutes in polar and nonpolar solvents in the case of GBSD/CIS/INDO/S2 and PCM/TDDFT calculations, respectively (compare the GSRF excitation energies to the corresponding cGSRF values in Tables 5, 6, 9, and 10). For the same reason, the cLR method is more accurate than the LR method.
The VEM protocol, which is both state-specific and self-consistent, is more accurate than the cGSRF scheme because it self-consistently equilibrates the fast component of the excited-state reaction field towards the excited-state electron density. Therefore, the VEM method is a better justified approach to calculate vertical excitation energies in solution. In general, the IESRF excitation energies are as accurate as those obtained using the VEM protocol and the same SMD Coulomb radii, making the IESRF method a better approximation to the VEM scheme than the original IBSF method.81 According to Table 13, the performance of IBSF/PCM can be improved by using the UFF radii scaled by 1.1 (i.e., the default choice of radii in Gaussian 09 for IBSF/PCM calculations) instead of the SMD Coulomb radii which we recommend for all other PCM calculations presented here.
Finally, we recall that the difference between ωLR and ωGSRF (Tables 9 and 10) is solely due to the term νPCMia,jb included in the LR scheme. As noted previously,79,112 the use of this term can partially recover the solute–solvent dispersion interaction, at least, implicitly. Table 14 shows calculated ωGSRF − ωLR values. The value of ωGSRF − ωLR averaged over all eight solutes is equal to 465 and 481 cm−1 in polar solvents and in nonpolar solvents, respectively. It is relatively small for acetone, acrolein, methanal, and pyridine, and it is relatively large for IM and JM. The difference ωGSRF − ωLR can serve as an estimate of solute–solvent dispersion, and it is always positive in our calculations, which is consistent in sign with previous estimates25,29,113,114 but different in magnitude.
6. Concluding remarks
We proposed a self-consistent state-specific vertical excitation model, called VEM, for electronic excitation in solution. This model uses the nonequilibrium formulation of the excited-state reaction field and the excited-state polarization free energy. This model is self-consistent in that it evaluates the excited-state reaction field iteratively (i.e., self-consistently with the excited-state electron density), and it is state-specific because the model computes the resulting nonequilibrium excited-state polarization free energy with account for the change in the solvent's reaction field in response to the solute's electronic excitation using the excited-state (i.e., state-specific) electronic density. This relaxation effect is treated by an explicit calculation of the last term of eqn (31), which signifies the fast polarization contribution to the excitation energy. We tested several other protocols as approximations to the VEM approach. We have found that approximations that do not compute the fast polarization contribution to the excitation energy explicitly (these methods are not state-specific) are generally poor in most of the studied cases, and they are less accurate than the VEM protocol.Acknowledgments
This work was supported in part by the U.S. Army Research Laboratory under grant no. W911NF09-100377 and by the National Science Foundation under grants no. CHE09-56776 and CHE09-52054.Notes and references
- N. S. Bayliss and E. G. McRae, J. Phys. Chem., 1954, 58, 1002 CrossRef CAS.
- N. S. Bayliss and E. G. McRae, J. Phys. Chem., 1954, 58, 1006 CrossRef CAS.
- E. M. Kosower, J. Am. Chem. Soc., 1958, 80, 3253 CrossRef CAS.
- W. Liptay, in Excited States, ed. E. C. Lim, Academic, New York, 1974, Vol. I, p. 129 Search PubMed.
- M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377 CrossRef CAS.
- C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, 3rd ed., Wiley-VCH, Weinheim, 2003 Search PubMed.
- E. M. Kober, B. P. Sullivan and T. J. Meyer, Inorg. Chem., 1984, 23, 2098 CrossRef CAS.
- G. Van der Zwan and J. T. Hynes, J. Phys. Chem., 1985, 89, 4181 CrossRef CAS.
- J. E. Brady and P. W. Carr, J. Phys. Chem., 1985, 89, 5759 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221 CrossRef CAS.
- K. V. Mikkelsen, H. Agren, H. J. A. Jensen and T. Helgaker, J. Chem. Phys., 1988, 89, 3086 CrossRef CAS.
- P. Suppan, J. Photochem. Photobiol., A, 1990, 50, 293 CrossRef CAS.
- M. M. Karelson and M. C. Zerner, J. Phys. Chem., 1992, 96, 6949 CrossRef CAS.
- J. Gao, J. Am. Chem. Soc., 1994, 116, 9324 CrossRef CAS.
- J. Gao, N. Li and M. Freindorf, J. Am. Chem. Soc., 1996, 118, 4912 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS.
- Y.-L. Lin and J. Gao, J. Chem. Theory Comput., 2007, 3, 1484 Search PubMed.
- A. Marini, A. Muñoz-Losa, A. Biancardi and B. Mennucci, J. Phys. Chem. B, 2010, 114, 17128 Search PubMed.
- J. Catalán and J. P. Catalán, Phys. Chem. Chem. Phys., 2011, 13, 4072 RSC.
- R. Rajamani, Y.-L. Lin and J. Gao, J. Comput. Chem., 2011, 32, 854 Search PubMed.
- Y.-K. Li, Q. Zhu, X.-Y. Li, K.-X. Fu, X.-J. Wang and X.-M. Cheng, J. Phys. Chem. A, 2011, 115, 232 Search PubMed.
- M. A. Aguilar, F. J. Olivares del Valle and J. Tomasi, J. Chem. Phys., 1993, 98, 7375 CrossRef CAS.
- R. Cammi and B. Mennucci, J. Chem. Phys., 1999, 110, 9877 CrossRef CAS.
- J. Li, C. J. Cramer and D. G. Truhlar, Int. J. Quantum Chem., 2000, 77, 264 CrossRef CAS.
- M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708 CrossRef CAS.
- D. M. Chipman, J. Chem. Phys., 2009, 131, 014103 Search PubMed.
- D. M. Chipman, J. Chem. Phys., 2009, 131, 014104 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2829 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- M. E. Casida, in Time-Dependent Density Functional Theory for Molecules, ed. D. P. Chong, World Scientific, Singapore, 1995, Vol. 1, p. 155 Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454 CrossRef CAS.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133 CrossRef.
- A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Phys. Rev. B: Condens. Matter, 1996, 53, 3764 CrossRef CAS.
- A. D. McLachlan and M. A. Ball, Rev. Mod. Phys., 1964, 36, 844 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. MontgomeryJr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. MontgomeryJr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.2, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef.
- F. Lipparini, G. Scalmani, B. Mennucci, E. Cancès, M. Caricato and M. J. Frisch, J. Chem. Phys., 2010, 133, 014106 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032 CrossRef.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151 CrossRef CAS.
- B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cancès, THEOCHEM, 1999, 464, 211 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef CAS.
- S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS.
- F. Santoro, V. Barone, C. Benzi and R. Improta, Theor. Chem. Acc., 2007, 117, 1073 Search PubMed.
- B. Mennucci, C. Cappelli, C. A. Guido, R. Cammi and J. Tomasi, J. Phys. Chem. A, 2009, 113, 3009 CrossRef CAS.
- G. J. Hoijtink, E. de Boer, P. H. van der Meij and W. P. Weijland, Recl. Trav. Chim. Pays-Bas, 1956, 75, 487 CAS.
- F. Peradejordi, Cahiers Phys., 1963, 17, 393 Search PubMed.
- G. Klopman, Chem. Phys. Lett., 1967, 1, 200 CrossRef CAS.
- O. Tapia, in Quantum Theory of Chemical Reactions, ed. R. Daudel, A. Pullman, L. Salem and A. Viellard, Wiley, London, 1981, Vol. 2, p 25 Search PubMed.
- S. C. Tucker and D. G. Truhlar, Chem. Phys. Lett., 1989, 157, 164 CrossRef.
- W. C. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127 CrossRef CAS.
- T. Grycuk, J. Chem. Phys., 2003, 119, 4817 CrossRef CAS.
- M. Cossi and V. Barone, J. Phys. Chem. A, 2000, 104, 10614 CrossRef CAS.
- S. I. Pekar, Untersuchungen über die Elektronentheorie der Kristalle, Akademie-Verlag, Berlin, Germany, 1954 Search PubMed; S. I. Pekar, Introduction to Electron Theory of Crystals, Technical Lit., Moscow, 1951[English translation] Search PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979 CrossRef CAS.
- M. A. Aguilar, J. Phys. Chem. A, 2001, 105, 10393 Search PubMed.
- M. H. Abraham, P. L. Grellier, D. V. Prior, P. P. Duce, J. J. Morris and P. J. Taylor, J. Chem. Soc., Perkin Trans. 2, 1989, 699 RSC.
- M. H. Abraham, Chem. Soc. Rev., 1993, 22, 73 RSC.
- M. H. Abraham, J. Phys. Org. Chem., 1993, 6, 660 CrossRef CAS.
- M. H. Abraham, in Quantitative Treatment of Solute/Solvent Interactions, Theoretical and Computational Chemistry SeriesVol. 1, ed. P. Politzer and J. S. Murray, Elsevier, Amsterdam, 1994, p 83 Search PubMed.
- A. W. Lange and J. M. Herbert, J. Phys. Chem. Lett., 2010, 1, 556 Search PubMed.
- M. Cossi and V. Barone, J. Chem. Phys., 2000, 112, 2427 CrossRef CAS.
- M. Orozco and F. J. Luque, Chem. Phys. Lett., 1997, 265, 473 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 2447 CrossRef CAS.
- A. Herzenberg, D. Sherrington and M. Süveges, Proc. Phys. Soc., 1964, 84, 465 Search PubMed.
- T. H. Dunning and V. McKoy, J. Chem. Phys., 1967, 47, 1735 CrossRef CAS.
- D. G. Truhlar, Int. J. Quantum Chem., 1973, 7, 807 CrossRef CAS.
- J. B. Foresman, M. Head-Gordon, J. A. Pople and M. J. Frisch, J. Phys. Chem., 1992, 96, 135 CrossRef CAS.
- K. Ruedenberg and K. R. Sundberg, in Quantum Science, ed. J. L. Calais, O. Goscinski, J. Linderberg and Y. Öhrn, Plenum Press, New York, 1976, p. 505 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029 CrossRef CAS.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef.
- R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513 CrossRef CAS.
- M. Caricato, B. Mennucci, J. Tomasi, R. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520 CrossRef.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 Search PubMed.
- J. E. Ridley and M. C. Zerner, Theor. Chim. Acta, 1973, 32, 111 CrossRef CAS.
- M. C. Zerner, Rev. Comput. Chem., 1991, 2, 313 Search PubMed.
- J. Li, B. Williams, C. J. Cramer and D. G. Truhlar, J. Chem. Phys., 1999, 110, 724 CrossRef CAS.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384 CrossRef CAS.
- The MG3S basis is available at the following website (accessed December 2, 2010): http://comp.chem.umn.edu/basissets/basis.cgi.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P.v. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS.
- T. Zhu, J. Li, G. D. Hawkins, C. J. Cramer and D. G. Truhlar, J. Chem. Phys., 1998, 109, 9117 CrossRef CAS ; errata: 1999, 111, 5624.
- J. Li, G. D. Hawkins, C. J. Cramer and D. G. Truhlar, Chem. Phys. Lett., 1998, 288, 293 CrossRef CAS.
- M. C. Zerner, J. E. Ridley, A. D. Bacon, W. D. Edwards, J. D. Head, J. McKelvey, J. C. Culberson, P. Knappe, M. G. Cory, B. Weiner, J. D. Baker, W. A. Parkinson, D. Kannis, J. Yu, N. Roesch, M. Kotzian, T. Tamm, M. M. Karelson, X. Zheng, G. Pearl, A. Broo, K. Albert, J. M. Cullen, J. Li, G. D. Hawkins, J. D. Thompson, C. P. Kelly, D. A. Liotard, A. V. Marenich, C. J. Cramer and D. G. Truhlar, ZINDOMN version 2011, Quantum Theory Project, University of Florida, Gainesville, and Department of Chemistry, University of Minnesota, Minneapolis, 2011 Search PubMed.
- J. Li, T. Zhu, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 2178 Search PubMed.
- J. Li, T. Zhu, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 1820 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291 CrossRef CAS.
- M. C. Zerner, J. E. Ridley, A. D. Bacon, W. D. Edwards, J. D. Head, J. McKelvey, J. C. Culberson, P. Knappe, M. G. Cory, B. Weiner, J. D. Baker, W. A. Parkinson, D. Kannis, J. Yu, N. Roesch, M. Kotzian, T. Tamm, M. M. Karelson, X. Zheng, G. Pearl, A. Broo, K. Albert, J. M. Cullen, J. Li, G. D. Hawkins, J. D. Thompson, C. P. Kelly, D. A. Liotard, C. J. Cramer and D. G. Truhlar, ZINDOMN version 1.2, Quantum Theory Project, University of Florida, Gainesville, and Department of Chemistry, University of Minnesota, Minneapolis, 2005 Search PubMed.
- N. C. Handy and H. F. Schaefer III, J. Chem. Phys., 1984, 81, 5031 CrossRef CAS.
- G. Mackinney and O. Temmer, J. Am. Chem. Soc., 1948, 70, 3586 Search PubMed.
- S. F. Mason, J. Chem. Soc., 1959, 1240 RSC.
- K. Inuzuka, Bull. Chem. Soc. Jpn., 1961, 34, 6 Search PubMed.
- A. F. Moskvin, O. P. Yablonskii and L. F. Bondar, Theor. Exp. Chem., 1966, 2, 469 Search PubMed [English translation].
- H. Baba, L. Goodman and P. C. Valenti, J. Am. Chem. Soc., 1966, 88, 5410 CrossRef CAS.
- S. W. Staley and T. D. Norden, J. Am. Chem. Soc., 1984, 106, 3699 CrossRef CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311 CrossRef CAS.
- A. M. Moran, D. S. Egolf, M. Blanchard-Desce and A. M. Kelley, J. Chem. Phys., 2002, 116, 2542 CrossRef CAS.
- W. Leng, F. Würthner and A. M. Kelley, J. Phys. Chem. A, 2005, 109, 1570 Search PubMed.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef.
- A. D. Kulkarni, B. Mennucci and J. Tomasi, J. Chem. Theory Comput., 2008, 4, 578 Search PubMed.
- I. Renge, J. Phys. Chem. A, 2009, 113, 10678 CrossRef CAS.
- S. Corni, R. Cammi, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 123, 134512 CrossRef CAS.
- N. Rösch and M. C. Zerner, J. Phys. Chem., 1994, 98, 5817 CrossRef.
- W. Liptay, Z. Naturforsch., 1965, 20A, 1441 Search PubMed.
Footnote |
| † Electronic Supplementary Information (ESI) available in two parts: Part I contains the Appendix to Section 2 with the proofs of eqn (21), (22), (31), (32)–(36), and (48) and more details on the PCM formalism used here; it also gives a description of the GB analog of the VEM(d,RD)/PCM method, and it contains the excitation energies of acetone, acrolein, methanal, and pyridine in water computed using the hydrogen-bonding contribution correction (ΔωH); Part II contains Cartesian coordinates of the molecular structures of all studied solute molecules optimized in the gas phase and in solution. See DOI: 10.1039/c1sc00313e |
| This journal is © The Royal Society of Chemistry 2011 |