Neutron diffraction, NMR and molecular dynamics study of glucose dissolved in the ionic liquid 1-ethyl-3-methylimidazolium acetate†
Tristan G. A.
Youngs
a,
John D.
Holbrey
b,
Claire L.
Mullan
b,
Sarah E.
Norman
b,
M. Cristina
Lagunas
b,
Carmine
D'Agostino
c,
Mick D.
Mantle
c,
Lynn F.
Gladden
c,
Daniel T.
Bowron
d and
Christopher
Hardacre
*b
aAtomistic Simulation Centre, School of Maths and Physics, Queen's University, Belfast, BT7 1NN, UK
bQUILL Research Centre, School of Chemistry and Chemical Engineering, Queen's University, Belfast, BT9 5AG, UK. E-mail: c.hardacre@qub.ac.uk
cDepartment of Chemical Engineering and Biotechnology, University of Cambridge, CB2 3RA, UK
dRutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK
First published on 9th June 2011
Abstract
β-D-glucose dissolved in the ionic liquid 1-ethyl-3-methylimidazolium acetate in a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (ionic liquid
1 molar ratio (ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose) has been studied by neutron scattering, NMR and molecular dynamics simulations. Good agreement was found between simulated neutron scattering profiles generated for isotopically substituted liquid systems and those experimentally determined as well as between simulated and experimental diffusion coefficients obtained by Pulsed Field Gradient NMR spectroscopy. The overriding glucose–ionic liquid interactions in the liquid are hydrogen-bonding between acetate oxygens and sugarhydroxyl groups. The ionic liquid cation was found to play only a minor role in the solvation of the sugar and does not participate in hydrogen-bonding with the sugar to any significant degree. NOESY experiments lend further evidence that there is no direct interaction between sugarhydroxyl groups and acidic hydrogens on the ionic liquid cation.
glucose) has been studied by neutron scattering, NMR and molecular dynamics simulations. Good agreement was found between simulated neutron scattering profiles generated for isotopically substituted liquid systems and those experimentally determined as well as between simulated and experimental diffusion coefficients obtained by Pulsed Field Gradient NMR spectroscopy. The overriding glucose–ionic liquid interactions in the liquid are hydrogen-bonding between acetate oxygens and sugarhydroxyl groups. The ionic liquid cation was found to play only a minor role in the solvation of the sugar and does not participate in hydrogen-bonding with the sugar to any significant degree. NOESY experiments lend further evidence that there is no direct interaction between sugarhydroxyl groups and acidic hydrogens on the ionic liquid cation.
Introduction
Recently, ionic liquids have been found to be excellent solubilisers of cellulose and its derivatives1 leading to interest in the application of ionic liquids in biomass processing,2 generation of polymeric materials3 and energy products4 (HMF, fermentable sugarsetc). Since ionic liquids have limited vapour pressure and high thermal stability this, coupled with their ability to solvate these high molecular weight polysaccharides, may form the basis for new, cleaner approaches to cellulose (re)processing. It is generally accepted that the mechanism for the dissolution of cellulose proceeds through disruption of the inter-strand hydrogen-bonding network between adjacent polymer chains, although the precise mechanism is hotly debated.5 The dissolution process has been achieved by derivatisation, as used for example in the viscose rayon process where xanthate esters are formed with CS2 and through solvent intercalation. The latter typically uses strongly hydrogen-bond accepting solvents which leads to swelling and breaking of the hydrogen-bonding network.Ionic liquids, while not necessarily strongly hydrogen-bonding between their constituent ions, often contain anions which make excellent hydrogen-bond acceptors for solvated OH-containing molecules such as water.6 It has been shown previously that weakly-coordinating, poor hydrogen-bond acceptor anions such as [BF4]− and [PF6]− do not permit the dissolution of cellulose, while ionic liquids containing anions that are strong hydrogen-bond acceptors (chloride, dimethylphosphate, acetate) solubilise high concentrations of cellulose. For example, it was found to be possible to dissolve at least 25 wt% cellulose in 1-butyl-3-methylimidazolium chloride ([C4mim]Cl) with microwave heating to form viscous polymer solutions that could be extruded as films or fibres.11-Ethyl-3-methylimidazolium ([C2mim][OAc]) has emerged as perhaps the “best” of the new ionic liquid cellulose solvent systems7 and, additionally, shows useful enzyme and environmentally-friendly characteristics8 and significant ability to capture CO2.9 The liquid structure of [C2mim][OAc] has been probed using vibrational spectroscopy10 and combined neutron scattering/molecular dynamics simulations.11
The structure and dynamics of both cellulose and short oligomer models (cellobiose and glucose) in either imidazolium chloride- or acetate-based ionic liquids has been studied previously by NMR,12–14neutron scattering,15rheometry,16 molecular dynamics (MD),14,15,17,18 and density functional theory computational approaches.19 All studies confirm that the predominant interaction between the carbohydrate moieties and the ionic liquid ions are hydrogen-bonding in nature between the anions and the sugarhydroxyl groups. In contrast, the role of the cation has been the subject of an ongoing debate.20 Weak interactions between cation and carbohydrate have also been found in MD simulations which have been postulated as being due to van der Waals or hydrogen bonding binding.17,18 The cation has also been suggested to participate in hydrogen-bonding with the carbohydrate on the basis of NMR experiments.13 The simplified model systems provide very detailed structural information concerning the interactions involved in the solvation process. Currently, it is not possible to study cellulose to the same degree experimentally or theoretically. Therefore, whilst glucose will not demonstrate the subtleties of the polymer matrix, the main structural features which are likely to dominate the solvation processes are similar.
Here, we describe the solvation of glucose monomers in [C2mim][OAc], derived from neutron scattering experiments collected over a wide Q range (0.05–50 Å) in the liquid state for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 glucose
6 glucose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ionic liquid ratios using H/D isotopic substitution on glucose and independently on the ionic liquid cation and anion. Independent classical molecular dynamics simulations have been used to validate and further describe the system. Self-diffusion constants have been calculated by MD and are compared with experimental data determined by pulsed field gradient (PFG) NMR spectroscopy. In addition, 2D nuclear Overhauser effect spectroscopy (NOESY) NMR experiments have been employed to probe close contacts between solute and ions. Through the analysis, we have extrapolated the information in order to provide a model of the primary interactions associated with cellulose dissolution.
ionic liquid ratios using H/D isotopic substitution on glucose and independently on the ionic liquid cation and anion. Independent classical molecular dynamics simulations have been used to validate and further describe the system. Self-diffusion constants have been calculated by MD and are compared with experimental data determined by pulsed field gradient (PFG) NMR spectroscopy. In addition, 2D nuclear Overhauser effect spectroscopy (NOESY) NMR experiments have been employed to probe close contacts between solute and ions. Through the analysis, we have extrapolated the information in order to provide a model of the primary interactions associated with cellulose dissolution.
Experimental details
Neutron scattering data were collected at the ISIS pulsed neutron and muon source at Rutherford Appleton Laboratory, UK, using the SANDALS instrument. The instrument has a wavelength range of 0.05 to 4.5 Å and data was collected over the Q range 0.1 to 50 Å−1. Each sample was contained in null scattering Ti0.68Zr0.32 flat plate cells of internal geometry of 1 × 35 × 35 mm with a wall thickness of 1 mm. During the measurements, the cell was maintained at a temperature of 323 K using a Julabo circulating heater. Measurements were made on each of the empty sample holders, the empty spectrometer and a 3.1 mm thick vanadium standard sample for the purposes of instrument calibration and data normalization. After appropriate normalization for the cell and the window material, good reproducibility was found between the sample cells.Four 1-ethyl-3-methylimidazolium acetate ionic liquids containing combinations of fully protiated or deuteriated cations and anions were prepared, as described previously.11Glucose-d7 was purchased from Aldrich and converted to glucose-d12, by repeated stirring in D2O followed by vacuum drying to obtain >97% perdeuteriated material, by 1H and 2H NMR spectroscopy. Neutron scattering data were collected with 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio mixtures of [C2mim][OAc] and glucose at 323 K for eight samples with a range of hydrogen isotope substitutions on the ionic liquid cation and anion with either protiated or deuteriated glucose (see Table 1).
1 mole ratio mixtures of [C2mim][OAc] and glucose at 323 K for eight samples with a range of hydrogen isotope substitutions on the ionic liquid cation and anion with either protiated or deuteriated glucose (see Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid
1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose systems investigated by neutron scattering
glucose systems investigated by neutron scattering
| Sample | Cation (H/D11) | Anion (H/D3) | Glucose (H/D12) |
|---|---|---|---|
| 1 | Protiated | Protiated | Protiated |
| 2 | Protiated | Deuteriated | Protiated |
| 3 | Protiated | Protiated | Deuteriated |
| 4 | Protiated | Deuteriated | Deuteriated |
| 5 | Deuteriated | Deuteriated | Protiated |
| 6 | Deuteriated | Deuteriated | Deuteriated |
| 7 | Deuteriated | Protiated | Protiated |
| 8 | Deuteriated | Protiated | Deuteriated |
Data analysis was performed using GUDRUN, based upon algorithms in the ATLAS package,21 to produce a differential scattering cross section for each sample. The experimental sample densities and scattering levels were consistent with the correct isotopic compositions of the samples. Calibration and background subtraction for single atom scattering was made to produce an interference differential scattering cross section for each sample. The neutron diffraction data were analysed using the empirical potential structure refinement (EPSR) approach.22 This refinement consists of a Monte Carlo simulation using Lennard-Jones potentials with atom-centred point charges comparing the residuals from the simulated data with experimental in Q-space. The modelling process combines this data with basic information about the structure of the ions and total atomic densities of the system to constrain the model in a chemically and physically reliable manner. The experimental total structure factor F(Q) extracted from the neutron scattering data for each of the eight samples was used to build and refine a three dimensional model of the liquid structure consistent with the experimental data using EPSR.
The EPSR refinement for the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid
1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system was initialised using an equilibrated Monte Carlo simulation of 240 ion pairs of the ionic liquid and 40 glucose molecules in a cubic box of dimension 40.967 Å at 323 K, corresponding to an atomic density of 0.105 atoms Å−3 equivalent to the experimentally determined molecular density of the fully protiated 6
glucose system was initialised using an equilibrated Monte Carlo simulation of 240 ion pairs of the ionic liquid and 40 glucose molecules in a cubic box of dimension 40.967 Å at 323 K, corresponding to an atomic density of 0.105 atoms Å−3 equivalent to the experimentally determined molecular density of the fully protiated 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid
1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose sample. The eight datasets obtained by varying the isotopic signature of the samples were compared with the simulation thus increasing the confidence in the EPSR derived structure. Partial radial distribution functions describing the distributions of cations, anions and glucose molecules around a central moiety were calculated using the SHARM routines within EPSR using the anion and glucose centres of mass and cation centre of mass of the imidazolium ring as positions of reference. Atom types were defined based on their unique positions in the molecular skeleton of the two ions. Reference potentials for the ionic liquid cation and anion were derived from OPLS-AA parameters with charges scaled by 0.8, and distance constraints for the ionic liquid ions were obtained from the averaged atomic coordinates in the single crystals of 1-ethyl-3-methylimidazolium salts and from the ab initio minimised geometry of the acetate anion using GAMESS-US23 at the MP2/6-31G(d) level of theory as previously reported.11 Reference potentials for glucose (Table 2) were derived from OPLS-AA parameters and distance and angular constraints for the model were constructed within the EPSR “makemole” subroutine using standardised bond lengths (Table 3). All angular constraints were set to idealised tetrahedral values of 109.466° and dihedral restraints set to ±60° around the glucose ring to generate an initial chair with equatorially positioned non-hydrogen substituents.
glucose sample. The eight datasets obtained by varying the isotopic signature of the samples were compared with the simulation thus increasing the confidence in the EPSR derived structure. Partial radial distribution functions describing the distributions of cations, anions and glucose molecules around a central moiety were calculated using the SHARM routines within EPSR using the anion and glucose centres of mass and cation centre of mass of the imidazolium ring as positions of reference. Atom types were defined based on their unique positions in the molecular skeleton of the two ions. Reference potentials for the ionic liquid cation and anion were derived from OPLS-AA parameters with charges scaled by 0.8, and distance constraints for the ionic liquid ions were obtained from the averaged atomic coordinates in the single crystals of 1-ethyl-3-methylimidazolium salts and from the ab initio minimised geometry of the acetate anion using GAMESS-US23 at the MP2/6-31G(d) level of theory as previously reported.11 Reference potentials for glucose (Table 2) were derived from OPLS-AA parameters and distance and angular constraints for the model were constructed within the EPSR “makemole” subroutine using standardised bond lengths (Table 3). All angular constraints were set to idealised tetrahedral values of 109.466° and dihedral restraints set to ±60° around the glucose ring to generate an initial chair with equatorially positioned non-hydrogen substituents.
| Atom type | ε (kJ mol−1) | σ (Å) | q (e) |
|---|---|---|---|
| HG | 0.20 | 2.500 | 0.23362 |
| HG1 | 0.20 | 2.500 | 0.05125 |
| OG | 0.80 | 3.166 | −0.63464 |
| CG | 0.50 | 3.500 | 0.17612 |
| OCG | 0.80 | 3.166 | −0.3076 |
| CG1 | 0.50 | 3.500 | 0.1615 |
PFG
NMR experiments were carried out using a Bruker Biospin DMX 300 spectrometer, operating at a 1H frequency of 300.13 MHz, equipped with a diffusion probe capable of producing magnetic field gradient strength pulses up to 11.6 T m−1. The measurements were performed between 293 and 323 K, at increments of 5 K to an accuracy of ±0.1 K. A Bruker digital variable temperature unit, BVT 3000, was used to set the required temperature for each experiment. Samples were prepared in gas-tight 5 mm NMR tubes fitted with Young's taps and filled to a vertical height of approximately 40 mm under nitrogen. At each temperature, the sample was left to stand for 15 min before starting the measurement, in order to reach thermal equilibrium. Diffusion measurements were carried out using a standard PGSTE pulse sequence.24 Sixteen spectra were acquired per sample with the gradient strength being varied between 0.05 and 10 T m−1. The observation time, Δ, was set to 50 ms. Typical values of δ were 3 and 3.5 ms. The numerical values of the diffusion coefficient, D, were obtained by fitting the NMR signal decay function to the following expression:
NOESY NMR experiments were carried out using a Bruker Avance 400 spectrometer using standard library sequences with mixing times, τm, of 30, 40, 50 and 300 ms. Measurements were performed at 323 K, with chemical shifts measured relative to an external standard consisting of a sealed capillary containing DMSO-d6 inside the NMR tube sample. Samples were prepared as outlined above. It should be noted that all the mixing times used led to similar data. This is not surprising given the slow pure liquid dynamics, coupled with the presence of glucose in the mixture. However, using the long mixing times (300 ms), significant T1 noise was observed and thus the shorter mixing time experiments (which were less prone to such noise) are reported, herein.
Theoretical details
The ionic liquid cation was modelled using the forcefield of Canongia Lopes et al.,25 while the necessary parameters for the acetate anion and glucose monomer were taken from OPLS-AA.26 Previous work on the pure [C2mim][OAc] ionic liquid showed that the system dynamics were too slow when using integer charges on the ions.11 In line with the findings of this work, charges on the ionic liquid ions were scaled by a factor of 0.85 in order to more properly model the diffusion processes occurring in the system. All C–H and O–H bonds were treated as constraints. Simulations of [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mole ratios of 10
glucose mole ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 6
1, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were performed in the NPT ensemble at 323 K and 1 atm with thermostat and barostat relaxation times of 0.1 and 0.2 ps, respectively. For each ratio, four separate simulations were conducted beginning from random initial configurations in order to reduce any bias in the results arising from the starting positions of ions and molecules. All simulations underwent a 3 ns equilibration period at a timestep of 1 fs during which statistics were discarded, followed by a production run of a further 3 ns. All calculated properties are averaged over the four resulting 3 ns production runs for a given ratio, with configurations saved every 1000 steps (1 ps). In each case, the number of ionic liquid ion pairs was 240 and all simulations were conducted with DL_POLY v2.20.27
1 were performed in the NPT ensemble at 323 K and 1 atm with thermostat and barostat relaxation times of 0.1 and 0.2 ps, respectively. For each ratio, four separate simulations were conducted beginning from random initial configurations in order to reduce any bias in the results arising from the starting positions of ions and molecules. All simulations underwent a 3 ns equilibration period at a timestep of 1 fs during which statistics were discarded, followed by a production run of a further 3 ns. All calculated properties are averaged over the four resulting 3 ns production runs for a given ratio, with configurations saved every 1000 steps (1 ps). In each case, the number of ionic liquid ion pairs was 240 and all simulations were conducted with DL_POLY v2.20.27
Results
General liquid structure
Experimental neutron diffraction total scattering functions are presented in Fig. 1 together with the EPSR and MD-derived data. In general, a good fit is observed for all isotopic substitutions across the Q range of interest (above 0.5 Å−1) between the experimental data and the EPSR derived model. In addition, excellent agreement is found with the MD simulations. We note that the major peak at 1.5 Å−1 is too intense in the MD results which suggests that the liquid is over-structured in these simulations. This peak corresponds to ion–ion or ion–glucose contacts and is dominated by the ionic liquid cation–anion interaction. Some of this discrepancy can be attributed to the lack of correction for line broadening in the MD calculated F(Q) which, if applied, may reduce all peak intensities by around 10%. Otherwise, this suggests that the cation–anion (or, alternatively, the anion–glucose) interaction may still be too strong, despite the scaling of the ionic charges.![Experimental (solid lines), EPSR refined (dotted lines) and MD simulated (dashed lines) distinct scattering profiles of all isotopically-substituted 6 : 1 [C2mim][OAc] : glucose mixtures examined.](/image/article/2011/SC/c1sc00241d/c1sc00241d-f1.gif) | ||
Fig. 1 Experimental (solid lines), EPSR refined (dotted lines) and MD simulated (dashed lines) distinct scattering profiles of all isotopically-substituted 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc] 1 [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixtures examined. glucose mixtures examined. | ||
The corresponding experimental and simulated centre-of-mass radial distribution functions (RDFs) for the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc]
1 [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system are shown in Fig. 2, together with those from the neat [C2mim][OAc] ionic liquid previously reported.11 It is immediately apparent that the general ionic liquid structure is not significantly perturbed by the presence of the solute despite its size. This has been observed previously for other systems with equally large solutes, for example as glucose in [C1mim]Cl,17benzene in [C1mim][PF6]28 and 1-methylnaphthalene in 1-methyl-4-cyanopyridinium bis{(trifluoromethyl)sulfonyl}imide,29 indicating that intermolecular ion–ion correlations dominate the observed F(Q). A slight expansion (approx. 0.4 Å) of the coordination shells in the 6
glucose system are shown in Fig. 2, together with those from the neat [C2mim][OAc] ionic liquid previously reported.11 It is immediately apparent that the general ionic liquid structure is not significantly perturbed by the presence of the solute despite its size. This has been observed previously for other systems with equally large solutes, for example as glucose in [C1mim]Cl,17benzene in [C1mim][PF6]28 and 1-methylnaphthalene in 1-methyl-4-cyanopyridinium bis{(trifluoromethyl)sulfonyl}imide,29 indicating that intermolecular ion–ion correlations dominate the observed F(Q). A slight expansion (approx. 0.4 Å) of the coordination shells in the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc]
1 [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system can be observed compared with the pure [C2mim][OAc] shown by a shift in the maxima of the RDFs to longer distances. The glucose–ion RDFs show short contacts with the glucose of ∼5 Å for both cation and anion, although the anion contacts dominate in the first solvation shell. Some glucose–glucose contacts are present in the MD data within this first solvation shell suggesting that occasional hydrogen-bonds between neighbouring sugars occur; however, the predominant glucose–glucose RDF peak is observed at 10 Å. A structural feature compatible with this length scale is the positioning of two sugar molecules hydrogen-bonding to a common bridging acetate anion through the two oxygen centres (the specific nature of these contacts is examined in detail below).
glucose system can be observed compared with the pure [C2mim][OAc] shown by a shift in the maxima of the RDFs to longer distances. The glucose–ion RDFs show short contacts with the glucose of ∼5 Å for both cation and anion, although the anion contacts dominate in the first solvation shell. Some glucose–glucose contacts are present in the MD data within this first solvation shell suggesting that occasional hydrogen-bonds between neighbouring sugars occur; however, the predominant glucose–glucose RDF peak is observed at 10 Å. A structural feature compatible with this length scale is the positioning of two sugar molecules hydrogen-bonding to a common bridging acetate anion through the two oxygen centres (the specific nature of these contacts is examined in detail below).
![Centre-of-mass radial distribution functions for a 6 : 1 [C2mim][OAc] : glucose system, as determined by EPSR fitting of experimental neutron diffraction data (solid lines with symbols) and MD simulation (solid line). MD data for the neat ionic liquid is also shown for comparison (dashed line). Top panel shows ionic liquid cation–anion (black), cation–cation (blue) and anion–anion (red) distributions. Bottom panel shows glucose–glucose (green), glucose–cation (blue) and glucose–anion (red) correlations.](/image/article/2011/SC/c1sc00241d/c1sc00241d-f2.gif) | ||
Fig. 2 Centre-of-mass radial distribution functions for a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc] 1 [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system, as determined by EPSR fitting of experimental neutron diffraction data (solid lines with symbols) and MD simulation (solid line). MD data for the neat ionic liquid is also shown for comparison (dashed line). Top panel shows ionic liquid cation–anion (black), cation–cation (blue) and anion–anion (red) distributions. Bottom panel shows glucose–glucose (green), glucose–cation (blue) and glucose–anion (red) correlations. glucose system, as determined by EPSR fitting of experimental neutron diffraction data (solid lines with symbols) and MD simulation (solid line). MD data for the neat ionic liquid is also shown for comparison (dashed line). Top panel shows ionic liquid cation–anion (black), cation–cation (blue) and anion–anion (red) distributions. Bottom panel shows glucose–glucose (green), glucose–cation (blue) and glucose–anion (red) correlations. | ||
The EPSR-derived glucose–glucose correlation shows weaker glucose–glucose correlation with a small, broad peak at ∼7 Å which can be attributed to the same close contacts in the liquid. The co-ordination numbers between species derived from MD and EPSR simulation models by integrating the area under the first peak in the radial distributions are shown in Table 4. Compared with the pure liquid, the cation–cation, anion–anion and anion–cation co-ordination numbers are reduced slightly, as expected, due to the presence of the solute and this is consistent with the idea that the acetate anions now also form close contacts with the dissolved sugar as well as with the ionic liquid cations. It is again noteworthy that the dominant 1st shell Coulombic cation–anion interaction has been only slightly perturbed, with the loss of only 0.6 anions from the primary solvation shell of the cation, on dissolution of the glucose. The largest decreases are seen for the like-ion values, but the sizeable spherical volume over which this loss is made makes a quantitative analysis of the location of the losses difficult. We may safely suggest that this is simply related to the presence of the glucose within the primary shell around anions, which affects the like-ion coordination numbers both directly, as a consequence of the sugar taking up space in the solvation shell and indirectly through a disruption of the cation–anion–cation and anion–cation–anion structural features, both of which are governed by the anion–cation interaction. In addition, the solubilisation leads to a reduction in density of the liquid. Around the glucose molecule we find an average of nearly five anions and, up to the same cutoff distance, nearly six (5.75) cations
| CNXY (Y around X) | Pure IL11 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 IL 1 IL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Glucose MD/EPSR Glucose MD/EPSR |
r max (Å) |
|---|---|---|---|
| Glucose–Glucose | — | 4.9 ± 0.4/4.7 ± 1.5 | 13 |
| Glucose–Anion | — | 4.7 ± 0.2/4.6 ± 1.2 | 7.1 |
| Glucose–Cation | — | 9.6 ± 0.2/8.9 ± 1.9 | 8.7 |
| Anion–Anion | 17.8 | 15.5 ± 0.1/16.0 ± 1.4 | 10.5 |
| Cation–Anion | 7.1 | 6.3 ± 0.1/6.4 ± 1.2 | 7.5 |
| Cation–Cation | 25.1 | 22.1 ± 0.2/22.7 ± 1.9 | 11.8 |
As shown by the comparison of the radial distribution functions (Fig. 2), spatial distributions of the anions around the cation are similar for both the pure ionic liquid and the liquid following dissolution of glucose (see Supporting Information†). Spatial probability distributions of ions around a central glucose, Fig. 3, reveal the likely positions of the cation and anion around the sugar. With respect to the acetate anion the positioning and thus predominant regions of density is guided almost entirely by hydrogen-bonding to the glucose hydroxyl groups. In contrast, high probability regions for the cation are generally found outside the anion density around the equator of the sugar and tend to suggest that the cation is positioned as a result of interaction with the anions rather than as a result of direct interaction with the sugar. This trend appears not to be followed in the vicinity of the ring oxygen (OG, Table 3). Around OG a clear band of cations is observed which does not immediately appear to be the result of neighbouring anions since there are no high probability regions in the same locality.
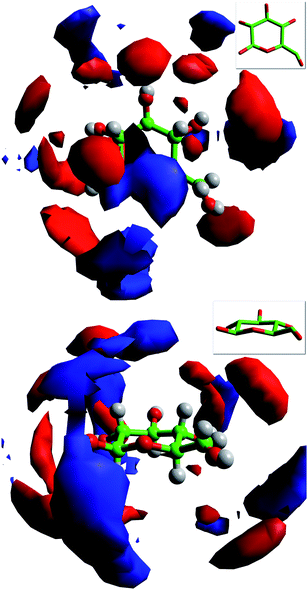 | ||
| Fig. 3 Spatial probability distributions of anions (red) and cations (blue) around a central glucose derived from the MD model. The surfaces are drawn to encompass regions containing greater than six anions or four cations times the bulk density of ions in the system. Inserts show the orientation of the central glucose molecule in each case, plan view (top) and side view (bottom). | ||
Fine solvation structure
A principal objective of this study was to model the IL–carbohydrate solvation interactions in order to try and understand the primary factors contributing to cellulose solubility in the ionic liquid and, therefore, examine why cellulose is dissolved more rapidly in acetate ionic liquids compared with the corresponding chloride based system. It is generally accepted that the most important property of an ionic liquid relevant to the solubilisation of cellulose is the presence of hydrogen-bond acceptor sites (in the anion) and that the driving force for solubilisation is the disruption of the inter-strand cellulose hydrogen-bonding network through competitive hydrogen-bonding to strongly hydrogen-bond accepting anions. More recently the suggestion has been made that the cation also has a direct role through hydrogen-bonding to the sugar.13 Previously, we reported that weak hydrogen bonding may exist between the cation and the glucose molecule for [C1mim]Cl ionic liquid systems.15,17 However, with the interactions observed being very weak it was difficult to definitively ascribe the binding to hydrogen bonding or van der Waals contacts. In order to resolve this uncertainty, in the present study a detailed analysis of the distance and angular distribution of anions, cations and glucose molecules has been undertaken. While there has always been debate surrounding the specific nature of hydrogen-bonds, it is usually stated that the interaction is 90% electrostatic. From the perspective of purely geometric criteria, some common definitions are often employed in order to ‘detect’ hydrogen-bonds in crystal structures and atomistic simulations. For example, a typical X–H⋯Y interaction may be considered a hydrogen-bond if rY⋯H < 2.5 Å and θX–H⋯Y > 150.0°.Fig. 4 shows the partial RDFs between various hydrogen/oxygen pairs on different species in the simulations, together with the related distance/angle map of the interaction. The numbering schemes for [C2mim]+ and glucose hydrogens are shown in Fig. 5. RDFs between glucose hydroxyls and acetate oxygens demonstrate strong hydrogen-bonding character according to the criteria defined above, with a strong, sharp peak at 1.7 Å and a clear tendency for the O⋯H–O angle to 180°. For all other interactions considered, the primary peak is located at distances greater than 2.55 Å and the range of X–H⋯Y angles encountered is larger and are generally found to be below 150°. In particular, the geometry of contacts between cation ring hydrogens and glucose oxygens is not indicative of any strong association. This data bears a significant resemblance to the aliphatic–H/O data presented here, for which hydrogen-bonding certainly does not occur. In addition, no strong trends are seen between the ring oxygen of the glucose and the ring hydrogens of the cation. This suggests that the localisation of the cation in this region observed in the probability distributions in Fig. 3 is again primarily a result of ion placement due to interaction with the anion rather than the sugar solute and is unlikely to be structure forming.
 | ||
| Fig. 4 Selected partial radial distribution functions between glucose molecules, anions and cations, and the distance/angle maps for the related X–H⋯Y interaction. Atom types are those listed in Table 3. Interactions between glucose oxygens and ionic liquid cation hydrogens are presented as averages over all similar centres (individual partial RDFs are provided in the Supporting Information for completeness†). | ||
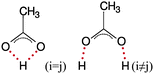
In our previous work on the neat [C2mim][OAc] system11 analysis of single cation–multiple anion contacts showed that approximately two thirds of the time a particular cation ring-hydrogen was involved in a hydrogen-bond to single acetate oxygen, while the bidentate case was observed for the majority of the remaining time. Herein, we have extended the concept to examine single anion–multiple cation contacts thus focusing on the environment of the anion in the liquid rather than the cation. Concentrating on the interactions with a given anion in the system, a cation ring-hydrogen or glucose hydroxyl hydrogen is considered to be interacting if the Hn⋯OA distance is less than 3.5 or 2.2 Å, respectively. These limits correspond to the positions of the first minima in the relevant partial RDFs. Considering the contacts in the pure ionic liquid shown in the top three entries in Table 5 we see that on average an anion has 4.59 short O/H contacts with cations, of which around half are single contacts and around one third are bidentate interactions where both acetate oxygens interact simultaneously with one ring hydrogen. The remaining contacts are attributed to bifurcated (one acetate oxygen shared between two ring hydrogens), bridging interactions (where both acetate oxygens interact simultaneously with different ring hydrogens) and interaction where three or more close contacts are made with a single cation. As noted previously,11 despite the ease with which one might expect the anion to bridge the HR4 and HR5 hydrogens on the ring, this interaction is rarely observed accounting for less than 1% of all anion–cation close contacts. These 4.59 short contacts are shared between 3.42 cations, indicating that approximately only half of the cations in the first coordination shell around the anion are interacting with any degree of strength or directionality, the remainder simply filling available space. The anion contacts with the isolated HR2 hydrogen are almost entirely described by single and bidentate interactions as is to be expected and accounting for the double-contact of the latter case translates into an observed likelihood of approximately 2.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in favour of the single O⋯H contact. Approximately 8% of all observed contacts involving HR4 and HR5 are attributed to the bifurcated case, while the bridging case makes up just 0.6%. In addition, the HR5 hydrogen closer to the ethyl chain participates in slightly fewer short contacts than does the HR4 site owing to the increased bulk and volume occupancy of the alkyl chain compared with the methyl side-chain.
1 in favour of the single O⋯H contact. Approximately 8% of all observed contacts involving HR4 and HR5 are attributed to the bifurcated case, while the bridging case makes up just 0.6%. In addition, the HR5 hydrogen closer to the ethyl chain participates in slightly fewer short contacts than does the HR4 site owing to the increased bulk and volume occupancy of the alkyl chain compared with the methyl side-chain.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid
1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixture. NC is the number of short contacts observed per cation (where C–H⋯Y is less than rmax). For each specific hydrogen centre on the cation the percentage breakdown of the individual OA⋯HRn contacts responsible is given. All contact patterns involving at most two hydrogens are treated explicitly, while the type ‘Other’ refers to all other multiple-centre contacts. The first matrix of percentages represent contacts involving only one acetate oxygen, with diagonal elements (HRi = HRj) representing single (pure) hydrogen bonds, and off-diagonal elements (HRi ≠ HRj) representing concomitant hydrogen bonds between two hydrogens and the same acetate oxygen. The second matrix represents contacts involving both acetate oxygens, with diagonal elements (HRi = HRj) representing bifurcated hydrogen bonding between a single hydrogen and both acetate oxygens, and off-diagonal elements (HRi ≠ HRj) representing simultaneous individual hydrogen bonds formed between two hydrogens and the two acetate oxygens
glucose mixture. NC is the number of short contacts observed per cation (where C–H⋯Y is less than rmax). For each specific hydrogen centre on the cation the percentage breakdown of the individual OA⋯HRn contacts responsible is given. All contact patterns involving at most two hydrogens are treated explicitly, while the type ‘Other’ refers to all other multiple-centre contacts. The first matrix of percentages represent contacts involving only one acetate oxygen, with diagonal elements (HRi = HRj) representing single (pure) hydrogen bonds, and off-diagonal elements (HRi ≠ HRj) representing concomitant hydrogen bonds between two hydrogens and the same acetate oxygen. The second matrix represents contacts involving both acetate oxygens, with diagonal elements (HRi = HRj) representing bifurcated hydrogen bonding between a single hydrogen and both acetate oxygens, and off-diagonal elements (HRi ≠ HRj) representing simultaneous individual hydrogen bonds formed between two hydrogens and the two acetate oxygens
| N C |
|
|
Other | |||||
|---|---|---|---|---|---|---|---|---|
| HR2 | 1.70 | 56.12 | <.01 | <.01 | 43.76 | 0.07 | 0.05 | <.01 |
| HR4 | 1.49 | — | 47.84 | 8.09 | — | 34.82 | 0.62 | 8.83 |
| HR5 | 1.40 | — | — | 48.33 | — | — | 32.58 | 10.07 |
| Pure | 4.59 | HR2 | HR4 | HR5 | HR2 | HR4 | HR5 | — |
| HR2 | 1.49 | 57.79 | <.01 | <.01 | 42.09 | 0.04 | 0.07 | <.01 |
| HR4 | 1.28 | — | 49.36 | 7.73 | — | 33.58 | 0.69 | 8.60 |
| HR5 | 1.21 | — | — | 49.85 | — | — | 31.40 | 10.26 |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
3.99 | HR2 | HR4 | HR5 | HR2 | HR4 | HR5 | — |
On the addition of glucose to the ionic liquid we observe a small decrease in the total number of short anion–cation O/H contacts from 4.59 to 3.98 but very little change in the populations of the different binding types shown in the last three entries of Table 5. The number of cations involved in these short contacts also decreases, from 3.42 to 3.00 in the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system. For the observed contacts between acetate oxygens and the glucose hydroxyl groups shown in Table 6, a rather different pattern is observed compared with the anion–cation case. The predominant interaction is the single contact (as was the case for the cation ring hydrogens) accounting for over 50% of the observed contacts for each hydroxyl hydrogen, but the bidentate interaction is now the least common of the four basic interaction types. It is most prevalent for the isolated H6 (2.04% of site contacts) but is rarely seen otherwise. Instead, bridging interactions between adjacent hydroxyl groups around the equator of the glucose are commonplace, with that between H1 and H2 particularly so (24.09% of site contacts). An acetate anion approaching the anomeric carbon will prefer to distance itself from the ring oxygen owing to electrostatic repulsion and hence promotes the H1/H2 bridge. Consequently, this enforces a bridging pattern of anions around the ring, with the following hydroxyl pair H2/H3 less likely to see a bridging contact (8 to 9% of site contacts) and the H3/H4 pair more likely (∼15% of site contacts). Analysing all instantaneous contact between anions and hydroxyl groups for individual sugar molecules shows that the situation where each hydroxyl is involved in a single hydrogen-bond with a different acetate anion occurs only 10% of the time, whereas three single hydrogen-bonds and one bridging interaction accounts for ∼25% of all environments. The total number of short OA⋯Hn contacts per anion is 0.77, corresponding to 4.67 contacts (hydrogen-bonds) per glucose or 0.93 hydrogen-bonds per hydroxyl group per glucose. We also note that at any instant almost half (47.22%) of all acetate anions have no short contacts with any glucose molecules. Coupled with the relatively minor reduction in cation–anion contacts, this suggests that sugar concentrations in excess of 14.3 mol% in [C2mim][OAc] are feasible.
1 system. For the observed contacts between acetate oxygens and the glucose hydroxyl groups shown in Table 6, a rather different pattern is observed compared with the anion–cation case. The predominant interaction is the single contact (as was the case for the cation ring hydrogens) accounting for over 50% of the observed contacts for each hydroxyl hydrogen, but the bidentate interaction is now the least common of the four basic interaction types. It is most prevalent for the isolated H6 (2.04% of site contacts) but is rarely seen otherwise. Instead, bridging interactions between adjacent hydroxyl groups around the equator of the glucose are commonplace, with that between H1 and H2 particularly so (24.09% of site contacts). An acetate anion approaching the anomeric carbon will prefer to distance itself from the ring oxygen owing to electrostatic repulsion and hence promotes the H1/H2 bridge. Consequently, this enforces a bridging pattern of anions around the ring, with the following hydroxyl pair H2/H3 less likely to see a bridging contact (8 to 9% of site contacts) and the H3/H4 pair more likely (∼15% of site contacts). Analysing all instantaneous contact between anions and hydroxyl groups for individual sugar molecules shows that the situation where each hydroxyl is involved in a single hydrogen-bond with a different acetate anion occurs only 10% of the time, whereas three single hydrogen-bonds and one bridging interaction accounts for ∼25% of all environments. The total number of short OA⋯Hn contacts per anion is 0.77, corresponding to 4.67 contacts (hydrogen-bonds) per glucose or 0.93 hydrogen-bonds per hydroxyl group per glucose. We also note that at any instant almost half (47.22%) of all acetate anions have no short contacts with any glucose molecules. Coupled with the relatively minor reduction in cation–anion contacts, this suggests that sugar concentrations in excess of 14.3 mol% in [C2mim][OAc] are feasible.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid
1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system. NC is the number of short contacts observed per hydroxyl hydrogen per frame (where O–H⋯Y is less than rmax). Contact pattern types are analogous to those for the acetate–cation case detailed in Table 5
glucose system. NC is the number of short contacts observed per hydroxyl hydrogen per frame (where O–H⋯Y is less than rmax). Contact pattern types are analogous to those for the acetate–cation case detailed in Table 5
| N C |
|
|
Other | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | 0.97 | 61.62 | 3.95 | 0.32 | 0.05 | 0.10 | 0.61 | 24.09 | 0.62 | 0.90 | 2.87 | 4.89 |
| H2 | 0.97 | — | 50.49 | 5.15 | 3.07 | 0.00 | — | 0.34 | 7.78 | 0.04 | 0.00 | 5.10 |
| H3 | 0.84 | — | — | 54.02 | 8.35 | 0.03 | — | — | 0.33 | 15.60 | 0.97 | 6.84 |
| H4 | 0.92 | — | — | — | 55.42 | 7.43 | — | — | — | 1.20 | 6.31 | 1.63 |
| H6 | 0.97 | — | — | — | — | 79.50 | — | — | — | — | 2.04 | 0.74 |
| All | 4.67 | H1 | H2 | H3 | H4 | H6 | H1 | H2 | H3 | H4 | H6 | — |
Previous work on [C1mim]Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose systems revealed the ability for the chloride anion to form bridging hydrogen-bond interactions with two hydroxyl groups simultaneously and this was found to be a fairly commonplace structural feature. In the present case, a high proportion of anion–glucose contacts involve a single group. The spherically-symmetric chloride anion may always interact with a second glucose no matter what the contact pattern with the first. Assuming similar interactions also exist on cellulose dissolution indicates that the initial separation of strands through disruption of the existing hydrogen-bonding may be potentially followed by the formation of a chloride hydrogen-bond bridge between the two strands. In effect, this presents a second hydrogen-bonding system which must also be disrupted before the strands become fully separated and enter into solution proper. For the acetate anion the chances of such secondary hydrogen-bonding structures are reduced since they are prevented somewhat by the hydrophobic methyl group.
glucose systems revealed the ability for the chloride anion to form bridging hydrogen-bond interactions with two hydroxyl groups simultaneously and this was found to be a fairly commonplace structural feature. In the present case, a high proportion of anion–glucose contacts involve a single group. The spherically-symmetric chloride anion may always interact with a second glucose no matter what the contact pattern with the first. Assuming similar interactions also exist on cellulose dissolution indicates that the initial separation of strands through disruption of the existing hydrogen-bonding may be potentially followed by the formation of a chloride hydrogen-bond bridge between the two strands. In effect, this presents a second hydrogen-bonding system which must also be disrupted before the strands become fully separated and enter into solution proper. For the acetate anion the chances of such secondary hydrogen-bonding structures are reduced since they are prevented somewhat by the hydrophobic methyl group.
Since bridging interactions involving a single acetate and two hydroxyl groups on the same sugar make up a significant portion of the observed contacts and, since this would aid the solvation of cellulose by reducing the propensity for inter-strand bridging after their initial separation, this may explain why acetate-based ionic liquids appear to be able to dissolve such material at a higher rate than other ionic liquid systems such as the corresponding halides, although the much lower relative viscosities of the acetates may also play an important role. This is illustrated schematically in Fig. 6. Unfortunately, from the spatial distribution functions, there is no clear spatial orientation of the cation around the glucose and, therefore, no information which would guide the positioning of the cation. However, it is likely that, due to the need for charge balance and the strong Coulombic interactions between the anion and the cation, that the cations will not be a significant distance from the anions following dissolution of the cellulose.
 | ||
| Fig. 6 Schematic illustration of acetate anion penetration and separation of cellulose strands (left) compared to potential formation of bridging intra-sheet hydrogen-bonds with chloride (right). | ||
NMR experiments (PFG and nOe)
The convergence of the results from the MD and EPSR simulations with the experimental data provides a high level of confidence in the quality of the MD model. Dynamical data such as self-diffusion constants for the motion of individual species in the liquid can be derived from the simulations and should, given the confidence in the quality of the MD, provide results consistent with independent experimental data.Diffusion coefficients as calculated from molecular dynamics simulation and as determined by PFG NMR are shown in Fig. 7. As found by Moyna et al., a decrease in the ion diffusion coefficients was found on dissolution of glucose compared with the pure ionic liquid with the decrease in diffusion coefficient larger with higher concentrations of dissolved glucose (Fig. 7b). This is as expected with the increase in viscosity and the strong hydrogen-bonding interactions between the glucose and the anion. Importantly, the agreement between the MD derived diffusion coefficients and those obtained experimentally is reasonable. Charge scaling was required to provide a similar agreement in the pure ionic liquid system,11 The same scaling factors were used in this study for the ionic liquid giving confidence that the model is transferable between systems and is, therefore, a reasonable description of the cation and anion. The MD simulations, in general, give slightly higher values for the diffusion coefficient compared with the NMR-derived data, suggesting that the charge scaling reduces the cation–anion cohesion by too great a factor. Thus, a reasonably consistent explanation for the discrepancy between the calculated RDFs and those obtained experimentally (as shown in Fig. 1) is the lack of correction for line broadening in the F(Q) data calculated by MD, rather than too strong ionic or hydrogen-bonding interactions defined in the force field which would result in a simulation model with significantly underestimated diffusion coefficients due to a higher degree of Coulombic structuring in the liquids.
![Self diffusion coefficients for the cation (blue), anion (red) and glucose (green) determined by PFG NMR spectroscopy (lines, from this work (a) and from ref. 12 (b)) and molecular dynamics simulations (circles, this work) for 6 : 1 [C2mim][OAc] : glucose mixtures as a function of (a) temperature and (b) [C2mim][OAc]:glucose mole ratio.](/image/article/2011/SC/c1sc00241d/c1sc00241d-f7.gif) | ||
Fig. 7 Self diffusion coefficients for the cation (blue), anion (red) and glucose (green) determined by PFG NMR spectroscopy (lines, from this work (a) and from ref. 12 (b)) and molecular dynamics simulations (circles, this work) for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc] 1 [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixtures as a function of (a) temperature and (b) [C2mim][OAc]:glucose mole ratio. glucose mixtures as a function of (a) temperature and (b) [C2mim][OAc]:glucose mole ratio. | ||
The NOE spectra of the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [C2mim][OAc]:glucose mixture (see Supporting Information†) shows no significant interaction between either the anion or cation with the hydroxyls or ring hydrogens of the glucose (10 and 2.5–4 ppm, respectively). However, some correlation was found between the glucose CH and OH hydrogens as well as the aliphatic hydrogens on the ionic liquid cation. These findings were consistent across all mixing times employed (30–50 ms). Selective deuteriation of the anion and cation were also performed in an attempt to reduce the observed T1 noise related to the strong contributions in the spectra arising from the large contribution of the ionic liquid protons, potentially swamping any signals related to interactions with the glucose (Fig. 8). A mixture of 95 mol% [C2mim-d8][OAc-d3] (all deuteriated except HR2, HR4 and HR5) + 5 mol% [C2mim-d8][OAc] (all deuteriated except HR2, HR4 and HR5 on the cation and methyl group on the anion) was prepared and used as the ionic liquid solvent in a 6
1 [C2mim][OAc]:glucose mixture (see Supporting Information†) shows no significant interaction between either the anion or cation with the hydroxyls or ring hydrogens of the glucose (10 and 2.5–4 ppm, respectively). However, some correlation was found between the glucose CH and OH hydrogens as well as the aliphatic hydrogens on the ionic liquid cation. These findings were consistent across all mixing times employed (30–50 ms). Selective deuteriation of the anion and cation were also performed in an attempt to reduce the observed T1 noise related to the strong contributions in the spectra arising from the large contribution of the ionic liquid protons, potentially swamping any signals related to interactions with the glucose (Fig. 8). A mixture of 95 mol% [C2mim-d8][OAc-d3] (all deuteriated except HR2, HR4 and HR5) + 5 mol% [C2mim-d8][OAc] (all deuteriated except HR2, HR4 and HR5 on the cation and methyl group on the anion) was prepared and used as the ionic liquid solvent in a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 IL
1 IL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose system. Using this system the signal from the substituted protons was significantly attenuated, as expected, allowing the remaining possible cross-correlations to be observed. The resulting spectrum shows that no significant interaction between cation ring hydrogens and glucose hydroxyls exists.
glucose system. Using this system the signal from the substituted protons was significantly attenuated, as expected, allowing the remaining possible cross-correlations to be observed. The resulting spectrum shows that no significant interaction between cation ring hydrogens and glucose hydroxyls exists.
![NOESY spectrum of 6 : 1 mixture of ionic liquid : glucose, where the ionic liquid is a 95 : 5 molar ratio of [C2mim-d8][OAc-d3] and [C2mim-d8][OAc]. The mixing time employed was 40 ms.](/image/article/2011/SC/c1sc00241d/c1sc00241d-f8.gif) | ||
Fig. 8
NOESY spectrum of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ionic liquid 1 mixture of ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose, where the ionic liquid is a 95 glucose, where the ionic liquid is a 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 molar ratio of [C2mim-d8][OAc-d3] and [C2mim-d8][OAc]. The mixing time employed was 40 ms. 5 molar ratio of [C2mim-d8][OAc-d3] and [C2mim-d8][OAc]. The mixing time employed was 40 ms. | ||
Effect of glucose loading
Centre-of-mass RDFs calculated from simulations of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 6
1, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratios of ionic liquid:glucose (see Supporting Information†) indicate clearly the minor structural effects imposed on the ionic liquid, even for the highest loading of 4
1 mole ratios of ionic liquid:glucose (see Supporting Information†) indicate clearly the minor structural effects imposed on the ionic liquid, even for the highest loading of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Aside from the glucose–glucose RDFs (which, since the glucose is randomly distributed throughout the ionic liquid, displays considerable noise) the largest change is seen in the anion–anion RDF, manifest as a slight decrease in the primary peak as more glucose is added into the system. Presumably, this is a result of the number of anions positioned around glucose molecules becoming large enough to perturb the correlation between those surrounding the cations.
1. Aside from the glucose–glucose RDFs (which, since the glucose is randomly distributed throughout the ionic liquid, displays considerable noise) the largest change is seen in the anion–anion RDF, manifest as a slight decrease in the primary peak as more glucose is added into the system. Presumably, this is a result of the number of anions positioned around glucose molecules becoming large enough to perturb the correlation between those surrounding the cations.
Averaged intermolecular interaction energies between species, Fig. 9, show clearly the relative strengths and nature of the interactions between glucose and ionic liquid ions in the system. We note first the relatively minor changes in the ion–ion interaction strengths on going from low pure IL to high glucose content (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) systems. All van der Waals energies become slightly less stabilising by a few kJ mol−1 per ion pair, as does the anion–anion electrostatic interaction. However, there is a significant decrease in the cation–anion electrostatic energy of almost 30 kJ mol−1 due to the reduced number of contacts as a result of the glucose content in the liquid. The cation–cation electrostatic energy in fact becomes more negative as more glucose is added, which is attributed to the introduction of preferential sites above and below the sugar ring, leading to less competing cation–cation close contacts around an anion centre. Between ionic liquid ions and glucose molecules all interactions are energetically favourable with the exception of the van der Waals glucose–anion energy which is weakly repulsive at all concentrations. All other intermolecular energies involving glucose molecules follow the same trend as the cation–anion interactions, becoming weaker as the mole fraction of glucose increases.
1) systems. All van der Waals energies become slightly less stabilising by a few kJ mol−1 per ion pair, as does the anion–anion electrostatic interaction. However, there is a significant decrease in the cation–anion electrostatic energy of almost 30 kJ mol−1 due to the reduced number of contacts as a result of the glucose content in the liquid. The cation–cation electrostatic energy in fact becomes more negative as more glucose is added, which is attributed to the introduction of preferential sites above and below the sugar ring, leading to less competing cation–cation close contacts around an anion centre. Between ionic liquid ions and glucose molecules all interactions are energetically favourable with the exception of the van der Waals glucose–anion energy which is weakly repulsive at all concentrations. All other intermolecular energies involving glucose molecules follow the same trend as the cation–anion interactions, becoming weaker as the mole fraction of glucose increases.
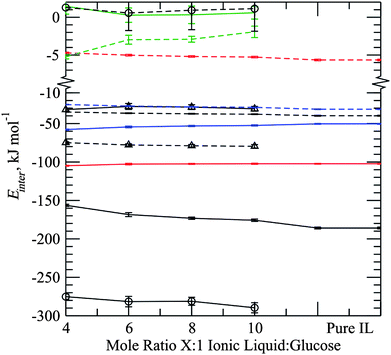 | ||
| Fig. 9 Interaction energies as a function of mole fraction loading between: cation-anion (black), anion-anion (red), cation-cation (blue), glucose-glucose (green), glucose-anion (circles) and glucose-cation (triangles). Solid and dashed lines represent electrostatic and van der Waals energies respectively. Interactions involving the sugar are normalised relative to the number of sugar molecules in the system, while those involving only the ionic liquid are normalised relative to the number of ion pairs in the system. | ||
As reported previously for glucose in the ionic liquid [C1mim]Cl the van der Waals interaction between sugar and cation is favourable.17,18 In the present case these interactions are found to have a favourable interaction of the order of 30 kJ mol−1. This interaction type is secondary to the glucose–anion interaction but still significant at approximately two sevenths the value and is over twice the glucose–cation electrostatic interaction energy. Taking the latter point into account and, given that a hydrogen-bond is typically considered to be 90% electrostatic interactions, we must conclude that the ability of the ionic liquid cation to stabilise the glucose-solvent interaction through van der Waals forces is considerably more important than the presence of any (weak) hydrogen-bond-like interactions. Absolute values of the calculated interaction energies are, in general, consistent with those for individual glucose sub-units of oligomers as studied by Liu et al.18 The anion–glucose interaction energy per glucose in the present case is of the order of −280 kJ mol−1, cf. −220 kJ mol−1 in Ref. 18, the latter being lower presumably because of the reduced number of free OH groups in the oligomeric structure. For the cation–glucose interaction the van der Waals and electrostatic energies per glucose are reported as −72.4 and −25.3 kJ mol−1, respectively, compared with around −170 and −30 kJ mol−1 in the present study. Thus, both simulation studies predict comparable values for the electrostatic aspect, but significantly different values for the van der Waals component. Again, reasons for this may be related to differences enforced in the local ionic liquid solvation environment on going from the monomeric to oligomeric case.
Discussion
Remsing et al.12 performed NMR experiments in order to determine any correlations between observed nuclei relaxation rates in [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cellobiose and [C2mim]Cl
cellobiose and [C2mim]Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cellobiose systems as a function of cellobiose concentration, in order to directly probe the predominant species contacts present in the system. It was concluded that subtle variations in 13C relaxation times were consistent with changes in solution viscosity rather than being indicative of any cation–carbohydrate interaction. Conversely, the observed strong dependence of acetate13C relaxation time with cellobiose concentration provides clear evidence of strong interaction with the carbohydrate. Subsequent NMR experiments by Zhang et al. focussed on the [C2mim][OAc]
cellobiose systems as a function of cellobiose concentration, in order to directly probe the predominant species contacts present in the system. It was concluded that subtle variations in 13C relaxation times were consistent with changes in solution viscosity rather than being indicative of any cation–carbohydrate interaction. Conversely, the observed strong dependence of acetate13C relaxation time with cellobiose concentration provides clear evidence of strong interaction with the carbohydrate. Subsequent NMR experiments by Zhang et al. focussed on the [C2mim][OAc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cellobiose system solvated in DMSO-d6.13 They reported the changes in chemical shift of all carbon atoms in cellobiose as a function of ionic liquid concentration, together with those for the ring hydrogens of the [C2mim]+ cation, concluding that the observed trends are consistent with the presence of hydrogen-bonding between carbohydrate and cation. None of the data in the present study provides compelling evidence for the presence of such interactions in the system. Analysis of molecular dynamics simulations reveals no geometric features indicative of hydrogen-bonding between HRn and On sites and NOESY experiments show no through-space interactions between the same groups. Energetic analysis of the present simulation data is consistent with both our earlier study on the [C1mim]Cl15 system and the work of Liu et al.,18i.e. that the significant favourable energetic interaction between cation and carbohydrate is van der Waals-like and the overall interaction energy is a fraction of that of the anion–carbohydrate interaction. Therefore, from both the previous chloride15 and current acetate studies, the predominant interactions of the ionic liquid with cellulose as a solute, in terms of dissolution, are likely to be with the anion and that any cation–solute interactions are not structure forming.
cellobiose system solvated in DMSO-d6.13 They reported the changes in chemical shift of all carbon atoms in cellobiose as a function of ionic liquid concentration, together with those for the ring hydrogens of the [C2mim]+ cation, concluding that the observed trends are consistent with the presence of hydrogen-bonding between carbohydrate and cation. None of the data in the present study provides compelling evidence for the presence of such interactions in the system. Analysis of molecular dynamics simulations reveals no geometric features indicative of hydrogen-bonding between HRn and On sites and NOESY experiments show no through-space interactions between the same groups. Energetic analysis of the present simulation data is consistent with both our earlier study on the [C1mim]Cl15 system and the work of Liu et al.,18i.e. that the significant favourable energetic interaction between cation and carbohydrate is van der Waals-like and the overall interaction energy is a fraction of that of the anion–carbohydrate interaction. Therefore, from both the previous chloride15 and current acetate studies, the predominant interactions of the ionic liquid with cellulose as a solute, in terms of dissolution, are likely to be with the anion and that any cation–solute interactions are not structure forming.
Conclusions
The detailed solvated structure of [C2mim][OAc] with glucose has been elucidated using EPSR simulations weighted to the experimentally determined liquid structure and pure molecular dynamics simulations. Good agreement between the methodologies has been observed together with a good match to the experimentally determined diffusion coefficient measurements. The detailed structure shows that, as in many cases of solutes dissolved in ionic liquids, the first shell ionic structure is not significantly perturbed by the presence of the glucose. Using a combination of the structural information with NOESY data it has also been possible to demonstrate that the primary interaction with glucose and, therefore, with cellulose is associated with the anion and little directional interactions with the cation are found. Differences have been reported between the solubilisation of cellulose between chloride and acetate based ionic liquid systems. This is thought to be due to the non-directional nature of hydrogen-bonding associated with the chloride anion compared with the acetate anion. In the former, although the chloride will disrupt the cellulose–cellulose hydrogen-bonding enabling the strands to be separated, the chloride can act as a binder between the strands limiting the solubility. In the case of acetate, bridging anions between the strands are unlikely leading to more complete disruption of the cellulose macrostructure. In addition, the rates of dissolution are likely to be influenced by the higher viscosity of the chloride based ionic liquid compared with the acetate based system.The authors gratefully acknowledge Petronas, QUILL and the EPSRC (Portfolio Partnership Grant (EP/D029538/1) and CASTech (EP/G012156/1)) for funding. We also thank the STFC for beamtime.
Notes and references
- R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974 CrossRef CAS.
- A. Pinkert, K. N. Marsh, S. Pang and M. P. Staiger, Chem. Rev., 2009, 109, 6712 CrossRef CAS; T. Heinze, S. Dorn, M. Schöbitz, T. Liebert, S. Köhler and F. Meister, Macromol. Symp., 2008, 262, 8 CrossRef CAS.
- H. Zhang, Z. G. Wang, Z. N. Zhang, J. Wu, J. Zhang and H. S. He, Adv. Mater., 2007, 19, 698 CrossRef CAS; J. H. Poplin, R. P. Swatloski, J. D. Holbrey, S. K. Spear, A. Metlen, M. Gratzel, M. K. Nazeeruddin and R. D. Rogers, Chem. Commun., 2007, 2025 RSC; R. P. Swatloski, J. D. Holbrey, J. L. Weston and R. D. Rogers, Chimica Oggi, 2006, 24, 31 Search PubMed; H. B. Xie, S. H. Li and S. B. Zhang, Green Chem., 2005, 7, 606 RSC; M. B. Turner, S. K. Spear, J. D. Holbrey and R. D. Rogers, Biomacromolecules, 2004, 5, 1379 CrossRef CAS.
- L. Vanoye, M. Fanselow, J. D. Holbrey, M. P. Atkins and K. R. Seddon, Green Chem., 2009, 11, 390 RSC; S. Q. Hu, Z. F. Zhang, Y. X. Zhou, B. X. Han, H. L. Fan, W. J. Li, J. L. Song and Y. Xie, Green Chem., 2008, 12, 1280 Search PubMed; B. H. Zhao, J. E. Holladay, H. Brown and Z. C. Zhang, Science, 2007, 316, 1597 CrossRef CAS; G. N. Sheldrake and D. Schleck, Green Chem., 2007, 10, 1044 Search PubMed; C. Lansalot-Matras and C. Moreau, Catal. Commun., 2003, 10, 517 Search PubMed.
- A. Pinkert, K. N. Marsh and S. Pang, Ind. Eng. Chem. Res., 2010, 49, 11121 Search PubMed; B. Lindman, G. Karlström and L. Stigsson, J. Mol. Liq., 2010, 156, 76 CrossRef CAS; H. Ohno and Y. Fukaya, Chem. Lett., 2009, 38, 2 CrossRef CAS.
- C. G. Hanke and R. M. Lynden-Bell, J. Phys. Chem. B, 2003, 107, 10873 CrossRef CAS.
- Y. Zhang and J. Y. G. Chan, Energy Environ. Sci., 2010, 3, 408 RSC; S. H. Lee, T. V. Doherty, R. J. Linhardt and J. S. Dordick, Biotechnol. Bioeng., 2009, 102, 1368 CrossRef CAS; N. Sun, M. Rahman, Y. Qin, M. L. Maxim, H. Rodríguez and R. D. Rogers, Green Chem., 2009, 11, 646 RSC; F. Hermanutz, F. Ga, E. Uerdingen, F. Meister and B. Kosan, Macromol. Symp., 2008, 262, 23 CrossRef CAS.
- H. Zhao, L. Jackson, Z. Y. Song and A. Olubajo, Tetrahedron: Asymmetry, 2006, 17, 2491 CrossRef CAS.
- M. B. Shiflett and A. Yokozeki, J. Chem. Eng. Data, 2009, 54, 108 CrossRef CAS.
- J. Kiefer, K. Obert, J. Fries, A. Bosmann, P. Wasserscheid and A. Leipertz, Appl. Spectrosc., 2009, 63, 1041 CrossRef CAS.
- D. T. Bowron, C. D'Agostino, L. F. Gladden, C. Hardacre, J. D. Holbrey, M. C. Lagunas, J. McGregor, M. D. Mantle, C. L. Mullan and T. G. A. Youngs, J. Phys. Chem. B, 2010, 114, 7760 Search PubMed.
- R. C. Remsing, G. Hernandez, R. P. Swatloski, W. W. Massefski, R. D. Rogers and G. Moyna, J. Phys. Chem. B, 2008, 112, 11071 CrossRef CAS.
- J. M. Zhang, H. Zhang, J. Wu, J. Zhang, J. S. He and J. F. Xiang, Phys. Chem. Chem. Phys., 2010, 12, 1941 RSC.
- I. D. Petrik, R. C. Remsing, Z. Liu, B. B. O'Brien, and G. Moyna, in “Ionic Liquids: From Knowledge to Application”, ed. N. V. Pletchkova, R. D. Rogers and K. R Seddon, ACS Symposium Series 1030, American Chemical Society, Washington DC, 2009, p 75 Search PubMed.
- T. G. A. Youngs, J. D. Holbrey, M. Deetlefs, M. Nieuwenhuyzen, M. F. Costa Gomes and C. Hardacre, ChemPhysChem, 2006, 7, 2279 CrossRef CAS.
- B. Kosan, C. Michels and F. Meister, Cellulose, 2008, 15, 59 CrossRef CAS.
- T. G. A. Youngs, C. Hardacre and J. D. Holbrey, J. Phys. Chem. B, 2007, 111, 13765 CrossRef CAS.
- H. B. Liu, K. L. Sale, B. M. Holmes, B. A. Simmons and S. Singh, J. Phys. Chem. B, 2010, 114, 4293 CrossRef CAS.
- J. X. Guo, D. J. Zhang, C. G. Duan and C. B. Liu, Carbohydr. Res., 2010, 345, 2201 CrossRef CAS.
- R. C. Remsing, I. D. Petrik, Z. Liu and G. Moyna, Phys. Chem. Chem. Phys., 2010, 12, 14827 RSC; J. Zhang, H. Zhang, J. Wu, J. Zhang, J. He and J. Xiang, Phys. Chem. Chem. Phys., 2010, 12, 14829 RSC.
- A. K. Soper, W. S. Howells and A. C. Hannon, ATLAS-Analysis of Time-of-Flight Diffraction Data from Liquid and Amorphous Samples, Rutherford Appleton Laboratory, Report RAL-89-046, 1989 Search PubMed; A. C. Hannon, W. S. Howells and A. K. Soper, Inst. Phys. Conf. Ser., 1990, 107, 193.
- A. K. Soper, Chem. Phys., 1996, 202, 295 CrossRef CAS; A. K. Soper, Chem. Phys., 2000, 258, 121 CrossRef CAS; A. K. Soper, Mol. Phys., 2001, 99, 1503 CrossRef CAS.
- M. S. Gordon, M. W. Schmidt, C. E. Dykstra, G. Frenking, K. S. Kim, and G. E. Scuseria (ed.), Theory and Applications of Computational Chemistry: the first forty years Advances in electronic structure theory: GAMESS a decade later Elsevier (Amsterdam), 2005, p. 1167 Search PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288 CrossRef CAS.
- J. N. Canongia Lopes and A. A. H. Padua, J. Phys. Chem. B, 2006, 110, 19586 CrossRef; J. N. Canongia Lopes, J. Deschamps and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 2038 CrossRef; J. N. Canongia Lopes, A. A. H. Padua and J. Deschamps, J. Phys. Chem. B, 2004, 108, 11250 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 110, 1657 Search PubMed.
- W. Smith, T. R. Forester, and I. T. Todorov, The DL_POLY_2.0 User Manual, Daresbury Laboratory, United Kingdom Search PubMed.
- M. Deetlefs, C. Hardacre, M. Nieuwenhuyzen, O. Sheppard and A. K. Soper, J. Phys. Chem. B, 2005, 109, 1593 CrossRef CAS.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, M. Nieuwenhuyzen, T. G. A. Youngs, D. T. Bowron and S. J. Teat, Phys. Chem. Chem. Phys., 2010, 12, 1842 RSC.
Footnote |
† Electronic supplementary information (ESI) available: Partial RDFs between individual glucose oxygen atoms and cation hydrogens, fully protiated NOESY NMR spectrum, centre-of-mass RDFs for different glucose loadings, and spatial distributions of anions around cations for pure ionic liquid and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic liquid 1 ionic liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose systems. See DOI: 10.1039/c1sc00241d glucose systems. See DOI: 10.1039/c1sc00241d |
| This journal is © The Royal Society of Chemistry 2011 |

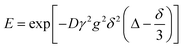
![Hydrogen numbering schemes used for [C2mim]+, [OAc]− and glucose in Fig. 4.](/image/article/2011/SC/c1sc00241d/c1sc00241d-f5.gif)