Symmetry related [Dy^III₆Mn^III₁₂] cores with different magnetic anisotropies

Abstract

Two heterometallic [Dy^III₆Mn^III₁₂] clusters comprising of the same [Mn^III₈O₁₃] fragment, four isolated Mn^III ions and two linear [Dy^III₃] units have been synthesised. Except for the same composition, the main difference of these two cores lies in the coordination environment and the orientations of the linear [Dy^III₃] units. This difference leads to an alternation in the symmetry of the two cores that significantly modulates their magnetic properties including ground spin state and slow relaxation behavior.

---

Since the first [Mn₁₂] cluster that exhibits slow relaxation of the magnetization was discovered in the 1990's,^1–4 considerable effort has been focused on exploring single-molecule magnets (SMMs).^5,6 These unique complexes require both a high spin ground-state (S_T) and an appreciable uniaxial magnetic anisotropy (D < 0), leading to an energy barrier between the bistable states that slows down magnetization reversal.^4,7,8 Although numerous SMMs have been reported, finding an SMM with both high ground spin-state and large magnetic anisotropy is still a challenge for synthetic chemists.

The importance of both factors for an SMM can be well illustrated by the example of the [Mn₁₉] complex,⁹ which holds a record ground spin state of S = ⁸³/₂, but fails to be an SMM because of the nearly absent magnetic anisotropy.^10,11 By deliberately replacing the central eight-coordinate Mn^II ion with the highly anisotropic Dy^III ion, slow relaxation of the magnetization was observed.¹² Another example of the significance of the magnetic anisotropy on the energy barrier of the SMMs is the large-spin (S = 37) molecule with an energy barrier of only 13 K due to the very small magnetic anisotropy.¹³

Inspired by the large magnetic anisotropy of the heavier lanthanides, great synthetic efforts have been devoted to, not only the pure 4f,^14–17 but also 3d–4f^12,18–23clusters in recent years. Although the magnetic interactions between the contracted 4f electrons are usually weak, the recently reported linear [Dy^III₃] and [Tb^III₃] complexes showed promising ferromagnetic coupling (up to J = +7.5 K) and thus, a high ground spin state.¹⁵ Besides the ground state the control of the magnetic anisotropy is also very important as can be seen in a triangular [Dy^III₃] molecule with non-collinearity of the principle axes.^16f,16g However, the intrinsic correlation between the spin-state and the magnetic anisotropy in these systems haven't been completely elucidated, which requires further exploration.

Herein we demonstrated two 3d–4f complexes by employing an extended in situ synthetic route we have isolated three new 3d–4fclusters (structures shown in Fig. 1), [Dy₆Mn₁₂O₇(OH)₁₀(OAc)₁₄(mpea)₈]·20H₂O·4MeOH (1) and [Ln₆Mn₁₂O₉(OH)₈(OAc)₁₀(mpea)₈(mp)₂(MeOH)₂(H₂O)₂]·solv (2. While Ln = Dy, solv = 26H₂O·2MeOH 2-Dy; Ln = Y, solv = 15H₂O·4MeOH 2-Y), where Hmp = 2-hydroxy-5-methyl-isophthalaldehyde and H₂mpea = 2-hydroxy-3-((2-hydroxy-ethylimino)methyl)-5-methylbenzaldehyde), with symmetry related [Ln^III₆Mn^III₁₂] cores. Interestingly, the two complexes 1-Dy and 2-Dy show different ground-state spins and slow magnetization behaviors, which may be influenced by the different symmetries of their cores (vide infra).

Fig. 1 a) Molecule structures of 1-Dy (left) and 2-Dy (right). b) The cluster cores of 1-Dy (left) and 2-Dy (right). Each Ln^III is highlighted as a green polyhedron and the Jahn–Teller axes of Mn^III ions are highlighted as blue sticks. Hydrogen atoms and lattice solvent molecules have been omitted for clarity.

After the Schiff-base was synthesized in situ, it was added to LnCl₃·6H₂O, Mn(OAc)₂·4H₂O, and triethylamine in different solvents. Complex 1 crystallizes in the orthorhombic space groupFddd while 2 is of lower symmetry and crystallizes in the triclinic P1̄ space group (see ESI†). As can be seen in Fig. 1, though isomeric, the [Ln^III₆Mn^III₁₂] cores possess D₂ site symmetry in 1 and C₁ symmetry in 2. All of the Mn and Ln ions in both compounds are trivalent, which are confirmed by bond-valence-sum (BVS) calculations (Table S1†),²⁴ charge considerations, and the observation of Jahn–Teller distortion around the Mn^III centers.

The cores can be described as being composed of five parts; ABCBA for 1 and AB′CB′′A for 2 (Figures S1 and S2†). Two isolated Mn^III ions capping a linear [Ln^III₃] trimer form fragment AB, while fragment C comprises a [Mn^III₈O₁₃] unit that contains a twisted [Mn^III₄O₅] tetragon that is capped by four Mn^III ions alternating above and below the tetragon with oxo-bridges. It should be mentioned that the central oxygen atom of [Mn^III₄O₅] acts as μ₄-oxo bridge binding the [Mn^III₄] unit in 1 and a μ₅-oxo bridge binding [Mn^III₄] and the central Ln^III ion of a [Ln^III₃] trimer in 2. The main symmetry differences between the two cores arise from the orientation of the [Ln^III₃] units which leads to differing orientations of the Jahn–Teller axes in the central twisted [Mn^III₄O₅] tetragon in 1 and 2.

The coordination environments and orientations of the two linear [Ln^III₃] units of 1 and 2 differ significantly. The coordination sphere of each Ln^III ion comprises only O atoms, presenting various types of coordination environments: (i) For 1, the central Ln^III of fragment B, [Ln^III₃O₆], is 8-coordinate, whereas both end-positions are 9-coordinate. The Ln^III polyhedra are all face-sharing within fragment B while the end polyhedra are vertex-sharing with the second B fragment in 1; (ii) For 2, the Ln^III ions in fragment B′, [Ln^III₃O₄], are all 8-coordinate edge-sharing polyhedra whereas fragment B′′, [Ln^III₃O₆], comprises three face-sharing 9-coordinate Ln^III polyhedra. In other words, two identical [Ln^III₃O₆] trimers link together with oxo-bridges to form a [Ln^III₆O₁₄] unit as a twisted hexagon in 1, while differing [Ln^III₃O₄] and [Ln^III₃O₆] timers remain magnetically separated from one another in 2. It is worth mentioning that the two [Ln^III₃] units are nearly parallel (∼11°) and perpendicular (∼83°) to one another in 1 and 2, respectively.

Dc magnetic susceptibility data were collected in the temperature range 1.8–300 K at 500 Oe (Fig. 2). At 300 K, the χ_MT values are 123.6 and 120.3 cm³ K mol⁻¹ for 1-Dy and 2-Dy, respectively, which are close to the expected value of 121.0 cm³ K mol⁻¹ for an uncoupled [Dy^III₆Mn^III₁₂] core (Dy^III: S = ⁵/₂, L = 5, ⁶H_15/2, g = ⁴/₃; Mn^III: S = 2, g = 2).^18,25 Upon lowering the temperature, the χ_MT value of 1-Dy remains roughly constant and then sharply increases to a maximum value of 409.5 cm³ K mol⁻¹ at 3.5 K, suggesting a high-spin ground state. The χ_MT value of 2-Dy first slightly decreases to 107.0 cm³ K mol⁻¹ at 23 K, then increases to a maximum of 117.9 cm³ K mol⁻¹ at 5 K and then lowers again sharply to 100.88 cm³ K mol⁻¹ at 2 K, which is likely attributed to competition between ferromagnetic and antiferromagnetic coupling and/or crystal field effects of Dy^III.^14a,26,27

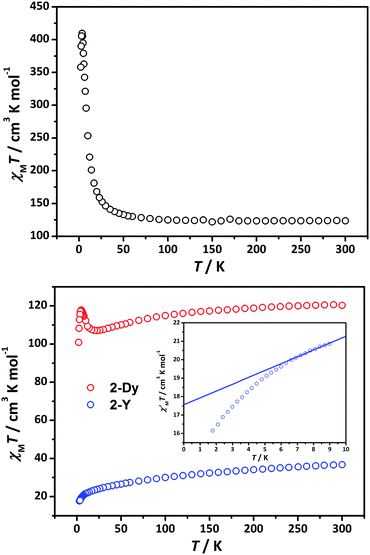Fig. 2 Temperature dependence of the χ_MT products at 500 Oe for 1-Dy (up), 2-Dy (bottom, red) and 2-Y (bottom, blue). Inset: The low-frequency χ_M′T data were extrapolated to 0 K for 2-Y.

Ac susceptibility measurements were carried out in a 5 Oe ac field oscillating at 1–1488 Hz, and with a zero dc field (Fig. 4, S3, S4†) in order to investigate the presence of SMM-like behavior.

An intriguing question is why the magnetic behaviour of 1-Dy and 2-Dy is so different (Fig. 2) despite common structural blocks. In order to further investigate the interactions of the spin carriers in 2, Y^III without spins are the candidate ions to replace the Dy^III ions, so we make a try to have a look at 2-Y. The decay of χ_MT data suggests the presence of an antiferromagnetic interaction between Mn⋯Mn. We can subtract the plot 2-Y from the plot 2-Dy (Figure S6†) to investigate the interactions between Ln⋯Ln and Ln⋯Mn. The resulting Δχ_MT values increase on low temperature, confirming the ferromagnetic interactions between Ln⋯Ln and/or Ln⋯Mn in 2-Dy. Going to the low-frequency (1 Hz) χ_M′T data extrapolated to 0 K for 2-Y (Fig. 2), the values of 17.7 cm³ K mol⁻¹ corresponds to an S = 3 [Mn^III₈O₁₃] unit (fragment C) and four uncoupled Mn^III (S = 2) ions as fragment A and C are magnetically separated by two [Y^III₃] units. Indeed, the S = 3 for the fragment [Mn^III₈O₁₃] in 2-Y is also apparently supported by the field-dependent magnetization measurement (Figure S5†), approaching a value of 22 μ_B at 7 T for 2-Y, which would be true in the case of four isotropic marginal Mn^III (S = 2) and an isotropic S = 3 for the central [Mn^III₈O₁₃].

However, the ab initio calculations of the four Mn^III fragments (see ESI† for details) reveal a zero-field splitting of the ground S = 2 of ca. 12 cm⁻¹. This relatively strong ionic anisotropy will induce the zero-field splitting of the ground term. Despite a much lower value of the supposed ground state spin (S = 3) compared to the maximal possible (S = 16) in this unit, the zero-field splitting of both these manifolds is expected to be of similar extent, as it was also the case in Mn₁₂ acetate complex.²⁸ Given their structural similarity, it is reasonable to suppose that the amplitude of zero-field splitting of the ground spin (S = 3) should be comparable to the latter compound, i.e. it cannot be ignored. As a result, the total molar magnetization at low temperature will be much lower than in the case of an isotropic spin. In conclusion, the total spin of the central fragment [Mn^III₈O₁₃] in 2-Yshould be larger than 3 but still lower than 8, in order to keep an overall antiferromagnetic coupling seen in susceptibility measurements.

This conclusion is also confirmed by the molar magnetization of 2-Dy which approaches 57 μ_B at fields of 7 T, a value higher than 52 μ_B corresponding to four isotropic Mn^III ions (4 × 4 = 16 μ_B), six Ising Dy(III) ions (6 × 5 = 30 μ_B) and an isotropic S = 3 (6 μ_B) of the central [Mn^III₈O₁₃] core. The difference is even larger if one takes into account the lowering of the magnetization due to zero-field splitting on marginal Mn^III ions and of the spin of the central [Mn^III₈O₁₃] core.

For the complex 1-Dy, the difference between the measured magnetization (71 μ_B) and the predicted one in the case of four Mn^III (4 × 4 = 16 μ_B), six Dy ions (6 × 5 = 30 μ_B) leads to a value of 25 μ_B, which clearly can only be expected in the case of predominantly ferromagnetic coupling (S > 8 total spin) of the [Mn^III₈O₁₃] core. This difference is, again, larger if one takes into account the lowering of the total magnetization due to the zero-field splitting, as discussed above.

The difference in the magnetic behavior between complexes 1-Dy and 2-Dy is therefore due to several factors: 1) the value of the spin of the [Mn^III₈O₁₃] central core is larger in 1-Dy compared to 2-Dy; 2) the orientations of the main anisotropy axes on Dy ions are different due to the structural arrangements of the [Dy^III₃] triades (see Tables S5 and S9†); 3) the exchange coupling between the [Dy^III₃] triades and the spin of the central [Mn^III₈O₁₃] core is ferromagnetic in 1-Dy and antiferromagnetic in 2-Dy. Note that whatever the sign of the exchange interaction between [Dy^III₃] triades and the central core, the arrangements of the total magnetic moments within each of [Dy^III₃] triades is ferromagnetic in both complexes.

The ab initio calculated²⁹ main anisotropy axes of the ground Kramers doublets on Dy sites in 1-Dy and 2-Dy are shown in Fig. 3 (see ESI† for computational details, energies local g tensors of the ground Kramers doublets on Dy sites and relative angles between main anisotropy axes in 1-Dy and 2-Dy).

Fig. 3 Local magnetic moments in the ground state on Dy ions of a) 1-Dy; b) 2-Dy. Dashed lines represent the local anisotropy axes, while the arrows show the orientation of the local magnetization.

Frequency-dependent out-of-phase (χ_M′′) signals in the ac susceptibility show that both complexes behave as SMMs but exhibit different slow relaxation of magnetization. For 1-Dy, one peak is observable at 3.7 K for 1488 Hz, while at 2.0 K for 2-Dy for 1488 Hz. A higher spin and the more colinear local anisotropy axes of 1-Dy are likely to enhance the blocking temperature (T_B) in contrast to 2-Dy. The ac susceptibilities, along with Cole-Cole plots showing quasi-semicircles and fitting Debye functions³⁰ for 1-Dy and 2-Dy (Figure S7, α₁ = 0.30–0.36, α₂ = 0.48–0.51†), indicate the presence of different distribution processes of slow relaxation. According to φ = (ΔT_p/T_p)/Δ(log f), the value of φ is, respectively, 0.14 for 1-Dy and 0.23 for 2-Dy (Figure S8†), suggesting a superparamagnetic-like behavior rather than spin glass behavior.³¹ Hence, the effective energy barriers (and characteristic relaxation time) can be obtained by fitting to the Arrhenius law giving Δ_eff/k_B = 35.1(5) K (τ₀ = 1.00 × 10⁻⁸ s) for 1-Dy and Δ_eff/k_B = 18.2(5) K (τ₀ = 3.02 × 10⁻⁸ s) for 2-Dy, respectively (insets of Fig. 4).

Fig. 4 Plots of ac susceptibility vs. temperature for 1-Dy (left) and 2-Dy (right) oscillating at 1–1488 Hz at H_ac = 5 G and H_dc = 0. Inset: The ln(τ)versus T⁻¹ plots obtained from χ_M′′(T) (△) and χ_M′′(ν) (○); The solid lines correspond to the Arrhenius law for 1-Dy (left) and 2-Dy (right).

However, no out-of-phase signals were observed under the resolution limit of the susceptometer above 1.8 K for 2-Y (Figure S4†). In terms of ac susceptibility, strong frequency-dependent signals were observed for 2-Dy while absent for 2-Y. We inferred it mainly originate from the [Dy^III₃] units. It is clear that introducing the highly anisotropic lanthanide ions into [Ln^III₆Mn^III₁₂] do play an important role, making it towards SMM.

In summary, we have generated two giant 3d–4fclusters with symmetry related [Dy^III₆Mn^III₁₂] cores which possess different molecular symmetry, resulting in different magnetic behaviors and energy barriers. For the high-symmetry one, the existing Dy^III ions do not only introduce large anisotropy but also enhances the ground-state simultaneously in this system. For the low-symmetry one, we successfully replace the anisotropic Dy^III with diamagnetic Y^III, confirming the ferromagnetic interaction of Dy⋯Dy and/or Dy⋯Mn and demonstrating the anisotropic lanthanide ions make it toward an SMM.

Acknowledgements

This work was supported by the NSFC (Grant No. 50872157, 90922009 and 20821001), the “973 Project” (2007CB815305), the Research Fund for the Doctoral Program of Higher Education (20100171110015) and the US NSF.

Notes and references

1. T. Lis, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2042.
2. P. D. W. Boyd, Q. Li, J. B. Vincent, K. Folting, H. R. Chang, W. E. Streib, J. C. Huffman, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1988, 110, 8537.
3. (a) A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141.
4. (a) R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804; (b) S. M. J. Aubin, Z. Sun, L. Pardi, J. Krzystek, K. Folting, L.-C. Brunel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329.
5. W. Wernsdorfer, Nat. Nanotechnol., 2009, 4, 145.
6. (a) K. Katoh, Y. Yoshida, M. Yamashita, H. Miyasaka, B. K. Breedlove, T. Kajiwara, S. Takaishi, N. Ishikawa, H. Isshiki, Y. F. Zhang, T. Komeda, M. Yamagishi and J. Takeya, J. Am. Chem. Soc., 2009, 131, 9967; (b) L. Margheriti, D. Chiappe, M. Mannini, P.-E. Car, P. Sainctavit, M.-A. Arrio, F. B. de Mongeot, J. C. Cezar, F. M. Piras, A. Magnani, E. Otero, A. Caneschi and R. Sessoli, Adv. Mater., 2010, 22, 5488; (c) W.-G. Wang, A.-J. Zhou, W.-X. Zhang, M.-L. Tong, X.-M. Chen, M. Nakano, C. C. Beedle and D. N. Hendrickson, J. Am. Chem. Soc., 2007, 129, 1014.
7. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789.
8. D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268.
9. A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926.
10. O. Waldmann, A. M. Ako, H. U. Güdel and A. K. Powell, Inorg. Chem., 2008, 47, 3486.
11. T. Glasera, I. Liratzis, A. M. Ako and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2296.
12. A. M. Ako, V. Mereacre, R. Clerac, W. Wernsdorfer, I. J. Hewitt, C. E. Anson and A. K. Powell, Chem. Commun., 2009, 544.
13. (a) E. E. Moushi, T. C. Stamatatos, W. Wernsdorfer, V. Nastopoulos, G. Christou and A. J. Tasiopoulos, Inorg. Chem., 2009, 48, 5049; (b) M. Atanasov, P. Comba and C. A. Daul, Inorg. Chem., 2008, 47, 2449; (c) S. A. Stoian, C. Paraschiv, N. Kiritsakas, F. Lloret, E. Münck, E. L. Bominaar and M. Andruh, Inorg. Chem., 2010, 49, 3387.
14. (a) P.-H. Lin, T. J. Burchell, R. Clérac and M. Murugesu, Angew. Chem., Int. Ed., 2008, 47, 8848; (b) M. T. Gamer, Y. Lan, P. W. Roesky, A. K. Powell and R. Clérac, Inorg. Chem., 2008, 47, 6581; (c) Y.-Z. Zheng, Y. Lan, C. E. Anson and A. K. Powell, Inorg. Chem., 2008, 47, 10813; (d) Y. Gao, G.-F. Xu, L. Zhao, J. Tang and Z. Liu, Inorg. Chem., 2009, 48, 11495.
15. (a) I. J. Hewitt, Y. Lan, C. E. Anson, J. Luzon, R. Sessoli and A. K. Powell, Chem. Commun., 2009, 6765; (b) F.-S. Guo, J.-L. Liu, J.-D. Leng, Z.-S. Meng, Z.-J. Lin, M.-L. Tong, S. Gao, L. Ungur and L. F. Chibotaru, Chem.–Eur. J., 2011, 17, 2458.
16. (a) B. Hussain, D. Savard, T. J. Burchell, W. Wernsdorferb and M. Murugesu, Chem. Commun., 2009, 1100; (b) P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489; (c) H. Ke, G.-F. Xu, L. Zhao, J. Tang, X.-Y. Zhang and H.-J. Zhang, Chem.–Eur. J., 2009, 15, 10335; (d) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538; (e) I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352; (f) J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729; (g) J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Phys. Rev. Lett., 2008, 100, 247205.
17. R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328.
18. C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369.
19. (a) A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 15648; (b) C. M. Zaleski, E. C. Depperman, J. W. Kampf, M. L. Kirk and V. L. Pecoraro, Angew. Chem., Int. Ed., 2004, 43, 3912; (c) A. Mishra, W. Wernsdorfer, S. Parsons, G. Christoua and E. K. Brechin, Chem. Commun., 2005, 2086; (d) V. Mereacre, A. M. Ako, R. Clérac, W. Wernsdorfer, G. Filoti, J. Bartolomé, C. E. Anson and A. K. Powell, J. Am. Chem. Soc., 2007, 129, 9248.
20. (a) V. Mereacre, A. M. Ako, R. Clérac, W. Wernsdorfer, I. J. Hewitt, C. E. Anson and A. K. Powell, Chem.–Eur. J., 2008, 14, 3577; (b) C. Papatriantafyllopoulou, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2011, 50, 421.
21. (a) N. Akhtar, Y.-Z. Zheng, Y. Lan, V. Mereacre, C. E. Anson and A. K. Powell, Inorg. Chem., 2009, 48, 3502; (b) A. M. Ako, V. Mereacre, R. Clérac, I. J. Hewitt, Y. Lan, G. Buth, C. E. Anson and A. K. Powell, Inorg. Chem., 2009, 48, 6713; (c) M. Andruh, J.-P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342; (d) J. Rinck, G. Novitchi, W. V. d. Heuvel, L. Ungur, Y. Lan, W. Wernsdorfer, C. E. Anson, L. F. Chibotaru and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 7583; (e) C. Papatriantafyllopoulou, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2011, 50, 421.
22. (a) G. Karotsis, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 9928; (b) G. Karotsis, S. Kennedy, S. J. Teat, C. M. Beavers, D. A. Fowler, J. J. Morales, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, J. Am. Chem. Soc., 2010, 132, 12983.
23. (a) C. Lampropoulos, T. C. Stamatatos, K. A. Abboud and G. Christou, Inorg. Chem., 2009, 48, 429; (b) T. Shiga, T. Onuki, T. Matsumoto, H. Nojiri, G. N. Newton, N. Hoshinoa and H. Oshio, Chem. Commun., 2009, 3568; (c) T. C. Stamatatos, S. J. Teat, W. Wernsdorfer and G. Christou, Angew. Chem., Int. Ed., 2009, 48, 521.
24. (a) I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244; (b) W. Liu and H. H. Thorp, Inorg. Chem., 1993, 32, 4102.
25. O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993.
26. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694.
27. J.-P. Sutter and M. L. Kahn, Magnetism: molecules to materials; Miller, J. S.; Drillon, M. ed.; Wiley-VCH: Weinheim, 2005; Vol. 5, pp 161–188.
28. O. Waldmann, Inorg. Chem., 2007, 46, 10035.
29. L. Chibotaru and L. Ungur. Computer programs SINGLE_ANISO and POLY_ANISO, University of Leuven, 2006.
30. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341.
31. J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor and Francis, London, 1993.

---

Footnote

† Electronic supplementary information (ESI) available: The ESI contains experimental details of the synthesis of 1-Dy, 2-Dy and 2-Y together with their X-ray structure determinations, magnetic susceptibility and ab initio calculations of the local magnetic properties on Dy sites in 1-Dy and 2-Dy. CCDC 779464 (1-Dy), 779465 (2-Dy), and 795483 (2-Y). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1sc00166c

---