A 58-electron superatom-complex model for the magic phosphine-protected gold clusters (Schmid-gold, Nanogold®) of 1.4-nm dimension

Abstract

We have re-investigated the structural identity of the famous gold-phosphine-halide Au:PR₃:X compound having 55–69 gold atoms and core size of 1.4 nm (similar to “Schmid gold” or Nanogold®) from the viewpoint of the Superatom-Complex (SAC) model for ligand protected metal clusters, and in consideration of the ligand-adatom groups observed previously for the structurally known 39-atom cluster [Au₃₉(PR₃)₁₄Cl₆]⁻¹. Density functional theory is used to define the formation energy of various compositions and structures, enabling a comparison of the stability of different cluster-sizes. In agreement with the SAC model, we find a strong correlation between optimal energy and delocalized electron shell closings: The 58 electron shell closing is a driving force behind the energetics. Of all compositions studied here, the energetically best one is [Au₆₉(PR₃)₂₀Cl₁₂]⁻¹ anion, which has a truncated decahedral 37-atom core encapsulated by 20 Au:PR₃ and 12 Au–Cl groups. It is energetically and chemically far superior to the standard models based on Au₅₅(PR₃)₁₂X₆. Critical comparisons are made to recent experiments (NMR and mass spectrometry).

---

Although known since ancient times, ligand protected small Gold particles experience currently a growing interest in particular if they are in the nanoscale regime. Their stability and tunable properties are promising for a wide variety of applications as functionalized nano-particles,¹ from building blocks for nanoscale electronics up to multivalent drug delivery.²Gold nanoparticles can be stabilized by different ligands and generally exhibit good chemical stability.³ In the case of phosphine⁴ and thiolate⁵ ligands, the preferential formation of certain “magic” clusters containing up to ca. 150 gold atoms is well known. The underlying reasons for this enhanced stability of particular sizes (and the instability of other sizes) have only recently become clear, mainly because of the work done on thiolate protected species. The well known phosphine stabilized “Schmid Au₅₅” cluster,⁶ originally formulated as Au₅₅(PPh₃)₁₂Cl₆,⁴ is one of the first and probably most utilized Gold nanoparticles. However, unlike its smaller homolog, [Au₃₉(PR₃)₁₄Cl₆]⁻¹,⁷ neither its definite composition nor its atomic structure have yet been determined.

In 2008 some of us proposed a unifying model that accounts for the special stability of structurally characterized ligand protected (both thiolates and phosphines) gold clusters in terms of their electronic properties.⁸ The magic stability of specific sizes was shown to be related to the appearance of shell closings of the delocalized electrons originating from the Au(6s) atomic orbitals. In this context the ligands play a key role. Each halogen or thiolate ligand effectively localizes one of the Au(6s) electrons in an energetically lower lying metal–ligand bonding orbital, making it in this way unavailable for the metallic subsystem. In most of the stable ligand-protected gold clusters that are known so far, the remaining metallic electrons in the clusters are able to close an angular momentum shell of delocalized orbitals. These orbitals are distributed over the entire gold-core of the cluster, which is therefore figuratively termed as “superatom complex” (SAC). Analogous to the atomic noble-gas configurations, the shell closings lead to chemical inertness and enhanced stability of the clusters. In contrast to halides and thiolates, the phosphine ligands do not localize Au electrons, affect the electronic structure only weakly, and mainly provide steric stabilisation. The application of this principle led to the correct prediction of the structure of the long sought and outstandingly stable Au₂₅(SR)₁₈⁻¹,⁹ which was solved experimentally just at the same time.¹⁰ The model applies even to gold-clusters doped with other transition metal atoms.¹¹ In the case of thiolates, the ligands are coordinated radially to atoms of the ‘metallic’ gold core but also bridge tangentially to Au ‘adatoms’. The halide ligands in ‘undecagold’¹² and [Au₃₉(PR₃)₁₄Cl₆]⁽⁻⁾⁷ are also coordinated radially to Au atoms, but in the larger complex these may be regarded as adatoms on a smaller (convex) core; similarly, the Au-PR₃ units are even clearer examples of ligand-adatom groups.

In the present work we apply the principles of the SAC model and the coordinative ligand-adatom group binding to the long-standing problem of the Schmid-gold compound.⁴ Similar cluster compounds (core-diameter of about 1.4 nm) are known commercially by the product name Nanogold®. The original structure assignment Au₅₅(PPh₃)₁₂Cl₆ was mainly guided by stoichiometry and the idea of an cubo-octahedral⁴ (later icosahedral or decahedral) gold core. Despite numerous experimental investigations of these clusters⁶ it has not been possible to obtain the precise mass or to obtain a crystal structure, however. There is some evidence that the original synthesis may lead to a mixture of different sizes.^13,14 Notably, an alternative synthesis by Weare et al.¹⁵ and Sharma et al.¹⁶ lead to assignments of average compositions of Au₁₀₁(PPh₃)₂₁Cl₅ and Au₉₉(PPh₃)₂₄Cl₁₂, respectively. In line with the observation of poly-sized clusters, mass spectroscopy of Au₅₅ cluster samples revealed three distinct peaks, suggesting the presence of three different sizes instead of only one.^17,18 None of the three sizes suggests the assumed structure assignment. This finding is contrasted by a recent matrix-assisted laser desorption ionisation study that seems to be consistent with the Au₅₅(PPh₃)₁₂Cl₆ model.¹⁹

Despite the experimental uncertainties the Au₅₅(PPh₃)₁₂Cl₆ model is used in numerous theoretical investigations^20,21 (see Fig. 1a for the model 1 used by Pei and co-workers²⁰). From the viewpoint of the superatom picture, a cluster composed of 55 gold atoms and 6 chlorines has nominally 49 metallic electrons. This number is far from any angular momentum shell closing.²² In addition, the cluster possesses an unpaired electron, which is a sign of a radical, hence the cluster should be very unstable chemically. From a structural viewpoint 55 atoms is a magic number for icosahedral, deacahedral and truncated octahedral clusters.²³ However, from gas-phase studies it is known that bare Au₅₅ clusters do not show geometric shell closures.²⁴ In general, geometric effects are expected to dominate for larger sizes, where the icosahedral 55 atom motive can indeed be found in the core of certain chemically stabilized metal clusters.²⁵ Here we perform a study of possible alternative structural motifs, guided by the SAC model and the principle of filling an angular momentum shell of 58 delocalized electrons in the gold core. We have found several candidate compositions and structures that show better energetics and improved chemical stability compared to Schmid's generic model Au₅₅(PPh₃)₁₂Cl₆. Fig. 1b) shows our energetically best structure: [Au₆₉(PR₃)₂₀Cl₁₂]⁻¹, to be discussed in detail later.

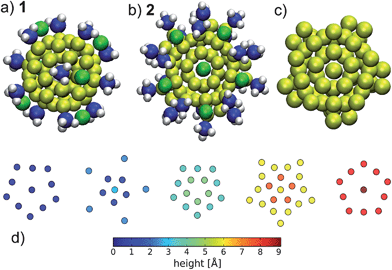Fig. 1 Structure of a) the Au₅₅(PH₃)₁₂Cl₆ literature model²⁰1 and b) our energetically best structure 2, Au: yellow, Cl: green, P: blue and H: white. The structure of the gold-core of 2 is shown in c) and it is shown as split into layers of different height perpendicular to the paper plane in d).

Even though the mass spectra observed by Fackler et al.¹⁷ were obtained under violent conditions leading to fragmentation of parent clusters, the data is useful for guiding thinking of construction of possible theoretical models and compositions for stable clusters that are larger than the generic Au₅₅. The three mass peaks reported in ref. 17 are located roughly at 8 kDa, 13 kDa and 18 kDa, and cannot be assigned to any known phosphine/halogen clusters, neither to the Teo-Zhang [Au₃₉(PPh₃)₁₄Cl₆]¹⁻ (11567 amu) nor to the generic Au₅₅(PPh₃)₁₂Cl₆ model (14193 amu). Interestingly, Fackler et al. assigned the two higher mass peaks to [Au₄₆(PPh₃)₁₂Cl₆] and [Au₆₇(PPh₃)₁₄Cl₈], respectively, corresponding to clusters of approximately 40 and 58 delocalized electrons in the Gold core. 40 and 58 electrons are both electron numbers of strong spherical shell closings.²² In this work, we concentrate on possible structures that provide a 58 delocalized electron shell closing. Note that this is the stabilising shell closing of the well known thiolate protected Au₁₀₂(p-MBA)₄₄.^8,26

We have constructed different models, where the basic building block consisted of the known approximately D_5h-symmetric Au₇₉ core of Au₁₀₂(p-MBA)₄₄, where the 10 surface gold atoms farthest from the symmetry axis where removed to obtain Au₆₉. From this structure further surface atoms can be removed to obtain Au₃₉ and by extracting the two capping Au atoms along the symmetry axis Au₃₇. Using these cores, Cl atoms, PH₃, AuCl, and/or AuPH₃ units where added to arrive at a structure with a theoretical 58 delocalized electron count in the SAC model. The structures constructed in this way are then relaxed to the nearest local energy minimum. The resulting structures are of different mass and composition and have fivefold symmetry by construction.

In order to compare the energetics of these clusters, we need a general measure of the cluster stability. In this respect, we compare the clusters' energy with that of a reservoir of its components. The reservoir consists of a piece of fcc bulk gold structure with the energy E_Au per gold atom together with an infinite reservoir of ligands (see supporting information (SI) for more detail). The reference for ligands is taken as the energies of stable gas-phase molecules PH₃ (E_PH3) and Cl₂ (E_Cl2). In case of negatively charged clusters (q<0), |q| of the chlorine energies are replaced by the energy of the atomic chlorine anion E_Cl. Using these values, we define the stabilisation energy as

withwhere N_Au, N_Cl, N_PH3 are the gold atom, chlorine atom and PH₃ group count, respectively [the charge q has to be taken in unit charges in (2)]. With these definitions we will find E_stab < 0 if the cluster production is endothermic with respect to bulk gold and the ligand reservoir, i.e. −E_stab gives the energetic cost to form the clusters.

We use density functional theory (DFT) to evaluate the energies and forces. The Kohn–Sham DFT calculations were performed with the program package GPAW.²⁷ It uses the projector augmented wave method²⁸ and represents the smooth wave functions on uniform real space grids. This approach provides a single convergence parameter, the grid-spacing, to control the accuracy of discretization. The exchange–correlation energy was approximated in a generalized gradient approximation (GGA) as proposed by Perdew, Burke and Ernzerhof (PBE).²⁹ The calculations were carefully tested on numerical convergence and the PBE energetics was found to be converged at a grid-spacing of 0.2 Å. All structures were geometry-optimized without any symmetry restriction and were considered to be relaxed if the residual forces fell below 0.05 eV Å⁻¹. The energetics was cross-checked using the meta-GGA functionals as proposed by Tao, Perdew, Staroverov and Scuseria (TPSS)³⁰ and as proposed by Zao and Thrular (M06-L)³¹ by a non-self consistent post-calculation using the PBE wave-functions and density. The meta-GGAs are known to give an improved description of the gold-gold interaction.³² A refinement of the grid-spacing to 0.18 Å was necessary for converged energetics in case of the meta-GGAs.

DFT calculations of such extended systems are challenging and therefore we were able to study only a limited number of candidate structures. Fig. 2 summarizes the masses, the HOMO–LUMO gaps and PBE energetics of all the structures considered in this work. The stabilisation energy for the best structures is found to be slightly positive, a result suggesting an energetic driving force for the formation of clusters out of the fcc bulk gold. This is an artefact of a too small cohesive energy of bulk gold in the PBE approximation and is corrected by the meta-GGAs as we will see below. We obtain a cohesive energy for bulk fcc of 3.03 eV, 3.26 eV and 3.58 eV for PBE, TPSS and M06-L respectively. The PBE value is in good agreement with the pseudopotential result of 3.15 eV³³ and the FLAPW value of 3.06 eV.³⁴ The PBE value is far too small compared to the experimental 3.81 eV³³ leading to the erroneous positive stabilisation energy.

Fig. 2 PBE stabilisation energy, HOMO–LUMO gaps and masses (corresponding to PPh₃ ligands) of the different structures considered. The compositions corresponding to the masses are given. The structures of the clusters are shown in the supporting information.†

Three structures are highlighted in the figure: 2 represents our energetically best structure [Au₆₉(PR₃)₂₀Cl₁₂]⁻¹ and 1 is the energetically best Au₅₅(PPh₃)₁₂Cl₆ model proposed by Pei et al.²⁰ In addition we have added a smaller cluster 3 [Au₆₉(PR₃)₁₅Cl₁₂]⁻¹ that offers good energetics for comparison (see SI for the structure of 3†). The differences in the stabilisation energies are not very large on absolute scale, but there is a clear gap of nearly 0.2 eV per gold atom between our best structure 2 and the generic Au₅₅ model 1. In fact, 1 represents one of the energetically most unfavourable structures of our set of clusters.

The mass in Fig. 2 is given corresponding to PPh₃ groups instead of the PH₃ ligands used in the calculation to enable a convenient comparison to the experimental mass spectra. In accordance with the SAC model, structure 2 not only shows the best energy, but also the largest HOMO–LUMO gap of all structures. Its mass could fit well to the high mass peak reported by Fackler et al.¹⁷ Generally, there is a correlation trend between a large gap and good energetics, but this relation is not definite. The generic model 1 shows a small gap even with a negative charge to avoid spin polarisation. As for 2, we also find a correlation between energetics and a large HOMO–LUMO gap for structure 3.

Table 1 shows the properties of 1–3 in more detail. The models are also compared to the experimentally known and fully characterized phosphine-halide stabilized clusters Au₁₁(PH₃)₇Cl₃¹² and [Au₃₉(PH₃)₁₄Cl₆]⁻¹.⁷ In contrast to PBE both MGGAs predict the gold bulk to be more stable than the clusters, i.e. the ligand protected clusters are only metastable forms. Varying the functional does not change the energetic ordering of the structures, however. The meaningfulness of E_stab is confirmed by the favourable values for the known clusters Au₁₁(PH₃)₇Cl₃ and [Au₃₉(PH₃)₁₄Cl₆]⁻¹. Interestingly, our best structure 2 appears to be energetically more favourable than the well-known [Au₃₉(PH₃)₁₄Cl₆]⁻¹. Table 1 again emphasises the small HOMO–LUMO gap as well as unfavourable energy of Schmid's generic structure 1.

Table 1 Structure, E_stab for PBE, TPSS, M06-L and the PBE HOMO–LUMO gap. The structures are characterized by N_Au, N_PH3, N_Cl, q. All values are given in eV (1 eV = 23.06 kcal mol⁻¹)

Structure NAu, NPH3, NCl, q	Gap	PBE	TPSS	M06-L
2 69,20,12,-1	0.60	0.01	−0.13	−0.21
3 69,15,12,-1	0.40	−0.06	−0.19	−0.3
1 55,12,6,-1	0.15	−0.18	−0.29	−0.37
39,14,6,-1	0.84	−0.03	−0.18	−0.32
11,7,3,0	2.02	0.14	−0.06	−0.23

---

We now want to describe further details of the structure 2. As shown in Fig. 1b), the cluster is of C₅ symmetry where the 10 peripheral AuPR₃ units arrange themselves in a propeller-like chiral conformation. The remainder, as defined via the removal of these 10 units, has additional mirror planes and C_5v symmetry. The gold-only substructure is shown in Fig. 1c) and is sectioned into layers along the 5-fold symmetry axis in Fig. 1d). Top and bottom layers each consist of Au₁₀ rings with an central Au-atom pointing slightly out of the cluster. All 12 Cl-atoms are coordinated to these axial atoms and to the inwardly displaced atoms of the Au₁₀ rings. The outer atoms of the rings are protected by the remaining 10 PR₃ units. The other layers could be sectioned with increasing height in 5 + [5 + 1] + 10 + 5 + 10 + [5 + 1] + 5 atom Au planes as depicted in Fig. 1d). There is no horizontal reflection plane and every attempt to force this symmetry leads to more unstable configurations. The inner Au₃₇ core (obtained after removing all AuPR₃ and AuCl units) closely resembles the structure of the second most stable Ni₃₉ cluster by Wetzel and DePristo³⁵ (see also ESI†) and thus differs from the core of Au₁₀₂(p-MBA)₄₄.²⁶

The applicability of the SAC model to this cluster can be further confirmed by a projection of the Kohn–Sham states on angular momentum eigenfunctions of the cluster as a whole.³² Here a “good” superatom shows a closing of a shell of similar angular momentum states around Fermi energy. Indeed, we have shown previously that the structurally known Au₁₁(PR₃)₇Cl₃ and [Au₃₉(PR₃)₁₄Cl₆]⁻¹ clusters fulfil closing of the angular momentum shells for 8 and 34 electrons, respectively.⁸ For the 58 electron shell closing relevant here, we expect the delocalized electron configuration 1S²1P⁶1D¹⁰2S²1F¹⁴2P⁶1G¹⁸ resulting in G symmetry for the occupied and H symmetry for the unoccupied states around the Fermi energy.²² We have performed this analysis for structures 1 and 2 as shown in Fig. 3. Due to near spherical symmetry of the icosahedral Au₅₅ core, the generic model 1 shows a clear development of the delocalized shells. The number of delocalized electrons leads to HOMO and LUMO levels that are in the middle of the 2P/1G shell, however. This explains the small HOMO–LUMO gap of this structure. Inspection of the angular momentum projected density of states of cluster 2 provides a qualitative explanation of the enhanced stability of this cluster. Indeed the HOMO states show pronounced 2P/1G symmetry and the LUMO states have 2D/1H symmetry as expected. There is some admixture of G symmetry also in these states however, most probably because of the non-spherical gold core in 2.

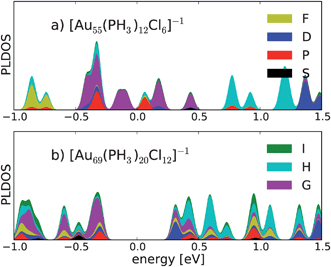Fig. 3 Angular momentum expansion of the Kohn–Sham states around Fermi energy (set to 0 eV) for the structures a) 1 and b) 2. The states are broadened by Gaussians of 0.03 eV width.

There are no decisive experimental electronic spectra of the Au₅₅ clusters in the literature. The reported optical spectra are featureless¹⁵ and the voltammetry yields no distinct peaks.¹⁴ The only featured data are powder XRD spectra. We compare the simulated powder XRD patterns³⁶ of the clusters 1 and 2 with available experimental data in Fig. 4. To our knowledge, there are two publications^13,37 reporting XRD data in the literature. Both experiments used similar X-ray frequencies so that the data can be superimposed in a single plot. Both structures 1 and 2 show qualitative agreement to experiment and none can be excluded simply because of this data. One has to note that the experimental samples used might represent mixtures of different sized clusters, however. The observed XDR are presumably the average over a distribution of sizes.

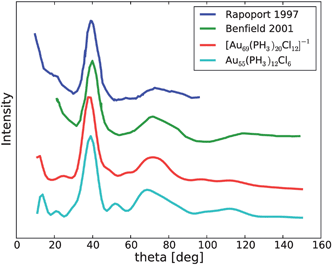Fig. 4 Simulation of the XRD signal in comparison with experiment. The experimental curves were extracted from Benfield et al.³⁷ and Rapoport et al.¹³

We finally note, that recent experimental investigations on 1.4-nm gold-phosphine clusters can also be interpreted in a manner consistent with the structure-model 2. Weare et al.¹⁵ reported an average composition of 100 : 21 : 5 (Au:P:halide) for a sample incorporating also clusters larger than 1.4 nm and an improved characterization by Sharma et al.¹⁶ of a similarly prepared sample gave a composition of 100 : 24 : 12 (Au:P:total halide). Both are quite close to the 69 : 20 : 12, considering again the presence of a minor fraction of larger (therefore Au-rich) clusters. Finally, Schaaff³⁸ described the electrospray ionization (ESI†) of size-purified sample of Nanogold® that showed a well defined strong peak at a mass of 14,7-kDa. This mass suggests a minimal fragmentation-resistant compound [Au₅₇(PR₃)₈]⁻¹ that would be consistent with an [Au₆₉(PR₃)₂₀Cl₁₂]⁻¹ that had lost 12 Au(PR₃)Cl units³⁶ (see also ESI for a more detailed discussion†).

In conclusion, we have provided an entirely new analysis, based on the general principles of the SAC model and the precedent of specific ligand-adatom structural groups, to account for the special stability and associated properties of the ubiquitous Schmid and Nanogold clusters, which have thus far resisted crystallographic structure-determination. We have shown that the stabilisation energy is a useful quantity to compare structures of different sizes and compositions. Clusters constructed to fulfil the 58 delocalized electron shell closing provide better stabilisation energy paired with better chemical stability (indicated by large HOMO–LUMO gaps) than Schmid's generic model. Naturally, there is huge variety of possible structures that fulfil the 58 electron shell closing. The available experimental data is far too scarce to provide a hard restriction on size or composition of the clusters. The demanding computational effort allowed only to test a limited amount of structures here. Nevertheless, the clearly improved energetics lets us believe that the structures found here are of more relevance for the experimental conditions than the generic Au₅₅ model used in the literature.

This work was carried out under the HPC-EUROPA2 project (project number: 228398), with the support of the European Community – Research Infrastructure Action of the FP7. M.W. thanks CSC/Espoo and RZ Karlsruhe for the computational resources, and Univ. of Jyväskylä for the hospitality. We thank O. Lopez-Acevedo for providing a modified version of the Au₃₇ core. Funding by the Deutsche Forschungsgemeinschaft and the Academy of Finland Distinguished Professor program is gratefully acknowledged.

Notes and references

1. M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293.
2. M.-C. Bowman, T. E. Ballard, C. J. Ackerson, D. L. Feldheim, D. M. Margolis and C. Melander, J. Am. Chem. Soc., 2008, 130, 6896.
3. M. Homberger and U. Simon, Philos. Trans. R. Soc. London, Ser. A, 2010, 368, 1405.
4. G. Schmid, R. Boese, R. Pfeil, F. Bandermann, S. Mayer, G. H. M. Calis and J. W. A. van der Velden, Chem. Ber., 1981, 114, 3634.
5. T. G. Schaaff, M. N. Shafigullin, J. T. Khoury, I. Vezmar, R. L. Whetten, W. G. Cullen, P. N. First, C. Gutierrez-Wing, J. Ascensio and M. J. Jose-Yacaman, J. Phys. Chem. B, 1997, 101, 7885.
6. G. Schmid, Chem. Soc. Rev., 2008, 37, 1909.
7. B. K. Teo, Xiaobo Shi and Hong Zhang, J. Am. Chem. Soc., 1992, 114, 2743.
8. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157; H. Häkkinen, Chem. Soc. Rev., 2008, 37, 1847.
9. J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756.
10. M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754.
11. D. Jiang and S. Dai, Inorg. Chem., 2009, 48, 2720; K. A. Kacprzak, L. Lehtovaara, J. Akola, O. Lopez-Acevedo and H. Häkkinen, Phys. Chem. Chem. Phys., 2009, 11, 7123; M. Walter and M. Moseler, J. Phys. Chem. C, 2009, 113, 15834.
12. D. M. P. Mingos, J. Chem. Soc., Dalton Trans., 1996, 561.
13. W. Vogel, W. Rosner and B. Tesche, J. Phys. Chem., 1993, 97, 11611; D. H. Rapoport, W. Vogel, H. Colfen and R. Schlögl, J. Phys. Chem. B, 1997, 101, 4175.
14. R. Balasubramanian, R. Guo, A. J. Mills and Royce W. Murray, J. Am. Chem. Soc., 2005, 127, 8126.
15. W. W. Weare, S. M. Reed, M. G. Warner and J. E. Hutchison, J. Am. Chem. Soc., 2000, 122, 12890.
16. R. Sharma, G. P. Holland, V. C. Solomon, H. Zimmermann, S. Schiffenhaus, S. A. Amin, D. A. Buttry and J. L. Yarger, J. Phys. Chem. C, 2009, 113, 16387.
17. J. P. Fackler Jr., C. J. McNeal, L. H. Pignolet and R. E. P. Winpenny, J. Am. Chem. Soc., 1989, 111, 6434.
18. E. Gutierrez, R. D. Powell, F. R. Furuya, J. F. Hainfeld, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Eur. Phys. J. D, 1999, 9, 647.
19. W. Chen and S. Chen, Angew. Chem., Int. Ed., 2009, 48, 4386.
20. Y. Pei, N. Shao, Y. Gao and X. C. Zeng, ACS Nano, 2010, 4, 2009.
21. A. Genest, S. Krüger and N. Rösch, Z. Naturforsch., 2009, 64b, 1246; G. Periyasamy and F. Remacle, Nano Lett., 2009, 9, 3007.
22. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611.
23. F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371.
24. H. Häkkinen, M. Moseler, O. Kostko, N. Morgner, M. Astruc Hoffman and B. von Issendorff, Phys. Rev. Lett., 2004, 93, 093401.
25. O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Grönbeck and H. Häkkinen, J. Phys. Chem. C, 2009, 113, 5035; N. T. Tran, D. R. Powell and L. F. Dahl, Angew. Chem., Int. Ed., 2000, 39, 4121.
26. P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430.
27. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109; J. Enkovaara, et al. , J. Phys.: Condens. Matter, 2010, 22, 253202.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
30. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
31. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
32. L. Ferrighi, B. Hammer and G. K. H. Madsen, J. Am. Chem. Soc., 2009, 131, 10605.
33. H. Grönbeck, A. Curioni and W. Andreoni, J. Am. Chem. Soc., 2000, 122, 3839.
34. T. Hayashi, Y. Morikawa and H. Nozoye, J. Chem. Phys., 2001, 114, 7615.
35. T. L. Wetzel and A. E. DePristo, J. Chem. Phys., 1996, 105, 572; E. K. Parks, K. P. Kerns and S. J. Riley, J. Chem. Phys., 1998, 109, 10207.
36. T. Iwasa and K. Nobusada, J. Phys. Chem. C, 2007, 111, 45.
37. R. E. Benfield, D. Grandjean, M. Kroll, R. Pugin, T. Sawitowski and G. Schmid, J. Phys. Chem. B, 2001, 105, 1961.
38. T. G. Schaaff, private communication.

---

Footnote

† Electronic supplementary information (ESI) available: Further remarks to the definition of the stabilisation energy and critical comparison to experiments, pictorial presentations of the Au₃₇ core of 2, coordinates of structures 2 and 3 and figures of all considered clusters shown in Fig. 2 and Table 1. See DOI: 10.1039/c1sc00060h

---