Heavy water hydration of mannose: the anomeric effect in solvation, laid bare

Abstract

The presence and consequences of the anomeric effect have been explored and directly exposed, through an investigation of the vibrational spectroscopy of the doubly and triply hydrated α and β anomers of phenylD-mannopyranoside, (PhMan) isolated under molecular beam conditions in the gas phase. The experiments have been aided by the simple trick of substituting D₂O for H₂O, which has the advantage of isotopically isolating the carbohydrate (OH) bands from the water (OD) bands. Recording the double resonance, IR-UV ion dip spectra of the hydrated complexes, α- and β-PhMan·(D₂O)_2,3 in a series of ‘proof of principle’ experiments, revealed that these heavy water molecules engage the key endocyclic oxygen atom, O5, allowing the anomeric effect to be probed through a combination of vibrational spectroscopy and quantum chemical calculations. Importantly, in the dihydrates, both anomers adopt the same conformation and the two water molecules occupy the same template. One of them acts as a remarkably sensitive reporter, able to sense and expose subtle stereoelectronic changes through the resulting changes in its hydrogen-bonded interaction with the substrate.

---

Introduction

The anomeric effect was first identified more than fifty years ago.¹ Since then it has become a text-book example of the influence of stereoelectronic factors on molecular, and biomolecular conformational landscapes.^1–6 The effect was initially associated with the stabilization of chair-form pyranose sugars when they have an axially oriented electronegative substituent at C1 (the endo-anomeric effect) but in its generalized interpretation, it can be extended to include both cyclic and acyclic molecules, in particular those containing the motifR-X-CH₂-Z, where Z is an electronegative atom and X is, typically, an O or S atom.⁷ Despite its long history however, its origins have continued to excite prolonged debate,^1,2,7–11 not least because of the difficulty of separating stereoelectronic effects from other potential influences including steric, electrostatic and hydrogen-bonded interactions, and solvation.

The great majority of measurements of the effect have necessarily been conducted in the condensed phase, unlike many calculations conducted in a ‘virtual’ gas phase environment. Separating the plethora of secondary factors which may modulate anomeric effects, particularly solvation, from those associated with intrinsic, particularly stereoelectronic factors, presents a major experimental challenge. To begin to address that challenge, the first essential requirement is knowledge of the conformational structures of the isolated anomers, i.e., those they can access when the solvent environment is stripped away. This can be achieved by transferring them into the gas phase through laser evaporation from the solid state into an expanding molecular beam, followed by their interrogation through conformer-selected, resonant two photon ionization (R2PI) spectroscopy. Subsequent double resonance, infrared-ultraviolet (IR-UV) spectroscopy, using the “ion-dip” technique,^12,13 provides their characteristic vibrational signatures, which can be interpreted and assigned through comparisons with simulations based upon a combination of molecular mechanics, density functional theory (DFT) and ab initio calculations.¹⁴ The comparisons lead to structural assignments and also identify the primary interactions within the isolated carbohydrate molecules that govern their intrinsic structural architectures.^14,15

Similar methods can then be used to probe their secondary interactions with neighbouring molecules, for example through the interrogation of ‘custom-made’ hydrated complexes of known stoichiometry, created and stabilized in seeded molecular beams under controlled conditions.¹⁶ The OH vibrational signatures of the carbohydrate and the bound water molecules, which are extremely sensitive to inter- and intra-molecular hydrogen-bonded interactions, can be thus recorded following appropriate mass selection. Likewise, in combination with theory, their vibrational spectroscopic signatures can be converted into conformational and intermolecular structures to reveal the interactions which sustain them.^17–19

This strategy has already proved to be highly successful in identifying a set of working rules governing the conformational preferences and regioselective binding in a representative series of singly hydrated monosaccharides,^18,19 but it does have a number of experimental limitations. These become increasingly apparent when the strategy is applied to multiply hydrated carbohydrates, since a rise in the number of bound water molecules necessarily increases the (already large) number of OH groups, and the OH vibrational spectra become increasingly congested and poorly resolved. Strong hydrogen bonded-interactions can further exacerbate the problem since they broaden the spectral widths of the associated OH vibrational bands, placing a further limitation on the attainable spectral resolution. When the core carbohydrate is an oligosaccharide the problem increases still further.

We describe here, a way of alleviating this problem and at the same time, facilitating the exploration of the anomeric effect in hydrated saccharides, isolated in the gas phase, simply by substituting D₂O (‘heavy’ water) for H₂O. The isotopic substitution conveniently separates the (OH) vibrational spectrum associated with the carbohydrate, lying in the range 3300–3700 cm⁻¹, from the (OD) vibrational spectrum associated with its hydration shell, lying in the range 2400–2800 cm⁻¹. This greatly reduces the incidence of spectral congestion and also provides additional data against which the reliability of previous spectral and structural assignments can be tested. Since the hydrated complexes are generated in the gas phase under molecular beam conditions there is no H/D isotope exchange.

The present work, which exploits this approach, begins with an initial set of ‘proof of principle’ experiments before leading into the central aim, to probe the anomeric effect in an isolated hydrated monosaccharide through a combination of experiment and theory. This goal combines two notable aspects. Firstly, determination of the anomeric effect at this first step of solvation and, secondly, by using the solvent itself as a probe, to report simultaneously on the effect and its role during (micro)solvation. The initial experiments provide qualitative comparisons between the vibrational (and R2PI) spectra of the α- and β-anomers of phenylD-mannopyranoside (Scheme 1) and their single, double and triple hydrates. (The phenyl ‘tag’, which is structurally benign,¹⁵ is needed to provide the UV chromophore required to exploit the infrared ion-dip detection technique). These provide a prelude to a detailed quantitative analysis of the vibrational spectra and conformational structures of the doubly hydrated anomers, α- and β-PhMan·(D₂O)₂. This choice was not an arbitrary one since earlier investigations¹⁸ of the doubly hydrated anomer, β-PhMan·(H₂O)₂, had already revealed a particularly stable and in the present context, apposite structure, shown in Fig. 1. The two water molecules occupy separate sites: one inserted between the OH4 and OH6 groups, the other between OH6 and the (axially oriented) OH2 group, which, crucially, locates it above O5 and close to the sites relevant to the anomeric effect. This second water molecule, (W2, in Fig. 1) acts as an extraordinarily sensitive reporter, able to sense subtle stereoelectronic changes associated with anomeric effects⁶ and to reveal them through their influence on the local OH vibrational signatures.

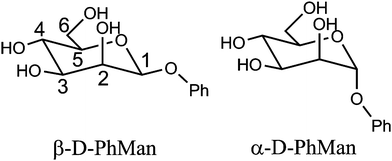Scheme 1 Molecular structures of phenyl α- and β-D-mannopyranoside.

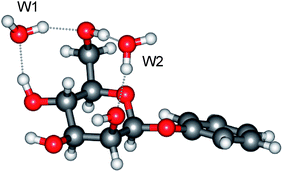Fig. 1 Molecular structure of the di-hydrate, β-PhMan·(H₂O)₂.

Results and discussion

Hydration with D₂O: a broad overview

Fig. 2 displays the mass-selected R2PI spectra of the hydrated saccharides, α- and β-PhMan·(D₂O)_0-3, recorded in each of their parent ion mass channels. The spectra are quite distinct and only one of them shows any evidence of cluster ion fragmentation: the R2PI spectrum of the β-di-hydrate also appears strongly in the singly hydrated ion channel but, intriguingly, this does not occur in the corresponding α-di-hydrate.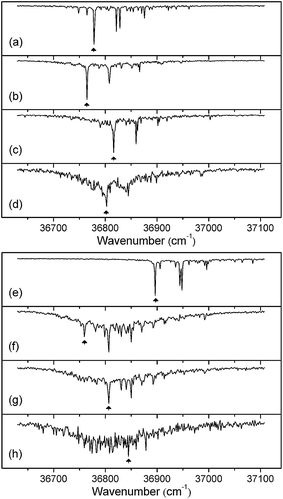

Fig. 2 R2PI spectra of the α (a–d) and β (e–h) anomers of phenylD-mannopyranoside. (a,e), the bare anomers; (b,f), (c,g) and (d,h), the mono-, di- and tri-hydrated complexes, α/β-PhMan·(D₂O)_1,2,3. The arrows indicate bands selected in recording the complementary IR-UV double resonance spectra presented in Fig. 3 and 4.

The full set of IR-UV ion-dip spectra are shown in Fig. 3 and 4, where they can be compared with the calculated vibrational spectra associated with their lowest energy conformations. There is no evidence of any IR absorption at ∼3740 cm⁻¹, where ‘free’ OH band(s) associated with the corresponding H₂O complexes, would appear, confirming the absence of any observable isotopic exchange between carbohydrate hydroxyls and D₂O.

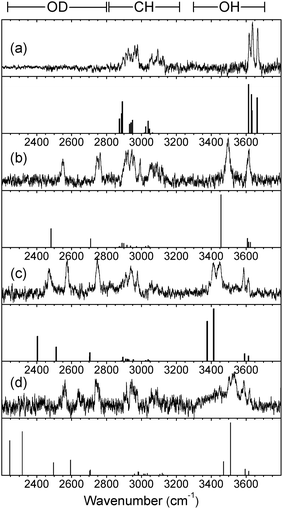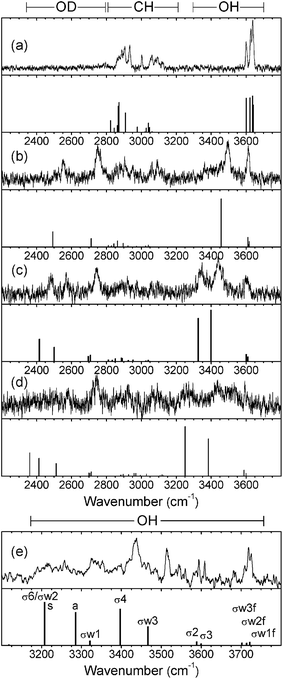
Fig. 3 Experimental IRID spectra of (a), phenyl α-D-mannopyranoside and (b,c,d), its hydrated clusters, α-PhMan·(D₂O)_1,2,3 recorded with the UV probe set on the bands identified by the arrows in Fig. 2(a–d). The calculated vibrational (stick) spectra are those associated with their lowest energy structures. (Note: the IRID signals are strongly attenuated at wavenumbers <2450 cm⁻¹ where the IR laser intensity falls away steeply).

Fig. 4 Experimental IRID spectra of (a), phenyl β-D-mannopyranoside; (b,c,d), its hydrated clusters, β-PhMan·(D₂O)_1,2,3 recorded with the UV probe set on the bands identified by the arrows in Fig. 2(e–h); and (e) β-PhMan·(H₂O)₃ reported earlier.¹⁷ The calculated vibrational (stick) spectra are those associated with their lowest energy structures. (Note: the IRID signals are strongly attenuated at wavenumbers <2450 cm⁻¹ where the IR laser intensity falls away steeply).

The R2PI spectra of the mono-hydrates, α/β-PhMan·(D₂O)₁, Fig. 2b and 2f, are identical to those reported earlier for the corresponding complex with H₂O.^18,19 Their IRID spectra, Fig. 3b and 4b, reflect the isotopic substitution and confirm the earlier assignments^18,19 of the lowest energy (H₂O)₁ hydrates to the insertion structure, cG-g +ins(4,6).‡ The bound and free OD modes of the D₂O molecule, inserted between OH4 and OH6, are associated with the two bands centred at ∼2540 cm⁻¹ and ∼2740 cm⁻¹; the strong band at ∼3500 cm⁻¹ in the carbohydrate region, is associated with OH4, and the remaining feature, centred at ∼3610 cm⁻¹, is an unresolved composite of the three overlapping ‘spectator’ bands OH2,3, and 6.

The insertion of additional D₂O molecules is reflected in the pattern and increasing number of OD bands. The ‘bound’ OD bands, displaced towards lower wavenumbers, increase to two in each of the di-hydrates, at ∼2470 cm⁻¹ and ∼2580 cm⁻¹ (Fig. 3c and 4c) and in the α-tri-hydrate, three bands are clearly resolved, at ∼2560 cm⁻¹, ∼2630 cm⁻¹ and ∼2760 cm⁻¹ (Fig. 3d and 4d). The free OD features remain at ∼2740 cm⁻¹ though they must now accommodate two, or three, overlapping bands. In the α-di-hydrate, α-PhMan·(D₂O)₂, the four carbohydrate OH bands, Fig. 3c, separate into two pairs, associated with the ‘spectator’ groups OH2 at ∼3590 cm⁻¹ and OH3 at ∼3610 cm⁻¹, and the hydrogen bonded groups, OH6 ∼3410 cm⁻¹ and OH4, at ∼3450 cm⁻¹. The complete OH/OD spectrum closely resembles the computed vibrational spectrum associated with the lowest energy structure, cG-g+.ins(4,6;6,2) shown in Fig. 5. The same is true for the corresponding β-dihydrate, β-PhMan·(D₂O)₂, although their spacings are not the same as those in the α-dihydrate—betraying a crucial difference, as will be seen below.

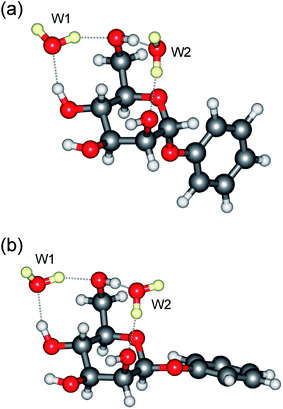Fig. 5 Molecular structure of the di-hydrates: (a) α-PhMan·(D₂O)₂ and (b) β-PhMan·(D₂O)₂.

The IRID spectra of the tri-hydrates, α- and β-PhMan·(D₂O)₃, also differ; unfortunately, the latter spectrum, shown in Fig. 4d, is poorly resolved but a better quality spectrum, recorded earlier¹⁷ for the complex with H₂O, is reproduced in Fig. 4e. Its principal features are in good accord with the vibrational spectrum¹⁷ associated with the lowest energy computed structure, cG-g +.ins[4,6;(6,2:6,2)]. It incorporates a single bound water molecule inserted into the 4,6 site and a bridging water dimer linking OH6 and O2, to create the cyclic hydrogen bonded sequence, OH4 → W1 → OH6 → W2 → W3 → OH2 → OH3 → OH4 shown in Fig. 6b. In the α-complex, however, the corresponding structure is predicted to lie at an energy 6.1 kJ mol⁻¹ above the global minimum, and the most favoured structure now incorporates a water trimer, bound into a branched hydrogen bonded network, shown in Fig. 6a. The vibrational spectrum associated with this structure is in reasonable accord with the experimental IRID spectrum presented in Fig. 3d. In each case the hydration ‘crown’ is located above the hydrophilic face of the host carbohydrate, D-mannose.

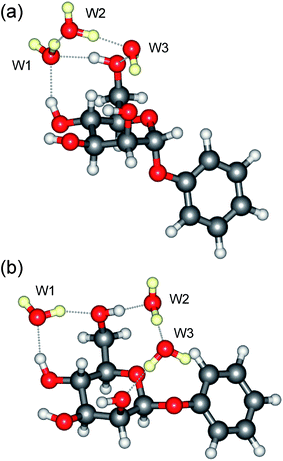Fig. 6 Molecular structure of the tri-hydrates: (a), α-PhMan·(D₂O)₃ and (b), β-PhMan·(D₂O)₃.

Comparisons between the experimental spectra and those associated with the six lowest energy structures of α-PhMan·(D₂O)_2,3 are included as Electronic Supplementary Information.†

The anomeric effect in phenyl α- and β-D-mannopyranoside

As noted above, although the patterns of the OH and OD bands in the two di-hydrates, α- and β-PhMan·(D₂O)₂, are very similar, reflecting their similar structures, there are also clear differences in the relative positions of the OH bands, which suggest some subtle structural variations. Their OH spectra are highlighted in Fig. 7.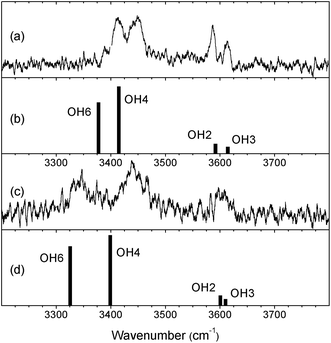

Fig. 7 The experimental and calculated OH vibrational spectra of (a,b) the α and (c,d) the β anomers of PhMan·(D₂O)₂.

The change from α to β results in a small relative displacement of the OH4 band, ∼10 cm⁻¹ towards lower wavenumber, and a much larger displacement, ∼65 cm⁻¹, in the OH6 band. Evidently, in the β-complex, there is a stronger H-bonded interaction between OH6 and the water molecule (W2) inserted between OH6 and O2, suggesting a re-positioning of W2. There is also a subtle change in the relative spacing of the OH2 and OH3 bands; although they lie near to the closely spaced doublet in the α-complex, they are no longer separately resolved.

This manifestation of key bonding changes seen in the gas phase for two structurally similar anomer complexes, closely resembles that observed in a recent investigation¹⁹ of methylD-galactopyranoside (where OH4 is axial, rather than OH2) in the gas phase: the interaction of its α and β anomers with N-acetylphenylalanine methyl amide (acting as a ‘sensor’) revealed a relative increase in the ‘lone pair’ electron density on O5 in the β-anomer. A similar relative increase in electron density in the β anomer of the mannopyranoside, would enhance the ‘lone pair’ repulsion between O5 and the oxygen in the bound water molecule, W2, located directly above it and generate a modified hydrate structure.

Comparing the experimental observations with the results of the DFT, B3LYP/6-311++G(d,p) calculations provides very strong evidence in support of this suggestion. The computed OH vibrational spectra (Fig. 7) associated with the minimum energy structures of the two anomer complexes (Fig. 1 and 5) reproduce both the relative shifts and the enhanced separation of the OH4 and OH6 bands in the β di-hydrate, and even the slight displacement and poorer resolution of the OH2 and OH3 bands. Additionally, while the broad cG-g+.ins(4,6; 6,2) structure is retained in going from the α to the β anomer, the calculations (Table 1) predict a large increase, 0.076 Å, in the O5–O(W2) separation. (This is also accompanied by a reorientation of the bound water molecule, W2: compare the orientations of its ‘free’ OD group, shown in Fig. 1 and Fig. 5).

Table 1 Calculated inter- and intramolecular bond distances (Å) in α- and β-PhMan·(D₂O)₂

Bond	α	β	δ(α → β)	Comments: β relative to α
OH4⋯W1	1.858	1.838	−0.020	Small increase in H-bonding
W1⋯OH6	1.785	1.796	+0.011	Slight decrease in H-bonding
OH6⋯W2	1.859	1.838	−0.021	W2 moves closer to OH6
W2⋯OH2	1.968	1.940	−0.028	W2 also moves closer to OH2
O5⋯O(W2)	3.016	3.092	+0.076	W2 pushed away from O5
C1–O5	1.403	1.416	+0.013	n(O1)→σ*(C1–O5): exo – small increase
C1–O1	1.417	1.395	-0.022	n(O5)→σ*(C1–O1): endo - larger decrease

---

The calculations (based on experimental spectroscopic data) also indicate a small increase, +0.013 Å, in the inter-atomic distance between the anomeric site, C1, and O5 in the pyranose ring, and a larger, 0.022 Å relative reduction in the C1–O1 distance. These changes are exactly those that would be anticipated if there were an enhanced exo-anomeric effect, associated with n(O1) → σ*(C1–O5) hyperconjugation, and a (more strongly) reduced endo-anomeric effect, n(O5) → σ*(C1–O1)), in going from the α to the β anomer. They would result in a relatively larger electron density on O5 in the β anomer – a result which is further supported by the natural bond order (NBO) analysis⁹ summarised in Table 2. It indicates a much reduced endo-anomeric effect in the β di-hydrate and a correspondingly larger lone pair occupancy on O5, increased by ∼0.06e. The increased density on O5 is consistent with the increased repulsion between O5 and O(W2), also observed, Table 1.

Table 2 Natural bond orbital analysis of the anomeric effect observed in α- and β-PhMan·(D₂O)₂. ΔE_nσ* is the second order perturbation energy associated with n–σ* orbital hyperconjugation

Orbital hyperconjugation	ΔEnσ*/kJ mol^−1	σ* occupancy/e	n(O) lone pair occupancy/e
n(O5)→σ*(C1–O1) (Endo)	α: 58.31	α: 0.061	α: 1.901
	β: 18.35	β: 0.039	β: 1.958
n(O1)→σ*(C1–O5) (Exo)	α: 49.16	α: 0.057	α: 1.848
	β: 53.25	β: 0.060	β: 1.844

---

Similar considerations may also contribute to the different structures of the hydration shells in the two triply hydrated anomers (see Fig. 6) although, due to their different overall structures, they cannot be directly compared. In the α complex, the distance between O5 and the oxygen atom in the neighbouring water molecule, W3, which lies above it, is 3.27 Å. In the β complex, although the carbohydrate has a similar conformation, the hydration structure changes and the distances between O5 and the oxygen atoms in W3 (and W2) increase to 3.49 Å (and 3.30 Å); the two neighbouring water molecules are both ‘pushed away’ from O5 and OH6 reorients to allow it to donate a second hydrogen bond to the oxygen on W2. Additionally, the water molecule, W1, while still accepting a hydrogen bond from OH4 at the 4,6 site, also re-orients and donates a hydrogen bond to OH6 rather than W2.

Conclusions

The anomeric effect in microsolvated D-mannose has been explored and directly exposed, through an investigation of the vibrational spectroscopy of the doubly and triply hydrated α and β anomers of phenylD-mannopyranoside, isolated under molecular beam conditions in the gas phase. The investigation has been greatly aided by the simple experimental trick of substituting D₂O for H₂O, which allows the (OH) vibrational bands associated with the saccharide to be separated from the (OD) bands associated with the bound water molecules. Subtle differences in the vibrational signatures of the hydrated α and β anomers can be interpreted in the light of complementary density functional theoretical calculations and a natural bond orbital analysis. The two singly hydrated anomers have identical structures, accessed in the β anomer through a change in the conformation of the monosaccharide, and the bound water molecule is located in the favoured water pocket at the 4,6 site. In the doubly hydrated anomers, the two water molecules again occupy the same template, bound on each side of the hydroxymethyl group, which places the additional W2 molecule at a site close to the anomeric region of the saccharide—but their structures, while similar, are not identical. The key structural change is mediated by changes consistent with ‘lone pair repulsion’ between the oxygen atom in the pyranose ring (O5) and the neighbouring water molecule. The extra water molecule thus acts as a remarkably sensitive ‘spy’, free from environmental influences and able to sense and expose subtle stereoelectronic changes through the resulting changes in its hydrogen-bonded interaction with the substrate. Similar effects appear to contribute to a change in the structure of the hydrogen bonded ‘hydration crown’ lying above the hydrophilic face of the carbohydrate, displayed in the triply hydrated anomers. These studies now provide precise structural data for the differences in solvation caused by the anomeric effect. They are likely to contribute to the striking differences between anomers found in nature, for example, between cellulose (a β1,4Glc polymer) and starch (an α1,4Glc polymer).

Experimental

General

Infrared “ion-dip” (IRID) vibrational spectroscopy,^12,13 conducted in the gas phase under molecular beam conditions, coupled with molecular mechanics, density functional theory (DFT) and ab initio calculations, provides an excellent method of determining the structures of carbohydrates and their hydrated clusters.^15–19IRID spectroscopy is a double resonance technique that depletes the ground state population of the target molecule whenever the IR radiation is ‘in tune’ with one of its fundamental vibrational modes. Monitoring the resulting dip in the resonant two photon ionization signal thereby provides a means of recording its vibrational spectrum. In the present system, the necessary UV chromophore is provided by the (structurally benign) phenyl ‘tag’.

Materials

The α- and β- anomers of phenyl D- mannopyranoside were synthesized following methods described previously.^17,18 Their hydrated (D₂O) complexes were generated in the gas phase using a combination of pulsed laser ablation and molecular beam procedures. Ground powdered samples of the carbohydrate were thoroughly mixed with graphite powder (∼20% graphite:80% sample, w/w), deposited as a thin uniform surface layer on a graphite substrate, and placed in a vacuum chamber close to and just below the exit of a pulsed, cylindrical nozzle expansion valve (0.8 mm diameter). The carbohydrates, desorbed by laser evaporation from the surface, were entrained and cooled in an expanding argon jet (∼4 bar backing pressure) seeded with D₂O, before passing into the detection chamber through a 2 mm diameter skimmer to create a collimated molecular beam. This was crossed by pulsed tunable UV and IR laser beams in the extraction region of a linear, Wiley-McLaren time-of-flight mass spectrometer (R. M. Jordan).

Spectroscopy

Mass-selected resonant two photon ionization spectra of individual molecular complexes were recorded using a frequency-tripled pulsed Nd:YAG-pumped dye laser (Sirah). Their conformer-specific vibrational spectra were subsequently recorded in the OH and OD stretch regions, through IRID spectroscopy, using IR radiation tuned over the range 2200–3800 cm⁻¹ and UV radiation tuned onto selected resonant two-photon ionization (R2PI) absorption bands. In these experiments the first laser (IR) was pulsed at 5 Hz while the second one (UV), delayed by ∼150 ns, ran at 10 Hz, to allow subtraction of the background signals. The IR radiation (line-width 2–3 cm⁻¹, ∼5–10 mJ/pulse) was provided by the idler output of an OPO/OPA laser system (LaserVision), pumped by a pulsed Nd:YAG laser (Continuum, Surelite II). Several spectra, typically ≥5, were recorded and averaged to achieve acceptable signal-to-noise levels.

Computation

Following the tried and tested strategies described elsewhere^18,20 analysis of the experimental data began with a series of unrestricted surveys of the many possible complex structures generated through a molecular mechanics conformational search. This was done using the mixed Monte Carlo multiple minimization and Large Scale low mode method as implemented in the MacroModel software (MacroModel v.8.5, Schrödinger, LLC21) until no additional new structures were obtained. All conformations with relative energies ≤10 kJ mol⁻¹, as well as a number of relevant higher energy structures, were subsequently submitted for geometry optimization using the Gaussian 03 suite of programs²¹ and density functional theory (DFT) at the B3LYP/6-311++G(d,p) level [α- and β-PhMan·(D₂O)_0–2] or B3LYP/6-31+G(d) level [α- and β-PhMan·(D₂O)₃]. This led to a new set of relative energies (corrected for zero point energies), molecular structures and (harmonic) vibrational spectra which could then be compared with experiment. More accurate energies were calculated for the optimized DFT structures, at the MP2/6-311++G(d,p) level of theory to take dispersion interaction into account. All energies were corrected for zero point energy (ZPE) using the unscaled DFT harmonic frequencies. Structural assignments were based primarily on the level of correspondence between the experimental and computed wavenumbers of the carbohydrate (OH) and water (OD) vibrational bands, scaled by the recommended²² appropriate ‘anharmonicity’ factor, 0.9533 (B3LYP/6-311++G(d,p)) or 0.9733 (B3LYP/6-31+G(d)), to bring them into better accord with experiment and secondly, on their calculated relative energies. Reassuringly, in all cases the best agreement between experiment and theory was obtained for the minimum energy structures. The full list of relative energies, optimized geometries and harmonic vibrational frequencies for the low energy structures is given as Electronic Supplementary Information.†

Acknowledgements

We appreciate the help of Drs David Gamblin and Eoin Scanlan, who synthesized the phenyl mannopyanoside samples; collaboration with Prof Benny Gerber and the support provided by the US Department of Energy Office of Science, Grant Number DE-FG02-09ER64762; the Laser Support Facility of the STFC; and the Leverhulme Trust for the award of an Emeritus Fellowship to JPS. BGD is a Royal Society Wolfson Research Merit Award recipient and is supported by an EPSRC LSI Platform grant.

References

1. J. T. Edward, Chem. Ind., 1955, 1102.
2. R. U. Lemieux, Pure Appl. Chem., 1971, 15, 527.
3. A. J. Kirby, The Anomeric Effect and Related Stereoelectronic Effects at Oxygen, Springer, Berlin, 1983.
4. P. Deslongchamps, Stereoelectronic effects in organic chemistry, Pergamon, Oxford, 1983.
5. E. Juaristi and G. Cuevas, Tetrahedron, 1992, 48, 5019.
6. G. R. J. Thatcher, The anomeric effect and associated stereoelectronic effects, ACS, Washington, 1993.
7. K. B. Wiberg and M. A. Murcko, J. Am. Chem. Soc., 1989, 111, 4821.
8. E. L. Eliel and S. H. Wilen, Stereochemistry of organic compounds, Wiley Interscience, New York, 1994.
9. U. Salzner and P. von Rague Schleyer, J. Org. Chem., 1994, 59, 2138.
10. A. Vila and A. Mosquera, J. Comput. Chem., 2007, 28, 1516.
11. Y. R. Mo, Nat. Chem., 2010, 2, 666.
12. T. S. Zwier, J. Phys. Chem. A, 2006, 110, 4133.
13. E. G. Robertson and J. P. Simons, Phys. Chem. Chem. Phys., 2001, 3, 1.
14. J. P. Simons, Mol. Phys., 2009, 107, 2435.
15. J. P. Simons, P. Çarçabal, B. G. Davis, D. P. Gamblin, I. Hünig, R. A. Jockusch, R. T. Kroemer, E. M. Marzluff and L. C. Snoek, Int. Rev. Phys. Chem., 2005, 24, 489.
16. J. P. Simons, B. G. Davis, E. J. Cocinero, D. P. Gamblin and E. C. Stanca-Kaposta, Tetrahedron: Asymmetry, 2009, 20, 718.
17. P. Çarçabal, R. A. Jockusch, I. Hünig, L. C. Snoek, R. T. Kroemer, B. G. Davis, D. P. Gamblin, I. Compagnon, J. Oomens and J. P. Simons, J. Am. Chem. Soc., 2005, 127, 11414.
18. E. J. Cocinero, E. C. Stanca-Kaposta, E. M. Scanlan, D. P. Gamblin, B. G. Davis and J. P. Simons, Chem.–Eur. J., 2008, 14, 8947.
19. E. J. Cocinero, P. Çarçabal, T. D. Vaden, J. P. Simons and B. G. Davis, Nature, 2011, 469, 76.
20. E. J. Cocinero, E. C. Stanca-Kaposta, M. Dethlefsen, B. Liu, D. P. Gamblin, B. G. Davis and J. P. Simons, Chem.–Eur. J., 2009, 15, 13427.
21. M. J. Frisch et al. Gaussian 03, Revision C.02; Gaussian, Inc.: Pittsburgh, PA, 2003.
22. Y. Bouteiller, J. C. Gillet, G. Grégoire and J.-P. Schermann, J. Phys. Chem. A, 2008, 112, 11656.

---

Footnotes

† Electronic supplementary information (ESI) available: Relative energies, vibrational frequencies and structural data for the low energy conformers of α- and β-PhMan·(D₂O)_0–3. See DOI: 10.1039/c1sc00002k

‡ “ins(4,6)” indicates insertion of the water molecule between OH4 (acting as a hydrogen-bond donor) and OH6 (the acceptor); “G-g+” indicates the gauche orientation of the exocyclic hydroxymethyl group and its terminal OH6 group, respectively; and “c” indicates the clockwise orientation of the peripheral OH groups, OH2–OH3–OH4.

---