A quantum-chemical perspective into low optical-gap polymers for highly-efficient organic solar cells
Chad
Risko
a,
Michael D.
McGehee
b and
Jean-Luc
Brédas
a
aSchool of Chemistry and Biochemistry and Center for Organic Photonics and Electronics, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
bDepartment of Materials Science and Engineering, Stanford University, Stanford, California 94305, USA
First published on 15th March 2011
Abstract
The recent and rapid enhancement in power conversion efficiencies of organic-based, bulk-heterojunction solar cells has been a consequence of both improved materials design and better understanding of the underlying physical processes involved in photocurrent generation. In this Perspective, we first present an overview of the application of quantum-chemical techniques to study the intrinsic material properties and molecular- and nano-scale processes involved in device operation. In the second part, these quantum-chemical tools are applied to an oligomer-based study on a collection of donor–acceptor copolymers that have been used in the highest-efficiency solar cell devices reported to date. The quantum-chemical results are found to be in good agreement with the empirical data related to the electronic and optical properties. In particular, they provide insight into the natures of the electronic excitations responsible for the near-infrared/visible absorption profiles, as well as into the energetics of the low-lying singlet and triplet states. These results lead to a better understanding of the inherent differences among the materials, and highlight the usefulness of quantum chemistry as an instrument for material design. Importantly, the results also point to the need to continue the development of integrated, multiscale modeling approaches to provide a thorough understanding of the materials properties.
I. Introduction
The conversion of solar radiation into electrical power through the photovoltaic effect offers considerable promise as a means of widespread, clean and sustainable energy generation. Moreover, the potential for low-cost, light-weight, large-area and flexible light-harvesting devices has been a key driver for the development of organic-based photovoltaics (OPV). As a result, there has been a tremendous push not only to design new materials for OPV applications, but also to develop device architectures that take account of the differing electronic and optical processes under which OPV cells operate vs. traditional inorganic devices. Considerable effort has been put forth toward the development of semiconducting and light-harvesting materials for bulk-heterojunction (BHJ)1–3 solar cells that are mainly based on phase-separated polymer–fullerene blends. Recent advances include the design of copolymers that combine electron-rich and electron-deficient moieties4–78 for use with fullerene derivatives. These materials combinations have pushed organic solar cells closer to commercial viability, as photovoltaic power conversion efficiencies have improved from a threshold value of 5% beyond 8% in a short period of time.9,11,20,24,33,43–45,50,60,63,67,78–80 A number of recent research accounts and reviews provide an overview of the development and applications of such copolymers.19,60,66,80–104The physical mechanisms at the molecular and nanoscopic scales that dictate the limits of OPV power conversion remain understood in a rather limited way. Based on the seminal work of Tang in 1986,105 the active layer within an OPV is generally composed of at minimum two distinct materials, an electron-donating/hole-transport material (HTM) and an electron-accepting/electron-transport material (ETM);106 these have, respectively, a correspondingly small ionization potential (electron rich and easily oxidized) and a large electron affinity (electron deficient and easily reduced). Within this active layer, the combination of five principal stages needs to be optimized for efficient OPV operation.89,94,95,98,100–102 The initial step (i) involves photoexcitation and formation of excitons – Coulombically-bound electron–hole pairs with no net charge; it is important to recall that exciton binding energies in π-conjugated systems usually reach several hundreds of millielectronvolts (meV), instead of the few meV found in inorganic semiconductors (where photon absorption at room temperature then results in the creation of free charge carriers). Prior to decay back to the ground state, the excitons have to dissociate into separated charges (in the form of positive and negative polarons) within the active layer. Thus, in step (ii), the excitons must diffuse within the active layer to the HTM/ETM interface;97 note that this migration is not influenced by the presence of an electric field as the exciton is charge neutral. For efficient exciton dissociation into separated charged polarons in the respective HTM and ETM components, step (iii), a process more complex than (simple) interfacial charge transfer, needs to follow; indeed, the Coulombic potential holding the hole in the HTM close to the electron in the ETM has to be overcome,107 either through differences in the chemical potentials of the HTM and ETM components or via involvement of higher-energy (‘hot’) charge-transfer states. The final charge-separated state is defined by the (adiabatic) ionization potential of the HTM and electron affinity of the ETM. In step (iv), the separated hole and electron migrate via drift and diffusion through the HTM and ETM phases, and in step (v) they are collected at the respective electrodes.
From a device perspective, these five steps translate into the readily measurable quantities of short-circuit current (JSC) and open-circuit voltage (VOC),89,98,108,109 parameters that require careful balance for high device performance. JSC directly depends on the external quantum efficiency, which can be associated with the efficiencies of the molecular- and nano-scale processes described above. The factors that determine VOC, on the other hand, are somewhat more difficult to define and have been of intense recent interest.89,98,108–117 In a number of instances, VOC has been shown to scale with the energetic difference between the ionization potential of the HTM and electron affinity of the ETM (or, as is often expressed in approximate terms in the literature, the HOMO energy of the HTM and the LUMO energy of the ETM).88 A related metric, the fill factor (FF), provides a means to compare the device operating performance (the maximum power density corresponding to JMAX × VMAX, the maximum current density and voltage, respectively, that the device is able to generate) to its upper limit (defined by JSC × VOC). Among the complications that hinder the understanding and optimization of JSC, VOC and FF are that these parameters are influenced by the molecular/polymer packing, morphology and electronic interactions at the HTM-ETM interface in the active layer.
Based on the five steps discussed above, a number of design guidelines have emerged regarding the intrinsic material properties of the HTM copolymers. First, low-energy (≈1.2–1.9 eV) first singlet excited states (i.e., small/low optical gaps) are needed to absorb a wide portion of the solar spectrum and generate a large photocurrent, in particular through photon absorption extended into the near-infrared region (the latter feature was actually the main initial driver in the development and application of these copolymers in BHJ solar cells). Second, molecules/polymers with large individual transition dipole moments are required to form films with high absorption coefficients for photon capture. Third, suitable ionization potentials and electron affinities are necessary for efficient charge transfer and charge separation at the organic/organic (HTM/ETM) interface and charge collection at the electrodes. Finally, planar conjugated backbone structures are preferable as they are susceptible to lead to tightly-packed stacking arrangements that can assist in providing large charge-carrier mobilities through strong intra- and intermolecular electronic coupling; minimal reorganization energies (i.e., geometry relaxation energies in going from the neutral state to the charged state and vice versa) are also desirable.96,118,119
Quantum-chemical methods provide a powerful tool set both for designing new copolymers and understanding their performance in BHJ devices as the intrinsic materials properties we described can be thoroughly addressed. Note that in the remainder of this Perspective, we will refer to these copolymers, which combine electron-rich and electron-deficient moieties, as donor–acceptor (DA) copolymers; it should be borne in mind, however, that these copolymers constitute the hole-transporting material in BHJ cells. The Perspective is structured as follows: In Section II, we provide a (non-exhaustive) review of recent literature pertaining to the application of quantum-chemical methods to the study of DA copolymer systems, in particular in relation to the five steps we presented above. In Section III, we describe the application of these methods to the study of a series of DA copolymers (see Fig. 1) used in the most highly-efficient BHJ solar cells reported to date.11,20,24,33,43–45,50,60,63,67,78,79 The geometric structure, electronic structure, and singlet and triplet excited-state properties will be detailed to gain insight into the structure–property relationships that make these copolymers such successful HTMs, in particular in comparison to poly-3-hexylthiophene (P3HT) that has long been used as the reference HTM component in OPVs.120–124
![Monomer structures for the DA copolymers of interest: P3HT poly(3-alkylthiophene); PCPDTBT poly[2,6-(4,4-bis-alkyl-4H-cyclopenta[2,1-b;3,4-b′]dithiophene)-alt-4,7-(2,1,3-benzothiadiazole)]; PCDTBT poly[N-alkyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole); PBDTTT-E poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-alkylester-thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-C poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-CF poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)-3-fluorothieno[3,4-b]thiophene-2,6-diyl]; PBDTTPD poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-N-alkylthieno[3,4-c]pyrrole-4,6-dione-1,3-diyl].125 (Unfortunately, even in top chemistry journals, these copolymers are most often referred to simply by their abbreviations; this is the reason why we will be using these abbreviations here as well).](/image/article/2011/SC/c0sc00642d/c0sc00642d-f1.gif) | ||
Fig. 1 Monomer structures for the DA copolymers of interest: P3HT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly(3-alkylthiophene); PCPDTBT poly(3-alkylthiophene); PCPDTBT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[2,6-(4,4-bis-alkyl-4H-cyclopenta[2,1-b;3,4-b′]dithiophene)-alt-4,7-(2,1,3-benzothiadiazole)]; PCDTBT poly[2,6-(4,4-bis-alkyl-4H-cyclopenta[2,1-b;3,4-b′]dithiophene)-alt-4,7-(2,1,3-benzothiadiazole)]; PCDTBT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[N-alkyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole); PBDTTT-E poly[N-alkyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole); PBDTTT-E ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-alkylester-thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-C poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-alkylester-thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-C ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-CF poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)thieno[3,4-b]thiophene-2,6-diyl]; PBDTTT-CF ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)-3-fluorothieno[3,4-b]thiophene-2,6-diyl]; PBDTTPD poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-alt-4-(alkyl-1-one)-3-fluorothieno[3,4-b]thiophene-2,6-diyl]; PBDTTPD ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-N-alkylthieno[3,4-c]pyrrole-4,6-dione-1,3-diyl].125 (Unfortunately, even in top chemistry journals, these copolymers are most often referred to simply by their abbreviations; this is the reason why we will be using these abbreviations here as well). poly[4,8-bis-alkyloxy-benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl-N-alkylthieno[3,4-c]pyrrole-4,6-dione-1,3-diyl].125 (Unfortunately, even in top chemistry journals, these copolymers are most often referred to simply by their abbreviations; this is the reason why we will be using these abbreviations here as well). | ||
II. Overview on the application of quantum-chemical methods for DA copolymers
Quantum-chemical methods can provide valuable information into both the intrinsic properties of the DA copolymer and in the description of interactions among neighboring molecules in the bulk and at the interface. Studies of model oligomer systems at both wave-function theory level (i.e., Hartree–Fock [HF] methods, post-HF methods that include electron correlation, and semiempirical HF methods) and density functional theory level (as well as combinations thereof) have been widely used in the design and understanding of small optical gap DA copolymers for organic-based electronics applications, and in particular for OPVs.8,12,20,23,26,27,48,49,51,62,68,70,73,75,126–153Detailed theoretical studies of the interplay between structural and chemical modifications of model oligomers and the resulting influence on the electronic structure allow for insight into the nature of the photoexcitation process, exciton formation, and exciton and charge migration through the DA copolymer. For an accurate description of the electronic and optical properties, relatively long oligomer systems need to be studied to ensure that the conjugation path length is sufficient to describe the polymer system.154 As such, semiempirical HF-based methods – e.g., the Austin Model 1 (AM1),155 Modified Neglect of Differential Overlap (MNDO),156 or Parameterized Method 3 (PM3)157,158 Hamiltonians – have been extensively employed as they formally scale as χ3, where χ represents the number of valence electrons in the system.73,127,128,139,141–143,146,150,152 Semiempirical methods have limitations, however, due to the need for parameterization with experimental results (which can include solvent polarizability dependence) and the use of small basis sets. In addition, semiempirical methods suffer from the explicit lack of a description of electron correlation in HF theory (though there is an implicit accounting of electron correlation through the parameterization), which can lead to over-localized solutions of the wave function; this in turn can affect the description of the electronic structure, oxidation and reduction properties and electronic excitations. While systematic improvements of HF methods to include electron correlation are available, the state-of-the-art post-HF methods quickly become computationally cumbersome even for systems of moderate size.
Density functional theory (DFT) has also been extensively applied to the geometric and electronic description of DA oligomers.12,20,26,48,49,51,62,68,70,75,129–135,138–140,144,145,147–149,151,153 DFT tends to provide a good balance between chemical accuracy and computational cost, though limitations in system size do arise because of larger computational demands in comparison to semiempirical methods since DFT methods normally scale as χ4; however, it should be noted that considerable efforts have been devoted to reduce this scaling, e.g., via linear scaling techniques,159–163 to allow DFT methods to be applied to very large systems. Additionally, traditional DFT methods suffer from the self-interaction error (the fact that an electron can interact with itself), which generally leads to an over-delocalized description of the wave function, and artifacts due to the approximations needed to describe the exchange functional. In addition to oligomer studies of electronic structure, DFT calculations that take into account periodic boundary conditions have been implemented in order to determine the electronic band structures of full polymeric materials.12,23,149
The impact of the geometric structure on the electronic properties manifests itself through the degree of bond-length alternation (BLA) across the polymer backbone, the aromatic stabilization of the constituent copolymer segments, inductive or mesomeric effects due to substitutions along the backbone, relative coplanarity of the conjugated backbone, and degree of intermolecular coupling in the solid state.81 A design principle initially associated with constructing small optical gap polymers (to extend photon absorption into the near-infrared) is the use of structures within the conjugated backbone that induce quinoidal character, for instance via the presence of a single conjugated carbon between arylene rings or via the use of fused structures.96,164–168 The quinoidal structure reduces the aromatic stabilization energy of the constituent parts, leading to a reduction in the energetic gap between the highest-occupied and lowest-unoccupied molecular orbitals, i.e., HOMO and LUMO.165 To investigate such geometric attributes, quinoidal character can be enforced within the oligomer by placing, for instance, terminal methylene (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) units at the oligomer ends and examining the differences in BLA vs. capping the oligomer with hydrogen atoms.135,169 As the oligomer length is increased, the relative stability of the quinoid vs. aromatic structures can be evaluated by comparing the energy per repeat unit.170,171 More recently, the design of small optical-gap copolymers has focused predominantly on the strategy, originally developed by Havinga and co-workers,172,173 of combining electron-rich (donor) moieties and electron-deficient (acceptor) moieties; the former are expected to lead to a high-energy HOMO and the latter to a low-energy LUMO, and thus to an overall small HOMO–LUMO gap.
CH2) units at the oligomer ends and examining the differences in BLA vs. capping the oligomer with hydrogen atoms.135,169 As the oligomer length is increased, the relative stability of the quinoid vs. aromatic structures can be evaluated by comparing the energy per repeat unit.170,171 More recently, the design of small optical-gap copolymers has focused predominantly on the strategy, originally developed by Havinga and co-workers,172,173 of combining electron-rich (donor) moieties and electron-deficient (acceptor) moieties; the former are expected to lead to a high-energy HOMO and the latter to a low-energy LUMO, and thus to an overall small HOMO–LUMO gap.
The degree of planarity within the conjugated backbone can not only influence the electronic and optical properties considerably, but from a practical computational viewpoint, it can also affect the cost associated with the calculations and analyses of longer oligomers. As a first approximation, planar conjugated backbones have been used in a variety of quantum-chemical oligomer analyses;137,138 this is particularly of benefit for the proper description of the optical properties of polythiophene (and like polymers) that are known to display (nearly) coplanar backbones in the solid state. However, forcing such geometric restrictions can have significant influence on the final optical properties, as differences ≥0.3 eV in the electronic excitation energies can easily be found in the case of flexible polymer chains.137,138,174 While generally more time consuming, allowing optimization of the torsional modes between the units within the conjugated backbone leads to a more accurate analysis of the geometric structure, in particular for highly flexible (amorphous) polymers and for comparison to UV-vis studies performed in solution (in a good solvent).
An additional consideration with regard to geometry concerns the orientation of the individual components along the conjugated backbone. As donor–acceptor components often contain heteroatoms, there exists the possibility of intramolecular van der Waals and electrostatic interactions that can stabilize particular configurations. For example, S⋯N (S⋯O) and hydrogen-bonding interactions have been hypothesized to stabilize particular orientations among the constituent parts along the conjugated backbone, for example, in the p-dithiophenebenzothiadiazole (dT-BT) oligomer.139,149,153 It is noteworthy that such interactions can in essence compete with each other and sometimes provide constituent orientations that are nearly isoenergetic and have little-to-no influence on the resulting electronic or excited-state properties. Interestingly in the case of dT-BT, the most significant difference among the orientations is the total dipole moment (Fig. 2), suggesting that particular orientations among constituent parts can be stabilized by variations in solvent polarity, which in turn can significantly affect the solid-state packing arrangements through dipole–dipole interactions (or lack thereof).
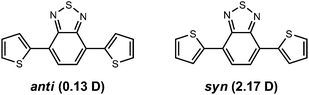 | ||
| Fig. 2 The anti- and syn-conformations of the p-dithiophenebenzothiadiazole (dT-BT) oligomer, along with the respective total dipole moments (Debye) as determined at the B3LYP/6-31G** level of theory. The anti-conformation is 1.5 kcal mol−1 energetically more stable in the ‘gas-phase’, B3LYP/6-31G** calculations. | ||
As mentioned earlier, intermolecular interactions can also alter the geometric structure of the DA copolymers. Indeed, the prediction of molecular packing arrangements in the solid state is a grand challenge of the computational chemistry community. In particular for aromatic systems, the task of predicting solid-state structures is hampered by the subtle interplay of dispersion and electrostatic forces. Such interactions require high-level ab initio calculations in order to properly describe the preferred geometric orientations,175–184 calculations that are often inapplicable to large systems. Density functional theory methods that include dispersion corrections do offer a cost-effective means of taking into account interactions amongst π-conjugated structures and have been recently used to predict preferred orientations and geometries of stacked oligomers.70,185 Such intermolecular interactions do impact the geometry of individual chains and are key in understanding exciton and charge transport through the system (vide infra).
The eigenvalues (energies) of the one-electron wave functions (i.e., molecular orbitals), in particular the frontier electronic levels (HOMO and LUMO), are often used to depict energy level (band) diagrams for organic electronic devices. Based within Hartree–Fock theory, Koopmans' theorem186 (i.e., ‘frozen orbital’ approximation) states that the ionization potential of the neutral ground state is given by the (sign inverse of the) HOMO energy and that the electron affinity is given by the LUMO energy. However, treating the HOMO and LUMO energies as ionization energies and vice versa should be done with caution. Most notably, the frozen orbital approximation neglects electron correlation, electron reorganization and vibronic coupling.187 With regard to the use of molecular orbital energies from DFT methods for the determination of ionization energies, there are even further questions given that a priori Kohn–Sham eigenvalues are auxiliary quantities; however, Janak's theorem188 has been used in the proof that there is a DFT counterpart to Koopmans' theorem.189 Though evaluations of the ionization potential and electron affinity of a given system tend to not be quantitative, qualitative trends among molecular systems can be found readily throughout the literature for well-behaved systems. An additional important note is that experimental estimates of the ionization energies derived from electrochemical measurements can be misleading. Electrochemical measurements (e.g., cyclic voltammetry and differential pulse voltammetry) of oxidation and reduction potentials are at best estimates of the bulk ionization energies, since the dielectric environment of the polymer in solution can differ considerably from that of the polymer in the solid state.
With a proper description of the geometric and electronic structure, quantum-chemical methods can be used to describe the processes involved during photoexcitation and exciton formation. As with the determination of the geometric properties, the most widely used methods for the determination of the (singlet) excited-state properties of DA oligomers are based on semiempirical HF8,75,127–130,138,141,142,146,150,151 and (time-dependent) density functional theory.48,49,51,70,129–134,136,138–140,144,145,147,153 The most common semiempirical HF method employed to date uses the Intermediate Neglect of Differential Overlap (INDO) Hamiltonian coupled with a Configuration Interaction scheme that allows for excitations of single electrons (CIS). As such, an important consideration in the use of these methods involves the proper choice of the CI active space; often, the chosen active space is one that allows for all π–π* transitions within the system to be considered. A recent benchmark study of eight semiempirical HF Hamiltonians suggests that the methods generally underestimate the vertical excitation energies, while only a few are able to reproduce reasonably well the oscillator strength (transition dipole moment); the orthogonalization-corrected approaches (e.g., OM1, OM2 and OM3) were rated as the most promising to describe vertical excitation processes in organic compounds.190
Time-dependent DFT (TDDFT) is an extension of DFT, whose foundations lie in the rigorous proof of correspondence between a time-dependent external potential and the time-dependent one-particle density.191,192 As with general DFT methods, TDDFT offers accurate results for well-behaved systems and efficient computational cost.193 However, the effects of electron self-interaction from the general DFT formalism do tend to lead to over-delocalization of the excited-state wave function, and hence a shift in the calculated vertical transition energies vs. experiment. The degree of the shift is largely dependent on the choice of functional, with improvements observed in general for hybrid functionals that include some quantity of HF exchange. Importantly, newer functionals that include long-range corrections to the exchange functional194–199 do offer the possibility to correct for these current limitations.
A major consideration, in particular in the context of designing polymers with relatively small optical gaps, is the correspondence between the calculated transition energies for oligomers vs. the optical excitation energies measured for the full polymers, a topic that has been reviewed recently.137 As such, a variety of extrapolation procedures – from simple linear and polynomial fits to extrapolation procedures derived empirically154,200 and theoretically137,201 – have been applied to extract the vertical transition energy (as well as the molecular orbital energy levels) at the polymer limit.48,49,51,70,75,129–133,136,138,141,146,202 For a series of increasing oligomer lengths, the calculated vertical transition energies are plotted as a function of the inverse of either (i) the number of repeat units in the structure (1/n) or (ii) the number of effective double bonds (1/Neff). The results of such analyses typically show at least two main regions within the plot – a linear regime where the vertical transition energy decreases with increasing oligomer size, and a saturation regime where continued increase of the oligomer length no longer influences the transition energy. The turnover point between the two regions has been described as the ‘effective conjugation length’200 or the ‘maximum conducive chain length’.137 Again, such extrapolation procedures should be used with caution, as the errors associated with the assumptions employed in the chosen computational methodology can outweigh appreciably the improvement in predicted value of the vertical transition energy at the polymer limit.137 The proper choice of extrapolation procedure can also change considerably depending on the particular polymer characteristic being analyzed for convergence behavior.202
In addition to excitation energies, information pertaining to the nature of the excited state203 – including the electronic configuration, transition dipole moment (oscillator strength), distribution of the correlated electron–hole pair, transition density and charge-density difference with the ground state – can be obtained readily and can provide insight into how the D/A moieties along the backbone interact in the excited state. The use of molecular orbitals (and their corresponding wave-function density distributions) are a natural way for chemists to describe the nature of low-lying electronic transitions in conjugated materials, as most systems involve transitions among the frontier π orbitals (for instance, HOMO → LUMO). For an electronic excitation, the probability that a transition will occur between two states is given by the electronic transition dipole moment:
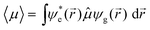 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and ψg(
) and ψg(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) are the excited-state and ground-state wave functions, and
) are the excited-state and ground-state wave functions, and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the dipole moment operator: e
is the dipole moment operator: e![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , with e the elementary charge. Eqn (1) is the basis of the orbital selection rules for electronic transitions. Note that both vibrational (i.e., Franck–Condon factor) and spin selection rules also play an important role in the probability of a transition, though they are not discussed here. The electronic transition dipole moment translates into the molar extinction coefficient (solution) or absorption coefficient (thin film), and thus provides direct information on absorption strengths.
, with e the elementary charge. Eqn (1) is the basis of the orbital selection rules for electronic transitions. Note that both vibrational (i.e., Franck–Condon factor) and spin selection rules also play an important role in the probability of a transition, though they are not discussed here. The electronic transition dipole moment translates into the molar extinction coefficient (solution) or absorption coefficient (thin film), and thus provides direct information on absorption strengths.
Beyond simple molecular orbital analyses, further scrutiny of the ground- and excited-state wave functions involved in the electronic transitions provides even deeper understanding. For example, correlated electron–hole distributions have been used to visualize how the electron and hole in the excited state (de)localize across the conjugated backbone.8,127,144,204 Furthermore, the transition density and charge-difference density give access to the areas of the conjugated system directly involved in the transition and the change in electron density on excitation, respectively.8,144,203
In complement to descriptions of the vertical excitation processes, both wave-function and DFT methods can be used to determine excited-state geometries and as a result the degree of relaxation and (de)localization of the exciton, of relevance with regard to intramolecular and intermolecular exciton diffusion within the bulk. While HF/CIS has been the principal method employed to date to determine the nature of the geometry in the first excited state,129–133,136TDDFT methods205 are being increasingly considered. Additionally, using the geometry of the first excited state with the methods described above allows one to simulate the expected fluorescence spectrum of the system of interest.
The nature and energies of the low-lying triplet states can also be evaluated with similar computational methodologies. Such information is important as the determination of triplet-state properties is often more difficult to assess experimentally.145,206 Both vertical and adiabatic energy differences with respect to the ground state, geometric consequences of triplet-state formation (e.g., localization of the triplet state), and singlet–triplet exchange energies127,128,141,145,146,207 are accessible. In the context of organic solar cells, characterization of the triplet states is very useful, since triplets can provide for energy-loss pathways.112,206,208
Accurate descriptions of exciton migration/diffusion in organic thin-films remain elusive.95 Typically, long-range Förster resonant energy transfer (FRET) theory has been applied to describe the diffusion of singlet excitons, though the use of the customary point-dipole model is inappropriate for energy transfer between nearby chromophores;209 on the other hand, short-range Dexter mechanisms have been used to describe the diffusion of triplet excitons.95 Important for the description of energy transfer is the determination of optical coupling between interacting sites.127,210 To deal with the limitations of the point-dipole model in FRET, optical coupling has been determined on the basis of atomic transition densities.211,212 Very recent theoretical work on oligoacene single crystals underlines the substantial contributions of charge-transfer configurations (that is, configurations in which the hole and the electron are found on separate, adjacent molecules) in the description of the lowest singlet exciton; this has significant implications for exciton diffusion.213
As with exciton diffusion, an unambiguous picture of the exciton dissociation process at the HTM-ETM interface is currently not present. This is mainly due to the fact that a number of factors very much complicate a straightforward description; these include: the nature of the ground state (e.g., relative molecular orientations, degree of charge transfer) at the heterojunction interface, polarization effects and the formation of heterojunction interface dipoles, the nature of the (singlet or triplet) exciton that reaches the interface, and the coupling between the exciton state and the charge-transfer (CT) states at the interface.95,117,214,215 Recent work has been performed on isolated HTM and ETM molecular pairs to probe the rates of charge-transfer, charge-separation and charge-recombination processes at the interface;117,214,216,217 however, no theoretical work to date has been done to evaluate these rates for DA oligomers.
The energy of the fully charge-separated state is defined as the energy difference between the (adiabatic) ionization potential of the HTM and the (adiabatic) electron affinity of the ETM. To determine such energies theoretically, the radical-cation and radical-anion states need to be evaluated. Both wave-function and DFT methods have been widely used to examine these states for isolated DA oligomers.49,129–133,136,140,147 Accurate evaluations of the polarization energies appearing in condensed phases, however, remain a challenging task.215,218–232 Since the vertical ionization potential and electron affinity can also be determined computationally, these values can be exploited in the determination of the intramolecular relaxation energies for ionization and the intramolecular reorganization energy for charge transport, see below.
Charge transport in organic thin films has been recently discussed in terms of semiclassical Marcus theory.118,119,233–236 In that context, charge-carrier mobility can be related to the rate of electron transfer, kab, between two adjacent molecules or polymer chain segments:
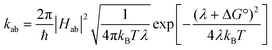 | (2) |
Finally, the quantum-chemical study of charge collection at the electrodes has to deal with the complexity of the organic–metal or organic–conducting oxide interfaces. Significant computational efforts have been undertaken recently to understand the nature of these interfaces, including how molecular orientations, chemical substitutions and charge-density redistributions, influence the energy-level alignment between the frontier molecular orbitals of the organic layer and the Fermi energy of the electrode.238–250 Such investigations have proven to be very useful to provide an understanding of results obtained from photoelectron spectroscopy experiments. To date, limited theoretical studies on oligomer constituents of polymers have been carried out, though a recent discussion of how oligothiophenes deposit on a gold surface detail an important dependence of the results on oligomer orientation.251
III. Application of quantum-chemical methods to highly-efficient DA copolymers
As the discussion in Section II underlines, quantum-chemical methods can provide a wealth of information concerning the intrinsic geometric, electronic and optical properties of DA copolymers for use in BHJ solar cells. At this point, we turn to the application of some of these methods to a series of DA copolymer systems, Fig. 1, that have been recently exploited in efficient laboratory BHJ solar cells.9,11,20,24,33,43–45,50,60,63,67,78–80PCPDTBT, synthesized by Brabec et al.,9,18 initially led to power conversion efficiencies (PCEs) of 3.2% when blended with [6,6]-phenyl C71-butyric acid methyl ester (PC71BM); importantly, incorporation of an alkanedithiol processing additive (few volume percent) provided a dramatic PCE enhancement to 5.5% by adjusting the BHJ morphology.79,99 Synthesized by Leclerc et al.,11,19,20,50PCDTBT blended with PC71BM yielded a PCE of 6.1% (5.96% certified) and 0.88 V VOC, with an internal quantum efficiency near 100%. The PBDTTT series, synthesized within the groups of Yu and Li,33,36,44,45 have notably shown how relatively minor modifications to the chemical structure of the copolymer repeat unit can lead to dramatic improvements in VOC and JSC for BHJ solar cells blended with PC71BM; these produced one of the largest literature-reported certified PCE of 6.77% (uncertified PCEs of 7.73% were also published). Recently, the groups of Leclerc,78 Fréchet,71 and Jen252 have independently shown that replacing the thienothiophene unit in the PBDTTT copolymers with thieno[3,4-c]pyrrole-4,6-dione can also provide for (uncertified) maximum PCEs of 4.0–6.8%, and 5.5% for a device with an active area of 1.0 cm2 in air. Poly(3-hexylthiophene) (P3HT), a proven, successful polymer in BHJ solar-cell architectures and the “fruit fly” of the community at large, will serve as a point of reference for this computational analysis; BHJ solar cells with P3HT blended with [6,6]-phenyl C61-butyric acid methyl ester (PC61BM) yield PCEs around 5%.120–123For the analysis, alternating DA oligomers ranging in size from n = 1–4 monomer units were evaluated at the DFT level using the hybrid, generalized gradient approximation (GGA) functional B3LYP253–255 and a 6-31G** basis set.256–258 Geometry optimizations of the ground state (S0) were performed for the entire oligomer series, while the lowest-lying triplet (T1) states were optimized for the tetramers. The recently developed hybrid meta exchange–correlation M06-2X functional259 was also used to evaluate the oligomer ground-state geometries; in general, the results were very similar: the twist angles between the donor and acceptor components were a few degrees larger and the BLA pattern along the carbon-carbon backbone was slightly more pronounced vs. the B3LYP-derived geometries, which is consistent with the larger fraction of Hartree–Fock exchange in M06-2X. All alkyl chains appended to the conjugated backbone were truncated to methyl groups to reduce the computational requirements. Note that the final (macro) shape of the oligomer can be highly dependent on the choice of monomer conformation and whether the oligomer is built in a random or regular fashion; for the purpose of this work, the alternating pattern between D and A moieties was chosen to occur in a regular fashion. Time-dependent DFT (TDDFT) calculations were performed to assess the excited-state vertical transition energies, oscillator strengths and electronic configurations. Two modern density functionals – the M06-2X functional and the long-range corrected hybrid ω-B97X functional198 – were also employed to examine the excited-state properties; for both functionals, the partial charge-transfer-like S0 → S1 transition energies were significantly blue shifted vs. both experiment and the B3LYP-derived energies. Absorption spectra were simulated through convolution of the vertical transition energies and oscillator strengths with Gaussian functions characterized by a full width at half-maximum (fwhm) of 0.3 eV. All calculations were performed with Gaussian 09 (Revision A.02)260 and molecular orbital density plots were generated with ArgusLab 4.0.1.261
a. Geometric and electronic properties
Table 1 collects the ionization energies, frontier molecular orbital energies and descriptions of the S0 → S1 transition for the donor and acceptor components of the polymers of interest (Fig. 3): carbazole (CBZ), cyclopentadithiophene (CPDT), benzodithiophene (BDT), benzothiadiazole (BT), p-dithiophenebenzodiathiazole (dT-BT), thieno[3,4-c]pyrrole-4,6-dione (TPD) and thienothiophene (TT). The calculated trends in the HOMO and LUMO energies, in general, track well the adiabatic ionization potentials (AIP) and adiabatic electron affinities (AEA), respectively. Benzodithiophene is the most readily oxidized donor component, followed by cyclopentadithiophene and carbazole. For an accurate determination of the AEA, an extended basis set (6-31++G**) that included the use of diffuse functions was employed. Based on these results, benzothiadiazole and the fluorine-substituted thienothiophene acceptors are the easiest to reduce. It is noteworthy, however, that the dithienyl substitution around benzothiadiazole stabilizes the AEA considerably while also decreasing the AIP; indeed, the AIP is similar to that of the donor components used in this polymer series.153 Moreover, there is minimal influence on the orientation of the thiophene units (synvs. anti) on the electronic structure.135,153 The most significant difference between the two conformations concerns the total dipole moment, which is substantially larger for the syn-conformation (vide supra) that had previously been considered theoretically.139 The anti-conformation is slightly more energetically stable and, therefore, has been used throughout the remainder of the oligomer study. Interestingly, subtle modifications to the electron-withdrawing groups appended to the thienothiophene unit can have a substantial effect on both the AIP and AEA. On replacing the methyloxy group (TT-COOCH3) on the thienothiophenecarbonyl substituent with a methyl group (TT-COCH3), both the AIP and AEA increase. Adding a fluorine substituent (TT-COCH3–F) further stabilizes both the AIP and AEA. Of the electron acceptor groups studied here, thieno[3,4-c]pyrrole-4,6-dione has the smallest AEA; it is worth noting that the choice of the extended basis set had the largest impact on the AEA of the thieno[3,4-c]pyrrole-4,6-dione, bringing it more in line with the other acceptor units.| Compounda | AIP b | AEA b | HOMO | LUMO | S0 → S1 | |||
|---|---|---|---|---|---|---|---|---|
| E vert | f | Electronic configuration | ||||||
a
CBZ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) carbazole, CPDT carbazole, CPDT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) cyclopentadithiophene, BDT cyclopentadithiophene, BDT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) benzodithiophene, BT benzodithiophene, BT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) benzothiadiazole, dT-BT benzothiadiazole, dT-BT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) p-dithiophenebenzodiathiazole, TPD p-dithiophenebenzodiathiazole, TPD ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) thieno[3,4-c]pyrrole-4,6-dione, TT thieno[3,4-c]pyrrole-4,6-dione, TT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) thienothiophene.
b Note that the ionization energies were determined as IE = E(radical-ion) − E(neutral).
c Results in parentheses determined at the B3LYP/6-31++G** level of theory. thienothiophene.
b Note that the ionization energies were determined as IE = E(radical-ion) − E(neutral).
c Results in parentheses determined at the B3LYP/6-31++G** level of theory.
|
||||||||
| Donor | CBZ | 6.94 | +0.87 (+0.29)c | −5.33 | −0.64 | 4.04 | 0.03 | HOMO → LUMO (92%) |
| CPDT | 6.73 | +0.49 (+0.04) | −5.19 | −1.02 | 3.92 | 0.31 | HOMO → LUMO (99%) | |
| BDT | 6.39 | +0.36 (−0.06) | −5.29 | −1.06 | 3.86 | 0.19 | HOMO → LUMO (90%) | |
| Acceptor | BT | 8.52 | −0.50 (−0.96) | −6.62 | −2.35 | 3.86 | 0.04 | HOMO → LUMO (97%) |
| dT-BT | 6.62 | −1.24 (−1.61) | −5.37 | −2.63 | 2.39 | 0.28 | HOMO → LUMO (97%) | |
| TPD | 9.04 | −0.06 (−0.63) | −7.30 | −1.79 | 4.17 | 0.00 | HOMO-2 → LUMO (95%) | |
| TT-COOCH3 | 7.55 | −0.29 (−0.71) | −5.80 | −1.78 | 3.65 | 0.07 | HOMO → LUMO (95%) | |
| TT-COCH3 | 7.62 | −0.43 (−0.88) | −5.87 | −1.99 | 3.51 | 0.07 | HOMO → LUMO (94%) | |
| TT-COCH3–F | 7.70 | −0.50 (−0.98) | −5.97 | −2.04 | 3.51 | 0.00 | HOMO-1 → LUMO (93%) | |
![Chemical structures of the donor and acceptor components. CPDT cyclopentadithiophene, CBZ carbazole, BDT benzodithiophene, BT benzothiadiazole, dT-BT p-dithiophenebenzodiathiazole, TT thienothiophene, TPD thieno[3,4-c]pyrrole-4,6-dione.](/image/article/2011/SC/c0sc00642d/c0sc00642d-f3.gif) | ||
Fig. 3 Chemical structures of the donor and acceptor components. CPDT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) cyclopentadithiophene, CBZ cyclopentadithiophene, CBZ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) carbazole, BDT carbazole, BDT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) benzodithiophene, BT benzodithiophene, BT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) benzothiadiazole, dT-BT benzothiadiazole, dT-BT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) p-dithiophenebenzodiathiazole, TT p-dithiophenebenzodiathiazole, TT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) thienothiophene, TPD thienothiophene, TPD ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) thieno[3,4-c]pyrrole-4,6-dione. thieno[3,4-c]pyrrole-4,6-dione. | ||
Based on these optimized component geometries, alternating oligomers ranging from n = 1–4 monomer units were built to represent the full polymer systems illustrated in Fig. 1. Note that we consider here isolated chains (“in the gas phase”). As shown in Fig. 4, there are noticeable differences with regard to the ground-state (S0) geometric shapes of the tetramers. The tetramer representing P3HT is relatively linear with dihedral angles between the thiophene rings on the order of 15°. Due to the inherent curvature of the cyclopentadithiophene unit62,73 (and the regular, alternating bonding pattern considered), the tetramer for PCPDTBT shows a definite arch shape, though the twist between adjacent cyclopentadithiophene and benzothiadiazole units is negligible (≈0°). On the other hand, the PCDTBT, PBDTTPD and PBDTTT longer oligomers each have a regular zigzag pattern – a geometric configuration that has been speculated as one of the key features behind the distinct film-forming properties and enhanced solar cell performance of the PBDTTT polymers,152,262 and recently implicated as a new design principle for conjugated polymers.263 For PCDTBT, the twist angles between the thiophene and carbazole units are on the order of 25–27° (due to steric hindrance between neighboring hydrogen atoms on the two constituents), while the thiophene–benzothiadiazole twist is ≈3–5°. PBDTTPD has a near 0° twist along the backbone. The PBDTTT chains have a slight asymmetry with respect to the twist between the benzodithiophene and thienothiophene units. In PBDTTT-E and PBDTTT-C, the backbone twist on the side of the thienothiophene unit containing sulfur is ≈15°, while the other backbone twist is ≈20°; for the fluorine-substituted PBDTTT-CF, these twist angles increase slightly to approximately 18 and 24°, respectively. We recall that, since the electronic properties such as ionization potential, electron affinity, or optical gap vary as a function of the cosine of the twist angle,264 the twist angles calculated here are not expected to lead to major differences with respect to coplanar conformations.
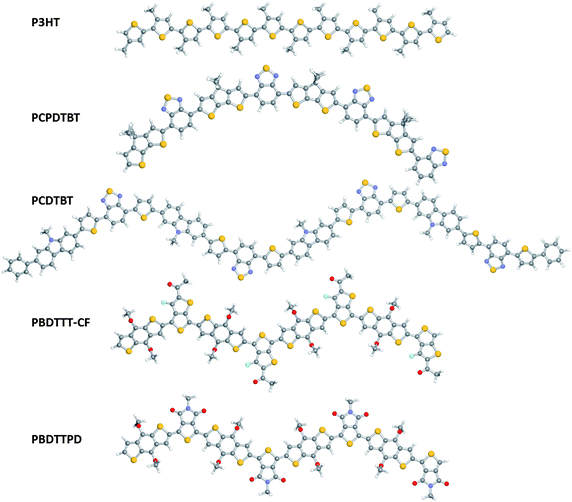 | ||
| Fig. 4 Optimized ground-state (S0) geometric structures for the tetramers as determined at the B3LYP/6-31G** level of theory. | ||
As noted above, the energies of the highest-occupied and lowest-unoccupied molecular orbitals (one-electron wave functions) can be used as first approximations of the ionization potential and electron affinity, respectively, via Koopmans' theorem. Fig. 5 shows the evolution of the (B3LYP/6-31G**) HOMO and LUMO energies as a function of oligomer length; for reference, the HOMO and LUMO energies of PC61BM and PC71BM (which are generally used as ETMs in BHJ solar cells) are plotted as well. Within the oligomer length range analyzed, there is a definite linear relationship between the HOMO (LUMO) energies and the inverse number of repeat units. As there is no apparent energetic saturation within this range, the use of typically-employed polynomial extrapolation procedures to evaluate the energies at the polymer limit is not appropriate; the lone exception could be the PCDTBT oligomer series, which does start to saturate due to the longer conjugation path length of the monomer unit with respect to the other systems.
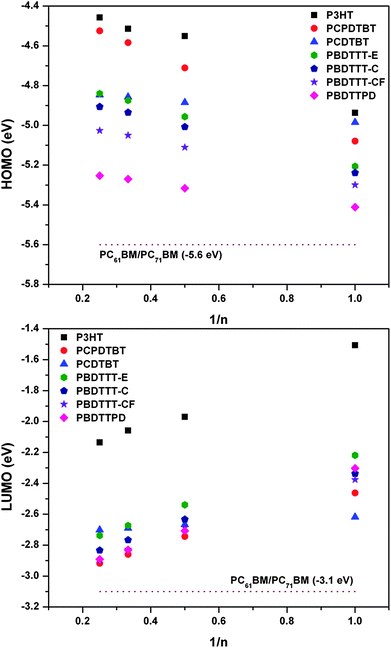 | ||
| Fig. 5 Evolution of the (top) HOMO and (bottom) LUMO energy (eV) with respect to the inverse number of repeat units (n) in the oligomer as determined at the B3LYP/6-31G** level of theory. For reference, the dashed line in each plot represents the HOMO (top) and LUMO (bottom) energy of PC61BM and PC71BM as determined at the B3LYP/6-31G** level of theory. | ||
As expected a priori, each DA copolymer system is more difficult to oxidize and easier to reduce vs. P3HT, while being easier to oxidize and more difficult to reduce vs. PC61BM/PC71BM. The HOMO energies for the tetramers suggest that the ionization potentials for the DA copolymers decrease on going from PCPDTBT < PCDTBT ≈ PBDTTT-E < PBDTTT-C < PBDTTT-CF < PBDTTTPD, while the LUMO energies indicate that the electron accepting ability follows PCPDTBT ≈ PBDTTT-CF ≈ PBDTTPD > PBDTTT-E ≈ PCDTBT. The benzodithiophene donor consistently provides the most energetically stabilized HOMO within the series. As suggested by Chen et al.,33 the subtle change in substitution pattern on the thienothiophene unit affects both the HOMO and LUMO of the chain. Importantly, the use of the thieno[3,4-c]pyrrole-4,6-dione acceptor stabilizes the HOMO even further, while also maintaining an energetically-stabilized LUMO. Unfortunately, a direct comparison between the computational results and the available electrochemical oxidation/reduction potentials available in the literature is not straightforward as the electrochemical measurements were either performed in a variety of solvents, and/or half-wave potentials or onset potentials were reported.
Fig. 6 shows pictorial representations of the one-electron HOMO and LUMO wave functions for selected oligomers in the series. Analysis of the HOMO for each system reveals a rather well delocalized wave function. This suggests that the positively-charged polaron of the fully charge-separated state could be fairly delocalized across the conjugated backbones in these polymers. The LUMO, on the other hand, shows a varying degree of (de)localization based on the component parts. For the systems containing the benzothiadiazole acceptor, the LUMO is mainly localized on the benzothiadiazole units; this is especially the case for PCDTBT where the additional thiophene units appended to the benzothiadiazole impart a great deal of isolation. The PBDTTT and PBDTTPD polymers, however, reveal a similar degree of delocalization for both the HOMO and LUMO; the benzodithiophene unit allows the thienothiophene (or thieno[3,4-c]pyrrole-4,6-dione) acceptors to couple more strongly together so as to allow for greater delocalization. These differences, then, would provide for variations in negative polaron distributions (i.e., delocalized in the PCPDTBT and the benzodithiophene-containing polymers and localized on the benzothiadiazole acceptor in PCDTBT) should the polymers be reduced. Importantly, they are expected to impact the nature/strength of the optical excitations (vide infra).
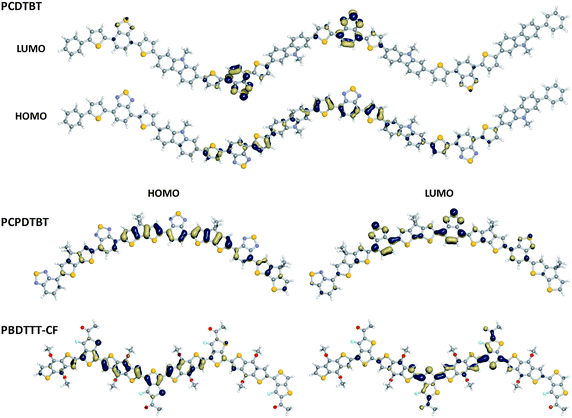 | ||
| Fig. 6 Pictorial representations of the single-electron HOMO and LUMO wave-function distributions as determined at the B3LYP/6-31G** level of theory. | ||
As noted above, VOC is observed in many instances to scale with the energetic difference between the ionization potential of the HTM and electron affinity of the ETM. Thus, if the same ETM material (e.g.PC61BM or PC71BM) is used in the solar cell, a direct comparison of the ionization potentials among the HTM polymers should provide a linear relationship. Fig. 7 shows a plot of the tetramer HOMO energies vs. the literature values of VOC for the polymers of interest. In general, there appears to be a rather good linear relationship between the tetramer HOMO energies and VOC. The lone exception is PCDTBT, which turns out to have the highest-reported VOC among these polymers (0.89 V).11 Since the exact nature and determination of VOC remains of considerable debate, it would seem particularly useful to try and better understand the origin of the PCDTBTVOC data. Importantly, recent analyses of bimolecular recombination dynamics in polymer–PCBM blends suggest that low charge-recombination rates can lead to lower dark currents and large VOC values.114
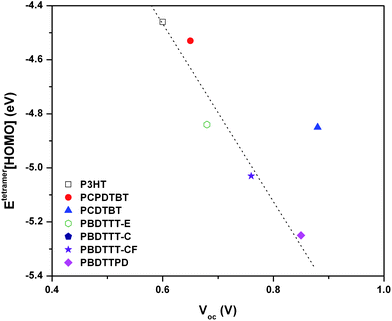 | ||
| Fig. 7 Tetramer HOMO energies (eV) determined at the B3LYP/6-31G** level of theory vs. literature-reported solar cellVOC (V)11,20,24,33,43–45,50,60,63,67,78,79 for the polymers of interest. Open data points are VOC determined in a device with PC61BM, while closed data points are for solar devices using PC71BM. As a point of reference, the LUMO energies of PC61BM and PC71BM determined at the B3LYP/6-31G** level of theory are −3.08 and −3.09 eV, respectively. | ||
b. Singlet excited-state transitions
We now turn our attention to the description of the optical excitation processes in these oligomers. Fig. 8 shows the evolution of the S0 → S1 vertical transition energies and transition dipole moments as a function of the number of repeat units as determined with time-dependent DFT at the B3LYP/6-31G** level of theory. As with the HOMO and LUMO energies, there occurs a reasonable linear relationship between the inverse number of repeat units and vertical excitation energy, which expectedly undergoes a systematic red-shift within the oligomer length range analyzed. The DA oligomers, as anticipated, present smaller singlet excited-state transition energies than the oligothiophenes. Overall, the calculated S0 → S1 vertical transition energies follow the reported measured absorption onsets for the polymers, with the calculated energies being slightly red-shifted with respect to the empirical data due to the effects of electron self-interaction in the general DFT formalism. There are, however, two exceptions: in the case of PBDTTPD, there appears to be a discrepancy between the time-dependent DFT results that appear to blue shift the transition energy vs. the reported absorption onset value, though it is noteworthy that the empirical spectrum is quite broad and the energetic difference reported between the absorption onset and maximum is ≈0.3 eV;71 for PCDTBT, the more extended conjugation path of the monomer induces too pronounced a red shift of the transition energy for the tetramer vs. the other considered tetramers.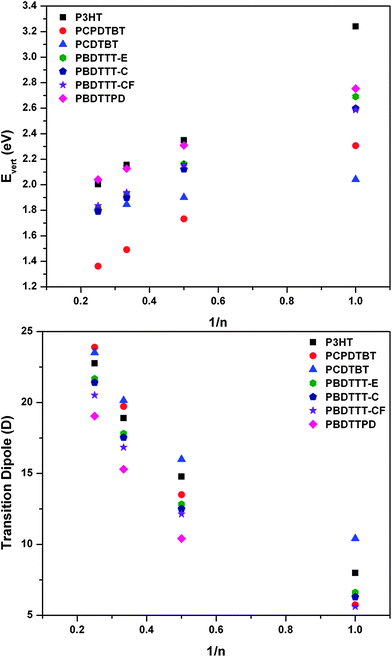 | ||
| Fig. 8 Evolution of the S0 → S1 (top) vertical transition energy (eV) and (bottom) transition dipole moment (Debye, D) with the inverse number of repeat units as determined with TDDFT at the B3LYP/6-31G** level of theory. | ||
Also as expected, the transition dipole moment, which is predominately directed along the long-axis of the oligomer backbone, increases with increasing oligomer length. The data reveal that the transition dipole moments for the benzodithiophene-containing polymers are consistently smaller than those of the other oligomer systems considered herein. However, this result could not be verified due to nominal molar extinction coefficient/absorption coefficient data in the literature.
Fig. 9 illustrates simulated absorption spectra based on Gaussian-function convolution (fwhm = 0.3 eV) of the tetramer vertical transition energies and oscillator strengths. Notably, good agreement exists between the overall shape of the simulated spectra for the tetramers and the literature-reported polymer (both solution and thin-film) absorption spectra.11,20,24,33,43–45,50,60,63,67,78,79 The spectra, in general, can be characterized as having one dominant, low-energy transition with large oscillator strength followed by a second, high-energy transition (or series of transitions) with smaller oscillator strengths. Two items of interest are evident for the benzodithiophene-containing polymers (PBDTTT series and PBDTTPD). First, as indicated above, the substitution of the thienothiophene acceptor by the thieno[3,4-c]pyrrole-4,6-dione leads to a blue shift of the low-energy optical absorption maximum; this appears to be consistent when comparing reported spectra for the copolymers containing the two acceptor units.33,36,44,71 Second, the low-energy band reported in the literature absorption spectra33,44,45,67,71,76,78 is comprised of two peaks that appear to have an energetic splitting on the order of 0.15–0.20 eV (∼1210–1615 cm−1), while the time-dependent DFT results reveal the presence of only one, dominant low-energy transition; this is related to the presence in the experimental data of a vibronic progression typical of the coupling of the electronic excitation with C–C stretching modes (such electron–vibration couplings have not been considered in the calculations reported here).
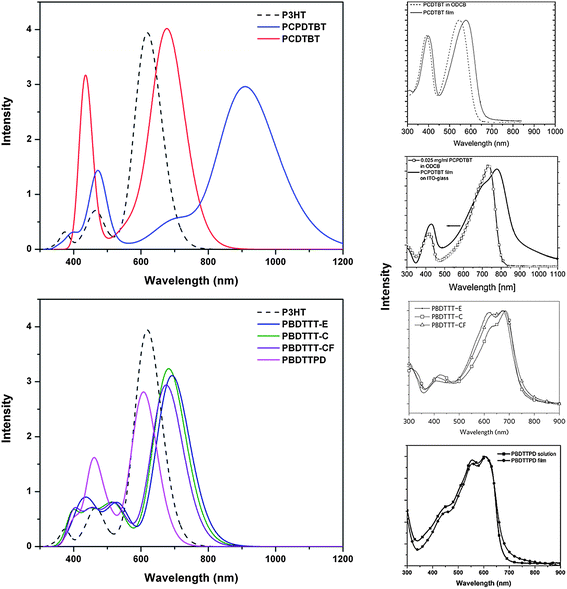 | ||
| Fig. 9 Simulated absorption spectra for the tetramers as determined with TDDFT at the B3LYP/6-31G** level of theory. P3HT (dashed line) is shown as a reference in both plots. Empirical UV-visspectra for the DA copolymers are shown for reference, adapted from refs. 9, 11, 33 and 252. | ||
As noted earlier, the use of molecular orbitals are a natural way to describe low-lying electronic transitions in conjugated materials. An alternative way to examine the nature of the electronic transition is through analysis of the transition density matrixvia natural transition orbitals (NTOs).265 NTOs are a convenient way to reduce the often complex descriptions of the mixed electronic configurations – i.e., linear combinations of multiple single-electron excitations among a number of occupied and unoccupied orbitals – that frequently describe an excited-state transition into a single hole–particle excitation – i.e., an excitation described by a single pair of generalized occupied and unoccupied orbitals. An eigenvalue λ denotes the fraction (e.g., weight) of the hole (in the occupied space)–particle (promoted into the unoccupied space) pair contribution for the given electronic transition described by the NTOs.203,265
Fig. 10 shows pictorial representations of the NTOs and corresponding λ values for the S0 → S1 transition of representative oligomers in the series. As the S0 → S1 transitions are predominantly HOMO → LUMO, the corresponding NTOs have character similar to the molecular orbital wave-function distributions depicted in Fig. 6. For PCPDTBT and the benzodithiophene-containing polymers, both the hole and electron are fairly well delocalized over the entire conjugated backbone, though there is a definite partial charge-transfer-like character to the excitation; indeed, the hole NTO is delocalized (through the acceptors) across the donor components, while the electron NTO has most of its density on the acceptor. The significant spatial overlap of the hole and electron leads to large transition dipole moments for these polymers.
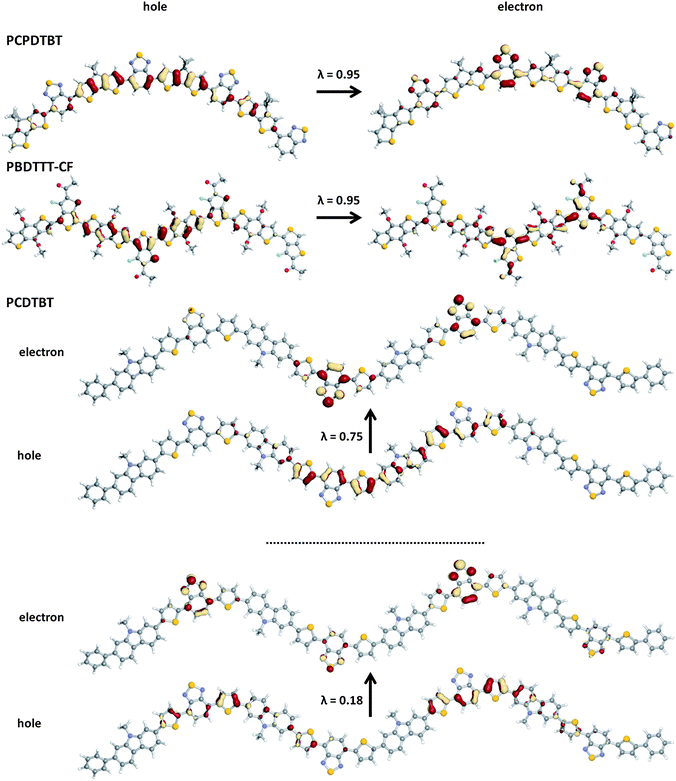 | ||
| Fig. 10 Pictorial representation of the natural transition orbitals (NTO) describing the S0 → S1 transition as determined with TDDFT at the B3LYP/6-31G** level of theory; λ is the fraction of the hole–particle contribution to the excitation. | ||
The situation is somewhat different for PCDTBT, where two sets of NTOs are needed to describe the transition (as the S0 → S1 transition is a linear combination of four single-electron excitations). Two items of interest stand out from these NTOs. First, while the predominant hole–particle couple is a partial charge-transfer-like transition, the hole maintains the fairly delocalized nature observed in the other oligomer systems while the electron is highly localized on the benzothiadiazole acceptors. Note, however, that the hole and electron reside within the same spatial extent of the oligomer, again leading to a rather large spatial overlap between the hole and electron NTOs, and, in turn, a significant transition dipole moment for the S0 → S1 transition. Second, the minor participant to the excited state is mostly localized on the p-dithiophenebenzothiadiazole subunits.
It is of interest, as well, to apply the NTO analysis to the examination of the transition largely responsible for the high-energy band, in particular because of the differences in absorption intensity within this region for these polymers. Fig. 11 shows the pictorial representations of the NTOs and corresponding λ values for the S0 → Sη transition of a number of oligomers in the series, where η is the number of the electronic transition dominating the high-energy absorbing feature. It is frequently stated in the DA copolymer literature that the secondary, high-energy band corresponds to a donor-localized π–π* transition. Referring back to Table 1, however, shows that the first electronic transition energies in the individual donor components – CBZ (4.04 eV, f = 0.03), CPDT (3.92 eV, f = 0.31) and BDT (3.86 eV, f = 0.19) – are considerably larger than where the high-energy bands appear in the simulated spectra (Fig. 7). The NTOs for these transitions reveal, in fact, that the high-energy transitions in the DA chains possess a substantial contribution of partial charge-transfer-like character. For the PBDTTT polymers, only one hole–particle couple is principally involved, and the NTOs are not as fully delocalized as in the S0 → S1 transition. For the other three polymers considered here, the electronic configurations are more highly mixed than the S0 → S1 transition; this provides an additional interesting contrast for PBDTTPDvs. the other PBDTTT polymers. For PCPDTBT and PCDTBT, which contain the benzothiadiazole acceptor, the hole in the main excitation is again delocalized, however, the electron also appears to be well delocalized over both the donor and acceptor, with the density on the benzothiadiazole unit confined to the thiadiazole. The secondary excitation in PCPDTBT is more reminiscent of the partial-charge-transfer transition observed for the S0 → S1 excitation, while in PCDTBT the secondary transition is (again) p-dithiophenebenzothiadiazole localized.
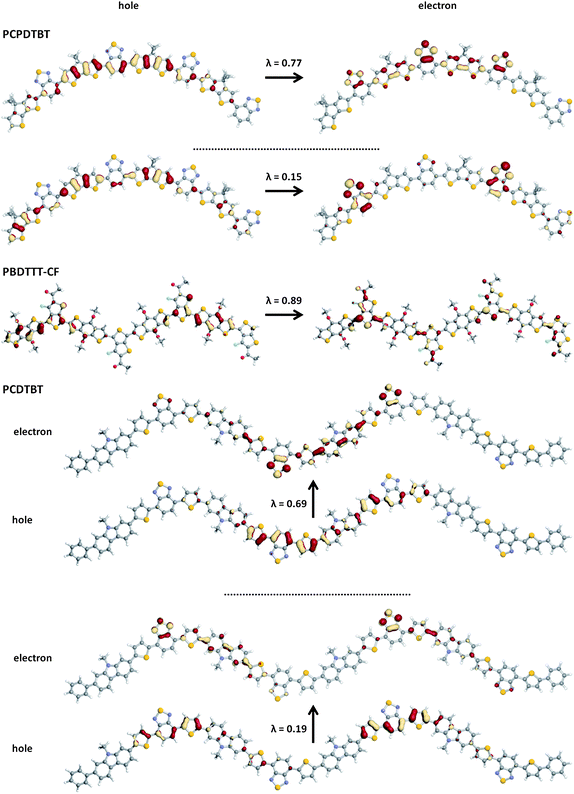 | ||
| Fig. 11 Pictorial representation of the natural transition orbitals (NTO) describing the S0 → Sη transition as determined with TDDFT at the B3LYP/6-31G** level of theory; λ is the fraction of the hole–particle contribution to the excitation; η = 14, 5 and 32 for PCPDTBT, PBDTTT-CF and PCDTBT, respectively. | ||
c. Triplet excited-state energies
Table 2 provides energies for the first triplet (T1) state for the tetramers and PC61BM/PC71BM at the B3LYP/6-31G** level of theory. The exchange energies (ΔEST), i.e., the differences between the S1 and T1 energies, were determined for the tetramers. Across the series, ΔEST was found to be on the order of 0.6 eV, consistent with previous experimental and theoretical evaluations for conjugated polymers.207| S0 → T1 | S0 → S1 | (ΔEST)a | |||
|---|---|---|---|---|---|
| ΔSCF | TDDFT | TDDFT | TDDFT | ||
| Adiabatic | Vertical | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| a ΔEST = E(S1) − E(T1). | |||||
| PC61BM | 1.69 | 1.83 | 1.52 | 1.93 | 0.41 |
| PC71BM | 1.50 | 1.68 | 1.48 | 2.01 | 0.53 |
| P3HT | 1.25 | 1.67 | 1.32 | 2.00 | 0.68 |
| PCPDTBT | 0.83 | 1.08 | 0.78 | 1.36 | 0.58 |
| PCDTBT | 1.53 | 1.74 | 1.20 | 1.82 | 0.62 |
| PBDTTT-E | 1.13 | 1.46 | 1.18 | 1.82 | 0.64 |
| PBDTTT-C | 1.11 | 1.44 | 1.15 | 1.79 | 0.64 |
| PBDTTT-CF | 1.13 | 1.50 | 1.22 | 1.84 | 0.62 |
| PBDTTPD | 1.51 | 1.75 | 1.43 | 2.04 | 0.61 |
The energetic positions of the HTM and ETM T1 states with respect to the charge-transfer state is a potentially important photocurrent loss mechanism in BHJ blends, as interfacial charge recombination might occur to the T1 state of either of the two materials.112 Whether determined by time-dependent DFT (vertical excitation only) or ΔSCF (both adiabatic and vertical excitations) methods, the T1 states of PCDTBT and PBDTTPD are higher than those of the other DA copolymers, while that of PCPDTBT is considerably lower, with the range of these energies covering approximately 0.4 eV (0.7 eV) via time-dependent DFT (ΔSCF). Focusing on the time-dependent DFT results, the T1 state energy for each of the DA copolymers studied herein is lower than that of either PC61BM or PC71BM. It would therefore be expected that if interfacial charge recombination to the T1 state were to occur that the recombination would occur on the polymer. Work is currently ongoing to determine the energetics of the charge-transfer states and rates of exciton dissociation and recombination for these polymer systems coupled with fullerenes; the results will be used to provide a better description of the efficiency of charge separation at the interface and identify potential loss mechanisms in devices made from these materials.
IV. Conclusions
We have provided an overview of the information an oligomer-based quantum-chemical characterization can provide on the intrinsic properties of polymers of interest for BHJ solar cell applications. The quantum-chemical methods were applied to the examination of a series of DA copolymer systems exploited in BHJ solar cells that have recently pushed forward the power conversion efficiencies of OPVs. The quantum-chemistry results show how the individual components that comprise the copolymers work in concert to provide some of their most important electronic and optical characteristics, and how the individual copolymers differ within the series.We need to keep in mind, however, that while such studies are very valuable, they constitute only a first component in the much broader multiscale modeling and experimental efforts that need to be performed to further push both the materials design and a complete understanding of the underlying photochemistry and device physics. For instance, while there are notable differences among the intrinsic properties of the DA copolymer systems, there is no single (or set of) intrinsic property (properties) that provides concrete evidence as to why the copolymers perform so well in BHJ solar cells.
Therefore, only an integrated multiscale theoretical approach, combined with experimental efforts for the determination of structure/morphology at the nano- and mesoscales, will develop the foundation required for broader understanding. While some examples of multiscale theoretical and/or empirical (or combinations thereof) studies exist, their frequency with regard to the rest of the literature is scarce.141,145,146,237,266,267 Such prospective multiscale theoretical efforts will have to examine not only how the donor–acceptor interactions in the polymer backbone control the intrinsic electronic and excited-state properties of the copolymers, but also how the intrinsic properties are affected by solid-state effects including polymer packing and film morphology and their dependence on molecular weight.
As an example, while the quantum-chemical calculations discussed above provide insight into the nature of the optical transition and the strength of the transition dipole moment of a single oligomer/polymer chain, the absorption coefficient of the thin film, which is a key parameter in the production of large photocurrents,48,94 is dependent on the intermolecular interactions and density of the polymer in the solid state; in other words, it is important to realize what leads either to a material having a rather poor absorption coefficient on the order of 104 cm−1 or to a material with an absorption coefficient on the order of 10−5–10−6 cm−1, which is desired to facilitate efficient thin-film devices. A further illustration concerns the recent report on the PBDTTT copolymers, suggesting that the preference of these polymers to adopt face-on orientations with respect to the substrate (vs. the edge-on orientation preferred by P3HT) as well as the ability to fine tune the inter-backbone distance by placing branched vs. straight alkyl chains along various parts of the copolymer backbone, play a key role in controlling the copolymer interactions with the fullerene ETM and ultimately provide a distinct reason behind the enhanced solar-cell power conversion efficiencies.262 Thus, the need to offer answers to such fundamental questions demands the development of integrated, multiscale modeling approaches that will enhance the theoretical understanding. It is through such systematic analyses that a more complete narrative will be gained and that concrete design principles for materials leading to high-efficiency device applications will truly become available.
Acknowledgements
This publication was based on work supported by the Center for Advanced Molecular Photovoltaics, Award No KUS-C1-015-21, made by King Abdullah University of Science and Technology (KAUST). The authors would like to thank Dr Veaceslav Coropceanu and Dr John Sears for valuable discussion and insight.VI. References
- J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti and A. B. Holmes, Nature, 1995, 376, 498–500 CrossRef CAS.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- G. Yu and A. J. Heeger, J. Appl. Phys., 1995, 78, 4510–4515 CrossRef CAS.
- A. Dhanabalan, J. L. J. van Dongen, J. K. J. van Duren, H. M. Janssen, P. A. van Hal and R. A. J. Janssen, Macromolecules, 2001, 34, 2495–2501 CrossRef CAS.
- A. Dhanabalan, J. K. J. van Duren, P. A. van Hal, J. L. J. van Dongen and R. A. J. Janssen, Adv. Funct. Mater., 2001, 11, 255–262 CrossRef CAS.
- S. A. Jenekhe, L. Lu and M. M. Alam, Macromolecules, 2001, 34, 7315–7324 CrossRef CAS.
- C. J. Brabec, C. Winder, N. S. Sariciftci, J. C. Hummelen, A. Dhanabalan, P. A. Van Hal and R. A. J. Janssen, Adv. Funct. Mater., 2002, 12, 709–712 CrossRef CAS.
- N.-K. Persson, M. Sun, P. Kjellberg, T. Pullerits and O. Inganäs, J. Chem. Phys., 2005, 123, 204718 CrossRef.
- D. Muhlbacher, M. Scharber, M. Morana, Z. G. Zhu, D. Waller, R. Gaudiana and C. Brabec, Adv. Mater., 2006, 18, 2884–2889 CrossRef.
- B. C. Thompson, Y.-G. Kim, T. D. McCarley and J. R. Reynolds, J. Am. Chem. Soc., 2006, 128, 12714–12725 CrossRef CAS.
- N. Blouin, A. Michaud and M. Leclerc, Adv. Mater., 2007, 19, 2295–2300 CrossRef CAS.
- K. F. Cheng, C. L. Liu and W. C. Chen, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 5872–5883 CrossRef CAS.
- K. Colladet, S. Fourier, T. J. Cleij, L. Lutsen, J. Gelan, D. Vanderzande, L. H. Nguyen, H. Neugebauer, S. Sariciftci, A. Aguirre, G. Janssen and E. Goovaerts, Macromolecules, 2007, 40, 65–72 CrossRef CAS.
- A. Gadisa, W. Mammo, L. M. Andersson, S. Admassie, F. Zhang, M. R. Andersson and O. Inganaes, Adv. Funct. Mater., 2007, 17, 3836–3842 CrossRef CAS.
- W. Tang, L. Ke, L. Tan, T. Lin, T. Kietzke and Z.-K. Chen, Macromolecules, 2007, 40, 6164–6171 CrossRef CAS.
- H. M. P. Wong, P. Wang, A. Abrusci, M. Svensson, M. R. Andersson and N. C. Greenham, J. Phys. Chem. C, 2007, 111, 5244–5249 CrossRef CAS.
- M. Zhang, C. Yang, A. K. Mishra, W. Pisula, G. Zhou, B. Schmaltz, M. Baumgarten and K. Mullen, Chem. Commun., 2007, 1704–1706 RSC.
- Z. Zhu, D. Waller, R. Gaudiana, M. Morana, D. Muhlbacher, M. Scharber and C. Brabec, Macromolecules, 2007, 40, 1981–1986 CrossRef CAS.
- N. Blouin and M. Leclerc, Acc. Chem. Res., 2008, 41, 1110–1119 CrossRef CAS.
- N. Blouin, A. Michaud, D. Gendron, S. Wakim, E. Blair, R. Neagu-Plesu, M. Belletete, G. Durocher, Y. Tao and M. Leclerc, J. Am. Chem. Soc., 2008, 130, 732–742 CrossRef CAS.
- J. Hou, H.-Y. Chen, S. Zhang, G. Li and Y. Yang, J. Am. Chem. Soc., 2008, 130, 16144–16145 CrossRef CAS.
- J. Hou, M.-H. Park, S. Zhang, Y. Yao, L.-M. Chen, J.-H. Li and Y. Yang, Macromolecules, 2008, 41, 6012–6018 CrossRef CAS.
- A. Kumar, J. G. Bokria, Z. Buyukmumcu, T. Dey and G. A. Sotzing, Macromolecules, 2008, 41, 7098–7108 CrossRef CAS.
- Y. Liang, S. Xiao, D. Feng and L. Yu, J. Phys. Chem. C, 2008, 112, 7866–7871 CrossRef CAS.
- A. J. Moule, A. Tsami, T. W. Buennagel, M. Forster, N. M. Kronenberg, M. Scharber, M. Koppe, M. Morana, C. J. Brabec, K. Meerholz and U. Scherf, Chem. Mater., 2008, 20, 4045–4050 CrossRef CAS.
- Q. Peng, K. Park, T. Lin, M. Durstock and L. Dai, J. Phys. Chem. B, 2008, 112, 2801–2808 CrossRef CAS.
- W. Walker, B. Veldman, R. Chiechi, S. Patil, M. Bendikov and F. Wudl, Macromolecules, 2008, 41, 7278–7280 CrossRef CAS.
- F. Zhang, J. Bijleveld, E. Perzon, K. Tvingstedt, S. Barrau, O. Inganaes and M. R. Andersson, J. Mater. Chem., 2008, 18, 5468–5474 RSC.
- E. Ahmed, F. S. Kim, H. Xin and S. A. Jenekhe, Macromolecules, 2009, 42, 8615–8618 CrossRef CAS.
- P. M. Beaujuge, W. Pisula, H. N. Tsao, S. Ellinger, K. Mullen and J. R. Reynolds, J. Am. Chem. Soc., 2009, 131, 7514–7515 CrossRef CAS.
- J. C. Bijleveld, M. Shahid, J. Gilot, M. M. Wienk and R. A. J. Janssen, Adv. Funct. Mater., 2009, 19, 3262–3270 CrossRef CAS.
- J. C. Bijleveld, A. P. Zoombelt, S. G. J. Mathijssen, M. M. Wienk, M. Turbiez, D. M. de Leeuw and R. A. J. Janssen, J. Am. Chem. Soc., 2009, 131, 16616–16617 CrossRef CAS.
- H.-Y. Chen, J. Hou, S. Zhang, Y. Liang, G. Yang, Y. Yang, L. Yu, Y. Wu and G. Li, Nat. Photonics, 2009, 3, 649–653 CrossRef CAS.
- D. Gedefaw, Y. Zhou, S. Hellstroem, L. Lindgren, L. M. Andersson, F. Zhang, W. Mammo, O. Inganaes and M. R. Andersson, J. Mater. Chem., 2009, 19, 5359–5363 RSC.
- S. Hellstroem, F. Zhang, O. Inganaes and M. R. Andersson, Dalton Trans., 2009, 10032–10039 RSC.
- J. Hou, H.-Y. Chen, S. Zhang, R. I. Chen, Y. Yang, Y. Wu and G. Li, J. Am. Chem. Soc., 2009, 131, 15586–15587 CrossRef CAS.
- J. Hou, H.-Y. Chen, S. Zhang and Y. Yang, J. Phys. Chem. C, 2009, 113, 21202–21207 CrossRef CAS.
- J. Hou, T. L. Chen, S. Zhang, H.-Y. Chen and Y. Yang, J. Phys. Chem. C, 2009, 113, 1601–1605 CrossRef CAS.
- L. Huo, H.-Y. Chen, J. Hou, T. L. Chen and Y. Yang, Chem. Commun., 2009, 5570–5572 RSC.
- L. Huo, J. Hou, H.-Y. Chen, S. Zhang, Y. Jiang, T. L. Chen and Y. Yang, Macromolecules, 2009, 42, 6564–6571 CrossRef CAS.
- O. Inganas, F. Zhang and M. R. Andersson, Acc. Chem. Res., 2009, 42, 1731–1739 CrossRef CAS.
- S. K. Lee, N. S. Cho, S. Cho, S.-J. Moon, J. K. Lee and G. C. Bazan, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 6873–6882 CrossRef CAS.
- Y. Liang, D. Feng, J. Guo, J. M. Szarko, C. Ray, L. X. Chen and L. Yu, Macromolecules, 2009, 42, 1091–1098 CrossRef CAS.
- Y. Liang, D. Feng, Y. Wu, S.-T. Tsai, G. Li, C. Ray and L. Yu, J. Am. Chem. Soc., 2009, 131, 7792–7799 CrossRef CAS.
- Y. Liang, Y. Wu, D. Feng, S.-T. Tsai, H.-J. Son, G. Li and L. Yu, J. Am. Chem. Soc., 2009, 131, 56–57 CrossRef CAS.
- L. J. Lindgren, F. Zhang, M. Andersson, S. Barrau, S. Hellstroem, W. Mammo, E. Perzon, O. Inganaes and M. R. Andersson, Chem. Mater., 2009, 21, 3491–3502 CrossRef CAS.
- J. G. Mei, N. C. Heston, S. V. Vasilyeva and J. R. Reynolds, Macromolecules, 2009, 42, 1482–1487 CrossRef CAS.
- R. Mondal, S. Ko, J. E. Norton, N. Miyaki, H. A. Becerril, E. Verploegen, M. F. Toney, J. L. Bredas, M. D. McGehee and Z. N. Bao, J. Mater. Chem., 2009, 19, 7195–7197 RSC.
- R. Mondal, N. Miyaki, H. A. Becerril, J. E. Norton, J. Parmer, A. C. Mayer, M. L. Tang, J.-L. Bredas, M. D. McGehee and Z. Bao, Chem. Mater., 2009, 21, 3618–3628 CrossRef CAS.
- S. H. Park, A. Roy, S. Beaupre, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–303 CrossRef CAS.
- T. T. Steckler, X. Zhang, J. Hwang, R. Honeyager, S. Ohira, X. H. Zhang, A. Grant, S. Ellinger, S. A. Odom, D. Sweat, D. B. Tanner, A. G. Rinzler, S. Barlow, J. L. Bredas, B. Kippelen, S. R. Marder and J. R. Reynolds, J. Am. Chem. Soc., 2009, 131, 2824–2826 CrossRef CAS.
- H. Xin, X. Guo, F. S. Kim, G. Ren, M. D. Watson and S. A. Jenekhe, J. Mater. Chem., 2009, 19, 5303–5310 RSC.
- S. Zhang, Y. Guo, H. Fan, Y. Liu, H.-Y. Chen, G. Yang, X. Zhan, Y. Liu, Y. Li and Y. Yang, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 5498–5508 CrossRef CAS.
- A. P. Zoombelt, M. Fonrodona, M. G. R. Turbiez, M. M. Wienk and R. A. J. Janssen, J. Mater. Chem., 2009, 19, 5336–5342 RSC.
- A. P. Zoombelt, M. Fonrodona, M. M. Wienk, A. B. Sieval, J. C. Hummelen and R. A. J. Janssen, Org. Lett., 2009, 11, 903–906 CrossRef CAS.
- A. P. Zoombelt, J. Gilot, M. M. Wienk and R. A. J. Janssen, Chem. Mater., 2009, 21, 1663–1669 CrossRef CAS.
- A. P. Zoombelt, M. A. M. Leenen, M. Fonrodona, Y. Nicolas, M. M. Wienk and R. A. J. Janssen, Polymer, 2009, 50, 4564–4570 CrossRef CAS.
- D. Baran, A. Balan, S. Celebi, B. Meana Esteban, H. Neugebauer, N. S. Sariciftci and L. Toppare, Chem. Mater., 2010, 22, 2978–2987 CrossRef CAS.
- P. M. Beaujuge, J. Subbiah, K. R. Choudhury, S. Ellinger, T. D. McCarley, F. So and J. R. Reynolds, Chem. Mater., 2010, 22, 2093–2106 CrossRef CAS.
- S. Beaupre, P.-L. T. Boudreault and M. Leclerc, Adv. Mater., 2010, 22, E6–E27 CrossRef CAS.
- C.-H. Chen, C.-H. Hsieh, M. Dubosc, Y.-J. Cheng and C.-S. Hsu, Macromolecules, 2010, 43, 697–708 CrossRef CAS.
- H.-Y. Chen, J. Hou, A. E. Hayden, H. Yang, K. N. Houk and Y. Yang, Adv. Mater., 2010, 22, 371–375 CrossRef CAS.
- J. Guo, Y. Liang, J. Szarko, B. Lee, H. J. Son, H. J. Son, B. S. Rolczynski, L. Yu and L. X. Chen, J. Phys. Chem. B, 2010, 114, 742–748 CrossRef CAS.
- L. Huo, J. Hou, S. Zhang, H.-Y. Chen and Y. Yang, Angew. Chem., Int. Ed., 2010, 49, 1500–1503 CAS.
- B.-S. Kim, B. Ma, V. R. Donuru, H. Liu and J. M. J. Frechet, Chem. Commun., 2010, 46, 4148–4150 RSC.
- J. Li and A. C. Grimsdale, Chem. Soc. Rev., 2010, 39, 2399–2410 RSC.
- Y. Liang, Z. Xu, J. Xia, S.-T. Tsai, Y. Wu, G. Li, C. Ray and L. Yu, Adv. Mater., 2010, 22, E135–E138 CrossRef CAS.
- B. Liu, A. Najari, C. Pan, M. Leclerc, D. Xiao and Y. Zou, Macromol. Rapid Commun., 2010, 31, 391–398 CrossRef CAS.
- C. F. N. Marchiori and M. Koehler, Synth. Met., 2010, 160, 643–650 CrossRef CAS.
- R. Mondal, H. A. Becerril, E. Verploegen, D. Kim, J. E. Norton, S. Ko, N. Miyaki, S. Lee, M. F. Toney, J.-L. Brédas, M. D. McGehee and Z. Bao, J. Mater. Chem., 2010, 20, 5823–5834 RSC.
- C. Piliego, T. W. Holcombe, J. D. Douglas, C. H. Woo, P. M. Beaujuge and J. M. J. Frechet, J. Am. Chem. Soc., 2010, 132, 7595–7597 CrossRef CAS.
- G. Qian and Z. Y. Wang, Can. J. Chem., 2010, 88, 192–201 CrossRef CAS.
- M. C. Scharber, M. Koppe, J. Gao, F. Cordella, M. A. Loi, P. Denk, M. Morana, H. J. Egelhaaf, K. Forberich, G. Dennler, R. Gaudiana, D. Waller, Z. G. Zhu, X. B. Shi and C. J. Brabec, Adv. Mater., 2010, 22, 367–370 CrossRef CAS.
- J.-S. Wu, Y.-J. Cheng, M. Dubosc, C.-H. Hsieh, C.-Y. Chang and C.-S. Hsu, Chem. Commun., 2010, 46, 3259–3261 RSC.
- X. Zhang, T. T. Steckler, R. R. Dasari, S. Ohira, W. J. Potscavage, Jr., S. P. Tiwari, S. Coppee, S. Ellinger, S. Barlow, J.-L. Bredas, B. Kippelen, J. R. Reynolds and S. R. Marder, J. Mater. Chem., 2010, 20, 123–134 RSC.
- Y. Zhang, S. K. Hau, H.-L. Yip, Y. Sun, O. Acton and A. K.-Y. Jen, Chem. Mater., 2010, 22, 2696–2698 CrossRef CAS.
- A. P. Zoombelt, S. G. J. Mathijssen, M. G. R. Turbiez, M. M. Wienk and R. A. J. Janssen, J. Mater. Chem., 2010, 20, 2240–2246 RSC.
- Y. Zou, A. Najari, P. Berrouard, S. Beaupre, B. Reda Aich, Y. Tao and M. Leclerc, J. Am. Chem. Soc., 2010, 132, 5330–5331 CrossRef CAS.
- J. Peet, J. Y. Kim, N. E. Coates, W. L. Ma, D. Moses, A. J. Heeger and G. C. Bazan, Nat. Mater., 2007, 6, 497–500 CrossRef CAS.
- Y. Liang and L. Yu, Acc. Chem. Res., 2010, 43, 1227–1236 CrossRef CAS.
- J. Roncali, Chem. Rev., 1997, 97, 173–205 CrossRef CAS.
- H. A. M. van Mullekom, J. Vekemans, E. E. Havinga and E. W. Meijer, Mater. Sci. Eng., R, 2001, 32, 1–40 CrossRef.
- A. Ajayaghosh, Chem. Soc. Rev., 2003, 32, 181–191 RSC.
- K. M. Coakley and M. D. McGehee, Chem. Mater., 2004, 16, 4533–4542 CrossRef CAS.
- H. Hoppe and N. S. Sariciftci, J. Mater. Res., 2004, 19, 1924–1945 CAS.
- H. Spanggaard and F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2004, 83, 125–146 CrossRef CAS.
- T. L. Benanti and D. Venkataraman, Photosynth. Res., 2006, 87, 73–81 CrossRef CAS.
- M. C. Scharber, D. Wuhlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. L. Brabec, Adv. Mater., 2006, 18, 789–794 CrossRef CAS.
- P. W. M. Blom, V. D. Mihailetchi, L. J. A. Koster and D. E. Markov, Adv. Mater., 2007, 19, 1551–1566 CrossRef CAS.
- E. Bundgaard and F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2007, 91, 954–985 CrossRef CAS.
- S. Guenes, H. Neugebauer and N. S. Sariciftci, Chem. Rev., 2007, 107, 1324–1338 CrossRef.
- J. Roncali, Macromol. Rapid Commun., 2007, 28, 1761–1775 CrossRef CAS.
- R. Kroon, M. Lenes, J. C. Hummelen, P. W. M. Blom and B. De Boer, Polym. Rev., 2008, 48, 531–582 Search PubMed.
- B. C. Thompson and J. M. J. Fréchet, Angew. Chem., Int. Ed., 2008, 47, 58–77 CrossRef.
- J. L. Bredas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1699 CrossRef CAS.
- Y. J. Cheng, S. H. Yang and C. S. Hsu, Chem. Rev., 2009, 109, 5868–5923 CrossRef CAS.
- P. Heremans, D. Cheyns and B. P. Rand, Acc. Chem. Res., 2009, 42, 1740–1747 CrossRef CAS.
- B. Kippelen and J. L. Bredas, Energy Environ. Sci., 2009, 2, 251–261 RSC.
- J. Peet, A. J. Heeger and G. C. Bazan, Acc. Chem. Res., 2009, 42, 1700–1708 CrossRef CAS.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS.
- A. W. Hains, Z. Liang, M. A. Woodhouse and B. A. Gregg, Chem. Rev., 2010, 110, 6689–6735 CrossRef CAS.
- D. Venkataraman, S. Yurt, B. H. Venkatraman and N. Gavvalapalli, J. Phys. Chem. Lett., 2010, 1, 947–958 Search PubMed.
- C. J. Brabec, S. Gowrisanker, J. J. M. Halls, D. Laird, S. Jia and S. P. Williams, Adv. Mater., 2010, 22, 3839–3856 CrossRef CAS.
- P.-L. Boudreault, A. Najari and M. Leclerc, Chem. Mater., 2011, 23, 456–469 CrossRef CAS.
- C. W. Tang, Appl. Phys. Lett., 1986, 48, 183–185 CrossRef CAS.
- We are using here the HTM and ETM notations to denote the two components of the active layer, instead of the more conventional donor and acceptor (D/A) notations, in order to prevent any confusion with the donor/acceptor character of the copolymers used in the BHJ solar cells.
- A. C. Morteani, P. Sreearunothai, L. M. Herz, R. H. Friend and C. Silva, Phys. Rev. Lett., 2004, 92, 247402 CrossRef.
- M. D. Perez, C. Borek, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9281–9286 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganas and J. V. Manca, Nat. Mater., 2009, 8, 904–909 CrossRef CAS.
- S. Westenhoff, I. A. Howard, J. M. Hodgkiss, K. R. Kirov, H. A. Bronstein, C. K. Williams, N. C. Greenham and R. H. Friend, J. Am. Chem. Soc., 2008, 130, 13653–13658 CrossRef CAS.
- H. Ohkita, S. Cook, Y. Astuti, W. Duffy, S. Tierney, W. Zhang, M. Heeney, I. McCulloch, J. Nelson, D. D. C. Bradley and J. R. Durrant, J. Am. Chem. Soc., 2008, 130, 3030–3042 CrossRef CAS.
- D. Veldman, S. C. J. Meskers and R. A. J. Janssen, Adv. Funct. Mater., 2009, 19, 1939–1948 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganas and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- A. Maurano, R. Hamilton, C. G. Shuttle, A. M. Ballantyne, J. Nelson, B. O'Regan, W. Zhang, I. McCulloch, H. Azimi, M. Morana, C. J. Brabec and J. R. Durrant, Adv. Mater., 2010, 22, 4987–4992 CrossRef CAS.
- T. M. Clarke, A. Ballantyne, S. Shoaee, Y. W. Soon, W. Duffy, M. Heeney, I. McCulloch, J. Nelson and J. R. Durrant, Adv. Mater., 2010, 22, 5287–5291 CrossRef CAS.
- R. D. Pensack and J. B. Asbury, J. Phys. Chem. Lett., 2010, 1, 2255–2263 Search PubMed.
- J. Lee, K. Vandewal, S. R. Yost, M. E. Bahlke, L. Goris, M. A. Baldo, J. V. Manca and T. V. Voorhis, J. Am. Chem. Soc., 2010, 132, 11878–11880 CrossRef CAS.
- J. L. Bredas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva, Y. Olivier, R. Silbey and J. L. Bredas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS.
- W. L. Ma, C. Y. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617–1622 CrossRef CAS.
- G. Li, V. Shrotriya, J. S. Huang, Y. Yao, T. Moriarty, K. Emery and Y. Yang, Nat. Mater., 2005, 4, 864–868 CAS.
- Y. Kim, S. Cook, S. M. Tuladhar, S. A. Choulis, J. Nelson, J. R. Durrant, D. D. C. Bradley, M. Giles, I. Mcculloch, C. S. Ha and M. Ree, Nat. Mater., 2006, 5, 197–203 CrossRef CAS.
- K. Kim, J. Liu, M. A. G. Namboothiry and D. L. Carroll, Appl. Phys. Lett., 2007, 90, 163511 CrossRef.
- M. D. Irwin, B. Buchholz, A. W. Hains, R. P. H. Chang and T. J. Marks, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2783–2787 CrossRef CAS.
- Note that the monomer length to represent P3HT was chosen to be three thiophene units so as to ensure a similar number of double bonds with the other systems studied herein.
- U. Salzner, J. B. Lagowski, P. G. Pickup and R. A. Poirier, J. Comput. Chem., 1997, 18, 1943–1953 CrossRef CAS.
- J. Cornil, I. Gueli, A. Dkhissi, J. C. Sancho-Garcia, E. Hennebicq, J. P. Calbert, V. Lemaur, D. Beljonne and J. L. Bredas, J. Chem. Phys., 2003, 118, 6615–6623 CrossRef CAS.
- J. C. Sancho-Garcia, C. L. Foden, I. Grizzi, G. Greczynski, M. P. de Jong, W. R. Salaneck, J. L. Bredas and J. Cornil, J. Phys. Chem. B, 2004, 108, 5594–5599 CrossRef.
- J.-F. Wang, J.-K. Feng, A.-M. Ren, X.-D. Liu, Y.-G. Ma, P. Lu and H.-X. Zhang, Macromolecules, 2004, 37, 3451–3458 CrossRef CAS.
- L. Yang, J.-K. Feng, Y. Liao and A.-M. Ren, Polymer, 2005, 46, 9955–9964 CrossRef CAS.
- L. Yang, J.-K. Feng and A.-M. Ren, J. Comput. Chem., 2005, 26, 969–979 CrossRef CAS.
- L. Yang, J.-K. Feng and A.-M. Ren, J. Org. Chem., 2005, 70, 5987–5996 CrossRef CAS.
- L. Yang, Y. Liao, J.-K. Feng and A.-M. Ren, J. Phys. Chem. A, 2005, 109, 7764–7774 CrossRef CAS.
- C.-L. Pai, C.-L. Liu, W.-C. Chen and S. A. Jenekhe, Polymer, 2006, 47, 699–708 CrossRef CAS.
- U. Salzner, O. Karalti and S. Durdagi, J. Mol. Model., 2006, 12, 687–701 CrossRef CAS.
- L. Yang, J.-K. Feng, A.-M. Ren and J.-Z. Sun, Polymer, 2006, 47, 1397–1404 CrossRef CAS.
- J. Gierschner, J. Cornil and H.-J. Egelhaaf, Adv. Mater., 2007, 19, 173–191 CrossRef CAS.
- B. M. Medina, A. Van Vooren, P. Brocorens, J. Gierschner, M. Shkunov, M. Heeney, I. McCulloch, R. Lazzaroni and J. Cornil, Chem. Mater., 2007, 19, 4949–4956 CrossRef CAS.
- A. S. Ozen, C. Atilgan and G. Sonmez, J. Phys. Chem. C, 2007, 111, 16362–16371 CrossRef.
- L. Yang, J.-K. Feng and A.-M. Ren, THEOCHEM, 2007, 816, 161–170 CrossRef CAS.
- B. P. Karsten, L. Viani, J. Gierschner, J. Cornil and R. A. J. Janssen, J. Phys. Chem. A, 2008, 112, 10764–10773 CrossRef CAS.
- A. Van Vooren, J.-S. Kim and J. Cornil, ChemPhysChem, 2008, 9, 989–993 CrossRef CAS.
- L. Zhang, Q. Y. Zhang, H. Ren, H. L. Yan, J. P. Zhang, H. P. Zhang and J. W. Gu, Sol. Energy Mater. Sol. Cells, 2008, 92, 581–587 CrossRef CAS.
- Y. Ding, J. F. Zhao, X. S. Wang, S. S. Liu and F. C. Ma, Chin. J. Chem. Phys., 2009, 22, 389–394 CrossRef CAS.
- B. P. Karsten, J. C. Bijleveld, L. Viani, J. Cornil, J. Gierschner and R. A. J. Janssen, J. Mater. Chem., 2009, 19, 5343–5350 RSC.
- B. P. Karsten, L. Viani, J. Gierschner, J. Cornil and R. A. J. Janssen, J. Phys. Chem. A, 2009, 113, 10343–10350 CrossRef.
- D. D. Liang, S. S. Tang, J. B. Liu, J. H. Liu and L. J. Kang, THEOCHEM, 2009, 908, 102–106 CrossRef CAS.
- Q. Peng, J. Xu and W. Zheng, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 3399–3408 CrossRef CAS.
- Y. H. Tian and M. Kertesz, Macromolecules, 2009, 42, 6123–6127 CrossRef CAS.
- J. M. Winfield, A. Van Vooren, M.-J. Park, D.-H. Hwang, J. Cornil, J.-S. Kim and R. H. Friend, J. Chem. Phys., 2009, 131, 035104 CrossRef.
- J. G. Kang, H. J. Kim, Y. K. Jeong, M. K. Nah, C. Park, Y. J. Bae, S. W. Lee and I. T. Kim, J. Phys. Chem. B, 2010, 114, 3791–3798 CrossRef CAS.
- J. M. Szarko, B. S. Rolczynski, J. Guo, Y. Liang, F. He, M. W. Mara, L. Yu and L. X. Chen, J. Phys. Chem. B, 2010, 114, 14505–14513 CrossRef CAS.
- S. Ko, R. Mondal, C. Risko, J. K. Lee, S. Hong, M. D. McGehee, J.-L. Bredas and Z. Bao, Macromolecules, 2010, 43, 6685–6698 CrossRef CAS.
- J. Rissler, Chem. Phys. Lett., 2004, 395, 92–96 CrossRef CAS.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902 CrossRef.
- M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977, 99, 4899 CrossRef CAS.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221–264 CrossRef CAS.
- C. A. White, B. G. Johnson, P. M. W. Gill and M. Head-Gordon, Chem. Phys. Lett., 1994, 230, 8–16 CrossRef CAS.
- C. A. White, B. G. Johnson, P. M. W. Gill and M. Head-Gordon, Chem. Phys. Lett., 1996, 253, 268–278 CrossRef CAS.
- G. E. Scuseria, J. Phys. Chem. A, 1999, 103, 4782–4790 CrossRef CAS.
- B. J. Zhou, V. L. Ligneres and E. A. Carter, J. Chem. Phys., 2005, 122, 044103 CrossRef.
- D. R. Bowler and T. Miyazaki, J. Phys.: Condens. Matter, 2010, 22, 074207 CrossRef CAS.
- F. Wudl, M. Kobayashi and A. J. Heeger, J. Org. Chem., 1984, 49, 3382–3384 CrossRef CAS.
- J. L. Bredas, J. Chem. Phys., 1985, 82, 3808–3811 CrossRef CAS.
- J. L. Bredas, A. J. Heeger and F. Wudl, J. Chem. Phys., 1986, 85, 4673–4678 CrossRef CAS.
- R. Jira and H. Braunling, Synth. Met., 1987, 17, 691–696 CrossRef CAS.
- H. Braunling and R. Jira, Synth. Met., 1987, 20, 375–378 CrossRef.
- I. Hoogmartens, P. Adriaensens, D. Vanderzande, J. Gelan, C. Quattrocchi, R. Lazzaroni and J. L. Bredas, Macromolecules, 1992, 25, 7347–7356 CrossRef CAS.
- C. X. Cui, M. Kertesz and Y. Jiang, J. Phys. Chem., 1990, 94, 5172–5179 CrossRef CAS.
- A. Karpfen and M. Kertesz, J. Phys. Chem., 1991, 95, 7680–7681 CrossRef CAS.
- E. E. Havinga, W. Tenhoeve and H. Wynberg, Polym. Bull., 1992, 29, 119–126 CAS.
- E. E. Havinga, W. Tenhoeve and H. Wynberg, Synth. Met., 1993, 55, 299–306 CrossRef CAS.
- G. Cirmi, D. Brida, A. Gambetta, M. Piacenza, F. D. Sala, L. Favaretto, G. Cerullo and G. Lanzani, Phys. Chem. Chem. Phys., 2010, 12, 7917–7923 RSC.
- M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887–10893 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2003, 107, 8377–8379 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690–7697 CrossRef CAS.
- E. C. Lee, B. H. Hong, J. Y. Lee, J. C. Kim, D. Kim, Y. Kim, P. Tarakeshwar and K. S. Kim, J. Am. Chem. Soc., 2005, 127, 4530–4537 CrossRef CAS.
- K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2006, 110, 4397–4404 CrossRef CAS.
- A. L. Ringer, M. O. Sinnokrot, R. P. Lively and C. D. Sherrill, Chem.–Eur. J., 2006, 12, 3821–3828 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 878–886 CrossRef CAS.
- S. Tsuzuki, T. Uchimaru and M. Mikami, J. Phys. Chem. A, 2006, 110, 2027–2033 CrossRef CAS.
- A. L. Ringer and C. D. Sherrill, J. Am. Chem. Soc., 2009, 131, 4574–4575 CrossRef CAS.
- J. Vura-Weis, M. R. Wasielewski, A. K. Thazhathveetil and F. D. Lewis, J. Am. Chem. Soc., 2009, 131, 9722–9727 CrossRef CAS.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- S. W. Staley and J. T. Strnad, J. Phys. Chem., 1994, 98, 116–121 CrossRef CAS.
- J. F. Janak, Phys. Rev. B, 1978, 18, 7165–7168 CrossRef CAS.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- M. R. Silva-Junior and W. Thiel, J. Chem. Theory Comput., 2010, 6, 1546–1564 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- E. K. U. Gross and W. Kohn, Phys. Rev. Lett., 1985, 55, 2850–2852 CrossRef CAS.
- J. Tao, S. Tretiak and J.-X. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235110 CrossRef.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106 CrossRef.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- H. Meier, U. Stalmach and H. Kolshorn, Acta Polym., 1997, 48, 379–384 CrossRef CAS.
- W. Kuhn, Helv. Chim. Acta, 1948, 31, 1780 CrossRef CAS.
- S. S. Zade, N. Zamoshchik and M. Bendikov, Acc. Chem. Res., 2011, 44, 14–24 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS.
- A. Kohler, D. A. dos Santos, D. Beljonne, Z. Shuai, J. L. Bredas, A. B. Holmes, A. Kraus, K. Mullen and R. H. Friend, Nature, 1998, 392, 903–906 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- A. Kohler and H. Bassler, Mater. Sci. Eng., R, 2009, 66, 71–109 CrossRef.
- A. Kohler and D. Beljonne, Adv. Funct. Mater., 2004, 14, 11–18 CrossRef.
- R. Schueppel, K. Schmidt, C. Uhrich, K. Schulze, D. Wynands, J. L. Bredas, E. Brier, E. Reinold, H. B. Bu, P. Baeuerle, B. Maennig, M. Pfeiffer and K. Leo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085311 CrossRef.
- H. Wiesenhofer, D. Beljonne, G. D. Scholes, E. Hennebicq, J. L. Bredas and E. Zojer, Adv. Funct. Mater., 2005, 15, 155–160 CrossRef.
- E. E. Neuteboom, S. C. J. Meskers, P. A. Van Hal, J. K. J. Van Duren, E. W. Meijer, R. A. J. Janssen, H. Dupin, G. Pourtois, J. Cornil, R. Lazzaroni, J.-L. Bredas and D. Beljonne, J. Am. Chem. Soc., 2003, 125, 8625–8638 CrossRef CAS.
- B. P. Krueger, G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 1998, 102, 5378–5386 CrossRef CAS.
- S. Marguet, D. Markovitsi, P. Millie, H. Sigal and S. Kumar, J. Phys. Chem. B, 1998, 102, 4697–4710 CrossRef CAS.
- H. Yamagata, J. E. Norton, E. Hontz, Y. Olivier, D. Beljonne, J. L. Bredas, R. J. Silbey and F. C. Spano, 2010, submitted for publication.
- T. Kawatsu, V. Coropceanu, A. J. Ye and J. L. Bredas, J. Phys. Chem. C, 2008, 112, 3429–3433 CrossRef CAS.
- M. Linares, D. Beljonne, J. Cornil, K. Lancaster, J. L. Bredas, S. Verlaak, A. Mityashin, P. Heremans, A. Fuchs, C. Lennartz, J. Ide, R. Mereau, P. Aurel, L. Ducasse and F. Castet, J. Phys. Chem. C, 2010, 114, 3215–3224 CrossRef CAS.
- Y. P. Yi, V. Coropceanu and J. L. Bredas, J. Am. Chem. Soc., 2009, 131, 15777–15783 CrossRef CAS.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Mater. Chem., 2011, 21, 1479–1486 RSC.
- P. J. Bounds and R. W. Munn, Chem. Phys., 1979, 44, 103–112 CrossRef CAS.
- P. J. Bounds and R. W. Munn, Chem. Phys., 1981, 59, 41–45 CrossRef CAS.
- P. J. Bounds and R. W. Munn, Chem. Phys., 1981, 59, 47–53 CrossRef CAS.
- I. Eisenstein, R. W. Munn and P. J. Bounds, Chem. Phys., 1983, 74, 307–320 CrossRef CAS.
- I. Eisenstein and R. W. Munn, Chem. Phys., 1983, 79, 189–195 CrossRef CAS.
- I. Eisenstein and R. W. Munn, Chem. Phys., 1983, 77, 47–61 CrossRef CAS.
- Z. G. Soos, E. V. Tsiper and R. A. Pascal, Chem. Phys. Lett., 2001, 342, 652–658 CrossRef.
- E. V. Tsiper and Z. G. Soos, Phys. Rev. B: Condens. Matter, 2001, 64, 195124 CrossRef.
- E. V. Tsiper, Z. G. Soos, W. Gao and A. Kahn, Chem. Phys. Lett., 2002, 360, 47–52 CrossRef CAS.
- E. V. Tsiper and Z. G. Soos, Phys. Rev. B: Condens. Matter, 2003, 68, 085301 CrossRef.
- J. E. Norton and J. L. Bredas, J. Am. Chem. Soc., 2008, 130, 12377–12384 CrossRef CAS.
- S. Verlaak and P. Heremans, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115127 CrossRef.
- F. Castet, P. Aurel, A. Fritsch, L. Ducasse, D. Liotard, M. Linares, J. Cornil and D. Beljonne, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115210 CrossRef.
- S. Verlaak, D. Beljonne, D. Cheyns, C. Rolin, M. Linares, F. Castet, J. Cornil and P. Heremans, Adv. Funct. Mater., 2009, 19, 3809–3814 CrossRef CAS.
- D. Beljonne, J. Cornil, L. Muccioli, C. Zannoni, J.-L. Bredas and F. Castet, Chem. Mater., 2010 Search PubMed , ASAP.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- J. Nelson, J. J. Kwiatkowski, J. Kirkpatrick and J. M. Frost, Acc. Chem. Res., 2009, 42, 1768–1778 CrossRef CAS.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Phys. Rev. Lett., 2006, 96, 196806 CrossRef.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Surf. Sci., 2006, 600, 4548–4562 CrossRef CAS.
- P. C. Rusu and G. Brocks, J. Phys. Chem. B, 2006, 110, 22628–22634 CrossRef CAS.
- P. C. Rusu and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 073414 CrossRef.
- L. Segev, A. Salomon, A. Natan, D. Cahen, L. Kronik, F. Amy, C. K. Chan and A. Kahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165323 CrossRef.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Nano Lett., 2007, 7, 932–940 CrossRef.
- A. Natan, L. Kronik, H. Haick and R. T. Tung, Adv. Mater., 2007, 19, 4103–4117 CrossRef CAS.
- P. B. Paramonov, S. A. Paniagua, P. J. Hotchkiss, S. C. Jones, N. R. Armstrong, S. R. Marder and J. L. Bredas, Chem. Mater., 2008, 20, 5131–5133 CrossRef CAS.
- P. J. Hotchkiss, H. Li, P. B. Paramonov, S. A. Paniagua, S. C. Jones, N. R. Armstrong, J. L. Bredas and S. R. Marder, Adv. Mater., 2009, 21, 4496–4501 CrossRef CAS.
- H. Li, Y. Q. Duan, P. Paramonov, V. Coropceanu and J. L. Bredas, J. Electron Spectrosc. Relat. Phenom., 2009, 174, 70–77 CrossRef CAS.
- P. C. Rusu, G. Giovannetti, C. Weijtens, R. Coehoorn and G. Brocks, J. Phys. Chem. C, 2009, 113, 9974–9977 CrossRef CAS.
- H. Li, P. Paramonov and J. L. Bredas, J. Mater. Chem., 2010, 20, 2630–2637 RSC.
- P. C. Rusu, G. Giovannetti, C. Weijtens, R. Coehoorn and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125403 CrossRef.
- G. Heimel, I. Salzmann, S. Duhm, J. P. Rabe and N. Koch, Adv. Funct. Mater., 2009, 19, 3874–3879 CrossRef CAS.
- Y. Zhang, S. K. Hau, H. L. Yip, Y. Sun, O. Acton and A. K. Y. Jen, Chem. Mater., 2010, 22, 2696–2698 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.2), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- M. A. Thompson, Planaria Software, LLC, Seattle, WA Search PubMed.
- J. M. Szarko, J. Guo, Y. Liang, B. Lee, B. S. Rolczynski, J. Strzalka, T. Xu, S. Loser, T. J. Marks, L. Yu and L. X. Chen, Adv. Mater., 2010, 22, 5468–5472 CrossRef CAS.
- R. Rieger, D. Beckmann, A. Mavrinskiy, M. Kastler and K. Mullen, Chem. Mater., 2010, 22, 5314–5318 CrossRef CAS.
- J. L. Bredas, G. B. Street, B. Themans and J. M. Andre, J. Chem. Phys., 1985, 83, 1323–1329 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- P. Brocorens, A. Van Vooren, M. L. Chabinyc, M. F. Toney, M. Shkunov, M. Heeney, I. McCulloch, J. Cornil and R. Lazzaroni, Adv. Mater., 2009, 21, 1193–1198 CrossRef CAS.
- C. Muller, E. G. Wang, L. M. Andersson, K. Tvingstedt, Y. Zhou, M. R. Andersson and O. Inganas, Adv. Funct. Mater., 2010, 20, 2124–2131 CrossRef.
| This journal is © The Royal Society of Chemistry 2011 |
