Conformational states of nucleic acid–peptide complexes monitored by acoustic wave propagation and molecular dynamics simulation†
Jonathan S.
Ellis‡
a and
Michael
Thompson
*ab
aInstitute of Biomaterials and Biomedical Engineering, University of Toronto, 164 College Street, Toronto, Canada
bDepartment of Chemistry, University of Toronto, 80 St. George Street, Toronto, ON, Canada. E-mail: mikethom@chem.utoronto.ca
First published on 15th November 2010
Abstract
Material properties, interfacial slip, and conformational changes are modelled for the immobilisation of HIV-1 TAR RNA and subsequent binding of tatpeptide fragments to the surface of a transverse-shear mode acoustic wave device. The modelling is based on previously-reported experimental results [N. Tassew, Ph.D. Thesis, 2003, University of Toronto, Toronto, Canada] and follows on from a previous modelling paper [J. S. Ellis and M. Thompson, Langmuir, 2010, 26, 11558]. A three-layer shear acoustic model is used to represent the system, where the layers describe the biomolecular monolayers and the contacting bulk buffer solution. Each layer is described by geometric, viscoelastic, and interfacial parameters, which are numerically fit to experimental values using a two-parameter minimisation algorithm. The neutravidin and TAR are described as distinct viscoelastic monolayers. Binding of tatpeptide fragment to the TAR monolayer is modelled using a complex slip parameter and a change in length, corresponding to a straightening of the molecule. Molecular dynamics (MD) simulations of the TAR-tat fragment system are performed to corroborate the modelling results. Starting structures are computed by molecular docking, and MD simulations of TAR complexed with various length tat fragments are described. The simulations are in general agreement with the modelling results and literature values from similar molecular dynamics experiments. A new parameter is introduced to describe biomolecule–solvent affinity, and is compared to interfacial coupling values obtained from modelling. This research demonstrates that acoustic wave devices can be used to detect conformational shifts in surface-attached biomolecules, provided molecular details about such shifts are known.
Introduction
The detection of conformational and structural changes in biomolecules is of great interest in basic biophysical chemistry, bioanalytical chemistry and the pharmaceutical sciences. Molecular conformation in a specific environment determines the behaviour and function of a biomolecule. In addition to interactions with other molecules, tertiary structure plays an important role in the biochemistry that lies behind many diseases. Many techniques exist for detecting molecular folding in solution, including nuclear magnetic resonance spectroscopy,1 circular dichroism,2 and gel electrophoresis.3,4 As well, protein folding can be predicted computationally using molecular dynamics simulations.5,6The conformation of biomolecules at the solid–liquid interface is also of great interest, especially in basic surface science and biosensor technology. For medical equipment and implants, the adsorption of biomolecules onto surfaces can have important implications with respect to the immune response. For this reason, fundamental knowledge concerning the nature of biomolecular adsorption to surfaces is essential. Accordingly, the ability to detect surface properties and conformation in real-time is of great interest in drug discovery and biosensing, yielding information on rate constants and binding pathways. A number of techniques exist to observe conformational dynamics on surfaces, such as atomic force microscopy,7surface plasmon resonance,8,9 and scanning probe technologies such as the scanning Kelvin nanoprobe.10–12 Of these techniques, only SPR offers real-time detection.
Acoustic physics has been recently proposed to detect conformational shifts of biomolecules attached to surfaces, specifically the transverse shear mode acoustic wave biosensor (TSM).13,14 The TSM device offers sensitive, label free, online detection of biochemical interactions, can also be employed in a flow injection system, and has potential for miniaturization. It has been applied widely in the field of bioanalytical chemistry in recent years, largely owing to these properties.13 Applications of the TSM include the detection of nucleic acid hybridization,15 immunochemistry,16 and protein interactions.17,18 This sensor has recently been used to detect living cells on surfaces.19–22 Traditionally, this device has been used as a gravimetric detector, but it is sensitive to many more factors than simple mass adsorption. These include viscoelastic effects of an adsorbed film and interfacial coupling between the surface and the contacting buffer liquid.
In particular, changes in the material and interfacial properties of an adsorbed biochemical monolayer on the sensor surface are converted to acoustic and electrical signals. Since conformational changes in an adsorbed biochemical monolayer can lead to mechanical and chemical changes at the surface, this sensor can be used to detect biomolecular interactions and structural changes. The challenge exists, however, in separating the sensor response due to monolayer mechanical properties from that due to mass adsorption, interfacial effects, and the buffer liquid. A number of recent studies have used this sensor to detect conformational shifts in representative proteins and nucleic acids, upon interaction with ligands known to induce such changes.23–25 In these studies, the device signals were contrary to conventional behaviour, which were attributed to conformational shifts or interfacial slip. However, these effects were only treated qualitatively, and not considered quantitatively. In addition, these various studies did not address the mechanical properties of the monolayer under consideration.
In this paper, we consider experimental results involving the immobilisation of biotinylated TAR, a segment of HIV-1 RNA involved in viral replication, to a modified surface of a transverse shear mode acoustic wave device (TSM).24 This is followed by the subsequent binding of fragments of HIV-1tatpeptide to the immobilised TAR, an interaction known to induce a conformational shift in the viral RNA.26 Adsorption of the macromolecule and subsequent binding of ligands lead to signals that are attributed to viscoelastic changes in the sensing layer, induced by macromolecular conformational changes. Furthermore, chemical events in the biomolecules can lead to changes in interfacial coupling between the monolayer and the solvent, which in turn can lead to interfacial slip. For a liquid under shear flow, slip occurs when the liquid particles directly adjacent to a surface have a finite velocity parallel to the surface. Slippage effects have been connected to hydrophobic surfaces under high hydrodynamic shear stress,27,28 and have been suggested as a possible explanation for anomalous results in acoustic wave biosensor studies.29
In order to evaluate these experimental results, we develop multi-layer, one-dimensional models describing the acoustic impedance of the combined systems. These models, and the experimental results they describe, follow a previous paper that considered the adsorption of neutravidin to the bare gold electrode surface of a TSM device.30 Size, viscoelastic and interfacial effects are included for all layers. The mechanical and coupling properties are numerically fit to the experimental results using a perturbation analysis of the acoustic response. We also present a series of molecular dynamics (MD) simulations of the TAR-tat system that test the coupling and structural behaviour at a molecular level, to corroborate the numerical modelling of the bulk experimental results. Finally, we introduce a molecular measure to compare the relative hydrophobicity of the various TAR-tat fragment complexes, determined from MD simulations, to the bulk slippage parameters which are determined from the numerical modelling.
Background
The thickness shear-mode acoustic wave biosensor
The general equations of TSM operation have been treated extensively elsewhere,30–32 so we present here only models relevant to this analysis. In general, the TSM device functions through the generation of a resonant shear wave in an electroded quartz wafer. At the resonant frequency, the acoustic wave travels through the quartz with very little dissipation, and is reflected at the solid interface to maintain the standing wave. Changes at the substrate surface affect the apparent thickness and acoustic properties of the quartz wafer, and can be measured as changes in the acoustic properties of the shear wave. In its simplest form, the device functions as a mass deposition sensor, whereby changes in the resonant frequency correspond to changes in the adsorbed mass, given by the well-known Sauerbrey equation, | (1) |
When the device is operated as a biosensor, measurements are often performed in a liquid environment, which leads to energy dissipation at the surface–liquid interface, as well as inertial storage, measured by the frequency fs. Dissipation can be measured by the motional resistance of the equivalent circuit of the crystal element, Rm. For a purely viscous layer of sufficient thickness, the sensor response in both fs and Rm are proportional to the root of the density–viscosity product, as shown in the Kanazawa–Gordon description in eqn (2),
 | (2) |
In many biosensing applications, multiple adsorbed layers need to be considered. As such, we require a model describing multiple layers, including the bulk liquid layer. A general model to describe these changes is the small load approximation,33–35 where the response is related to the lumped acoustic impedance of all layers in contact with the device surface, given by
 | (3) |
 | (4) |
 is the acoustic impedance of layer i, ρi, Gi and hi are its density, shear modulus, and thickness, respectively, and
is the acoustic impedance of layer i, ρi, Gi and hi are its density, shear modulus, and thickness, respectively, and  is the wave number. Further layers can be incorporated into eqn (4) (cf. Eq. 26 in ref. 31).
is the wave number. Further layers can be incorporated into eqn (4) (cf. Eq. 26 in ref. 31).
In a previous paper,30 we described the surface load impedance for a neutravidin monolayer on a TSM surface, which incorporated the layer thickness, viscoelasticity, and interfacial effects. That analysis will serve as the starting point for the one here, which will demonstrate that the acoustic impedance can be used to describe conformational shifts in the biomolecular layer.
Before we describe the impedance model in full, we present a necessary brief description of the HIV-1 TAR-tat system and discuss conformational shifts observed in the molecules when the complex is formed.
The HIV-1 TAR-tat complex
Recent research into drug treatments for human immunodeficiency virus (HIV) has focused on interference in the metabolic and replication processes of the virus. One target is the interaction between the trans-activation region (TAR) on the viral RNA and the viral tatpeptide, an 86-amino acid protein that recognizes the TAR region and initiates transcription. HIV-1 TAR RNA has a conserved trinucleotide hairpin bulge and a hexanucleotide loop, which are important for recognition by the tatpeptide. Only a nine-residue basic region of the tatpeptide is required for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric binding to RNA, but flanking amino acid residues contribute to the binding affinity and kinetic and structural stability of the TAR-tat complex in vitro.36 There is evidence for a conformational shift in the TAR RNA upon tat binding,26 which is likely mediated by the length of the tatpeptide. tatpeptides of at least 30 amino acids are apparently required for the full conformational change, although binding of shorter peptides may lead to smaller changes. A schematic of the nucleic acid sequence of HIV-1 TAR RNA and the tatprotein amino acid sequence are shown in Fig. 1 and 2.
1 stoichiometric binding to RNA, but flanking amino acid residues contribute to the binding affinity and kinetic and structural stability of the TAR-tat complex in vitro.36 There is evidence for a conformational shift in the TAR RNA upon tat binding,26 which is likely mediated by the length of the tatpeptide. tatpeptides of at least 30 amino acids are apparently required for the full conformational change, although binding of shorter peptides may lead to smaller changes. A schematic of the nucleic acid sequence of HIV-1 TAR RNA and the tatprotein amino acid sequence are shown in Fig. 1 and 2.
 | ||
| Fig. 1 Molecular schematic of HIV-1 TAR RNA, showing the bulge and loop regions, obtained from PDB coordinates 1ARJ.37 The nucleotides are colour coded, with U – green, G – blue, C – purple, and A – red. | ||
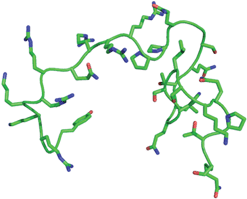 | ||
| Fig. 2 Molecular schematic of HIV-1tatpeptide. This representation is the 30-mer, containing amino acids Tyr-47 to Gln-76. The PDB coordinates, showing the backbone and residues, are obtained from 1JFW.38 | ||
A previously-reported experiment using the acoustic biosensor24 studied the binding of various lengths of tatpeptide to surface-immobilised TAR RNA. TAR was biotinylated and attached to a neutravidin-modified surface, and exposed to solutions containing tatpeptides of amino acid lengths 12, 20, 22, 25, 27 and 30. For all lengths, the tatpeptides began with Tyr-47 and contained the entire basic region. For instance, tat-12 consisted of Tyr-47 to Pro-58 and tat-30 comprised Tyr-47 to Gln-76. Addition of the tatpeptides to the surface-immobilised TAR RNA results in decreases in Rm and, depending on the peptide length, either large increases, no discernible change, or a large decrease, in fs. Under normal conditions, fs and Rm should change in opposite directions, so if their shift is in the same direction, a more complex interaction is occurring. All the experimental results from ref. 30 are summarized in Table 1.
| Load | Δf/Hz | ΔRm/Ω |
|---|---|---|
| Neutravidin | −181(8) | 1.7(0.5) |
| bTAR | −53(4) | 1.7(0.2) |
| tat | ||
| tat-12 | 32(5) | −3.5(0.6) |
| tat-20 | 25(9) | −2.7(0.8) |
| tat-22 | 18(7) | −2.4(0.6) |
| tat-25 | 18(4) | −2.3(0.6) |
| tat-27 | 0(8) | −1.8(0.8) |
| tat-30 | −21(6) | −2.3(0.5) |
Even though binding of the tatpeptides to the immobilized TAR RNA occurs in all cases, simply adding a few amino acids to the tatpeptide completely changes the way in which the device responds. Since the difference in molecular mass between the tatpeptides is negligible, this indicates that the device responds to changes in the conformation of the nucleotide-peptide complex, causing changes in the viscoelastic properties of the layers, or its coupling to the liquid.
The binding of tatpeptides of various lengths to immobilised TAR RNA yield very different results, the most interesting of which (decreases in both fs and Rm) occurs for tat-30. It is possible that the sensor is detecting a conformational shift in the TAR-tat complex. In interpreting these results, the conventional microbalance approach should not be applied to model the response, since in all cases, the mass effect would either be too small or predict signals in the wrong direction entirely. Viscoelastic changes in the sensing layer, induced by the conformational change in the protein, could be responsible for the biosensor responses, as this would determine the acoustic impedance.
Significant changes in the viscoelastic properties can be required to generate the large shifts, and these are generally proportionally larger in Rm than fs, which is not always the case in the experimental results. A possible candidate for such effects is slip at the surface–liquid interface. Slip has been described at solid–liquid interfaces for a number of systems, most notably for cases under high shear stress and for confined liquids. For a liquid under shear flow, slip occurs when the liquid particles directly adjacent to a surface have a finite velocity parallel to the surface. Recent work with aqueous flows at hydrophobic39–42 and even hydrophilic43–45 surfaces has shown that slip can occur at the microscopic scale. A number of authors have discussed the possibility of slip at the surface–liquid interface of an acoustic biosensor.29,31,46–56 Since slip depends on the surface–liquid affinity and surface morphology, it is likely that biomolecular conformational changes due to binding of an analyte to a surface-immobilised moiety could lead to interfacial slip.
These effects would influence acoustic wave propagation, making interpretation of the signal more difficult. The ability to predict the effects of slip is essential to the interpretation and understanding of biosensor signals.
Slip and the TSM device
A complete discussion of slip theory is not required for this analysis, and has been covered in depth by others,27,28,42,44,57–59 including at a TSM surface.29,31,48,49,52,54,60–62 Instead, we review some of recent reports that have presented evidence for slip, and then consider the slip models used in the Modelling section, as they pertain to acoustic wave devices.Due to the high shear rates and small length scales involved in acoustic biosensor operation, it is highly likely that slip is possible at the surface liquid interface. Slip can be included at the solid-liquid interface by (i) a frictional stress in the shear stress balance between the surface and the liquid or (ii) a slip parameter in the displacement/velocity boundary equation. Ferrante et al.29 included slip in the displacement boundary equation between the surface and the liquid, with a complex slip parameter, α, so that uliq,x(z = h) = αuads,x(z = h), where the ui,x are the particle displacements in the horizontal direction, h is the thickness of the quartz wafer and the location of the surface–liquid boundary, and α is a complex coefficient. For highly coupled systems, the no slip condition is α = 1 + j0, whereas for full slip, α = 0 + j0, equivalent to the device operating in a vacuum. Hayward and Thompson52 extended the slip parameter model to four layers, adding a purely elastic electrode layer and a viscoelastic polymer film. They allowed for complex slip at each interface, but only included slip between the film and liquid. For slip at the surface–liquid interface, the load impedance is
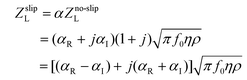 | (5) |
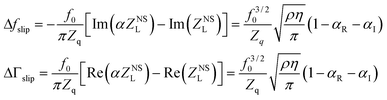 | (6) |
A common description of slip is the slip length. For a finite slip velocity vs at the solid wall, the slip length b is an imaginary extrapolation length into the solid wall required to recover the no-slip condition, such that vs = b(∂vs/∂z)z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. Ellis and Hayward50 showed mathematically that, for purely viscous liquids at an ideal elastic solid boundary, the complex parameter α is related to the slip length b by
0. Ellis and Hayward50 showed mathematically that, for purely viscous liquids at an ideal elastic solid boundary, the complex parameter α is related to the slip length b by
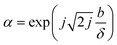 | (7) |
Daikhin et al.47 modelled slip at the adsorbate–liquid interface, where the adsorbate is rigidly coupled to the surface, by including a dissipation term in the wave equation of the device and a slip length boundary condition. Inclusion of slip resulted in extra frequency and bandwidth effects of the form
 | (8) |
McHale et al.31 used a similar description of slip, but modelled it at different layers using a slip parameter for layer i, si = 1/k. For slip at the surface–liquid interface, their model yields the same result as eqn (8). The acoustic load impedance for an adsorbed layer with slip at the adsorbate interface is
 | (9) |
 | (10) |
It is important to note that a, s, and b, are single-valued parameters, so they may not be able to fit all data. As well, as can be seen from eqn (8), Δf is much less sensitive to the effects of slip than ΔΓ, by a factor of approximately 1/a, which could be on the order of 102. For this reason, the single-valued slip models are not sensitive enough to describe some situations involving amorphous biochemical monolayers, where a large amount of energy is being transferred or lost within a very thin layer. For this reason, the complex α slip parameter may be more suitable for certain biochemical monolayers that involve significant changes in viscoelasticity in very thin layers.
Slip at the substrate–liquid interface is suitable for modelling situations of a liquid slipping on a viscoelastic support, such as biochemical monolayers under certain conditions. In some cases, however, the velocity discontinuity may exist between the substrate and the adsorbate, such as in the case of a very thin linker layer connecting the biochemical sensing layer to the surface. Slip may occur at intermediate layers, which can be described using similar models to those considered above.
The various models and manifestations of slip can be used to describe the sensor responses obtained for the experimental systems described above. This includes the immobilisation of biotinylated TAR RNA to an adsorbed neutravidin monolayer, and the subsequent binding of tatpeptides. The motivation for using slip to describe these results is that conventional models do not apply and the detection and quantification of adsorption is masked by other processes. By including slip in the model, the event of interest can be separated from other physical processes, and sensor performance can be improved.
To clarify these effects, we numerically fit the model described by eqn (4) to experimental values for (a) the binding of biotinylated TAR RNA to an adsorbed neutravidin surface30 and (b) the complexation of various length tatpeptide fragments to TAR. As required, the various descriptions of slip are included in the acoustic models.
Along with the numerical modelling, we perform molecular dynamics (MD) simulations to determine the molecular properties and conformational structures of various TAR-tat complexes. These properties include the length, shape, and volume of the macromolecules, and the hydrophilic and hydrophobic solvent accessible surface area (SASA). This last property should give an indication of the relative differences in solvent affinity and possibly slip between two molecules. To determine valid starting structures for the various TAR-tat complexes, we perform docking simulations with AutoDock prior to the MD simulations.
The numerical modelling and molecular simulations, including determination of the initial structures with AutoDock, are discussed in the Methodology.
Methodology
Hardware and software
Most computations were performed on an Apple PowerMac G4 (Apple Inc, Sunnyvale, USA) running MacOS 10.4. Some MD simulations were performed on an Apple iMac G5, also running MacOS 10.4.All modelling calculations were performed using Octave 3.0.1.64,65 All molecular dynamics simulations were performed with the Gromacs 3.3 simulation package.66,67 Molecular graphics and structure modification were done with MacPyMol.68 Docking simulations were performed using AutoDock 3.0.569 and AutoDock Tools 3.0.5.70 Gromacs was compiled on the Apple PowerMac with G4 PowerPC processor under the Darwin 8 operating system, using the GNU C compiler  (http://gcc.gnu.org). Single precision was used, to take advantage of the Altivec vector processor on the PowerPC.71
(http://gcc.gnu.org). Single precision was used, to take advantage of the Altivec vector processor on the PowerPC.71
Molecular dynamics
 function in MacPyMol.
function in MacPyMol.
Two separate docking and molecular dynamics strategies were undertaken. In the first series, MD runs of 2 or 3 ns were done on docked structures determined separately for each of tat-12, tat-22, and tat-30. The docked structures were evaluated solely on their final docked energies. The second strategy involves performing a single docking study, and using the same docked structures for both the tat-12 and tat-30 runs. These structures were then used to perform large-scale simulations of 20 ns.
In the initial strategy, 20 potential structures were found for each of tat-12, tat-22, and tat-30. The grid spacing was set to 0.75 Å. The GA population size was different for each run, with the top individual surviving to the next generation. The individual AutoDock configurations for tat-12, -22, and -30 are shown in the ESI (Figs. S.1 and S.2).† The names of the runs are arbitrary and serve solely as markers. These structures were selected solely based on their final docked energy as selection criterion, so no checks were made for impossible linkages or docking. As a result, some of the initial runs could not be used. The two lowest energy structures were selected for each configuration, and used for molecular dynamics runs.
For the second strategy, the tat-30 peptide was used for the docking, and then truncated for the tat-12 runs, using the tat-30 docking results. Random initial coordinates, quaternion rotations, and dihedrals were used, with the tat molecule centred around [13.43,−0.38,−5.08]. For both strategies, the number of active torsion molecules was set to 30. The GA population size was set to 150, with the top individual surviving to the next generation. The maximum number of generations and energy evaluations was set to 1500000 and 27000, respectively.
Of the 30 final configurations, the three with the lowest final docked energies were selected for the MD runs. These were runs 10, 12, and 13 and will be referred to as TARtatn.10, TARtatn.12, and TARtatn.13, where n is either 12 or 30, the length of the tatpeptide fragment. The output.pdb files for the lowest-energy runs were incorporated into the TAR.pdb files to create a starting configuration of the TAR-tat complex. To generate the tat-12 molecule, the tat-30 molecule was truncated at R57 and capped with –COOH, as described above.
 , for a final initial box size of 5.602 × 5.272 × 4.981 nm. The molecular topology was generated using the Amber99ϕ force field ported to Gromacs.72 The Gromacs program
, for a final initial box size of 5.602 × 5.272 × 4.981 nm. The molecular topology was generated using the Amber99ϕ force field ported to Gromacs.72 The Gromacs program  was then used to fill the box with solvent molecules at density 1 g cm−3, which corresponds to 5539 solvent molecules. The solvent used was the Amber tip4p water model,73 which has been adapted for use with Gromacs.72 To balance the charges and neutralise the macromolecule, 22 Na+ ions were added using the Gromacs
was then used to fill the box with solvent molecules at density 1 g cm−3, which corresponds to 5539 solvent molecules. The solvent used was the Amber tip4p water model,73 which has been adapted for use with Gromacs.72 To balance the charges and neutralise the macromolecule, 22 Na+ ions were added using the Gromacs  code, replacing 22 of the solvent molecules.
code, replacing 22 of the solvent molecules.
Following pre-processing, a steepest-descent energy minimisation (EM) was performed to eliminate bad solvent contacts. PME electrostatics were used74 and rigid water molecules were enforced with the SETTLE algorithm.75 In general, two to three minimisations were performed to ensure that a local minimum was found. The tolerances were reduced before each subsequent minimisation run. Once EM was complete, 50-ps position restrained dynamics were run, with a 2-fs timestep, PME, and coupling to Berendsen temperature and pressure baths,76 with Tref = 300 K, τT = 0.1, Pref = 1.0 bar, τP = 0.5, and coefficient of compressibility βV = 4.5 × 10−5. Linear constraints were maintained with the LINCS algorithm.77
The full MD simulations in this case were performed for 3 ns at 2-fs timesteps. During the runs, coordinates, velocities, and energy were recorded every 100 steps. The neighbour list for cutoff interactions was updated every 10 steps, and the neighbour cutoff was 9 Å. Periodic boundary conditions were used in all directions and the vdW cutoff radius was rvdW = 10 Å. PME electrostatics were used with rcoul = 9 Å. The PME order was set to 4, with tolerance 10−5 and three-dimensional geometry. The spacing of the Fourier grid for PME was 0.9 Å. The LINCS algorithm with order 4 was used for constraints.
For the second strategy, the MD settings were the same as above, although padding of 1.0 nm on each side of the macromolecule with editconf, for a final initial box size of 6.002 × 5.67 × 5.381 nm. The full MD simulations in this case were performed for 20 ns at 2-fs timesteps. In the case of apoTAR, the run was 20 ns.
Runs that were interrupted prematurely or extended were restarted using the  code. As well,
code. As well,  and
and  were used to link concatenate interrupted trajectories and energy files upon completion, and
were used to link concatenate interrupted trajectories and energy files upon completion, and  was used to convert high-resolution .trr trajectory files to lower resolution .xtc files. In some cases, part of the TAR-tat complex moved out of the box into a periodic image. Since this makes analysis impossible, the molecules were made whole again with the command
was used to convert high-resolution .trr trajectory files to lower resolution .xtc files. In some cases, part of the TAR-tat complex moved out of the box into a periodic image. Since this makes analysis impossible, the molecules were made whole again with the command  .
.
 .
.
The energy, temperature, pressure and density of different groups can be monitored with the tool  . RMS deviation from starting positions of different groups relative to one another can be monitored using
. RMS deviation from starting positions of different groups relative to one another can be monitored using 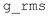 and
and  . The solvent accessible surface area and excluded volume can be monitored using
. The solvent accessible surface area and excluded volume can be monitored using  . This tool computes hydrophilic, hydrophobic, and total accessible area, based on a solvent probe. In our analysis, a probe radius of 1.4 Å was used.
. This tool computes hydrophilic, hydrophobic, and total accessible area, based on a solvent probe. In our analysis, a probe radius of 1.4 Å was used.
Two analysis tools were programmed in-house, both of which made use of the  program to determine the raw atomic coordinates.
program to determine the raw atomic coordinates.
Bend and twist angle. The first calculates the bend and twist angles between the lower and upper stem of TAR RNA molecule. Using a coordinate system similar to that established by Mu and Stock,78 we tested the bend angle of the apoTAR and of the different complexes. A coordinate system was defined where the average positions of the lower and upper stem base pairs define two straight lines that represent the orientation of the RNA base pairs. In our system, the z-axis was defined by the averaged sum of vectors orthogonal to the planes formed by the 4, 5, and 6 carbons of each base. This axis represents the direction of stacking of base-pairs in the lower and upper stems. The x-axis was the averaged sum of vectors orthogonal to the plane formed by the z-axis and the phosphorous atoms of each base-pair. Its direction is from the minor groove to the major groove. This is shown in Fig. 3. The bend angle is then formed as the angle between the averaged z-axes of the upper and lower stems.
 | ||
| Fig. 3 Definition of axes for determination of bend angles. The top frame shows the configuration of an RNA base pair with the atoms of interest indicated. The bottom frame shows the same marked atoms, as they define the coordinate axes. The z-axis is perpendicular to the plane defined by the 4, 5, and 6 carbons. The x-axis is orthogonal to the z-axis and a vector connecting the phosphorous atoms on the backbone. The top frame also indicates the major and minor grooves. | ||
Maximum atom pair distance. The second in-house tool calculates the maximum atom-pair distances between all particles in a trajectory. The
 tool is used to determine each atom location and the distance between all particles is determined. The largest separation at each time step is then the largest maximum pair distance (MPD). To save computation time, hydrogen atoms were excluded and only TAR molecule distances were calculated.
tool is used to determine each atom location and the distance between all particles is determined. The largest separation at each time step is then the largest maximum pair distance (MPD). To save computation time, hydrogen atoms were excluded and only TAR molecule distances were calculated.
Results and discussion
Modelling
In this section, we describe numerical fitting of experimental values for the binding of biotinylated TAR RNA to an adsorbed neutravidin surface and its subsequent interaction with various-length tatpeptides.The main model to be used is the thin-film approximation, eqn (4), as well as the various descriptions of slip considered above. Numerical fitting is performed using the  tool from Octave 3.0.1.
tool from Octave 3.0.1.  implements the MINPACK
implements the MINPACK  subroutine, which numerically finds a root for a system of N equations with N variables. The system of equations is provided by the user, and the first-order matrix of partial derivatives is calculated by a forward-difference approximation.79
subroutine, which numerically finds a root for a system of N equations with N variables. The system of equations is provided by the user, and the first-order matrix of partial derivatives is calculated by a forward-difference approximation.79
Initial values for neutravidin adsoption from previous study
The material properties of the neutravidin (NAv) layer, used as a linker moiety, were determined in a previous analysis.30 NAv was modelled as a hydrated viscoelastic monolayer with a surface concentration of 1.5 pmol cm−2. Upon modelling, it was found that interfacial slip occurred on the bare gold surface prior to NAv adsorption. The slip length values on bare gold were between 6 to 10 nm, which is consistent with other studies of slip on gold under shear flow.Since each adsorption of the NAv layer was followed by subsequent binding of bTAR, we treat each case separately, using the individual values from each NAv run. The average values for the NAv complex shear modulus were G′ + jG′′ = (1.2 + j0.56) × 106 dyne cm−2. For reference, the full dataset of NAv shear moduli are shown in the ESI (Table S.1).†
Biotinylated TAR binding to neutravidin
The adsorption of bTAR to the NAv surface was modelled as a second viscoelastic layer above the NAv. A no-slip boundary condition was used between the bTAR and the contacting liquid.As above, the data are from ref. 24 and have been reanalysed for consistency. The immobilisation of bTAR on the NAv surface was detected from changes in frequency and resistance. The responses are obtained before exposure to bTAR in solution, and after subsequent washing with buffer, so that ΔfbTAR = fnbTAR − fNAv and ΔRbTAR = RnbTAR − RNAv, where the nbTAR indicates NAv-bTAR complex formation in buffer. Table 2 shows the Δf and ΔR results for the adhesion of bTAR to the NAv surface.
| Expt. | Δf/Hz | ΔR/Ω | Expt. | Δf/Hz | ΔR/Ω |
|---|---|---|---|---|---|
| b1 | −56.0 | 2.06 | b16 | −38.6 | 1.37 |
| b2 | −54.1 | 1.81 | b17 | −70.2 | 2.20 |
| b6 | −55.3 | 1.91 | b18 | −55.8 | 2.14 |
| b7 | −35.4 | 0.46 | b19 | −62.8 | 2.12 |
| b8 | −69.1 | 1.91 | b20 | −64.9 | 1.65 |
| b9 | −63.9 | 2.39 | b21 | −62.6 | 1.97 |
| b10 | −36.3 | 0.20 | b22 | −31.7 | 1.18 |
| b11 | −42.0 | 0.78 | b23 | −43.2 | 1.25 |
| b12 | −65.7 | 2.40 | b24 | −62.0 | 1.15 |
It is important to note that there is significant variability in the bTAR data, with a standard error in Δf of 0.25. The error in ΔR is also relatively large for both NAv and bTAR adsorption (0.35 and 0.22, respectively).
Adsorption of biotinylated TAR and mechanical properties
The first test to perform is whether bTAR binding is purely gravimetric. From radio-labelling studies,80 the surface concentration of bTAR is approximately 1 pmol cm−2. With molar mass 9939 pg pmol−1,§ gravimetric adsorption of bTAR should result in a shift of approximately Δf ≅ −2 Hz (eqn (1)). Obviously, the responses in Table 2 could not be due to gravimetric adsorption alone. Even if there is significant error in the accuracy of the radio-labelling data for bTAR, and it is as high as 5 pmol cm−2 (close-packing of neutravidin based on molecular dimensions), the response would be less than −10 Hz, still significantly below the measured responses.It is also possible that significant hydration of the bTAR layer will result in water bound to the bTAR layer, which could add to the density of the layer. The box dimensions of the bTAR molecule are approximately 4.0 × 3.7 × 3.3 nm, obtained from PDB file 1ARJ structure 2.37 If the largest dimension is normal to the surface, then the footprint of the molecule is 12 nm2. If the rest of the surface is filled by water, then the density of the composite hydrated bTAR layer is ρw,bTAR = 0.92 g cm−3, which is close to that for the hydrated neutravidin layer (0.88 g cm−3). The gravimetric response for such a layer is −40 Hz. This response is within the margin of error for those obtained above. However, this model does not account for the ΔR = 1.7 Ω, which corresponds to a bandwidth shift of ∼27 Hz. Changes in the resistance/bandwidth indicate some changes in the viscoelastic properties of the layer.
Viscoelastic properties of the bTAR layer
One option is to model the neutravidin–bTAR complex as a single acoustic layer, having composite dimensional and material properties of both the neutravidin and the bTAR. This model is realistic since there is not a well-defined linear boundary between the neutravidin and the bTAR and the presence of bTAR may alter the properties of the neutravidin. However, there is likely enough of a difference between the bTAR, which is a nucleic acid chain, and sparsely populated on the surface, and the neutravidin, which is a globular protein and forms a denser layer. In addition, the thickness of the NAv layer is uniform on gold,81 so it is reasonable to assume that the boundary between NAv and bTAR is well delineated. The proposed system is shown schematically in Fig. 4.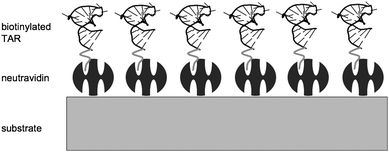 | ||
| Fig. 4 Schematic representation of neutravidin–bTAR binding configuration. The dark grey molecules on the surface are NAv, which bind the biotin in one of the pockets. | ||
An additional layer is incorporated into the model by solving the equations of motion to find the load impedance. The impedance for the kth layer is given by82
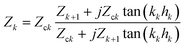 | (11) |
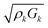 , kk and hk are the wavevector and thickness, and Zk+1 is the combined impedance of all higher layers. The total load impedance ZL is the impedance for k = 1. For the NAv-bTAR system in liquid, a three-layer system, the load impedance ZL is given by
, kk and hk are the wavevector and thickness, and Zk+1 is the combined impedance of all higher layers. The total load impedance ZL is the impedance for k = 1. For the NAv-bTAR system in liquid, a three-layer system, the load impedance ZL is given by | (12) |
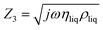 ,
,  , and
, and 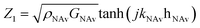 . Eqn (12) is incorporated into an Octave script with the previously determined parameters for NAv. The model was solved for the complex shear modulus GbT = μbT + jωηbT, with ρbT = 1.006 g cm−3, hbT = 4.8 nm, and the NAv values from ref. 30. The average bTAR shear modulus values were log(ηbTAR) = 2.5 ± 0.5 and log(μbTAR) = 5.8 ± 0.1. The full solution set is shown in the ESI (Table S.2).†
. Eqn (12) is incorporated into an Octave script with the previously determined parameters for NAv. The model was solved for the complex shear modulus GbT = μbT + jωηbT, with ρbT = 1.006 g cm−3, hbT = 4.8 nm, and the NAv values from ref. 30. The average bTAR shear modulus values were log(ηbTAR) = 2.5 ± 0.5 and log(μbTAR) = 5.8 ± 0.1. The full solution set is shown in the ESI (Table S.2).†
In almost all the cases, the viscosity and the elasticity both decreased from the NAv values, so the bTAR layer is less stiff and less resistant to flow than the NAv layer. This makes sense, since the NAv is a globular protein, and the bTAR will have more liquid penetration.
Detection of conformational changes on binding of tatpeptides
| tat peptide length | Primary structure | M w/Da |
|---|---|---|
| 12 | YGRKKRRQRRRP | 3738 |
| 20 | YGRKKRRQRRRPPQGSQTHQ | 6279 |
| 22 | YGRKKRRQRRRPPQGSQTHQVS | 6934 |
| 25 | YGRKKRRQRRRPPQGSQTHQVSLSK | 7911 |
| 27 | YGRKKRRQRRRPPQGSQTHQVSLSKQP | 8448 |
| 30 | YGRKKRRQRRRPPQGSQTHQVSLSKQPTSQ | 9498 |
The tat fragments go from the short 12-mer peptide containing only the basic region necessary for binding to TAR RNA (Y47–P58), to the 30-mer that contains the entire basic binding region and the glutamine-rich region responsible for structural changes in TAR (Y47–Q76). Based on the molecular masses of the tat fragments, the expected gravimetric frequency shifts should be on the order of −1.0 Hz for tat-12 and −2.6 Hz for tat-30. As is evident from Table 4, the shifts, including changes in resistance, where very different.
| tat length | No. of samples | Δfavg/Hz | ΔRavg/Ω |
|---|---|---|---|
| 12 | 2 | 32 ± 5 | −3.5 ± 0.6 |
| 20 | 8 | 26 ± 9 | −2.7 ± 0.9 |
| 22 | 3 | 15 ± 2 | −2.2 ± 0.3 |
| 25 | 4 | 18 ± 4 | −2.3 ± 0.6 |
| 27 | 5 | −0.2 ± 8 | −1.8 ± 0.8 |
| 30 | 3 | −21 ± 6 | −2.3 ± 0.5 |
As the peptide length increases, ΔR remains relatively constant, while Δf goes from positive to negative. In fact, for tat-30, the frequency and resistance shifts are both negative, which is contrary to the normal gravimetric functioning of the device. The normal gravimetric interpretation of an increase in frequency of 32 Hz would be that mass is being lost from the surface. Since the resistance shift remains relatively constant throughout all the tat runs, it is unlikely that mass is being lost, so a different interpretation is required. To understand some possible reasons behind this shift, we consider conformational shifts in TAR RNA on binding of tat fragments of different lengths.
Upon binding the full tatprotein, TAR is known to undergo a significant conformational shift. The bulge region of the TAR RNA (U22-U24) is straightened, causing the bend angle to decrease from 50° to 10°, and the entire complex stiffens and becomes more ordered. This is shown schematically in Fig. 5. Simple binding of the peptide occurs for tat-12, but the full conformational shift only occurs for longer peptides, with tat-30 believed to be the minimum length required for the full conformational shift.83 However, shorter peptides could induce partial conformational shifts and shape changes, which may explain the frequency shifts observed above. From this description, some combination of stiffness, layer thickness, and slippage effects could also be responsible for the observed shifts.
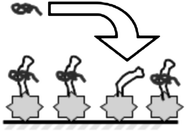 | ||
| Fig. 5 tat peptides delivered in solution bind to immobilized TAR, inducing possible conformation shift. | ||
Modelling approach
The modelling approach begins by assigning average values for the tat-30 runs, for which we do not have any data for NAv or bTAR adsorption, only for the addition of tat-30 itself. To account for this, the tat-30 system parameters are calculated from average results for all other previous NAv and bTAR runs. Using the averaged mechanical properties to predict the averaged responses for NAv and bTAR did not work, since the predicted response is significantly affected by small perturbations in the input parameters. To avoid this problem, the average mechanical parameters for the NAv and bTAR layers were estimated by solving the systems with the average sensor signals (Δfavg and ΔRavg) as inputs.However, as opposed to bTAR, which was modelled separately from the neutravidin layer, the binding of tat will be modelled as a change in the bTAR layer from the pre-binding state. The TAR-tat complex cannot be separated into discrete bTAR and tat layers. Instead, the complex has a composite macromolecular structure that is treated together. As well, it will be instructive to observe the changes in the layer upon TAR-tat complex formation for the different length peptides, as this will provide information on how the device can be used to detect peptide–nucleic acid binding.
Viscoelastic shifts are one possible explanation for the observed sensor responses. To test this hypothesis, a similar solving algorithm was used as that to fit the bTAR properties, eqn (11), with initial estimate for μTAR-tat and ηTAR-tat the same as the values found for the bTAR layer. However, this model could not fit any of the data expect tat-27, for which it showed an increase in viscosity and a decrease in stiffness. This sort of behaviour may be indicative of conformational shifts involving straightening of RNA molecules, as proposed by Tsortos et al.14 However, since this model was unsuccessful in fitting the data, we turn to alternative descriptions of the system in an attempt to elucidate the physical phenomena present.
Another potential scenario involves the stiffness of the TAR-tat layer and surface–liquid coupling at the interface. However, this algorithm could only fit the same result as the η–μ algorithm. In both cases, the stiffness and viscosity increased, and there was an onset of slip. This behaviour is consistent with the formation of the TAR-tat complex, since the ordering of the RNA occurs for all tat fragment lengths, but complexation may lead to exposure of hydrophobic domains that are blocked by the longer fragments. A similar model was fit to interfacial slip and changes in monolayer viscosity, instead of stiffness. However, as with the fit of slip and stiffness, this model cannot explain most of the results, so a different description is required.
As mentioned above, the binding of the full tatprotein to TAR results in a straightening of the bend in the TAR RNA, and a stiffening/ordering of the TAR-tat complex. When the shorter peptide fragments bind, the straightening does not occur or occurs only to a small extent. The degree of straightening on binding could manifest as various degrees of ordering at the interface, or as a different interfacial liquid viscosity near the device surface. This would be in addition to the changes in length of the TAR molecule. Ordering at the interface can be modelled as slip, so a possible model involves changes in thickness and slip. Since many of the thickness values are negative, this model cannot be used to fit the results. In all cases, the slip values are negative, indicating that the surface becomes more ordered and coupling increases because of the conformational shift. However, these results should not be given too much credibility, because of the unphysical nature of the thickness values. Attempts to fit the thickness and stiffness were also unsuccessful (not shown) because of the small layer thicknesses involved. The model is not sensitive enough to these changes.
Describing the TAR-tat surface complex using changes in shape (thickness), the material properties, or a real-valued slip parameter is unsuccessful. The thin-film approximation is not sensitive enough to model the observed results, even with slip included. As well, for a sparse, soft surface, it is unlikely that the conditions required for a real-valued slip parameter are satisfied. In a recent analysis, Willmott and Tallon55 found that a real-valued slip parameter is insufficient for the description of oscillating surfaces, and that a complex slip value could be required. While this may not be the case on the unmodified gold surface considered in ref. 30, a complex slip parameter is likely required on the biochemical surface considered here.
The complex slip parameter α described above is a suitable slip model. It is easily included in the impedance model with the substitution Zi → αZi, where Zi is the load impedance of layers i, i + 1…n. We include slip at the surface–liquid interface, between the TAR-tat layer and the liquid, so Zliq → αZliq. The fitted slip values for this model are shown in Fig. 6, with the full solution set in the ESI (Table S.4).†
 | ||
| Fig. 6 Outer slip magnitude (a) and phase shift (b). The results for inner slip are almost identical. | ||
The slip magnitude remains relatively constant for the shorter peptides, increasing slightly for tat-27, and becoming close to the no-slip condition |α| = 1.0 for tat-30. Concurrently, the slip phase increases slightly as the peptide length increases.
From a biophysical standpoint, when the tat fragments bind to the surface-immobilised TAR molecules, the RNA undergoes a conformational straightening and previously unexposed regions become exposed to the interface. This straightening (the unbound form is bent at approximately 50°), would appear as an increase in the thickness of the TAR layer on the surface. In the traditional functioning of the TSM biosensor, an increase in the thickness on the surface should appear as an increase in the effective wavelength, which corresponds to a decrease in the frequency. However, since this is a storage effect, there should be no change in the dissipation, resistance or bandwidth.
The TAR-tat results, shown in Table 4, all involve a decrease in the resistance Rm. This indicates that, in all cases, the amount of acoustic energy lost into the liquid is decreasing when tat binds. As discussed above, this sort of behaviour could be indicative of an onset of slip. Since the increase in ΔR remains relatively constant across the different length peptides, it is likely that a decrease in coupling at the interface is occurring equally for all the tat fragments.
A limitation of the complex slip/thickness description is that, since there are only two experimental values, there can be only two fitting parameters. We cannot therefore fit the complex slip parameter α and the layer thickness. A suitable slip model that uses the complex slip parameter but only has a single fitting parameter is the sliptime model proposed by Smith et al.84
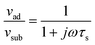 | (13) |
 | ||
| Fig. 7 Model fitting results for TAR-tat layer thickness hTAR-tat (a) and sliptime ωτs (b). The error bars represent one standard deviation. | ||
The computed thickness changes in all cases are negative, indicating a decrease in thickness of the TAR-tat complex when tat binds to the immobilised TAR surface. This shift is contrary to what would be expected, since the TAR molecule should undergo a lengthening. However, the decrease is much lower, approximately 1 nm, for the tat-30 fragments, compared to the values for the other peptide lengths. The model does not differentiate between the actual layer thickness and the apparent location of the reflecting surface, so the introduction of slip could have the effect of shifting the plane of reflection. It is encouraging that this model at least shows the expected pattern, if not the precise expected values. We will consider the actual quantification of these shifts, and what they reveal about the precise structure and interaction at the RNA-protein complex/liquid interface, in the Discussion section.
Molecular dynamics
In the previous section, we modelled the interaction of surface-immobilised HIV-1 TAR RNA with tatpeptide fragments of different lengths. As the length of the tatpeptide increased from 12 to 30 amino acids, the signal underwent a complex shift that was explained as an increase in the thickness of the TAR-tat complex on the surface, upon binding. This was accompanied by a change in interfacial coupling at the surface–liquid interface, modelled as the onset of slip. The larger tat molecules appeared to induce a larger increase in thickness at the surface.In this section, we present results of molecular docking and subsequent molecular dynamics simulations of the TAR RNA and the TAR-tat complex for peptide lengths of 12, 22, and 30 amino acids. These results are then compared to the modelling discussed in the previous section. Specifically, we are interested in the size, shape and exposure of the solvent to hydrophobic domains of the TAR-tat complex, as compared to the unbound, TAR molecule.
The initial structures and MD simulations were discussed above. Since two strategies were used for docking and MD simulation, we present each docking/simulation strategy separately. First, a series of 3 ns simulations are presented for tat-12, -22, and -30, where the dockings are performed individually for each different length. Second, a number of 20 or 30 ns simulations are described, where the same docked structure was used for both tat-12 and tat-30. These are compared to a 20 ns simulation of unbound apoTAR.
AutoDock results
The aim of the docking studies is to find energetically favourable structures that are accurate representations RNA–peptide interactions. The starting structure is important because an energetically favourable structure increases the likelihood that simulation will produce a stable, realistic structure that demonstrates accurate dynamics.As described in the Methodology, each peptide length (tat-12, 22, and 30) was docked individually, and the lowest energy structures were selected. The docked energies of the selected runs are shown in Table 5 and the structures are shown in the ESI.† The numbers following the peptide lengths are used solely as identifiers.
| Name and tat-length | Final docked energy/kcal mol−1 |
|---|---|
| t12.3 | −25.20 |
| t12.12 | −21.52 |
| t22.15 | −11.91 |
| t22.18 | −5.94 |
| t30.1 | −10.47 |
| t30.18 | −7.97 |
Molecular simulation results with Gromacs
In this section, we describe MD analyses to (a) evaluate the quality of the simulations and (b) to extract structural, size, and conformational information from the simulations. The analyses include calculation of the RMS deviations from initial structures, the bend angle between the upper and lower stems created by the bulge that is reduced by tat binding, the hydrophilic and hydrophobic solvent accessible surface areas, and molecular length and volume.All RMSD values are calculated with respect to the minimised, position restrained structure. The results are displayed in the ESI (Fig. S.3)† for the RMSD of the full TAR-tat complex, the tatpeptide, and the domains of the RNA (lower stem, upper stem, bulge, and loop), compared to the unbound TAR, for Str1. The runs are in general agreement with published results of 1 ns MD simulations,85 at least for the first nanosecond of these 3 ns simulations. The unbound TAR RMSD values are all higher than the bound forms, indicating that the bound conformations are less mobile and the presence of the tatpeptide stabilises the macromolecule. The loop is the most flexible area of the TAR, likely since any mobility in the upper stem induces motion in the loop. The variation in RMSD values is similar to that between the bound structures within NMR values, as reported by Nifosi et al.85
The deviation in the RMSD values for Str2, from the initial structure of the RNA elements (stems, bulge, and loop) is more random for the bound forms than for the unbound TAR, which only has an RMSD value of 5 Å for the total simulation. It is possible that the unbound TAR stabilises, while the TAR-tat complexes are reorganising to a more stable structure. The unbound TAR does experience significant motion in the lower and upper stems, as compared to the bound forms. This has been observed in other molecular dynamics studies of TAR RNA bound to argininamide.85 Motion of the unbound TAR molecule remained relatively constant over the whole 20 ns simulations, and did not vary significantly from the first 3 ns.
For the bound TAR, the deviation of the individual elements remained constant between Str1 and Str2, but the total motion of the bound TAR molecule was much larger for the 20-ns Str2 simulations, compared to the Str1 runs. This is likely due to the combined contributions of small changes in the RMSD values for all the individual elements. There is no significant difference in the overall motion of the TAR between the tat-12 and tat-30 runs, although the mobility of the lower stem and bulge were greater for Tat12. This could be due to stabilisation of these elements in the TAR due to the longer tat-30 peptide. Motion of the tatpeptide remained relatively constant for both simulations, with mean values around 5 Å.
For the most part, the 3 ns simulations demonstrate an equilibration period for the free TAR simulations. There is a large amount of oscillations in the unbound TAR element, especially in the bulge and loop. Similarly, there is a large amount of variability in the full 20 ns simulation, although the RMSDs of all elements in the freeTAR appear to reach equilibrium values within 7 or 8 ns. When considering the bound forms, there are few discernible patterns between the shorter and longer tatpeptides for the 3 ns simulations. The bulge and loop are less stable than the other elements, except in the case of Tat30.1, where all RMSD values were very low. In fact, Tat30.1 appears to be stable in general. For the 20 ns runs, the tat-30 simulations were more stable for the lower stem and bulge, although there was no pattern in the upper stem and loop. This is the case for the full TAR-tat complex, and the tatpeptide motion as well.
 | ||
| Fig. 8 Comparison of bend angles for the different runs for Str1. Each bar represents a different run: (1) Tat12.3; (2) Tat12.12; (3) Tat22.15; (4) Tat22.18; (5) Tat30.1; (6) Tat30.18; (7) FreeTAR. The error bars display one standard deviation. | ||
The bend angles followed similar patterns for Str2. For the unbound TAR, the bend angle remained relatively constant throughout Str2, and agree with similar studies.78,85 There are large differences between the bound forms for both Str1 and Str2, and the unbound TAR. However, for the longer simulations, the shorter tat-12 peptides actually converged to slightly lower angles than the longer tat-30 peptides.
 program, which applies the double cubic lattice method.89
program, which applies the double cubic lattice method.89
The number of accessible atoms or residues that are hydrophilic or hydrophobic was determined. An atom was deemed hydrophobic if its absolute charge was less than 0.2e, where e is the elementary charge. Since the various TAR-tat complexes in this study are different in size, the relative hydrophobicity of a macromolecule was measured as the ratio of the hydrophilic to hydrophobic accessible surface areas.
For both the Str1 and Str2 simulations, the relative hydrophobicities are shown in Fig. 9, which displays ratios of hydrophilic:hydrophobic areas for the different runs. The difference in relative hydrophobicity between the bound and unbound molecules is very evident. The ratio decreases as the tat length increases, indicating that the larger tatpeptide may block more hydrophilic zones on the TAR RNA. However, as before, this difference is not significant.
 | ||
| Fig. 9 Comparison of the ratio of hydrophilic:hydrophobic solvent accessible surface area for the different runs for (a) Str1 and (b) Str2. For Str1, the run identifiers are the same as in Fig. 8, and for Str2, they are: (1) 12.10, (2) 12.13, (3) 30.10, (4) 30.13, and (5) FreeTAR. The error bars display one standard deviation. | ||
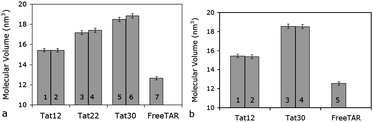
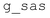 . This is the amount of space that the macromolecule displaces. We can use these values to compare to the estimated density. Comparisons of volume values for Str1 and Str2 are shown in Fig. 10. The molecular volume increases linearly with the molecular mass, with an R2 of 0.9904. The molecular volume of TAR alone is 12.7 ± 0.2 nm3, and the averaged molecular volumes for Str1 are 15.4 ± 0.2, 17.3 ± 0.3, and 18.9 ± 0.3 nm3, for tat-12, -22, and -30, respectively. These values, and their errors, remain consistent for the 20 ns simulations of Str2. Values of the volume for the full simulations are shown in the ESI (Fig. S.6).†
. This is the amount of space that the macromolecule displaces. We can use these values to compare to the estimated density. Comparisons of volume values for Str1 and Str2 are shown in Fig. 10. The molecular volume increases linearly with the molecular mass, with an R2 of 0.9904. The molecular volume of TAR alone is 12.7 ± 0.2 nm3, and the averaged molecular volumes for Str1 are 15.4 ± 0.2, 17.3 ± 0.3, and 18.9 ± 0.3 nm3, for tat-12, -22, and -30, respectively. These values, and their errors, remain consistent for the 20 ns simulations of Str2. Values of the volume for the full simulations are shown in the ESI (Fig. S.6).†
 | ||
| Fig. 11 Comparison between the maximum pair distances for the various tat lengths and unbound TAR. The run identifiers are the same as in Fig. 8 and 9, and the error bars display one standard deviation. | ||
The MPD for Str1 does show an increase as the peptide length increases. There is no apparent difference between the tat-12 and tat-22 (4.5 ± 0.2 nm), but there is an increase of 3 Å for tat-30 (4.8 ± 0.3 nm). The maximum separation for the unbound TAR RNA was similar to the tat-30 runs at 4.7 ± 0.2 nm, although it does have more variation, and does decrease after significant fluctuations between 0.5 and 2 ns. Values of the MPD for the full simulations are shown in the ESI (Fig. S.7 and S.8).†
Comparison of simulation strategies and validation of results
The two different docking and simulation strategies yielded different results, even though the general structures where similar. In Str1, the lowest energy structures were taken for each of tat-12, -22 and -30. For Str2 the lowest energy structures of tat-30 were selected for simulation and then truncated to tat-12, with the same structure. As a result, the docked structures of Str1 were tailored to the specific length of the peptide, and thus represent a more physical model of the bound structures. On the other hand, the Str2 structures were tailored only to tat-30, so the tat-12 complexes may have been unrealistic. This could be why they resulted in inconsistent values for the bend angle and MPD in most cases.Throughout the simulations, it became evident that 3 ns and even 20 ns is not enough to obtain a complete picture of the conformational dynamics of the TAR-tat system. While in some cases an equilibrium value was reached, in most of the simulations the structures oscillated between multiple equilibrium values. The dynamics of biomolecular motion have features that become apparent on different time scales, so we are only observing a subsection of the conformational ensemble of the TAR-tat complex. More and longer simulations are required to fully capture the structural dynamics of this system.
There were similarities between the two strategies that can be applied to the TAR-tat system. Namely, these were the molecular volume and the ratio of hydrophilic to hydrophobic surfaces. Despite the differences in the other structural properties calculated from the simulations, these remain constant throughout the simulations and provide useful information about the size and hydrophobicity of the macromolecules.
Str1 appears to be a better strategy than Str2, and these runs should have been used for the extended 20 ns simulations. The docked structures selected for each individual tatpeptide length could be more physically realistic and specific than the truncated tat-12 peptides of Str2. However, the simulations of Str2 provide interesting information into the specificity of the conformational dynamics of the TAR-tatmacromolecule. When the tat-12 peptide was docked in a configuration favourable for tat-30, the conformational changes were similar to those obtained for tat-30.
This could indicate that the presence of only the minimal basic region can induce the conformational shift, if it binds in a favourable way. To bind in this specific way, the surrounding amino acids of the glutamine-rich region (Fig. 2a) must be present. This point, however, is speculative, and would require further study for validation.
Comparison of modelling and simulations
The main objective of this study was to characterise a model that can explain TAR-tat binding on the acoustic wave device, and then verify it through molecular simulations. The modelling revealed that the biotinylated TAR layer behaved as a viscoelastic monolayer with no slip between the monolayer surface and the contacting liquid. The TAR-tat complex was modelled as a similar viscoelastic monolayer with a different thickness and interfacial slip. Recall that the thickness increased and the slip increased very slightly as the tat length increased. In this section, we corroborate the modelling results with what was observed in the MD simulations.TAR layer as a viscoelastic layer with no slip
A main finding of the modelling was that there was no slip on the hydrated neutravidin surface. Furthermore, adsorption of the bTAR layer did not affect the no-slip condition. The hydrophilic:hydrophobic SASA ratio calculated for the unbound TAR molecule was approximately 3, indicating there were over three times more hydrophilic atoms in contact with the solvent than hydrophobic atoms. It is therefore reasonable that there would be little slip of the liquid on the TAR monolayer.The bTAR molecules were modelled using a dry (non-hydrated) molecular volume of 49 nm3 and hydrated density for the monolayer of 1.01 g cm−3. The solvent accessible volume found for TAR molecule from the MD studies was found to be 12.6 ± 0.2 nm3, which is significantly lower than the 49 nm3 used for the modelling. The latter figure was estimated by taking the product of the cubic box dimensions, which does not take into account the volume occupied by solvent.
The dry density was estimated by multiplying the molecular weight Mm by the surface concentration csurf and dividing by the thickness of the monolayer/length of the molecule. The hydrated density was then determined from the mass of solvent occupying the non-excluded space of the molecule, which was determined from the footprint of the molecule itself, and the total area separating two individual molecules (Atot = 100 nm2). Previously, we used the largest box dimension as the thickness, which was 4.0 nm, and the other two dimensions as the footprint area, 12 nm2. However, the MPD for unbound TAR gave a molecule length of 4.8 nm, so treating the molecule as box of equivalent volume, we have a molecular footprint of 2.6 nm2. The dry density, with csurf = 1.5 pmol cm−2, is ρbTAR = 0.031 g cm−3, compared to 0.037 g cm−3 used in the modelling section. The hydrated density is then ρbTAR = 1.0 g cm−3, which is equivalent to that of water. As before, this value is a rough estimate.
Recalculating the viscoelasticity estimates for the bTAR layer with the MD values for TAR length and volume results in increases in the viscosity and decreases in the stiffness from those listed in Table 2. The time constants (τ = η/μ) increased by 1.5 to 4 times. The average updated shear modulus values for the bTAR layer are log(μbTAR) = 5.7 ± 0.1 and log(ηbTAR) = −2.1 ± 0.1. The full solution set is shown in the ESI (Table S.5).†
TAR-tat binding affects layer thickness and slip
Various models of TAR-tat binding were used, including as a viscoelastic layer, and as changes in layer thickness, stiffness, and slip. A variety of slip models were evaluated. It was found that the best model involved fitting the monolayer thickness and a slip model based on the sliptime τs (eqn (13)).The main results of the TAR-tat molecular simulations showed that as the length of the tatpeptide was increased, the volume of the system increased, the ratio of hydrophilic:hydrophobic surface area decreased gradually, and the maximum pair distance (MPD) increases. However, the MPD value decreased in most cases from that of the unbound TAR value.
As in the bTAR case, we reinterpret the molecular volume and monolayer density in terms of the volumes obtained from the simulations. The initial modelling results imply that the binding of the tatpeptides caused a decrease in the thickness of the layer (the TAR layer was assumed to have a thickness of 40 Å), with the shortest peptides resulting in decreases so as to make the layer disappear entirely. While such a situation is possible, it is unlikely, since the TAR is still on the surface following binding. Now that a new estimate is available for the TAR thickness and volume, we can recalculate the thickness-sliptime model for the TAR-tat system, with the molecular area footprint included in the calculation. The areas were fitted to all experimental peptide lengths with a linear regression analysis¶ of the MD volumes divided by the MPD lengths.
As shown in Table 6, the values determined from simulation do not have much effect on the fitted values. As before, there is a steady increase in overall TAR-tat length as the peptide length increases, and gradual decreases in sliptime. However, the errors in the peptide length averages are higher in the new fitted values than in the old ones.
| tat | No. of samples | Old values | New values | ||
|---|---|---|---|---|---|
| h TAR-tat/nm | ωτ s (×10−2) | h TAR-tat/nm | ωτ s (×10−2) | ||
| 12 | 2 | −0.3 (0.5) | −1.5 (0.1) | −0.2 (0.5) | −1.3 (0.1) |
| 20 | 8 | 0.1 (0.4) | −1.4 (0.2) | 0.2 (0.5) | −1.2 (0.3) |
| 22 | 3 | 0.8 (0.4) | −1.4 (0.3) | 1.2 (0.6) | −1.2 (0.3) |
| 25 | 4 | 0.7 (0.7) | −1.5 (0.5) | 1.9 (0.6) | −1.7 (0.2) |
| 27 | 5 | 1.5 (0.7) | −1.7 (0.4) | 2.2 (1.1) | −1.7 (0.6) |
| 30 | 3 | 3.05 (0.05) | −1.8 (0.4) | 3.7 (0.1) | −1.8 (0.4) |
Another interpretation is that since the numerical modelling is a two-parameter fit, other material properties are lumped into the two selected fitting parameters. Since we now have estimates for the volume and thickness (from the MPD) of the TAR-tat molecules, we can include these in the model, and potentially determine other parameters. To determine the density, we require an estimate for the surface area footprint of the TAR-tat complex. Estimates of the molecular areas were obtained from the MD volumes obtained above. The length of each TAR-tat complex was determined by fitting an exponential model|| to the values obtained from the MD simulations.
The modelling strategies used were recalculated with the new fitting approach. These included:
• stiffness–viscosity (μ–η)
• stiffness–sliptime (μ–ωτs)
• stiffness–thickness (μ–h)
• viscosity–sliptime (η–ωτs)
• viscosity–thickness (η–h)
• thickness–sliptime (h–ωτs)
• α-slip
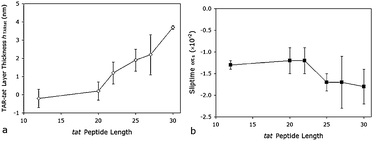
Only the thickness-sliptime and alpha-slip models converged for most of the experimental values, and of these two, only the α-slip model converged for all observations. The thickness-slip values are shown in Fig. 12. The thickness shifts (Fig. 12a) are similar to those obtained before the MD values were included.
 | ||
| Fig. 12 Recalculated model results for the thickness-sliptime fit as a function of tatamino acid length for (a) the layer thickness and (b) the sliptime. | ||
Turning to the sliptime fits, while there is an increase in the sliptime, the error is large and a difference in the sliptime between −1.7 × 10−2 and 4 × 10−2 corresponds to a decrease in the α-slip phase from 2.3° to 0.97°, which is small. With this model, there is no correlation between the degree of slip and the peptide length, only that slip does occur. This corresponds to behaviour observed in the MD simulations for both the hydrophilic:hydrophobic ratio and the RMSD of the various TAR-tatmacromolecules. The ratio of hydrophilic:hydrophobic surface atoms decreases slightly on TAR-tat binding, so it is reasonable that there is an onset of slip on binding of the tatpeptides. However, as is evident from Fig. 9, there is not a significant difference in the ratios between the different length peptides. Using this model, there is also no significant difference in the degree of slip; however, the onset of slip is evident. While the device and our model are sensitive enough to detect the onset of changes in interfacial coupling, it cannot detect the small differences in interfacial coupling between the different TAR-tat complexes.
We can draw similar conclusions regarding the revised α-slip fit, shown in Fig. 13. The re-evaluated slip estimates are similar to the initial values shown in Fig. 6, although the values for the slip angle are higher. Recall that even though α-slip models interfacial coupling, it combines all interfacial effects at the surface, including small changes in the viscoelasticity and thickness.
 | ||
| Fig. 13 Recalculated model results for the α-slip fit, showing slip magnitude (a) and phase (b). The error bars represent one standard deviation. | ||
It is evident that there is an onset of slip with the binding of tat. At the same time however, in this model, the lag between the surface layer and the liquid layer increases as the peptide length increases. This could be indicative of the excess drag due to the longer and heavier TAR-tat molecules. Since the difference (in length and mass) is small, the difference in angle is small too. The small decrease in the magnitude of the α parameter as the tatpeptide gets shorter could be due to small changes in the hydrophilic:hydrophobic ratios at shorter peptides, although, as mentioned above, this difference was not significant.
Solvent-accessible surface area as an indicator for slip
The ratio of the hydrophilic to hydrophobic SASA was used as an indicator of the relative hydrophilicity of a biomolecule and, by extension, of the monolayer. In an aqueous solution, the degree of hydrophilicity of a monolayer could reveal the relative slip of the solution across the surface. A more likely indicator of the surface-liquid affinity would be the shift in this ratio as the system changes states.In the previous sections, we used two measurements of interfacial coupling to describe the interaction between the TAR-tat monolayer and the adjacent aqueous buffer. The first was the complex α-slip parameter, and the second was the sliptime ωτs, where α = 1/(1 + jωτs). These values constitute experimentally determined system parameters, which have been fitted by numerical modelling.
The slip values can be compared to the SASA ratio to establish a relationship between hydrophobicity of a biochemical monolayer and interfacial coupling. Fig. 14 shows a comparison between the computed α-slip value from Fig. 13 and the SASA ratio for Str1, from Fig. 9. The x-axis shows the difference in the ratios between the MD values for unbound TAR and the various TAR-tat complexes, which represents the difference in affinity between the two states. The slip phase increases as the SASA difference between states increases, so the phase could be a good indicator of changes in surface affinity. However, the slip magnitude also increases for larger changes in affinity, which indicates that slippage is decreasing for decreasing affinity, so this is not a good marker for changes in affinity. This is because all interfacial changes are combined in the slip measurement, so changes in layer thickness or viscoelasticity are also modelled by α.
 | ||
| Fig. 14 Relationship between numerically fit α-slip parameter and the solvent affinity determined from MD simulations. The x-axis shows the difference between the hydrophilic:hydrophobic SASA ratios for unbound TAR and TAR-tat complexes, obtained from simulation. The y-axes are the slip magnitude and phase determined from experiment. The black diamonds show the magnitude, and the grey boxes the phase. The error bars represent one standard deviation, and the lines are drawn for display only. | ||
The sliptime description may be more appropriate for comparing the slip modelling with the MD simulations, since the change in monolayer thickness is modelled separately. In Fig. 15, the same difference in the SASA ratio is plotted against the magnitude and phase of α, as determined from the fitted sliptime ωτs in Table 6. In this case, because the length change is isolated in the thickness variable, the interfacial coupling effects are better isolated. As a result, the magnitude calculated from the sliptime decrease as the hydrophobicity increases, and the phase increases. This indicates that the change in surface area hydrophobicity from one state to another may be a good indicator of interfacial coupling. Conversely, changes in interfacial coupling may be useful as a predictor of conformational changes in a biochemical monolayer, provided a change in surface hydrophobicity occurs.
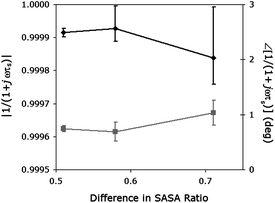 | ||
| Fig. 15 Relationship between numerically fit sliptime ωτs and the solvent affinity determined from MD simulations. The x-axis shows the difference between the hydrophilic:hydrophobic SASA ratios for unbound TAR and TAR-tat complexes, obtained from simulation. The y-axes are the magnitude and phase of the sliptime slip determined from experiment. The black diamonds show the magnitude, and the grey boxes the phase. The error bars represent one standard deviation, and the lines are drawn for display only. | ||
Evaluation of models
TAR adsorption as a viscoelastic layer
TAR was described as a second overlayer, above the NAv layer.30 The choice to do this, as opposed to incorporating it in a single NAv-bTAR layer, is that there is likely a clear interface between the two. Both the shear viscosity and the shear stiffness were lower for the bTAR layer than for the NAv layer. This is to be expected, since the globular protein NAv would form a more ordered, packed layer than the RNA, allowing more hydration by the surrounding solvent. This would reduce the overall energy storage of the layer, since more energy can be lost into the surrounding hydration layer, since the layer will be more liquid-like.Since no studies have been done previously on modelling the shear behaviour of TAR RNA, we cannot compare our results to the literature. However, we can relate them to other values for nucleic acids on acoustic biosensor surfaces. Few studies have actually quantified the viscoelastic properties of sheared nucleic acid layers. Stengel et al.18 observed changes in viscosity on partial hybridisation of ssDNA on a streptavidin-modified acoustic sensor surface. They found that the shear viscosity for both short strands of ssDNA and a combination of ds-DNA and ss-DNA were on the order of 3 × 10−2 g cm−1s−1. Binding of a large peptide led to a 60% increase in the viscosity. Peh et al.17 measured the binding of estrogen response element DNA (Mw = 21 kDa) to an estrogen receptor protein (Mw = 66 kDa) on an acoustic device, followed by binding of agonist and antagonist ligands. The immobilised DNA alone was found to have shear modulus and viscosity values of 2 × 106 g cm−1s−2 and 2 × 10−2 g cm−1s−1, respectively. This would correspond to a time constant ωτ = 0.31 for the 5-MHz crystals used. Binding of the peptide led to increases in both the modelled shear modulus and viscosity, to 5.5 × 106 g cm−1s−2 and 4.3 × 10−2 g cm−1s−1, yielding ωτ value of 0.24. Binding of agonist and antagonist ligands to the complex results in less increase in the viscoelasticity values.
These values indicate that our numerically fitted mechanical properties are in the correct range for nucleic acid monolayers on the TSM. However, there is a difference in the sizes of the complexes discussed in the above papers, and those considered here. As well, we have considered RNA molecules in this study, which are easier to deform and likely have more intrinsic disorder than dsDNA of equal size.90 This is evident from the fact that the TAR layer shows lower shear viscosity (8 × 10−3 g cm−1s−1) and modulus (5 × 105 g cm−1s−2) than most of the DNA structures discussed above.
TAR-tat interactions as a conformational change in the layer
The experimental results for TAR-tat binding show a consistent decrease in Rm across all peptide lengths, although the decrease was slightly larger for the tat-12 peptide. The frequency, on the other hand, went from a large increase for the tat-12 to a large decrease for the tat-30. A main reason for the decrease in resistance on binding of tat is that in the unbound form, TAR exists in two distinct conformers.87 In both of these, the nucleotides around the tri-nucleotide bulge do not stack, which would lead to greater mobility and thus greater dissipation. When tat binds, the base-pairs stack and straighten the bulge, leading to a stiffer molecule with less mobility,26 thereby decreasing the dissipation.We now turn to the modelled values for α-slip for the different tat lengths. The averaged computed values are shown in Table 7. Note that although there is a difference in the values, they are all very close to unity. This description indicates that there is only an onset of partial slip upon binding of tatpeptides, and in fact for tat-30, the difference in velocities between the surface and the liquid is only 0.5%. This difference is the same between the load impedance with slip and without. However, the phase angle increases for the longer tatpeptides.
| tat | |α|outer | ∠αouter (°) | b/nm |
|---|---|---|---|
| 12 | 0.972 (0.005) | 0.6 (0.1) | 5.1 (1.0) |
| 20 | 0.976 (0.007) | 0.8 (0.1) | 4.4 (1.3) |
| 22 | 0.979 (0.004) | 0.77 (0.05) | 3.9 (0.7) |
| 25 | 0.977 (0.005) | 0.9 (0.3) | 4.2 (0.9) |
| 27 | 0.987 (0.006) | 1.1 (0.2) | 2.3 (1.1) |
| 30 | 0.9950 (0.0004) | 0.9 (0.2) | 0.9 (0.1) |
The onset of partial slip upon binding of tat is expected from the MD results (Fig. 9), due to the decrease in hydrophilic contacts from TAR to TAR-tat. However, the MD simulations do not corroborate the decrease in slip as the tat length increases. Instead, we consider alternate interpretations of the meanings of the slip parameter. The complex slip α represents the difference in velocity at the interface by its magnitude, whereas the phase angle represents the lag in velocity between the surface and liquid. Considering first the magnitude, Ellis and Hayward50 showed that the effect of α can be estimated with the slip length, as b = −δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lnα, where δ is the decay length. The average values are shown in Table 7. These values are lower than those found for solvent on bare gold, since there is only a small difference in frequency shifts compared to the large shift for NAv from bare gold.
lnα, where δ is the decay length. The average values are shown in Table 7. These values are lower than those found for solvent on bare gold, since there is only a small difference in frequency shifts compared to the large shift for NAv from bare gold.
Interpretation of the phase angle is more complicated. The phase lag increases slightly for increasing tat lengths. If indeed the increase in lag represents an actual physical quantity, it makes sense that the larger TAR-tat complexes should experience more drag, which would result in a lag of the liquid particles adjacent or bound to the biochemical surface. To evaluate the physical meaning of the phase lag, we treat it as the time delay for the liquid particles to “catch up” to the surface. If we assume no slip for the TAR surface, the adjacent liquid layer will move in phase with the surface. A phase lag of 1° indicates that 1/360 of the period, or 0.0028/f0, would have elapsed before the liquid catches up to the surface. For the tat-12 complex, the 0.6° lag corresponds to a delay of 190 ps, and for the tat-30 complex, 290 ps. The increase in lag could correspond to an increase in energy loss due to drag or the increased mass.
Turning to the description of the thickness/slip model, numerical fitting showed a change in layer thickness and an onset of slip. As discussed above, the onset of slip is expected from the increase in hydrophobic surface contacts on binding of tatpeptides (Fig. 14 and 15). Interpretation of the length change estimates is more complex, since the values in Table 6 are for the thickness of the entire layer, not simply the change in thickness. Because of this, it appears as though the layer disappears completely for the tat-12 binding, and is smaller than the unbound TAR layer by at least 1 nm for even tat-30. Considering the difference between the tat-12 and tat-30, this is still unrealistic, since the layer thickness could not change by 3.5 nm due to binding.
Instead, we assume an average slip length as determined from the values in Table 7 of 3.6 nm. We then assume that all shifts in Rm are due to slippage effects, since the changes in Rm for adsorption of the different tat lengths are relatively similar. Using the slip response description from Daikhin et al.,47 we have
 | (14) |
Any residual frequency shift will be due to the change in thickness of the adsorbate layer, Δftot = Δfslip + Δfa. The change in frequency due to the change in thickness can be estimated as half the change in the effective wavelength. To a first approximation, we ignore the shear mechanical properties of the adsorbate, since its thickness is small compared to the thickness of the quartz. The effective thickness change is then given by
 | (15) |
 | ||
| Fig. 16 Change in effective thickness for the various tatpeptides, as determined from ΔR and eqn (14) and 15. The error bars show one standard deviation. | ||
The TAR RNA is known to straighten on binding of the full tatprotein. This reduces the bend angle at the bulge from 50° to close to straight. From a geometrical argument, we can obtain an estimate for what the actual change in thickness of this layer should be. In its bent form, the distance between the base of the bent RNA and the loop is 40 Å. Assuming the RNA is attached at the base and that the lower stem is oriented perpendicular to the surface, the theoretical thickness of the tat-bound layer is approximately 45 Å.91 This value is precisely the increase in thickness for the tat-30 molecule, as predicted from eqn (15). The same model predicts no change in thickness for the tat-27 case, and decreases in thickness of up to 6.5 Å for the shorter peptides. The predictions for the tat-30 and tat-27 shown in Fig. 16 are reasonable, since the full stable conformational change is only expected for tat fragments of at least 30 amino acids. Binding of the tat-27 molecule may indeed stabilise the complex, without inducing the full conformational shift.
A possible explanation for why all peptides shorter than tat-27 display a decrease in length in Fig. 16 is that none of these molecules form fully stable complexes. This is evident from the fact that the resistance/bandwidth measurements are higher for the shorter peptides. In eqn (14), we assumed that the entire shift in Rm from was due to slippage. However, from the range of Rm values, a more likely description is that some portion of the Rm shift for the shorter peptides is due to increases in dissipation within the film. This could occur if the unstable complexes are more mobile, resulting in an irregular layer thickness. The actual plane of reflection becomes more ambiguous, and thus lower, than for the stiffer, more stable compounds.
It is important to note that the viscoelasticity and slip values obtained herein are based on the fitting process and model parameters from the literature. Errors in these parameters may have a large effect on the reliability of the solutions. While a full sensitivity analysis is beyond the scope of this paper, the influence of such errors should be determined in greater detail, and is suggested for future work.
Conclusions
We have demonstrated that the TSM device can be applied to measure conformational shifts in biochemical monolayers in the liquid phase. We have performed quantitative treatments of interfacial slip and viscoelastic properties of protein fragments and nucleic acids that are comparable to similar systems found in the literature. Quantitative modelling of interfacial coupling for biomolecules immobilised on the surface of an acoustic biosensor has not been done before. Finally, we have introduced a molecular parameter, the ratio of hydrophilic to hydrophobic solvent accessible surface area that could be used to predict the interfacial coupling behaviour between a biochemical surface and an adjacent buffer.There are a number of experimental descriptions of viscoelastic changes in biological adsorbate layers on acoustic sensor surfaces.17,18 However, none of these has included slip at any interface, in spite of mounting evidence that interfacial coupling should be considered. While studies have treated hydration of proteins92,93 and conformational changes,14,94 none have considered situations where the changes in frequency and resistance are in the same direction, as we have in the present work
The molecular dynamics simulations of TAR RNA and the TAR-tat complex exhibited interesting patterns concerning the different length tatpeptides. In particular, they demonstrated changes in the bend angle, SASA ratios and overall length from the unbound TAR structure. However, longer simulations and a broader sampling are required to fully characterise the structural changes on TAR-tat binding. In particular, separate AutoDock simulations should be done for each tat length, as in Str1, compared to the truncation performed in Str2. There was an interesting result from Str2, suggesting that the presence of only the minimal basic region can induce the conformational shift, if it binds in the right way. However, further analysis is required to verify this.
This work has highlighted viscoelastic and interfacial properties of biological adsorbate layers, which can be compared with other similar studies. It also demonstrates the promise of using molecular dynamics in this area, but highlights some potential problems. Finally, this study considered the physical phenomenon of interfacial slip in a system where it likely has a significant effect on the device response. The quantitative material properties established will provide a framework for future study of multilayered biochemical systems. Additionally, it will hopefully encourage further coupling of molecular dynamics with biosensing of proteins and nucleic acids to predict interfacial properties of biochemical surfaces.
Acknowledgements
The authors are grateful for support of this work from the Natural Sciences and Engineering Research Council of Canada and a NATO Science for Peace Grant. JSE would like to thank the Ontario Graduate Scholarship (OGS) and the Victoria Noakes Ontario Graduate Scholarship in Science and Technology (OGSST) Programs for financial support. The authors wish to express their appreciation to Professors Gordon Hayward (University of Guelph), Glen McHale (The Nottingham Trent University), and Michael Urbakh (Tel-Aviv University), and Drs. David Stone (University of Toronto) and Nardos Tassew (Toronto Western Hospital) for much very helpful discussion.Notes and references
- H. J. Dyson and P. E. Wright, Annu. Rev. Phys. Chem., 1996, 47, 369–395 CrossRef CAS.
- N. J. Greenfield, Anal. Biochem., 1996, 235, 1–10 CrossRef CAS.
- D. P. Goldenberg and T. E. Creighton, Anal. Biochem., 1984, 138, 1–18 CrossRef CAS.
- P. G. Righetti and B. Verzola, Electrophoresis, 2001, 22, 2359–2374 CrossRef CAS.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS.
- W. F. van Gunsteren, P. H. Hunenberger, A. E. Mark, P. E. Smith and I. G. Tironi, Comput. Phys. Commun., 1995, 91, 305–319 CrossRef CAS.
- S. Scheuring, D. Fotiadis, C. Möller, S. A. Müller, A. Engel and D. J. Müller, Single Mol., 2001, 2, 59–67 CrossRef CAS.
- K. Robert, J. Mol. Recognit., 2004, 17, 151–161 CrossRef CAS.
- C. Boozer, G. Kim, S. Cong, H. Guan and T. Londergan, Curr. Opin. Biotechnol., 2006, 17, 400–405 CrossRef CAS.
- L. E. Cheran, M. Chacko, M. Q. Zhang and M. Thompson, Analyst, 2004, 129, 161–168 RSC.
- L. E. Cheran, S. Sadeghi and M. Thompson, Analyst, 2005, 130, 1569–1576 RSC.
- H. Huo, L. E. Cheran and M. Thompson, in New Approaches in Biomedical Spectroscopy, ed. K. Kneipp, R. Aroca, H. Kneipp and E. Wentrup-Byrne, American Chemical Society, Washington DC, 2007, pp. 312–337 Search PubMed.
- B. A. Cavic, G. L. Hayward and M. Thompson, Analyst, 1999, 124, 1405–1420 RSC.
- A. Tsortos, G. Papadakis, K. Mitsakakis, K. A. Melzak and E. Gizeli, Biophys. J., 2008, 94, 2706–2715.
- X. D. Su, Y. J. Wu and W. Knoll, Biosens. Bioelectron., 2005, 21, 719–726 CrossRef CAS.
- J. Zhang, X. D. Su and S. J. O'Shea, Biophys. Chem., 2002, 99, 31–41 CrossRef CAS.
- W. Y. X. Peh, E. Reimhult, H. F. Teh, J. S. Thomsen and X. D. Su, Biophys. J., 2007, 92, 4415–4423 CrossRef CAS.
- G. Stengel, F. Hook and W. Knoll, Anal. Chem., 2005, 77, 3709–3714 CrossRef CAS.
- S. J. Braunhut, D. McIntosh, E. Vorotnikova, T. Zhou and K. A. Marx, Assay Drug Dev. Technol., 2005, 3, 77–88 CrossRef CAS.
- L. E. Cheran, S. L. Cheung, A. Al Chawaf, J. S. Ellis, D. D. Belsham, W. A. MacKay, D. Lovejoy and M. Thompson, Analyst, 2007, 132, 242–255 RSC.
- K. A. Marx, T. Zhou, A. Montrone, H. Schulze and S. J. Braunhut, Biosens. Bioelectron., 2001, 16, 773–782 CrossRef CAS.
- X. M. Wang, J. S. Ellis, C. D. Kan, R. K. Li and M. Thompson, Analyst, 2008, 133, 85–92 RSC.
- E.-L. E. Lyle, University of Toronto, 2004.
- N. G. Tassew, Ph.D., University of Toronto, 2003.
- X. Wang, University of Toronto, 2008.
- M. Zacharias and P. J. Hagerman, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 6052–6056 CrossRef CAS.
- V. S. J. Craig, C. Neto and D. R. M. Williams, Phys. Rev. Lett., 2001, 87, 054504 CrossRef CAS.
- C. Neto, V. S. J. Craig and D. R. M. Williams, Eur. Phys. J. E, 2003, 12, S71–S74 CAS.
- F. Ferrante, A. L. Kipling and M. Thompson, J. Appl. Phys., 1994, 76, 3448–3462 CrossRef CAS.
- J. S. Ellis and M. Thompson, Langmuir, 2010, 26, 11558–11567 CrossRef CAS.
- G. McHale, R. Lucklum, M. I. Newton and J. A. Cowen, J. Appl. Phys., 2000, 88, 7304–7312 CrossRef CAS.
- C. E. Reed, K. K. Kanazawa and J. H. Kaufman, J. Appl. Phys., 1990, 68, 1993–2001 CrossRef CAS.
- F. Eggers and T. Funck, J. Phys. E: Sci. Instrum., 1987, 20, 523 CrossRef CAS.
- D. Johannsmann, K. Mathauer, G. Wegner and W. Knoll, Phys. Rev. B: Condens. Matter, 1992, 46, 7808 CrossRef.
- L. Tessier, F. Patat, N. Schmitt, M. Lethiecq, Y. Frangin and D. Guilloteau, Sens. Actuators, B, 1994, 19, 698–703 CrossRef CAS.
- K. M. Weeks, C. Ampe, S. C. Schultz, T. A. Steitz and D. M. Crothers, Science, 1990, 249, 1281–1285 CAS.
- F. Aboul-ela, J. Karn and G. Varani, J. Mol. Biol., 1995, 253, 313–332 CrossRef.
- J. M. Peloponese, C. Gregoire, S. Opi, D. Esquieu, J. Sturgis, E. Lebrun, E. Meurs, Y. Collette, D. Olive, A. M. Aubertin, M. Witvrow, C. Pannecouque, E. De Clercq, C. Bailly, J. Lebreton and E. P. Loret, C. R. Acad. Sci., Ser. III, 2000, 323, 883–894 CAS.
- J. H. J. Cho, B. M. Law and F. Rieutord, Phys. Rev. Lett., 2004, 92.
- R. Pit, H. Hervet and L. Leger, Tribol. Lett., 1999, 7, 147–152 CrossRef CAS.
- D. C. Tretheway and C. D. Meinhart, Phys. Fluids, 2004, 16, 1509–1515 Search PubMed.
- Y. X. Zhu and S. Granick, Phys. Rev. Lett., 2002, 88, 106102 CrossRef.
- E. Bonaccurso, H. J. Butt and V. S. J. Craig, Phys. Rev. Lett., 2003, 90, 144501 CrossRef.
- E. Bonaccurso, M. Kappl and H. J. Butt, Phys. Rev. Lett., 2002, 88, 076103 CrossRef.
- C. Cottin-Bizonne, S. Jurine, J. Baudry, J. Crassous, F. Restagno and E. Charlaix, Eur. Phys. J. E, 2002, 9, 47–53 CAS.
- M. Cieplak, E. D. Smith and M. O. Robbins, Science, 1994, 265, 1209–1212 CAS.
- L. Daikhin, E. Gileadi, V. Tsionsky, M. Urbakh and G. Zilberman, Electrochim. Acta, 2000, 45, 3615–3621 CrossRef CAS.
- B. Du, I. Goubaidoulline and D. Johannsmann, Langmuir, 2004, 20, 10617–10624 CrossRef CAS.
- W. C. Duncan-Hewitt and M. Thompson, Anal. Chem., 1992, 64, 94–105 CrossRef CAS.
- J. S. Ellis and G. L. Hayward, J. Appl. Phys., 2003, 94, 7856–7867 CrossRef CAS.
- J. S. Ellis and M. Thompson, Chem. Commun., 2004, 1310–1311 RSC.
- G. L. Hayward and M. Thompson, J. Appl. Phys., 1998, 83, 2194–2201 CrossRef CAS.
- J. Krim, MRS Bull., 1998, 23, 20–21.
- M. Rodahl and B. Kasemo, Sens. Actuators, A, 1996, 54, 448–456 CrossRef.
- G. R. Willmott and J. L. Tallon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 066306 CrossRef CAS.
- M. S. Yang, M. Thompson and W. C. Duncan-Hewitt, Langmuir, 1993, 9, 802–811 CrossRef CAS.
- J. L. Barrat and L. Bocquet, Phys. Rev. Lett., 1999, 82, 4671–4674 CrossRef CAS.
- J. Baudry, E. Charlaix, A. Tonck and D. Mazuyer, Langmuir, 2001, 17, 5232–5236 CrossRef CAS.
- S. Granick, Y. X. Zhu and H. Lee, Nat. Mater., 2003, 2, 221–227 CrossRef CAS.
- J. S. Ellis and M. Thompson, Phys. Chem. Chem. Phys., 2004, 6, 4928–4938 RSC.
- F. Lu, H. P. Lee and S. P. Lim, J. Phys. D: Appl. Phys., 2004, 37, 898–906 CrossRef CAS.
- M. Salomaki and J. Kankare, Langmuir, 2004, 20, 7794–7801 CrossRef.
- G. McHale and M. I. Newton, J. Appl. Phys., 2004, 95, 373–380 CrossRef CAS.
- J. W. Eaton, GNU Octave Manual, Network Theory Limited, 2002 Search PubMed.
- J. W. Eaton, Octave, 2007 Search PubMed.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317 CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- W. L. DeLano, MacPyMOL: A PyMOL-based Molecular Graphics Application for MacOS X, ( 2007) DeLano Scientific LLC, Palo Alto, CA, USA Search PubMed.
- G. M. Morris, D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew and A. J. Olson, J. Comput. Chem., 1998, 19, 1639–1662 CrossRef CAS.
- M. F. Sanner, J. Mol. Graph. Model., 1999, 17, 57–61 CAS.
- S. Olivier, J. Prins, J. Derby and K. Vu, Proceedings of 8th IEEE International Workshop on Parallel and Distributed Scientific and Engineering Computing, Long Beach, CA, 2007 Search PubMed.
- E. J. Sorin and V. S. Pande, Biophys. J., 2005, 88, 2472–2493 CrossRef CAS.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- Y. G. Mu and G. Stock, Biophys. J., 2006, 90, 391–399 CrossRef CAS.
- J. J. Moré, B. S. Garbow and K. E. Hillstrom, User Guide for MINPACK-1, Argonne National Laboratory, Argonne, IL, 1980 Search PubMed.
- L. M. Furtado, H. B. Su, M. Thompson, D. P. Mack and G. L. Hayward, Anal. Chem., 1999, 71, 1167–1175 CrossRef CAS.
- R. C. Ebersole, J. A. Miller, J. R. Moran and M. D. Ward, J. Am. Chem. Soc., 1990, 112, 3239–3241 CrossRef CAS.
- R. Lucklum and P. Hauptmann, Faraday Discuss., 1997, 107, 123–140 RSC.
- K. M. Weeks and D. M. Crothers, Biochemistry, 1992, 31, 10281–10287 CrossRef CAS.
- E. D. Smith, M. O. Robbins and M. Cieplak, Phys. Rev. B: Condens. Matter, 1996, 54, 8252–8260 CrossRef CAS.
- R. Nifosi, C. M. Reyes and P. A. Kollman, Nucleic Acids Res., 2000, 28, 4944–4955 CrossRef CAS.
- G. Aboul-ela, J. Karn and G. Varani, Nucleic Acids Res., 1996, 24, 4598–4598.
- K. S. Long and D. M. Crothers, Biochemistry, 1999, 38, 10059–10069 CrossRef CAS.
- B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379 CrossRef CAS.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef CAS.
- A. Perez, A. Noy, F. Lankas, F. J. Luque and M. Orozco, Nucleic Acids Res., 2004, 32, 6144–6151 CrossRef CAS.
- J. D. Puglisi, L. Chen, S. Blanchard and A. D. Frankel, Science, 1995, 270, 1200–1203.
- G. V. Lubarsky, M. R. Davidson and R. H. Bradley, Biosens. Bioelectron., 2007, 22, 1275–1281 CrossRef CAS.
- X. Su and J. Zhang, Sens. Actuators, B, 2004, 100, 309–314.
- C. D. Gwenin, J. P. Jones, M. Kalaji, T. J. Lewis, J. P. Llewellyn and P. A. Williams, Sens. Actuators, B, 2007, 126, 499–507 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: General remarks and additional figures. See DOI: 10.1039/c0sc00423e |
| ‡ Present address: Dept. of Mechanical & Industrial Engineering, Faculty of Applied Science & Engineering, University of Toronto, 5 King’s College Road, Toronto, Canada. |
| § This value is obtained from the molecular weights of TAR (9695 Da) and biotin (244 Da). |
| ¶ The polyfit linear regression function in Octave3 was used to fit the areas for the TAR-tat complexes. The equation obtained was A = 0.02987L + 3.074. L is the peptide length and A is the molecular area to input to the model. The parameters were fitted to the average values from Str1, and the R2 value was 0.94. |
| || The exponential function h = αeβ(L−d) + D was fit using a Levenberg–Marquardt non-linear regression analsysis in Octave3.0.1, yielding α =5.29 × 10−3, β = 0.744, d = 25.4 and D = 4.54. L is the peptide length and h is the layer thickness to input to the model. The parameters were fit to the average values from Str1, and the R2 value was 0.999. |
| This journal is © The Royal Society of Chemistry 2011 |