Copper(I) speciation in mixed thiosulfate-chloride and ammonia-chloride solutions: XAS and UV-Visible spectroscopic studies

Abstract

Thiosulfate and ammonia mixtures may be more environmentally benign alternatives to cyanide for leaching Au from ores. In this method, the Cu(I)/Cu(II) couple acts as a redox mediator aiding in the oxidative dissolution of metallic Au. Information about the speciation of Cu(I) and Cu(II) in these lixiviant solutions is paramount to the optimization of gold ore processing conditions. With this in mind, we have carried out XANES, EXAFS and UV-Vis spectroscopic studies of the speciation of Cu(I) in mixed thiosulfate-chloride and ammonia-chloride solutions. In thiosulfate-chloride solutions, the EXAFS studies indicate that the geometry of the predominant Cu(I) complex is distorted trigonal (triangular planar), with an average of 2 sulfur atoms + 1 oxygen atom occupying the coordination sphere. This indicates that the stability of the [Cu(S₂O₃)₃]⁵⁻ complex is lower than previously proposed. Formation constants for Cu(I) thiosulfate complexes have been derived on the basis of systematic UV-Vis measurements of solutions with varying [S₂O₃]/[Cl] ratios. Only one mixed chloride-thiosulfate complex, [Cu(H₂O)(S₂O₃)Cl]²⁻, was found to predominate over the range of conditions investigated. For Cu(I) in ammonia-chloride solutions, our results confirm the broad stability of [Cu(NH₃)₂]⁺ and we have also identified a stable mixed amminechlorocopper(I) complex, [CuCl(NH₃)]⁺. XAS reveals that these two complexes share a linear geometry. This study demonstrates that combinations of methods are required to decipher the geometry and thermodynamic properties of transition metal complexes in mixed ligand chemical systems where many species may coexist. Our results allow more comprehensive predictions of solution speciation and contribute to efforts to design improved methods to process gold ore with thiosulfate and ammonia lixiviants.

---

1. Introduction

Gold is typically extracted using the cyanidation/carbon-in-pulp process, a method that is effective and economical when applied to ores containing relatively low gold concentrations (0.5–3 ppm Au).¹ Increasing pressure from environmental protection agencies and public perception, which frown upon cyanide due to its toxicity and potential volatility, has resulted in the investigation of more benign lixiviants, such as thiosulfate and ammonia.^2,3 In these alternative methods, the copper(I)/(II) couple acts as a redox mediator aiding in the oxidative dissolution of gold. Metallic Au is oxidized by Cu(II), and the resulting Cu(I) can be oxidized back to Cu(II) by reaction with atmospheric oxygen to complete the catalytic cycle. In addition, since Cu(II) can also oxidize thiosulfate to tetrathionate, an understanding of the solution speciation and stability of individual species is important for decreasing the amount of reactant needed during processing.² The chemistry of the ammonia–thiosulfate–copper(I)/(II) system is complicated due to the presence of two complexing ligands, ammonia and thiosulfate. Given that gold processing plants in arid and semi-arid regions (e.g., Australia) may need to use highly saline local groundwaters, it is also important to investigate the effect of chloride (e.g., “Water Management at KCGM”⁴). Copper(I) speciation is important in the gold oxidation cycle and, thus, there is a need to understand the nature and properties of Cu(I) complexes that form in these chemical environments, in order to design new hydrometallurgical methods that optimize leaching parameters, extract gold more efficiently and quickly, and minimize the amounts of lixiviants.

The complexation of Cu(I) by chloride ligands from ambient temperature to 500 °C has been the subject of recent solubility and spectroscopic studies.^5–11 The consensus emerging from these studies is that the linear complexes [H₂O–Cu–Cl]⁰ and [Cl–Cu–Cl]⁻ dominate the speciation of Cu(I) in acidic chloride brines. The trigonal planar [CuCl₃]²⁻ ion exists at low temperature (< 200 °C) and high [Cl⁻] (> 2 m), but detailed XAS studies showed that the tetrahedral complex [CuCl₄]³⁻, commonly found in solids, does not exist in solution,⁵ a result independently corroborated by ab initio molecular dynamic simulations.¹² Herein, the thermodynamic constants for Cu(I) chloro-complexes from Brugger et al.⁵ are used.

Fewer data are available for thiosulfatocopper(I) complexes, and little information is available on their geometry. According to Smith and Martell,¹³ [Cu(S₂O₃)]⁻ predominates over a broad range of S₂O₃²⁻ activities (e.g., up to ∼16 mM S₂O₃²⁻ in a 1 mM Cu⁺ solution at pH 9.25), whereas [Cu(S₂O₃)₂]³⁻ and [Cu(S₂O₃)₃]⁵⁻ form at higher [S₂O₃²⁻] (Fig. 1). Only two studies report formation constants for [Cu(S₂O₃)]⁻,^14,15 and they are in relatively poor agreement (log β = 8.91/9.91 and 10.35, respectively; Table 1). The study of Golub et al.¹⁴ does not provide sufficient details on the reaction conditions (e.g., metal ion concentrations are not reported), and hence this study does not meet the quality criteria outlined by Martell and Motekaitis,¹⁶ so we cannot assess the reliability of their results. A good consensus exists for the formation constant of [Cu(S₂O₃)₂]³⁻, with three of four studies in broad agreement (11.69 < log β < 12.30;^15,17,18; Table 1). Two studies^15,19 provide a consistent formation constant for [Cu(S₂O₃)₃]⁵⁻ (13.64 < log β < 14.30), which is much higher than the log β = 10.35/11.75 reported by Golub et al.¹⁴ (Table 1). Only one study has investigated mixed chloride-thiosulfate complexes. Using potentiometric methods, Boos and Popel²⁰ proposed that [Cu(S₂O₃)₂Cl]⁴⁻ was the predominant species present for [Cl⁻] from 0.01 to 0.1 M and [S₂O₃²⁻] from 1.5 to 5.4 mM, which are reflected in Fig. 1a.

Fig. 1 Distributions of Cu(I) species in the thiosulfate-ammine-chloride system. Full circles and number labels refer to solution compositions from Tables S1 and S3. Activity of Cu species 10⁻³, T = 25 °C.

Table 1 Selected literature thermodynamic data for copper(I)-chloride, thiosulfate and ammine complexes. Stability constants are for the formation reactions, Cu⁺ + x S₂O₃²⁻ + y Cl⁻ + z [NH₃]⁰ = Cu(S₂O₃²⁻)_xCl_y(NH₃)_z^1−2x−y at 25 °C. Uncertainties (1−δ) are indicated in parentheses

Complex	Stability constants (Log β)	Ionic strength (m)	Medium	References
a N.B. Golub et al.^43 also reported formation constants of 11.5/12.38 for [Cu(S2O3)4^7^− in Na2SO4/K2SO4. b Preferred value in Smith and Martell.^13 c Ka for the reaction [Cu(NH3)2]^+ + NH3(aq) = [Cu(NH3)3]^+. d Solis et al.^21 also report minor amounts (< 15%) of other mixed ligand complexes, and hence impossible to characterize precisely. e Cited by Black.^49
Cu(I) chloride complexes
CuCl^0	4.17	0	NaCl	5
CuCl2^−	5.46	0	NaCl	5
CuCl3^2^−	4.75	0	NaCl	5
Cu(I) thiosulfate complexes
Cu(S2O3)^−	10.35^b	0.1–7	Na2SO4	15
	8.91/9.91		Na2SO4/K2SO4	43
	8.5	0		Recommended.This study
Cu(S2O3)2^3^−	12.27^b	1.6	Na2SO4	15
	12.30	n.r.	n.r.	18
	11.69 (18 °C)	Variable	Variable	17
	9.32/10.6		Na2SO4/K2SO4	43
	12.0(5)	0		Recommended. This study
Cu(S2O3)3^5^−^a	14.30	1.2	KNO3	19
	13.70^b	1.6	Na2SO4	15
	13.64	1.0	Na2SO4	15
	10.34/11.75		Na2SO4/K2SO4	43
	9.9(5)	0		Recommended. This study
Cu(I) mixed thiosulfate-chloride complexes
Cu(S2O3)2Cl^4^−	12.89	n.r.	n.r.	20
Cu(S2O3)Cl2^3^−	7.63(15)	0		Recommended. This study
Cu(S2O3)Cl^2^−	9.61(15)	0		Recommended. This study
Cu(I) ammine complexes
Cu(NH3)^+	5.74^b	2.0	NH4NO3	44
	5.80	3.0	(NH4)2SO4	45
Cu(NH3)2^+	9.92^b	0.1	KNO3	46
	11.38	1	NaClO4	21
	10.7(+ 0.2/−0.5)	0		Recommended. This study
Cu(NH3)3^+	Ka = ∼0.04	0.5	NaClO4	47
	Ka = 0.05	1.0	NaClO4	48
	Ka = 0.05	3.0	(NH4)2SO4	45
	∼10.5	0		Recommended. This study
Cu(I) mixed ammine-chloride complexes
Cu(NH3)Cl^0	8.92	1.0	NaClO4	21
	8.38(+ 0.2/−0.3)	0		Recommended. This study

---

Investigations of speciation in the Cu(I)–NH₃ system (Table 1) indicate that [Cu(NH₃)₂]⁺ is the main amminecopper(I) complex, and that [Cu(NH₃)]⁺ and [Cu(NH₃)₃]⁺ play only minor roles (Fig. 1). A single study (Solis et al.²¹) examined the presence of mixed chloro-ammine complexes by polarography and concluded that the most abundant complex is [Cu(NH₃)Cl]⁰, although the data suggested that other minor mixed complexes are present (e.g., [Cu(NH₃)Cl₂]⁻).

The formation constants for Cu(I)–S₂O₃²⁻ and Cu(I)–NH₃ species are approximately 4–8 orders of magnitude larger than those for the Cu(I)–Cl⁻ complexes (Table 1); hence even in chloride-rich solutions (e.g. 1 m Cl⁻; Fig. 1), Cu(I) speciation is expected to be dominated by ammine and thiosulfato complexes. This study aims to investigate the significance of mixed chloride complexes in the Cu(I)–Cl⁻–S₂O₃²⁻ and Cu(I)–Cl⁻–NH₃ systems, to characterize the composition and geometry of the predominant ammine and thiosulfato complexes using a combination of X-ray Absorption Spectroscopy (XAS) and UV-Vis spectroscopy, and to provide a reliable set of formation constants for Cu(I) complexes that is consistent with existing information for Cu(I) complexation in the Cl⁻–NH₃–S₂O₃²⁻ system. This will provide more comprehensive numerical models for these complex chemical systems, which can be used in the refinement and optimization of methods for extracting gold.

2. Experimental methods and data analysis

2.1 Starting materials and solutions preparation

Freshly synthesized copper(I) chloride was dissolved with the requisite amounts of sodium chloride, sodium thiosulfate, ammonium chloride and sodium hydroxide in water to achieve the solution compositions listed in the supplementary data Tables S1–S4.† All chemicals were of analytical-grade or better and were used as received. All solutions were prepared by weighing and, to minimize oxidation of Cu(I) to Cu(II), they were prepared from double-deionized water degassed of oxygen by boiling and bubbling nitrogen gas through the solution for at least 15 min, immediately before preparation in a glove box under nitrogen atmosphere. Samples were then loaded, in the glove box, into either stopped PTFE solution cells that were used to obtain XAS data under ambient conditions or stoppered quartz cuvettes for UV-Vis spectrophotometry. Stock solutions of copper(I) chloride were filtered through Millipore 0.22 μm membrane filters before mixing with ammonia and thiosulfate stocks. Identical solutions could not be measured for both the XAS and UV-Vis experiments, due to the higher Cu(I) concentration and consequently higher S₂O₃²⁻ and NH₃ concentrations (in order to prevent precipitation of copper compounds) required for the XAS experiments, which resulted in covering a different range of compositions to that for the UV-Vis experiments. The pH values of stocks and samples containing ammonia were measured outside of the glove box using a glass electrode calibrated with freshly prepared sodium tetraborate (pH_25 °C 9.2) and phosphate (pH_25 °C 7.2) buffer solutions.²² The pH of thiosulfate solutions was not adjusted and was self-buffered at ∼5.5. Copper(I) hydrolysis is not expected to be important as the pH of the solutions was well below the first hydrolysis constant for Cu(I) (log K [Cu(OH)]⁰_(aq) = 11.36 at 25 °C).^10,23 Thus, under these experimental conditions, the speciation and thermodynamic properties could be determined whilst minimising the impact of mixed hydroxide complexes.

2.2 UV-Vis measurements and interpretation

Spectrophotometric measurements were carried out at 25 °C using a Varian CARY® 5G UV-Vis-NIR instrument equipped with a water-regulated temperature controller. The sample solutions were placed in 1 cm path length quartz cuvettes in the nitrogen glove box, and sealed with a screw on cap and Teflon o-ring. For each solution, the baseline spectrum of a solution with the same composition but containing no Cu was collected before measuring the spectrum of the Cu-bearing solution. The baseline spectrum was subtracted from the spectrum of each sample solution to correct for detector response, and for the absorption of the cell and solution matrices. The absorbance of each solution was measured at 1 nm increments between 1200 and 200 nm. It was typically in the range of 0–2.5 absorbance units, with a reproducibility of 0.01 units.

Solution UV-Vis-NIR spectrophotometry measures a variety of electronic transitions including those between orbitals on the metals and ligands (and vice versa) and the complexes and solvent. It can therefore provide information about the electronic structure of the complex, e.g., the oxidation state of the metal, the geometry of the complex, and the nature of the ligands. The intensity of electronic transitions (molar absorbances ∼1000–5000 M⁻¹ cm⁻¹) occurring in the 210–320 nm region for the Cu(I) system indicates that these bands originate from charge transfer transitions. Systematic measurements of UV-Vis spectra for solutions containing varying amounts of ligands were used to identify the complexes present in the experiments and derive their apparent formation constants, providing a test of the validity of proposed speciation models. The interpretation is based on the Beer–Lambert law, which relates the absorbance (A) at a given wavelength (λ) to the molar absorptivity (ε_i,λ) and the molar concentrations (M_i) of each of the i absorbing species present in solution:

where n is the number of the absorbing species and l is the path length of the cell. The procedure used to fit the spectra is similar to the method established by Brugger et al.²⁴ for experiments on Cu(II)-chloro complexes. The data were processed using the BeerOz program.²⁵

When considering more than one wavelength, the Beer–Lambert law (eqn 1) can be written in a matrix form as:

A = C*E (2)

where A is the matrix of measured absorbance (number of solutions × number of wavelengths), C is the matrix of concentration of absorbing species (number of solutions × number of absorbing species) and E is the matrix of molar absorptivity for all absorbing species (number of absorbing species × number of wavelengths). The goal of data analysis is to find the matrices C and E that best reproduce the observed absorbance spectra, i.e., matrix A, by optimizing both formation constants and molar absorptivities for each absorbing complex. Practically, this simple linear algebra problem has an infinite number of solutions, whereas there is only one physical solution. This unique solution can be obtained by introducing physical constraints (e.g., concentrations and molar absorptivities as positive numbers; chemical mass action or mass balance) into the model. This usually renders the problem non-linear and non-linear least-square techniques are required to retrieve E and C.²⁵

On the basis of preliminary analysis and taking into account available literature information, a chemical speciation model can be established. The final quantitative analysis is conducted using non-negativity constraints for the molar absorptivity coefficients, and a complete speciation model to calculate the matrix C (i.e., the elements of C are constrained by mass balance and mass action equations). This analysis delivers a set of equilibrium constants (Log K) for the formation of the different Cu(I) complexes. For the distribution of species calculations, activity coefficients were estimated with the “b-dot” equation,²⁶ using the b-dot parameters listed for NaCl solutions from Helgeson and Kirkham.²⁷ The ion size parameters were set to 5 Å for Cu(I)-complexes, 9 Å for H⁺, and 4 Å for all other charged ions and complexes.²⁸ The ionic strength of solutions ranged from ∼0.5 to 5 molal (Tables S3 and S4†), which is within the limit for the b-dot model description of NaCl solutions.^24,29

2.3 X-ray absorption spectroscopy measurement and analysis

2.3.1 XAS measurements. Copper K-edge (8979 eV) X-ray Absorption Near Edge Structure (XANES) and Extended X-ray absorption Fine Structure (EXAFS) spectra were measured at the 20-BM-B beamline (XOR/PNC sector), at the Advanced Photon Source (APS), in Chicago, USA. The APS is a 7 GeV ring and operates in top-up mode with a current of 102 mA. 20-BM-B is a bending magnet beam line with a Si(111) monochromator and an energy resolution (ΔE/E) of 1.4 × 10⁻⁴ (at 10 keV).³⁰ A focused beam size of 1 × 5 mm² was used. The incident and transmitted beam intensity I₀ and I₁ were measured with ion chambers. A 12 element solid-state Ge detector was used for detecting fluorescence data. The energy was calibrated with a Cu foil, such that the maximum of the first derivative was at 8979 eV. For each solution, 2 to 6 scans were collected, allowing an assessment of the effect of beam damage;⁵ the replicate spectra were reproducible (to within 5%) indicating there was no measurable impact of beam damage. The Cu step height in a blank sample was also measured and found to be three orders of magnitude lower in intensity than the samples studied, and thus has a negligible effect for EXAFS analysis.

2.3.2 Standards for XANES & EXAFS. In EXAFS data analysis, it is crucial to estimate the value of S₀² (“scale factor”), as the magnitude of the Fourier transformed EXAFS peak is fitted, among other parameters, as the product of S₀² and the number of scattering atoms.³¹ In this study, an aqueous solution containing 0.0089 m CuCl₂ and 0.53 m lithium chloride was used to determine S₀². Note that it is preferable to use a solution as a standard rather than the Cu foil as S₀² should be determined under as similar conditions as possible. Although the geometry of the Cu(II) aqua-ion may be tetragonal, this does not affect the EXAFS fitting and the suitability of the aqua ion as an EXAFS standard.^5,32 With a k² weighting, 2 ≤ k ≤ 11.0 Å⁻¹ and a Hanning window, S₀² was refined to be 0.75(9) (the number in the parentheses is the one standard deviation error). This value of S₀² was used in all subsequent refinements, and is similar to that used by other authors for aqueous Cu(I) speciation studies (e.g., 0.71⁵ and 0.81³²). The determination of S₀² was performed using a distorted octahedral model, with four oxygen atoms at a distance of 1.96(1) Å plus two oxygen atoms at a longer distance of 2.54(8) Å.

2.3.3 XANES data preparation for simulation and analysis. XANES spectra arise from the excitation of core electrons to higher electronic states, and contain information about oxidation state and coordination symmetry. Kau et al.³³ compared the XANES spectra of 19 Cu(I) compounds with two-, three- and four-fold coordination. They were able to relate the position of the pre-edge (attributed to the 1s → 4p_xy transition) and the intensity of this transition relative to the edge height to the coordination geometry of copper in the compound. Linear Cu(I) compounds have a sharp pre-edge with an average normalized absorption amplitude of 1.08. In contrast, this amplitude decreases to 0.63 in trigonal Cu(I) compounds. For four coordinate Cu(I) compounds the pre-edge is broad, the average normalized absorption amplitude is 0.72, and the crest is shifted by ∼1.5 eV towards higher energy compared to linear and trigonal compounds.³³

XANES spectra for a given stoichiometry and geometry of Cu(I) thiosulfato and ammine complexes were calculated ab initio using the FDMNES package developed by Joly,³⁴ following the procedure outlined in Brugger et al.⁵ and Testemale et al.³⁵. The final states and resulting absorption cross sections were calculated using the Finite Difference Method (FDM) to solve the Schrödinger equation in the cluster. This method allows a totally free potential shape, thus avoiding the limitations imposed by the Muffin Tin approximation. Compared to methods that rely on the Muffin Tin approximation, FDM is of particular interest in the case of low symmetry and/or non-dense structures, as in the case of the low-symmetry aqueous complexes considered here.^5,34

Brugger et al.⁵ calculated the XANES spectra for linear, trigonal planar and tetrahedral Cu(I)-chloro complexes. A comparison between calculations for the crystalline solids cubic Cu₂O_(s) and cubic CuCl_(s) performed with different cluster sizes demonstrated that there are only minor differences between calculations that include only the first coordination shell and those that include atoms beyond the first shell in the case of ‘dense’ coordination, as is the case for CuCl_(s) in which the Cu is tetrahedral and coordinated by four chloride ions. However, in the case of more open structures, such as Cu₂O_(s) in which Cu is linear and coordinated by two oxygen atoms, inclusion of second-shell atoms resulted in significant improvements between the calculated and experimental spectra of the crystalline compound.

The raw calculations represent the photo-absorption cross-section related to the transition amplitudes between initial and final states. To make these calculated spectra comparable with the experimental spectra, these calculations are convoluted with a Lorentzian function that has an energy-dependent width in order to reproduce the core-hole lifetime broadening (1.55 eV for the Cu K-edge³⁶) and the inelastic plasmon interactions with the photoelectron, and with a Gaussian function to reproduce the experimental resolution, 1.26 eV in this case (Cu K-edge × ΔE/E = 8979 × 1.4 × 10⁻⁴). Note that these values are set a priori and not fitted in the subsequent analyses, and that the calculated peak shapes tend to be sharper than the experimental data as thermal effects and the inelastic mean free path are not taken into account.³⁷

The atoms were kept neutral for all the calculations and the evolution of the charges on the atoms was not studied, as the experimentally observed changes are essentially structural. Atomic charges need to be considered in the case of a stable structure that changes very little during the experiment and in which the evolution of charges is likely to be detectable.^38,39 In the present study, however, the XANES calculations are used essentially to confirm the nature (i.e., geometry and stoichiometry) of the main Cu species present in the aqueous solutions.

2.3.4 EXAFS data preparation and analysis. EXAFS spectra represent a final state interference effect arising from the scattering of the outgoing photoelectron from neighboring atoms. The amplitude and frequency of the sinusoidal modulation of absorbance vs. energy depends on the type and bonding of the neighboring atom and their distances. Refinement of EXAFS data provides information on the number and nature of nearest neighbors and the distances between them, and can be used to test the speciation model derived from the XANES data and provide additional characterization of the complexes and their changes with temperature and salinity. The data used in the EXAFS fits ranged from k = 2.0 to 10.0 Å⁻¹ (CuS₂O₃_09, CuNH₃_01, MCuNH₃_09) and 11.0 Å⁻¹ (CuS₂O₃_06). The fitting was done in R-space in the range [1.0–4.3 Å], with a Hanning window and k² weighting. To quantify the coordination changes of Cu(I)–S₂O₃²⁻ ± Cl⁻ and Cu(I)–NH₃⁰ ± Cl⁻ complexes, EXAFS data were analyzed with the HORAE package,³¹ calculations being performed using FEFF version 8.⁴⁰ Self-absorption effects were checked for the fluorescence data using the SABCOR⁴¹ self-absorption correction routine that is incorporated into ATHENA (part of the HORAE package) and were found to be negligible.

3. Results and discussion

The determination of a speciation model that incorporates all the available data (current measurements as well as published results) is an iterative process, where the results of one experiment, or previously published study, are used in the analysis of the other datasets until a self-consistent model is obtained. In the following sections, we first present the qualitative XANES analysis and ab initio simulation of the XANES spectra to identify the possible geometries and, thus, the allowable stoichiometries of the species. This is followed by the analysis of EXAFS data for ‘end-member’ solutions, i.e., solutions containing the most contrasting speciation, usually corresponding to solutions with, for example, the least and most amounts of chloride. Finally, the systematic UV-Vis spectral measurements are used to confirm the nature of the species present and to retrieve their formation constants. The results for the thiosulfate system are presented first followed by those for the ammonia system.

A note regarding notation: because the information from XAS solution data is generally limited to first shell/nearest neighbors interactions, only those atoms involved in the simulation or fit will be indicated within parentheses, i.e., (CuSClO). For fitting the UV-Vis data and for the thermodynamic interpretation, we use a stoichiometric notation for the entire complex, which will be indicated by square brackets, i.e., [Cu(S₂O₃)Cl(H₂O)]³⁻. Finally, we follow the usual convention in thermodynamic modeling that excludes coordinated water molecules from the species names; no parenthesis is used for this notation, e.g. Cu(S₂O₃)Cl²⁻.

3.1 The Cu–S₂O₃–Cl system

3.1.1 Qualitative XANES results. A series of XAS measurements were conducted for the solution compositions listed in Table S1.† The S₂O₃²⁻/Cu ratio was varied from 2 to 3, at chloride concentrations of 0.5 and ∼4 m (CuS₂O₃_01 to 06; Table S1†). Several other solution compositions were also measured (CuS₂O₃_07 to 11; Table S1†).

XANES spectra for all solutions are broadly similar (Fig. 2), the main difference being an increase in the intensity of the pre-edge with increasing S₂O₃²⁻/Cu ratio. Solutions with the same S₂O₃²⁻/Cu ratio and varying chloride concentrations have very similar XANES spectra; i.e., for these compositions the effect of chloride is small. The XANES features strongly suggest that Cu(I) exists predominantly as three-coordinate complexes.³³ A linear structure can be excluded on the basis of the low intensity of the pre-edge (see [Cl–Cu–Cl]⁻,⁵ [HS–Cu–SH]⁻⁴²), as can a tetrahedral geometry because of the lack of a shift in the position of the pre-edge to higher energy.^5,33 The differences between the spectra shown in Fig. 2 result from either structural distortions and/or variation in the ligands occupying the Cu(I) coordination sphere, but not from a change in coordination geometry.

Fig. 2 Examples of XANES data for Cu(I)–S₂O₃²⁻–Cl⁻ solutions, showing the effect of varying Cu(I), S₂O₃²⁻ and Cl⁻ concentrations.

3.1.2 Ab initio XANES calculations. Typical examples of both the raw spectra (i.e. not convoluted with the experimental broadening factors) and convoluted spectra are shown in Fig. 3. The former spectra allow the individual peaks contributing to the spectrum to be distinguished, while the latter enable easier comparison with experimental data. The end-member solutions for experiments with variable Cl concentration and fixed S₂O₃²⁻/Cu ratio, CuS₂O₃_06 and CuS₂O₃_09, are used to identify the geometry of the complexes in the solutions.

Fig. 3 XANES simulations (raw spectra only) of the Cu–S₂O₃²⁻–Cl⁻ system, compared with experimental data. (a) Effect of changing geometry. (b) Effect of changing distance. (c) Effect of ligand substitution.

Fig. 3a illustrates the effect of geometry on the XANES spectra. XANES simulations demonstrate that both end-member solutions can be modeled well using a distorted trigonal planar geometry. When the atoms are arranged in an equilateral triangle (symmetry C₃), the peaks in the resulting calculated spectrum do not match the positions of the peaks in the experimental spectra. In contrast, a close agreement was found between observed and calculated spectra for a near-T-shaped geometry or a Y-shaped geometry (Fig. 3a). Slight distortion of the T-shaped geometry (i.e. rotating one or more atoms by 5°) results in a decrease in the intensity of the second peak; this small effect virtually disappears when the spectra are convoluted (i.e., broadened by the experimental resolution) (Fig. 3a).

All the raw calculated spectra have a small peak, indicated with dashed line 2 in Fig. 3a, between the two main large peaks (indicated with 1 and 3). This small feature was not observed in the measured spectra, but this is probably an effect of experimental resolution; indeed this feature was absent when the spectra were convoluted with an experimental broadening routine (Fig. 3a). The shift in position of peak ‘3’ can also be accounted for by slight changes in S bond lengths (Fig. 3b). For example, for the (CuS₂O) entity, an increase in the Cu-S distance from 2.20 to 2.25 Å causes a 0.3 eV shift in the peak 3 position for the T- and Y-shaped geometries (Fig. 3b). A change in Cu–O bond length from 2.0 to 2.1 Å (leaving the Cu–S distance at 2.25 Å) does not affect the position of peak ‘3’, but slightly drops its intensity, as well as shifting the position of the minor peak ‘2’.

Fig. 3c shows the effect of substituting O, S and Cl ligands. Although the spectra shown are for a T-shaped geometry, the trends are the same for Y-shaped geometries. Distances used for these calculations were Cu–O = 2.0 Å, Cu–Cl = 2.25 Å and Cu–S = 2.25 Å, which were optimized from XANES FDMNES calculations and are similar to those determined by EXAFS (see section 3.1.3). The change in ligand is reflected mainly by a shift in the position of the peak number ‘3’; a similar shift is observed in the experimental data. The spectra that least resemble the experimental spectra are those containing more than one oxygen atom in the coordination sphere (i.e., (CuO₂S), (CuO₂Cl), (CuO₃)). All the other calculated spectra have four peaks within the first 20 eV, labeled by the numbers ‘1’ to ‘4’ on Fig. 3c. Peak no. ‘3’ is at a too low energy in the calculated (CuS₃), (CuCl₃), and (CuCl₂S) spectra (i.e., models with longer bond lengths). However, the spectra calculated for complexes with one oxygen ligand are close to the experimental data. The main change between the two experimental spectra is a shift of the peak number ‘3’ to lower energy from solution CuS₂O₃_09 to solution CuS₂O₃_06. Such a shift can be explained by a change from (CuS₂O) to (CuCl₂O), but is also consistent with a change from (CuS₂O) to (CuSClO).

3.1.3 Quantitative EXAFS analysis for the Cu–S₂O₃–Cl system. The results of the EXAFS refinements for the two end-member solutions are tabulated in Table 2, and the data and fits are shown in Fig. 4. The data for the two end-members were refined simultaneously in order to reduce the number of fit parameters; in the final fits the Debye Waller factors were set to be the same for all oxygen and for all sulfur atoms, respectively, and the total number of ligands was set to three as determined from XANES. Due to the close scattering factors for Cl and S, initial fits were conducted only with S and O ligands. We found that the data for both ‘end-member’ solutions can be fitted with ∼2 sulfur and ∼1 O atom (CuS₂O) (Table 2). To check on the effect of Cl, a fit to the data for solution CuS₂O₃_06 was carried out in which Cl was substituted for S. This fit was almost as good as that using two S plus one oxygen atom (Table 2), indicating that EXAFS cannot distinguish between a S and a Cl ligand in this case.

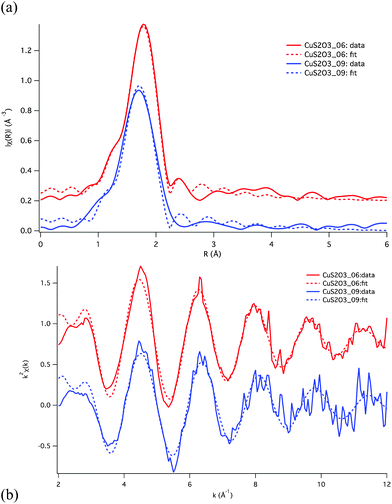Fig. 4 EXAFS fits for the Cu–S₂O₃²⁻–Cl⁻ system, shown in R-space (a) and k-space (b). The fit parameters are listed in Table 2. Fits were conducted simultaneously on both the CuS₂O₃_06 and CuS₂O₃_09 solutions, and are based on the assumption that speciation is dominated by trigonal complexes.

Table 2 Summary of bond lengths and other parameters derived for Cu(I) aqueous complexes from EXAFS refinements. All solutions were measured at room temperature and at 1 bar

	Model	donor	N	R (Å)	δ ^2 (Å^2)	ΔE0 (eV)	χ^2red
a Constrained to be the same for the Cl and N atoms.
Solution CuS2O3_
06	Trigonal	S	2.1(3)	2.24(1)	0.006(3)	7(2)	25.8
		O	0.9(3)	2.11(4)	0.009(20)
09	Trigonal	S	1.8(3)	2.20(3)	0.006(3)	7(2)	25.8
		O	1.2(3)	2.10(5)	0.009(20)
06	Trigonal	Cl	1.9(3)	2.223(9)	0.005(2)	7(2)	35.4
		O	1.1(3)	2.13(5)	0.026(23)
09	Trigonal	S	1.6 (fix)	2.21(2)	0.005(2)	7(4)	23.9
		O	1.4 (fix)	2.09(4)	0.019(22)
Solution CuNH3_
01	linear	N	2	1.90(1)	0.002(1)	2(1)	39
09	Trigonal	Cl	2.1(4)	2.27(32)	0.04(15)	5(2)	12.7
		N	0.9(4)	2.21(1)	0.008(3)
09	Trigonal: 50%	Cl	3 (fix) × 0.50	2.219(9)	0.004(1)	0(1)	32
	linear: 21%	Cl	1 (fix) × 0.21	2.10(2)	0.003(2)^a
		N	1 (fix) × 0.21	1.94(10)	0.003(2)^a
	linear: 21%	Cl	2 (fix) × 0.21	2.10(2)	0.003(2)^a
	linear: 7%	N	2 (fix) × 0.07	2.14 (fix)	0.003(2)^a

---

These XAS results suggest some discrepancy with the speciation predicted using available thermodynamic properties (Fig. 1a; Table 1). The XANES data unambiguously reveal that the copper(I) geometry and ligation change little over the range of conditions investigated. This result is confirmed by EXAFS that reveals that the average coordination in solutions CuS₂O₃_09 and _06 consists of ∼2 (Cl + S) and ∼1 oxygen, in contrast to the transition from 1S + 2O (i.e. [Cu(S₂O₃)(H₂O)₂]⁻) (solution 9) to 2S + 1Cl (i.e. [Cu(S₂O₃)₂Cl]⁴⁻) (solution 06) inferred using the available thermodynamic properties. In the following section a speciation model for Cu(I) in mixed thiosulfate-chloride solutions will be developed that is consistent with the XAS data and the systematic UV-Vis data.

The bond lengths determined from EXAFS compare well with bond lengths published in the literature. As can be seen in Table 3, Cu(I) coordinated to two ligands, either sulfur or chlorine have similar bond lengths (∼2.15 Å). Similarly Cu(I) coordinated to three sulfur or chlorine ligands has a longer bond length around 2.27 Å, and Cu(I) in a four-fold coordination with sulfur or chlorine has a bond length around 2.35 Å. This indicates that the Cu-S bond length is influenced by the number of coordinating atoms. In the context, the Au(I)-S distance measured by EXAFS on Au(I)-hydrosulfide solutions under hydrothermal conditions is similar to the Au(I)-S distance found in solids with similar (linear) coordination geometry (Table 3). As expected, the Cu(I)–O and Cu(I)–N bond lengths are shorter than Cu(I)–S or Cu(I)–Cl bond lengths (Table 2). In summary, the bond lengths determined from EXAFS refinements are consistent with a three-fold coordination around the Cu(I) atom.

Table 3 Comparison of bond lengths for selected Cu(I), Ag(I) and Au(I) bisulfide, thiosulfate and chloride complexes in solids and solutions for different coordination geometries

Structure	Coordination number	Shortest Bond length	Ref.
a Solid state structure. b Solution.
Copper(I)
Na4(Cu(NH3)4)–(Cu(S2O3)2)2	Four, Cu(I)–S (S from thiosulfate)	2.357 Å^a	50
CuFeS2 (chalcopyrite)	Four, Cu(I)–S	2.279 Å^a	51
CuCl (nantokite)	Four, Cu(I)–Cl	2.345 Å^a	52
K5Cu(S2O3)3.(2.25)H2O	Three, Cu(I)–S	2.225(1) Å^a	62
		2.232(1) Å^a
	(S from thiosulfate)	2.288(1) Å^a
Cu2S Chalcocite-Q	Three, Cu–S	2.307 Å^a	53
Cu2S Chalcocite-low	Three, Cu(I)–S	2.265 Å^a	54
2 & 3 coordinated Cu	Two, Cu(I)–S	2.171 Å^a
Cu(I) in 12.88 m LiCl solution at 25 °C, 1 b	Three, Cu(I)–Cl	2.267(7) Å^b	5
Cu(I) in 15.58 m LiCl solution at 25 and 400 °C, 600 b	Three, Cu(I)–Cl	2.272(7) Å^b (25 °C)	5
	Two, Cu(I)–Cl	2.152(7) Å^b (400 °C)
Cu(I) in 2 m NaHS solution at 428 °C, 600 b	Two, Cu(I)–S	2.147(9) Å^b	42
0.4 m Cu(I) in 2 m NaCl + 0.03 m HCl solution at 325 °C (La structure)	Two, Cu(I)–Cl [CuCl2]^−	2.13 Å^b	7
Cu2O, cuprite	Two, Cu(I)–O	1.848 Å^a	55
0.4 m Cu(I) in 0.03 m HCl solution at 325 °C (Lb structure)	Two, Cu(I)–O [CuClO](aq)	1.88 Å^b	7
Gold(I)
Na3Au(S2O3)2(H2O)2	Two, Au(I)–S (S from thiosulfate)	2.272 Å^a	56
Na3Au(S2O3)2(H2O)2	Two, Au(I)–S (S from thiosulfate)	2.280 Å^a	57
Au2S	Two, Au(I)–S	2.174 Å^a	58
Au(I) in the H2O–S–NaOH–Na2SO4 solution at 300–450 °C, 300–600 b	Two, Au(I)–S [Au(HS)2]^−	2.29–2.30 Å^b	59
Silver(I)
NaAgS2O3(H2O)	Four, Ag–S (3S + 1O) (S from thiosulfate)	2.481 Å^a	60
Ag2S Argentite (stable > 450 K)	Four, Ag–S	2.430 Å^a	61
Na3Ag(S2O3)2.(1.5)H2O	Ag^1–S	2.5994(6) Å^a	62
	Ag^1–S	2.5379(5) Å^a
	Ag^1–S	2.4384(6) Å^a
	Ag^2–S	2.5637(5) Å^a
	Ag^2–S	2.7505(6) Å^a
	Ag^2–S	2.4458(6) Å^a
	Ag^3–S	2.5518(5) Å^a
	Ag^3–S	2.6055(6) Å^a
	Ag^4–S	2.4381(6) Å^a
	Ag^4–S	2.7480(6) Å^a
	Ag^4–S	2.5396(5) Å^a
	Ag^4–S	2.4372(7) Å^a
	Three (4 times)
	S from thiosulfate

---

3.1.4 UV-Vis spectrophotometry. A total of 47 solutions containing 0.1–1 mmolal Cu and varying thiosulfate (0–2.5 mmolal) and chloride (0.5–4 m) concentrations were measured by UV-Vis spectrophotometry (Fig. S1a; Table S2†). Principal Component Analysis (PCA)²⁵ reveals that a total of 7 species are required to describe the dataset. Addition of the 6th species causes a large improvement in residuals (from ∼0.1% to 0.03%), but the 7th species has only a small effect–although this effect is still about twice as large as that expected for random noise (Fig. S1b†). Comparison of two series of spectra obtained at two chloride concentrations (2 and 4 m) with varying thiosulfate concentrations (Fig. 5) reveals a slight difference, which is most likely related to the presence of mixed chloro-thiosulfato complexes under these conditions.

Fig. 5 UV-Visible spectra of Cu(I) chloride solutions at different salt concentrations (see Fig. S1): (a) subset I at 2 m total chloride concentration, and (b) subset II at 4 m total chloride concentration.

Under our experimental conditions, a total of three chloro-complexes and three thiosulfato-complexes are expected (Table 1). Assuming a trigonal geometry for the complexes, as established on the basis of the XAS results, the possible mixed chloro-complexes include [CuCl(S₂O₃)(H₂O)]²⁻, [CuCl₂(S₂O₃)]³⁻, and [CuCl(S₂O₃)₂]⁴⁻. The system is clearly underdetermined from a statistical point of view, since 7 species are sufficient to explain the whole dataset, 5 explaining 99.9% of the variance (Figure. S1b†). In addition to the large number of possible species, some of those species are expected to have similar spectra or to exist in relatively small proportion, and difficult to identify via UV-Vis spectrophotometry. Hence, it is important to use all the available chemical information in order to obtain a model that is self-consistent.

In all the fits, the formation constants of Cu(I)-chloro-complexes (Log K) in Table 1 were used. The molar absorbance spectra of these species were obtained from a fit of a series of spectra obtained under thiosulfate-free conditions (total chloride concentrations of 0.5 to 4 m) and then fixed for the rest of the fitting. As linear [CuCl(H₂O)]⁰ is a minor species (< 10 mole%) with low molar absorption coefficients, we assumed that its absorption spectrum is equal to that of [CuCl₂]⁻, in a manner similar to Liu et al.⁹ and Brugger et al.⁵ The spectra retrieved for linear [CuCl₂]⁻ and trigonal [CuCl₃]²⁻ are similar to those reported in ref. 5 (Fig. 6a). Slight changes in the UV-Vis spectrum above ∼4 m Cl concentrations are due to distortion of the trigonal [CuCl₃]²⁻ complex and not to a change in complex stoichiometry.⁵

Fig. 6 Results of UV-Vis data analysis for the thiosulfate-chloride dataset at 25 °C. (a) Molar absorbance spectra for individual Cu(I) complexes. (b–d) Calculated distributions of species as a function of thiosulfate concentration, for different total chloride concentrations.

Similarly, the formation constant for [Cu(S₂O₃)₂(H₂O)]³⁻ was taken from the literature (Table 1). For [Cu(S₂O₃)(H₂O)₂]⁻, EXAFS data reveal that it is less stable than expected from the study of Toropova et al.¹⁵ (Fig. 1a). A Log K value of 8.5 was chosen as a maximum stability for this complex consistent with our EXAFS data; this value is close to that of Golub et al.⁴³

In the final analysis, the formation constants for [Cu(S₂O₃)₃]⁵⁻, [CuCl(S₂O₃)(H₂O)]²⁻ and [Cu(S₂O₃)Cl₂]³⁻ were optimized. Three-dimensional residual maps show that the UV-Vis data provide only a maximum value for the formation constant of [Cu(S₂O₃)₃]⁵⁻ (Figure. S2†). The value of 9.9 for the formation of [Cu(S₂O₃)₃]⁵⁻ was chosen on the basis of the EXAFS analysis and comparison with previous studies, and corresponds to the maximum stability of this species consistent with the EXAFS data. Note that attempts to include [Cu(S₂O₃)₂Cl]⁴⁻, the mixed ligand complex proposed by Boos and Popel,²⁰ resulted in poor fits, and this complex is also inconsistent with the EXAFS data. Differences between the calculated and measured absorbance values are ≤ 0.10 absorbance unit. These relatively large differences (analytical reproducibility ∼0.01 absorbance unit) are attributed to the difficulty in distinguishing the spectra of the individual Cu(I) thiosulfato complexes. In the final analysis, the spectra of the three thiosulfato complexes were constrained to be equal to each other; in the absence of this constraint, fits were erratic and calculated spectra for the individual Cu(I) thiosulfato complexes were not physically realistic. Such problems are expected because of the relatively low concentrations of some of these complexes across the experimental solutions and the similarity of their molar absorbance spectra.

The final model (Table 1; Fig. 5,6) is consistent with the EXAFS results. The predicted stability of [CuCl(S₂O₃)(H₂O)]²⁻ is lower than that reported by Toropova et al.¹⁵ Our proposed model provides a different picture of the Cu(I) speciation in thiosulfate-rich solutions (Fig. 1b), with reduced stability of the [Cu(S₂O₃)(H₂O)₂]⁻ and [Cu(S₂O₃)₃]⁵⁻ complexes compared to the previous consensus (Fig. 1a).

3.2 The Cu–NH₃–Cl system

3.2.1 XANES spectroscopy. XAS measurements were conducted on solutions with compositions listed in Table S3.† The NH₃/Cu ratio was varied from 0.38 to 15, at ∼4 m Cl⁻ (solutions CuNH₃_04 to 10, Table S3). Solutions with NH₃/Cu ratios of 25 and 50 were also measured, but with Cl⁻ concentration < 1 m (solutions CuNH₃_01 to 03, Table S3). There is a smooth transition with decreasing NH₃/Cu ratio (Fig. 7; Solutions CuNH₃_05 to CuNH₃_09). The intensities of the first and second peaks decrease with decreasing NH₃/Cu ratio. There is also a shift of the position of the second peak to lower energy with decreasing NH₃/Cu ratio. There is no obvious trend with varying Cl⁻ concentration (solutions 1–4, Table S3), and the solutions with high NH₃/Cu ratio but different Cl⁻ concentrations (0.7 vs. 4 m) look similar (CuNH₃_01 and CuNH₃_05, Fig. 7). The three isosbestic points imply that only two spectroscopically distinct species can account for the observed spectra.

Fig. 7 XANES spectra for solutions in the Cu–NH₃–Cl system, showing a smooth transition with decreasing NH₃/Cu ratio (max for CuNH₃_01, min for CuNH₃_09). Note the three isosbestic points, labeled ‘1’ to ‘3’.

Comparison of these spectra with those of Kau et al.³³ indicates that the number of ligands coordinated to Cu(I) under these conditions changes from two (Sols 1 and 5, Table S3†) to three (Sol 9, Table S3†). The trigonal complex is stable at high chloride concentration, and may contain the [CuCl₃]²⁻ species described by Brugger et al.⁵ This hypothesis is supported by the fact that intermediary spectra (e.g., CuNH₃_09) can be reproduced well by a linear combination of the spectra CuNH₃_01 (mainly linear Cu(I) amine complex) and Cu_16mLiCl (mainly [CuCl₃]²⁻,⁵) (Fig. 8b).

Fig. 8 XANES simulations of the Cu(I)–NH₃–Cl system, compared with experimental data. (a) Linear end-member: solution NH₃_001 (Table S3). Only raw spectra are shown. (b) Trigonal end-member: solution NH₃_009 (Table S3). Fine dotted lines are convoluted spectra, all other spectra are raw calculations.

3.2.2 Ab initio XANES calculations for Cu–NH₃–Cl. Solution CuNH₃_001 can be modeled by the linear species (CuN₂) with Cu–N = 1.90 Å (Fig. 8a). A mixed linear (CuNO), with either (i) both Cu–N and Cu–O at 1.90 Å or (ii) the same molecule but bent from straight linear by about 20°, did not fit as well, mainly because the first peak was shifted to a lower energy by ∼0.3 eV. Similarly for a linear (CuO₂) with Cu–O = 1.85 Å, the first peak was also at a lower energy, even though the next peak compared well with the experimental spectrum. For the (CuN₂) configuration, the best agreement between calculated spectrum and spectrum NH₃_001 was obtained for a linear structure with two N at 1.90 Å (Fig. 8a), in agreement with the solid state structures.⁸

As mentioned in Section 3.2.1, solution CuNH₃_009 can be modeled as a linear combination of the experimental solutions CuNH₃_001 (29%) and Cu_16mLiCl (71%) (Fig. 8b). Solution Cu_16mLiCl contains mainly a distorted trigonal planar [CuCl₃]²⁻ complex.⁵ XANES calculations for this complex⁵ showed that while the peak positions were modeled well, the intensities were poorly reproduced; this discrepancy was attributed to second shell effects. Fig. 8b also shows calculated spectra for the (CuN₃) entity for different trigonal planar geometries, with Cu–N = 1.95 Å (Fig. 8b). The convoluted spectra are quite featureless, making them difficult to distinguish from that obtained for the (CuCl₃) entity. The main difference is that the spectra for distorted trigonal configurations (T or Y shapes) show a broad peak at about 14 eV above the edge, in agreement with the experimental spectrum.

3.2.3 Quantitative EXAFS analysis for the Cu–NH₃–Cl system. EXAFS is not expected to be able to distinguish between N and O as these atoms vary by only one electron. Therefore, the (CuN₂) model was used to fit the data for Solution CuNH₃_001 using: (i) two identical Cu–N bond lengths; and (ii) two slightly different Cu–N bond lengths. The best fit was obtained using two identical Cu–N bond lengths (Table 2). Solution CuNH₃_009 can be fitted using two models: (i) a simple mixture of ∼2 Cl and ∼1 N atoms constrained to add to a total of three atoms (which approximates the model of a linear combination of (CuCl₃) + (CuN₂)) and (ii) the model predicted by UV-Vis analysis, namely 50% (CuCl₃) + 21% (CuClN) + 21% (CuCl₂) + 7% (CuN₂); see section 3.2.4 below). Visually both models fit equally well (Fig. 9), although the fit parameters are better for the first (simpler) model. The results of the EXAFS refinements for the two end-member solutions are tabulated in Table 2, and the data and fits are shown in Fig. 9.

Fig. 9 EXAFS fits in R space (a) and k-space (b) for the Cu–NH₃–Cl system. For CuNH₃_9 results from two models are displayed: a fully trigonal model, and a fit resulting from the speciation derived from the analysis of the UV-Vis data, including trigonal and linear species.

3.2.4 UV-Vis spectrophotometry. Forty solutions containing 0.23–0.57 mmolal Cu and varying ammonia (0–0.158 m) and chloride (0.53–5.24 m) concentrations were measured by UV-Vis spectroscopy (Figure S3a; Table S4). PCA reveals that the dataset requires at least 7 species for explanation (Figure S3b). The ammonia-free dataset shows that the increase of the peak at 275 nm is characteristic of the increasing concentration of trigonal planar [CuCl₃]²⁻ replacing linear [CuCl₂]⁻ with increasing chloride concentration (Fig. 10a^5,9). The evolution of the spectra collected in 4 m Cl⁻ shows a decrease of the band characteristic of the trigonal species (ca. 275 nm) with increasing ammonia concentration. This suggests the formation of a linear ammine complex. Fig. 10b illustrates these changes with a broad shoulder in the lower UV (< 260 nm) becoming the predominant feature with increasing [NH₃] relative to [Cu⁺] and [Cl⁻].

Fig. 10 Changes in UV-Visible spectra of Cu(I) ammonia solutions at different salt concentrations for the Cu(I)–Cl–NH₃ system (see Fig. 11): (a) subset III varying Cl⁻ concentration at ∼0.05 m ammonia and (b) subset I at [Cl_tot] ∼4, varying NH₃ concentration. Lines are experimental data, crosses represent spectra calculated using the final fit.

We performed a least squares fitting of the whole dataset in order to test the nature of the ammine complexes and possible mixed chloride-ammonia species. In addition to the known copper chloride species ([CuCl(H₂O)]⁰, [CuCl₂]⁻, [CuCl₃]²⁻), linear [CuNH₃(H₂O)]⁺, [Cu(NH₃)₂]⁺, and [Cu(NH₃)Cl]⁺ complexes, the trigonal [Cu(NH₃)₃]⁺ and the trigonal mixed ammine-chloro-complexes [Cu(NH₃)Cl₂]⁻ and [Cu(NH₃)₂Cl]⁻ were also considered. In fitting the data, the formation constants for Cu(I)-chloro complexes were taken from Brugger et al.,⁵ and their molar absorbance spectra fixed from a fit of the ammonia-free solutions. Similarly, the formation constant of the [Cu(NH₃)(H₂O)]⁺ complex was taken from the literature (log β = 5.74; Table 1), since two studies provide consistent values, and this complex is expected to be present in only minor (< 10%) concentrations ^44,45. In the final analysis, an excellent fit was obtained with 6 complexes [CuCl(H₂O)]⁰, [CuCl₂]⁻, [CuCl₃]²⁻, [Cu(NH₃)(H₂O)]⁺, [Cu(NH₃)₂]⁺ and [Cu(NH₃)Cl]⁰. The maximum differences in absorbance between calculated and experimental spectra were ± 0.06 absorbance units. We attribute the 7th factor in the PCA analysis (Figure S3b) to a deviation from Beer–Lambert law affecting the [CuCl₃]²⁻ species at high salinity.⁵ The calculated molar absorbance spectrum for [CuCl(NH₃)]⁰ and [Cu(NH₃)₂]⁺ are consistent with linear species (Fig. 11a). The calculated distribution of species show that [Cu(NH₃)₂]⁺ is the dominant species under most conditions in ammine-bearing solutions (Fig. 11b,c); mixed chloride-amine complexes are important only under specific Cl/NH₃ ratios (Fig. 11c). Fits that included mixed trigonal chloride-ammine species were statistically identical, but the molar absorbance spectra for the trigonal species were unrealistic, usually resembling the spectrum of [CuCl₂]⁻. Also of note is that under the investigated ammonia concentrations, [Cu(NH₃)₃]⁺ is not expected to be present in significant amounts; this is consistent with the formation constant reported by previous studies (Table 1). Figure S4 plots residual contours from the fit of the data as a function of the log K for the formation of the linear diamminecopper(I) and amminechlorocopper(I) complexes. A well-constrained 90% confidence interval gives an estimate of the Log Ks for [Cu(NH₃)₂]⁺ = 10.7(+ 0.2/−0.5) and [CuClNH₃]⁰ = 8.38(+ 0.2/−0.3) at 25 °C.

Fig. 11 Results of UV-Vis data analysis for the NH₃-chloride dataset at 25 °C. (a) Molar absorbance spectra for individual Cu(I) complexes. Note that the spectrum of Cu(NH₃)₃⁺ could not be retrieved because it is a minor component in the investigated solutions. (b,c) Calculated distributions of species as a function of NH₃ concentration for 0.0 and 4.0 m NaCl solutions.

4. Conclusions

By combining UV-Vis and XAS data, this study has provided a speciation model for copper(I) in mixed thiosulfate-chloride and ammonia-chloride systems consistent with UV-Vis and XAS data (Fig. 1). The new formation constants derived in our study allow to refine the prediction of Cu(I) speciation in ammonia-chloride solutions. For the thiosulfate-chloride system, our results indicate that the [Cu(S₂O₃)₂(H₂O)]³⁻ complex is more stable than previously thought. We demonstrate the existence of mixed thiosulfate-chloride complexes ([Cu(S₂O₃)Cl(H₂O)]²⁻ and [Cu(S₂O₃)Cl₂]³⁻), with the former complex being dominant under some conditions (Fig. 1b). The results of our study allow more comprehensive predictions of speciation which can be applied in the design of efficient hydrometallurgical gold processing methods using thiosulfate lixiviants, including where using chloride-rich waters commonly encountered in gold deposits in semi-arid environments.

This study illustrates the complexity of studying speciation in apparently ‘simple’ inorganic systems. This complexity is related to the fact that many species can co-exist in solution; that is, in many cases individual species cannot be isolated due to the presence of significant amounts of other species (see speciation diagrams in Fig. 6b–d and 10b,c), which may be only minor components (≤ 15%). As a consequence, in order to study these complex systems effectively, multiple experimental methods, such as XAS and UV-Visible spectrophotometry, are necessary.

Our approach emphasizes the importance of understanding the coordination geometry when studying the speciation in such systems. XANES spectroscopy in particular is a powerful tool to establish the geometry of the dominant complexes in solution, thereby constraining the number of possible species that may exist in solution. Information about the coordination geometry of the complexes is also important in assessing their catalytic potential, or in comparing results from theoretical molecular dynamic studies with experimental results (e.g., see ref. ¹²).

Acknowledgements

This work was supported by the Australian Synchrotron Research Program, which is funded by the Commonwealth of Australia under the Major National Research Facilities Program and the Australian Research Council through the Centre for Green Chemistry. Use of the Advanced Photon Source was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Contract No.W-31-109-Eng-38. JB acknowledges an Australian Research Council Professorial Fellowship.

References

1. G. J. Sparrow and J. T. Woodcock, Extractive Metall. Rev., 1995, 14, 193–247.
2. M. G. Aylmore and D. M. Muir, Miner. Eng., 2001, 14, 135–174.
3. M. G. Aylmore and D. M. Muir, Miner. Metall. Proc., 2001, 18, 221–227.
4. Water Management at KCGM. URL: http://www.superpit.com.au/Environment/Water/tabid/129/Default.aspx..
5. J. Brugger, B. Etschmann, W. Liu, D. Testemale, J.-L. Hazemann, H. Emerich, W. van Beek and O. Proux, Geochim. Cosmochim. Acta, 2007, 71, 4920–4941.
6. L. Ciavatta and M. Iuliano, Ann. Chim., 1998, 88, 71–89.
7. J. L. Fulton, M. M. Hoffmann and J. G. Darab, Chem. Phys. Lett., 2000, 330, 300–308.
8. W. H. Liu, J. Brugger, B. Etschmann, D. Testemale and J. L. Hazemann, Geochim. Cosmochim. Acta, 2008, 72, 4094–4106.
9. W. Liu, J. Brugger, D. C. McPhail and L. Spiccia, Geochim. Cosmochim. Acta, 2002, 66, 3615–3633.
10. W. Liu, D. C. McPhail and J. Brugger, Geochim. Cosmochim. Acta, 2001, 65, 2937–2948.
11. Z. Xiao, C. Gammons and A. Williams-Jones, Geochim. Cosmochim. Acta, 1998, 62, 2949–2964.
12. D. M. Sherman, Geochim. Cosmochim. Acta, 2007, 71, 714–722.
13. R. M. Smith and A. E. Martell, Critical Stability Constants, Vol. 4: Inorganic Complexes, Plenum Press, 1976.
14. A. M. Golub, S. S. Butsko and L. P. Dobryanskaya, Z. Neorganich. Khim., 1975, 20, 2728–2732.
15. V. F. Toropova, I. Sirotina and T. Lisova, Uchenye Zapiski Kazanskogo Gosudarst. Univ., 1955, 115, 43–52.
16. A. E. Martell, R. J. Motekaitis, Determination and Use of Stability Constants, VCH Publishers, Inc., 1988.
17. A. I. Stabrovskii, Z. Obshch. Khim., 1951, 21, 1223–1237.
18. E. A. Ukshe and A. I. Levin, Z. Fizich. Khim., 1953, 27, 1396–1403.
19. D. G. Davis, Anal. Chem., 1958, 30, 1729–1732.
20. G. A. Boos and A. A. Popel, Russian J. Inorg. Chem., 1970, 15, 792–793.
21. J. S. Solis, G. Hefter and P. M. May, Aust. J. Chem., 1995, 48, 1293–1300.
22. A. I. Vogel, Vogel's Textbook of Quantitative Inorganic Analysis Including Elementary Instrumental Analysis, Longman Inc., 1978.
23. L. N. Var'yash, Geochem. Int., 1989, 26, 80–90.
24. J. Brugger, D. C. McPhail, J. Black and L. Spiccia, Geochim. Cosmochim. Acta, 2001, 65, 2691–2708.
25. J. Brugger, Comput. Geosci., 2007, 33, 248–261.
26. H. C. Helgeson, Am. J. Sci., 1969, 267, 729–804.
27. H. Helgeson and D. H. Kirkham, Am. J. Sci., 1974, 274, 1089–1198.
28. J. Kielland, J. Am. Chem. Soc., 1937, 59, 1675–1678.
29. H. C. Helgeson, D. H. Kirkham and G. C. Flowers, Am. J. Sci., 1981, 281, 1249–1516.
30. S. M. Heald, D. L. Brewe, E. A. Stern, K. H. Kim, D. T. Jiang, E. D. Crozier and R. A. Gordon, J. Synchrotron Radiat., 1999, 6, 347–349.
31. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
32. J. Chaboy, A. Munoz-Paez, P. J. Merkling and E. S. Marcos, J. Chem. Phys., 2006, 124, 064509-1–064509-9.
33. L.-S. Kau, D. J. Spira-Solomon, J. E. Penner-Hahn, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1987, 109, 6433–6442.
34. Y. Joly, Phys. Rev., 2001, 125120-1–125120-10.
35. D. Testemale, J. Brugger, W. Liu, B. Etschmann and J.-L. Hazemann, Chem. Geol., 2009, 264, 295–310.
36. M. O. Krause and J. H. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329.
37. J. D. Bourke, C. T. Chantler and C. Witte, Phys. Lett. A, 2006, A360, 702–706.
38. Y. Joly, D. Cabaret, H. Renevier and C. R. Natoli, Phys. Rev. Lett., 1999, 82, 2398–2401.
39. D. Testemale, J. L. Hazemann, G. S. Pokrovski, Y. Joly, J. Roux, R. Argoud and O. Geaymond, J. Chem. Phys., 2004, 121, 8973–8982.
40. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B, 1998, 58, 7565–7576.
41. C. H. Booth and F. Bridges, Physica Scripta, 2005, 2005, 202–204.
42. B. E. Etschmann, W. Liu, D. Testemale, H. Müller, N. A. Rae, O. Proux, J. L. Hazemann and J. Brugger, Geochim. Cosmochim. Acta, 2010, 74, 4723–4739.
43. A. M. Golub, L. P. Dobryanskaya and S. S. Butsko, Z. Neorganich. Khim., 1976, 21, 2733–2737.
44. J. Bjerrum, Kgl. Danske Videnskab. Selskab, Math.-fys. Medd., 1934, 12, 67pp.
45. T. V. Stupko, V. E. Minorov and G. L. Pashkov, Z. Priklad. Khim., 1998, 71, 1087–1090.
46. S. Lurdes, S. Gonçalves and L. Sigg, Electroanalysis, 1991, 3, 553–557.
47. J. Bjerrum, Acta Chem. Scand., 1986, A40, 223–235.
48. O. Horvath and K. L. Stevenson, Inorg. Chem., 1989, 28, 2548–2551.
49. S. B. Black, The Thermodynamic Chemistry of the Aqueous Copper-Ammonia Thiosulfate System, PhD thesis, Murdoch University, 2006, 261pp.
50. A. Ferrari, A. Braibanti and A. Tiripicchio, Acta Crystallogr., 1966, 21, 605.
51. R. Ramirez, C. Mujica, A. Buljan and J. Llanos, Bol. Soc. Chilena De Quimica, 2001, 46, 235–245.
52. J. C. Monier and R. Kern, Comptes Rendus Hebdomadaires Des Seances De L Academie Des Sciences, 1955, 241, 69–71.
53. A. Janosi, Acta Crystallogr., 1964, 17, 311–312.
54. H. T. Evans, Nature Physical Science, 1971, 232, 69–70.
55. A. Kirfel and K. Eichhorn, Acta Cryst. A, 1990, 46, 271–284.
56. H. Ruben, A. Zalkin, M. O. Faltens and D. H. Templeton, Inorg. Chem., 1974, 13, 1836–1839.
57. R. F. Baggio and S. Baggio, J. Inorg. Nucl. Chem., 1973, 35, 3191–3200.
58. K. Ishikawa, T. Isonaga, S. Wakita and Y. Suzuki, Solid State Ionics, 1995, 79, 60–66.
59. G. S. Pokrovski, B. R. Tagirov, J. Schott, E. F. Bazarkina, J. L. Hazermann and O. Proux, Chem. Geol., 2009, 259, 17–29.
60. L. Cavalca, A. Mangia, C. Palmieri and G. Pelizzi, Inorg. Chim. Acta, 1970, 4, 299–304.
61. R. J. Cava, F. Reidinger and B. J. Wuensch, J. Solid State Chem., 1980, 31, 69–80.
62. E. J. Chan, B. W. Skelton and A. H. White, Z. Anorg. Allg. Chem., 2008, 634, 2825–2844.

---

Footnote

† Electronic Supplementary Information (ESI) available: composition of solutions for XAS and UV-Visible measurements (Tables S1–S4); results of principle component analysis and residual maps for the thiosulfate-chloride and ammonia-chloride data UV-Visible data (Figures S1–S4). See DOI: 10.1039/c1ra00708d/

---