Made-to-order nanocarbons through deterministic plasma nanotechnology

Abstract

Through a combinatorial approach involving experimental measurement and plasma modelling, it is shown that a high degree of control over diamond-like nanocarbon film sp³/sp² ratio (and hence film properties) may be exercised, starting at the level of electrons (through modification of the plasma electron energy distribution function). Hydrogenated amorphous carbon nanoparticle films with high percentages of diamond-like bonds are grown using a middle-frequency (2 MHz) inductively coupled Ar + CH₄ plasma. The sp³ fractions measured by X-ray photoelectron spectroscopy (XPS) and Raman spectroscopy in the thin films are explained qualitatively using sp³/sp² ratios 1) derived from calculated sp³ and sp² hybridized precursor species densities in a global plasma discharge model and 2) measured experimentally. It is shown that at high discharge power and lower CH₄ concentrations, the sp³/sp² fraction is higher. Our results suggest that a combination of predictive modeling and experimental studies is instrumental to achieve deterministically grown made-to-order diamond-like nanocarbons suitable for a variety of applications spanning from nano-magnetic resonance imaging to spin-flip quantum information devices. This deterministic approach can be extended to graphene, carbon nanotips, nanodiamond and other nanocarbon materials for a variety of applications

---

1. Introduction

Nanocarbons^1–4 in a range of structural configurations including graphene,^5–8nanotubes,^9–15nanowires,^{16, 17} nanocones,¹⁸ nanotips^19–21nanofibres²² and a wealth of other variations have been the subject of intense research interest over the last few decades due to their unique mechanical, optical, electronic and other properties. Whilst some structures, e.g., nanotubes are ‘holey’ with factors like chirality affecting their behavior,²³ nanocarbons that are fully filled such as nanotips, nanoparticlesetc. contain mixtures of sp²- and sp³-hybridized carbons, the relative amounts of which, to a great extent control their properties.

It has been noted that sp³-hybridized carbons are largely responsible for the elastic and mechanical properties of nanocarbons such as diamond-like nanocarbon (DLNC), whereas the optical and electronic properties are controlled by the clustering of the sp² phase.^24,25 The ability to tailor the ratio of sp³ to sp² bonds so the properties of the film are suited for a specific application is crucial. For example, some applications require water repellent coatings/lubricants, Paul et al.²⁶ found that hydrophobicity in DLNC films increases with higher sp³/sp² ratios. In DLNC films, high compressive stress limits applications to use of films of thickness 100 nm or less,²⁷ however, Cheng et al. found that decreases in the sp³/sp² ratio led to a reduction in internal stress.²⁸ As the sp² clustering in particular, is highly dependent on the specifics of the growth environment,²⁵ choosing the most flexible and controllable fabrication technique is key to the efficient manufacturing of made-to-order diamond-like nanocarbon films for a broad range of applications spanning from nanoelectromechanical systems, to magnetic hard disc coatings to biomedical coatings for joint implants.²⁹ Moreover, by achieving high percentages of sp³carbon in nanoparticles, one can produce nanodiamond clusters,^30,31 which are particularly promising materials for nano-magnetic resonance imaging³² and spintronics.³³ However, enabling sp³/sp² control simultaneously with optimization of nanodiamond size and structure remains extremely challenging.

Many fabrication methods including ion beam deposition,³⁴magnetron sputtering,²⁶ filtered cathodic vacuum arc³⁵ and chemical vapor deposition (CVD)³⁶ have been used to make nanocarbon films. Inductively coupled plasma (ICP) CVD is a promising growth route as ICPs have a high plasma density, low ion bombardment energies (hence less damage to the forming film) and excellent uniformity.^37–39 Reactive plasmas^40,41 consist of a diverse range of species which undergo many chemical reactions in the plasma bulk.^42,43 Some of the newly created radicals and ions, however, may detract from the desired film structure, composition and properties. Hence, intense modeling efforts are required to account for species production and loss,^19,44 to enable us to optimize the production of plasma-generated species that will enhance rather than detract from the intended properties of ‘made-to-order’ diamond-like nanocarbon films.

However, despite numerous plasma modeling papers^19,44 and experimental examinations of DLNC films^24,26,34,45 the relationship between sp³/sp² concentration in the gas phase (or plasma influx) and in the deposited nanoparticle film has not been sufficiently developed. Clearly elucidating this link, with particular attention to the effect of plasma parameters such as discharge power and hydrocarbon source gas flow rate and thus proposing a comprehensive combinatorial⁴⁶ approach to DLNC nanoparticle film growth are the main aims of this paper. This approach incorporates theory, simulation and experiment and serves as an important road mark on the way to deterministic plasma fabrication of made-to-order diamond-like nanocarbon films and may ultimately be extended to produce highly tailored nanodiamonds and other nanocarbon films including graphene. For nanostructured films manufactured using plasma-based fabrication techniques, a high level of control is required even at the level of electrons (fostering such a capability was highlighted as a grand scientific challenge by the US Department of Energy⁴⁷). In this work, we show that such a level of control may be exercised by modifying plasma parameters to fine tune the electron energy distribution function (EEDF) which influences the production of ions and neutral radicals in the plasma bulk.³⁸ These plasma-generated species in turn, influence the film composition (i.e., sp³/sp² ratio) and hence the film properties and potential applications.

The paper is structured as follows: the experimental set-up and methodology are presented in Section 2, with the results of a global plasma discharge model, plasma diagnostics and DLNC nanoparticle film deposition described in Section 3. A further discussion and comparison of the results is presented in Section 4, whereas Section 5 is a summary and outlook for future work.

2. Experiment and methodology

This section begins with a flow chart (Sec. 2.1) which provides an overview of the steps required to get from a Ar +CH₄ plasma to a tailored DLNC nanoparticle film. Subsequent sections 2.2, 2.3 and 2.4 describe the physical experiment (including the deposition system and plasma diagnostics), the global discharge model and the characterization of the DLNC films, respectively, in greater detail.

2.1. Process flowchart

A flow chart provided in Fig. 1 details the links between the experiment, theory and simulation tasks described in more detail in Sections 2.2, 2.3 and 2.4. The steps required to get from an Ar + CH₄ ICP (described in Sec. 2.2) to a tailored diamond-like nanocarbon thin film are as follows. Firstly, the EEDF is calculated based on the measured plasma parameters. Electron temperature and number density (T_e and n_e, respectively) are derived from the EEDF in Step P1, which leads to the first decision - will n_e and T_e result in appropriate rates of electron impact reactions (K_e)? If not, the EEDF must be adjusted by varying the process parameters (e.g., P_in). If the resultant K_e is acceptable, it will be input into the global discharge model (described in Sec. 2.3) which will calculate the expected sp³/sp²-hybridized precursor species densities in the plasma discharge. The projected gas phase sp³/sp² ratio from the global discharge model is calculated in Step P2.

Fig. 1 . (Color online) Flow-chart for design of DLNC thin films. The red dashed line indicates one of the aims of this paper - to link the sp³/sp² ratio in the gas phase to the sp³/sp² ratio in the thin film (see in Sec. 3.4). Steps [P1] - [P4] are as follows: [P1] is the derivation of n_e and T_e from the EEDF, [P2] is calculation of the sp³/sp² ratio based on the global discharge model, [P3] is the calculation of the sp³/sp² ratio based on the plasma diagnostics measurements and [P4] is the measurement of the sp³/sp² ratio in the film using Raman spectroscopy and/or XPS. See Secs. 2.1–2.4 for further details.

Note, as indicated by the red dashed line in Fig. 1, one of the main aims of this paper is to elucidate the link between sp³/sp² ratios in the plasma bulk and in the DLNC nanoparticle film. This will provide us with an indication of what the sp³/sp² gas phase ratio should be in order to produce the desired sp³/sp² ratio in the film (this will be addressed in Sec. 3.4). If the plasma sp³/sp² is not appropriate, then return to the EEDF stage. If the ratio is acceptable, proceed to experimental measurements [Optical emission spectroscopy (OES) and Quadrupole mass spectroscopy (QMS)] of the species densities in the plasma discharge and in Step P3 calculate the actual gas phase sp³/sp² ratio using the measured data. The ratio in Step P3 should be close to the ratio measured in Step P2, if not, return to the global discharge model and recalculate. If the ratio is acceptable, commence ICP-CVD deposition of the film and in Step P4 measure the film sp³/sp² ratio using Raman spectroscopy and/or X-ray photoelectron spectroscopy (XPS). If the film sp³/sp² ratio is not acceptable, return to the global discharge model stage. However, if the sp³/sp² is as anticipated, then a diamond-like nanocarbon film with the desired properties should be obtained.

2.2. Experimental details

A middle frequency (2MHz) inductively coupled plasma source,³⁸ depicted both schematically [Fig. 2 (a)] and pictorially [Fig. 2 (b)] was used to deposit DLNC nanoparticle films on Si (111) substrates with varying input power (P_in) and methane flow rate (J_CH4). The DC bias voltage applied to the substrate holder was used to control the ion flux and energy, in this work it was maintained at −50 V. The temperature of the substrate holder is an important parameter for neutral particle flux and was kept at 300 °C. The deposition time was 40 min.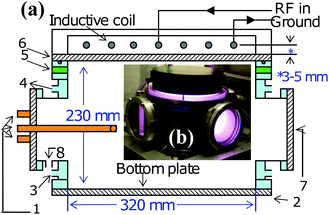

Fig. 2 (Color online) (a) Schematic of the ICP experimental set-up, where 1: Diagnostic ports for Langmuir probe, OES and QMS measurements; 2: Vacuum chamber; 3: Cooling water in; 4: Cooling water out; 5: Gas inlet; 6: Quartz window; 7: Observation window; 8: To vacuum pump. (b) Photograph of the ICP source operating in H-mode Ar discharge.

A single Langmuir probe was used to obtain the I–V curve, the second derivative of which is proportional to the EEDF, f_e(V), which can be expressed as follows:

where A is the surface collection area of the single radio frequency (RF)-compensated Langmuir probe (where the RF compensation was specifically designed for the 13.56 MHz operation frequency), e is the electron charge and m_e is the electron mass. The electron number density and temperature, n_e and T_e may be extracted from the EEDF (Step P1 from Fig. 1) as follows:

n_e(ε) = ∫^∞₀f_e(ε)dε (2)

The optical emission was measured by inserting a collimator into the holes at the sideport of the ICP chamber (recall Fig. 2 (a), port is designated as 1), the collected optical emission signal was transferred via optical fiber to the entrance slit of the SpectroPro-775 spectrometer (with a line resolution of 0.023 nm). Data acquisition was controlled by the SpectraSenser program. The Quadrupole Mass Analyzer system used to conduct QMS was “Microvision Plus” (manufactured by MKS Instrument Spectra Products), with data acquisition controlled by “Process Eye 2000” software.

2.3. Global discharge model

Electron impact ionization and dissociation, neutral–neutral reactions, neutral–ion reactions, proton impact ionization, and dissociative recombination reactions were included in a global, spatially-averaged model (190 reactions, 48 neutral and ionic species) which was used to predict the particle densities (fluxes of CH⁺₄ and CH⁺₃ obtained from the simulation are included in Table 1) for Ar + CH₄ plasmas. Supported by previous experimental measurements,^48,49 the plasma density was assumed to be uniform in the processing chamber. The rate constants for electron impact reactions were K_e = ∫f(ε)σ(ε)ν_e(ε)d(ε), where ν_e(ε) is the electron velocity, f(ε) is the EEDF and σ(ε) is the reaction cross section. As a weakly ionized Ar + CH₄ (electropositive) plasma was considered, anions were not accounted for and it was assumed that upon ionization neutral particles would be singly ionized.

Table 1 Measured electron density, n_e [1 × 10¹¹cm⁻³] and temperature, T_e [eV] of Ar + CH₄ plasma for varying input power, P_in [W], typical sp³ species flux (calculated from global discharge model) - CH⁺₄[1 × 10¹² cm⁻²s⁻¹], typical sp² species flux (calculated from global discharge model) - CH⁺₃ [1 × 10¹² cm⁻²s⁻¹], sp³/sp² [%] (measured using XPS)

P in	n e	T e	CH^+4	CH^+3	sp^3/sp^2 (XPS) [%]
400	1.29	3.78	7.63	6.61	7.1
800	2.53	3.64	7.44	6.48	12.0
1200	3.59	3.53	6.72	5.80	17.2
1600	4.41	3.75	6.43	5.50	19.0
2000	4.85	3.76	5.83	4.94	21.3

---

Some carbon containing species may be sp²- or sp³-hybridized in the gas-phase. As noted, the ratio of sp³- to sp²-hybridized carbons in nanomaterials can be used to tailor structure and properties to ensure that the resulting materials conform to the requirements of a given application. This paper seeks to establish a link between the EEDF, the hybridization in the gas-phase/plasma-bulk to hybridization in the DLNC film (as indicated by the red line in Fig. 1). Hence in our discussion of the plasma influx (both experimentally measured and simulated) we will focus on the following sets of species [CH⁺₄, C₂H⁺₆, C₂H₅] and [CH₃, CH⁺₃, C₂H⁺₅, CH₂, C₂H₃] as representative of plasma-generated species containing sp³ and sp²-hybridized carbons, respectively (this will be elaborated on in Sec. 4). Non-radical neutrals were not considered to directly insert into films as their sticking coefficients were assumed zero due to their saturated electronic structure.⁵⁰

2.4. Characterisation of DLNC films

The sp³/sp² ratio of DLNC thin films was estimated by Raman measurement and XPS (Step P4 in Fig. 1), compared to the plasma influx sp³/sp² ratio and related to plasma parameters: input power, P_in and methane inlet, J_CH4. X-ray diffraction was used to examine the effect of the plasma parameters on the crystalline structure of the samples.

3. Results

3.1. Electron energy distribution

The effect of increasing P_in on the EEDF is an increase in the number of electrons, including those in the high-energy tail of the distribution - shown in the inset in Fig. 3. The electron number density, n_e and temperature, T_e have been derived from the EEDF and are listed in Table 1. The number and temperature of electrons (particularly those in the high-energy tail as the threshold energy for electron impact reactions, including ionization and dissociation, is typically around 10 eV as indicated by the dashed line in Fig. 3), influence the rate constants for electron impact reactions, K_e. Explicitly, K_e increases with P_in as f(ε) increases with n_e and ν_e(ε) increases with T_e. If K_e increases, then more electron impact reactions will occur which will affect the relative densities of hydrocarbon ions and neutral radical species in the plasma bulk, the sp³/sp² ratio in the plasma-generated flux incident to the substrate and hence, ultimately, the sp³/sp² ratio in the DLNC nanoparticle films. The EEDF was used for the calculation of K_e in the global discharge model described in Sec. 2.3.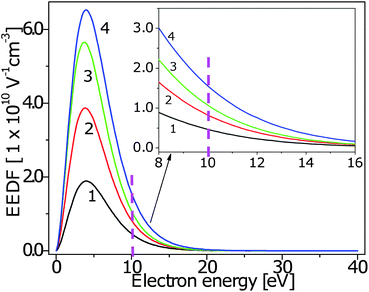

Fig. 3 (Color online) The experimental EEDF of Ar + CH₄ ICP at 1.5 Pa, J_Ar = 35 sccm and J_CH4 = 8 sccm, inset shows a high-energy tail of the EEDF. P_in varies as follows 1: 400 W, 2: 800 W, 3: 1200 W, 4: 1600 W. EEDF calculated using I–V measurements obtained by a single RF-compensated Langmuir probe. Dashed line shows a typical energy threshold for electron impact reactions.

3.2. Plasma generated species

Fig. 4 presents the results both of the global discharge model and data from the experimentally produced Ar + CH₄ discharge, specifically, the effect of input power, P_in on the densities of ions and neutral radicals in the plasma bulk. The results of the Optical Emission Spectroscopy and Quadrupole Mass Spectrometry of a 2 MHz ICP plasma (J_Ar = 35 sccm, J_CH4 = 8 sccm) discharge in a Ar + CH₄ gas mixture at 1.5 Pa with different input powers (0 – 2000 W) are presented in Fig. 4 (a) and (b), respectively. For the majority of the 48 species included in the global model, the OES and QMS results are largely consistent with number density tendencies found in the modeling. Experimentally and computationally obtained neutral radical and ion fluxes are presented in Fig. 4 (c) and (d), respectively.

Fig. 4 (Color online). (a) OES relative intensity of species α to Ar (416 nm), I_a/I_{Ar_416}, with different P_in. The legend represents neutral radicals as follows: 1: CH(387), 2: H₂(420), 3: CH(431), 4: H_γ (434), 5: H₂(471), 6: H_β (486), 7: C₂(517), 8: H_α (656), 9: C(833). (b) The partial pressures of radicals where J_Ar = 35 sccm and J_CH4 = 8 sccm at 1.5 Pa with varying P_in. The fluxes (cm⁻²s⁻¹) of (c) radicals containing sp³ and sp² carbons, (d) ions containing sp² and sp³ carbons, where: 1: CH⁺₄ (sp³), 2: CH⁺₃ (sp²), 3: C₂H⁺₅ (sp²), 4: C₂H⁺₆ (sp³).

The relative intensity of OES lines of species α to Ar (416 nm) lines, I_α/I_{Ar_416}, with different P_in up to 2000 W is plotted in Fig. 4 (a). The intensities of the optical emission lines with varying P_in serves as a qualitative representation of the neutral radicals densities and enables us to verify the validity of the global discharge model without interfering with the ongoing discharge. The OES results in Fig. 4 (a) show an increase of intensities of H_β and H_α emissions and a decline of intensities of CH, H₂, H_γ, C₂ and C lines with increasing P_in. Whilst these species are not the ones that we have singled out for analysis in Fig. 4 (c) and (d), they may play an important role in determining the concentration of relevant sp³ and sp² hybridized hydrocarbons through reactions in the plasma discharge. We emphasize that the OES results are in a good level of agreement with species densities predicted by the global discharge model (specific comparisons are omitted for space considerations).

The partial pressures of C, CH, H, CH₂, C₂H₅ and CH₃versusP_in measured by QMS are plotted in Fig. 4 (b). We will single out CH₂, C₂H₅ and CH₃ for the purpose of this discussion. The density of a CH₂ radical initially decreases with increased P_in until P_in = 1200 W, when it begins to rise with further increased P_in. As in Fig. 4 (c), the QMS results show that the concentration/flux of C₂H₅ is much lower than the other species of interest. The density of a methyl radical is shown by QMS to increase with P_in until 1200 W, whereupon it begins to decrease. For radicals, the flux plotted in Fig. 4 (c) is calculated by Ψ_j = 0.25n_jν_th,iγ_j, where γ_j is the sticking coefficient, ν_th,j is the thermal speed and n_j is the radical density. Fluxes of all species appear to decrease with greater P_in except for CH₂ which increases. There is better agreement between the CH₃ and CH₂ radical fluxes and QMS results at higher powers. Fig. 4 (d) presents ion fluxes - both from simulation and experimentally obtained by measuring the current on the substrate and taking into account the relative intensity ratio of the ions. It should be noted that the ion fluxes are comparable, if not higher than the plotted neutral radicals in Fig. 4 (c). This, combined with the higher sticking probability of ions versus radicals points to the importance of the ion flux to the deposited film properties.

The simulated fluxes with J_CH4 varying between 8 and 32 sccm, with P_in = 1600 W are plotted in Fig. 5. Unsurprisingly, with increased methane influx, all species increase with increasing J_CH4, excepting CH₂ which decreases. This decrease could be due to more chemical reactions involving CH₄ favouring consumption of CH₂ rather than production.

Fig. 5 (Color online). Ion/radical number densities (simulated) with varying methane flow rate, where P_in is 1600 W and 1: CH₃(sp²), 2: CH₂(sp²), 3: C₂H₃ (sp²), 4: CH⁺₄ (sp³), 5: CH⁺₃ (sp²), 6: C₂H₅ (sp³), 7: C₂H⁺₅ (sp²), 8: C₂H⁺₆ (sp³).

3.3. DLNC films

Fig. 6 presents scanning electron microscope (SEM) images of DLNC films with varied discharge power and methane inlet. The SEM image at low power [Fig. 6 (a)] shows uniform coverage of nanoparticles with an approximate size of 40 nm. The cobble-like nanoparticles congregate into a film, with average nanoparticle size increasing to approximately 100 nm at 1600 W as shown in Fig. 6 (b). It can be clearly observed from SEM micrographs that lower P_in and higher J_CH4 [Fig. 6 (a) and (c)] result in a more graphite-like surface morphology (indicating a higher percentage of sp² bonding, see Fig. 7 for further justification). On the other hand, at lower J_CH4 and higher P_in, Fig. 6 (b) shows the emergence of some faceted diamond-like crystalline structure (sp³ bonding). This is emphasized in Fig. 6 (e) which is a zoomed-in inset of Fig. 6 (b) and shows a clear, faceted structure, indicating the increased crystallinity (crystallinity of the samples will be discussed further using X-ray diffraction (XRD) results plotted in Fig. 7).

Fig. 6 (Color online) SEM images of DLNC thin films on Si(111) deposited at: (a) P_in = 400 W, J_CH4 = 8 sccm (b) P_in = 1600 W, J_CH4 = 8 sccm (c) P_in = 1600 W with J_CH4 = 32 sccm. (d) XPS where P_in = 400 W, J_CH4 = 8 sccm, legend as follows: 1) Pristine peak, Deconvoluted peaks: 2) C-sp², 3) C-sp³, 4) C–O, 5: C = 0, (e) Zoomed in inset of (b) showing crystalline facets [sp³]. (f) XPS where P_in = 1600 W, J_CH4 = 32 sccm, legend as in (d).

Fig. 7 (Color online) Raman spectra of DLNC thin films on Si(111) varying as a function of (a) P_in,(b) J_CH4. D and G peak positions marked. Increase of I_D/I_G with P_in clearly visible. XRD patterns with varying (c) P_in and (d) J_CH4.

This illustrates that the sp³/sp² ratio is higher for lower methane flow rates. The observation of more sp² bonding for lower P_in [Fig. 6 (a)] and higher J_CH4 [Fig. 6 (c)] is supported by X-ray photoelectron spectroscopy (XPS) measurements in Fig. 6 (d) and (f), respectively. The XPS spectra both show a strong contribution of the C-sp² peak [series 2] to the experimental data, in marked contrast to a relatively weak contribution from the C-sp³ peak [series 3]. The sp³/sp² ratio may be calculated by taking the ratio of the areas under the sp² and sp³ peaks. For Fig. 6 (d) it is 7.1%, whereas for 1600 W [Fig. 6 (f)] it is 19.0% (see Table 1). Hence, we can conclude that high methane flow rates and low P_in result in a lower sp³/sp² ratio in the DLNC films.

For varying power, the behavior of the sp³ fraction of the films may also be derived from the visible Raman spectra plotted in Fig. 7 (a), application of the 3 stage model of Ferrari and Robertson²⁴ and X-ray diffraction results [Fig. 7 (b)]. The ratio of the D peak to the G peak (I_D/I_G) clearly increases with P_in. Hence we recognize that the films are in stage 2 (nanocrystalline[NC]-graphite to a-C), thus the sp³ fraction is between 10% ∼ 20% and qualitatively note that the sp³/sp² will increase with P_in [in agreement with the conclusion drawn from the XPS in Fig. 6 (d) and (f)]. Crystallinity is also an important factor in tailoring film properties, the only direct information of crystalline graphite is the weak peak G(002) at 2θ = 26.2° shown for the 1600 W series, but not observable for the 2000 W series in Fig. 7 (b). Hence, it could be argued that XRD also shows a shift from NC-graphite to a-C with increasing P_in (supporting our classification of the films being in stage 2 of the Ferrari-Robertson model²⁴). Therefore, the sp³ fraction of carbon thin films indeed strongly depends on the input power.

The corresponding Raman and XRD spectra for the varying J_CH4 case are shown in Fig. 7 (c) and (d), respectively. The slight shift of the G peak in Fig. 7 (c) towards lower wavenumbers with increased J_CH4 indicates that the composition of the film is changing from amorphous carbon to NC-graphite, placing it in stage 2 of the Ferrari-Robertson model,²⁴ predicting a decline of sp³/sp² with increased J_CH4. The trend towards a NC-graphite structure with greater methane fraction is supported by the XRD spectra presented in Fig. 7 (d), specifically, the clear increase of the (101) and (202) phases for graphite at 2θ = 44.4° and 51.4°, respectively. The increase in intensity of the D and G peaks with increased J_CH4 in the Raman spectra in Fig. 7 (c) leads us to conclude that the increase of the peaks at 2θ = 44.4° and 51.4° in the XRD spectra is due to graphite - the G(101) and G(202) phases, respectively. These results suggest that sp² content increases with J_CH4, whereas sp³ content decreases.

3.4. Comparison of sp³/sp² for influx species and DLNC films

Recall from Fig. 1 that one of the primary aims of this paper was to establish a link between the sp³/sp² ratio in the gas phase to the sp³/sp² ratio in the DLNC film. Fig. 8 compares the normalized sp³/sp² ratios in the XPS-measured films to the measured (Langmuir probe) and calculated (global discharge model) plasma species densities. The effect of discharge power, P_in is considered in Fig. 8 (a). The film composition is normalized with respect to the sp³/sp² ratio (0.213) at 2000 W, whereas, the fluxes of the plasma species are normalized with respect to the sp³/sp² ratio at 2000 W derived from the measured and simulated fluxes. For the purpose of this work, the following ion and neutral radical species were taken into account when calculating the sp³ and sp² contributions - (sp³): CH⁺₄, C₂H⁺₆, C₂H₅ and (sp²): CH₃, CH⁺₃,C₂H⁺₅,CH₂,C₂H₃.

Fig. 8 (Color online). The normalized sp³/sp² ratio in the total fluxes from model analysis and the bond ratio in the DLNC thin film by XPS measurement with varying (a) input power [E refers to experimentally measured ion flux, T refers to ion fluxes obtained through the global discharge model](b) CH₄ flow rate.

It is shown that sp³/sp² increases as P_in is increased from 400 to 2000 W, indicating that the relative amount of sp³ increases as power is increased. It is observed that the normalized sp³/sp² ratio for the plasma species increases less rapidly than film composition at high sp³/sp² and high P_in. Similarly, the effect of CH₄ flow rate was considered both on the plasma species and the film composition in Fig. 8 (b). The sp³/sp² ratio was normalized with respect to the maximum value obtained at 8 sccm (19%). It can be seen that sp³/sp² decreases as J_CH4 increases [supported by Fig. 6 (b) and (c)], with increased disparity between sp³/sp² for the plasma species and film composition at higher methane inputs. Hence, the normalised sp³/sp² ratio for the film composition decreases at more marked rate than the plasma species. Given the correspondence between the sp³/sp² ratio behaviour of the plasma species and film composition, the species density variation with plasma parameters may be used to predict the sp³/sp² ratios for DLNC films as indicated in Fig. 1.

4. Discussion

As mentioned in Sec. 3, whilst the global discharge model accounts for 48 species, we singled out the following eight ion and neutral radical species for analysis due to their relative abundance in the discharge: CH⁺₄, CH₃, C₂H⁺₆, C₂H₅, CH⁺₃, C₂H⁺₅, CH₂ and C₂H₃. Recall, non-radical neutrals were not considered to directly contribute to developing films as their sticking coefficients are close to zero due to their saturated electronic structure.⁵⁰ We will now expand on our assignation of various species as sp²- or sp³-hybridized. hybridization is a fundamental issue for carbon-containing species, however, it is not always entirely straightforward. The methyl radical, CH₃, for example, has been assigned as sp²-hybridized.⁵¹ It has a planar structure,⁵² with the unpaired electron residing in a vacant p orbital and the 3 sp² orbitals doubly occupied.⁵¹ Qualitatively, the sp² orbitals are more stable in this case as the electrons will be closer to the nucleus - i.e., the sp² orbitals have more of an ‘s’ character than sp³.⁵¹ This assignment is supported in the literature by both theoretical (Molecular Orbital Theory⁵³) and experimental data (Infrared spectroscopy,⁵⁴ microwave studies,⁵⁵etc.). It is, however, noted in Electron Spin Resonance studies⁵⁶ that whilst the trigonal planar structure is more stable, there is only a small additional amount of energy needed to favour a shallow pyramidal (sp³) structure.⁵⁷ Note, the methyl cation (CH⁺₃) is also classified as sp²,⁵⁸ whilst the methane cation (CH⁺₄), by contrast, is clearly sp³ (pyramidal).⁵⁹

One indication of sp² -hybridization is the presence of a π-bond. Whilst this is indeed the case for the vinyl radical (C₂H₃) which is documented as sp² hybridized,^57,60–62 the distinction is not always so clear cut. For example, the CH₂ radical does not have a double bond, yet it is clearly sp²-hybridized (even though it has a ‘bent’ structure, it can be rotated so it is planar). The ethyl cation (C₂H⁺₅), in the gas phase, exhibits a bridge structure (with a π-bond) as this is a more stable configuration than the classical open isomer,⁵⁷ thus we have classified it as sp². It should be noted that this cation is hyperconjugated⁶³ and hence exhibits a higher degree of stability than a non-hyperconjugated structure.

The ethyl radical and C₂H⁺₆ in particular, bear mentioning due to their asymmetrical nature - only one side may be definitively designated as sp³ hybridized, the other is unknown - it bears mentioning, however, that the ethyl radical has been widely studied and it has been noted that the radical centre should be non-planar in terms of stability arguments.⁶⁴ The asymmetry of these two species is not accounted for in our model and both have been assigned as sp³.

A common belief is that the methyl radical is the most important species for DLNC deposition,^65–67 this is the view put forward by Shiratani et al.⁶⁷ who found that CH₃ contributed a maximum of 60% to film growth and Teii et al.⁶⁸ who noted that CH₃ represented the major adspecies in diamond CVD. It has also been stated that the methyl radical is the most important species in promoting diamond-like (or sp³) bonds in deposited films,^69,70 this is despite its sp² hybridization. An alternative interpretation is that of Dagel et al., who numerically and experimentally considered hard carbon film growth in RF methane plasmas⁶⁶ and concluded that whilst CH₃ was important, it did not appreciably contribute to a-C:H film growth, rather it was of interest as it produced C₂H₆ through the following recombination reaction 2CH₃→C₂H₆.⁶⁶Ethane (a non-radical neutral, hence not directly incorporated in the film) could undergo dissociation reactions in the plasma, the products of which (i.e.C₂H₅, C₂H⁺₅etc.) contribute to film growth. Recall from Table 1 that the electron number density increases with P_in. This implies that more electron impact reactions are likely to take place, i.e., ionization such as e⁻ + C₂H₆→C₂H⁺₆ + 2e⁻, e⁻ + C₂H₆→C₂H⁺₅ + H + 2e⁻ and dissociation such e⁻ + C₂H₆→C₂H₅ + H + e⁻. So whilst C₂H₆ may not directly contribute to film growth, its ions and radical products created through increased electron impact reactions can incorporate in the film. In this way the density of CH₃ (sp²) can be linked with the densities of C₂H⁺₆ (sp³), C₂H⁺₅ (sp²) and C₂H₅ (sp³) and hence the sp³/sp² gas phase ratio may be compared to the sp³/sp² ratio in the film.

As noted in Sec. 3, the fluxes of ion species were comparable with the fluxes of neutral radicals. This is because applied external voltage [-50 V] accelerated cations and remarkably increased the ion flux. The increased flux, in combination with their higher (than radical) sticking coefficients (which in most cases are close to unity⁷¹) points to importance of ion species in determination of the film composition/properties. This is in line with the investigation of Miyagawa et al.⁷² who considered the effect of the ion(CH⁺₃)/neutral radical (CH₃) arrival ratio on the sp³ fraction of DLNC films in a plasma-based ion implantation process using a Monte Carlo simulation. They found that higher sp³ fractions were obtained for higher ion/neutral ratios at lower ion energies (∼50–150 eV).

What happens on the surface, i.e. film formation, whilst influenced by the plasma chemistry is not solely determined by it. We also have to consider how radicals/ions incorporate into the growing film, the influence of substrate conditions, etc. An in-depth modelling of reactions (i.e., radical recombinations, adsorption, desorption, energy transfer in plasma-surface interactions, etc.) on the surface of forming DLNC films was beyond the scope of this study. However, using logic and similar available studies^52,65,66,72 we can qualitatively describe what is likely to happen on the surface under relevant experimental conditions.

The plasma species upon arriving at the surface of the forming film will undergo surface reactions, i.e., adsorption, desorption etc.Hydrogen atoms from the gas phase remove surface H [H(gas) + H(surface) → H₂(gas)] thus creating dangling bonds which can then either be passivated by atomic H or act as radical sites for the chemisorption of hydrocarbon radicals/ions.⁷³ Similarly, Ar⁺ may also serve to activate the surface and create dangling bonds.⁴⁴ Radicals may undergo recombination and be released (as non-radical neutrals) back into the plasma to undergo subsequent gas-phase reactions. Ions, as well as directly incorporating into the film, can lead to loss/damage due to etching or sputtering or can further facilitate the incorporation of radicals into the film through stitching.⁶⁵ It is noted that the direct chemisorption of a methyl radical at a surface site is the rate-limiting step in CVD modelling of film growth using methane plasmas.⁷³ Moreover, Hori and Goto note that due to its planar structure CH₃ is only very weakly physisorbed on the surface - thus to enable the chemisorption of CH₃ both H abstraction and ion bombardment are required. It is commonly believed that film growth proceeds mainly by direct incorporation of ions or through the transformation of a physisorbed layer of radicals into a chemisorbed state that the surface of the growing film rather than by direct incorporation of radicals into chemisorbed sites.⁷¹ This is in accordance with our earlier assertion about the relative importance of the ion flux over the radical flux for tailoring film properties.

Surface processes can influence the plasma influxes - i.e. through ‘backflux’⁷¹ resulting from the desorption of radicals from the surface, the subsequent radical recombinations leading to the expulsion of non-radical neutral products from the surface to the plasma where they can undergo further reactions. As we do not model surface fluxes, this backflux is not accounted for and could also contribute to the discrepancy between theoretical (simulated) and measured ion fluxes mentioned above and in Sec. 3. It should also be noted that we do not take into account displacement damage due to ion irradiation or the possibility of random network stabilization⁷⁴ - both are surface effects which can contribute to modification of bonding (and by extension, mechanical and optoelectronic properties) in the film. Hence, the plasma species sp³/sp² ratio alone does not provide an exact indication of the sp³/sp² ratio in the film. It does, however, give a reasonable idea of the expected film sp³/sp² ratio trend variation with plasma parameters such as P_in and J_CH4.

We have also considered the effect of varying the substrate temperature and the applied bias on DLNC films. This study suggests that increasing bias will increase the ion flux incident to the substrate. We found that whilst the deposition rate was increased, higher applied bias had very little effect on the composition of the films. This can be seen to support our assertion in Sec. 3 that it is the ions that are the significant constituents of the films formed even at lower substrate bias. Higher substrate temperature was observed to increase the sp³/sp² ratio of the films, this is possibly due to its role in reducing neutral density (recall Γ_j = 0.25n_jγ_jν_th,j), whilst the ions are controlled by the bias voltage. We should note that whilst raising the temperature of the substrate would enable us to obtain higher fractions of sp³ in deposited films, it would negate the benefit of a low temperature plasma process and limit the range of applications - thus a better way to tailor the sp³ content is by manipulating plasma parameters (i.e., P_in and J_CH4) rather than surface parameters such as the substrate temperature or the applied bias.

Investigations such as these fall at the intersection of plasma physics, materials science and surface science, given the massive number of reactions both in the gas phase (i.e., electron impact, etc. as accounted for in our global discharge model) and occurring on the surface (i.e., self-sputtering, ion-induced damage, sub-plantation, etc.) the plasma-based deposition of DLNC may be easily classified as a complex system. In such systems, a combination of experimental studies and advanced multi-stage modeling (there are about 9 orders of magnitude that need to be accounted for in order to model the whole deposition process from the ICP system down to diffusion of adatoms/adions about the substrate surface⁴²) is required to come up with effective (both in terms of cost and time) fabrication recipes for tailor made carbon-based films and nanostructures. As we noted, whilst there exist papers which link plasma parameters to the sp³/sp² ratio in DLNC films^71,75 the link between the sp³/sp² ratio in the plasma influx to sp³/sp² in the deposited film remains largely unexplored. Clarifying this issue was one of the main aims of this paper. Moreover, this work may be made applicable to a range of carbon-based nanostructures, by combining it with relevant growth and surface modelling.^19,21–23

Potential extensions of this work include noting that the percentage of the total number of electrons with energies above the dissociation threshold can be estimated using the areas (in the same energy range) under the EEDF plot; thus it is also possible to tailor the percentage of mid-energy electrons to produce excited species relevant for DLNC fabrication as excitation will require less energy. Note also that whilst in this work, OES and QMS were used to indicate the relative densities of reactive neutral species, such species can also be measured unambiguously using other techniques such as fiber optic catalytic probes;^77,78 incorporating such a diagnostic technique may further improve the process framework presented in this paper.

5. Conclusions

We have demonstrated a deterministic approach for the fabrication of DLNC thin films, with a reasonable level of control starting from electrons in the plasma to sp³/sp² ratios in the deposited film. We have also shown that the sp³/sp² ratio is higher for increased input power and lower methane flow rate. By tuning the sp³/sp² ratio one is able to tailor the elastic, mechanical and optoelectronic properties of diamond-like nanocarbon thin films. Given the close relationship between sp³/sp² in the plasma influx and deposited film, we have shown that one may effectively tailor nanostructured film properties, to the level of bond lengths,⁷⁶by careful adjustment of plasma parameters at the level of electrons by controlling the EEDF. This highlights the importance of controlling species production in the plasma bulk by manipulation of parameters such as discharge power and gas composition in order to effect a higher level of control over the characteristic properties, not only of diamond-like nanocarbon thin films but also a variety of other solid/filled carbon nanostructures including nanoparticles, nanotips and highly tailored nanodiamonds. The integral role of predictive modeling in modern, deterministic fabrication processes, in particular has been highlighted as crucial in order to fully realize the potential of plasma nanofabrication all the way to made-to-order carbon-based nanostructures/films for a range of advanced applications. This approach can also be used for the production of graphene, nanodiamond, nanotips and other nanocarbon materials.

Acknowledgements

S.X. and Y.P.R acknowledge support from the National Research Foundation of Singapore, A.E.R. was supported by an APA and the CSIRO PSS, K.O. acknowledges the partial support from the CSIRO's Science Leadership Program and the Australian Research Council (ARC).

References

1. L. Y. Chiang, R. Anandakathir, T. S. Hauck, L. Lee, T. Canteenwala, P. A. Padmawar, K. Pritzker, F. F. Bruno and L. A. Samuelson, Nanoscale, 2010, 2, 535.
2. R. K. F. Lee, B. J. Cox and J. M. Hill, Nanoscale, 2010, 2, 859.
3. J. A. Rodriguez-Manzo, A. Tolvanen, A. V. Krasheninnikov, K. Nordlund, A. Demortiere and F. Banhart, Nanoscale, 2010, 2, 901.
4. N. Wang and L. H. Guan, Nanoscale, 2010, 2, 893.
5. J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470.
6. R. Mas-Balleste, C. Gomez-Navarro, J. Gomez-Herrero and F. Zamora, Nanoscale, 2010 10.1039/C0NR00323A.
7. S. Malik, A. Vijayaraghavan, R. Erni, K. Ariga, I. Khalakhan and J. P. Hill, Nanoscale, 2010, 2, 2139.
8. M. K. Singh, E. Titus, G. Goncalves, P. A. A. P. Marques, I. Bdikin, A. L. Kholkin and J. J. A. Gracio, Nanoscale, 2010, 2, 700.
9. M. Keidar, I. Levchenko, T. Arbel, M. Alexander, A. M. Waas and K. Ostrikov, Appl. Phys. Lett., 2008, 92, 043129.
10. Z. J. Han, B. K. Tay, M. Shakerzadeh and K. Ostrikov, Appl. Phys. Lett., 2009, 94, 223106.
11. M. Keidar, J. Phys. D: Appl. Phys., 2007, 40, 2388.
12. R. M. Sankaran and W. H. Chiang, Nat. Mater., 2009, 8, 882.
13. O. Volotskova, I. Levchenko, A. Shashurin, Y. Raitses, K. Ostrikov and M. Keidar, Nanoscale, 2010, 2, 2281.
14. F. Villalpando-Paez, H. Muramatsu, Y. A. Kim, H. Farhat, M. Endo, M. Terrones and M. S. Dresselhaus, Nanoscale, 2010, 2, 406.
15. B. C. Thompson, J. Chen, S. E. Moulton and G. G. Wallace, Nanoscale, 2010, 2, 499.
16. I. Levchenko, K. Ostrikov, D. Mariotti and V. Švrček, Carbon, 2009, 47, 2379.
17. I. Levchenko, K. Ostrikov and D. Mariotti, Carbon, 2009, 47, 344.
18. Z. L. Tsakadze, I. Levchenko, K. Ostrikov and S. Xu, Carbon, 2007, 45, 2022.
19. I. B. Denysenko, S. Xu, P. P. Rutkevych, J. D. Long, N. A. Azarenkov and K. Ostrikov, J. Appl. Phys., 2004, 95, 2713.
20. I. B. Denysenko and K. Ostrikov, Appl. Phys. Lett., 2007, 90, 251501.
21. I. Levchenko, K. Ostrikov, M. Keidar and S. Xu, J. Appl. Phys., 2005, 98, 064304.
22. I. Denysenko and K. Ostrikov, J. Phys. D: Appl. Phys., 2009, 42, 015208.
23. E. Tam and K. Ostrikov, Nanotechnology, 2009, 20, 375603.
24. A. C. Ferrari and J. Robertson, Philos. Trans. R. Soc. London, Ser. A, 2004, 362, 2477.
25. J. Robertson, Surf. Coat. Technol., 1992, 50, 185.
26. R. Paul, S. N. Das, R. N. Gayen, R. K. Roy, R. Bhar and A. K. Pal, J. Phys. D: Appl. Phys., 2008, 41, 055309.
27. D. H. Lee, S. Fayeulle, K. C. Walter and M. Nastasi, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 148, 216.
28. Y. Cheng, Y. Wu, J. Chen, D. Xu, X. Qiao and C. Xie, Surf. Coat. Technol., 1999, 111, 141.
29. C. Casiraghi, J. Robertson and A. C. Ferrari, Mater. Today, 2007, 10(1–2), 44.
30. J. E. Butler and A. V. Sumant, Chem. Vap. Deposition, 2008, 14, 145.
31. A. S. Barnard, Cryst. Growth Des., 2009, 9, 4860.
32. L. M. Manus, D. J. Mastarone, E. A. Waters, X. Q. Zhang, E. A. Schultz-Sikma, K. W. MacRenaris, D. Ho and T. J. Meade, Nano Lett., 2010, 10, 484.
33. C. Bradac, T. Gaebel, M. Naidoo, M. J. Sellars, J. Twamley, L. I. Brown, A. S. Barnard, T. Plakhotnik, A. V. Zvyagin and J. R. Rabeau, Nat. Nanotechnol., 2010, 5, 345.
34. A. Grigonis, Ž. Rutkūnienė, V. Kopustinskas, G. J. Babonas and A. Rėza, Vacuum, 2005, 78, 593.
35. N. Yasui, H. Inaba and N. Ohtake, Appl. Phys. Express, 2008, 1, 035002.
36. Q. J. Cheng, S. Xu, J. D. Long, Z. H. Ni, A. E. Rider and K. Ostrikov, J. Phys. D: Appl. Phys., 2008, 41, 055406.
37. S. Xu, K. Ostrikov, J. D. Long and S. Y. Huang, Vacuum, 2006, 80, 621.
38. Y. P. Ren, J. D. Long and S. Xu, Phys. Plasmas, 2007, 14, 073301.
39. Q. J. Cheng, E. Tam, S. Xu and K. Ostrikov, Nanoscale, 2010, 2, 594.
40. U. Cvelbar, B. Markoli, I. Poberaj, A. Zalar, L. Kosec and S. Spaić, Appl. Surf. Sci., 2006, 253, 1861.
41. K. Ostrikov, I. Levchenko, U. Cvelbar, M. Sunkara and M. Mozetic, Nanoscale, 2010, 2, 2012.
42. K. Ostrikov, Rev. Mod. Phys., 2005, 77, 489.
43. K. Ostrikov and A. B. Murphy, J. Phys. D: Appl. Phys., 2007, 40, 2223.
44. K. Ostrikov, H. J. Yoon, A. E. Rider and S. V. Vladimirov, Plasma Processes Polym., 2007, 4, 27.
45. R. Kleber, M. Weiler, A. Krüger, S. Sattel, G. Kunz, K. Jung and H. Ehrhardt, Diamond Relat. Mater., 1993, 2, 246.
46. A. D. Arulsamy, A. E. Rider, Q. J. Cheng, S. Xu and K. Ostrikov, J. Appl. Phys., 2009, 105, 094314.
47. “Directing Matter and Energy: Five Challenges for Science and the Imagination”, BESAC Subcommittee on Grand Challenges for Basic Energy Sciences, http://www.sc.doe.gov/bes/reports/list.html Report prepared at Lawrence Berkeley National Laboratory, Editor: Arthur L. Robinson (Advanced Light Source Division), Writer: Lynn Yarris (Communications Department).
48. S. Xu, K. N. Ostrikov, Y. Li, E. L. Tsakadze and I. R. Jones, Phys. Plasmas, 2001, 8, 2549.
49. K. N. Ostrikov, S. Xu and A. B. M. S. Azam, J. Vac. Sci. Technol., A, 2002, 20, 251.
50. J. Perrin, M. Shiratani, P. Kae-Nune, H. Videlot, J. Jolly and J. Guillon, J. Vac. Sci. Technol., A, 1998, 16, 278.
51. M. K. Fox and J. K. Whitesell, Organic Chemistry, Jones and Bartlett Publishers, Inc., USA, 3rd edn, 2004.
52. M. Hori and T. Goto, Appl. Surf. Sci., 2007, 253, 6657.
53. F. M. Bickelhaupt, T. Ziegler and P. von Ragué Schleyer, Organometallics, 1996, 15, 1477.
54. L. Andrews and G. C. Pimentel, J. Chem. Phys., 1967, 47, 3637.
55. M. C. Lawrence and G. N. Robertson, J. Phys. Chem., 1983, 87, 3375.
56. M. Karplus and G. K. Fraenkel, J. Chem. Phys., 1961, 35, 1312.
57. F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, Springer, New York, 5th edn, 2007.
58. D. A. Dixon and A. J. Arduengo III, J. Phys. Chem., 1991, 95, 4180.
59. F. Penotti, J. Gerratt, D. L. Cooper and M. Raimondi, THEOCHEM, 1988, 169, 421.
60. T. Fujii, H. Tokiwa and H. Ichikawa, THEOCHEM, 1995, 339, 209.
61. L. A. Curtiss and J. A. Pople, J. Chem. Phys., 1988, 88, 7405.
62. K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 1997, 106, 4119.
63. S. Ajith Perera, R. J. Bartlett, P. von, R. Schleyer and J. Am, J. Am. Chem. Soc., 1995, 117, 8476.
64. J. Pacansky and M. Dupuis, J. Chem. Phys., 1978, 68, 4276.
65. N. V. Mantzaris, E. Gogolides, A. G. Boudouvis, A. Rhallabi and G. Turban, J. Appl. Phys., 1996, 79, 3718.
66. D. J. Dagel, C. M. Mallouris and J. R. Doyle, J. Appl. Phys., 1996, 79, 8735.
67. M. Shiratani, J. Jolly, H. Videlot and J. Perrin, Jpn. J. Appl. Phys., 1997, 36(7B), 4752.
68. K. Teii, M. Hori and T. Goto, J. Appl. Phys., 2002, 92, 4103.
69. R. Chakrabarti, K. Chakrabarti, A. B. Maity, S. Chaudhuri and A. K. Pal, Diamond Relat. Mater., 1997, 6, 991.
70. F. G. Celii, P. E. Pehrsson, H. T. Wang and J. E. Butler, Appl. Phys. Lett., 1988, 52, 2043.
71. W. Möller, Appl. Phys. A: Mater. Sci. Process., 1993, 56, 527.
72. Y. Miyagawa, Nakadate, M. Ikeyama, S. Nakao and S. Miyagawa, Diamond Relat. Mater., 2003, 12, 927.
73. J. C. Richley, J. N. Harvey and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 11416.
74. J. C. Angus and F. Jansen, J. Vac. Sci. Technol., A, 1986, 6, 1778.
75. W. Möller, Appl. Phys. Lett., 1991, 59, 2391.
76. C. Q. Sun, Prog. Mater. Sci., 2009, 54, 179.
77. U. Cvelbar, M. Mozetic and A. Ricard, IEEE Trans. Plasma Sci., 2005, 33, 834.
78. D. Babic, I. Poberaj and M. Mozetic, Rev. Sci. Instrum., 2001, 72, 4110.

---