Synergistic folding of two intrinsically disordered proteins: searching for conformational selection

Abstract

Intrinsically disordered proteins (IDPs) lack stable structures under physiological conditions but often fold into stable structures upon specific binding. These coupled binding and folding processes underlie the organization of cellular regulatory networks, and a mechanistic understanding is thus of fundamental importance. Here, we investigated the synergistic folding of two IDPs, namely, the NCBD domain of transcription coactivator CBP and the p160 steroid receptor coactivator ACTR, using a topology-based model that was carefully calibrated to balance intrinsic folding propensities and intermolecular interactions. As one of the most structured IDPs, NCBD is a plausible candidate that interacts through conformational selection-like mechanisms, where binding is mainly initiated by pre-existing folded-like conformations. Indeed, the simulations demonstrate that, even though binding and folding of both NCBD and ACTR is highly cooperative on the baseline level, the tertiary folding of NCBD is best described by the “extended conformational selection” model that involves multiple stages of selection and induced folding. The simulations further predict that the NCBD/ACTR recognition is mainly initiated by forming a mini folded core that includes the second and third helices of NCBD and ACTR. These predictions are fully consistent with independent physics-based atomistic simulations as well as a recent experimental mapping of the H/D exchange protection factors. The current work thus adds to the limited number of existing mechanistic studies of coupled binding and folding of IDPs, and provides a first direct demonstration of how conformational selection might contribute to efficient recognition of IDPs. Interestingly, even for highly structured IDPs like NCBD, the recognition is initiated by the more disordered C-terminal segment and with substantial contribution from induced folding. Together with existing studies of IDP interaction mechanisms, this argues that induced folding is likely prevalent in IDP–protein interaction, and emphasizes the importance of understanding how IDPs manage to fold efficiently upon (nonspecific) binding. Success of the current study also further supports the notion that, with careful calibration, topology-based models can be effective tools for mechanistic study of IDP interaction and regulation, especially when combined with physics-based atomistic simulations and experiments.

---

Introduction

Cellular signaling and regulation frequently involve proteins or protein segments that lack stable tertiary folds under physiological conditions and instead exist as heterogeneous and presumably dynamic ensembles of disordered structures.^1–5 Such intrinsically disordered proteins (IDPs) often fold into stable structures upon binding to specific targets. It is important to understand the mechanisms of these coupled binding and folding interactions, as they underlie the organization of regulatory networks for cellular signaling and decision-making. IDPs are also extensively implicated in various human diseases including cancer, neurodegenerative diseases and diabetes.⁶ Mechanistic understanding of IDP interactions and regulation can thus aid in assessing related human diseases and devising rational strategies to modulate IDP functions for therapeutic purposes. In particular, signaling and regulatory IDPs arguably represent a novel class of potential drug targets.⁷ Several small molecules have been successfully developed to bind IDPs and interfere with their interactions using high-throughput screening.^8–10 However, the structural plasticity that allows IDPs to function as versatile regulators poses a significant challenge for rational optimization of the potential drug molecules. The structure of the bound IDP complex alone is not likely going to be sufficient. Instead, an in-depth understanding of how coupled binding and folding occurs and how this process might be modulated by drug molecules is expected to be necessary.

At the baseline level, coupled binding and folding could follow two ideal mechanisms, namely, induced folding and conformational selection. These two extreme mechanisms differ in the kinetic ordering of the binding and folding events: (nonspecific) binding precedes folding in induced folding, and vice versa in conformational selection. Importantly, these mechanisms emphasize different conformational properties of IDPs for interaction. Conformational selection requires the pre-existence of folded-like conformations in the unbound state, and further argues that such preformed structural elements play a main role in initiating recognition.^11–13 In contrast, induced folding emphasizes intrinsic flexibility and nonspecific binding for efficient interaction. Under induced folding scenario, the specific features of the residual structures in the unbound state do not directly affect recognition. Instead, it is the overall level of residual structures that plays a functional role, which is to modulate the binding thermodynamics through the entropic cost of folding. Therefore, such a seemingly semantic classification of the baseline mechanism provides a necessary starting point for understanding how recognition of a specific IDP may be regulated or modulated, such as by post-translational modifications, amino acid replacements, cellular environment, and drug molecules. Note that actual IDP interactions are not expected to follow either ideal mechanism exclusively. Both mechanisms could play roles, such as at different stages of coupled binding and folding.^14,15 There might also be dependence on the solution conditions¹⁶ and even the nature of the specific target.

Residual structures often persist in unbound IDPs.¹ Intriguingly, these residual structures often resemble the folded conformations adopted in complexes.^12,17,18 Such observations have been frequently considered as evidence for conformational selection-like mechanisms of IDP interactions.^{12,13,17–19} However, pre-existence of folded-like conformations is not sufficient evidence for conformational selection. Instead, one needs to further clarify whether the preformed structures play a significant role in initiating binding, such as by examining the free energy surfaces and transition state ensembles of coupled binding and folding or, more directly, by comparing the time-scales (or equivalently rate constants) of binding and folding transitions.^16,20 For example, previous atomistic simulations of the extreme C-terminus of tumor suppressor p53 reveal that, while the free peptide appears to sample several distinct folded-like conformations observed experimentally in various complexes, its interaction with one of its specific targets, S100B(ββ), is mainly initiated by nonspecific binding of unfolded conformations.²¹ Interestingly, the p53 peptide does not appear to be an unusual case, and evidence has recently accumulated to suggest that induced folding is likely prevalent in IDP–protein interactions.^5,22 Induced folding has been consistently observed in mechanistic studies of IDP interaction from experiments^23–25 and simulations.^26–30 Additional evidence of induced folding comes from kinetic data showing that stabilizing native-like structures in unbound IDPs actually reduce the binding rate.^31,32 Theoretical considerations based on the dynamic energy landscape view have predicted that induced folding would prevail with stronger and longer-range intermolecular interactions.³³ This appears to be the case for IDP–protein interactions: structural plasticity for adopting distinct folded states is considered a hallmark of regulatory IDPs;^34,35 therefore, intermolecular interactions do overwhelm intrinsic folding prior to binding and dictate binding-induced folding of IDPs.

Despite the compelling arguments that can be made above for the prevalence of induced folding, conformational selection could play important or even dominant roles for some IDPs. One such possible example is the nuclear-receptor co-activator binding domain (NCBD) of transcription coactivator CREB-binding protein (CBP). It is one of the most structured IDPs that have been characterized so far. Free NCBD is highly helical with molten globule characteristics.^36,37 Four folded structures of NCBD have been determined, in complex with the trans-activation domain (TAD) of tumor suppressor p53,³⁸ the p160 steroid receptor co-activator ACTR,³⁹ the steroid receptor co-activator 1 (SRC1),⁴⁰ and the interferon regulatory factor 3 (IRF3),⁴¹ respectively. In these complexes, NCBD adopts two distinct folds, which mainly differ in the tertiary packing of three similar helices. Two representative folded structures of NCBD, as observed in the NCBD/ACTR and NCBD/IRF3 complexes, are shown in Fig. 1. The structures of NCBD in complex with SRC1 and p53 are similar to that with ACTR. NCBD appears to have a strong tendency to pre-fold, and it is possible to stabilize various conformational sub-states of the unbound NCBD by tuning the solution conditions. For example, two structures of free NCBD have been determined by solution nuclear magnetic resonance (NMR).^18,42 Intriguingly, the recent NMR structure of free NCBD turns out to be very similar to the folded structure in the NCBD/ACTR complex, and this was considered strong evidence for conformational selection in coupled binding and folding of NCBD.¹⁸ However, as we previously demonstrated in the case of the p53 extreme C-terminus, pre-existence of folded-like conformations is only a necessary but insufficient condition of conformational selection. Nonetheless, given the highly helical nature and apparent tendency to pre-fold, NCBD does seem to represent one of the most probable cases of conformation selection, if any IDP could rely on preformed structures for efficient initiation of specific recognition.

Fig. 1 (a) The NMR structure of the NCBD/ACTR complex (PDB: 1kbh).³⁹NCBD is shown in green and ACTR in orange. All helices of NCBD and ACTR are labeled. (b) An overlay of two representative folded structures of NCBD. The conformation in complex with ACTR is shown in green, and the one with IRF3 in yellow (PDB: 1zoq).⁴¹ Only the structured segment (residues 2066–2112) is shown, and the two structures are aligned using the backbone atoms of the second helix (residues 2085–2093).

This work exploits topology-based modeling as an effective means to determine the mechanism of NCBD/ACTR interaction and to test whether conformation selection indeed could play a dominant role for highly structured IDPs like NCBD. The NCBD/ACTR interaction is particularly interesting also because ACTR is an IDP as well. Such synergistic folding of two IDPs has not yet been investigated in detail. Topology-based modeling is based on the conceptual framework of minimally frustrated energy landscape for natural proteins,⁴³ which argues that natural proteins achieve efficient and robust folding by evolving to possess smooth, funneled underlying free energy landscapes. There is a strong correlation between the free energy and fraction of native contacts. In other words, native interactions largely shape the protein energy landscape and non-native ones do not play significant roles. Therefore, given the folded topology, one can derive a list of native contacts and construct effective energy functions that capture the gross features of the true energy landscape. These energy functions are often referred to as Gō- or Gō-like models. These models are extremely efficient and allow direct simulation of folding and unfolding transitions to characterize both kinetics and thermodynamics of folding. Indeed, topology-based modeling has provided impressive correspondence between experiment and theory for many proteins.^43,44 In principle, it should be applicable to binding-induced folding of IDPs, as binding and folding are analogous processes^45,46 and the topology of the folded complex ought to dictate the gross aspects of recognition mechanism. However, there do exist important differences between sequence and interfacial characteristics of IDPs and globular proteins. For example, IDPs are enriched with charged and polar residues and lack large hydrophobic residues.⁴⁷ At the same time, IDPs rely more on hydrophobic contacts for interfacial interactions.⁴⁸ These differences can translate into a significant shift in the balance of local folding and intermolecular binding, which subsequently determines important aspects of coupled binding and folding, such as whether the baseline mechanism follows induced folding or conformational selection. Therefore, existing Gō-like models designed for globular proteins might not be directly applied to IDP complexes.

Using well-characterized model IDP complexes,²⁹ we have recently illustrated that, even with sequence-flavoring, existing Gō-like models need to be re-calibrated to balance the intrinsic folding propensities and the intermolecular interaction strength. Such calibration requires additional (experimental) information including the binding affinity and the level of residual structures in the unbound states. We have further shown that, once calibrated, topology-based models do not only appear to predict the correct baseline mechanism of interaction, but are also capable of capturing nontrivial specific details of binding-induced folding. For example, the calibrated Gō-like model predicts that the phosphorylated kinase inducible domain (pKID) of transcription factor CREB initiates binding to the KIX domain of CBPvia the C-terminus in disordered conformations, followed by binding and folding of the rest of the C-terminal helix and finally the N-terminal helix. This multi-step sequential binding-induced folding mechanism of pKID is surprisingly consistent with several key observations derived from a recent NMR study,²³ and provides a molecular interpretation of key NMR-derived kinetic rates. In this work, we applied a similar approach to construct a balanced topology-derived model of the NCBD/ACTR complex and investigate the mechanism of the synergistic folding of NCBD and ACTR. While important limitations clearly exist with such simplistic protein models derived from the folded topology,²⁹ these models can be expected to capture important aspects of the NCBD/ACTR recognition and provide an effective means to generate initial insights that may be further investigated by detailed simulations and/or experiments.

Methods

Topology-based modeling of NCBD/ACTR

An initial sequence-flavored Gō-like model was first derived from the PDB structure of the NCBD/ACTR complex (PDB: 1kbh)³⁹ (see Fig. 1a), using the Multiscale Modeling Tools for Structural Biology (MMTSB) Gō-Model Builder (http://www.mmtsb.org).^49,50 The model represents each residue using a single C_α-bead and treats the C_α-based native interactions using the Miyazawa–Jernigan (MJ) statistical potentials⁵¹ to provide residue-specific energetic biases. In addition, it includes knowledge-based sequence-dependent, but native-structure independent, pseudo-torsional potentials. The underlying idea is that a sequence could provide differing statistical weights to the populations of structural elements during folding to modulate their prevalence as observable intermediates and affect folding kinetics. The sequence-flavored Gō-like models have been shown to recapitulate subtle differences in folding mechanisms and kinetics that arise from sequence differences in topologically analogous proteins.^52,53 Therefore, it is particularly suitable for extension to modeling IDPs. The initial model was then calibrated by first uniformly scaling the strengths of sets of intra-molecular native contact interaction strengths based on experimental knowledge of the overall level of residual structures in unbound NCBD and ACTR. The strengths of inter-molecular contacts were then scaled to match the simulated and experimental binding affinities of the complex. Both NCBD and ACTR fold into three helices in the complex. The three NCBD helices are (in mouse CBP numbering): α1 (2066–2076; N_intra = 12, N_inter = 13), α2 (2085–2092; N_intra = 8, N_inter = 8), and α3 (2094–2112; N_intra = 18, N_inter = 41); the three ACTR helices are (in human ACTR numbering): α1 (1044–1058; N_intra = 18, N_inter = 32), α2 (1063–1071; N_intra = 9, N_inter = 16), and α3 (1072–1080; N_intra = 9, N_inter = 12). N_inter denotes the number of native inter-molecular contacts, and N_intra is the number of native contacts within the individual helix. All 76 native intermolecular contacts and the corresponding strengths of interactions from the original sequence-flavored Gō-like model are listed in the ESI‡, Table S1. The total number of intra-molecular contacts is 49 for ACTR and 78 for NCBD. As shown in Fig. S1 (ESI‡), while NCBD contains a small number of tertiary contacts that define the α1–α2 interface and the short α2–α3 turn, ACTR largely lacks tertiary contacts.

Simulation protocols

The complex was simulated in a 105 Å cubic box with periodic boundary conditions using CHARMM.^54,55 Langevin dynamics simulations were performed with a dynamic time step of 15 fs and a friction coefficient of 0.1 ps⁻¹. Lengths of all virtual bonds were fixed with SHAKE,⁵⁶ and the cutoff distance for non-bonded interactions was 25 Å. For the calibration of the intra-molecular interactions, free NCBD and ACTR were simulated at 300 K for 750 ns. Due to the tight binding, enhanced sampling with replica exchange (REX)⁵⁷ is necessary for reliable calculation of K_d to calibrate the intermolecular interactions. All REX simulations were performed with the MMSTB Toolset^49,50 with eight replicas spanning 270 to 370 K. The lengths of calibration REX simulations range from 2 to 5 μs. Once the model was properly calibrated, a 30 μs production simulation was initiated from the PDB structure near the melting temperature (T_m ≈ 315 K), which was used to calculate all the free energy profiles shown in the rest of this paper. Ten additional productions simulations were initiated from randomly selected folded and unfolded conformations sampled in the REX calibration run (see Fig. S2a, ESI‡). These simulations allow better transition statistics for the construction of the conformational space network (CSN). As summarized in Table S2 (ESI‡), a total of 268 folding/binding and unfolding/unbinding transitions were sampled in all production simulations. Representative time traces of the fractions of inter- and intra-molecular contacts are shown in Fig. S2b (ESI‡).

Data analysis

All the analysis was carried out using CHARMM and additional in-house scripts. A given native contact is considered formed if the inter-C_α distance is no more than 1 Å greater than the distance in the PDB structure. For equilibrium simulations of free NCBD and ACTR, the helicity was calculated as the fraction of 1–5 (backbone) native contacts formed. For REX simulations of the complex, a weighted histogram analysis method (WHAM) was used to combine information from all temperatures to compute either C_v curves or unbiased probability distributions.⁵⁸ The unbound state was identified as the one without any native intermolecular contacts formed, and the dissociation constants were calculated from the bound and unbound probabilities aswhere V₀ is the periodic box volume in units of ų. For production simulations at T_m, all free energy surfaces are converted directly from the corresponding histograms. The surfaces were then shifted such that the bound minima were at zero. Helix cross angles were calculated using the Chothia–Levitt–Richardson algorithm⁵⁹ as implemented in CHARMM.

To construct the CSN, all conformations sampled during all 11 production simulations at 315 K were first assigned to discrete microscopic states (nodes) using 8 fractions of native contacts as descriptors, including the fraction of intra-molecular contacts of ACTR (Q^ACTR_intra), the fraction of tertiary contacts of NCBD (Q^NCBD_intra-tert), the fractions of inter-molecular contacts made by the three ACTR helices (Q^ACTR-α1_inter, Q^ACTR-α2_inter and Q^ACTR-α3_inter), and the fractions of inter-molecular contacts made by the three NCBD helices (Q^NCBD-α1_inter, Q^NCBD-α2_inter and Q^NCBD-α3_inter). Distribution along each descriptor was divided evenly into 5 bins except for Q^NCBD_intra-tert, where five non-uniform bins were used with 0.1, 0.2, 0.4 and 0.8 as the dividing values. The reason for using non-uniform sub-states is to resolve natural conformational states along Q^NCBD_intra-tertwithout having to use more bins. The total possible number of conformational states using the above setup is 5⁸ = 390 625. For clarity, only the most populated nodes with additional nodes from the transition paths were included in the CSN. The transition paths were defined as those where the system left either the bound or the unbound state and entered the other state without revisiting the originating state. The fraction of the total native intermolecular contacts formed (Q_inter) was used as the order parameter for defining the bound and unbound states for transition path identification. Q_inter = 0.15 was used as the upper bound of the unbound state, and Q_inter = 0.4 as the lower bound of the bound state. Inclusion of nodes on the transition paths is necessary to preserve different transition pathways when a limited number of nodes are used to construct the CSN. The resulting network was visualized with stress minimization using visone (www.visone.de). The node sizes and link thickness in the final CSNs shown reflect the statistical weights in the logarithmic scale.

Results and discussion

Calibration of the sequence-flavored Gō-like model

Previous NMR secondary chemical shift analysis has estimated that the free NCBD has native-like helical content and the free ACTR is highly disordered with low residual helicity.³⁷Fig. 2a compares the overall helicity distributions of unbound ACTR with different levels of scaling of the strengths of all intra-molecular interactions. Clearly, it shows that the original sequence-flavored Gō-like model overestimates the residual structure level. The scaling factor of ACTR intra-molecular interaction strengths was chosen to be 0.4 in the final model, which yields an average helicity of ∼30%. Note that, due to the coarse-grained nature, the Cα-only model has a limiting helicity of nearly 20% even without any specific intra-molecular interactions (e.g., see the 0.1 trace in Fig. 2a). A helicity of ∼30% is thus near the “random coil” limit within the context of the peptide model. For NCBD, it turned out that no scaling of the intra-molecular interaction strengths was necessary. As shown in Fig. 2b, all three helices of NCBD in the unbound state are nearly as stable as in the bound state. It is interesting that sequence-flavoring alone correctly predicts NCBD-α3 to be the least stable helix in the unbound state. This is consistent with the results of NMR secondary chemical shift analysis.³⁷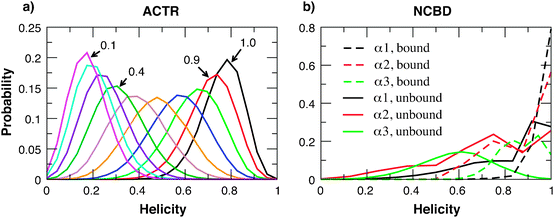

Fig. 2 (a) Probability distributions of the overall helicity of the unbound ACTR, calculated with various uniform scaling of the intra-molecular interaction strengths. (b) Probability distributions of the helicities of three NCBD helical segments in the unbound and bound states. The unbound state was calculated without any scaling of the intra-molecular interaction strengths, and the bound state distributions were calculated from a 1 μs simulation of the complex using the final calibrated model (see main text).

Once the scaling factors of the intra-molecular interaction strengths were determined, multiple REX simulations were carried out using different scaling of the intermolecular interaction strengths. The free energy profiles as a function of Q_inter with a few different scaling factors are provided in Fig. S3a, ESI.‡ The original model yields K_d∼μM, nearly two orders of magnitude weaker than the experimental value of K_d = 34 ± 8 nM.³⁶ The optimal scaling of the intermolecular interaction strengths turns out to be 1.1, which yields K_d ≈ 23 nM and T_m ≈ 315 K. The heat capacity as a function of temperature calculated from a 4.9 μs REX simulation using the final model is shown in Fig. S3b, ESI.‡ Surprisingly, with sequence flavoring, the topology-derived models appear to consistently predict strong structural fluctuations within the folded complex, such that the folded minimum centers at Q_inter ≈ 0.6 even with substantial strengthening of the intermolecular interactions (e.g., with scaling factors up to 1.5; data not shown). Further examination of the list of all native intermolecular contacts (see Table S1, ESI‡) reveals that it contains many contacts involving small hydrophobic residues and/or charged ones. These contacts are weak in the MJ scale,⁵¹ and frequently involve the C-termini of ACTR and NCBD. Indeed, the root-mean-squared fluctuation (RMSF) profiles computed from a control simulation of the complex at 300 K using the calibrated model reveal significantly elevated fluctuation at the C-termini of both ACTR-α3 and NCBD-α3 (see Fig. S4, ESI‡). Interestingly, a previous NMR relaxation analysis has also revealed fluctuating contacts between ACTR-α3 and NCBD-α3.³⁷ In addition, a recent H/D exchange mass spectrometry (H/D-MS) study⁶⁰ showed that, within the folded regions of NCBD and ACTR, peptide segments that map to the C-termini of both ACTR-α3 and NCBD-α3 had the smallest protection factors. Therefore, it appears that the strong structural fluctuations predicted by the calibrated sequence-flavored model are realistic, and no adjustment to the model was applied to further stabilize the complex.

The baseline mechanism: induced folding vs. conformational selection

With careful calibration, the final sequence-flavored Gō-like model is able to reproduce the experimental data on the binding affinity and the level of residual structures in the unbound proteins. Therefore, the model properly reflects the balance between the intrinsic folding propensities of NCBD and ACTR and the strength of their interactions. This balance should allow a reliable prediction of the baseline mechanism. For this, we examine the free energy surfaces along appropriate binding and folding reaction coordinates, where the most probable transition paths can be identified as the minimum free energy paths connecting various basins. In the context of topology-based modeling, the fractions of native contacts provide natural reaction coordinates for describing folding, and analogously, binding.⁶¹Fig. 3 examines the 2D binding and folding free energy surfaces of NCBD and ACTR, using the total fractions of inter- and intra-molecular contacts as order parameters. Apparently, both NCBD and ACTR bind and fold in a highly cooperative fashion, as Q^ACTR_intra and Q^NCBD_intra gradually increase together with Q_inter. In particular, even though the free NCBD is highly helical (see Fig. 2b), Q^NCBD_intra does not appear to increase any faster than Q_inter, i.e., folding does not precede binding on the whole protein level. Therefore, on the baseline level, neither NCBD nor ACTR follows either induced folding or conformational selection. Not surprisingly, folding of NCBD and ACTR are highly synergistic. As shown in Fig. 3c, neither protein displays any significant folding without binding (and folding) of the partner.

Fig. 3 2D free energy surfaces of the synergistic binding and folding of NCBD and ACTR. Q^ACTR_intra and Q^NCBD_intra are the fractions of native intra-molecular contacts formed by ACTR and NCBD, respectively. Contour levels are drawn at every kT.

A key intermediate state of the NCBD/ACTR interaction

The free energy surfaces in Fig. 3 also reveal a key intermediate state of the NCBD/ACTR interaction, at Q_inter ≈ 0.25. To further characterize the nature of this state, conformations sampled during the production simulation were grouped to three states: Q_inter = 0 for the unbound state, 0.21 < Q_inter < 0.32 for the intermediate state (corresponding to 16 to 24 native contacts formed), and Q_inter > 0.5 for the bound state. Structural analysis of the resulting ensembles reveals that in the intermediate state NCBD and ACTR mainly interact through the C-terminal segments that include both α2 and α3, while α1 helices from both proteins are largely unbound (see Fig. 4). At the intermediate state, α2 and α3 from both proteins are similarly folded compared to the bound state, while α1 helices remain as (un)structured as in the unbound state (see Fig. S5, ESI‡). Further analysis of the helix–helix packing geometry including helix center distances and cross angles (see Fig. S6, ESI‡) demonstrates that the C-terminal segments of NCBD and ACTR adopt highly folded-like tertiary conformations in this intermediate state, which is consistent with the Q^{NCBD-α2α3–ACTR-α2α3}_inter distributions shown in Fig. 4b. Therefore, the C-terminal segments of NCBD and ACTR appear to serve as a mini folding core prior to complete binding and folding (e.g., see Fig. 4c). As discussed above, NMR, H/D-MS and the current simulations all suggest significant structural fluctuation in interactions between NCBD-α3 and ACTR-α3. The observation that the C-terminal α2 and α3 regions of these two proteins form the key folding core and play a major role in initiating specific recognition can thus be surprising. Nonetheless, this prediction is fully consistent with independent atomistic unfolding and unbinding simulations using physics-based explicit and implicit solvent protein force fields.⁶² Furthermore, it also appears to be consistent with the recent H/D-MS study,⁶⁰ where peptide segments within the α2 and α3 regions of both NCBD and ACTR were shown to have much larger protection factors compared to those mapped into other folded regions of the complex.

Fig. 4 Probability distributions of the fraction of native intermolecular contacts formed (a) by NCBD-α1, Q^NCBD-α1_inter, and (b) between the C-terminal segments of NCBD and ACTR, Q^{NCBD-α2α3-ACTR-α2α3}_inter. The unbound state has no native intermolecular contact by definition and is thus not shown. (c) A representative snapshot of the intermediate state, with all helical segments colored and marked.

Mechanism of coupled binding and tertiary folding of NCBD

NCBD is highly helical in the unbound state (see Fig. 2b), and only forms a limited number of tertiary intra-molecular contacts upon folding and binding to ACTR (see Fig. S1b, ESI‡). The total fraction of intra-molecular contacts (Q^NCBD_intra) is thus not a sensitive measure of NCBD tertiary folding. To better understand the interplay between binding and NCBD tertiary folding, Fig. 5a examines the free energy surface as a function of Q_inter and the fraction of tertiary intra-molecular contacts of NCBD, Q^NCBD_intra-tert. At the baseline level (e.g., assuming an inability to resolve the details along the pathways connecting the unbound and bound states), it appears that the increase in Q_inter precedes and thus presumably drives that of Q^NCBD_intra-tert, i.e., an induced folding-like mechanism. However, such a baseline mechanistic classification appears to break down once the additional details of the transition pathways are taken into consideration. Instead, conformational selection appears to play key roles during different stages of binding and tertiary folding of NCBD. Specifically, the transition between the unbound and intermediate states follows both induced folding and conformational selection-like pathways, as indicated by the yellow and dark green dashed lines connecting states U and I in Fig. 5a. Furthermore, the conformational selection-like pathway has lower free energy barrier (by ∼1 kT), and is thus slightly favored. More notably, the intermediate-bound transition appears to mainly follow conformational selection on the tertiary level, where NCBD quickly folds before forming additional native contacts with ACTR (e.g., see the green dashed line connecting states I and B in Fig. 5a). Such a staged mechanism of coupled binding and tertiary folding of NCBD resembles the extended conformational selection model recently discussed by Csermely, Palotai and Nussinov,¹⁵ which emphasizes a multi-stage mutual adjustment process that involves both induced folding and conformational selection.

Fig. 5 2D free energy surfaces of coupled binding and tertiary folding of NCBD. Q^NCBD_intra-tert is the fraction of native tertiary intra-molecular contacts formed by NCBD. θ_α2–α3 is the cross angle between NCBD-α2 and α3, and θ_α1–α2 is that between NCBD-α1 and α2. In panel (a), the unbound, intermediate and bound states are marked with U, I and B, respectively. Contour levels are drawn at every kT.

With largely folded helices in the unbound state, the tertiary folding of NCBD mainly involves packing of the three helical segments. The analysis above (e.g., see Fig. 4) has shown that the unbound-intermediate transition mainly involves the folding of NCBD-α2 and α3 and the next step involves that of NCBD-α1. In Fig. 5b and c, we directly examine the coupling between intermolecular interactions and formation of native-like helix–helix packing as reflected in the helix–helix cross-angles. The analysis shows that the transition pathways between the unbound and intermediate states indeed have a very broad distribution, and there is a continuum between two extreme mechanisms of induced folding and conformational selection for (binding-induced) tertiary packing of NCBD-α2 and α3 (as indicated by multiple dashed lines in Fig. 5b). In the intermediate state, NCBD-α1 remains nearly as dynamic as in the unbound state, but with a slight enrichment of folded-like conformations (also see ESI‡, Fig. S6, red traces). These folded-like conformations appear to play a key role in initiating the binding and folding of the rest of the complex. One way to understand the conformational selection-like transition between the intermediate and bound states is that, as the most stable helix, NCBD-α1's packing with the folded core of NCBD-α2 and α3 is defined by only a few degrees of freedom. Thus, NCBD-α1 can readily adopt native-like packing upon making a few additional intermolecular contacts, which appears to drive the formation of the remaining intermolecular contacts.

Folding and binding of individual helical segments of NCBD and ACTR

We have further examined coupled binding and folding of individual helices of NCBD and ACTR. As shown in Fig. 6a and b, NCBD-α1 and α2 are very stable in the unbound state, and bind largely as pre-folded helices as expected. The least stable helix of NCBD, α3, appears to fold concurrently with binding (Fig. 6c). In contrast to NCBD helices, all ACTR helices are largely unstructured in the unbound state, and they appear to mainly follow induced folding-like mechanisms. As shown in Fig. 6d–f, Q_inter increases faster than various Q_intra of individual helices during transitions, either between the unbound and intermediate states (ACTR-α2 and α3) or between the intermediate and bound states (ACTR-α1). In other words, intermolecular interactions drive the (secondary) folding of ACTR. Taken together, the current topology-based simulation suggests that NCBD provides pre-folded structural elements on both secondary and tertiary levels, which allow efficient binding of ACTR in unstructured conformations and drive specific folding of ACTR during different stages of the recognition.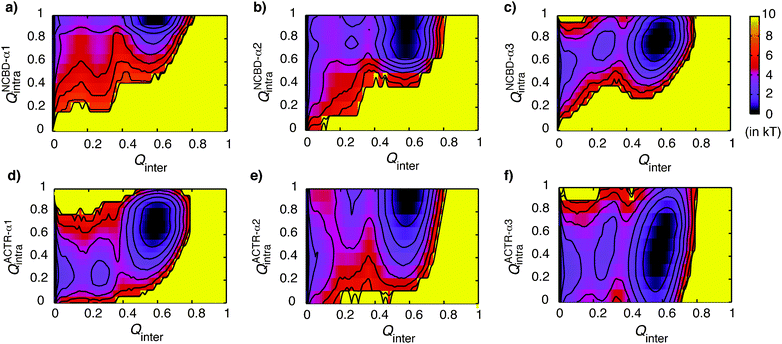

Fig. 6 2D free energy surfaces as functions of Q_inter and the fraction of intra-molecular native interactions formed within individual helices of NCBD and ACTR. Contour levels are drawn at every kT.

Fig. 7 and 8 further examine the sequence of binding of all ACTR and NCBD helices by comparing the free energy projections along various combinations of the fractions of native intermolecular contacts formed by different helical segments. Examination of the minimum free energy paths connecting various basins along these projections reveals detailed (kinetic) ordering of binding and folding of individual segments. The analysis supports the above observation that α2 and α3 from both proteins drive the recognition by forming the folded core at the intermediate state. Specifically, binding of ACTR-α2 and α3 precedes that of ACTR-α1 (Fig. 7d and e), and binding of NCBD-α2 and α3 precedes that of NCBD-α1 (Fig. 8d and e). Furthermore, NCBD-α3 and ACTR-α2 appear to be most frequently involved in initiating the recognition. NCBD-α3 has the largest number of native intermolecular contacts (N_inter = 41) and its role in initiating binding and folding may thus be expected.⁶³ However, ACTR-α2 does not have the highest density of native contacts and its role in initiating recognition is unexpected from simple consideration of native contact density. Interestingly, these free energy surfaces also reveal a co-existence of many parallel pathways of the NCBD/ACTR recognition. For example, Fig. 8a shows that, along the dominant pathway (indicated by the yellow dashed line), Q^NCBD-α_inter¹ does not increase from near zero until Q_inter exceeds ∼0.25. That is, NCBD-α1 binds only after a significant number of native intermolecular interactions are formed. At the same time, there exists a minor pathway where binding is initiated by NCBD-α1 (indicated by the green dashed line in Fig. 8a). These parallel pathways are also evident in Fig. 8d. In fact, the free energy surfaces shown in Fig. 7 and 8 suggest that all helices of NCBD and ACTR could initiate binding, albeit at different levels of prevalence. Such diversity in folding and binding pathways is not surprising, and is actually expected to be generally true based on the funneled energy landscape theory.⁶⁴ The importance of examining the recognition mechanism using multiple sets of order parameters should also be emphasized. For example, the Q^NCBD_intra-tert–Q_inter free energy surface shown in Fig. 5a alone could lead to an overly simplified view that the recognition occurs through a well-defined pathway that involves folding and binding of α2 and α3, followed by binding and folding of α1 helices. This is a limitation of free energy analysis along pre-selected order parameters, which can mask important heterogeneity and complexity along orthogonal degrees of freedom.

Fig. 7 2D free energy surfaces as functions of the fractions of native intermolecular contacts formed by various segments of ACTR. Contour levels are drawn at every kT.

Fig. 8 2D free energy surfaces as functions of the fractions of native intermolecular contacts formed by various segments of NCBD. Contour levels are drawn at every kT.

Network analysis of the complex pathways of coupled binding and folding

CSN analysis does not rely on pre-determined order parameters as required in the traditional free energy analysis, and can thus allow better visualization of the heterogeneous pathways of protein folding and binding.^65–67 One of the key challenges in constructing the CSN is the need to divide the continuous protein conformational space into discrete microstates. The discretization has been mainly achieved either by conformational clustering^68–71 or by using a reduced set of (structural) descriptors.^67,72 In the context of topology-based modeling, various fractions of native contacts do provide natural reaction coordinates and are thus appropriate for defining microstates. Fig. 9 shows a CSN of the synergetic folding of NCBD and ACTR derived from all 11 production simulations, by including only the most populated 100 nodes and additional 200 nodes from the transition paths. The total number of links is 15 161. Including additional nodes does not change the appearance of the CSN (e.g., see Fig. S7, ESI‡). Even though powerful analysis can be done to further analyze the kinetic portioning and connectivity of the conformational space, the goal here is mainly to illustrate and visualize the complexity of multiple pathways of binding and folding of NCBD and ACTR. With the nodes distributed with minimized stress (as implemented in visone), the CSN shows a natural segregation of different (meta-)stable free energy states that include the unbound (labeled in blue), intermediate (green), and fully bound (red) states. It further illustrates the co-existence of two main groups of recognition pathways. While the peptides mostly initiate binding through the C-terminal α2 and α3 and go through the intermediate state toward the bound state, they can also initiate binding through α1 helices (e.g., the link between nodes 37 and 218) and reach the bound state through an intermediate state that is mainly stabilized by interactions between α1 helices (purple nodes). Interestingly, it appears that NCBD needs to pre-fold with 0.4 < Q^NCBD_intra-tert < 0.8 to initiate binding through α1. Along the major pathway, the CSN shows three key routes initiated by nodes 202, 248 and 270. These routes appear to correspond to conformational selection (node 202) and induced folding initiated by NCBD-α2 (node 248) and α3 (node 270) for the unbound–intermediate transitions observed from the free energy analysis (e.g., see Fig. 5a). Transitions from the intermediate to the bound state mainly go through an intermediate state where NCBD becomes pre-folded (orange nodes), even though highly cooperative binding and folding of α1 helices also appear to be possible (e.g., see direct links between green and red nodes). Taken together, the CSN appears to provide a clear and concise illustration of the heterogeneous pathways of the NCBD/ACTR recognition that is fully consistent with the observations derived from analysis of multiple free energy surfaces.

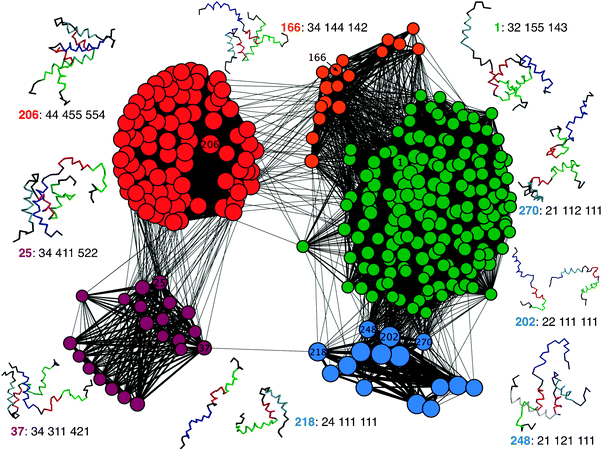Fig. 9 The CSN of the synergetic folding of NCBD and ACTR. The nodes represent the conformational microstates, and the links represent the transitions between them. The node sizes and link widths reflect the statistical weights in the logarithmic scale. The colors of the nodes are assigned according to states of NCBD: blue: unfolded and unbound; green: partially folded and bound with ACTR through NCBD-α2 and α3; orange: folded and bound with ACTR through NCBD-α2 and α3; red: folded and bound; and purple: partially folded and bound to ACTR through NCBD-α1. Representative snapshots are shown for selected nodes, where NCBD and ACTR helices are colored using the same scheme as in Fig. 4. The notation is the node ID (in bold fonts) followed by the bin indices (1 through 5) along the 8 structural descriptors (Q^ACTR_intra, Q^NCBD_intra-tert, Q^ACTR-α1_inter, Q^ACTR-α2_inter, Q^ACTR-α3_inter, Q^NCBD-α1_inter, Q^NCBD-α2_inter, Q^NCBD-α3_inter; see Methods for details).

Conclusions

Topology-based modeling has been successfully applied to investigate the synergistic folding of two IDPs with drastically different residual stabilities in the unbound states. Through careful calibration based on additional experimental data besides the complex structure, the topology-based model was able to properly capture the balance between the intrinsic folding propensities of NCBD and ACTR and the strength of their intermolecular interaction. Subsequent simulations revealed several important mechanistic features of the coupled binding and folding processes. Despite a drastic difference in the residual structural level, both NCBD and ACTR bind and fold in a highly cooperative fashion on the baseline level that involves a key intermediate state. In the intermediate state, the C-terminal helices α2 and α3 of NCBD and ACTR form a mini folding core that allows rapid folding and binding of α1 helices. Interestingly, due to the highly structured nature of the unbound NCBD, conformational selection appears to play significant roles in the formation of both the intermediate state and the final specific complex. The binding-induced tertiary folding of NCBD involves multiple stages of selection and induced folding, and is clearly an example of “extended conformational selection”.^15,73 Importantly, key mechanistic features predicted by the current topology-based modeling, such as regarding individual helix folding and binding, tertiary folding, and intermolecular interactions, are surprisingly consistent with independent atomistic simulations using implicit solvent protein force fields.⁶² Several key aspects of the predicted mechanism are also consistent with the protection factor mapping derived from a recent H/D-MS study of NCBD/ACTR.⁶⁰

Nonetheless, it is interesting to note that, even for an unusually structured IDP like NCBD, the recognition is initiated by the more flexible C-terminal segment and with substantial contribution from induced folding. Formation of the meta-stable mini folding core appears to be necessary for conformational selection to play an even larger role during later stages of recognition, where NCBD-α1 readily forms native-like packing with the folded core and allows rapid binding and folding of the rest of the complex. Combined with existing experimental and theoretical evidence (see Introduction), the current work further supports the notion that induced folding is very likely the prevalent mechanism of specific IDP–protein interactions. Even when conformational selection does play a role, it will likely be limited to the local (secondary) structure level and later stages of the recognition process. A fundamental question is then why and how induced folding might confer functional advantages for IDP recognition. The need for proteins to remain unstructured in the unbound state is believed to arise from certain functional constraints, particularly in signaling and regulation, such as to allow high specificity coupled with low affinity binding, inducibility by posttranslational modifications, structural plasticity for binding multiple targets, and thermo-instability for allosteric regulation.^74,75 It has also been proposed that disordered proteins could enhance the (nonspecific) binding rate up to 1.6 folds due to larger capture radii (i.e., the fly-casting effects).^76,77 However, recent studies show that unbound IDPs tend to be compact^78–80 and thus may not have much greater capture radii to have the full fly-casting effects. Furthermore, the rate-enhancing effect due to increased capture radii will be largely offset by slower diffusion.⁸¹ Therefore, it is not obvious that intrinsic disorder itself could provide any significant kinetic advantages.

Instead, it appears that while required for satisfying other functional constraints, intrinsic disorder could lead to a kinetic bottleneck that must be overcome to allow facile recognition in signaling and regulation. This bottleneck arises from the requirement of (partial or full) folding during specific binding, as protein folding is usually a slow process (compared to translational and orientational diffusion) with an estimated “speed limit” of μs.⁸² Indeed, the recent dual-transition state model developed by Zhou²⁰ predicts that the diffusion-limited binding rate provides an upper bound of the binding rate, which is achieved only if the protein can rapidly undergo folding transition upon nonspecific binding. This limit corresponds to the case of induced folding. In contrast, conformational selection arises in the limit of slow conformational transitions and actually defines the lower bound of the binding rate. Interestingly, existing experimental binding rates show that IDPs bind no slower than globular proteins.⁸¹ This suggests that IDPs are able to overcome the kinetic bottleneck of folding and achieve rates near or at the diffusion limit. This is consistent with the notion that induced folding is the prevalent mechanism for coupled binding and folding of IDPs. A key question is then how IDPs manage to fold so rapidly upon nonspecific binding, often at rates beyond the traditional folding speed limit. The constraint of rapid folding could explain why the interaction motifs of IDPs are usually short and often fold into simple topologies with low contact orders upon binding. Furthermore, it is likely that IDPs (and their binding targets) may exploit additional physical properties to achieve rapid folding. For example, previous studies of IDP interactions²¹ and protein–DNA interactions^83,84 have suggested that long-range electrostatic interactions may play an important role.

While it is encouraging that simple models derived from the folded complex topology can reliably predict important features of coupled binding and folding, several inherent limitations of such models should not be overlooked. For example, topology-derived models cannot faithfully describe specific details of the unbound states, particularly non-native-like residual structures,⁸⁵ or properly model the encounter complexes, a critical step that often involves transient nonspecific contacts.^23,24 Importantly, non-native interactions can play an important role in stabilizing nonspecific encounter complexes and/or folding intermediates, leading to nontrivial consequences in binding and folding pathways and kinetics.^86,87 Given the prevalence of charges in IDPs, long-range electrostatic interactions do not only modulate the conformational properties of the unbound states,^80,88 but can also play a key role in the binding and folding interactions.²¹ Explicit charges could be introduced into the conventional topology-derived models to account for long-range electrostatic interactions.^89,90 Nonetheless, even though more sophisticated Gō-like models might be exploited,⁹¹ contributions of specific yet non-native interactions are not encoded in the topology per se and cannot be expected to be properly accounted for in topology-based modeling in general. It is also important to emphasize that detailed characterization of disordered protein states and transient structures represents a broader challenge beyond topology-based modeling. Due to the heterogeneous and dynamic nature of such states, experiments alone generally do not provide sufficient restraints for unambiguous determination of the unfolded ensembles.^92–94 Arguments can be made that de novo molecular simulations are necessary to provide the missing structural details of free IDPs,^5,95,96 even though such simulations are limited by both sample capability and force field accuracy. At present, only small free IDPs could be modeled using physics-based force fields with reasonable reliability, and direct simulations of the coupled binding and folding processes are largely out of reach. As such, it is important to tightly integrate hypothesis-driven topology-based modeling, physics-based de novo simulation, and various biochemical and biophysical characterizations to obtain better understanding of how the structure and interaction of IDPs are precisely controlled and regulated.

Acknowledgements

The authors thank Dr David D. Weis for helpful discussions and for sharing his unpublished manuscript on the H/D-MS study of NCBD/ACTR. This work was supported by NSF through Award MCB 0952514 to JC. This work is contribution 11-379-J from the Kansas Agricultural Experiment Station.

References

1. H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208.
2. L. M. Iakoucheva, C. J. Brown, J. D. Lawson, Z. Obradovic and A. K. Dunker, J. Mol. Biol., 2002, 323, 573–584.
3. V. N. Uversky, C. J. Oldfield and A. K. Dunker, J. Mol. Recognit., 2005, 18, 343–384.
4. R. G. Smock and L. M. Gierasch, Science, 2009, 324, 198–203.
5. T. H. Click, D. Ganguly and J. Chen, Int. J. Mol. Sci., 2010, 11, 5292–5309.
6. V. N. Uversky, C. J. Oldfield and A. K. Dunker, Annu. Rev. Biophys., 2008, 37, 215–246.
7. A. K. Dunker and V. N. Uversky, Curr. Opin. Pharmacol., 2010, 10, 782–788.
8. D. I. Hammoudeh, A. V. Follis, E. V. Prochownik and S. J. Metallo, J. Am. Chem. Soc., 2009, 131, 7390–7401.
9. G. Mustata, A. V. Follis, D. I. Hammoudeh, S. J. Metallo, H. Wang, E. V. Prochownik, J. S. Lazo and I. Bahar, J. Med. Chem., 2009, 52, 1247–1250.
10. S. J. Metallo, Curr. Opin. Chem. Biol., 2010, 14, 481–488.
11. V. Receveur-Brechot, J. M. Bourhis, V. N. Uversky, B. Canard and S. Longhi, Proteins, 2006, 62, 24–45.
12. M. Fuxreiter, I. Simon, P. Friedrich and P. Tompa, J. Mol. Biol., 2004, 338, 1015–1026.
13. C. J. Tsai, B. Ma, Y. Y. Sham, S. Kumar and R. Nussinov, Proteins, 2001, 44, 418–427.
14. D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796.
15. P. Csermely, R. Palotai and R. Nussinov, Trends Biochem. Sci., 2010, 35, 539–546.
16. G. G. Hammes, Y. C. Chang and T. G. Oas, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13737–13741.
17. S. G. Sivakolundu, D. Bashford and R. W. Kriwacki, J. Mol. Biol., 2005, 353, 1118–1128.
18. M. Kjaergaard, K. Teilum and F. M. Poulsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12535–12540.
19. J. Song, L. W. Guo, H. Muradov, N. O. Artemyev, A. E. Ruoho and J. L. Markley, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1505–1510.
20. H. X. Zhou, Biophys. J., 2010, 98, L15–L17.
21. J. H. Chen, J. Am. Chem. Soc., 2009, 131, 2088–2089.
22. P. E. Wright and H. J. Dyson, Curr. Opin. Struct. Biol., 2009, 19, 31–38.
23. K. Sugase, H. J. Dyson and P. E. Wright, Nature, 2007, 447, 1021–1025.
24. R. Narayanan, O. K. Ganesh, A. S. Edison and S. J. Hagen, J. Am. Chem. Soc., 2008, 130, 11477–11485.
25. A. Bachmann, D. Wildemann, F. Praetorius, G. Fischer and T. Kiefhaber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3952–3957.
26. A. G. Turjanski, J. S. Gutkind, R. B. Best and G. Hummer, PLoS Comput. Biol., 2008, 4, e1000060.
27. Q. Lu, H. P. Lu and J. Wang, Phys. Rev. Lett., 2007, 98, 128105.
28. G. M. Verkhivker, D. Bouzida, D. K. Gehlhaar, P. A. Rejto, S. T. Freer and P. W. Rose, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5148–5153.
29. D. Ganguly and J. Chen, Proteins: Struct., Funct., Bioinf., 2011, 79, 1251–1266.
30. J. Wang, Y. Wang, X. Chu, S. J. Hagen, W. Han and E. Wang, PLoS Comput. Biol., 2011, 7, e1001118.
31. T. Zor, B. M. Mayr, H. J. Dyson, M. R. Montminy and P. E. Wright, J. Biol. Chem., 2002, 277, 42241–42248.
32. E. A. Bienkiewicz, J. N. Adkins and K. J. Lumb, Biochemistry, 2002, 41, 752–759.
33. K. I. Okazaki and S. Takada, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 11182–11187.
34. C. J. Oldfield, J. Meng, J. Y. Yang, M. Q. Yang, V. N. Uversky and A. K. Dunker, BMC Genomics, 2008, 9(suppl 1), S1.
35. A. K. Dunker, M. S. Cortese, P. Romero, L. M. Iakoucheva and V. N. Uversky, FEBS J., 2005, 272, 5129–5148.
36. S. J. Demarest, S. Deechongkit, H. J. Dyson, R. M. Evans and P. E. Wright, Protein Sci., 2004, 13, 203–210.
37. M. O. Ebert, S. H. Bae, H. J. Dyson and P. E. Wright, Biochemistry, 2008, 47, 1299–1308.
38. C. W. Lee, M. A. Martinez-Yamout, H. J. Dyson and P. E. Wright, Biochemistry, 2010, 49, 9964–9971.
39. S. J. Demarest, M. Martinez-Yamout, J. Chung, H. W. Chen, W. Xu, H. J. Dyson, R. M. Evans and P. E. Wright, Nature, 2002, 415, 549–553.
40. L. Waters, B. Yue, V. Veverka, P. Renshaw, J. Bramham, S. Matsuda, T. Frenkiel, G. Kelly, F. Muskett, M. Carr and D. M. Heery, J. Biol. Chem., 2006, 281, 14787–14795.
41. B. Y. Qin, C. Liu, H. Srinath, S. S. Lam, J. J. Correia, R. Derynck and K. Lin, Structure, 2005, 13, 1269–1277.
42. C. H. Lin, B. J. Hare, G. Wagner, S. C. Harrison, T. Maniatis and E. Fraenkel, Mol. Cell, 2001, 8, 581–590.
43. P. G. Wolynes, Q. Rev. Biophys., 2005, 38, 405–410.
44. R. D. Hills and C. L. Brooks, Int. J. Mol. Sci., 2009, 10, 889–905.
45. C. J. Tsai, B. Y. Ma and R. Nussinov, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9970–9972.
46. Y. Levy, P. G. Wolynes and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 511–516.
47. A. K. Dunker, J. D. Lawson, C. J. Brown, R. M. Williams, P. Romero, J. S. Oh, C. J. Oldfield, A. M. Campen, C. R. Ratliff, K. W. Hipps, J. Ausio, M. S. Nissen, R. Reeves, C. H. Kang, C. R. Kissinger, R. W. Bailey, M. D. Griswold, M. Chiu, E. C. Garner and Z. Obradovic, J. Mol. Graphics Modell., 2001, 19, 26–59.
48. B. Meszaros, P. Tompa, I. Simon and Z. Dosztanyi, J. Mol. Biol., 2007, 372, 549–561.
49. J. Karanicolas and C. L. Brooks, Protein Sci., 2002, 11, 2351–2361.
50. J. Karanicolas and C. L. Brooks, J. Mol. Biol., 2003, 334, 309–325.
51. S. Miyazawa and R. L. Jernigan, J. Mol. Biol., 1996, 256, 623–644.
52. J. Karanicolas and C. L. Brooks, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3954–3959.
53. R. D. Hills and C. L. Brooks, J. Mol. Biol., 2008, 382, 485–495.
54. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217.
55. B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614.
56. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
57. Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151.
58. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
59. C. Chothia, M. Levitt and D. Richardson, J. Mol. Biol., 1981, 145, 215–250.
60. T. R. Keppel, B. A. Howard and D. D. Weis, Biochemistry, (submitted).
61. S. S. Cho, Y. Levy and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 586–591.
62. W. Zhang, D. Ganguly and J. Chen, PLoS Comput. Biol., 2011 (to be submitted).
63. R. D. Hills and C. L. Brooks, Biophys. J., 2008, 95, L57–L59.
64. J. N. Onuchic, Z. LutheySchulten and P. G. Wolynes, Annu. Rev. Phys. Chem., 1997, 48, 545–600.
65. A. Caflisch, Curr. Opin. Struct. Biol., 2006, 16, 71–78.
66. D. Gfeller, P. De Los Rios, A. Caflisch and F. Rao, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1817–1822.
67. S. Muff and A. Caflisch, Proteins, 2008, 70, 1185–1195.
68. G. R. Bowman, K. A. Beauchamp, G. Boxer and V. S. Pande, J. Chem. Phys., 2009, 131, 124101.
69. G. R. Bowman and V. S. Pande, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10890–10895.
70. V. A. Voelz, V. R. Singh, W. J. Wedemeyer, L. J. Lapidus and V. S. Pande, J. Am. Chem. Soc., 2010, 132, 4702–4709.
71. M. Andrec, A. K. Felts, E. Gallicchio and R. M. Levy, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6801–6806.
72. F. Rao and A. Caflisch, J. Mol. Biol., 2004, 342, 299–306.
73. B. Ma and R. Nussinov, Curr. Opin. Chem. Biol., 2010, 14, 652–659.
74. P. E. Wright and H. J. Dyson, J. Mol. Biol., 1999, 293, 321–331.
75. V. J. Hilser and E. B. Thompson, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8311–8315.
76. B. A. Shoemaker, J. J. Portman and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8868–8873.
77. E. Trizac, Y. Levy and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2746–2750.
78. X. L. Wang, A. Vitalis, M. A. Wyczalkowski and R. V. Pappu, Proteins, 2006, 63, 297–311.
79. H. T. Tran, A. Mao and R. V. Pappu, J. Am. Chem. Soc., 2008, 130, 7380–7392.
80. A. H. Mao, S. L. Crick, A. Vitalis, C. L. Chicoine and R. V. Pappu, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8183–8188.
81. Y. Huang and Z. Liu, J. Mol. Biol., 2009, 393, 1143–1159.
82. J. Kubelka, J. Hofrichter and W. A. Eaton, Curr. Opin. Struct. Biol., 2004, 14, 76–88.
83. Y. Levy, J. N. Onuchic and P. G. Wolynes, J. Am. Chem. Soc., 2007, 129, 738–739.
84. D. Vuzman and Y. Levy, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21004–21009.
85. E. Shakhnovich, Chem. Rev., 2006, 106, 1559–1588.
86. Z. Zhang and H. S. Chan, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2920–2925.
87. Y. Huang and Z. Liu, PLoS One, 2010, 5, e15375.
88. J. A. Marsh and J. D. Forman-Kay, Biophys. J., 2010, 98, 2383–2390.
89. A. Azia and Y. Levy, J. Mol. Biol., 2009, 393, 527–542.
90. P. Weinkam, E. V. Pletneva, H. B. Gray, J. R. Winkler and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1796–1801.
91. C. Clementi, Curr. Opin. Struct. Biol., 2008, 18, 10–15.
92. D. Eliezer, Curr. Opin. Struct. Biol., 2009, 19, 23–30.
93. H. J. Dyson and P. E. Wright, Chem. Rev., 2004, 104, 3607–3622.
94. D. Ganguly and J. Chen, J. Mol. Biol., 2009, 390, 467–477.
95. D. Ganguly and J. H. Chen, J. Am. Chem. Soc., 2009, 131, 5214–5223.
96. A. Vitalis and R. V. Pappu, J. Comput. Chem., 2009, 30, 673–699.

---

Footnotes

† Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins; Guest Editor: M. Madan Babu.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c1mb05156c

---