Integrated computational model of cell cycle and checkpoint reveals different essential roles of Aurora-A and Plk1 in mitotic entry

Abstract

Understanding the regulation of mitotic entry is one of the most important goals of modern cell biology, and computational modeling of mitotic entry has been a subject of several recent studies. However, there are still many regulation mechanisms that remain poorly characterized. Two crucial aspects are how mitotic entry is controlled by its upstream regulators Aurora-A and Plk1, and how mitotic entry is coordinated with other biological events, especially G2/M checkpoint. In this context, we reconstructed a comprehensive computational model that integrates the mitotic entry network and the G2/M checkpoint system. Computational simulation of this model and subsequent experimental verification revealed that Aurora-A and Plk1 are redundant to the activation of cyclin B/Cdk1 during normal mitotic entry, but become especially important for cyclin B/Cdk1 activation during G2/M checkpoint recovery. Further analysis indicated that, in response to DNA damage, Chk1-mediated network rewiring makes cyclin B/Cdk1 more sensitive to the down-regulation of Aurora-A and Plk1. In addition, we demonstrated that concurrently targeting Aurora-A and Plk1 during G2/M checkpoint recovery achieves a synergistic effect, which suggests the combinational use of Aurora-A and Plk1 inhibitors after chemotherapy or radiotherapy. Thus, the results presented here provide novel insights into the regulation mechanism of mitotic entry and have potential value in cancer therapy.

---

Introduction

Mitotic entry is one of the most important events in eukaryotic cell cycle, and understanding its regulation mechanism is an immediate goal of modern cell biology.¹ Currently, it has been widely accepted that mitotic entry is driven by a regulatory network comprising cyclin B/Cdk1, Cdc25, and Wee1.² Mathematical models describing the cyclin B/Cdk1-Cdc25-Wee1 network have been well established by Tyson, Novák, Ferrell, and others,^3–6 which quantitatively revealed that the irreversible mitotic entry is strictly controlled through the positive feedbacks between cyclin B/Cdk1 and Cdc25, and the double-negative feedbacks between cyclin B/Cdk1 and Wee1.

Recently, the research focus has shifted to a fundamental question, namely, what and how to regulate these feedback loops.² A few studies have demonstrated that Polo-like kinase 1 (Plk1) phosphorylates and activates Cdc25, and phosphorylates and inactivates Wee1.^7,8 Seki et al.⁹ and Macůrek et al.¹⁰ independently reported that the initial activation of Plk1 during mitotic entry is mediated cooperatively by Aurora-A and Bora. Besides, Aurora-A also directly phosphorylates and promotes the activation of Cdc25.¹¹ These suggest that Aurora-A and Plk1 participate in the positive regulation of mitotic entry. Furthermore, the cyclin B/Cdk1-Cdc25-Wee1 network is also controlled by G2/M checkpoint regulatory network.¹² Upon DNA damage in G2, Chk1-mediated phosphorylation induces Cdc25 sequestration with 14-3-3 proteins, with the consequent inhibition of mitotic entry.^13,14 After the completion of DNA repair, cells regain the ability to enter mitosis (i.e.G2/M checkpoint recovery), which involves Plk1-mediated phosphorylation and after degradation of Claspin.¹⁵

Despite these increased understanding of the regulation of mitotic entry, there are still many contrary phenomena difficult to interpret. One of the most critical aspects is that although it has been shown that Aurora-A and Plk1 participate in the regulation of mitotic entry,^8,11 further analyses indicated that inhibition of either Aurora-A or Plk1 failed to prevent mitotic entry,¹⁶ which disagrees with our intuition. In another aspect, little is known about the coordination between mitotic entry and G2/M checkpoint in the context of the full regulation networks.¹⁷ To address these questions, there needs to be an in-depth understanding of the regulatory network of mitotic entry at the systems level, which, however, is challenged by the presence of multiple feedback and feed-forward loops. Mathematical modeling and simulations have been demonstrated to be a powerful tool to elucidate the dynamic behaviors of cellular regulatory networks.^18,19 To our knowledge, however, such a quantitative and systematic study of mitotic entry and G2/M checkpoint has not been fully described.

In addition, our previous studies and others have revealed that many components of mitotic entry network, especially Aurora-A and Plk1, are aberrantly regulated in human cancer cells and thus have been regarded as important therapeutic targets for cancer treatment.^20–23 In spite of that, several inhibitors against these targets do not show significant therapeutic efficiency as expected.²⁴ One of the most important reasons seems to be due to the robustness of the regulatory network of mitotic entry.¹² Thus identifying an effective strategy, especially synergistic drug combination,²⁵ to control the abnormal mitotic entry in malignant human cells is a priority for biomedical research. Using computational model of cellular regulatory network to identify an optimal drug combination is increasingly regarded as a potentially more productive strategy.^18,26,27

Taking all these facts together, we here investigate the regulation of mitotic entry by combination of experimental measurement with the development of an integrated computational model that incorporates the cyclin B/Cdk1-Cdc25-Wee1 network and its upstream regulatory network consisting of Aurora-A, Plk1, Chk1 etc. Our current study focuses not only on normal mitotic entry (i.e. unperturbed by G2/M checkpoint), but also on G2/M checkpoint recovery (i.e. mitotic re-entry after G2/M checkpoint arrest). The dynamic properties of the reconstructed computational model are then systematically characterized. The simulation results and experimental verifications reveal some novel insights, particularly the different essential roles performed by Aurora-A and Plk1 in normal mitotic entry and in G2/M checkpoint recovery. Finally, a synergistic drug combination targeting the abnormal regulatory network of mitotic entry is identified, which has potential value for future anticancer therapy.

Results

Reconstruction of the computational model of mitotic entry and checkpoint recovery

In this study, the computational model scope is defined as the cyclin B/Cdk1-Cdc25-Wee1 network and its upstream regulatory network, which involves normal mitotic entry, G2/M checkpoint arrest and recovery. To obtain a complete and correct network representation, both the information obtained from public databases KEGG²⁸ and Reactome,²⁹ and the information retrieved from the literature was used for the reconstruction of the computational model. A schematic representation showing individual molecular species and their biochemical interactions is presented in Fig. 1. In order to characterize the network dynamics, these biochemical interactions were formulated as a set of ordinary differential equations (ODE) according to the law of mass action (full list in ESI,† Table S1). A brief description of these interactions will be given below; and detailed information including initial values of species, model parameters, and biological evidence can be found in the ESI,† Table S1.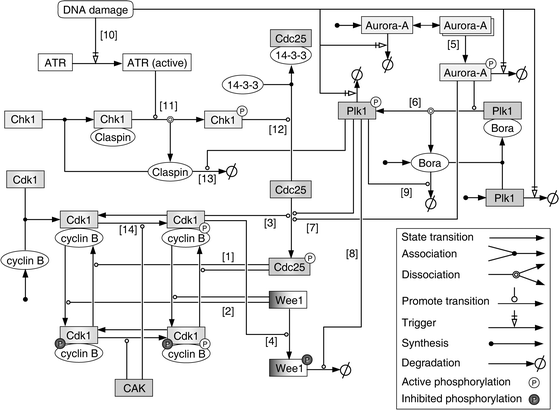

Fig. 1 A schematic representation showing the biochemical interactions of individual molecular species in the computational model. The standard Systems Biology Graphical Notation (SBGN) is used for ease of interpretation. The model involves the cyclin B/Cdk1-Cdc25-Wee1 network, its upstream regulators Aurora-A and Plk1, and signaling pathways related to G2/M checkpoint arrest and recovery. Note: Aurora-A can directly phosphorylate Plk1 without Bora but with a very low reaction rate, which is not shown here for concision.

The cyclin B/Cdk1-Cdc25-Wee1 network in our model is similar to the models of Tyson-Novák^3,4 and that of Ferrell-Pomerening.^5,6 The key regulator of mitotic entry is the cyclin B/Cdk1 complex, whose activity is promoted by Cdc25 phosphatases (see [1] in Fig. 1) and is restrained by kinase Wee1¹ (see [2] in Fig. 1). Following activation, cyclin B/Cdk1 will promote the phosphorylation of Cdc25 and Wee1³⁰ (see [3] and [4] in Fig. 1). Consistent with previous studies, the synthesis of cyclin B and the degradation of Wee1 during mitotic entry were considered in our model, whereas the total amount of Cdk1 and Cdc25 was assumed constant.^3,31 And four different phosphorylation states of cyclin B/Cdk1³ were also modeled here (Fig. 1).

Most importantly, our model incorporates the upstream regulators Aurora-A, Plk1, Bora, and the signaling pathways related to G2/M checkpoint arrest and recovery (Fig. 1), which have not been fully considered in previous computational models. In the case of Aurora-A and Plk1, we considered the amount of protein molecules begins to rise during G2 and peaks in M phase.⁹ The kinase activity of Aurora-A depends on its autophosphorylation,³² therefore, we included dimmer formation reaction for its activation (see [5] in Fig. 1). Activated Aurora-A will phosphorylate and promote the activation of Plk1, which is greatly enhanced by Bora^9,10 (see [6] in Fig. 1). We considered this effect by using different parameter values for reactions with or without Bora. Both Aurora-A and Plk1 phosphorylate Cdc25 and thereby stimulate its phosphatase activity¹⁶ (see [7] in Fig. 1). Plk1-mediated phosphorylation also facilitates the degradation of Wee1 and Bora^33,34 (see [8] and [9] in Fig. 1).

In the case of G2/M checkpoint arrest and recovery, our model describes the following mechanisms: in response to DNA damage, the activity of ATR kinase is triggered (see [10] in Fig. 1), which will then phosphorylate and activate checkpoint kinase Chk1 in the assistance of Claspin^35,36 (see [11] in Fig. 1). Once activated, Chk1 will inhibit the activity of Cdc25 by promoting its association with decoy protein 14-3-3¹³ (see [12] in Fig. 1). After the completion of DNA repair, G2/M checkpoint recovery is initiated with the termination of ATR signal and the Plk1-mediated degradation of Claspin^37,38 (see [13] in Fig. 1).

Model parameter optimization using ensemble modeling

Some parameter values in our computational model were directly obtained from preceding studies (see the footnote of Table S1 in ESI†), and others without experimentally determined values were estimated by fitting model outputs to experimental quantitative data, which has already become a regular solution.^39–41 The experimental data comprises the measurement of eight proteins at different time points after the release of human Hela cells from G1/S arrest, which was acquired from previously published dataset.^9,42,43 Hela cells were used largely for their well-known cell cycle profiles. The parameter estimation was performed using an optimal algorithm developed in this study, which is named HQEM (hybrid quasi ensemble modeling). Ensemble modeling (EM) approach will construct an ensemble of models with variant network structures⁴⁴ or with different sets of parameter values,⁴⁵ all of which are capable of reproducing experiment observations. EM with variations in parameter values was chosen here because it has been widely adopted to deal with the parametric uncertainty that prohibits the reliable estimation of precise parameter value.^45,46 Compared with general EM method, our HQEM algorithm has two major improvements. Firstly, scrambled Halton sequence, which has global and uniform sampling ability and has no dimensional limitation,⁴⁷ is employed instead of random numbers that have been used in EM. Secondly, the sampling points generated by scrambled Halton sequence are further subjected to a trust-region reflective optimization, which owns the property of fast local convergence speed in solving large-scale nonlinear problems.⁴⁸ The algorithm of HQEM is detailed in the section of “Materials and methods” and is illustrated in Fig. S1 in ESI†.

The computational results indicate that HQEM exhibits superior performance in accuracy. The parameter sets obtained by EM nearly always have the model produce undesired simulation results that are far away from the experimental data (Fig. S2 in ESI†). Conversely, using HQEM, we obtained an ensemble of 114 parameter sets (Table S2), all of which have relative errors below 1.5% and thus guarantee the absolute consistency of our model simulations with experimental observations (Fig. 2). Consequently, by sampling the parameter space more uniformly and globally, HQEM can construct an ensemble model that more accurately describes the experimental observations.

Fig. 2 Ensemble model simulations and experimental data for the time courses of the amount of active Aurora-A (pT288), active Plk1 (pT210), Bora, inactive cyclin B/Cdk1 (pY15), Claspin, Wee1 during normal mitotic entry; inactive cyclin B/Cdk1 (pY15) during checkpoint recovery; and active Plk1 (pT210) when Bora is depleted. The ensemble simulation results based on the obtained 114 parameter sets, which have errors below 1.5% of the average error of all the sampling parameter sets, are shown for each protein. In each panel, the fit having the lowest error is indicated by a black line, and slightly less good fits (113 sets) are indicated by gray lines.

In addition, an identifiability analysis, recently proposed by Balsa-Canto et al.,⁴⁹ was conducted to evaluate the quality of our parameter estimation (Fig. S3 in ESI†). It can be seen that the computational model is insensitive to changes in the value of some parameters, thus using HQEM method can ensure that the observed model outputs are not due to specific parameter values and thereby reduces the ambiguity of model predictions. In the following studies, all of the 114 ensemble parameter sets are used for the model simulations, and it has been found that our model predictions given by using the ensemble parameter sets are closely coincident (see Fig. S4 in ESI† for a detailed presentation of ensemble simulation results). Therefore, it can be concluded that our calibrated ensemble model is capable of reproducing quantitative features of G2/M transition networks and is suitable for further simulations. For concise presentation, only the representative simulation results are given below.

Aurora-A and Plk1 are redundant for Cdk1 activation in normal mitotic entry

Using the calibrated computational model, we first analyzed the activation process of Aurora-A and Plk1 during mitotic entry. In Fig. 3A, we plot the amount of activated Aurora-A at 11 h as a function of the different initial values of Aurora-A. The 11 h time point was used as a reference here because it corresponds to the M phase of Hela cells after double thymidine release. It can be seen that for small amounts of Aurora-A (15% or less) there is very little activity of Aurora-A, but larger amounts (35% or more) will induce considerable activated Aurora-A (Fig. 3A). This is largely due to that the autophosphorylation of Aurora-A provides its own positive feedback loop (Fig. 3B). In addition, since Aurora-A directly phosphorylates Plk1, the effect of the total amount of Aurora-A on Plk1 activity was also analyzed, and similar behavior can be observed (Fig. 3A). On the other hand, the protein expression levels of Aurora-A and Plk1 are also highly controlled during mitotic entry (Fig. 3C). Therefore, these two aspects (i.e. the positive-feedback regulation and the protein expression pattern) guarantee that the activities of Aurora-A and Plk1 are stimulated at the desired stage of mitotic entry, which is believed to be important to regulate the activity of cyclin B/Cdk1.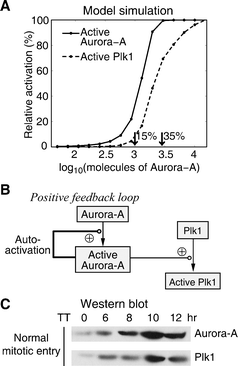

Fig. 3 Aurora-A and Plk1 activation during normal mitotic entry. (A) Dose-response curves revealing the influence of different amount of Aurora-A to its own activation and to the activation of Plk1. (B) The auto-activation of Aurora-A forms a positive feedback loop. (C) Hela cells were synchronized and samples were collected at the indicated times and processed for immunoblot analysis with antibodies to Aurora-A and Plk1.

Subsequently, the effect of altering the total amount of Aurora-A and Plk1 on the activity of cyclin B/Cdk1 during normal mitotic entry was examined. Only the simulation results before 11 h time point are considered here since our primary interest is in studying the control of mitotic entry. From Fig. 4A, it can be seen that when the amount of Aurora-A was reduced to half (50%), the percentage of activated cyclin B/Cdk1 at 11 h was decreased about 9% (i.e. from 78% in control to 69%). Furthermore, similar result was obtained from the analysis of the influence of altering Plk1 concentration on the activity of cyclin B/Cdk1 (Fig. 4B). Besides, the ensemble simulations gave the coincident model predictions (shown in Fig. S4B,C in ESI†) and thus confirmed that our results did not depend on the values of individual parameters. Therefore, it can be concluded that Aurora-A and Plk1 are redundant for the activation of cyclin B/Cdk1 during normal mitotic entry.

Fig. 4 Simulations of normal mitotic entry, G2 checkpoint arrest and recovery. (A–D) Simulated time courses of activated cyclin B/Cdk1 in response to different amount of Aurora-A and Plk1 reveal the redundant functions of (A) Aurora-A and (B) Plk1 during normal mitotic entry; and the crucial functions of (C) Aurora-A and (D) Plk1 during G2/M checkpoint recovery. (E, F) Inappropriate hyperactive Aurora-A promotes (E) the abnormal deactivation of Chk1 and (F) the abnormal activation of cyclin B/Cdk1 even in the presence of DNA-damage signaling. The Aurora-A and Plk1 percentages are related to their total amount under normal circumstances.

Essential roles of Aurora-A and Plk1 for Cdk1 activation in checkpoint recovery

Next, we were particularly interested in investigating how different levels of Aurora-A and Plk1 affect the activity of cyclin B/Cdk1 during G2/M checkpoint recovery. To mimic checkpoint arrest and recovery, the amount of ATR was set to the maximum level and kept for one hour, and terminated afterwards. Our results clearly show that when the concentration of Aurora-A is reduced to half (50%), activated cyclin B/Cdk1 at 11 h is dramatically decreased about 39% (i.e. from 75% in control to 36%) (Fig. 4C). On the contrary, in normal mitotic entry, the impact on the amount of activated cyclin B/Cdk1 is only about 9% (Fig. 4A). In addition, the activity of cyclin B/Cdk1 is also crucially dependent on Plk1 during G2/M checkpoint recovery (Fig. 4D), compared with that in normal mitotic entry (Fig. 4B). The decrease of Plk1 amount to 10% resulted in the reduction of activated cyclin B/Cdk1 about 39% (i.e. from 75% in control to 36%) (Fig. 4D). In normal mitotic entry, however, this impact is only about 7% (i.e. from 78% in control to 71%) (Fig. 4B). In conclusion, the simulation results demonstrate that Aurora-A and Plk1 play more important roles in ensuring the activation of cyclin B/Cdk1 in a reasonable time during G2/M checkpoint recovery, which is further confirmed by our experiments (see the subsection of ‘Experimental validation of simulation results’ below for a detailed description).

Considering the significance of Aurora-A and Plk1 to G2/M checkpoint recovery, further simulations were performed to examine the impact caused by the abnormal hyperactivity of Aurora-A and Plk1 during DNA damage-induced G2/M checkpoint arrest. The simulations show that an excessive amount of Aurora-A does not affect the onset of DNA-damage response, since the same time course of Chk1 activation is observed despite the changes in Aurora-A concentrations (Fig. 4E). However, it can be seen that more amount of Aurora-A significantly shortens the duration of activated Chk1 signal (Fig. 4E) and allows the abnormal activation of cyclin B/Cdk1 even in the presence of DNA damage (Fig. 4F). An important function of G2/M checkpoint is to assess DNA damage prior to mitosis.¹² Whereas, according to our simulations, the elevated activation of Aurora-A and Plk1, which is often observed in cancer cells,^20,23 will override G2/M checkpoint arrest and thus enable cancer cells to proliferate abnormally.

Analysis of network regulation mechanisms

In order to understand why alterations of Aurora-A and Plk1 largely affect G2/M checkpoint arrest and recovery, additional simulations were carried out. Firstly, it has been shown that cyclin B/Cdk1 activation can be observed even when Aurora-A and Plk1 is inhibited during normal mitotic entry (Fig. 4A and B). The main reason lies in that cyclin B/Cdk1 can be partially phosphorylated and activated by Cdk-activating kinase (CAK)⁵⁰ (see [14] in Fig. 1). And in normal mitotic entry, there is plenty of freedom form of Cdc25. Thus, the positive feedback loop “cyclin B/Cdk1 → Cdc25 → cyclin B/Cdk1” itself can promote the complete activation of cyclin B/Cdk1 without Aurora-A and Plk1 (Fig. 5A).

Fig. 5 Analysis of the network regulation mechanisms. (A) Simulation of the response of activated cyclin B/Cdk1 by altering the amount of Cdc25 during normal mitotic entry. In this case, the total amount of Aurora-A was reduced to 5% in order to neglect its function. (B) Chk1 modulates the strength of positive/double-negative feedback loops (i.e. by inhibiting Cdc25), and thereby increases the activation threshold of cyclin B/Cdk1 for mitotic entry. (C) Chk1 also incorporates into a feed-forward loop for cyclin B/Cdk1 activation, and thus modulates the Aurora-A-dependent cyclin B/Cdk1 activation during G2/M checkpoint recovery. (D) Dose–response analysis reveals that the sensitivity of cyclin B/Cdk1 activation to changes in the amount of Aurora-A is up-regulated in response to Chk1. The calculation of the sensitivity matrix is defined in the section of “Materials and methods”. (E) Plk1 incorporates into a feed-forward loops that modulates the Aurora-A-dependent cyclin B/Cdk1 activation during G2/M checkpoint recovery.

In response to DNA-damage signal, the activated Chk1 will modulate the strength of the positive/double-negative feedback loops by magnifying the sequestration effect of 14-3-3 on Cdc25 (Fig. 1), which brings the activation threshold of cyclin B/Cdk1 higher than the in vivo concentration³¹ of cyclin B, thereby keeps the activity of cyclin B/Cdk1 in an inactive state (Fig. 5B). Besides, by participating in a feed-forward loop (Fig. 5C), Chk1 also up-regulates the threshold of Aurora-A and Plk1 that will directly influence the cyclin B/Cdk1 activation during G2/M checkpoint recovery (Fig. 5C). Since the activity of Chk1 will not immediately return to baseline, the proper activities of Aurora-A and Plk1 are required to shift the activation threshold of cyclin B/Cdk1 back to normal level during G2/M checkpoint recovery (see Fig. S5 in ESI†). This is also reflected in that the increase of the sensitivity of cyclin B/Cdk1 to the alteration of Aurora-A and Plk1 is proportional to the activity of Chk1 (Fig. 5D). In this scenario, Aurora-A and Plk1 are more required in G2/M checkpoint recovery than in normal mitotic entry to promote the appropriate activation of cyclin B/Cdk1.

Furthermore, as a downstream regulator, Plk1 incorporates into several coherent feed-forward loops between Aurora-A and cyclin B/Cdk1, for instance, “Aurora-A → Plk1 → Cdc25 → cyclin B/Cdk1” (Fig. 5E). Thus, additional analysis on the function of Plk1 was performed. It was found that Plk1 significantly increases the maximum activity of cyclin B/Cdk1 that can be achieved under the same amount of Aurora-A (Fig. 5E). And the alteration of cyclin B/Cdk1 activity is very sensitive to the initial increase of the amount of Plk1. It can be seen that when the total amount of Plk1 increase from 0% to 25%, there is an obvious activation of cyclin B/Cdk1 (Fig. 5E). Therefore, by forming feed-forward loops, Plk1 enlarges and expands the role of Aurora-A in promoting cyclin B/Cdk1 activation.

Synergistic effect of combinational inhibition of Aurora-A and Plk1 in checkpoint recovery

Aurora-A and Plk1 have recently become the favorite therapeutic targets for cancer treatment,^20,51 and many chemical inhibitors are under development.¹⁶ But due to the complexity of the regulatory networks, agent inhibiting one single target often has a limited effect.^18,24 Combination therapies by simultaneously inhibiting multiple targets are considered as a good choice to tackle this problem.^25,26,52 Considering that Aurora-A positively regulates Plk1 and both of them control the activity of cyclin B/Cdk1, we speculate that a combination of Aurora-A inhibitor with Plk1 inhibitor will produce a synergistic effect. This is because many known synergistic drug combinations share the similar molecular mechanism (i.e. different targets of related pathways that regulate the same molecule) as thoroughly analyzed by Jia et al.²⁵

Previous studies have shown that network simulation provides a cheap and rapid approach to testing the possible synergistic effect of combinational use of agents inhibiting different targets.^26,53 Accordingly, we further attempt to address this issue by applying a network perturbation to our computational model (see reactions r54-r57 of Table S1 in ESI†). The synergistic effect of a drug combination is typically determined relative to the expectation that is calculated from the single agent activities based on standard non-interaction reference models.⁵³ One of such models commonly used is Bliss independence model, which is theoretically appropriate for agents acting on different targets.^26,53,54 Here, a comparison between simulated dose-response surface and Bliss additive surface at varying inhibitor concentrations²⁶ was used to identify if there is a possible synergistic effect between Aurora-A and Plk1 inhibitors.

Interestingly, our computational simulations gave a striking result. During G2/M checkpoint recovery, the combinational inhibition of Aurora-A and Plk1 produces strong synergistic effect in inhibiting the activity of cyclin B/Cdk1 (Fig. 6), which supports our previous hypothesis. The synergy contour, which was obtained by subtracting the inhibition in Bliss additive surface from that in simulated dose-response surface, highlights the region of synergy where extra inhibition exceeds 30% (Fig. 6, bottom right panel). On the contrary, in normal mitotic entry, no significant extra inhibition can be observed when Aurora-A and Plk1 are targeted at the same time (Fig. S6 in ESI†). This is understandable since the above simulations have already demonstrated that Aurora-A and Plk1 are dispensable for cyclin B/Cdk1 activation during normal mitotic entry. Therefore, a potential new synergistic drug combination, in which Aurora-A and Plk1 are simultaneously targeted during G2/M checkpoint recovery, was revealed to efficiently control the abnormal mitotic entry network in human malignant cells.

Fig. 6 Response surface simulation of concurrently targeting Aurora-A and Plk1 during G2/M checkpoint recovery. The synergy contours, which is obtained by subtracting the inhibition in Bliss independence surface (i.e. additive reference model) from that in simulated dose-response surface, highlights the region of synergy where extra inhibition exceeds 30% (bottom right panel). The simulations of dose-response surface and Bliss additive surface at varying inhibitor concentrations were carried out according to Fitzgerald et al.²⁶ A checkerboard of 900 dose pairs was used here.

Experimental validation of simulation results

In order to validate our simulation results, further experiments were carried out. Hela cells were treated by Aurora-A inhibitor VX-680⁵⁵ (300 nM) and Plk1 inhibitor BI-2536⁴² (100 nM). These concentrations were chosen primarily because they fall into the concentration region that can produce synergistic effect as suggested by the computational simulations (Fig. 6). DNA-damage agent doxorubicin was used to induce G2/M checkpoint arrest, and caffeine was subsequently added to stimulate G2/M checkpoint recovery.¹⁰ The amount of inactivated Cdk1 (phosphorylated on Y15) was determined by immunoblotting at indicated time points. As expected, in normal mitotic entry, inhibition of Aurora-A and Plk1 either alone or in combination has minimal impact on the activation of cyclin B/Cdk1 (Fig. 7A). After a preceding treatment with doxorubicin and caffeine, inhibition of either Aurora-A or Plk1 alone moderately influences the activation of cyclin B/Cdk1 (Fig. 7A), confirming the importance of Aurora-A and Plk1 to the cyclin B/Cdk1 activation during G2/M checkpoint recovery (Fig. 4C and D). Further, cyclin B/Cdk1 activation is largely inhibited when both Aurora-A and Plk1 inhibitors are used after a preceding doxorubicin and caffeine treatment (Fig. 7A), which is in agreement with our simulation of drug combinations (Fig. 6).

Fig. 7 Experimental validation of simulation results. (A) Hela cells were synchronized to G1/S boundary by a double thymidine treatment (TT). Respective drugs, such as doxorubicin (dox), caffeine (caf), VX-680 (VX), and BI-2536 (BI), were added at corresponding time. Levels of certain proteins at indicated time points after double thymidine release were analyzed by Western blotting. Cdk1-pY15 represents the inactive Cdk1 phosphorylated on Tyr15. α-tubulin serves as a loading control. All studies were performed in triplicate with similar results. (B) Hela cells were treated as in (A), and the percentage of mitotic cells based on cell cycle distribution profile was plotted. n = 3 for each. (C) Hela cells were treated with different drugs as in (A), and the percentage of apoptotic and death cells was measured using Cell Counting Kit-8 assay. n = 3 for each.

Because the activity of cyclin B/Cdk1 determines mitotic entry, we further measured the proportion of mitotic cells to explore the distinct impacts brought by different drug perturbations. Again, inhibition of Aurora-A and Plk1 either alone or in combination during normal mitotic entry has minor effect on the rate of mitotic cells (Fig. 7B). The perturbations of either Aurora-A or Plk1 alone in G2/M checkpoint recovery indeed exert an apparent influence on the cell cycle profile (Fig. 7B). And the low mitotic index (27%) of cells at 12 h recovered from DNA-damage checkpoint arrest with VX-680 and BI-2536 treatment (Fig. 7B) confirms the synergistic effect predicted by our model simulations (Fig. 6).

In addition, several previous studies have provided evidences that if G2/M DNA-damage checkpoint is efficiently arrested long enough, cells may enter senescence or undergo apoptosis.¹ Our model simulations have shown that simultaneously inhibition of Aurora-A and Plk1 can produce synergistic effect and thus seriously delay G2/M checkpoint recovery, which is expected to induce more cell apoptosis and death. In order to test this hypothesis, we measured cell viability (i.e. the percentage of apoptosis and dead cells in population) after the drug treatments. The ultimate outcome has indicated that, when compared with those cells treated only with doxorubicin and VX-680, or with doxorubicin and BI-2536, the cells treated with doxorubicin, VX-680, and BI-2536 have shown a larger apoptotic/death fraction (Fig. 7C). Additionally, the combinational use of lower or higher levels of VX-680 and BI-2536 does not show obvious synergistic effect on induction of apoptosis (Fig. S7 in ESI†), which supports our simulation results (Fig. 6).

Discussion and conclusions

Several computational modeling of cell cycle have been carried out,^4,5,56,57 and an excellent review on this subject by Csikász-Nagy is available.¹⁷ Obviously, the current main challenge in this research area is to determine how cell cycle is coordinated with other biological events such as checkpoints.¹⁷ Thus, by integrating computational modeling with experimental studies, we investigate the regulation of the core mitotic entry network (i.e. cyclin B/Cdk1-Cdc25-Wee1) during not only the normal mitotic entry but also the G2/M checkpoint arrest and recovery. The systems level study here allows us gain insights into the dynamic properties of the complex regulatory network of mitotic entry, and the connections between the deregulation of mitotic entry and the development of cancer.

Our dynamic simulations and experimental verifications have characterized the perturbation effect of Aurora-A and Plk1 on cyclin B/Cdk1 activation in different cellular contexts. In normal mitotic entry, the influence of altering the amount of Aurora-A and Plk1 on cyclin B/Cdk1 activation is minor. The reasonable interpretation is that, in normal mitotic entry, the activation threshold of cyclin B/Cdk1 is lower than the in vivo concentration of cyclin B, and thus Aurora-A and Plk1 would be dispensable to the activation of cyclin B/Cdk1. On the contrary, in response to DNA damage, activated Chk1 will up-regulate this threshold to keep cyclin B/Cdk1 in its inactive state. And activated Chk1 also up-regulates the threshold of Aurora-A and Plk1 that will influence the cyclin B/Cdk1 activation. Thus, during G2/M checkpoint recovery, proper activities of Aurora-A and Plk1 are required to reduce the threshold to a normal level and thereby promote the activation of cyclin B/Cdk1. This rationalizes why interference of Aurora-A and Plk1 function during G2/M checkpoint recovery has significant impact on cyclin B/Cdk1 activation, but not during normal mitotic entry. On the other hand, by regulating the strength of positive/double-negative feedback and feed-forward loops, the upstream regulators (such as Aurora-A, Plk1, ATR, and Chk1) ensure the cyclin B/Cdk1-Cdc25-Wee1 network can produce appropriate outputs in response to different cellular signals (e.g. DNA-damage signal, proliferative signal). We propose that such a regulation mechanism might be general since many biological networks contain the same feedback and feed-forward architecture.^58,59

Most importantly, the simulation and experimental results have provided several useful suggestions on how to efficiently control the abnormal mitotic entry network. Firstly, it is shown that continual activation of Aurora-A and Plk1 affords the cancer cells the ability to override the G2/M checkpoint arrest and to proliferate continually even in the presence of DNA damage. Thus, the cancer cells that under the stress of DNA damage are addicted to Aurora-A and Plk1 for their survival, and such kinds of phenomena have been termed as ‘oncogene addiction’.^60,61 Consistently, we found that the preceding use of DNA-damage agent could turn Aurora-A and Plk1 into the crucial nodes of mitotic entry network, whose inhibition will result in a system failure. Therefore, it is proposed that the phenomenon of ‘oncogene addiction’ can be created by network perturbations with molecularly targeted agents, which implicates a new concept for future cancer treatment.

Secondly, simultaneous inhibition of Aurora-A and Plk1 during G2/M checkpoint recovery produces synergistic combination effect, which could not be observed in that during normal mitotic entry. This finding indicates that multi-targeted agents could produce distinct drug interactions in different cellular contexts, and thus highlights the necessity of using systems biology approaches to design optimal drug combination strategies, which has also been emphasized more recently by others.^25,62 Finally, the simulation and experiment results presented here suggest that further in vivo studies could be carried out to assess the potential clinical benefit of the combinational use of Aurora-A and Plk1 inhibitors after chemotherapy or radiotherapy for cancer treatment.

Materials and methods

Cell culture, synchronization and drug treatments

Human Hela cell line was obtained from the American Type Culture Collection (http://www.atcc.org). All cells were maintained in Dulbecco's modified Eagle's medium (DMEM) that was supplemented with 10% fetal calf serum (Invitrogen), penicillin (100 U ml⁻¹, Sigma), and streptomycin (100 μg ml⁻¹, Sigma). For synchronization at G1/S transition, Hela cells were treated twice with thymidine (2 mM, Sigma) for 18 h intermitted by 9 h release. Cells were subsequently washed and incubated in fresh medium to be released from the double thymidine block. To induce DNA damage in G2, pulse treatment of Hela cells with doxorubicin (0.5 μM, Sigma) was performed for 1 h at 5 h after the release from the thymidine block. Doxorubicin was then washed away and caffeine (5 mM, Sigma) was immediately added to terminate the DNA damage signaling and to allow mitotic entry. Where indicated, Aurora-A inhibitor VX-680 (300 nM, Dakang Pharm.) and Plk1 inhibitor BI-2536 (100 nM, Axon Medchem) were added at 6 h after the release from the thymidine block. Nocodazole (100 ng ml⁻¹, Sigma) was used to trap cells in mitosis. Cell cycle distribution was determined as described.^9,10

Sample preparation and western blotting

Hela cells were lysed at indicated time points with 50 μl RIPA ice-cold lysis buffer (50 mM Tris-HCl pH 7.5, 150 mM NaCl, 1% NP-40, 0.1% SDS) supplemented with protease inhibitor cocktail (Sigma) for 10 min. Lysate was centrifuged at 4 °C for 15 min at 14 000 rpm. Protein concentrations were measured using Bradford protein assay kit (Bio-Rad). 20 μl of each lysate was separated on 10% SDS-PAGE and transferred to PVDF (Millipore). The membranes were blocked with 5% BSA in TBS/T and stained with primary antibodies at a 1 : 1000 dilution overnight at 4 °C. Membranes were then probed with peroxidase conjugated secondary antibody at a 1 : 5000 dilution and visualized by enhanced chemiluminescence assay (Amersham) on a Kodak image station. Primary antibodies used for western blotting were anti-Cdk1-pY15 rabbit antibody (Abcam), anti-Aurora-A mouse antibody (Abcam), anti-Plk1 mouse antibody (Cell Signaling), and anti-α-tubulin rabbit antibody (Cell Signaling). Secondary antibodies used were peroxidase conjugated goat anti-rabbit antibody and goat anti-mouse antibody (ZSGB-BIO).

Analysis of cell viability using MTT assay

Hela cells were seeded in 96 well plates and cultured for 12 h in DMEM. Where indicated, doxorubicin (0.5 μM, Sigma), caffeine (5 mM, Sigma), VX-680 (300 nM, Dakang Pharm.), and BI-2536 (100 nM, Axon Medchem) were added in triplicate to the culture medium. The Hela cells were further cultured for 72 h. Cell viability was evaluated using Cell Counting Kit-8 (Dojindo Molecular Technologies). In brief, Hela cells plated in 96-well plates were incubated with CCK-8 reagents for 2 h at 37 °C. The extent of the reduction of WST-8 to formazan was quantified by measuring OD at 450 nm.

Computational model formulation and simulations

The implementation of the computational model, and all the numerical simulations were performed within Matlab (MathWorks, MA, USA, http:// www.mathworks.com). Ordinary differential equations were numerically solved by Sundials method.⁶³ The computational model is available in Systems Biology Markup Language (SBML) format and in Matlab SimBiology project format as Dataset S1 in ESI†.

Algorithm of HQEM

The algorithm of HQEM consists of two main steps. Firstly, a d-dimensional scrambled Halton sequence P is constructed to generate quasi-random numbers; d is the number of parameters that need to be estimated. Secondly, the generated random numbers are used as the initial value for a trust-region reflect optimization to find a set of optimum parameters p that will produces a local minimum of the objective function formulated as:
The expression g(p) is the model simulated values based on the parameter set p; g′ is the corresponding experimental measured values; ω is the weight that is used to normalize the contributions of each term to the objective function E(p); p_LB and p_UB are the lower and upper boundary parameter constrains.

The scrambled Halton sequence⁴⁷P is constructed according to:

P = {(ψ_m1(n), …, ψ_mr(n), …, ψ_md(n))^∞_n=1}

ψ_m(n) = σ_m(b₀)m⁻¹ + σ_m(b₁)m⁻² + σ_m(b₂)m⁻³ + … + σ_m(b_k)m^−k−1

where ψ_m(n) is the base-m radical inverse function for natural number n; m is a prime number, thus m_r (1 ≤ r ≤ d) represents d distinct prime numbers; b_l ∈ {0,1, …, m−1} for l = 0, 1, …, k; and σ_m is different permutation functions for corresponding bases m.

The trust-region reflective optimization⁴⁸ is performed from a starting point p₀ in a d-dimensional space. A simpler approximation function f is computed, which reasonably reflects the behavior of function E(p) in a neighborhood N around the point p₀ (i.e. trust region). Thus formulates the trust-region subproblem:

where s is a trial step; g is the gradient of E(p) at the current point p₀; H is the symmetric matrix of second derivatives; D is a diagonal scaling matrix; Δ is a positive scalar; and ‖…‖ is the 2-norm. The current point p₀ is updated to be (p₀ + s) if E(p₀ + s) < E(p₀); otherwise, the current point p₀ remains unchanged and the trust region N is shrunk and the trial step computation is repeated.

The HQEM algorithm was written in MatLab and designed to run in parallel. The source code of the algorithm is available in Dataset S2 in ESI†.

Sensitivity analysis

Sensitivity analysis was applied to examine the relative changes of protein concentrations x (i.e. activated cyclin B/Cdk1 at time 11 h) as a result of the relative changes of the protein concentrations y (i.e. Aurora-A and Plk):

s = (dx/x)/(dy/y)

where s corresponds to the normalized relative sensitivity of molecule x with respect to the perturbed total amount of molecule y. The sensitivity matrix displayed in Fig. 5D was calculated by simultaneously varying the total amount of Aurora-A and Chk1.

Acknowledgements

We are grateful for funding support from the National S & T Major Project of China (grant 2009ZX09501-001, 2009ZX09103-133; S.Y.Y.), and the National Natural Science Foundation of China (grant 20872100; S.Y.Y.).

References

1. M. Malumbres and M. Barbacid, Nat. Rev. Cancer, 2009, 9, 153–166.
2. A. Lindqvist, V. Rodríguez-Bravo and R. H. Medema, J. Cell Biol., 2009, 185, 193–202.
3. B. Novák and J. J. Tyson, J. Cell Sci., 1993, 106, 1153–1168.
4. B. Novák, J. J. Tyson, B. Gyorffy and A. Csikasz-Nagy, Nat. Cell Biol., 2007, 9, 724–728.
5. J. R. Pomerening, E. D. Sontag and J. E. Ferrell, Nat. Cell Biol., 2003, 5, 346–351.
6. J. R. Pomerening, S. Y. Kim and J. E. Ferrell, Cell, 2005, 122, 565–578.
7. T. Takaki, K. Trenz, V. Costanzo and M. Petronczki, Curr. Opin. Cell Biol., 2008, 20, 650–660.
8. V. Archambault and D. M. Glover, Nat. Rev. Mol. Cell Biol., 2009, 10, 265–275.
9. A. Seki, J. A. Coppinger, C.-Y. Jang, J. R. Yates and G. Fang, Science, 2008, 320, 1655–1658.
10. L. Macůrek, A. Lindqvist, D. Lim, M. A. Lampson, R. Klompmaker, R. Freire, C. Clouin, S. S. Taylor, M. B. Yaffe and R. H. Medema, Nature, 2008, 455, 119–123.
11. G. Vader and S. M. Lens, Biochim. Biophys. Acta, 2008, 1786, 60–72.
12. M. Lobrich and P. A. Jeggo, Nat. Rev. Cancer, 2007, 7, 861–869.
13. M. Donzelli and G. F. Draetta, EMBO Rep., 2003, 4, 671–677.
14. R. Boutros, V. Lobjois and B. Ducommun, Nat. Rev. Cancer, 2007, 7, 495–507.
15. I. Mamely, M. A. Vugt, V. A. Smits, J. I. Semple, B. Lemmens, A. Perrakis, R. H. Medema and R. Freire, Curr. Biol., 2006, 16, 1950–1955.
16. S. Taylor and J.-M. Peters, Curr. Opin. Cell Biol., 2008, 20, 77–84.
17. A. Csikasz-Nagy, Briefings Bioinf., 2009, 10, 424–434.
18. R. P. Araujo, L. A. Liotta and E. F. Petricoin, Nat. Rev. Drug Discovery, 2007, 6, 871–880.
19. J. Vera, J. Schultz, S. Ibrahim, Y. Raatz, O. Wolkenhauer and M. Kunz, Mol. BioSyst., 2010, 6, 264–273.
20. K. Strebhardt and A. Ullrich, Nat. Rev. Cancer, 2006, 6, 321–330.
21. X. Q. Deng, H. Y. Wang, Y. L. Zhao, M. L. Xiang, P. D. Jiang, Z. X. Cao, Y. Z. Zheng, S. D. Luo, L. T. Yu, Y. Q. Wei and S. Y. Yang, Chem. Biol. Drug Des., 2008, 71, 533–539.
22. H. Y. Wang, Z. X. Cao, L. L. Li, P. D. Jiang, Y. L. Zhao, S. D. Luo, L. Yang, Y. Q. Wei and S. Y. Yang, Bioorg. Med. Chem. Lett., 2008, 18, 4972–4977.
23. J. R. Pollard and M. Mortimore, J. Med. Chem., 2009, 52, 2629–2651.
24. S. Lapenna and A. Giordano, Nat. Rev. Drug Discovery, 2009, 8, 547–566.
25. J. Jia, F. Zhu, X. Ma, Z. W. Cao, Y. X. Li and Y. Z. Chen, Nat. Rev. Drug Discovery, 2009, 8, 111–128.
26. J. B. Fitzgerald, B. Schoeberl, U. B. Nielsen and P. K. Sorger, Nat. Chem. Biol., 2006, 2, 458–466.
27. B. Schoeberl, E. A. Pace, J. B. Fitzgerald, B. D. Harms, L. Xu, L. Nie, B. Linggi, A. Kalra, V. Paragas, R. Bukhalid, V. Grantcharova, N. Kohli, K. A. West, M. Leszczyniecka, M. J. Feldhaus, A. J. Kudla and U. B. Nielsen, Sci. Signaling, 2009, 2, ra31.
28. M. Kanehisa and S. Goto, Nucleic Acids Res., 2000, 28, 27–30.
29. G. Joshi-Tope, M. Gillespie, I. Vastrik, P. D'Eustachio, E. Schmidt, B. de Bono, B. Jassal, G. R. Gopinath, G. R. Wu, L. Matthews, S. Lewis, E. Birney and L. Stein, Nucleic Acids Res., 2004, 33, D428–D432.
30. H. Hochegger, S. Takeda and T. Hunt, Nat. Rev. Mol. Cell Biol., 2008, 9, 910–916.
31. T. Arooz, C. H. Yam, W. Y. Siu, A. Lau, K. K. Li and R. Y. Poon, Biochemistry, 2000, 39, 9494–9501.
32. M. G. Manfredi, J. A. Ecsedy, K. A. Meetze, S. K. Balani, O. Burenkova, W. Chen, K. M. Galvin, K. M. Hoar, J. J. Huck, P. J. LeRoy, E. T. Ray, T. B. Sells, B. Stringer, S. G. Stroud, T. J. Vos, G. S. Weatherhead, D. R. Wysong, M. Zhang, J. B. Bolen and C. F. Claiborne, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4106–4111.
33. N. Watanabe, H. Arai, J. Iwasaki, M. Shiina, K. Ogata, T. Hunter and H. Osada, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11663–11668.
34. A. Seki, J. A. Coppinger, H. Du, C.-Y. Jang, J. R. Yates and G. Fang, J. Cell Biol., 2008, 181, 65–78.
35. D. Branzei and M. Foiani, Nat. Rev. Mol. Cell Biol., 2008, 9, 297–308.
36. H. C. Reinhardt and M. B. Yaffe, Curr. Opin. Cell Biol., 2009, 21, 245–255.
37. M. A. Vugt, A. Bras and R. H. Medema, Cancer Res., 2005, 65, 7037–7040.
38. N. Mailand, S. Bekker-Jensen, J. Bartek and J. Lukas, Mol. Cell, 2006, 23, 307–318.
39. W. S. Hlavacek, Mol. Syst. Biol., 2008, 5, 240.
40. M. Ashyraliyev, Y. Fomekong-Nanfack, J. A. Kaandorp and J. G. Blom, FEBS J., 2009, 276, 886–902.
41. J. R. Banga, BMC Syst. Biol., 2008, 2, 47.
42. P. Lenart, M. Petronczki, M. Steegmaier, B. D. Fiore, J. J. Lipp, M. Hoffmann, W. J. Rettig, N. Kraut and J.-M. Peters, Curr. Biol., 2007, 17, 304–315.
43. A. Peschiaroli, N. V. Dorrello, D. Guardavaccaro, M. Venere, T. Halazonetis, N. E. Sherman and M. Pagano, Mol. Cell, 2006, 23, 319–329.
44. L. Kuepfer, M. Peter, U. Sauer and J. Stelling, Nat. Biotechnol., 2007, 25, 1001–1006.
45. W. W. Chen, B. Schoeberl, P. J. Jasper, M. Niepel, U. B. Nielsen, D. A. Lauffenburger and P. K. Sorger, Mol. Syst. Biol., 2008, 5, 239.
46. C. C. Wang, M. Cirit and J. M. Haugh, Mol. Syst. Biol., 2009, 5, 246.
47. C. Schlier, Appl. Numer. Math., 2008, 58, 1467–1478.
48. R. H. Byrd, J. C. Gilbert and J. Nocedal, Math. Program., 2000, 89, 149–185.
49. E. Balsa-Canto, A. Alonso and J. Banga, BMC Syst. Biol., 2010, 4, 11.
50. D. Desai, H. Wessling, R. Fisher and D. Morgan, Mol. Cell. Biol., 1995, 15, 345–350.
51. N. Keen and S. Taylor, Nat. Rev. Cancer, 2004, 4, 927–936.
52. H. Kitano, Nat. Rev. Drug Discovery, 2007, 6, 202–210.
53. J. Lehár, A. S. Krueger, W. Avery, A. M. Heilbut, L. M. Johansen, E. R. Price, R. J. Rickles, G. F. Short, J. E. Staunton, X. Jin, M. S. Lee, G. R. Zimmermann and A. A. Borisy, Nat. Biotechnol., 2009, 27, 659–666.
54. C. I. Bliss, Ann. Appl. Biol., 1939, 26, 585–615.
55. E. A. Harrington, D. Bebbington, J. Moore, R. K. Rasmussen, A. O. Ajose-Adeogun, T. Nakayama, J. A. Graham, C. Demur, T. Hercend, A. Diu-Hercend, M. Su, J. M. Golec and K. M. Miller, Nat. Med., 2004, 10, 262–267.
56. T. Haberichter, B. Madge, R. A. Christopher, N. Yoshioka, A. Dhiman, R. Miller, R. Gendelman, S. V. Aksenov, I. G. Khalil and S. F. Dowdy, Mol. Syst. Biol., 2007, 3, 84.
57. A. Faure and D. Thieffry, Mol. BioSyst., 2009, 5, 1569–1581.
58. T. Y. Tsai, Y. S. Choi, W. Ma, J. R. Pomerening, C. Tang and J. E. Ferrell, Science, 2008, 321, 126–129.
59. U. Alon, Nat. Rev. Genet., 2007, 8, 450–461.
60. I. B. Weinstein, Science, 2002, 297, 63–64.
61. J. Luo, N. L. Solimini and S. J. Elledge, Cell, 2009, 136, 823–837.
62. Z. A. Knight, H. Lin and K. M. Shokat, Nat. Rev. Cancer, 2010, 10, 130–137.
63. A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, Assoc. Comput. Mach., Trans. Math. Software, 2005, 31, 363–396.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1–S7, Table S1–S2, Dataset S1–S2. See DOI: 10.1039/c0mb00004c

‡ These authors contributed equally to this work.

---