Theoretical discussions on electron transport properties of perylene bisimide derivatives with different molecular packings and intermolecular interactions

Abstract

Seven perylene bisimide derivatives with different molecular packings and intermolecular interactions were investigated in detail within Marcus-Levich-Jortner formalism at the level of density functional theory (DFT). In theory, we further proved the report that different halogen substitutions in the core position of perylene bisimide lead to different molecular packings in their single crystals and thus obviously different electron transport properties. Here, insight into the geometries, the character of the frontier molecular orbitals, the decompositions of reorganization energies and transfer integrals in different directions was provided to shed light on the relationship between structures and properties. The molecular dynamics (MD) simulations and band structures calculations were also employed to give a multiscale understanding of their transport properties. The results show that there are small discrepancies of the intramolecular electron reorganization energies among these compounds and the transfer integrals determine their electron transport properties. Compounds 1a, 3a and 3b, with typical “brick” packing, π-stacked face-to-face packing and “herringbone” packing, respectively, have larger electron mobilities among these systems and possess different transport dimensionalities. Moreover, we also find there is close relationship between the intermolecular interaction energy and the transfer integral.

---

1. Introduction

The availability of both n- and p-type semiconductors is essential for diodes and complementary circuits with high operating speeds and low power consumption.^1–4 However, the operational performance and stability of organic n-type materials significantly lag behind their p-type counterparts, which has been one of the major challenges confronting the field of organic electronics.⁵ As we know, one of the major hurdles for n-channel organic semiconductors is the vulnerability of the n-type charge carrier to air conditions. In general, from the perspective of an experimentalist, the main solutions to this problem are (i) lowering redox potential to prevent ambient oxidation^6,7 and (ii) designing dense solid state packing to create kinetic barriers to slow down the diffusion of ambient oxidants into the active channel area.^8,9

During the past few years, a large number of organic electron transport materials have been reported, such as oligothiophenes,^10–12thiazole derivatives,¹³ perfluorinated pentacene,¹²terthienoquinoid derivatives,¹²fullerene^14,15 and so on. In particular, derivatives of perylene bisimides (PBIs) are of increasing interest, due to their exceptional geometries and electronic properties such as large π-conjugation spreading over the whole core, the ability to form well ordered π-stacked aggregates. It should be particularly emphasized that the solid–state packing and concomitant properties of PBIs (e.g.transport properties), can be tailored specifically either by introduction of appropriate substituents in the imide position or by core substitution in the bay region.^7,16–20PBI derivatives have been well-known as organic high-performance pigments and the influence of intermolecular interactions on the optical properties have been investigated in depth, both experimentally and theoretically.^21–24 For example, Klebe et al. investigated 24 different structures of PBI derivatives and presented an empirical fit to correlate the absorption maxima with arrangement between next-neighbor PBIs.²¹ Fink et al. and Zhao et al. successfully evaluated excitation energies of the PBI crystal structure.^23,24 Surprisingly, more and more attention has been paid to the transport properties of PBI derivatives in an attempt to explore some better n-type materials. In an experiment, Bao, J. Marks and Wurthner have presented a comprehensive analysis of the charge transport properties of the halogenated PBIs.^{16–19,25,26} Recently, some theoretical discussions on the transport properties of derivatives of PBIs have also appeared.^27–29 Vura-Weis et al.²⁷ mapped the relationship between stacking geometry, binding energy, and electronic coupling for PBI and calculated the couplings for 20 PBI derivatives with different substituents in the imide position based on density functional theory (DFT). Delgado et al.²⁹ used DFT to investigate the effect of the type, number and positions of the substituents on charge-transport parameters of 30 end-substituted PBIs and 7 core- and core/end-substituted PBIs. The calculations of band structure and transfer integral provided a compelling illustration of the impact of intermolecular packing on the transport properties.

In the present work, the molecular models are shown in Fig. 1. Compared with series 3 (3a, 3b), larger torsional angles (>25°) of the perylene bisimide core of series 2 (2a–2c) weaken π–π stack with small distance and thus induce lower electron mobilities. Whereas 1a with eight chlorine substituents was reported to have better transport performance although the torsional angle of its perylene bisimide core is very large (35.8°). This phenomenon aroused our great interest. The transport properties of seven perylene bisimide derivatives with various halogen substitutions in core positions were investigated by combining DFT calculations with molecular dynamics (MD) simulations to attempt to demonstrate the structure–property relationships and help design n-type semiconductors with high mobilities. Especially, the present work intensely focuses on the influence of different halogen substituents on the crystal packings and transport properties through changing molecular structure and inducing various intermolecular interactions. Here, we employed the Marcus–Levich–Jortner formalism to evaluate electron mobilities, which was proved to give good estimates of the values. The relationship between molecular alignments in crystal, the thermal fluctuation of the transfer integrals and intermolecular interactions was mapped. Finally, we hope that our work can provide a useful guideline for the synthetic study and reasonable design of high-performance n-type semiconductor with high mobility.

Fig. 1 Molecular models of the PBI derivatives investigated in this work.

2. Computational methodology

The equilibrium structures of the neutral and anion species were optimized at DFT level using the B3LYP functional and the 6-31G(d,p) basis set.^30,31 Harmonic vibrational frequencies were calculated at the same theoretical level based on the optimized geometries and also employed to estimate the vibrational contributions to the intramolecular reorganization energies³² (See in the Electronic Supplementary Information† (ESI)). The intramolecular reorganization energies were computed employing the adiabatic potential approach based on B3LYP/6-31G(d,p).^33,34 The B3LYP functional has been considered to give better a description of ultraviolet photoelectron spectroscopy (UPS)-derived values for oligoacenes.^32,35,36 Recently, the DFT estimate of the reorganization energy was reported to strongly depend on the ratio (Ax) between the HF-like and density functional exchange.^37–39 To determine the effect of different functionals on the reorganization energy, a series of functionals with different ratio, namely BLYP (Ax = 0), B3LYP (Ax = 0.2), BλLYP (Ax = 0.2533) and BHHLYP (Ax = 0.5), were employed to calculate the reorganization energies of 1a and 3b. The results presented in Fig. S1† show that the reorganization energies of 1a and 3b increase obviously with Ax increasing, which is consistent with the conclusion on familiar oligmers, such as pentacene, rubrene and so on, reported by Sancho-Darcia and Pérez-Jiménez in ref. 37–39. The optimized geometries and the electronic structures (e.g. energy level of LUMO) of 1a and 3b obtained from these functionals mentioned above were compared with experimental values (listed in Table S1†) to further illustrate the effect of various methods on the molecular structures. The results listed in Table S1 show that the discrepancies between the bond lengths and bond angles obtained from different functionals are small both for 1a and 3b, and B3LYP (Ax = 0.2) and BλLYP (Ax = 0.2533) among these functionals lead to values closer to the experimental ones, especially for energy levels of LUMO. Furthermore, in order to investigate the influence of basis set, three basis sets, 6-31G(d,p), 6-31+G(d,p) and 6-31++G(d,p), were also employed to calculate the reorganization energy of 1a using B3LYP functional. The results depicted in Fig. S2† suggest that the effect of the diffusion functions on reorganization energy is negligible. Meanwhile, basis set superposition error (BSSE) using a counterpoise correction scheme was taken into account during the calculation of interaction energies for main hopping pathways in all systems at the level of M06-2x/6-31G(d,p), which was not assumed as a BSSE-free one. M06-2X functional is considered to be suitable for the description of noncovalent interactions such as π–π interaction, H-bond interaction.⁴⁰ All the calculations were performed using the Gaussian 09 software package.⁴¹

Currently, there are mainly two mechanisms describing charge transport in organic crystal semiconductors: a) the coherent band model, and b) the incoherent hopping model. In general, for perfectly ordered defect-free organic crystals at low temperatures the band theory or its extensions are employed. An analysis presented by Cheng et al. indicated that band-like transport model is not tenable above 150 K for organic materials.⁴² Here, all the compounds were investigated about assumed 300 K, at which point the thermal disorder may strongly localize the charge and the lattice phonons are strongly coupled with the charge motion, suggesting that the hopping may dominate.^43,44 From the discussion of the thermal fluctuations of transfer integrals hereinafter described, the fluctuations are found to be almost of the same order of magnitude as the average values, indicating charge transport should be treated by thermal disorder. The hopping mechanism was thus employed to calculate electron mobilities for all molecules.

In hopping regime, the electron-transfer (ET) rate between two adjacent molecular sites i and j is given in the Marcus-Levich-Jortner formulation:^45,46

Where, λ_class is the classical contribution to the reorganization energy (generally the outer sphere contribution), t_ij represents charge transfer integral between molecular site i and j, which was computed at the M06-2X/6-31G(d,p) level following site-energy corrected method in this manuscript (depicted in the supplementary information†).⁴⁷ It should be pointed out that this functional was proved to give a little larger values of transfer integral than B3LYP functional⁴⁷ and PW91 functional⁴⁸ here (shown in Fig. S3†), but this functional can give a better estimate of noncovalent interactions. This formulation includes the quantum description of nonclassical degrees of freedom represented by a single effective mode of frequency ω_eff, and associated Huang–Rhys factor S_eff.^49,50 In general, when ħω ≫ k_BT, quantum mechanical correction (vibrational factors) must be treated and thus the Marcus–Levich–Jortner formulation should be adopted; when ħω ≪ k_BT, it can be assumed classical and the simpler Marcus-type expression can be employed.⁴⁹ Wherein, ℏ is the Planck constant divided by 2π, k_B is the Boltzmann constant, and T is the temperature and defined as 300 K. Here, eqn (1) was employed by reference to the effective frequency calculated in the section of reorganization energy.

Assuming a Brownian motion of charge carrier in the absence of applied electric field, electron mobility is calculated from the diffusion coefficient D with the Einstein–Smoluchowshi equation:

Where, the diffusion coefficient D can be approximately evaluated from the electron-transfer rate k as, , i represents a specific hopping pathway with r_i being the electron hopping distance; d is spatial dimension. While, is the relative probability for electron hopping to the ith neighbor. The calculations of all parameters mentioned above were performed on the basis of the three–dimensional crystal structures for all compounds investigated here.

To give a detailed discussion on the effect of different substitutions on molecule packing in the crystal and to investigate the modulation of the transfer integrals by thermal motions, preliminary MD simulations were run on supercells (4 × 3 × 3) of the crystal unit cells of compounds 1a, 3a and 3d.^19,26 The molecular MD simulations with fixed lattice constants was carried out with COMPASS force field within the Material Studio package.^51,52 100 ps MD simulations in the NPT ensemble and at 300 K were run, using the Berendsen thermostat.⁵³

Meanwhile, to investigate the main directions of electron transport, the electronic band-structure calculations were performed with VASP^54–56 using the PBE (Perdew–Burke–Ernzerhof) exchange–correlation functional⁵⁷ and a plane-wave basis set. The band structure calculations were based on the optimized crystal structure, and the cell constants were fixed at the experimental values during optimization, with a Monkhorst–Pack mesh of 10 × 4 × 2 k-points.

3. Results and discussion

3.1 Geometry and frontier molecular orbital

Based on the crystal structures,^19,26,58 all the molecular geometries were fully optimized at B3LYP/6-31G(d,p) level. The results are in good agreement with the experimental values, and the differences between optimized geometries and the experimental values were summarized in Table S2.† In view of substantial π–π packing and stronger hydrogen-bond interactions between adjacent molecules in the crystal lattice, the torsion angle of the core of 1a calculated for the isolated molecule has a slightly larger discrepancy against experimental data (5.6°) than other compounds (<2.1°). For 2a, each molecule has two different torsion angles in the bay area, 19.8° and 25.3°, which has been ascribed experimentally to packing effects and intermolecular interactions in the crystal lattice; but the two torsion angles become uniform 25° after geometry optimization. It can be seen that different types (F, Cl, Br) or different number (eight, four, two) substituents induce greatly different distortions of the perylene core (3a<3b<2a<2b<2c<1b<1a) caused by steric hindrance. It has been long recognized that high electronic performance requires strong π-orbital overlap between adjacent organic molecules in solid state, planar systems thus have mostly been focused on up to now. So series 3 with small torsion angles of the cores (<6°) is expected to have better transport performance.

The frontier molecular orbitals of all compounds are shown in Fig. 2. Both the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) levels posses π orbital features and spread over the whole core, as displayed by other calculations.^28,29 As can be seen in Fig. 2, various halogen substituents bring a little difference between orbital occupations as a result of small contributions of halogens to molecular orbitals. However, the energy levels of frontier molecular orbitals are effectively tuned. The adiabatic ionization potentials (electron affinities), vertical ionization potentials (electron affinities) and the LUMO levels for all compounds are listed in Table 1. The results of 2a, 3a and 3b are consistent with the calculated values in ref. 28 and 29. Combining Fig. 2 with Table 1, some conclusions were drawn as follows: (i) The LUMO energy of compound 1a is the lowest among these compounds. Also, the electron affinity is the maximum, which is clearly in the range of air-stable n-channel semiconductors according to Marks et al.⁷ Moreover, the low energy of the LUMO is extremely favorable to injection of electrons from metal electrode to organic layer in organic photoelectric devices, for instance, OLED, OTFT and so on. (ii) The LUMO levels of series 2 are lowered by four halogens substituents in the core and the lowering degree increases in the order of F, Br, Cl. (iii) The difluorinated substituents in bay positions do not significantly promote the ionization potential and the electron affinity of 3b. To demonstrate these observations to some extent, natural population analysis (NPA)⁵⁹ was carried out and the partial charges are listed in Table 2. For NPA, the analysis of electron density distribution in a molecular system is built on the orthonormal natural atomic orbitals. It has been shown to exhibit good numerical stability and agreement with other theoretical calculations of charger distribution.⁶⁰ In particular, the distinguished feature of this method is that it alleviates the basis set dependence problem encountered in the Mulliken population analysis.⁶⁰ For 1b, electron-donating methyls slightly weaken the electron withdrawing ability of carbonyls, which may result in a poorer electron delocalization than 1a and thus slightly higher HOMO/LUMO energy than 1a. Meanwhile, the slightly negative natural charges of C1, C2, C3, C4 and slightly positive natural charges of eight Cl atoms indicate the donating-resonance effect of Cl atoms.⁶¹ For 2a, Table 2 shows that the natural charges of C2 and C3 are positive and the natural charges of F atoms are negative, which suggests that the attracting-inductive effect of F atoms may be dominated. While for 2b and 2c, the donating-resonance effect of Cl and Br atoms may play a decisive role from the negative natural charges of C2, C3 and positive natural charges of R₃2′, R₄3′. Meanwhile, the effect of donating-resonance of Cl atoms is found to be slightly stronger than Br atoms. Thereby, the HOMO/LUMO energy of 2a is higher than that of 2b and 2c, and 2b has the lowest HOMO/LUMO energy among compounds 2a–2c. Compared to 3a with no substituent in core, the natural charge of C3 of 3b with two F atoms substituents is positive, which may increase electron delocalization in the case of no change of planarity of the whole molecule. Accordingly, 3b has a slightly lower HOMO/LUMO energy than 3a. Furthermore, more uniform distribution of natural charges of series 1 than series 2 and 3 suggests that the electron delocalizations of series 1 are better although the planarities of cores are destroyed. So the HOMO/LUMO energy of 1a is the lowest among our systems investigated here.

Table 1 Adiabatic ionization potentials (electron affinities), vertical ionization potentials (electron affinities) and LUMO energies for all compounds based on B3LYP/6-31G(d,p) level. (Energies in eV)

	1a	1b	2a	2b	2c	3a	3b
a Adiabatic ionization potentials (IP) and adiabatic electron affinities (EA). b Vertical ionization potentials and vertical electron affinities. c Data from ref. 19 and ref. 26. d The calculated values in ref. 29 are −3.85 eV and 3.78 eV for 2a and 3b, respectively. e The calculated values in ref. 28 is 3.78 eV for 3a.
IP ^a	7.92	7.76	7.58^e	7.68	7.60	7.43	7.48
IP ^b	8.02	7.87	7.70	7.80	7.71	7.52	7.59
EA ^a	3.15	3.08	2.78	2.99	2.99	2.63	2.68
EA ^b	2.99	2.92	2.62	2.84	2.83	2.48	2.53
LUMO	−4.16	−4.07	−3.86 ^d	−4.02	−3.99	−3.73 ^e	−3.77 ^d
LUMO ^c	−4.23	—	−3.93	−406	−4.10	−3.85 ^f	−3.88

---

Table 2 Natural charges of C atoms at the edge of PDI core and their substituted atoms for each compound based on B3LYP/6-31G(d,p) level.^a

	1a	1b	2a	2b	2c	3a	3b
a Due to structural symmetry of each compound, only half molecule was analyzed.
C1	−0.016	−0.017	−0.227	−0.177	−0.177	−0.159	−0.161
R21′	0.106	0.102	0.287	0.288	0.288	0.273	0.273
C2	−0.035	−0.035	0.458	−0.017	−0.088	−0.202	−0.203
R32′	0.076	0.074	−0.311	0.049	0.121	0.244	0.267
C3	−0.035	−0.035	0.459	−0.017	−0.088	−0.202	0.448
R43′	0.076	0.074	−0.310	0.050	0.120	0.244	−0.324
C4	−0.016	−0.016	−0.227	−0.178	−0.177	−0.159	−0.224
R24′	0.106	0.102	0.287	0.288	0.288	0.273	0.287

---

Fig. 2 Illustration of the frontier molecular orbitals for all compounds at B3LYP/6-31G(d,p) level.

3.2 Reorganization energy

Reorganization energy is one key parameter governing the hopping rate. In general, it is cast into contributions from intramolecular vibrations and surrounding medium, namely internal reorganization energy and the external reorganization energy, respectively. Here, the intramolecular reorganization energies of all compounds (listed in Table 3) were evaluated from adiabatic potential-energy surfaces based on B3LYP/6-31G(d,p). Simultaneously, normal-mode (NM) analysis was employed to provide the partition of the total geometry relaxation into the contributions from individual vibrational mode (see the ESI†). As seen in Fig. S4, the overall distributions of vibrations of 1a and 1b are basically consistent except for twisting vibration of methyl of 1b in low frequency region. For series 2 (a–c), the contributions of torsion vibrations in low frequency region increase in the order of F, Cl, Br, depicted in Fig. 3. The vibrations in low frequency region mainly include torsion of the two naphthalene subunits and swing of side chains, and their degrees would become larger with the mass of substitutions in bay position increasing (F, Cl, Br). In a similar manner, there are the similar performances for 3a and 3b (Fig. S5†). Besides, since same density functional (B3LYP) selected, the intramolecular reorganization energies of 2a, 3a and 3b have little deviation from the results reported in ref. 28 and 29.

Table 3 Intramolecular electron reorganization energies λ (in eV) calculated from the adiabatic potential-energy surfaces of neutral/cation or neutral/anion species, the classical contributions to reorganization energy λ_classical (in eV), effective frequencies ω_eff (in eV), and effective Huang–Rhys factors S_eff of all compounds investigated here based on B3LYP/6-31G(d,p)

	1a	1b	2a	2b	2c	3a	3b
a The values in ref. 29 are 0.322 eV and 0.309 eV for 2a and 3b, respectively. b The value in ref. 28 is 0.30 eV for 3a.
λ	0.326	0.330	0.321^a	0.318	0.308	0.298^b	0.311^a
λ classical	0.005	0.009	0.045	0.040	0.038	0.047	0.048
ωeff	0.076	0.077	0.110	0.106	0.120	0.117	0.118
Seff	4.22	4.26	2.91	3.00	2.57	2.55	2.64

---

Fig. 3 The contributions of vibrations to the geometry relaxation for 2a (red label), 2b (green label) and 2c (blue label) respectively. The distributions in low frequency regions (below 500 cm⁻¹) are amplified, while the whole distributions are shown in the insert figure.

It is known that the effect of quantum behavior can be contained by treating only a few modes quantum mechanically by mode averaging.⁴⁹ In this case, vibrations in a frequency range are averaged to give an effective mode of frequency ω_eff and associated Huang–Rhys factor S_eff,

S_eff = λ_int/ℏω_eff (4)

Because the vibrations in low frequency region are mainly torsion vibrations for our systems mentioned above, there is possible anharmonicity. So the contributions for frequencies below 200 cm⁻¹ were not included when the effective frequencies and Huang–Rhys factors were evaluated²⁸ The calculated values summarized in Table 3 show that the effective frequencies of series 1 have the same order of magnitude with k_BT (∼0.025 eV), so the classical approximation, namely simpler Marcus-type theory, may give a better description of series 1, which would be discussed below.

The classical contributions to reorganization energy (λ_classical) are generally considered as the outer-sphere reorganization energy, which is not easily estimated in crystal environment.^62,63 Here, we have set a radix (0.005 eV) of λ_classical for our systems and calculated them employing the method proposed in ref. 28. The detailed description was shown in the supplementary information (Table S3†). λ_classical for each compound is also listed in Table 3. However, it must be noted that the value of outer-sphere reorganization energy would affect the transfer rate strongly from eqn (1) and the selection of 0.005 eV here based on ref. 62, in which the external reorganization energies calculated for familiar organic semiconductors (naphthalene, pentacene, and rubrene) in crystal environment are among 0.001∼0.007 eV. Furthermore, the purpose of this work is to provide a detailed description of structure–property relationship and not the absolute charge carrier mobility, so the theoretical model and the external reorganization energies selected are reasonable.

3.3 Transfer integral and intermolecular interaction

Crystal structures and main charge hopping pathways of 1a, 3a and 3b are depicted in Fig. 4, Fig. 5 and Fig. 6. While the related information of 1b and series 2 (a–c) is shown in Fig. S6–S9.† The solvent molecules in single crystals of 1b, 2b and 2c were omitted for clarity.²⁶

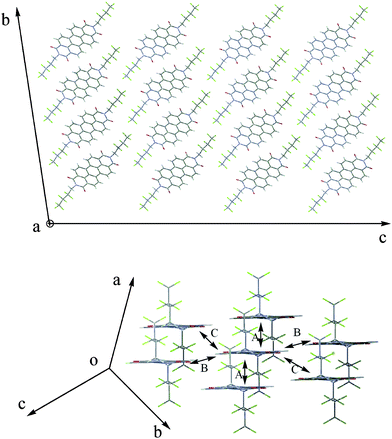
Fig. 4 Crystal of 1a. A b-c plane of a 3 × 3 × 3 supercell structure (top panel); Main charge hopping pathways in a-b plane extracted from the supercell (bottom panel). According to the crystal symmetry of 1a, the four main pathways can be assigned to a typical dimer A, in which neighbors are displaced by about 6.9 Å relative to each other along a axis.

Fig. 5 Crystal of 3a. A b-c plane of a 4 × 3 × 3 supercell structure (top panel); Main charge hopping pathways in a-b-c plane extracted from the supercell (bottom panel). According to the crystal symmetry of 3a, the six main pathways can be assigned to three typical dimers A, B and C, in which the centers of mass of the adjacent molecules are diagonally displaced by about 4.9 Å, 9.2 Å and 12.0 Å respectively.

Fig. 6 Crystal of 3b. An a-c plane of a 3 × 3 × 3 supercell structure (top panel); Main charge hopping pathways in a-b-c plane extracted from the supercell (bottom panel). According to the crystal symmetry of 3b, the six main pathways can be assigned to two typical dimers A and B, in which the neighbors for dimer A are shifted by about 3.8 Å along short axis of the perylene bisimide core and the neighbors for dimer B are tilted with the centers of mass separated by 8.1 Å.

For 1a, eight chlorine substituents form a slipped two-dimensional π-stacked arrangement, namely a ‘brick’ stack, in which the NH imide groups are envisioned to enforce a close hydrogen-bond contact between adjacent molecules.¹⁹ In the a–b plane, we can find that there are four nearest neighbors for each molecule to form main charge hopping pathways, which can be assigned to a typical dimer A according to the crystal symmetry (depicted in Fig. 4). The larger electron transfer integral for dimer A (50 meV) was ascribed to face-to-face π stacking of two adjacent half molecules with a close distance (about 3.5 Å). It is noted that the other adjacent molecules except for the four molecules were not described here because of their smaller transfer integrals with large relative distances. Meanwhile, 1a was inferred to have two-dimensional (2-D) transport behavior in terms of the four analogous hopping pathways in a-b plane, which would be further confirmed by band structure (vide infra). Furthermore, to demonstrate the role of eight chlorine substituents, the transfer integral of the dimer A with all chlorines replaced by hydrogen atoms was also calculated, the value decreased from 50 meV to 32.5 meV, not taking the change of configuration into account. Therefore, eight chlorine substituents have important influence on the electron transfer integral of 1a. However, compared with 1a, two methyl substituents on the imide nitrogens induce a very different crystal structure of 1b (shown in Fig. S6†). The smaller orbital overlaps and larger distances between adjacent molecules lead to smaller transfer integrals in main hopping pathways selected. In terms of the almost same reorganization energy parameters, the electron mobility of 1b was inferred to be smaller than 1a. For 2a, two molecules with opposite chirality have been observed in the crystal structure in a 1 : 1 ratio; i.e., a racemate is given in the solid state.²⁶ So the crystal structure of 2a is relatively complicated and thus there are four distinct charge transfer pathways around random molecule. From Fig. S7,† transfer integrals of the four different dimers were calculated and three of them are large (144 meV, 64 meV and 61 meV, respectively). While for 2b and 2c, their crystal structures are similar, each molecule has six main charge transfer pathways assigned to two typical dimers A and B (depicted in Fig. S8 and S9, respectively†) and the transfer integrals are small owing to small orbital overlaps and weak intermolecular interactions (5 meV and 1 meV for 2b, 0.7 meV and 15 meV for 2c, respectively). As seen in Fig. 5 and 6, the crystals of 3a and 3b take on the familiar slip-stacked π–π arrangement and the “herringbone” arrangement, respectively. Their transfer integrals in main hopping pathways show two uncommon features: (i) For 3a, the transfer integral of dimer C with little direct π–π overlap²⁶ is also very large (53 meV). It was ascribed to the close contacts between the molecular edges (C–C distance is 2.986 Å). (ii) The transfer integral (0.92 meV) of dimer A with a large π–π overlap (50%) of 3a is much smaller than the value (155.87) meV of dimer A with a little π–π overlap (less than 5%) of 3b. This abnormality is at variance with the conventional view that face-to-face π-stacked arrangement is more favorable for charge transport than “herringbone” arrangement. We will give an interpretation according to an analysis of stronger thermal fluctuation of the transfer integrals of 3a.²⁸

The classical MD simulations based on supercells (4 × 3 × 3) of the crystal unit cells of 1a, 3a and 3d were performed in order to obtain a deeper comprehension of charge transport in different crystal packing modes, “brick” arrangement, slip-stacked arrangement and “herringbone” arrangement, respectively. The MD simulation with fixed lattice constants was carried out with COMPASS force field within the Material Studio package, which was proved to reproduce the experimental crystal structure of oligoacenes extremely well.^52,64 Dynamic trajectories were extracted every 500 fs with a total 200 snapshots and the transfer integral of representative dimer A for 1a, 3a and 3b, respectively, at each snapshot were calculated to estimate the strength of the nonlocal source of electron–phonon interaction.^65,66 Because large computational cost is needed for calculating a time series of transfer integrals for a given pair of molecules (200 transfer integrals for each dimer) and the charge transport property is determined by main charge hopping pathways, only representative dimer A (major charge hopping direction) for each compounds was investigated in the process of investigating the thermal fluctuation of the transfer integral, as justified by ref. 27, 28 and 52. In general, the energy splitting in dimer (ESD) approximation overestimates the real values for non-centrosymmetric dimers. Here, the transfer integrals with ESD approximation have been checked against the results of site-energy corrected method for the dimer A of 1a, 3a and 3b. No significant discrepancies have been observed between these two method, such as 52.5 meV compared to 50.0 meV for 1a, 7.5 meV compared to 0.9 meV for 3a (the difference is very small compared with the time average value 56 meV), 155.6 meV compared to 155.8 meV for 3b. Thus ESD approximation was employed to calculate the transfer integral for each snapshot to reduce the prohibitive computational efforts. The thermal fluctuation of the transfer integrals of 3a is depicted in Fig. 7, while the corresponding informations on 1a and 3b were depicted in Fig. S10 and Fig. S11,† respectively. For 3a with slip-stacked face-to-face arrangement, the thermal fluctuation of the transfer integrals is very large (almost three times the average value 56 meV) and thus the corresponding standard deviation σ_t (the calculated method refers to ref. 64) is also very large (23 meV). Comparing with the average value (56 meV), it indicates that the contribution of the nonlocal interactions appears stronger to results in obvious vibration-modulated contribution to the charge transport. The origin was speculated that there are stronger intermolecular interactions including stronger repulsions between molecules along face-to-face packing direction with close distance (3.31 to 3.35 Å) and no strong interactions in other directions. This may induce a relatively strong effect by intermolecular vibrations. While for 1a with “brick” arrangement and 3b with “herringbone” arrangement, the thermal fluctuations of the transfer integrals of dimer A are both small (about one-fifth and one-ninth of the average values, respectively) and the corresponding standard deviations are 2 meV and 7 meV, respectively, which are small in comparison to their average values (52 meV and 176 meV, respectively). It indicates that dynamic disorder has less influence on the transfer integrals of 1a and 3b than the transfer integrals of 3a. This result inferred that there are stronger hydrogen bond interactions along a axis (2.9 Å) and Cl–Cl short contact along c axis (3.2 Å), besides π–π interactions along b axis in 1a crystal and stronger C–H…π interactions in surrounding dimer B stackings (2.8∼3.2 Å), except for b axis in 3b crystal. These additional interactions may stabilize the molecules in crystal environments. The main intermolecular interactions for 1a, 3a and 3b are marked in Fig. S12.†

Fig. 7 Thermal fluctuation of the transfer integral of 3a (dimer A) at 300 K.

In addition, it is well-known that the crystal packing is governed by the intermolecular interaction forces and the intermolecular transfer integrals are determined by the crystal packing. So the relationship between intermolecular interactions with their corresponding transfer integral is to be investigated. Herein, intermolecular interaction energies of the major hopping pathways for each molecule were calculated and all the values are listed in Fig. 8 with the corresponding transfer integrals. The results show that there is a certain corresponding relationship between them with the exception of 3a. For 3a, the intermolecular interaction energy of dimer A is very large due to stronger π–π interaction with short distance between molecules, but the corresponding transfer integral is very small. This abnormal performance was attributed to some deviations of the transfer integral of static dimer A as mentioned above.

Fig. 8 Charge transfer integrals and their corresponding intermolecular interaction energies for the representative dimers (the major hopping pathways) of all compounds investigated here. The interaction energy was given by the expression ΔE = E_dimer−(E_monomer1 + E_monomer2).

3.4 Mobility calculation

Combining the parameters mentioned above with eqn (1, 2), we estimated the electron mobilities of all compounds here. The results are listed in Table 4. We found that these results are in good agreement with experimental values, except for 2a and 3b. It proves the reliability of our methods, although there are some approximations. In addition, the results of 3a and 3b have some deviations from previously calculated results,^28,29 this could be attributed to different theoretical methods selected. Note that neither the intramolecular reorganization energies nor classical reorganization energies for all compounds differ markedly. From Table 4, the differences of electron mobilities calculated for these compounds are significant. Thus, we can anticipate that the transfer integral plays a decisive role, in other words, the molecular packings determine the electron mobilities for these compounds. Among these compounds, 1a, 3a and 3b, with typical “brick” packing, π-stacked face-to-face packing and “herringbone” packing, respectively, have larger electron mobilities. Both the perylene bisimide cores of 3a and 3b possess nearly planar configuration, which is favorable for π–π stacking. While for 1a, although the torsional angle of perylene bisimide core is very large, eight chlorine substituents induce unique “brick” packing in crystal by more strong hydrogen bond interactions and π–π interactions. Thus the electron mobility of 1a is also higher.

Table 4 Electron mobility (in cm² V⁻¹ s) of all compounds investigated here based on Marcus–Levich–Jortner formulations, compared to the experimental value

	1a	1b	2a	2b	2c	3a	3b
a The calculated value in ref. 28 is 0.04 cm^2 V^−1·s. b The calculated value in ref. 29 is 0.4 cm^2 V^−1·s. c Data from ref. 19 and ref. 26.
μ	0.34	0.007	0.99	0.003	0.025	0.37^a	1.49^b
μexp^c	0.91		0.03^c	0.0005^c	0.0003^c	0.67–0.72^c	0.35

---

There are some deviations of calculated results from experimental values for 2a and 3b, which can be rationalized in terms of their molecular packing. For 2a, alternative packing of two different enantiomers induces asymmetry in the backward and forward electron transfer probabilities along a given direction. As a result, charge carrier is easily trapped inside a dimer without transport forward, which is analogous to the situation as described in ref. 28. Besides, the theoretical model of charge transport selected here is suitable for homogeneous isotropic arrangement; slight overestimation of electron mobility is also possible for inhomogeneous molecular arrangement of 2a. While the large difference of molecular packing in single crystal and in thin film was considered to be the main factor for overestimation of electron mobility of 3b. According to ref. 26, the cell parameters of thin film are quite different from that of the single crystal.

In addition, based on the same order of magnitude for the effective frequencies (∼0.076 eV) and k_BT (∼0.025 eV), the simple Marcus formula was also employed to calculate the mobilities of 1a and 1b, which are 0.51 cm² V⁻¹ s and 0.01 cm² V⁻¹ s, respectively. It can be found that the simple Marcus formula and Marcus–Levich–Jortner formulations give the similar results and the simple Marcus formula could give a better value compared to the experimental value of 1a.¹⁹ Simultaneously, according to the reorganization energies calculated employing the different functions mentioned above, the electron mobilities of 1a and 3b were also evaluated and the results are summarized in Fig. S13.† It is found that the selection of functionals has an important influence on the values of calculated mobilities. The more the percentage of HF exchange in different DFT-based methods is, the smaller the values are. However, the relative magnitudes of charge mobility between 1a and 3b from different functionals are consistent.

3.5 Band structure

Although the hopping model was selected, in order to have a further understanding on the anisotropy of charge transport in single crystals, we also examined the band structures of 1a, 3a and 3b (shown in Fig. 9). In view of the primitive unit cells of 1a and 3b containing two inequivalent molecules, two subbands appear both in their valence bands and conduction bands. While 3a has only one molecule in the primitive unit cell, thus the valence (conduction) band consists of one subband. In general, the appearance of both dispersive and flat bands is indication of anisotropy for the charge-transport properties of the crystal, and the stronger dispersion of band is, the larger carrier mobility is. As seen in Fig. 9, the strong conduction band dispersion occurs in the ΓX and ΓY subzone for 1a and 3a, corresponding to a axis and b axis in real space, respectively. With respect to 3b, there is strong dispersion for conduction band in the ΓY direction (b axis). For 1a and 3b, the flat valance bands in all directions suggests that their hole mobilities are very low and thus they could be used only as electron transport materials. To our surprise, for 3a, the presence of the strongly dispersive valence band along ΓX direction suggests the hole mobility may be very high along the a axis, namely in the direction of slip-stacked face-to-face arrangement. This bipolar transport was confirmed by our calculation on the hole mobility of 3a, which is as high as 0.84 cm² V⁻¹ s using the formalism selected in this manuscript.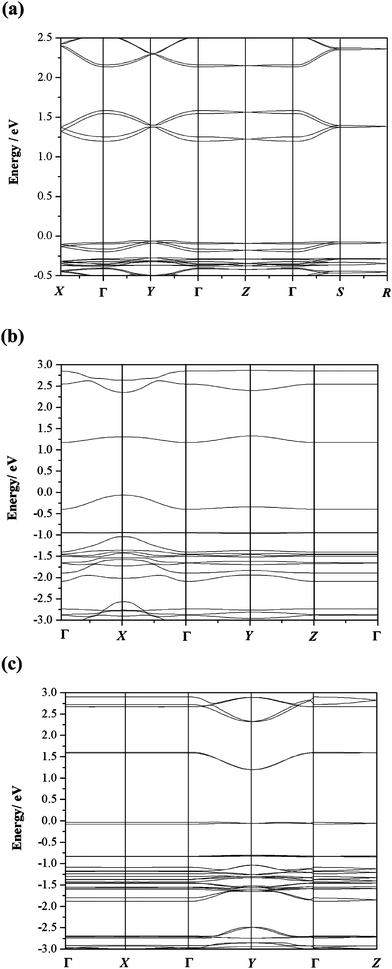

Fig. 9 Band structures of three crystals: (a) 1a (Orthorhombic space group Pbcn, a = 14.46 Å, b = 7.36 Å, c = 20.03 Å, and α = β = γ = 90°), (b) 3a (Triclinic space groupP1̄, a = 4.91 Å, b = 8.48 Å, c = 16.29 Å, and α = 97.49°, β = 94.37°, γ = 98.03°) and (c) 3b (Monoclinic space groupP2₁/c, a = 17.46 Å, b = 5.28 Å, c = 15.28 Å, α = γ = 90°, β = 110.90°). The energies are plotted along directions in the first Brillouin zone connecting the point: Γ = (0, 0, 0), X = (0.5, 0, 0), Y = (0, 0.5, 0), Z = (0, 0, 0.5), S = (0.5, 0.5, 0) and R = (0.5, 0.5, 0.5) for the band structure of 1a; Γ = (0, 0, 0), X = (0.5, 0, 0), Y = (0, 0.5, 0), and Z = (0, 0, 0.5) for the band structures of 3a and 3b. The zero of the energy scale is set as the Fermi level.

In addition, stronger dispersions of conduction bands in two different directions for 1a and 3a indicate that they present 2-D electron transport behavior, while stronger conduction band dispersion only along one direction for 3b indicates 1-D electron transport behavior.

4 Conclusions

In conclusion, we employed the Marcus–Levich–Jortner formalism at the level of DFT and MD simulations to investigate the transport properties of seven perylene bisimide derivatives, which have various halogen substitutions in the core position of perylene bisimide. The influence of different halogen substituents on the crystal packings and transport properties through changing molecular structure and inducing various intermolecular interactions was focused on. We find that there are small discrepancies of the intramolecular electron reorganization energies among these compounds and the transfer integrals determine their electron transport properties. The investigation on the thermal fluctuation of the transfer integrals in different molecular packings, namely “brick” arrangement, π-stacked face-to-face arrangement and “herringbone” arrangement indicate that the transport behavior of 3a may be phonon-assisted by dynamic disorder and compound 1a and 3b have smaller thermal fluctuations of the transfer integrals than 3a. These phenomena were ascribed to richer intermolecular interactions in crystals of 1a and 3b than those in crystal of 3a. The calculations of the electron mobilities for all compounds and band structures for 1a, 3a and 3b further proved the different transport performances of perylene bisimide derivatives. Furthermore, insights into the relationship between molecular interaction and charge transport are under study to provide with more detailed strategies, that is, how to tune charge transport by molecular modification.

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Project No. 20903020; 20703008), Chang Jiang Scholars Program (2006), Program for Changjiang Scholars and Innovative Research Team in University (IRT0714), National Basic Research Program of China (973 Program-2009CB623605), the Science and Technology Development Project Foundation of Jilin Province (20090146), the Training Fund of NENU's Scientific Innovation Project (NENU-STC08005 and -STC08012), The Project-sponsored by SRF for ROCS, SEM. And we also thank Patrik Callis (MSU) for supplying the Bozesuite program. We thank the state key laboratory of theoretical and computational chemistry of Jilin University for supplying the Material Studio package and VASP program.

References

1. K. F. Brennan and A. S. Brown, Theory of Modern Electronic Semiconductor Devices, John Wiley & Sons, Inc.: New York, 2002, 448.
2. T. H. Jung, B. Yoo, L. Wang, A. Dodabalapur, B. A. Jones, A. Facchetti, M. R. Wasielewski and T. J. Marks, Appl. Phys. Lett., 2006, 88, 183102.
3. K. Hizu, T. Sekitani, T. Someya and J. Otsuki, Appl. Phys. Lett., 2007, 90, 093504.
4. H. Klauk, U. Zschieschang, J. Pflaum and M. Halik, Nature, 2007, 445, 745–748.
5. Z. N. Bao, Adv. Mater., 2000, 12, 227–230.
6. Y. G. Wen and Y. Q. Liu, Adv. Mater., 2010, 22, 1331–1345.
7. B. A. Jones, A. Facchetti, M. R. Wasielewski and T. J. Marks, J. Am. Chem. Soc., 2007, 129, 15259–15278.
8. C. R. Newman, C. D. Frisbie, D. A. da Silva, J. L. Bredas, P. C. Ewbank and K. R. Mann, Chem. Mater., 2004, 16, 4436–4451.
9. H. E. Katz, A. J. Lovinger, J. Johnson, C. Kloc, T. Siegrist, W. Li, Y. Y. Lin and A. Dodabalapur, Nature, 2000, 404, 478–481.
10. M. H. Yoon, A. Facchetti, C. E. Stern and T. J. Marks, J. Am. Chem. Soc., 2006, 128, 5792–5801.
11. J. A. Letizia, A. Facchetti, C. L. Stern, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 13476–13477.
12. S. Handa, E. Miyazaki, K. Takimiya and Y. Kunugi, J. Am. Chem. Soc., 2007, 129, 11684–11685.
13. S. Ando, R. Murakami, J. Nishida, H. Tada, Y. Inoue, S. Tokito and Y. Yamashita, J. Am. Chem. Soc., 2005, 127, 14996–14997.
14. T. W. Lee, Y. Byun, B. W. Koo, I. N. Kang, Y. Y. Lyu, C. H. Lee, L. Pu and S. Y. Lee, Adv. Mater., 2005, 17, 2180–2184.
15. S. Kobayashi, T. Takenobu, S. Mori, A. Fujiwara and Y. Iwasa, Appl. Phys. Lett., 2003, 82, 4581–4583.
16. M. M. Ling, P. Erk, M. Gomez, M. Koenemann, J. Locklin and Z. N. Bao, Adv. Mater., 2007, 19, 1123–1127.
17. Y. Li, L. Tan, Z. H. Wang, H. L. Qian, Y. B. Shi and W. P. Hu, Org. Lett., 2008, 10, 529–532.
18. R. Schmidt, M. M. Ling, J. H. Oh, M. Winkler, M. Konemann, Z. N. Bao and F. Wurthner, Adv. Mater., 2007, 19, 3692–3695.
19. M. Gsanger, J. H. Oh, M. Konemann, H. W. Hoffken, A. M. Krause, Z. N. Bao and F. Wurthner, Angew. Chem., Int. Ed., 2010, 49, 740–743.
20. Y. Avlasevich, C. Li and K. Mullen, J. Mater. Chem., 2010, 20, 3814–3826.
21. G. Klebe, F. Graser, E. Hädicke and J. Berndt, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 69–77.
22. P. M. Kazmaier and R. Hoffmann, J. Am. Chem. Soc., 1994, 116, 9684–9691.
23. R. F. Fink, J. Seibt, V. Engel, M. Renz, M. Kaupp, S. Lochbrunner, H.-M. Zhao, J. Pfister, F. Wurthner and B. Engels, J. Am. Chem. Soc., 2008, 130, 12858–12859.
24. H.-M. Zhao, J. Pfister, V. Settels, M. Renz, M. Kaupp, V. C. Dehm, F. Wurthner, R. F. Fink and B. Engels, J. Am. Chem. Soc., 2009, 131, 15660–15668.
25. P. Osswald and F. Wurthner, J. Am. Chem. Soc., 2007, 129, 14319–14326.
26. R. Schmidt, J. H. Oh, Y. S. Sun, M. Deppisch, A. M. Krause, K. Radacki, H. Braunschweig, M. Konemann, P. Erk, Z. A. Bao and F. Wurthner, J. Am. Chem. Soc., 2009, 131, 6215–6228.
27. J. Vura-Weis, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 1738–1739.
28. E. Di Donato, R. P. Fornari, S. Di Motta, Y. Li, Z. H. Wang and F. Negri, J. Phys. Chem. B, 2010, 114, 5327–5334.
29. M. C. R. Delgado, E. G. Kim, D. A. da Silva and J. L. Bredas, J. Am. Chem. Soc., 2010, 132, 3375–3387.
30. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
31. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
32. M. Malagoli, V. Coropceanu, D. A. da Silva and J. L. Bredas, J. Chem. Phys., 2004, 120, 7490–7496.
33. H. Z. Gao, C. S. Qin, H. Y. Zhang, S. X. Wu, Z. M. Su and Y. Wang, J. Phys. Chem. A, 2008, 112, 9097–9103.
34. G. C. Yang, Y. Liao, Z. M. Su, H. Y. Zhang and Y. Wang, J. Phys. Chem. A, 2006, 110, 8758–8762.
35. F. Wurthner, Chem. Commun., 2004, 1564–1579.
36. V. Coropceanu, D. A. da Silva Filho, R. Friedlein, W. Osikowicz, R. Murdey, C. Suess, W. R. Salaneck and J.-L. Bredas, J. Phys. Chem. B, 2006, 110, 18904–18911.
37. J. C. Sancho-Garcia, Chem. Phys., 2007, 331, 321–331.
38. J. C. Sancho-Garcia and A. J. Perez-Jimenez, J. Phys. Chem. A, 2008, 112, 10325–10332.
39. J. C. Sancho-Garcia and A. J. Perez-Jimenez, J. Chem. Phys., 2008, 129, 024103.
40. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01; Gaussian, Inc., Wallingford CT, 2009.
42. Y. C. Cheng, R. J. Silbey, D. A. da Silva, J. P. Calbert, J. Cornil and J. L. Bredas, J. Chem. Phys., 2003, 118, 3764–3774.
43. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Bredas, Chem. Rev., 2007, 107, 926–952.
44. X. Yang, L. Wang, C. Wang, W. Long and Z. Shuai, Chem. Mater., 2008, 20, 3205–3211.
45. R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978.
46. J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867.
47. E. F. Valeev, V. Coropceanu, D. A. da Silva, S. Salman and J. L. Bredas, J. Am. Chem. Soc., 2006, 128, 9882–9886.
48. X. D. Yang, Q. K. Li and Z. G. Shuai, Nanotechnology, 2007, 18, 424029.
49. P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168.
50. J. L. Bredas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003.
51. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
52. L. J. Wang, Q. K. Li, Z. G. Shuai, L. P. Chen and Q. Shi, Phys. Chem. Chem. Phys., 2010, 12, 3309–3314.
53. H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
54. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558–561.
55. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1994, 49, 14251–14269.
56. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
58. M. Sadrai, G. R. Bird, J. A. Potenza and H. J. Schugar, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 637–640.
59. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
60. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
61. A. Facchetti, Y. Deng, A. C. Wang, Y. Koide, H. Sirringhaus, T. J. Marks and R. H. Friend, Angew. Chem., Int. Ed., 2000, 39, 4547–4551.
62. D. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946.
63. S. Di Motta, E. Di Donato, F. Negri, G. Orlandi, D. Fazzi and C. Castiglioni, J. Am. Chem. Soc., 2009, 131, 6591–6598.
64. N. G. Martinelli, Y. Olivier, S. Athanasopoulos, M. C. R. Delgado, K. R. Pigg, D. A. da Silva, R. S. Sanchez-Carrera, E. Venuti, R. G. Della Valle, J. L. Bredas, D. Beljonne and J. Cornil, ChemPhysChem, 2009, 10, 2265–2273.
65. A. Troisi and G. Orlandi, J. Phys. Chem. A, 2006, 110, 4065–4070.
66. V. Coropceanu, R. S. Sanchez-Carrera, P. Paramonov, G. M. Day and J. L. Bredas, J. Phys. Chem. C, 2009, 113, 4679–4686.

---

Footnote

† Electronic supplementary information (ESI) available: The computational methods about normal mode analysis, the site energy corrected method and evaluation of classical reorganization energy; the influences of different functionals and basis sets on the reorganization energy and transfer integral; normal mode analyses of series 1 and 3; the crystal structures of 1b, 2a, 2b, and 3c; Thermal fluctuations of the transfer integrals of 1a and 3b (dimer A for each molecule). See DOI: 10.1039/c0jm02119a

---