Communication theory and multicellular biology

Abstract

In this Perspective, we propose that communication theory—a field of mathematics concerned with the problems of signal transmission, reception and processing—provides a new quantitative lens for investigating multicellular biology, ancient and modern. What underpins the cohesive organisation and collective behaviour of multicellular ecosystems such as microbial colonies and communities (microbiomes) and multicellular organisms such as plants and animals, whether built of simple tissue layers (sponges) or of complex differentiated cells arranged in tissues and organs (members of the 35 or so phyla of the subkingdom Metazoa)? How do mammalian tissues and organs develop, maintain their architecture, become subverted in disease, and decline with age? How did single-celled organisms coalesce to produce many-celled forms that evolved and diversified into the varied multicellular organisms in existence today? Some answers can be found in the blueprints or recipes encoded in (epi)genomes, yet others lie in the generic physical properties of biological matter such as the ability of cell aggregates to attain a certain complexity in size, shape, and pattern. We suggest that Lasswell's maxim “Who says what to whom in what channel with what effect” provides a foundation for understanding not only the emergence and evolution of multicellularity, but also the assembly and sculpting of multicellular ecosystems and many-celled structures, whether of natural or human-engineered origin. We explore how the abstraction of communication theory as an organising principle for multicellular biology could be realised. We highlight the inherent ability of communication theory to be blind to molecular and/or genetic mechanisms. We describe selected applications that analyse the physics of communication and use energy efficiency as a central tenet. Whilst communication theory has and could contribute to understanding a myriad of problems in biology, investigations of multicellular biology could, in turn, lead to advances in communication theory, especially in the still immature field of network information theory.

---

Insight, innovation, integration

One of the major transitions in evolution is the emergence and radiation of complex multicellular organisms from single cells. At the heart of multicellular biology, ancient and modern, lies the dynamic and reciprocal exchange of “information” within and between cells and their environment. The concept of “communication” is not restricted to evolutionary developmental biology, normal or aberrant, and pathology. Communication theory is a field of mathematics concerned with the problems of signal transmission, reception, and processing. Currently, this field is primarily the province of telecommunications engineering. In this Perspective, we propose that communication theory provides an invaluable theoretical framework for exploring problems relevant to multicellularity. A key virtue of communication theory is its ability to be blind to molecular and/or genetic mechanisms. By analysing the physics of communication and using energy efficiency as a central tenet, communication theory has the potential to enhance understanding of and yield unexpected insights about biology that are of theoretical and experimental utility.

1. Introduction

1.1 The major transitions in evolution

A central idea in contemporary biology is that of information. Developmental biology can be seen as the study of how information in the genome is translated into adult structure, and evolutionary biology of how the information came to be there in the first place. Our excuse for writing an article concerning topics as diverse as the origins of genes, of cells and of languages is that all are concerned with the storage and transmission of information… there is sufficient formal similarity between the various transitions to hold out the hope that progress in understanding any one of them will help to illuminate others.¹

Who says what to whom in what channel with what effect. Harold Lasswell's working definition of communication.

The major evolutionary transitions are from replicating molecules to molecules in compartments, independent genes to chromosomes, RNA to DNA plus RNA, DNA plus RNA to the genetic code and proteins, prokaryotes to eukaryotes, asexual clones to sexual populations, single cells to complex multicellular organisms, chemically- to neurally-integrated individuals, solitary individuals to colonies and social groups, and primate groups to human linguistic communities.^1,2 One broad class of transitions led to new entities constructed from previously autonomously reproducing units (protocells, chromosomes, eukaryotic cells, populations and species, multicellular organisms, and integrated social groups). The other class of transitions led to the sophistication of the internal organisation and information processing capacity of an entity (cells with DNA, cells with translation, animals with nervous systems, and linguistic societies).

A hallmark of these evolutionary transitions is changes in the way information—autocatalytic systems, (epi)genetic, behavioural, and symbolic—is stored, transmitted, and processed.^1,2 Information can be stored in protocells, chromosomes, DNA, populations, differential gametes, social networks and symbolic networks, as codes, and encoded in neural impulses and circuits. Information transmission between generations can occur through reproduction (replicating molecules transmitted as groups, genes transmitted synchronously in linked groups, DNA replication, coordinated reproduction of the new entity, and segregation and recombination) or through communication (social learning, and linguistic communication). Information transmission among cells and individuals can occur via(bio)chemical communication (multicellular organisms) or neural communication (animals with nervous systems). Irrespective of the mode of storage and means of transmission, whenever there is a flow or exchange of information, there is, as embodied in Lasswell's maxim, communication.

1.2 The lexicon of communication

The biological literature is replete with communication-related terms such as “information” and its “coding,” “decoding,” “transport,” “fidelity,” “cross-talk,” and “interference.” Biosemiotics is the study of signs and meanings in living systems.^3–5 Code biosemiotics⁶ focuses on organic codes, codes that can be divided broadly into ones that take part in processes that manufacture biological objects such as the genetic code and splicing code, and codes that organise existing objects into functioning supramolecular structures such as the signal transduction code and compartment code. Other examples of organic codes include the sugar code (“glycocode”), cytoskeleton code, adhesive code, histone code, DNA structure code, and metabolic code. The appearance of new organic codes is associated with the major events of macroevolution.

Although both biosemiotics and communication theory consider the transmission, reception and processing of signals from one place or instant to another, they provide different perspectives on Lasswell's maxim. With its roots in philosophy and linguistics, biosemiotics is primarily a descriptive and qualitative study of the semantics of communication in living systems. The engineering origin of communication theory means that this mathematical and quantitative study of communication addresses challenges such as point-to-point communication and information collection by sensor networks, topics that are relevant to biology across a wide range of spatiotemporal scales such as from molecules to languages.

To date, information- and coding-theoretic studies have focused on molecular biology and neuroscience problems pertaining to sequencing technology (polymerase chain reaction, sequence related data-compression, DNA base calling), molecular interactions (proteins and nucleic acids, proteins and domains, biological networks), theoretical sequence analysis (DNA mutations and disease, whole genome alignment), heredity, ensembles of neurons, neural spike trains and higher functions of cognitive systems.^7–19Nucleic acid- and protein-related studies of this type have the potential to shed light on organic codes because these two classes of molecules contribute to the synthesis and primary structures of the basic macromolecular components of all cells. However, scant attention has been paid to another ubiquitous class: carbohydrates (glycans or sugars)—a term that includes monosaccharides, oligosaccharides, polysaccharides, and derivatives of these compounds—as well as glycoconjugates, glycans attached covalently to other molecules such as proteins and lipids.^20–24

Superficially, the paucity of information- and coding-theoretic studies of carbohydrates can be explained by glycomics being a less mature field than genomics and proteomics.^25–28 A deeper explanation is the more complex and dynamic nature of the glycome—the entire complement of carbohydrates, whether free or present in more complex molecules, of an organism or a cell.^29–35 In humans, the size of the glycome is orders of magnitude larger than the proteome and ∼2% of the genome is estimated to encode proteins that make, modify, localise or bind carbohydrates. The distinctive features of carbohydrates include their branched structure, the diversity of secondary modifications of monosaccharides, the importance of the spatiotemporal and molecular context in which they occur, and the indirect relationship of carbohydrates to the genome.

Communication theoretic studies of the glycome and the glycocode, the complex information conveyed by glycans and glycoconjugates, would increase understanding of the major events in macroevolution and extant multicellular biology. For example, the biological communication mediated by glycans underlies diverse molecular, cellular, and tissue functions and plays critical roles in development, health and disease.

1.3 Communication theory and multicellular biology

In multicellular ecosystems and many-celled structures, the local and global (a)biotic milieu of each cell is important.^36–41 Dynamic and reciprocal exchanges of information underpin the cohesive and coherent social relations that exist between cells and their environment(s). By eavesdropping, broadcasting, and intercepting messages, the cohabitants of such ecosystems and structures can be coerced into cooperative or adversarial behavioural modifications, either for the common good or for the benefit of one subset of the population of cells over another. Communication within and between species and kingdoms plays a role in normal and aberrant multicellular biology.^42–44 For example, specific commensal bacteria are essential for development and homeostasis in many eukaryotes and their absence results in phenotypes as surely as mutations to the genomes.^45,46Quorum sensing is an interbacterial communication system that utilises small diffusible molecules (autoinducers) to regulate bacterial gene expression. Colonisation of the large intestine in humans and cattle by enterohemorrhagic Escherichia coli involves cross-communication between cell-to-cell biochemical signalling systems of the bacterial pathogen (quorum sensing) and the eukaryotic host (hormones, epinephrine).^43,47

Reliable intra- and intercellular communication is essential for not only multi-species and multi-kingdom multicellular ecosystems, but also for every multicellular plant and animal species. In metazoans for example, such communication is a component of homeostasis (the ability of tissues, organs and organ systems to maintain a relatively constant internal environment regardless of the conditions in the external environment) and resilience (the capacity of a system to recover from a stochastic or deterministic shock, insult or disturbance). The issues of homeostasis and resilience in Metazoa permeate the work of Dr Mina Bissell, the honouree of this themed issue of Integrative Biology. Her research examines microenvironmental influences on gene expression and tissue specificity in normal and malignant breast tissues.^48,49 She has highlighted the need to culture mammalian cells in physiologically relevant three-dimensional (3D) microenvironments and demonstrated that such experimental techniques generate reasonable ex vivo many-celled structures that approximate the ducts, acini, and other functional units and architectural elements observed in the breast.

A fundamental question in evolutionary developmental biology is how single-celled organisms coalesced to produce many-celled forms that diversified and evolved into the varied microbiomes and multicellular organisms in existence today. We suspect that ex vivo 3D organotypic cell culture models are useful systems for probing both ancient and modern metazoans. For example, models of the basic “building blocks” of tissues and organs may provide physicochemical and structural insights about the hollow balls, tubes, many-celled forms and other morphotypes postulated to have existed during the emergence and radiation of multicellularity. Architectural and functional insights may emerge from comparative analyses: a 3D organotypic model of a mammary gland acinus—a hollow ball of cells—can be seen as but a lumen away from the rosette-shaped colony of Salpingoeca rosetta, a choanoflagellate that can exist either as single cells or ∼4–50 cells arranged in closely packed spheres.⁵⁰

Here, we propose that communication theory provides a new quantitative lens for multicellular biology and illustrate how the intersection of these fields is a fertile ground for re-examining existing topics and exploring new subjects. We suggest information- and coding-theoretic approaches that could be used to analyse aspects of the glycocode, an organic code critically important for multicellularity and its (dys)functions. We probe the fundamental question “How much information is necessary to specify a physical structure?” This issue is woven through Dr Bissell's genotype-phenotype studies: what, when, where, why and how is information exchanged amongst and between cells and their microenvironment, and what is the relationship between dynamic reciprocal communication and tissue form and function, normal and aberrant. We consider the information–physical structure question from the stand point of two “structural codes” and outline some possible research avenues. The first code is the stochastic mapping between the spatiotemporal organisation of chromosome territories in the cell nucleus, an increasingly important epigenetic mechanism, and the phenotype of the cell: communication theoretic studies might help to clarify the role of nuclear architecture in evolutionary developmental biology and cell (de)differentiation. The second code is the stochastic mapping between the orientation of the mitotic spindle and the plane of cell division in the context of single cells and many-celled structures: communication theoretic studies might help to reveal what a cell could possibly know in the isolated versus collective state.

Our abstraction that communication theory is an organising principle for multicellular biology is in accord with and responsive to recent arguments for “a new kind of molecular biology, the molecular biology of organization” and studies centred on the cell, a fundamental unit of structure, function, and organisation.⁵¹ This initial foray into building bridges between two seemingly disparate fields focuses less on genes and more on principles governing the origins (evolutionary developmental biology), generation (morphogenesis), maintenance (homeostasis and resilience), subversion (infectious and chronic diseases such as cancer and immune disorders), and decline (ageing) of multicellularity. Here, we explore flows and exchanges of information that have the potential to address basic questions in the biology of Metazoa and that could illuminate (dys)functions of cells, tissues and organs.

This Perspective is organised as follows. Section 2 provides an overview of the evolutionary developmental biology of multicellular animals, and the Developmental Genetic Toolkit implicated in metazoan evolution. Section 3 summarises existing work on Dynamical Patterning Modules (DPMs), physical forces and processes mobilised by subsets of the molecules in the toolkit. A new DPM, mitotic spindle orientation, is proposed and examined with respect to the coherent growth of and (re)shaping of many-celled structures (hollow balls and tubes) and a possible role in normal and malignant epithelial tissue biology. Section 4 discusses communication theory as an organising principle for multicellular biology, provides a primer on well known and useful concepts and theorems, and describes some extant illustrative applications of information and coding theory. Section 5 provides the broad brush strokes of how concepts and ideas from information theory, coding theory, and communication theory might be utilised to address topics that are relevant to multicellular ecosystems and many-celled structures in general, and metazoan tissues and organs in particular. Section 6 explores what communication theory might contribute to multicellular biology and vice versa.

2. Evolutionary developmental biology

2.1 From single cells to multicellular animals

The evolution of multicellular animals from their single-celled ancestors likely involved the emergence of simple colonies of equipotent cells followed by the organisation and integration of cell function and behaviour within an individualised organism.^52,53 The main innovations that mediated this transition were cell adhesion (binding of a cell to another cell or to a surface), cell signalling (communication within and between cells), cell differentiation (a division of labour facilitated by multiple types of cells), and recognition of self from non-self (immunity). Subsequent elaboration and regulation of gene families required for these functions enabled developmental patterning, morphogenesis, and the functional integration of tissues.

Choanoflagellates are a group of free-living unicellular and colonial flagellate eukaryotes considered to be the closest living relatives of Metazoa. Their ultrastructural and functional characteristics are conserved in the specialised “feeding cells” of sponges, eukaryotes considered to be living models of the last common metazoan ancestor. Choanoflagellates can attach to and engulf bacteria, a process that could be the single-cell antecedent to cellular adhesion. Protozoa can respond to both other organisms and their environment based on secreted proteins, a potential precursor to the kind of cell-to-cell signalling essential for multicellularity. The genome of the choanoflagellate Monosiga brevicollis harbours versions of metazoan cell signalling and cell adhesion gene families.⁵⁴

Placozoa are small, flattened non-parasitic multicellular animals with a simple body that consists of an outer layer of simple epithelium enclosing a loose sheet of stellate cells resembling the mesenchyme of some more complex animals. The genome of the only named placozoan Trichoplax adhaerens harbours versions of transcription factors and components of pathways such as cell signalling and cell adhesion that are associated typically with diverse cell types and developmental processes in more complex metazoans.⁵⁵

Sponges have simple body plans that lack organs, muscles, and nerve cells. They are a somewhat loose association of cells in which the internal and external environments are undifferentiated (in terms of ionic homeostasis) and possess some of the most ancient tissue (differentiated epithelia). Sponges lack abundant intercellular junctions and a basement membrane, two features that contribute to the architecture and mechanical and absorptive/transport properties of eumetazoan epithelial cells. The genome of the marine sponge Amphimedon queenslandica harbours genes associated with processes that are the hallmarks of Metazoa and whose dysfunctions can drive diseases such as cancer, a failure of social controls on multicellularity, and autoimmune disorders, the disruption of distinctions between self and non-self.⁵⁶ These processes are cell–cell and cell–extracellular matrix adhesion, developmental signalling and gene regulation, regulated cell cycling and growth, programmed cell death, specialised cell types, and allorecognition (an event central to adaptive immunity, the ability to recognise and remember specific pathogens and to mount stronger attacks each time the pathogen is encountered) and innate immunity (an older, evolutionarily conserved, “non-specific” defense mechanism that defends the host from infection by other organisms). Thus, almost all/most of the key genetic prerequisites for Metazoa were in place well before sponges split from other animals.

2.2 Developmental Genetic Toolkit

Morphogenesis and pattern formation in Metazoa are mediated by evolutionarily conserved genetic loci, elements of a Developmental Genetic Toolkit.⁵⁷ The cardinal features of this toolkit are the ability of cells to stick to their neighbours and to send signals to them, to divide and grow in a coordinated fashion, to develop into specialised cell types, to distinguish themselves from cells belonging to other organisms, and to die if they are in the wrong place or misbehaving. Comparative genomics and other analyses have not only identified the molecular players in this toolkit in invertebrates and living models for the transition from unicellular to multicellular organisms, but also shed light on (dys)functions of multicellularity.^{52,54–56,58}

Neither choanoflagellates nor placozoans nor sponges possess true tissues organised into germ layers and an embryo that goes through a gastrula stage. Despite this, the presence of the toolkit in these organisms attests to their value as living models of the generation, maintenance, subversion, and decline of mammalian tissues and organs. Therefore, insights about microenvironmental influences on gene expression and tissue specificity in normal and malignant human breast tissues are likely to emerge from studies of species in the order Choanoflagellida, phylum Placozoa, and phylum Porifera. Indeed, 3D organotypic models where mammalian cells are replaced by cells from such species could illuminate not only normal biology and pathology, but also the evolution and diversification of Metazoa.

3. Dynamical patterning modules

In addition to blueprints or recipes encoded in (epi)genomes, the generic physical properties of biological matter are implicated in the earliest events in metazoan history and in the assembly and sculpting of extant multicellular animals.^59–63 Pattern formation and morphogenesis in the earliest metazoans as well as the hollow, multilayered and segmented morphotypes in the gastrulation stage embryos of modern metazoans are believed to involve processes generic to living and non-living viscoelastic, chemically excitable materials: free diffusion, immiscible liquid behaviour, oscillation and multistability of chemical state, reaction-diffusion coupling, and mechanochemical responsivity. Changes in the local physical milieu and physical forces of a system modify such processes providing novel contexts and ways for genes that were already present to interact with each other and their environment. Slight differences in the rates or in the interaction parameters between molecules and cells generate new morphogenetic fields and self-organising dynamics that serve as a medium for the formation of novel structures.

All metazoan body plans and organs are hypothesized to have emerged via a process of self-organisation using a “pattern language” for multicellular form, that is, a collection of Dynamical Patterning Modules (DPMs).^59,60,62,63 A DPM consists of a set of molecules (usually proteins) produced by a cluster of cells and the suite of physical processes they mobilise so as to generate an aspect or to alter the form (shape, size, topology) or pattern (specific arrangement of cell types) of the cluster. Table 1 lists DPMs that have been enunciated to date.

Table 1 Dynamical patterning modules (DPMs) that have been defined to date.^60,62 The physical effects mobilised by the molecular constituents of DPMs are cell–cell adhesion, phase separation of differentially adhesive cell populations, short-range laterally acting inhibition, generation of structural anisotropy across individual cells, alteration of the rheological properties of the microenvironment, oscillations in cells' biochemical state, and diffusion across cell masses. The non-living condensed matter analogues of these physical behaviours are cohesion (ADH) and phase separation (DAD) in liquids, chemical reaction (LAT), self-assembly of anisotropic polymers (POL), chemical oscillation (OSC), molecular diffusion (MOR), reaction-diffusion instability (TUR), and solidification and dispersal of colloids and phase transitions (ECM)

DPM	Molecular constituents	Physical principles	Role in evolution and development
ADH	Cadherins	Adhesion	Multicellularity
LAT	Notch	Lateral inhibition	Coexistence of alternative cell states
DAD	Cadherins	Differential adhesion	Phase separation, tissue multilayering
POLa	Wnt	Cell surface anisotropy	Topological change, interior cavities
POLp	Wnt	Cell shape anisotropy	Tissue elongation
ECM	Chitin, collagen	Stiffness, dispersal	Tissue solidification, elasticity, epithelial mesenchymal transformation
OSC	Wnt + Notch	Chemical oscillation	Segmentation, periodic patterning
MOR	TGF-β/BMP, FGF, Hh	Diffusion	Pattern formation
TUR	MOR + Wnt + Notch	Dissipative structure	Segmentation, periodic patterning
ASM	FGFs	Asymmetric interaction	Induction; epithelial-mesenchymal interaction
MIT	MAPK	Mass increase	(Differential) growth
APO	Bcl-2	Mass decrease	(Differential) cell loss

---

DPMs connect molecules that coordinate organismal development and the physical properties and processes of form. Developmental Transcription Factors (DTFs) are gene regulatory molecules that mediate cell type- and region-specific functions. DPMs were present in unicellular organisms but assumed their physical role—rapid and exhaustive exploration of many-celled forms—only in the context of multicellularity. Although DTFs are as ancient as DPM genes, their role in the unicellular world was mediating transcriptional responses to internal and external signals. Given their highly conserved nature, DPM molecules and DTFs can be seen as two broad categories of the toolkit.

The actions and interactions of DPMs on single-celled organisms as well as transient and variable many-celled forms generated polymorphic multicellular structures such as internal body cavities, appendages, segmentation, and primitive organs such as hearts and eyes. DTFs switched on and off certain genes and their main role was mediating the cell- or tissue-specific effects of DPMs and hardwiring the molecular players of DPMs in regulatory networks. Natural selection built upon, fine-tuned, stabilised, and locked in already-emerged but highly plastic ancient many-celled forms rendering these innovations in structure robust. Although extant DPMs play a role in the development of Metazoa, the price paid for stable body plans and organs is severe constraints on the ability of these DPMs to explore morphospace freely.

3.1 Molecular homology—analogy paradox

The framework of DPMs resolves the apparent paradox that disparate organisms employ homologous genes when building structurally dissimilar but functionally similar structures categorised traditionally as analogous—eyes in insects and vertebrates, wings in bird and flies, and so on.^62,64 Given the same set of ingredients, the non-linear dynamics of tissues, cells, and the molecules they produce are capable of making structures that are very different from one another. Variation in the local (a)biotic environment of a group of ancestral single cells or a minor genetic change in several different cell populations could have produced clusters that were hollow, multilayered, segmented and so on. Some gene products tend to cause cell sheets to bend and to protrude in certain ways so when the context changed in a particular manner, analogous appendages could have formed in different evolutionary lineages. The vertebrate limb bud and limb pattern may have arisen from changes in the size and/or shape of the surface of the embryo—an outpocketing of the animal body wall. The context and state of the many-celled form allowed genes that had evolved for other functions to play new “approximate” (not-yet-programmed) functions in clusters of cells. Natural selection could pick from this wide palette of forms choosing those that were suitable for given ecological niches.

Tissue mass structures are made using molecules that are predisposed to mobilising certain processes of the physical world. The adhesion DPM (ADH in Table 1) is the sine qua non of multicellularity: the single-celled ancestors of Metazoa had cadherins on their surfaces even though those cells did not use cadherins to stick to each other.⁶⁵ Since the function of a cell surface cadherin as a sticky protein is environmentally dependent, only certain milieus would have allowed cadherin-bearing single-cell organisms to clump together. The integrin family of metazoan extracellular matrix adhesion molecules are critical mediators of the actions of many DPMs. Although homologues are present in choanoflagellates, true integrins are found in the sponges where they mediate both adhesion and outside-in signaling. Thus, integrins acquired a novel morphogenetic function with the emergence of multicellularity and the organisational architecture provided by an extracellular matrix.

3.2 Tissues: epithelia

A fundamental component of organogenesis, disease progression and ageing is the development and homeostasis of epithelia, sheets of tightly adherent cells that line internal and external surfaces in many metazoans.^66–69 The essential architectural features of this tissue are cells polarised in an apical/basal manner, cell–cell junctions, a paracellular diffusion barrier, specialised plasma membrane proteins, and directional transport in the form of secretion and absorption. Some aspects of epithelial morphogenesis are not directed explicitly by genetic control but emerge from the complex interactions between geometric and biomechanical properties of epithelial tissues.⁷⁰Cell pattern geometry can influence the mechanical properties of tissues and key biological processes such as planar polarisation, tissue remodelling, and cell division. In epithelial forms, the tight coupling between cell adhesion and cellular proliferation constrains cellular geometry (cell shape), cellular topology (connectivity among cells), and tissue organisation.

Tubes and hollow balls are two many-celled forms that approximate key functional units and architectural elements observed in many tissues and organs. In the mammary gland for example, a luminal epithelial cell layer forms the ducts (tubular structures) and secretory acini (balls of cells containing a central lumen), and a basal myoepithelial cell layer provides the forces for secretion. This epithelium is embedded in a fat pad composed of adipocytes, blood vessels, fibroblasts and immune cells. Human cancer mortality is attributable largely to the local invasion of tumours into adjacent normal tissues and the dissemination and metastasis of tumour cells to distant sites—processes that can be viewed as epithelial morphogenesis gone awry.^{40,41,48,71,72}

3.3 A new DPM: mitotic spindle orientation

Cytokinesis is the last step of the cell cycle that results in the division of a mother cell into two daughter cells that are approximately equal in size and have similar fates (symmetric cell division) or, depending on environmental conditions and cell type, have unequal sizes and differing fates (asymmetric cell division).^73–75 In addition to increasing cell numbers, cytokinesis plays a role in shaping how tissues grow and pattern themselves and in sustaining tissue form and function. Achieving the right balance between cell expansion and cell differentiation requires precise spatiotemporal regulation of cell division site positioning. Mitotic spindle orientation is a valuable, if imperfect, predictor of eventual cell division plane orientation.^76,77Cell–extracellular matrix contacts, cellular geometry, cellular topology, cell–cell signalling, and apical–basal polarity cues contribute to orienting the mitotic spindle.⁷⁸ During cell differentiation events that accompany development in the embryo and tissue homeostasis in the adult, mitotic spindle movement is directed by crosstalk between the cell periphery and the microtubule cytoskeleton.⁷⁹

We propose that mitotic spindle orientation is a new DPM, a single-cell function that antedated the evolution of multicellularity and takes on unanticipated roles when acting in a social context. For example, Cdc42, a Rho-GTPase common to animal cells and yeast, directs the mitotic spindle in one cell toward the point of contact with another in some immune responses.⁸⁰ Assuming this interaction arose early, the role of this new DPM in evolution and development is postulated to be the coherent growth of and (re)shaping of tissue mass. Fig. 1 illustrates how this new DPM might play a role in normal and aberrant tissue biology.

Fig. 1 The physical consequences of mitotic spindle orientation, a single-cell effect, in many-celled forms and a possible role for this behaviour in the collective state in tissue morphogenesis and cancer. Top Acini (balls of cells containing a central lumen) and ducts (tubular structures) are building blocks of many tissues and organs. One aspect of their formation can be abstracted as cell divisions, local events, in the context of a multicellular structure whose global architecture is a tube or a hollow ball. MiddleCytokinesis in the plane of a cell layer results in expansion of the layer (left). In a hollow ball, cell division at a point on the surface along any tangent increases the ball's radius. In a tube, cell division at a point on the surface along a direction parallel to the long axis L increases the tube's length, whereas division perpendicular to L increases its radius. Cytokinesis out of the plane of a cell layer can result in growth towards the lumen (for example, the first stage in ductal carcinoma in situ) (middle) or towards the basal cell direction (for example, branch initiation) (right). Bottom Globally oriented spindles could be induced by the local biochemical milieu (for example, the presence of morphogens) and/or physical forces (for example, tension generated by cell–cell, cell–extracellular matrix, and cytoskeleton–spindle interactions) on one or both faces of a cell layer and be distributed in a uniform or localised manner (green; only one spindle orientation in one cell is shown). Other putative globalisation mechanisms include a domino-like effect or something akin to magnetisation (local cell interactions nucleated by a domain of oriented cells).

4. Communication theory as an organising principle for multicellular biology

In the context of multicellular biology, a message can be any information conveyed by the environment (abiotic such as oxygen concentration, or biotic such as cells from the same or a different multicellular system or the extracellular matrix), a cell, or a group of cells. Cells respond to messages by displaying certain discrete behaviours (for example, DPM action) and in turn compose messages to other cells and their environment by activating (or lending their voice to) certain behaviours. The organisation of cellular and tissue responses into discrete sets provides a foundation amenable to analysis at a number of levels using communication theory, a theory which couches explicitly the transfer of information into discrete units and considers explicitly the energy expenditure associated with message construction, transmission and reception.

4.1 Information theory and coding theory: a primer

Typically, information theorists use “bits” to describe information. Somewhat paradoxically, “information” is what is not already known. A “bit” of information is essentially an “answer” to a yes/no question such as “Did the fair coin turn up heads or tails?” or “Did a mother cell divide into two daughters via symmetric or asymmetric cell division?” Questions with multiple answers can be posed such as “Will this haematopoietic stem cell become a red blood cell, a white blood cell, or a platelet?” or “Are these cells derived primarily from endoderm, ecotoderm, or mesoderm?” or “What protein should be produced?” The answers could be specified using a sequence of binary digits {0,1} or some other set of m-ary digits—for instance, {a,b,c,d,e} depending upon the alphabet available. In a computer, the alphabet is {0,1}. In biology, 20 natural amino acids comprise the protein alphabet whereas 4 natural nucleotides comprise the DNA alphabet. Since “bits” is a somewhat arbitrary unit, “trits” might be defined as the fundamental unit for a ternary alphabet. No matter what size alphabet is used, the “information content” of the “answer set” can always be specified in bits.

Compact (short length) representations are desirable for reasons that can almost always be related to efficient energy usage, a key desideratum of both human-engineered and natural biological systems. Consider the following question,

Given a set of unknown outcomes {a_m}, with relative frequencies (probabilities) {p_m}, m = 1,…,M, what is the minimum average number of alphabet symbols needed to specify unequivocally which outcome occurred?

The answer is provided by the Coding Theorem⁸¹ which states that the minimum average number of symbols R(n) necessary to code the {a_m} using an n-ary alphabet obeys

where H_n() is the base-n entropy in “nits” of the answer probability distribution. Using a binary coding scheme, the minimum number of bits necessary is
where H₂(p) = (log₂n)H_n(p). Thus, we can always specify the information necessary to provide an answer in units of bits regardless of the coding alphabet size. From here on, log will denote log₂ unless specified otherwise.

Consider the communication problem associated with the “signal transduction code,” for example, a cell (sender) transmits signals to its environment (receiver) seeking direction about whether to divide symmetrically or asymmetrically, how to orient its mitotic spindle, whether to self-renew or to differentiate into a specialised cell type, and so on. Suppose this direction takes the form of a signal sequence {X_i} emitted by the sender and is interpreted by the receiver as some external (or internally processed) corresponding set of signals {Y_i} that are corrupted by various sources of uncertainty. It is important to note that the physics behind the {X_i} and {Y_i} are assumed arbitrary. All that is necessary is some stochastic mapping X → Y from sender to receiver summarised by a probability distribution f_Y|X().

Given our previous description of the number of bits necessary on average to provide answers, the natural fundamental question is how many bits per “channel use” (transmission of an X_i in this case) can the sender possibly convey in a reliable fashion? The term “reliable” means “where the probability of error can be made arbitrarily small by employing codes which span multiple channel uses.” A “code” is simply a sequence of symbols which correspond to a message. The answer is provided by the powerful Channel Coding Theorem⁸¹ which states that the capacity, C, of the channel is

where I(X;Y) is the mutual information between X and Y and is defined as
This maximisation can be modified to handle continuous X and Y and is in most practical situations further constrained by energy—the cost of producing signal X or interpreting the signal Y.

This question of continuous versus discrete descriptions of an underlying reality cannot be and is not ignored. Often, we cannot simply assume discrete representations, for example, a membrane voltage or a chemical concentration. Rate distortion theory^81,82 specifies how much information is necessary to approximate an information source under some fidelity criterion when a complete source specification is too large. With distortion measure d(X,q(X)) where q(X) is a finite (or “quantized”) representation of X, we can then ask how many bits per source symbol, R(ε), are required on average to represent an information source X under an average acceptable fidelity criterion ε. Rate distortion theory tells us

Just as important, rate distortion theory also tells us that any coding rate below R(ε) results in an unacceptable average distortion. Similar to the previously mentioned source coding theorem, this prevents us from seeking impossible “perpetual motion” strategies.

Consider the scenario where the signal upon which a receiver acts lies at the end of a cascade of intermediate processes. If these processes are deterministic, we could imagine them summarised by Z = g(Y) where Y is, say, the first signal that impinges on the cellular sensing apparatus and Z is the signal upon which the cell acts. The Data Processing Theorem⁸¹ states

I(Z;X) = I(g(Y);X) ≤ I(Y;X)

Thus, the number of bits per channel use that can be delivered to the receiver is upper-bounded by the channel capacity between X and Y. This theorem also holds if the mapping between Y and Z is stochastic. Thus, signaling cascades such as X → Y → Z → Ω result in

I(Ω;X) ≤ I(Y;X)

Note that nowhere has a particular coding scheme been specified. The information-theoretic concepts described provide bounds on information transfer regardless of the scheme used. That is, information theory is in some sense “mechanism blind.”

4.2 What simplifications does information theory offer?

The identification of signalling agents as well as their mechanisms of action and regulation in uncertain environments requires sophisticated experimental studies. However, many details are not necessary to employ usefully communication theory because knowledge of the specific methods (coding) by which information is conveyed does not affect the bounds on how much information there is, or how rapidly it can be delivered reliably. In other words, the beauty of pursuing a communication theoretic approach is that biological systems are not required to practice any particular style of coding or transmission. Rather, communication theory places fundamental physical limits on any method biological systems use to perform information transfer. Once the physical substrate is described, communication theory provides mechanism-blind bounds.

The well-known signal to noise ratio (SNR) is a simple but powerful example of mechanism-blindness in telecommunications theory. Consider a channel described by

r(t) = s(t) + w(t)

where s(t) is the information-bearing signal, w(t) is noise, and r(t) is the received signal. This type of additive signaling model arises naturally in a number of biological settings. There are infinite potential signal and receiver structures that could be used to carry information over the channel. However, if w(t) is white Gaussian noise, communication theory tells us that the figure of merit is the energy carried by signal s(t) relative to the impinging noise energy—the SNR.^81,83–85 The detailed structure of the coder, receiver, and signal do not affect the theoretical bounds on information flow.

A variety of similar bounds exist for efficient coding of specific objects and networks of communicating elements.⁸¹ It is this generality and implicit reduction of complexity that constitutes the power of a communication theoretic lens. Therefore, by analysing the physics of communication and using energy efficiency as a central tenet, communication theory may help to refine and to extend our understanding of communication in multicellular systems, be they natural or human-engineered, ancient or modern.

Perhaps the most overlooked and important feature of communication theory is that it can be used to determine what a cell can possibly know based only on the physics of the problem as opposed to detailed knowledge of genes, molecules, and networks—essentially an application of the data processing theorem to determine what is and is not possible for molecular, cellular and tissue behaviour. In other words, communication theory is blind to genetic and/or molecular mechanisms. This key notion is illustrated by the following examples.

4.3 Molecular machines

The relationship between information and energy was investigated for a “molecular machine”—a single macromolecule or macromolecular complex that performs a specific function for a living system—operating under isothermal conditions.⁸⁶ Restating the channel capacity theorem as a molecular machine capacity theorem allowed derivation of the minimum amount of energy the machine must dissipate in order to gain one bit of information: E_min = k_BTln(2) Joules per bit (k_B is the Boltzmann constant and T is the absolute temperature). In this context, the term “bits” is a measure of the molecular-state entropy. Since the quantity of interest is change in state, large numbers of “before” and “after” microstates (particular machine configurations) are irrelevant and so it is possible to speak about single bits for changes in a macroscopic object without knowledge of the detailed state of its molecules.

Information transmission in a molecular machine was studied⁸⁷ by comparing the implicit information necessary for protein binding to a specific DNA site and the energy involved in the transformation from bound to unbound state. That is, for DNA binding proteins, the before and after states correspond to the molecule bound to a non-specific site anywhere on a DNA molecule and to a specific functional site respectively. The isothermal efficiency of binding (for which neither external energy is supplied nor is any energy extracted from the system) was computed using the minimum energy dissipation required by a molecular machine to gain one bit of information (E_min = k_BTln(2)) and the information in DNA sequences bound specifically by proteins (sequence logos). For a bistable molecular machine in which the two states are distinct, the maximal isothermal efficiency was calculated to be 70%.

Although these studies pertain to molecular machines in a cell rather than multicellular systems, their basic ethos is the same as ours. We hope to identify physical quantities of interest, include explicitly energy usage and then seek to understand the limits of operation (characterised essentially by information transfer) based on available energy. The specific result that DNA binding proteins make efficient use of energy gives us hope that the operation of biological systems at higher levels of organisation can be treated similarly. That is, efficient energy usage is a hallmark of biological systems and might be used to narrow the range of potential mechanisms by excluding those which provably cannot achieve the requisite information transfer with the available energy. That said, the extent to which the results for DNA–protein macromolecular complexes can be applied to other molecular machines and to multicellular systems remains to be seen.

4.4 Chemotaxis in slime mould

Both unicellular and multicellular organisms exhibit chemotaxis, the ability to sense spatial heterogeneities in the concentration of extracellular molecules and to respond by polarising and migrating towards the source. In mammals, this process plays major roles in development and in adults, it is important in normal biology (for example, immune function and tissue repair) and pathology (for example, metastasis and inflammation).⁸⁸

Dictyostelium discoideum is a eukaryote that transitions from a collection of unicellular amoebae into a multicellular slug and then into a fruiting body within its life time. Information theory was employed to investigate how this organism can chemotax even when it is unclear whether the physics of the situation (cell/receptor positioning and stochasticity) could allow reliable measurement of spatial chemoattractant gradients.^88,89 The study considered two random variables: the true gradient and the direction in which a cell moves. The underlying, seemingly counterintuitive, idea was that given the direction chosen by the cell, the less information provided by the true direction, the better the cell's decision must be. That is, if the cell generally chooses something approximating the correct direction, knowledge of the true direction does not add much additional knowledge. Thus, the study sought to minimise the mutual information between the true direction and the chosen direction.

The theoretical analysis found that the organism can chemotax efficiently by temporally sampling the gradient during directed stochastic cell motion. Furthermore, this observation explained the apparently puzzling result that cells could chemotax even when they lacked direct gradient information.^88,90 Overall, information theory—the mutual information between the environmental and behavioural variables of interest—allowed the bounds of what was possible to be outlined without explicit consideration of the specific molecular workings of cells.

From a true communication theory perspective, the analysis was limited by its neglect of energy. Since cell mobility requires energy expenditure, it would be interesting to consider the energetics of mobile cell-driven gradient sensing compared to the maintenance of structures that perform spatial sensing in other ways, for example, anisotropic proliferation/retraction of surface receptors or even extension of (possibly mobile) filopodia to amplify spatial gradients. Put another way, a communication theoretic approach would consider what information is potentially available and then what cost in energy is required to secure the information. Hence, communication theory has the potential to both explain existing biology and perhaps even to identify under- or unappreciated biological solutions to a given problem.

4.5 Quorum sensing in bacteria

The small diffusible molecules involved in the luminescence of Vibrio harveyi are moderately well understood. Information theory was employed to investigate how these bacterial cells integrate and interpret the information contained within these autoinducer signals.⁹¹ The study used the known kinetics and physics of the receptor system to examine what is effectively mutual interference between two known autoinducers, AI-1 and AI-2. The theoretical analysis found that the mutual interference between AI-1 and AI-2 signals resulted in loss of information about the local environment and so bacteria may have evolved active strategies to limit mutual interference.

To the best of our knowledge, this is the first use of information theory in a biological system where a single observable is related to more than one “channel input” (in this case, AI-1 and AI-2 receptor occupancies). From our perspective, the most encouraging result is that the information-theoretic approach generated new insights amenable to subsequent experimental investigation without explicit knowledge of biochemical/signalling circuits and mechanisms.

4.6 Pheromone signalling in yeast

The unicellular eukaryote Saccharomyces cerevisiae finds potential mating partners using information about the extracellular concentration of a secreted pheromone. Mutual information was employed to investigate the alignment between two random variables: dose (secreted ligand concentration and receptor binding) and response (downstream intracellular mechanisms which respond to receptor occupancy).⁹² The theoretical analysis found that matching the dose and response characteristics results in better transmission of information about potential mates to the receiving cell. This result is not too surprising because the behaviour of sensors and actuators tends to be sigmoidal. By definition, a saturated sensor has a limited dynamic range and generally higher relative noise level; an actuator driven alternately to saturation and quiescense (“bang bang control”) with no middle ground in between has the same problem. That is, a graded response conveys information well and dose–response mismatch mutes a graded response.

Perhaps the most striking finding is that cells might have evolved the capacity to combat information suppressing mismatch by employing a feedback mechanism to adjust dose response. A known signalling protein (Sst2) was found to have a previously uncharacterised role in generating such feedback. Overall, an information theoretic approach increased understanding of cell signalling, once again, without a search for explicit mechanisms and signaling agents.

4.7 Molecular codes

Coding theory is the study of the properties of codes and their fitness for a specific application. A code described as a two-way information channel encodes meanings as symbols, reads the symbols, and then decodes their meanings. Because the forward mapping (meanings to symbols, the encoder) and backward mapping (symbols to meanings, the decoder) are coupled, the code and message co-evolve. Thus, the code can reassign meanings to symbols at later stages of its evolution. A code described as a one-way information channel encodes meanings as symbols, reads symbols, and then decodes their meanings. However, the encoder and decoder are uncoupled so symbols and meanings do not co-evolve resulting in a less flexible code. The costs associated with a biological coding system include the energy and resources required to initially construct and subsequently maintain its components, and to transmit information in an energy efficient and reliable fashion.

Molecular codes, mappings that relate symbols and meanings written in one molecular language into another, are components of evolutionary transitions. For example, cells with translation possess the redundant, error-correcting genetic code which reads DNA base triplets (codons) and decodes them as amino acids or a stop signal. Information theoretic concepts were used to model the genetic code as a one-way noisy information channel that receives an input of codons (symbols) and outputs the corresponding amino acids (meanings).⁹³ The statistical physics model was used to optimise a quantity representing the conflicting needs for error tolerance, diversity, and minimal energy cost. A code emerged when the benefits of specificity, the controlled synthesis of functional proteins due to non-random associations of codons and amino acids, exceeds the cost of producing and maintaining molecules able to recognise and distinguish targets from lookalikes. A similar topological rate distortion analysis has been applied to the problem of protein folding.⁹⁴ The evolution of the genetic code was been studied using rate distortion theory and non-equilibrium dynamics constrained by the availability of environmental metabolic free energy.⁹⁵

5. Metazoans: cellular conversations

Next, we discuss subjects ranging from molecules to organs that have a more direct bearing on multicellularity than the preceding biological topics and where further communication theoretic studies are warranted. We sketch some communication problems and suggest possible research avenues that could be pursued to address them.

5.1 Communication theory and organic codes: glycocode

The three main features of an organic code are a correspondence between the objects of two independent worlds, a system of molecular adaptors, and a set of rules that guarantee biological specificity.⁶ Ignoring the semantics of the message and considering only the information conveyed, one communication theoretic interpretation of these features is the stochastic mapping between symbols and meanings, a noisy information channel, and the transmission of information in an energy efficient and reliable fashion respectively. Such an interpretation opens up new avenues for exploring existing and yet-to-be-defined organic codes. Which aspects of the glycocode can be described as noisy information channels? What part do galectins, a family of carbohydrate binding proteins, play in the energy efficient and reliable transmission of glycan-encoded information?

In order to analyse organic codes within a communication theoretic framework, two basic issues need to be addressed: source coding, replacing an initial message by a shorter but fully equivalent one, and channel coding, protecting an initial message against transmission errors (the introduction of redundancy and replacement of the original message by a longer one). Having addressed the issues of source coding and channel coding—undoubtedly, tasks that are more readily explicated than solved—information theory concepts and theorems can be applied. Given an organic code, one starting point is developing mathematical abstractions of the information conveyed by messages, for example, a sequence of symbols from a finite-size alphabet where each letter can be distinguished unambiguously from the others.

Biological communication mediated by the glycome. Glycans and glycoconjugates are ubiquitous: they can be found on the surfaces of all cells, in the cytoplasm and nucleus of eukaryotes, and within the extracellular matrix.^29–35 Complex glycans at the cell surface are targets of microbes and viruses, regulate cell adhesion and development, influence metastasis of cancer cells, and regulate myriad receptor:ligand interactions. Intracellularly, glycans within the secretory pathway regulate protein quality control, turnover, and trafficking of molecules to organelles. In the nucleus, crosstalk between nucleocytoplasmic O-linked N-acetylglucosamine and phosphorylation regulates signalling, cytoskeletal functions, and gene expression in response to nutrients and stress. Thus, elements of the glycome are at the forefront of molecular and cellular communication, not least the flow and exchange of information required to transform a collection of cells into a society. In unicellular organisms, glycans function generally as structural components of the cell membrane. In multicellular organisms, they have a broader and deeper repertoire of roles, mobilising many, if not most, of the forces, processes, and phenomena linked to normal and aberrant biology.

In broad terms, glycome-mediated communication consists of encoding information in the primary structure, density and presentation of glycans and glycoconjugates, deciphering messages by, for example, carbohydrate binding-molecules, and transducing the decoded messages by multiple signalling pathways. The glycocode is not a static organic code because the complex information conveyed by glycans and glycoconjugates is susceptible to internal and external influences such as age, diet, lifestyle, xenobiotic compounds, and microbiomes. Whilst the amino acid sequence of a protein is determined by the corresponding gene, glycans lack a direct template for their biosynthesis. Since a glycan is generated by the coordinated action of many enzymes in the subcellular compartments of a cell, its final structure depends on the expression, activity, accessibility, and interactions of many molecules. Thus, the glycocode is dynamically and reciprocally linked to both an organism's genome and to environmental factors (direct effects on individual enzymatic processes or indirect induction of epigenetic changes that modify gene expression patterns).

Encoding carbohydrate messages: primary structure of glycans. A first step in communication theoretic studies of the glycome and the glycocode is encoding the meaning specified by carbohydrates. Doing so will require taking into account not only the primary structure of glycans, but also factors such as glycan density and presentation. Since compact representations of signals are desirable for reasons that can almost always be related to efficient energy usage, an important task is developing short length representations that capture the complex information conveyed by glycans and glycoconjugates. Here, we restrict ourselves to the problem of describing the primary structure of carbohydrates as a sequence of symbols from a glycan specification alphabet.

The protein and DNA specification alphabets have 20 and 4 letters respectively and even lipids can be represented by 8 categories.²⁰ Glycans present greater challenges because compared to amino acids and nucleic acids, the number of naturally occurring monosaccharides is larger and ill-defined, a pair of residues can be linked in several ways, and a residue can be connected to three or four others. Glycans have been proposed to be derived initially from 32, possibly more, monosaccharides²⁰ but this includes residues with secondary modifications. Thus, the exact size and precise nature of a glycan specification alphabet is an open question—∼100 is a reasonable guess for the number of “parent” monosaccharides (residues without substitutions) present in all three kingdoms of life.

DNA and protein molecules can be represented, at least in their most basic forms, as simple linear strings but glycan chains are complex branched structures. Permutations of the phosphodiester and peptide bonds are the main source of coding capacity in nucleic acids and proteins. The superior coding capacity of glycans can be attributed to (i) linkage options for the glycosidic bond (for example, 1–2, 1–3, 1–4 or 1–6 when L-fucose is conjugated to glycans), (ii) anomeric bond configuration (α or β; the only difference between glycogen/starch and cellulose), (iii) ring size (pyranose or furanose), and (iv) branches.³⁰ With 20 different letters, ∼10⁷ hexapeptides are possible but there are ∼10¹⁵ theoretically possible hexasaccharides. Given five monosaccharides, there are ∼10⁴ possible glycan isomers if the monomers are identical and ∼10⁶ if they are different—far more that the number of proteins that could be created from five amino acids.²⁴

Entropy and mutual information are measures that have been used for protein- and nucleic acid-related statistical machine learning tasks such as alignment and searching. Thus, information theoretic studies of glycans are likely to have many practical applications. Given a glycan specification alphabet, the primary structure of a glycan could be represented as a graph where nodes correspond to monosaccharides and edges to glycosidic bonds. Information theoretic measures for graphs have been developed⁹⁶ but the entropy of two glycans with the same graph topology would be identical even if they differed in their constituent monosaccharides and anomeric bond configurations. However, this coding scheme could be modified by “colouring” both nodes and edges and a theoretical upper bound obtained for the information necessary to specify glycans.

Whilst the graph theoretic approach offers an analytic bound, it is useful also to catalogue glycan types directly so that we can begin to quantify glycan specification information empirically. By enumerating glycan structures and their relative frequencies, an entropy can be calculated which provides an empirical but still quantitative lower bound on the amount of information—from whatever sources—necessary to produce glycans. From there, with the known map from genes to proteins as a guide, one can begin to provide quantitative lower bounds on, for example, how many genes are necessary to determine glycan structure—without specific knowledge of which genes are responsible or even the enzymes that determine glycan structure. That is, the data processing theorem requires that whatever the original source for glycan specification, the original amount of information necessary is at least as large as the entropy of glycan specification. Resources for such studies include EUROCarbDB whose central database of carbohydrate structures contains ∼13 500 unique glycan sequences currently.³⁵

Reading carbohydrate messages: protein–glycan interactions. One mechanism for deciphering the information conveyed by the glycocode is recognising stereochemical determinants of glycans and glycoconjugates using molecules such as lectins, receptors, toxins, microbial adhesins, antibodies, and enzymes. Here, we focus on galectins, an evolutionarily conserved family of glycan-binding proteins that lie at the crossroads of health and disease and are associated with most of the processes that are the hallmarks of multicellularity.^97–100 Most galectins are bivalent or multivalent with regard to their carbohydrate-binding activities and have the potential to form distinct types of lattices with multivalent glycans. Secreted galectins mediate communication between immune cells not by binding to cell surface receptors but by recognising a preferred set of cell surface glycoconjugates. Protein–glycan interactions are as key to deciphering the glycome as protein–nucleic acid interactions are to decoding the genome.

Mutual information has been used to examine protein–nucleic acid interactions such as the properties of protein sequences and structures that are most useful in binding DNA.^18,101,102 Thus, information theoretic investigations of protein–glycan interactions in general and galectin–glycan binding in particular are likely to have many practical applications. As discussed earlier, the isothermal efficacy of information transmission in a DNA binding protein–DNA complex has been examined.⁸⁷ Whilst a protein–glycan macromolecular complex can be seen also as a “molecular machine,” a similar analysis is more challenging: sequence logos can be used to compute the information in DNA sequences bound by specific proteins but there is, at present, no analogous method for computing the information in glycans bound by specific glycan binding molecules.

5.2 Communication theory and structural codes

The chromosome territory code. A mammalian cell spends the majority of its time in a phase where the DNA of each chromosome is folded such that it occupies a discrete, spatially restricted nuclear subvolume called a chromosome territory (CT). CTs can overlap, have limited movement and their global spatial organisation is non-random and probabilistic.^103–110 The spatiotemporal position of a CT in a cell nucleus is influenced by internal and external factors such as chromosome size and overall gene density, cell type, shape of cell nucleus, pre- and post-embryonic developmental stage, disease state, age, and species. Cell types that share a common developmental and/or differentiation pathway may have similar CT position patterns and the patterns in a given cell type are conserved evolutionarily. Since cell differentiation is one of the innovations that mediated the transition from single cells to multicellular organisms, CT position patterns provide a window into multiple facets of multicellularity.

Here, we propose a novel structural code, the CT code—a stochastic mapping between the spatial position pattern of the CTs in a cell nucleus (CT configuration) and a cell with a particular suite of architectural and functional characteristics (cellular phenotype). We assume the existence of machinery that encodes and decodes CT configurations and cellular phenotypes. We posit that CT configurations reside in a CT configuration space where a point corresponds to a particular arrangement of CTs in a nucleus. A cellular phenotype corresponds to a region in CT configuration space, that is, many CT position patterns are compatible with a particular cellular phenotype. This tolerance captures the probabilistic and non-random nature of CT organisation so that, for example, the spatial organisation of CTs in mammary gland luminal epithelial cell nuclei cannot be described by a single CT configuration. In essence, a cellular phenotype is a probability distribution on CT configuration space. Whilst the information needed to encode a particular cellular phenotype is degenerate, this degeneracy is constrained by a functional requirement to control the spatiotemporal locations of CTs.

Energy and resources are required to construct and maintain the components of this structural coding system, and to ensure that information transmission is both energy efficient and reliable. Information is conveyed only when CT configuration and cellular phenotype are correlated, even partially, that is, there is an association between a particular non-random arrangement of CTs and a specific set of cell behaviours. One proxy for cellular phenotype is a cell's molecular fingerprint, its profile of transcripts, proteins, glycans, metabolites and so on. Thus, cellular phenotypes and differences between them could be quantified by exploiting extant repositories of experimentally determined molecular profiling data. Since different regions of CT configuration space correspond to different phenotypes, paths through this space could correspond to processes associated with normal and/or aberrant biology, for example, the differentiation, dedifferentiation and dysdifferentiation of mammary gland luminal epithelial cells.

An important open problem is the stochastic mapping between CT configurations and cellular phenotypes, in general as well as for specific species. Currently, it is not feasible to determine experimentally the spatiotemporal position patterns of CTs in the nuclei of a large number of cells of the same let alone different type. One theoretical abstraction that may be useful is to treat the problem as a geometric packing problem: the arrangement of a defined number of objects (ellipsoids representing CTs) inside a container (an ellipsoid representing the cell nucleus) subject to constraints such as the allowable overlap between objects, and the relative and absolute position of an object with respect to both the container and other objects. A simple geometric model of a generic human cell nucleus consisting of spherical CTs of different radii packed randomly inside a spherical nucleus has been developed but the underlying technique has many limitations including an inability to handle constraints.¹¹¹ Methods in mathematical and robust optimisation could be used to formulate more general purpose geometric packing problems that include constraints. However, finding feasible solutions to and suitable approximations for non-convex optimisation problems will be challenging.^112,113

The CT code lends itself to a variety of communication problems. For example, a mammary gland luminal epithelial cell might transmit signals to its (a)biotic environment seeking direction about whether to be “normal” or “malignant.” Assume this takes the form of a signal sequence {X_i} emitted by the cell nucleus and interpreted by the environment as the corresponding set of signals {Y} that are corrupted by uncertainty. All that we require is some stochastic mapping X → Y summarised by a probability distribution f_Y|X(). This problem might be elaborated to include feedback: the environment transmits information to the cell nucleus with one outcome being an altered CT configuration.

Mitotic spindle code. Earlier, we suggested that mitotic spindle orientation is a new DPM (Fig. 1). Here, we propose a novel structural code, the mitotic spindle code—a stochastic mapping between spindle orientation and the plane of cell division in the context of single cells and many-celled structures.

The relationship between interphase cell–substrate adhesion and mitotic spindle orientation in adherent cells has been studied using two-dimensional (2D) patterns of fibronectin generated using microfabricated stamps.⁷⁸ By controlling both cellular geometry and cell adhesion, the spindle axis in cells was induced to take up a variety of shapes and a predictive mathematical model of the process was developed to determine how novel patterns of interphase cell–substrate adhesions would be interpreted by the spindle (Fig. 2). From an information theoretic perspective, a cell might choose to minimise the mutual information between what it considers to be the “correct” orientation of its mitotic spindle and the true orientation required by its environment. For any DPM, communication theory might allow the bounds of what is possible to be outlined without explicit consideration of the specific workings of cells, for example, by making use of the mutual information between variables of interest in the single-cell and collective state, the cost of producing and interpreting signals associated with the molecular components of the DPM, and the energetics of the physical forces and processes mobilised by the DPM.

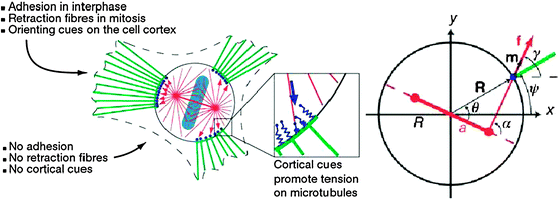Fig. 2 Spindle orientation and cortical forces in adherent cells (adapted from ref. 78). Left A spherical cell during mitosis (circle) linked by retraction fibres (green) to adhesion sites. The density of retraction fibres at the cortex activates cortical force generators (blue), which exert pulling forces on astral microtubules. The resultant torque on the spindle (red) rotates it as well as the metaphase plate (cyan) until a stable orientation angle is attained. RightSpindle geometry and cortical forces. Spindle poles (red) are separated by a distance 2a in a cell of radius R. Cortical force generators exert a pulling force f tangential to the orientation of astral microtubules, the unit vector m. This force exerts a torque R × f on the spindle. R is the vector pointing to the cortical position at which the force acts.

Assume that a given cell senses its surroundings through extensions (filaments, fibres). An information theoretic perspective would then ask how much spatial information is conveyed to the cell through such tetherings. Modulo determining typical environments (the entropy of the milieus in which a cell might find itself), the data processing theorem and channel capacity theorems should allow determination of the precision with which a spindle can be oriented.

In addition to physical tethering, cells communicate in a panoply of ways and a plethora of mechanisms could be imagined through which a cell might gather data and learn about its environment. For example, the environment could produce anisotropic distributions of signalling molecules which diffuse through the extracellular spaces. A cell might produce auto-inducing signalling agents whose local concentrations are affected by anisotropic signal uptake in the surrounding medium. That is, cellular extensions are but one of many possible ways a cell could learn about its local environment. This begs the question: why might one data and knowledge gathering method be chosen over another?

Communication theory suggests an organising principle that might provide a path towards an answer. Energy is a fundamental resource in biology and is often, if not always, conserved where possible. Hence, the milieu-sensing problem could be cast in a formal communication theory context: how might a cell use energy resources most efficiently to determine, for example, the geometry of its surroundings? Given our knowledge of protein synthesis, it is relatively straightforward to calculate energy budgets for a variety of methods such as the construction of filaments and fibres and the diffusion of signalling molecules. It would be interesting to determine the circumstances under which what seems like an energy intensive method (assembly/disassembly of cellular extensions) is more energy efficient than synthesizing diffusive signalling molecules and maintaining an appropriate number and distribution of receptors. Doing so might yield unexpected results, as was the case for interstellar communication where sending information-bearing physical artifacts was found to be far more energy efficient than communicating via electromagnetic signals.¹¹⁴

5.3 Single and combinatorial actions of DPMs

The molecular constituents of DPMs are associated with physical properties of meso- to macroscopic systems that are amenable to modification by external parameters and extrinsic forces (Table 1). Spatiotemporal combinations of DPMs can mobilise novel mesoscale physical phenomena and so mediate the primary transformations believed to have produced morphologically complex body plans from clusters of cells.⁶⁰ These transformations establish stable mixtures of cells occupying more than one biochemical state, form distinct non intermixing cell layers, produce internal cavities, generate non-uniform patterns of cell occupying different biochemical states, and disperse subpopulations of cells without disintegrating the organism. The genetic programs observed in organisms are the products of evolution in which forms organised by inherent properties were stabilised by post-hoc genetic circuitry. In essence, genetic programs are seen as an epiphenomenon of self-organisation.

If each discrete action implemented by a DPM is considered to be a “primitive” operation, multicellular systems of varying size and complexity can be “built” through a sequence of discrete actions in space and time. However, the molecules and actions mobilised by DPMs are not “orthogonal”—for example, “Cadherins” are part of both the ADH and DAD DPMs (Table 1)—and the sequential application of different DPMs can generate multiple paths to the same many-celled form. Biologically, this overlap is useful because different genes can achieve the same outcome, a way perhaps to hedge evolutionary bets. However, from the analytic standpoint of determining form and function from genome/proteome/glycome specification (reliable code-to-structure/function transformation), such non-orthogonality presents obvious combinatorial difficulties. When presented with such dependencies, communication theory seeks to determine a set of independent actions and effects which through combinations can be used to describe the dependent system.

An “orthogonal” set of DPMs would allow easy quantification of the information content embodied by biological form which could then be related to the eminently quantifiable information content of relevant genome portions. Even if such DPMs or similar entities exist, they may not have physical analogues in cells, that is, there may be no set of molecular signals and/or operations that define independent actions. Nonetheless, realisable/observed actions could by definition be constructed analytically from “basis actions” to help quantify specification and thence information flow in multicellular systems. Whether such a decomposition is actually possible remains to be seen.

5.4 Tissues and organs: building a mammary gland

Three basic unit operations of morphogenesis have been proposed: assembly from basic building blocks, sculpting from a block of material, and folding 2D surfaces into 3D structures.¹¹⁵ Examples include muscular and skeletal structures assembled from different cells that are specified in one region and delivered to another, separate fingers sculpted from limbs by the removal of extra cells, and tissue layers and other shapes formed by folding sheets composed of epithelial cells. These operations are regulated spatially and temporally in a combinatorial manner, and the underlying molecular mechanisms and cellular processes are conserved across tissue types and species. For example, mammary gland epithelial patterning might involve a gradient of chemical signals (morphogens) that generate a localised force which deforms the cellular layer. Proteins secreted by one or more sources bind to cell surface receptors, the activated receptors initiate a cascade of intracellular signals that regulate gene expression, the new pattern of expressed genes gives rise to changes in cellular properties such as shape and mobility, and these altered properties specify the cellular activities and mechanical modifications necessary to generate epithelial folds.

We might seek to decompose the operations that generate a tissue or an organ into a collection of interacting actions—some combination of DPMs, DTFs, strategies similar to those underlying chemotaxis in slime mould, quorum sensing in bacteria, and pheromone signalling in yeast, approaches that generate many-celled forms, and so on. As interesting and important as this type of “recipe” might be, this is only the beginning from a communication theory perspective. By enumerating steps, we inherently provide some measure of the information necessary to construct, say, a mammary gland, and implicitly, some measure of the genome portion size associated with this task.

5.5 Ageing: reliable information transfer

The origin and evolution of multicellularity likely involved a dialectic of stability and change, certainty and uncertainty. Interactions between cells and their environment that involved too much certainty and predictability might have restricted the depth and breadth of possible morphotypes thereby rendering adaptation to the full range of potential internal and external conditions difficult or impossible. The early history of multicellular animals may have required maximising the outcomes of relations rather than initial encounters.

Extant organisms maintain form reliably, generating the same stable structures time and again, generation after generation. Since molecular, cellular, and tissue events are inherently stochastic and incomplete knowledge is pervasive, decision-making under uncertainty is the norm. The current and anticipated future state of the environment need to be inferred from noisy data, a cost–benefit analysis of each potential response in light of the predicted future and past history is required, the time taken to decide and generate a response needs to be considered, and decisions are made in the presence of other cooperative and/or competitive decision-makers.¹¹⁶ Tissues, organs and organisms require a web of intercommunicating processes that are stable in their ability to maintain form and function, yet flexible in their responses to the environment. Dysfunctions of multicellularlity likely reflect changes in efficiency (throughput) and resilience (adaptability).

Ageing is characterised by a systemic decline of the capacity to respond to internal and external stresses, leading to increased mortality. In most tissues and organs, the process of progressive loss of adaptive abilities is accompanied by functional decline but the exact pattern of phenotypic changes varies from one individual to the next and depends upon genotype as well as environmental conditions. In metazoans with renewable tissues, longevity is affected by the balance between stem cell quantity and quality.¹¹⁷Cellular senescence, an aggregate of phenotypes that arrests rather than kills would-be tumour cells, mobilises the systemic and local tissue milieu for resolution of tissue damage, a mobilisation that can be beneficial (tumour suppression and tissue repair in young organisms) or detrimental (tumour promotion and ageing in late life).⁶⁹Ageing is thought to be a time-dependent process of cell dysdifferentiation and is associated with increased stochastic deregulation of cellular gene expression.¹¹⁸ As cell-to-cell heterogeneity increases over time and tissues become cellular mosaics, the energy efficiency and reliability of information transmission changes—communication, ageing, and uncertainty are intimately connected.

Probability distributions are central to communication theory. For example, the stochastic mapping from sender to receiver is summarised by f_Y|X(), and the noise in a channel described by an additive signalling model, w(t), is usually a white Gaussian. A communication theoretic analysis of ageing might benefit from the use of different classes of probability distributions such as members of the exponential, Cauchy, uniform, and Laplace families. Instead of the same distribution, we might seek to sample from a distribution of distributions, either at random or in a time dependent manner.

The Channel Coding Theorem addresses the question of conveying signals in a reliable fashion where the probability of error can be made arbitrarily small by employing codes which span multiple channel uses. A number of questions arise if ageing is associated with increasingly less reliable signal transmission and/or changes in the cost of producing or interpreting signals. Does this apply to signals from some or all organic codes? Is it cell- and/or tissue-type dependent? Are there fewer channel uses over time? Does the mutual information between the sent and received signals change over time? With respect to rate distortion theory, is ageing associated with changes in how much information is necessary to approximate an information source such as an organic code—increasing the number of wild-goose chases (attempts to seek perpetual motion strategies)?

If a sense of the information flow necessary to determine tissue, organ, organism and multicellular structure can be determined, then an immediate question arises. Given the physics of the communication channels between cells, what limits are placed on the interaction of cells and their various actions? Answers to such questions could help illuminate the limits of stable biological systems and/or suggest the possibility of previously unexplored portions of morphospace that might be engineered artificially for specific purposes.^119–124

6. Communication theory to multicellular biology and back again

We have described some key concepts in information and coding theory and showed how they have been used to study a variety of organisms (unicellular eukaryotes, bacteria) and phenomena (gradient sensing, ligand-receptor interactions, signal transduction, organic codes). Our primer provided but a glimpse of the elegance, beauty and power of communication theory. For example, the increasingly studied area of network information theory—a field which seeks to provide bounds on reliable information passage between multiple senders and receivers—cannot but help and be relevant to multicellular biology, ancient and modern.

From simple representation and coding of macromolecules to the more complicated behaviours of morphogenesis and ageing, a communication theoretic approach allows quantitative statements to be made about the processes involved. The inherent mechanism-blind nature of communication theory means that a lack of a priori detailed molecular and/or genetic knowledge of agents and mechanisms does not preclude the provision of guidance about what signalling modalities are probable or improbable under energy constraints. We suspect communication theory could be of value in “forensic” retrospective studies that seek likely evolutionary developmental pathways and in experiments whose aim is to uncover (or rule out) detailed mechanisms.

So far, we have highlighted how communication theory has and could contribute to understanding a myriad of problems in biology. In turn, we expect the study of multicellular biology could lead to advances in communication theory, especially in the still immature field of network information theory.⁸¹ It is possible, if not likely, that biological systems, having had billions of years to evolve, will provide new insights into an area that has thus far been perceived as the sole domain of telecommunications engineering and for which it is proving devilishly difficult to derive a complete theory.

Communication in biological systems may have something to contribute even to the well-understood body of “classical” communication theory. For instance, it is well known that feedback over memoryless channels does not increase channel capacity but the same cannot be said of channels with memory.⁸¹ As a matter of mathematical convenience therefore, it is not uncommon for communication theorists to recast channels with memory into memoryless analogues for subsequent analysis and engineering. That is, codes are designed for the memoryless analogue and then inverse-transformed for use on the actual channel with memory. Modern wireless systems with arrays of transmit and receive antennas (Multiple-Input Multiple-Output or MIMO for short)^125,126 are an obvious example of this design ethos. However, the ubiquity of feedback in biological systems and an assumption about evolved energy-efficiency suggests that communication theory, rather than viewing channels with memory as a complication or an annoyance, should consider the potential engineering advantages that channels with memory might afford.

Acknowledgements

This work was supported in part by NSF Grant CDI-0835592, A Communications Theory Approach to Morphogenesis and Architecture Maintenance. Work by I.S.M. was supported also by an unrestricted gift from Kasian Franks, SeeqPod, Inc. We thank Ramray Bhat, Stuart Newman and Tom Schneider for comments and discussions. We are grateful to two referees whose careful, thoughtful and considered comments helped to shape, clarify and improve the manuscript greatly.

References

1. E. Szathmáry and J. Maynard Smith, The major evolutionary transitions, Nature, 1995, 374, 227–232.
2. E. Jablonka and M. J. Lamb, The evolution of information in the major transitions, J. Theor. Biol., 2006, 239, 236–246.
3. M. Barbieri, A short history of biosemiotics, Biosemiotics, 2009, 2, 221–245.
4. G. Battail, Applying semiotics and information theory to biology: A critical comparison, Biosemiotics, 2009, 2, 303–320.
5. K. Kull, T. Deacon, C. Emmeche, J. Hoffmeyer and F. Stjernfelt, Theses on biosemiotics: Prolegomena to a theoretical biology, Biol. Theory, 2009, 4, 167–173.
6. M. Barbieri, Biosemiotics: a new understanding of life, Naturwissenschaften, 2008, 95, 577–599.
7. T. D. Schneider, Claude Shannon: biologist. The founder of information theory used biology to formulate the channel capacity, IEEE Eng. Med. Biol. Mag., 2006, 25, 30–33.
8. T. D. Schneider, Twenty Years of Delila and Molecular Information Theory: The Altenberg-Austin Workshop in Theoretical Biology Biological Information, Beyond Metaphor: Causality, Explanation, and Unification, Biol. Theory, 2006, 1, 250–260.
9. C. Adami, Information theory in molecular biology, Phys. Life Rev., 2004, 1, 3–22.
10. M. K. Gupta, The quest for error correction in biology, IEEE Eng. Med. Biol. Mag., 2006, 25, 46–53.
11. G. Sicot and R. Pyndiah, Study on the genetic code: comparison with multiplexed codes, in IEEE Int Symp Information Theory, 2007, pp. 2666–2670.
12. R. A. Gatenby and B. R. Frieden, Information theory in living systems, methods, applications, and challenges, Bull. Math. Biol., 2007, 69, 635–657.
13. P. Nurse, Life, logic and information, Nature, 2008, 454, 424–426.
14. R. Giancarlo, D. Scaturro and F. Utro, Textual data compression in computational biology: a synopsis, Bioinformatics, 2009, 25, 1575–1586.
15. Ö. U. Nalbantog̃lu, D. J. Russell and K. Sayood, Data compression concepts and algorithms and their applications to bioinformatics, Entropy (Basel), 2010, 12, 34–52.
16. G. Battail, Heredity as an encoded communication process, IEEE Trans. Inf. Theory, 2010, 56, 678–687.
17. O. Milenkovic, G. Alterovitz, G. Battail, T. P. Coleman, J. Hagenauer, S. P. Meyn, N. Price, M. F. Ramoni, I. Shmulevich and W. Szpankowski, Introduction to the special issue on information theory in molecular biology and neuroscience, IEEE Trans. Inf. Theory, 2010, 56, 649–652.
18. A. D. Fernandes and G. B. Gloor, Mutual information is critically dependent on prior assumptions: would the correct estimate of mutual information please identify itself?, Bioinformatics, 2010, 26, 1135–1139.
19. C. G. Bowsher, Information processing by biochemical networks: a dynamic approach, J. R. Soc. Interface, 2010, 8, 186–200.
20. J. D. Marth, A unified vision of the building blocks of life, Nat. Cell Biol., 2008, 10, 1015.
21. Essentials of Glycobiology, ed. A. Varki, R. Cummings, J. Esko, H. Freeze, P. Stanley, C. Bertozzi, G. Hart and M. Etzler, Cold Spring Harbor Laboratory Press, 2008.
22. L. L. Kiessling and R. A. Splain, Chemical approaches to glycobiology, Annu. Rev. Biochem., 2010, 79, 619–653.
23. H.-J. Gabius, H.-C. Siebert, S. André, J. Jimínez-Barbero and H. Rüdiger, Chemical biology of the sugar code, ChemBioChem, 2004, 5, 740–764.
24. G. Lauc and V. Zoldoš, Protein glycosylation—an evolutionary crossroad between genes and environment, Mol. BioSyst., 2010, 6, 2373–2379.
25. K. F. Aoki-Kinoshita, An introduction to bioinformatics for glycomics research, PLoS Comput. Biol., 2008, 4, e1000075.
26. M. Frank and S. Schloissnig, Bioinformatics and molecular modeling in glycobiology, Cell. Mol. Life Sci., 2010, 67, 2749–2772.
27. Y. Akune, M. Hosoda, S. Kaiya, D. Shinmachi and K. F. Aoki-Kinoshita, The RINGS resource for glycome informatics analysis and data mining on the Web, OMICS, 2010, 14, 475–486.
28. G. W. Hart and R. J. Copeland, Glycomics hits the big time, Cell, 2010, 143, 672–676.
29. C. H. Chay and K. J. Pienta, Evidence for lectin signaling to the nuclear matrix: cellular interpretation of the glycocode, J. Cell. Biochem., 2000, 35, 123–129.
30. H. J. Gabius, Glycans: bioactive signals decoded by lectins, Biochem. Soc. Trans., 2008, 36, 1491–1496.
31. R. D. Cummings, The repertoire of glycan determinants in the human glycome, Mol. BioSyst., 2009, 5, 1087–1104.
32. D. J. Harvey, A. H. Merry, L. Royle, M. P. Campbell, R. A. Dwek and P. M. Rudd, Proposal for a standard system for drawing structural diagrams of N- and O-linked carbohydrates and related compounds, Proteomics, 2009, 9, 3796–3801.
33. S. Herget, R. Ranzinger, K. Maass and C.-W. v. d. Lieth, GlycoCT—a unifying sequence format for carbohydrates, Carbohydr. Res., 2008, 343, 2162–2171.
34. The Carbohydrate-Active enZYmes Database: families of structurally-related catalytic and carbohydrate-binding modules (or functional domains) of enzymes that degrade, modify, or create glycosidic bonds. http://www.cazy.org/.
35. EuroCarbDB: a repository of carbohydrate structures, experimental evidence, and carbohydrate-oriented research and analysis tools. http://www.ebi.ac.uk/eurocarb.
36. R. I. Schwarz and M. J. Bissell, Dependence of the differentiated state on the cellular environment: modulation of collagen synthesis in tendon cells, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 4453–4457.
37. J. B. Kim, R. Stein and M. J. O'Hare, Three-dimensional in vitro tissue culture models of breast cancer—a review, Breast Cancer Res. Treat., 2004, 85, 281–291.
38. L. G. Griffith and M. A. Swartz, Capturing complex 3D tissue physiology in vitro, Nat. Rev. Mol. Cell Biol., 2006, 7, 211.
39. C. R. Woese and N. Goldenfeld, How the microbial world saved evolution from the Scylla of molecular biology and the Charybdis of the modern synthesis, Microbiol. Mol. Biol. Rev., 2009, 73, 14–21.
40. R. Xu, A. Boudreau and M. J. Bissell, Tissue architecture and function: dynamic reciprocity via extra- and intra-cellular matrices, Cancer Metastasis Rev., 2009, 28, 167–176.
41. D. C. Radisky, M. Stallings-Mann, Y. Hirai and M. J. Bissell, Single proteins might have dual but related functions in intracellular and extracellular microenvironments, Nat. Rev. Mol. Cell Biol., 2009, 10, 228–234.
42. S. Atkinson and P. Williams, Quorum sensing and social networking in the microbial world, J. R. Soc. Interface, 2009, 6, 959–978.
43. D. T. Hughes, D. A. Terekhova, L. Liou, C. J. Hovde, J. W. Sahl, A. V. Patankar, J. E. Gonzalez, T. S. Edrington, D. A. Rasko and V. Sperandio, Chemical sensing in mammalian host–bacterial commensal associations, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9831–9836.
44. I. Sekirov, S. L. Russell, L. C. Antunes and B. B. Finlay, Gut microbiota in health and disease, Physiol. Rev., 2010, 90, 859–904.
45. L. Dethlefsen, M. McFall-Ngai and D. A. Relman, An ecological and evolutionary perspective on human–microbe mutualism and disease, Nature, 2007, 449, 811–818.
46. N. King, Nature and nurture in the evolution of cell biology, Mol. Biol. Cell, 2010, 21, 3801–3802.
47. V. Sperandio, A. G. Torres, B. Jarvis, J. P. Nataro and J. B. Kaper, Bacteria–host communication: the language of hormones, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8951–8956.
48. J. L. Inman and M. J. Bissell, Apical polarity in three-dimensional culture systems: where to now?, J. Biol., 2010, 9, 2.
49. C. M. Ghajar and M. J. Bissell, Tumor engineering: the other face of tissue engineering, Tissue Eng. A, 2010, 16, 2153–2156.
50. S. R. Fairclough, M. J. Dayel and N. King, Multicellular development in a choanoflagellate, Curr. Biol., 2010, 20, R875–R876.
51. S. Brenner, Sequences and consequences, Philos. Trans. R. Soc. London, Ser. B, 2010, 365, 207–212.
52. S. A. Nichols, M. J. Dayel and N. King, Genomic, phylogenetic, and cell biological insights into metazoan origins, in Animal Evolution: Genes, Genomes, Fossils and Trees, ed. M. J. Telford and D. T. J. Littlewood, Oxford University Press, 2008.
53. M. Abedin and N. King, Diverse evolutionary paths to cell adhesion, Trends Cell Biol., 2010, 20, 734–742.
54. N. King, M. J. Westbrook, S. L. Young, A. Kuo, M. Abedin, J. Chapman, S. Fairclough, U. Hellsten, Y. Isogai, I. Letunic, M. Marr, D. Pincus, N. Putnam, A. Rokas, K. J. Wright, R. Zuzow, W. Dirks, M. Good, D. Goodstein, D. Lemons, W. Li, J. B. Lyons, A. Morris, S. Nichols, D. J. Richter, A. Salamov, J. G. I. Sequencing, P. Bork, W. A. Lim, G. Manning, W. T. Miller, W. McGinnis, H. Shapiro, R. Tjian, I. V. Grigoriev and D. Rokhsar, The genome of the choanoflagellate Monosiga brevicollis and the origin of metazoans, Nature, 2008, 451, 783–788.
55. M. Srivastava, E. Begovic, J. Chapman, N. H. Putnam, U. Hellsten, T. Kawashima, A. Kuo, T. Mitros, A. Salamov, M. L. Carpenter, A. Y. Signorovitch, M. A. Moreno, K. Kamm, J. Grimwood, J. Schmutz, H. Shapiro, I. V. Grigoriev, L. W. Buss, B. Schierwater, S. L. Dellaporta and D. S. Rokhsar, The Trichoplax genome and the nature of placozoans, Nature, 2008, 454, 955–960.
56. M. Srivastava, O. Simakov, J. Chapman, B. Fahey, M. E. A. Gauthier, T. Mitros, G. S. Richards, C. Conaco, M. Dacre, U. Hellsten, C. Larroux, N. H. Putnam, M. Stanke, M. Adamska, A. Darling, S. M. Degnan, T. H. Oakley, D. C. Plachetzki, Y. Zhai, M. Adamski, A. Calcino, S. F. Cummins, D. M. Goodstein, C. Harris, D. J. Jackson, S. P. Leys, S. Shu, B. J. Woodcroft, M. Vervoort, K. S. Kosik, G. Manning, B. M. Degnan and D. S. Rokhsar, The Amphimedon queenslandica genome and the evolution of animal complexity, Nature, 2010, 466, 720–726.
57. D. H. Erwin, Early origin of the bilaterian developmental toolkit, Philos. Trans. R. Soc. London, Ser. B, 2009, 364, 2253–2261.
58. T. Domazet-Lošo and D. Tautz, Phylostratigraphic tracking of cancer genes suggests a link to the emergence of multicellularity in metazoa, BMC Biol., 2010, 8, 66.
59. S. A. Newman, G. Forgacs and G. B. Müller, Before programs: the physical origination of multicellular forms, Int. J. Dev. Biol., 2006, 50, 289–299.
60. S. A. Newman and R. Bhat, Dynamical patterning modules: physico-genetic determinants of morphological development and evolution, Phys. Biol., 2008, 5, 015008.
61. C.-M. Chuong, Limb pattern, physical mechanisms and morphological evolution—an interview with Stuart A. Newman, Int. J. Dev. Biol., 2009, 53, 663–671.
62. S. A. Newman and R. Bhat, Dynamical patterning modules: a “pattern language” for development and evolution of multicellular form, Int. J. Dev. Biol., 2009, 53, 693–705.
63. S. A. Newman, R. Bhat and N. V. Mezentseva, Cell state switching factors and dynamical patterning modules: complementary mediators of plasticity in development and evolution, J. Biosci., 2009, 34, 553–572.
64. S. A. Newman, The developmental genetic toolkit and the molecular homology--analogy paradox, Biol. Theory, 2005, 1, 12–16.
65. M. Abedin and N. King, The premetazoan ancestry of cadherins, Science, 2008, 319, 946–948.
66. A. Krtolica and J. Campisi, Cancer and aging: a model for the cancer promoting effects of the aging stroma, Int. J. Biochem. Cell Biol., 2002, 34, 1401–1414.
67. A. Krtolica and J. Campisi, Integrating epithelial cancer, aging stroma and cellular senescence, Adv. Gerontol., 2003, 11, 109–116.
68. R. S. Gray, K. J. Cheung and A. J. Ewald, Cellular mechanisms regulating epithelial morphogenesis and cancer invasion, Curr. Opin. Cell Biol., 2010, 22, 640–650.
69. J. Campisi, Cellular senescence: putting the paradoxes in perspective, Curr. Opin. Genet. Dev., 2010, 21, 107–112.
70. W. T. Gibson and M. C. Gibson, Cell topology, geometry, and morphogenesis in proliferating epithelia, Curr. Top. Dev. Biol., 2009, 89, 87–114.
71. V. A. Spencer, R. Xu and M. J. Bissell, Gene expression in the third dimension: the ECM-nucleus connection, J. Mammary Gland Biol. Neoplasia, 2010, 15, 65–71.
72. D. J. Andrew and A. J. Ewald, Morphogenesis of epithelial tubes: Insights into tube formation, elongation, and elaboration, Dev. Biol., 2010, 341, 34–55.
73. T. D. Pollard and J.-Q. Wu, Understanding cytokinesis: lessons from fission yeast, Nat. Rev. Mol. Cell Biol., 2010, 11, 149–155.
74. S. Oliferenko, T. G. Chew and M. K. Balasubramanian, Positioning cytokinesis, Genes Dev., 2009, 23, 660–674.
75. G. Normand and R. W. King, Understanding cytokinesis failure, Adv. Exp. Med. Biol., 2010, 675, 27–55.
76. G. Zeng, S. M. Taylor, J. R. McColm, N. C. Kappas, J. B. Kearney, L. H. Williams, M. E. Hartnett and V. L. Bautch, Orientation of endothelial cell division is regulated by VEGF signaling during blood vessel formation, Blood, 2007, 109, 1345–1352.
77. P. Kunda and B. Baum, The actin cytoskeleton in spindle assembly and positioning, Trends Cell Biol., 2009, 19, 174–179.
78. M. Théry, A. Jiménez-Dalmaroni, V. Racine, M. Bornens and F. Jülicher, Experimental and theoretical study of mitotic spindle orientation, Nature, 2007, 447, 493–496.
79. J. K. Moore and J. A. Cooper, Coordinating mitosis with cell polarity: Molecular motors at the cell cortex, Semin. Cell Dev. Biol., 2010, 21, 283–289.
80. J. Pulecio, J. Petrovic, F. Prete, G. Chiaruttini, A. M. Lennon-Dumenil, C. Desdouets, S. Gasman, O. R. Burrone and F. Benvenuti, Cdc42-mediated MTOC polarization in dendritic cells controls targeted delivery of cytokines at the immune synapse, J. Exp. Med., 2010, 207, 2719–2732.
81. T. M. Cover and J. A. Thomas, Elements of Information Theory, Wiley-Interscience, 1991.
82. R. G. Gallager, Information Theory and Reliable Communication, Wiley, 1968.
83. J. M. Wozencraft and I. M. Jacobs, Principles of Communication Engineering, Wiley, 1965.
84. H. L. Van Trees, Detection, Estimation, and Modulation Theory, Part I, Wiley, New York, 1968.
85. S. Haykin, Communication Systems, John Wiley & Sons, 1994.
86. T. D. Schneider, Theory of molecular machines. II. Energy dissipation from molecular machines, J. Theor. Biol., 1991, 148, 125–137.
87. T. D. Schneider, 70% efficiency of bistate molecular machines explained by information theory, high dimensional geometry and evolutionary convergence, Nucleic Acids Res., 2010, 38, 5995–6006.
88. P. A. Iglesias and P. N. Devreotes, Navigating through models of chemotaxis, Curr. Opin. Cell Biol., 2008, 20, 35–40.
89. B. W. Andrews and P. A. Iglesias, An information-theoretic characterization of the optimal gradient sensing response of cells, PLoS Comput. Biol., 2007, 3, e153.
90. O. Hoeller and R. R. Kay, Chemotaxis in the absence of PIP3 gradients, Curr. Biol., 2007, 17, 813–817.
91. P. Mehta, S. Goyal, T. Long, B. L. Bassler and N. S. Wingreen, Information processing and signal integration in bacterial quorum sensing, Mol. Syst. Biol., 2009, 5, 325.
92. R. C. Yu, C. G. Pesce, A. Colman-Lerner, L. Lok, D. Pincus, E. Serra, M. Holl, K. Benjamin, A. Gordon and R. Brent, Negative feedback that improves information transmission in yeast signalling, Nature, 2008, 456, 755–761.
93. T. Tlusty, A colorful origin for the genetic code: information theory, statistical mechanics and the emergence of molecular codes, Phys. Life Rev., 2010, 7, 362–376.
94. R. Wallace, Without magic bullets: the biological basis for public health interventions against protein folding disorders. http://precedings.nature.com/documents/4847/version/2, 2010.
95. R. Wallace, Metabolic constraints on the evolution of genetic codes: Did multiple “preaerobic” ecosystem transitions entrain richer dialects via Serial Endosymbiosis? http://precedings.nature.com/documents/4120/version/3, 2010.
96. M. Dehmer and A. Mowshowitz, Inequalities for entropy-based measures of network information content, Appl. Math. Comput., 2010, 215, 4263–4271.
97. M. E. Taylor and K. Drickamer, Paradigms for glycan-binding receptors in cell adhesion, Curr. Opin. Cell Biol., 2007, 19, 572–577.
98. R. Y. Yang, G. A. Rabinovich and F. T. Liu, Galectins: structure, function and therapeutic potential, Expert Rev. Mol. Med., 2008, 10, e17.
99. G. A. Rabinovich and M. A. Toscano, Turning ‘sweet’ on immunity: galectin–glycan interactions in immune tolerance and inflammation, Nat. Rev. Immunol., 2009, 9, 338–352.
100. M. Salatino and G. A. Rabinovich, Fine-tuning antitumor responses through the control of galectin–glycan interactions: an overview, Methods Mol. Biol., 2011, 677, 355–374.
101. C. Kauffman and G. Karypis, An analysis of information content present in protein–DNA interactions, Pac. Symp. Biocomput., 2008, 13, 477–488.
102. I. Erill and M. C. O'Neill, A reexamination of information theory-based methods for DNA-binding site identification, BMC Bioinformatics, 2009, 10, 57.
103. K. J. Meaburn and T. Misteli, Cell biology: chromosome territories, Nature, 2007, 445, 379–781.
104. E. Heard and W. Bickmore, The ins and outs of gene regulation and chromosome territory organisation, Curr. Opin. Cell Biol., 2007, 19, 311–316.
105. K. J. Meaburn, T. Misteli and E. Soutoglou, Spatial genome organization in the formation of chromosomal translocations, Semin. Cancer Biol., 2007, 17, 80–90.
106. T. Takizawa, K. J. Meaburn and T. Misteli, The meaning of gene positioning, Cell, 2008, 135, 9–13.
107. M. J. Zeitz, L. Mukherjee and S. Bhattacharya, J. Xu and R. Berezney. A probabilistic model for the arrangement of a subset of human chromosome territories in WI38 human fibroblasts, J. Cell. Physiol., 2009, 221, 120–129.
108. N. V. Marella, B. Seifert, P. Nagarajan, S. Sinha and R. Berezney, Chromosomal rearrangements during human epidermal keratinocyte differentiation, J. Cell. Physiol., 2009, 221, 139–146.
109. T. Cremer and M. Cremer, Chromosome territories, Cold Spring Harbor Perspect. Biol., 2010, 2, a003889.
110. J. Postberg, H. J. Lipps and T. Cremer, Evolutionary origin of the cell nucleus and its functional architecture, Essays Biochem., 2010, 48, 1–24.
111. W. R. Holley, I. S. Mian, S. J. Park, B. Rydberg and A. Chatterjee, A model for interphase chromosomes and evaluation of radiation induced aberrations, Radiat. Res., 2002, 158, 568–580.
112. S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004.
113. A. Bental, L. El Ghaoui and A. Nemirovski, Robust Optimization, Princeton University Press, 2009.
114. C. Rose and G. Wright, Inscribed matter as an energy-efficient means of communication with an extraterrestrial civilization, Nature, 2004, 431, 47–49.
115. J. J. Zartman and S. Y. Shvartsman, Unit operations of tissue development: Epithelial folding, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 231–246.
116. T. J. Perkins and P. S. Swain, Strategies for cellular decision-making, Mol. Syst. Biol., 2009, 5.
117. A. Y. Maslov and J. Vijg, Genome instability, cancer and aging, Biochim Biophys Acta, 2009, 1790(10), 963–969.
118. S. Gravina and J. Vijg, Epigenetic factors in aging and longevity, Pflugers Arch, 2010, 459, 247–25.
119. M. M. Kämpf and W. Weber, Synthetic biology in the analysis and engineering of signaling processes, Integr. Biol., 2010, 2, 12–24.
120. A. S. Khalil and J. J. Collins, Synthetic biology: applications come of age, Nat. Rev. Genet., 2010, 11, 367–379.
121. V. G. Yadav and G. Stephanopoulos, Reevaluating synthesis by biology, Curr. Opin. Microbiol., 2010, 13, 371–376.
122. ETC Group, The new biomasters-synthetic biology and the next assault on biodiversity and livelihoods, 2010, http://www.etcgroup.org/en/node/5232.
123. Friends of the Earth. Synthetic solutions to the climate crisis: The dangers of synthetic biology for biofuels production, 2010, http://www.foe.org/healthy-people/synthetic-biology.
124. H. Wallace, Biosciences for Life?, Who decides what research is done in health and agriculture?, GeneWatch, UK, 2010, http://www.genewatch.org.
125. G. J. Foschini and M. J. Gans, On Limits of Wireless Communications in a Fading Environment Using Multiple Antennas, Wireless Personal Communications, 1998, 6, 311–335.
126. A. Goldsmith, S. A. Jafar, N. Jindal and S. Vishwanath, Capacity Limits of MIMO Channels, J. Selected Areas in Communication, 2003, 21, 684–702.

---

Footnote

† Published as part of an Integrative Biology themed issue in honour of Mina J. Bissell: Guest Editor Mary Helen Barcellos-Hoff.

---