Short-range correlations in d–f cyanido-bridged assemblies with XY and XY-Heisenberg anisotropy

Abstract

Two new d–f cyanido-bridged 1D assemblies [RE(pzam)₃(H₂O)Mo(CN)₈]·H₂O (RE = Sm(III), Er(III)) were synthesized and their magneto-structural properties have been studied by field-dependent magnetization and specific heat measurements at low temperatures (≥0.3 K). Below ≈ 10 K the ground state of both the Sm(III) and Er(III) ions is found to be a Kramers doublet with effective spin S = 1/2. From analyses of the low-temperature magnetic specific heat and magnetization the exchange coupling between these RE(III) effective spins and the Mo(V) spins S = 1/2 along the structural chains has been determined. It is found to be antiferromagnetic, with J_∥/k_B = −2.6 K and Ising–Heisenberg symmetry of the interaction (J_∥/J_⊥ = 0.3) for RE = Sm(III), whereas the compound with RE = Er(III) behaves as a pure XY chain, with J_⊥/k_B = −1.0 K. For the compound [Sm(pzam)₃(H₂O)Mo(CN)₈]·H₂O a small λ-type anomaly in the specific heat is observed at about 0.6 K, which is ascribed to a transition to long-range magnetic ordering induced by weak interchain interactions of dipolar origin. No evidence for 3D interchain magnetic ordering is found in the Er(III) analogue.

---

Introduction

Heterobimetallic d–f metal complexes provide a rich source for the study of the magnetic interactions between d and f metal ions.^1–17 It has been predicted theoretically that the magnetic exchange interactions of 4fⁿ ions with other paramagnetic species will be ferromagnetic for n > 7 and antiferromagnetic for n < 7.¹⁸ However, the studies reported so far do not fully corroborate this prediction. The magnetic exchange interactions involving the f electrons are weak, and often masked by the crystal field effects on the magnetic susceptibility. Therefore, the analysis of the experimental data often proves to be difficult. To ascertain the nature of the magnetic exchange interaction between rare-earth(III) ions and transition metal ions in cyanido-bridged assemblies derived from hexacyanidometallate building-blocks, an experimental methodology has been developed in which the intrinsic rare-earth(III) ion magnetic properties are determined separately by comparing the χ_MT vs.T curves for two isostructural analogues (i.e. RE-M and RE-M′ where RE is a rare-earth ion M and M′ represent a paramagnetic and a diamagnetic transition metal ion).^19–22 However, in several cases, this approach has likewise failed in correctly determining the strength and/or type of the d–f exchange interaction. Consequently, a more precise estimate of the d–f exchange interaction should preferably include measurements of other thermodynamic properties besides the magnetic susceptibility, in order to more reliably separate the effects of the ligand field splittings from the contributions arising from the (anisotropic) exchange coupling. In this respect, the experimental study of the low-temperature magnetic specific heat of heterobimetallic d–f assemblies has proven to be a useful tool since it provides a direct determination of the magnetic ground state of the f metal ion¹⁶ resulting from the ligand field splittings, as well as a valuable estimate of the strength and type of the d–f exchange interaction.

As a part of a detailed study of cyanido-bridged complexes with low-dimensional magnetic networks, we have previously shown that a combination of magnetic and low-temperature specific heat measurements advantageously allows a rigorous determination of the exchange interactions between neighbouring metal ions and their correlation to the structure.^23–25 In this paper, we extend these studies to two new RE members of this series, namely [RE(pzam)₃(H₂O)Mo(CN)₈]·H₂O (RE(III) = Sm 1, Er 2).

Structural and experimental details

The synthesis and complete crystallographic studies of the complexes of general formula [RE(pzam)₃(H₂O)Mo(CN)₈]·H₂O have been reported earlier.^23–25 They crystallize in the space group Pna21 and their crystal structure is formed by chains of cyanido-bridged alternating arrays of [Mo(CN)₈]³⁻ and [RE(pzam)₃(H₂O)]³⁺ fragments running along the b crystallographic axis. Each chain is surrounded by six other equivalent chains through hydrogen bonding interactions, giving rise to a three-dimensional network.

Temperature dependent magnetic susceptibility and magnetization measurements were performed with a Quantum Design MPMS-5 5T SQUID magnetometer in the temperature range 1.8–300 K and up to 5 T. Data were corrected for the magnetization of the sample holder and for diamagnetic contributions as estimated from the Pascal constants. The presence of next-nearest neighbour magnetic interactions, i.e.RE(III)–RE(III) or Mo(V)–Mo(V) within the chains has been verified by studying the magnetic properties of the lanthanum diamagnetic derivative.²⁴ In that case, we have found no evidence for a magnetic interaction between the 4d Mo(V) ions via the La(III) ion. It may then also be safely assumed that the magnetic interaction between the 4f RE(III) ions mediated through the Mo(V) ion can be neglected.²⁴

Heat capacity measurements in different magnetic fields were carried out in the range 0.3 K to 25 K with a commercial ³He set-up (PPMS), using the relaxation method. The investigated samples were in the form of polycrystalline powders. The measured specific heat of both complexes has been analyzed in terms of two additive contributions, namely the lattice (phonon) contribution (C_l) and the magnetic contribution (C_m). The phonon contribution can be deduced from the zero-field measurements, in combination with the field-independent part of the high-temperature in-field data (the data for T > 10 K). As explained previously,²⁵C_l is given by a polynomial function above 8 K of which the lowest order (T³) can be interpreted in terms of the Debye model, yielding an estimate of the Debye temperature. By numerical integration of the magnetic heat capacity the magnetic entropy can be obtained, giving a direct determination of the number of spin states involved in the magnetic ordering process and thus the magnetic ground states of the RE(III) ion involved.

Results and discussion

Temperature and field dependent magnetizations above 1.8 K

As alluded to in the above, it is often not straightforward to determine the nature of the interaction between a RE(III) ion with a first-order orbital momentum and a paramagnetic transition metal ion without ambiguity. This is because the free-ion states of the RE(III) ions having the same J but arising from different ^2S+1Γ_J terms may mix through spin–orbit coupling. In addition, the resulting states are split further and mixed by the ligand field, such that the spectrum of the low-lying states that determine the magnetic properties at low temperature may become rather complicated. The presence of excited states further up in energy above the ground state may also add a significant temperature-independent contribution to the magnetic susceptibility. However, for small magnetic interactions a first analysis of the magnetic data can be done using an approximate approach²⁶ where the RE(III) ions are considered as non-interacting, as discussed below.

The 4f⁵ electronic configuration of Sm(III) gives ⁶H_J as the ground term, which splits into six J-multiplets under the spin–orbit interaction and yields the multiplet with J = 5/2 as the ground state. Crystal fields lift the degeneracy of the J-manifolds, giving rise to Kramers doublets, and within the process also states belonging to different J-multiplets become mixed (the so-called crystal field J–Jmixing). Since for Sm(III) the J-multiplets are closely spaced (10³ cm⁻¹) as compared to other rare-earth(III) ions, the crystal field J–Jmixing is quite appreciable and thus its effect on the magnetic properties can be profound. As seen in Fig. 1a, the χ_MT value of 1 measured at 300 K is 1.04 cm³ K mol⁻¹, considerably higher than the theoretical value of 0.46 cm³ K mol⁻¹ calculated on the basis of the free ion approximation taking only the ⁶H_5/2ground state into consideration (J = 5/2, g_J = 2/7 for Sm(III) and S = 1/2 and g = 2 for Mo(V)). It seems likely that the admixtures from the ⁶H_7/2 excited multiplet within the ⁶H_5/2 ground state multiplet are responsible for the observed difference. In fact, spin-relaxation studies performed on several Sm(III) compounds have shown that even small admixtures from the ⁶H_7/2 level produce large effects, i.e. increases in the g_Sm factors.^27,28 When lowering the temperature, the χ_MT value is seen to decrease smoothly, reaching a minimum value of 0.76 cm³ K mol⁻¹ at ca. 20 K followed by a sharp increase to a value of 1.31 cm³ K mol⁻¹ at 1.8 K. On the basis of literature data, one may expect the J = 5/2 multiplet to be split into three Kramers doublets, the distance of the two excited doublets being of the order of 100 K above the ground doublet. Lowering of the temperature will therefore produce a progressive depopulation of the excited levels and thus a temperature dependence of the χ_MT product. Based on the specific heat data presented below, we find indeed that at temperatures below ca. 20 K only the lowest Kramers doublet remains thermally populated. In addition, the already mentioned presence of the excited states arising from the J = 7/2 multiplet will entail a temperature-independent contribution to the magnetic susceptibility, i.e. an upward shift of the χ_MT vs. T curve. The need for including such an additional contribution can be seen when comparing the experimental χ_MT vs. T curve with the theoretical one based on the expression of χ_Sm as a function of λ reported previously,²⁶ assuming a spin–orbit coupling parameter λ = 210 cm⁻¹, as typical for Sm(III), and the expectedχ_MT value of 0.38 cm³ K mol⁻¹ for Mo(V) (Fig. 1a). Finally, the abrupt increase in the χ_MT vs. T curve at low temperature can be attributed to the magnetic exchange interaction between Sm(III) and Mo(V), as will be further discussed below.

Fig. 1 (a) Temperature dependence of χ_MT for 1 (○) and χ_M (•) as measured in a field of 0.1 T. Blue circles represent the calculated product χ_SmT as a function of λ = 210 cm^-1. (b) The temperature dependence of χ_MT for 2 (○) and χ_M (•) as measured in a field of 0.1 T.

Temperature-dependent magnetic susceptibility data of 2 are shown in Fig. 1b, likewise as plots of χ_MT vs. T and χ_Mvs. T. The χ_MT product measured at 300 K is 11.7 cm³ K mol⁻¹, equal within errors to the expected value of 11.8 cm³ K mol⁻¹ based on the non-interacting free-ion approximations (J = 15/2, g_J = 1/5 for Er(III) and S = 1/2 and g = 2 for Mo(V)). When the temperature is lowered, the χ_MT product gradually decreases and reaches the value of 6.55 cm³ K mol⁻¹ at 1.8 K. The Er(III) ion with its electron configuration 4f¹¹ has the ⁴I_15/2 ground multiplet. The first excited state ⁴I_13/2 is located at about 6470 cm⁻¹ above the ground state and therefore its contribution to the magnetic susceptibility is only about 1% at room temperature and can be neglected.^29,30 In crystal fields of low symmetry, the 16-fold degeneracy of the free ion is removed by the splitting of the ground multiplet in eight Kramers doublets over an energy range of the order of 500 K.³¹ Consequently, the gradual depopulation of the excited doublets can be held responsible for the observed variation in the χ_MT product with temperature. When fitting the χ_M data in the paramagnetic region (T > 50 K) to the Curie–Weiss law, the Curie constant and Curie–Weiss temperature are obtained as 12.2 cm³ K mol⁻¹ and −13.7 K, respectively. The large Curie–Weiss temperature is clearly a result of the strong crystal field effects and should not be attributed to exchange interactions.

To get more insight in the type of magnetic interactions in 1 and 2, the field dependence of the magnetization was recorded at different temperatures in the range 1.8–8 K, as shown in Fig. 2 and 3. For 1, the measured curves are compared to the Brillouin function calculated for the non-interacting ions, with the expected spin S = 1/2 for Mo(V) and an effective spin of S = 1/2 for Sm(III) in view of the specific heat data to be discussed below. In agreement with the field-dependence observed for the magnetic specific heat, we have adopted a powder g_Sm value of 0.6, which is in the range observed for Sm(III) in sites of low-symmetry.³² The ground multiplet of Sm(III), ⁶H_5/2, is split by a cubic crystal field into a doublet Γ₇ and a quartet Γ₈.³³ In crystal fields of lower symmetry, the quartet Γ₈ splits into two Kramer doublets Γ₆ and Γ₇.³³ Experimental determinations of the g-values for Sm(III) compounds have shown that the Γ₆ doublet is the ground state for the axial symmetry whilst for lower symmetry, i.e. monoclinic, the ground state is the Γ₇ doublet. In most cases, the average g-value is close to 0.6.³² As seen in the Fig. 2, the non-interacting limit describes the data at 8 K rather well. The data at 2 and 4 K show deviations attributable to weak magnetic interactions, to be further discussed below.

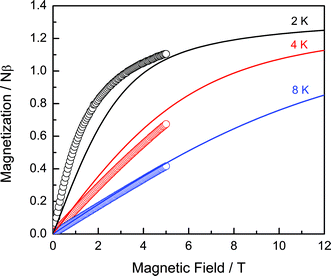Fig. 2 Field dependence of the magnetization of 1 as measured at 2, 4 and 8 K. Solid lines represent the Brillouin function for non-interacting Sm(III) and Mo(V) ions assuming S_Sm = 1/2, g_Sm = 0.6, S_Mo =1/2, g_Mo = 2, as calculated for the same temperatures.

Fig. 3 (a) Field dependence of the magnetization of 2 as measured at 1.8, 2, 4 and 8 K. (b) Field dependence of the magnetization as measured at 2 K with the contribution above 4 T from excited levels (inset) removed. The solid line represents the calculated Brillouin curve for non-interacting Er(III) and Mo(V) ions assuming S_Er = 1/2, g_Er = 6.7, S_Mo =1/2, g_Mo = 2.

In the case of complex 2, from the magnetization curve taken at 1.8 K it appears that a field of ca. 3 T is sufficient to reach saturation of the magnetic moment of the Er(III) ground state, since the subsequent slow and nearly linear increase of the magnetization can be attributed to the contributions from the excited levels (Fig. 3a). Indeed, the slope of this high-field part gives χ ≈ 0.28 cm³ mol⁻¹, about equal to the value measured in low fields at T ≈ 30 K. By extrapolating the magnetization M(B) measured at the higher fields (B > 4 T) to B = 0 we obtain the intercept M^total ≈ 4.4 Nβ (Fig. 3b). Since M^total = M^Er + M^Mo and M^Mo = 1 Nβ, we obtain an effective powder g value of g_p^Er ≈ 6.8 for the Er(III) ion when assuming only a lowest Kramers doublet with an effective spin S = 1/2 to be populated at 2 K for Er(III) ion (see the specific heat data below). This value agrees well with the presence of Er(III) in sites of low symmetry.^34,35

In Fig. 3b, we show the calculated Brillouin function for non-interacting Er(III) and Mo(V) ions at 1.8 K. The origin of the small deviations observed for the magnetization data measured at 1.8 K (with the high-field contribution of the excited levels subtracted) can likewise be ascribed to weak exchange effects, in this case between Er(III) and Mo(V) ions.

Specific heat at very low temperatures

Fig. 4a and 5a show the measured temperature dependence of the specific heat of 1 and 2 in the temperature range 0.3–25 K in zero field and in various applied magnetic fields. From the (field-independent) data above about 10 K and the zero-field curve down to about 7 K, the lattice contribution C_l could be estimated and fitted to the simple Debye model, yielding a Debye temperature, θ_D, of 51 ± 2 K for 1 and 49 ± 2 K for 2, respectively. Fig. 4b and 5b display the magnetic specific heat curves obtained by subtracting C_l from the total specific heat. By integrating the C_m data, we have calculated the magnetic entropies of 1 and 2, which are plotted as insets in Fig. 4b and 5b. As can be seen, the magnetic entropy, ΔS/R, reaches the value of 1.36 J mol⁻¹ K⁻¹ for both. This value is equal, within the errors, to the theoretical value of ΔS/R = 2ln2 = 1.38 J mol⁻¹ K⁻¹ expected for two spins S = 1/2, implying that the ground state of both Sm(III) and Er(III) ions is a doublet with effective spin S = 1/2.

Fig. 4 (a) Molar heat capacity of 1 as measured in zero field and in constant magnetic fields up to 7 T. Solid curve shows the estimated (field-independent) lattice contribution. (b) Magnetic heat capacity of 1 as obtained by subtracting the lattice contribution (Inset: magnetic entropy curves obtained by integration of the magnetic heat capacity).

Fig. 5 (a) Molar heat capacity of 2 as measured in zero field and in constant magnetic fields up to 5 T. Solid curve shows the estimated (field-independent) lattice contribution. (b) Magnetic heat capacity of 2 as obtained by subtracting the lattice contribution (Inset: magnetic entropy curves obtained by integration of the magnetic heat capacity).

As can be seen from the temperature range of the zero-field C_m data in Fig. 4b and 5b, the magnetic exchange interactions (J) between Sm(III) or Er(III) with Mo(V) are rather weak, in particular for Er(III). Nevertheless, they are clearly discernable in the specific heat, leading to broad anomalies with maxima at 1.4 K and 0.7 K for 1 and 2, respectively. In view of the chain-like crystal packing, these broad anomalies can be ascribed to short-range magnetic correlations along the chains, as typically observed for 1D magnetic systems. In addition, compound 1 is found to display a λ-type peak at T_C = 0.60 K under zero-field, which can be attributed to a cooperative transition to a 3D ordered magnetic arrangement resulting from weak interchain interactions. Since no direct superexchange paths connecting magnetic ions in neighbouring chains can be discerned in the crystal structure, such interchain interactions are most likely of dipolar origin and thus quite weak.

The specific type of magnetic exchange interaction (J/k_B) along the 1D chains in 1 and 2 is governed by the intrinsic anisotropic properties of the Sm(III) and Er(III) magnetic ground states. Since the shape and the height of the specific heat maximum (C^max/R) are sensitive to the type of anisotropy, a determination of the type of 1D chain can be done by comparison of the magnetic specific heat anomalies as measured in zero field with theoretical predictions for the various model Hamiltonians (Ising, XY, Heisenberg and intermediate symmetries).³⁶ The observed heights of the specific heat maxima for 1 and 2 are equal to 0.80 R and 0.64 R, respectively, occurring at T_max ≈ 1.33 K and 0.65 K, respectively. When comparing with the calculations of Blöte³⁶ for magnetic chain models with different symmetry of interaction, it appears that the antiferromagnetic chain model with S = 1/2 and intermediate Ising–Heisenberg symmetry of the interaction provides the best description of the observed anomaly of compound 1 (Fig. 6a). The appropriate spin-Hamiltonian reads:

H = −2 Σ [J_⊥{S_ixS_jx + S_iyS_jy} + J_‖S_izS_jz] (1)

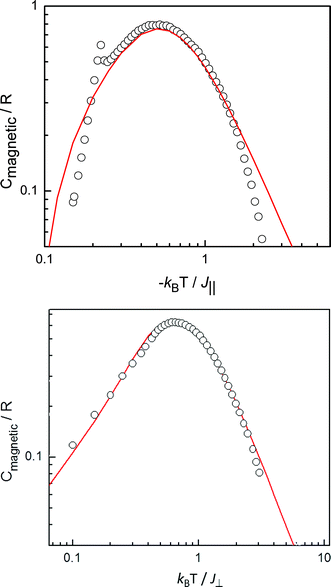Fig. 6 a) Comparison of the zero-field magnetic specific heat anomaly of 1 (taking J_∥/k_B = −2.6 K) with the prediction for the specific heat of the antiferromagnetic chain model with S = 1/2 and intermediate Ising-Heisenberg symmetry of the interaction (J_⊥/J_∥ = 0.3). (b) Comparison of the zero-field specific heat maximum of 2 (taking J_⊥/k_B = 1 K) with the prediction for the specific heat of the magnetic XY chain model with S = ½ (and J_∥ = 0).

The ratio of the exchange constants J_⊥ and J_∥ found from the fit is J_⊥/J_∥ = 0.3. From this comparison we estimate a value of the antiferromagnetic exchange interaction of J_∥/k_B = −2.6 K. On the other hand, as shown in Fig. 6b, the magnetic specific heat of 2 can be fitted quite well to the theoretical prediction³⁶ for the (pure) XY linear chain model (J_⊥ ≠ 0, J_∥ = 0), leading to |J_⊥|/k_B = 1.0 K. This planar anisotropy agrees with the symmetry of the g-tensor often observed for Er(III). For instance, EPR studies on different Er(III) compounds have shown that the g-values are highly anisotropic with mostly g_∥<g_⊥ and an average g-value equal to 7.^37–40 Since the symmetry of the interaction can be roughly related to that of the g-tensor by the expression: J_///J_⊥ ≈ (g_///g_⊥)², the strong XY symmetry demonstrated by the specific heat anomaly would be well explained. We remind that for the pure XY model the specific heat is the same for ferro- or antiferromagnetic J_⊥ so that the sign of J_⊥ remains to be determined.

With regards to the in-field data, a detailed quantitative analysis in terms of these theoretical models is not possible since in the experiment we are not dealing with equal magnetic moments (gS) at all chain sites but with ferrimagnetic chains due to the non-equivalent RE(III) and Mo(V)g-values. In addition, only powder data are available, so that the experimental field-dependent properties are averages over non-equivalent crystallographic directions. Nevertheless, a rough qualitative analysis can be done for the case of the Er(III)–Mo(V) (compound 2), for which the Zeeman energies corresponding to the applied fields of 3 T and 5 T are (relatively) large compared to the exchange interaction. As described previously,²⁵ we can then try to analyze the in-field specific heat data in terms of a mean-field model, in which the total splitting Δ_tot of each doublet is the addition of the Zeeman splitting, Δ_Z = gβB_appl due to the applied field B_appl, and the exchange splitting Δ_ex = 2zS|J| due to the exchange interaction J/k_Binterpreted in terms of an exchange field:

B_ex = 2zS|J_⊥|/gβ = Δ_ex/gβ (2)

Since for all ions involved S = 1/2, the number of magnetic neighbours along the chain is z = 2 and β/k_B ≈ 2/3 × K/T, these formulae reduce to

Δ_Z/k_B = 2/3 × gB_appl (3)

and

Δ_ex/k_B = 2|J_⊥|/k_B (4)

Each split doublet will contribute a two-level Schottky anomaly to the specific heat, with different splitting factors g_RE and g_Mo for the Δ_Z/k_B of RE(III) and Mo(V), whereas Δ_ex/k_B ≈ 2 K for |J_⊥|/k_B ≈ 1 K, independent of the g-value. We show in Fig. 7 the fit for compound 2 for the data collected at 5 T obtained by subtracting an exchange field B_ex = −Δ_ex/gβ from the applied field values, corresponding to − 3/7 T for Er(III) taking g_Er = 7, i.e. close to the value determined above from the magnetization fit, and to − 3/2 T for Mo(V) (g_Mo = 2). Keeping in mind that powder data are involved, the agreement obtained appears to be reasonable. The negative sign of B_ex implies that the interaction J_⊥ is likewise antiferromagnetic for RE = Er(III). A similar analysis for the Sm(III)–Mo(V) (compound 1) is not useful since the condition Δ_Z ≪ Δ_ex needed for applying the model is not reached even in highest field due to the larger value of J/k_B.

Fig. 7 Magnetic specific data at 5 T applied field compared to the (sums of the) calculated Schottky anomalies corresponding to the Zeeman splittings Δ_Er/k_B and Δ_Mo/k_B of the Er(III) and Mo(V) doublets, taking g_Mo = 2.0, g_Er = 7 and applying a correction for the exchange splitting of Δ_ex/k_B = 2 K (subtracted from the calculated Zeeman splittings).

Finally, in order to estimate the effects of the weak interchain coupling (J′), we will assume that, similar as for the previously studied RE(III)–Mo(V) chains, it is of dipolar origin, corresponding to an interaction of strength J′/k_B ≈ 0.02 K. To estimate the 3D ordering temperature T_c^3d resulting from such an interaction, we adopt the well known³⁶ mean-field formula:

k_BT_c^3d ≈ ξ_1d(T_c)J′S² (5)

where ξ_1d(T) is the magnetic correlation length along the individual magnetic chains. The argument basically equates the thermal energy at the transition temperature with the interaction energy at T = T_c of a reference spin with a correlated spin segment in the adjacent chain. In the case of compound 1, with its Ising-like character, we take for the intrachain correlation length the Ising prediction:

ξ_1d(T) = (1/k_BT)exp(J/k_BT) (6)

Taking J_∥/k_B = 2.6 K and S = 1/2 one obtains T_C^3D ≈ 0.6 K, just equal to the experimental value. For the XY chain compound 2, we use instead the prediction for the pure XY chain: ξ_1d(T) = J/k_BT (again for S = 1/2), leading with |J_⊥|/k_B = 1 K to the estimate T_C^3D ≈ 0.07 K, i.e. far below the lowest temperature reached in our specific heat measurements. The fact that the T_C^3D is so much higher for compound 1 can thus be clearly attributed to the exponential temperature dependence of ξ_1d(T) characteristic for an Ising-type chain. This simple argument clearly explains why the presence of 3D ordering was only observed in the case of compound 1, in spite of the close similarities between the two materials in other respects.

Conclusions

We have synthesized two new 1D cyanido-bridged coordination polymers based on [Re(pzam)₃(H₂O)]³⁺ (RE = Sm(III), Er(III)) and [Mo(CN)₈]³⁻ fragments and studied their magnetic properties in detail. The field-dependent magnetization and specific heat measurements at low temperatures reveal the presence of antiferromagnetic superexchange interactions between the RE(III) and Mo(V) ions, of magnitude J_∥/k_B = −2.6 K and Ising–Heisenberg symmetry of the interaction (J_∥/J_⊥ = 0.3) for RE = Sm and J_⊥/k_B = −1.0 K and a strong XY-type (planar) anisotropy for RE = Er(III). Further work on the investigation of the magnetic properties of isostructural compounds in this series containing W(V) is currently in progress.

Acknowledgements

This research was supported by a Veni grant from the Netherlands Organization for Scientific Research (NWO) to S. T. One of the authors (M. E.) thanks the Spanish MICINN for grants MAT2009-13977-C03 and CSD 2007-00010.

Notes and references

1. S. A. Stoian, C. Paraschiv, N. Kiritsakas, F. Lloret, E. Munck, E. L. Bominaar and M. Andruh, Inorg. Chem., 2010, 49, 3387–3401.
2. M. Andruh, J. P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342–3359.
3. F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Inorg. Chem., 2010, 49, 4355–4361.
4. T. Yamaguchi, Y. Sunatsuki, H. Ishida, M. Kojima, H. Akashi, N. Re, N. Matsumoto, A. Pochaba and J. Mrozinski, Inorg. Chem., 2008, 47, 5736–5745.
5. V. Chandrasekhar, B. M. Pandian, R. Boomishankar, A. Steiner, J. J. Viftal, A. Houri and R. Clerac, Inorg. Chem., 2008, 47, 4918–4929.
6. V. Mereacre, A. M. Ako, R. Clerac, W. Wernsdorfer, I. J. Hewitt, C. E. Anson and A. K. Powell, Chem.–Eur. J., 2008, 14, 3577–3584.
7. A. Okazawa, T. Nogami, H. Nojiri and T. Ishida, Chem. Mater., 2008, 20, 3110–3119.
8. X. J. Kong, Y. P. Ren, L. S. Long, Z. P. Zheng, G. Nichol, R. B. Huang and L. S. Zheng, Inorg. Chem., 2008, 47, 2728–2739.
9. P. Przychodzen, R. Pelka, K. Lewinski, J. Supel, M. Rams, K. Tomala and B. Sieklucka, Inorg. Chem., 2007, 46, 8924–8938.
10. V. Chandrasekhar, B. M. Pandian, R. Azhakar, J. J. Vittal and R. Clerac, Inorg. Chem., 2007, 46, 5140–5142.
11. T. Hamamatsu, K. Yabe, M. Towatari, S. Osa, N. Matsumoto, N. Re, A. Pochaba, J. Mrozinski, J. L. Gallani, A. Barla, P. Imperia, C. Paulsen and J. P. Kappler, Inorg. Chem., 2007, 46, 4458–4468.
12. F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Chem.–Eur. J., 2007, 13, 1602–1609.
13. M. Ferbinteanu, T. Kajiwara, K. Y. Choi, H. Nojiri, A. Nakamoto, N. Kojima, F. Cimpoesu, Y. Fujimura, S. Takaishi and M. Yamashita, J. Am. Chem. Soc., 2006, 128, 9008–9009.
14. S. Tanase and J. Reedijk, Coord. Chem. Rev., 2006, 250, 2501–2510.
15. C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2387.
16. M. Evangelisti, M. L. Kahn, J. Bartolome, L. J. de Jongh, C. Meyers, J. Leandri, Y. Leroyer and C. Mathoniere, Phys. Rev. B: Condens. Matter, 2003, 68.
17. O. Kahn, Acc. Chem. Res., 2000, 33, 647–657.
18. M. L. Kahn, C. Mathoniere and O. Kahn, Inorg. Chem., 1999, 38, 3692–3697.
19. A. Figuerola, J. Ribas, M. Llunell, D. Casanova, M. Maestro, S. Alvarez and C. Diaz, Inorg. Chem., 2005, 44, 6939–6948.
20. A. Figuerola, J. Ribas, D. Casanova, M. Maestro, S. Alvarez and C. Diaz, Inorg. Chem., 2005, 44, 6949–6958.
21. A. Figuerola, C. Diaz, J. Ribas, V. Tangoulis, J. Granell, F. Lloret, J. Mahia and M. Maestro, Inorg. Chem., 2003, 42, 641–649.
22. A. Figuerola, C. Diaz, J. Ribas, V. Tangoulis, C. Sangregorio, D. Gatteschi, M. Maestro and J. Mahia, Inorg. Chem., 2003, 42, 5274–5281.
23. F. Prins, E. Pasca, L. J. de Jongh, H. Kooijman, A. L. Spek and S. Tanase, Angew. Chem., Int. Ed., 2007, 46, 6081–6084.
24. S. Tanase, L. J. de Jongh, F. Prins and M. Evangelisti, ChemPhysChem, 2008, 9, 1975–1978.
25. S. Tanase, M. Evangelisti, L. J. de Jongh, J. M. M. Smits and R. de Gelder, Inorg. Chim. Acta, 2008, 361, 3548–3554.
26. O. Kahn, Molecular Magnetism, John Wiley & Sons, New York, 1993.
27. G. H. Larson and C. D. Jeffries, Phys. Rev., 1966, 141, 461–478.
28. P. L. Scott and C. D. Jeffries, Phys. Rev., 1962, 127, 32–51.
29. http://vog.tsin.scisyhp/PhysRefData/ASD/levels_form.html .
30. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, 1970.
31. M. Ferbinteanu, T. Kajiwara, F. Cimpoesu, K. Katagiri and M. Yamashita, Polyhedron, 2007, 26, 2069–2073.
32. M. Falin, H. Bill and D. Lovy, J. Phys.: Condens. Matter, 2004, 16, 1293–1298.
33. K. R. Lea, M. J. M. Leask and W. P. Wolf, J. Phys. Chem. Solids, 1962, 23, 1381–1405.
34. F. B. I. Cook and M. J. A. Smith, J. Phys. C: Solid State Phys., 1973, 6, 3785–3796.
35. T. C. Ensign and N. E. Byer, Phys. Rev. B: Solid State, 1972, 6, 3227–3239.
36. H. W. J. Blöte, Physica B, 1975, 79, 427–466.
37. C. A. Hutchison and E. Wong, J. Chem. Phys., 1958, 29, 754–760.
38. B. Bleaney and H. E. D. Scovil, Proc. R. Soc. A, 1951, 64, 204–205.
39. J. W. Orton, An introduction to transition group ions in crystals, Gordon and Breach Science Publishers Inc., New York, 1969.
40. G. H. Bellesis, S. Simizu and S. A. Friedberg, J. Appl. Phys., 1987, 61, 3286–3288.

---

Footnote

† Current Address: Van't Hoff Institute of Molecular Sciences, University of Amsterdam, Science Park 904,1098 XH, Amsterdam, The Netherlands. Fax: +31 (0)20 525 5604; Tel: +31 (0)20 525 6477; E-mail: s.grecea@uva.nl

---