HRTEM and molecular modeling of the MoS₂–Co₉S₈ interface: understanding the promotion effect in bulk HDS catalysts

Abstract

As environmental regulations increase, more selective transition metal sulfide (TMS) catalytic materials for hydrotreating applications are needed. Highly active TMS catalysts become more and more desirable triggering new interest for unsupported Co-promoted MoS₂-based systems that have high volumetric activity as reported here. Contrary to the common observation for alumina-supported MoS₂-based catalysts, we found in our previous studies with dibenzothiophene (DBT) hydrodesulfurization (HDS) that the catalytic activity is directly proportional to the increase of surface area of the sulfide phases (Co₉S₈ and MoS₂) present in Co-promoted MoS₂ unsupported catalysts. This suggests that activity is directly connected with an increase of the contact surface area between the two sulfide phases. Understanding of the nature of the possible interaction between MoS₂ and Co₉S₈ in unsupported catalytic systems is therefore critical in order to get a more generalized overview of the causes for synergy. This has been achieved herein through the detailed characterization by XRD, XPS, and HRTEM of the highly active Co₉S₈/MoS₂ catalyst resulting in a proposed model for a Co₉S₈/MoS₂ interface. This model was then subjected to a DFT analysis to determine a reasonable description of the surface contact region between the two bulk phases. Modelling of the interface shows the creation of open latent vacancy sites on Mo atoms interacting with Co and formation of direct Co–Mo bonds. Strong electron donation from Co to Mo also occurs through the intermediate sulfur atom bonded to both metals while an enhanced metallic character is also found. These changes in coordination and electronic properties are expected to favor a synergetic effect between Co and Mo at the proposed localized interface region between the two bulk MoS₂ and Co₉S₈ phases.

---

1. Introduction

Molybdenum sulfide is a key phase of any industrial hydrotreating catalysts used today. However, MoS₂ by itself is only moderately active for desulfurization purposes. Addition of a cobalt or nickel promoter is necessary to achieve highly active catalytic systems for hydrodesulfurization (HDS).¹ The description of the promoted phase has been extensively studied since the 1970's leading to different proposals for explaining the promotion effect from Co or Ni. The first attempt to describe the promoted phase was formulated by Farragher and Cossee who considered that Co was localized at octahedral sites at the periphery of the edge planes of the MoS₂ layered phase in a so-called “pseudo-intercalation” position.² At the same time, Delmon and co-workers found that the unsupported catalysts they prepared that had the MoS₂ and Co₉S₈ phases present were able to work together by being in close contact.³ This approach offered a good description of the synergy effect at the macroscopic level by identifying the bulk phases present, by noting the absence of a ternary bulk promoted phase and by showing that hydrodesulfurization occurs at the interface between these two bulk sulfide phases. However, their model was not able to give insight about how these two bulk phases interact to produce a synergetic effect. Topsøe et al. were the first to provide experimental evidence about a specific Co environment. Small amounts of ⁵⁷Co introduced into bulk MoS₂ led to the observation of a specific emission Mössbauer spectroscopy (EMS) signal different from Co₉S₈ called the “CoMoS” phase.⁴ Using XAFS, they were also able to show that the atomic local structure of MoS₂ was preserved.⁵

This model is nowadays generally accepted for supported CoMo or NiMo systems and has unambiguously demonstrated the specific interaction of Co or Ni with the edges of MoS₂ slabs (CoMoS “decoration” model). In this respect, in the last few years, development of quantum computational calculations by integration of Density Functional Theory (DFT) has provided a substantial progress in understanding the localization of Co (or Ni) at the edges of MoS₂ layers assuming the decoration model.^6–10

These models are very helpful in providing an explanation for the cause of the synergetic effect. However, they also suffer from the absence of a unified description able to explain the appearance of the synergetic effect when bulk Co₉S₈ and MoS₂ phases are present. Also the question of at what level of Co addition does the Co₉S₈ phase appear in catalytically stabilized unsupported catalytic systems is still open.

In a little known paper, Phillips and Fote reported that promoted systems should be considered as mixtures of two immiscible phases (Co₉S₈ and MoS₂) that interact by forming surface phases.¹¹Fig. 1 illustrates this concept through a hypothetical phase diagram of Co/Mo/S catalytic systems participating in a synergetic effect. This description of the different promoted systems was called “symmetrical synergy” by Chianelli et al. and is composed of three different domains as Co is added to the system (this approach can be similarly considered with Ni added to MoS₂ or WS₂).¹² The left-hand portion of this diagram corresponds to the most accessible zone (in terms of preparation) for supported systems. In this region, as Co is added, the promotion effect increases until a maximum is reached. This maximum occurs typically between Co/Mo ratios of 0.10–0.30. Co₉S₈ is not detected in this region in supported systems and only the Co/Mo/S surface phase is found. The maximum activity will then correspond to the optimal accommodation of cobalt at the edges of MoS₂ layers and its exact position will depend on the MoS₂ edge area available (and therefore on its slab size). The Co/Mo/S surface phase equates with the CoMoS phase.

Fig. 1 Hypothetical phase diagram for Co/Mo/S catalytic materials illustrating the symmetrical synergy model.¹²

Further addition of cobalt favors Co₉S₈ segregation leading to a region in which both bulk phases coexist. This region can be described as the “synergy by contact” region dominated by the two immiscible phases. On the right-hand portion of the diagram, a Mo/Co/S surface phase exists which is analogous to the Co/Mo/S surface phase but with Mo promoting Co₉S₈. Due to the difficulty to prepare high surface area Co₉S₈, this region has not been explored. However, very recent reports have actually demonstrated that promotion can also be observed in Co₉S₈-(or NiS_x-) rich regions in the presence of few MoS₂ (WS₂) slabs. Le et al. have observed for unsupported NiW catalysts that the highest HDS activity per surface area was achieved on catalysts formed of NiS bulk particles covered with WS₂ slabs.¹³ Similarly, Olivas et al. have found highly active unsupported NiW systems presenting molar ratios of R (R = Ni/(Ni + W)) in the range of 0.8–0.9.¹⁴ Finally, Wang et al. have found unsupported NiMoW catalysts that are very active in the HDS of 4,6-DMDBT if MoS₂ or WS₂ slabs are well dispersed on a Ni₇S₆ substrate.¹⁵

In the presence of both bulk phases (Co₉S₈ and MoS₂), the HDS activity will then be the resultant of the mixture of the two surface-enriched phases.¹² This symmetrical synergy can be applied to other promoted systems. Because of the immiscibility, surface phases exist in which the bulk crystal phase is surface enriched with the other metal. The magnitude of this enrichment and therefore of the synergetic effect will depend on the surface area of the crystalline phases present. Moreover, it should be remembered that in any discussion of the synergetic effect, two questions are still open:

(1) Co₉S₈ (Ni₃S₂) can be promoted with Mo or W,

(2) at what concentrations does Co₉S₈ (Ni₃S₂) separate from MoS₂ (WS₂) in catalytically stabilized materials.

Any description not addressing these points is incomplete. Furthermore, the nature of the promoting effect is electronic by nature thanks to the electron donation of Co to Mo weakening the metal–sulfur bond strength up to values corresponding to optimized HDS performance.^16,17

Formation of surface phase Co/Mo/S or Mo/Co/S would then permit the charge transfer from Co to Mo responsible for promotion.¹² This effect is expected to occur whatever the bulk crystalline phases present. While the Co/Mo/S surface phase is well described in the literature, the region where Co₉S₈ and MoS₂ actually coexist is not completely understood. For example, Delmon and co-workers reported the presence of Co₉S₈ at lower levels that shown in Fig. 1.³ The region where MoS₂ and Co₉S₈ coexist is very often characterized by a lower but still existing synergetic effect which could result from an ineffective use of Co (or Mo) to form the surface phase, part of Co₉S₈ or MoS₂ not being in contact with each other to form such a promoted surface phase.

Comprehension of the nature of the possible interaction between MoS₂ and Co₉S₈ in this region where bulk phases can coexist is therefore critical in order to get a generalized overview of the possible causes for synergy. Comprehension of this synergetic effect is also important taking into account the high volumetric activity of unsupported Co/MoS₂ catalysts. The objective of the present study is therefore to provide information about the local structure of the MoS₂/Co₉S₈ interface. For this purpose, unsupported Co-promoted systems in which Co₉S₈ and MoS₂ phases coexist will be first evaluated in the hydrodesulfurization (HDS) of dibenzothiophene (DBT), a model molecule representative of the refractory sulfur compounds present in diesel fuels before being carefully characterized to propose a possible model for the Co₉S₈/MoS₂ interface. This model will then be subjected to computational modeling and DFT calculations in order to determine a reasonable description of the surface contact region between the two bulk phases. Consequences in terms of electronic properties of the formation of such an interface will also be presented.

2. Experimental

2.1. Preparation of the bimetallic precursors

2.1.1. Preparation of the Co/(NH₄)₂MoS₄ precursor. The bimetallic precursor was prepared in two steps. In a first step, ammonium tetrathiomolybdate, (NH₄)₂MoS₄ (ATM), was prepared according to methods reported elsewhere.¹⁸ATM was generally prepared by bubbling H₂S into an aqueous solution (30 mL distilled water) of 10 g of ammonium heptamolybdate, (NH₄)₆Mo₇O₂₄·6H₂O and 100 mL of NH₄OH for about 2 h. In a second step, the molybdenum precursor was mixed with CoCl₂ in aqueous solution; 1.6 g of (NH₄)₂MoS₄ in 20 mL of water was added under stirring at room temperature to a second solution of 0.47 g of CoCl₂·1/2H₂O dissolved into 10 mL of water. A black precipitate immediately formed. The bimetallic precursor is then filtered and dried at room temperature overnight. This compound was amorphous in nature. The obtained Co/Mo molar ratio in this bimetallic precursor is 0.3 in agreement with the possible stoichiometric reaction:

3(NH₄)₂MoS₄ + CoCl₂ → (NH₄)₄Co(MoS₄)₃ + 2NH₄Cl.

However, instability in air probably transformed this precursor into an amorphous polymeric compound of the type Co_x(MoS₄)_3x keeping a Co/Mo ratio of 0.3.¹⁹

2.1.2. Preparation of the Co/(NR₄)₂MoS₄ precursors. For comparison purposes, some cobalt-containing tetraalkylammonium thiomolybdate precursors have been considered here for which carbon does not contribute significantly to the total surface area. One of these precursors contains a tetramethylammonium thiomolybdate group (called here Co/TMATM) while the other one is formed from a tetrapentylammonium thiomolybdate precursor (called Co/TPenATM). Their preparation has been detailed elsewhere and does not differ substantially from the Co/ATM method of preparation.^19,20

The (NR₄)₂MoS₄ (R = C₁, C₅) precursors were first synthesized at room temperature by simply stirring ATM with the respective tetraalkylammonium bromide salts in a 1 : 2 molar ratio in the presence of NaOH until formation of a precipitate:

(NH₄)₂MoS₄ + 2R₄NBr + 2NaOH → (NR₄)₂MoS₄ + 2NH₄OH + 2NaBr

The precipitate is then filtered in vacuum and dried overnight at room temperature.

The appropriate amount of (NR₄)₂MoS₄ precursor to yield 1 g of MoS₂ (2.3 g of [(CH₃)₄N]₂MoS₄ or 5.1 g of [(C₅H₁₁)₄N]₂MoS₄) was then dissolved into 20 mL of water for [(CH₃)₄N]₂MoS₄ or into 50 mL of 1 : 1 ethanol/water solution for [(C₅H₁₁)₄N]₂MoS₄) while stirring. 10 mL of a 0.47 g of CoCl₂·1/2H₂O aqueous solution was then added. A black precipitate then formed immediately. The black material was then filtered and dried overnight at room temperature.

2.2. Preparation of the unsupported Co/MoS₂ catalyst

2.2.1. Hydrothermal technique. Co/MoS₂ catalysts could be obtained through decomposition of the bimetallic precursor under hydrothermal conditions.²¹ For this purpose, 5 g of the precursor were added to water and placed inside a 0.5 L high-pressure batch reactor. The reactor was purged with N₂ at room temperature before increasing temperature and pressure to 300 °C and 1200 psi (82.7 bars) or 1400 psi (96.5 bars). Temperature was maintained at 300 °C for 2 h. The desired pressure was developed autogenously by the appropriate amount of water addition to the closed system (for instance 50 mL of water for a pressure of 1200 psi). After cooling down to room temperature, the recovered product was washed with isopropanol.

2.2.2. In situ technique. Another approach to synthesize the Co/MoS₂ catalysts is to use either ex situ or in situ methods of activation. The ex situ method consists in decomposing the precursors under H₂/H₂S at 400 °C for 4 h. The resulting solid generally presents very low surface area and will not be considered here.²² In the in situ approach, the bimetallic precursors are decomposed in the reaction media during the HDS of dibenzothiophene (see below). Like for the hydrothermal method, the high pressure present in the batch reactor during the catalytic test favors the formation of high surface area unsupported Co/MoS₂ catalysts.

2.3. Catalytic activity measurements

The hydrodesulfurization (HDS) of dibenzothiophene (DBT) that has been extensively used as a model of HDS of petroleum feedstock was carried out in a 2 L Parr model 4522 high-pressure batch reactor. Approximately 1 g of Co/MoS₂ catalyst (or the appropriate amount of precursor to yield 1 g of Co/MoS₂ catalyst using the in situ technique), along with the reactant mixture (6.6 g of DBT in 150 mL of decalin; [DBT]₀ = 0.239 mol L⁻¹), was placed in the reactor, then pressurized to 490 psi (33.8 bars) with hydrogen, and heated to 350 °C at a rate of 10 °C min⁻¹. After the working temperature was reached, sampling for chromatographic analysis was taken during the course of each run to determine conversion versus time dependence. Reaction runs averaged about 5 h. The reaction products were analyzed using a Perkin–Elmer model Auto-system chromatograph with a 6 ft long, 1/8 inch packed column containing OV-3 (phenyl methyl dimethyl silicone 10% phenyl) as a separating phase supplied by Supelco.

2.4. Morphological studies

All morphological studies were performed after a test on a steady-state stabilized catalyst working in the dibenzothiophene hydrodesulfurization. Sorption surface analyses were performed on a NOVA 1000 instrument with a Quantachrom Autosorb-1 model by nitrogen adsorption using the BET isotherm method. Samples were degassed under Ar flow at 200 °C for 2 h before nitrogen adsorption.

X-Ray Diffraction (XRD) patterns of catalysts were obtained on a Phillips X Pert MPD diffractometer operating at 43 kV and 30 mA and equipped with a curved graphite monochromator using Cu Kα radiation (λ = 1.54056 Å) in the 2θ range of 7–80°.

X-Ray photoelectron spectroscopy (XPS) studies were performed on a Axis Ultra DLD (Kratos Analytical) spectrometer equipped with a dual Al/Mg anode. The spectra were excited using Al Kα radiation (1486.6 eV). The XPS spectra of Co 2p signals were recorded and their binding energies (BE) referred to the energy of the Al 2p peak (BE 74.2 eV).

High-resolution transmission electron microscopy (HRTEM) analysis was performed using a Schottky field emission electron microscope FEI Tecnai TF20 (200 kV). The unit is equipped with a STEM unit, high-angle annular dark-field (HAADF) detector, and X-Twin lenses with a resolution of ∼ 2 nm. The sample was prepared by adding 0.05 g of catalytic powder in ethanol in a glass vial. The solution was placed in ultra-sonic bath for particle dispersion. One drop of the diluted solution was deposited onto a lacey Cu/C 200 mesh grid. The sample was left to dry at RT for 2 h. Energy Dispersive X-Ray (EDX) microanalysis was performed using an EDAX detector with a solid angle of 0.13 sr. Evaluation of slab lengths and stacking degree of MoS₂ particles was performed using SigmaScan Pro5 software.

TEM simulation was carried out using the simulaTEM software in the Cerius2 analytical 2 molecular package. The physical meaning and principle of the TEM simulator software is described in detail by Gómez-Rodríguez et al.²³ Basically, TEM simulator performs a full dynamical calculation by a multi-slice method using projected potential , where a_i and b_i are coefficients to be determined. The variable U = (u, v, w) is used to represent coordinates in reciprocal space (Fourier space) quantities (spatial frequencies). f(U) is the atomic dispersion factor. TEM simulations were calculated at two defocus conditions with the parameters used for the Tecnai TF20 (200 kV). The following conditions were used for simulation: chromatic Cc and spherical Cs aberration coefficients were, respectively, 1.4 mm and 2.7 mm; the defocus condition was −485.2 Å with a beam spread of 0.3 mrad. The aperture diameter centered at reciprocal space origin was 0.7 Å⁻¹. All calculations were performed with a 512 × 512 sampling and slide thickness of 20 Å. The general procedure used to perform HRTEM simulation is described in Fig. 2.

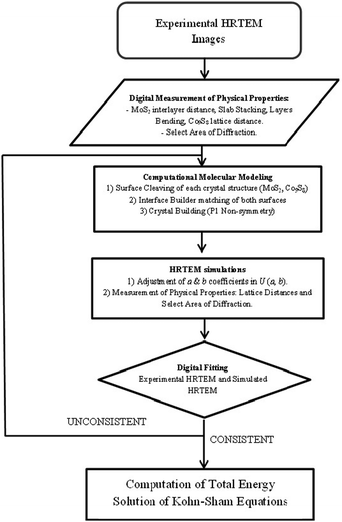Fig. 2 Flow chart diagram of the procedure used to build an interface model based on HRTEM simulation.

2.5. Density functional theory calculations

Using information obtained by conventional HRTEM observations, an interface model was constructed using Cerius2 Package and subjected to validation using projected potential TEM simulator. Further investigations were carried out on a selected interface model in order to understand the role of synergic contact area between MoS₂ and Co₉S₈ bulk species. Calculations of Total Energy in Band Structure (BS) and Density of States (DOS) were achieved using CASTEP code,²⁴ as contained in Accelrys Inc. Materials Studio package. To solve Kohn–Sham equations, a numerical expansion of the k-wave functions was completed using a plane wave basis (PWB) set. The exchange–correlation functional was revised by Perdew–Burke–Ernzerhof (RPBE)²⁵ and ultrasoft pseudopotentials were used considering the ion-core to be frozen (ion cores are not involved in chemical bonding). The PWB cutoff energy was 300 eV with a self-consistent field tolerance of 1 × 10⁻⁶ eV per atom for gamma point only in reciprocal space. The system was relaxed and geometrically optimized during DOS and BS calculations using a thermal smearing of 0.1 eV. Since the bulk interface model consisted of more than 100 atoms and to reduce computational time, just a representative portion called “seed” was subjected to electronic calculations. The “seed” was treated as a crystal using a supercell with lattice parameters, a = 14.0 Å, b = 20.0 Å and c = 6.0 Å and α = β = γ = 90° (P1 non-symmetry) leaving sufficient empty space between adjacent neighboring atoms to reduce electron interactions in the periodic structure. The k-point path for band structure calculations was set as: G(0, 0, 0), F(0, ½,0), Q(0, ½, ½) and Z(0, 0, ½).

3. Results and discussion

3.1. Unsupported CoMo catalysts: correlation between DBT HDS activity and specific surface area

The objective of the present study is to develop a reasonable description of unsupported CoMo catalysts for which the presence of bulk Co₉S₈ and MoS₂ phases is clearly determined. Therefore, our first objective was to optimize the synthesis of unsupported CoMo catalysts for which both MoS₂ and Co₉S₈ bulk phases coexist and for which a strong synergetic effect exists. Previous studies made by our research group have been centered on the preparation of unsupported CoMo catalysts using several synthesis methods. The different approaches include (1) the use of carbon-containing thiomolybdate precursors for which a beneficial role of carbon on the final HDS activity was confirmed,^19,20,26,27 and (2) hydrothermal or open-flow hot isostatic pressing (OFHIP) techniques providing high surface area materials.²¹ The detailed HDS characterization of these unsupported CoMo catalysts can be found elsewhere and will therefore not be discussed here extensively.^19–21

Unsupported CoMo catalysts prepared from tetraalkylammonium precursors will only be considered here if carbon coming from the thiosalts does not contribute significantly to the total surface area. Therefore, Table 1 lists unsupported CoMo catalysts prepared by hydrothermal or in situ techniques. Samples are labeled L (low), M (medium) or H (high) according to their respective surface areas. Comparison is also provided with unsupported MoS₂ and commercial CoMo/Al₂O₃ catalyst. The HDS activity values can vary in a large extent from 7.2 × 10⁻⁷ mol s⁻¹ g⁻¹ up to 32.0 × 10⁻⁷ mol s⁻¹ g⁻¹. These values are much higher than those expected for a MoS₂ sample prepared from ATM (Table 1). Therefore, experimental conditions for the preparation of unsupported CoMo catalysts appear critical in achieving a high synergetic effect. In this respect, the pressure applied in the autoclave during the decomposition of the bimetallic precursor into the unsupported CoMo catalyst plays a key role in increasing the HDS activity. The samples prepared under hydrothermal conditions at 1200 psi (82.7 bars) (Co/MoS₂-H₁) or 1400 psi (96.5 bars) (Co/MoS₂-H₂) present very high activities, respectively, 3.1 and 3.4 times higher than for the Co/MoS₂-L₂ catalyst obtained by in situdecomposition of Co/ATM at 31 bars. Moreover, in all cases, the increase of the autoclave pressure during the decomposition of the bimetallic precursor into the final CoMo catalyst also leads to a very marked increase in the surface area (Table 1). A direct link between the increase in surface area and the enhancement in HDS activity is therefore observed as shown in Fig. 3. Since MoS₂ is an anisotropic compound, direct correlation between surface area and HDS activity is normally unexpected since HDS active sites are formed only at the edges of MoS₂ layers.²⁸ One possible reason for such a difference in activity could be related to a higher MoS₂ dispersion for high surface area CoMo catalysts, i.e. a higher MoS₂ edge area. However, the determination by TEM of the MoS₂ slab size for Co/MoS₂-H₁ and for Co/MoS₂-L₂ does not sustain this hypothesis. Indeed, while Co/MoS₂-H₁ presents an average slab size of 62 Å (see Section 3.2.3 for a more detailed TEM characterization), Co/MoS₂-L₂ exhibits a better MoS₂ dispersion with an average slab size of 39 Å even if less active in HDS.

Table 1 Specific surface area, DBT HDS activity and HYD/DDS ratio of unsupported CoMo catalysts formed from either in situ or hydrothermal techniques. Co/MoS₂ samples are labelled L (low), M (medium) or H (high) according to their respective surface areas. Comparison to an unpromoted and unsupported MoS₂ catalyst and to a commercial CoMo/Al₂O₃ is provided

Catalyst	Method of preparation	Specific surface area/ m^2 g^−1	Rate constants (10^−7 mol s^−1 g^−1)	HYD/DDS ratio
a From ref. 20. b From ref. 19. c From ref. 21.
MoS2^a	ATM precursor (Patm, 400 °C)	—	1.7	1.40
Co/MoS2-L1^a	Co/ATM precursor (prepared at 60 °C) and in situ decomposed under DBT HDS conditions (31 bars, 350 °C)	37	7.2	0.60
Co/MoS2-L2^b	Co/ATM precursor (prepared at RT) and in situ decomposed under DBT HDS conditions (31 bars, 350 °C)	53	9.4	0.35
Co/MoS2-M^a	Co/TMATM precursor (prepared at 60 °C) and in situ decomposed under DBT HDS conditions (31 bars, 350 °C)	117	15.4	0.41
Co/MoS2-H1^c	Co/ATM precursor decomposed under hydrothermal conditions (1200 psi (82.7 bars), 300 °C)	210	29.0	0.31
Co/MoS2-H2^c	Co/TPenATM precursor decomposed under hydrothermal conditions (1400 psi (96.5 bars), 300 °C)	250	32.0	0.37
CoMo/Al2O3	Commercial	—	15.0	0.40

---

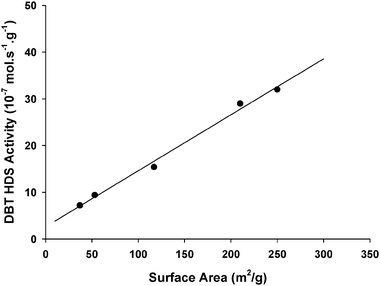Fig. 3 Dibenzothiophene HDS activity vs. specific surface area for the different unsupported CoMo catalysts listed in Table 1. The straight line is added only to guide the eye and emphasizes the existing linear correlation.

Therefore, no direct correlation between the MoS₂ edge area (and the possible degree of accommodation of Co) and the evolution of the HDS activity can be found. On the other hand, the fact that the HDS activity correlates with the surface area of the unsupported CoMo catalyst (then combining the surface areas of both bulk MoS₂ and Co₉S₈ and not only the MoS₂ edge area) is a stronger argument (even if not a direct proof) of the necessity to get high surface contact area between the two bulk sulfide phases in order to increase the possibility to form surface Co/Mo and Mo/Co species at the MoS₂/Co₉S₈ interface as predicted in the symmetrical synergy model.¹²

Finally, compared to unpromoted samples, the synergetic effect can be evaluated not only through comparison of activity values but also through the examination of the selectivity variations. Indeed, the HDS of DBT presents two parallel pathways: (1) the hydrogenating (HYD) pathway leading to the formation of tetrahydrodibenzothiophene through hydrogenation of one of the two aromatic rings of DBT followed by C–S bond breaking and formation of cyclohexylbenzene, and (2) the direct desulfurization (DDS) pathway leading to direct C–S bond rupture and formation of biphenyl. The main effect of the cobalt promotion on MoS₂ is electronic by nature,^16,29 and leads to a strong enhancement of the DDS pathway.^30–32 The MoS₂ catalyst formed by in situdecomposition of the ATM precursor under HDS conditions shows a HYD/DDS ratio of 1.40 that shifts to 0.3–0.6 for the different Co/MoS₂ catalysts (Table 1). A strong DDS selectivity is then achieved characteristic of a promoting effect of cobalt on MoS₂ whatever the unsupported CoMo samples.

3.2. Characterization by N₂ adsorption, XRD, XPS and (HR)TEM

In the next section of this study, one of the unsupported CoMo catalysts presenting the most optimized textural and catalytic properties (Co/MoS₂-H₁) is characterized to better determine the morphological characteristics of the MoS₂ phase and the presence of an eventual Co₉S₈ phase which would be susceptible to interact with molybdenum sulfide through a hypothetic interface. This catalyst was systematically characterized under HDS steady-state conditions and therefore it reflects the stabilized catalytic morphology under reaction conditions.

3.2.1. N₂ adsorption–desorption isotherms. The N₂ adsorption–desorption isotherms of the Co/MoS₂ unsupported catalyst were recorded before and after the hydrodesulfurization (HDS) of dibenzothiophene (DBT) (Fig. S1, ESI†).

Except for a decrease in the N₂ adsorbed volume, the isotherm curves do not present any real change after the catalytic test and still present a composite profile closer to the one expected for a type II than for a type IV solid suggesting that the catalyst does not present (or presents poorly) mesoporous organization. The hysteresis loop is also closer to H3 type confirming that the porosity observed is mainly due to voids inside aggregates. Therefore, the catalyst is in fact formed of aggregated particles without any real mesoporosity, any value of porous volume being due to intergranular porosity. This aggregated morphology without any real mesoporosity suggests that the surface area exposed by the solid only results from the external surface area of the bulk phases present. This situation differs from unsupported CoMo catalysts obtained from tetraalkylammonium thiometallates precursors for which mesoporosity was formed through the decomposition of the organic moieties.^33–37

3.2.2. X-Ray diffraction: turbostraticity and bending effects. The XRD pattern of the Co/MoS₂ unsupported catalyst is reported in Fig. 4. A typical XRD profile characteristic of a poorly crystalline phase was obtained showing a disordered MoS₂ structure. Molybdenum disulfide is a layered structure formed of 2D Mo–S–Mo layers stacked in the c direction.³⁸MoS₂ slabs can be maintained stacked but only through weak Van der Waals interactions. Moreover, this stacking is often imperfect leading to some rotations of MoS₂ layers with respect to each other, i.e. turbostraticity. MoS₂ particles can also present strong bending curvature effects. All these features make MoS₂ a structure presenting a very disordered state also called “rag” structure”.³⁹

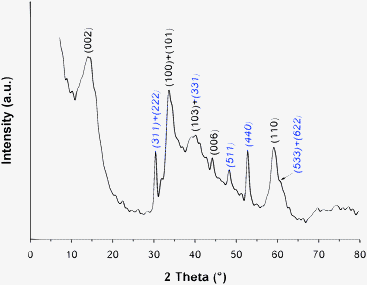Fig. 4 X-Ray diffractogram of the Co/MoS₂ unsupported catalyst. The main MoS₂ and Co₉S₈ diffraction peaks are shown on the pattern; peaks for the Co₉S₈ phase are shown in italics.

Debye–Scherrer equation applied to the full width at half maximum (FWHM) of the (002) MoS₂ diffraction peak (Fig. 4) provides estimation of the crystalline order along the [001] direction and thus information about the stacking degree. A D₀₀₂ value of 29.2 Å was found corresponding to an average stacking n of 4.6 layers. However, this average stacking value only gives information about the stacking degree of MoS₂ particles presenting a multiple-layered structure (n ≥ 2) since applied to the (002) diffraction peak. Excess scattering at low angles underneath the (002) peak can also be noticed in Fig. 4. Previous studies have shown that this excess scattering is related to the fraction of unstacked layers which is not taken into account in the calculation of the average stacking value based on the Debye–Scherrer equation.^38,40

The presence of this excess scattering shows that a non-negligible proportion of unstacked layers is present. Turbostraticity and bending effects can also influence the morphology of MoS₂-based solids. A slight displacement of the position of the (002) and (100) reflections is generally related to such stacking faults.⁴¹ Peak displacements are indeed observed here resulting in a shift of the (002) diffraction peak from 2θ = 14.4° (d₀₀₂ = 6.17 Å) to 13.9° (d₀₀₂ = 6.37 Å) and of the (100) diffraction peak from 2θ = 32.7° to 33.6°. These peak shifts can reflect rotation either along the a-axis (basal plane direction) or along the c-axis (stacking direction). However, while rotation along the c-axis only results in a shift of the (002) diffraction peak to lower angle values without any shift of the (100) diffraction peak, rotation along the a-axis is expected to shift the (002) and (100) diffraction peaks, respectively, to lower and higher angle values.⁴¹ Therefore, turbostraticity based on an interlayer rotation along the a-axis is observed on the Co/MoS₂-H₁ catalyst. It is worth noting that the shift of the (002) diffraction peak can also result from an increase of the interlayer distance. The turbostratic effect is also responsible for the strong anisotropy of the (100) MoS₂ envelope.⁴² Previous studies have also shown that bending of the layers led to higher (110)/(100) intensity ratios than expected from a perfectly crystalline bulk sample (I(110)/I(100) = 0.52).^26,43 The actual I(110)/I(100) ratio (0.60) is slightly higher than the expected value for highly crystalline bulk MoS₂ suggesting that bending of the layers occurs either from a minor proportion of very bent slabs or from a large proportion of slabs but with small bending angles.

Diffraction peaks of the Co₉S₈ phase (JCPDS: 01-086-2273) are also observed at 30.4°, 48.2°, and 52.7° corresponding to the (311) + (222), (511), and (440) reflections, respectively. The (331) Co₉S₈ reflection overlapped with the (103) MoS₂ diffraction peak around 2θ = 40° while the (533) + (622) Co₉S₈ reflections give rise to an anisotropy of the (110) MoS₂ envelope at 2θ = 61°.

In summary, the X-ray diffraction analysis reveals the coexistence of both MoS₂ and Co₉S₈ bulk phases. The MoS₂ phase is poorly organized and is formed of slabs presenting a high degree of stacking faults and possibly some minor bending effects. This poorly crystalline and disorganized morphology hampers the possibility to precisely characterize the eventual presence of an interface between MoS₂ and Co₉S₈. However, partly destacked slabs and turbostratic effects are morphological parameters which might favor the increase of the contact surface area between the two bulk sulfide phases.

3.2.3. XPS characterization. X-Ray photoelectron spectroscopy was used to determine the electronic state of the cobalt species on the Co/MoS₂-H₁ unsupported catalyst. After sulfidation, the Co 2p core level spectrum generally reveals the presence of three distinct phases: surface cobalt(II) oxide, the mixed so-called “CoMoS” phase where Co is in decoration of MoS₂ edge planes, and Co₉S₈. XPS can therefore help to distinguish between “CoMoS” and Co₉S₈ even if the positions in binding energy (BE) between these two sulfide Co species differ only by 0.5 eV which is the experimental resolution limit.⁴⁴Fig. 5 reports the Co 2p core level spectra of Co/MoS₂-H₁ before and after HDS reaction. Before HDS reaction, the Co 2p_3/2 signal exhibits a maximum at 778.1 eV with a minor contribution at 780.5 eV due to Co(II) oxide species (Fig. 5). The Co 2p_3/2 signal for Co₉S₈ is generally reported to be at BEs ranging between 777.8 eV and 778.1 eV while the signal for “CoMoS” is found at 778.6 eV.^44,45 Therefore, the Co 2p_3/2XPS signature of Co sulfide species is close to the value expected for Co₉S₈ suggesting a low proportion of Co atoms in decoration of MoS₂ edges if any. After DBT HDS reaction, the maximum intensity of the Co 2p_3/2 signal slightly shifts (0.3 eV) to lower BEs (777.8 eV) while the Co(II) oxide contribution remains at 780.5 eV suggesting an even lower proportion of the “CoMoS” phase (if any) after HDS reaction. To confirm this point, the decomposition of the Co XPS spectrum was performed before and after the DBT HDS reaction in order to determine the relative proportion of both CoO_x and Co₉S₈ species and assuming a third contribution coming from a CoMoS phase. Results show a very small proportion of the CoMoS phase (≤ 4%) before HDS further reduced to only 2% after HDS. Therefore, a much lower value than the error uncertainty commonly observed for the decomposition of XPS spectra (±10%) is found. Results are reported in Table 2. A CoMoS phase (if present) should then represent only a negligible amount insufficient to explain by itself the HDS catalytic properties of this highly HDS active unsupported CoMo catalyst. Only one study has previously reported a decomposition of the Co XPS spectrum of an unsupported CoMo sulfide showing a low proportion of the CoMoS phase.⁴⁶ It should however be noted that even if already low, this proportion was overestimated in this previous study since the proportion of cobalt present in the CoO_x phase was not taken into account. This confirms that the synergetic effect observed on this unsupported Co/MoS₂ catalyst cannot be ascribed to cobalt atoms in decoration of MoS₂ slabs as commonly observed for supported catalysts.

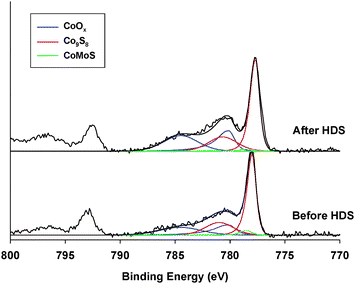Fig. 5 Co 2p XPS core level spectra of the unsupported Co/MoS₂-H₁ catalyst before and after dibenzothiophene HDS reaction.

Table 2 Results of the decomposition of the Co XPS spectra of the Co/MoS2-H₁ unsupported catalyst before and after HDS reaction showing the different proportions of Co species (the corresponding binding energy values are given in parentheses)

Co/MoS2-H1	% CoOx	% Co9S8	% CoMoS
Before HDS	32 (780.2 eV)	64 (778.0 eV)	4 (778.5 eV)
After HDS	41 (780.1 eV)	57 (777.7 eV)	2 (778.5 eV)

---

3.2.4. TEM characterization. TEM images show the presence of characteristic fringes of molybdenum disulfide with the interplanar d₀₀₂ spacing of about 0.64 nm (Fig. 6). Samples are formed of bundles of intermingled MoS₂ layers that are fairly stacked. Determination of MoS₂ slab dimensions shows an average length along the basal direction of 6.2 nm with sizes ranging from 2 to 20 nm. Similarly, an average stacking degree of 3.7 was found relatively close to the value determined by XRD.

Fig. 6 TEM image showing characteristic fringes of MoS₂ particles. Layers are quite disordered leading to many stacking faults as observed in the inset.

However, the stacking degree determined by XRD (4.6) was calculated based on the Debye–Scherrer equation applied to the (002) diffraction peak and was then overestimated since neglecting the presence of monolayers. The value found by TEM is therefore closer to the real value even if still probably overestimated. Quite large stacking distribution was once again obtained reaching values up to nine stacked slabs.

The composition of the Co/MoS₂-H₁ unsupported catalyst was analyzed through EDX analyses of images acquired in the STEM bright field mode confirming the presence of the Co, Mo and S elements on large analyzed regions with a 1 : 0.3 : 2.1 Mo : Co : S molar ratio. This ratio is similar to the one determined by elemental analysis suggesting good homogeneity of the composition. Examination of TEM pictures show that slabs often present small bending effects. This confirms that bending occurs on a large proportion of slabs but with generally low angles of curvature. Low angles of curvature are expected since bending of MoS₂ layers results in strain effects along the basal plane leading to unstable structures if the curvature angle becomes too high.^47–49

This instability could favor the breaking of slabs. Examples of such curved slabs are shown in Fig. 7 in which some slabs present a stronger bending effect. Careful observation of these MoS₂ slabs showed that they are in fact broken at the position where torsion of the slabs and therefore strain effects are expected to be the most important (inset, Fig. 7). Finally, a highly disordered organization of stacked layers can be easily observed showing imperfect stacking of layers leading to a marked turbostratic effect. These results are in agreement with previous XRD conclusions confirming that MoS₂ is present under the form of poorly organized slabs with many stacking faults and limited bending effects.

Fig. 7 TEM image showing MoS₂ fringes with a strong bending effect of almost 90° of angle. Inset: zoom in on the curved particle showing that slabs are in fact broken at the point of highest torsion.

The interpretation of the Co₉S₈ phase by TEM appears less straightforward than by XRD. The main reason for such difficulty is related to the poorly crystalline structure of molybdenum sulfide that hampers a correct visualization of cobalt sulfide. However, as shown in Fig. 8A, it could be clearly observed that the MoS₂ slabs are in fact spread on a Co₉S₈ substrate which leads to a limited number of TEM zones where MoS₂ and Co₉S₈ are both clearly visualized. Fast Fourier transform of the substrate showed a hexagonal array of diffraction spots corresponding to the (111) plane of Co₉S₈ (inset, Fig. 8A). However, some spreading of these spots can also be noticed suggesting some slight disorganized arrangement of the Co₉S₈ substrate. A HRTEM image of another region in which the Co₉S₈ substrate can be seen is presented in Fig. 8B in which a honeycomb-like hexagonal arrangement of the lattice atoms can be clearly observed. The presence of a cobalt sulfide substrate on which MoS₂ is spread suggests that Co₉S₈ might form first during the decomposition of the bimetallic precursor followed by nucleation of the MoS₂ phase from this substrate. This might be expected since Co₉S₈ is expected to be sulfided first before MoS₂ as observed by Geantet et al.⁵⁰

Fig. 8 (A) TEM image of a highly stacked slab presenting some curving effects and interacting with the Co₉S₈ substrate. The cobalt sulfide phase can be clearly visualized as shown for example in the white-squared zone. Fast Fourier Transform of the square region (inset) showing a hexagonal arrangement of diffraction spots. (B) HRTEM image of another region on which MoS₂ is spread onto a Co₉S₈ substrate. The honeycomb-like arrangement of lattice cobalt atoms is clearly visualized. (C) Modelling of a Co₉S₈ (111) plane (blue: cobalt, yellow: sulfur). (D) Simulated TEM picture of the Co₉S₈ (111) model shown in (C) showing the same honeycomb-like arrangement than found experimentally in (B).

The HRTEM image of the Co₉S₈ substrate presented in Fig. 8B was further analyzed to confirm the preferential surface exposed. For this purpose, a Co₉S₈ (111) molecular model was constructed (Fig. 8C). TEM simulations performed on this model (Fig. 8D) show a clear correspondence between the experimental HRTEM image and the simulation based on the Co₉S₈ (111) model.

Further calculations of the side-to-side distance of this hexagonal lattice arrangement led to a value of 0.724 nm vs. 0.737 nm found experimentally confirming undoubtedly the preferential exposition of the (111) plane on Co₉S₈ as a substrate for a possible interaction between MoS₂ and Co₉S₈ bulk phases. This result will be considered later in this study as a starting point to propose a molecular model of the MoS₂/Co₉S₈ interface from which DFT calculations will be performed.

Therefore, if an interface should be present at the contact area between MoS₂ and Co₉S₈ bulk phases, this interface region can only be obtained between the (111) plane of Co₉S₈ and the edge area of MoS₂ slabs. Indeed, since MoS₂ exhibits a layered nature, dangling bonds are expected only at the termination planes of MoS₂ particles and are therefore the preferential region for interaction with cobalt sulfide. As said before, due to the preferential deposition of MoS₂ onto the Co₉S₈ substrate, the visualization of both MoS₂ and Co₉S₈ is however expected to be limited to regions at the periphery of the aggregated unsupported Co/MoS₂ catalyst. Nevertheless, the situation observed in Fig. 8 is also found on other zones of visualization of both MoS₂ and Co₉S₈ like in Fig. S2 (ESI†) in which MoS₂ slabs look like as emerging from the Co₉S₈ substrate from its edges.

3.3. Modeling the MoS₂/Co₉S₈ interface

3.3.1. TEM simulation. The preceding section has shown that the unsupported Co/MoS₂ catalyst is mainly composed of poorly crystalline MoS₂ slabs, slightly bent, and highly stacked with a strong turbostratic character. This “rag” MoS₂ phase is spread onto a Co₉S₈ substrate limiting its visualization to the periphery of the analyzed zones. In the regions where the two bulk sulfide phases can be observed, Co₉S₈ seems to preferentially expose (111) planes in close proximity to MoS₂. Therefore, if an interface exists between the two bulk sulfide phases, it would be found at the contact region between the MoS₂ edge planes and the Co₉S₈ (111) substrate. This conclusion must be however considered cautiously due to: (1) the difficulty in visualizing mixed zones comprising both MoS₂ and Co₉S₈, (2) the inherent “local” character of a TEM analysis, and (3) the too low TEM resolution which cannot be used to clearly visualize the formation of such an interface. Moreover, in the present case, only initial bulk MoS₂ and Co₉S₈ phases were considered without taking into account a possible influence of the ratio of partial pressures between H₂ and H₂S which would modify the edge states of MoS₂ and/or Co₉S₈. Therefore, the procedure developed here should be considered as a first approach to a more complex catalytic system which would be more reactive to its environment composed of H₂, H₂S and hydrocarbon compounds.

TEM characterization therefore can be used to provide tracks from direct observations to determine how the two bulk Co₉S₈ and MoS₂ sulfide phases would interact with each other but TEM cannot provide definitive conclusion about the existence of a real interface. To more deeply analyze this possibility, one must then shift to molecular modeling simulations to better define the feasibility of such an interface. Therefore, a model interface was then built between a cleaved (111) Co₉S₈ moiety and the (010) edge plane of MoS₂ (Fig. 9). The building of the interface was a challenging task due to the complexity of both MoS₂ and Co₉S₈ structures. The positional tensor matrix σ_ij which indicates each individual atom in the structure has indeed many coefficient coordinates. However, formation of an interface between (010) MoS₂ and (111) Co₉S₈ through modeling simulation was found to be possible by simulating TEM pictures from tentative models and confronting them to experimental HRTEM pictures of MoS₂ and Co₉S₈ interacting with each other as shown in Fig. 10. In a first step, on the selected experimental TEM image, line profile analysis was performed to determine the MoS₂ interlayer spacing and slab thickness. The experimental TEM image was also digitalized before to obtain a molecular representation of the interface using interface builder from Accelrys which matches the matrix vector for each crystal plane in a (h, k, l) form to its parity neighbour crystal making a Ax = B matrix with A the (010) MoS₂ plane, x the (111) Co₉S₈ plane, and B the interface. This approach allows us to calculate bonding after building the interface based on electronic parity between species leading to a reliable model (Fig. S3, ESI†). A simulated HRTEM image was then determined with appropriate Scherzer Cs coefficient and defocus and slide thickness conditions while keeping similar MoS₂ interlayer spacing (Fig. 10). Every data produced by TEM simulation are then fitted with experimental TEM results with an accuracy of ±0.005%. Finally, a digitalized image of the simulated picture was generated leading to a simulated molecular representation using a similar procedure than for the experimental TEM image. Both models were then superimposed until a good fit is obtained. A portion of the interface corresponding to the best fit (Fig. 11) is then chosen to generate a “seed” interface model for which further analysis of band structure, density of states and Mulliken calculations are performed in the following sections.

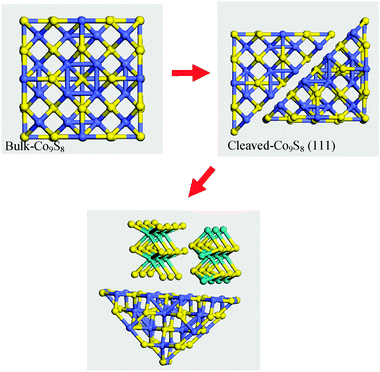Fig. 9 Schematic representation of the procedure used to build the model interface between a cleaved (111) Co₉S₈ moiety and the (010) edge plane of MoS₂.

Fig. 10 Comparison between experimental and simulated HRTEM images of the interface region between the two bulk MoS₂ and Co₉S₈ phases. The simulated HRTEM picture is then used as a reference to build the model interface.

Fig. 11 (A) The resulting model interface between the layered MoS₂ (010) plane and the Co₉S₈ (111) plane. The atoms are coloured as follows: cobalt (blue), sulfur (yellow) and molybdenum (green), (B) portion of the interface called “seed” (red dashed line) used for DFT calculations, (C) zoom on a cobalt cubic cluster arrangement connected to Mo atoms, and (D) another view of (B).

3.3.2. Description of the MoS₂–Co₉S₈ interface model. Before describing in detail the local interface structure, it should be noted at this point that Co₉S₈ presents a complex structure. Two types of Co atoms are present: an octahedrally coordinated Co atom with six S neighbors and a tetrahedrally coordinated Co atom with (1) 4 nearest S neighbors plus three other S atoms at a distance only 0.009 Å larger and (2) three Co neighbors forming a cubic array. A close look at the model interface shows that each MoS₂ slab interacts with the cobalt atoms forming the cubic arrangement (Fig. 11). The interfacial energy is 1.5 eV/atom. In half of the cobalt cubic clusters interacting with molybdenum, two Mo atoms interact with Co atoms. However, while one of the Mo atoms only interacts with one Co atom, the second Mo atom is connected to two Co atoms of the cubic array (Fig. 11C). Both Mo atoms are fivefold coordinated showing the existence of latent vacancy sites (in bulk MoS₂, Mo is six-fold coordinated). These vacancies may play an important role in HDS providing sites for coordinating sulfur-containing reactants. For the other half of the cobalt cubic cluster interacting with molybdenum, two Mo atoms also form bonds with Co atoms. One of the Mo atoms is coordinated to only one Co atom of the cubic array while the other one is coordinated to two Co atoms of the cubic array but also to one single octahedral Co atom. The higher coordination number of Mo atoms shows the absence of latent vacancy sites in this case. Another interesting point of the proposed interface molecular model is the shift of the interlayer distance to 6.4 Å. This value is identical to the one observed experimentally by XRD (Fig. 4) and comes from the shift to lower angles of the (002) diffraction peak. Therefore, this shift of the (002) diffraction seems to be explained by both an increase of the interlayer distance between MoS₂ slabs due to the formation of the MoS₂/Co₉S₈ interface and also probably from rotation of the MoS₂ layers from each other about the a-axis.

3.3.3. Mulliken charge analysis. The presence of direct Co–Mo bonds is an interesting feature found in our molecular interface model. The interface model was then further analyzed to determine the possible modifications of electronic properties induced by the presence of these Co–Mo bonds and their influence on the catalytic efficiency in hydrodesulfurization mainly regarding a possible electron donation from Co to Mo. The two sets of Mo atoms connected to cobalt cluster arrays were then analyzed separately through Mulliken population analysis. For the set of highly coordinated Mo atoms, Mulliken calculations lead to charges of +0.49 to +0.53 for the Mo atoms. In bulk MoS₂, the Mo charge is +0.61. The direct bonding between Co and Mo therefore results in a limited charge donation from cobalt to molybdenum. Inversely, cobalt atoms of the cubic array that are directly connected to Mo show much more negative (or less positive) charges (−0.07 and + 0.03) than those expected for similar Co atoms in bulk Co₉S₈ (+0.16). Consequently, one of the first Co neighbors to these Mo-coordinated Co atoms in the cubic cluster shows inversely much more positive charge values ranging from +0.28 to +0.30 while the second first Co neighbors present more negative values than expected from the bulk Co₉S₈ (−0.15 and −0.07). Finally, the Co atoms of the cubic cluster located at the farthest atomic positions compared to Mo present the closest charge values to bulk cobalt sulfide (+0.14 and +0.16). This result coupled with the absence of sulfur atoms shared between this cobalt cluster array and the highly coordinated Mo atoms shows that the direct electron donation is in this case quite limited. The more negative charge values of Co connected to Mo combined with the higher positive charges on some of their first Co neighbors suggest that donation of electrons (probably induced by a destabilization effect of Mo) propagates inside the cubic cluster array resulting in a formal reduction of some Co atoms and a formal oxidation of some of their Co neighbors. However, this redistribution of charges inside the cubic cluster only results in a limited donation from cobalt to molybdenum.

For the set of fivefold-coordinated Mo atoms, the situation appears different. While for the Mo atom coordinated to two Co atoms of the cubic cluster, a positive charge value of +0.53 (very similar to the previous case) is obtained suggesting once again a limited electron donation from Co through direct Co–Mo bonds, the second Mo atom coordinated to only one cobalt presents a much lower charge of +0.25 showing in this case a strong electron donation. This latter Mo atom is also the only type of molybdenum atoms that possesses bonding to a sulfur atom connected to the cobalt cluster array and not only presenting direct Co–Mo bonds (Fig. S4, ESI†). Electron donation from cobalt atoms of the cobalt cluster array to molybdenum is therefore more effective through intermediate sulfur shared between the two metallic atoms. This is also confirmed by the more negative charge value of this sulfur atom (−0.22) compared to sulfur atoms in similar crystallographic positions but only connected to cobalt (−0.09 and −0.11). The resulting Mo–S bond of this Mo–S–Co entity is then expected to be particularly weakened and is therefore the most susceptible to form coordinatively unsaturated sites. The charges on Co atoms of the cubic array associated to these fivefold coordinated Mo atoms present a similar situation to the previous case: a more negative value on the Co atoms directly connected to Mo and a highly positive value on one of their first Co neighbors.

Fivefold coordinated Mo atoms engaged in a Mo–S–Co moiety with the cobalt cubic array therefore not only possess latent vacancy sites but also are the most susceptible to create CUS sites through a strong electron donation. It should be finally noted that similar Mo–S–Co moieties but with octahedral Co atoms that are not directly bonded to Mo do not result in an effective electron donation. Therefore, the direct Co–Mo bond seems necessary to perturb electronically the cobalt cubic array inducing an electronic donation but only through an intermediate sulfur atom shared between Mo and Co. These results confirm that electron donation from Co to Mo is effective in Co–S–Mo moieties and result into more labile sulfur atoms.^51,52 The presence of latent vacancy sites is also in full agreement with a recent DFT study by Moses et al. suggesting that the Co–Mo–S edge in its equilibrium state under HDS conditions can perform hydrogenation and C–S bond scission without the necessity to initially create vacancies.⁵³ This result is also in agreement with previous theoretical calculations showing that to be effective, electron donation from Co to Mo should occur only when Mo t_2g orbitals in a MoS₂ environment lie between the t_2g and e_g orbitals of Co. The presence of sulfur bonds between Mo and Co then seems necessary to shift downward the Co 3d energy bands compared to Mo 4d t_2g levels.¹⁶

3.4. Electronic properties

In order to determine the consequences in terms of electronic properties of the formation of such a MoS₂/Co₉S₈ interface, band structure and density of states (DOS) calculations were performed. For comparison purposes, the same procedure was applied first separately for finite-size MoS₂ and Co₉S₈ samples to investigate if results are coherent with previous studies before considering the MoS₂/Co₉S₈ interface. The results obtained using a PWB set in CASTEP calculations for band structure calculations of bulk MoS₂, Co₉S₈ and “seed” (MoS₂/Co₉S₈) indicate a semiconductor behavior for bulk MoS₂ structure⁵⁴ as presented in Fig. 12. No irreducible points are observed in bulk MoS₂ due to its strong semiconductor character. For bulk Co₉S₈, two Fermi wave vector values k_F at ∼0.17Å⁻¹ and ∼0.43 Å⁻¹ were found showing a metallic character in the first Brillouin zone. For our “seed” interface model, an interesting metallic character was found with three Fermi wave vector values k_F at ∼0.37Å⁻¹, 0.43 Å⁻¹ and 0.56 Å⁻¹. The Fermi wave vector k_F value of 0.37 Å⁻¹ is in agreement with Bollinger et al. which obtained a value of 0.39Å⁻¹ for a two-dimensional MoS₂ stripe exposing mainly Mo-edges.⁵⁵ This characteristic k_F value is related to a strong metallic character due to superposition of p_x orbitals along the edge of MoS₂. Similarly, the k_F value at ∼0.43 Å⁻¹ originates from Co₉S₈ while a new metallic state is observed at k_F ≈ 0.56 Å⁻¹. This new metallic state results from the formation of the interface and might be related to the creation of direct Co–Mo bonds. This leads to a conclusion of mixing states in the interface model due to the superposition of p_x orbitals in two parallel sulfur chains along the MoS₂ edge which are in direct contact with Co species.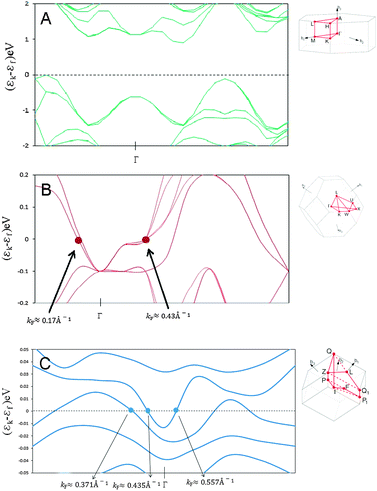

Fig. 12 Band structure calculations for bulk MoS₂ (A) and Co₉S₈ (B) and for the MoS₂/Co₉S₈ (C) interface model. For each band structure calculation, the path used for integrating periodic functions of the wave vector in the Brillouin zone is indicated.

Fig. 13 reports the DOS for the MoS₂ (A) and Co₉S₈ samples (B), and for the MoS₂/Co₉S₈ interface (C). The DOS found for MoS₂ reflects a semiconducting behavior with a weak band gap of 0.7 eV at the Fermi level (Fig. 13A). This value is close to the one found previously (0.89 eV) showing that the DOS for a finite MoS₂ system with sulfur-saturated Mo surface atoms is quite close to the bulk DOS.^56,57 In the layered MoS₂ structure, the coordination of the metal atom is trigonal prismatic. The ligand-field effect on Mo d states resulting from the covalent Mo d–S p bonding under a trigonal distortion led to the splitting of t_2g orbitals into a non-degenerate a_1g and doubly degenerate e_g sets. Therefore, the Fermi level falls at the upper edge of the a_1g band while the e_g complex forms the lowest group of conduction bands. However, substantial mixing of the Mo 4d character with the S 3p band occurs.

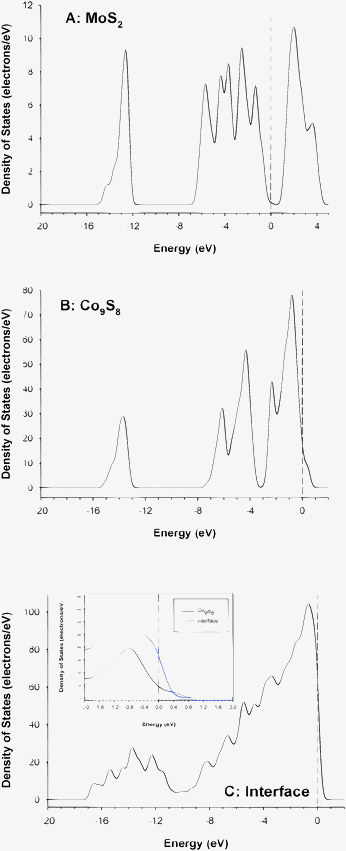Fig. 13 Total electronic density of states of (A) MoS₂, (B) Co₉S₈, and (C) of the “seed” from the MoS₂/Co₉S₈ interface. The inset in (C) shows a comparison of the densities of states between Co₉S₈ and the interface at the Fermi level (after normalization).

As previously explained, Co₉S₈ presents two types of cobalt atoms: an octahedrally coordinated cobalt atom with six sulfur neighbors and a tetrahedrally coordinated cobalt atom forming a cubic array through coordination to three other cobalt neighbors. Due to the presence of these Co–Co bonds, the DOS for Co₉S₈ presents a metallic character (Fig. 13B). However, the Fermi level (EF) corresponds to an inflection point showing the presence of lower and upper parts of mainly the Co 3d band. Hybridization with S 3p σ* states is more expected on the upper part of the Co 3d band above EF.

The DOS for the MoS₂/Co₉S₈ interface presents a metallic character due to the presence of both Co–Co and Co–Mo bonds (Fig. 13C). However, due to the Co–Mo interaction, the distribution of the electronic density of the d bands appears broader with a lower part going from −10 eV to just above EF.

Particular attention paid to the DOS profile at EF shows that the electronic density is however more localized at the Fermi level for the interface with a higher electron density at 0 eV than for Co₉S₈ going back to zero for a less positive value of energy of 0.7 eV versus 1.3 eV for Co₉S₈.

Therefore, the metallic character is more localized at the region close to the Fermi level. This effect could be related to the shift of the unoccupied Mo d_yz states below (or close to) the Fermi level due to their filling by cobalt as previously stated for the CoMoS decoration model.¹⁶ This would suggest that similarities would exist between CoMoS and the Co₉S₈/MoS₂ interface in terms of electronic properties confirming that a similar synergy effect applies in the present case. This is expected to modify significantly the HDS catalytic properties of the MoS₂/Co₉S₈ interface increasing its hydrogenating character but probably less than the formation of latent vacancy sites on fivefold coordinated Mo atoms of the interface.

3.5. Comparison to previous results based on DFT, EXAFS, NMR or organometallic studies

3.5.1. Comparison to previous organometallic studies. Comparison of the model MoS₂/Co₉S₈ interface is possible in relation with previous organometallic studies trying to modelize Co/Mo/S clusters in order to study the HDS mechanism. Types of reactions exhibited by organometallic compounds in solution often occur on the surface of heterogeneous catalysts and can give valuable information about the HDS mechanism. Co/Mo/S clusters used in the organometallic approach often present Co–Mo bonds. Examples can be found in studies made by Curtis and co-workers,^58–61 Brenner et al.,⁶² and by Halbert et al.⁶³ Curtis et al. found that in the cluster desulfurization reactions can occur on Co sites bonded to Mo and presenting latent vacancy sites.⁶¹ Using the same organometallic cluster presenting direct Co–Mo bonds with intermediate S atoms as in the present interface model, Brenner et al. observed that this cluster led to a much higher turnover frequency in the HDS of thiophene than a classical CoMo/Al₂O₃ catalyst.⁶² These authors concluded that the activity was increased by the presence of molecular scale ensembles containing molybdenum, cobalt and sulfur. Using XPS, they also observed that the presence of such direct Co–Mo bonds presenting shared intermediate sulfur atoms led to a strong donation of electrons from Co to Mo. Halbert et al. studied the Mo₂Co₂S₄(S₂CNEt₂)₂(CH₃CN)₂(CO)₂ cluster presenting a thiocubane Co₂Mo₂(μ₃-S)₄ core (Fig. 14).⁶³ In this cluster, Mo atoms are coordinated to two Co atoms. When the cobalt fragments bind to the terminal Mo=S groups, open sites on the Mo centers are produced as also observed in the MoS₂/Co₉S₈ interface. The formation of Co–Mo bonds in this cluster was suggested to favor the electronic donation from Co to Mo weakening Mo–S bonds and making the d_z², d_xz, and d_yz orbitals of molybdenum more available as acceptor orbitals.⁶³ This would make “open” sites analogous to vacancies whose affinity for ligands will be enhanced by cobalt. This situation can also be expected on the fivefold coordinated Mo atoms of the interface. Fig. 15 reports the DOS found for the Mo₂Co₂S₄(S₂CNEt₂)₂(CH₃CN)₂(CO)₂ cluster acquired considering only the thiocubane Co₂Mo₂(μ₃-S)₄ core. As expected due to the presence of direct Co–Mo bonds in this thiocubane cluster, the DOS presents a strong metallic character which seems even more amplified compared to the MoS₂/Co₉S₈ interface. As a matter of fact, the DOS profile for the thiocubane Co₂Mo₂(μ₃-S)₄ core is essentially similar to the one observed for the interface model but with a stronger localization of d orbitals reaching maximum almost at the Fermi level. This confirms that the formation of direct Co–Mo bonds with sulfur ligands led to an enhanced hydrogenating character of the resulting catalyst.

Fig. 14 Drawing of Co₂Mo₂(μ₃-S)₄(S₂CNEt₂)(CO)₂·(CH₃CN)₂cluster. Adapted from ref. 63 (blue: cobalt, green: molybdenum, yellow: sulfur, red: oxygen, grey: carbon, dark blue: nitrogen, white: hydrogen).

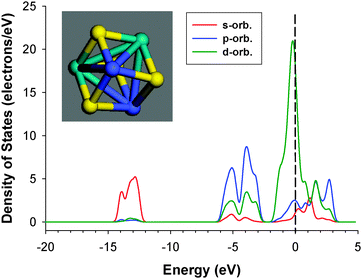Fig. 15 Density of states of the thiocubane Co₂Mo₂(μ₃-S)₄ core of the Co₂Mo₂(μ₃-S)₄(S₂CNEt₂)(CO)₂·(CH₃CN)₂cluster. Inset: representation of the thiocubane core (blue: cobalt, green: molybdenum, yellow: sulfur).

3.5.2. Comparison to previous EXAFS, NMR and DFT studies. The Co₉S₈/MoS₂ model interface can also be confronted to previous EXAFS results acquired on CoMo samples about Co–Mo distances. In this respect, EXAFS studies have generally reported Co–Mo distances varying between 2.73 and 2.80 Å.^64,65 Taking into account all the first Co neighbors of Mo atoms in the model interface, a value of 2.758 Å is found in complete agreement with those determined by EXAFS. The structural model interface found herein would lead to similar Co–Mo distances as those obtained experimentally using X-ray absorption techniques.

⁵⁹Co NMR was rarely envisaged to study Co-promoted MoS₂-based catalysts. Co salt precursors or oxides are generally paramagnetic and alumina, the most common support used for CoMo catalysts, impairs the analysis of these solids through ⁵⁹Co NMR. Only SiO₂-supported CoMo catalysts were studied using this technique.⁶⁶ Using ⁵⁹Co NMR, structural information can be retrieved from the measurement of the quadrupolar interaction related to the symmetry of the local environment. The local electronic structure is also given by the Knight shift and the relaxation time. For instance, in a Co₉S₈ reference, octahedral Co presents a long longitudinal relaxation time while tetrahedral Co exhibits a short relaxation time reflecting very different electronic surroundings with metallic Co neighbors for tetrahedral Co and only sulfur neighbors for octahedral Co. In CoMo/SiO₂, new distorted tetrahedral Co sites were detected resulting from the sharing of sulfur atoms between the MoS₂ phase and cobalt atoms engaged in the cubic cluster unit. Such a situation would favor a higher electron donation from Co to Mo.⁶⁷ This result is in agreement with the present conclusions about the inactivity of octahedral Co atoms and the formation of highly active Co–Mo entities presenting sulfur ligands and formed with tetrahedral Co atoms of the cubic clusters of Co₉S₈ at the interface of the two sulfide phases.

The presence of potentially highly active sites on fivefold coordinated Mo atom directly connected to Co has also to be compared with previous DFT studies about the localization of Co onto the edges of MoS₂ slabs for supported cobalt-promoted MoS₂ catalysts. In this respect, formation of direct Co–Mo bonds was already found by DFT calculations modeling the localization of cobalt on the Me-edge of MoS₂ particles.^7,68 Under a very large P_H2S/P_H2 range, formation of these direct Co–Mo bonds was found to correspond to the most stable configuration of cobalt on the Me-edge of MoS₂. Stable morphology of CoMo nanocrystallites would correspond to an equal proportion of 50% of S-edge and 50% of Me-edge. Co coverage on the S-edge and Me-edge would be, respectively, 100% and 50%. Moreover, Mo atoms on the Co-promoted Me-edge can exhibit five-fold coordination. Recent DFT calculations of the localization of cobalt on MoS₂ nanocrystallites have also shown that the maximum in HDS activity is generally reached at a Co/Mo ratio of 0.3 and corresponds to the optimum formation of mixed CoMoS sites with direct Co–Mo bonds.⁶⁹ These mixed CoMoS sites also possess intermediate metal–sulfur bond energy corresponding to the highest HDS activity achievable in the spirit of the Sabatier principle.¹⁶ Therefore, some similarity is observed here between the model interface that is proposed as occurring at the interface between bulk MoS₂ and Co₉S₈ phases and the local Co/Mo/S structure on the Me-edge of MoS₂ as determined by DFT.

3.6. Significance of the present interface model compared to previous descriptions of the synergy effect on supported systems

Results presented here can be compared to the previous models of cobalt decoration,⁴ and of synergy by contact.³ In agreement with this latter model, our results suggest that MoS₂ and Co₉S₈ phases are able to interact with each other in HDS through their interface: the higher hydrogenating character due to cobalt would enhance the hydrogen supply to Mo on which sulfur-containing reactants would be preferably bound. Results are also partly comparable to the more “nanoscopic” view of the decoration model. As already observed in Section 3.5.2, similar Co–Mo bonds and five-fold coordination of Mo would occur on the most stable Co-promoted Me-edge configuration under typical HDS conditions. Therefore, some similarity can be expected.

However, some discrepancies should also be noted. First of all, the formation of the synergetic phase on a support is believed to occur through migration of cobalt to MoS₂ edge planes (which can be really effective only if cobalt is not sulfided before its migration to already sulfided Mo). In this case, an intimate mixing of Co and Mo occurred. In the present case, due to the fact that Co is expected to be easily sulfided first while Mo must be reduced from +VI (MoS₄²⁻) to +IV (MoS₂), MoS₂ seems to “nucleate” from the Co₉S₈ substrate. With respect to the symmetrical synergism model and its Co/Mo phase diagram, the segregation of MoS₂ from a Co₉S₈ substrate would correspond to the second optimum in activity observed on the right side of the phase diagram (Fig. 1). The proposed model interface would then correspond to the situation prevailing in the Co-rich regions. It is also worth noting that the Co/Mo ratio of 0.3 should be considered cautiously since a large proportion of MoS₂ and Co₉S₈ are expected not to interact with each other in such a case. This situation also differs from the one observed on supported systems for which the optimum on the left side of the phase diagram is expected to be reached. One characteristic feature of the optimum observed on the right side of the symmetrical phase diagram is that the synergetic effect is generally less amplified due to the difficulty to obtain high surface area Co₉S₈. This “surface dependency” of the synergetic effect is clearly observed in this study for Co/MoS₂ unsupported catalysts in the HDS of DBT. The difficulty to obtain a highly surface contact with Co₉S₈ is partly overwhelmed here through the formation of a very high surface area solid obtained thanks to an increase of the pressure used during the preparation and resulting in a high surface contact between reactant and catalyst. The last point to consider in a future study will be the influence of the replacement of sulfur by carbide-like entities as observed in steady-state DBT HDS stabilized catalysts and also to determine how DBT molecules can interact with these interfacial sites in order to perform HDS reaction.^26,27

4. Conclusion

The present study showed that contrary to the common assumption observed for supported MoS₂-based catalysts, the HDS activity of Co-promoted MoS₂ unsupported catalysts is directly related to the increase of the respective surface areas of the pure phases. This suggests that the HDS activity could be related to the contact area of a possible interface between bulk MoS₂ and Co₉S₈ phases. This point led us to reinvestigate carefully highly active unsupported Co/MoS₂ catalysts. This approach helps us to define a model interface between MoS₂ and Co₉S₈ in accord with HRTEM experimental observations. This model was then confronted to a DFT approach to determine its feasibility as a reasonable description of the interface region between the two bulk sulfide phases.

Modeling of the interface shows the creation of open latent vacancy sites on half of the Mo atoms interacting with cobalt and formation of Co–Mo bonds. Strong electron donation from Co to Mo occurs through intermediate sulfur atom bonded to both metals. Calculations of the density of states for this interface showed an enhanced metallic character at the region close to the Fermi level consecutively to the MoS₂–Co₉S₈ interaction. These modifications of coordination and electronic properties may play a major role in explaining the synergetic effect present at the interface where Co and Mo interact with each other. Results particularly confirm the presence of latent vacancy sites, a higher hydrogenation character and the weakening of the Mo–S bond strength in Mo–Co–S entities. These results are in agreement with our previous work comparing the synergic systems such as MoS₂/Co₉S₈ with binary transition metal sulfides.¹² It confirms that these synergic systems behave as pseudo-binary sulfides mimicking the electronic structure of very HDS active noble metal sulfides.⁷⁰

Acknowledgements

M. Ramos thanks CONACYT, Mexico doctoral scholarship program #207997, the MRTI of UTEP, Cotton Trust UTEP, the Microlectronics Research Lab of UT-Austin and Departamento de Educación y Cúltura of Gobierno del Estado de Chihuahua. We would like also to thank Dr Marc-Jacques Ledoux for his strong support and fruitful discussion on this subject. The authors want to particularly dedicate this paper to the memory of Dr Edward F. Stiefel because of his contributions to the field of organometallic catalyst and who, as described in the text, predicted the inorganic structure of the promoted sites prior to 1985.

References

1. B. Torres, G. Berhault and R. R. Chianelli, Metal Sulfides in Encyclopedia of Catalysis, Wiley, New York, 2002 DOI:10.1002/0471227617.
2. A. L. Farragher and P. Cossee, Proceedings of the 5th International Congress on Catalysis, North-Holland, Amsterdam, 1973, p. 1301.
3. G. Hagenbach, P. Courty and B. Delmon, J. Catal., 1973, 31, 264.
4. H. Topsøe, B. S. Clausen, R. Candia, C. Wivel and S. Mørup, J. Catal., 1981, 68, 433.
5. R. Candia, B. S. Clausen, J. Bartholdy, N. Y. Topsøe, B. Lengeler and H. Topsøe, Proceedings of the 8th International Congress on Catalysis, Dechema, Frankfurt-an-Main, 1984, vol. 2, p. 375.
6. P. Raybaud, Appl. Catal., A, 2007, 322, 76.
7. E. Krebs, A. Daudin and P. Raybaud, Oil Gas Sci. Technol., 2009, 64, 707.
8. H. Schweiger, P. Raybaud and H. Toulhoat, J. Catal., 2002, 212, 33.
9. M. Sun, A. E. Nelson and J. Adjaye, J. Catal., 2004, 226, 32.
10. J. V. Lauritsen, J. Kibsgaard, G. H. Olesen, P. G. Moses, B. Hinnemann, S. Helveg, J. K. Nørskov, B. S. Clausen, H. Topsøe, E. Lægsgaard and F. Besenbacher, J. Catal., 2007, 249, 220.
11. R. W. Phillips and A. A. Fote, J. Catal., 1976, 41, 168.
12. R. R. Chianelli and G. Berhault, Catal. Today, 1999, 53, 357.
13. Z. Le, P. Afanasiev, D. Li, X. Long and M. Vrinat, Catal. Today, 2008, 130, 24.
14. A. Olivas, G. Alonso and S. Fuentes, Top. Catal., 2006, 39, 175.
15. L. Wang, Y. N. Zhang, Y. L. Zhang, Z. Jiang and C. Li, Chem.–Eur. J., 2009, 15, 12571.
16. R. R. Chianelli, G. Berhault, P. Raybaud, S. Kasztelan, J. Hafner and H. Toulhoat, Appl. Catal., A, 2002, 227, 83.
17. M. J. Ledoux, O. Michaux, G. Agostini and P. Panissod, J. Catal., 1986, 102, 275.
18. D. Genuit, P. Afanasiev and M. Vrinat, J. Catal., 2005, 235, 302.
19. H. Nava, C. Ornelas, A. Aguilar, G. Berhault, S. Fuentes and G. Alonso, Catal. Lett., 2003, 86, 257.
20. L. Alvarez, J. Espino, C. Ornelas, J. L. Rico, M. T. Cortez, G. Berhault and G. Alonso, J. Mol. Catal. A: Chem., 2004, 210, 105.
21. M. H. Siadati, G. Alonso, B. Torres and R. R. Chianelli, Appl. Catal., A, 2006, 305, 160.
22. J. Espino, L. Alvarez, C. Ornelas, J. L. Rico, S. Fuentes, G. Berhault and G. Alonso, Catal. Lett., 2003, 90, 71.
23. A. Gómez-Rodríguez, L. M. Beltrán del Río and R. Herrera-Becerra, Ultramicroscopy, 2010, 110, 95.
24. M. D. Segall, P. J. D. Langan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and S. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
26. G. Berhault, A. Mehta, A. Pavel, J. Yang, L. Rendon, M. J. Yácaman, L. Cota, A. Duarte and R. R. Chianelli, J. Catal., 2001, 198, 9.
27. S. P. Kelty, G. Berhault and R. R. Chianelli, Appl. Catal., A, 2007, 322, 9.
28. S. J. Tauster, T. A. Pecoraro and R. R. Chianelli, J. Catal., 1980, 63, 515.
29. S. Harris and R. R. Chianelli, J. Catal., 1986, 98, 17.
30. T. Kabe, A. Ishihara and Q. Zhang, Appl. Catal., A, 1993, 97, 1.
31. P. Marchand, J. L. Lemberton and G. Pérot, Appl. Catal., A, 1998, 169, 343.
32. M. Breysse, G. Berhault, S. Kasztelan, M. Lacroix, F. Maugé and G. Pérot, Catal. Today, 2001, 66, 15.
33. G. Alonso, G. Berhault, F. Paraguay, E. Rivera, S. Fuentes and R. R. Chianelli, Mater. Res. Bull., 2003, 38, 1045.
34. J. A. Lumbreras, R. Huirache-Acuña, E. M. Rivera-Muñoz, G. Berhault and G. Alonso, Catal. Lett., 2010, 134, 138.
35. L. Alvarez, G. Berhault and G. Alonso, Catal. Lett., 2008, 125, 35.
36. W. Trakarnpruk and B. Seentrakoon, Ind. Eng. Chem. Res., 2007, 46, 1874.
37. V. Sundaramurthy, A. K. Dalai and J. Adjaye, J. Mol. Catal. A: Chem., 2008, 294, 20.
38. G. Berhault, M. Perez De la Rosa, A. Mehta, M. J. Yácaman and R. R. Chianelli, Appl. Catal., A, 2008, 345, 80.
39. R. R. Chianelli, E. B. Prestridge, T. A. Pecoraro and J. P. deNeufville, Science, 1979, 203, 1105.
40. M. Perez de la Rosa, S. Texier, G. Berhault, A. Camacho, M. J. Yácaman, A. Mehta, S. Fuentes, J. A. Montoya, F. Murrieta and R. R. Chianelli, J. Catal., 2004, 225, 288.
41. K. S. Liang, R. R. Chianelli, F. Z. Chien and S. C. Moss, J. Non-Cryst. Solids, 1986, 79, 251.
42. R. R. Chianelli, Int. Rev. Phys. Chem., 1982, 2, 127.
43. H. Nava, J. Espino, G. Berhault and G. Alonso, Appl. Catal., A, 2006, 302, 177.
44. A. D. Gandubert, E. Krebs, C. Legens, D. Costa, D. Guillaume and P. Raybaud, Catal. Today, 2008, 130, 149.
45. D. G. Castner and P. R. Watson, J. Phys. Chem., 1991, 95, 6617.
46. A. F. Lamic, A. Daudin, S. Brunet, C. Legens, C. Bouchy and E. Devers, Appl. Catal., A, 2008, 344, 198.
47. R. R. Chianelli, G. Berhault, P. Santiago, D. Mendoza, A. Espinosa, J. A. Ascencio and M. J. Yacamán, Mater. Technol. Adv. Perf. Mater., 2000, 15, 54.
48. A. K. Datye, S. Srinivasan, L. F. Allard, C. H. F. Peden, J. R. Brenner and L. T. Thompson, J. Catal., 1996, 158, 205.
49. Y. Iwata, Y. Araki, K. Honna, Y. Miki, K. Sato and H. Shimada, Catal. Today, 2001, 65, 335.
50. C. Geantet, Y. Soldo, C. Glasson, N. Matsubayashi, M. Lacroix, O. Proux, O. Ulrich and J. L. Hazemann, Catal. Lett., 2001, 73, 95.
51. G. Berhault, M. Lacroix, M. Breysse, F. Maugé, J.-C. Lavalley, H. Nie and L. Qu, J. Catal., 1998, 178, 555.
52. F. Bataille, J. L. Lemberton, P. Michaud, G. Pérot, M. Vrinat, M. Lemaire, E. Schulz, M. Breysse and S. Kasztelan, J. Catal., 2000, 191, 409.
53. P. G. Moses, B. Hinnemann, H. Topsøe and J. K. Nørskov, J. Catal., 2009, 268, 201.
54. W. Li, J. F. Chen, Q. He and T. Wang, Phys. B, 2010, 405, 2498.
55. M. V. Bollinger, J. V. Lauritsen, K. W. Jacobsen, J. K. Nørskov, S. Helveg and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 196803.
56. P. Raybaud, J. Hafner, G. Kresse and H. Toulhoat, Surf. Sci., 1998, 407, 237.
57. P. Raybaud, J. Hafner, G. Kresse and H. Toulhoat, J. Phys.: Condens. Matter, 1997, 9, 11107.
58. M. D. Curtis, J. E. Penner-Hahn, J. Schwank, O. Baralt, D. J. McCabe, L. Thompson and G. Waldo, Polyhedron, 1981, 7, 2411.
59. U. Riaz, O. Curnow and M. D. Curtis, J. Am. Chem. Soc., 1991, 113, 1416.
60. U. Riaz, O. Curnow and M. D. Curtis, J. Am. Chem. Soc., 1994, 116, 4357.
61. M. D. Curtis and S. H. Druker, J. Am. Chem. Soc., 1997, 119, 1027.
62. J. R. Brenner, B. T. Carvill and L. T. Thompson, Appl. Organomet. Chem., 1992, 6, 463.
63. T. R. Halbert, S. A. Cohen and E. I. Stiefel, Organometallics, 1985, 4, 1690.
64. B. R. G. Leliveld, J. A. J. van Dillen, J. W. Geus, D. C. Koningsberger and M. de Boer, J. Phys. Chem. B, 1997, 101, 11160.
65. A. J. Dugulan, E. J. M. Hensen and J. A. R. van Veen, Catal. Today, 2008, 130, 126.
66. M. J. Ledoux, O. Michaux, G. Agostini and P. Panissod, J. Catal., 1985, 96, 189.
67. M. J. Ledoux, G. Maire, S. Hantzer and O. Michaux, Proceedings of the 9th International Congress on Catalysis, Calgary, 1988, vol. 1, p. 74.
68. E. Krebs, B. Silvi, A. Daudin and P. Raybaud, J. Catal., 2008, 260, 276.
69. K. Marchand, C. Legens, D. Guillaume and P. Raybaud, Oil Gas Sci. Technol., 2009, 64, 719.
70. R. R. Chianelli, T. A. Pecoraro, T. R. Halbert, W. H. Pan and E. I. Stiefel, J. Catal., 1984, 86, 226.

---

Footnote

† Electronic supplementary information (ESI) available: N₂ adsorption–desorption isotherms of the Co/MoS₂-H₁ catalyst; a TEM image showing interaction between edge planes of molybdenum sulfide with Co₉S₈, a schematic of the procedure used to simulate HRTEM pictures, a fragment of the “seed” from the interface model. See DOI: 10.1039/c1cy00126d

---