 Open Access Article
Open Access Article
On the influence of basis sets and quantum chemical methods on the prediction accuracy of COSMO-RS†
Received
15th July 2011
, Accepted 9th September 2011
First published on 2nd November 2011
Abstract
This paper examines how the accuracy of activity coefficients at infinite dilution calculated from the conductor-like screening model for real solvents (COSMO-RS) depends on the basis set and the quantum chemical method used. Activity coefficients at various temperatures serve as experimental parameters for optimising the COSMO-RS parameters. A modification of the electrostatic misfit term of the energy function of COSMO-RS is presented that leads to a slightly higher accuracy. COSMO-RS parameter sets for nine different systematically varied basis sets using the density functional theory with the BP86 functional show that at least a valence double-zeta basis set is necessary for good accuracy. Larger basis sets show no advantages. Investigations of eight different quantum chemical calculation methods using a valence triple-zeta basis set are documented. Hartree–Fock and local density approximations give relatively poor results. The gradient-corrected density functionals investigated and the B3LYP hybrid functional show practically identical accuracy. The most accurate parameterisation was obtained with MP2.
1. Introduction
The conductor-like screening model for real solvents (COSMO-RS) method1,2 for calculating the mixed-phase thermodynamic properties is now a well established tool for semi-quantitative prediction of substance data.3
At the core of the COSMO-RS method is the statistical thermodynamic treatment of an ensemble of surface screening charge densities, serving as a model for the interactions in a molecular assembly. The surface screening charges are determined by quantum chemical calculations for molecules placed in a dielectric continuum. The continuum solvation model COSMO (COnductor-like Screening MOdel)4 is used here, with the dielectric constant set to infinity, ε → ∞, for calculation of the surface screening charges used in COSMO-RS. The reference state of the system is thus the chemical potential of a molecule in a perfect electrical conductor. In the COSMO-RS model, intermolecular interaction is described in terms of pairwise interaction of the screening charge densities on discrete surface segments. For a given cavity construction algorithm, the calculated surface screening charges depend directly on the details of the quantum chemical method. The effect of these dependencies on the parameters of the semi-empirical COSMO-RS method is naturally of both fundamental and practical interest. Despite a series of published parameterisations, such as in ref. 2 and 5–10, no study has been published so far on comparative investigations of the influence of the quantum chemical method used to compute the surface screening charges on the accuracy of the resulting COSMO-RS parameterisation. The object of the present study is therefore to investigate the prediction accuracy of COSMO-RS parameterisations with systematic variation of the quantum chemical computation methods. The work is organized in the following way. The first section lists the equations necessary for an understanding of the COSMO-RS method, describes the quantum chemical methods used, and specifies the target function for the parameterisation and the experimental data set on which the parameterisation is based. The results obtained are then documented and discussed. The work concludes with a summary and outlook. The detailed working equations for COSMO-RS are listed in the Appendix.
2. Methods
The central equation of the COSMO-RS method is| |  | (1) |
where μS(σ) is the chemical potential of an ensemble S as a function of the surface screening charge density σ. R is the universal gas constant and T is the absolute temperature. aeff is the effective contact area between two segments. PS(σ) is a probability density and is called the σ-profile of the ensemble S. The function ε(σ,![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) describes the interaction between two charged surface segments as a function of the screening charge densities. The σ-profile of an ensemble S containing NM different components M with mole fractions xM is defined as:
) describes the interaction between two charged surface segments as a function of the screening charge densities. The σ-profile of an ensemble S containing NM different components M with mole fractions xM is defined as:| | 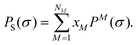 | (2) |
PM(σ) is here the σ-profile of molecule M. Eqn (1) belongs to the class of non-linear integral equations of the Hammerstein type.11 It can be solved either purely numerically1 or semi-analytically.11 The residual contribution to the chemical potential of a substance M in ensemble S, which is ascribed to intermolecular interactions, can be calculated in the COSMO-RS model by integration over the surface screening charge density:| |  | (3) |
Together with the combinatorial contribution to the chemical potential μMCS that describes the size of the molecules (see eqn (A7) in the Appendix for the functional form), the chemical potential is then defined as:| | μMS = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) MS + μMCS. MS + μMCS. | (4) |
The limiting activity coefficient of a component i at infinite dilution in component j is of the utmost importance in mixed-phase thermodynamics (see for example ref. 3 and 12). This key parameter is easily calculated from the knowledge of the chemical potentials:| |  | (5) |
An important field of application of the COSMO-RS method is the prediction of this parameter (see for example ref. 13). If a suitable COSMO-RS parameter set is available no experimental data are necessary; only quantum chemical calculations with the dielectric continuum model COSMO for the isolated molecules i and j are required. The Appendix shows the working equations of the COSMO-RS method, with its parameters to be fitted to an experimental data set. The methods used for the quantum chemical calculations include, in addition to the density functional theory (DFT), the Hartree–Fock (HF) method14–16 and 2nd order Møller–Plesset perturbation theory (MP2).17 All of the quantum chemical calculations were performed using the TURBOMOLE suite of programs.18 The functionals used in the DFT calculations are the S-VWN functional (a variant of the local density approximation, LDA),19,20 the BP8620,21 and PBE22 functionals which are based on the generalised gradient approximation (GGA), the B3LYP hybrid functional,20,23 as well as the meta-GGA-based functional TPSS24 and its hybrid variant TPSSH.25 In the DFT and HF calculations, the highly efficient RI-J method was used.26 The MP2 calculations were carried out with the rimp2 program.27 The COSMO dielectric continuum model implemented in TURBOMOLE is described in ref. 28. The screening charge densities of the MP2-COSMO calculations were calculated using the PTED variant29 of continuum solvation models implemented in TURBOMOLE.30 The following basis sets were used: the minimal basis set STO-3G,31 the valence double-zeta basis sets 3-21G,324-31G,33 6-31G*34 and SV(P),35 the valence triple-zeta basis sets TZVP36 and def2-TZVPP37, the def2-TZVPPD valence triple-zeta basis set expanded by diffuse functions,38 and the valence quadruple-zeta basis set def2-QZVPP.39
A root mean square (RMS) value serves as a measure of the goodness of our optimisation. The RMS is typically used as a parameter for assessing the predictions of a model. This parameter has two important properties: cancelling of negative and positive deviations is suppressed by the sum of the error squares, and large errors are more heavily weighted than small deviations. Our chosen target function for parameter optimisation for the COSMO-RS model is the following RMS value:
| |  | (6) |
where
Ti is the absolute temperature of system
i. The selected RMS value has the dimension of a chemical potential and is thus an energy equivalent on the logarithmic scale. In this way, properties other than activity coefficients (
e.g., partition coefficients) could also in principle be incorporated simultaneously into the parameter optimisation. The present work investigates only activity coefficients at infinite dilution; optimisation is therefore carried out exclusively for this key parameter in mixed-phase thermodynamics. The choice of the experimental limiting activity coefficients here is a problem that must not be underestimated, because these are very often associated with large errors. A carefully validated data set has been provided by Voutsas and Tassios
40 in a publication on predictive calculations using group-contribution methods. A subset of this data set has been studied by Putnam
et al. in connection with the accuracy of the COSMO-RS method.
41 The data set given in
ref. 41 serves as the basis for the parameter optimisations in the present work. The set contains 70 molecules for which limiting activity coefficients are given for at least one, and generally for three or four, temperatures. The data set contains a total of 375 data points, 85 of which describe aqueous systems. The classes of molecules included in the set—
alkanes,
cycloalkanes,
alkenes,
cycloalkenes,
ketones,
alcohols,
carboxylic acids, and
chloroalkanes—distinguish this data set as being particularly relevant for typical fields of work in the chemical industry. In addition to this data set, we considered for our work another data set consisting of
alkanes and
alkenes in alkanols and alkenols containing 368 data points for binary combinations. This latter set is also distinguished by very high experimental accuracy. It is based on data from Miyano
42–44 and Miyano and Fukuchi,
45 and has been used in a recently published study evaluating the goodness of predictive methods for calculation of Henry coefficients.
46
3. Results and discussion
The starting point of the optimisations documented here is the procedure described in ref. 2. For this purpose the molecular geometries were optimised using the COSMO solvation model with ε → ∞, employing the BP86 functional and the TZVP basis set. In ref. 2 a second set of averaged charge densities is used for a quantitative description of the correlation of the polarization charge densities (see eqn (A4) in the Appendix); the weighting of this set is adjusted by the parameter fcorr. Entry 1 of Table 1 shows the calculated parameters and an RMS value of 0.33 kcal mol−1 that was obtained. For this calculation fcorr was set to fcorr = 2.4 as described in ref. 2. The second entry in Table 1 shows the parameter set obtained when fcorr is also optimised. The values, particularly of α and fcorr, now differ significantly from those of the first optimisation but result in an improvement of only about 2% in the RMS value.
Table 1 Optimised parameters for various basis sets and methods
| Entry |
Method and basis set used for calculating 
|
Method and basis set used for geometry optimisation |
RMSa |
α
b
|
α
1
b
|
α
2
b
|
α
3
b
|
r
av
c
|
a
eff
d
|
f
corr
e
|
c
hb
b
|
σ
hb
f
|
f
h2o
e
|
λ
0
e
|
λ
1
e
|
λ
2
e
|
|
In kcal mol−1.
In (kcal Å2) (mol e2)−1.
In Å.
In Å2.
Dimensionless.
In e Å−2.
Variable parameters during the optimisation are denoted by ‘v’ and fixed parameters by ‘f’.
|
| 1 |
BP86(RI), TZVP |
BP86(RI), TZVP (cosmo) |
0.333 |
2588 |
vg |
— |
— |
— |
0.68 |
v |
3.52 |
v |
2.40 |
f |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 132 |
v |
0.00894 |
v |
0.889 |
v |
0.23 |
v |
0.512 |
v |
−0.00168 |
v |
| 2 |
BP86(RI), TZVP |
BP86(RI), TZVP (cosmo) |
0.325 |
1157 |
v |
— |
— |
— |
0.46 |
v |
3.56 |
v |
11.36 |
v |
7726 |
v |
0.00893 |
v |
0.890 |
v |
1.01 |
v |
0.532 |
v |
−0.00304 |
v |
| 3 |
BP86(RI), TZVP |
BP86(RI), TZVP (gas) |
0.324 |
1281 |
v |
— |
— |
— |
0.49 |
v |
3.54 |
v |
11.56 |
v |
7609 |
v |
0.00859 |
v |
0.885 |
v |
0.92 |
v |
0.587 |
v |
−0.00168 |
v |
| 4 |
B3LYP(RI), TZVP |
B3LYP(RI), TZVP (gas) |
0.327 |
1282 |
v |
— |
— |
— |
0.48 |
v |
3.29 |
v |
11.01 |
v |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017 |
v |
0.01001 |
v |
0.902 |
v |
1.07 |
v |
0.573 |
v |
−0.00183 |
v |
| 5 |
BP86(RI), TZVP |
BP86(RI), TZVP (gas) |
0.278 |
— |
699 |
v |
4243 |
v |
8981 |
v |
0.85 |
v |
4.48 |
v |
— |
5767 |
v |
0.00350 |
v |
0.879 |
v |
1.00 |
f |
0.616 |
v |
−0.00036 |
v |
| 6 |
BP86(RI), TZVP |
BP86(RI), TZVP (cosmo) |
0.278 |
— |
444 |
v |
3192 |
v |
7805 |
v |
0.85 |
v |
4.68 |
v |
— |
5684 |
v |
0.00339 |
v |
0.888 |
v |
1.00 |
f |
0.561 |
v |
−0.00056 |
v |
| 7 |
BP86, STO-3G |
BP86, STO-3G (gas) |
0.601 |
— |
1366 |
v |
7724 |
v |
124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
v |
0.47 |
v |
3.50 |
v |
— |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
v |
0.00560 |
v |
0.921 |
v |
1.00 |
f |
0.639 |
v |
−0.00736 |
v |
| 8 |
BP86, 3-21G |
BP86, 3-21G (gas) |
0.368 |
— |
404 |
v |
363 |
v |
96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784 784 |
v |
0.45 |
v |
3.88 |
v |
— |
6967 |
v |
0.00715 |
v |
0.895 |
v |
1.00 |
f |
0.843 |
v |
−0.00239 |
v |
| 9 |
BP86, 4-31G |
BP86, 4-31G (gas) |
0.283 |
— |
533 |
v |
4343 |
v |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165 165 |
v |
0.60 |
v |
4.80 |
v |
— |
3348 |
v |
0.00390 |
v |
0.875 |
v |
1.00 |
f |
0.661 |
v |
−0.00212 |
v |
| 10 |
BP86, 6-31G* |
BP86, 6-31G* (gas) |
0.287 |
— |
519 |
v |
801 |
v |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
v |
0.42 |
v |
4.62 |
v |
— |
4037 |
v |
0.00591 |
v |
0.872 |
v |
1.00 |
f |
0.736 |
v |
−0.00203 |
v |
| 11 |
BP86, SV(P) |
BP86, SV(P) (gas) |
0.285 |
— |
1203 |
v |
6885 |
v |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351 351 |
v |
0.73 |
v |
4.57 |
v |
— |
5088 |
v |
0.00385 |
v |
0.859 |
v |
1.00 |
f |
0.587 |
v |
−0.00168 |
v |
| 12 |
BP86(RI), SV(P) |
BP86(RI), SV(P) (gas) |
0.287 |
— |
1156 |
v |
6292 |
v |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 228 |
v |
0.70 |
v |
4.76 |
v |
— |
4577 |
v |
0.00394 |
v |
0.861 |
v |
1.00 |
f |
0.548 |
v |
−0.00154 |
v |
| 13 |
BP86, TZVP |
BP86(RI), TZVP (gas) |
0.278 |
— |
642 |
v |
3948 |
v |
9426 |
v |
0.79 |
v |
4.68 |
v |
— |
5186 |
v |
0.00354 |
v |
0.881 |
v |
1.00 |
f |
0.585 |
v |
−0.00137 |
v |
| 14 |
BP86(RI), def2-TZVPP |
BP86(RI), TZVP (gas) |
0.278 |
— |
972 |
v |
4395 |
v |
8782 |
v |
1.02 |
v |
4.34 |
v |
— |
6919 |
v |
0.00320 |
v |
0.884 |
v |
1.00 |
f |
0.576 |
v |
−0.00197 |
v |
| 15 |
BP86(RI), def2-TZVPPD |
BP86(RI)
TZVP (gas) |
0.279 |
— |
1009 |
v |
5606 |
v |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081 081 |
v |
1.15 |
v |
4.33 |
v |
— |
7404 |
v |
0.00299 |
v |
0.908 |
v |
1.00 |
f |
0.557 |
v |
−0.00134 |
v |
| 16 |
BP86(RI), def2-QZVPP |
BP86(RI), TZVP (gas) |
0.281 |
— |
1188 |
v |
4491 |
v |
9078 |
v |
1.11 |
v |
4.34 |
v |
— |
6443 |
v |
0.00318 |
v |
0.895 |
v |
1.00 |
f |
0.558 |
v |
−0.00116 |
v |
| 17 |
HF(RI), TZVP |
HF(RI), TZVP (gas) |
0.308 |
— |
865 |
v |
2725 |
v |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 511 |
v |
0.67 |
v |
4.81 |
v |
— |
3429 |
v |
0.00579 |
v |
0.910 |
v |
1.00 |
f |
0.475 |
v |
−0.00110 |
v |
| 18 |
S-VWN
TZVP
|
S-VWN, TZVP (gas) |
0.299 |
— |
638 |
v |
3595 |
v |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174 174 |
v |
0.75 |
v |
4.69 |
v |
— |
4512 |
v |
0.00387 |
v |
0.876 |
v |
1.00 |
f |
0.552 |
v |
−0.00043 |
v |
| 19 |
PBE(RI), TZVP |
PBE(RI), TZVP (gas) |
0.279 |
— |
684 |
v |
3941 |
v |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 225 |
v |
0.76 |
v |
4.76 |
v |
— |
4838 |
v |
0.00366 |
v |
0.879 |
v |
1.00 |
f |
0.575 |
v |
−0.00123 |
v |
| 20 |
TPSSH(RI), TZVP |
TPSSH(RI), TZVP (gas) |
0.280 |
— |
1044 |
v |
3706 |
v |
7089 |
v |
0.90 |
v |
4.27 |
v |
— |
5119 |
v |
0.00370 |
v |
0.880 |
v |
1.00 |
f |
0.606 |
v |
−0.00038 |
v |
| 21 |
TPSS(RI), TZVP |
TPSS(RI), TZVP (gas) |
0.278 |
— |
592 |
v |
3522 |
v |
8645 |
v |
0.75 |
v |
4.75 |
v |
— |
4817 |
v |
0.00348 |
v |
0.884 |
v |
1.00 |
f |
0.569 |
v |
−0.00278 |
v |
| 22 |
B3LYP(RI), TZVP |
B3LYP(RI), TZVP (gas) |
0.282 |
— |
656 |
v |
3716 |
v |
7597 |
v |
0.91 |
v |
4.50 |
v |
— |
5573 |
v |
0.00325 |
v |
0.887 |
v |
1.00 |
f |
0.558 |
v |
−0.00008 |
v |
| 23 |
RI-MP2, def2-TZVPP |
RI-MP2, def2-TZVPP (gas) |
0.264 |
— |
691 |
v |
4819 |
v |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
v |
0.61 |
v |
5.12 |
v |
— |
4029 |
v |
0.00410 |
v |
0.892 |
v |
1.00 |
f |
0.630 |
v |
−0.00308 |
v |
| 24 |
RI-MP2, def2-TZVPP |
BP86(RI), TZVP (gas) |
0.263 |
— |
711 |
v |
5324 |
v |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442 442 |
v |
0.61 |
v |
5.18 |
v |
— |
4104 |
v |
0.00431 |
v |
0.893 |
v |
1.00 |
f |
0.649 |
v |
−0.00287 |
v |
As described above, the parameterisation of COSMO-RS has so far usually been performed on the basis of molecular geometries obtained by optimisation of the molecule in a perfect electrical conductor. The only exception of which we are aware is the parameterisation published in ref. 10, based on calculations with the Amsterdam density functional (ADF) package. The third entry in Table 1 shows the results of a parameter optimisation based on the optimised molecular structures in the gas phase. A subsequent single-point calculation with COSMO for ε → ∞ then gives the screening charge densities. It is seen that despite the differences in the parameters of this optimisation compared with those based on optimisation with COSMO for ε → ∞, the RMS value hardly changes. We have observed the same effect also in other parameterisations, which are not published here. With one exception, all of the following parameterisations documented in this work are based on molecular geometries in the gas phase. We share the view expressed in ref. 10 that the geometry of a molecule in a perfect electrical conductor is not a good starting point for most solvents. These conditions favour relatively strong charge separation, which can lead to minimum geometries that are not favoured in non-polar environments. In view of the typical polarities of solvents that are important in practice, it appears to us that the preferred compromise is to avoid optimisation in the electrical conductor. However, we regard the advantages described in ref. 10 of a better parameter fit for COSMO-RS and faster convergence in optimisations of geometry as less important than another computational advantage: in general, time-consuming quantum-chemical investigations—for example of reaction mechanisms, which often involve hundreds of molecular structures—are considered in the gas phase in the first step, provided that the solvents used are not markedly polar. If now, for example, the influence of the solvent on kinetic constants is to be estimated using COSMO-RS (see for instance ref. 47 and 48), all the molecular structures would have to be optimised a second time. A parameterisation based on gas-phase structures has the major advantage that only one set of molecular structures needs to be generated and handled.
The results of the COSMO-RS parameter optimisation with the use of the B3LYP functional instead of BP86 can be seen in entry 4 of Table 1. The RMS value remains almost the same as the one for BP86 (entry 3). From this result no advantage is discernible for B3LYP, and the BP86 functional represents the better choice because of the savings in computing time in the DFT calculation.
The results presented so far have been based on the traditional parameterisation of COSMO-RS using the approach of ref. 2. For the remaining studies presented below, a slightly modified approach for the electrostatic misfit energy as a function of two orthogonal sets of charge densities has been used. Instead of the function according to ref. 2:
| |  | (7) |
where
α and
fcorr are parameters to be optimised, and
σα and
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) α
α with
α =
i, j represent the two sets of screening charge densities (see Appendix for details), we use the function:
| | α1(σj + σi)2 + α2(σj + σi)(![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) j + j + ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i) + α3( i) + α3(![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) j + j + ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i)2 i)2 | (8) |
with
α1,
α2 and
α3 as the parameters to be fitted. The first two terms of
eqn (8) are a reformulation of
eqn (7), the third term can be interpreted as an additional weight for the self-energy arising from the second, orthogonalised set of charges. In order not to increase the total number of parameters to be fitted, which would cause additional computational effort, the parameter
λ0 in the combinatorial contribution to the chemical potential is fixed at 1 in our optimisations, which are based on
eqn (8). (For the form of the combinatorial contribution see
eqn (A7) in the Appendix.) Comparison of entry 5 with entry 3 in
Table 1 reveals that the use of function
(8) produces a 14% improvement in the RMS value to 0.28 kcal mol
−1. To demonstrate for this variant of COSMO-RS that the use of the gas-phase molecular structure has no effect on the result of optimisation goodness, entry 6 of
Table 1 shows the values obtained using the geometries from optimisation in a perfect electrical conductor.
Entries 7 to 11 of Table 1 show the results of studies on parameter optimisation with COSMO-RS using basis sets smaller than TZVP. BP86 is used as the functional in all these computations. With the use of the STO-3G minimal basis set, the RMS value more than doubles to 0.60 kcal mol−1, but decreases significantly on using the 3-21G basis set. Although the STO-3G basis set has the same number of primitive functions as the 3-21G basis, the latter provides a significantly better description of the details of screening charge density (RMS value of 0.37 kcal mol−1); this is ascribed to the higher flexibility in the valence shell, in which it has twice as many functions as STO-3G. Increasing the number of valence functions, as in the 4-31G basis set, improves the RMS to 0.28 kcal mol−1. The 6-31G* basis set, with two more primitives to describe the core orbitals and one additional polarization function of non-hydrogen atoms, interestingly brings no improvement in the optimisation of the COSMO-RS parameters. In agreement with this finding, the SV(P) basis set brings no improvement either. Entry 12 of Table 1 shows the results for the SV(P) basis set using the RI-J method. It is seen that this method can be used with no loss of accuracy. This applies also to the use of the TZVP basis set, as is clear from entry 13. If the results for the TZVP basis set (entries 5 and 13 in Table 1) are now re-examined, it is clear that there is practically no improvement over the valence double-zeta basis sets. Entries 14 to 16 of Table 1 show parameterisations for calculation of screening charge densities with even larger basis sets, the molecular geometries in each case being calculated with the TZVP basis set in the gas phase. The use of a def2-TZVPP basis set that has been optimised relative to the TZVP basis set and provided with a further set of polarisation functions does not yield any improvement in fitting of the COSMO-RS parameters; neither does the use of the def2-TZVPPD basis set that is especially suitable for electrical properties such as dipole moments and polarisabilities, and nor do calculations with the def2-QZVPP valence quadruple-zeta basis set with two sets of polarization functions.
It is quite remarkable that using the split valence basis set SV(P) which is known not to describe the dipole moment of polar molecules well, a similar quality for the activity coefficients can be achieved compared to the valence triple-zeta basis set TZVP. In Fig. 1 the distribution of the screening charge densities over the molecular surface computed with STO-3G, SV(P) and TZVP is shown for water. It can be seen that the σ-profiles calculated with SV(P) and TZVP are much more similar to each other than to the one calculated with STO-3G. From the sigma profiles, it can be understood why the STO-3G basis set leads to a much bigger deviation from the TZVP basis set with respect to the RMS value of the COSMO-RS optimization than the SV(P) basis set.
 |
| | Fig. 1
σ-Profiles for water employing the BP86 functional and three different basis sets. | |
The studies on the influence of various quantum chemical computing methods on the accuracy of COSMO-RS parameterisation are shown from entry 17 onwards in Table 1. All of the calculations except those using the MP2 method are performed with the TZVP basis set. Compared to the calculations with BP86 discussed above (entry 5 in Table 1), Hartree–Fock yields significantly poorer accuracy, with an RMS value of 0.31 kcal mol−1. The use of the local S-VWN functional also leads to a poorer result of 0.30 kcal mol−1. In contrast, all the gradient-corrected functionals as well as the B3LYP hybrid functional show practically identical RMS values. We achieved the highest accuracy in our investigations with the MP2 method using the def2-TZVPP basis set. The RMS, at 0.26 kcal mol−1, showed an improvement of circa 4% relative to the non-local density functionals. This value is also obtained when the molecular geometries are calculated by a DFT method, using for example the BP86 functional, instead of with MP2.
Applications of some of the parameterisations presented here to the above-mentioned second data set (see ref. 46) are shown in Table 2. For this data set the RMS value is generally somewhat lower than for the training set, but shows for the most part a similar dependence on the selected basis set or method.
Table 2 Results of activity coefficient predictions for the test data set employing selected parameter sets of Table 1 using eqn (8)
| Method and basis set used for calculating 
|
Method and basis set used for geometry optimisation |
RMS/kcal mol−1 |
|
BP86, STO-3G |
BP86, STO-3G (gas) |
0.204 |
|
BP86, 4-31G |
BP86, 4-31G (gas) |
0.194 |
|
BP86(RI), SV(P) |
BP86(RI), SV(P) (gas) |
0.202 |
|
BP86(RI), TZVP |
BP86(RI), TZVP (gas) |
0.216 |
|
RI-MP2, def2-TZVPP |
RI-MP2, def2-TZVPP (gas) |
0.188 |
4. Conclusions and outlook
The present work provides for the first time a systematic study of the influence of the quantum chemical method used on the accuracy of COSMO-RS parameterisations. The target function for the optimisation consists of activity coefficients at infinite dilution, which are key parameters in mixed-phase thermodynamics. The data presented here show that at least a valence double-zeta basis set should be used. Larger basis sets, however, at least when used with gradient-corrected DFT methods, offer no improvement in the accuracy of the COSMO-RS parameterisation. Screening charge densities calculated by the Hartree–Fock method or by the LDA variant of DFT give significantly less accurate parameterisation than when gradient-corrected functionals or the B3LYP hybrid functional are used. The differences in the accuracy of COSMO-RS for the non-local functionals used here are negligibly small. The most accurate parameterisation is based on screening charge densities calculated by the MP2 method. We believe that some further potential exists for moderate improvements in the RMS value, although possibly less in the underlying quantum mechanical methods than in the form of the energy expression ε(σ,![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) for the COSMO-RS method. In our view, a deeper mathematical investigation of the parameter optimisation space should also lead to an improved choice of empirical correction parameters for the physically motivated COSMO-RS approach. Other possible starting points for improvements include the calculation method of the averaged screening charge densities and the method used for the construction of the cavity for the screening charges. In view of the good performance of MP2, we believe that it would be of interest to investigate screening charge densities calculated by the coupled electron pair approximation (CEPA) method49–52 as a basis for COSMO-RS parameterisation. The power of this now somewhat forgotten method for very efficient calculation of electron correlation effects was recently brought to mind in a study based on its implementation in a modern quantum chemical program package.53
) for the COSMO-RS method. In our view, a deeper mathematical investigation of the parameter optimisation space should also lead to an improved choice of empirical correction parameters for the physically motivated COSMO-RS approach. Other possible starting points for improvements include the calculation method of the averaged screening charge densities and the method used for the construction of the cavity for the screening charges. In view of the good performance of MP2, we believe that it would be of interest to investigate screening charge densities calculated by the coupled electron pair approximation (CEPA) method49–52 as a basis for COSMO-RS parameterisation. The power of this now somewhat forgotten method for very efficient calculation of electron correlation effects was recently brought to mind in a study based on its implementation in a modern quantum chemical program package.53
Appendix. COSMO-RS working equations
Let the solvent accessible surface of a molecule M be divided into nM distinct tesserae. Assume that on all tesserae i with i∈{1,…,nM} the screening charge densities 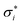 calculated by the COSMO model for ε → ∞ are known. Assume further that the area of the ith tessera, Ai, is known. The averaged screening charge density used in COSMO-RS is then:
calculated by the COSMO model for ε → ∞ are known. Assume further that the area of the ith tessera, Ai, is known. The averaged screening charge density used in COSMO-RS is then:| |  | (A1) |
where| |  | (A2) |
In (A2)rj is the averaged radius of tessera j. This is determined by  . The term dji is the distance between the centres of the two tesserae j and i. The term rav is a parameter to be fitted.
. The term dji is the distance between the centres of the two tesserae j and i. The term rav is a parameter to be fitted.
Let a mixture S consist of NM molecules and let k∈{1,…,NM}. Let the mole fraction of the kth species be xk. The integral eqn (1) can now be rewritten in the form of an equation that on the right-hand side contains a double sum in the numerator and denominator:
| |  | (A3) |
The effective contact area
aeff here is a parameter to be fitted to the experimental data.
In addition to σi, another charge density is now introduced, designated as σi. It is obtained from  through eqn (A1), with the term rav in (A2) being substituted by 2·rav. An orthogonal set of charge densities is now generated in accordance with
through eqn (A1), with the term rav in (A2) being substituted by 2·rav. An orthogonal set of charge densities is now generated in accordance with
| | ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i = σi − λorth·σi i = σi − λorth·σi | (A4) |
The parameter
λorth is 0.816 according to
ref. 2. The term describing the interaction energy of the screening charge densities is given by:
| |  | (A5) |
with the two parameters
α and
fcorr to be fitted and the function for the hydrogen-bonding energy given by
| | | εHB(σj, σi) = cHB·max(0,max(σj, σi) − σHB)·min(0,min(σj, σi) + σHB). | (A6) |
The parameters
cHB and
σHB are obtained by fitting to
experimental data.
The combinatorial contribution to the chemical potential is described as follows:
| |  | (A7) |
In
(A7),
VM and
AM are the volume and surface area of molecule
M;

and

. The terms
λ0,
λ1 and
λ2 are parameters to be fitted to
experimental data.
In addition to the fitted parameters mentioned above, a scaling factor fH2O is also used. This factor, which scales the screening charge densities of the water molecule, was introduced by Klamt in ref. 6.
The following atomic radii were used in cavity construction for the COSMO calculation: rH = 1.3 Å, rC = 2.0 Å, rO = 1.72 Å, rN = 1.83 Å, rF = 1.72 Å, rCl = 2.05 Å.
References
- A. Klamt, J. Phys. Chem., 1995, 99, 2224 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074 CrossRef CAS.
-
G. M. Kontogeorgis and G. K. Folas, Thermodynamic Models for Industrial Applications, Wiley, Chichester, 1st edn 2010 Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 799 CAS.
- S.-T. Lin and S. I. Sandler, Ind. Eng. Chem. Res., 2002, 41, 899 CrossRef CAS.
- A. Klamt, Fluid Phase Equilib., 2003, 206, 223 CrossRef CAS.
- H. Grensemann and J. Gmehling, Ind. Eng. Chem. Res., 2005, 44, 1610 CrossRef CAS.
- T. Banerjee, M. K. Singh and A. Khanna, Ind. Eng. Chem. Res., 2006, 45, 3207–3219 CrossRef CAS.
- S. Wang, S. I. Sandler and C.-C. Chen, Ind. Eng. Chem. Res., 2007, 46, 7275 CrossRef CAS.
- C. C. Pye, T. Ziegler, E. van Lenthe and J. Louwen, Can. J. Chem., 2009, 87, 790 CrossRef CAS.
- R. Franke and J. Friedrich, Chem. Phys., 2009, 356, 110 CrossRef CAS.
-
R. C. Reid, J. M. Prausnitz and B. E. Poling, The Properties of Gases & Liquids, McGraw-Hill, New York, 4th edn, 1987 Search PubMed.
- R. Franke, J. Krissmann and R. Janowsky, Chem.-Ing.-Tech., 2002, 74, 85 CrossRef CAS.
- D. R. Hartree, Proc. Cambridge Philos. Soc., 1928, 24, 89–111 CrossRef CAS.
- V. Fock, Z. Phys., 1930, 61, 126 CrossRef.
- J. C. Slater, Phys. Rev., 1930, 35, 210 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- F. Bloch, Z. Phys., 1929, 57, 545 CrossRef CAS; P. A. M. Dirac, Proc. Cambridge Philos. Soc., 1930, 26, 376 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; J. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS; A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283 CrossRef CAS.
- F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331 CrossRef CAS.
- A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187 RSC.
- F. J. Olivares del Valle and J. Tomasi, Chem. Phys., 1991, 150, 139 CrossRef CAS.
-
M. Diedenhofen, in High Performance Computing in Chemistry, ed. Johannes Grotendorst, Publication Series of the John von Neumann Institute for Computing (NIC), Jülich, 2005, vol. 25 Search PubMed.
- W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657 CrossRef CAS; W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1970, 52, 2769 CrossRef.
- J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939 CrossRef CAS; M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797 CrossRef.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Chem. Phys. Lett., 1972, 16, 217 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753 CrossRef CAS.
- E. C. Voutsas and D. P. Tassios, Ind. Eng. Chem. Res., 1996, 35, 1438 CrossRef CAS.
- R. Putnam, R. Taylor, A. Klamt, F. Eckert and M. Schiller, Ind. Eng. Chem. Res., 2003, 42, 3635 CrossRef CAS.
- Y. Miyano, J. Chem. Thermodyn., 2005, 37, 459 CrossRef CAS.
- Y. Miyano, J. Chem. Eng. Data, 2005, 50, 2045 CrossRef CAS.
- Y. Miyano, J. Chem. Eng. Data, 2005, 50, 211 CrossRef.
- Y. Miyano and K. Fukuchi, Fluid Phase Equilib., 2004, 226, 183 CrossRef CAS.
- R. Franke, B. Hannebauer and S. Jung, Chem.-Ing.-Tech., 2010, 82, 265 CrossRef CAS; R. Franke, B. Hannebauer and S. Jung, Chem. Eng. Technol., 2010, 33, 251 CrossRef.
- R. Franke, C. Borgmann, D. Hess and K.-D. Wiese, Z. Anorg. Allg. Chem., 2003, 629, 2535 CrossRef CAS.
- P. Deglmann, I. Müller, F. Becker, A. Schäfer, K.-D. Hungenberg and H. Weiß, Macromol. React. Eng., 2010, 3, 496 CrossRef.
- W. Meyer, Int. J. Quantum Chem., 1971, 5, 341 CrossRef CAS; W. Meyer, J. Chem. Phys., 1973, 58, 1017 CrossRef.
- R. Ahlrichs, H. Lischka, V. Staemmler and W. Kutzelnigg, J. Chem. Phys., 1975, 62, 1225 CrossRef CAS; R. Ahlrichs, F. Driessler, H. Lischka, V. Staemmler and W. Kutzelnigg, J. Chem. Phys., 1975, 62, 1235 CrossRef; R. Ahlrichs, F. Keil, H. Lischka and W. Kutzelnigg, J. Chem. Phys., 1975, 63, 455 CrossRef; R. Ahlrichs, H. Lischka, B. Zurawski and W. Kutzelnigg, J. Chem. Phys., 1975, 63, 4685 CrossRef.
- V. Staemmler and R. Jaquet, Theor. Chim. Acta, 1981, 59, 48 Search PubMed.
- R. Fink and V. Staemmler, Theor. Chim. Acta, 1993, 87, 129 CrossRef CAS.
- F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108 CrossRef.
Footnote |
| † This paper is dedicated to Volker Staemmler on the occasion of his 70th birthday. |
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) describes the interaction between two charged surface segments as a function of the screening charge densities. The σ-profile of an ensemble S containing NM different components M with mole fractions xM is defined as:
) describes the interaction between two charged surface segments as a function of the screening charge densities. The σ-profile of an ensemble S containing NM different components M with mole fractions xM is defined as: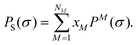

![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) MS + μMCS.
MS + μMCS.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017
017![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710
710![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784
784![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165
165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384
384![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351
351![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228
228![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081
081![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511
511![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174
174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225
225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756
756![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442
442
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) α with α = i, j represent the two sets of screening charge densities (see Appendix for details), we use the function:
α with α = i, j represent the two sets of screening charge densities (see Appendix for details), we use the function:![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) j +
j + ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i) + α3(
i) + α3(![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) j +
j + ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i)2
i)2
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) for the COSMO-RS method. In our view, a deeper mathematical investigation of the parameter optimisation space should also lead to an improved choice of empirical correction parameters for the physically motivated COSMO-RS approach. Other possible starting points for improvements include the calculation method of the averaged screening charge densities and the method used for the construction of the cavity for the screening charges. In view of the good performance of MP2, we believe that it would be of interest to investigate screening charge densities calculated by the coupled electron pair approximation (CEPA) method49–52 as a basis for COSMO-RS parameterisation. The power of this now somewhat forgotten method for very efficient calculation of electron correlation effects was recently brought to mind in a study based on its implementation in a modern quantum chemical program package.53
) for the COSMO-RS method. In our view, a deeper mathematical investigation of the parameter optimisation space should also lead to an improved choice of empirical correction parameters for the physically motivated COSMO-RS approach. Other possible starting points for improvements include the calculation method of the averaged screening charge densities and the method used for the construction of the cavity for the screening charges. In view of the good performance of MP2, we believe that it would be of interest to investigate screening charge densities calculated by the coupled electron pair approximation (CEPA) method49–52 as a basis for COSMO-RS parameterisation. The power of this now somewhat forgotten method for very efficient calculation of electron correlation effects was recently brought to mind in a study based on its implementation in a modern quantum chemical program package.53
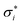 calculated by the COSMO model for ε → ∞ are known. Assume further that the area of the ith tessera, Ai, is known. The averaged screening charge density used in COSMO-RS is then:
calculated by the COSMO model for ε → ∞ are known. Assume further that the area of the ith tessera, Ai, is known. The averaged screening charge density used in COSMO-RS is then:

 . The term dji is the distance between the centres of the two tesserae j and i. The term rav is a parameter to be fitted.
. The term dji is the distance between the centres of the two tesserae j and i. The term rav is a parameter to be fitted.

 through eqn (A1), with the term rav in (A2) being substituted by 2·rav. An orthogonal set of charge densities is now generated in accordance with
through eqn (A1), with the term rav in (A2) being substituted by 2·rav. An orthogonal set of charge densities is now generated in accordance with![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i = σi − λorth·σi
i = σi − λorth·σi

 and
and  . The terms λ0, λ1 and λ2 are parameters to be fitted to experimental data.
. The terms λ0, λ1 and λ2 are parameters to be fitted to experimental data.


