 Open Access Article
Open Access ArticleElectronic structure of pyridine-based SAMs on flat Au(111) surfaces: extended charge rearrangements and Fermi level pinning†
ZhongYun
Ma
a,
Ferdinand
Rissner
b,
LinJun
Wang
a,
Georg
Heimel
c,
QiKai
Li
a,
Zhigang
Shuai
*ad and
Egbert
Zojer
*b
aKey Laboratory of Organic Solids, Beijing National Laboratory for Molecular Sciences (BNLMS), Institute of Chemistry, Chinese Academy of Sciences, 100190 Beijing, People's Republic of China
bInstitute of Solid State Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: egbert.zojer@tugraz.at
cInsitut für Physik, Humboldt-Universität zu Berlin, Brook-Taylor-Strasse 6, 12489 Berlin, Germany
dDepartment of Chemistry, Tsinghua University, 100084 Beijing, People's Republic of China. E-mail: zgshuai@tsinghua.edu.cn
First published on 18th April 2011
Abstract
Density functional theory calculations are used to investigate the electronic structure of pyridine-based self-assembled monolayers (SAMs) on an Au(111) surface. We find that, when using pyridine docking groups, the bonding-induced charge rearrangements are frequently found to extend well onto the molecular backbone. This is in contrast to previous observations for the chemisorption of other SAMs, e.g., organic thiolates on gold, and can be explained by a pinning of the lowest unoccupied states of the SAM at the metal Fermi-level. The details of the pinning process, especially the parts of the molecules most affected by the charge rearrangements, strongly depend on the length of the molecular backbone and the tail-group substituent. We also mention methodological shortcomings of conventional density functional theory that can impact the quantitative details regarding the circumstances under which pinning occurs and highlight a number of peculiarities associated with bond dipoles that arise from Fermi-level pinning.
1. Introduction
Self-assembled monolayers (SAMs) formed by the chemisorption of dipolar organic molecules provide a convenient technique for tuning the effective work function of metallic electrodes.1–10 Using this approach, the barriers for charge-carrier injection/extraction into/from the functional organic materials forming the active layers in devices can be well adjusted.1,4,8 Besides, SAMs also have promising applications in molecular electronics, where the SAMs act as a linker between two electrodes.11–17 In both cases, the electronic structure of the SAM/metal interface plays the dominant role for the overall device performance and, thus, has triggered a significant number of experimental3,18–24 and theoretical25–31 investigations. The main quantities of interest in this context are the SAM-induced work-function modification, ΔΦ, and the level alignment between the highest occupied and the lowest unoccupied π-states of the SAM (the HOPS and the LUPS) and the metal Fermi-level.25,26 The energetic offsets will be denoted as ΔEHOPS and ΔELUPS in the following.Processes crucially important for these quantities are the charge density rearrangements at the interface, Δρbond, which are caused by the chemical bonding between the organic molecules and the metal surface. They induce a bond dipole (BD) at the interface that directly modifies ΔΦ, ΔEHOPS, and ΔELUPS by an amount ΔEBD.25 In previous studies dealing with various molecules on Au(111) or Ag(111) surfaces, it has been found that the charge rearrangements in most instances are very much localized in the immediate vicinity of the docking group and the adjacent Au atoms.32 This is in particular true for the commonly used thiolates, as has recently been confirmed by a comparative cluster-based study using density functional theory and Hartree–Fock based methods including also hybrid functionals.33
In thiolates, one, however, encounters a complication: as for the adsorption of thiols, the sulfur–gold bond is not directly “formed” but rather replaces a sulfur–hydrogen bond, there have been inconsistencies in the literature regarding the definition of the bond-dipole; i.e., one can either follow the bond-replacement view or understand the SAM formation as a binding of –S˙ to the Au surface (see also extended discussion in ref. 31). This leads to values of ΔEBD for similar systems hugely varying in magnitude and also in sign.8,34–38 This puzzle has been resolved only recently and it has been shown that viewing the process as bond replacement rather than bond formation provides chemically more intuitive results.39 Such ambiguities do not occur for the adsorption of pyridine docking groups as, there, one is clearly dealing with the formation of a new bond.
For pyridine docking groups, bonding-induced charge rearrangements confined to the interface have been found in certain systems.40 However, especially for more extended conjugated backbones, they have also been observed to extend over a significant part of the molecules.41 This has been attributed to Fermi-level pinning, which gives rise to particularly small charge injection barriers turning pyridine into a promising linker in molecular electronics for efficient electronic conductivity. In fact, pyridines have been used to secure molecular wires onto metal surfaces and between two metal electrodes,42–48 and the pyridine–gold interaction was considered as both reasonably strong and highly flexible.40
Here, we pursue two main goals: using density-functional theory (DFT) based band-structure calculations, we will first provide an in depth analysis of the electronic structure of pyridine linked SAMs, discussing the impact of both the length of the conjugated backbone and various tail-group substitutions (cf., Fig. 1a). Secondly, as the main focus of this paper, we will provide a detailed description of the pinning process and discuss different pinning situations. For that, the systems studied here are an ideal test-bed, as, depending on the length of the backbone and the tail-group substituent, the frontier orbitals at which pinning occurs are localized on different parts of the molecules. Even if the latter were to some extent affected by shortcomings of current state of the art DFT (as will be discussed in the Methodology section), this does not affect the main conceptual conclusions of the paper linking orbital localization and Fermi-level pinning.
 | ||
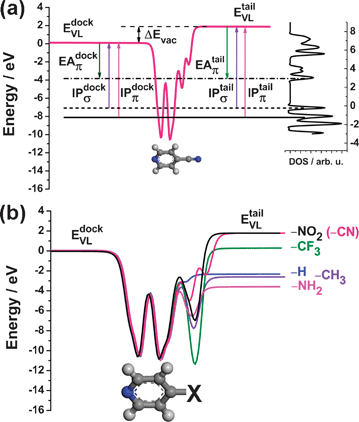
| Fig. 1 (a) Top: Schematic representation of the metal/SAM systems investigated in this work. The SAM consists of the docking group (dock), the π-conjugated core (π), and the tail group (tail); bottom: nomenclature and chemical structures of the investigated molecules. ‘X’ denotes the tail-group substituent (see text). (b) Side and (c) top view of Pyr|2P|NH2 as a representative SAM on a five-layer Au(111) slab. The red rectangle in (c) highlights the p(√3 × 3) surface unit cell. The various Au layers are displayed with different shading to ease the comparison between top- and side-view. | ||
After a brief description of the studied model systems, we will describe and then critically evaluate the applied methodology and discuss the adsorption geometry of the SAM. As a next step, it is useful to separately analyze first the hypothetical case of free-standing monolayers (i.e., the situation in the absence of the gold substrate) and then the charge rearrangements resulting from the metal–SAM bonding with a particular focus on the details of pinning. Finally, we will use the results of these analyses to discuss the SAM-induced work-function modifications and the level alignment.
2. Studied model systems
In Fig. 1a, we show the schematic structure of the SAM/metal interface. As a substrate, we choose a flat Au(111) surface as a reasonable first approximation, considering the fact that even for the much more widely investigated thiolates on Au, the details of the surface structure are still heavily debated (cf. corresponding discussion in refs. 23 and 26). Also for pyridines, different docking structures have been considered: Hou et al.49 have shown by computational modelling that when pyridines adsorb on an Au ad-atom rather than a flat Au surface, this results in a shift of the molecular levels relative to the metal states in a way that Fermi-level pinning of the LUPS is favoured. For the systems investigated here it can, thus, be concluded that the main impact of adsorption through an ad-atom would be the occurrence of Fermi-level pinning also in some of the few cases in which it does not happen on a flat surface. For systems that are pinned already on a flat surface docking through an ad-atom would merely increase the magnitude of the involved charge rearrangements.It should also be mentioned that a variety of contact geometries has been considered in transport studies paying particular attention to the role of additional Au atoms in hollow sites on the Au(111) surface adjacent to the docking site. Both, for pyridine docked to a nominally flat surface50 as well as for pyridines docked through ad-atoms46 the calculations showed that the extra Au atoms shift the transmission spectra to higher energies. In fact, for transport measurements also the orientation of the molecular backbone relative to the electrodes has been shown to play a crucial role.48 While such strongly tilted molecules are a realistic scenario in break-junction transport measurements, they should, however, not occur in the densely packed SAMs considered here.
The SAMs consist of three components, the docking groups, the backbones, and the tail-group substituents. In the present study, docking to the Au(111) surface occurs through the N atom of a pyridine ring, –Pyr; the length of the conjugated backbone varies from one to three rings (1P, 2P and 3P), and one electron donating (–NH2) and two electron accepting (–CN and –NO2) substituents have been considered for all conjugation lengths (see Fig. 1a). To get a comprehensive understanding of the tail-group substituent effect on the electronic structure of SAM-modified gold surfaces, we additionally include –H, –CH3 and –CF3 tail groups for the shortest backbone, 1P. In this context it should be mentioned that the dipole moments due to the tail-group substituents might have an adverse effect on the SAM-forming properties in experimental studies using the above-mentioned molecules. Monolayers of related molecules docked via thiolates have, however, been successfully investigated employing a variety of polar tail group substituents.51–58
In the following, we will use the nomenclatures Pyr|nP|X and Au|Pyr|nP|X, with nP denoting a backbone with n rings (where the first ring is always the pyridine) and ‘X’ specifying the tail-group substituent. The former syntax denotes the isolated monolayer, while the latter specifies the SAM bonded to the Au substrate.
To realize periodicity in two dimensions, we employed the repeated-slab approach. Five layers of gold atoms were used to represent the Au(111) surface (Fig. 1b), and two pyridine-based molecules were arranged in a p(√3 × 3) surface unit cell in a typical herringbone pattern (Fig. 1c). Following Bilić et al.,40 we chose close to upright standing pyridines with the nitrogen atoms in the pyridine ringson-top of Au atoms as a starting geometry. A vacuum gap of >20 Å was introduced between the uppermost atom of the molecule and the subsequent periodic image of the slab to exclude spurious electronic interaction between neighbouring slabs; to suppress the artificial electric field arising from imposing the periodic boundary conditions on the asymmetric slabs, a self-consistently determined dipole layer was introduced into the vacuum gap.59 Isolated molecules were calculated in a 3D periodic box with the dimensions of 40 × 40 × 40 Å.
3. Methodology
All calculations presented here are carried out using the Vienna ab initio Simulation Package (VASP)60–63 at the DFT level. The PW91 exchange–correlation (xc) functional is chosen64 using a plane-wave basis set with an energy cutoff of 20 Ryd. The projector augmented-wave method (PAW)65,66 was applied to describe the valence-core interactions, which allows the use of the relatively low kinetic energy cutoff. For the self-consistent field calculations, we used an 8 × 5 × 1 Monkhorst–Pack grid67 of k-points together with a Methfessel–Paxton occupation scheme68 and a broadening of 0.2 eV. Only spin-restricted (i.e., unpolarized) calculations are reported here. When performing geometry optimizations, all atoms of the SAM and the top two gold layers were fully relaxed until the largest remaining force component was smaller than 0.01 eV Å−1, while the bottom three gold layers were kept fixed at their bulk positions with a lattice constant of afcc = 4.175 Å.69 A previous study based on optimizations with Cartesian coordinates in VASP has shown that the total energy is rather insensitive to the tilt angle of the long axes of the molecules with respect to the surface normal up to tilts of 15°.40 In view of the tilt angle being a crucial parameter for the determination of the SAM-induced work-function modification and, thus, to obtain a better converged value for the molecular tilt, a recently developed geometry optimization scheme based on internal coordinates and the Direct Inversion in the Iterative Subspace (DIIS) algorithm has been used in combination with the external optimisation tool GADGET.70 In all systems studied here, the energy of the configuration obtained applying this strategy is lower than that achieved by the conventional strategy69 employing the native damped molecular dynamics optimizer of VASP together with Cartesian coordinates. Although the differences are small (<0.02 eV) for all pyridine based systems studied here, we found that the internal coordinate based optimizations give geometries that depend less on the initial starting geometries, making the results significantly more reproducible. All 3D isodensity representations shown throughout this paper and in the Electronic Supplementary Information (ESI†) are produced using XCrySDen.71The binding energy (Ebind) in the following is defined as Ebind = [Esystem − (Eslab + Emonolayer)]/2, where Esystem is the energy for the SAM/metal combined system containing two molecules per unit cell, Eslab and Emonolayer are the energy of metal slab and molecular monolayer respectively, and the division by 2 accounts for the two molecules in the unit cell. The structures of the slab and the monolayer are frozen to those of the combined system. In this way, Ebind is a direct measure for the electronic interaction energy between the monolayer and the metal and is not affected by geometric relaxations and the inter-molecular interaction within the SAM.
As in this work we will mainly be interested in pinning effects, a crucial parameter is the energetic alignment between the various SAM states and the metal Fermi-level. Therefore, especially the well known incorrect description of energy gaps by conventional DFT calculations needs to be addressed. The encountered problems include (i) the lack of derivative discontinuity of the functionals and the occurrence of the self-interaction error,72 and (ii) the fact that screening at the metal–organic interface is not captured properly.73 Factor (i) results in a too small gap and, therefore, “favours” Fermi level pinning;74 this complication is, however, at least partially offset by (ii), as the screening-induced narrowing of the gap of molecules above a metal is not captured by DFT; i.e., one is dealing with a fortuitous partial cancellation of errors. Indeed, using the approach outlined above, good agreement between theory and experiment has been obtained for physical observables such as the adsorption-induced work-function change in a number of pinned systems. These include the strong acceptor F4TCNQ75 and also PTCDA76,77 lying more or less flat on the (111) surfaces of all coinage metals and also the strong donors MV078 and TDAE79 on Au(111). In fact, we are not aware of a case in which contradicting theoretical and experimental results have been documented. This is, however, certainly also a consequence of most investigated systems (especially all mentioned above) representing “strongly pinned” situations where very large charge transfer from/to the frontier orbitals occurs. In such cases, an incorrect description mostly affects the exact amount of transferred charge but not the level alignment. Regarding the nature of the frontier orbitals, one also must not forget that the self-interaction error more severely affects localized than delocalized orbitals,80 which can result in some re-ordering of the states.
In isolated molecules, the use of hybrid functionals usually yields eigenvalues which compare well with experiment.81–85 For extensive periodic calculations including metal substrates, hybrid functionals are, however, prohibitively expensive and would also not account for the above mentioned polarization effects (thus, potentially adversely affecting the above mentioned fortuitous cancellation of errors). Moreover, when studying the adsorption of CO on late 4d and 5d transition metal (111) surfaces using a number of non-local functionals, Stroppa and Kresse found that including non-local exchange “improves some but worsens other properties”.86 Nevertheless, we performed single-point calculations with the HSE functional on suitably small test systems, namely the free-standing Pyr|1P|H and Pyr|1P|NH2 monolayers. There we did not observe inconsistencies compared to the PW91 calculations (for more details see ESI†)
Another shortcoming of (semi)local DFT, namely the neglect of van der Waals interactions is less of an issue here: First, it has been shown by Bilić et al.40 that the PW91 functional provides a very reasonable description of the Au–pyridine bond. Secondly, the dimensions of the SAM unit cell are primarily determined by the periodicity of the Au(111) surface. Thus, van der Waals interactions, in a first approximation, will only affect the backbone tilt of the molecules. As we are dealing with densely packed SAMs, also this effect can be expected to be small. This can, for example, be inferred from a comparison of the measured reorientation of anthracene under hydrostatic pressure with calculations based on the local-density approximation as well as on gradient-corrected functionals.87
Finally, especially for the amine-substituted systems, also the choice of the basis set turns out to be an important issue, as is discussed in detail in the ESI†. There, we show that with an atomic-orbital type basis that does not include diffuse basis functions, qualitatively incorrect results are obtained. With the plane-wave basis used in the VASP calculations one is, however, on the safe side and close to the situation that has been characterized as the complete-basis-set limit in ref. 40.
In conclusion, as far as quantitative predictions are concerned, the following results are certainly adversely affected by the above discussed, well known, shortcomings of DFT. Nevertheless, the main physical consequences, in particular the fundamental conclusions, through what mechanisms pinning occurs in SAMs and how it can, in general, influence bonding-induced charge rearrangements should not be affected.
4. Results and discussion
The geometry optimizations do not change any of the basic characteristics of the initially chosen adsorbate structures, i.e., the molecules are bonded to the gold surface with the N atoms of the pyridine rings at the on-top adsorption sites. As the Au–N bond lengths (RAu–N) for the two symmetry-inequivalent molecules in the surface unit cell are always very close, only the average values are given in Table 1. They vary from 2.50 to 2.69 Å depending on the tail group and the chain length. Typically, the shorter bond lengths are observed for those systems that in the following will be identified as being in the Fermi-level pinning regime. They are printed in italics in Table 1. This indicates that pinning strengthens the bond between the pyridine and the Au surface. Due to the interaction with the pyridine molecules, the bonding Au atoms are raised from the top gold layer by ca. 0.1 Å along the surface normal (i.e., the z-direction). Very small tilt angles (α, at most 5.5°) for the long axes of the molecules with respect to the surface normal are observed.88 The binding energies listed in Table 1 follow the trends for RAu–N, i.e., one typically finds larger binding energies in systems with shorter Au–N bond lengths.| Systems | R Au–N/Å | α/° | E bind/kcal mol−1 |
|---|---|---|---|
| Au|Pyr|1P|H | 2.68 | 0.4 | −3.17 |
| Au|Pyr|1P|CH3 | 2.69 | 0.4 | −3.15 |
| Au|Pyr|1P|CF3 | 2.64 | 5.5 | −3.18 |
| Au|Pyr|1P|NH 2 | 2.60 | 1.9 | −3.61 |
| Au|Pyr|2P|NH 2 | 2.57 | 1.2 | −3.74 |
| Au|Pyr|3P|NH 2 | 2.51 | 1.1 | −4.18 |
| Au|Pyr|1P|CN | 2.68 | 3.4 | −3.11 |
| Au|Pyr|2P|CN | 2.53 | 2.7 | −3.80 |
| Au|Pyr|3P|CN | 2.51 | 1.3 | −4.34 |
| Au|Pyr|1P|NO 2 | 2.50 | 1.3 | −4.58 |
| Au|Pyr|2P|NO 2 | 2.50 | 1.8 | −4.57 |
| Au|Pyr|3P|NO 2 | 2.51 | 1.8 | −4.60 |
4.1 Electronic structure of the isolated molecular monolayer
To understand the electronic structure of the interfaces formed between the metal and the SAM, it is useful to first discuss the hypothetical case of a free-standing monolayer (i.e., in the absence of the gold substrate). In these calculations, the SAM atoms are frozen at the positions that they adopt in the optimized geometry of the combined system. In Fig. 2a, the calculated electron electrostatic energy averaged over the x,y-plane of the unit cell is shown for Pyr|1P|CN as a representative example. As expected from fundamental electrostatics, the dipolar layer that the SAM approximately represents splits space into a region “left” of the docking-group ends of the monolayer with a vacuum level denoted by EdockVL and a region “right” of the tail-group end of the monolayer with a vacuum level at EtailVL. The jump in vacuum energies, ΔEvac, is related to the component of the molecular dipole moments perpendicular to the substrate, μ⊥, per unit-cell area, A, attenuated by an effective parameter describing depolarization by the neighbouring dipoles, εeff: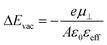 | (1) |
 | ||
| Fig. 2 Plane-averaged electron electrostatic energy of free-standing 2D molecular layers consisting of donor- and acceptor-substituted pyridines. (a) shows the representative case Pyr|1P|CN. For this layer also the two highest occupied and the lowest unoccupied bands are included and the meanings of the various ionisation potentials and electron affinities used throughout the manuscript are explained. These include the docking-group side and tail-group side vacuum level energy (EdockVL and EtailVL), the corresponding ionization potentials (IPdockσ, IPtailσ, IPdockπ and IPtailπ), as well as the electron affinities (EAdockπ and EAtailπ). The IP and EA values for all tail groups are given in Table 2. The plot to the right shows the density of states (DOS) of the layer. (b) shows equivalent electrostatic energy plots for all one-ring SAMs. They are aligned to EdockVL, which is justified by the resulting very similar average electrostatic energies in the region of the pyridine rings. | ||
| Systems | μ ⊥,mol a/e Å−1 | ΔEvac/eV | IP dockσ/eV | IP dockπ(1)/eV | IP dockπ(2)/eV | EA dockπ/eV | IP tailσ/eV | IP tailπ(1)/eV | IP tailπ(2)/eV | EA tailπ/eV |
|---|---|---|---|---|---|---|---|---|---|---|
| a To convert to Debye, multiply by 4.8. b The highest occupied σ-state overlaps with another state of π-character. c In this SAM the two types of π-states are so close in energy that they overlap with each other. d In this SAM, there is a second occupied σ-state above the highest π-state. This state, in contrast to the highest σ-state, is localized on the –NO2group. e In these SAMs, the LDOS associated with the first peak in the DOS corresponds to a superposition of the two σ-states found in the one-ring system and mentioned in the previous footnote. Note that for some of the above listed IPs, one is actually dealing with a double-peak structure in the PDOS (e.g., peak (III) in Fig. 4a). This is a consequence of the two inequivalent molecules in the unit cell and we report here the position of the higher energy peak. For all above footnotes see also discussion in the main text and data provided in the ESI. | ||||||||||
| Pyr|1P|H | 0.47 | −2.33 | 7.15 | 8.69 | 8.04 | 3.46 | 4.82 | 6.37 | 5.72 | 1.13 |
| Pyr|1P|CH3 | 0.59 | −2.61 | 7.23 | 8.48 | 8.08 | 3.54 | 4.62 | 5.87 | 5.47 | 0.93 |
| Pyr|1P|CF3 | −0.11 | 0.30 | 7.19 | 8.69 | 8.04 | 3.65 | 7.49 | 8.99 | 8.34 | 3.95 |
| Pyr|1P|NH 2 | 0.83 | −3.62 | 7.25 | 7.74 | 8.09 | 3.21 | 3.63 | 4.13 | 4.48 | −0.41 |
| Pyr|2P|NH 2 | 1.12 | −3.53 | 7.23 b | 7.23 | — | 4.14 | 3.70 b | 3.70 | — | 0.61 |
| Pyr|3P|NH 2 | 1.26 | −3.62 | 7.26 b | 7.26 | — | 4.62 | 3.64 b | 3.64 | — | 1.00 |
| Pyr|1P|CN | −0.44 | 1.78 | 7.21 | 8.10 c | 8.10 | 3.97 | 8.99 | 9.89 | 9.89 | 5.75 |
| Pyr|2P|CN | −0.52 | 1.77 | 7.24 | 7.64 | — | 4.54 | 9.00 | 9.40 | — | 6.31 |
| Pyr|3P|CN | −0.61 | 1.90 | 7.30 b | 7.30 | — | 4.66 | 9.21 b | 9.21 | — | 6.56 |
| Pyr|1P|NO 2 | −0.48 | 1.80 | 7.24 d | 8.59 | 7.94 | 4.85 | 9.04 d | 10.39 | 9.74 | 6.65 |
| Pyr|2P|NO 2 | −0.67 | 1.79 | 7.29 e | 7.99 | — | 4.95 | 9.08 e | 9.78 | — | 6.74 |
| Pyr|3P|NO 2 | −0.90 | 1.79 | 7.26 e | 7.66 | — | 5.02 | 9.05 e | 9.45 | — | 6.81 |
 | ||
| Fig. 3 Dependence of the step in the electron electrostatic energy across the molecular monolayer, ΔEvac, on the molecular dipole moment perpendicular to the substrate surface, μ⊥,mol. The dashed lines are linear fits to the data points for the one-ring systems and to the –NH2, –CN, –NO2 substituted SAMs with different chain lengths (1P, 2P and 3P), respectively. They serve as guides to the eye to illustrate the presence of three different regimes. | ||
 | ||
| Fig. 4 (a) Density of states projected onto the hydrogen (H), carbon (C) and nitrogen (N) atoms as well as their sum (MDOS) for the Pyr|1P|NH2 free-standing monolayer (not including the Au substrate). The highest occupied peaks are denoted as I, II and III and the lowest unoccupied state by ii. The first very weak (note ref. 93) feature in the unoccupied PDOS, denoted by i, is significant for the pinning process discussed below. (b) Local density of states, LDOS, associated with these peaks for one unit cell. It has been obtained by integrating over an energy interval of ±0.10 eV around the peak maxima. The energy axis is aligned at the onset of the HOMO peak. | ||
Due to the two different vacuum levels, the energy to remove (add) an electron from (to) the docking-group side differs from that for the tail-group side (see Fig. 2). Consequently, there are two ionisation potentials (electron affinities), IPdock and IPtail (EAdock and EAtail). Interestingly, as described first in ref. 32 for thiolates, changing the tail-group modifies the electrostatic energy only in the region of the substituent. The energy landscape in the region of the pyridine ring remains virtually unaffected by the different substituents (see Fig. 2b).
A complication when determining IPdock and IPtail for pyridine-containing systems is that the choice of the most suitable frontier state for defining those quantities is ambiguous, especially in view of the fact that the free-standing monolayer is only an auxiliary system that shall later help to understand the bonded SAM. Thus, it is not useful to strictly associate the IP with the highest occupied state independent of its character and one needs to identify the nature of the state(s) associated with the peaks in the DOS.
In all one-ring systems, the molecular HOMO is calculated to be a σ-orbital concentrated in the vicinity of the N atom. As discussed already in ref. 40 and 49, this state “disappears” when the pyridine is adsorbed on a flat Au(111) surface, since the hybrid orbitals are smeared out over a wide energy range due to the strong interaction with the metal states. Therefore, one needs to include also ionisation energies associated with the removal of electrons from the highest occupied π-states, whose signatures can also be identified in the adsorbed monolayers. Fig. 4 illustrates the case for Pyr|1P|NH2: the highest occupied state, peak I, is the above described σ-state. The next two peaks correspond to bands derived from two π-states. Peak II has a large density on the axial C atoms and on the substituent (type-(1)), while peak III is localized on the pyridine ring and the axial C atoms are within a nodal plane of the associated density (type-(2)). As shown in the ESI†, the two types of π-states also differ by the extent to which they are localized on the substituents and, therefore, their order changes as a function of the tail group (see Table 2). For the longer backbones, especially the type-(1) π-state is destabilized and the shapes of the calculated LDOS imply that it overlaps with the σ-state localized in the vicinity of the N-atom91 with a somewhat modified situation for the –NO2 substituent.92
As far as the lowest unoccupied states are concerned, the situation is much more straightforward, and they are always of π-character. The values for EAdockπ and EAtailπ are listed in Table 2. Interestingly, for Pyr|1P|NH2 and Pyr|2P|NH2 we find some overlap of the first strong peak in the PDOS with a dispersing substituent-derived band (feature (i) in Fig. 4)93 that will become relevant below when describing the charge-rearrangements.
Regarding the evolutions of the various IPs and EAs with the substituent group we find that IPdockσ remains virtually constant, i.e., the values of the twelve considered systems lie within 0.15 eV (see Table 2). This can be understood from the fact that these orbitals are highly localized on the pyridine ring, where the electron electrostatic energy is hardly affected by the substituent (cf.Fig. 2b). When an electron is removed from such an orbital to the docking-group side of the SAM, it does not “feel” the potential modifications that are confined to the vicinity of the tail-group side of the SAM as first described in ref. 32 (see also discussion in refs. 26 and 94). The same applies to the variations in the IPdockπ(2) of the one-ring systems with different substitutions, which can again be rationalized by the fact that the type-(2) orbitals have hardly any density in the regions where the potential is strongly modified by the substituents. Only for the –NO2 substituent the situation is somewhat different (see ESI†). Much larger variations in IPdockπ (up to 1 eV) are found for the type-(1) occupied π-orbitals and the lowest unoccupied states consistent with their shapes (see ESI†). Still, the overall substituent effect is much larger for the IPtailπ and EAtailπ, where changes of around 5 to 6 eV are observed when comparing, for example, the –NH2 and –CN substituted systems. The reduced π-gap upon extending the conjugated backbone manifests itself in a decreased difference between IPπ and EAπ in the two- and three-ring systems.95
4.2 Interaction-induced charge rearrangements and the bond dipole
The next aspects that need to be understood before arriving at a conclusive picture of the electronic properties of the SAM-modified gold surfaces are the charge rearrangements upon bond-formation with the substrate, Δρbond, the associated amount of net charge transfer, Qbond, and the resulting bond dipole, ΔEBD.Δρbond can be expressed as:
| Δρbond(z) = ρsystem(z) − [(ρslab(z) + ρmonolayer(z)], | (2) |
 | ||
| Fig. 5 Charge rearrangements upon bond formation, Δρbond, net charge transfer, Qbond, as well as the resulting change in electrostatic energy, Ebond, for the –NH2 (solid line), –CN (dotted line) and –NO2 (dashed line) substituted monolayers. (a), (b) and (c) show the situations for the one-, two- and three-ring systems, respectively. The vertical dashed lines mark the positions of the top Au layer, the N atom of the pyridine ring, and the topmost atom of the molecules. | ||
For the shortest chain, 1P, Δρbond of Au|Pyr|1P|CN is mainly localized around the SAM/metal interface, i.e., only very localized charge rearrangements between the metal and the docking group occur. This situation is strongly reminiscent of what has been observed for other docking groups including isocyanides and also thiolates,29,41 at least when describing the bonding as a replacement of an S–H by an S–Au gold bond (see extensive discussion in ref. 39). The situation is very similar for Au|Pyr|1P|H, Au|Pyr|1P|CH3, and Au|Pyr|1P|CF3 as shown in ESI†. The bonding-induced charge rearrangements in Au|Pyr|1P|NH2 and Au|Pyr|1P|NO2, however, are qualitatively different. They extend along the whole backbone, and for the former, even significant charge rearrangements occur in the region of (respectively above) the substituent. Increasing the chain length (see Fig. 5b and c) results in charge rearrangements that extend along the whole backbone for all substituents. The fact that the –NO2 substituent gives rise to the most pronounced charge rearrangements for all chain lengths is consistent with the observation that these SAMs also display the largest binding energies (cf., Table 1).
Further insight to what extent the charge rearrangements describe long-range charge transfer or local polarization can be obtained by integrating Δρbond over z.96 The quantity Qbond(z), defined as:
| Qbond(z) = ∫z−∞Δρ(z′) dz′, | (3) |
The succession of regions with depletion and accumulation of electron density can in a simplified 1D-picture be viewed as a series of dipole layers. To quantify the modification of the electrostatic energy, Ebond, one needs to solve the 1D Poisson equation,
 | (4) |
| Systems | ΔΦ/eV | ΔEBD/eV | IPSAM/eV | EASAM/eV | ΔEHOPS(1)/eV | ΔEHOPS(2)/eV | ΔELUPS/eV | E LUMOcorr/eV |
|---|---|---|---|---|---|---|---|---|
| a Note that in all –NO2 substituted systems, the two close-lying highest occupied states also in the bonded SAM are of σ-character. They are localized on the substituent and have also a non-vanishing density at the N-atom of the pyridine. The highest of these peaks is found at −2.02, −1.85 and −1.72 eV from the Fermi energy in the combined one-, two- and three-ring systems, respectively. The values listed in the table correspond to the highest π-state(s). Note that for some of the above described listed values of ΔEHOPS, one is actually dealing with a double-peak structure in the PDOS. This is a consequence of the two inequivalent molecules in the unit cell and we report here the position of the higher energy peak. | ||||||||
| Au|Pyr|1P|H | −3.27 | −0.94 | 5.62 | 1.13 | −4.54 | –3.69 | 0.79 | 0.00 |
| Au|Pyr|1P|CH3 | −3.56 | −0.95 | 5.37 | 0.88 | −4.26 | –3.71 | 0.77 | 0.05 |
| Au|Pyr|1P|CF3 | −0.81 | −1.11 | 8.21 | 3.92 | −4.65 | –3.80 | 0.49 | 0.03 |
| Au|Pyr|1P|NH 2 | −3.77 | −0.16 | 4.63 | 0.14 | −3.20 | −3.70 | 1.29 | −0.55 |
| Au|Pyr|2P|NH 2 | −3.81 | −0.28 | 4.22 | 1.08 | −2.82 | — | 0.31 | −0.47 |
| Au|Pyr|3P|NH 2 | −3.95 | −0.33 | 3.59 | 1.00 | −2.33 | — | 0.26 | 0.00 |
| Au|Pyr|1P|CN | 0.82 | −0.96 | 9.86 | 5.67 | −3.82 | –3.82 | 0.36 | 0.08 |
| Au|Pyr|2P|CN | 1.39 | −0.38 | 9.44 | 6.35 | −2.82 | — | 0.27 | −0.04 |
| Au|Pyr|3P|CN | 1.62 | −0.28 | 9.21 | 6.62 | −2.35 | — | 0.24 | −0.06 |
| Au|Pyr|1P|NO 2 a | 1.72 | −0.08 | 10.23 | 6.73 | −3.46 | –2.76 | 0.23 | −0.08 |
| Au|Pyr|2P|NO 2 a | 1.90 | 0.11 | 9.79 | 6.90 | −2.65 | — | 0.24 | −0.16 |
| Au|Pyr|3P|NO 2 a | 1.99 | 0.20 | 9.50 | 7.01 | −2.27 | — | 0.22 | −0.20 |
In fact, one can distinguish between two contributions to Ebond(z) (cf., bottom plots in Fig. 5): a sharp decrease between the top Au layer and the nitrogen atoms and a more or less gradual increase along the backbone. For Au|Pyr|1P|NH2 and Au|Pyr|2P|NH2 one can even identify a third region corresponding to a relatively sharp increase around the substituent. The latter two contributions lead to a significant reduction of the large negative potential energy shift that arises from the charge rearrangements in the immediate Au–N region. As a consequence, while ΔEBD is about −1.00 eV in all systems, where only the sharp drop in Ebond at the interface occurs (i.e., in the one-ring systems with –H, –CH3, –CF3, and –CN substituents), it is reduced to a mere −0.16 and −0.08 eV in Au|Pyr|1P|NH2 and Au|Pyr|1P|NO2, respectively and becomes even positive for the more extended –NO2 substituted SAMs. In the –CN substituted systems, the partial cancellation due to the opposing (positive) bond-dipole contributions manifests itself in a decrease of the absolute magnitude of ΔEBD with chain length.
4.3 Reason for the delocalization of the charge rearrangements—Fermi-level pinning
To understand the origin of the unusual charge rearrangements in most of the systems discussed above, it is useful to first take a look at the corresponding densities of states projected onto the molecular parts at the interfaces. For the –NH2, –CN and –NO2 substituted systems with one and three rings they are shown in Fig. 6. For comparative reasons, Au|Pyr|1P|H is also included in that plot. In the latter system, EF lies clearly inside the band gap of the SAM; for Au|Pyr|1P|NH2, which displays the charge rearrangements “above” the substituent, we find the Fermi-level of the combined system at the location of feature (i) from Fig. 4. For Au|Pyr|1P|CN, EF is right at the onset of the LUPS related peak, i.e., the LUPS-derived states are not filled. In contrast, in the other systems EF is somewhat shifted into the peak and the LUPS-derived band is partially occupied, albeit only to a very small degree. | ||
| Fig. 6 Density of states projected onto the molecular region, MDOS, of the combined SAM-metal systems for the –NH2, –CN and –NO2 substituted monolayers with one (1P) and three (3P) conjugated rings. The PDOS of Au|Pyr|1P|H is also included to show a system far from Fermi level pinning. The Fermi levels are aligned to zero, and the positions of the LUPSs are indicated by arrows. The dashed arrow in the panel of Au|Pyr|1P|NH2 highlights the dispersing band (cf., feature (i) in Fig. 4a) pinned at the Fermi level. | ||
The latter is a manifestation of the fact that the systems are in the regime of Fermi-level pinning and Au|Pyr|1P|CN might be considered to be right at the onset of pinning. This process shall be briefly explained for the three-ring systems in the following: When joining metal substrate and SAM, to a first approximation, the electrostatic energy of the combined system is given by a superposition of the individual systems, with the potential landscape of the SAM shifted by ΔEBD relative to that of the metal.26,41 For the relative alignment between the unoccupied states in the SAM and the metal Fermi-level, this means that it is approximately given by the work function of the metal, Φ, minus the docking-side electron affinity of the SAM, EAdockπ, plus the bond-dipole ΔEBD. As for an Au(111) surface, Φ is calculated to be 5.22 eV, this would mean that the lowest unoccupied levels of all three-ring SAMs investigated (cf., Table 2) here would come to lie below EF, if ΔEBD was −1.0 eV like in the cases where no pinning occurs. This is inconsistent with the establishment of thermodynamic equilibrium. As a consequence, charges need to be rearranged to induce extra dipole(s) that shift the molecular levels in a way that their occupation is consistent with thermodynamic equilibrium, which means that they will (partially) overlap with EF.
For flat-lying adsorbates, this is usually achieved by a charge-transfer between metal and the adsorbate layer.98,99 The amount of charge transfer and, consequently, the exact position of EF relative to the molecular levels is, in a first approximation, determined by the magnitude of the bond-dipole that needs to be established to shift back the LUMO, although also more complex situations involving charge forward and backward donation have been observed.75,100
Interestingly, in SAMs the realignment does not proceed via long-range charge transfer, but is achieved by a polarization of the SAM (cf. Δρbond(z) and Q(z) plots in Fig. 5). The fact that the primary effect of pinning is not a (partial) filling of the LUPS is also clearly seen when comparing the associated local density of states with a 3D isodensity representation of the charge rearrangements. Such a comparison is shown in Fig. 7 for the particularly instructive case of a three-ring SAM bearing –NO2 substituents. The LUPS (Fig. 7b) displays typical features of the molecular LUMO (Fig. 7a); the charge rearrangements (Fig. 7c and d), however, do not even resemble the LUPS and a polarization of several bonds is clearly resolved. Of note, a similar type of Fermi-level pinning that proceeds via the polarization of a molecular backbone rather than via long-range charge transfer has also been observed for a “pinned” molecular layer on top of a SAM.94
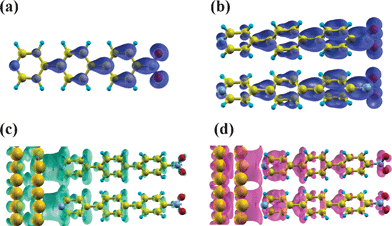 | ||
| Fig. 7 The local density of states (LDOS) of the LUMO for the isolated Pyr|3P|NO2 molecule (a), and of the LUPS of the Au|Pyr|3P|NO2 combined system (b). (c), (d) A 3D isodensity representation of charge rearrangement for Au|Pyr|3P|NO2 (only the top two layers of the Au-slab are shown). Electrons flow from regions shown in (c) to those depicted in (d). | ||
A finding that appears particularly surprising, at first glance, is that for the three-ring systems the same kind of pinning occurs for both donor and acceptor substitution. While a deep-lying LUMO prone to pinning does not come as a surprise for the acceptor substituted systems, donor substitution results in very small electron affinities in isolated molecules, rendering the unoccupied states high in energy. The latter, indeed, manifests itself in the tail-group side EAs reported for the –NH2 substituted molecules in Table 2. But, as mentioned above, what determines the level alignment is EAdockπ, which is only weakly affected by the substitution due to the peculiarities of “SAM electrostatics”.26,30 As a consequence, there is not necessarily a direct connection between simple molecular properties and the occurrence of pinning in a SAM.
What remains to be explained is the electron accumulation above the –NH2groups in Au|Pyr|1P|NH2 and Au|Pyr|2P|NH2, i.e., the unusual pinning level encountered in these systems. It is associated with an unoccupied σ-state in the region of the –NH2group that spreads out far into space and, as a consequence, gives rise to a strongly dispersing band in the monolayer (cf., feature (i) in Fig. 4a and ESI†). Pinning now occurs at the bottom of that band (cf., Au|Pyr|1P|NH2 in Fig. 6).
To check to what extent the occurrence of this quite “unusual” state is an artefact of the used programs and methodologies, we performed an extensive series of tests employing a variety of band-structure and molecule-based codes using either plane-wave or different atomic-orbital type basis sets. These tests, which are reported in detail in the ESI†, showed that (i) such a state is found in all calculations and (ii) for sufficiently large basis sets it becomes the lowest-lying unoccupied state for the short-chained, –NH2 substituted molecules. The relative position of that state might still be affected by the self-interaction error present in all DFT calculations based on (semi)local functionals (see discussion in the Methodology section). Nevertheless, the observations reported here for Au|Pyr|1P|NH2 and Au|Pyr|2P|NH2 still provide valuable insight into what happens, when the electronic state responsible for Fermi-level pinning is not delocalized along the molecular backbone, but is rather found relatively far away from the immediate interface region. Such cases can also be encountered when studying pinned SAMs in which the conjugated backbone is separated from the metal by a non-conjugated spacer.
4.4 Work-function modifications
The above considerations provide us with all the information necessary for understanding the change in the work function of the substrate due to the adsorption of the SAM, ΔΦ. The values of ΔΦ for all studied SAMs are listed in Table 3. ΔΦ arises from a simple superposition of the bond dipole and the change in the electrostatic potential induced by the hypothetical free-standing SAM;1–4,8,32i.e., it is given by:| ΔΦ = ΔEvac + ΔEBD | (5) |
Substitution with a donor gives rise to a larger work-function decrease, as here ΔEBD and ΔEvac are of the same sign. In the case of the –NH2 substituted SAMs, the net effect is, however, smaller than what one might have expected, as a consequence of the significantly reduced (negative) ΔEBD because of Fermi-level pinning.
For the case of acceptor substitution in the absence of Fermi-level pinning, the large negative “intrinsic” ΔEBD of the pyridine docking group limits the achievable work-function change. In fact, for Au|Pyr|1P|CF3, ΔΦ remains negative and for Au|Pyr|1P|CN it adopts “only” a value of +0.82 eV. Only when ΔEBD becomes less negative for the pinned two- and three-ring –CN substituted SAMs and Au|Pyr|1P|NO2, a significant increase of the work function can be expected. This is further enhanced for Au|Pyr|2P|NO2 and Au|Pyr|3P|NO2, where ΔEBD becomes positive (vide supra). The relative order of ΔΦ in the latter SAMs is then not determined by the order of ΔEvac (a property of the monolayer) but rather by how “positive” ΔEBD gets due to pinning (a consequence of the interaction between the SAM and the metal).
In the pinning cases, an expression alternative to eqn (5) can be used to describe the work-function of the SAM-covered metal, Φmod. In a way, it reflects the involved physics more directly as it relates Φmod to the energy of the pinning level: Because the position of the LUPS is fixed at a difference ΔELUPS from the metal Fermi-level, the effective work function Φmod differs from the tail-group side electron affinity EAtail only by this value (plus a typically small correction term ELUMOcorr explained in the following section) yielding:101
| Φmod = Φ + ΔΦ = EAtail + ΔELUPS − ELUMOcorr | (6) |
4.5 Level alignment
The quantities most relevant for charge-carrier injection into the SAM are the energy difference between the frontier levels in the organic layer and the Fermi level of metal, i.e., ΔELUPS and ΔEHOPS. They can be viewed as arising from the properties of (i) the free standing layer (IPdock and EAdock), (ii) the metal substrate (characterized by its work function Φ), and (iii) the charge-rearrangements upon bonding (ΔEBD). In addition, the change in “intrinsic” electronic structure of the molecules that arises from the charge rearrangements needs to be considered. These correction energies (EHOMOcorr and ELUMOcorr) can be obtained from the difference of the tail-group side IPs (EAs) of the free-standing layer and those of the bonded SAM.41 The latter are listed in Table 3 and are referred to as IPSAM and EASAM, respectively. They are the experimentally accessible quantities usually used to characterize the electronic structure of the SAM. In this way, one obtains:41| ΔEHOPS = Φ − IPdock + ΔEBD + EHOMOcorr | (7a) |
| ΔELUPS = Φ − EAdock + ΔEBD + ELUMOcorr | (7b) |
 | ||
| Fig. 8 Density of states projected onto the molecular region, MDOS, of the Au|Pyr|3P|CN combined SAM–metal system. The insets show the local density of states (LDOS) of the corresponding HOPS and LUPS, only the top two Au layers are shown. The Fermi energy is set to zero. | ||
As far as the occupied states are concerned, no strong features reminiscent of the σ-state localized in the vicinity of the nitrogen atom are observed, in accord with a strong hybridisation of that state with metal orbitals as suggested already by Bilić et al.40 As far as the occupied π-states are concerned, the same situation as for the free-standing monolayer is obtained. I.e., one finds type-(1) and type-(2) π-states and which of them lies higher in energy depends on the substituent. This is not particularly surprising, as ΔEBD shifts all states in the same manner and Ecorr remains small apart from the one- and two-ring NH2 substituted systems (vide supra). As far as the non-pinned SAMs are concerned, the trends as a function of the substituents remain the same as in Table 2; for example, the ΔEHOPS associated with the type-(2) π-states are very similar. This is no longer the case for the pinned SAMs (italics in Table 3), where ΔEBD varies with the substituent. As pinning always results in a less negative ΔEBD, it results in a reduction of ΔEHOPS that becomes more efficient for more strongly pinned systems where one deals with less negative values of ΔEHOPS.
5. Summary and conclusions
To summarize, we have systematically investigated the interfacial properties of pyridine-docked SAMs on Au(111) at the DFT level. The electronic structure of the hypothetical free-standing monolayers, as a starting point for the investigations, is relatively complex involving close lying σ- and π-states, where the order of the latter changes as a function of the substituent. Otherwise the typical properties of SAMs are observed25,26 with the substitution primarily affecting ionisation potentials (electron affinities) for removing (adding) an electron through the tail-group side of the SAM (the “tail” quantities), at least as long as the states of interest have only little weight on the substituents.Significant deviations from more conventional SAMs are observed for the bonded layers, where in most studied systems the Fermi level gets pinned at the lowest unoccupied molecular states. This gives rise to charge-rearrangements that extend along the whole molecular backbone, which are not associated with long-range charge transfer but rather with a local polarization of the SAM. As a net-effect, the magnitude of the bond-dipole, which amounts to –1 eV in the non-pinned systems, is reduced and the bond-dipole becomes even positive for –NO2 substituted systems containing two or three rings along the backbone. What appears somewhat surprising at first glance is that (beyond a certain chain length) an equivalent pinning situation is observed for strongly donating and strongly accepting substituents, in spite of the fact that the associated molecular electron affinities differ significantly. This can again be explained by the peculiarities of SAM electrostatics.
The main impact of the pinning at the LUPS on the SAM-induced work-function modifications is that it reduces the work-function reduction by donor substituted SAMs and boosts the work-function increase due to acceptor substituted SAMs. As far as the level alignment between the Fermi level and the SAM states is concerned, a very small barrier to electron injection is found for all pinned systems. As without pinning the unoccupied molecular states would come to lie even below EF, pinning at the unoccupied states essentially reduces the injection barriers for holes into the occupied states.
The results of this work highlight how much Fermi-level pinning can alter the electronic properties of SAMs, showing that it can be beneficial for certain quantities and types of SAMs, while it is detrimental for others.
Acknowledgements
The authors thank Leeor Kronik and Amir Natan for stimulating discussions regarding the shortcomings of density functional theory and Tomáš Bučko for providing and acquainting us with the GADGET code. Financial supports by the Ministry of Science and Technology of China through the 973 program (Grants 2011CB932304, and 2011CB8084050), National Science Foundation of China (Grants 20833004 and 20920102031) and by the Austrian Science Fund FWF through project P20972-N20, are gratefully acknowledged.References
- I. H. Campbell, S. Rubin, T. A. Zawodzinski, J. D. Kress, R. L. Martin, D. L. Smith, N. N. Barashkov and J. P. Ferraris, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R14321 CrossRef CAS.
- B. de Boer, A. Hadipour, M. M. Mandoc, T. van Woudenbergh and P. W. M. Blom, Adv. Mater., 2005, 17, 621 CrossRef CAS.
- D. M. Alloway, M. Hofmann, D. L. Smith, N. E. Gruhn, A. L. Graham, R. Colorado, V. H. Wysocki, T. R. Lee, P. A. Lee and N. R. Armstrong, J. Phys. Chem. B, 2003, 107, 11690 CrossRef CAS.
- I. H. Campbell, J. D. Kress, R. L. Martin, D. L. Smith, N. N. Barashkov and J. P. Ferraris, Appl. Phys. Lett., 1997, 71, 3528 CrossRef CAS.
- C. Ganzorig, K. J. Kwak, K. Yagi and M. Fujihira, Appl. Phys. Lett., 2001, 79, 272 CrossRef CAS.
- R. A. Hatton, S. R. Day, M. A. Chesters and M. R. Willis, Thin Solid Films, 2001, 394, 292 CrossRef CAS.
- H. Yan, Q. L. Huang, J. Cui, J. G. C. Veinot, M. M. Kern and T. J. Marks, Adv. Mater., 2003, 15, 835 CrossRef CAS.
- R. W. Zehner, B. F. Parsons, R. P. Hsung and L. R. Sita, Langmuir, 1999, 15, 1121 CrossRef CAS.
- L. Zuppiroli, L. Si-Ahmed, K. Kamaras, F. Nüesch, M. N. Bussac, D. Ades, A. Siove, E. Moons and M. Grätzel, Eur. Phys. J. B, 1999, 11, 505 CrossRef CAS.
- D. Fragouli, T. N. Kitsopoulos, L. Chiodo, F. Della Sala, R. Cingolani, S. G. Ray and R. Naaman, Langmuir, 2007, 23, 6156 CrossRef CAS.
- C. Zhou, M. R. Deshpande, M. A. Reed, L. Jones II and J. M. Tour, Appl. Phys. Lett., 1997, 71, 611 CrossRef CAS.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252 CrossRef CAS.
- J. Chen, M. A. Reed, A. M. Rawlett and J. M. Tour, Science, 1999, 286, 1550 CrossRef CAS.
- H. B. Akkerman, P. W. M. Blom, D. M. de Leeuw and B. de Boer, Nature, 2006, 441, 69 CrossRef CAS.
- A. J. Kronemeijer, H. B. Akkerman, T. Kudernac, B. J. van Wees, B. L. Feringa, P. W. M. Blom and B. de Boer, Adv. Mater., 2008, 20, 1467 CrossRef CAS.
- J. G. Kushmerick, D. B. Holt, J. C. Yang, J. Naciri, M. H. Moore and R. Shashidhar, Phys. Rev. Lett., 2002, 89, 086802 CrossRef CAS.
- J. R. Heath, Annu. Rev. Mater. Res., 2009, 39, 1 CrossRef CAS.
- M. Zharnikov and M. Grunze, J. Phys.: Condens. Matter, 2001, 13, 11333 CrossRef CAS.
- C. D. Zangmeister, S. W. Robey, R. D. van Zee, Y. Yao and J. M. Tour, J. Phys. Chem. B, 2004, 108, 16187 CrossRef CAS.
- W. Chen, C. Huang, X. Y. Gao, L. Wang, C. G. Zhen, D. Qi, S. Chen, H. L. Zhang, K. P. Loh, Z. K. Chen and A. T. S. Wee, J. Phys. Chem. B, 2006, 110, 26075 CrossRef CAS.
- M. Kind and C. Wöll, Prog. Surf. Sci., 2009, 84, 230 CrossRef CAS.
- V. de Renzi, Surf. Sci., 2009, 603, 1518 CrossRef CAS.
- C. Vericat, M. E. Vela, G. Benitez, P. Carro and R. C. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805 RSC.
- S. G. Ray, H. Cohen, R. Naaman, H. Liu and D. H. Waldeck, J. Phys. Chem. B, 2005, 109, 14064–14073 CrossRef CAS.
- G. Heimel, L. Romaner, E. Zojer and J. L. Brédas, Acc. Chem. Res., 2008, 41(6), 721 CrossRef CAS.
- G. Heimel, F. Rissner and E. Zojer, Adv. Mater., 2010, 22, 2494 CrossRef CAS.
- Q. Sun and A. Selloni, J. Phys. Chem. A, 2006, 110, 11396 CrossRef CAS.
- E. Fabiano, M. Piacenza, S. D'Agostino and F. Della Sala, J. Chem. Phys., 2009, 131, 234101 CrossRef CAS.
- P. C. Rusu, G. Giovannetti and G. Brocks, J. Phys. Chem. C, 2007, 111, 14448 CrossRef CAS.
- A. Natan, L. Kronik, H. Haick and R. T. Tung, Adv. Mater., 2007, 19, 4103 CrossRef CAS.
- A. Bilić, J. R. Reimers and N. S. Hush, J. Chem. Phys., 2005, 122, 094708 CrossRef.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Phys. Rev. Lett., 2006, 96, 196806 CrossRef.
- F. Della Sala, E. Fabiano, S. Laricchia, S. D'Agostino and M. Piacenza, Int. J. Quantum Chem., 2010, 110, 2162 CrossRef CAS.
- V. De Renzi, R. Rousseau, D. Marchetto, R. Biagi, S. Scandolo and U. del Pennino, Phys. Rev. Lett., 2005, 95, 046804 CrossRef CAS.
- P. C. Rusu and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 073414 CrossRef.
- P. C. Rusu and G. Brocks, J. Phys. Chem. B, 2006, 110, 22628 CrossRef CAS.
- G. Heimel, L. Romaner, E. Zojer and J. L. Brédas, Organic Optoelectronics and Photonics III, ed. P. L. Heremans, M. Muccini and E. A. Meulenkamp, Proc. SPIE, 2008, vol. 6999, p. 699919 Search PubMed.
- M. Malicki, Z. Guan, S. D. Ha, G. Heimel, S. Barlow, M. Rumi, A. Kahn and S. R. Marder, Langmuir, 2009, 25, 7967 CrossRef CAS.
- L. J. Wang, G. M. Rangger, Z. Y. Ma, Q. K. Li, Z. Shuai, E. Zojer and G. Heimel, Phys. Chem. Chem. Phys., 2010, 12, 4287 RSC.
- A. Bilić, J. R. Reimers and N. S. Hush, J. Phys. Chem. B, 2002, 106, 6740 CrossRef CAS.
- G. Heimel, L. Romaner, E. Zojer and J. L. Brédas, Nano Lett., 2007, 7, 932 CrossRef.
- P. Hébert, A. Le Rilie, W. Q. Zheng and A. Tadjeddine, J. Electroanal. Chem., 1998, 447, 5 CrossRef CAS.
- J. Lipkowski and L. Stolberg, Adsorption of Molecules at Metal Electrodes, ed. J. Lipkowski and P. N. Ross, VCH, New York, 1992, p. 171 Search PubMed.
- M. J. Crossley, P. L. Burn, S. J. Langford and J. K. Prashar, J. Chem. Soc., Chem. Commun., 1995, 1921 RSC.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221 CrossRef CAS.
- R. Stadler, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 241401 CrossRef.
- X. Li, J. Hihath, F. Chen, T. Masuda, L. Zang and N. Tao, J. Am. Chem. Soc., 2007, 129, 11535 CrossRef CAS.
- M. Kamenetska, S. Y. Quek, A. C. Whalley, M. L. Steigerwald, H. J. Choi, S. G. Louie, C. Nuckolls, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, J. Am. Chem. Soc., 2010, 132, 6817 CrossRef CAS.
- S. Hou, J. Ning, Z. Shen, X. Zhao and Z. Xue, Chem. Phys., 2006, 327, 1 CrossRef CAS.
- C. Wang, A. S. Batsanov, Martin R. Bryce, S. Martín, R. J. Nichols, S. J. Higgins, V. M. García-Suáez and C. J. Lambert, J. Am. Chem. Soc., 2009, 131, 15647–15654 CrossRef CAS.
- J. F. Kang, S. Liao, R. Jordan and A. Ulman, J. Am. Chem. Soc., 1998, 120, 9662 CrossRef CAS.
- S. Liao, Y. Shnidman and A. Ulman, J. Am. Chem. Soc., 2000, 122, 3688 CrossRef CAS.
- J. F. Kang, A. Ulman, S. Liao, R. Jordan, G. Yang and G. Liu, Langmuir, 2001, 17, 95 CrossRef CAS.
- W. Azzam, C. Fuxen, A. Birkner, H.-T. Rong, M. Buck and C. Wöll, Langmuir, 2003, 19, 4958 CrossRef CAS.
- N. Ballav, B. Schüpbach, O. Dethloff, P. Feulner, A. Terfort and M. Zharnikov, J. Am. Chem. Soc., 2007, 129, 15416–15417 CrossRef CAS.
- M. Malicki, Z. Guan, S. D. Ha, G. Heimel, S. Barlow, M. Rumi, A. Kahn and S. R. Marder, Langmuir, 2009, 25, 7967–7975 CrossRef CAS.
- M. Manolova, H.-G. Boyen, J. Kucera, A. Groß, A. Romanyuk, P. Oelhafen, V. Ivanova and D. M. Kolb, Adv. Mater., 2009, 21, 320 CrossRef CAS.
- L. Kankate, A. Turchanin and A. Gölzhäuser, Langmuir, 2009, 25, 10435 CrossRef CAS.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS; A. Natan, L. Kronik and Y. Shapira, Appl. Surf. Sci., 2006, 252, 7608 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- S. Tsuzuki and H. P. Lüthi, J. Chem. Phys., 2001, 114, 3949 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Surf. Sci., 2006, 600, 4548 CrossRef CAS.
- T. Bučko, J. Hafner and J. G. Ángyán, J. Chem. Phys., 2005, 122, 124508 CrossRef.
- A. Kokalj, Comput. Mater. Sci., 2003, 28, 155 CrossRef CAS . Code available from http://www.xcrysden.org/.
- S. Kümmel and L. Kronik, Rev. Mod. Phys., 2008, 80, 3 CrossRef.
- D. M. Newns, Phys. Rev., 1969, 178, 1123 CrossRef CAS; Y. Li, D. Lu and G. Galli, J. Chem. Theory Comput., 2009, 5, 881 CrossRef CAS.
- Note that the resulting incorrect description of the charge transfer can under certain circumstances also result in an incorrect value for the charging-induced shifts of the orbital energies. For isolated molecules, this effect can be very large,31 although in the SAM its impact will be mediated by the very different far-field arising from collective effects, that has been discussed by Natan et al.30.
- L. Romaner, G. Heimel, J. L. Brédas, A. Gerlach, F. Schreiber, R. L. Johnson, J. Zegenhagen, S. Duhm, N. Koch and E. Zojer, Phys. Rev. Lett., 2007, 99, 256801 CrossRef; G. M. Rangger, O. T. Hofmann, L. Romaner, G. Heimel, B. Bröker, R.-P. Blum, R. L. Johnson, N. Koch and E. Zojer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165306 CrossRef.
- L. Romaner, D. Nabok, P. Puschnig, E. Zojer and C. Ambrosch-Draxl, New J. Phys., 2009, 11, 053010 CrossRef.
- The only complication in the case of PTCDA is that there the neglect of van der Waals interactions results in a non-bonded situation and agreement with experiment is found only, when the adsorbate layer is put to the experimental adsorption distance.
- B. Bröker, R.-P. Blum, J. Frisch, A. Vollmer, O. T. Hofmann, R. Rieger, K. Müllen, J. P. Rabe, E. Zojer and N. Koch, Appl. Phys. Lett., 2008, 93, 243303 CrossRef.
- J. Böhlin, M. Unge and S. Stafström, J. Phys.: Condens. Matter, 2008, 20, 315008 CrossRef.
- T. Körzdörfer, S. Kümmel, N. Marom and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 201205 CrossRef.
- N. Dori, M. Menon, L. Kilian, M. Sokolowski, L. Kronik and E. Umbach, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195208 CrossRef.
- N. Marom, O. Hod, G. E. Scuseria and L. Kronik, J. Chem. Phys., 2008, 128, 164107 CrossRef.
- N. Marom and L. Kronik, Appl. Phys. A: Mater. Sci. Process., 2008, 95, 159.
- M. Palummo, C. Hogan, F. Sottile, P. Bagalá and A. Rubio, J. Chem. Phys., 2009, 131, 084102 CrossRef.
- J. Sauther, J. Wüsten, S. Lach and Ch. Ziegler, J. Chem. Phys., 2009, 131, 034711 CrossRef CAS.
- A. Stroppa and G. Kresse, New J. Phys., 2008, 10, 063020 CrossRef.
- K. Hummer, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 184105 CrossRef.
- Due to the steric restriction by the two H atoms bonded to the C atoms next to the N atom, the molecular axes can primarily tilt along the direction that is perpendicular to the molecular plane. In this respect, pyridines differ from SAMs docked, e.g., via thiolates or isocyanides. Those docking groups separate the molecular backbone farther from the substrate, giving the molecules more freedom to tilt.
- L. Romaner, G. Heimel, C. Ambrosch-Draxl and E. Zojer, Adv. Funct. Mater., 2008, 18, 3999 CrossRef CAS.
- L. J. Wang, G. M. Rangger, L. Romaner, G. Heimel, T. Bučko, Z. Y. Ma, Q. K. Li, Z. Shuai and E. Zojer, Adv. Funct. Mater., 2009, 19, 3766 CrossRef CAS.
- In the more extended systems, the relative ordering of the rather localized σ- and more delocalized π-orbitals, however, needs to be taken with a grain of salt, as the self-interaction error (cf. Methodology section) will affect the two types of orbitals differently due to their different degree of localization80.
- There the HOMO arises from an overlap of the two highest σ-orbitals.
- One of the reasons, why this peak is so weak is that the corresponding states are very delocalized and, thus, extend to far above the substituent groups (cf., discussion in the ESI†). As a consequence, they are not fully captured in the scheme that calculates projected densities of states in the VASP program. (For comparison, see the total DOS in Figure S7b in the ESI.).
- F. Rissner, G. M. Rangger, O. T. Hofmann, A. M. Track, G. Heimel and E. Zojer, ACS Nano, 2009, 3, 3513 CrossRef CAS.
- For the EA values and in Pyr|nP|NO2 also for the IP values this yields a monotonic evolution of the π-related quantities with chain-length; in contrast, for the –NH2 and –CN substituted systems, where σ- and π-states overlap, the IPπ's are virtually the same for two and three rings.
- L. Romaner, G. Heimel and E. Zojer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045113 CrossRef.
- In this context it should be noted that Bilić et al. described the pyridine-Au binding as “dispersive in nature, with significant contributions from the charge polarization effects but minimal contributions from charge transfer and covalent bonding”40.
- N. Koch, ChemPhysChem, 2007, 8, 1438 CrossRef CAS.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450 CrossRef CAS.
- R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601 CrossRef CAS.
- When evaluating equations 6 and 7 using the quantities from Tables 2 and 3, small inconsistencies on the order of a few hundredths of an eV occur. This is a consequence of the finite extent of the metal slab, as the Fermi energy slightly varies between the systems due to different amounts of charge transfer at the interface.
- The actual value of ΔELUPS in a pinned system is, of course, also influenced by the chosen broading of the DOS.
- N. Crivillers, C. Munuera, M. Mas-Torrent, C. Simao, S. T. Bromley, C. Ocal, C. Rovira and J. Veciana, Adv. Mater., 2009, 21, 1177 CrossRef CAS.
- G. Heimel, E. Zojer, L. Romaner, J. L. Brédas and F. Stellacci, Nano Lett., 2009, 9, 2559 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the nature of the highest occupied states and the lowest unoccupied states of the isolated monolayer as well as the SAM-metal systems; detailed discussion of “unusual” charge rearrangements in certain amine-substituted SAMs; description of test calculations using hybrid functionals. See DOI: 10.1039/c0cp02168g |
| This journal is © the Owner Societies 2011 |
