Photodissociation and photoelectron imaging of molecular ions: probing multisurface and multichannel dynamics

Abstract

High-resolution ion and electron imaging techniques have been used to explore a series of problems in the reaction dynamics of gas phase ions. These have applications ranging from fundamental dynamical studies to atmospheric chemistry and astrochemistry. In this minireview we illustrate these approaches with several examples from our recent work. We examine the conformationally- and vibrationally-mediated photodissociation dynamics of propanal and ethylene cations, and show how these can reveal reaction dynamics across multiple electronic potential surfaces of these molecules. Recent results for methylamine cation photodissociation provide insight into the rich chemistry of the ionosphere of Saturn's great moon, Titan. The combination of high-resolution ion and photoelectron imaging, REMPI spectroscopy and state-of-the-art ab initio calculations yields a powerful multifaceted approach to studying photoionization and photofragmentation dynamics in ions.

---

Prashant Chandra Singh

Prashant Chandra Singh obtained his PhD from the Indian Institute of Technology, Bombay, in 2008. He then moved to Wayne State University for postdoctoral research and worked under the guidance of Prof. Arthur Suits. He has been awarded JSPS and FPR fellowships and is currently working with Prof. Tahara at RIKEN, Japan. His main research interests are the dynamics of molecules in the gas phase and at interfaces.

Lei Shen

Lei Shen obtained his BS degree from the University of Science and Technology of China, and PhD from Wayne State University with Prof. Arthur G. Suits. Currently he is carrying out postdoctoral work in Prof. Poul B. Petersen's group at Cornell University.

Myung Hwa Kim

Myung Hwa Kim obtained his BS degree in Chemistry and MS degree in Physical Chemistry at Korea University in Seoul. He obtained his PhD at the State University of New York at Stony Brook in Chemical Physics under the guidance of Prof. Arthur G. Suits. He performed postdoctoral research in the laboratory of Prof. Alec. M. Wodtke at the University of California at Santa Barbara. In 2009, he joined Ewha Womans University, Seoul, in the Department of Chemistry & Nano Science as an Assistant Professor.

Arthur G. Suits

Arthur G. Suits is a Professor of Chemistry and Member of the Academy of Scholars at Wayne State University. He obtained his PhD from the University of California, Berkeley, in the group of Y. T. Lee. Following postdoctoral work at Cornell University with Paul Houston, he joined the staff at Lawrence Berkeley National Laboratory. From 2000–2004 he held joint appointments at Stony Brook University and Brookhaven National Laboratory. In 2004, he joined the faculty at Wayne State. His research interests are in chemical reaction dynamics, chemical physics, and astrochemistry. He is a Fellow of the American Physical Society.

---

Introduction

Dynamical studies of gas phase molecular cations have been widely pursued for their fundamental interest as well as their importance in atmospheric, astrochemical and biological problems. In one aspect of these investigations, state-prepared ion photodissociation^1–5 and ion-molecule reaction dynamics studies^6–12 have been used to explore aspects of the excited state potential energy surfaces and product branching, initial alignment of the molecule and its impact on photoionization, and to study vibrational mode-dependent reactivity. These studies are analogous to the vibrationally-mediated studies of neutrals pursued notably by Crim, Rosenwaks and others.^13–18 Two general strategies have been used to prepare polyatomic cations with initial excitation in different vibrational modes or in different conformations: resonance-enhanced multiphoton ionization (REMPI)^1–4 and mass-analyzed threshold ionization (MATI) techniques.¹⁹ In a simple REMPI scheme, the vibrational state or conformer selection in the cation can be achieved by excitation of an intermediate Rydberg state followed by ionization by an additional photon. This REMPI ionization process will often produce singly-charged vibrational and conformational states quite selectively because the state of the ion that results is largely determined by the nature of the Rydberg state that is initially excited. This is owing to the fact that, in general, the geometry of the Rydberg state strongly resembles the ion – after all, a Rydberg state is a molecule well on its way to becoming an ion. The photoionization process itself may be the subject of interest in some cases, or these state-prepared ions may then be used for further study of reaction or photodissociation dynamics. The recently developed DC sliced ion-imaging technique²⁰ is very well suited for these studies, as photolysis of the cations necessarily results in the formation of charged photo-products that may be detected directly. Photoelectron imaging is a powerful related technique that gives structural and dynamical information on the prepared ions, and also aids in assigning the observed REMPI spectra.^21,22 Furthermore, photoelectron imaging may readily be performed in any ion imaging apparatus simply by reversing the polarity of the electrodes and adjusting the potential appropriately. REMPI, photoelectron imaging and DC sliced ion imaging techniques in conjunction provide a powerful approach to understand the state-selective structural and photochemical properties of ions.^23,24 This minireview presents a snapshot of our work over several years applying imaging methods to various processes in the reaction dynamics of ions. We have used these techniques to investigate mode selectivity in the photodissociation of the ethylene cation (C₂H₄⁺),^25,26 and conformationally-selective photodissociation dynamics in propanal,^27,28 isobutanal²³ and butanone²⁴ cations, to study photoionization processes and product branching in multiphoton ionization of CO,²⁹ to probe alignment effects and product branching in the acetaldehyde cation,³⁰ and to explore photoionization dynamics in the methylamine cation.³¹ This work is strongly coupled to theory, and indeed the strong interaction with theory is one of the hallmarks of chemical dynamics investigations. Although our chief focus is to explore fundamental dynamical issues, there are sometimes immediate practical implications of these studies in diverse areas such as atmospheric chemistry and astrochemistry, as well as in biological chemistry. In this minireview, we will discuss the photoionization/photodissociation of propanal, ethylene and methylamine cations to illustrate these approaches.

Experimental approach

The experiments described here were performed in a unique reflectron imaging machine that can be used in either reflectron multimass or conventional velocity map/DC sliced or photoelectron imaging mode. The apparatus has been described in detail elsewhere,³² and only a brief description is given here. The machine is made up of a source chamber in which a pulsed molecular beam is generated, and the main chamber, where the ionization and photodissociation of polyatomic cations occurs. For conventional velocity map imaging, a 120 cm long flight tube is connected with the main source chamber. In the multimass imaging setup there are two additional components in the main chamber. First, a set of deflection plates in which a transverse voltage pulse is used to induce mass separation. Second, after the ions are spatially dispersed by mass, they enter a single stage reflectron consisting of a stack of 36 electrodes. In this region, the ions turn around due to the retarding field of the reflectron and are redirected towards the detector through another field free region. Finally, the ions with different mass-to-charge ratios arrive at distinct positions on the surface of the position-sensitive detector, and recoil velocity distributions and relative branching may be obtained for multiple masses simultaneously. For photoelectron imaging, or slice imaging of a single product mass, the apparatus can be operated in a linear mode. In either configuration, images of the ion impacts on the detector are recorded using CCD camera in-house image acquisition software, then transformed from velocity to translational energy.³³

Preparation, characterization, and selective photodissociation of ion conformers

Molecular conformational isomerism is central to a broad range of chemical phenomena from protein folding^34,35 to the development of molecular motors,^36–38 and the role of electronic excitation in isomerization dynamics is central to the chemistry of vision and photosynthetic systems.³⁹ Perhaps surprisingly, there has only been limited direct experimental evidence of conformationally-selective photodynamics in the literature.^19,40,41 To explore these issues, we used DC sliced ion imaging and photoelectron imaging, in conjunction with theoretical calculations from the Martinez group, to characterize the different conformers of the propanal cation, and to reveal surprising conformationally-selective photodissociation dynamics in this system.²⁸

Propanal exists in two different conformational forms, cis and gauche, in which the cis form has a planar CCCO backbone, while the gauche form has an out-of-plane carbonyl group. The neutral gauche form is 270 to 400 cm⁻¹ higher in energy than the cis form and the transition barrier is 800 cm⁻¹.⁴² However, while the cations are similar in structure to the neutrals, the gauche form cation is slightly lower in energy and the transition barrier to the cis form is 344 cm⁻¹.²⁷ Furthermore, the Rydberg states also have a large difference in energy, so resonant ionization may readily be used to produce one ion or the other, even though both neutral conformers are initially present in the molecular beam.

These experiments were performed for both ions and electrons in the multimass imaging apparatus operated in the linear mode. cis or gauche propanal was selectively prepared in a beam of neutral propanal via the 3s Rydberg state on a two-photon resonance (∼370 nm) and ionized by a third photon.⁴³ The cation so produced largely remains in the same conformational and vibrational level as the initially excited Rydberg state owing to the similarities of the Rydberg and ion geometries. This “diagonal” ionization is documented by photoelectron imaging as shown in Fig. 1.²⁷ The photoelectron images and the photoelectron kinetic energy distribution were measured for the cis and gauche propanal ionization via the 3s Rydberg state at two-photon energies of 53943.9 cm⁻¹ and 54785.3 cm⁻¹, respectively. The image recorded on the cis origin of the 3s Rydberg state has two sharp rings, while for that from the gauche origin of the 3s Rydberg state, a single intense ring is prominent. The main peak corresponding to the cis cation has 0.0325 eV of electron kinetic energy, and is readily assigned to formation of the vibrational ground level of the cis form of the ion. The second, cis photoelectron peak, of much lower intensity, is shifted by about 29.8 meV (237 cm⁻¹), from the vibrationless ground state of the cis propanal cation, and is assigned to one quantum in the v₁₅⁺ (CCCO deformation) mode on the basis of the theoretical predictions of the frequencies and the modes likely to be active in the photoionization. For the gauche photoelectron data, a single sharp peak at 0.242 eV is seen with very weak peaks at higher binding energy. From the theoretical calculations, the peak position for the vibrationless ions of the gauche conformer is expected to be about 0.245 eV, which is in nice agreement with the peak at 0.242 eV. This peak is thus assigned as the origin for the gauche conformer cation. From our photoelectron spectra, the vertical ionization potentials for the cis and gauche conformers of propanal are determined to be 9.999(3) and 9.944(3) eV, which give a significant reduction in the associated uncertainty from the earlier determination of 9.98 eV.⁴⁴ From the photoelectron imaging results, we conclude that the conformer ion preparation takes place with >98% purity, and the vibrational level preparation with >80% purity, following the initially excited Rydberg level.

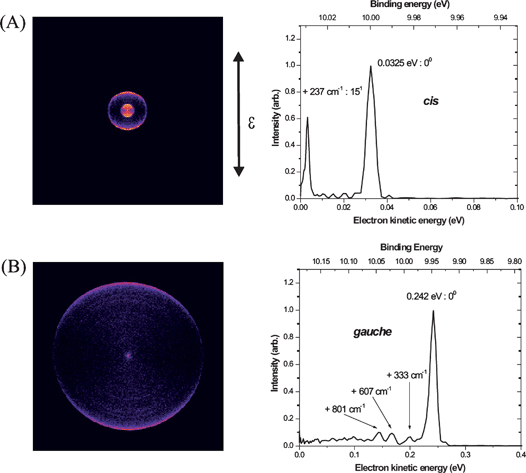Fig. 1 Photoelectron images and photoelectron kinetic energy distributions measured for propanal via (A) the cis transition at 53943.9 cm⁻¹ and (B) the gauche transition at 54785.3 cm⁻¹.

Fig. 2 shows ion images of the C₃H₅O⁺ product from the dissociation of the cis (Fig. 2A) and gauche (Fig. 2B) propanal cation in the ground vibrational level, and also for one quantum (Fig. 2C) and two quanta excitation (Fig. 2D) of the v₁₅⁺ mode for the cis form. Fig. 2E shows the translational energy distributions of the cis and gauche conformers in the ground vibrational state obtained from their respective images. In all images there appear two rings: for the cis form there is one intense central ring and a weak outer ring. For the gauche form, the outer ring is much stronger. The translational energy distributions for the two conformers thus each have two product peaks but with different relative intensities. The faster component accounts for ∼18% of the dissociation yield in the case of the cis conformer but ∼48% of the dissociation yield for the gauche form. The other striking feature of the images is the sharp truncation of the two rings on the low energy side. This feature is characteristic of cases in which slower-recoiling products, which have vibrational excitation exceeding some threshold energy, undergo secondary decomposition. Based on these observations, the two peaks can be assigned to distinct product isomers. One of these is identified as the propanoyl cation, CH₃CH₂CO⁺ + H, which has 2.9 eV available energy as shown in Fig. 3A.⁴⁵ The onset of secondary decomposition of propanoyl, leading to ethyl cation + CO, is at ∼2.3 eV above the ion ground level; therefore, propanoyl cations produced with less than ∼1.1 eV of translational energy will undergo additional fragmentation and will not appear in the C₃H₅O⁺ mass images. This fragmentation accounts for the abrupt cut off of the fast peak at translational energies lower than ∼1.1 eV, and allows definitive assignment of the fast peak to the CH₃CH₂CO⁺ + H channel. The other product isomer, identified as hydroxyallyl cation, CH₂CHCHOH⁺, has a higher energy threshold; therefore, we expect this product to show a lower translational energy release.⁴⁶ Furthermore, this isomer has a secondary fragmentation pathway to HCO⁺ + C₂H₄ with a threshold energy of ∼3.15 eV above the cation origin. This indicates that hydroxyallyl cations formed with less than ∼0.2 eV translation energy will undergo fragmentation and will not appear at mass 57. Precisely this behavior is observed for the slow peak; we therefore assign the slow peak to the hydroxyallyl isomer.

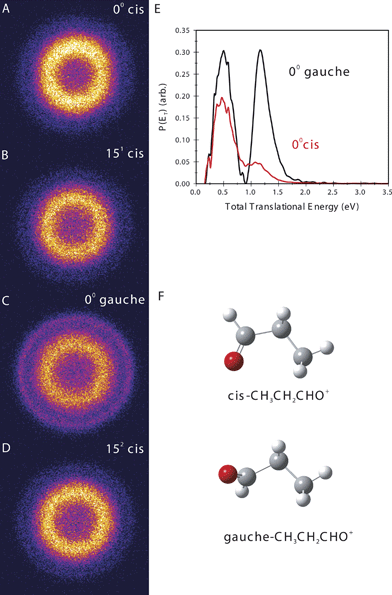Fig. 2 Sliced ion images of the C₃H₅O⁺ product of propanal cation photodissociation, starting from the indicated conformer and vibrational level (A–D). (E) Total translational energy distributions from the images in (A) to (D) for dissociation from the cis origin (red line) and gauche origin (black line). (F) Equilibrium structures for the indicated propanal cation conformers.

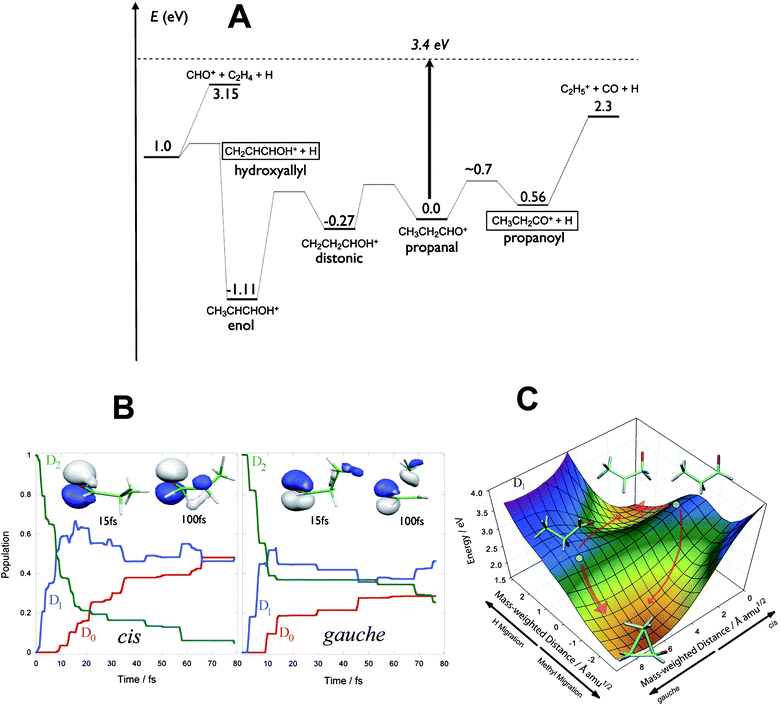Fig. 3 (A) Energy level diagram for key isomers and products of propanal cation dissociation relative to the cation ground state. The excitation energy is shown as a dashed line. (B) Electronic population for cis (left) and gauche (right) conformers of the propanal cation after photoexcitation to D₂ from AIMS calculations. (C) Two-dimensional cut of the D₁ potential energy surface for the propanal cation showing reaction pathways from the Franck–Condon points (shown as a solid circle for each of the cis and gauche conformers) to the hydrogen-migration and methyl-migration minima for cis and gauche conformers.

Although we are able to assign these peaks to the two different isomers clearly on the basis of energetics, to understand the dramatically different branching ratios exhibited by the two conformers, ab initio multiple spawning (AIMS) dynamical calculations were performed by Tao and Martinez. In both cation conformers, the singly occupied molecular orbital (SOMO) in the ground electronic state is a nonbonding (n) orbital primarily localized on the carbonyl group. The first excited electronic state (D₁), with a π SOMO, is dark, while the second excited state (D₂), with a σ SOMO, is optically bright. The experiment thus excites both conformers to D₂. However, as shown in Fig. 3B, the AIMS calculations show that decay from D₂ to D₁ is extremely fast, with more than half of the population undergoing internal conversion to D₁ within 10 fs. This rapid and efficient quenching stems from a conical intersection that connects D₂ and D₁ very close to the initially excited geometries. The key dynamics leading to conformer-specific behavior then takes place on the D₁ surface. There, the cis conformation has a high probability of undergoing hydrogen migration to form CH₃CHCH₂O⁺, which converts rapidly to the D₀ state through another conical intersection. On the ground state, H migration from the methyl group to the O atom, followed by a loss of H from C1, leads to the hydroxyallyl cation. The gauche conformation instead more often undergoes methyl migration, as the charge in this case is localized on the methyl carbon. When this structure converts to D₀, the methyl group reverts to the original site, yielding an energetic propanal cation in the starting geometry. Fig. 3C shows the key region of the D₁ potential energy surface containing the cis and gauche Franck–Condon points (i.e., the geometry of maximum overlap between the excited state and the ground state of the ion), the ridge connecting them, and the two local D₁ minima. The difference in slope for each of the two pathways in each conformer is significant, and the distinct product branching can be directly related to the gradient of the D₁ potential energy surface at the Franck–Condon point for these two molecules. Thus, excitation of cis and gauche conformers leads ultimately to different intermediate structures in the ground state, which in turn fragment through chemically distinct pathways to give the observed experimental results. Dramatically different product branching ultimately seen on the ground state is controlled by subtle differences in the excited state potential surface leading to the two conical intersections.

Vibrational mediated photodissociation of the ethylene cation

Vibrationally-mediated photodissociation is a powerful tool to control unimolecular reaction dynamics and probe features of the ground and excited state potential surfaces.^13–15 In this approach, an initial vibrational level is prepared by infrared excitation, opening Franck–Condon-mediated access to different regions of the excited state surfaces. Using REMPI, analogous vibrational state preparation in ions is possible as we have just shown for conformational selectivity. This has been exploited to great effect in ion-molecule reaction studies by Anderson and co-workers.^6–12 We illustrate this approach for ion photodissociation in a multimass imaging study of the dissociation of the ethylene cation. The thresholds for H and H₂ elimination from open shell ethylene cation (X ²B_3u) are very close in energy and exhibit different correlations to the electronic states involved in dissociation.^47–53 We studied the photodissociation of the ethylene cation using the reflectron multimass velocity map imaging apparatus to gain insight into the multisurface dynamics in this system.

Multimass velocity map images for the photodissociation of state selected C₂H₄⁺, produced via the various vibronic bands of (π, 3s) and (π, 3p) Rydberg states through (2 + 1) REMPI⁵⁴ and its translational energy derived from the images are shown in Fig. 4. Photoelectron imaging experiments were also used to confirm the nature of the initial state of the prepared ions, as described in the preceding section for the propanal cation. In all the images, the rightmost spot is the residual parent C₂H₄⁺ ion as it has no recoil velocity. The next two adjacent images are C₂H₃⁺ and C₂H₂⁺, respectively, which originate from H loss and H₂ loss following electronic excitation from the initial vibrational state of the C₂H₄⁺ ion. Photofragment images for the C₂H₃⁺ and C₂H₂⁺ are structureless and isotropic in nature, though careful inspection shows subtle differences in the shape of the images for the H and H₂ loss channels originating from the different initial vibrational states of C₂H₄⁺. For all the transitions, the measured translational energies for both H and H₂ elimination channels are small compared to the total available energy in the system; as in the example of the 4³ level where the average translational energies for H and H₂ loss channels are 0.21 eV and 0.10 eV, respectively, compared to available energies of 1.0 and 1.08 eV for these reactions.

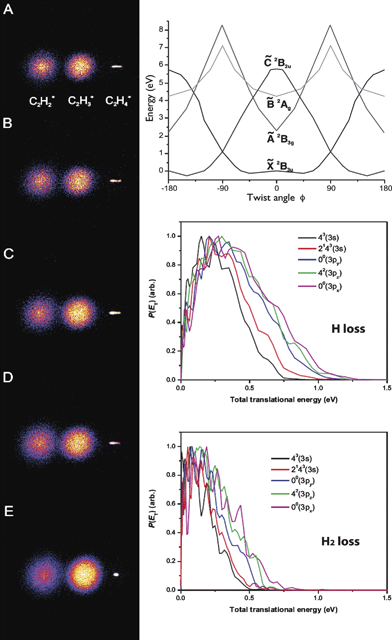Fig. 4 Left: Photofragment images from the photodissociation of C₂H₄⁺ produced by (2 + 1) REMPI through the (A): 4¹ (3s), (B): 2¹3¹ (3s), (C): 0⁰ (3p_y), (D): 4¹(3p_z), and (E): 0⁰ (3p_x) vibrational levels, respectively. Top right: Schematic potential energy diagrams for C₂H₄⁺ adapted from ref. 34. Bottom right: The total translational energy distributions for both H and H₂ elimination channels.

A molecular dissociation process that takes place over a significant “reverse barrier” typically peaks at a translational energy some significant fraction of the barrier height. The barrier generally represents Pauli repulsion of the newly formed molecules created in close proximity. This repulsive potential energy is then largely converted to recoil translational energy as the dissociation takes place. In contrast, in a barrierless process such as is seen, for example, when a bond simply breaks to form two radicals, the most probable translational energy is near zero. This is because there are many more possible states when the energy is partitioned into rotational and vibrational excitation of the products than when it is all partitioned into translation. One exception to this is for H atom elimination, in which often the translational energy distribution peaks at some small non-zero value owing to angular momentum effects.^55,56 The translational energy distributions thus can be used to gain insight into the reaction paths and dynamics. One of the interesting features of the ethylene cation dissociation is that all of the translational energy distributions obtained for the H₂ elimination channel follow the typical statistical unimolecular decay pattern, which represents the maximum intensity close to zero kinetic energy, whereas the peaks are slightly shifted to higher kinetic energy for H elimination. Therefore, the appearances of the P(E_T) and the isotropic angular distribution suggest that, for the H₂ channel, dissociation ultimately takes place on the ground electronic state following internal conversion, consistent with Lorquet and co-workers'⁵⁰ theoretical results as shown in Fig. 4. Furthermore, based on the experimental and theoretical results, the initially excited B̃²A_g excited state is believed to undergo rapid internal conversion to the vibrationally excited electronic ground state x̃²B_3u through the C̃²B_2u or the òB_3g state. After internal conversion, the likely mechanism for H₂ elimination is that, on the ground electronic state, the system follows the reaction path connecting a bridged intermediate structure to ethylidene (CH₃CH⁺) by hydrogen transfer. This ultimately leads to the C₂H₂⁺ + H₂ dissociation by 1,1 elimination. For the H loss mechanism, after internal conversion the vibrationally excited C₂H₄⁺ on the ground electronic state couples to the òB_3g state via conical intersection C as one of C–H bonds is stretched. Finally, H elimination takes place along this nonadiabatic pathway to give rise to the ground state C₂H₃⁺. Alternatively, the B̃²A_g state can undergo internal conversion to the òB_3g state directly. For the H atom product, the peak is slightly shifted from zero, but previous studies showed no evidence of an exit channel barrier correlating with the C₂H₃⁺ + H channel along the C–H stretching coordinate.⁵⁰ As mentioned above, this peak away from zero energy is not unusual for H elimination in barrierless processes.

Branching ratios between the H and H₂ elimination channels were also measured from the direct integration of the images. Branching to the H elimination channel increases with increasing total energy, while the H₂ elimination branching is favored by pure torsional excitation (3p_z, 4²) and by its combination with a C–C stretching mode (3s, 2¹ 4³) as compared to the vibrationless excitation via the 3p_y 0⁰ and 3p_z 0⁰ levels. These results indicate that vibrational state selection of the ground electronic state of C₂H₄⁺ (X̃ ²B_3u) has a significant effect upon the detailed dissociation dynamics, likely by governing access to the coupling regions in a fashion similar to that shown above for the propanal cation.

Photodissociation of the methylamine cation and Titan's atmosphere

Titan's ionosphere is of great current interest as it plays a crucial role in the chemical and thermal balance of Titan's upper atmosphere, it establishes a link between Saturn's magnetosphere and the dense neutral atmosphere of Titan,^57–61 and it may play an important role in the formation of Titan's dense aerosol haze layers. To explore the features of the ionosphere, the Cassini space mission currently in the Saturnian system performed the first in situ measurements with the Ion and Neutral Mass Spectrometer (INMS) experiment, and found the presence of a total of 45 different ions in Titan's ionosphere.^62,63 The most abundant ion detected, with m/z = 28, was assigned as HCNH⁺. After these initial missions, several experimental and theoretical studies have been performed which demonstrate the importance of HCNH⁺ in many ion-neutral reactions, including those suspected in Titan's ionosphere. However, its formation mechanism and the details of its role in the ionospheric chemistry have not been clearly revealed.^64,65 In order to understand the pathways involved in the formation of HCNH⁺, and to investigate features of the ionic potential energy surfaces relevant to nitrogen chemistry in Titan's ionosphere, we studied photodissociation of the CH₃NH₂⁺ cation using DC sliced ion imaging methods, augmented by high-level (CBS-APNO) ab initio calculations from Zhou and Schlegel et al.³¹

Fig. 5 shows the DC sliced images and translational energy release derived from these images for the photodissociation products of CH₃NH₂⁺ at 41690 cm⁻¹. The images are similar for all channels except for the H₂ loss channel, in which the image appears to have a “hole” inside it. The hydrogen atom loss channel from CH₃NH₂⁺ has two possible pathways: (1) CH₂NH₂⁺ + H and (2) CH₃NH⁺ + H. The translational energy release for hydrogen loss has a peak around 0.4 eV and extends to 1.5 eV, which is consistent with the calculations for the CH₃NH⁺ + H channel, having a maximum available energy of 1.5 eV. The CH₂NH₂⁺ product has an available energy of 5.1 eV; however, the translational energy release is found to be between 0.1 and 1.5 eV, which likely excludes this as the observed hydrogen loss product. Rather, the agreement between experimental and theoretical results suggests CH₃NH⁺ is the product detected as the hydrogen loss channel. The other possible product, CH₂NH₂⁺, can further dissociate to HCNH⁺ by direct H₂ loss. The ab initio calculations show this pathway has a barrier of 4.03 eV, which is within the available energy of the primary CH₂NH₂⁺ product. This suggests that any CH₂NH₂⁺ formed may further dissociate to HCNH⁺ + H₂, while the higher energy CH₃NH⁺ is the H loss product detected.

Fig. 5 (A) Ion images and total translational energy distribution for (a) m/z = 30 (H loss) (b) m/z = 29 (H₂ loss) and (c) m/z = 28 (H + H₂) loss channels of CH₃NH₂⁺ dissociation at 41690 cm⁻¹. (B) Potential energy profiles for the dissociation pathways of CH₃NH₂⁺. The energy values given in bold were calculated at the CBS-APNO level of theory while those in italics were calculated at the B3LYP/6-311 g(d, p) level of theory.

Direct H₂ loss from CH₃NH₂⁺ could follow two pathways, via CH₂NH⁺ or CHNH₂⁺. However, theoretical calculations of Zhou and Schlegel show that only CH₂NH⁺ + H₂ is energetically possible. The H₂ loss image shows a dearth of low recoil energy products. The translational energy release shows a peak around 0.5 to 1.9 eV, and extends out to 3 eV. This hole in the H₂ loss image may either correspond to an energy barrier for H₂ loss from CH₃NH₂⁺ or it could be the result of secondary decomposition of the primary products, just as for the propanal cation discussed above. The only possible channel for H₂ loss from CH₃NH₂⁺ is via the formation of CH₂NH⁺, with a 3.7 eV barrier to the process. This product has a 2.8 eV available energy after the barrier, which is consistent with the translation energy release plot for H₂ loss shown in Fig. 5. This suggests that the hole in the H₂ loss image is due to the barrier for the H₂ loss from the CH₃NH₂⁺ to CH₂NH⁺. The CH₂NH⁺ product can dissociate further to HCNH⁺ + H via a barrier of 1.5 eV. This energy barrier from CH₂NH⁺ to HCNH⁺ is less than the available energy of 2.8 eV, though the available energy depends upon the partitioning of energy in the exit channel. Even if the decay does not allow the transfer of all excess energy to CH₂NH⁺, the 1.7 eV available energy in CH₂NH⁺ is enough to overcome the barrier for formation of the HCNH⁺ product. Fig. 5 also shows the translational energy for H + H₂ loss, which peaks around 0.7 eV and extends to 3.0 eV, in good agreement with the maximum available energy for the HCNH⁺ + H + H₂ product of 3.1 eV. This channel is thus associated to the HCNH⁺ product.

The branching ratio for these photofragmentation channels is estimated to be 4.2 : 1 : 2.5 (m/z = 30 : 29 : 28) from the integration of their respective images. This shows that starting with the open shell CH₃NH₂⁺ ion, at this energy, subsequent formation of the closed shell ions at m/z = 30 and 28 is favored, consistent with strategies used in modeling Titan's ionosphere.^62,65 Studies such as these can aid in the construction of these models of Titan's ionosphere, particularly in the challenging effort to couple the ion chemistry to the neutral chemistry there and in the stratosphere, and help to understand the complex chemistry underlying haze formation as well.

Conclusion and outlook

We have shown the application of high-resolution ion and electron imaging, in particular DC slice and multimass imaging, to address fundamental problems in chemical dynamics and also problems related to atmospheric and astrochemistry. These experimental results are interpreted with the aid of state-of-the-art theoretical calculations performed by our collaborators. The systems presented here are drawn from our recent investigations providing insight into a range of problems: from vibrationally-mediated photodissociation and conformationally-selective photodissociation dynamics to the ion chemistry relevant to Titan's ionosphere.

Future applications of ion and electron imaging hold great promise for further investigations of the issues raised herein. In our studies we have not yet been successful in identifying additional examples of conformationally-selective chemistry, but we note that very recently, the Ashfold group at Bristol has shown remarkably conformationally-selective photodissociation of neutral morpholine.⁶⁶ There is much we can learn from these studies about the important influence of subtle geometrical changes in controlling chemical outcomes. The chemistry of planetary atmospheres will certainly profit from additional studies such as those described here for methylamine, as the complex ion-neutral chemistry is now seen to play a central role. Indeed, we have ongoing work on ethylamine, propyne, and phenylacetylene cations underway in our laboratory. Finally, we suggest that the full potential of photoelectron imaging has not at all been tapped – it has surprisingly seen more application to anion photodetachment than to neutrals. The use of photoelectron imaging to study radicals, we believe, represents an important scientific opportunity whose time is ripe.

Acknowledgements

We are extremely grateful to our theoretical collaborators Hongli Tao and Todd Martinez on the propanal cation studies, and Jia Zhou and H. Bernhard Schlegel on the methylamine studies. This work was supported by the National Science Foundation under award numbers CHE-0715300 and CHE-0627854.

References

1. N. H. Nahler, O. P. J. Vieuxmaire, J. R. Jones, M. N. R. Ashfold, A. Eppink, A. M. Coriou and D. H. Parker, J. Phys. Chem. A, 2004, 108, 8077–8083.
2. O. P. J. Vieuxmaire, N. H. Nahler, J. R. Jones, R. N. Dixon and M. N. R. Ashfold, Mol. Phys., 2005, 103, 1677–1692.
3. O. P. J. Vieuxmaire, M. G. D. Nix, J. A. J. Fitzpatrick, M. Beckert, R. N. Dixon and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2004, 6, 543–554.
4. C. S. Chang, C. Y. Luo and K. Liu, J. Phys. Chem. A, 2005, 109, 1022–1025.
5. A. D. Webb, N. H. Nahler and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 3773–3778.
6. S. L. Anderson, Acc. Chem. Res., 1997, 30, 28–36.
7. R. J. Green, J. Qian, H. T. Kim and S. L. Anderson, J. Chem. Phys., 2000, 113, 3002–3010.
8. H. T. Kim, R. J. Green and S. L. Anderson, J. Chem. Phys., 2000, 112, 10831–10837.
9. H. T. Kim, J. B. Liu and S. L. Anderson, J. Chem. Phys., 2001, 115, 5843–5858.
10. J. B. Liu and S. L. Anderson, Int. J. Mass Spectrom., 2005, 241, 173–184.
11. J. B. Liu, B. Van Devener and S. L. Anderson, J. Chem. Phys., 2003, 119, 200–214.
12. J. B. Liu, B. Van Devener and S. L. Anderson, J. Chem. Phys., 2004, 121, 11746–11759.
13. M. L. Hause, Y. H. Yoon and F. F. Crim, J. Chem. Phys., 2006, 125, 174309–174307.
14. F. F. Crim, Annu. Rev. Phys. Chem., 1993, 44, 397–428.
15. F. F. Crim, J. Phys. Chem., 1996, 100, 12725–12734.
16. Y. Cohen, I. Bar and S. Rosenwaks, J. Chem. Phys., 1995, 102, 3612–3616.
17. R. P. Schmid, T. ArusiParpar, R. J. Li, I. Bar and S. Rosenwaks, J. Chem. Phys., 1997, 107, 385–391.
18. I. Bar and S. Rosenwaks, Int. Rev. Phys. Chem., 2001, 20, 711–749.
19. S. T. Park, S. K. Kim and M. S. Kim, Nature, 2002, 415, 306–308.
20. D. Townsend, M. P. Minitti and A. G. Suits, Rev. Sci. Instrum., 2003, 74, 2530–2539.
21. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
22. R. Mabbs, E. R. Grumbling, K. Pichugin and A. Sanov, Chem. Soc. Rev., 2009, 38, 2169–2177.
23. L. Shen, P. C. Singh, M. Kim, B. Zhang and A. G. Suits, J. Phys. Chem. A, 2009, 113, 68–74.
24. L. Shen, B. Zhang and A. G. Suits, J. Phys. Chem. A, 2010, 114, 3114–3120.
25. M. H. Kim, B. D. Leskiw, L. Shen and A. G. Suits, J. Phys. Chem. A, 2007, 111, 7472–7480.
26. M. H. Kim, B. D. Leskiw and A. G. Suits, J. Phys. Chem. A, 2005, 109, 7839–7842.
27. M. H. Kim, L. Shen and A. G. Suits, Phys. Chem. Chem. Phys., 2006, 8, 2933–2939.
28. M. H. Kim, L. Shen, H. Tao, T. J. Martinez and A. G. Suits, Science, 2007, 315, 1561–1565.
29. W. Li, S. A. Lahankar, C. S. Huang, P. S. Shternin, O. S. Vasyutinskii and A. G. Suits, Phys. Chem. Chem. Phys., 2006, 8, 2950–2957.
30. S. K. Lee, R. Silva, M. H. Kim, L. Shen and A. G. Suits, J. Phys. Chem. A, 2007, 111, 6741–6745.
31. P. C. Singh, L. Shen, J. Zhou and A. G. Suits, Astrophys. J., 2010, 710, 112.
32. B. D. Leskiw, M. H. Kim, G. E. Hall and A. G. Suits, Rev. Sci. Instrum., 2005, 76, 104101–104106.
33. W. Li, S. D. Chambreau, S. A. Lahankar and A. G. Suits, Rev. Sci. Instrum., 2005, 76, 063106–063107.
34. X. Michalet, S. Weiss and M. Jager, Chem. Rev., 2006, 106, 1785–1813.
35. W. Min, B. P. English, G. Luo, B. J. Cherayil, S. C. Kou and X. S. Xie, Acc. Chem. Res., 2005, 38, 923–931.
36. P. Bodis, M. R. Panman, B. H. Bakker, A. Mateo-Alonso, M. Prato, W. J. Buma, A. M. Brouwer, E. R. Kay, D. A. Leigh and S. Woutersen, Acc. Chem. Res., 2009, 42, 1462–1469.
37. J. Clayden, S. P. Fletcher, S. J. M. Rowbottom and M. Helliwell, Org. Lett., 2009, 11, 2313–2316.
38. B. Takacs, N. Billington, M. Gyimesi, B. Kintses, A. Malnasi-Csizmadia, P. J. Knight and M. Kovacs, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6799–6804.
39. G. Uyeda, J. C. Williams, M. Roman, T. A. Mattioli and J. P. Allen, Biochemistry, 2010, 49, 1146–1159.
40. L. Khriachtchev, M. Pettersson and M. Rasanen, J. Am. Chem. Soc., 2002, 124, 10994–10995.
41. E. Martinez-Nunez, S. A. Vazquez, I. Borges, A. B. Rocha, C. M. Estevez, J. F. Castillo and F. J. Aoiz, J. Phys. Chem. A, 2005, 109, 2836–2839.
42. G. F. Metha, M. A. Buntine, D. C. McGilvery and R. J. S. Morrison, J. Mol. Spectrosc., 1994, 165, 32–56.
43. N. C. Shand, C. L. Ning, M. R. F. SIggel, I. C. Walker and J. Pfab, J. Chem. Soc., Faraday Trans., 1997, 93, 2883–2888.
44. J. Randell, J. A. Handy and A. P. Cox, J. Chem. Soc., Faraday Trans. 2, 1988, 84, 1199–1212.
45. J. Dannacher and J.-P. Stadelmann, Int. J. Mass Spectrom., 2001, 208, 147–157.
46. C. E. Hudson, D. J. McAdoo, L. L. Griffin and J. C. Traeger, J. Am. Soc. Mass Spectrom., 2003, 14, 136–142.
47. M. Desouter-Lecomte, C. Sannen and J. C. Lorquet, J. Chem. Phys., 1983, 79, 894–904.
48. J. M. Luis, M. Torrent-Sucarrat, M. Sola, D. M. Bishop and B. Kirtman, J. Chem. Phys., 2005, 122, 184104–184113.
49. J. E. Pollard, D. J. Trevor, J. E. Reutt, Y. T. Lee and D. A. Shirley, J. Chem. Phys., 1984, 81, 5302–5309.
50. C. Sannen, G. Raseev, C. Galloy, G. Fauville and J. C. Lorquet, J. Chem. Phys., 1981, 74, 2402–2411.
51. R. Stockbauer and M. G. Inghram, J. Chem. Phys., 1975, 62, 4862–4870.
52. P. Wang, X. Xing, S. J. Baek and C. Y. Ng, J. Phys. Chem. A, 2004, 108, 10035–10038.
53. S. Willitsch, U. Hollenstein and F. Merkt, J. Chem. Phys., 2004, 120, 1761–1774.
54. B. A. Williams and T. A. Cool, J. Chem. Phys., 1991, 94, 6358–6366.
55. J. P. Cole and G. G. Balint-Kurti, J. Chem. Phys., 2003, 119, 6003–6016.
56. E. J. Feltham, R. H. Qadiri, E. E. H. Cottrill, P. A. Cook, J. P. Cole, G. G. Balint-Kurti and M. N. R. Ashfold, J. Chem. Phys., 2003, 119, 6017–6031.
57. C. Elachi, S. Wall, M. Allison, Y. Anderson, R. Boehmer, P. Callahan, P. Encrenaz, E. Flamini, G. Franceschetti, Y. Gim, G. Hamilton, S. Hensley, M. Janssen, W. Johnson, K. Kelleher, R. Kirk, R. Lopes, R. Lorenz, J. Lunine, D. Muhleman, S. Ostro, F. Paganelli, G. Picardi, F. Posa, L. Roth, R. Seu, S. Shaffer, L. Soderblom, B. Stiles, E. Stofan, S. Vetrella, R. West, C. Wood, L. Wye and H. Zebker, Science, 2005, 308, 970–974.
58. F. M. Flasar, R. K. Achterberg, B. J. Conrath, P. J. Gierasch, V. G. Kunde, C. A. Nixon, G. L. Bjoraker, D. E. Jennings, P. N. Romani, A. A. Simon-Miller, B. Bezard, A. Coustenis, P. G. J. Irwin, N. A. Teanby, J. Brasunas, J. C. Pearl, M. E. Segura, R. C. Carlson, A. Mamoutkine, P. J. Schinder, A. Barucci, R. Courtin, T. Fouchet, D. Gautier, E. Lellouch, A. Marten, R. Prange, S. Vinatier, D. F. Strobel, S. B. Calcutt, P. L. Read, F. W. Taylor, N. Bowles, R. E. Samuelson, G. S. Orton, L. J. Spilker, T. C. Owen, J. R. Spencer, M. R. Showalter, C. Ferrari, M. M. Abbas, F. Raulin, S. Edgington, P. Ade and E. H. Wishnow, Science, 2005, 308, 975–978.
59. D. E. Shemansky, A. I. F. Stewart, R. A. West, L. W. Esposito, J. T. Hallett and X. Liu, Science, 2005, 308, 978–982.
60. S. P. Synnott, C. F. Peters, B. A. Smith and L. A. Morabito, Science, 1981, 212, 191–192.
61. E. H. Wilson and S. K. Atreya, Planet. Space Sci., 2003, 51, 1017–1033.
62. J. Cui, R. V. Yelle, V. Vuitton, J. H. Waite Jr, W. T. Kasprzak, D. A. Gell, H. B. Niemann, I. C. F. Müller-Wodarg, N. Borggren, G. G. Fletcher, E. L. Patrick, E. Raaen and B. A. Magee, Icarus, 2009, 200, 581–615.
63. J. H. Waite, Jr., H. Niemann, R. V. Yelle, W. T. Kasprzak, T. E. Cravens, J. G. Luhmann, R. L. McNutt, W.-H. Ip, D. Gell, V. De La Haye, I. Muller-Wordag, B. Magee, N. Borggren, S. Ledvina, G. Fletcher, E. Walter, R. Miller, S. Scherer, R. Thorpe, J. Xu, B. Block and K. Arnett, Science, 2005, 308, 982–986.
64. V. Vuitton, J. F. Doussin, Y. Bénilan, F. Raulin and M. C. Gazeau, Icarus, 2006, 185, 287–300.
65. V. Vuitton, R. V. Yelle and M. J. McEwan, Icarus, 2007, 191, 722–742.
66. T. A. A. Oliver, G. A. King and M. N. R. Ashfold, Chem. Sci., 2010, 1, 89.

---

Footnotes

† Present address: Molecular Spectroscopy Laboratory, ASI, RIKEN, Saitama, Japan.

‡ Present address: Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, USA.

---