Less is more – multiscale modelling of self-assembling multivalency and its impact on DNA binding and gene delivery
Paola
Posocco
*a,
Sabrina
Pricl
*a,
Simon
Jones
b,
Anna
Barnard
b and
David K.
Smith
*b
aMolecular Simulations Engineering (MOSE) Laboratory, Department of Materials and Natural Resources (DMNR), University of Trieste, Piazzale Europa 1, 34127, Trieste, Italy. E-mail: POSOCCO@dicamp.units.it; SABRINA.PRICL@dicamp.units.it
bDepartment of Chemistry, University of York, Heslington, York, UK YO10 5DD. E-mail: dks3@york.ac.uk; Fax: +44 1904 432516
First published on 9th July 2010
Abstract
This edge article reports the multiscale modelling of spermine-functionalised dendrons designed to bind DNA and deliver it into cells. The modelling provides an insight into the mode of self-assembly of the dendrons, in particular aggregate charge density and shape, and hence suggests explanations for some of the unexpected experimental observations. In particular, the self-assembly model helps explain why the first generation dendron is more effective in binding DNA than the second generation analogue, even though the second generation system has a greater number of surface spermine ligands. Effective self assembly of the first generation dendron leads to a high charge density assembled structure – more effective than the larger number of ligands on the second generation dendron – i.e., less is more. The modelling also suggests an alternative shape of self-assembly for the system with two hydrophobic cholesterol units (rather than one) at the dendron focal point – this may help explain why this system shows much enhanced gene delivery in vitro.
Introduction
In recent years, multivalency has emerged as a key strategy for enhancing interactions between synthetic ligands and biological targets.1 Multivalency is of particular importance when the biological target has multiple binding sites – in such a case, after the first ligand has bound to the target, the presence of proximate additional ligating groups lowers the entropic penalty associated with subsequent binding events. It can also be considered that there is a higher effective local concentration of the ligand, which enhances the interaction between the synthetic system and the biological target. Dendritic molecules represent one of the most effective strategies for organising multivalent arrays of ligands and there have been numerous reports in which such molecules have been shown to bind polyvalent biological targets with high affinity.2 Of particular interest have been the interactions which can be established between dendritic molecules and nucleic acid targets such as DNA, RNA and siRNA.3 Polycationic amine-derived dendrimers can exhibit high-affinity binding of polyanionic nucleic acids, with multiple electrostatic interactions being established between the binding partners. Furthermore, such dendrimers can act as effective vectors for the delivery of genetic material into cells. Indeed, Superfect™ (a fractured PAMAM dendrimer) is now one of the standard commercial agents applied for in vitro gene delivery work.4 It has been well established that higher generation dendrimers bind DNA more strongly, owing to their higher positive charge, and furthermore, that they are more effective in terms of gene delivery, due to the proton sponge effect in which protonation of some of the additional amines enables the difficult step of endosomal escape after cellular uptake.5Recently, we have developed an interest in the ability of relatively small, multivalent dendrons, with spermine surface groups to bind DNA.6 Spermine is a tetraamine present in all eukaryotic cells at millimolar levels, and plays a key role in the natural processes of DNA folding.7 In previous work we demonstrated that higher generation dendrons bound DNA more strongly, due to their ability to establish a larger number of contacts with the target – i.e. multivalency in action. Furthermore, we have used a combined experimental and theoretical approach to demonstrate that for higher generation systems, the binding was independent of salt concentration, and explained this observation by developing a new paradigm in multivalency, in which some of the surface ligands ‘sacrificed’ their interactions with DNA in order to shield the remaining spermine–DNA interactions from the competitive influence of sodium cations.8
In general terms, however, the synthesis of high generation, well-defined dendrimers with the required levels of purity, is demanding, and we have therefore become interested in developing alternative approaches to enhancing multivalency, whilst limiting the synthetic input. With this goal in mind, we reasoned that rather than using covalent synthesis to put the multivalent array in place, simple dendron self-assembly processes could achieve the same goal, with the self-assembled dendrimer behaving somewhat like a higher generation covalently constructed system (Fig. 1).9 We reasoned that by combining simple dendron chemistry with self-assembly, we could achieve a cost-effective approach to tunable nano-assemblies with high-affinity for biological targets. Recently, there has been increasing interest in the development of self-assembling multivalent arrays to bind diverse biological targets such as glycoproteins,10 integrins11 and collagen.12 In general, to achieve this goal, target-specific ligands are appended with a hydrophobic chain and then inserted into liposome assemblies, with the overall assemblies being multivalent. It should also be pointed out that cationic lipids are well-known to bind and deliver DNA.13 We therefore decided to design surfactant-like dendrons capable of self-assembly into higher order aggregates. There has been considerable interest in the development of self-assembling dendrons.14 Indeed, the groups of Diederich, Florence and others have previously used this type of strategy to generate dendrons with enhanced gene delivery potential.15 We therefore decided to modify our dendrons and provide them with some inherent capacity to self-assemble. In this edge article, we use multiscale modelling to gain a unique understanding of the impacts of self-assembly on biological activity.
 | ||
| Fig. 1 Schematic figure showing self-assembling dendrons for DNA binding and gene delivery. | ||
Results and discussion
Summary of key experimental data
In 2008, we made a preliminary report of the synthesis of dendrons Chol-G1, Chol-G2 and Chol2-G1 (Fig. 2), and their application in the binding of DNA and its delivery into cells.16 These compounds bind DNA as a consequence of electrostatic interactions between protonated cationic spermine ligands and anionic polyphosphate DNA. In this edge article, we compare their experimental behaviour with that of related Z-protected compounds,6a,b and relate this to multiscale modelling data. We hoped that these modelling studies would provide us with a theoretical understanding of our dendrons, and more importantly, provide us with ground rules to enable the synthesis of new dendrons capable of more effective DNA binding and gene delivery. | ||
| Fig. 2 Compounds used for DNA binding and delivery studies: Z-G1, Z-G2, Chol-G1, Chol-G2 and Chol2G1. | ||
DNA binding ability was assessed using ethidium bromide (EthBr) exclusion assays (using calf thymus DNA) and gel electrophoresis studies (using pGL3 plasmid DNA). A summary of the key data from these assays is presented in Table 1. The N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios represent the ratio between protonatable cationic amines on the dendron and anionic phosphate groups on the DNA required to achieve 50% EthBr displacement (in the EthBr exclusion assay) or to retain the plasmid DNA in the loading well (in the gel electrophoresis assay).
P ratios represent the ratio between protonatable cationic amines on the dendron and anionic phosphate groups on the DNA required to achieve 50% EthBr displacement (in the EthBr exclusion assay) or to retain the plasmid DNA in the loading well (in the gel electrophoresis assay).
| Data from EthBr exclusion assay | Data from gel electrophoresis | Gene delivery | |
|---|---|---|---|
N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratioa P ratioa |
N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratioa P ratioa |
Max. % of PEI control | |
a The N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios represent the ratio between protonatable cationic amines on the dendron and anionic phosphate groups on the DNA required to achieve 50% EthBr displacement (in the EthBr exclusion assay) or to retain the plasmid DNA in the loading well (in the gel electrophoresis assay).
b Transfection performed in the presence of chloroquine. P ratios represent the ratio between protonatable cationic amines on the dendron and anionic phosphate groups on the DNA required to achieve 50% EthBr displacement (in the EthBr exclusion assay) or to retain the plasmid DNA in the loading well (in the gel electrophoresis assay).
b Transfection performed in the presence of chloroquine.
|
|||
| Z-G1 | 2.70 | 2.21 | <2b |
| Chol-G1 | 0.52 | 0.34 | ca. 25b |
| Chol2-G1 | 0.49 | 0.85 | 60 |
| Z-G2 | 0.76 | 1.07 | ca. 5b |
| Chol-G2 | 1.35 | 0.51 | 10 |
It is evident that when there is a simple Z-protecting group at the focal point, the N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios for DNA binding decrease on going from first to second generation dendron. This indicates that for Z-G2, a smaller amount of amine is required to condense the DNA, and that it is therefore a significantly more effective DNA binder than Z-G1 (Fig. 2). This is in agreement with the hypothesis that the surface spermine groups act as a multivalent array and collaborate in binding the DNA, with the presence of more surface ligands enhancing binding. We have previously used molecular dynamics methods to model the 1
P ratios for DNA binding decrease on going from first to second generation dendron. This indicates that for Z-G2, a smaller amount of amine is required to condense the DNA, and that it is therefore a significantly more effective DNA binder than Z-G1 (Fig. 2). This is in agreement with the hypothesis that the surface spermine groups act as a multivalent array and collaborate in binding the DNA, with the presence of more surface ligands enhancing binding. We have previously used molecular dynamics methods to model the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 interaction between the dendron and DNA double helix and hence gain a detailed understanding of the multivalency effects in this system.8 However, when a cholesterol unit is at the focal point of the dendron, surprisingly, Chol-G1 (and Chol2-G1) have significantly lower N
1 interaction between the dendron and DNA double helix and hence gain a detailed understanding of the multivalency effects in this system.8 However, when a cholesterol unit is at the focal point of the dendron, surprisingly, Chol-G1 (and Chol2-G1) have significantly lower N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios than Chol-G2. This was a surprising result, indicating that the first generation systems were much more effective DNA binders than their second generation analogues – i.e., less is more – even though the cholesterol unit cannot be directly involved in forming interactions with the DNA. It is also worth noting that whilst changing the Z group for a cholesterol unit significantly improved the DNA binding of the G1 dendrons, the same structural modification had a lesser effect on the binding ability of the G2 dendron. The nature of this binding enhancement for Chol-G1 could not be meaningfully modelled using simple molecular dynamics methods on the 1
P ratios than Chol-G2. This was a surprising result, indicating that the first generation systems were much more effective DNA binders than their second generation analogues – i.e., less is more – even though the cholesterol unit cannot be directly involved in forming interactions with the DNA. It is also worth noting that whilst changing the Z group for a cholesterol unit significantly improved the DNA binding of the G1 dendrons, the same structural modification had a lesser effect on the binding ability of the G2 dendron. The nature of this binding enhancement for Chol-G1 could not be meaningfully modelled using simple molecular dynamics methods on the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dendron
1 dendron![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA complex, because the spermine-functionalised surfaces of Z-G1 and Chol-G1 are, in their own right, identical, yet the degrees of binding are very different.
DNA complex, because the spermine-functionalised surfaces of Z-G1 and Chol-G1 are, in their own right, identical, yet the degrees of binding are very different.
Gene delivery ability of the dendrons was assessed in (e.g.) HEK293, C2C12 and MDA-MB-231 cells, and compared against branched PEI as a control.6b,16 As is evident, many of the dendrons, although effective DNA binders, were ineffective in gene delivery. Compounds Z-G1 and Z-G2 both required the addition of chloroquine, a known endosomal escape agent,17 in order for transfection to be observed. However, the cholesterol-modified derivatives were better in terms of gene delivery. Compound Chol-G1 still required the addition of chloroquine, but demonstrated quite effective gene delivery, while Chol-G2 and Chol2G1 showed very good levels of transfection even in the absence of chloroquine – notably Chol2G1 was particularly effective and furthermore, a combination of the two vectors improved transfection levels up to ca. 200% of the positive control.16
The cytotoxicity of these dendrons was assessed using a cell titre blue assay.16 All dendrons were relatively non-toxic at transfection concentrations. It was noteworthy that Chol-G1 and Chol-G2 were slightly more toxic than PEI giving 50% cell viability at 10 μg mL−1, whilst Chol2-G1 was somewhat less toxic (50% cell viability at 25 μg mL−1).
In summary, therefore, we found that the addition of a hydrophobic unit at the focal point of the dendron had a significant impact on the ability of the compound to bind and deliver DNA. In our original paper,16 we proposed that the hydrophobic units were able to self-assemble, and hence generate multivalent arrays of spermine ligands in situ, and that therefore Chol-G1 was more effective than Z-G1. However, there were a number of interesting experimental observations which we were unable to fully explain. In particular:
(i) Why are lower generation Chol-G1 compounds more effective DNA binders than their higher generation Chol-G2 analogues – even though they have fewer spermine ligands on their surfaces?
(ii) Why was Chol2G1 significantly more effective in terms of gene delivery into cells than the Chol-G1 – how does the extra cholesterol unit assist gene delivery?
We therefore hoped to probe the nature of the DNA binding and propose answers to these questions using multiscale modelling methods.
Multiscale molecular modeling of dendrons
In order to provide an insight into the DNA binding processes of these ligands, it was necessary to move beyond the simple molecular dynamics approaches employed in our previous studies, which treated these systems as isolated 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes,8 and instead employ a multiscale approach. In simplistic terms, this approach takes the dendrons and DNA simulated by molecular dynamics, parameterises them, and hence converts them into much simpler (e.g., coarse-grained) representations. It is then within the realms of computer power for many of these simplified building blocks to be refined simultaneously in a large solvent box (containing 150 mM aqueous NaCl in this case). By refining multiple dendrons together, it is possible to monitor dendron self assembly and to gain an insight into the types of aggregates which may be formed. Furthermore, by refining the dendrons in the presence of DNA, it is possible to gain an understanding of interactions between the dendron aggregates which form and DNA. The methodology is described in full detail in the methods section at the end of the paper.
1 complexes,8 and instead employ a multiscale approach. In simplistic terms, this approach takes the dendrons and DNA simulated by molecular dynamics, parameterises them, and hence converts them into much simpler (e.g., coarse-grained) representations. It is then within the realms of computer power for many of these simplified building blocks to be refined simultaneously in a large solvent box (containing 150 mM aqueous NaCl in this case). By refining multiple dendrons together, it is possible to monitor dendron self assembly and to gain an insight into the types of aggregates which may be formed. Furthermore, by refining the dendrons in the presence of DNA, it is possible to gain an understanding of interactions between the dendron aggregates which form and DNA. The methodology is described in full detail in the methods section at the end of the paper.
Initially, we modelled Chol-G1 and Chol-G2 using this approach, in the absence of DNA, in order to gain an insight into why Chol-G1 unexpectedly showed greater affinity for DNA, even though it has fewer spermine surface ligands. On refining Chol-G1 it was evident that the self-assembly of these ligands into aggregates was a favoured process. In Fig. 3a, the green beads represent the cholesterol units and the yellow beads represent the spermine dendron part. Clearly, the cholesterol units self-assemble within the water. In Fig. 3b these cholesterol aggregates are represented volumetrically as green spheres. On increasing the volume fraction (concentration) of dendron within the box (Fig. 4), the aggregates increase in number, but do not significantly change in terms of morphology or composition. Comparing the modelling of Chol-G2 gives results which appear, at first sight, similar to those obtained with Chol-G1 (Fig. 4). Spherical aggregates are formed, driven by the hydrophobicity of the (green) cholesterol units, which want to separate themselves from the aqueous phase. Analogous to Chol-G1, increasing the volume fraction of the dendron does not significantly change the proposed aggregate morphology. Stable supramolecular dendritic micelles related to these have recently been used to explore biotin–avidin binding.18
 | ||
| Fig. 3 Mesoscale modelling of Chol-G1 showing aggregation into micellar objects. (a) Yellow beads represent dendrons and green beads represent cholesterol units; (b) green spheres represent hydrophobic regions and yellow beads represent dendron units. | ||
 | ||
| Fig. 4 Mesoscale modelling of Chol-G1 and Chol-G2 with increasing volume fraction. Chol-G1 and Chol-G2 form stable micellar aggregates across all volume fractions. | ||
Following the expectations stemming from geometrical considerations, both Chol-G1 and Chol-G2 predominantly form spherical monodisperse micelles with average diameters of 3.4 and 3.8 nm, respectively. This is a net consequence of their conical shape, with a large cationic headgroup connected to a comparatively small lipophilic tail (vide infra). However, when the aggregates of Chol-G1 and Chol-G2 are considered in more detail, there is a significant difference between them. Fig. 5 represents the effective positive charge density on the surfaces of the aggregates. Clearly Chol-G1 gives rise to a more highly charged aggregate (represented in red) than Chol-G2 (represented in blue). This may seem counterintuitive, because Chol-G2 has twenty seven protonatable amine groups on the surface, whereas Chol-G1 has only nine. However, the self-assembly process is significantly more effective for Chol-G1 than the Chol-G2 analogue, and this means that Chol-G1 gives rise to a much more effectively packed aggregate with a tightly packed positively charged surface. Conversely, for the aggregates of Chol-G2, the surface charge is spread more diffusely. This argument is supported by evaluation of the surface charge densities σm for both micellar systems. In the case of Chol-G1, the estimated aggregation number Nagg = 21 leads to a σm value of 5.3 e nm−2, whilst for Chol-G2Nagg = 7 and, hence, σm = 4.2. In this way, we propose that self-assembly controls the surface charge of the aggregate, and hence the relative affinities of these systems for DNA. In this sense, less is more, and the smaller dendron is actually better able to bind DNA once the multivalency becomes expressed on the nanoscale through dendron self-assembly
 | ||
| Fig. 5 Mesoscale modelling of Chol-G1 and Chol-G2 representing surface positive charge of the aggregates. Chol-G1 forms aggregates with a significantly higher charge density. | ||
We then performed modelling studies on Chol2-G1, which is actually the most effective dendron for the purposes of cellular gene delivery. In Fig. 6, the cholesterol units are represented in green and the dendron units in purple. At low volume fractions, this dendron once again formed roughly spherical or short elongated micellar aggregates. However, on increasing the volume fraction, the mode of assembly changed dramatically, to give a cylindrical micellar hexagonal phase morphology, in which the hydrophobic cholesterol tails are located inside the cylinders with the hydrophilic dendritic heads being on the surface. Neither Chol-G1 or Chol-G2 exhibited this type of behaviour, with spherical micelles (supramolecular dendrimers) being the dominant and stable aggregate form. We propose that the combined action of a greater degree of hydrophobicity of Chol2-G1 and of a reduced like-charge repulsion in the dendritic cationic headgroup exerted by the ionic strength encourages this phase change in the nature of the aggregate. Notably, with respect to lipid-based molecules used as nanovectors, members of this Chol-based dendron series have a hydrophobic tail the characteristics of which are (i) a high number of carbon atoms (28 for 1 Chol-moiety vs. 10–14 for, e.g., aliphatic fatty alcohols), (ii) higher steric hindrance, and (iii) higher rigidity of the hydrophobic part, as the four condensed rings constitute a fairly stiff skeleton.
 | ||
| Fig. 6 Mesoscale modelling of Chol2-G1 with increasing volume fraction. The self-assembled morphology evolves from a roughly spherical micellar form to hexagonally packed cylindrical micelles. | ||
Israelachvili's rules can be used to predict micellar phases based on molecular-level structural aspects of lipids.19 As the geometry and the degree of order of the eventual aggregate architectures are determined by the enforced curvature in the assembly from the relative sizes of the polar and apolar domains of the amphiphiles, the dimensionless packing parameter P, originally developed for small amphiphiles in water,19 can be generalized and used to define the relative size of the hydrophobic region of the Chol-modified dendrons. Accordingly, the balance between the solvent-phobic and solvent-philic interactions gives rise to an optimal surface area of the solvent-phobic block at the interface between the polar and apolar parts of the molecule (α0). This, together with the length lc and the volume of the insoluble domain νh, contributes to the packing parameter defined as  . As a general guideline, spherical micelles are formed when P ≤ 1/3; cylindrical micelles are formed at 1/3 < P ≤ 1/2; if 1/2 < P < 1, bilayers with a spontaneous curvature (vesicles) are produced; for P = 1, planar bilayers will be formed; and, lastly, if P > 1, micellar aggregates with a reverse curvature will be generated.
. As a general guideline, spherical micelles are formed when P ≤ 1/3; cylindrical micelles are formed at 1/3 < P ≤ 1/2; if 1/2 < P < 1, bilayers with a spontaneous curvature (vesicles) are produced; for P = 1, planar bilayers will be formed; and, lastly, if P > 1, micellar aggregates with a reverse curvature will be generated.
Simple molecular modeling considerations allowed us to calculate the packing parameter for all Chol-based dendrons in hydrated conditions: the volume νh (391 Å3), and the length lc (16.4 Å) of the hydrophobic tail are close to the data reported in the literature.20 The estimated values of the surface areas at the interface α0 are 96 Å2 for Chol-G1 and Chol2-G1, and 194 Å2 for Chol-G2. By using these values, packing parameters P of 0.24 and 0.12 could be calculated for Chol-G1 and Chol-G2, respectively, thus predicting spherical aggregate formation. For Chol2-G1, however, the estimated value of P = 0.47 theoretically supports the formation of cylindrical micelles for this molecular series. Cylindrical dendritic micellar assemblies have been widely explored by Percec and co-workers.14d
As the concentration of the solution is increased, Chol-dendron–solvent interactions become more significant. In order to minimize the free energy, the local packing of the aggregate may change, leading to a decrease in the curvature of the local assembly. In other terms, derivatized-dendrons, which at low concentration form spherical aggregates, assemble into cylindrical and eventually membrane-like aggregates as the concentration increases. Hence, again as a general rule, on moving from low to high concentrations, spherical micelles pack into cubic phases, followed by hexagonally packed cylinders and, finally, lamellae. This is the case for Chol2-G1, for which the balance between hydrophobic and hydrophilic is such that, in order to avoid contact between the solvent and the cholesterol moiety, a higher level of molecular frustration, and hence a higher curvature is attained on increasing dendron concentration.
These morphological proposals also provide a rationale for the results of the EthBr exclusion assay shown in Table 1. In the case of the assembled systems characterized by smaller micelles (i.e., Chol-G1 and Chol-G2), the overall DNA surface will be less covered (patch-like coverage) which allows for better residual binding of small molecules like EthBr. Therefore, in order to “fill the gaps”, higher concentrations of dendrons are necessary to attain the same result displayed by the cylindrical micelles formed by Chol2-G1. However, Chol-G1 has a significantly higher surface charge density than Chol2-G1 (for which Nagg = 34 and σm = 1.7 e nm−2) and this effect partly compensates for the ‘patchy’ DNA coverage of Chol-G1, making it comparable as a DNA binder to its more hydrophobic counterpart, Chol2-G1.
Importantly, it has previously been demonstrated for cationic lipid gene delivery agents that the mode of aggregation plays a key role during endosomal escape, with hexagonal phases being known to destabilise endosomal membranes most effectively.21 We therefore propose that the multiscale modelling of the Chol2-G1 may offer an explanation as to why this dendron shows the most effective gene delivery and lower cytotoxicity (vide infra).
Multiscale molecular modeling of dendron–DNA assemblies
We then modelled dendron assembly in the presence of DNA. Fig. 7 shows the way in which an aggregate can interact with the DNA through electrostatic interactions, with the anionic (red) DNA inserting into the cationic spermine shell of the dendron aggregate (green). In general terms, the presence of DNA did not significantly modify the self-assembly of the dendrons and all three dendrons retained their distinctive modes of self-assembly in the presence of DNA (Fig. 8). There is a tendency for the DNA (red) to wrap itself around the dendron aggregates (green), but with different mechanisms and, hence, different overall structures. As highlighted in Fig. 7, in the case of the spherical micellar systems, the DNA molecules are loosely packed without a well-defined inter-helical pattern or distances. The micelles appear to undergo a small degree of deformation in the complexes, with a tendency to elongate along the DNA longitudinal direction presumably to enhance the adhesion with the rather planar, extended surface of DNA. In these cases, the DNA molecules seem to comply with the well-known “bead-on-a-string” model,22 according to which some regions of the nucleic acid are engulfed by the micelles (see yellow circle in Fig. 7) whilst some others are no longer surrounded by them. Thus, the DNA helices are partially embedded within the micellar organization and partially exposed to the solution environment, where Na+ ions originating from the electrolyte provide the charge neutralization required for eventual condensation. | ||
| Fig. 7 Mesoscale modelling of the interaction between DNA (red) and the aggregates of Chol-G1 (green) – direct contact is highlighted by the yellow circle. | ||
 | ||
| Fig. 8 Mesoscale modelling of the interaction between DNA (red) and the aggregates of (a) Chol-G1, (b) Chol-G2 and (c) Chol2-G1. | ||
To a first approximation, the average number of DNA base pairs covered by the Chol-G1 and Chol-G2 micelles of Fig. 8a,b can be estimated by the simple relationship:
 | (1) |
Dendron Chol2-G1 can form cylindrical dendritic micelles; the DNA chains inserted into the regular interspace of the cylinders. We note that such a system would be expected to (i) bind and compact DNA efficiently, (ii) protect DNA from degradation, (iii) achieve efficient DNA release.21 It is generally known that the DNA double helix behaves as a semi-flexible coil; thus, the cylindrical shape of the micelles formed by Chol2-G1 is better able to comply with the wrapping pattern of the semi-rigid DNA helix than the small spherical micelles generated by the other dendrons. As can be easily understood from Fig. 8, this mesoscopic organization of Chol2-G1 with DNA results in more efficient and well-organized DNA compaction and, hence, potential protection from degradation during DNA delivery.
Applying eqn (1) to this system yields a value of nbp = 44.7. In line with the underlying discussion, the cylindrical shape of the resulting Chol2-G1 dendron aggregates, although having overall lower surface charge density (σm = 1.7 e nm−2), can not only exploit the surface charge distribution more efficiently by following the seemingly cylindrical shape of the semi-rigid DNA duplex, but can also complex a considerably larger number of DNA bases per aggregate with respect to its less hydrophobic counterparts.
It is also not difficult to infer from the mesoscale simulation images, that the spherical micellar systems actually contain more water space than the cylindrical ones. Again at first approximation, given the average center-to-center distance of the cylinders dcyl/cyl = 5.9 nm, and some simple geometrical considerations, the volume fraction of water ϕcylw in the hexagonal lattice formed by Chol2-G1 can be calculated as 0.42. Although the same approach cannot be applied to the alternative micellar systems due to the absence of a long-range regular structure, the comparison of the density maps of water for the Chol2-G1/- and Chol-G2/DNA systems support this concept (Fig. 9). The higher water content in the Chol-G2 spherical micellar system may imply that a significant fraction of dendron and DNA charges are wasted in terms of mutual interactions. This is in line with the illustrations in Fig. 7 and 8, as a notable fraction of the periphery of the spherical dendron micelles fail to contact DNA and vice versa.
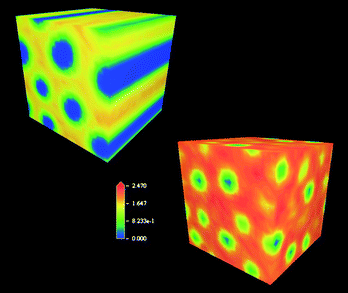 | ||
| Fig. 9 Three-dimensional density distribution of water molecules in the Chol2-G1/- (top, left) and Chol-G2/DNA (bottom, right) complexes. The higher level of intermicellar hydration is apparent in the Chol-G2-based system. | ||
Very importantly, the coupling of simulation/experimental evidence concurs to show that these Chol2-G1/DNA complexes, capable of forming a cylindrical phase, efficiently transfect cells. It is tempting to speculate that the existence of a regular and continuous DNA sub-organisation may facilitate the release of the DNA cargo, as in principle, all DNA is accessible once a part of it is exposed to the inside of the cell. This is in contrast to both the spherical micellar systems, where DNA in less efficiently wrapped and, hence, less protected and organised, and the widely employed lipid-based lamellae-forming nanovectors, in which the enveloping lipid bilayers have to be removed layer-by-layer to release all of the encapsulated DNA.
The main findings from the present work allow us to speculate on the possible structure–activity relationship according to the following line of thought. Endocytosis is the dominant mechanism of cellular entry by dendron-based nanocarriers.3 After cellular uptake, the nanovectors and their cargoes must escape from endosomes, in order for DNA to progress towards the cell nucleus and avoid the rather rapid degradation of the endosome content. Endosomal escape is usually initiated by destabilisation of the endosome membrane that results in flip-flop of the anionic lipids predominantly located on the cytoplasmic face of the membrane.13 These anionic lipids can then laterally diffuse into the complex and form charge-neutralised ion pairs with the cationic part of the nanocarriers. This displaces the cargo DNA from the complex and generates a mechanical and osmotic stress that further contributes to the rupture of the endosomal bilayer and release of DNA into the cytoplasm. The importance of endosomal escape as a barrier to transfection can be assessed by performing transfection experiments in the presence of chloroquine.17 Several experiments performed with cationic lipids as DNA carriers supported the idea that nanovector/DNA complexes with lower surface charge densities σm may remain trapped within the endosome,15d as they are not able to induce either flip-flop of the membrane lipids or osmotic pressure increase for membrane bursting. At the same time, however, σm is not the only transfection modulating physicochemical parameter – inherent biomembrane fusogenicity and complex rigidity play major roles in transfection efficiency.
With these ideas in mind, we can postulate that, in the case of Chol-G1, for which an enhancement of the transfection efficiency was achieved only in the presence of chloroquine, the high charge density which will favor endosomal escape is counteracted by the more compact packing of the amphiphiles in the spherical micellar aggregates (Nagg = 21). This, in turn, imparts an overall higher rigidity to the corresponding nanovectors which are thus less likely to fuse efficaciously with both the cellular and endosomal membranes. In the case of Chol-G2, the larger cationic headgroup and consequent higher Coulombic repulsion among like-charges leads to the formation of micelles with a smaller aggregation number (Nagg = 7) and a smaller surface charge than Chol-G1. This results in a lower DNA affinity but, at the same time, in a less tightly packed and hence more flexible micelle with respect to its lower generation counterpart. Therefore, the enhanced transfection efficiency of Chol-G2 over Chol-G1 (see Table 1) could be ascribed to a better capacity of this nanovector to fuse with the anionic lipid components of the endosomal membrane and to partially effective complex dissociation in the endosome/cytoplasm due to the lower DNA–micelle attractive interactions. Lastly, in the case of the most effective vector Chol2-G1, we propose that the coupling of a different mesoscopic assembly, aggregate dimensions, surface charge value and, last but not least, DNA encasing and wrapping patterns probably represents the best compromise between binding and transfection efficiency.21 The result obtained through the use of a relatively small and rigid amphiphile of unusual shape (a large hydrophobic portion coupled with a very large hydrophilic head) is a cylindrical nanostructure showing an enhancement of binding for the target DNA and improved transfection efficiency. This enhancement may be attributed to three effects: (1) the reduced competition of water molecules for the binding of DNA within the partially desolvated interface, (2) the presence of a flexible linker moiety which endows the resulting cylindrical micelle with the proper degree of flexibility for effective fusion with the cellular/endosomal membrane, and (3) the enhanced multivalency effect derived from the presence of multiple DNA anchoring points in close proximity and structurally well matched to the DNA.
We propose that these factors, as observed from the modelling, help explain the more effective gene delivery observed with this vector.
Further experimental studies of aggregation
In order to gain some insight into whether the results from multiscale modeling were realistic, we performed further experimental studies of the dendron![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA complexes.
DNA complexes.
Initially, the ability of Chol-G1 to self-assemble in the absence of DNA was tested using a Nile red solubilisation fluorescence assay, in which hydrophobic Nile red dye is used to report on the formation of a hydrophobic domain within an assembled nanostructure.23 Nile red is only solubilised when the dendron itself self-assembles into a nanostructure with a hydrophobic domain. Fig. 10 demonstrates that self-assembling behaviour was observed for Chol-G1, with a discontinuity in the fluorescence intensity of Nile red, plotted against increasing dendron concentration, occurring at the critical aggregation concentration (CAC), above which assembly occurs. Using this approach, the CAC could be quantified as 15 μM. This demonstrates that these dendrons are capable of self-assembly processes.
 | ||
| Fig. 10 Fluorescence intensity data from Nile red solubilisation assay to determine the critical aggregation concentration (CAC) of Chol-G1. | ||
We used dynamic light scattering (DLS) methods to monitor the aggregation of all five dendrons in the presence of pGL3 plasmid DNA. The dimensions of the uncomplexed plasmid DNA were 66 nm. As is clear from Fig. 11, there are significant differences between the dendrons in terms of their ability to aggregate with plasmid DNA. In the presence of plasmid DNA, all of the dendrons modified with cholesterol units gave rise to larger aggregates than the previously investigated Z-G1 and Z-G2.6b Dendrons Chol-G1 and Chol-G2 both formed assemblies which increased in size as the loading of dendron went up (and the N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio consequently increased). Interestingly, Chol-G1 formed significantly larger aggregates with DNA than Chol-G2, even though it is a smaller dendron. This is the reverse of what was observed for Z-G1 and Z-G2 where the latter compound gave rise to larger aggregates with plasmid DNA on account of its multivalency. These observations may be indicative of the greater surface charge of the self-assembled Chol-G1 supramolecular dendrimers compared with those of Chol-G2, as was proposed from the multiscale modeling – hence leading to more effective DNA binding and the formation of larger combined aggregates. This is in agreement with simple self-assembly arguments, in that the small but highly charged aggregates formed from Chol-G1, encourage the formation of larger overall aggregate structures, whereas the less highly charged Chol-G2 assemblies give rise to less aggregation of the plasmid DNA. As the loadings of both dendrons increase, and with it the overall positive charge, the observed diameter, and hence degree of dendron aggregation also increase. Intriguingly, the interaction of Chol2-G1 with DNA as monitored by DLS was relatively independent of N
P ratio consequently increased). Interestingly, Chol-G1 formed significantly larger aggregates with DNA than Chol-G2, even though it is a smaller dendron. This is the reverse of what was observed for Z-G1 and Z-G2 where the latter compound gave rise to larger aggregates with plasmid DNA on account of its multivalency. These observations may be indicative of the greater surface charge of the self-assembled Chol-G1 supramolecular dendrimers compared with those of Chol-G2, as was proposed from the multiscale modeling – hence leading to more effective DNA binding and the formation of larger combined aggregates. This is in agreement with simple self-assembly arguments, in that the small but highly charged aggregates formed from Chol-G1, encourage the formation of larger overall aggregate structures, whereas the less highly charged Chol-G2 assemblies give rise to less aggregation of the plasmid DNA. As the loadings of both dendrons increase, and with it the overall positive charge, the observed diameter, and hence degree of dendron aggregation also increase. Intriguingly, the interaction of Chol2-G1 with DNA as monitored by DLS was relatively independent of N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio, and was markedly different in nature to the aggregation of either Chol-G1 or Chol-G2, giving aggregates with an apparently smaller diameter. However, the aggregates were still significantly larger than those observed for Z-G1. This would be in agreement with the results of multiscale modeling in which Chol2-G1 was observed to assemble into a different nanoscale morphology, with much more effective packing of the DNA, as a consequence of the greater degree of hydrophobicity at the dendron focal point. These light scattering studies are, therefore, in qualitative agreement with the multiscale modelling study.
P ratio, and was markedly different in nature to the aggregation of either Chol-G1 or Chol-G2, giving aggregates with an apparently smaller diameter. However, the aggregates were still significantly larger than those observed for Z-G1. This would be in agreement with the results of multiscale modeling in which Chol2-G1 was observed to assemble into a different nanoscale morphology, with much more effective packing of the DNA, as a consequence of the greater degree of hydrophobicity at the dendron focal point. These light scattering studies are, therefore, in qualitative agreement with the multiscale modelling study.
 | ||
Fig. 11 Dynamic light scattering results indicating the polyamine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA N DNA N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio and the approximate dimensions (nm) of the aggregate formed in each case, assuming spherical aggregation. In the absence of polyamine, light scattering of the pGL3 plasmid DNA indicated a diameter of 66 nm. P ratio and the approximate dimensions (nm) of the aggregate formed in each case, assuming spherical aggregation. In the absence of polyamine, light scattering of the pGL3 plasmid DNA indicated a diameter of 66 nm. | ||
Conclusions
In conclusion, multiscale modelling is demonstrated to be a very powerful approach, providing further insight into the behaviour of self-assembling dendrons and their multivalent interaction with biological targets. In particular, we have demonstrated that in terms of multivalency, less really can be more, with the smaller Chol-G1 dendron assembling more effectively than Chol-G2 to yield an aggregate with higher charge density which binds DNA more effectively – a hypothesis supported by new experimental observations. Furthermore, modelling predicts that the Chol2-G1 dendron, which shows the most effective gene delivery, has a significantly different phase behaviour/morphology in terms of its self-assembly – in agreement with new dynamic light scattering results. This demonstrates how modelling can provide an insight into experimental structure–activity relationships which can otherwise be difficult to interpret. These results demonstrate how the careful structural optimisation of self-assembling dendrons is of great importance in designing biologically active systems. We note that the synthesis of Chol2-G1, the most effective vector, is somewhat onerous,16 and we therefore hope that the future application of this type of multiscale modelling will now enable us to design modified self-assembling dendrons which exhibit similar proposed aggregation phase behaviour but are synthetically simpler and more accessible. In this way, we suggest that future experimental work in this field will be increasingly informed by the results of predictive multiscale molecular modelling in order to yield biological constructs with enhanced activity.Experimental and computational methods
Experimental methods
The synthesis of compounds Z-G1 and Z-G2 was described in ref. 6a and the synthesis of Chol-G1, Chol-G2 and Chol2-G1 was described in ref. 16.Ethidium bromide (EthBr) exclusion assays were performed in PIPES buffer at pH 7.4, in the presence of 150 mM NaCl. The concentration of calf thymus DNA (per nucleotide) was 2.0 μM, and the concentration of EthBr was 2.54 μM. The concentration of ligand required to displace 50% of the EthBr was determined by fluorescence spectroscopy. Full details can be found in ref. 6a, 16.
Gel electrophoresis assays were performed with pGL3 plasmid DNA and increasing amounts of dendron. Full details can be found in ref. 6b, 16.
Nile red solubilisation fluorescence assays were performed in aqueous solution with increasing concentrations of dendron, and excitation at 550 nm. Nile red emission was monitored at 635 nm.
Dynamic light scattering studies were performed in PBS buffer using dendrons and pGL3 plasmid DNA. The solutions were vortexed and then left to stand for 10 min before the sizes were measured on a Brookhaven instruments corporation 90Plus particle size analyzer at 25 °C, at 1 min per run and 5 runs per sample.
Gene delivery studies were performed using a variety of cell lines, including HeLa, HEK293, C2C12 and MDA-MB-231 cells using a luciferase assay with pGL3. Data quoted in Table 1 are the maximal observed transfection levels at any N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P loading of the dendron. Once again, full details of degrees of transfection and cell lines at different loadings can be found in the original experimental literature – ref. 6b and 16.
P loading of the dendron. Once again, full details of degrees of transfection and cell lines at different loadings can be found in the original experimental literature – ref. 6b and 16.
Computational methods
Similar to MD, in a DPD run, the time evolution of each DPD particle can be calculated by solving Newton's second law:
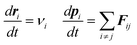 | (2) |
 , rij = ri − rj, rij = |ri − rj|, and νij = (vi − vj). wC, wD, and wR are the conservative, dissipative, and random r dependent weight functions. The θij term is a Gaussian white noise function with symmetry properties (i.e., θij = θji).
, rij = ri − rj, rij = |ri − rj|, and νij = (vi − vj). wC, wD, and wR are the conservative, dissipative, and random r dependent weight functions. The θij term is a Gaussian white noise function with symmetry properties (i.e., θij = θji).
All of the above forces are acting within a sphere of interaction or cut-off radiusrc, which is the length scale parameter of the system. γ and σ are the coefficients of the dissipative and random forces, respectively. In analogy with the fluctuation-dissipation theorem, Español and Warren26 obtained the detailed balanced condition for the DPD as:
 | (3) |
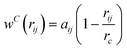 in which rij ≤ rc and zero otherwise, and
in which rij ≤ rc and zero otherwise, and 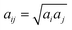 is the repulsion parameter.
is the repulsion parameter.
This fundamental DPD parameter aij can be determined as a function of the DPD number density ρ and system temperature by matching the compressibility condition:27,28
 | (4) |
The dissipative and random weight functions take the general form:29
 | (5) |
 , where ζij is an independent increment in a stochastic process, which is represented by a uniform distribution of random numbers the mean of which is zero with unit variance, and generated independently for different pairs of particles at each simulation time step.
, where ζij is an independent increment in a stochastic process, which is represented by a uniform distribution of random numbers the mean of which is zero with unit variance, and generated independently for different pairs of particles at each simulation time step.
In this edge article, we used standard DPD particles to represent the chain beads, and the DNA molecule was modeled as a string of DPD particles which are sequentially connected through the WLC spring with the pairwise interaction force given by:
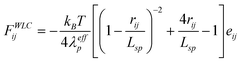 | (6) |
However, the DPD particles can pass through each other without restriction. In order to enforce self-avoidance of the chain, we therefore applied the Lennard-Jones potential ULJ between beads as in Symeonidis et al.31 It is noted that the Lennard-Jones potential applied here is defined at a mesoscopic level and not at the microscopic level as in molecular dynamics. When the beads get close, the repulsion force derived from the Lennard-Jones potential will dominate and push them apart. The repulsion force is calculated as follows:
 | (7) |
Moreover, in order to correctly derive the electrostatic interactions between charged beads (i.e. present in dendron and DNA molecules), the electrostatic force FEij between charged beads i and j was analyzed following the approach reported in Groot's work.32 According to this study, the electrostatic field is solved by smearing the charges over a lattice grid, the size of which is determined by a balance between the fast implementation and the correct representation of the electrostatic field.
Concerning the modeling of the mesoscale architecture, we modeled the dendron molecules at a coarse-grained level using a branched and flexible amphiphilic chain made up of three bead types: a neutral bead type, Ch, as a cholesterol building block, a positively charged bead type Sp, as spermine repeating unit, and a neutral bead type L, linking the two parts together (when present). According to the chemical structures reported in Fig. 2, and satisfying the theoretical criteria for which each bead type should be of similar volume, the coarse-grained models of each dendritic system were obtained, as shown in Fig. 12. Solvent molecules were simulated by single bead types W, and an appropriate number of counterions of a charge of ±1 were added to preserve charge neutrality and to account for the experimental solution ionic strength. The inclusion of explicit counterions was necessary because counterion condensation and the interactions between the counterions and the charged groups may affect the complex structure to a certain extent. Each DNA chain was represented as a series of 500 negatively charged particles D linked linearly through springs.
 | ||
| Fig. 12 Schematic representation of the DPD models of the Chol-modified dendrons considered in this work. The colours of the beads stand for hydrophilic spermine beads Sp (yellow), hydrophobic cholesterol bead Ch (green), and linker bead L (purple). | ||
Having set the reference volume of one bead and the density of the system to a value of ρ = 3, then the cut-off radius rc, which sets the length scale of the system, corresponds approximately to 0.76 nm. All simulations were performed in a 3D-periodic cubic box of 20 × 20 × 20 r3c, equivalent to a bulk system of 3510 nm3. The appropriate number of dendrons and DNA molecules were added to the simulation box in order to fit experimental concentrations.
A characteristic time scale was then defined as 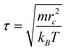 . Accordingly, the physical time scale unit in the present simulations was τ ≈ 0.009 ns. Since 5 × 106 time steps were performed in each DPD run, the total physical time of each calculation was about 2.3 μs.
. Accordingly, the physical time scale unit in the present simulations was τ ≈ 0.009 ns. Since 5 × 106 time steps were performed in each DPD run, the total physical time of each calculation was about 2.3 μs.
The intra- and intermolecular interactions between DPD particles are expressed by the conservative parameter aij, defined by eqn (4). This quantity accounts for the underlying chemistry of the system considered. In this work, we employed a well-validated strategy that correlates the interaction energies estimated from atomistic molecular dynamics (MD) simulations to the mesoscale aij parameter values.33 Following this computational recipe, for each dendron type a 30 base-pair double-stranded DNA with a randomly generated sequence was generated with the Nucgen module of AMBER 9.34 The molecular models of the three dendron structures (Chol-G1, Chol2-G1, and Chol-G2) were then built and geometry optimized using the Antichamber module of AMBER 9 and the GAFF force field.35
The corresponding bimolecular complexes were generated by placing the dendron molecule close to the DNA major groove, solvating the resultant assembly with a box of TIP3P water molecules36 extending at least 10 Å from the solute in each direction. The appropriate number of counterions (Na+ and Cl−) were added to neutralize the system and to generate the 0.15 M ionic strength. Each system was then relaxed and equilibrated by MD in the microcanonical ensemble (constant volume–constant temperature, or NVT) for 200 ps at 300 K, using the Pmemd module of AMBER 9. Equilibrium density was then reached by performing 5 ns isobaric–isothermal (NPT) MD simulations. These were followed by 10 ns production runs under NVT conditions (T = 300 K), using an integration time step for the equations of motion of 2 fs, the Langevin thermostat, a cut-off for long-range interaction of 12 Å, and the Particle Mesh Ewald technique37 to treat the system electrostatics.
The interaction energies between the system's molecular constituents were estimated using the Molecular Mechanics/Poisson–Boltzmann Surface Area (MM/PBSA) methodology,38 and then rescaled onto the corresponding mesoscale segments adapting the procedure described in detail in ref. 30. The bead–bead interaction parameter for water was set equal to aww = 25, in agreement with the correct value of DPD density ρ = 3 (see eqn (4)).24 The maximum level of hydrophobic/hydrophilic repulsion was captured by setting the interaction parameter aij between the positively charged spermine bead Sp and the lipophilic cholesterol bead Ch as 80. The counterions were set to have the interaction parameters of water.29 Once these parameters were assigned, all the remaining bead–bead interaction parameters for the DPD simulations were easily obtained, starting from the atomistic interaction energy values, as described in the previous work.30 The entire set of DPD interaction parameters employed in this work are summarized in Table 2.
| a ij | Sp | Ch | L | D | W |
|---|---|---|---|---|---|
| Sp | 45 | 80 | 30 | 10 | 15 |
| Ch | 80 | 25 | 40 | 80 | 80 |
| L | 30 | 40 | 25 | 30 | 35 |
| D | 10 | 80 | 30 | 45 | 15 |
| W | 15 | 80 | 35 | 15 | 25 |
Acknowledgements
We thank Nathan P. Gabrielson and Prof. Daniel W. Pack for assistance with the gene transfection studies, which were carried out in the Department of Chemical Engineering at University of Illinois at Urbana-Champaign. D.K.S. also acknowledges the EPSRC (C534395/1) in funding this research. D.K.S. and S.P. acknowledge the support of COST action TD0802, ‘Dendrimers in Biomedical Applications’, in enabling this collaborative program of research.Notes and references
- (a) M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef; (b) L. L. Kiessling, J. E. Gestwicki and L. E. Strong, Curr. Opin. Chem. Biol., 2000, 4, 696–703 CrossRef CAS; (c) A. Mulder, J. Huskens and D. N. Reinhoudt, Org. Biomol. Chem., 2004, 2, 3409–3424 RSC; (d) J. D. Badjic, A. Nelson, S. J. Cantrill, W. B. Turnbull and J. F. Stoddart, Acc. Chem. Res., 2005, 38, 723–732 CrossRef CAS; (e) J. Huskens, Curr. Opin. Chem. Biol., 2006, 10, 537–543 CrossRef CAS; (f) D. J. Diestler and E. W. Knapp, J. Phys. Chem. C, 2010, 114, 5287–5304 CrossRef CAS.
- (a) F. Vögtle, G. Richardt, N. Werner and A. J. Rackstraw, Dendrimer Chemistry – Concepts, Syntheses, Properties, Applications, Wiley-VCH, Weinheim, 2009 Search PubMed; (b) G. R. Newkome and C. N. Moorefield, Handbook of Dendrimers: Synthesis, Nanoscience and Applications, Wiley-VCH, Weinheim, 2009 Search PubMed; (c) D. A. Tomalia, Prog. Polym. Sci., 2005, 30, 294–324 CrossRef CAS; (d) U. Boas, J. B. Christensen and P. M. H. Heegaard, Dendrimers in Medicine and Biotechnology, Royal Society of Chemistry, Cambridge, 2006 Search PubMed; (e) B. Klajnert and M. Bryszewska, Dendrimers in Medicine, Nova Science, UK, 2007 Search PubMed; (f) I. J. Majoros and J. R. Baker, Dendrimer-Based Nanomedicine, Pan Stanford Publishing, Singapore, 2008 Search PubMed; (g) N. Joshi and M. Grinstaff, Curr. Top. Med. Chem., 2008, 8, 1225–1236 CrossRef CAS; (h) Y. M. Chabre and R. Roy, Curr. Top. Med. Chem., 2008, 8, 1237–1285 CrossRef CAS; (i) W.-D. Jang, K. M. K. Selim, C.-H. Lee and I.-K. Kang, Prog. Polym. Sci., 2009, 34, 1–23 CrossRef CAS; (j) P. M. H. Heegaard, U. Boas and N. S. Sorensen, Bioconjugate Chem., 2010, 21, 405–418 CrossRef CAS.
- (a) C. Dufes, I. F. Uchegbu and A. G. Schatzlein, Adv. Drug Delivery Rev., 2005, 57, 2177–2202 CrossRef CAS; (b) M. Guillot-Nieckowski, S. Eisler and F. Diederich, New J. Chem., 2007, 31, 1111–1127 RSC; (c) H. S. Parekh, Curr. Pharm. Des., 2007, 13, 2837–2850 CrossRef CAS; (d) D. K. Smith, Curr. Top. Med. Chem., 2008, 8, 1187–1203 CrossRef; (e) A.-M. Caminade, C. O. Turrin and J.-P. Majoral, Chem.–Eur. J., 2008, 14, 7422–7432 CrossRef CAS.
- (a) J. Haensler and F. C. Szoka, Bioconjugate Chem., 1993, 4, 372–379 CrossRef CAS; (b) J. F. Kukowska-Latallo, A. U. Bielinska, J. Johnson, R. Spindler, D. A. Tomalia and J. R. Baker, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 4897–4902 CrossRef CAS; (c) A. Bielinska, J. F. Kukowska-Latallo, J. Johnson, D. A. Tomalia and J. R. Baker, Nucleic Acids Res., 1996, 24, 2176–2182 CrossRef CAS; (d) M. X. Tang, C. T. Redemann and F. C. Szoka, Bioconjugate Chem., 1996, 7, 703–714 CrossRef CAS.
- N. D. Sonawane, F. C. Szoka and A. S. Verkman, J. Biol. Chem., 2003, 278, 44826–44831 CrossRef CAS.
- (a) M. A. Kostiainen, J. G. Hardy and D. K. Smith, Angew. Chem., Int. Ed., 2005, 44, 2556–2559 CrossRef CAS; (b) J. G. Hardy, M. A. Kostiainen, D. K. Smith, N. P. Gabrielson and D. W. Pack, Bioconjugate Chem., 2006, 17, 172–178 CrossRef CAS; (c) J. G. Hardy, C. S. Love, N. P. Gabrielson, D. W. Pack and D. K. Smith, Org. Biomol. Chem., 2009, 7, 789–793 RSC; (d) M. A. Kostiainen, D. K. Smith and O. Ikkala, Angew. Chem., Int. Ed., 2007, 46, 7600–7604 CrossRef; (e) D. J. Welsh, S. P. Jones and D. K. Smith, Angew. Chem., Int. Ed., 2009, 48, 4047–4051 CrossRef CAS; (f) M. A. Kostiainen and H. Rosilo, Chem.–Eur. J., 2009, 15, 5656–5660 CrossRef CAS; (g) M. A. Kostiainen, G. R. Szilvay, D. K. Smith, M. B. Linder and O. Ikkala, Angew. Chem., Int. Ed., 2006, 45, 3538–3542 CrossRef CAS; (h) M. A. Kostiainen, G. R. Szilvay, J. Lehtinen, D. K. Smith, M. B. Linder, A. Urtti and O. Ikkala, ACS Nano, 2007, 1, 103–113 CrossRef CAS.
- (a) D. Bancroft, I. D. Williams, A. Rich and M. Egli, Biochemistry, 1994, 33, 1073–1086 CrossRef CAS; (b) V. A. Bloomfield, Biopolymers, 1997, 44, 269–282 CrossRef CAS; (c) I. Rouzina and V. A. Bloomfield, Biophys. J., 1998, 74, 3152–3164 CrossRef CAS; (d) M. Saminathan, T. Anthony, A. Shirahata, L. H. Sigal, T. Thomas and T. J. Thomas, Biochemistry, 1999, 38, 3821–3830 CrossRef CAS; (e) L. D. Williams, Annu. Rev. Biophys. Biomol. Struct., 2000, 29, 497–521 CrossRef CAS; (f) H. Deng, V. A. Bloomfield, J. M. Benevides and G. J. Thomas, Nucleic Acids Res., 2000, 28, 3379–3385 CrossRef CAS; (g) V. Vijayanathan, T. Thomas, A. Shirahata and T. J. Thomas, Biochemistry, 2001, 40, 13644–13651 CrossRef CAS; (h) Y. Burak, G. Ariel and D. Andelman, Biophys. J., 2003, 85, 2100–2110 CrossRef CAS; (i) L. D'Agostino, M. di Pietro and A. Di Luccia, FEBS J., 2005, 272, 3777–3787 CrossRef CAS; (j) D. Pastre, O. Pietrement, F. Landousy, L. Hamon, I. Sorel, M. O. David, E. Delain, A. Zozime and E. Le Cam, Eur. Biophys. J., 2006, 35, 214–223 CrossRef CAS; (k) X. Qiu, K. Andresen, J. S. Lamb, L. W. Kwok and L. Pollack, Phys. Rev. Lett., 2008, 101, 228101 CrossRef.
- (a) G. M. Pavan, A. Danani, S. Pricl and D. K. Smith, J. Am. Chem. Soc., 2009, 131, 9686–9694 CrossRef CAS; (b) S. P. Jones, G. M. Pavan, A. Danani, S. Pricl and D. K. Smith, Chem.–Eur. J., 2010, 16, 4519–4532 CrossRef CAS.
- D. K. Smith, Chem. Commun., 2006, 34–44 RSC.
- (a) B. S. Kim, D. J. Hong, J. Bae and M. Lee, J. Am. Chem. Soc., 2005, 127, 16333–16337 CrossRef CAS; (b) Y. Lim and M. Lee, Org. Biomol. Chem., 2007, 5, 401–405 RSC; (c) M. K. Müller and L. Brunsveld, Angew. Chem., Int. Ed., 2009, 48, 2921–2924 CrossRef CAS.
- (a) X. Montet, M. Funovics, K. Montet-Abou, R. Weissleder and L. Josephson, J. Med. Chem., 2006, 49, 6087–6093 CrossRef CAS; (b) M. O. Guler, L. Hsu, S. Soukasene, D. A. Harrington, J. F. Hulvat and S. I. Stupp, Biomacromolecules, 2006, 7, 1855–1863 CrossRef CAS; (c) X.-B. Xiong, A. Mahmud, H. Uludag and A. Lavasanifar, Biomacromolecules, 2007, 8, 874–884 CrossRef CAS; (d) Z. Huang, T. D. Sargeant, J. F. Hulvat, A. Mata, P. Bringas, C.-Y. Koh, S. I. Stupp and M. L. Snead, J. Bone Miner. Res., 2008, 23, 1995–2006 CrossRef; (e) M. Zhou, A. M. Smith, A. K. Das, N. W. Hodgson, R. F. Collins, R. V. Ulijn and J. E. Gough, Biomaterials, 2009, 30, 2523–2530 CrossRef CAS.
- S. W. A. Reulen, P. Y. W. Dankers, P. H. H. Bomans, E. W. Meijer and M. Merkx, J. Am. Chem. Soc., 2009, 131, 7304–7312 CrossRef CAS.
- (a) P. P. Karmali and A. Chaudhuri, Med. Res. Rev., 2007, 27, 696–722 CrossRef CAS; (b) S. Bhattacharya and A. Balaj, Chem. Commun., 2009, 4632–4656 RSC; (c) N. M. Rao, Chem. Phys. Lipids, 2010, 163, 245–252 CrossRef CAS.
- (a) D. K. Smith, A. R. Hirst, C. S. Love, J. G. Hardy, S. V. Brignell and B. Huang, Prog. Polym. Sci., 2005, 30, 220–293 CrossRef CAS; (b) K. T. Al-Jamal, C. Ramaswamy and A. T. Florence, Adv. Drug Delivery Rev., 2005, 57, 2238–2270 CrossRef; (c) D. K. Smith, Adv. Mater., 2006, 18, 2773–2778 CrossRef CAS; (d) B. M. Rosen, C. J. Wilson, D. A. Wilson, M. Peterca, M. R. Imam and V. Percec, Chem. Rev., 2009, 109, 6275–6540 CrossRef CAS.
- (a) D. Joester, M. Losson, R. Pugin, H. Heinzelmann, E. Walter, H. P. Merkle and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1486–1490 CrossRef CAS; (b) M. Guillot, S. Eisler, K. Weller, H. P. Merkle, J. L. Gallani and F. Diederich, Org. Biomol. Chem., 2006, 4, 766–769 RSC; (c) M. Guillot-Nieckowski, D. Joester, M. Stohr, M. Losson, M. Adrian, B. Wagner, M. Kansy, H. Heinzelmann, R. Pugin, F. Diederich and J. L. Gallani, Langmuir, 2007, 23, 737–746 CrossRef CAS; (d) A. Ahmad, H. M. Evans, K. Ewert, C. X. George, C. E. Samuel and C. R. Safinya, J. Gene Med., 2005, 7, 739–748 CrossRef CAS; (e) K. K. Ewert, H. M. Evans, A. Zidovska, N. F. Bouxsein, A. Ahmad and C. R. Safinya, J. Am. Chem. Soc., 2006, 128, 3998–4006 CrossRef CAS; (f) D. S. Shah, T. Sakthivel, I. Toth, A. T. Florence and A. F. Wilderspin, Int. J. Pharm., 2000, 208, 41–48 CrossRef CAS; (g) H. K. Bayele, C. Ramaswamy, A. F. Wilderspin, K. S. Srai, I. Toth and A. T. Florence, J. Pharm. Sci., 2006, 95, 1227–1237 CrossRef CAS.
- S. P. Jones, N. P. Gabrielson, D. W. Pack and D. K. Smith, Chem. Commun., 2008, 4700–4702 RSC.
- (a) J. H. Felgner, R. Kumar, C. N. Sridhar, C. J. Wheeler, Y. J. Tsai, R. Border, P. Ramsey, M. Martin and P. L. Felgner, J. Biol. Chem., 1994, 269, 2550–2561 CAS; (b) P. Erbacher, A. C. Roche, M. Monsigny and P. Midoux, Exp. Cell Res., 1996, 225, 186–194 CrossRef CAS; (c) M. L. Forrest and D. W. Pack, Mol. Ther., 2002, 6, 57–66 CrossRef CAS.
- M. A. Azagarsamy, V. Yesilyurt and S. Thayumanavan, J. Am. Chem. Soc., 2010, 132, 4550–4551 CrossRef CAS.
- (a) J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC; (b) J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, Biochim. Biophys. Acta, Biomembr., 1977, 470, 185–201 CrossRef CAS.
- V. V. Kumar, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 444–448 CrossRef CAS.
- (a) I. S. Zuhorn, J. B. F. N. Engberts and D. Hoekstra, Eur. Biophys. J., 2007, 36, 349–362 CrossRef CAS; (b) J. O. Radler, I. Koltover, T. Salditt and C. R. Safinya, Science, 1997, 275, 810–814 CrossRef CAS; (c) A. El Ouahabi, M. Thiry, V. Pector, R. Fuks, J. M. Ruysschaert and M. Vandenbranden, FEBS Lett., 1997, 414, 187–192 CrossRef CAS; (d) I. Koltover, T. Salditt, J. O. Radler and C. R. Safinya, Science, 1998, 281, 78–81 CrossRef CAS.
- H. Wong, J. M. Victor and J. Mozziconacci, PLoS One, 2007, 2(9), e877 CrossRef.
- (a) P. Greenspan, E.P. Mayer and S.D. Fowler, J. Cell Biol., 1985, 100, 965–973 CAS; (b) E. R. Gillies, T. B. Jonsson and J. M. J. Fréchet, J. Am. Chem. Soc., 2004, 126, 11936–11943 CrossRef CAS.
- P. J. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Español, Europhys. Lett., 1997, 40, 631–636 CrossRef CAS.
- P. Español and P. B. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS.
- X. Fan, N. P.-T., S.o. Chen, X. Wu and T. Y. Ng, Phys. Fluids, 2006, 18, 63102–63110 Search PubMed.
- E. Moeendarbary, T. Y. Ng, H. Pan and K. Y. Lam, Microfluid. Nanofluid., 2010, 8, 243–254 CrossRef CAS.
- V. Symeonidis, G. E. Karniadakis and B. Caswell, Phys. Rev. Lett., 2005, 95, 076001 CrossRef.
- R. D. Groot, J. Chem. Phys., 2003, 118, 11265–11277 CrossRef CAS.
- (a) G. Scocchi, P. Posocco, A. Danani, S. Pricl and M. Fermeglia, Fluid Phase Equilib., 2007, 261, 366–374 CrossRef CAS; (b) G. Scocchi, P. Posocco, M. Fermeglia and S. Pricl, J. Phys. Chem. B, 2007, 111, 2143–2151 CrossRef CAS; (c) G. Scocchi, P. Posocco, J.-W. Handgraaf, J. G. E. M. Fraaije, M. Fermeglia and S. Pricl, Chem.–Eur. J., 2009, 15, 7586–7592 CrossRef CAS; (d) R. Toth, D.-J. Voorn, J.-W. Handgraaf, J. G. E. M. Fraaije, M. Fermeglia, S. Pricl and P. Posocco, Macromolecules, 2009, 42, 8260–8270 CrossRef CAS.
- D. A. Case, T. A. Darden, T. E. Cheatham, III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, K. M. Merz, D. A. Pearlman, M. Crowley, R. C. Walker, W. Zhang, B. Wang, S. Hayik, A. Roitberg, G. Seabra, K. F. Wong, F. Paesani, X. Wu, S. Brozell, V. Tsui, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, P. Beroza, D. H. Mathews, C. Schafmeister, W. S. Ross, and P. A. Kollman, AMBER 9, University of California, San Francisco, 2006 Search PubMed.
- (a) J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef; (b) A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS; (c) A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- J. Srinivasan, T. E. Cheatham, P. Cieplak, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 1998, 120, 9401–9409 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
