DOI:
10.1039/C0SC00274G
(Perspective)
Chem. Sci., 2010,
1, 663-674
Future perspectives of nonadiabatic chemical dynamics
Received
21st April 2010
, Accepted 3rd June 2010
First published on
9th August 2010
Abstract
A variety of chemical phenomena are governed by non-adiabatic transitions at conical intersections of potential energy surfaces, if not directly, but indirectly in the midst of the processes. In other words, the non-adiabatic transition makes one of the most significant key mechanisms in chemical dynamics. Since the basic analytical theory is now available to treat the transitions, it is possible to comprehend the dynamics of realistic chemical and biological systems with the effects of transitions taken into account properly. Another important quantum mechanical effect of tunneling can also be taken into account. Furthermore, it becomes feasible to control chemical dynamics by controlling the non-adiabatic transitions at conical intersections, and also to develop new molecular functions by using peculiar properties of non-adiabatic transitions. These may be realized, if we apply appropriately designed laser fields. This perspective review article explains the above mentioned ideas based on the authors' recent activities. The non-adiabatic chemical dynamics is expected to open a new dimension of chemistry.
 Shinkoh Nanbu | Shinkoh Nanbu was born in Miyagi, Japan, in 1964. He completed his doctorate in Chemistry at Keio University, Japan, in 1994. From 1991 to 1992, he was a JSPS doctoral fellow at Keio University. In 1992, he became an Assistant Professor at the Computer Centre of the Institute for Molecular Science. He moved to the Computer Centre of Kyushu University in 2005. Since 2009, he has been a Professor in the Faculty of Science and Technology at Sophia University, Tokyo. His current interests include photochemistry, nonadiabatic phenomena, and isotope fractionation in atmospheric chemistry. |
 Toshimasa Ishida | Toshimasa Ishida was born in Tokyo and completed his doctorate of Science at the University of Tokyo, Japan. He worked at Shizuoka University, Institute for Molecular Science. He has been an associate professor in Fukui Institute for Fundamental Chemistry at Kyoto University since October 2004. His current interests are photochemistry and reactions of biomolecules. |
 Hiroki Nakamura | Hiroki Nakamura is the former Director General of IMS and the Executive Director and Vice President of NINS (National Institute of Natural Sciences). He received his PhD from The University of Tokyo. His scientific interests are the theory of chemical dynamics, semiclassical theory, and nonadiabatic transition. |
1. What is non-adiabatic chemical dynamics?
Electronically excited states play crucial roles in a variety of chemical phenomena. Even when the initial or final states are not excited states, in many cases they play important roles in the midst of chemical processes. This means that it is inevitable to comprehend the time evolution of chemical phenomena, namely, to comprehend the dynamics of the phenomena. Non-adiabatic chemical dynamics is defined as chemical processes in which excited electronic states are involved or transitions among two or more electronically adiabatic potential energy surfaces, which are called “non-adiabatic transition”, take place.1 Since such a transition cannot be described by classical mechanics, non-adiabatic transition is a quantum mechanical effect. The most typical non-adiabatic transition in chemistry is a transition at the conical intersection of potential energy surfaces (see Fig. 1(a)). A conical intersection of adiabatic potential energy surfaces in a multi-dimensional space with N degrees of freedom can have at most (N − 2) – dimensional surface crossing which makes an apex of crossing cones. The non-adiabatic transition occurs efficiently near the apex; in other words, it does not occur efficiently when the two potential energy surfaces are energetically far apart. When a trajectory just hits the apex, the transition occurs from one cone to the other with unit probability. When it crosses the potential energy surfaces nearby the apex, it splits into two. One transits to the other adiabatic potential energy surface with a certain transition probability p, which is called non-adiabatic transition probability, and the other stays on the same adiabatic potential energy surface with the probability 1 − p. There are two more typical examples of potential energy surface crossings: crossing seam (Fig. 1(b)) and glancing intersection (Renner–Teller type) (Fig. 1(c)). The crossing seam can be regarded as a part of the conical intersection. Usually, the intersection point is located at infinity. When it comes to analysis of chemical processes, attention should always be paid to whether any excited electronic states are involved in the process or they are located nearby the transition state. Although the transition state is a well known important concept in chemical dynamics, care should always be taken whether there is an excited state nearby or not. In some cases, the transition state, i.e., the potential barrier, is created due to the crossing of two diabatic potential energy surfaces. If that is the case, the dynamics becomes different from the ordinary one. Non-adiabatic transition and conical intersection are the theoretical concepts, but they are inevitable to comprehend the mechanisms of chemical dynamics.
 |
| | Fig. 1 Schematic view of (a) conical intersection, (b) crossing seam, and (c) glancing intersection. | |
Chemistry is now beyond phenomenology and empiricism, and understanding of mechanisms has become more and more important. One more thing to be noted is that photo-excitation is also regarded as a non-adiabatic transition. When a strong laser field is applied, the excitation process cannot be treated by the simple perturbation theory, but should be treated as a non-perturbative non-adiabatic transition. There are two types of one-dimensional potential energy curve crossing as shown in Fig. 2, in which (a) is called the non-adiabatic tunneling (NT) type and (b) is called the Landau–Zener (LZ) type. In the former (latter) case, the two coupled diabatic potential curves [dash lines in Fig. 2] cross with the opposite (same) signs of slope. After diagonalization of these two diabatic potential energy curves, we have two adiabatic potential energy curves (solid lines) as shown in Fig. 2. The non-adiabatic transitions occur locally at the diabatic crossing point where the two adiabatic potential energy curves come close together. This is called avoided crossing of adiabatic potential energy curves. It should be noted that the non-adiabatic transitions play significant roles, even when the transitions are energetically forbidden, namely, even when the total energy of the system is lower than the energy of the avoided crossing point. These cases correspond to the energy EL in Fig. 2 and are called classically forbidden transitions. In the case of Fig. 2(a), the upper adiabatic state is totally inaccessible at this energy, but the tunneling through the lower adiabatic potential energy curve is affected by the existence of this excited state. Usually, this is not understood properly. After a long history of theoretical studies pioneered by Landau,2 Zener3 and Stueckelberg,4 the whole set of one-dimensional curve crossing problems was solved completely by Zhu and Nakamura.1,5,6 This is now called the Zhu-Nakamura theory. Real chemical systems are naturally multi-dimensional and both non-adiabatic tunneling and the Landau–Zener type of avoided crossing of potential energy curves take place depending on the geometry of the conical intersection, if we cut the potential energy surfaces, say for instance, along a classical trajectory.
 |
| | Fig. 2 (a) Non-adiabatic tunneling type and (b) Landau–Zener type of potential energy curve crossing. | |
Now the reader may be convinced that non-adiabatic dynamics plays key roles in many chemical processes such as structural changes of molecules, chemical reactions and manifestations of molecular functions, and that the non-adiabatic transition at the conical intersection presents an important microscopic basic mechanism of these chemical phenomena as a quantum mechanical effect. The well known phenomenon governed by the non-adiabatic transition is photo-isomerization of a molecule. One typical example is photo-chromism, in which the structural change due to the isomerization causes the color change of the molecule. The fundamental mechanism of eyesight is also photo-isomerization of a retinal molecule. Once the over-all mechanisms of chemical dynamic processes are understood, it becomes possible to think about enhancing the efficiency of desirable chemical processes, controlling chemical dynamics, and revealing new molecular functions. For these purposes theories to describe the non-adiabatic transitions, hopefully analytical as much as possible, are very useful, even if they are just one-dimensional theories. In many cases of organic chemical reactions and even biological phenomena, it seems that the so-called steric effects restrict a mechanistically important region to a low dimensional space so that the fundamental mechanisms can work efficiently. Thus the analytical theories are useful even for multi-dimensional problems. It should also be noted that the fact that the non-adiabatic coupling is a vector which specifies the direction of transition supports the good applicability of the one-dimensional theories. In the case of the NT type of transition shown in Fig. 2(a), very interesting phenomenon of complete reflection occurs as demonstrated in Fig. 3. At energies higher than the bottom of the upper adiabatic potential, the transmission probability oscillates as a function of energy and becomes completely zero at certain discrete energies. This phenomenon occurs whenever we have NT type of curve crossing, irrespective of the shape of potential energy curves. The reflection is complete only in one-dimension, but the phenomenon may survive to some extent in multi-dimensional systems and interesting molecular functions can be manifested. Some examples will be shown in Section 4.
 |
| | Fig. 3 Transmission probability against energy in the NT-type of potential energy curve crossing. | |
This perspective review article is intended to give a theoretical overview and potential future perspectives of non-adiabatic chemical dynamics for the general broad readership as much as possible. The contents are mainly based on our recent activities presented in Refs. 5 and 7 together with some additional results. In the next section we propose to comprehend the dynamics of large scale real chemical and biological systems by generalizing the trajectory surface hopping method and the semiclassical frozen-Gaussian propagation method. The generalization is made by incorporating the Zhu-Nakamura(ZN) formulas of non-adiabatic transitions. These methods acronymized as ZN-TSH (Trajectory Surface Hopping) and ZN-SC (Semi-Classical), respectively, are appropriate for comprehending the non-adiabatic chemical dynamics occurring in Nature. The ZN-TSH is more so, since this can be easily applied to large systems. Its numerical application to the photo-isomerization of retinal molecules is presented in Section 2.8 In Section 3 we will discuss about the possibilities of controlling chemical dynamics. Thanks to the recent rapid development of laser technology, now we may be able to design laser fields to control chemical dynamics in a desirable way. Non-adiabatic transitions, not only at naturally existing conical intersections but also induced by an external laser field, play roles as key mechanisms, and thus the basic theories are again useful. The recent progress of nano-science and its related fine technologies promotes the discussions about molecular functions such as molecular machines and switches.9,10 Here non-adiabatic dynamics would again play roles as a basic pivotal mechanism for various molecular functions to work. In Section 4 we present some examples of controlling non-adiabatic transitions and utilizing the complete reflection phenomenon. Section 5 concludes our discussions about future perspectives.
2. How to comprehend the dynamics
First of all, it is fundamental to theoretically comprehend the dynamics occurring in Nature. Namely, theoretical methodologies should be developed so that we can analyze real high-dimensional chemical dynamics with quantum mechanical effects taken into account properly. Although considerable efforts have been made to develop quantum mechanical methods to treat multi-dimensional systems such as the multi-configuration time-dependent Hartree (MCTDH) method,11 it is unfortunately formidable to treat high-dimensional chemical systems quantum mechanically accurately. Some kind of quantum-classical hybrid methods are necessary to be developed. The molecular dynamics (MD) simulation method based on classical mechanics is commonly employed as a powerful methodology.12 However, this is purely classical and quantum mechanical effects are not taken into account at all. Various attempts have been made to develop methods to take into account quantum mechanical effects with use of the practically convenient classical mechanics. The basic idea is to run classical trajectories on the potential energy surfaces with quantum mechanical effects somehow taken into account along them. The simplest such method is the trajectory surface hopping (TSH) method, in which non-adiabatic transitions are treated by the hopping of classical trajectories from one potential energy surface to the other. The reaction probability is calculated from the number of classical trajectories ended up in the product region relative to the total number of trajectories. The TSH method was first proposed by Bjerre and Nikitin13 and by Tully and Preston.14 After these works, various modifications have been made by Tully15 and by Truhlar and coworkers.16 In order to take into account the effects of phases, we have to rely on the so-called semiclassical (SC) theory in which the phase is accumulated along classical trajectory and the transition amplitude is evaluated. There are basically two types of formulations: one is to use classical trajectories directly with the quantized initial condition (initial value representation: IVR-SC)17 and the other is to propagate frozen Gaussian wave packets that are used to expand the initial total wave function (HK-SC).18 These theories have been developed basically for adiabatic processes, namely, for the dynamics on a single adiabatic potential energy surface. We have generalized these methods by simply incorporating our ZN formulas of non-adiabatic transitions.19,20,21 As mentioned above, these are called as ZN-TSH and ZN-HKSC. By doing this, we can overcome various problems encountered in the procedure of taking into account quantum mechanical effects. The most crucial point is that the ZN formulas can treat the classically forbidden non-adiabatic transitions by simple analytical formulas, which is not possible by the other conventional TSH methods. Even the phases induced by the transition can be taken into account analytically. Quantum mechanical tunneling effects can also be taken into account by detecting caustics (turning point in one-dimensional case) along classical trajectories and running appropriate tunneling trajectories from there.21,22 Actual numerical applications of these methods to realistic systems are presented below. When we treat the dynamics of real chemical systems, accurate information of potential energy surfaces is inevitable. When that is available or can be computed in the whole range of important molecular configuration space of the system including excited potential energy surfaces, we can directly employ the above mentioned ZN-TSH or ZN-HKSC methods. However, this is not the ordinary case, unfortunately. The practically useful way is the so called on-the-fly method in which the potential energies are computed in an ab initio quantum chemical way while running each classical trajectory. This on-the-fly ab initio method is used also in MD and MC(Monte Carlo) methods.23,24 On the other hand, it is important to have at least qualitative knowledge about in what molecular configurations conical intersections and dynamically important tunneling regions are located. This kind of prior knowledge is very helpful to carry out the full computations, since high-cost high-level quantum chemical computations can be restricted to these regions. In other words, it should be noted that potential energies in the vicinity of conical intersections and tunneling barriers should be calculated accurately by the high-level of quantum chemical methods. The minimum requirement before starting the full computations is to draw the energy correlation diagram of the system. Fig. 4 shows a simple example in the case of photo-conversion between cyclohexadiene and hexatriene which will be discussed in the next section. The two conical intersections seem to play important roles in the dynamics in this energy range.
After these preparations the computations based on the ZN-TSH or ZN-HKSC methods can be carried out. Unless the phases are expected to play significant roles, it is better to use ZN-TSH method, because this is far simpler. An example in which the phases are important is laser control of dynamics, since the coherence plays a crucial role in this case. The actual calculation procedure of ZN-TSH is rather simple. While running classical trajectories, the minimum adiabatic potential energy separation is detected along each trajectory, which defines the position of non-adiabatic transition. At this point the direction of transition should be determined. If the non-adiabatic coupling vector is available or can be computed, that defines the direction of transition. If it is not available, the direction can be estimated to a good approximation from the Hessian matrix there.5,20 The multi-dimensional potential energy surfaces are cut along this direction and we have one-dimensional potential energy curves with avoided crossing like those in Fig. 2 to which the ZN formulas can be applied. If the ZN-probability is larger than a random number generated there, the trajectory jumps to the other potential energy surface. Otherwise, it stays on the initial surface. Even when the energy is lower than the avoided crossing point, this procedure can be performed, since the over-all transition probability including not only the non-adiabatic transition at the avoided crossing point but also the tunneling from the turning point on the initial potential energy curve to that on the other potential energy curve (see the case of EL in Fig. 2) can be provided by the ZN theory. This cannot be done by any other conventional methods based on the LZ formulas or even by the numerical solution of time-dependent Schrödinger equations along classical trajectories. Fig. 5 shows the cumulative reaction probability for H2(v = 2) + D+→H + (HD)+ for J(total angular momentum) = 026 and clearly demonstrates that the commonly used LZ formula is not good enough and that the classically forbidden transitions play crucial roles. The “exact” [dashed line] is the quantum mechanically exact numerical solution. The “new” (“old”) TSH means the result of the ZN-TSH (LZ-TSH). The oscillatory structure of the exact result is due to resonances which are neglected in the TSH calculations by discarding the long lived trajectories. Fig. 5 guarantees that the ZN-TSH works alright and can reproduce the quantum mechanical results properly. Successful applications of the ZN formulas have been made to various other systems such as the non-adiabatic chemical reactions in the C + H220 and H2 + D+(H+)27 systems, the photo-dissociation of bromoacetylchloride,28 and the electron transfer in 2,7-dinitronaphthalene.29 Thus the method can now be applied to large chemical systems which cannot be treated quantum mechanically exactly.
![Initial vibrational state specified cumulative reaction probabilities for H2(v = 2) + D+→H + HD +. dashed line : exact quantum mechanical numerical solution, solid line : ZN-TSH, dash-dot line : LZ-TSH. Taken from Ref. [26].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f5.gif) |
| | Fig. 5 Initial vibrational state specified cumulative reaction probabilities for H2(v = 2) + D+→H + HD +. dashed line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exact quantum mechanical numerical solution, solid line exact quantum mechanical numerical solution, solid line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZN-TSH, dash-dot line ZN-TSH, dash-dot line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LZ-TSH. Taken from Ref. [26]. LZ-TSH. Taken from Ref. [26]. | |
As an example of such applications, numerical calculations of photo-isomerization of a retinal molecule are presented here. The model used is the 12-π system shown in Fig. 6 in which two methyl groups are removed from the Schiff base of retinal. On-the-fly classical dynamics calculations combined with ab initio quantum chemical computations of electronic states including excited states are carried out with non-adiabatic transitions taken into account by the ZN formulas.8 The electronic state calculations are the state averaged 6 electron orbital complete active space self-consistent field (CAS(6,6)SCF) scheme with the 6-31G basis set. The initial geometry of the ground state is determined by the optimization by the B3LYP-DFT method. The initial velocity was provided randomly according to the Boltzmann distribution at T = 300 K and ninety-eight classical trajectories were run. The procedure is summarized as follows. When the energy difference between the two adjacent adiabatic potential energy surfaces is a local minimum, the non-adiabatic coupling vector is calculated. The one-dimensional adiabatic potential energy curves are calculated in the direction of the coupling vector and the type of crossing is identified, i.e., the NT-type or the LZ-type. In the former, the signs of the potential slopes are different, while in the latter, the two potential curves cross with the same sign of slope. The transition probability is estimated using the ZN formulas from these adiabatic potentials. The transition probability calculated is compared to a uniform random number generated and the decision is made whether the transition to the adjoining surface occurs or the trajectory stays on the same surface. A non-vertical hop, which corresponds to the classically forbidden transition, is taken into account when the kinetic energy is not enough for the vertical hop which corresponds to the classically allowed transition. Although such classically forbidden transitions have turned out not to occur in the present system, the classically allowed transitions at the energies near the crossing point occur rather frequently and can be accurately treated in the present scheme. The optimized geometry and the velocity distribution on the ground state in the 11-cis form mentioned above are employed to start classical trajectories on the photo-excited state. The energy diagram relevant to the present system is depicted in Fig. 7 which shows two conical intersections leading to 11-cis and 9-cis conformations.
 |
| | Fig. 6 12 – π molecular model of retinal. | |
 |
| | Fig. 7 Energy diagram for isomerization of retinal. Energy is in Kcal/mol. The blue and red lines indicate the ground and exited states, and CI stands for conical intersection. | |
Fig. 8 shows the time evolution of potential energy difference between the ground and excited states along each trajectory. Note that when the relevant trajectory is on the excited state, the energy is taken to be positive while the value is taken to be negative when the trajectory runs on the ground state. It is revealed that the energy relaxation occurs in two steps, as is seen in Fig. 8. All-trans, 9-cis, and 11-cis forms are generated in vacuo in the present calculation, although the 9-cis form is not observed in Rhodopsin protein.30 This suggests that the generation of 9-cis form is prevented by the protein environment in reality.
 |
| | Fig. 8 Time evolution of energy difference between the ground and excited states along each trajectory. Taken from 8. | |
Fig. 9 shows the time evolution of dihedral angles in the case of all-trans formation. Interestingly, the –C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– bond rotates clockwise when the –C11
C10– bond rotates clockwise when the –C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12– bond rotates counterclockwise in any routes to the products. Note that the –C9
C12– bond rotates counterclockwise in any routes to the products. Note that the –C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– rotation occurs even when the system goes back to the reactant, i.e. to the 11-cis form. Since the rotation of the –C9
C10– rotation occurs even when the system goes back to the reactant, i.e. to the 11-cis form. Since the rotation of the –C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– bond activates the motion directed to the 9-cis form, the channel to the 9-cis form is open in addition to that to the all-trans form. In this sense, the two conical intersections, one between the 11-cis and all-trans forms and the other between the 11-cis and 9-cis forms, are almost equally accessed in vacuo to make a transition to the ground state. As mentioned above, in the Rhodopsin protein environment, on the other hand, the 9-cis form is not generated. This indicates that in Rhodopsin the route to 9-cis form is blocked by the surrounding protein and only the route to the all-trans form (and reverted 11-cis form) is left open. The branching ratio of all-trans, 9-cis and 11-cis forms at the final stage is 1
C10– bond activates the motion directed to the 9-cis form, the channel to the 9-cis form is open in addition to that to the all-trans form. In this sense, the two conical intersections, one between the 11-cis and all-trans forms and the other between the 11-cis and 9-cis forms, are almost equally accessed in vacuo to make a transition to the ground state. As mentioned above, in the Rhodopsin protein environment, on the other hand, the 9-cis form is not generated. This indicates that in Rhodopsin the route to 9-cis form is blocked by the surrounding protein and only the route to the all-trans form (and reverted 11-cis form) is left open. The branching ratio of all-trans, 9-cis and 11-cis forms at the final stage is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Since the 9-cis form is counted as trans with respect to the 11-position, the ratio of the 11-trans form to the 11-cis form is 1
2. Since the 9-cis form is counted as trans with respect to the 11-position, the ratio of the 11-trans form to the 11-cis form is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The experimental quantum yield of isomerization is 0.67 in protein and 0.15 in solutions.31,32 Since we can assume safely from the discussion above that the protein environment in Rhodopsin suppresses the 9-cis form and leads to the all-trans product, the present result in vacuo is closer to the value in protein.
1. The experimental quantum yield of isomerization is 0.67 in protein and 0.15 in solutions.31,32 Since we can assume safely from the discussion above that the protein environment in Rhodopsin suppresses the 9-cis form and leads to the all-trans product, the present result in vacuo is closer to the value in protein.
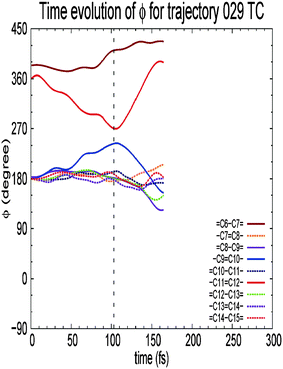 |
| | Fig. 9 Time evolution of dihedral angles of the backbone in retinal along trajectories leading to the all-trans form. | |
As mentioned above, another good example of non-adiabatic dynamics is electron transfer which constitutes an important process in biology. The Marcus theory is widely known,33 but it sometimes does not work well, because it relies on the first order perturbation theory with respect to the electronic coupling. We have been successful in improving that theory by incorporating the ZN-formulas.34 The rate constant is given as:
with
| |  | (2) |
where
kMarcus is the Marcus formula defined by:
| |  | (3) |
H
AD
is the electronic coupling between acceptor and donor, ΔG is the exothermicity, λ is the reorganization energy, β is the Boltzman factor, and ω is the frequency of the harmonic oscillator. The probability ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) is given as:
is given as:
| | ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) (β) = β∫∞0dE exp(−βE)PZN(E,Q0) (β) = β∫∞0dE exp(−βE)PZN(E,Q0) | (4) |
where
PZN is the overall non-adiabatic transition probability calculated from the Zhu-Nakamura theory and
Q0 represents the potential crossing point. Thus the factor
κ takes into account the effects of non-adiabatic transition and tunneling properly. It should also be noted that the electronic coupling
HAD is assumed to be constant in the Marcus formula, but this is not necessary in the present formulation. The coupling
HAD cancels out in
k of
eqn (1) and the Zhu-Nakamura probability can be calculated from the information of adiabatic potentials.
The Marcus formula naturally breaks down when the electronic coupling is strong. But even when the coupling is weak, it does not work well at low temperatures, since the classically forbidden non-adiabatic transitions cannot be treated properly. Fig. 10 shows an example of such a case.35
![Arrhenius plot of the electron transfer rate in the weak coupling (HAD = 0.001au) case. Solid circle : exact perturbation theory, solid line : present result, dotted line : Marcus' high temperature theory, dash line : result with use of the LZ formula. Taken from Ref. [35].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f10.gif) |
| | Fig. 10 Arrhenius plot of the electron transfer rate in the weak coupling (HAD = 0.001au) case. Solid circle![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exact perturbation theory, solid line exact perturbation theory, solid line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) present result, dotted line present result, dotted line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Marcus' high temperature theory, dash line Marcus' high temperature theory, dash line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) result with use of the LZ formula. Taken from Ref. [35]. result with use of the LZ formula. Taken from Ref. [35]. | |
The next question is whether we can treat another important quantum mechanical effect, namely, tunneling, in the same framework. The answer is yes. In order to do this, first, we have to detect caustics along each trajectory that represents the boundary between classically allowed and forbidden regions and is equivalent to the turning point in one-dimensional case. This is not trivial at all in multi-dimensional space, but can now be carried out by solving the non-linear Riccati differential equation for the following matrix A:22
| |  | (5) |
where
p and
q represent the momentum and coordinate. The differential equation satisfied by this matrix along the classical trajectory is given by:
| |  | (6) |
where
Hαβ(
α,
β =
p,
q) are the matrices of the second derivative of the Hamiltonian taken along the classical trajectory, namely, ∂
2H/∂
q∂
p,
etc. During the propagation, the inverse of the matrix
A becomes zero at caustics, by which the caustics can be easily detected.
Once the caustics are detected, we run a tunneling classical trajectory from there on the upside down potential energy surface. However, it is a bit too much to run those tunneling trajectories at every caustics. This is why it is so important to have knowledge about the important tunneling region in advance. Besides, when the action calculated along the trajectory is expected to be too large and the corresponding tunneling probability is too small compared to the pre-determined criterion, we can neglect the contribution from such a trajectory. We will not go into the details here, and the reader should refer to previous reports.5,22 As explained above, the ZN-TSH can be usefully utilized to comprehend the non-adiabatic chemical dynamics of large systems with the tunneling effects also taken into account. From the authors' viewpoint, the MD simulation method should now be improved with non-adiabatic dynamics and tunneling effects taken into account. The modifications must be simple, as expected from the procedure of ZN-TSH. When it is necessary to take into account the effects of phases, we have to employ the semiclassical theory as explained before. We do not go into the details here and give only a brief explanation. The initial state is expanded in terms of frozen Gaussian wave packets and the center of each frozen wave packet is propagated along a classical trajectory.18 When it comes to the non-adiabatic transition point, the transition is made by using the electronic transition matrix based on the Zhu-Nakamura theory and then further propagation is carried out on a new potential energy surface. Along these propagations, all the phases not only along the classical trajectories but also due to the non-adiabatic transitions are taken into account. One of the applications of this formulation to laser control will be presented in the next section.
In concluding this section, it should be noted that the ZN-TSH and ZN-HKSC calculations should be performed in the adiabatic state representation, since the transitions are well localized in the crossing region and the methods can be applied even in the dissipative systems. The reader interested in the ZN-TSH method can download the code from our website36 to use it for practical applications.
3. Control of non-adiabatic chemical dynamics
Since non-adiabatic transitions play crucial roles in chemical dynamics, it would be nice if we could control them in a desirable way. Catalyst chemistry has a long history and it is generally believed that catalysts lower the transition states and enhance the desirable reactions.37 Non-adiabatic transitions at conical intersections may also be involved in those reactions and it would be interesting to analyze those reactions from the present view point. Here we consider controlling non-adiabatic transitions by a laser field. It is again important to have knowledge about the local geometrical structures of potential energy surfaces in the vicinity of conical intersections. The desirable direction of transition there can be known in advance and we can change the wave packet momentum vector into that direction. This can actually be done by designing a laser field. This is called the directed momentum method. A pre-determined momentum vector can be given to the initial wave packet. Roughly speaking, the laser field should be parallel to the derivative with respect to the molecular internal coordinates of dipole moment vector in the direction of the desirable momentum.7 Actual design of laser pulse can be done by using the semiclassical guided optimal control theory.5,38,39 Numerical demonstration is given here by taking the photo-conversion of cyclohexadiene (CHD) to hexatriene (HT) as an example.25 The schematic potential energy diagram is shown in Fig. 4. Another important factor in this kind of photo-induced process is to enhance the efficiency of initial photo-excitation. The high efficiency close to 100% can be achieved by the quadratic laser frequency chirping, namely by appropriately changing the laser frequency quadratically as a function of time. The photo-excitation probability is usually estimated by the first order perturbation theory. This is alright, as far as the laser intensity is not high. When the laser is strong enough, however, the perturbation theory does not hold and it is better to use the dressed state picture and consider the photo-excitation process as a non-adiabatic transition between the excited state and the upward dressed ground state that crosses the excited state. This is a time-dependent non-adiabatic transition process and the coupling is the laser-dipole interaction. If we chirp the laser frequency quadratically (or periodically), we can create two (or more) crossings and the overall transition probability can be made unity by designing the chirping appropriately to satisfy the constructive interference condition (see Fig. 11). This figure shows the 100% efficiency of selective excitation of one of the two closely lying energy levels. This idea is applicable also to pump-dump of wave packet, although the quadratic chirping should be done quickly before the wave packet moves out from the transition region in space.
![Selective and complete excitation from the ground level to one of the excited level 2 by the quadratic frequency chirping in the case of three-level model. Taken from Ref. [40].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f11.gif) |
| | Fig. 11 Selective and complete excitation from the ground level to one of the excited level 2 by the quadratic frequency chirping in the case of three-level model. Taken from Ref. [40]. | |
By using the directed momentum method and the quadratic chirping of photo-excitation, the photo-conversion efficiency from CHD to HT can be made much higher than in the ordinary case. Fig. 12 demonstrates the enhancement of HT production obtained from the numerical computations of the 2D model of the system.25Fig. 13 shows a numerical demonstration of pump and dump of the initial vibrational wave packet to dissociate a diatomic molecule NaK.41 In Fig. 13(a) the wave packet at the left turning point on the ground state is the one before the final pump and does not have a smooth shape, but is quite bumpy, since this is prepared by the pump and dump method from the ground vibrational state. The overall dissociation probability can, however, be quite high (∼ 90%). The excitation efficiency of this bumpy wave packet is shown in Fig. 13(b). Fig. 13(c) shows the pump of the initial ground vibrational state on the ground electronic state and the dump of thus excited wave packet at the right turning point on the excited state. There are many other numerical applications to demonstrate the effectiveness of this quadratic chirping method.1,5,7,41 It would be possible, at least theoretically, to control various chemical dynamics by combining the above mentioned methods:7 the directed momentum method, the quadratic chirping method and the method to guide wave packet motion by the semiclassical optimal control theory.
![Time variation of wave packet populations on S0 and S1 states after the initial excitation. (a) and (b) with and without the directed momentum method, respectively. Taken from Ref. [25].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f12.gif) |
| | Fig. 12 Time variation of wave packet populations on S0 and S1 states after the initial excitation. (a) and (b) with and without the directed momentum method, respectively. Taken from Ref. [25]. | |
![Highly efficient dissociation of a NaK molecule by using the quadratically chirped pulses within the pump-dump mechanism. (a) Potential energy curves of the ground and excited states and dipole moment. The bumpy wave packet is created by the pump-dump scheme from the ground vibrational state on the ground electronic potential curve and is finally pumped up by another quadratically chirped pulse to dissociate. (b) Time variation of the population of this bumpy wave packet on the ground and excited states. (c) Time variation of population of the wave packet to prepare the bumpy packet by pumping up from the ground vibrational state and dumping at the right turning point on the excited state. Taken from Ref. [41].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f13.gif) |
| | Fig. 13 Highly efficient dissociation of a NaK molecule by using the quadratically chirped pulses within the pump-dump mechanism. (a) Potential energy curves of the ground and excited states and dipole moment. The bumpy wave packet is created by the pump-dump scheme from the ground vibrational state on the ground electronic potential curve and is finally pumped up by another quadratically chirped pulse to dissociate. (b) Time variation of the population of this bumpy wave packet on the ground and excited states. (c) Time variation of population of the wave packet to prepare the bumpy packet by pumping up from the ground vibrational state and dumping at the right turning point on the excited state. Taken from Ref. [41]. | |
| | 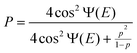 | (7) |
where p is the non-adiabatic transition probability for one passage of the crossing point and Ψ is the phase along the upper adiabatic potential curve at energy E plus the contribution due to the non-adiabatic transition. Thus, the complete reflection occurs when the following condition is satisfied:| | | Ψ(E) = (n + 1/2)π, (n = 0, 1, 2,…) | (8) |
This is complete only in the one-dimensional system, but the phenomenon can survive to some extent even in multi-dimensional systems, depending on the potential energy surface topography. Actually, some possible applications have been discussed so far.1,5,44 Examples are state-selective photo-dissociation of HI molecule (HI→H + I(2P3/2),H + I(2P1/2)),45 the bond-selective photo-dissociation of HOD and CH3SH,46 and the two-dimensional molecular switch.44 In these photo-induced processes, the dressed state picture is useful. As is schematically shown in Fig. 14, an attractive ground state is dressed up by the photon energy ℏω and the two NT-type crossings are created. By adjusting the laser frequency, the complete reflection condition is satisfied at the right or the left crossing, and photo-dissociation to the right side or to the left side can be stopped, respectively.
 |
| | Fig. 14 Schematic potential energy diagram of selective photo-dissociation. The attractive ground state V1(r) is dressed up by the laser to the dashed curve and two NT-type crossings are created with the repulsive excited state V2(R). By adjusting the laser frequency the complete reflection condition can be created either at the right or the left side, and thus the selective photo-dissociation can be achieved. | |
As a first example of molecular functions, here we explain the possibility of molecular switching. It is well known that the complete transmission occurs whenever we have a periodic set of potentials whatever the potential shapes are. In addition to this, if the potentials are the NT-type, we have two possibilities of complete transmission and complete reflection. This means that we can switch the transmission to reflection or vice versa by somehow modifying the potential systems. Fig. 15 demonstrates this phenomenon.47 At the origin of the coordinate, two units of the same NT-type of potentials are set and a wave packet with the central energy at the complete transmission condition is sent in from the right. At the time ts when one-third of the wave packet has transmitted the potential units already, the potential shape is modified to satisfy the condition of complete reflection. As is clearly seen in the figure, the residual two-thirds cannot transmit and are completely reflected back.
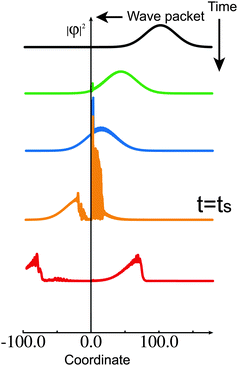 |
| | Fig. 15 Numerical demonstration of switching with use of a wave packet propagation. Two NT-type potential units are put at the origin. At time t = ts, one of the potential units is modified so that the complete reflection condition coincides with the wave packet energy. The residual two-thirds of the wave packet is reflected back. | |
The second example is the hydrogen transmission through a carbon ring of a nanomaterial.48,49,50 An example shown here (Fig. 16) is a modified coronene molecule C19H12BF6 in which six fluorine atoms are attached to the second layer of carbon atoms and one carbon atom in the first layer is replaced by boron. This molecular system represents a part of a modified nano-tube. The adiabatic interaction potentials are shown in Fig. 17. This corresponds to the interaction between a hydrogen atom and the molecular system when the hydrogen incidents in the direction perpendicular to the molecular surface. As seen in this figure, there are two avoided crossings designated as α and because of these the transmission probability depicts resonant type peaks and dips as seen in Fig. 18. If this kind of phenomenon would happen in nano-tubes with hydrogen molecules, this could be used to encapsulate or to store hydrogen molecules. Resonant peaks would be convenient for the incident hydrogen to be trapped inside, since it cannot come out easily because of energy loss. The present study is just a first step towards this kind of goal. It should be noted, however, that non-adiabatic transitions play a sort of key element to manifest molecular functions.
 |
| | Fig. 16 Molecular structure of the fluorinated hexa boron-substituted coronenyl radical C19H12BF6. | |
![Adiabatic potential energy curves for the hydrogen incidence perpendicularly to the molecular surface. The NT-type avoided crossings are designated as α. Taken from Ref. [50].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f17.gif) |
| | Fig. 17 Adiabatic potential energy curves for the hydrogen incidence perpendicularly to the molecular surface. The NT-type avoided crossings are designated as α. Taken from Ref. [50]. | |
![Transmission probability against energy. Taken from Ref. [50].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f18.gif) |
| | Fig. 18 Transmission probability against energy. Taken from Ref. [50]. | |
5. Concluding remarks
Now, we believe that many of chemical dynamical processes are actually governed by non-adiabatic transitions in various ways. They are not only ubiquitous and play crucial roles in a variety of phenomena occurring in Nature, but also they are versatile in manifesting various functions. Thus, it is crucial to take into account the effects of non-adiabatic transitions properly into simulations in order to comprehend chemical and biological dynamics occurring in Nature. The commonly employed molecular dynamics (MD) simulation method is purely classical mechanical and is based on the model interaction potentials. The ab initio MD method is now developed to improve the second defect.23,24 We can now overcome the first defect by incorporating non-adiabatic transitions and tunneling effects with use of the analytical formulas along classical trajectories. The on-the-fly ZN-TSH method with tunneling effects included can be usefully utilized for this purpose.8,20 This could be a useful tool to attack large scale real chemical and biological systems.
Not just comprehending the dynamics going on in Nature, but we can now think of controlling them and also developing new molecular functions.5 An appropriate combination of controlling the elementary processes, such as pump-dump of wave packet, non-adiabatic transition at conical intersections, and wave packet motion on a single adiabatic potential energy surface, would enable us to control various chemical dynamics as we desire. In a variety of molecular functions exemplified by photo-chromism, on the other hand, non-adiabatic transitions play a role of pivotal mechanism and their conversion efficiency can be enhanced by controlling the transitions. From the viewpoint of non-adiabatic transition, we should be able to find and develop new molecular functions. As examples, the molecular switch with use of the complete reflection phenomenon and hydrogen encapsulation or storage by carbon nano-materials have been discussed in this review. Many examples other than those discussed in this review article can be thought of. In order to further develop and realize these ideas, it would be definitely necessary and important to build up an effective system of interplay and collaboration of scientists from various fields. Theoreticians from electronic structure, chemical dynamics, statistical chemistry, and MD simulations, and also experimentalists from synthetic chemistry, laser science and chemistry, and spectroscopy should be able to work together. A new field of non-adiabatic chemical dynamics would hopefully be opened up in near future.
Acknowledgements
The authors would like to thank the support by a Grant-in-Aid for specially Promoted Research on Studies of Non-adiabatic chemical dynamics based on the Zhu-Nakamura theory from the MEXT of Japan.
References
-
Nonadiabatic Transition: Concepts, Basic Theories, and Applications by Hiroki Nakamura, World Scientific, Singapore, 2002 Search PubMed.
- L. D. Landau, Phys. Zts. Sov., 1932, 2, 46 Search PubMed.
- C. Zener, Proc. Roy. Soc., 1932, A137, 696 CrossRef.
- E. C. G. Stueckelberg, Hel. Phys. Acta., 1932, 5, 369 Search PubMed.
- H. Nakamura, Adv. Chem. Phys., 2008, 138, 95–212 CAS.
- H. Nakamura and C. Zhu, Comments on Atomic and Molecular Physics, 1996, 32, 249 Search PubMed.
- A. Kondorskiy, S. Nanbu, Y. Teranishi and H. Nakamura, J. Phys. Chem., 2010, A114, 6171 Search PubMed.
- T. Ishida, S. Nanbu and H. Nakamura, J. Phys. Chem. A, 2009, 113, 4356 CrossRef CAS.
-
Molecular Machines and Motors(Structure and Bonding) edited by J.-P. Sauvage, Springer, Berlin, 2001 Search PubMed.
-
Molecular Devices and Machines: A journey into the Nanoworld by Vincenzo Balzani, Margnertia Venturi, and Alberto Credi, Wiley-VCH, Weinheim, Germany, 2003 Search PubMed.
-
Multi-Dimensional Quantum Dynamics edited by H-D Meyer, F Gatti and G. A. Worth, John Wiley and Sons, Hoboken, NJ, 2009 Search PubMed.
-
Molecular Dynamics Simulation of Statistical Mechanical Systems edited by G. Ciccotti and W. G. Hoover, North-Holland, Amsterdam, Holland, 1986 Search PubMed.
- A. Bjerre and E. E. Nikitin, Chem. Phys. Lett., 1967, 1, 179 CrossRef CAS.
- J. C. Tully and R. Preston, J. Chem. Phys., 1970, 54, 4297.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
-
A. Jasper, B. K. Kendrick, C. A. Mead, and D. G. Truhlar, in Modern Trends in Chemical Reaction Dynamics: Experiment and Theory edited by K. Liu and X. Yang, World Scientific, Singapore, 2004 Search PubMed.
- W. H. Miller, J. Phys. Chem., 2001, 105, 2942 Search PubMed.
- M. F. Herman and E. Kluk, Annu. Rev. Phys. Chem., 1994, 45, 83 CrossRef CAS.
- A. Kondorskiy and H. Nakamura, J. Chem. Phys., 2004, 120, 8937 CrossRef CAS.
- P. Oloyede, G. Mil'nikov and H. Nakamura, J. Chem. Phys., 2006, 124, 144110 CrossRef.
- H. Nakamura, J. Phys. Chem. A, 2006, 110, 10929 CrossRef CAS.
- P. Oloyede, G. Mil'nikov and H. Nakamura, J. Theor. Comput. Chem., 2004, 3, 91 CrossRef CAS.
- T. Taketsugu and M. S. Gordon, J. Phys. Chem., 1995, 99, 8462 CrossRef CAS.
-
Ab Initio Molecular Dynamics by D. Marx and J. Hutter, Cambridge Univ. Press, New York, 2009 Search PubMed.
- H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 125, 034307 CrossRef.
- C. Zhu, H. Kamisaka and H. Nakamura, J. Chem. Phys., 2002, 116, 3234 CrossRef CAS.
- B. Li and K.-L. Han, J. Chem. Phys., 2008, 128, 114116 CrossRef.
- F. Zhang, W.-J. Ding and W. H. Fang, J. Chem. Phys., 2006, 125, 184305 CrossRef.
- Y. Zhao and H. Nakamura, J. Theor. Comp. Chem., 2004, 5, 209.
- R. Hubbard and A. Kropf, Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 130 CrossRef CAS.
- J. B. Hurley, T. G. Ebrey, B. Ilonig and M. Ottolenghi, Nature, 1977, 270, 540 CAS.
- Y. Koyama, K. Kubo, M. Komori, H. Yasuda and Y. Mukai, Photochem. Photobiol., 1991, 54, 433 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochem. BioPhys. Acta, 1985, 811, 265 CrossRef CAS.
- Y. Zhao, W. Liang and H. Nakamura, J. Phys. Chem. A, 2006, 110, 8204 CrossRef CAS.
- Y. Zhao, M. Han, W. Liang and H. Nakamura, J. Phys. Chem., 2007, 111, 2047 Search PubMed.
-
S. Nanbu, T. Ishida, and H. Nakamura, http://pweb.cc.sophia.ac.jp/nanbu_lab/index_e.html.
- See, for instance, H.-J. Freund, Chap.5 in Handbook of Heterogeneous Catalysis edited by G. Ertl, H. Knozinger, F. Schuth, and J. Weitkamp, Wiley-VCH, Weinheim, 2008 Search PubMed.
- A. Kondorskiy, G. Mil'nikov and H. Nakamura, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 041401 CrossRef.
- A. Kondorskiy and H. Nakamura, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 043407 CrossRef.
-
K. Nagaya, Y. Teranishi, and H. Nakamura, ACS Symposium Series 821, American Chemical Society, Washington DC, 2002, ch. 7.
- S. Zou, A. Kondorskiy, G. Mil'nikov and H. Nakamura, J. Chem. Phys., 2005, 122, 084112 CrossRef.
- H. Nakamura, J. Chem. Phys., 1992, 97, 256 CrossRef CAS.
- C. Zhu and H. Nakamura, J. Chem. Phys., 1992, 97, 8497 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1993, 98, 6208 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1994, 101, 4855 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1998, 108, 7501 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1994, 101, 10630 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1995, 102, 7448 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1998, 109, 4689 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1997, 106, 2599 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1997, 107, 7839 CrossRef CAS; C. Zhu and H. Nakamura, Chem. Phys. Lett., 1996, 258, 342 CrossRef CAS; C. Zhu and H. Nakamura, J. Chem. Phys., 1997, 274, 205 CAS; C. Zhu and H. Nakamura, Comput. Phys. Commun., 1993, 74, 9 CrossRef CAS.
- H. Nakamura, J. Chem. Phys., 1999, 110, 10253 CrossRef CAS.
- H. Fujisaki, Y. Teranishi and H. Nakamura, J. Theor. Comput. Chem., 2002, 1, 245 CrossRef CAS.
- K. Nagaya, Y. Teranishi and H. Nakamura, J. Chem. Phys., 2000, 113, 6197 CrossRef CAS.
- S. Nanbu, F. Goodman and H. Nakamura, J. Chem. Phys., 1997, 107, 5445 CrossRef CAS.
- S. Nanbu, T. Ishida and H. Nakamura, Chem. Phys., 2006, 324, 721 CrossRef CAS.
- H. Zhang, S. C. Smith, S. Nanbu and H. Nakamura, Aust. J. Chem., 2010, 63, 371 CrossRef CAS.
- H. Zhang, S. C. Smith, S. Nanbu and H. Nakamura, J. Phys.: Condens. Matter, 2009, 21, 144209 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. 





![Energy diagram of the photo-conversion between cyclohexadiene and hexatriene. Taken from Ref. [25].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f4.gif)
![Initial vibrational state specified cumulative reaction probabilities for H2(v = 2) + D+→H + HD +. dashed line : exact quantum mechanical numerical solution, solid line : ZN-TSH, dash-dot line : LZ-TSH. Taken from Ref. [26].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f5.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exact quantum mechanical numerical solution, solid line
exact quantum mechanical numerical solution, solid line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZN-TSH, dash-dot line
ZN-TSH, dash-dot line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LZ-TSH. Taken from Ref. [26].
LZ-TSH. Taken from Ref. [26].


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– bond rotates clockwise when the –C11
C10– bond rotates clockwise when the –C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12– bond rotates counterclockwise in any routes to the products. Note that the –C9
C12– bond rotates counterclockwise in any routes to the products. Note that the –C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– rotation occurs even when the system goes back to the reactant, i.e. to the 11-cis form. Since the rotation of the –C9
C10– rotation occurs even when the system goes back to the reactant, i.e. to the 11-cis form. Since the rotation of the –C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10– bond activates the motion directed to the 9-cis form, the channel to the 9-cis form is open in addition to that to the all-trans form. In this sense, the two conical intersections, one between the 11-cis and all-trans forms and the other between the 11-cis and 9-cis forms, are almost equally accessed in vacuo to make a transition to the ground state. As mentioned above, in the Rhodopsin protein environment, on the other hand, the 9-cis form is not generated. This indicates that in Rhodopsin the route to 9-cis form is blocked by the surrounding protein and only the route to the all-trans form (and reverted 11-cis form) is left open. The branching ratio of all-trans, 9-cis and 11-cis forms at the final stage is 1
C10– bond activates the motion directed to the 9-cis form, the channel to the 9-cis form is open in addition to that to the all-trans form. In this sense, the two conical intersections, one between the 11-cis and all-trans forms and the other between the 11-cis and 9-cis forms, are almost equally accessed in vacuo to make a transition to the ground state. As mentioned above, in the Rhodopsin protein environment, on the other hand, the 9-cis form is not generated. This indicates that in Rhodopsin the route to 9-cis form is blocked by the surrounding protein and only the route to the all-trans form (and reverted 11-cis form) is left open. The branching ratio of all-trans, 9-cis and 11-cis forms at the final stage is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Since the 9-cis form is counted as trans with respect to the 11-position, the ratio of the 11-trans form to the 11-cis form is 1
2. Since the 9-cis form is counted as trans with respect to the 11-position, the ratio of the 11-trans form to the 11-cis form is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The experimental quantum yield of isomerization is 0.67 in protein and 0.15 in solutions.31,32 Since we can assume safely from the discussion above that the protein environment in Rhodopsin suppresses the 9-cis form and leads to the all-trans product, the present result in vacuo is closer to the value in protein.
1. The experimental quantum yield of isomerization is 0.67 in protein and 0.15 in solutions.31,32 Since we can assume safely from the discussion above that the protein environment in Rhodopsin suppresses the 9-cis form and leads to the all-trans product, the present result in vacuo is closer to the value in protein.


![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) is given as:
is given as:![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) (β) = β∫∞0dE exp(−βE)PZN(E,Q0)
(β) = β∫∞0dE exp(−βE)PZN(E,Q0)![Arrhenius plot of the electron transfer rate in the weak coupling (HAD = 0.001au) case. Solid circle : exact perturbation theory, solid line : present result, dotted line : Marcus' high temperature theory, dash line : result with use of the LZ formula. Taken from Ref. [35].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f10.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exact perturbation theory, solid line
exact perturbation theory, solid line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) present result, dotted line
present result, dotted line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Marcus' high temperature theory, dash line
Marcus' high temperature theory, dash line![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) result with use of the LZ formula. Taken from Ref. [35].
result with use of the LZ formula. Taken from Ref. [35].

![Selective and complete excitation from the ground level to one of the excited level 2 by the quadratic frequency chirping in the case of three-level model. Taken from Ref. [40].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f11.gif)
![Time variation of wave packet populations on S0 and S1 states after the initial excitation. (a) and (b) with and without the directed momentum method, respectively. Taken from Ref. [25].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f12.gif)
![Highly efficient dissociation of a NaK molecule by using the quadratically chirped pulses within the pump-dump mechanism. (a) Potential energy curves of the ground and excited states and dipole moment. The bumpy wave packet is created by the pump-dump scheme from the ground vibrational state on the ground electronic potential curve and is finally pumped up by another quadratically chirped pulse to dissociate. (b) Time variation of the population of this bumpy wave packet on the ground and excited states. (c) Time variation of population of the wave packet to prepare the bumpy packet by pumping up from the ground vibrational state and dumping at the right turning point on the excited state. Taken from Ref. [41].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f13.gif)
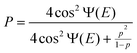



![Adiabatic potential energy curves for the hydrogen incidence perpendicularly to the molecular surface. The NT-type avoided crossings are designated as α. Taken from Ref. [50].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f17.gif)
![Transmission probability against energy. Taken from Ref. [50].](/image/article/2010/SC/c0sc00274g/c0sc00274g-f18.gif)
