Quantitative structure–reactivity modeling of copper-catalyzed atom transfer radical polymerization

Abstract

In this work, we present the first successful application of in silico modeling to the construction of quantitative and predictive relationships between the set of constants k_act, k_deact and K_ATRP and the structures and properties of various ATRP catalysts and initiators. The results are consistent not only with the generally accepted ATRP mechanistic picture but also provide valuable insights into this complex polymerization reaction. The models, built using the genetic function approximation algorithm, highlight and quantify the pivotal roles played in the ATRP process by energetic and steric factors of both catalysts and initiators as well as by the reaction medium. Moreover, the models suggest the existence of long-range interactions in catalyst–initiator recognition and subsequent binding. We believe that the approach will prove to be a powerful tool for the discovery of improved catalysts for ATRP.

---

Introduction

In order to lower the cost and shorten the time to market of new compounds, automated high-throughput synthesis, screening and characterization techniques have become increasingly common in chemical laboratories.^1–11 Notwithstanding the capability of these methodologies to carry out thousands of experiments per day, it has become apparent that a thorough exploration of the chemical space,¹² which is believed to exceed 10⁶⁰ compounds, is materially impossible. This has led to a greater use of computer-aided molecular design (CAMD) with the objective of finding a more reasonable number of molecules covering the chemical space as efficiently as possible.^13–22 The first step in a typical CAMD approach usually consists of the creation, on the basis of literature data, chemical knowledge and intuition, of virtual libraries of compounds (reaction space) whose structural and chemical properties are translated into numerical terms by calculating, for each of them, hundreds of molecular descriptors. The descriptors are mathematically treated, for instance with principal component analysis (PCA),^23–25 in order to select subsets of test items that cover the largest spread of molecular properties (diversity search). Once the actual experiments have been carried out and the reaction responses recorded, the reaction space is mathematically correlated with the response space by means of regression techniques. The resulting models are then used to design, in silico, the subsequent libraries of compounds to be tested in vitro. In general, when an initial hit is identified, new sets of compounds that sample smaller regions of the space around it are created and evaluated (similarity search). Several modeling/experiment cycles may be necessary before finding a compound with the specific combination of properties. While extensively employed in pharmaceutical^17,19,20 and agrochemical^16,18,21 research, virtual screening approaches have only started to be applied to the development of catalysts^26–41 and materials^42–47 recently.

Atom transfer radical polymerization (ATRP)^48–51 is one of the methods for controlled radical polymerization that have revolutionized the field of polymer chemistry in the last decade, the others being nitroxide mediated (NMP)^52,53 and reversible addition–fragmentation chain transfer (RAFT)^53,54 radical polymerizations. Macromolecules with precisely controlled architecture and functionality have been synthesized from a wide range of monomers under conditions that are much less stringent than those previously required for ionic living polymerizations.^50–52,54 Mechanism wise, ATRP is a redox-based process in which a transition-metal complex acts as a mediator for the intermittent generation of propagating radicals from alkyl halides (Scheme 1).^48,49 The polymerization control depends largely on the appropriate equilibrium between the activation (generation of radicals, k_act) and the deactivation (formation of alkyl halides, k_deact) processes, which determines the concentration of radicals and thus the rates of polymerization and termination as well as polydispersities. In particular, K_ATRP = k_act/k_deact should be sufficiently small in order to maintain a low concentration of radicals and to minimize termination reactions, whereas both k_act and k_deact should be large enough (though k_act ≪ k_deact) to provide good control over the polymerization while providing a reasonable polymerization rate. The values of K_ATRP, k_act and k_deact depend on the catalyst, initiator and monomer structure, as well as on the type of solvent and the reaction conditions. Understanding how these parameters affect the three reaction constants is crucial for the rational development of more efficient ATRP catalysts.

Scheme 1 Atom transfer radical polymerization equilibrium.

Recently, large datasets of K_ATRP, k_act and k_deact, either experimentally determined^55,56 or extrapolated by using the constant selectivity principle, were reported for a number of copper catalysts and alkyl halide initiators.⁵⁷ Semi-quantitative correlations between the structures of these compounds and K_ATRP⁵⁷ or k_act^57–59 were also described. In contrast, due to the difficulty of measuring the relative fast process, no such correlations are presently available for k_deact.

In this work, we present the first, successful application of in silico modeling to the construction of fully quantitative relationships between the set of constants k_act, k_deact and K_ATRP and the structures and properties of ATRP catalysts and initiators.

Computational details

All calculations were performed with the software package Materials Studio® 4.4⁶⁰ on a Windows Server 2008 SP1 64-bit equipped with 16 Intel Xeon 2.6GHz CPUs and 20GB RAM.

Geometry optimization

The geometry of catalysts and initiators was first pre-optimized with Forcite, an advanced classical molecular mechanics tool, using the Universal force field⁶¹ together with the SMART minimizer at the ultrafine quality level. The resulting conformers were taken as input structures in Dmol³,^62,63 a software for DFT calculations, using the following settings. Functional: generalized gradient approximation (GGA)^64,65 in combination with Becke exchange^66,67 plus Lee–Yang–Parr correlation⁶⁸ (BLYP); Basis set: double numerical plus d-function (DND); Basis file: 3.5; Core treatment: all electrons; Quality: fine; Integration accuracy: fine; SCF tolerance: fine; Max. SCF cycles: 50; Multipolar expansion: octapolar; DIIS: yes; DIIS size: 6; Orbital cutoff quality: fine; Orbital cutoff scheme: global; Solvation model: COSMO; Solvent: acetonitrile; Symmetry: yes; Energy convergence tolerance: 10⁻⁵ Ha; Max. force convergence tolerance: 2 × 10⁻³ Ha Å⁻¹; Max. displacement convergence tolerance: 5 × 10⁻³ Å; Max. iterations: 50; Max. step size: 0.3 Å.

Molecular descriptors

A large variety of molecular descriptors were calculated for both catalysts and initiators, including: quantum mechanical descriptors (total energy, HOMO, LUMO, HOMO–LUMO gap, binding energy, dielectric energy, solvation energy, surface area, cavity volume and dipoles, via Dmol³); molecular mechanical descriptors (bond and non-bond energies, van der Waals energy, electrostatic energy, valence energy (diagonal terms), angle energy, torsion energy and inversion energy, via Forcite); topological descriptors (Wiener index, Zagreb index, Balaban indices, ^mχ connectivity indices, ^mχ^v valence connectivity indices, ^mκ shape indices, α-modified ^mκ shape indices, molecular flexibility index, subgraph counts, edge adjacency and distance (magnitude), vertex adjacency and distance (magnitude and equality), bond, complementary and structural information content); electrotopological descriptors (E-state indices); spatial descriptors (molecular area, molecular volume, molecular density, principal moments of inertia, moments of inertia, radius of gyration, ellipsoidal volume, shadow areas, shadow area fractions, shadow lengths, shadow ratio, molecular shadow areas, molecular shadow area fractions, molecular shadow lengths, molecular shadow ratio, Connolly surface area, Connolly surface occupied volume, van der Waals surface area, solvent surface area, solvent-accessible surface area, van der Waals surface occupied volume, solvent surface occupied volume, and solvent-accessible occupied volume); thermodynamical descriptors (molecular refractivity, AlogP, and AlogP98); and constitutional descriptors (total molecular mass, atom count, element count, average N–Cu bond length, Cu–X bond length, C–X bond length, and count of various molecular fragments).⁶⁹

Principal components analysis (PCA)

PCA was carried out by standardizing the descriptor data by using the mean and scaling the results using unit standard deviation. Among all the resulting principal components, only those with an eigenvalue ≥ 1 were used subsequently.

Hierarchical cluster analysis (HCA)

Hierarchical cluster analysis was performed by applying the Ward's clustering method⁷⁰ along with Murtagh's reciprocal nearest neighbors (RNN) algorithm⁷¹ to the first n principal components for which the total variance explained was ≥0.9. The data were centered on the mean.

Regression analysis

Quantitative structure–reactivity relationships (QSRR) were built using the genetic function approximation (GFA) algorithm.⁷² Unless otherwise specified, the literature values of k_act and k_deact for copper complexes used in this study were those reported at 22 °C in MeCN with EtBriB as the initiator, whereas those of k_act and K_ATRP for the initiators refer to those reported at 22 °C in MeCN with PMDETA/CuBr as the catalyst.⁵⁷ Basis functions: linear polynomial and spline; Additional terms: none; Initial equation length: 5 terms; Maximum equation length: 9 terms; Population: up to 2000; Maximum generations: up to 5000; Number of top equations returned: 10; Mutation probability: 0.4; Total spline mutation probability: 0.1; Knot shift mutation probability: 0.5; Maximum knot shift fraction: 0.1; Random number seed: 9999; Minimum prediction fraction for term inclusion: 0.0001; Scoring function: Friedman's LOF;⁷³ Scaled LOF smoothness parameter: 0.5.

Results and discussion

Catalysts

Quantitative structure–reactivity relationship (QSRR) models were constructed utilizing 20 complexes that contain copper and multidentate nitrogen-based ligands (Chart 1) for which the values for the set of constants k_act, k_deact and K_ATRP had been reported in the literature.⁵⁷ In particular, the rate constants k_act and k_deact were quantitatively correlated with what are believed to be the structures of the activators and the deactivators in solution, respectively.

Chart 1 Ligands for copper-catalyzed atom transfer radical polymerization used in this study.

The complexes with Cu^IX and either bidentate (bpy, dNbpy, NPPMI, NOPMI) or tetradentate (HMTETA, [2.2.3], [2.3.2], [3.2.3], BPED, Me₆TREN, Et₆TREN, MA₆TREN, BA₆TREN, AN₆TREN, TPMA, Me₄Cyclam, DMCBCy) ligands have been reported to exist in solution preferentially as [Cu^I(κ²-Lig)₂]⁺ and [Cu^I(κ⁴-Lig)]⁺ respectively, whereas those with Cu^IIX₂ as [Cu^II(κ²-Lig)₂X]⁺ and [Cu^II(κ⁴-Lig)X]⁺.^74,75 On the other hand, in the presence of tridentate ligands such as PMDETA and BPMPA, Cu^IX and Cu^IIX are likely to form neutral complexes of the type [Cu^I(κ³-Lig)X] and [Cu^II(κ³-Lig)X₂] though the displacement of a halogen atom by the solvent or monomer is feasible in both species.^74,75 Finally, the complex with Cu^IX and TPEN may exist both as a binuclear tricoordinated complex, [Cu^I(κ³-TPEN)X]₂, and a mononuclear pentacoordinated complex, [Cu^I(κ⁵-TPEN)]⁺, the latter likely being the active species, while Cu^IIX₂ with TPEN can only exist as a mononuclear and hexacoordinated compound [Cu^II(κ⁵-TPEN)X]⁺.⁷⁶

After optimizing the geometries, molecular descriptors were calculated for each of the copper complexes above, and PCA was performed on the Cu(I) and Cu(II) species separately. The first 6 principal components (PCs) of each of the two groups of complexes were subjected to hierarchical cluster analysis (Fig. S1 and S2, ESI†). Test sets of diverse molecules were obtained by selecting one complex from each of the 4 most distant clusters such that the corresponding points in the figure-of-merit space were homogeneously spaced out. Accordingly, [Cu^I(NPPMI)Br], [Cu^I(Me₆TREN)]⁺, [Cu^I(MA₆TREN)]⁺ and [Cu^I(TPEN)]⁺ were chosen as a test set for the modeling of k_act, whereas [Cu^II(BPMPA)Br₂], [Cu^II(MA₆TREN)Br]⁺, [Cu^II(DMCBCy)Br]⁺ and [Cu^II(TPEN)Br]⁺ as a test set for k_deact. Furthermore, in order to ensure the inclusion of the most relevant molecular information, the initial group of descriptors used for modeling the remaining 16 activators and 16 deactivators (training sets) was chosen among the peripheral points in the loading plots PC1 vs. PC2 vs. PC3 (Fig. S3 and S4, ESI†). Generally accepted mechanistic considerations of the ATRP process were also taken into consideration. The number of descriptors was progressively reduced by iteratively subjecting them to GFA algorithm and discarding, after each regression cycle, those with the lowest occurrences in the populations.

Of all the molecular descriptors calculated for Cu(I) complexes, HOMO energy (HOMO), cavity volume (CV), molecular area (MA), moment of inertia Z (I_Z), van der Waal's surface area (vSA), solvent surface area (SSA), ⁵χ_path, ⁵χ_chain, ⁵χ^v_chain, ⁶χ_path, and ⁶χ^v_path survived the selection process for k_act. These were used to build quantitative structure–reactivity relationships and the GFA algorithm with linear polynomials returned the top 10 models in Table 1. The values of Friedman's LOF, R², adjusted R², cross-validated R², significance-of-regression (SOR) F-value, and critical SOR F-value (95%) indicate that all the regressions are statistically significant. Interestingly, eqn (10) rather than the one with the lowest Friedman's LOF value yields the best prediction for the test set (Fig. 1). A close look at the models reveals a direct proportionality between k_act and HOMO, which mirrors the experimental observation that the higher the reducing power of a Cu(I) complex, the higher its ATRP activity.⁵⁷ The regressions highlight also the pivotal role played in the reactivity of Cu(I) compounds by topological descriptors, which differentiate the molecules according to their size, degree of branching, flexibility and overall shape. It is worth noting that only few of the tens of topological indices computed in the present study ended up in the models. This should minimize the risk of “fortuitous explanation” of the figure-of-merit that is sometimes observed with relationships containing a large number of such parameters.⁷⁷ Surface area-based descriptors, which measure the extent to which molecules expose themselves to the external environment, have been generally related to molecular factors such as transport and solubility. It is therefore interesting to find out that MA and vSA, although positively correlated, not only have opposite effects on k_act but also, as pointed out by control GFA analysis, both parameters need to be present in the model in order to obtain a reliable regression. According to the role of CV in the equations, metal accessibility is another parameter that should be taken into consideration when designing an ATRP catalyst (vide infra). The moments of inertia depend on both the mass of each atom in the molecule and the overall molecular geometry. The presence of I_z in five out of ten models can be therefore taken as a further evidence of the importance of the geometry of the activator on the activation process. In contrast, the absence of the average N–Cu bond length in all the models may be symptomatic of a secondary role, with respect to the other parameters, played by the stability of Cu(I) complexes in the activation process. The relatively small preference of Cu(I) for specific donor atoms as well as the much smaller variation, compared to Cu(II) compounds, of the stabilities of its complexes as the ligand is altered have been recently pointed out.⁷⁸

Table 1 Top 10 models and relative statistical analysis for log(k_act) of Cu(I) activators obtained with genetic function approximation algorithm. The models are in order of increasing Friedman's LOF values and the one with the best prediction for the test set is given in bold

	Model	Friedman's LOF	R ^2	Adjusted R^2	Cross-validated R^2	SOR F-value	Critical SOR F-value (95%)
1	log(kact) = 47(HOMO) + 6.7 × 10^−3(CV) − 3.1(^5χpath) + 5.1(^6χpath) + 42(^5χ^vchain) − 4.3(^6χ^vpath) + 0.46(MA) + 1.6 × 10^−3(IZ) − 0.54(vSA) + 11	0.450	0.990	0.974	0.937	63.6	4.15
2	log(kact) = 58(HOMO) + 8.1 × 10^−3(CV) − 2.5(^5χpath) + 30(^5χchain) + 4.0(^6χpath) − 3.2(^6χ^vpath) + 0.37(MA) + 1.8 × 10^−3(IZ) − 0.47(vSA) + 12	0.497	0.988	0.971	0.807	57.6	4.15
3	log(kact) = 59(HOMO) + 7.9 × 10^−3(CV) − 3.5(^5χpath) + 5.9(^6χpath) + 45(^5χ^vchain) − 5.3(^6χ^vpath) + 0.54(MA) − 0.64(vSA) + 12	0.510	0.978	0.952	0.874	38.3	3.75
4	log(kact) = 58(HOMO) + 11 × 10^−3(CV) − 3.4(^5χpath) + 5.6(^6χpath) + 44(^5χ^vchain) − 5.2(^6χ^vpath) + 0.55(MA) − 0.67(vSA) + 7.3 × 10^−3(SSA) + 11	0.588	0.986	0.966	0.780	48.5	4.15
5	log(kact) = 71(HOMO) + 13 × 10^−3(CV) − 2.8(^5χpath) + 32(^5χchain) + 4.5(^6χpath) − 4.2(^6χ^vpath) + 0.47(MA) − 0.61(vSA) + 8.7 × 10^−3(SSA) + 11	0.611	0.986	0.964	0.742	46.7	4.15
6	log(kact) = 73(HOMO) + 9.5 × 10^−3(CV) − 2.9(^5χpath) + 32(^5χchain) + 4.8(^6χpath) − 4.3(^6χ^vpath) + 0.47(MA) − 0.56(vSA) + 12	0.612	0.973	0.942	0.553	31.7	3.75
7	log(kact) = 36(HOMO) − 2.3 × 10^−3(CV) − 1.6(^5χpath) + 26(^5χchain) + 2.2(^6χpath) + 5.4 × 10^−3(IZ) − 14 × 10^−3(SSA) + 12	0.906	0.935	0.879	0.735	16.6	3.51
8	log(kact) = 63(HOMO) + 8.3 × 10^−3(CV) − 3.3(^5χpath) + 9.9(^5χchain) + 5.6(^6χpath) + 31(^5χ^vchain) − 5.0(^6χ^vpath) + 0.52(MA) − 0.61(vSA) + 12	0.927	0.979	0.946	0.554	30.6	4.15
9	log(kact) = 38(HOMO) − 1.6(^5χpath) + 26(^5χchain) + 2.1(^6χpath) + 5.1 × 10^−3(IZ) − 20 × 10^−2(vSA) − 8.9 × 10^−3(SSA) + 12	0.967	0.931	0.871	0.518	15.4	3.51
10	log(k act ) = 35(HOMO) − 2.8( ^5 χ path ) + 4.6( ^6 χ path ) + 41( ^5 χ ^v chain ) − 3.0( ^6 χ ^v path ) + 0.32(MA) + 3.5 × 10 ^−3 (I Z ) − 0.34(vSA) + 11 × 10 ^−3 (SSA) + 12	0.986	0.977	0.943	0.762	28.7	4.15

---

Fig. 1 Calculated vs. experimental log(k_act) values for Cu(I) activators obtained by genetic function approximation analysis with linear polynomials. Training and test sets are represented by the symbols “” and “”, respectively.

As to k_deact, which is responsible for the control in ATRP reactions, the following descriptors for Cu(II) complexes outlasted the selection process: ⁴χ^v_path, ⁴χ^v_path/cluster, ⁵χ^v_path/cluster, electrostatic energy (EE), valence energy (VE), binding energy (BE), LUMO–HOMO energy (L–H), dipole Y (δ_Y), surface area (SA), average N–Cu bond length (N–Cu), and Cu–Br bond length (Cu–Br). The comparison of these parameters with those obtained for the activation reaction highlights a higher incidence of energetic terms on the deactivation reaction. The GFA algorithm with linear polynomials returned the statistically significant top 10 models in Table 2. To the best of our knowledge, this is the first time that correlations between k_deact and the structure of ATRP catalysts are reported. Similar to what was found for k_act, model 14 rather than the one with the lowest Friedman's LOF value exhibits the highest predictive power (Fig. 2), despite the negative value of cross-validated R². Likewise topological descriptors, whose importance has already been discussed above, L–H and SA appear in all the 10 equations. In particular, the fact that the rate of deactivation is roughly proportional to the width of the L–H gap is consistent with the known, high kinetic reactivity of compounds having a narrow band gap.⁷⁹ On the other hand, the direct proportionality between SA and k_deact can be rationalized on the basis of the different affinities of Cu(II) complexes for the reaction medium. The Cu–Br bond length, which turns out to be inversely proportional to the deactivation rate constant, is another important parameter that emerges from the modeling. Intuitively it is expected that the shorter the length of the Cu–Br bond, the stronger is the bond and hence the more favored is the deactivation process. This relates also to the concept of metal “halidophilicity”. It is experimentally observed that the degree of control in ATRP is lower in the presence of metal complexes with low halide affinity and/or of solvents that, like water, favor the dissociation of halides by effectively solvating them, thus reducing the amount of deactivator in solution.^80,81 Interestingly, albeit not included in model 14, N–Cu is present in four out of the ten regressions suggesting that, unlike Cu(I), the stabilities of Cu(II) complexes should be taken into consideration when designing an ATRP catalyst.^82,83

Table 2 Top 10 models and relative statistical analysis for log(k_deact) of Cu(II) deactivators obtained with genetic function approximation algorithm. The models are in order of increasing Friedman's LOF values and the one with the best prediction for the test set is given in bold

	Model	Friedman's LOF	R ^2	Adjusted R^2	Cross-validated R^2	SOR F-value	Critical SOR F-value (95%)
11	log(kdeact) = −2.3(^4χ^vpath) − 1.8(^4χ^vpath/cluster) + 1.4(^5χ^vpath/cluster) − 9.1 × 10^−3(VE) + 1.3(BE) + 4.1 × 10^2(L–H) − 0.25(δY) + 19 × 10^−3(SA) − 0.25	1.30	0.906	0.800	−1.37	8.48	3.75
12	log(kdeact) = −2.0(^4χ^vpath) − 1.0(^4χ^vpath/cluster) + 0.90(^5χ^vpath/cluster) − 20 × 10^−3(VE) + 14(N–Cu) − 6.1(Cu–Br) + 4.3 × 10^2(L–H) + 8.2 × 10^−3(SA) − 10	1.40	0.899	0.784	0.0716	7.81	3.75
13	log(kdeact) = −2.1(^4χ^vpath) − 1.2(^4χ^vpath/cluster) + 1.1(^5χ^vpath/cluster) − 9.6 × 10^−3(VE) − 5.0(Cu–Br) + 0.82(BE) + 4.3 × 10^2(L–H) + 14 × 10^−3(SA) + 13	1.54	0.889	0.762	0.0711	7.02	3.75
14	log(k deact ) = −2.0( ^4 χ ^v path ) − 1.0( ^4 χ ^v path/cluster ) + 0.79( ^5 χ ^v path/cluster ) + 4.3 × 10 ^−3 (EE) − 5.9(Cu–Br) + 4.0 × 10 ^2 (L–H) − 0.18(δ Y ) + 8.0 × 10 ^−3 (SA) + 17	1.78	0.872	0.725	−3.40	5.94	3.75
15	log(kdeact) = −2.0(^4χ^vpath) − 1.4(^4χ^vpath/cluster) + 1.0(^5χ^vpath/cluster) + 2.5 × 10^−3(EE) − 0.87(BE) + 3.6 × 10^2(L–H) − 0.25(δY) + 14 × 10^−3(SA) + 0.59	1.81	0.869	0.720	−4.52	5.82	3.75
16	log(kdeact) = −1.9(^4χ^vpath) − 1.1(^4χ^vpath/cluster) + 0.97(^5χ^vpath/cluster) − 12 × 10^−3(VE) + 9.3(N–Cu) + 0.76(BE) + 4.2 × 10^2(L–H) + 13 × 10^−3(SA) − 18	1.95	0.859	0.699	−3.68	5.35	3.75
17	log(kdeact) = −2.0(^4χ^vpath) − 0.91(^4χ^vpath/cluster) + 0.81(^5χ^vpath/cluster) + 2.6 × 10^−3(EE) − 5.1 × 10^−3(VE) − 7.6(Cu–Br) + 4.4 × 10^2(L–H) + 7.7 × 10^−3(SA) + 21	1.98	0.857	0.693	−3.88	5.24	3.75
18	log(kdeact) = −1.8(^4χ^vpath) − 0.78(^4χ^vpath/cluster) + 0.69(^5χ^vpath/cluster) + 2.7 × 10^−3(EE) − 5.1(Cu–Br) + 0.40(BE) + 3.8 × 10^2(L–H) + 9.8 × 10^−3(SA) + 14	2.06	0.852	0.682	−6.90	5.03	3.75
19	log(kdeact) = −1.8(^4χ^vpath) − 0.73(^4χ^vpath/cluster) + 0.65(^5χ^vpath/cluster) + 3.5 × 10^−3(EE) − 0.99(N–Cu) − 7.0(Cu–Br) + 4.1 × 10^2(L–H) + 7.0 × 10^−3(SA) + 22	2.23	0.839	0.655	−3.89	4.56	3.75
20	log(kdeact) = −2.0(^4χ^vpath) − 1.2(^4χ^vpath/cluster) + 0.94(^5χ^vpath/cluster) − 19 × 10^−3(VE) + 18(N–Cu) + 3.9 × 10^2(L–H) − 0.17(δY) + 8.2 × 10^−3(SA) − 32	2.32	0.833	0.643	−2.52	4.37	3.75

---

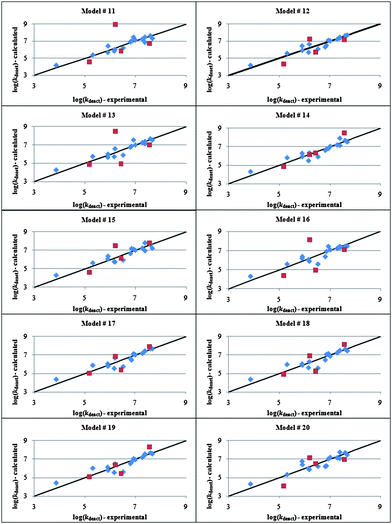Fig. 2 Calculated vs. experimental log(k_deact) values for Cu(II) deactivators obtained by genetic function approximation analysis with linear polynomials. Training and test sets are represented by the symbols “” and “”, respectively.

When linear splines were employed as basis functions in the GFA algorithm, the resulting models not only contained a smaller number of molecular descriptors (Tables S1 and S2, ESI†) but also provided better predictions for the training set (Fig. S5 and S6, ESI†). None of them, however, was able to produce reliable predictions for the test set.

Initiators

The procedure used to build QSRR models for the ATRP initiators was identical to that described above for the catalysts. In particular, the constants k_act and K_ATRP were quantitatively correlated to the structures of the 21 alkyl halides depicted in Chart 2. In contrast, since the function k_deact = f(structure of active radicals) is not bijective as different values of k_deact (e.g., for CH₃OCOCH₂Cl and CH₃OCOCH₂Br) may correspond to the structure of a single radical (i.e., CH₃OCOCH₂˙), it was not possible to model the deactivation rate constants directly. With the help of HCA carried out on the first 6 principal components (Fig. S7, ESI†), MClAc, tBBrP, BrAN and ECPA were chosen as the test set for k_act, whereas MClAc, tBBrP, BrAN and AllBr as the one for K_ATRP.

Chart 2 Alkyl halide initiators for atom transfer radical polymerization used in this study.

The descriptors selected for k_act, namely nitrile fragment counts (CN), total molecular mass (M_w), molecular volume (MV), molecular refractivity (MR), Wiener index (W), ¹κ, ⁰χ^v, ³χ_path, ³χ_cluster, principal moment of inertia X (I_X), radius of gyration (RoG), ellipsoidal volume (EV), solvation energy (SE) and LUMO energy (LUMO) were used in the GFA algorithm, which returned the top 10 linear polynomials in Table 3. Interestingly, both regression 22 and 30, which have the second lowest and the highest Friedman's LOF value, respectively, show the highest predictive power for the test set (Fig. 3). The models suggest that shape- and size-based descriptors play a crucial role also in the reactivity of the initiators. This can be rationalized as follows. Since ATRP is believed to occur through an inner sphere electron transfer (ISET) mechanism,⁸⁴ the halogen of the alkyl halide needs to be in the first coordination sphere of the metal center in order for the atom transfer to take place. It is therefore reasonable to imagine that the more compatible the shape of the initiator is with the steric neighborhood of the metal center in the activator, the more effective is the activation reaction (vide supra). The fact that the solvation energy appears in a number of regressions underlines further the importance of the solvent in the ATRP equilibrium.⁸¹ Another remarkable finding is the inverse proportionality between k_act and LUMO energy. This is consistent with the fact that the alkyl halide is the electron acceptor in the activation reaction and hence the lower the energy of the LUMO, the faster is the reduction. Moreover, the beneficial effect on the activation process resulting from the presence of a nitrile on the activator is due to the ability of this group to stabilize radicals by resonance, a property exploited in azo initiators for conventional free radical polymerization for example the use of 2,2′-azobisisobutyronitrile (AIBN).

Table 3 Top 10 models and relative statistical analysis for log(k_act) of alkyl halide initiators obtained with genetic function approximation algorithm. The models are in order of increasing Friedman's LOF values and the ones with the best prediction for the test set are given in bold

	Model	Friedman's LOF	R ^2	Adjusted R^2	Cross-validated R^2	SOR F-value	Critical SOR F-value (95%)
21	−log(kact) = −1.9(CN) − 22 × 10^−3(W) − 1.6(^0χ^v) + 0.16(MV) − 5.0(RoG) + 41(LUMO) + 9.1	0.312	0.972	0.955	0.0595	57.5	3.23
22	−log(k act ) = −2.8(CN) − 25 × 10 ^−3 (W) − 1.8( ^0 χ ^v ) + 0.19(MV) − 7.4(RoG) − 1.9 × 10 ^2 (SE) + 45(LUMO) + 9.9	0.379	0.978	0.961	0.353	57.5	3.30
23	−log(kact) = −33 × 10^−3(W) − 1.8(^0χ^v) + 0.13(MV) + 43(LUMO) + 2.2	0.455	0.919	0.893	0.675	34.3	3.31
24	−log(kact) = −25 × 10^−3(W) − 1.4(^0χ^v) + 0.10(MV) + 1.9 × 10^2(SE) + 39(LUMO) + 4.7	0.477	0.938	0.910	0.629	33.3	3.22
25	−log(kact) = −1.9(CN) − 22 × 10^−3(W) + 12 × 10^−3(^3χpath) − 1.5(^0χ^v) + 0.16(MV) − 5.1(RoG) + 42(LUMO) + 9.1	0.488	0.972	0.950	−0.0681	44.3	3.30
26	−log(kact) = −0.85(CN) − 30 × 10^−3(W) − 1.8(^0χ^v) + 0.12(MV) + 34(LUMO) + 2.7	0.498	0.935	0.906	−1.08	31.8	3.22
27	−log(kact) = −6.8 × 10^−3(W) + 3.9 × 10^2(SE) + 46(LUMO) + 9.8	0.546	0.874	0.845	0.684	30.0	3.57
28	−log(kact) = −15 × 10^−3(W) + 0.60(^3χpath) + 3.8 × 10^2(SE) + 45(LUMO) + 9.1	0.580	0.897	0.863	0.752	26.2	3.31
29	−log(kact) = −31 × 10^−3(W) − 1.7(^0χ^v) + 0.14(MV) − 1.4(RoG) + 49(LUMO) + 3.8	0.582	0.924	0.890	0.696	26.9	3.22
30	−log(k act ) = −3.3(CN) − 26 × 10 ^−3 (W) − 0.48( ^3 χ path ) − 2.2( ^0 χ ^v ) + 0.22(MV) − 7.6(RoG) − 2.8 × 10 ^2 (SE) + 40(LUMO) + 8.5	0.582	0.981	0.962	0.386	52.0	3.45

---

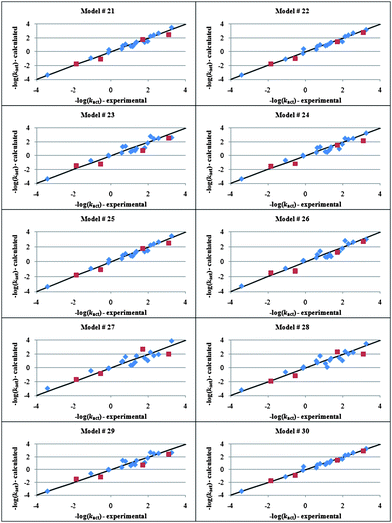Fig. 3 Calculated vs. experimental log(k_act) values for alkyl halide initiators obtained by genetic function approximation analysis with linear polynomials. Training and test sets are represented by the symbols “” and “”, respectively.

As far as K_ATRP is concerned, the following descriptors were found to be important for the modeling: nitrile fragment counts (CN), element count (EC), molecular density (MD), molecular refractivity (MR), Balaban index X (J_X), Balaban index Y (J_Y), ²χ, principal moment of inertia X (I_X), dipole Z (δ_Z), shadow area ZX plane (ShA_ZX), solvent surface occupied volume (SSOV), solvation energy (SE), total energy (TE), binding energy (BE), HOMO energy (HOMO), LUMO–HOMO energy (L–H) and C–X bond distance (C–X). When these parameters were used with the GFA algorithm, the linear polynomials in Table 4 were obtained, among which models 38 and 40 distinguished themselves for the reliability of the predictions (Fig. 4). The presence in the models of the highly discriminating Balaban index, whose value is substantially independent of the size of the molecule, as well as of the solvent surface occupied volume and solvation energy adds to what has already been said about the relevance of, respectively, topological descriptors and reaction medium in ATRP. By the same token, the fact that most equations contain the moment of inertia I_x goes back to the previously discussed importance of the geometry of the species involved in the ATRP equilibrium. Notably, since dipolar properties have been correlated to long-range electrostatic interactions,⁶⁹ which are believed to strongly influence the mutual orientation of ligands and receptors prior to Brownian collision and subsequent binding,⁸⁵ the inclusion of δ_Z in the regressions may indicate the existence of analogous long-range recognition processes between ATRP catalysts and initiators. Last but not least, a thorough analysis of the models points out the marked incidence of the total energy of the initiator on K_ATRP. TE is a measure of the overall reactivity of a molecule and can be related, in the present case, to both the reactivity of the carbon–halogen bond and the presence of radical stabilizing groups in the initiators.

Table 4 Top 10 models and relative statistical analysis for log(K_ATRP) of alkyl halide initiators obtained with genetic function approximation algorithm. The models are in order of increasing Friedman's LOF values and the ones with the best prediction for the test set are given in bold

	Model	Friedman's LOF	R ^2	Adjusted R^2	Cross-validated R^2	SOR F-value	Critical SOR F-value (95%)
31	−log(KATRP) = 5.9(EC) − 2.5(MR) + 2.7(JY) − 4.8(^2χ) − 6.6 × 10^−3(IX) − 1.5 × 10^2(SE) − 3.5 × 10^−3(TE) − 15(BE) + 13	86.7 × 10^−3	0.996	0.992	0.956	259	3.45
32	−log(KATRP) = −6.1(JX) + 7.9(JY) − 3.4(^0χ^v) − 8.8 × 10^−3(IX) + 49 × 10^−3(SSOV) + 45(HOMO) − 1.2(δZ) + 9.9(C–X) − 8.0	88.5 × 10^−3	0.996	0.992	0.977	254	3.45
33	−log(KATRP) = −19(JX) + 21(JY) − 1.5(^0χ^v) + 3.1(MD) − 9.7 × 10^−3(IX) − 39 × 10^−3(SSOV) + 1.1 × 10^3(SE) − 69(LUMO) − 3.3(δZ) − 1.1	92.5 × 10^−3	0.998	0.995	0.983	342	3.70
34	−log(KATRP) = 4.1(EC) − 1.9(MR) + 2.4(JY) − 4.0(^2χ) − 7.2 × 10^−3(IX) − 2.7 × 10^−3(TE) − 13(BE) − 0.58(δZ) + 12	93.5 × 10^−3	0.996	0.992	0.984	240	3.45
35	−log(KATRP) = 4.6(EC) − 2.3(MR) − 2.2(^2χ) − 7.6 × 10^−3(IX) − 0.14(ShAZX) − 3.3 × 10^−3(TE) − 16(BE) + 22	98.1 × 10^−3	0.993	0.988	0.966	186	3.30
36	−log(KATRP) = −11(JX) + 12(JY) − 1.0(^0χ^v) − 9.3 × 10^−3(IX) + 21 × 10^−3(SSOV) + 4.7 × 10^2(SE) − 2.6 × 10^−4 (TE) − 31(L–H) − 2.0(δZ) + 11	99.7 × 10^−3	0.998	0.994	0.970	320	3.70
37	−log(KATRP) = −2.1(CN) − 0.59(EC) + 2.5(JY) − 3.5(^0χ^v) − 9.8 × 10^−3(IX) + 66 × 10^−3(SSOV) − 1.8(δZ) + 9.2(C–X) − 21	0.107	0.995	0.990	0.965	207	3.45
38	−log(K ATRP ) = −9.5(J X ) + 10(J Y ) − 9.8 × 10 ^−3 (I X ) + 4.8 × 10 ^2 (SE) − 3.4 × 10 ^−4 (TE) − 0.89(BE) − 1.7(δ Z ) + 9.1	0.109	0.992	0.986	0.974	167	3.30
39	−log(KATRP) = 6.1(EC) − 2.7(MR) + 2.9(JX) − 5.5(^2χ) − 6.4 × 10^−3(IX) − 2.1 × 10^−3(SE) − 3.8 × 10^−3 (TE) − 18(BE) + 14	0.111	0.995	0.990	0.960	202	3.45
40	−log(K ATRP ) = −9.1(J X ) + 10(J Y ) − 10 × 10 ^−3 (I X ) + 10 × 10 ^−3 (SSOV) + 51 × 10 ^2 (SE) − 2.8 × 10 ^−4 (TE) − 1.8(δ Z ) + 6.6	0.111	0.992	0.986	0.961	163	3.30

---

Fig. 4 Calculated vs. experimental log(K_ATRP) values for alkyl halide initiators obtained by genetic function approximation analysis with linear polynomials. Training and test sets are represented by the symbols “” and “”, respectively.

As seen with the catalysts, when linear splines were used as basis functions in the GFA algorithm, the resulting models, while containing less molecular descriptors (Tables S3 and S4, ESI†) and providing better predictions for the training set, failed to return reliable values for the test set (Fig. S8 and S9, ESI†).

Conclusions

In this work, in silico modeling has been applied for the first time to the construction of quantitative and predictive relationships between the set of constants k_act, k_deact and K_ATRP and the structures and properties of various ATRP catalysts and initiators. The results are consistent not only with the generally accepted mechanistic picture for ATRP but also provide unprecedented insight into the factors governing this complex reaction. The models highlight and quantify the crucial roles played in ATRP by (i) the absolute and relative HOMO and LUMO energies and (ii) the topology (i.e., size, flexibility, geometry, overall shape etc.) of both catalysts and initiators; (iii) the compatibility between the shape of the initiator and the steric neighborhood of the metal center in the activator; (iv) the presence of radical stabilizing groups in the initiator; (v) the Cu–Br and the average N–Cu bond lengths in the deactivator; and (vi) the affinity of both catalysts and initiators for the reaction medium. Moreover, the regressions suggest the existence of long-range interactions in catalyst–initiator recognition and subsequent reaction. The approach is expected to greatly facilitate the design of new generations of atom transfer radical polymerization catalysts of wider academic and industrial interest.

Acknowledgements

The Agency for Science, Technology and Research, Singapore, is gratefully acknowledged for financial support.

Notes and references

1. B. Jandeleit, D. J. Schaefer, T. S. Powers, H. W. Turner and W. H. Weinberg, Angew. Chem., Int. Ed., 1999, 38, 2494–2532.
2. J. P. Stambuli and J. F. Hartwig, Curr. Opin. Chem. Biol., 2003, 7, 420–426.
3. J. G. de Vries and A. H. M. de Vries, Eur. J. Org. Chem., 2003, 799–811.
4. C. Gennari and U. Piarulli, Chem. Rev., 2003, 103, 3071–3100.
5. I. Takeuchi, J. Lauterbach and M. J. Fasolka, Mater. Today, 2005, 8, 18–26.
6. W. F. Maier, K. Stoewe and S. Sieg, Angew. Chem., Int. Ed., 2007, 46, 6016–6067.
7. D. L. Kale, S. C. Chaturvedi, D. Patil and R. B. Kakde, Pharm. Rev., 2008, 6, 46–51.
8. L. M. Mayr and D. Bojanic, Curr. Opin. Pharmacol., 2009, 9, 580–588.
9. J. Inglese and D. S. Auld, in Wiley Encyclopedia of Chemical Biology, ed. T. P. Begley, John Wiley & Sons, Inc., Hoboken, NJ, 2009, pp. 260–274.
10. H. W. Turner, A. F. Volpe and W. H. Weinberg, Surf. Sci., 2009, 603, 1763–1769.
11. V. Busico, R. Pellecchia, F. Cutillo and R. Cipullo, Macromol. Rapid Commun., 2009, 30, 1697–1708.
12. P. Kirkpatrick and C. Ellis, Nature, 2004, 432, 823 and references therein.
13. W. P. Walters, M. T. Stahl and M. A. Murcko, Drug Discovery Today, 1998, 3, 160–178.
14. R. Carlson, J. Carlson and A. Grennberg, J. Chemom., 2001, 15, 455–474.
15. B. K. Shoichet, Nature, 2004, 432, 862–865.
16. S. D. Lindell and J. Scherkenbeck, Comb. Chem. High Throughput Screening, 2005, 8, 555–562.
17. C. McInnes, Curr. Opin. Chem. Biol., 2007, 11, 494–502.
18. K.-J. Schleifer, Virtual Screening in Crop Protection Research, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007.
19. U. Rester, Curr. Opin. Drug Discovery Dev., 2008, 11, 559–568.
20. J. M. Rollinger, H. Stuppner and T. Langer, Prog. Drug Res., 2008, 65, 211–249.
21. S. D. Lindell, L. C. Pattenden and J. Shannon, Bioorg. Med. Chem., 2009, 17, 4035–4046.
22. A. Varnek and A. Tropsha, Chemoinformatics Approaches to Virtual Screening, Royal Society of Chemistry, Cambridge, UK, 2009.
23. K. Pearson, Philos. Mag., 1901, 2, 559–572.
24. H. Hotelling, J. Educ. Psychol., 1933, 24, 417–441.
25. H. Hotelling, J. Educ. Psychol., 1933, 24, 498–520.
26. R. Scordamaglia and L. Barino, Macromol. Theory Simul., 1998, 7, 399–405.
27. R. Scordamaglia and L. Barino, Macromol. Theory Simul., 1998, 7, 407–419.
28. S. Yao and Y. Tanaka, Macromol. Theory Simul., 2001, 10, 850–854.
29. K. B. Lipkowitz and M. C. Kozlowski, Synlett, 2003, 1547–1565.
30. E. Burello, D. Farrusseng and G. Rothenberg, Adv. Synth. Catal., 2004, 346, 1844–1853.
31. E. Burello, P. Marion, J.-C. Galland, A. Chamard and G. Rothenberg, Adv. Synth. Catal., 2005, 347, 803–810.
32. V. L. Cruz, J. Ramos, S. Martinez, A. Munoz-Escalona and J. Martinez-Salazar, Organometallics, 2005, 24, 5095–5102.
33. J. B. van der Linden, E.-J. Ras, S. M. Hooijschuur, G. M. Klaus, N. T. Luchters, P. Dani, G. Verspui, A. A. Smith, E. W. P. Damen, B. McKay and M. Hoogenraad, QSAR Comb. Sci., 2005, 24, 94–98.
34. E. Burello and G. Rothenberg, Int. J. Mol. Sci., 2006, 7, 375–404.
35. G. Occhipinti, H.-R. Bjørsvik and V. R. Jensen, J. Am. Chem. Soc., 2006, 128, 6952–6964.
36. J. A. Hageman, J. A. Westerhuis, H.-W. Fruhauf and G. Rothenberg, Adv. Synth. Catal., 2006, 348, 361–369.
37. V. L. Cruz, J. Martinez, J. Martinez-Salazar, J. Ramos, M. L. Reyes, A. Toro-Labbe and S. Gutierrez-Oliva, Polymer, 2007, 48, 7672–7678.
38. V. L. Cruz, S. Martinez, J. Martinez-Salazar, D. Polo-Cero, S. Gomez-Ruiz, M. Fajardo and S. Prashar, Polymer, 2007, 48, 4663–4674.
39. M. L. Drummond and B. G. Sumpter, Inorg. Chem., 2007, 46, 8613–8624.
40. A. G. Maldonado, J. A. Hageman, S. Mastroianni and G. Rothenberg, Adv. Synth. Catal., 2009, 351, 387–396.
41. A. G. Maldonado and G. Rothenberg, Chem. Soc. Rev., 2010 10.1039/b921393g.
42. C. H. Reynolds, J. Comb. Chem., 1999, 1, 297–306.
43. J. S. Duca, Y.-F. Tseng and A. J. Hopfinger, Adv. Mater., 2001, 13, 1713–1717.
44. J. R. Smith, A. Seyda, N. Weber, D. Knight, S. Abramson and J. Kohn, Macromol. Rapid Commun., 2004, 25, 127–140.
45. N. Adams and P. Murray-Rust, Macromol. Rapid Commun., 2008, 29, 615–632.
46. T. Puzyn, D. Leszczynska and J. Leszczynski, Small, 2009, 5, 2494–2509.
47. D. Farrusseng, F. Clerc, C. Mirodatos and R. Rakotomalala, Comput. Mater. Sci., 2009, 45, 52–59.
48. K. Matyjaszewski and J. Xia, Chem. Rev., 2001, 101, 2921–2990.
49. M. Kamigaito, T. Ando and M. Sawamoto, Chem. Rev., 2001, 101, 3689–3745.
50. K. Matyjaszewski and N. V. Tsarevsky, Nat. Chem., 2009, 1, 276–288.
51. M. Ouchi, T. Terashima and M. Sawamoto, Chem. Rev., 2009, 109, 4963–5050.
52. C. J. Hawker, A. W. Bosman and E. Harth, Chem. Rev., 2001, 101, 3661–3688.
53. G. Moad, E. Rizzardo and S. H. Thang, Acc. Chem. Res., 2008, 41, 1133–1142.
54. G. Moad, E. Rizzardo and S. H. Thang, Polymer, 2008, 49, 1079–1131.
55. T. Pintauer, P. Zhou and K. Matyjaszewski, J. Am. Chem. Soc., 2002, 124, 8196–8197.
56. W. Tang, N. V. Tsarevsky and K. Matyjaszewski, J. Am. Chem. Soc., 2006, 128, 1598–1604.
57. W. Tang, Y. Kwak, W. Braunecker, N. V. Tsarevsky, M. L. Coote and K. Matyjaszewski, J. Am. Chem. Soc., 2008, 130, 10702–10713 and references therein.
58. W. Tang and K. Matyjaszewski, Macromolecules, 2006, 39, 4953–4959.
59. W. Tang and K. Matyjaszewski, Macromolecules, 2007, 40, 1858–1863.
60. Accelrys Software Inc., San Diego, CA, USA, http://accelrys.com/products/materials-studio/.
61. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. I. Goddard and W. M. Skid, J. Am. Chem. Soc., 1992, 114, 10024–10035.
62. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
63. B. Delley, Theor. Comput. Chem., 1995, 2, 221–254.
64. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1992, 46, 6671–6687.
65. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
66. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
67. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
68. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
69. R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, Wiley-VCH, Weinheim, 2002.
70. J. H. Ward, J. Am. Stat. Assoc., 1963, 58, 236–244.
71. F. Murtagh, Comput. J., 1983, 26, 354–359.
72. D. Rogers and A. J. Hopfinger, J. Chem. Inf. Comput. Sci., 1994, 34, 854–866.
73. J. H. Friedman, Ann. Stat., 1991, 19, 1–67.
74. T. Pintauer and K. Matyjaszewski, Coord. Chem. Rev., 2005, 249, 1155–1184.
75. T. Pintauer and K. Matyjaszewski, Top. Organomet. Chem., 2009, 26, 221–251.
76. H. Tang, N. Arulsamy, J. Sun, M. Radosz, Y. Shen, N. V. Tsarevsky, W. A. Braunecker, W. Tang and K. Matyjaszewski, J. Am. Chem. Soc., 2006, 128, 16277–16285.
77. J. Devillers, Topological Indices and Related Descriptors in QSAR and QSPR, Gordon and Breach Science Publishers, Amsterdam, 1999, ch. 1, and references therein.
78. D. B. Rorabacher, Chem. Rev., 2004, 104, 651–697.
79. A. Rauk, Orbital Interaction Theory of Organic Chemistry, Wiley-Interscience, New York, 2000, ch. 13, and references therein.
80. W. A. Braunecker, W. C. Brown, B. C. Morelli, W. Tang, R. Poli and K. Matyjaszewski, Macromolecules, 2007, 40, 8576–8585.
81. W. A. Braunecker, N. V. Tsarevsky, A. Gennaro and K. Matyjaszewski, Macromolecules, 2009, 42, 6348–6360.
82. N. V. Tsarevsky, W. A. Braunecker, W. Tang, S. J. Brooks, K. Matyjaszewski, G. R. Weisman and E. H. Wong, J. Mol. Catal. A: Chem., 2006, 257, 132–140.
83. N. V. Tsarevsky and K. Matyjaszewski, Chem. Rev., 2007, 107, 2270.
84. K. Matyjaszewski, Macromol. Symp., 1998, 134, 105–118.
85. L. N. Drozdov-Tikhomirov, D. M. Linde, V. V. Poroikov, A. A. Alexandrov, G. I. Skurida, P. V. Kovalev and V. Y. Potapov, Mol. Biol., 2003, 37, 148–155.

---

Footnote

† Electronic supplementary information (ESI) available: cluster analysis dendrograms, loading plots, linear spline models and best fits. See DOI: 10.1039/c0py00058b

---