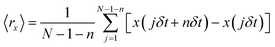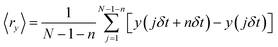Force applied to a single molecule at a single nanogate molecule filter

Abstract

We have investigated the origin of molecule filtering system based on a chemical potential barrier produced by thermodynamically driven molecular flow in a nanoscopic space at nanogates. Single molecule tracking experiments prove that the highly localized potential barrier allows for selective manipulation of the target molecule. We propose the presence of a force, a few fN per molecule, to decelerate the molecule's movement at the nanogate, which is comparable to or larger than the force applied by conventional electrophoretic operation. The present force can be tuned by changing the nanogate width at the nanometre level. These findings allow us to propose an accurate design of novel devices for molecular manipulation on an ultra small scale using a very small number of molecules without any external biases.

---

Molecules confined in nanospace exhibit peculiar motion, different from that in macroscopic space.^1–4 Molecular separation systems based on this unique molecular motion have recently received considerable attention because of their higher performance, novel separation mechanism and possibility of miniaturizing a separation device driven by ultra-small energy.^5–7 The Brownian ratchet,^7–9 entropic trap^5,6,10 and Ogston sieve^11,12 are typical examples that have been proposed based on molecular manipulation in small spaces. However, the fact that they are based on electrophoresis is an important disadvantage to these procedures because an uncharged molecule cannot be manipulated. Instead of using the electric field, systems using pressure-driven flow have been proposed, such as hydrodynamic chromatography^13,14 and shear driven chromatography.^15,16 In these systems, small molecules such as coumarin dyes have been successfully separated without applying an electric field.¹⁶ However, these systems need a long working channel of several hundreds of micrometres. Furthermore, they still need an external bias to cause molecular flow. This is a crucial obstacle for the miniaturization of the system. Even when using nanospaces to induce molecular rectification, the use of an external driving system, such as electrodes, power suppliers or syringe pumps, will spoil all of these efforts.

Instead of using an external bias, molecular flow driven under external force-free condition is currently attracting much attention as the novel molecular transport medium in ultra-small devices. A successful example is the use of a self-spreading lipid bilayer, which is a thermodynamically driven collective molecular flow that appears on a solid/liquid interface.^17–20 Recent experimental demonstrations have proposed the novel molecular filtering ability of the nanoscopic gate (nanogate) by using the self-spreading lipid bilayer as the molecular transport and filtering medium.^21–23 This system relies on the formation of a chemical potential barrier at the nanogate, caused by a local structural change in the self-spreading lipid bilayer. Change in the chemical potential, i.e., change in the molecular solubility, at the nanogate acts as a filter for the molecules. Since molecular transport is driven by the self-spreading behavior, this system can be operated under completely external force-free conditions; there is no need to apply any external bias, such as electric field or shear flow. Furthermore, the chemical potential barrier in the lipid bilayer enables comprehensive recognition of molecules, i.e., the chemical potential barrier can recognize the difference in any molecular parameter, such as size, charge, polarity, hydrophilicity, or chirality. Although the principle of the chemical potential barrier has been demonstrated by comparing the filtering efficiency for several molecules with different structures,²¹ its phenomenological understanding is still unclear. In order to establish a versatile molecular filtering device based on this system, it is important to determine how the molecules feel the chemical potential abnormality in close proximity to the nanogate.

Here, we investigate the diffusion dynamics of individual target molecules in a self-spreading lipid bilayer under the condition where the nanogate filtering phenomenon occurs. Observations based on single molecule tracking enable the precise characterization of molecular diffusion dynamics.²⁴ The presence of the chemical potential barrier for the molecule can be detected as a modulation in diffusion dynamics. Our results provide a new mechanistic insight into how molecules feel the chemical potential barrier during the nanogate filtering process. We further estimate the force imposed on each molecule near the nanogate, which is as high as those generated in the electrophoretic system, despite the fact that no external bias is imposed on the present system.

Periodically ordered Au nanogates shown in Fig. 1 were fabricated on a coverslip using a high-resolution electron beam lithography (EBL) system. Microchannels of 100 µm width × 600 µm length were fabricated, which contain at the middle of the channel a square lattice of Au obstacles with a diagonal length of 1.0 µm that are separated by intervals d with each other. The interval d is defined as the gate width. The channel without an Au nano-obstacle array is denoted as the control channel. Atomic force microscopy (AFM) images in Fig. 1c–f show successful preparation of the Au nano-obstacle, 10 nm in height. In the channels designated as d = 75, 100, and 200 nm, the real gate widths were estimated as 82, 128, and 218 nm, respectively, by scanning electron microscopy (SEM) observations. The nanogate channels were named 82 nm Gate, 128 nm Gate, and 218 nm Gate according to the designated gate width.

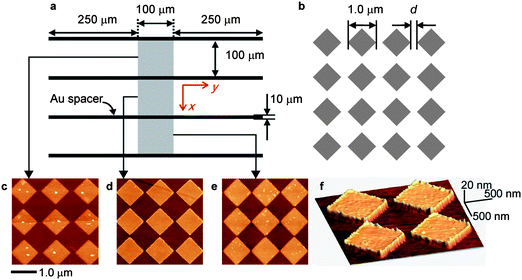Fig. 1 Schematics of the (a) microchannels separated by Au spacer and (b) periodic Au nanogate array fabricated in the middle of each microchannels. (c–e) Two dimensional AFM images of the nanogate fabricated at the100 µm × 100 µm region in the middle of each channel. The gate width d is (c) 218 nm (d) 128 nm (e) 82 nm. (f) Three dimensional AFM image with d = 128 nm.

To characterize molecular motion in the self-spreading bilayer, we tracked individual TR-DHPE molecules in the self-spreading DLPC bilayer using objective-type total internal reflection fluorescence microscopy (TIRFM). Although the trajectories in the control channel show typical random motion of the TR-DHPE molecule in the bilayer (Fig. 2a), those in the nanogate channels show hop diffusion moving among the compartments surrounded by the Au nano-obstacles through the nanogates (Fig. 2b–d). The trajectories were first analyzed through mean square displacement (MSD), 〈r²〉. For random diffusion and random hopping among small compartments, 〈r²〉 is described as

〈r²〉 = 4Dt (1)

where D is diffusion coefficient and t is time interval.²⁵ Based on this eqn (1), D was obtained as 4.0, 2.9, 2.2, and 2.2 µm² s⁻¹ for the control, 218 nm Gate, 128 nm Gate, and 82 nm Gate channels, respectively.

Fig. 2 Typical trajectories in (a) control, (b) 218 nm Gate, (c) 128 nm Gate and (d) 82 nm Gate channels tracked for 439, 343, 466, 412 frames, respectively.Mean displacement (MD) as a function of time in (e) x- and (f) y-direction. The lines and the markers represent the plots for individual molecules and ensemble averages, respectively. Ensemble averaged MD plots in (g) x- and (h) y-direction extracted from e and f, respectively.

Although MSD analysis enables to characterize the change in molecular diffusivity, the ensemble net displacement is well-characterized by the mean displacement (MD) analysis, 〈r〉. Biased motion can be characterized by the net movement of the molecule in either or both x- and y-direction. In the present system, the self-spreading direction is defined as y, and then the perpendicular direction as x. We analyzed MD from single molecule trajectories for both directions. In the x-direction analyses, the distribution of the plots for individual molecules was symmetric (Fig. 2e) and the averaged MD plot remained at zero (Fig. 2e and g). This result indicates that TR-DHPE molecules move randomly without biased motion in the direction perpendicular to the self-spreading. In the y-direction, the majority of the plots had a positive slope (Fig. 2f), and averaged MD plots increased linearly with t (Fig. 2f and h). The positive value of 〈r_y〉 indicates that the motion of the TR-DHPE molecule is biased toward the spreading direction of the bilayer.

Using the slopes of the MD plots, the averaged velocities of the TR-DHPE molecule, u, were calculated to be 610, 422, 468, and 256 nm s⁻¹ for the control, 218 nm Gate, 128 nm Gate, and 82 nm Gate channels, respectively. It was found that u was decreased with the lowering in d, though 218 nm Gate and 128 nm Gate demonstrated almost similar effect within the experimental error. One reason for the velocity lowering is the deceleration of the self-spreading velocity due to the presence of nanogate.^21,22 The spreading velocity can be quantitatively characterized by tracking the time-course of the spreading edge for the bilayer containing 1 mol% TR-DHPE (Fig. S1 in the ESI†). The spreading velocities, v, were obtained as 245, 196, 167, and 165 nm s⁻¹ for the control, 218 nm Gate, 128 nm Gate, and 82 nm Gate, respectively. The effect of the nanogate on u and v was depicted in Fig. 3, with comparing the control and 82 nm Gate systems. The plot shows several characteristic features of single molecule observation in the self-spreading bilayer at nanogate.

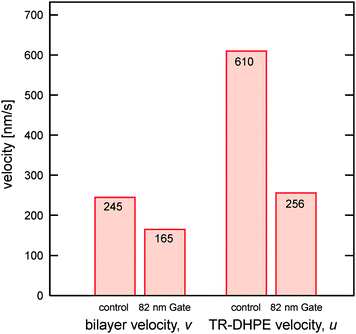Fig. 3 Velocities of the self-spreading bilayer and TR-DHPE in the self-spreading bilayer on the control and 82 nm Gate channels.

First, u was found to be higher than v for both channels. An internal-rolling mechanism,¹⁸ in which only the top monolayer spread with the bottom monolayer fixed on the substrate, can explain at least twice the enhancement in u compared with v if we assume that TR-DHPE distributes only at the top monolayer (Fig. S2 in the ESI†). Furthermore, it is also possible to assume that TR-DHPE molecule is not transported solely by the self-spreading behaviour, i.e., other bias is imposed to accelerate the TR-DHPE velocity along the spreading direction in the single molecule observation system. One possibility is the acceleration caused by the continuous supply of the TR-DHPE from the lipid lump to the lipid bilayer. Nissen et al. have shown concentration gradient of the TR-DHPE in the self-spreading lipid bilayer, in which TR-DHPE was likely to accumulate at the advancing spreading edge¹⁸ (see also Fig. S1 in the ESI†). This has been explained as the results of the density gradient of the lipid molecules in the spreading bilayer. Due to friction between the spreading bilayer and the solid substrate, the lipid density is not homogeneous and gradually decreases toward the spreading edge. According to this lipid density distribution, a bulky molecule such as TR-DHPE distributes with the opposite concentration gradient. This causes the accumulation of TR-DHPE at the spreading edge region with less lipid density. In the case of a single molecule tracking experiment, the concentration of TR-DHPE in the self-spreading lipid bilayer is extremely low. These facts lead to a continuous supply of TR-DHPE at the spreading edge until reaching an equilibrium concentration distribution, in which no accelerated diffusion will be observed at the equilibrium. The need to accumulate more TR-DHPE at the spreading edge is thought to cause the observed acceleration along the y-direction. Since linear density gradient is induced in the bilayer,¹⁸ this acceleration effect is supposed to be not position-dependent, because this acceleration is caused by a diffusion promoted by this linear gradient at each time. Although it is hard to discuss these two effects separately, the fact of u > v was evident when u was characterized via single molecule observation experiment.

Another interesting feature is the drastic decrease in u on 82 nm Gate. Although v was also decelerated on 82 nm Gate, decrease in u cannot be explained by considering only the decrease in v. The observed results strongly suggest that the progress of TR-DHPE was more retarded than the progress retardation for the bilayer spreading. This fact is the direct evidence of the appearance of nanogate molecular filtering. The observed decrease in u could be discussed quantitatively by estimating the additional force F applied to the TR-DHPE molecule moving toward the spreading edge.

The u value can be expressed with two components, one being the contribution from the self-spreading (v) and the other being the acceleration from the lump (u′):

u = v + u′ (2)

The relative velocity between the lipid bilayer and the diffusing molecule in the bilayer can be rewritten as

u′ = u − v (3)

D, u′, and the force on the diffusing molecule F can be related by the following equation:²⁵

D = u′k_BT/F (4)

where k_B is the Boltzmann constant and T is the absolute temperature. Based on eqn (4), at T = 300 K, F was calculated to be 0.38 and 0.17 fN per molecule for the control and the 82 nm Gate channel, respectively. Then, the force acting on TR-DHPE as the deceleration (F′) on the 82 nm Gate channel can be estimated as 0.21 fN per molecule. This calculation indicates that the force of 0.21 fN per molecule is imposed on TR-DHPE when spreading on the 82 nm Gate channel, which resulted in the reduction in the advancing power of TR-DHPE from 0.38 (control) to 0.17 fN per molecule (82 nm Gate). This value was found to be on the same order as the electrostatic force (0.40 fN per molecule) required for generating a molecular concentration gradient in the homogeneous lipid membrane with applying field strength of 10–15 V cm⁻¹.²⁶ This implies that a molecular distribution control as effective as that of the electric-field dependent system is achievable without any external field when we use the self-spreading lipid bilayer as the molecular transport medium.

It is necessary to note that F′ calculated above is a spatially averaged value, i.e., we assume that the deceleration occurs not only at the gate region but also at any place on the channel. This is not adequate for the nanogate filtering effect, in which the filtering is brought from the local chemical potential barrier only at the nanogate region.²¹ Therefore, we can consider the contribution of the effective deceleration width (w) defined by the structure of the nanogate as shown in Fig. 4. This means that within a single period of the nanogate array (1000 + d nm), only the narrow part with w is responsible to the deceleration. From a simple geometrical solution, F′ that is assumed to be imposed only at the part of w can be estimated by multiplying F′ with (1000 + d)/w, and the results were plotted as the function w (Fig. 4). As can be expected, F′ increases with decreasing w. In order to consider the plausible range of w, it is important to recall that the filtering effect was non-linearly increased when the gate width was decreased below 200 nm.²¹ In other words, confinement of the self-spreading lipid bilayer below 200 nm is important to yield a significant filtering effect. In the case of 82 nm Gate configuration (d = 82 nm), the position that the gate width (l) reaches 200 nm is at w = 60 nm. Thus, the dark area shown in inset of Fig. 4 (d = 82 nm, l = 200 nm, w = 60 nm) can be considered as a working area that induces strong filtering effect. At w = 60 nm, F′ reaches 4 fN per molecule, which is ten times higher than the values in the electrophoretic system. Further decreases in the gate width will yield a much higher deceleration force at the nanogate, leading to the fabrication of a truly nanometre scale molecular filtering system without any external bias. It should be also noted that this force is from the same origin of the chemical potential barrier in the nanogate that had been described in our previous manuscript.²¹ Since the present study offered more quantitative analysis, we were able to discuss in terms of force on molecules, which corresponds to a derivative form of the chemical potential in the nanogate.

Fig. 4 Applied force F′ for TR-DHPE locally imposed at single nanogate as a function of w. The inset shows the schematic illustration of nanogate region. The dark region can be considered as the area that induces filtering effect.

In the present system, the movement of TR-DHPE in the self-spreading direction was decelerated by the presence of nanogates. The mechanism of this deceleration seems to be quite different from those in previously documented methods, such as the entropic trap⁵ and Ogston sieving,¹¹ because the nanospace used in these systems is almost comparable to the size of the molecules of interest. For example, the sizes of the nanospace and the target molecules are both a few tens to hundreds of nanometres in the above systems, while the size of d in the present system is two orders of magnitude larger than the size of TR-DHPE in the present study. This means that the present system does not rely on steric hindrance to distinguish and separate molecules. This is a great difference between the present system and previous ones. Although it may be possible to induce entropic trap or Ogston sieving in our system together with the chemical potential barrier by reducing d to molecular size, this is out of the current purpose and would be our next step. By taking advantage of using a chemical potential barrier as the filtration mechanism, it would be possible to filtrate, separate, purify, and manipulate molecules by distinguishing them not only by size, but also by charge, conformation, polarity, specific functional group, or chirality. A part of molecular dependency has already demonstrated as the difference in the filtering efficiency.²¹ The present report yielded the first direct information on how a molecule feels the chemical potential barrier and how a molecule diffuses at the nanogate when the chemical potential barrier is on. Since it may become possible to visualize the deceleration effect as the asymmetric distribution of TR-DHPE across the nanogate if we dope TR-DHPE with much higher concentration, we will discuss on this matter in the separate report. Our findings in the present paper greatly aid in the design of the nanogate configuration for use in truly external force-free and nanoscopic molecular manipulation architectures.

In conclusion, mechanistic insight into how a molecule diffuses in a new class of molecular manipulation system, a chemical potential barrier at a nanogate, has been clarified by single molecule tracking experiments. We have found that this kind of nanogate is critically effective in creating the chemical potential barrier that can control the molecular diffusivity. For the molecule confined to these narrow nanogates, a force as high as 4 fN per molecule, which is an order of magnitude higher than the forces generated in conventional electrophoretic manipulation on the charged lipids, was imposed without any external bias. Present findings also provide the possibility of precise control of the local chemical potential barrier and the consequent deceleration force by the nanogate design with nanometre resolution, which will open up a systematic control of molecular filtering efficiency and selectivity in this novel molecular manipulation system.

Experimental methods

Coverslips were cleaned with piranha solution (H₂O₂/H₂SO₄ = 1/4 vol% mixture). Au nanogates were fabricated using a high-resolution EBL system (ELS-7700H, Elionix Co., Ltd., Japan) working at 100 kV voltage. A copolymer resist (ZEP-520a, Zeon) diluted with ZEP thinner (1 : 1) was spin-coated onto the coverslip (1000 rpm for 10 s, and 4000 rpm for 90 s). After pre-baking on a hot plate for 3 min at 180 °C, the substrates were exposed to an electrical current of 30 pA. After development in developer solution, 2 nm chromium and 10 nm gold layers were successively deposited by sputtering (ULVAC, MPS-4000, Japan). Then, the resist layer was removed by immersion in acetone solution for 2 min and in remover solution for 2 min in an ultrasonic bath. The fabricated structures were characterized using atomic force microscopy (AFM; Nanoscope IIIA, Digital Instruments) and field emission scanning electron microscopy (FE-SEM; JSM-6700FT, JEOL). The substrate was cleaned by sonication in chloroform, acetone and Milli-Q water, followed by immersion in concentrated nitric acid before use.

The self-spreading lipid bilayer was prepared as follows: 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC) was dissolved in chloroform with a concentration of 1.0 mg ml⁻¹; then, the dye-labeled lipid molecule Texas Red 1, 2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (TR-DHPE) was mixed to the desired molecular ratio. A drop of the solution was positioned on the substrate using a clean Teflon rod and then dried under ambient conditions. After evaporation, a lipid lump was left on the substrate. By the immersion of the substrate into 100 mM Na₂SO₄ aqueous solution, the lipid bilayer spread spontaneously from the lipid lump on the substrate.

For single molecule observation, a total internal reflection microscope (TIRFM) IX-71 (Olympus) equipped with a 100× objective lens (NA = 1.45) and 532 nm laser was used. The images were projected on a Hamamatsu charge coupled device (CCD) camera C9018 (Hamamatsu Photonics). Contrast enhancement of the images was achieved using an image intensifier unit C9016-02 (Hamamatsu Photonics). In TIRFM images, the individual TR-DHPE molecules were seen as bright spots composed of several pixels. The molecular trajectories were obtained by recording the centers of mass of the bright spots using Image-Pro Plus 5.1 (Media Cybernetics). The trajectories over 120 frames (2 s) were analyzed numerically using mean square displacement (MSD) 〈r²〉 and mean displacement (MD) 〈r〉 as a function of time interval t. MSD was calculated based on following equation:

while MD was calculated based on the following equations:

where δt is the video frame time, (x(jδt + nδt), y(jδt + nδt)) describes the particle position following a time interval nδt after starting at position (x(jδt), y(jδt)), N is the total number of frames in the video recording sequence, and n and j are positive integers, with n determining the time increment.

Acknowledgements

This work was partially supported by the Grant-in-Aid for scientific research 19049003, 20750001, and 21350001, from the Ministry of Education, Science and Culture, Japan. Especially, that on Priority Area “Strong Photon-Molecule Coupling Fields (no. 470)” is acknowledged.

Notes and references

1. R. Karnik, R. Fan, M. Yue, D. Li, P. Yang and A. Majumdar, Electrostatic control of ions and molecules in nanofluidic transistors, Nano Lett., 2005, 5, 943–948.
2. M. Krishnan, I. Monch and P. Schwille, Spontaneous stretching of DNA in a two-dimensional nanoslit, Nano Lett., 2007, 7, 1270–1275.
3. R. J. Mashl, S. Joseph, N. R. Aluru and E. Jakobsson, Anomalously immobilized water: a New water phase induced by confinement in nanotubes, Nano Lett., 2003, 3, 589–592.
4. D. Nykypanchuk, H. H. Strey and D. A. Hoagland, Brownian motion of DNA confined within a two-dimensional array, Science, 2002, 297, 987–990.
5. J. Han and H. G. Craighead, Separation of long DNA molecules in a microfabricated entropic trap, Science, 2000, 288, 1026–1029.
6. J. Fu, R. B. Schoch, A. L. Stevens, S. R. Tannenbaum and J. Han, A patterned anisotropic nanofluidic sieving structure for continuous-flow separation of DNA and proteins, Nat. Nanotechnol., 2007, 2, 121–128.
7. A. van Oudenaarden and S. G. Boxer, Brownian ratchets: molecular separation in lipid bilayers supported on patterned arrays, Science, 1999, 285, 1046–1048.
8. C.-F. Chou, O. Bakajin, S. W. P. Turner, T. A. J. Duke, S. S. Chan, E. C. Cox, H. G. Craighead and R. H. Austin, Sorting by diffusion: an asymmetric obstacle course for continuous molecular separation, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13762–13765.
9. K. Loutherback, J. Puchalla, R. H. Austin and J. C. Sturm, Deterministic microfluidic ratchet, Phys. Rev. Lett., 2009, 102, 045301.
10. A. K. R. Paul, Activated barrier crossing of macromolecules at a submicron-size entropic trap, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061801.
11. J. Fu, J. Yoo and J. Han, Molecular sieving in periodic free-energy landscape created by patterned nanofilter arrays, Phys. Rev. Lett., 2006, 97, 018103.
12. J. Fu, P. Mao and J. Han, Nanofilter array chip for fast gel-free biomolecule separation, Appl. Phys. Lett., 2005, 87, 263902.
13. E. Chmela, R. Tijssen, M. T. Blom, H. J. G. E. Gardeniers and A. van den Berg, A chip system for size separation of macromolecules and particles by hydrodynamic chromatography, Anal. Chem., 2002, 74, 3470–3475.
14. M. T. Blom, E. Chmela, R. E. Oosterbroek, R. Tijssen and A. van den Berg, On-chip hydrodynamic chromatography separation and detection of nanoparticles and biomolecules, Anal. Chem., 2003, 75, 6761.
15. W. De Malsche, D. Clicq, H. Eghbali, V. Fekete, H. Gardeniers and G. Desmet, An automated injection system for sub-micron sized channels used in shear-driven-chromatography, Lab Chip, 2006, 6, 1322–1327.
16. V. Fekete, D. Clicq, W. De Malsche, H. Gardeniers and G. Desmet, State of the art of shear driven chromatography: advantages and limitations, J. Chromatogr., A, 2007, 1149, 2–11.
17. J. Rädler, H. Strey and E. Sackmann, Phenomenology and kinetics of lipid bilayer spreading on hydrophilic surfaces, Langmuir, 1995, 11, 4539–4548.
18. J. Nissen, S. Gritsch, G. Wiegand and J. O. Rädler, Wetting of phospholipid membrane on hydrophilic surfaces—concepts toward self-healing membrane, Eur. Phys. J. B, 1999, 10, 335–344.
19. H. Nabika, A. Fukasawa and K. Murakoshi, Control of the structure of self-spreading lipid membrane by changing electrolyte concentration, Langmuir, 2006, 22, 10927–10931.
20. H. Nabika, A. Fukasawa and K. Murakoshi, Tuning the dynamics and molecular distribution of the self-spreading lipid bilayer, Phys. Chem. Chem. Phys., 2008, 10, 2243–2248.
21. H. Nabika, N. Iijima, B. Takimoto, K. Ueno, H. Misawa and K. Murakoshi, Segregation of molecules in lipid bilayer spreading through metal nano-gates, Anal. Chem., 2009, 81, 699–704.
22. H. Nabika, A. Sasaki, B. Takimoto, Y. Sawai, S. He and K. Murakoshi, Controlling molecular diffusion in self-spreading lipid bilayer using periodic array of ultra-small metallic architecture on solid substrate, J. Am. Chem. Soc., 2005, 127, 16786–16787.
23. Y. Kashimura, J. Durao, K. Furukawa and K. Torimitsu, Self-spreading behavior of supported lipid bilayer through single sub-100 nm gap, Jpn. J. Appl. Phys., 2008, 47, 3248–3252.
24. B. Takimoto, H. Nabika and K. Murakoshi, Single molecular observation of hop diffusion in a lipid bilayer at metallic nanogates, J. Phys. Chem. C, 2009, 113, 3127–3132.
25. P. G. Saffman and M. Delbruck, Brownian motion in biological membranes, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113.
26. J. T. Groves, S. G. Boxer and H. M. McConnell, Electric field-induced reorganization of two-component supported bilayer membranes, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 13390–13395.

---

Footnote

† Electronic supplementary information (ESI) available: Spreading velocity and molecular filtration characteristics (Figure S1) and asymmetric distribution of TR-DHPE in the self-spreading lipid bilayer (Figure S2). See DOI: 10.1039/c0nr00455c

---