Influence of anion on the kinetics of copper island growth

Abstract

We compare the kinetics of copper island growth in the kinetic regime in the presence and absence of anion adsorption and show that the growth exponents are inconsistent with a direct attachment model. In sulfate solution, anion adsorption leads to instantaneous nucleation, equal lateral and vertical growth exponents, and suppressed vertical growth. In perchlorate solution, island growth is characterized by progressive nucleation, enhanced vertical growth, and different lateral and vertical growth exponents. Avrami analysis and analysis of the surface power spectra suggest that island growth is controlled by surface diffusion to the island perimeter.

---

Introduction

Electrodeposition of a metal onto a foreign substrate in the overpotential regime usually proceeds by the growth and coalescence of three-dimensional islands, so-called Volmer–Weber island growth. At moderate to high overpotentials, island growth is controlled by bulk diffusive transport of metal ions to the growing island,^1–3 whereas at low overpotentials, island growth is slow and under kinetic control.⁴

For island growth in the kinetic regime there are two possible rate limiting steps: (1) direct attachment by electrochemical reduction of metal ions at the island surface and (2) indirect attachment resulting from adatom formation on the substrate and subsequent surface diffusion to the island perimeter. In either case, metal ion reduction can occur on the substrate, on the surface of the island, or at the island perimeter.

The mechanism of island growth can be determined from the exponents associated with the kinetics of vertical and lateral growth. In the literature, it is usually assumed that island growth in the kinetic regime is limited by direct attachment (metal ion reduction) at the island surface, and for this case the island growth kinetics are characterized by power law behavior with vertical (h) and lateral (L) growth exponents of one (h ∝ t¹ and L ∝ t¹). However, other island growth mechanisms can lead to different exponents. For example, rate limiting surface diffusion of adatoms to the island perimeter leads to a lateral growth exponent of 0.5 (L ∝ t^0.5). In this case, the electrochemical reaction is still in the kinetic regime, but the rate limiting step for lateral island growth is the surface diffusion of adatoms.

A consequence of the kinetic deposition regime is that the island shape is dictated by the surface energy of the different crystallographic planes leading to the formation of faceted islands.⁵ The surface energy can be independently controlled by introducing species that preferentially adsorb on specific crystal planes, thus enabling the control of island shape.⁶

The study of island growth in the kinetic regime requires a system where (1) the nucleation overpotential is sufficiently small so that island growth is not limited by the bulk transport of metal ions to the island surface and (2) the island orientation is not influenced by inhomogeneities in the microstructure of the substrate, e.g. individual grains in a polycrystalline substrate or microstructural defects such as grain boundaries.⁴ There are relatively few systems that satisfy these requirements. A small nucleation overpotential (for systems that do not exhibit underpotential deposition) is unusual; most systems exhibit values of 100 mV or more so that the kinetic regime cannot be accessed.^4,7–12 To avoid the influence of grain boundaries and microstructural defects means that either single crystal or amorphous substrates are preferred.

In previous work we have reported on the growth kinetics of copper islands on ruthenium oxide from sulfate solution in the kinetic regime.¹³ This is a model system for studies of island growth since ruthenium oxide is amorphous and hence the island orientation is dictated by the thermodynamically low energy orientation, which is a 〈111〉 surface normal for cubic crystals. In addition, the nucleation overpotential is very small allowing access to the kinetic deposition regime. Preferential adsorption of sulfate on the {111} planes of copper¹⁴ results in the formation of faceted islands.^13,15 In contrast, perchlorate does not specifically adsorb onto copper,¹⁶ resulting in approximately hemispherical islands.

In this paper we compare deposition of copper in sulfate and perchlorate solution to elucidate the influence of anion adsorption on island growth kinetics. We discuss the kinetics of island growth in terms of the contributions to vertical and lateral growth, and build upon these results using Avrami analysis of the island coverage and analysis of the power spectra of the surface topology.

Experimental

Copper islands were electrodeposited on polycrystalline ruthenium with a 2 nm thick amorphous oxide.¹³ All experiments were performed at room temperature and at a potential of −64 mV (vs. Cu²⁺/Cu), which is sufficiently small that deposition is rate-limited by the interfacial reaction kinetics. Island growth was studied in 0.1 M CuSO₄ (99.999%, Alfa Aesar) and 0.2 M H₂SO₄ (99.9999%, Alfa Aesar) or 0.1 M Cu(ClO₄)₂ (99.999%, Alfa Aesar) and 0.2 M HClO₄ (99.9999%, Alfa Aesar). AFM images (50 µm × 50 µm) were acquired at multiple random locations (Molecular Imaging Pico-Plus) after deposition. Experimental details have been reported elsewhere.¹³ At each deposition time, a minimum of four images were analyzed. The volume, projected area, and height were obtained for each island in the image. In sulfate solution, the total number of islands analyzed was N = 279 at 20 s, N = 402 at 50 s, and N = 363 at 100 s. In perchlorate solution, the total number of islands analyzed was N = 151 at 100 s, N = 262 at 200 s, and N = 363 at 500 s. The local charge density obtained from the total volume of islands in the images was in excellent agreement with the charge density obtained by integration of the current transients recorded at each deposition time indicating that the island distribution is uniform across the surface and that the AFM images are representative of the whole electrode. The island orientation was studied using X-ray diffraction (Philips X'Pert 4-circle system).

The power spectral density (PSD) of the surface topology was calculated using two-dimensional (2D) fast Fourier transform algorithm¹⁷ of the surface height from the AFM images (512 × 512 pixels). The resulting two dimensional PSD, g(q_x, q_y), was then simplified to a one dimensional PSD, g(|q|), by taking the angular average in polar coordinates.

Results and discussion

Fig. 1 shows the AFM images of islands formed in 100 mM Cu(II) sulfate or perchlorate solution at −64 mV (vs. Cu²⁺/Cu), illustrating the two island morphologies. X-Ray diffraction patterns (Fig. 2a) show that the out-of-plane orientation is predominantly perpendicular to the Cu (111) plane in both sulfate and perchlorate solution. At longer times, close to the onset of island coalescence, contributions are also seen from Cu (200) and Cu (220). As shown in Fig. 2b, the Cu (111) peak is observed at the onset of deposition and increases with time during island growth.

Fig. 1 AFM images (5 µm × 5 µm) of Cu islands electrodeposited from (a) 0.1 M CuSO₄ + 0.2 M H₂SO₄ for 200 s and (b) 0.1 M Cu(ClO₄)₂ + 0.2 M HClO₄ for 500 s. Deposition on ruthenium oxide substrate at −64 mV (vs. Cu²⁺/Cu). Larger area AFM images (50 µm × 50 µm) in (c) sulfate and (d) perchlorate solution under the same conditions.

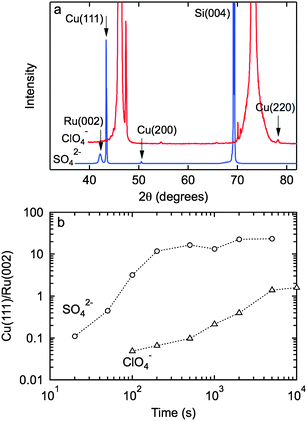Fig. 2 (a) X-Ray diffraction patterns for copper deposited from 0.1 M CuSO₄ + 0.2 M H₂SO₄ for 200 s and 0.1 M Cu(ClO₄)₂ + 0.2 M HClO₄ for 500 s at −64 mV (vs. Cu²⁺/Cu). (b) The intensity of the Cu (111) peak normalized to the Ru (002) peak versus deposition time in sulfate and perchlorate solution.

The shape of the hexagonal disk-shaped islands formed in sulfate solution is due to preferential anion adsorption on the (111) planes. Since the substrate is non-crystalline, the copper islands adopt the thermodynamically favorable orientation with the close-packed (111) planes of fcc copper parallel to the surface.^13,18 The island height is much smaller than the island width, resulting in an aspect ratio of about 1/12. The image in Fig. 1c shows the lack of in-plane order which is expected on a non-crystalline substrate.^13,18 In contrast, islands formed in perchlorate solution exhibit a distinct shape intermediate between a hemisphere and a cone (Fig. 1b). Despite the fact that the islands are not faceted, they retain the preferred (111) in-plane orientation, illustrating that island shape and orientation can be controlled independently.

The difference in island shape, under otherwise identical conditions, highlights the crucial role of specific adsorption on island growth. In sulfate solution, suppression of growth along the 〈111〉 direction, which corresponds to the surface normal, results in low aspect ratio disk-shaped islands. In contrast, the lack of specific adsorption on copper in perchlorate solution results in approximately isotropic growth, and hence hemispherical islands.

The island growth kinetics are analyzed using a method that we developed previously to study copper island growth in sulfate solution.¹³Fig. 3 shows the island volume (V) versus the projected area (A) for all islands at different times. The volume and projected area of each island are obtained from analysis of AFM images. The solid line represents the isotropic growth of ideal hemispherical islands (V = 2A^3/2/3√π).¹⁹ As we have shown previously, if V ∝ A^m then the lateral (L) and vertical (h) dimensions of the islands can be described by L ∝ t^a and h ∝ t^b, where a and b are the growth exponents.¹³ The lateral and vertical dimensions are obtained from the volume and projected area (L = A^1/2 and h = V/A) from which it is seen that m = 1 + b/2a.

Fig. 3 Volume versus projected area for copper disk-shaped islands deposited from sulfate solution and hemispherical islands deposited from perchlorate solution as a function of deposition time. The dotted lines are power law fits to the data. The solid line corresponds to the isotropic growth of hemispherical islands.

The disk-shaped islands formed in sulfate solution show power law behavior according to V ∝ A^m, where m = 1.5, but the line is shifted below that for isotropic growth indicating enhanced lateral growth. From the shift, we obtain an average aspect ratio of 1/12. From the exponent m = 1.5 for disk-shaped island growth in sulfate solution, we have b/a = 1, indicating that the aspect ratio (h/L ∝ t^b-a) remains constant over time. The hemispherical islands formed in perchlorate solution also follow power law behavior with m = 1.26, however, the line is shifted above that for isotropic growth, indicating a faster vertical growth rate especially for the smaller islands during the early stages of deposition. From the exponent we have b/a = 0.52, indicating a stronger time-dependence of lateral growth (a > b) and hence decreasing aspect ratio over time. The island growth exponents in sulfate and perchlorate solution are summarized in Table 1.

Table 1 Summary of growth exponents for copper islands in sulfate and perchlorate solution

Parameter		Sulfate	Perchlorate
m	(V ∝ A^m)	1.50	1.26
a	(L ∝ t^a)	0.50	0.50
b	(h ∝ t^b)	0.50	0.26
b/a		1.0	0.52
N(t)	Nucleation	Instantaneous, N(t) = N0	Progressive, N(t) = N0knt^0.74
n	Avrami exponent	0.95	1.7
w	PSD exponent	4.1	4.1

---

Comparison of the island dimensions after 100 s (Fig. 3) shows that the volume of the copper islands is 2.43 ± 1.3 µm³ in sulfate solution and 1.25 ± 0.44 µm³ in perchlorate solution. The corresponding projected areas are 8.43 ± 3.22 µm² in sulfate solution and 1.72 ± 0.48 µm² in perchlorate solution. While the average volume is about two times larger in sulfate solution, the projected area is almost five times larger, highlighting the fact that lateral growth is faster in sulfate solution and vertical growth is faster in perchlorate solution.

In summary, sulfate adsorption results in enhanced lateral growth and constant aspect ratio, whereas in the absence of specific adsorption we see enhanced vertical growth and a decrease in the aspect ratio with time. Furthermore, for isolated island growth, the lateral growth rate in sulfate solution > the vertical growth rate in perchlorate solution > the lateral growth rate in perchlorate solution > the vertical growth rate in sulfate solution. At longer times (data not shown), both disk-shaped islands and hemispherical islands deviate from the corresponding scaling relations shown in Fig. 3, indicating different growth kinetics due to the onset of island–island interactions.

For three dimensional island growth in the kinetic regime, it is usually considered that the electrochemical reduction of metal ions onto the growing island is the rate limiting step, in which case the lateral and vertical growth rates are expected to be constant²⁰ and a = b = 1. The mechanism of island growth can be elucidated using Avrami analysis of the transformed area resulting from randomly distributed islands:²¹f = 1 − exp [−S(t)] = 1 − exp (−ktⁿ)where f is islands surface coverage, S(t) is the extended surface coverage assuming independent growth, and exponent n is an integer value from 1 to 4. To determine the island growth mechanism, we first need to determine the nucleation mechanism (Fig. 4a). In sulfate solution, nucleation is complete in the first 20 s, consistent with instantaneous nucleation (N(t) = N₀), and the island density remains about constant up to about 500 s prior to the onset of island coalescence. In contrast, in perchlorate solution nucleation continues up to the onset of island coalescence at about 2000 s, consistent with progressive nucleation (N(t) = k_nN₀t). The slope in the plot of log N(t) versus log t is 0.74, less than the expected value of 1.

Fig. 4 (a) The time dependence of island densities in (○) sulfate and (△) perchlorate and disk solution. (b) Plot of −ln (1 − f) versus ln (t) according to the Avrami equation. The coverage f was obtained from analysis of all islands in at least four randomly selected AFM images (50 µm × 50 µm).

From the Avrami analysis (Fig. 4b) we obtain n = 0.95 in sulfate solution and n = 1.7 in perchlorate solution. An exponent n = 1 indicates instantaneous nucleation and surface diffusion limited growth, whereas n = 2 is consistent with progressive nucleation and surface diffusion limited growth. The exponent in sulfate solution (n = 0.95) is in good agreement with the value for instantaneous nucleation and surface diffusion limited island growth. The exponent in perchlorate solution is slightly lower than the value for progressive nucleation and surface diffusion limited growth, presumably due to the nucleation growth exponent of 0.74. These results indicate that indirect attachment via surface diffusion and not direct attachment is the rate limiting step during island growth from both sulfate and perchlorate solution. These results also highlight the importance of the amorphous substrate in avoiding microstructural defects that can serve as sinks for adatoms diffusing along the surface. The lateral growth exponent for rate limiting surface diffusion is a = 0.5, from which we obtain b = 0.5 in sulfate solution and b = 0.26 in perchlorate solution.

For deposition in sulfate solution where nucleation is instantaneous, the growth exponents a and b can also be obtained from the time dependence of the average island dimensions. This is difficult for systems that exhibit progressive nucleation due to the large dispersion in island size. From the analysis of the average island dimensions in sulfate solution we obtain a = 0.47 and b = 0.45,¹³ in excellent agreement with the values obtained from Avrami analysis.

In summary, Avrami analysis suggests that the rate limiting step for island growth in sulfate and perchlorate solution is the surface diffusion of adatoms to the island perimeter (L ∝ t^0.5). In sulfate solution, the vertical growth exponent is equal to the lateral growth exponent (h ∝ t^0.5) resulting in a constant aspect ratio and anion adsorption suppresses vertical growth resulting in faceted islands with an aspect ratio of 1/12. In perchlorate solution, the vertical growth is not suppressed, however, we do not observe isotropic hemispherical island growth. Surface diffusion remains rate limiting (L ∝ t^0.5) and the time dependence of the vertical growth rate becomes weaker (h ∝ t^0.26), resulting in a decrease in aspect ratio with time. Interestingly, nucleation is also dependent on anion (Fig. 4a), with instantaneous nucleation in sulfate solutions and progressive nucleation in perchlorate solution.

Finally, we compare the power spectra describing the evolution of the surface morphology with time during island growth (Fig. 5).^22,23 The power spectral density (PSD), g(|q|), where q is the wave vector with units of inverse length, is obtained from the two dimensional Fourier transform of the autocovariance function that describes the correlation in height between points on the surface:²⁴

G(r) = 〈h(r′)h(r′ − r)〉

where h is the surface height.

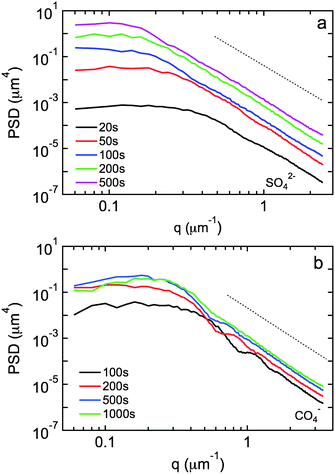Fig. 5 Power spectral densities of surface topology obtained from 50 µm × 50 µm AFM images as a function of time during island growth in (a) sulfate and (b) perchlorate solution. The dotted lines represent an exponent w = 4.

Fig. 5 shows PSDs for copper island growth in sulfate and perchlorate solution before island coalescence. The PSDs exhibit two distinct regimes, a plateau at smaller wave vectors (longer length scales) and a power law decay at larger wave vectors (shorter length scales). A constant value of g(|q|) with wavelength is indicative of stochastic roughening of the surface. In our case this is due to island growth that results in increasing height differences between the islands and the bare substrate at random locations on the surface. The power law decay at larger wave vectors is indicative of smoothing processes and the slope is dependent on the smoothening mechanism. An exponent w = 1 corresponds to viscous flow, w = 2 corresponds to evaporation–condensation, w = 3 corresponds to bulk diffusion, and w = 4 corresponds to surface diffusion.²⁴

The exponents in the power law regime are w = 4.1 ± 0.2 in sulfate solution and w = 4.1 ± 0.1 in perchlorate solution. These values are very close to the value w = 4 for surface diffusion smoothening^25,26 and consistent with the results from Avrami analysis.

In sulfate solution, the magnitude of the PSDs increases with time due to the roughening associated with vertical growth of the isolated islands and the constant aspect ratio. The crossover frequency k_c between the two regimes decreases with time consistent with enhanced lateral island growth. In perchlorate solution, the increase in the magnitude of the PSDs with time is less pronounced, presumably due to the fact that the island aspect ratio decreases with time. In addition, we observe peaks at about 0.2 µm⁻¹ due to additional roughening contribution from new islands (progressive nucleation).²⁴

Conclusions

In summary, we present a detailed comparison of copper deposition in the kinetic regime in sulfate solution (anion adsorption) and perchlorate solution (no anion adsorption). The island growth exponents are inconsistent with a direct attachment model. Avrami analysis and analysis of the surface PSDs show that island growth is controlled by surface diffusion of adatoms to the island perimeter. In sulfate solution anion adsorption leads to instantaneous nucleation, equal lateral and vertical growth exponents corresponding to a constant aspect ratio, and suppressed vertical growth. In perchlorate solution, with no anion adsorption, we observe progressive nucleation, slightly enhanced vertical growth, and different lateral and vertical growth exponents resulting in a decrease in aspect ratio with time. These results uncover time-dependent growth rates which are unexpected from a classical view of electrocrystallization in the kinetic regime and highlight the critical role of surface-diffusion in island growth in this system.

Acknowledgements

The authors gratefully acknowledge support from NSF (grant number CHE-0905869).

Notes and references

1. B. Scharifker and G. Hills, Electrochim. Acta, 1983, 28, 879–889.
2. G. Gunawardena, G. Hills, I. Montenegro and B. Scharifker, J. Electroanal. Chem., 1982, 138, 225–239.
3. G. Oskam, P. M. Vereecken and P. C. Searson, J. Electrochem. Soc., 1999, 146, 1436–1441.
4. L. Guo and P. C. Searson, Electrochim. Acta, 2010, 55, 4086–4091.
5. J. W. Mullin, Crystallization, Butterworth-Heinemann, Oxford, Boston, 2001.
6. M. J. Siegfried and K. S. Choi, J. Am. Chem. Soc., 2006, 128, 10356–10357.
7. A. Radisic, Y. Cao, P. Taephaisitphongse, A. C. West and P. C. Searson, J. Electrochem. Soc., 2003, 150, C362–C367.
8. A. Radisic, J. G. Long, P. M. Hoffmann and P. C. Searson, J. Electrochem. Soc., 2001, 148, C41–C46.
9. A. Radisic, A. C. West and P. C. Searson, J. Electrochem. Soc., 2002, 149, C94–C99.
10. P. M. Hoffmann, A. Radisic and P. C. Searson, J. Electrochem. Soc., 2000, 147, 2576–2580.
11. J. J. Whalen, J. D. Weiland and P. C. Searson, J. Electrochem. Soc., 2005, 152, C738–C743.
12. G. Oskam, J. G. Long, A. Natarajan and P. C. Searson, J. Phys. D: Appl. Phys., 1998, 31, 1927–1949.
13. L. Guo, S. L. Zhang and P. Searson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051601.
14. P. Broekmann, M. Wilms, M. Kruft, C. Stuhlmann and K. Wandelt, J. Electroanal. Chem., 1999, 467, 307–324.
15. L. Guo and P. C. Searson, Langmuir, 2008, 24, 10557–10559.
16. A. Hamelin, T. Vitanov, E. Sevastyanov and A. Popov, J. Electroanal. Chem., 1983, 145, 225–264.
17. M. K. Debe and K. K. Kam, Thin Solid Films, 1990, 186, 289–325.
18. L. Guo, A. Radisic and P. C. Searson, J. Electrochem. Soc., 2006, 153, C840–C847.
19. S. Fletcher, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 467–479.
20. E. Budevski, G. Staikov and W. J. Lorenz, Electrochemical Phase Formation and Growth, VCH, New York, 1996.
21. M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112.
22. W. U. Schmidt, R. C. Alkire and A. A. Gewirth, J. Electrochem. Soc., 1996, 143, 3122–3132.
23. W. Schwarzacher, J. Phys.: Condens. Matter, 2004, 16, R859–R880.
24. W. M. Tong and R. S. Williams, Annu. Rev. Phys. Chem., 1994, 45, 401–438.
25. C. Herring, J. Appl. Phys., 1950, 21, 301–303.
26. W. W. Mullins, J. Appl. Phys., 1959, 30, 77–83.

---