In situ X-ray diffraction study of the hydrothermal crystallization of hierarchical Bi₂WO₆ nanostructures

Abstract

The hydrothermal crystallization of hierarchical Bi₂WO₆ nanostructures has been monitored with in situ energy-dispersive X-ray diffraction (EDXRD). The kinetic data analysis according to the Avrami-Erofe'ev model suggests that the formation of nanostructured Bi₂WO₆ is diffusion controlled with Avrami exponents around 0.5 and that the growth mechanism is temperature independent in the interval from 150 to 180 °C. Furthermore, the reaction kinetics and the crystal structure of the resulting hydrothermal products depend on the pH value of the Bi(NO₃)₃·5H₂O/K₂WO₄ hydrothermal system.

---

Introduction

Bismuth tungstate (Bi₂WO₆) is a key representative of the family of Aurivillius type oxides with [WO₄]_n²⁻ sheets consisting of corner-sharing WO₆ octahedra alternating with [Bi₂O₂]_n²⁺ slabs as a common structural motif.¹ Bi₂WO₆ has numerous important physical and chemical properties, e.g. oxide anion conductivity, ferroelectricity, non-linear dielectric susceptibility and luminescent properties that render it suitable for many applications.^2–5 Therefore, Bi₂WO₆ keeps attracting research attention, especially due to its highly promising photocatalytic activity with respect to O₂ evolution and the visible-light-driven degradation of organic compounds.^6,7 The photocatalytic performance of semiconductors in general can be remarkably enhanced through their transformation onto the nanoscale with special emphasis on particle size and morphology control. As a consequence, intense research efforts have been focused on the synthesis of nanostructured Bi₂WO₆^8–10 so that different hydrothermal pathways to 3D hierarchical Bi₂WO₆ nanostructures composed of individual nanosheet building blocks were recently reported.^11–14 Interestingly, their photocatalytic activities were found to be superior to bulk Bi₂WO₆ with particle sizes of several tens of micrometers. However, the formation principles of these catalytically active Bi₂WO₆ particles still remain to be fully understood: in the first place, organic additives, such as polyvinylpyrrolidone (PVP) and block copolymers, were considered indispensable for the formation of hierarchical morphologies.^11,15–17 On the other hand, several other groups including some of us accessed hierarchically structured Bi₂WO₆ architectures via additive-free approaches.^12,14,18,19 The only thread among all these protocols are strongly acidic reaction media and the resulting multitude of preparative options clearly illustrates the importance of understanding hydrothermal formation mechanisms: there is a growing need for general principles that can be easily applied to plan the production of hierarchically structured nanomaterials. In contrast to this trend, however, hydrothermal autoclaves are still widely operated as “black boxes”, because the fundamental study of hydrothermal kinetics and possible intermediate phases in solution²⁰ is still limited to a number of selected examples. A more general concept of these processes would provide materials and industrial scientists with extremely powerful tools for the phase and morphology control of hydrothermal products, e.g. for future catalyst design.²¹ This goal requires the widespread use of in situ techniques that offer unique opportunities to track reaction pathways, thereby providing key information about hydrothermal crystallization kinetics.^22–27 Such insights would be complementary to high-throughput hydrothermal parameter optimizations.²⁸ Over the past years, we have successfully applied in situ methods to understand the formation mechanisms of different nanoscale oxide materials, such as MoO₃ fibers,²⁹ hexagonal tungsten bronzes^30,31 and Bi₆S₂O₁₅ nanowires.³² Among the growing spectrum of in situ techniques, energy-dispersive X-ray diffraction (EDXRD) which uses polychromatic radiation and energy discriminating detectors, has proven particularly efficient to investigate crystallization kinetics and to identify crystalline intermediates.^33,34 Moreover, in situ EDXRD offers a higher degree of flexibility for experimental setups in comparison with angular dispersive XRD techniques. This permits the convenient determination of the key experimental parameters that influence the crystallization kinetics and the product formation steps.

In the present study, we investigate the hydrothermal crystallization of hierarchical Bi₂WO₆ nanostructures (for representative SEM images cf.Fig. 1a–b)¹⁹ using in situ EDXRD methods with special emphasis on the role of the reaction temperature and the pH value. The resulting insights into the reaction kinetics were verified through comparison with ex situ measurements (XRD and scanning electron microscopy (SEM)).

Fig. 1 (a) and (b): SEM images of hierarchical Bi₂WO₆ nanostructures obtained under conventional hydrothermal synthesis conditions;¹⁹ (c) time-resolved EDXRD patterns measured during the crystallization of Bi₂WO₆ at 160 °C (pH 1.1); the indices of the intense lines of the product and W K_α fluorescence lines are marked (escape peak at 15 keV); inset: close-up SEM image of hierarchical Bi₂WO₆ nanostructures.

Experimental

In situ EDXRD experiments

In situ EDXRD experiments were performed at HASYLAB (Hamburg) bending magnet beamline F3 that provides an energy range of 13.31–62.54 keV with a maximum intensity at about 26 keV. The d-spacing is given by d = 6.199/E sinθ (with d in Å and E in keV). A solid state Ge detector cooled with liquid nitrogen was used for all experiments. With a detector angle of 4.9° the observable d-spacing range is 1.16 Å to 5.46 Å. The energy resolution Δd/d is about 10⁻² above 26 keV. The beam was collimated to 0.2 mm for optimum results. More detailed experimental information can be found in ref. 35 and 36. For the in situ experiments, autoclaves with glass liners (internal diameter of 10 mm and a volume of 10 mL) were used. Hierarchical Bi₂WO₆ microspheres were synthesized according to our previous studies.¹⁹ In a representative experiment, 97 mg (0.2 mmol) Bi(NO₃)₃·5H₂O, 33 mg (0.1 mmol) K₂WO₄ and 2 mL 20 vol.-% acetic acid were used as reactants. The reactions were performed at 150, 160, 170 and 180 °C, respectively. The pH of the suspension was adjusted to a specific value using 8 M NaOH solution, if required. Data collection was started immediately after the introduction of the autoclave into the oven. The acquisition time per frame for the in situ data measured in these experiments was 120 s. After the in situ experiments, the solid products were filtrated, collected, washed with distilled water and ethanol, and dried in air for further characterizations. It is noteworthy that the reactions have to be performed under rapid stirring to keep the measurement conditions constant by avoiding the sedimentation of the high density product particles.

Data analysis

The in situ EDXRD data analysis starts with the integration of the peak intensity in the individual spectra using a Gaussian function. Next, the integrated intensities of the product reflections were normalized against the intensity of the W K_α fluorescence line. The value of the extent of reaction, α, at a given time, t, can be calculated from the appearance of a Bragg reflection (hkl) according to α(t) = I_hkl(t)/I_hkl(t_∞), where I_hkl(t) is the normalized intensity of a reflection (hkl) with time t, and I_hkl(t_∞) represents the intensity normalized to the maximum Bragg peak area. To obtain detailed information on the kinetics of the crystallization process, kinetic evaluations were performed after subtracting of the induction time t_ind (defined as the time interval until the first reflections are observed) from the given time t, using the well-known Avrami-Erofe'ev equation which is a model to simulate nucleation-growth crystallisation:^37–39

α = 1 − exp{−[k(t − t_ind)]^m} (1)

k represents the rate constant and the exponent m is often used to distinguish between different reaction mechanisms.⁴⁰ The value of m is most easily visualized with the aid of a Sharp-Hancock (SH) plot using the following equation:⁴¹

ln[−ln(1 − α)] = mln(t − t_ind) + mlnk (2)

When ln[−ln(1 − α)] is plotted vs. ln(t − t_ind), a straight line is obtained if that part of the reaction follows the same mechanism. A change of the mechanism results in a change of the slope of the curve. The exponent m can be derived from the slope of the curve, while k can be obtained from the intercept with the y axis. Although this method has been widely used to study the reaction kinetics of zeolites,^42,43 oxides⁴⁴ and metal–organic frameworks,²³ one should keep in mind that the precise value of m often depends on the chosen strategy for data analysis with the determination of the induction time being an especially crucial parameter. The Avrami-Erofe'ev equation was developed to simulate nucleation and growth of crystalline solids using ideal conditions, e.g. spherical particles of identical size. These criteria are seldom fulfilled in real systems. Therefore, the evaluation of kinetic data applying the Avrami-Erofe'ev equation is performed in the following to get an impression whether changes of the synthetic conditions alter the overall dominating crystallization kinetics.

Analytical characterization

Powder X-ray diffraction (XRD) was performed on a STOE STADI P diffractometer in transmission mode (flat sample holders, Ge monochromator and Cu K_α1 radiation) operated at 40 kV and 40 mA and equipped with a position sensitive detector. Scanning electron microscopy (SEM) was performed on a Zeiss SUPRA 50 VP microscope. The specimens were investigated without conductive coating at rather low voltage (2 kV) to minimize charging effects.

Results and discussion

A three-dimensional stack plot of the in situ EDXRD patterns recorded at 160 °C and pH 1.1 during the hydrothermal reaction is shown in Fig. 1. After a short induction time of around 8 min (cf.Table 1), several diffraction peaks corresponding to the reflections of orthorhombic Bi₂WO₆ appeared and their intensity increased with the reaction time. The reaction is complete after ca. 70 min and no crystalline intermediates could be observed. Most importantly, the induction time has been considerably reduced with respect to the conventional hydrothermal synthesis that takes more than 1 h until the onset of product formation.^19a This is probably due to a combination of stirring and different heating conditions.

Table 1 Summary of the Avrami-Erofe'ev kinetic parameters for the hydrothermal growth of Bi₂WO₆ under different reaction conditions

T/°C	pH	t ind/min	t 0.5/min	m
a The reaction was too fast to generate sufficient data points for analysis.
150	1.1	12	28	0.54
160	1.1	8	16	0.52
170	1.1	6	14	0.49
180	1.1	4	12	0.57
160	4.0	4	10	0.77
160	4.6	4	7

---

The extent of reaction α for the most intense reflections ((002), (260) and (191)) of Bi₂WO₆ is plotted against the reaction time t in Fig. S1, ESI.† The sigmoidal curves are typical for a crystallization process that proceeds rapidly after an initial induction period, followed by completion of crystal growth. All growth curves have the same basic shape in common so that no crystallographic direction is obviously favored (Fig. S1, ESI†). This is in line with previous reports on the isotropic growth process of the related Aurivillius type oxide Bi₂MoO₆.⁴⁵ Therefore, the (260) reflection was selected for the following kinetic analysis.

The in situ EDXRD patterns monitoring the formation of Bi₂WO₆ at other temperatures (150, 170 and 180 °C) closely resemble the patterns recorded at 160 °C as shown in Fig. 1. Within this temperature range, the product is directly formed from the amorphous precursors in the absence of any crystalline intermediate phase. Moreover, Fig. 2 illustrates that higher reaction temperatures lead to a remarkable reduction of both the time t_ind and half-life time t_0.5 of Bi₂WO₆ formation: t_ind and t_0.5 decreased from 12 to 4 min and from 28 to 12 min, respectively, when the temperature was raised from 150 to 180 °C (Table 1). Nevertheless, the shape of the Bi₂WO₆ growth curves varied only little with the reaction temperature, thereby indicating that the growth mechanism is temperature independent in the given interval that is within our previously reported temperature window of 120–180 °C for the formation of hierarchical Bi₂WO₆ microspheres (cf.Fig. 3).^19a The Sharp-Hancock plots based on the kinetic data derived from the monitoring of the (260) reflection of Bi₂WO₆ are compared for different reaction temperatures in Fig. 3: all graphs are linear for 0.2 < α < 0.85 and thus point to common crystallization kinetics for the growth of Bi₂WO₆. This is well in line with the values of the Avrami exponents m evaluated from the linear part of the curves that are all close to 0.5 (Table 1). Their low average value (∼0.5) furthermore suggests that Bi₂WO₆ is formed via a diffusion-controlled process under the applied conditions, because the exponent m should be 1 or larger for all other reaction mechanisms.^35,40,42,43 Until now, it has been suggested in previous studies that diffusion-limited conditions are required for the formation of 3D hierarchical Bi₂WO₆ nanostructures, but this hypothesis has never been backed with according data for this hydrothermal system.¹⁸ However, our previous in situ studies on the formation of morphologically related hierarchical W/Mo-oxides point into the same direction, because they are also formed via a diffusion-controlled mechanism with Avrami exponents around 0.55.⁴⁶ Hence, the present in situ results support the hypothesis that diffusion-controlled mechanisms are obviously a common denominator for the self-organization of nanosized building blocks into hierarchical structures for chemically different hydrothermal systems. The rate constant (k) values have not been added to Table 1 due to the following reasons: once the crystallization process of a diffusion-controlled reaction is started, the reaction rate is not significantly influenced by the nucleation rate any more, but it depends on the diffusion rates of the species in solution to the crystallization sites.^40,42 Increasing the temperature should in principle increase the diffusion rates. On the other hand, the vigorous stirring during the reaction may exert a much higher influence on k than the investigated temperature range, thereby leading to opposite trends that are almost impossible to differentiate. In addition, the experimental errors of k are rather high and difficult to estimate precisely so that a discussion of general trends is more appropriate. As mentioned in the experimental part, rapid stirring is important to conduct the present in situ experiments and it reduces the induction times for Bi₂WO₆ formation to several minutes in comparison with hour scale induction periods in the absence of stirring under conventional laboratory conditions.¹⁹ Obviously, the aforementioned rate-determining diffusion step can be significantly accelerated by an improved transport of the individual species to the nucleation sites through stirring. Therefore, the reaction constant k may depend more strongly on the stirring rate rather than on the inherent diffusion rate which is also supported by preceding investigations.⁴²

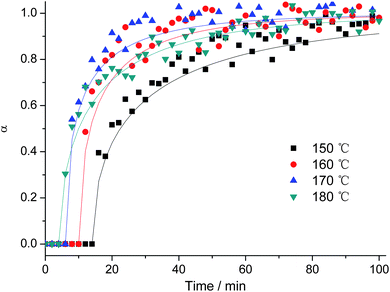Fig. 2 Extent of reaction α versus time for the (260) reflection of Bi₂WO₆ recorded at different temperatures.

Fig. 3 Sharp-Hancock plots for the kinetic data recorded at different temperatures over a range of 0.2 < α < 0.85.

As discussed in the introduction, strongly acidic reaction conditions are an indispensable parameter for the formation of hierarchical Bi₂WO₆ microspheres,^12,14 because they disintegrate into their individual nanoplate building blocks at higher pH values and other phases are formed above a pH threshold of 13.^19a In order to optimize the hydrothermal growth of catalytically active Bi₂WO₆ nanoparticles, understanding the influence of the pH on the reaction pathways and kinetics is crucial. Therefore, we performed a series of in situ experiments at constant temperature (160 °C) whilst the pH value of the precursor solution was varied by adding 8 M NaOH solution. The fast crystallization kinetics and the very short half-life time t_0.5 observed at pH 4 (cf.Fig. 4 and Table 1) illustrate how the pH value of the reaction system can accelerate the formation of Bi₂WO₆ that most likely proceeds as follows:⁴⁷

2Bi³⁺ + WO₄²⁻ + 2H₂O → Bi₂WO₆↓ + 4H⁺

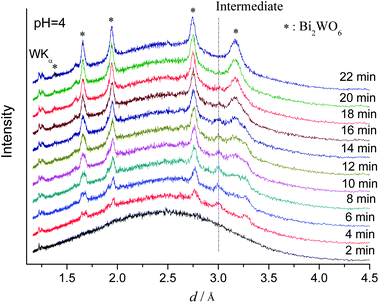Fig. 4 In situ EDXRD patterns for the formation of Bi₂WO₆ recorded at 160 °C (pH 4.0).

From the thermodynamic point of view, it is obvious that low pH values around 1.1 probably shift the equilibrium towards the precursors and thus restrain the formation of Bi₂WO₆.

In this context, it is very interesting that an additional reflection at 3.0 Å appeared after 4 min of reaction time at pH 4 that disappeared again after 22 min (Fig. 4). As shown in Fig. S2, ESI,† the same phenomenon occurred at pH 4.6 and it is probably caused by the presence of a crystalline intermediate. The observation that this unknown temporary phase could not be detected under strongly acidic conditions (pH 1.1, cf.Fig. 1) underscores the significant effect of the pH on the course of the reaction. This is also evident from the kinetic analysis (cf.Table 1): at pH 4.6, the reaction is even too fast to generate sufficient data for detailed analysis. Moreover, the Avrami exponent m also increases to 0.77 (pH 4.0) and this points again to a change of the reaction kinetics with the pH value of the hydrothermal system. Given that Avrami exponents around 1.0 were reported for the hydrothermal formation of Aurivillius type Bi₂MoO₆ nanoplates,⁴⁵ the above change in the crystallization kinetics probably causes the disintegration of Bi₂WO₆ spheres into their plate-shaped building blocks at higher pH.

As these insights are in line with our previous observations on hierarchical tungstate structures formed by diffusion-controlled processes⁴⁶ (i.e. reaction exponents ∼0.5), it would be worthwhile to pursue more extended studies in the field to reveal whether this is a general trend. If so, such principles could offer new strategies to control the morphology of hydrothermal products by adjusting the reaction kinetics.⁴⁸

A further pH increase to 11.0 leads to a phase change of the product so that cubic Bi_3.84W_0.16O_6.24 was obtained instead of orthorhombic Bi₂WO₆ (Fig. 5 and Fig. S3, ESI†). This phase change is due to the high solubility of WO₄²⁻ in alkaline media where [Bi₂O₂]²⁺ and WO₄²⁻ can precipitate.⁴⁹ As the formation of Bi_3.84W_0.16O_6.24 is based on this rapid precipitation process, no induction time at all was observed. Finally, pure monoclinic Bi₂O₃ is formed at pH 13.0 according to our previous studies.^19a

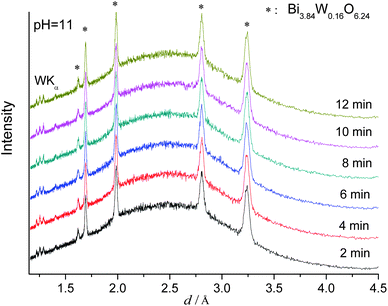Fig. 5 In situ EDXRD patterns for the formation of Bi_3.84W_0.16O_6.24 recorded at 160 °C (pH 11.0).

Generally, the morphologies and phases obtained from in situ experiments may differ from those observed in the course of the corresponding ex situ experiments due to the different autoclave setups and stirring conditions.⁵⁰ In order to prevent the discussion of relative artefacts, all solid products were collected after the in situ EDXRD experiments and they were analyzed by ex situ XRD and SEM. The XRD patterns of all ex situ products agree well with those of the phases grown under in situ conditions (Fig. S3, ESI†). Likewise, the in situ dependence of the morphology on the pH value corresponds with the trends observed for the ex situ experiments (Fig. 6): hierarchical Bi₂WO₆ microspheres are formed at pH 1.1 (Fig. 6a) and they disintegrate into their nanosheet building blocks at higher pH values (pH 4.6, cf.Fig. 6b). The phase change to cubic Bi_3.84W_0.16O_6.24 at pH 11.0 is reflected in a morphological transition to nanoparticles with diameters below 100 nm (Fig. 6c).

Fig. 6 SEM images of the products synthesized at different pH values (ex situ): (a) pH 1.1; (b) pH 4.6; (c) pH 11 (the SEM image of the samples synthesized at pH 4 is similar to the results obtained at pH 4.6. cf. Fig. 6b).

Conclusions

In summary, we have directly monitored the hydrothermal crystallization of hierarchical Bi₂WO₆ nanostructures with in situ EDXRD methods. The crystallization kinetics were assigned according to the Avrami-Erofe'ev model and we found that the growth of Bi₂WO₆ is diffusion controlled with Avrami exponents of ∼0.5 in the temperature range from 150 to 180 °C. A pH raise to 4.0 leads to a significant acceleration of the reaction kinetics along with an increased Avrami exponent m of ca. 0.77. This points to a pH-dependent reaction kinetics in the Bi(NO₃)₃·5H₂O/K₂WO₄ hydrothermal system that is accompanied by the disintegration of the hierarchically structured Bi₂WO₆ nanospheres into their individual building blocks. Furthermore, the emerging phases can also be steered through the pH, because cubic Bi_3.84W_0.16O_6.24 is formed through a rapid precipitation reaction at pH 11.0 due to the enhanced solubility of WO₄²⁻ in alkaline media and monoclinic Bi₂O₃ finally occurs at pH 13.0.

Our results indicate that diffusion-controlled processes with Avrami exponents around 0.5 are an essential prerequisite for the formation of hierarchical nanostructures. Therefore, they open up interesting perspectives for the control of nanomaterials fabrication through the understanding of mechanistic principles. Further studies on bismuth containing functional oxides are now in progress to apply these insights to their morphology tuning and to the development of sensors and photocatalysts.

Acknowledgements

We thank HASYLAB (DESY, Hamburg, Germany) for providing beamtime at beamline F3 for in situ EDXRD experiments. Beatrix Seidlhofer and Jing Wang (University of Kiel) are acknowledged for their kind assistance during the in situ experiments. The support of the Electron Microscopy ETH Zurich, EMEZ and Center for Microscopy and Image Analysis, University of Zurich, is acknowledged. We thank the Swiss National Science Foundation (SNF Professorship PP002-114711/1) and the University of Zurich for financial support.

Notes and references

1. J. Ricote, L. Pardo, A. Castro and P. Millan, J. Solid State Chem., 2001, 160, 54.
2. Z. G. Yi, Y. X. Li, Z. Y. Wen, S. R. Wang, J. T. Zeng and Q. R. Yin, Appl. Phys. Lett., 2005, 86, 192906.
3. N. A. McDowell, K. S. Knight and P. Lightfoot, Chem.–Eur. J., 2006, 12, 1493.
4. M. Hamada, H. Tabata and T. Kawai, Thin Solid Films, 1997, 306, 6.
5. O. M. Bordun, Inorg. Mater., 1998, 34, 12.
6. A. Kudo and S. Hijii, Chem. Lett., 1999, 1103.
7. J. W. Tang, Z. G. Zou and J. H. Ye, Catal. Lett., 2004, 92, 53.
8. C. Zhang and Y. F. Zhu, Chem. Mater., 2005, 17, 3537.
9. H. B. Fu, C. S. Pan, W. Q. Yao and Y. F. Zhu, J. Phys. Chem. B, 2005, 109, 22432.
10. H. B. Fu, L. W. Zhang, W. Q. Yao and Y. F. Zhu, Appl. Catal., B, 2006, 66, 100.
11. L. S. Zhang, W. Z. Wang, L. Zhou and H. L. Xu, Small, 2007, 3, 1618.
12. L. S. Zhang, W. Z. Wang, Z. G. Chen, L. Zhou, H. L. Xu and W. Zhu, J. Mater. Chem., 2007, 17, 2526.
13. F. Amano, A. Yamakata, K. Nogami, M. Osawa and B. Ohtani, J. Am. Chem. Soc., 2008, 130, 17650.
14. F. Amano, K. Nogami, R. Abe and B. Ohtani, Chem. Lett., 2007, 36, 1314.
15. Y. Y. Li, J. P. Liu, X. T. Huang and G. Y. Li, Cryst. Growth Des., 2007, 7, 1350.
16. J. Wu, F. Duan, Y. Zheng and Y. Xie, J. Phys. Chem. C, 2007, 111, 12866.
17. S. W. Liu and J. G. Yu, J. Solid State Chem., 2008, 181, 1048.
18. F. Amano, K. Nogami, R. Abe and B. Ohtani, J. Phys. Chem. C, 2008, 112, 9320.
19. (a) Y. Zhou, K. Vuille, A. Heel and G. R. Patzke, Z. Anorg. Allg. Chem., 2009, 635, 1848; (b) Y. Zhou, F. Krumeich, A. Heel and G. R. Patzke, Dalton Trans., 2010, 39, 6043.
20. K. Byrappa, M. Yoshimura, Handbook of Hydrothermal Technologies, William Andrew Publishing, New Jersey, 2001.
21. S. Marx, W. Kleist, J. Huang, M. Maciejewski and A. Baiker, Dalton Trans., 2010, 39, 3795.
22. R. I. Walton and D. O'Hare, Chem. Commun., 2000, 2283.
23. F. Millange, M. I. Medina, N. Guillou, G. Férey, K. M. Golden and R. I. Walton, Angew. Chem. Int. Ed., 2010, 49, 763.
24. Y. Du, K. M. Ok and D. O'Hare, J. Mater. Chem., 2008, 18, 4450.
25. (a) H. Jensen, M. Bremholm, R. P. Nielsen, K. D. Joensen, J. S. Pedersen, H. Birkedal, Y.-S. Chen, J. Almer, E. G. Søgaard, S. B. Iversen and B. B. Iversen, Angew. Chem., Int. Ed., 2007, 46, 1113; (b) M. Bremholm, M. Felicissimo and B. B. Iversen, Angew. Chem., Int. Ed., 2009, 48, 4788.
26. C. Kongmark, V. Martis, A. Rubbens, C. Pirovano, A. Lofberg, G. Sankar, E. Bordes-Richard, R. N. Vannier and W. Van Beek, Chem. Commun., 2009, 4850.
27. F. Fan, Z. Feng, K. Sun, M. Guo, Q. Guo, Y. Song, W. Li and C. Li, Angew. Chem., Int. Ed., 2009, 48, 8743.
28. N. Stock, Microporous Mesoporous Mater., 2010, 129, 287.
29. A. Michailovski, J.-D. Grunwaldt, A. Baiker, R. Kiebach, W. Bensch and G. R. Patzke, Angew. Chem., Int. Ed., 2005, 44, 5643.
30. A. Michailovski, R. Kiebach, W. Bensch, J.-D. Grunwaldt, A. Baiker, S. Komarneni and G. R. Patzke, Chem. Mater., 2007, 19, 185.
31. R. Kiebach, N. Pienack, W. Bensch, J.-D. Gruwaldt, A. Michailovski, A. Baiker, T. Fox, Y. Zhou and G. R. Patzke, Chem. Mater., 2008, 20, 3022.
32. Y. Zhou, J.-D. Gruwaldt, F. Krumeich, K. Zheng, G. Chen, J. Stötzel, R. Frahm and G. R. Patzke, Small, 2010, 6, 1173.
33. R. Kiebach, N. Pienack, M.-E. Ordolff, F. Studt and W. Bensch, Chem. Mater., 2006, 18, 1196.
34. A. M. Fogg, S. J. Price, R. J. Francis, S. O'Brien and D. O'Hare, J. Mater. Chem., 2000, 10, 2355.
35. L. Engelke, M. Schäfer, M. Schur and W. Bensch, Chem. Mater., 2001, 13, 1383.
36. L. Engelke, M. Schäfer, F. Porsch and W. Bensch, Eur. J. Inorg. Chem., 2003, 506.
37. M. J. Avrami, J. Chem. Phys., 1939, 7, 1103.
38. M. J. Avrami, J. Chem. Phys., 1940, 8, 212.
39. M. J. Avrami, J. Chem. Phys., 1941, 9, 177.
40. S. F. Hulbert, J. Br. Ceram. Soc., 1969, 6, 11.
41. J. D. Hancock and J. H. Sharp, J. Am. Ceram. Soc., 1972, 55, 74.
42. R. J. Francis, S. O'Brien, A. M. Fogg, P. S. Halasyamani, D. O'Hare, T. Losieau and G. Férey, J. Am. Chem. Soc., 1999, 121, 1002.
43. R. I. Walton, T. Loiseau, D. O'Hare and G. Férey, Chem. Mater., 1999, 11, 3201.
44. (a) R. I. Walton, F. Millange, R. I. Smith, T. C. Hansen and D. O'Hare, J. Am. Chem. Soc., 2001, 123, 12547; (b) R. Kiebach, M. Schaefer, F. Porsch and W. Bensch, Z. Anorg. Allg. Chem., 2005, 631, 369.
45. A. M. Beale and G. Sankar, Chem. Mater., 2003, 15, 146.
46. Y. Zhou, N. Pienack, W. Bensch and G. R. Patzke, Small, 2009, 5, 1978.
47. D. Ma, S. Huang, W. Chen, S. Hu, F. Shi and K. Fan, J. Phys. Chem. C, 2009, 113, 4369.
48. H. Imai and Y. Oaki, MRS Bulletin, 2010, 35, 138.
49. S. Yao, J. Wei, B. Huang, S. Feng, X. Zhang, X. Qin, P. Wang, Z. Wang, Q. Zhang, X. Jing and J. Zhan, J. Solid State Chem., 2009, 182, 236.
50. P. Norby, Curr. Opin. Colloid Interface Sci., 2006, 11, 118.

---

Footnote

† Electronic supplementary information (ESI) available: Extent of reaction α versus time for different reflections of Bi₂WO₆ at 160 °C, in situ EDXRD patterns for the reaction at pH 4.6 and ex situ XRD patterns of products synthesized at different pH values. See DOI: 10.1039/c0nr00340a

---