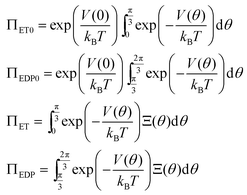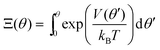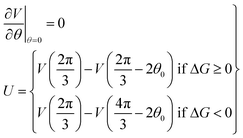FoF1-ATPase, rotary motor and biosensor
Yao-Gen
Shu
*a,
Jia-Chang
Yue
*b and
Zhong-Can
Ou-Yang
a
aInstitute of Theoretical Physics, CAS, Beijing, 100190, China. E-mail: shuyg@itp.ac.cn
bInstitute of Biophysics, CAS, Beijing, 100101, China. E-mail: yuejc@sun5.ibp.ac.cn
First published on 18th May 2010
Abstract
FoF1-ATPase is an amazing molecular rotary motor at the nanoscale. Single molecule technologies have contributed much to the understanding of the motor. For example, fluorescence imaging and spectroscopy revealed the physical rotation of isolated F1 and Fo, or FoF1 holoenzyme. Magnetic tweezers were employed to manipulate the ATP synthesis/hydrolysis in F1, and proton translation in Fo. Here, we briefly review our recent works including a systematic kinetics study of the holoenzyme, the mechanochemical coupling mechanism, reconstituting the δ-free FoF1-ATPase, direct observation of Fo rotation at single molecule level and activity regulation through external links on the stator.
 Yao-Gen Shu | Y.-G. Shu was born on January 4, 1964 in Zhejiang province, China. He received his Bachelor of Electronic Engineering in July 1985 at Zhejiang University, and then worked on industrial automation till 1999. He received his Ph. D. in 2004 at the Department of Physics of Xiamen University. From 2004 to 2009, he worked with Prof. Zhong-Can Ou-Yang at the Institute of Theoretical Physics (Chinese Academy of Sciences) and Prof. Pik-Yin Lai at the National Central University (Taiwan), respectively. Currently, he is a research fellow at the Institute of Theoretical Physics. His research focuses on molecular motors, cell motion, biosensor, nanodevices, and so on. |
 Jia-Chang Yue | Prof. Jia-Chang Yue is the leader of the molecular motor group at the Institute of Biophysics at the Chinese Academy of Sciences. He has held positions as a visiting scholar at Tohoku University, Japan and Hong Kong Polytechnic University. Previously he researched at the Department of Engineering Physics, Tsinghua University, China. Current research interests include: the structure and function of the rotary molecular motor FoF1-ATPase, and developing biosensors based on FoF1-ATPase. |
 Zhong-Can Ou-Yang | Prof. Zhong-Can Ou-Yang was born on January 25, 1946 in Fujian province, China. He received his Ph.D. in 1984 from Tsinghua University (Beijing). From 1987–1988, he worked with Prof. W. Helfrich at the Freie University (Berlin) as an Alexander von Humboldt fellow. He has been a professor at the Institute of Theoretical Physics, Chinese Academy of Sciences since 1992, and Director from 1998–2007. His research focuses on soft condensed matter physics and theoretical biophysics. He received the Achievement in Asia Award from the Overseas Chinese Physics Association in 1993 and is a member of Chinese Academy of Sciences and the Third Word Academy of Sciences. |
I. Introduction
FoF1-ATPase is a ubiquitous rotary motor that uses the transmembrane electrochemical potential to synthesize ATP in the plasma membrane of bacteria, chloroplasts and mitochondria. The holoenzyme is a complex of two rotary motors, Fo and F1, which are mechanically coupled by a common central stalk (“rotor”), cnεγ. The membrane embedded Fo unit converts the proton motive force (p.m.f.) into mechanical rotation of the “rotor”, thereby causing cyclic conformational change of α3β3 crown (“stator”) in F1 and driving ATP synthesis. A striking characteristic of this motor is its reversibility. It may rotate in the reverse direction for ATP hydrolysis and utilize the excess energy to pump protons across the membrane.1–6The basic hypothesis, “binding change mechanism”,7 however, had not been confirmed until direct observation of the rotation of F1-ATPase at the single molecule level in 1997,8 although it was partly proven by the eccentric structure of the γ subunit in 1994.9 Single molecule technologies have contributed much to the understanding of the motor. For example, fluorescence imaging and spectroscopy revealed the physical rotation of isolated F18,10–12 and Fo,13,14 or F1Fo holoenzyme.15–17 Magnetic tweezers also be employed to manipulate the ATP synthesis/hydrolysis in F1,18,19 and proton translation in Fo.20 Nevertheless, the fundamental relation between the rotation speed and substrate/product concentrations, transmembrane p.m.f. and damping coefficient is important in the time frame of enzymatics.21
II. Systematic kinetics of the holoenzyme
A few theoretical approaches have been proposed, aiming for a better understanding of the operating mechanism of this reversible motor. Some work focused on the hydrolysis or synthesis of F1. For example, Oster et al. constructed a 43 states model for the couplings among three catalytic sites and provided a physical view of the dynamics.22–24 However, this model is too sophisticated to be investigated analytically. Some other models studied the mechanism of torque generation of Fo with a turbine or all-atom model.25–27 The kinetics of the motor have also been investigated by Pänke et al. with simulations or storage of elastic energy model.28,29 Here, we focus on an analytical investigation of the systematic kinetics of the holoenzyme, that is, the fundamental relation between the rotation speed and substrate/product concentrations, transmembrane p.m.f. and damping coefficient.21It is well established that the mechanical process in Fo and the chemical reactions in F1 are tightly coupled. Therefore, it is possible to construct a theory which can systematically describe the whole machine. From the view point of enzymatics, conventional theory generally concerned with irreversible reaction on a single substrate which can be described by Michaelis–Menten kinetics. But ATP can be reversibly synthesized and hydrolyzed in FoF1-ATPase, and the reaction involves several substrates/products, thus there is an need for a quantitative theory which describes the multi-substrate/product enzymatics. Furthermore, analytical results could presumably allow for a deeper insight for the working principles of the motor.
FoF1-ATPase, in particular, is an amazing reversible motor. ATP hydrolysis does spontaneously occur in F1, whereas the thermodynamically unfavorable reaction, ATP synthesis, has to be driven by harnessing the transmembrane proton flow in Fo. If the motor functions as a synthase, the two substrates, ADP and Pi, are recombined into one product, ATP. The binding order of the two substrates is a characteristic attribute of the synthase. On the basis of inhibition studies, a compulsory order with binding of ADP preceding that of Pi was proposed.30 Enzyme kinetic analysis, on the other hand, indicated a random order in their binding.31,32
Another challenging question is whether the main kinetic enhancement occurs upon filling the second or the third site. Based on measurements of the dependence of ATP synthesis rate on ADP concentration, Boyer and Cross proposed that rapid net synthesis of MF1 is attained when a second catalytic site is filled.33,34 Results from the laboratories of Senior,35 Allison36 and Kinosita,11 however, provided evidence that three catalytic sites are filled when sufficient ATP is present for rapid catalysis by EcF1 or TF1. A crystal structure37 also indicated that all three sites are filled, one with ATP, one with ADP and Pi and one half closed site with ADP and Pi.
Different from the bi-site scenario, the tri-site one guarantees that the synthesis and the hydrolysis follow the same reaction pathway, which corresponds to the basic scheme that is proposed by Nakamoto, Senior and Kinosita.12,38–40 Here, we propose a tri-site filled scenario with random order of ADP and Pi binding (shown in Fig. 1) and systematically investigate the kinetics of FoF1-ATPase with p.m.f. The following details are taken into account:
 | ||
| Fig. 1 The detailed coupling reaction scheme of the holoenzyme FoF1-ATPase. Synthesis pathway runs from right to left (red solid line), whereas hydrolysis one runs from left to right (blue dashed dots). T, D and P represent ATP, ADP and Pi respectively. The green, blue and red β subunits denote “open”, “loose” and “tight” conformations (labeled by the superscripts O, L and T of β respectively) and correspond to βE, βDP and βT in the Walker structure.9 The inset shows the reversible reaction pathways of the enzyme F1.21 | ||
1. The synthesis and hydrolysis follow the same reaction pathway. One ATP is consumed if the motor moves 120° counterclockwise (CCW, blue pathway). Conversely, one ATP is synthesized if it moves 120° clockwise (CW, red pathway).
2. Before each step, all three αβ pairs display different conformations depicted as “open” (green), “loose” (blue) and “tight” (red). The exchange of substrates is practically restricted to the “open” conformation.
3. The binding of ATP and ADP/Pi to the “open” site is taken to be competitive while that of ADP and Pi is random.
4. CCW 120° movement of γ drives conformational changes of the three sites as “open” → “tight”, “tight” → “loose” and “loose” → “open” respectively.
5. Chemical reaction, ADP + Pi ⇌ ATP + H2O, takes place during the “tight” ⇌ “loose” conformational change, and is tightly coupled with transmembrane proton transport in Fo by the rotation of “rotor”.
Five states involved in this model are denoted by E, ET, EDP, ED and EP respectively. E is a two-site filled state and it has been indicated in the crystal structure9 that one site binds ATP and the other grips ADP and Pi. All others are three-site filled states. The structure of EDP has also been crystallized.37 Different from the bi-site model, the present model suggests that ATP synthesis, in the presence of adequate p.m.f., requires ADP and Pi to occupy the third (open) site; while for ATP hydrolysis, if the p.m.f. is low or absent, it requires that ATP occupies the same site.
The kinetics of this reversible reaction (shown in Fig. 1)21 may be described by the equations governing the probabilities (denoted by PE, PET, PEDP, PED, and PEP) of these five states
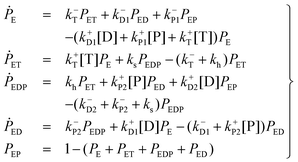 | (1) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) k±D and k±P1 = k±P2
k±D and k±P1 = k±P2 ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) k±P, it can be put into an apparent Michaelis–Menten equation. In addition, clamped ΔpH experiment41 has shown that binding and unbinding of a substrate (at cosubstrate saturation) are rapid processes as compared to the synthesis/hydrolysis step (mechanical rotation), which means that ks/h ≪ kL
k±P, it can be put into an apparent Michaelis–Menten equation. In addition, clamped ΔpH experiment41 has shown that binding and unbinding of a substrate (at cosubstrate saturation) are rapid processes as compared to the synthesis/hydrolysis step (mechanical rotation), which means that ks/h ≪ kL ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) k+P[P] + k+D[D] + k−P + k−D. Within the framework of steady-state conditions for eqn (1), the clockwise revolution rate of the motor at steady state is given by ⅓(ksPEDP − khPET) and is computed to be
k+P[P] + k+D[D] + k−P + k−D. Within the framework of steady-state conditions for eqn (1), the clockwise revolution rate of the motor at steady state is given by ⅓(ksPEDP − khPET) and is computed to be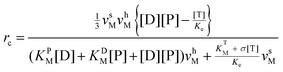 | (2) |
the definition and meaning of various quantities in the above equation are given below:
v sM and vhM are the saturated rates of synthesis and hydrolysis and are given by
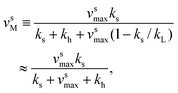 | (3) |
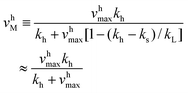 | (4) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) k−T and vhmax
k−T and vhmax ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) k−Pk−D/(k−P + k−D).
k−Pk−D/(k−P + k−D).
The corresponding Michaelis constants are given by
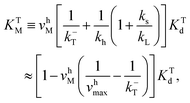 | (5) |
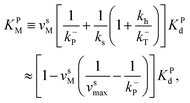 | (6) |
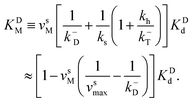 | (7) |
The equilibrium constant is given by 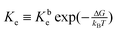 , where Kbe
, where Kbe ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) KTd/(KDdKPd) and the dissociations constant are K1d = k−1/k+1 with the subscript I = T, D, P respectively. The equilibrium constant varies exponentially with p.m.f.
KTd/(KDdKPd) and the dissociations constant are K1d = k−1/k+1 with the subscript I = T, D, P respectively. The equilibrium constant varies exponentially with p.m.f.
The inhibitions between substrates and products are complicated because ATP or ADP/Pi binds competitively to the same “open” site no matter which motor functions as the synthase or hydrolase. For convenience, we express the inhibitions in an uncompetitive hydrolysis form with the parameter: σ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) 1 + [P]/KTP1 + [D]/KTD1 + [D][P]/KTDP1, where KTP1
1 + [P]/KTP1 + [D]/KTD1 + [D][P]/KTDP1, where KTP1 ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) KPdχk−D/k−P, KTD1
KPdχk−D/k−P, KTD1 ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) KDdχk−P/k−D,
KDdχk−P/k−D, 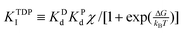 , and
, and 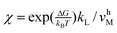 .
.
Eqn (2) implies that the motor is a synthase if rc > 0, a hydrolase if rc < 0, and at equilibrium if rc = 0. However, the relation between the rotation speed, p.m.f. and damping coefficient is still unclear. Now we use a stochastic mechanochemical coupling model to set the relation between kh/ks, ΔpH and the damping coefficient of the “rotor”.
III. Stochastic mechanochemical coupling model
The ensemble average behavior of FoF1-ATPase can be described phenomenologically by standard chemical kinetics if the reaction rates and mechanical rotation rate are related and their dependence on proton translocation is known. On the microscopic scale, FoF1-ATPase is more naturally described as a small mechanical device driven by a series of cyclic conformational states including rapid chemical events, such as binding and unbinding of substrates/products, and incessant, fast, thermal fluctuations which is essential to the molecular mechanism.42–44 It is at this level of microscopic fluctuations that the mechanical reversible rotation speed and chemical quantities such as concentrations of substrates/products and p.m.f. can be most naturally connected.It is rather well-established that different phenomena, such as the reversible chemical transition ET ⇌ EDP, the cyclic conformational changes of α3β3 crown, the couplings/communications among the three catalytic sites, and the stochastic 2π/3 rotation of the “rotor”, originate from the same process and occur simultaneously. In our model, E is the substrate “waiting” state, ED and EP are also substrate “waiting” states if the motor functions as a synthase. In these states, the barrier is too high for the chemical transition ET ⇌ EDP in β2 to take place (dashed curve in Fig. 2). According to the binding change mechanism,7,45 catalysis at one of the three sites is strongly promoted by additional substrate binding. For the hydrolysis pathway, ATP binding to the nucleotide-free site (β1) opens the gate by reducing the barrier as shown in Fig. 2(solid curve), which allows another ATP in β2 to be hydrolyzed. The free energy change of this step is given by:
ΔG = ΔG0 − mΔ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) H+ H+ | (8) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) +H, is usually expressed in terms of the transmembrane pH difference, ΔpH
+H, is usually expressed in terms of the transmembrane pH difference, ΔpH ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) pHin − pH out, and the transmembrane electric potential, Δϕ
pHin − pH out, and the transmembrane electric potential, Δϕ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ϕout − ϕin, as
ϕout − ϕin, as Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) H+ = 2.3kBTΔpH + eΔϕ H+ = 2.3kBTΔpH + eΔϕ | (9) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Δ
Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) H+/e = Δϕ + 59ΔpH. Eqn (9) shows that ΔpH and Δϕ are energetically equivalent, which is an essential feature of chemiosmotic theory.52 Experimental results on steady-state synthesis rates obtained with reconstituted ATP synthase from both spinach chloroplasts53,54 and chromatophores of R. capsulatus55 also indicated this feature.
H+/e = Δϕ + 59ΔpH. Eqn (9) shows that ΔpH and Δϕ are energetically equivalent, which is an essential feature of chemiosmotic theory.52 Experimental results on steady-state synthesis rates obtained with reconstituted ATP synthase from both spinach chloroplasts53,54 and chromatophores of R. capsulatus55 also indicated this feature.
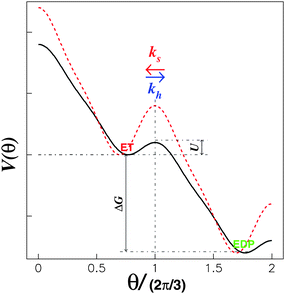 | ||
| Fig. 2 Model energy landscape with a periodic tilt, ΔG > 0. The drop in the barrier from the red dotted curve to the black solid curve takes place once the corresponding substrate binds to the substrate “waiting” site.21 | ||
Here, we introduce a two-dimensional energy landscape, V(x1, x2), with chemical and position variables. The kinetics of the enzyme may then be investigated by a random walk on the energy surface. As required for cyclic chemical turnovers and mechanical rotations, the surface is periodic along the chemical and position axes except for a uniform tilt of ΔG. In the tight mechanochemical coupling step, ET ⇌ EDP, however, the two-dimensional V(x1, x2) may be reduced to an one-dimensional V(θ), where θ represents the relative position between the “rotor” and the “stator”. The energy difference, ΔG, is periodically coupled into V(θ) completely due to the tight coupling between the γ rotation and α3β3 crown conformational changes. The stochastic theory, thereby, makes it possible to obtain the rates of hydrolysis and synthesis as a function of p.m.f. since ΔG is included in V(θ).
At steady state, all quantities about the stochastic rotation of the “rotor”, including the probability density of the “rotor” at an angle θ, ρ(θ), and the associated probability current, J, are constant in time, namely
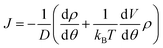 | (10) |
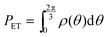 and
and 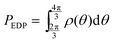 respectively. Finally, J is derived and compared with the form expected for a first-order chemical reaction at steady state, khPET − ksPEDP. The desired expressions for the rates of hydrolysis and synthesis as a function of ΔG can therefore be obtained:56–60
respectively. Finally, J is derived and compared with the form expected for a first-order chemical reaction at steady state, khPET − ksPEDP. The desired expressions for the rates of hydrolysis and synthesis as a function of ΔG can therefore be obtained:56–60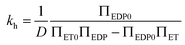 | (11) |
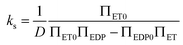 | (12) |
and
For a potential with two wells separated by a barrier, as in Fig. 2, the rate constants are most sensitive to the distances from the well bottoms to the barrier top, the size of each well, the barrier height (U), and the energy difference between wells (ΔG). Once these parameters are specified, the detailed shape of the potential has relatively little effect.
At equilibrium the net probability current, J, must be zero, and
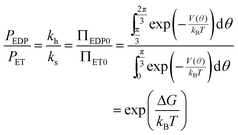 | (13) |
In order to calculate the rates of hydrolysis and synthesis that are tightly coupled to the diffusive rotation of the “rotor”, the one-dimensional energy landscape is phenomenologically constructed as (see Fig. 2):
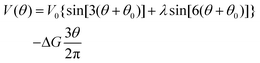 | (14) |
This asymmetric ratchet potential can be used to describe simultaneously the chemical transition between the two metastable states, ET and EDP, and the stochastic rotation of the “rotor” because the chemical transition ET ⇌ EDP is tightly coupled to the 2π/3 step rotation. The potential is constructed so that the barrier position can shift with varying ΔG. Under the conditions favoring ATP hydrolysis, that is, the p.m.f. is so low that ΔG > 0, the barrier position approaches the state ET. On the other hand, under conditions favoring ATP synthesis, the barrier position is close to the state EDP. If ΔG = 0, the ratchet potential will become symmetric. Such a construction is phenomenologically reasonable for the reversible motor.
Eqn (3), (6) and (7) can be directly used to quantitatively interpret the ensemble synthesis experiment of the holoenzyme28 as shown in Fig. 3. For an isolated TF1 with an attached long actin filament on the “rotor”,10 the hydrolysis step is the rate-limiting step because of the large damping of the long filament. Thus the hydrolysis kinetics can be easily analyzed by our model. Here, ks ≈ 0, and σ ≈ 1 due to vhM ≈ kh ≪ kL. Eqn (2) may be simplified into a normal Michaelis form:
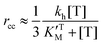 | (15) |
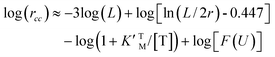 | (16) |
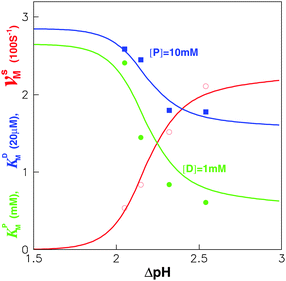 | ||
| Fig. 3 Experimental data28 of vsM, KDM and KPMversus ΔpH fitted by our model with vsmax = 250 s−1(≪ k−P), KDd = 57μM, KPd = 2.65 mM and k−D = 500 s−1. Here, Δϕ = 0 mV, m = 4,62,63 and U = 3kBT. Damping coefficient ξr = 6πηbhr2, is mainly contributed by the friction between c-ring and membrane, where h = 10 nm, is the “rotor” height, and r = 5 nm, is its radius.64 The bilayer viscosity is taken to be ηb = 10−7 pN s nm−2.21,25 | ||
![The CCW rotational rate of an isolated TF1versus L at different ATP concentrations. Symbols come from experiment10 while curves are fitted by our model with parameters K′MT = 0.8 μM and U = 2kBT. Here ξr = (π/3)ηL3/[ln(L/2r) − 0.447]61 with the radius of filament r = 5 nm and the medium viscosity η = 10−9 pN s nm−2.21](/image/article/2010/NR/b9nr00411d/b9nr00411d-f4.gif) | ||
| Fig. 4 The CCW rotational rate of an isolated TF1versus L at different ATP concentrations. Symbols come from experiment10 while curves are fitted by our model with parameters K′MT = 0.8 μM and U = 2kBT. Here ξr = (π/3)ηL3/[ln(L/2r) − 0.447]61 with the radius of filament r = 5 nm and the medium viscosity η = 10−9 pN s nm−2.21 | ||
IV. Direct observation of the light-driven rotation of Fo motor
Single molecule experiments had indicated the rotation of the F1 motor with a fluorescent filament attached the γ subunit.8,10 The relative rotation between the stator and rotor of the holoenzyme also had been detected by the FRET between the ε and b subunits.16 Fo is an ion-driven rotary motor. Its “rotor” is the proton channels cn and is connected the γ subunit by the ε subunit. Its “stator” consists of the a and b2 subunits and is fixed to the α3β3 crown of F1 by the δ subunit. Once the δ subunit is deleted, the two “stators” are no longer coupled, and the α3β3 crown will accompany the “rotor” on rotation. This is named δ-free FoF1-ATPase. We had developed a method to reconstitute the hybrid δ-free FoF1-ATPase and bacteriorhodopsins (BRs) into a liposome.13,65 BR converts light energy into transmembrane p.m.f., while the liposome functions as a battery to drive the motor. Employing a fluorescent actin filament attached to the β subunit, we have observed the light-driven rotation of δ-free FoF1-ATPase motor directly at the single molecule level.13The procedure of δ subunit deletion of FoF1-ATPase is briefly shown in Fig. 5. The proteoliposome containing FoF1-ATPase and BR was incubated with 2 M LiCl, 0.1 mM tricine-NaOH, 10 mM MgCl2, and 1 mM ATP for 20 min at 4 °C. Then the proteoliposome was washed and isolated by centrifuging. Because some α and β subunits may also be removed during δ deletion, the LiCl-treated proteoliposome needs incubation with purified α3β3γ(or β) subunits at 4 °C for 60 min (for each divided subunit of F1 with buffer 0.1 mM tricine-NaOH, 10 mM MgCl2, 50 mM KCl, 0.5 mM NaCl, and 1 mM ATP), and then is cultured at 37 °C for 60 min (for reconstituting the δ-free FoF1-ATPase). The proteoliposome needs to be isolated to obtain the reconstituted δ-free FoF1-ATPase.66–68
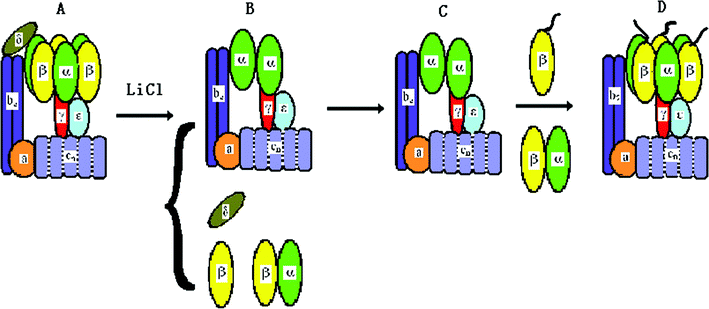 | ||
| Fig. 5 The procedure for reconstituting δ-free FoF1-ATPase motor. (A) FoF1-ATPase; (B) FoF1-ATPase is treated by LiCl to remove δ subunit; (C) rebinding of purified β and α subunits; (D) the reconstituted δ-free FoF1-ATPase motor.13 | ||
To visualize the rotation of Fo in proteoliposome, a fluorescently labeled actin filament was attached to β subunits through His-tag, and the proteoliposome was immobilized onto the glass surface through the biotin–streptavidin–biotin complexes (Fig. 6A). The sample was exposed under the cooled light source with a 570 nm filter for 30 min to initiate the rotation of the Fo motor. Before illumination, the buffer containing 2 mM NaN3 and 2 mM ADP was infused into the chamber. The clockwise rotation of the actin filament was traced directly by an Olympus IX71 fluorescent microscope equipped with an ICCD camera (Roper Scientific, Pentamax EEV 512 × 512 FT) viewing from Fo side to the F1 side. Fig. 6B shows an example of the sequential clockwise rotation images with 100 ms interval. We have selected six rotational data points with different length filaments to show in Fig. 6C. The rotation displays occasional pause or even reversal due to Brownian fluctuation. The rotation speed decreases with the increasing length of filament , which is in agreement with the results of single molecule experiments of F18,10 as expected.
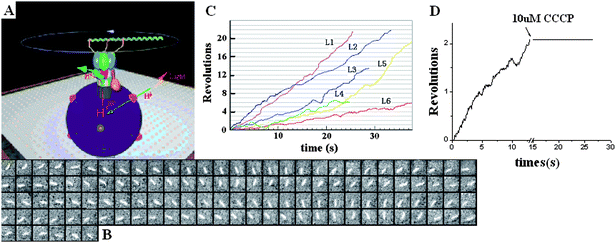 | ||
| Fig. 6 (A) The system used for observation of the Fo in the proteoliposome which was immobilized on the cover glass with biotin–streptavidin–biotin. (B) The sequential images of a clockwise rotating fluorescent actin filament. Time interval is 100 ms. (C) Time courses of the actin filament rotation with different lengths. The fluorescent filament was attached to the β subunits through His-tag. The length of filaments denoted L1, L2, L3,L4 ,L5 and L6 are 1.7, 1.9, 2.0, 2.3, 2.8 and 3.3 μm respectively. (D) The rotation was inhibited by adding CCCP, which verified the motor was indeed driven by transmembrane ΔpH.13 | ||
Several control experiments were performed to confirm that the observed rotation is driven by transmembrane proton flow. As shown in Fig. 6D, the rotation stopped immediately once 5 μl of 10 μM CCCP was added. It was also found that if the sample is in the dark or is incubated with DCCD before illumination, no rotation was observed (data not shown) because CCCP destroyed the transmembrane p.m.f. as well as DCCD blocked the proton channels. Furthermore, if NaN3 and ADP disappeared in the buffer, no rotation of filament was found because NaN3 and ADP prevented the α3β3 crown from sliding to the γ subunit.69 These results demonstrated that the rotation of filaments depended on the p.m.f. produced in proteoliposome. It is interesting that the ΔpH transmembrane of proteoliposome can persist for a long time. After the illumination, some filaments rotated continuously for more than 20 min. Therefore, the proteoliposome functions as a recharge battery to supply energy to the rotary motor.
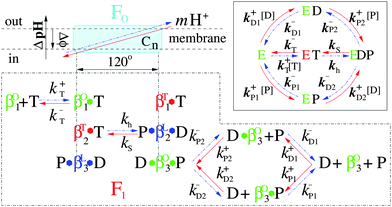
V. FoF1-ATPase activity regulated by external links on the stator
The activity regulation of the holoenzyme is an interesting topic. Traditional methods are chemical, which depend on either the concentration of substrate or the transmembrane electrochemical potential.12,28,62,63 In fact, FoF1 motor actively converts a chemical reaction (ATP hydrolysis in F1 or proton transfer in Fo) into unidirectional physical rotation of the “rotor”, which is accompanied by the cyclic conformational change of the “stator”. Single molecule assays have indicated that the activity of F110,18 or the speed of Fo (δ free FoF1 motor)13,20 can be regulated by varying the load on the “rotor” and the eccentric rotation of γ subunit is mechanically coupled with the cyclic conformational change of α3β3 crown at a high efficiency. However, how to regulate the holoenzyme (including Fo and F1) activity with a physical method instead a chemical one is still challenging. One of the reasons is that the “rotor” of FoF1 motor is mostly enwrapped by the “stator” α3β3 crown. The other reason is that the exposed fraction of the “rotor” is also partly shaded by the b2 subunit. Thus, it becomes very difficult to directly regulate the holoenzyme activity by a load on the “rotor”.Considering that the unidirectional rotation of “rotor” is tightly coupled with the cyclic conformational change of the “stator”, what will happen to the activity of the rotary motor if external complexes bind to the “stator”? To study regulation of the FoF1-ATPase activity by a simple physical method, the influenza H9 virus and its special antibody were employed as external links on the β subunit. Firstly, the chromatophore was prepared from the cells of Rhodopseudomonas palustris according to ref. 70, in which Fo was embedded in the chromatophore,71 whereas F1 protruded outside (structure 0).72 Next, the β antibody was bound to each β subunit (structure 1); then, streptavidin was connected to the β antibody (structure 2), and the H9 antibody was bound to the streptavidin in series via biotin (structure 3). Finally, the H9 virus was captured specifically by the H9 antibody (structure 4) (see Fig. 7). The holoenzyme activities of the five structures were measured by the luciferin–luciferase method with a computerized ultra-weak luminescence analyzer. All structures with different external links were treated as coordinates.73–76
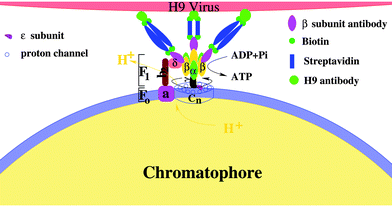 | ||
| Fig. 7 A schematic illustration of the activity regulation assay. The holoenzyme is a complex of two rotary motors Fo and F1. Fo motor was constituted by a subunit (stator) and n channel (cn, rotor). α3β3 crown (stator) and γ subunit (rotor) formed the F1 motor. The complex of b2 and δ subunits fixed the two stators, whereas the two rotors are mechanically coupled by the ε subunit. External complexes are linked on β subunits to regulate the holoenzyme activity. | ||
The activity of native FoF1-ATPase was used as a control and other structures were compared with the native value. When the β antibody was bound, the FoF1-ATPase (structure 1) activities in both synthesis and hydrolysis decreased, and its relative value was about 85% of the native form (structure 0). If streptavidin was joined to the β antibody (structure 2), the enzyme synthesis/hydrolysis activities decreased to 87% of the activity of structure 1. After the H9 antibody was connected to streptavidin (structure 3), the enzyme activity was inhibited continuously, with a relative value of 75% of structure 2. Once H9 virus was captured by its antibody (structure 4), however, the motor was activated, and its relative synthesis and hydrolysis activities were about 210% of that of structure 3. It is amazing that the activity of the modified holoenzyme, in which a series of external complexes are linked on the stator, can exceed the native level. These results are indicated in Fig.8.77
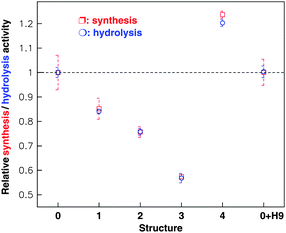 | ||
| Fig. 8 Relative synthesis (red) and hydrolysis (green) activities of the holoenzyme with different links on the β subunit as shown in Fig. 7. The statistical value (mean s.e.m.) of each structure was computed from 50–60 samples. The experiment has been repeated independently more than five times (10 samples each time). The native FoF1-ATPase (structure 0) activity was taken as a control and others were expressed in proportion to the control. Structures 1, 2, 3 and 4 represent the FoF1-ATPase linking in series on the β antibody, streptavidin, H9 antibody and H9 virus respectively. 0 + H9 represents the holoenzyme mixed directly with the H9 virus. | ||
To identify whether the H9 virus directly affects FoF1-ATPase activity, we measured the activity of native buffer (structure 0) incubated with H9 virus. The results shown in Fig. 8 prove that the H9 virus doesn't have any direct effect on the holoenzyme activity no matter if the enzyme functions as a synthase or hydrolase.
The abnormal regulation from structure 3 to 4 implied that structure 3 has great potential in design of a rapid, unlabeled, sensitive and selective biosensor78 though the underlying mechanism is still unclear.
VI. Conclusions
In contrast to human-made machines, motor proteins operate in a world where Brownian motion and viscous forces dominate. The relevant energy scale is kBT, which amounts to 4 pN nm. This may be compared to the ∼80 pN nm of energy derived from hydrolysis of a single ATP molecule at physiological conditions. Thermal, nondeterministic motion is thus an important aspect of the dynamics of molecular motors.ATP hydrolysis does spontaneously occur in F1, whereas the thermodynamically unfavorable reaction, ATP synthesis, has to be driven by harnessing the transmembrane proton flow in Fo. The mechanism of ATP formation in the F1 part is well described by the “binding change mechanism”. This has been developed in great detail by many techniques, and understanding of the mechanism has been claimed to be “almost complete”. However, if the motor functions as a synthase, the two substrates, ADP and Pi, are recombined into one product, ATP. The binding order of the two substrates is still unclear. Another challenging question is whether the main kinetic enhancement occurs upon filling the second or the third site. For Fo, the torque generation between a and cn in Fo is still covered. In addition, It has remained unsettled whether the entropic (chemical) component of Δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) +H relates to the difference in the proton activity between two bulk water phases (ΔpHB) or between two membrane surfaces (ΔpHS).79
+H relates to the difference in the proton activity between two bulk water phases (ΔpHB) or between two membrane surfaces (ΔpHS).79
It is of interest to ponder whether we can employ FoF1-ATPase nanomachines in artificial environments outside the cell to perform tasks that we design to our benefit.80 One striking demonstration is the construction of a nickel nanopropeller that rotates through the action of an engineered F1-ATPase motor.81 A metal-binding site was engineered into the motor and acted as a reversible on–off switch by obstructing the rotation upon binding of a zinc ion,82 similar to the action of putting a stick between two cogwheels. Other examples worth highlighting are the sol–gel packaging of vesicles containing bacteriorhodopsin, a light driven proton pump, and FoF1-ATP synthase,83,84 or FoF1-ATPase embedded chromatophore.76 Upon illumination, protons are pumped into the vesicles and ATP is created outside the vesicle by the ATP synthase. Besides the excellent stability of these gels (bacteriorhodopsin continued functioning for a few months), this technology provides a convenient packaging method and a way to use light energy for fuelling devices. Therefore, these nanodevices with a battery can be employed to design a rapid, unlabeled, sensitive and selective biosensor,73–75,77 or construct a micro-mixer to accelerate thrombolysis.67 Of course, many of these applications are little more than proof-of-principle examples.
Acknowledgements
This work was supported by the National Basic Research Program of China (973 Program) under the grant No. 2007CB935903 and No. 2007CB935901References
- P. D. Boyer, The ATP synthase—A splendid molecular machine, Annu. Rev. Biochem., 1997, 66, 717–749 CrossRef CAS.
- W. Junge, Protons, Proteins and ATP, Photosynth. Res., 2004, 80, 197–221 CrossRef CAS.
- J. Weber and A. E. Senior, ATP synthesis driven by proton transport in F1Fo-ATP synthase, FEBS Lett., 2003, 545, 61–70 CrossRef CAS.
- C. von Ballmoos, A. Wiedenmann and P. Dimroth, Essentials for ATP synthesis by F1Fo ATP synthase, Annu. Rev. Biochem., 2009, 78, 649–672 CrossRef CAS.
- B. A. Feniouk and M. Yoshida, Regulatory mechanisms of proton-translocating F1Fo- ATP synthase, Results Probl. Cell Differ., 2008, 45, 279–308 Search PubMed.
- M. Saraste, Oxidative phosphorylation at the fin de siècle, Science, 1999, 283, 1488–1493 CrossRef CAS.
- P. D. Boyer, R. L. Cross and W. Momsen, A new concept for energy coupling in oxidative phosphorylation based on a molecular explanation of the oxygen exchange reactions, Proc. Natl. Acad. Sci. U. S. A., 1973, 70, 2837–2839 CrossRef CAS.
- H. Noji, R. Yasuda, M. Yoshida and K. Kinosita Jr., Direct observation of the rotation of F1-ATPase, Nature, 1997, 386, 299–302 CrossRef CAS.
- J. P. Abrahams, A. G. W. Leslie, R. Lutter and J. E. Walker, Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria, Nature, 1994, 370, 621–628 CrossRef CAS.
- Y. Yasuda, H. Noji, K. Kinosita Jr. and M. Yoshida, F1-ATPase is a highly efficient molecular motor that rotates with discrete 120° steps, Cell, 1998, 93, 1117–1124 CrossRef CAS.
- T. Nishizaka and et.al, Chemomechanical coupling in F1-ATPase revealed by simultaneous observation of nucleotide kinetics and rotation, Nat. Struct. Mol. Biol., 2004, 11, 142–148 CrossRef CAS.
- K. Adachi and et.al, Coupling of rotation and catalysis in F1-ATPase revealed by single-molecule imaging and manipulation, Cell, 2007, 130, 309–321 CrossRef CAS.
- Y. H. Zhang and et.al, Rotary torque produced by proton motive force in F1Fo motor, Biochem. Biophys. Res. Commun., 2005, 331, 370–374 CrossRef CAS.
- M. G. Düser and et.al, 36° step size of proton-driven c-ring rotation in F1Fo-ATP synthase, EMBO J., 2009, 28, 2689–2696 CrossRef.
- G. Kaima and et.al, Coupled rotation within single F1Fo enzyme complexes during ATP synthesis or hydrolysis, FEBS Lett., 2002, 525, 156–163 CrossRef CAS.
- M. Diez and et.al, Proton-powered subunit rotation in single membrane-bound F1Fo-ATP synthase, Nat. Struct. Mol. Biol., 2004, 11, 135–141 CrossRef CAS.
- H. Ueno and et.al, ATP-driven stepwise rotation of FoF1-ATP synthase, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1333–1338 CrossRef CAS.
- H. Itoh and et.al., Mechanically driven ATP synthesis by F1-ATPase, Nature, 2004, 427, 465–468 CrossRef CAS.
- Y. Rondelez and et.al, Highly coupled ATP synthesis by F1-ATPase single molecules, Nature, 2005, 433, 773–777 CrossRef CAS.
- X. L. Liu and et.al, Mechanically driven proton conduction in single δ-free FoF1-ATPase, Biochem. Biophys. Res. Commun., 2006, 347, 752–757 CrossRef CAS.
- Y. G. Shu and P. Y. Lai, Systematic kinetics study of F1Fo-ATPase: Analytic results and comparison with experiments, J. Phys. Chem. B, 2008, 112, 13453–13459 CrossRef CAS.
- J. Xing, J. C. Liao and G. Oster, Making ATP, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16539–16546 CrossRef CAS.
- S. X. Sun, H. Wang and G. Oster, Asymmetry in the F1-ATPase and its implications for the rotational cycle, Biophys. J., 2004, 86, 1373–1384 CrossRef CAS.
- H. Wang and G. Oster, Energy transduction in the F1 motor of ATP synthase, Nature, 1998, 396, 279–282 CrossRef CAS.
- T. Elston, H. Wang and G. Oster, Energy transduction in ATP synthase, Nature, 1998, 391, 510–513 CrossRef CAS.
- G. Oster, H. Wang and M. Grabe, How Fo-ATPase generates rotary torque, Philos. Trans. R. Soc. London, Ser. B, 2000, 355, 523–528 CrossRef CAS.
- A. Aksimentiev, I. A. Balabin, R. H. Fillingame and K. Schulten, Insights into the molecular mechanism of rotation in the Fo sector of ATP synthase, Biophys. J., 2004, 86, 1332–1344 CrossRef CAS.
- O. Pänke and B. Rumberg, Kinetic modelling of the proton translocating CFoCF1-ATP synthase from spinach, FEBS Lett., 1996, 383, 196–200 CrossRef CAS.
- O. Pänke and B. Rumberg, Kinetic modeling of rotary CFoF1-ATP synthase: storage of elastic energy during energy transduction, Biochim. Biophys. Acta, Bioenerg., 1999, 1412, 118–128 CrossRef CAS.
- B. R. Selman and S. Selman-Reiner, The steady state kinetics of photophosphorylation, J. Biol. Chem., 1981, 256, 1722–1726 CAS.
- C. Kayalar, J. Rosing and P. D. Boyer, An alternating site sequence for oxidative phosphorylation suggested by measurement of substrate binding patterns and exchange reaction inhibitions, J. Biol. Chem., 1977, 252, 2486–2491 CAS.
- J. A. Pérez and S. J. Ferguson, Kinetics of oxidative phosphorylation in Paracoccus denitrificans. 1. Mechanism of ATP synthesis at the active site(s) of FoF1-ATPase, Biochemistry, 1990, 29, 10503–10518 CrossRef CAS.
- P. D. Boyer, Catalytic site forms and controls in ATP synthase catalysis, Biochim. Biophys. Acta, Bioenerg., 2000, 1458, 252–262 CrossRef CAS.
- Y. M. Milgrom and R. L. Cross, Rapid hydrolysis of ATP by mitochondrial F1-ATPase correlates with the filling of the second of three catalytic sites, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13831–13836 CrossRef CAS.
- A. E. Senior, S. Nadanaciva and J. Weber, The molecular mechanism of ATP synthesis by F1Fo-ATP synthase, Biochim. Biophys. Acta, Bioenerg., 2002, 1553, 188–211 CrossRef CAS.
- C. Dou, P. A. G. Fortes and W. S. Allison, The α3(βY341W)3γ subcomplex of the F1-ATPase from the thermophilic bacillus PS3 fails to dissociate ADP when MgATP is hydrolyzed at a single catalytic site and attains maximal velocity when three catalytic sites are saturated with MgATP, Biochemistry, 1998, 37, 16757–16764 CrossRef CAS.
- R. I. Menz, J. E. Walker and A. G. W. Leslie, Structure of bovine mitochondrial F1-ATPase with nucleotide bound to all three catalytic sites: implications for the mechanism of rotary catalysis, Cell, 2001, 106, 331–341 CrossRef CAS.
- M. K. Al-Shawi, C. J. Ketchum and R. K. Nakamoto, The Escherichia coli FoF1γM23K uncoupling mutant has a higher K0.5 for Pi. transition state analysis of this mutant and others reveals that synthesis and hydrolysis utilize the same kinetic pathway, Biochemistry, 1997, 36, 12961–12969 CrossRef CAS.
- J. A. Baylis Scanlon, M. K. Al-Shawi, N. P. Le and R. K. Nakamoto, Determination of the partial reactions of rotational catalysis in F1-ATPase, Biochemistry, 2007, 46, 8785–8797 CrossRef.
- J. Weber and A. E. Senior, ATP synthase: what we know about ATP hydrolysis and what we do not know about ATP synthesis, Biochim. Biophys. Acta, Bioenerg., 2000, 1458, 300–309 CrossRef CAS.
- G. Kothen, O. Schwarz and H. Strotmann, The kinetics of photophosphorylation at clamped ΔpH indicate a random order of substrate binding, Biochim. Biophys. Acta, Bioenerg., 1995, 1229, 208–214 CrossRef.
- J. Howard, Mechanics of motor proteins and the cytoskeleton, Sinauer Associates, Sunderland, MA ( 2001) Search PubMed.
- M. Schliwa, Molecular motors, Weinheim, Wiley-VCH, 2003 Search PubMed.
- F. Jülicher, A. Ajdari and J. Prost, Modeling molecular motors, Rev. Mod. Phys., 1997, 69, 1269–1281 CrossRef CAS.
- P. D. Boyer, The binding change mechanism for ATP synthase-Some probabilities and possibilities, Biochim. Biophys. Acta, Bioenerg., 1993, 1140, 215–250 CrossRef CAS.
- D. Stock, A. G. W. Leslie and J. E. Walker, Molecular architecture of the rotary motor in ATP synthase, Science, 1999, 286, 1700–1705 CrossRef CAS.
- H. Seelert; et.al. Structural biology: Proton-powered turbine of a plant motor. 2000, 405, pp. 418–419.
- W. P. Jiang, J. Hermolin and R. H. Fillingame, The preferred stoichiometry of c subunits in the rotary motor sector of Escherichia coli ATP synthase is 10, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 4966–4971 CrossRef CAS.
- N. Mitome, T. Suzuki, S. Hayashi and M. Yoshida, Thermophilic ATP synthase has a decamer c-ring: Indication of noninteger 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 H+/ATP ratio and permissive elastic coupling, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12159–12164 CrossRef CAS.
3 H+/ATP ratio and permissive elastic coupling, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12159–12164 CrossRef CAS. - D. Pogoryelov and et.al, The c15 ring of the Spirulina platensis F-ATP synthase: F1/Fo symmetry mismatch is not obligatory, EMBO Rep., 2005, 6, 1040–1044 CrossRef CAS.
- T. Meier and et.al, A tridecameric c ring of the adenosine triphosphate (ATP) synthase from the thermoalkaliphilic Bacillus sp. strain TA2.A1 facilitates ATP synthesis at low electrochemical proton potential, Mol. Microbiol., 2007, 65, 1181–1192 CrossRef CAS.
- P. Mitchell, Coupling of phosphorylation to electron and hydrogen transfer by a chemi-osmotic type of mechanism, Nature, 1961, 191, 144–148 CAS.
- U. Junesch and P. Gräber, Influence of the redox state and the activation of the chloroplast ATP synthase on proton-transport-coupled ATP synthesis/hydrolysis, Biochim. Biophys. Acta, Bioenerg., 1987, 893, 275–288 CrossRef CAS.
- U. Junesch and P. Gräber, The rate of ATP-synthesis as a function of ΔpH and ΔΦ catalyzed by the active, reduced H+-ATPase from chloroplasts, FEBS Lett., 1991, 294, 275–278 CrossRef CAS.
- P. Turina, Influence of the transmembrane electrochemical proton gradient on catalysis and regulation of the H+-ATP synthase from, Bioelectrochem. Bioenerg., 1994, 33, 31–34 CrossRef CAS.
- D. Keller and C. Bustamante, The mechanochemistry of molecular motors, Biophys. J., 2000, 78, 541–556 CAS.
- Y. G. Shu and H. L. Shi, Cooperative effects on the kinetics of ATP hydrolysis in collective molecular motors, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021912 CrossRef.
- Y. G. Shu and H. L. Shi, The effect on mechanical tension on DNA polymerase activity studied with a two-state model, Mod. Phys. Lett. B, 2007, 21, 1097–1105 CrossRef CAS.
- Y. G. Shu and Z. C. Ou-Yang, Motility of molecular motor, J.Comput. Theor. Nanosci, 2007, 4, 71–76 CAS.
- M. Li, Y. G. Shu and Z. C. Ou-Yang, Mechanochemical coupling of kinesin studied with a neck-linker swing model, Commun. Theor. Phys., 2009, 51, 1143–1148 CrossRef CAS.
- A. J. Hunt, F. Gittes and H. Howard, The force exerted by a single kinesin molecule against a viscous load, Biophys. J., 1994, 67, 766–781 CrossRef CAS.
- P. Turina, D. Samoray and P. Gräber, H+/ATP ratio of proton transport-coupled ATP synthesis and hydrolysis catalysed by CFoF1-liposomes, EMBO J., 2003, 22, 418–426 CrossRef CAS.
- S. Steigmiller, P. Turina and P. Gräber, The thermodynamic H+/ATP ratios of the H+-ATPsynthases from chloroplasts and, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3745–3750 CrossRef CAS.
- B. Böttcher and P. Gräber, Structural interpretations of Fo rotary function in the Escherichia coli F1Fo ATP synthase, Biochim. Biophys. Acta, Bioenerg., 2000, 1458, 404–416 CrossRef CAS.
- Y. Moriyama, A. Iwamoto, H. Hanada, M. Maeda and M. Futai, One-step purification of Escherichia coli H+-ATPase (F1Fo) and its reconstitution into liposomes with neurotransmitter transporters, J. Biol. Chem., 1991, 266, 22141–22146 CAS.
- T. Su and et.al, Constructing a novel Nanodevice powered by δ-free F1Fo-ATPase, Biochem. Biophys. Res. Commun., 2006, 350, 1013–1018 CrossRef CAS.
- N. Tao, J. Cheng and J. C. Yue, Using F1Fo-ATPase motors as micro-mixers accelerates thrombolysis, Biochem. Biophys. Res. Commun., 2008, 377, 191–194 CrossRef CAS.
- J. Y. Liao, J. Q. Yin and J. C. Yue, A novel biosensor to detect microRNAs rapidly, Journal of Sensors, 2009 DOI:10.1155/671896.
- E. Muneyuki and et.al, Inhibitory effect of NaN3 on the FoF1 ATPase of submitochondrial particles as related to nucleotide binding, Biochim. Biophys. Acta, Bioenerg., 1993, 1144, 62–68 CrossRef CAS.
- S. Philosoph, A. Binder and Z. Gromet-Elhanan, Coupling factor ATPase complex of Rhodospirillum rubrum. Purification and properties of a reconstitutively active single subunit, J. Biol. Chem., 1977, 252, 8747–8752 CAS.
- B. A. Feniouk and et.al, Chromatophore vesicles of Rhodobacter capsulatus contain on average one FoF1-ATP synthase each, Biophys. J., 2002, 82, 1115–1122 CrossRef CAS.
- T. Geyer and V. Helms, A spatial model of the chromatophore vesicles of Rhodobacter sphaeroides and the position of the cytochrome bc1 complex, Biophys. J., 2006, 91, 921–926 CrossRef CAS.
- X. L. Liu and et.al, FoF1-ATPase as biosensor to detect single virus, Biochem. Biophys. Res. Commun., 2006, 342, 1319–1322 CrossRef CAS.
- Z. T. Deng and et.al., Green and orange CdTe quantum dots as effective pH-sensitive fluorescent probes for dual simultaneous and independent detection of viruses, J. Phys. Chem. B, 2007, 111, 12024–12031 CrossRef CAS.
- Y. Zhang and et.al, Using cadmium telluride quantum dots as a proton flux sensor and applying to detect H9 avian influenza virus, Anal. Biochem., 2007, 364, 122–127 CrossRef.
- Y. B. Cui, Z. Fan and J. C. Yue, Detecting proton flux across chromatophores driven by FoF1-ATPase using N-(fluorescein-5-thiocarbamoyl)-1,2-dihexadecanoyl- sn-glycero- 3-phosphoethanolamine, triethylammonium salt, Anal. Biochem., 2005, 344, 102–107 CrossRef CAS.
- J. Cheng, X. A. Zhang, Y. G. Shu and J. C. Yue, FoF1-ATPase activity regulated by external links on β subunits, Biochem. Biophys. Res. Commun., 2010, 391, 182–186 CrossRef CAS.
- J. York, D. Spetzler, F. S. Xiong and W. D. Frasch, Single-molecule detection of DNA via sequence-specific links between F1-ATPase motors and gold nanorod sensors, Lab Chip, 2008, 8, 415–419 RSC.
- D. A. Cherepanov, B. A. Feniouk, W. Junge and A. Y. Mulkidjanian, Low dielectric permittivity of water at the membrane interface: effect on the energy coupling mechanism in biological membranes, Biophys. J., 2003, 85, 1307–1316 CrossRef CAS.
- M. G. L. van den Heuvel and C. Dekker, Motor proteins at work for nanotechnology, Science, 2007, 317, 333–336 CrossRef.
- R. K. Soong, G. D. Bachand, H. P. Neves, A. G. Olkhovets, H. G. Craighead and C. D. Montemagno, Powering an inorganic nanodevice with a biomolecular motor, Science, 2000, 290, 1555–1558 CrossRef CAS.
- H. Liu, J. J. Schmidt, G. D. Bachand, S. S. Rizk, L. L. Looger, H. W. Hellinga and C. D. Montemagno, Control of a biomolecular motorpowered nanodevice with an engineered chemical switch, Nat. Mater., 2002, 1, 173–177 CrossRef CAS.
- T.-J. M. Luo, R. Soong, E. Lan, B. Dunn and C. Montemagno, Photo-induced proton gradients and ATP biosynthesis produced by vesicles encapsulated in a silica matrix, Nat. Mater., 2005, 4, 220–224 CrossRef CAS.
- H. J. Choi and C. D. Montemagno, Artificial Organelle: ATP Synthesis from cellular mimetic polymersomes, Nano. Lett., 2005, 5, 1538–1542.
| This journal is © The Royal Society of Chemistry 2010 |