Progress of nanocrystalline growth kinetics based on oriented attachment
Jing
Zhang
,
Feng
Huang
* and
Zhang
Lin
*
Key Laboratory of Optoelectronic Materials Chemistry and Physics, State Key Lab of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, People's Republic of China. E-mail: fhuang@fjirsm.ac.cn; zlin@fjirsm.ac.cn
First published on 5th October 2009
Abstract
The crystal growth mechanism, kinetics, and microstructure development play a fundamental role in tailoring the materials with controllable sizes and morphologies. The classical crystal growth kinetics—Ostwald ripening (OR) theory is usually used to explain the diffusion-controlled crystal growth process, in which larger particles grow at the expense of smaller particles. In nanoscale systems, another significant mechanism named “oriented attachment (OA)” was found, where nanoparticles with common crystallographic orientations directly combine together to form larger ones. Comparing with the classical atom/molecular-mediated crystallization pathway, the OA mechanism shows its specific characteristics and roles in the process of nanocrystal growth. In recent years, the OA mechanism has been widely reported in preparing low-dimension nanostructural materials and reveals remarkable effects on directing and mediating the self-assembly of nanocrystals. Currently, the interests are more focused on the investigation of its role rather than the comprehensive insight of the mechanism and kinetics. The inner complicacy of crystal growth and the occurrence of coexisting mechanisms lead to the difficulty and lack of understanding this growth process by the OA mechanism.
In this context, we review the progress of the OA mechanism and its impact on materials science, and especially highlight the OA-based growth kinetics aiming to achieve a further understanding of this crystal growth route. To explore the OA-limited growth, the influence of the OR mechanism needs to be eliminated. The introduction of strong surface adsorption was reported as the effective solution to hinder OR from occurring and facilitate the exclusive OA growth stage. A detailed survey of the nanocrystal growth kinetics under the effect of surface adsorption was presented and summarized. Moreover, the development of OA kinetic models was systematically generalized, in which the “molecular-like” kinetic models were built to take the OA nanocrystal growth behavior as the collision and reaction between molecules. The development of OA growth kinetics can provide a sufficient understanding of crystal growth, and the awareness of underlying factors in the growth will offer promising guidance on how to control the size distribution and shape development of nanostructural materials.
 Dr Jing Zhang | Dr Jing Zhang was born in 1979. He received his PhD in Physical Chemistry in 2007 under the supervision of Prof. Zhang Lin with a thesis on "Nanocrystal Growth Kinetics Controlled by the Surface Adsorption Effect". Currently, he works as a post-doctoral researcher in the Soft Matter Group of the Solid State Research Institute in the Forschungszentrum Juelich, Germany, where he investigates nonionic water-in-oil microemulsions and their effects on the nucleation and growth of nanocrystals. |
 Professor Feng Huang | Professor Feng Huang received his PhD in Condensed Matter Physics in 1999 from Institute of Physics, CAS. From 2000 till 2004, he worked as post-doctoral researcher in University of Wisconsin-Madison and University of California-Berkeley, USA. He is interested in the thermodynamics, phase transformation and growth kinetics of nanoparticles. |
 Professor Zhang Lin | Professor Zhang Lin received her PhD in Physical Chemistry in 1999 from Institute of Chemistry, CAS. Afterwards, she worked as post-doctoral researcher in Department of Chemistry, University of Wisconsin-Madison and Lawrence Berkeley National Lab. Currently, she is investigating biogenic nanoparticles, the growth kinetics of nanoparticles and the relevant environmental applications. |
1. Introduction
Nanoscale materials are defined as materials having at least one dimension in the 1–100 nm range, in which nanocrystals are the major investigated subjects. Since Gleiter and coworkers successfully synthesized Fe nanoparticles in 1984,1,2 nanostructural materials have received extensive interest for their unique and fascinating properties and potential applications that are superior to their bulk counterparts. For example, semiconductor nanocrystals have exhibited a wide range of size-dependent properties for optics and electricity.3–5 The fundamental characteristics from phase stability to electronic structure can be influenced by the size and surface absorption status of nanoparticles.6–8 A detailed investigation of quantum size effects requires the preparation of nanoscale materials with a controllable size and morphology. The synthetic approaches for preparing nanoscale materials are various, and mainly include chemical methods,9,10 physical techniques,11,12 and biological means.13 Among them, the advantages of wet chemical methods are that the synthesis can be realized in a massively parallel fashion and with a simple facility (e.g. hydrothermal conditions). But its disadvantage mainly lies in that the size and shape are difficult to control in the process, as they undergo rapid nucleation and growth, readily impacted by surrounding interactions. Especially for nanostructured materials synthesized by chemical synthesis, the study on the crystal growth kinetics shows its scientific and practical significance for understanding and controlling the evolution of size and shape.Detailed investigations on the nanocrystalline growth mainly involve the growth mechanisms, the kinetic rules of size and morphology, and the accompanying phase transformation. By observing the microscopic structures of nanocrystals, the growth mechanisms will be found and judged. Then, the corresponding growth kinetic models will be proposed to describe and explain the crystal growth behavior. An understanding of the factors that affect crystal growth kinetics and the microstructure development in nanocrystals is fundamental to tailor new types of nanostructures and control material properties. Accordingly, research in the field of crystal growth kinetics attracts increasing attentions.7,14–16
As classical growth kinetics, the OR theory has shown great progress made in the past forty years or more. Various theories have been developed to describe and predict this atom-by-atom growth process, and the agreeable results between experimental and theoretical work can be well achieved.17 When the crystal size decreases to the nanometre level, in some circumstances, the crystal growth may be dominated by the newly developed OA mechanism,18 the direct self-organization of two particles into a single crystal by sharing a common crystallographic orientation. In contrast to the classical crystal growth pattern, the OA mechanism shows a peculiar growth pathway and characteristics, even contradicting the former. The aggregation-based growth mode attracts the interest of many researchers and presents its significant role in the construction and formation of nanostructural materials.16,19,20 As the OA is the assembly of primary particle units, the way of bottom-up fabrication can produce the novel objects with versatile properties, probably retaining the original structures and properties of their building blocks. It will give us a clue to tailor the products by tuning the raw materials. Also, the OA is an effective approach in favor of manufacturing anisotropic nanostructures, such as particle attachment always generating one-dimension nanowires or nanorods in one orientation.4,21,22 As for the crystal growth process, the unique mechanism can give rise to the critical information related to the shape and size evolution distinctively away from the classical growth pathway.
Extensive reports declare the importance and versatility of the OA mechanism for the material design and preparation, while detailed and in-depth investigations of the physical basis behind the OA-limited process are absent currently. The main challenge in exploring the OA mechanism is the acquisition of direct data and evidence from the complicated crystal growth process, especially on a nanoscale, which yields the difficulties of building the growth kinetic models and fitting the experimental data. Inspiringly, a series of work on the OA-based growth kinetics has been gradually carried out with efforts to explain the process in theory. The first OA kinetic model was developed in 2003,23 which takes the direct coalescence of particles as the reaction between the molecules and well fits the experimental results of particle size vs. time. After that, Penn19 and Ribeiro et al.24 respectively advanced the models from the viewpoint of the electrostatic interaction and colloid coagulation. In the view of aggregation, this crystal growth model is similar to the Smoluchowsky theory,25 which has been widely used to explain and fit the aggregation of molecules and colloids , and to describe the dynamical nucleation process. Generally, it was found that the mixed mechanisms coexisting in the growth bring the difficulty to obtain the systematical experimental data (such as the growth rate) and hinder the progress of the OA growth kinetics.23
In the study on OA growth kinetics, the effects of surface adsorption and surface charge were discussed to be the important factors for the crystal growth process and the OA mechanism. It is viewed that by adding ligands and passivating agents or by changing the particle surface one can control the growth by the OA mechanism.19,23 It was also reported that the nanocrystal growth rate is dependent on the adsorption of anions and a stronger adsorption leads to a slower OR growth rate.26,27 It is known that in nanoscale systems, the surface contributions to the total energy become increasingly important as the particle size decreases, even determining the structures and phase stability.6 The remarkable effects of surface functionalization with various molecular weight ligands may bring different assembly behaviors.28–30Nanocrystals have a higher surface energy, which facilitates the “reaction” on the surface, such as the direct bonding and crystallization between particles.18 Factors that directly modify the surface of nanocrystals will be a promising way to direct and mediate the crystal growth modes.
In this review, we summarize the progress of the OA-based growth kinetics, highlighting recent endeavours on the nanocrystal growth kinetics under the strong organic/inorganic surface adsorption, and the corresponding OA kinetic models. The introduction of the strong surface adsorption aims to adjust the crystal growth mode and realize the growth via the solo OA mechanism, which will simplify the experimental investigation for theoretical fitting. The advance in kinetic models can provide a comprehensive understanding of the OA-based growth behavior, as well as a potential guide to find a full satisfactory approach for the growth kinetics. The studies on the growth kinetics also offer the physical and chemical parameters and information that is meaningful for the control of the growth rate and size distribution in the system.
2. The classical growth kinetics for coarsening—Ostwald ripening
When giving an overview for the crystal growth kinetics, we can't overlook the influence and power of the classical kinetic model—Ostwald ripening (OR) mechanism.31–33 Early studies on the kinetic model for coarsening of crystals were almost based on the OR mechanism, which involves the growth of larger particles at the expense of smaller ones. The driving force for this process is the decrease in total surface free energy. According to the Gibbs–Thomson equation,34 the equilibrium solute concentration at the surface of larger particles is lower than that of smaller ones and the resulting concentration gradients lead to solute ions flowing from small particles to larger ones. The coarsening mechanism is often controlled by the diffusion, particle growth via addition of ions to the particle surface from solution. Fig. 1a illustrates the crystal growth via the OR mechanism. The classical kinetic model for the OR mechanism is known as the LSW model which is based on the Gibbs–Thomson equation.33,35 The general kinetic equation for these cases can be written as:![[D with combining macron]](https://www.rsc.org/images/entities/char_0044_0304.gif) n − n − ![[D with combining macron]](https://www.rsc.org/images/entities/char_0044_0304.gif) n0 = k(t − t0) n0 = k(t − t0) | (1) |
![[D with combining macron]](https://www.rsc.org/images/entities/char_0044_0304.gif) and
and ![[D with combining macron]](https://www.rsc.org/images/entities/char_0044_0304.gif) 0 are the mean particle sizes at time t and t0. k is a temperature-dependent material constant, and n is an exponent relevant to the coarsening mechanism. For example, for n = 3, the most often case, the coarsening kinetics are controlled by the volume diffusion of ions in the matrix.31–33 From eqn (1), it can be seen that the growth curve of size vs. time fits the parabola, and the crystal size increases continuously with time increasing.
0 are the mean particle sizes at time t and t0. k is a temperature-dependent material constant, and n is an exponent relevant to the coarsening mechanism. For example, for n = 3, the most often case, the coarsening kinetics are controlled by the volume diffusion of ions in the matrix.31–33 From eqn (1), it can be seen that the growth curve of size vs. time fits the parabola, and the crystal size increases continuously with time increasing.
 | ||
| Fig. 1 Scheme of nanocrystal growth controlled by: (a) Ostwald ripening mechanism; (b) oriented attachment mechanism. | ||
The OR mechanism has been used widely to describe and explain the crystal growth of particles with a relatively large size in solution. Experimentalists have confirmed the validity of the LSW theory.17 Though the OR growth kinetics tend to be satisfactory, some small disagreements between experimentally reported particle distribution and that predicted by the OR theories, still remain. So, in understanding the OR mechanism, more experimental and theoretical work is necessary in this field. In recent years, with the development of research in the nanoscale regime, findings in crystal growth often cannot be explained and fitted by the OR kinetics, especially to nanocrystals with a relatively small size. The typical cases are listed as follows.
(i) The crystal growth curve of particle size against time cannot be fitted properly by the LSW model. Peng et al. have reported the “focusing” of size distribution in the nanocrystal growth, and under these conditions, the smaller nanocrystals grow faster than the larger ones.36 The result is obviously inconsistent with the OR theory. Previously, it was found that using eqn (1) to fit the first stage of growth during hydrothermal coarsening of mercaptoethanol-capped nano-ZnS yielded an exponent with no physical meaning (n > 10).23
(ii) The crystal growth in solid phases (such as coarsening in air) often cannot be fitted and explained by the OR mechanism.37,38 Krill et al. found that the crystal growth rate of nanosized Fe (<150 nm) follows a liner relationship with time.37 Other examples demonstrate that the fitting results to the OR theory deviate from the proper physical explanation.38
(iii) Extensive work revealed that all kinds of irregular, even anisotropic morphologies were obtained in the synthesis of nanostructural materials, such as elongated crystals (chains), butterflies, horseshoes, etc.21,39–43 Moreover, the microstructure features of nanocrystals often exhibit the incorporation of defects, e.g., dislocation and planar defects (twins, stacking faults, etc.). These remarkable features scarcely occur in the crystal growth via the OR mechanism.
All of the above cases indicate that the growth of nanocrystals is controlled by an alternative mechanism.
3. The oriented attachment (OA) mechanism
In 1998, Penn and Banfield discovered an important crystal growth mechanism named “oriented attachment”.18,44 The mechanism involves spontaneous self-organization of adjacent particles, as grown by addition of solid particles to surface, so that they share a common crystallographic orientation, followed by joining of these particles at a planar interface. Crystal growth via the OA mechanism often leads to the formation of nanoparticles with irregular shapes by consuming primary nanocrystals as “building blocks”, and the growth rate is size-dependent.23,38As a non-classical crystallization mechanism,20 it brings much disputation when a newly developed mechanism appears. But after that, as shown in Table 1, adequate experiment observation eliminates the doubt and proves the validity of the OA mechanism. Gradually, the OA mechanism has attracted preponderant interests, for it is fundamental to design and explore materials with size- and morphology-controllability. Fig. 1b illustrates the crystal growth via the OA mechanism.
| Year | First-author | Matter | Morphology | Ref. |
|---|---|---|---|---|
| 1998 | Penn | TiO2 | various morphologies | 18,39 |
| 1998 | Scolan | TiO2 | oriented aggregates | 45 |
| 1999 | Penn | TiO2 | rutile elbows; anatase twins | 46 |
| 1999 | Penn | TiO2 | twins; intergrowths; | 44 |
| 1999 | Lee | CeO2 | twins and octahedral attached across{110} | 47 |
| 1999 | Audinet | CdS/ZnS | rounded particles with dimples and defects | 48 |
| 1999 | Chemseddine | TiO2 | elongated and corrugated | 49 |
| 1999 | Ricolleau | CdS | twins, stacking faults | 50 |
| CdS-ZnS | rounded and dimpled shapes | |||
| 1999 | de Moor | zeolite | round | 51 |
| 2000 | Zhang | sulfides, oxides | prisms, spindles, needles | 52 |
| 2000 | Nikolakis | zeolite | round | 53 |
| 2000 | Kuo | α-Ti, TiC | rounded aggregate | 54 |
| 2000 | Wang | Pt | elongated morphology | 40 |
| 2001 | Shen | ZrO2 | coalescence twins | 55 |
| 2001 | Penn | Fe2O3 | rounded hematite particles | 56 |
| FeOOH | irregular feroxyhite plates | |||
| CoOOH | hexagonal plates | |||
| anatase | Varied shapes | |||
| 2001 | Banfield | ZnS | twins, stacking faults, intergrowths; varied morphologies | 57 |
| 2001 | Shen | MCM-41 (silicate) | mesoporous | 58 |
| 2002 | Pacholski | ZnO | nanorods | 59 |
| 2002 | Niederberger | Hematite | rounded hexagonal plates | 60 |
| 2002 | Sampanthar | β-Co(OH)2 | “butterflies” | 41 |
| 2003 | Guyodo | α-FeOOH | nanorods | 61 |
| 2003 | Nesterova | FeOOH | various | 62 |
| 2003 | Lou | TiO2 | horseshoes | 42 |
| 2003 | Cozzoli | ZnO | elongated particles | 63 |
| 2003 | Jun | TiO2 | bullet, diamond, elongated rod | 64 |
| 2003 | Huang | ZnS | irregular-shape | 23 |
| 2004 | Deng | Bi2Te3 | nanorod | 65 |
| 2004 | Liu | ZnWO4 | nanorod | 66 |
| 2004 | Tsai | TiO2 | nanoparticles | 67 |
| 2004 | Adachi | TiO2 | nanowire | 68 |
| 2004 | He | Co3O4 | hollow spheres | 68 |
| 2005 | Liu | CdS | rings | 70 |
| 2005 | Wu | ZnO | nanorods | 71 |
| 2005 | Yu | ZnS | nanorods | 72 |
| 2005 | Gehrke | CaCO3 | hexagon crystals, lens-shaped | 73 |
| 2005 | Cho | PbSe | straight, zigzag, helical, branched, and tapered nanowires; nanorings | 74 |
| 2005 | Zitoun | MnO2 | multipods | 75 |
| 2005 | Cheng | PbMoO4 | dendrite | 76 |
| 2005 | Frandsen | α-Fe2O3 | chains | 77 |
| 2005 | Zhang | CuO | ellipsoidal nanoarchitectures | 78 |
| 2006 | Penn | α-FeOOH | nanorods | 79 |
| 2006 | Bao | NdF3 | plate-built chain | 80 |
| 2006 | Pradhan | CdSe | nanowire | 81 |
| 2006 | Wen | Ag | dendrite | 82 |
| 2006 | Calderone | SrTiO3 | hexagon | 83 |
| 2006 | Lu | Sb2S3 | nanorod-bundles | 84 |
| 2006 | Zhang | CuO | shuttle-like | 85 |
| 2006 | Shen | CaCO3 | olive-shape, lens-shape, hexagonal platelets | 86 |
| 2006 | Lu | Ag | dendrite | 87 |
| 2007 | Deng | Sb2O3 | nanorods and nanowires | 88 |
| 2007 | Halder | Au | nanowires | 89 |
| 2007 | Portehault | MnO2 | nanowires | 90 |
| 2007 | Yong | ZnTe | nanowires | 91 |
| 2007 | Klokkenburg | PbSe/CdSe | dipolar nanostructures | 92 |
| 2007 | Ribeiro | TiO2/SnO2 | heterostructural nanoparticles | 93 |
| 2007 | Du | NiSe2 | six-horn nanostars | 94 |
| 2008 | Zhang | Au | mesoporous spheres | 95 |
| 2008 | Zhou | CeO2 | nanoflowers | 96 |
| 2008 | Hawaldar | PbCrO4 | nanorods | 97 |
| 2008 | Xu | SnO2 | nanowires | 98 |
| 2008 | Yu | CdSe | nanorods | 99 |
Here, we present some selected examples to illustrate the typical OA phenomena. Usually, the crystal growth controlled by the OA mechanism tends to produce peculiar structures and morphologies. As shown in Fig. 2, the anatase nanoparticles assemble into a chain-like single crystalline structure.39 From the view of thermodynamics, combination in a coherent crystallographic orientation will eliminate the interfaces of nanocrystals. Reduction in surface energy in this way is the primary driving force for OA-based growth, though the detailed assembly process between the primary particles is under studied.
 | ||
| Fig. 2 A chain-like single crystal of anatase that was hydrothermally coarsened in 0.001 M HCl and grown by the OA mechanism. Reproduced with permission from Geochim. Cosmochim. Acta, 1999, 36, 1549. Copyright 1999 Elsevier. | ||
This example demonstrates the potential of OA for building anisotropic nanostructures. Other interesting OA examples include TiO2nanorods64 and PbSenanowires,74 from which we can see that the structures and shapes of primary “building blocks” act heavily on the OA growth and the product materials. As shown in Fig. 3 and 4, the primary unit is a polyhedral nanocrystal. The difference of surface energy at each face leads to the coalescence of primary particles in specific crystallographic orientation, such as the one-dimension growth in [001] of TiO2nanorods (Fig. 3) and in [111] of PbSenanowires (Fig. 4). Furthermore, during the OA growth, the primary units may keep or partially keep the original structure and configuration, which helps us to judge and study the OA growth kinetics.
![HRTEM analyses and simulated three-dimensional shape of anatase nanocrystals. (a) A bullet, (b) a diamond, (c) a short rod, (d) a long rod, and (e) a branched rod. The nanorods are formed by the OA mechanism with the primary units of truncated octagonal bipyramid. The long axes of the nanocrystals are parallel to the c-axis of the anatase structure in the [001] direction and the branched shape is a result of the growth along [101] directions starting from the hexagon shape. Scale bar: 3 nm. Reproduced with permission from J. Am. Chem. Soc., 2003, 125, 15981. Copyright 2003 American Chemical Society.](/image/article/2010/NR/b9nr00047j/b9nr00047j-f3.gif) | ||
| Fig. 3 HRTEM analyses and simulated three-dimensional shape of anatase nanocrystals. (a) A bullet, (b) a diamond, (c) a short rod, (d) a long rod, and (e) a branched rod. The nanorods are formed by the OA mechanism with the primary units of truncated octagonal bipyramid. The long axes of the nanocrystals are parallel to the c-axis of the anatase structure in the [001] direction and the branched shape is a result of the growth along [101] directions starting from the hexagon shape. Scale bar: 3 nm. Reproduced with permission from J. Am. Chem. Soc., 2003, 125, 15981. Copyright 2003 American Chemical Society. | ||
 | ||
| Fig. 4 TEM and high-resolution TEM images of PbSe zigzag nanowires. Single crystal helical PbSenanowires (3b, 3c, 3d) were formed by the OA mechanism. The primary building blocks are octahedral PbSenanocrystals (3a) and from Fig. 3e, the assembly process of PbSenanowires was captured. Reproduced with permission from J. Am. Chem. Soc., 2005, 127, 7140. Copyright 2005 American Chemical Society. | ||
As the OA mechanism is the direct coalescence of particles, it provides a route for the incorporation of defects, such as twins, stacking faults, and misorientation. The microstructural features and crystal morphology yield important clues to understand the OA mechanism in detail. As shown in Fig. 5, the growth of mercaptoethanol-capped nanosized ZnS is controlled by the OA mechanism.23 The big single crystal is composed by five small particle units which are signed as A, B, C, D, and E in Fig. 5a. Arrowheads mark indentations, interpreted to be the interfaces between assembly units. The schematic outlined in Fig. 5b illustrates the features in Fig. 5a and the defects during the OA growth, e.g. twin (T), stacking faults (SF). Once formed during the attachment, it is possible to preserve the defects in the following growth process, since transformation from one state into another needs extra energy.88 Obviously, these structural defects are the source of nonradiative recombination centers, which reduce the internal quantum efficiency of emission.
 | ||
| Fig. 5 HRTEM image of ZnSnanocrystal formed by the OA mechanism. Reproduced with permission from Nano Lett., 2003, 3, 373. Copyright 2003 American Chemical Society. | ||
The above cases well illustrate the characteristics and roles of OA mechanism in the preparation of nanostructural materials. Plenty of work has emphasized the importance of the OA mechanism in the process of crystal growth and morphology evolution of nanoscale materials which have been summarized in other previous papers,20,100,101 but most of the reports only demonstrate the OA mechanism occurring and simply illustrate the ongoing process. The inner complication of the OA mechanism appears to be the major challenge delaying the further advance of the growth kinetics. The exploration of the basic principles of the OA process mainly involves open problems such as: why OA happens? Which factors facilitate OA? What is the OA growth rate? How the assembly units collide and then attach each other, and which one is dominant? How about the microscopic process of the OA, such as the removal of the surface-absorbed molecules and the bonding at the interface? How OA-based growth influences microstructure, shape, phases, and structure–property relationships?
The advance of OA growth kinetics depends on the understanding of the mechanism; inversely, the studies on the OA growth kinetics will offer critical information (e.g. the growth rate) to understand the mechanism. As an increasingly important crystal growth mechanism, the OA needs and deserves an in-depth exploration for potentially controlling the development of size and morphology during the growth. Unfortunately, the OA and OR mechanisms often co-exist during the crystal growth.102 The mixed growth mode brings difficulty for the further investigation in the growth kinetics. Our preferential work reveals that the effect of surface adsorption should be one of the effective controlling ways to simplify the nanocrystal growth via a solo OA mechanism.
3.1 The OA kinetics under the strong surface adsorption
OA crystal growth phenomena have more often been observed for nanoparticles with a relatively small size and weight.23,38 Also, the attachments between secondary particles, even larger ones, are observed.19,23,102 It was found that under general conditions, OA and OR growth mechanisms occur simultaneously,102 sometimes accompanied with the phase transformation.103 All of these lead to difficulties for investigating this size dependent crystal growth mechanism, especially kinetically.During systematic studies on the nanocrystal growth kinetics,23,104–106 the effect of strong surface adsorption was proved to be the key to thermodynamically hinder the OR growth in the initial stage and attributed to the pure OA growth.
When primary ZnSnanoparticles are free of strong capping (H2O-ZnS), the coarsening process in water is consistently controlled by the mixed (OA + OR) mechanism.102 Though the OA mechanism is major in early stage and the OR acts heavily in the latter, there is no knot to divide the whole growth process, as shown in Fig. 6.
 | ||
| Fig. 6 Experimental data and fitting results for particles sizes vs. time at different temperatures. The whole growth process of ZnSnanoparticles in water is controlled by the (OA + OR) mechanism; inset are enlarged plots for the OA-dominated coarsening at the initial stage. Reproduced with permission from J. Phys. Chem. B, 2003, 107, 10470. Copyright 2003 American Chemical Society. | ||
When observing the growth process of mercaptoethanol-capped nano-ZnS (HS-ZnS) coarsening in water,23 it was discovered that the growth of nanocrystals could be divided into two stages. In the first stage, the asymptotic growth curve cannot be fitted by the OR theory—parabola growth kinetics (see Fig. 7). High-resolution transmission electron microscope (HRTEM) data display the nanocrystal growth limited by the OA mechanism (typical image shown in Fig. 5); the growth curve of two stages show distinct modes and have a dividing knot. These conclude that the growth in the first stage was controlled by the pure OA mechanism. Comparing with the (H2O-ZnS) system, it can be concluded that the strong surface adsorption of mercaptoethanol is the key to produce the exclusive OA growth.
 | ||
| Fig. 7 Two-stage growth of mercaptoethanol-capped nano-ZnS in aqueous solution. In the first stage, the growth is controlled by the pure OA mechanism, as shown in enlarged insets. Reproduced with permission from Nano Lett., 2003, 3, 373. Copyright 2003 American Chemical Society. | ||
The surface adsorption of capping ligands resulting in a pure OA growth stage can also be confirmed by the system of thiol-PbS.104 In this system, the observed growth curves show similar rules as the system of mercaptoethanol-capped ZnS. Also, as shown in Fig. 8, HRTEM data confirm the existing OA mechanism. But as an organic ligand, thiol is an unstable surface adsorption agent under hydrothermal treatment. During coarsening, it can be destroyed and desorbed into water. So the pure OA stage in these systems reveals the rule of a relatively small size range, ceasing at the size of about double the volume of a primary particle.
 | ||
| Fig. 8 Typical HRTEM images of the nanocrystal growth controlled by the OA mechanism in the thiol-PbS system. Larger crystals are constructed by smaller attached nanocrystals with size equal to primary particles (4–5 nm). The white parallel lines highlight the misorientation between two regions of the assembled particle. Schematic outlines of each image illustrate the attachment scheme of OA. Scale bars: 5 nm. Reproduced with permission from J. Phys. Chem. B, 2007, 111, 1449. Copyright 2007 American Chemical Society. | ||
Under more strong and stable surface adsorption, the pure OA stage may hold for a longer time and larger size. Concentrated NaOH shows its strong surface adsorption effect and even leads to the negative interfacial free energy.8 So, when ZnSnanoparticles are hydrothermally treated in 4 M NaOH solution,105 the crystal growth, limited by the exclusive OA mechanism, occurs at a large size scale in the first stage and the primary particles grow into a size over hundred times the original volume (see Fig. 9).
 | ||
| Fig. 9 Two-stage growth of ZnSnanocrystals in 4 M NaOH solution. In the first stage, the growth at a large size scale is controlled exclusively by the OA mechanism, as shown in enlarged insets. Reproduced with permission from J. Am. Chem. Soc., 2006, 128, 12981. Copyright 2006 American Chemical Society. | ||
Why does the effect of strong surface adsorption make the nanocrystal growth in the initial stage via the pure OA mechanism? Further investigation reveals that the effect can slow down the dissolution of particles in solution, so that the OR mechanism is thermodynamically prohibited in an unsaturated solution. Thus, the OA mechanism will be the only growth mode during the initial growth and the time period is prolonged with the increase of surface adsorption. As shown in Fig. 10, the concentration of zinc ions in the supernatant of the ZnS-NaOH system was checked during coarsening. It needs a relatively long time before the solution reaches saturation and during the period, crystal growth is limited by the pure OA mechanism.105 Comparing with Fig. 9a, it can be seen that the time point for saturation matches that of the pure OA growth ceasing.
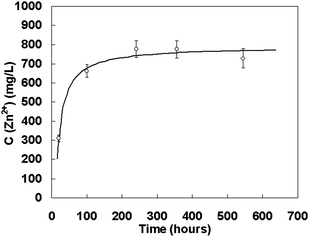 | ||
| Fig. 10 The Zn2+ concentration in the supernatant of ZnS-NaOH system at 100 °C vs. coarsening time. Reproduced with permission from J. Am. Chem. Soc., 2006, 128, 12981. Copyright 2006 American Chemical Society. | ||
Actually, research from Searson and coworkers also revealed that surface adsorption of anions (i.e.Br−, CH3CO2−, and ClO4−) on the nanoparticles can slow down the OR growth rate.26,27 Combining with the above examples, it can be seen that to select strong and stable surface adsorption of inorganic ions will be the effective means to obtain the pure OA growth and keep it for a long time period.
3.2 OA-based crystal growth kinetic models
Based on the characteristics of the OA mechanism, the first OA growth kinetic model was developed to fit the experimental growth curves (particle size vs. growth time).23 As shown in Fig. 7, in the first stage of hydrothermal treatment mercaptoethanol-capped nano-ZnS, the primary particles quickly double in average volume. It meant that two primary particles attached and combined into a larger secondary particle according to the relation of volume between the primary particle and the second one.
A nanoparticle is tens to thousands of times larger than a small molecule but far smaller than a macroscopic crystallite. So it is possible that the growth of nanoparticlesvia OA may share some characteristics with the collision reactions of molecules from the point of view that both processes produce a whole entity right after the reaction.18,107 Under hydrothermal coarsening, the Brownian motion of nanoparticles are assumed to be drastic. When two adjacent primary particles collide, the coalescence may occur on the premise that these two particles share a common crystallographic orientation. Thus two primary particles attach to each other and combine into a secondary one. The OA kinetic model can be interpreted as the following “reaction”:
 | (2) |
 | (3) |
On the basis of the above kinetic model, further studies were proceeded to gain a more thorough understanding of the growth behavior. Penn discussed the OA growth from the degree of the electrostatic interaction between particles in solution.19 The interactions such as electrostatic force and van der Waals are assumed as the main ingredients determining the kinetic rate constant. While Ribeiro et al. described the growth behavior of nanoparticles by considering the diffusion and coagulation of colloids ,24 and drew a conclusion that the viscosity of the liquid medium played an important role in growth by the OA mechanism, which is governed by an inverse proportional relationship with respect to the rate constant. Their models presented more detailed physical meanings for the possible OA-growth pathway and for the OA-based growth rate.
However, the above model only discussed the “reaction” between the primary particles (A1 + A1). That is, only primary particles are assumed to combine into secondary particles, then the “reaction” will stop. So in the system, there only exists two kinds of nanoparticles: primary particles and secondary particles. In fact, the attachment between two other particles such as a primary particle and a secondary one, even a multilevel one also exists, and is often experimentally observed.19,23,102 So based on the experimental observation, a more sophisticated OA growth kinetic model was developed as follows.104
 | ||
| Fig. 11 Schematic graph illustrating the growth of nanocrystals by oriented attachment: two primary particles collide and coalesce in the same crystallographic orientation (A1 + A1). Then, a secondary particle comes into being. The attachments also occur between primary particle and multilevel particle, such as (A1 + A2), (A1 + A3), etc. But the attachment between Ai and Aj (i ≥ 2, ,j ≥ 2) is neglected. Reproduced with permission from J. Phys. Chem. B, 2007, 111, 1449. Copyright 2007 American Chemical Society. | ||
The OA-based growth of nanoparticles can be analogous to the reaction between molecules, which is classically described by the Smoluchowski equation.25 The Smoluchowski equation has been used universally in the fields of colloid chemistry, aerosol dynamics, and atmospheric science. But most of the research is focused on the theoretical prediction of the structure and properties of aggregation by using computer simulations, especially in fractal geometry.108–111 In recent years, the Smoluchowski equation has also been used to describe the aggregation of nanocrystals and coagulation of colloids in theory, and to predict the size distribution.112–115 But only a little work was done to fit the experimental data by the Smoluchowski theory, for both the complicated solution of the equation and the difficulty in controlling the experiments. Zhang and coworkers adopted the equation to fit the transformation kinetics of crystallization and growth in the solid phase of titania.103 The fitting is greatly simplified by neglecting the influence of temperature and the concentration of particles on the OA-based growth for dry titania samples. As to the OA-based growth of nanoparticles in solution, these influence factors should be considered. The latter is closer to the essence described by the Smoluchowski equation.25
The “addition model” of the Smoluchowski equation is a limiting case of aggregation.110,116 It involves monomer–monomer reactions and monomer–multimer reactions. The multimer–multimer reaction can be neglected. It has been found that the modified “addition model” of the Smoluchowski equation is suitable for describing the OA growth kinetics under easily destroyed surface adsorption, such as organic capping agents.104 The monomers for OA under hydrothermal conditions are the primary nanoparticles. When the primary particles are exhausted, the crystal growth goes into the second stage. The growth via OA can be described as follows:
 | (4) |
 | (5) |
So the time evolution of the concentration of A1 and Ai are:
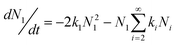 | (6) |
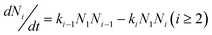 | (7) |
| ki = 4π(R1 + Ri)D1 | (8) |
| Ri = i⅓R1 | (9) |
For eqns (6)–(9), a numerical simulation is used to get the particle distribution at different times. Euler's polygon method is introduced to the program and a first-order expression of Taylor's formula is used as follows:118
 | (10) |
By this solution, the size distribution of particles can be obtained at a certain time. According to the definition of the volume-weighted average particle size,119 the average particle size, deq, which is consistent with the average particle size determined by XRD line broadening, can be expressed as:
| deq = ∑ Nkd4k/∑ Nkd3k | (11) |
The multistep OA growth agrees with the Smoluchowski theory.105 In the multistep OA kinetics model (Ai + Aj), the “reaction” of collision and coalescence may occur between any of two multilevel nanoparticles in the system. So, the collision and coalescence between particles here are unlimited and closer to the actual growth behaviors. As the size of the nanoparticle increases, the collision cross-section of the particle enlarges, while the motion rate of the particle decreases rapidly. Putting these two together produces an effect that with particle size increasing, OA-based growth slows down quickly and will finally stop. The process of growth in this way is illustrated in Fig. 12a and Fig. 12b and shows the typical HRTEM observation of crystal growth in this way.
 | ||
| Fig. 12 (a) Scheme of the OA-based growth of nanoparticles: two primary particles collide like molecules, and coalesce in the case of the same crystallographic orientation (1 + 1). After self-recrystallization, a secondary particle comes into being. The same “reactions” will take place between two other particles, such as (2 + 1) and (2 + 2), and further multistep “reactions” occur. (b) HRTEM image showing two ZnSnanoparticles attached to each other in the common crystallographic orientation. Reproduced with permission from J. Am. Chem. Soc., 2006, 128, 12981. Copyright 2006 American Chemical Society. | ||
The multistep OA-based growth kinetic model can be described as follows:
 | (12) |
 | (13) |
The rate matrix Kij is given by the Smoluchowski formula:25
| Kij = 4π(Ri + Rj)(Di + Dj) | (14) |
The proposed model was also based on the modified Smoluchowski equation and by numerical simulation, the experimental data can be fitted with the built kinetic model (Fig. 9). Because all of the possible binary interactions between nanoparticles in the systems are considered, the OA kinetic model shows its generalization. But on the other hand, the complexity and calculation magnitude of numerical simulations are greatly amplified.
The series of kinetic models tends to be gradually closer to the realistic growth behavior controlled by the OA mechanism. To take OA-based nanocrystal growth as the collision and reaction between molecules reveals the characteristics of nanoparticles at the transition state of molecules and bulk materials. The “molecular-like” kinetic models provide the deep insight of the OA-based crystal growth and by fitting experimental data, meaningful physical parameters and rules can be obtained to understand the microscopic crystal growth process.
For example, the activation energy can be obtained by using the OA kinetic models to fit the experimental data. The activation energy is an important parameter determined by the process of step-controls. Due to the scarcity of data directly from experiments, systemic studies on the activation energy of the OA growth were hardly reported. By fitting the OA growth kinetics, we can get the apparent activation energy from the experimental data of growth rate, which can be used to further analyze the microscopic dynamic process of controlling the growth.105
Another example is the effect of the OA mechanism in controlling the particle size distribution. In the chemical solution synthesis of nanocrystals, organic surfactants are broadly introduced to minimize the size distribution.120 However, the achievements from kinetically control often largely rely on the experience in experiments. The deficiency in fully understanding the inner mechanism will result in little effective approaches taken to control the synthesis in purpose. From the above growth kinetics, we know that strong surface adsorption (organic and inorganic) helps to generate the exclusive OA growth in the initial stage. During the OA growth, small particles diffuse fast due to their low mass. So, the smaller particles grow faster than the larger ones in the system, which facilitates a narrow size distribution. It has been reported that a “focusing” of size distribution was found during the nanocrystal growth in the CdSe-TOPO system and the InAs-TOP system.36 The authors suggested that continuous monitoring and adjustment of the monomer concentration could reliably prepare larger amounts of uniform nanoparticles, especially when the growth approaches the equilibrium of the asymptotic curve. Obviously, the OA growth kinetics are the major factor that determines the size distribution and the variety of shapes for nanosynthesis via surface capping.
Until now, studies on the OA-based growth kinetic models mainly focused on the systems of nanoparticles (zero dimension nanoscale materials), and little on two- or three-dimensions. Ribeiro et al.121 adopted the classical stepwise polymerization model122–124 to discuss the formation of anisotropic nanoparticles (one-dimension) by the OA mechanism. The main problem in these systems is not the building and solving of mathematical models, but the physical interpretation related to the kinetic models, such as the kinetic driving force and controlling factors of primary particles assembling in a certain direction. Also, the branch occurring on the one-dimensional structures enlarges the difference between calculated results and experimental statistical data. In fact, a homogenous one-dimensional structure formed by the OA mechanism is scarcely reported, due to the difficulties of changing from isotropy to anisotropy.125
3.3 Further understanding of microscopic OA dynamics
The OA undergoes two reaction steps: first, the nanocrystals (i-mers and j-mers) diffuse in the solution until collisions form a complex:
 | (15) |
 | (16) |
For a ZnS system, a series of activation energies was obtained by fitting the experimental data of growth rate.105 By comparing, it is concluded that under strong surface adsorption, the diffusion of nanocrystals is the slowest step for OA, though one can imagine that the strong adsorption also makes the disposal of surface ligands more difficult.
 | ||
| Fig. 13 Schematic of the particle rotation to get a structurally consistent nanocrystal during the process of OA. | ||
The grain rotation is likely induced by the thermal energy provided by the electron beam, which provides the opportunity to directly observe the OA dynamic process. For example, in the system of heterostructural SnO2/TiO2 nanoparticles,93 after 1 min of electron irradiation, the nanoparticles began a spontaneous counterclockwise rotational motion. Finally, after 15 min, the particles undergo some diffusional motion, relaxing the surface and concluding the OA process. The whole process is illustrated in Fig. 14.
 | ||
| Fig. 14 Spontaneous orientation by rotation alignment of SnO2 over TiO2 tip. The white bars show SnO2 planes and are a guide to the eyes in the rotation during the process of OA. Each image corresponds to a time interval of 1 min. Reproduced with permission from Appl. Phys. Lett., 2007, 91, 103105. Copyright 2007 American Institute of Physics. | ||
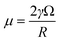 | (17) |
 | ||
| Fig. 15 Schematic of self-recrystallization after the particle coalescence by the OA mechanism. | ||
The oriented attached nanoparticle might undergo state A, state B, and state C. In experiments, though state A is formed via OA firstly, it is almost not observed in most systems by the TEM technique. Thus, it is supposed that the self-recrystallization from state A to state B is very rapid. But one can believe that the self-recrystallization from state B to state C might be slow, thus irregular small particle attachment geometries (state B) are captured frequently when the sizes of the assembling units are small. On the other hand, when the sizes of the assembling units become larger, the possibility of OA growth decreases, so there is enough time for nanoparticles to self-recrystallize into round shapes (state C).
The most recent development in studying the growth process of nanoparticles by the OA mechanism was by Zheng et al.,129 where the first direct microscopic observation of OA dynamics was fulfilled by using TEM with a liquid cell. The recrystallization during the OA process is clearly observed and by this technology, we promisingly obtain more detailed and in situ information for the microscopic dynamics of OA-based growth.
Summary and outlook
This article summarizes the OA-based growth kinetics, especially the control over obtaining the pure OA mechanism under the strong surface adsorption and the progress of OA kinetic models. The effect of surface adsorption was demonstrated to impact more on the OR growth kinetics than on the OA growth process. The influence to the former can lead to thermodynamic prohibition, while to the latter, the adsorption/desorption only brings the kinetic limitation. It is interesting that the OA growth occurs by direct particle coalescence, regardless of the strong surface adsorption. Further exploration in this area will probably generate a general understanding of crystallization itself. The “molecular-like” OA growth models can provide the microscopic understanding of the OA growth process, taking the OA growth behaves as the collision and reaction between molecules. The proposed growth kinetics will be meaningful to the self-assembly strategies for materials including colloids , polymers, and even biologic species.The OA mechanism has shown its increasing importance and role in self-assembly preparation. Kinetic modeling of crystal growth can provide critical information regarding the growth mechanism. To understand the microscopic process of nanocrystal growth by the OA mechanism can makes us utilize its positive roles in the preparation of nanostructural materials (e.g. the self-assembly of anisotropic crystals), and avoid its negative effects to properties (e.g. structural defects). Currently, the methods to produce controllable and uniform size and morphology are mainly based on the kinetic control. Besides the scientific significance, studies on the crystal growth kinetics are possible to generate effective methods to tailor and predict the properties of materials in the synthesis and growth. Just like that the effect of surface adsorption has been proved to greatly act on the nanocrystal growth. Other factors such as solvents, electric field, and magnetic field, are assumed to impact the nanocrystal growth behaviors and the corresponding products. By adjusting these effects, the crystal growth will possibly be controlled, which facilitates the further exploration of the OA-based growth kinetics.
The growth of nanocrystals is a rich field of research that needs progress in the theories and experiments. Further studies on the microscopic growth behaviors via the OA mechanism will help us to understand the crystallization process and control the development of structures. Exploitation of more powerful facilities may capture the real and in situ dynamic information. Alternatively, molecular simulation will provide the proper explanation on the molecular scale, as the OA-based growth process often fails to be directly observed, such as the adsorption and desorption of molecular, the collision mode and process, and bonding.
Acknowledgements
Financial supports for this study were provided by the National Natural Science Foundation of China (20501021) and (20803082), the Outstanding Youth Fund (50625205), Foundation for Overseas Scholar Fellowship and One Hundred Talent Program in Chinese Academy of Sciences, and Special Starting Foundation for Excellent Doctors in Chinese Academy of Sciences.References
- H. Gleiter and P. Marquardt, Nanocrystalline Structures – an Approach to New Materials, Metallkd Z., 1984, 75, 263–267 Search PubMed.
- R. Birringer, H. Gleiter, H. P. Klein and P. Marquardt, Nanocrystalline Materials an Approach to a Novel Solid Structure with Gas-like Disorder, Phys. Lett. A, 1984, 102, 365–369 CrossRef.
- A. P. Alivisatos, Perspectives on the Physical Chemistry of Semiconductor Nanocrystals, J. Phys. Chem., 1996, 100, 13226–13239 CrossRef CAS.
- Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, One-Dimensional Nanostructures: Synthesis, Characterization, and Applications, Adv. Mater., 2003, 15, 353–389 CrossRef CAS.
- C. Burda, X. Chen, R. Narayanan and M. A. El-Sayed, Chemistry and Properties of Nanocrystals of Different Shapes, Chem. Rev., 2005, 105, 1025–1102 CrossRef CAS.
- F. Huang, B. Gilbert, H. Zhang and J. F. Banfield, Reversible, Surface-Controlled Structure Transformation in Nanoparticles Induced by Aggregation-Disaggregation, Phys. Rev. Lett, 2004, 92 Search PubMed , 155501.
- F. Huang and J. F. Banfield, Size-Dependent Phase Transformation Kinetics in Nanocrystalline ZnS, J. Am. Chem. Soc., 2005, 127, 4523–4529 CrossRef CAS.
- Z. Lin, B. Gilbert, Q. Liu, G. Ren and F. Huang, A Thermodynamically Stable Nanophase Material, J. Am. Chem. Soc., 2006, 128, 6126–6131 CrossRef CAS.
- B. L. Cushing, V. L. Kolesnichenko and C. J. O'Connor, Recent Advances in the Liquid-Phase Syntheses of Inorganic Nanoparticles, Chem. Rev., 2004, 104, 3893–3946 CrossRef CAS.
- D. S. Wang, T. Xie and Y. D. Li, Nanocrystals: Solution-Based Synthesis and Applications as Nanocatalysts, Nano Res., 2009, 2, 30–46 Search PubMed.
- P. H. Shingu, Mechanical Alloying, Mat. Sci. Forum, 1992, 88–90.
- K. Ploog, Microscopical Structuring of Solids by Molecular Beam Epitaxy-Spatially Resolved Materials Synthesis, Angew. Chem., Int. Ed. Engl., 1988, 27, 593–621 CrossRef.
- H. K. Moon, C. I. Chang, D.-K. Lee and H. C. Choi, Effect of nucleases on the cellular internalization of fluorescent labeled DNA-functionalized single-walled carbon nanotubes, Nano Res., 2008, 1, 351–360 Search PubMed.
- V. F. Puntes, K. M. Krishnan and A. P. Alivisatos, Colloidal Nanocrystal Shape and Size Control: The Case of Cobalt, Science, 2001, 291, 2115–2117 CrossRef CAS.
- T. Hyeon, S. S. Lee, J. Park, Y. Chung and H. B. Na, Synthesis of Highly Crystalline and Monodisperse Maghemite Nanocrystallites without a Size-Selection Process, J. Am. Chem. Soc., 2001, 123, 12798–12801 CrossRef CAS.
- Nanoparticles and the Env ironment; J. F. Banfield, A. Navrotsky, eds., Reviews in Mineralogy & Geochemistry, vol. 44, Geochemical Society and Mineralogical Society of America, Washington, DC, 2001 Search PubMed.
- A. Baldan, Review: Progress in Ostwald Ripening Theories and Their Applications to Nickel-base Superalloys, Part I: Ostwald Ripening Theories, J. Mater. Sci., 2002, 37, 2171–2202 CrossRef CAS.
- R. L. Penn and J. F. Banfield, Imperfect Oriented Attachment: Dislocation Generation in Defect-Free Nanocrystals, Science, 1998, 281, 969–971 CrossRef CAS.
- R. L. Penn, Kinetics of Oriented Aggregation, J. Phys. Chem. B, 2004, 108, 12707–12712 CrossRef CAS.
- M. Niederberger and H. Cölfen, Oriented Attachment and Mesocrystals: Non-classical Crystallization Mechanisms Based on Nanoparticle Assembly, Phys. Chem. Chem. Phys., 2006, 8, 3271–3287 RSC.
- Z. Y. Tang, N. A. Kotov and M. Giersig, Spontaneous Organization of Single CdTe Nanoparticles into Luminescent Nanowires, Science, 2002, 297, 237–240 CrossRef CAS.
- D. V. Talapin, E. V. Shevchenko, C. B. Murray, A. Kornowski, S. Forster and H. Weller, CdSe and CdSe/CdS Nanorod Solids, J. Am. Chem. Soc., 2004, 126, 12984–12988 CrossRef CAS.
- F. Huang, H. Zhang and J. F. Banfield, Two-Stage Crystal-Growth Kinetics Observed during Hydrothermal Coarsening of Nanocrystalline ZnS, Nano Lett., 2003, 3, 373–378 CrossRef CAS.
- C. Ribeiro, E. J. H. Lee, E. Longo and E. R. Leite, A Kinetic Model to Describe Nanocrystal Growth by the Oriented Attachment Mechanism, ChemPhysChem, 2005, 6, 690–695 CrossRef CAS.
- M. V. Smoluchowski, Versuch einer Mathematischen Theorie der Kogulations-kinetik Kolloider Lsungen, Z. Phys. Chem., 1917, 92, 129–168 Search PubMed.
- Z. Hu, G. Oskam, R. L. Penn, N. Pesika and P. C. Searson, The Influence of Anion on the Coarsening Kinetics of ZnO Nanoparticles, J. Phys. Chem. B, 2003, 107, 3124–3130 CrossRef CAS.
- G. Oskam, Z. Hu, R. L. Penn, N. Pesika and P. C. Searson, Coarsening of Metal Oxide Nanoparticles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011403 CrossRef.
- J. Polleux, N. Pinna, M. Antonietti and M. Niederberger, Ligand-Directed Assembly of Preformed Titania Nanocrystals into Highly Anisotropic Nanostructures, Adv. Mater., 2004, 16, 436–439 CrossRef CAS.
- M. Niederberger, G. Garnweitner, F. Krumeich, R. Nesper, H. Cölfen and M. Antonietti, Tailoring the Surface and Solubility Properties of Nanocrystalline Titania by a Nonaqueous In Situ Functionalization Process, Chem. Mater., 2004, 16, 1202–1208 CrossRef CAS.
- S. H. Yu and H. Cölfen, Bio-Inspired Crystal Morphogenesis by Hydrophilic Polymers, J. Mater. Chem., 2004, 14, 2124–2147 RSC.
- C. Wagner, Theory of Precipitate Change by Redissolution, Z. Elektrochem, 1961, 65, 581–591 CAS.
- M. V. Speight, Growth Kinetics of Grain-boundary Precipitates, Acta Metall., 1968, 16, 133–135 CrossRef CAS.
- H. O. K. Kirchner, Coarsening of Grain-Boundary Precipitates, Metall. Trans., 1971, 2, 2861–2864 Search PubMed.
- C. T. Campbell, S. C. Parker and D. E. Starr, The Effect of Size-Dependent Nanoparticle Energetics on Catalyst Sintering, Science, 2002, 298, 811–814 CrossRef CAS.
- R. L. Joesten, Kinetics of Coarsening and Diffusion-controlled Mineral Growth, Rev. Mineral., 1991, 26, 507–582 Search PubMed.
- X. Peng, J. Wickham and A. P. Alivisatos, Kinetics of II–VI and III–V Colloidal Semiconductor Nanocrystal Growth: “Focusing” of Size Distributions, J. Am. Chem. Soc., 1998, 120, 5343–5344 CrossRef CAS.
- C. E. Krill III, L. Helfen, D. Michels, H. Natter, A. Fitch, O. Masson and R. Birringer, Size-Dependent Grain-Growth Kinetics Observed in Nanocrystalline Fe, Phys. Rev. Lett., 2001, 86, 842–845 CrossRef.
- H. Zhang and J. F. Banfield, New Kinetic Model for the Nanocrystalline Anatase-to-rutile Transformation Revealing Rate Dependence on Number of Particles, Am. Mineral., 1999, 84, 528–535 CAS.
- R. L. Penn and J. F. Banfield, Morphology Development and Crystal Growth in Nanocrystalline Aggregates under Hydrothermal Conditions: Insights from Titania, Geochim. Cosmochim. Acta, 1999, 63, 1549–1557 CrossRef CAS.
- Z. L. Wang, Transmission Electron Microscopy of Shape-Controlled Nanocrystals and Their Assemblies, J. Phys. Chem. B, 2000, 104, 1153–1175 CrossRef CAS.
- T. Sampanthar and H. C. Zeng, Arresting Butterfly-Like Intermediate Nanocrystals of β-Co(OH)2via Ethylenediamine-Mediated Synthesis, J. Am. Chem. Soc., 2002, 124, 6668–6675 CrossRef CAS.
- X. W. Lou and H. C. Zeng, Complex α-MoO3 Nanostructures with External Bonding Capacity for Self-Assembly, J. Am. Chem. Soc., 2003, 125, 2697–2704 CrossRef CAS.
- B. A. Korgel and D. Fitzmaurice, Self-Assembly of Silver Nanocrystals into Two-Dimensional Nanowire Arrays, Adv. Mater., 1998, 10, 661–665 CrossRef CAS.
- R. L. Penn and J. F. Banfield, Oriented Attachment and Growth, Twinning, Polytypism, and Formation of Metastable Phases: Insights from Nanocrystalline TiO2, Am. Mineral., 1998, 83, 1077–1082 CAS.
- E. Scolan and C. Sanchez, Synthesis and Characterization of Surfaceprotected Nanocrystalline Titania Particles, Chem. Mater., 1998, 10, 3217–3223 CrossRef CAS.
- R. L. Penn and J. F. Banfield, Formation of Rutile Nuclei at Anatase{112} Twin Interfaces and the Phase Transformation Mechanism in Nanocrystalline Titania, Am. Mineral., 1999, 84, 871–876 CAS.
- W. H. Lee and P. Y. Shen, On the Coalescence and Twinning of Cubeoctahedral CeO2 Condensates, J. Cryst. Growth, 1999, 205, 169–176 CrossRef CAS.
- L. Audinet, C. Ricolleau, M. Gandais, T. Gacoin, J. P. Boilot and P. A. Buffat, Structural Properties of Coated Nanoparticles: the CdS/ZnS Nanostructure, Philos. Mag., 1999, 79, 2379–2396 Search PubMed.
- A. Chemseddine and T. Moritz, Nanostructuring Titania: Control over Nanocrystal Structure, Size, Shape, and Organization, Eur. J. Inorg. Chem, 1999, 235–245 CrossRef CAS.
- C. Ricolleau, L. Audinet, M. Gandais and T. Gacoin, Structural Transformations in II–VI Semiconductor Nanocrystals, Eur. Phys. J. D, 1999, 9, 565–570 CrossRef CAS.
- P. de Moor, T.-P. M. Beelen, B. U. Komanschek, L. W. Beck, P. Wagner, M. E. Davis and R. A. van Santen, Imaging the Assembly Process of the Organic-Mediated Synthesis of a Zeolite, Chem.–Eur. J., 1999, 5, 2083–2088 CrossRef CAS.
- J. Z. Zhang, Interfacial Charge Carrier Dynamics of Colloidal Semiconductor Nanoparticles, J. Phys. Chem. B, 2000, 104, 7239–7253 CrossRef CAS.
- V. Nikolakis, E. Kokkoli, M. Tirrell, M. Tsapatsis and D. G. Vlachos, Zeolite Growth by Addition of Subcolloidal Particles: Modeling and Experimental Validation, Chem. Mater., 2000, 12, 845–853 CrossRef CAS.
- L. Y. Kuo and P. Y. Shen, On the Condensation and Preferred Orientation of TiC Nanocrystals - Effects of Electric Field, Substrate Temperature and Second Phase, Mater. Sci. Eng., A, 2000, 276, 99–107 CrossRef.
- P. Shen and W. H. Lee, (111)-Specific Coalescence Twinning and Martensitic Transformation of Tetragonal ZrO2 Condensates, Nano Lett., 2001, 1, 707–711 CrossRef CAS.
- R. L. Penn, G. Oskam, T. J. Strathmann, P. C. Searson, A. T. Stone and D. R. Veblen, Epitaxial Assembly in Aged Colloids, J. Phys. Chem. B, 2001, 105, 2177–2182 CrossRef CAS.
- J. F. Banfield and H. Zhang, Nanoparticles in the Environment, Rev. Mineral. Geochem., 2001, 44, 1–58 CAS.
- P. Shen, Y. Y. Fahn and A. C. Su, Imperfect Oriented Attachment: Accretion and Defect Generation of Hexagonal Inorganic-Surfactant Nanoparticles, Nano Lett., 2001, 1, 299–303 CrossRef CAS.
- C. Pacholski, A. Kornowski and H. Weller, Self-Assembly of ZnO: From Nanodots, to Nanorods, Angew. Chem., Int. Ed., 2002, 41, 1188 CrossRef CAS.
- M. Niederberger, F. Krumeich, K. Hegetschweiler and R. Nesper, An Iron Polyolate Complex as a Precursor for the Controlled Synthesis of Monodispersed Iron Oxide Colloids, Chem. Mater., 2002, 14, 78–82 CrossRef CAS.
- Y. Guyodo, A. Mostrom, R. L. Penn and S. K. Banerjee, From Nanodots to Nanorods: Oriented Aggregation and Magnetic Evolution of Nanocrystalline Goethite, Geophys. Res. Lett., 2003, 30, 1512 CrossRef.
- M. Nesterova, J. Moreau and J. F. Banfield, Model Biomimetic Studies of Templated Growth and Assembly of Nanocrystalline FeOOH, Geochim. Cosmochim. Acta, 2003, 67, 1185–1187 CrossRef.
- P. D. Cozzoli, M. L. Curri, A. Agostiano, G. Leo and M. Lomascolo, ZnO Nanocrystals by a Non-hydrolytic Route: Synthesis and Characterization, J. Phys. Chem. B, 2003, 107, 4756–4762 CrossRef CAS.
- Y. Jun, M. F. Casula, J. Sim, S. Y. Kim, J. Cheon and A. P. Alivisatos, Surfactant-Assisted Elimination of a High Energy Facet as a Means of Controlling the Shapes of TiO2 Nanocrystals, J. Am. Chem. Soc., 2003, 125, 15981–15985 CrossRef CAS.
- Y. Deng, C.-W. Nan and L. Guo, A Novel Approach to Bi2Te3 Nanorods by Controlling Oriented Attachment, Chem. Phys. Lett., 2004, 383, 572–576 CrossRef CAS.
- B. Liu, S.-H. Yu, L. Li, F. Zhang, Q. Zhang, M. Yoshimura and P. Shen, Nanorod-Direct Oriented Attachment Growth and Promoted Crystallization Processes Evidenced in Case of ZnWO4, J. Phys. Chem. B, 2004, 108, 2788–2792 CrossRef CAS.
- M. H. Tsai, S. Y. Chen and P. Shen, Imperfect Oriented Attachment: Accretion and Defect Generation of Nanosize Rutile Condensates, Nano Lett., 2004, 4, 1197–1201 CrossRef CAS.
- M. Adachi, Y. Murata, J. Takao, J. Jiu, M. Sakamoto and F. Wang, Highly Efficient Dye-Sensitized Solar Cells with a Titania Thin-Film Electrode Composed of a Network Structure of Single-Crystal-like TiO2 Nanowires Made by the “Oriented Attachment” Mechanism, J. Am. Chem. Soc., 2004, 126, 14943–14949 CrossRef CAS.
- T. He, D. R. Chen, X. L. Jiao, Y. Y. Xu and Y. X. Gu, Surfactant-Assisted Solvothermal Synthesis of Co3O4 Hollow Spheres with Oriented-Aggregation Nanostructures and Tunable Particle Size, Langmuir, 2004, 20, 8404–8408 CrossRef CAS.
- B. Liu and H. C. Zeng, Semiconductor Rings Fabricated by Self-Assembly of Nanocrystals, J. Am. Chem. Soc., 2005, 127, 18262–18268 CrossRef CAS.
- L. Wu, Y. Wu, W. Lu, H. Wei and Y. Shi, Morphology Development and Oriented Growth of Single Crystalline ZnO Nanorod, Appl. Surf. Sci., 2005, 252, 1436–1441 CrossRef CAS.
- J. H. Yu, J. Joo, H. M. Park, S. I. Baik, Y. W. Kim, S. C. Kim and T. Hyeon, Synthesis of Quantum-Sized Cubic ZnS Nanorods by the Oriented Attachment Mechanism, J. Am. Chem. Soc., 2005, 127, 5662–5670 CrossRef.
- N. Gehrke, H. Cölfen, N. Pinna, M. Antonietti and N. Nassif, Superstructures of Calcium Carbonate Crystals by Oriented Attachment, Cryst. Growth Des., 2005, 5, 1317–1319 CrossRef CAS.
- K.-S. Cho, D. V. Talapin, W. Gaschler and C. B. Murray, Designing PbSe Nanowires and Nanorings through Oriented Attachment of Nanoparticles, J. Am. Chem. Soc., 2005, 127, 7140–7147 CrossRef CAS.
- D. Zitoun, N. Pinna, N. Frolet and C. Belin, Single Crystal Manganese Oxide Multipods by Oriented Attachment, J. Am. Chem. Soc., 2005, 127, 15034–15035 CrossRef CAS.
- Y. Cheng, Y. Wang, D. Chen and F. Bao, Evolution of Single Crystalline Dendrites from Nanoparticles through Oriented Attachment, J. Phys. Chem. B, 2005, 109, 794–798 CrossRef CAS.
- C. Frandsen, C. R. H. Bahl, B. Lebech, K. Lefmann, L. T. Kuhn, L. Keller, N. H. Andersen, M. von Zimmermann, E. Johnson, S. N. Klausen and S. Morup, Oriented Attachment and Exchange Coupling of α-Fe2O3 Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214406 CrossRef.
- Z. P. Zhang, H. P. Sun, X. Q. Shao, D. F. Li, H. D. Yu and M. Y. Han, Three-Dimensionally Oriented Aggregation of a Few Hundred Nanoparticles into Monocrystalline Architectures, Adv. Mater., 2005, 17, 42–47 CrossRef CAS.
- R. L. Penn, J. J. Erbs and D. M. Gulliver, Controlled growth of alpha-FeOOH nanorods by exploiting-oriented aggregation, J. Cryst. Growth, 2006, 293, 1–4 CrossRef CAS.
- F. Bao, Y. Wang, Y. Cheng and Y. Zheng, Self-Assembly of Mono-Crystalline NdF3 Nanostructures during Hydrothermal Process, Mater. Lett., 2006, 60, 389–392 CrossRef CAS.
- N. Pradhan, H. Xu and X. Peng, Colloidal CdSe Quantum Wires by Oriented Attachment, Nano Lett., 2006, 6, 720–724 CrossRef CAS.
- X. Wen, Y.-T. Xie, M. W. C. Mak, K. Y. Cheung, X.-Y. Li, R. Renneberg and S. Yang, Dendritic Nanostructures of Silver: Facile Synthesis, Structural Characterizations, and Sensing Applications, Langmuir, 2006, 22, 4836–4842 CrossRef CAS.
- V. R. Calderone, A. Testino, M. T. Buscaglia, M. Bassoli, C. Bottino, M. Viviani, V. Buscaglia and P. Nanni, Size and Shape Control of SrTiO3 Particles Grown by Epitaxial Self-Assembly, Chem. Mater., 2006, 18, 1627–1633 CrossRef CAS.
- Q. Lu, H. Zeng, Z. Wang, X. Cao and L. Zhang, Size and Shape Control of SrTiO3 Particles Grown by Epitaxial Self-Assembly, Nanotechnology, 2006, 17, 2098–2104 CrossRef CAS.
- Y. Zhang, S. Wang, X. Li, L. Chen, Y. Qian and Z. Zhang, CuO Shuttle-like Nanocrystals Synthesized by Oriented Attachment, J. Cryst. Growth, 2006, 291, 196–201 CrossRef CAS.
- Q. Shen, L. C. Wang, Y. P. Huang, J. L. Sun, H. H. Wang, Y. Zhou and D. J. Wang, Oriented Aggregation and Novel Phase Transformation of Vaterite Controlled by the Synergistic Effect of Calcium Dodecyl Sulfate and n-Pentanol, J. Phys. Chem. B, 2006, 110, 23148–23153 CrossRef CAS.
- L. Lu, A. Kobayashi, Y. Kikkawa, K. Tawa and Y Ozaki, Oriented Attachment-Based Assembly of Dendritic Silver Nanostructures at Room Temperature, J. Phys. Chem. B, 2006, 110, 23234–23241 CrossRef CAS.
- Z. Deng, D. Chen, F. Tang, X. Meng, J. Ren and L. Zhang, Orientated Attachment Assisted Self-Assembly of Sb2O3 Nanorods and Nanowires: End-to-End versus Side-by-Side, J. Phys. Chem. C, 2007, 111, 5325–5330 CrossRef CAS.
- A. Halder and N. Ravishankar, Ultrafine Single-Crystalline Gold Nanowire Arrays by Oriented Attachment, Adv. Mater., 2007, 19, 1854–1858 CrossRef CAS.
- D. Portehault, S. Cassaignon, E. Baudrin and J.-P. Jolivet, Morphology Control of Cryptomelane Type MnO2 Nanowires by Soft Chemistry: Growth Mechanisms in Aqueous Medium, Chem. Mater., 2007, 19, 5410–5417 CrossRef CAS.
- K.-T. Yong, Y. Sahoo, H. Zeng, M. T. Swihart, J. R. Minter and P. N. Prasad, Formation of ZnTe Nanowires by Oriented Attachment, Chem. Mater., 2007, 19, 4108–4110 CrossRef CAS.
- M. Klokkenburg, A. J. Houtepen, R. Koole, J. W. J. de Folter, B. H. Erne and E. van Faassen, Vanmaekelbergh D. Dipolar Structures in Colloidal Dispersions of PbSe and CdSe Quantum Dots, Nano Lett., 2007, 7, 2931–2936 CrossRef CAS.
- C. Ribeiro, E. Longo and E. R. Leite, Tailoring of heterostructures in a SnO2/TiO2 system by the oriented attachment mechanism, Appl. Phys. Lett., 2007, 91, 103105 CrossRef.
- W. Du, X. Qian, X. Niu and Q. Gong, Symmetrical Six-horn Nickel Diselenide Nanostars Growth from Oriented Attachment Mechanism, Cryst. Growth Des., 2007, 7, 2733–2737 CrossRef CAS.
- Y. Zhang and H. Zeng, Surfactant-Mediated Self-Assembly of Au Nanoparticles and Their Related Conversion to Complex Mesoporous Structures, Langmuir, 2008, 24, 3740–3746 CrossRef CAS.
- H. Zhou, Y. Zhang, H. Mai, X. Sun, Q. Liu, W. Song and C. Yan, Spontaneous Organization of Uniform CeO2 Nanoflowers by 3D Oriented Attachment in Hot Surfactant Solutions Monitored with an In Situ Electrical Conductance Technique, Chem.–Eur. J., 2008, 14, 3380–3390 CrossRef CAS.
- R. R. Hawaldar, S. D. Sathaye, A. Harle, R. S. Gholap and K. R. Patil, Kinetics of PbCrO4 Nanorod Growth by Oriented Attachment at the Air – Water Interface, J. Phys. Chem. C, 2008, 112, 7557–7561 CrossRef CAS.
- X. Xu, J. Zhuang and X. Wang, SnO2 Quantum Dots and Quantum Wires: Controllable Synthesis, Self-Assembled 2D Architectures, and Gas-Sensing Properties, J. Am. Chem. Soc., 2008, 130, 12527–12535 CrossRef CAS.
- Z. Yu, M. A. Hahn, S. E. Maccagnano-Zacher, J. Calcines, T. D. Krauss, E. S. Alldredge and J. Silcox, Small-Angle Rotation in Individual Colloidal CdSe Quantum Rods, ACS Nano, 2008, 2, 1179–1188 CrossRef CAS.
- H. C. Zeng, Oriented Attachment: A Versatile Approach for Construction of Nanomaterials, Int. J. Nanotechnol., 2007, 4, 329–346 Search PubMed.
- Q. Zhang, S. Liu and S. Yu, Recent Advances in Oriented Attachment Growth and Synthesis of Functional Materials: Concept, Evidence, Mechanism, and Future, J. Mater. Chem., 2009, 19, 191–207 RSC.
- F. Huang, H. Zhang and J. F. Banfield, The Role of Oriented Attachment Crystal Growth in Hydrothermal Coarsening of Nanocrystalline ZnS, J. Phys. Chem. B, 2003, 107, 10470–10475 CrossRef CAS.
- H. Zhang and J. F. Banfield, Kinetics of Crystallization and Crystal Growth of Nanocrystalline Anatase in Nanometer-Sized Amorphous Titania, Chem. Mater., 2002, 14, 4145–4154 CrossRef CAS.
- J. Zhang, Y. Wang, J. Zheng, F. Huang, D. Chen, Y. Lan, G. Ren, Z. Lin and C. Wang, Oriented Attachment Kinetics for Ligand Capped Nanocrystals: Coarsening of Thiol-PbS Nanoparticles, J. Phys. Chem. B, 2007, 111, 1449–1454 CrossRef CAS.
- J. Zhang, Z. Lin, Y. Lan, G. Ren, D. Chen, F. Huang and M. Hong, A Multistep Oriented Attachment Kinetics: Coarsening of ZnS Nanoparticles in Concentrated NaOH, J. Am. Chem. Soc., 2006, 128, 12981–12987 CrossRef CAS.
- Y. Wang, J. Zhang, Y. Yang, F. Huang, J. Zheng, D. Chen, F. Yan, Z. Lin and C. Wang, NaOH Concentration Effect on the Oriented Attachment Growth Kinetics of ZnS, J. Phys. Chem. B, 2007, 111, 5290–5294 CrossRef CAS.
- J. F. Banfield, S. A. Welch, H. Z. Zhang, T. T. Ebert and R. L. Penn, Aggregation-Based Crystal Growth and Microstructure Development in Natural Iron Oxyhydroxide Biomineralization Products, Science, 2000, 289, 751–754 CrossRef CAS.
- F. Family, P. Meakin and J. Deutch, Kinetics of Coagulation with Fragmentation: Scaling Behavior and Fluctuations, Phys. Rev. Lett., 1986, 57, 727–730 CrossRef CAS.
- P. Meakin, Fractal Aggregates, Adv. Colloid Interface Sci., 1987, 28, 249–331 CrossRef.
- N. V. Brilliantov and P. L. Krapivsky, Non-scaling and Source-induced Scaling Behaviour in Aggregation Models of Movable Monomers and Immovable Clusters, J. Phys. A: Math. Gen., 1991, 24, 4789–4803 CrossRef.
- J. A. Dirksen and T. A. Ring, Fundamentals of Crystallization-Kinetic Effects on Particle-Size Distributions and Morphology, Chem. Eng. Sci., 1991, 46, 2389–2427 CrossRef CAS.
- V. Privman, D. V. Goia, J. Park and E. Matijeviæ, Mechanism of Formation of Monodispersed Colloids by Aggregation of Nanosize Precursors, J. Colloid Interface Sci., 1999, 213, 36–45 CrossRef CAS.
- J. Park, V. Privman and E. Matijeviæ, Model of Formation of Monodispersed Colloids, J. Phys. Chem. B, 2001, 105, 11630–11635 CrossRef CAS.
- S. Libert, V. Gorshkov, D. V. Goia, J. Park, E. Matijeviæ and V. Privman, Model of Controlled Synthesis of Uniform Colloid Particles: Cadmium Sulfide, Langmuir, 2003, 19, 10679–10683 CrossRef CAS.
- T. O. Drews, M. A. Katsoulakis and M. Tsapatsis, A Mathematical Model for Crystal Growth by Aggregation of Precursor Metastable Nanoparticles, J. Phys. Chem. B, 2005, 109, 23879–23887 CrossRef CAS.
- E. M. Hendricks and W. H. Ernst, Exactly Soluble Addition and Condensation Models in Coagulation Kinetics, J. Colloid Interface Sci., 1984, 97, 176–194 CrossRef.
- G. H. Weiss, Overview of theoretical models for reaction rates, J. Stat. Phys., 1986, 42, 3–36 CrossRef.
- K. F. Kelton, A. L. Greer and C. V. Thompson, Transient Nucleation in Condensed Systems, J. Chem. Phys., 1983, 79, 6261–6276 CrossRef CAS.
- E. Kaelble. Handbook of X-Rays; Mcgraw-Hill: New York, 1967; pp 17–8 Search PubMed.
- X. Wang, J. Zhuang, Q. Peng and Y. Li, A General Strategy for Nanocrystal Synthesis, Nature, 2005, 437, 121–124 CrossRef CAS.
- C. Ribeiro, E. J. H. Lee, E. Longo and E. R. Leite, Oriented Attachment Mechanism in Anisotropic Nanocrystals: A “Polymerization” Approach, ChemPhysChem, 2006, 7, 664–670 CrossRef CAS.
- W. Chalmers, The Mechanism of Macropolymerization Reactions, J. Am. Chem. Soc., 1934, 56, 912–922 CrossRef CAS.
- P. J. Flory, Molecular Size Distribution in Linear Condensation Polymers, J. Am. Chem. Soc., 1936, 58, 1877–1885 CrossRef CAS.
- S. Kuchanov, H. Slot and A. Stroeks, Development of a Quantitative Theory of Polycondensation, Prog. Polym. Sci., 2004, 29, 563–633 CrossRef CAS.
- Z. Tang and N. A. Kotov, One-Dimensional Assemblies of Nanoparticles: Preparation, Properties, and Promise, Adv. Mater., 2005, 17, 951–962 CrossRef CAS.
- D. Moldovan, V. Yamakov, D. Wolf and S. R. Phillpot, Scaling Behavior of Grain-Rotation Induced Grain Growth, Phys. Rev. Lett., 2002, 89, 206101 CrossRef.
- E. R. Leite, T. R. Giraldi, F. M. Pontes, E. Longo, A. Beltran and J. Andrés, Crystal Growth in Colloidal Tin Oxide Nanocrystals Induced by Coalescence at Room Temperature, Appl. Phys. Lett., 2003, 83, 1566–1568 CrossRef CAS.
- Z. Zhuang, J. Zhang, F. Huang, Y. Wang and Z. Lin, Pure Multistep Oriented Attachment Growth Kinetics of Surfactant-Free SnO2 Nanocrystals, Phys. Chem. Chem. Phys., 2009, 11, 8516–8521 RSC.
- H. Zheng, R. K. Smith, Y.-W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Observation of Single Colloidal Platinum Nanocrystal Growth Trajectories, Science, 2009, 324, 1309–1312 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
