One is enough: insights into the two-metal ion nuclease mechanism from global analysis and computational studies

Abstract

The mechanistic details of metallonuclease reactions, typically supported by Mg(II), have a long and contentious history. Two-metal ion mechanisms have enjoyed much favor, based largely in the multitude of X-ray crystal structures of these enzymes with more than one metal ion per active site. Most recently, this mechanism has come under challenge. Reviewed herein are the applications of different experimental strategies that collectively support a mechanism in which only one metal ion is necessary for nucleic acid hydrolysis. Based on global kinetic analysis, analysis of reactions in which the nonsupportive Ca(II) is added, and a number of computational approaches, secondary sites are proposed to either be occupied by activity-modulating metal ions or occupied in turn by a single metal that changes position during the course of the reaction.

---

Cynthia M. Dupureur

Cynthia Dupureur received her Bachelor's degree in chemistry from Missouri State University and earned her PhD at Ohio State University. Following an NSF postdoctoral fellowship at the California Institute of Technology, she was an Assistant Professor of Biochemistry and Biophysics at Texas A&M University. She is currently Associate Professor of Chemistry and Biochemistry at the University of Missouri St. Louis. Her interests include enzymology and nucleic acid–ligand interactions.

---

Introduction

Nucleases comprise a class of enzymes that catalyze the hydrolytic degradation of phosphodiester bonds in RNA and DNA. This activity is very abundant in cells and often a component activity of other nucleic acid processing functions that include polymerization, splicing, repair, and recombination.¹ Exonucleases are enzymes that cleave terminal mononucleotides. Endonucleases cut nucleic acids internally, yielding poly or oligonucleotide products. While exonucleases typically do not exhibit sequence specificity, there are examples of both nonspecific (e.g., DNaseI) and sequence specific endonucleases (e.g., restriction enzymes).

It is generally agreed upon that the basic elements of phosphoester hydrolysis (either mono- or diester) are activation of the nucleophilic water, attack of the scissile phosphodiester, and protonation of the leaving group. As summarized in Fig. 1, these mechanisms can be characterized as dissociative (D_N + A_N), in which the nucleophile becomes bonded to phosphate after the leaving group departs; associative (A_N + D_N), that is, a pentacovalent transition state is formed in which both the nucleophile and leaving group moieties are transiently bonded to the phosphorus; and finally, a concerted mechanism (A_ND_N) in which the nucleophile attacks the phosphorus and the leaving group departs simultaneously.

Fig. 1 Summary of mechanisms of phosphodiester hydrolysis. Dissociative (D_N + A_N), associative (A_N + D_N) and concerted (A_ND_N) mechanisms of phosphodiester hydrolysis, with roles for two metal ions A and B depicted. In one-metal ion mechanisms, Metal A performs the functions of both metal ions, or other active site groups contribute to nucleophile activation and/or leaving group facilitation. See Fig. 2 for examples. Adapted from ref. 42.

Because phosphodiester bonds are especially stable, and the substrates are highly polyanionic, hydrolysis of nucleic acids presents a special challenge. Bioinorganic chemists will immediately recognize the particular suitability of metal ion cofactors for this kind of reaction, and indeed many nucleases are metal ion-dependent. As summarized in Fig. 1, metal ions possess ideal properties to activate and/or stabilize nucleophiles, provide Lewis acid stabilization of the charge buildup in the transition state, and orient water molecules facilitating leaving group departure. As proposed classically by Steitz and Steitz,² in nuclease active sites featuring two metal ions, Metal A is associated with the first two steps; Metal B is often but not universally associated to the latter two steps (transition state stabilization is frequently depicted as shared by both metal ions). Interestingly, while Lewis acid catalysis is the most universally accepted role for a metal ion in phosphodiester hydrolysis enzyme mechanisms, work with model complexes indicate that the potential for this contribution is dwarfed by roles in nucleophile activation and leaving group departure, (up to 100-fold in rate enhancement over the uncatalyzed reaction vs. 10⁸ to 10⁹-fold rate enhancement for the latter two contributions).³

As has been discussed in detail previously,^4,5 Mg(II) is by far the most common nuclease metal ion cofactor. In vitro, Mn(II) is a common substitute in cleavage studies, since it typically exhibits comparable activity often at lower concentrations than Mg(II).⁴ Ca(II) supports only a few nucleases as a native cofactor;⁴ in many others, it is commonly used as a nonreactive cofactor substitute in binding and crystallographic studies.⁴ A few of the more newly characterized metallonucleases are Zn(II) dependent.⁶ While any of these ions can polarize phosphoesters and/or orient water for leaving group facilitation, the suitability of specific metal ions to serve in nucleophile activation depends very strongly on the pK_as of metal-bound hydroxides; this issue has been discussed in detail previously.⁴

Crystallography has enjoyed a long reign as the favored technique for elucidating various aspects of the metallonuclease mechanism,^2,7–9 and this form of evidence is still in heavy use.^10,11 The number and identity of metal ions detected via this technique, their locations, the identities of the active site groups, and the type of structure (free enzyme, a DNA complex, a product complex) have been used to make arguments about the number of metal ions involved and their roles in the reaction (Fig. 2).^4,9,12,13 Some of the structures used in these debates are summarized in Table 1, and other similar tables can be found in ref. 4,13–15.

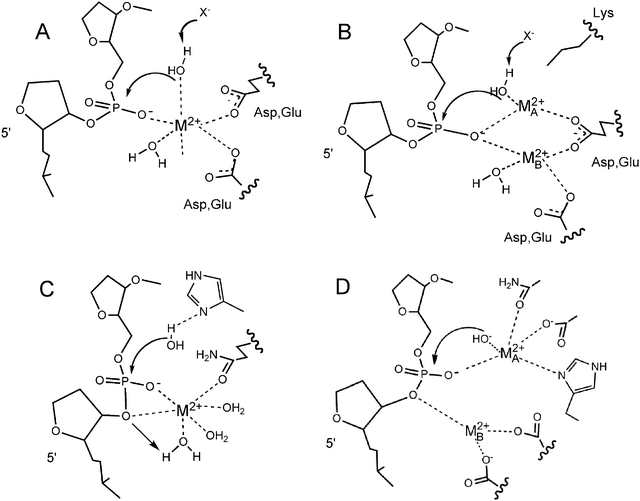Fig. 2 Examples of general metal ion driven mechanisms in protein metallonucleases. (A) One-metal ion mechanism in an acidic active site (after EcoRI endonuclease⁴); (B) Two-metal ion mechanism in an acidic active site (after EcoRV endonuclease⁴); (C) One-metal ion mechanism with His as a general base (after I-PpoI⁷²); (D) Two-metal ion mechanism with active site His (after APE-1 endonuclease¹⁶).

Table 1 Selected metallonuclease crystal structures^a

Enzyme	Metal ion	PDB	Reference
a Other similar tables can be found in ref. 4,13–15. b For a comprehensive list of EcoRV structures, see ref. 14.
EcoRV	Mg(II), Mg(II)	1RVB	62
EcoRV^b	Mn(II), Mn(II)	1SX8	9
PvuII	Ca(II), Ca(II)	1F0O	36
3′5′exo Klenow	Zn(II), Mg(II)	1DPI	2
RNase H E. coli	Mg(II)	1RDD	18
RNase H HIV RT	Mn(II), Mn(II)	1HRH	63
RNase H B. haldurans	Mg(II), Mg(II)	1ZBL	64
Tn5 5′exo	Mn(II), Mn(II)	1EXN	65
TnsA	Mg(II), Mg(II)	1F1Z	66
Tn5	Mn(II), Mn(II)	1MUS	67
MutH	Ca(II), Ca(II)	2AOR	68
Group I intron	Mg(II), Mg(II)	1ZZN	69
I-CreI	Ca(II), Ca(II)	1G94	12
Endo IV	Zn(II), Zn(II), Zn(II)	1QTW	70
Hammerhead Rzm	Mg(II)	300D	71
Ape1	Pb(II), Pb(II)	1E9N	16
BamHI	Ca(II), Ca(II)	2BAM	45

---

Where there is more than one crystallographically defined metal ion binding site, two-metal ion mechanisms have been favored.^2,9,15 Indeed, multiple mechanisms can be drawn in which metal ions can participate in some or all of the mechanistic steps in chemically reasonable ways. In active sites that feature amino acid sidechains that can serve as nucleophiles and/or general bases (i.e., His and/or Tyr),¹⁶ a second metal ion could be mechanistically gratuitous and arguments for a one-metal ion mechanism are easily defended.^10,17

Old problem

The issue is more complex for the more classic, older crystal structures of nucleases (e.g. 3′5′ exonuclease of Klenow fragment and EcoRV endonuclease, Fig. 2B). These metallonuclease active sites do not feature convenient nucleophiles and/or general bases among sidechains. Instead, these are rich in acidic residues, which are ideal ligands for multiple Mg(II) ions but are generally poor candidates for other mechanistic functions in phosphodiester hydrolysis. In these active sites, the mechanistic burden on a single metal ion is relatively heavy, and the frequency of more than one metal ion in crystal structures of this subclass of nucleases is high.¹⁵ In these enzymes, arguments for the importance of two metal ions (one for nucleophile activation (Metal A) and one for assistance in leaving group departure (Metal B)) would appear to be more convincing.

However, as pointed out recently by Pingoud et al.,¹³ enzymes from this group that are closely related structurally have been crystallized with differing numbers of metal ions. Among multiple examples, EcoRI endonuclease has always crystallized with one metal ion and BamHI, a close structural relative, with two metal ions.¹³ Similarly, the RNaseH domain of reverse transcriptase crystallized with two metal ions; RNaseH from E. coli contains only one metal ion.¹⁸ While there are some differences in conserved active site groups among these enzymes that might be used to defend one- or two-metal ion binding sites, clearly there are limits to the interpretation of structures when it comes to mechanism.

The most stubborn question remaining is this: For those systems that do not have active site amino acids that ionize in the physiological range, how many metal ions does it take to cut a nucleic acid? While two-metal ion mechanisms have enjoyed a lot of support historically,^2,9,12 there has been an increase in the sophistication of experimental approaches to this question in the past couple of years and a concomitant shift in favor of one-metal ion mechanisms in this class of enzyme. In this scenario, only one metal ion is required with the second metal ion modulating the activity, rather than two being absolutely required, even in those systems that lack mechanistically handy amino acid sidechains in the active site. This view is based on recent studies that demonstrate an increased level of sophistication. While these techniques are not by themselves new to biochemistry, they are relatively new to the metallonuclease field. It is the aim of this review to survey and comment on these efforts.

Metal ion dependence of cleavage activity

Observing the metal ion concentration dependence of cleavage kinetics is really the most direct experimental doorway to assessing metal ion involvement in a nuclease reaction. It is here that we directly observe the metal dependent productivity of the reaction. Clearly this is not a new strategy; examples of this type of experiment go back a decade or more and have been briefly reviewed.⁴ However, there is a wide range of sophistication to these experiments and there has been a clear trend toward more complex analyses in recent years. This has resulted in new mechanistic insights.

The most basic analysis of the metal ion concentration dependence of activity (k_cat, k_obs) is the analysis of the shape of this behavior. For example, noting more than one concentration phase (implying two classes of sites) or sigmoidicity (reflective of cooperativity), often in the form of a Hill coefficient, has been used to build mechanistic arguments. Historically this has been the most common level of interpretation for data of this form, and a number of examples have been cited in an earlier review.⁴ Slightly more sophisticated is fitting these data to models that express the cleavage rate constant as a function of metal ion binding constants, which may or may not be known a priori. Two older examples from the ribozyme field showed advanced sophistication and are the precursors to global analysis. In a detailed kinetic study of the Tetrahymena group I ribozyme,¹⁹ various cleavage experiments are used to estimate metal ion binding constants. In an RNase P study, both kinetic and equilibrium Mg(II) binding measurements were used to flesh out a reaction scheme.²⁰ Two older examples from the protein metallonuclease literature also illustrate the strategy. The first is a study of EcoRV endonuclease,²¹ a longstanding favorite two-metal ion mechanism enzyme. The authors work with active site variants and Mn(II) in addition to wildtype and Mg(II), which are all used to evaluate apparent sigmoidal dependence of kinetic constants on the metal ion concentration. This investigation is detailed, but in this system the metal ion binding constants have yet to be determined via independent experiment. This is unfortunate, since relatively small changes in these values can affect this kind of analysis in palpable ways.^22,23 These authors argue that two metals are involved in enzyme–substrate interactions, but both are not involved in catalysis. The second is of the 3′-5′ exonuclease activity of Klenow by Cowan and coworkers.²⁴ Although this study was less detailed, metal ion binding constants were measured in separate experiments and used as input for the one- and two- metal ion mechanism models. Based on their data, the authors argue for a one-metal ion mechanism for this system. This result runs counter to the favored two-metal ion mechanism for this activity.^2,25

A very recent example of a similar analysis has been published for T5 flap endonuclease,²³ an enzyme crystallized with the characteristic two metal ions.²⁶ First, both log-log plots of k_cat and K_mvs. Mg(II) concentration both yield slopes of 2, and k_cat/K_mvs. Mg(II) concentration yields a slope of 3. These data are fit to multiple models that feature metal ion binding constants, which typically converge to one tighter Mg(II) site (K_d, less than 1 mM) and one weaker Mg(II) site (above 2 mM). The authors argue for the involvement of two metal ions for optimum rate acceleration, with the involvement of a third, more weakly binding (above 3 mM) metal ion that could be replaced by Ca(II) (see below). This study is clearly an example that is counter to the trend toward one-metal ion mechanisms for metallonucleases.

Ca(II) doping studies

A variation on the above kinetic experiment is the effect of a second metal ion (usually Ca(II)) on the Mg(II) or Mn(II)-dependent activity of the nuclease. When a stimulation of activity is observed (typically at low concentrations), the most common interpretation is that two equiv. of metal ions are required for the reaction, and further, a metal of slightly different characteristics (Ca(II) is larger and has different coordination preferences relative to Mg(II)) can be tolerated in one metal ion binding site. This implies a more secondary, electrostatic role for what is assumed to be Metal B. The degree of sophistication of these studies varies widely, ranging from single timepoint reactions to global analysis.²⁷

The best cited Ca(II) doping study is of EcoRV endonuclease.²⁸ When this activity is supported by Mn(II), Ca(II) stimulates steady state reaction rates. Steady state, Mg(II)-dependent EcoRV activity toward noncognate DNA was stimulated at low Ca(II) and inhibited at higher Ca(II) concentrations (>2 mM).²⁸ Presumably Ca(II) successfully competes with Mg(II) under these conditions, resulting in an inactive complex. This work inspired less detailed studies of endonuclease V,²⁹ ApeI endonuclease,¹⁶ and TaqI endonuclease,³⁰ all of which exhibit stimulation of activity upon doping with Ca(II).

There are three interesting recent applications of this experiment. The first is a survey study of a number of enzymes of the EcoRI family (BamHI, MboI, NgoMIV, PspGI, SsoII). Collectively, the authors present evidence of reaction stimulation by Ca(II), mostly at high concentrations (in excess of 10 mM). This points to a very weak ancillary Ca(II) site, which the authors argue is regulatory.¹³

The central issue with the interpretation of such Ca(II) doping experiments is that what is observed depends on the relative affinities of each metal ion for each site (which determines the distribution of multiple enzyme–metal ion species), and the extent to which each metal ion supports cleavage. This makes it possible to have data supporting the involvement of multiple metal ions in a reaction without seeing stimulation by Ca(II). Ca(II) inhibition was also recently studied in T5 flap endonuclease²³ and PvuII endonuclease.²⁷ In both cases, Ca(II) was not found to be stimulatory, but other kinetic evidence for the influence of a second Mg(II) ion on the reaction was reported.^23,31 This issue is examined more systematically using global kinetic analysis for PvuII endonuclease (see below). However, at the level of simpler kinetic experiments, if one sees stimulation by Ca(II), it can be quite persuasive. However, in its absence one cannot draw any conclusions regarding the involvement of a second metal ion without a much more detailed analysis.

Global analysis of reaction schemes

While the above examples are more detailed than many routine metallonuclease studies, there are some important limitations. One is the certainty with which one knows the metal ion binding constants. Small differences in these constants can have an effect on fits^23,27 and thus comparisons of fits to various models. The other issue is working with steady state parameters. k_cat is strongly influenced by the rate limiting step, which is often not a chemical step but a physical step like product release.²² In addition, K_m is a function of 3 parameters (association and dissociation rate constants for substrate binding, and k₂, the rate constant for the chemical step) and can carry large error.²³ These difficulties provide strong motivation for global analysis of single turnover rate constants.

Global analysis involves the simultaneous fitting of multiple data sets (often time dependent) to obtain unknown parameters. For enzyme kinetics, these data are often of the form of product concentration vs. time as a function of concentration of a species upon which the rate depends (usually substrate and/or an effector). In single turnover kinetics, the enzyme concentration is in large excess of that of the substrate and the rate is independent of the former value, i.e., the reaction becomes pseudo-first order. This is preferred over steady state kinetics because the steps for product release can be neglected, since this process does not contribute to the observed rate under these conditions. Often trial experiments must be performed to establish conditions under which the observed rate reflects the chemical step and not some other process upon which the rate depends (e.g. protein oligomerization, ligand binding). With these issues in mind, this technique has a convincing history in the enzyme kinetics community^19,20,32 and can be applied with confidence. Finally, this technique reduces the number of rate constants needed for the fit. This is an important feature, as the greater the number of unknown constants, the greater the uncertainty in fits and parameter determinations.

Data are fit to a series of differential equations that are derived from reaction schemes (Fig. 3) to yield unknown rate constants. There are a number of computer programs (e.g., KinTekSim, DynaFit,³³ and Berkeley Madonna) that facilitate this process as well as the actual fitting and simulation of data. Finally, one inputs the values of known rate constants and makes initial estimates of unknown parameters. Since reaction schemes usually involve a large number of steps and pathways, the accuracy of this process is greatly aided by the inclusion of parameter values obtained via independent experiment. Examples can include association and dissociation rate constants for ligand binding and the rate constant for the chemical step. By comparing fits to variations in mechanistic schemes, one can determine which pathways reasonably represent the data. For example, does substrate bind enzyme in the absence of an effector, or is the enzyme active when only one of two metal ion binding sites are occupied? In making these judgments, it is helpful to utilize uncertainty in an individual parameter as well as the overall standard deviation relative to another model, and the ability of the model to reproduce the data (simulation; see below). Also useful is whether or not the value of a parameter obtained from the fit is reasonable given what is known about the system (e.g., the right order of magnitude). Finally, with multiple unknowns, it may not be possible to discriminate among alternate models, particularly if what is varied is not part of a critical pathway.

Fig. 3 General reaction scheme for a metalloenzyme. This example features a system that could be dependent upon more than one metal ion for substrate binding (steps 0, 2, and 4) and/or cleavage (steps 5 and 6). Product release steps 7, 8 and 9 can be eliminated via the application of single turnover kinetics.

Global analysis has been in use in ligand binding, spectroscopy and enzymology studies for many years.^32,34,35 In 2008, Xie et al. conducted a detailed study of PvuII endonuclease, a homodimeric restriction enzyme that has been crystallized with two Ca(II) ions and DNA.³⁶ Here global analysis of single turnover data and independently determined binding and cleavage parameters were used to establish the following mechanistic features of this reaction: First, the enzyme prefers to bind metals first, then the substrate. This result has its roots in a study of the metal ion dependence of DNA binding (using Ca(II)), in which it was noted that association rate constants for DNA binding are 6000-fold slower in the absence of Ca(II) than at 10 mM.³⁷ Other central insights emerge from the fact that with this analysis, it is possible to dissect out the contributions of a species containing only one metal ion per active site (EM₂ and EM₂S, where E is a homodimer and S is duplex DNA) to substrate binding and cleavage. From this we learn that while Ca(II) supports higher affinity for DNA via a faster association rate constant, for both Ca(II) and Mg(II), individual metal ions contribute nearly equally to DNA binding affinity. This finding is supported by X-ray crystal structures that show the scissile phosphate as a bridging ligand between two metal ions.³⁶ And finally, the enzyme species in which one metal ion occupies each active site is indeed capable of cleaving DNA (EM₂S, k = 0.01 s⁻¹); however, when two metal ions are present per active site (EM₄S), the rate constant is 100-folder higher (1 s⁻¹). Put another way, a second Mg(II) ion stimulates cleavage activity. This an important result, because for the first time individual metallonuclease cleavage rate constants are established for two enzyme species that exist as a dynamic mixture in solution. There is simply no other way to assess the activity of the EM₂S species (i.e., one metal per active site), and it shows that at least for PvuII endonuclease, widely perceived as a “two-metal ion mechanism” enzyme, only one metal ion is strictly required for DNA cleavage. As for assigning metal ions to specific sites or locations in the active site, no kinetic method alone is capable of providing this information. One is obligated to assume that when there is one metal ion per active site, it occupies the A site, that is, the site that is considered to be responsible for nucleophile and transition state stabilization (top metal in Fig. 2B).²²

Other pieces of useful mechanistic information also emerge from this kind of study. Capitalizing on the constants that resulted from the above analysis, the same authors were able to test models of metal ion binding cooperativity.²² Indeed, as has been surmised from an earlier Ca(II) binding study of PvuII³⁸ and recently noted for T5 flap endonuclease,²³ the metal ion binding sites are either weakly positively cooperative or simply independent. This is somewhat surprising, as chemical intuition would suggest that two proximal positive charges would represent some interacting or cooperative effects, possibly negative. However, other factors like the local negative charge must mitigate this.

Finally, global analysis was used to examine the pathways to product release in the PvuII endonuclease system.²² It has long been established that product release is rate limiting among metallonucleases.²² Of greater mechanistic interest is the role of metal ions in this process and their stoichiometry. This has been used to make arguments for the movement of metal ions during the course of the metallonuclease reaction.¹¹

One can reasonably expect that the affinity for cleavage products would not be high in a metallonuclease, and certainly no stronger than that for nonspecific DNA among those sequence-specific metallonucleases. Using equilibrium experiments, the authors establish that this is the case for PvuII endonuclease, with affinities estimated to be in the low micromolar range. Interestingly, this estimate could be obtained only in the absence of metal ions. In their presence, no enzyme product complex could be detected using fluorescence anisotropy. This suggests that product affinity is discouraged by metal ions. Steady state data, which is acutely sensitive to rate limiting processes like product release, were then globally fit to alternate models for product release. From this analysis it was clear that metal ions are retained in the active site when product is released.

All of the aforementioned analyses on PvuII endonuclease were leveraged to dissect the behaviors of various species in Ca(II)-doped reactions. When there are two different metal ions in the reaction and two potential sites, the number of species increases dramatically. Instead of relying on statistics and some simplifying assumptions about differential metal ion affinities (the more common strategy in this type of experiment^28,29), global analysis can be applied to address questions regarding which enzyme species bound simultaneously by both Mg(II) and Ca(II) are active, if any, and what those characteristic cleavage rate constants are. The input data in this case are progress curves obtained at a variety of Mg(II) and Ca(II) concentrations, with both being varied in turn. As mentioned earlier, PvuII is one of the metallonucleases for which Ca(II) does not stimulate activity at either or low or high concentrations. An additional complication is that PvuII binds Ca(II) with two different binding constants, 120 μM and 2 mM. This required a series of trial fits to establish which site, A or B, bound Ca(II) more tightly. With that established, fits were used to used to determine which species were populated under what conditions and which were active. Indeed, due to the high affinity of site (B) for Ca(II), only one mixed metal enzyme species dominates, and its activity is comparable to that when only one Mg(II) is present per active site (presumably at site A). This is the first analysis that dissects the behaviors of individual metallonuclease species that exist as dynamic mixtures across wide concentration ranges.

While the power of global kinetic analysis cannot be disputed, there are multiple reasons why this approach has not enjoyed widespread use thus far: one is that it requires high quality kinetic data. For nucleases, these experiments are quite tedious. There are no convenient real-time assays for nucleases that reflect only the chemical step, leaving us to quench reaction timepoints, separate reaction components via electrophoresis, and analyze digitized gel images. This commitment of time and labor eliminates casual interest in the experiment. While obtaining benchtop rates may not be so demanding for most, determining fast single turnover rates often involve an expensive and complicated quench flow apparatus. Second, obtaining an array of rates in any time regime is time consuming, especially when the assay is discontinuous. Third, it requires a great deal of comfort with curve fitting programs, simulations, and plotting of data. Fourth, the more independently determined constants, the more convincing the testing of models, and the easier it is to discriminate among models as it reduces the number of unknowns in the global fit. There are only a handful of enzymes for which extensive thermodynamic and kinetic data already exist.

Simulation of experimental data

Simulating experimental data is a valuable resource that has historically been underutilized in the metallonuclease mechanism. It is useful in establishing the limits of an experiment, evaluating mechanistic models (binding or kinetic), and characterizing species distributions under any experimental conditions. Fortunately, the recent metallonuclease literature indicates an increased enthusiasm for this approach. Simple applications to evaluate alternate metal ion binding models appear in a couple of studies of PvuII endonuclease.^39,40 Xie et al.^22,31 utilized simulations to determine the best reaction scheme models in the global analysis of the PvuII reaction. Put simply, how well does a model reaction scheme with particular input or fit parameters simulate experimental data? An example is featured in Fig. 4.³¹ The parameters obtained from the fit were used to simulate experimental data, which was then plotted and compared to the experimental data. In this fashion, it is easy to determine which model(s) best represent the data.

Fig. 4 Simulation of kinetic data using alternate kinetic models. Single turnover rate constants k_obsvs. [Mg(II)] for PvuII endonuclease. Experimental data are indicated with closed circles. Data points simulated from models A1 (two metal ions are necessary for cleavage) and B1 (enzyme is active with both one and two metal ions per active site) are as indicated. This is one means by which models can be evaluated. Taken from ref. 31 and reprinted with permission from the American Chemical Society.

More recently, Pingoud et al.¹³ made some basic assumptions to simulate the metal ion dependence of Ca(II)-stimulated behavior. They noted that Ca(II)-stimulated steady state cleavage activity could be simulated when Ca(II) binding into site B enhanced affinity for Mg(II) in site A. This result is counter to that observed on PvuII and T5 flap endonuclease, where in both cases metal ion binding sites were not found to be significantly cooperative, but consistent with molecular dynamics calculations included in the same paper.

A useful application of simulations appears in the PvuII endonuclease study of Ca(II) doped reactions.²⁷ Using the results of the fits, species distributions and their individual contributions to activity were constructed from the determined parameters and model reaction schemes (Fig. 5). It is here that certain realities emerge. Predictably, if binding constants are weak, species are poorly populated. An example in this case is EC_2AM_2BS, where Ca(II) occupies the A site with weak affinity. Since site B binds Ca(II) more tightly, this species is basically not only inactive, it does not form appreciably, either. Simulations were also used to determine what rate constants could be responsible for an observed stimulation of metallonuclease activity by Ca(II). Interestingly, the rate constant for cleavage by a mixed species is much more critical than whether one is observing steady state vs. single turnover cleavage behavior. Further, weaker affinity for Ca(II) can blunt or obscure an observation of stimulated activity, which is the likely reason why stimulation by Ca(II) is not observed in some so-called “two-metal ion mechanism” systems.

Fig. 5 Distribution of species and contributions to product. Plots represent PvuII endonuclease cleavage data simulated at 5 mM Mg(II) as a function of Ca(II) concentration. The simulation is based on parameters obtained from applying to the data a model in which one enzyme–Mg(II)–Ca(II) species is active and site B is the strong Ca(II) site. (A) Enzyme–metal–substrate species distribution at 10 s. (B) Enzyme–metal–substrate species distribution at 50 s. (C) Percent contribution to product at 10 s. (D) Percent contribution to product at 50 s. Red EC_2AC_2BS; green EM_2AS; blue EM_2AC_2BS, black EM_2AM_2BS. The remaining species are not visible on this scale. Reprinted with kind permission from Springer Science+Business Media: J. Bioinorg. Chem., Characterizing Metalloendonuclease Mixed Metal Complexes by Global Kinetic Analysis, 15, 2010, p. 544, Charulata B. Prasannan, Fuqian Xie, and Cynthia M. Dupureur, Fig. 8, © SBIC 2010.

And finally, simulation can be used to provide insights into the two-metal ion mechanism. In the PvuII study²⁷ (Fig. 5) and a recent survey of EcoRI family enzymes,¹³ weak metal ion binding constants for Ca(II) and Mg(II) and simulation were used to determine the relative populations of species of interest, particularly as they might exist in a cell. If a stimulatory Ca(II) binds at concentrations beyond 10 mM, the case for a number of EcoRI family enzymes, this is not physiologically relevant. The same can be said of the EM₄S species of PvuII: this species exists in very low abundance at cellular Mg(II) concentrations (low mM; Fig. 5). The implication of this is that the most abundant species is a single metal ion species. For PvuII endonuclease, this is a slow species. However, metallonucleases are not known for their speed, nor does it appear to be necessary for their in vivo function. Faster, more efficient enzyme species, like EM₄S and the Mg(II)–Ca(II) species of the EcoRI family, exist only on the bench.

Computational studies

Like complex kinetic analysis, computational techniques were applied in the metallonuclease field over a decade ago,⁴¹ displayed a quiescence during the height of crystallographic analysis, and then recently resurged with fresh mechanistic insights.

With regard to the issue at hand, the most compelling are studies that examine the energetics of one- and two-metal ion mechanisms. A recent fundamental look at the problem comes from recent calculations of potential energy surfaces, presented by Kamerlin and Wilkie as More O'Ferrall–Jencks plots for phosphomonoester hydrolysis in the absence and presence of metal ions.⁴² A dissociative mechanism is most favorable when no metal ion is present. More interesting are the differences between one- and two-metal ion mechanisms. While a dissociative mechanism is clearly more favorable for the two-metal ion mechanism, when only one metal ion is present, a concerted mechanism is most favored. This is in spite of the high energy barrier for this mechanism, which the authors attribute to the position of a single metal ion interfering with either nucleophilic attack or leaving group departure.

More recently, Imhof et al. explored both associative and dissociative phosphodiester mechanisms for both a model Mg(II) complex and the enzyme EcoRV using QM/MM and MD. ⁴³ In contrast to the above results with phosphomonoesters, the associative mechanism was found more favorable for the model complex, while dissociative character was found to be more favorable in the EcoRV reaction. The authors state that due to the enzyme active site environment, the inversion of configuration so often seen in phosphoesterases can be observed in mechanisms with either character. The authors did not examine the impact of metal ion stoichiometry in these processes.

The observations of Kamerlin and Wilkie are based on a simple model in which the metal ion does not move, a possibility introduced a number of years ago based on EcoRV endonuclease crystal structures.^6,9 This mechanism is considered in molecular dynamics (MD) studies of the BamHI endonuclease structure,⁴⁴ an enzyme that crystallized with two Ca(II) ions and DNA⁴⁵ and for which the mechanism has been debated. In an ironic twist on a proposed two-metal ion mechanism, Fuxreiter and colleagues interpret their results as indicating a pathway for one metal ion, beginning with nucleophile activation at the commonly discussed site A, a ground state position (Fig. 6). During the course of the reaction, the metal ion moves along a trajectory to site A′, less than 1 Å from site A, and then to site M. This position is between the A and B sites and is a favorable location from which to contribute to transition state stabilization. Regarding Metal B, they noted a great deal of variability for the position of this metal ion in various enzymes and variants thereof, and propose that this second metal ion is regulatory, serving to attenuate activity rather than be critical for it.

Fig. 6 Summary of metal ion trajectory in BamHI endonuclease. Mg(II) moves from site A to A′ (less than 1 Å away) to M during the course of the reaction. This pathway is based on calculations described in ref. 44.

A similar proposal emerges from a study of the repair enzyme APE-1 endonuclease.¹⁷ For our purposes, it should be noted that this enzyme features one active site His residue, making it electrostatically distinct from the largely acidic active sites of the classic metallonucleases with two metal ion binding sites. Working with a variety of crystal structures of this enzyme, the authors examined the positions of metal ions during the reaction and identified two general metal ion binding sites (A and B). When two metal ions fill these sites, they are repulsive in the calculations, moving far enough away from each other to preclude a commonly accepted condition of proximity (4 Å) for simultaneous interaction with the scissile phosphate.^4,11 Based on this result, the authors propose that one metal is required and moves along a trajectory during the reaction, similar to that proposed by Fuxreiter and colleagues. The idea of metal ion movement is echoed in the aforementioned study by Imhof et al., in which the movement or relocalization of metal ions is a dominant theme, and the second Mg(II) appears to have a far less critical role than the first.⁴³

In another computational study of BamHI endonuclease,⁴⁶ QM/MM calculations were used to determine the activation barriers for variations on the mechanism. This study appears to have been inspired by Warshel's earlier work with the exonuclease domain of the Klenow fragment of DNA polymerase I.⁴¹ More specifically, the source of nucleophile activation was varied to involve an amino acid sidechain (Glu 113), an active site water molecule, or water from bulk solution. The authors report that the last scenario was most energetically favorable, lessening the extent of metal ion involvement in the reaction. Secondly, they calculated activation barriers when metal ions are located at sites A and B. Interestingly, whether a metal ion is present in site B affects the energy barrier very little; if site A is not occupied, the catalytic power of the enzyme is severely compromised. This is basis of the authors' proposal that the second metal ion at site B in BamHI endonuclease is “auxiliary”.⁴⁶

Recent studies with ribozymes (metallonucleases composed of RNA) provide an interesting contrast to these conclusions. Car–Parrinello DFT (density functional theory) calculations were applied to a simple ribozyme model to evaluate the contributions of each metal ion in a two-metal ion mechanism. Results indicate that both metal ions make significant contributions to lowering the activation barrier, and that additional catalytic power comes from the presence of an active site hydroxyl group.⁴⁷ Karplus also addressed this issue by performing DFT calculations on a hammerhead ribozyme model. Energies were evaluated at several points along the reaction coordinate for pathways involving no metal, one metal, and two metal ions. The energy barrier for nucleophile activation is highest for a metal ion-independent mechanism and it is higher for one metal than for two.⁴⁸ These insights seem to run counter to the trend toward one-metal ion mechanisms among the protein metallonucleases. While the explanation for this is probably complex, the fact that ribozymes are composed entirely of polyanionic nucleic acid is likely to be a significant factor.

Since metal ion occupancy is critical for the proposed mechanisms, metal ion binding affinities are of earnest interest. Unfortunately, experimental data on various metallonucleases remains limited, probably due to the technical demands of the measurements.⁴ This led to a computational approach to understanding metal ion binding site occupancy for BamHI endonuclease. QM/MM methods were used to calculate the free energies of moving active site metal ions from specific active site positions to bulk solvent.¹³ The data support two general conclusions: Metals are held more loosely in site B, and Mg(II) in site A and Ca(II) in site B is the most stable configuration. While this dovetails nicely with cleavage kinetic observations in this paper, it is not a universal observation: In PvuII endonuclease, both equilibrium and kinetic data collected experimentally indicate that in this system Ca(II) is held more tightly in site B when Mg(II) is present.²⁷ When Mg(II) is the only cofactor, the K_ds for the sites are basically interchangeable and binding is not cooperative.²²

Another area of computational studies of metallonucleases involves the calculation or prediction of pK_as of active site groups. This behavior is indeed relevant to the one- vs. two-metal ion mechanism debate, as this information clarifies metal ion contributions to the mechanism. Fuxreiter and coworkers utilized the protein dipoles/Langevin dipoles (PDLD/S) method, the EVB/FEP method, QM/MM calculations and MD simulations of reaction energy barriers to support an extrinsic mechanism that refers to introduction of OH⁻ into the active site from bulk solution. The nucleophilic water is further stabilized by metal ion ligation.^46,49 Most recently, Xie et al. used the linear form of the Poisson Boltzmann equation to calculate the pK_a of nucleophilic waters in a subclass of metallonucleases that feature a conserved Lys group in the active site (PD…(D/E)xK). Surprisingly neutral pK_as were noted. They subsequently used the tool to assess the contributions of the conserved Lys and Metal A to nucleophile activation.⁵⁰ More specifically, by noting the increase in the water pK_a when either group is neutralized and/or moved, they showed that in a number of these enzymes (PvuII, EcoRV, T7 endonuclease I, TnsA, and NgoMIV endonuclease), both groups contribute to stabilization of the nucleophile. Studies of model metal complexes featuring a pendant amine in a mononuclear Zn(II) complex provide experimental support for this conclusion.⁵¹ The pK_a of the nucleophile is reduced by 2 log units in complexes featuring the pendant amine.

In a recent QM/MM study of EcoRV endonuclease,⁴³ the conserved Lys was characterized as important in stabilizing the metaphosphate intermediate for nucleophilic attack in an associative pathway, while Asp90 was characterized as the general base. While proposals that acidic groups serve in this role are almost always controversial, the idea that this group could be involved in the catalytic step has some support: Horton and Perona note that metal ion movement in their model could alter the pK_a of this group in a direction favorable to this proposal.⁹ Thus it would appear that there is conflicting computational support for the role of the conserved Lys group obtained from using different approaches. Clearly additional studies would be of great interest.

Putting it together

The most informative experimental data on the one- vs. two-metal ion mechanism issue is global kinetic analysis that shows that PvuII endonuclease, an enzyme with two metal ion binding sites, can cut DNA with one metal ion, and the rate enhancement above the uncatalyzed reaction with one metal ion is just two orders of magnitude short of that observed when the second metal ion is present³¹ (Table 2). Given that a rate enhancement of 10¹⁷ over the uncatalyzed reaction is estimated to be required to cleave DNA in a few minutes,³ this difference is quite small. Stimulation of Mg(II)-supported activity by Ca(II) observed in a number of systems lends additional support for a second, activity-modulating metal ion. This latter observation requires at least two metal ion binding sites and, unless three metal ions are involved, a single metal ion for the unmodulated activity. Finally, there are multiple computational studies that support a mechanism with one critical metal ion with a second, ancillary metal ion to modulate activity. A recent crystallographic analysis provides additional support.¹⁰ All of these conclusions leave room for the possibility that a second metal ion makes the reaction more efficient, even if the conditions are in vitro rather than in vivo in nature.

Table 2 Summary of kinetic constants comparing protein and artificial metallonucleases

Agent	k obs, s^−1	k/M^−1 s^−1
a Toward 2-hydroxypropyl-4-nitrophenyl phosphate. See ref. 52. b Single turnover rate constant for cleavage of target DNA. ref. 31. c Second order rate constant obtained by dividing kobs by Km (30 nM and fairly constant across a wide range of Mg(II) concentrations^31). kcat is limited by product release under multiple turnover conditions and therefore not useful here.
Zn(L1OH)	0.1^a	0.25
Zn2(L2O)	5e-3^a	0.0013
PvuII, one Mg(II)	0.01^b	3.3e5^c
PvuII, two Mg(II)	1.1^b	3.3e7^c

---

While studies of synthetic model metal complexes are very seldom cited in this literature, here it is quite relevant to do so. There is plenty of evidence that, all other things being equal, dinuclear complexes are generally more efficient hydrolytic agents than mononuclear complexes.^52,53 When targeting DNA and the more labile RNA, the vast majority of model complex literature focuses on dinuclear complexes.^3,54 From the standpoint of catalytic power, the advantages of two over one metal ion are clear in these studies: In a study of Zn(II) complexes cleaving phosphoesters, the fold difference in second order rate constants for mono and dinuclear Zn(II) complexes is two hundred⁵² (Table 2). Based on their analysis, the authors attribute this to differences in transition state stabilization and nucleophile activation. Other examples can be found in the same literature.⁵⁵ For PvuII endonuclease, the difference in the rate constants (when two Mg(II) ions are present vs. one) is about 100-fold. Of course, with one metal ion binding occupied, PvuII endonuclease is still a better cleavage agent toward the very stable DNA than the above dinuclear Zn(II) complex toward a more labile chromogenic phosphoester by about 10-fold.

Can nucleic acids be hydrolyzed with one metal ion? Yes, they can, as demonstrated by the activities of both natural and artificial metallonucleases. Therefore the second metal ion is not necessary to achieve that goal, but can clearly increase the rate in a measurable way in some systems. But it is important to note that in many cases, the second site is not likely to be occupied to an appreciable extent in a cell. For these systems, a two metal ion enzyme complex is a largely an in vitro species.

This being the case, why then are two sites so often detected in metallonucleases, particularly in those with a wealth of acidic active site groups? Here is where the proposal of metal ion movement is a welcome reconciliation. In an enzyme active site, which architecturally is a cloistered pocket of participating chemical groups, it is certainly possible for one metal ion to occupy more than one site along the reaction coordinate, moving as the reaction proceeds, without diffusing away. If the two sites are positions in a trajectory, then it is more plausible for one metal to perform the functions of more than one metal ion binding site. This is obviously not possible in a model metal complex, where metal ions must serve dual roles in structure and catalysis. Metal ion movement was first alluded to by Fothergill,⁴¹ proposed in detail by Horton and Perona,⁹ and has been recently reviewed.^4,6

If one accepts this explanation, then what about the enzymes for which there are three metal ion binding sites identified in one structure? While not as abundant as enzymes crystallized with two metal ions, there are a number of metallonucleases and other related hydrolases which crystallized with three metal ion binding sites (alkaline phosphatase,⁵⁶ nuclease P1,⁵⁷ I-CreI endonuclease,⁵⁸ endonuclease IV,⁵⁹ among others).

Once the discussion moves from two to three metals, the mechanism becomes more complex for a variety of reasons. I-CreI endonuclease has three active site metal ions, but one is shared between two active sites, and as such should be considered a variation on the two-metal ion structures.⁵⁸ As exemplified by endonuclease IV,⁵⁹ some of these enzymes have more than one activity, which may necessitate a more complex active site. Next, many of these enzymes utilize Zn(II). Unlike Mg(II), Zn(II) can often be a structural cofactor, binding Cys and or His residues in a tetrahedral geometry, and is almost always held more tightly than Mg(II). This appears to be the case for nuclease P1, the structure of which features three active site Zn(II) ions: the scissile phosphate is a bridging ligand for two of these cations; the third is off to the side, held by 2 His residues and one acidic group,⁵⁷ a configuration more typical of a structural and/or electrostatic role than a direct catalytic role and certainly reminiscent of the one-metal ion metallonuclease structures mentioned in the introduction. Finally, as lately computational methods and global kinetic analysis have been applied to two-metal ion nucleases, these issues are even less developed in these three-metal ion systems. One recent study of alkaline phosphatase proposes a three-metal ion mechanism based on a combination of crystallographic analysis and site-directed mutagenesis,⁶⁰ which incidentally is the same experimental basis of the three metal ion sites located in EcoRV endonuclease.⁹ This is supported by another study of alkaline phosphatase active site variants.⁶¹ The involvement of three metal ions has been proposed for T5 flap endonuclease based on analysis of steady state kinetics.²³ As for the application of binding and kinetic data to various models tested using global analysis of three metal ion systems, this will be challenging, as it is very difficult to collect data of high enough qualify to discriminate between mechanistic models involving two equiv. of cofactor vs. three equiv. Based on this evidence, it is not prudent to extend recent conclusions about the involvement of two metal ions in metallonculease active sites to those with three.

Finally, applications of the aforementioned tools in the metallonuclease literature assure us that interest and motivation in this area is not waning, despite its long history. It seems a safe prediction that additional studies will continue to emerge to lend unique and critical mechanistic insight to this interesting class of metalloenzymes.

References

1. N. Mishra, Nucleases-Molecular Biology and Applications, Wiley & Sons, Hoboken, 2002.
2. T. A. Steitz and J. A. Steitz, A general two-metal ion mechanism for catalytic RNA, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 6498–6502.
3. N. Williams, B. Takasaki, M. Wall and J. Chin, Structure and Nuclease Activity of Simple Dinuclear Metal Complexes: Quantitative Dissection of the Role of Metal Ions, Acc. Chem. Res., 1999, 32, 485–493.
4. C. M. Dupureur, An integrated look at metallonuclease mechanism, Curr. Chem. Biol., 2008, 2, 159–173.
5. J. A. Cowan, The Biological Chemistry of Magnesium, VCH, New York, 1995.
6. C. M. Dupureur, Roles of Metal Ions in Nucleases, Curr. Opin. Chem. Biol., 2008, 12(2), 250.
7. A. K. Aggarwal, Structure and function of restriction endonucleases, Curr. Opin. Struct. Biol., 1995, 5, 11–19.
8. E. A. Galburt and B. L. Stoddard, Catalytic mechanisms of restriction and homing endonucleases, Biochemistry, 2002, 41, 13851–13860.
9. N. C. Horton and J. J. Perona, DNA Cleavage by EcoRV endonuclease: Two metal ions in three metal ion binding sites, Biochemistry, 2004, 43, 6841–6857.
10. W. Yang, An equivalent metal ion in one- and two-metal-ion catalysis, Nat. Struct. Mol. Biol., 2008, 15, 1228–1231.
11. W. Yang, J. Y. Lee and M. Nowotny, Making and breaking nucleic acids: two-Mg²⁺-ion catalysis and substrate specificity, Mol. Cell, 2006, 22, 5–13.
12. B. Chevalier, D. Sussman, C. Otis, A. J. Noel, M. Turmel, C. Lemieux, K. Stephens, R. J. Monnat, Jr. and B. L. Stoddard, Metal-dependent DNA cleavage mechanism of the I-CreI LAGLIDADG homing endonuclease, Biochemistry, 2004, 43, 14015–14026.
13. V. Pingoud, W. Wende, P. Friedhoff, M. Reuter, J. Alves, A. Jeltsch, L. Mones, M. Fuxreiter and A. Pingoud, On the divalent metal ion dependence of DNA cleavage by restriction endonucleases of the EcoRI family, J. Mol. Biol., 2009, 393, 140–160.
14. F. Winkler and A. Prota, in Nucleic Acids and Molecular Biology, ed. A. Pingoud, Springer Verlag, 2004, vol. 14, pp. 179–214.
15. J. R. Horton, R. Blumenthal and X. Cheng, in Nucleic Acids and Molecular Biology, ed. A. Pingoud, Springer Verlag, 2004, vol. 14, pp. 361–392.
16. P. T. Beernink, B. W. Segelke, M. Z. Hadi, J. P. Erzberger, D. M. Wilson, 3rd and B. Rupp, Two divalent metal ions in the active site of a new crystal form of human apurinic/apyrimidinic endonuclease, Ape1: implications for the catalytic mechanism, J. Mol. Biol., 2001, 307, 1023–1034.
17. N. Oezguen, C. H. Schein, S. R. Peddi, T. D. Power, T. Izumi and W. Braun, A “moving metal mechanism” for substrate cleavage by the DNA repair endonuclease APE-1, Proteins: Struct., Funct., Bioinf., 2007, 68, 313–323.
18. K. Katayanagi, M. Okumura and K. Morikawa, Crystal structure of Escherichia coli RNase HI in complex with Mg²⁺ at 2.8 A resolution: proof for a single Mg(2+)-binding site, Proteins: Struct., Funct., Genet., 1993, 17, 337–346.
19. S. O. Shan and D. Herschlag, Probing the role of metal ions in RNA catalysis: kinetic and thermodynamic characterization of a metal ion interaction with the 2′-moiety of the guanosine nucleophile in the Tetrahymena group I ribozyme, Biochemistry, 1999, 38, 10958–10975.
20. J. A. Beebe, J. C. Kurz and C. A. Fierke, Magnesium ions are required by Bacillus subtilis ribonuclease P RNA for both binding and cleaving precursor tRNA^Asp, Biochemistry, 1996, 35, 10493–10505.
21. D. H. Groll, A. Jeltsch, U. Selent and A. Pingoud, Does the Restriction Endonuclease EcoRV Employ a Two-Metal-Ion Mechanism for DNA Cleavage?, Biochemistry, 1997, 36, 11389–11401.
22. F. Xie and C. M. Dupureur, Kinetic analysis of product release and metal ions in a metallonuclease, Arch. Biochem. Biophys., 2009, 483, 1–9.
23. K. Syson, C. Tomlinson, B. R. Chapados, J. R. Sayers, J. A. Tainer, N. H. Williams and J. A. Grasby, Three metal ions participate in the reaction catalyzed by T5 flap endonuclease, J. Biol. Chem., 2008, 283, 28741–28746.
24. C. B. Black and J. A. Cowan, A critical evaluation of metal-promoted Klenow 3′-5′ exonuclease activity: calorimetric and kinetic analyses support a one-metal-ion mechanism, JBIC, J. Biol. Inorg. Chem., 1998, 3, 292–299.
25. H. Han, J. M. Rifkind and A. S. Mildvan, Role of Divalent Cations in 3′5′-Exonuclease Reaction of DNA Polymerase I, Biochemistry, 1991, 30, 11104–11108.
26. M. Feng, D. Patel, J. J. Dervan, T. Ceska, D. Suck, I. Haq and J. R. Sayers, Roles of divalent metal ions in flap endonuclease-substrate interactions, Nat. Struct. Mol. Biol., 2004, 11, 450–456.
27. C. B. Prasannan, F. Xie and C. M. Dupureur, Characterizing metalloendonuclease mixed metal complexes by global kinetic analysis, JBIC, J. Biol. Inorg. Chem., 2010, 15, 533–545.
28. I. B. Vipond, G. S. Baldwin and S. E. Halford, Divalent Metal Ions at the Active Sites of the EcoRV and EcoRI Restriction Endonucleases, Biochemistry, 1995, 34, 697–704.
29. H. Feng, L. Dong and W. Cao, Catalytic mechanism of endonuclease V: a catalytic and regulatory two-metal model, Biochemistry, 2006, 45, 10251–10259.
30. W. Cao and J. Lu, Exploring the catalytic center of TaqI endonuclease: rescuing catalytic activity by double mutations and Mn2+, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 2001, 1546, 253–260.
31. F. Xie, S. Qureshi, G. A. Papadakos and C. M. Dupureur, One and Two Metal Ion Catalysis: Global Single Turnover Kinetic Analysis of PvuII Endonuclease Mechanism, Biochemistry, 2008, 47, 12540.
32. K. Johnson, in The Enyzmes, Academic Press, New York, 1992, vol. XX, pp. 1–61.
33. P. Kuzmic, Program DYNAFIT for the analysis of enzyme kinetic data: application to HIV proteinase, Anal. Biochem., 1996, 237, 260–273.
34. J. M. Beechem, Global analysis of biochemical and biophysical data, Methods Enzymol., 1992, 210, 37–54.
35. M. T. Henzl, J. D. Larson and S. Agah, Estimation of parvalbumin Ca(2+)- and Mg(2+)-binding constants by global least-squares analysis of isothermal titration calorimetry data, Anal. Biochem., 2003, 319, 216–233.
36. J. R. Horton and X. Cheng, PvuII endonuclease contains two calcium ions in active sites, J. Mol. Biol., 2000, 300, 1049–1056.
37. L. H. Conlan and C. M. Dupureur, Multiple metal ions drive DNA association by PvuII endonuclease, Biochemistry, 2002, 41, 14848–14855.
38. T. J. José, L. H. Conlan and C. M. Dupureur, Quantitative evaluation of metal ion binding to PvuII restriction endonuclease, JBIC, J. Biol. Inorg. Chem., 1999, 4, 814–823.
39. G. A. Papadakos, H. Nastri, P. Riggs and C. M. Dupureur, Uncoupling metallonuclease metal ion binding sites via nudge mutagenesis, JBIC, J. Biol. Inorg. Chem., 2007, 12, 557–569.
40. L. M. Bowen, G. Muller, J. P. Riehl and C. M. Dupureur, Lanthanide spectroscopic studies of the dinuclear and Mg(II)-dependent PvuII restriction endonuclease, Biochemistry, 2004, 43, 15286–15295.
41. M. Fothergill, M. F. Goodman, J. Petruska and A. Warshel, Structure-Energy Analysis of the Role of Metal Ions in Phosphodiester Bond Hydrolysis by DNA Polymerase I, J. Am. Chem. Soc., 1995, 117, 11619–11627.
42. S. C. Kamerlin and J. Wilkie, The role of metal ions in phosphate ester hydrolysis, Org. Biomol. Chem., 2007, 5, 2098–2108.
43. P. Imhof, S. Fischer and J. C. Smith, Catalytic mechanism of DNA backbone cleavage by the restriction enzyme EcoRV: a quantum mechanical/molecular mechanical analysis, Biochemistry, 2009, 48, 9061–9075.
44. L. Mones, I. Simon and M. Fuxreiter, Metal-binding sites at the active site of restriction endonuclease BamHI can conform to a one-ion mechanism, Biol. Chem., 2007, 388, 73–78.
45. H. Viadiu and A. K. Aggarwal, The role of metals in catalysis by the restriction endonuclease BamHI, Nat. Struct. Biol., 1998, 5, 910–916.
46. L. Mones, P. Kulhanek, J. Florian, I. Simon and M. Fuxreiter, Probing the two-metal ion mechanism in the restriction endonuclease BamHI, Biochemistry, 2007, 46, 14514–14523.
47. M. Boero, M. Tateno, K. Terakura and A. Oshiyama, Double-metal-ion/single-metal-ion mechanisms of the cleavage reaction of ribozymes: first-principles molecular dynamics simulations of a fully hydrated model system, J. Chem. Theory Comput., 2005, 1, 925–934.
48. F. Leclerc and M. Karplus, Two-metal ion mechanism for hammerhead-ribozyme catalysis, J. Phys. Chem. B, 2006, 110, 3395–3409.
49. M. Fuxreiter and R. Osman, Probing the general base catalysis in the first step of BamHI action by computer simulations, Biochemistry, 2001, 40, 15017–15023.
50. F. Xie, J. M. Briggs and C. M. Dupureur, Nucleophile activation in PD.(D/E)xK metallonucleases: An experimental and computational pK(a) study, J. Inorg. Biochem., 2010, 104(6), 665–672.
51. R. Bonomi, G. Saielli, U. Tonellato, P. Scrimin and F. Mancin, Insights on nuclease mechanism: the role of proximal ammonium group on phosphate esters cleavage, J. Am. Chem. Soc., 2009, 131, 11278–11279.
52. O. Iranzo, A. Y. Kovalevsky, J. R. Morrow and J. P. Richard, Physical and kinetic analysis of the cooperative role of metal ions in catalysis of phosphodiester cleavage by a dinuclear Zn(II) complex, J. Am. Chem. Soc., 2003, 125, 1988–1993.
53. Z. L. Lu, C. T. Liu, A. A. Neverov and R. S. Brown, Rapid three-step cleavage of RNA and DNA model systems promoted by a dinuclear Cu(II) complex in methanol. energetic origins of the catalytic efficacy, J. Am. Chem. Soc., 2007, 129, 11642–11652.
54. J. R. Morrow and O. Iranzo, Synthetic metallonucleases for RNA cleavage, Curr. Opin. Chem. Biol., 2004, 8, 192–200.
55. D. Wahnon, A. Lebuis and J. Chin, Hydrolysis of a phosphate diester doubly coordinated to a dinuclear cobalt(III) complex: A novel mechanism, Angew. Chem., Int. Ed. Engl., 1995, 34, 2412–2414.
56. B. Stec, K. M. Holtz and E. R. Kantrowitz, A revised mechanism for the alkaline phosphatase reaction involving three metal ions, J. Mol. Biol., 2000, 299, 1303–1311.
57. A. Volbeda, A. Lahm, F. Sakiyama and D. Suck, Crystal structure of Penicillium Citrinum P1 nuclease at 2.8 Å resolution, EMBO J., 1991, 10, 1607–1618.
58. B. S. Chevalier, R. J. Monnat and B. L. Stoddard, The homing endonuclease I-CreI uses three metals, one of which is shared between the two active sites, Nat. Struct. Biol., 2001, 8, 312–316.
59. E. D. Garcin, D. J. Hosfield, S. A. Desai, B. J. Haas, M. Bjoras, R. P. Cunningham and J. A. Tainer, DNA apurinic-apyrimidinic site binding and excision by endonuclease IV, Nat. Struct. Mol. Biol., 2008, 15, 515–522.
60. D. Koutsioulis, A. Lyskowski, S. Maki, E. Guthrie, G. Feller, V. Bouriotis and P. Heikinheimo, Coordination sphere of the third metal site is essential to the activity and metal selectivity of alkaline phosphatases, Protein Sci., 2010, 19, 75–84.
61. J. G. Zalatan, T. D. Fenn and D. Herschlag, Comparative enzymology in the alkaline phosphatase superfamily to determine the catalytic role of an active-site metal ion, J. Mol. Biol., 2008, 384, 1174–1189.
62. D. Kostrewa and F. K. Winkler, Mg²⁺ binding to the active site of EcoRV endonuclease: A crystallographic study of complexes with substrate and product DNA at 2 Å resolution, Biochemistry, 1995, 34, 683–696.
63. J. F. Davies, Z. Hostomska, Z. Hostomsky, S. R. Jordan and D. A. Matthews, Crystal structure of the ribonuclease H domain of HIV-1 reverse transcriptase, Science, 1991, 252, 88–95.
64. M. Nowotny, S. A. Gaidamakov, R. J. Crouch and W. Yang, Crystal structures of RNase H bound to an RNA/DNA hybrid: substrate specificity and metal-dependent catalysis, Cell, 2005, 121, 1005–1016.
65. T. A. Ceska, J. R. Sayers, G. Stier and D. Suck, A helical arch allowing single-stranded DNA to thread through T5 5'-exonuclease, Nature, 1996, 382, 90–93.
66. A. B. Hickman, Y. Li, S. V. Mathew, E. W. May, N. L. Craig and F. Dyda, Unexpected structural diversity in DNA recombination: the restriction endonuclease connection, Mol. Cell, 2000, 5, 1025–1034.
67. M. Steiniger-White, I. Rayment and W. S. Reznikoff, Structure/function insights into Tn5 transposition, Curr. Opin. Struct. Biol., 2004, 14, 50–57.
68. J. Y. Lee, J. Chang, N. Joseph, R. Ghirlando, D. N. Rao and W. Yang, MutH complexed with hemi- and unmethylated DNAs: Coupling base recognition and DNA cleavage, Mol. Cell, 2005, 20, 155–166.
69. M. R. Stahley and S. A. Strobel, Structural evidence for a two-metal-ion mechanism of group I intron splicing, Science, 2005, 309, 1587–1590.
70. D. J. Hosfield, Y. Guan, B. J. Haas, R. P. Cunningham and J. A. Tainer, Structure of the DNA repair enzyme endonuclease IV and its DNA complex: Double-nucleotide flipping at abasic sites and three-metal-ion catalysis, Cell, 1999, 98, 397–408.
71. W. G. Scott, J. B. Murray, J. R. Arnold, B. L. Stoddard and A. Klug, Capturing the structure of a catalytic RNA intermediate: the hammerhead ribozyme, Science, 1996, 274, 2065–2069.
72. E. A. Galburt, B. Chevalier, W. Tang, M. S. Jurica, K. E. Flick, R. J. Monnat, Jr. and B. L. Stoddard, A novel endonuclease mechanism directly visualized for I-PpoI, Nat. Struct. Biol., 1999, 6, 1096–1099.

---