Spatial assessment of Langat river water quality using chemometrics†
Hafizan
Juahir
*a,
Sharifuddin Md
Zain
b,
Ahmad Zaharin
Aris
a,
Mohd Kamil
Yusoff
a and
Mazlin Bin
Mokhtar
c
aDepartment of Environmental Sciences, Faculty of Environmental Studies, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia. E-mail: hafizan@env.upm.edu.my; zaharin@env.upm.edu.my; mkamil@env.upm.edu.my; Fax: +603 8946 7463; Tel: +603 8946 7455
bDepartment of Chemistry, Faculty of Science, Universiti Malaya, 50603, Kuala Lumpur, Malaysia. E-mail: smzain@um.edu.my
cInstitute for Environment and Development (LESTARI), Universiti Kebangsaan Malaysia, 43300 UKM Bangi, Selangor, Malaysia. E-mail: mazlin@ukm.my
First published on 4th September 2009
Abstract
The present study deals with the assessment of Langat River water quality with some chemometrics approaches such as cluster and discriminant analysis coupled with an artificial neural network (ANN). The data used in this study were collected from seven monitoring stations under the river water quality monitoring program by the Department of Environment (DOE) from 1995 to 2002. Twenty three physico-chemical parameters were involved in this analysis. Cluster analysis successfully clustered the Langat River into three major clusters, namely high, moderate and less pollution regions. Discriminant analysis identified seven of the most significant parameters which contribute to the high variation of Langat River water quality, namely dissolved oxygen, biological oxygen demand, pH, ammoniacal nitrogen, chlorine, E. coli, and coliform. Discriminant analysis also plays an important role as an input selection parameter for an ANN of spatial prediction (pollution regions). The ANN showed better prediction performance in discriminating the regional area with an excellent percentage of correct classification compared to discriminant analysis. Multivariate analysis, coupled with ANN, is proposed, which could help in decision making and problem solving in the local environment.
Environmental impactRiver water pollution is mainly the result of anthropogenic activities that occur within the river basin. In order for a river to be properly managed, these activities need to be identified and functionally related to the water pollution parameters. This is a rather challenging undertaking. This task can be simplified by analyzing water quality parameters using several chemometric methods without focusing on the anthropogenic factors. This work shows that these methods are able to predict three regions within the Langat River Basin which correspond to different pollution levels. With the identification of these regions, ascertaining anthropological activities will be a less strenuous exercise. The generalization ability of artificial neural networks in the analysis manifests their comparative superiority in predicting the three regions. |
1. Introduction
The Langat River catchment straddles the main urban conurbation in the Klang Valley, Peninsular Malaysia, forming parts of the growing urban complex of the Selangor State. Since 1970, urban expansion has occurred in the Langat River catchment, including extensive land conversion from agriculture use to an urban-industrial-commercial landscape. The changes of land use and land cover are particularly related to an increase of population and intensive agriculture.1 From the government census reports of 1970, 1980 and 1991, Selangor is one of the most populated states in Malaysia that has recorded a rapid growth from a total of less than one million in the 1970 Population Census, to 1.4 million in 1980, to close to 2.3 million in the 1991 Census. It has been estimated that the population in 1998/1999 was around 3.1 million people.2 Based on the inventory list from the Department of Environment of the State of Selangor, there were 693 potential sources of pollutant in the Langat River Basin.The spatial analysis should be conducted to evaluate the most significant water quality parameters to be taken into consideration due to land use activities. The transformation of a particular type of land use to another, such as agriculture and forest area to industrial or municipal area, will change the types of pollutant loadings into the river system. Spatial analysis is one of the most important methods that should be conducted within a river basin in order to investigate the effects of various land uses types on water quality.3–5 This is due to the fact that the effects of the spatial dimensions of land uses, and thus their effect on water quality, remain unclear.6,7
Since there are too many PSs (point sources) and NPSs (non point sources) of pollution along the Langat River, it is quite a challenge to identify the origin of each pollutant observed in the water. Regular monitoring by DOE provides the spatial and temporal variation data needed to attempt this. However, the huge amount of data collected is itself a challenge, especially in interpreting them. In order to interpret these huge and complex data matrices comprising of a large number of physico-chemical parameters, one often needs to use correct methods of data interpretation.8,9
Chemometrics is deemed to be the best approach to avoid misinterpretation of large amounts of complex environmental monitoring data.10 Chemometric methods have been widely used in drawing meaningful information from masses of environmental data. These methods have often been used in exploratory data analysis tools for the classification11,12 of samples (observations) or sampling stations and the identification of pollution sources.13–15 Chemometrics have also been applied to characterize and evaluate the surface and freshwater quality, as well as verifying spatial and temporal variations caused by natural and anthropogenic factors.16,17 Recently, multivariate analysis methods have become an important tool in environmental sciences18,19 to reveal and evaluate complex relationships in a wide variety of environmental applications.20–22 In this study, the most common multivariate methods used for clustering are the hierarchical agglomerative cluster analysis (HACA)23 and these methods are commonly supported by discriminant analysis (DA) as a confirmation for HACA. Both methods are usually referred to as pattern recognition methods.24 The application of different pattern recognition techniques to reduce the complexity of large data sets has been proven to give a better interpretation and understanding of water quality data.25,26
Applications of ANNs to environmental problems are becoming more common.27–31 The application of ANNs, which are computing systems that were originally designed to simulate the structure and function of the brain,32 is a relatively new concept in environmental modeling. If trained properly, a neural network model is capable of ‘learning’ linear as well as the nonlinear features in the data.33
An ANN consists of a set of simple processing units (neurons) arranged in a defined architecture and connected by weighted channels which act to transform remotely-sensed data into a classification. According to Schalkoff,34 the classification techniques of ANN is unlike the conventional ones. It is distribution-free, may sometimes use small training sets35 and, once trained, it is rapid computationally, which will be of value in processing large data sets.36 Furthermore, ANNs have been shown to be able to map land cover more accurately compared to many widely used statistical classification techniques37 and alternatives such as evidential reasoning.38
It has been proposed that the best tool to model non-linear environmental relationship is the ANN.39,40 Research has been undertaken at Imperial College, London which attempted to investigate the capability of the ANN approach in modeling spatial and temporal variations in river water quality.41 ANNs were used as a predictive models to predict salinity in the River Murray at Murray Bridge, South Australia.42 Silets et al.43 have also used an ANN to predict salinity. Ha and Stenstrom44 proposed a neural network approach to examine the relationship between stormwater water quality and various types of land use. Astel et al.45 studied the use of self-organizing maps (SOM) to classify a large environmental data set. They compared the performance of the SOM classification with the more traditional methods of principal component analysis (PCA) and cluster analysis (CA).
In Malaysia, the use of ANNs have been considered in several instances. For example, an ANN could be directly beneficial in identifying spatial and temporal sampling sites that are significant in terms of its contribution to water quality monitoring activities. Since the activity of water quality monitoring, at least in the Langat river basin, is an expensive endeavour, identifying redundant stations can result in significant cost reduction and allow more effective and efficient river quality management activities. Another example is the use of ANNs in predicting short and possible long term time series of various water quality parameters. To this effect, Hafizan Juahir et al.46 have showed that the ANN model gives better performance compared to the autoregressive integrated moving average (ARIMA) model in forecasting DO; the use of ANN for river regulation47 and the application of the second order backpropagation method48 on water quality of the Langat River. Such information could provide opportunities for better river basin management to control river water pollution in Malaysia.
The three of the main objectives of this paper are (i) to evaluate spatial and temporal variations in river water quality data matrix of the Langat River (Peninsular Malaysia) using chemometric methods, (ii) to determine the best ANN input parameters for the spatial (regional areas) prediction given by HACA, and (iii) to develop the best ANN models based on the best input parameters selected in objective (ii).
2. Materials and methods
2.1 Study site
Seven water quality stations were selected from the upstream to downstream of the Langat River. These stations are managed by the Department of Environment (DOE) under the Ministry of Natural Resource and Environment, Malaysia. The Langat Basin catchment area is illustrated in Fig. 1, whereas Table 1 shows the description of sampling points located in the study area. All the stations were identified based on the availability of recorded data from September 1995 to May 2002. The sub-basins that are involved include Pangsoon and Ulu Lui (SB01), Hulu Langat (SB02), Cheras (SB03), Kajang (SB04), Putrajaya (SB05), Teluk Datok (SB06) and Teluk Panglima Garamg (SB07). The first three sites (SB01 to SB03) are areas of relatively low river pollution and are in the upstream of the Langat River. Stations SB04 and SB05 are in the middlestream region of moderate river pollution. The last five sites (SB04–SB07) are regions of high river pollution as there are a number of wastewater drains and are in the middle and downstream of the Langat River basin. It should also be noted that in the data, there are stations which are missing. Furthermore, not all stations were consistently sampled throughout the sampling years. | ||
| Fig. 1 Schematic map showing the geographical locality of the study site. | ||
| DOE Station No. | Cumulative sub-basin coding | Distance from estuary/km | Grid reference | Location |
|---|---|---|---|---|
| 2814602 | SB07 | 4.19 | 2d 52.027′ 101d 26.241′ | Kampung Air Tawar (end of road) |
| 2815603 | SB06 | 33.49 | 2d 48.952′ 101d 30.780′ | Telok Datuk, near Banting Town |
| 2817641 | SB05 | 63.43 | 2d 51.311′ 101d 40.882′ | Bridge at Kampung Dengkil |
| 2918606 | SB04 | 81.14 | 2d 57.835′ 101d 47.030′ | Near West Country Estate |
| 2917642 | SB03 | 86.94 | 2d 59.533′ 101d 47.219′ | Kajang bridge |
| 3017612 | SB02 | 93.38 | 3d 02.459′ 101d 46.387′ | Junction to Serdang, Cheras at Bt. 11 |
| 3118647 | SB01 | 113.99 | 3d 09.953′ 101d 50.926′ | Bridge at Bt. 18 |
2.2 The data
Initially, the multivariate analysis and ANN models were developed using all available data consisting of 23 water quality variables and 305 samples data sets [data matrix: 23 × 305]. The main data used in this study were recorded from September 1995 to June 2002 from seven monitoring stations managed by the Department of Environment, Malaysia. These data are arranged in sequence by date throughout the years (1995–2002) from upstream to downstream of seven water quality monitoring stations along the main Langat River. Fig. 2 shows the number of data points obtained and used in the development of the ANN prediction model from the high pollution source (HPS), moderate pollution source (MPS) and low pollution source (LPS) regions duly assigned by the cluster analysis. Regional boundaries of HPS, MPS and LPS are represented by stations that show significant changes in selected water quality parameters along the river. | ||
| Fig. 2 The number of data points used in the development of ANN prediction model obtained from seven monitoring station. | ||
Preliminary work was done on the data matrix which included the assembling and transformation of the data. Data which were below the detection limit were complemented with values equal to half the detection limit. Normal distribution tests were carried out with the help of the W (Shapiro-Wilk) test; the agreement of the distribution of the physico-chemical parameters of water with the normal distribution was checked.49 Variables with a distribution other than normal were subjected to a transformation. In the case of variables, where their post-transformation distribution differed significantly from the normal one, those parameters were not taken into consideration when making the environmetric analyses.49
The ANN models were developed using 305 raw data points and were divided into training, testing and validation phases for river class prediction model, spatial water quality pattern recognition and inverse prediction model. In preparing data for ANN, the main concerns are; (i) the division of the data into sets intended for ANN training, testing and validation and, (ii) the selection of the best sets of input parameters based on the available data sets. The division of the data affects the prediction performance of the ANN. Poor prediction performance is expected when the validation data contain values outside of the ‘range’ of training. Training, testing and validation data should thus be selected from the same population. However, validation data can be difficult to assemble if the availability of the data is limited. Traditionally, to determine whether the neural network has been trained successfully for a task, it is validated using a “validation set”. In the validation process, the ANN is given the input data (commonly referred to as “unknown sample inputs”) from samples that have not been previously used in training and testing. It is then required to determine the corresponding output value. To evaluate the accuracy of the ANN outputs, they are compared to the set target output data using conventional methods of analysis.
The ANNs developed in this study were trained, tested and validated using the available data sets and methods as described. Division of data into training, testing and validation were carried out randomly from the chronologically arranged observations. The validation data is at least 10% of the whole data set. The balance is then used as training (68%) and testing (22%).50 Environmental modeling requires data of at least one year to be included with regard to the date of sampling.
2.3 Cluster analysis
In this study HACA was employed to investigate the grouping of sampling sites (spatial) within the study regions. HACA is a common method to classify51 variables or cases (observations/samples) into classes (clusters) with high homogeneity level within the class and high heterogeneity level between classes with respect to a predetermined selection criterion.52 Ward's method, using Euclidean distances as a measure of similarity53–55 within HACA has proved to be a very efficient method. The result is illustrated by a dendogram, presenting the clusters and their proximity.56 The Euclidean distance (linkage distance) is reported as Dlink/Dmax, which represents the quotient between the linkage distance divided by the maximal distance. The quotient is usually multiplied by 100 as a way to standardize the linkage distance represented by the y-axis.15,572.4 Discriminant analysis
Discriminant analysis (DA) determines the variables that discriminate between two or more naturally occurring groups/clusters. It constructs a discriminant function (DF) for each group.58 DFs are calculated using equation:where i is the number of groups (G), ki the constant inherent to each group, n the number of parameters used to classify a set of data into a given group and wj is the weight coefficient assigned by DF analysis (DFA) to a given parameter (Pj). In this study, DA was applied to determine whether groups differ with regards to the mean of a variable, and to use that variable to predict group membership. Two groups of temporal (two seasons) and three groups of spatial (three sampling regions) data, which were determined from CA, were selected. DA was applied to the raw data by using the standard, forward stepwise and backward stepwise modes. These were used to construct DFs to evaluate both spatial and temporal variations in the river water quality. The stations (spatial) were the grouping (dependent) variables, while all the measured parameters constitute the independent variables. In the forward stepwise mode, variables are included step-by-step beginning from the most significant variable until no significant changes are obtained. In backward stepwise mode, variables are removed step-by-step beginning with the less significant variable until no significant changes are obtained.
2.5 Spatial pattern recognition (S-ANN)
The main aims of designing and building S-ANN are (i) to investigate the possibility of using commonly determined water quality physico-chemical parameters to build supervised classifiers to discriminate the regions of differing water quality, and (ii) to obtain a decision rule which allows the discrimination of unknown patterns, i.e. samples which have not been used in the training and testing phases. These spatial classification ANN models were developed in order to investigate the ability of the models in classifying the seven monitoring station along the Langat River into three different regions (HPS, MPS and LPS) as given by HACA. When the classification of some samples are known a priori (given by HACA – as in this case) the final classification of samples in groups (pattern recognition) is often carried out using supervised techniques (e.g. DA and ANN).The input variables for this model are the water quality parameters, while the outputs are the regions within the Langat River Basin which fits the description based on these parameters. An example of the input/output data sets is presented in Table 2. The data used in this study consists of 305 data sets (observations). Supervised pattern recognition techniques require the splitting of data from the samples, whose classification is known a priori, into two sets: training (205 data sets) and testing (69 data sets). These two data sets are used to build the ANN model whose predictive ability on unknown samples is validated during the validation phase (31 data sets).
| Station no. | Inputs | Output | ||||||
|---|---|---|---|---|---|---|---|---|
| DO | BOD | COD | Mg | Na | E. coli | Coliform | Region | |
| SB07 | 1.1 | 0.3 | 1011 | 714.1 | 5768.7 | 0.001 | 5.42 × 10−5 | HPS |
| SB06 | 2.7 | 2.8 | 40 | 263.8 | 2077.5 | 0.00175 | 3.83 × 10−5 | HPS |
| SB05 | 0.17 | 10.6 | 110 | 5.9 | 10.31 | 0.0005 | 0.00042 | HPS |
| SB04 | 2.5 | 6 | 23 | 1.29 | 10 | 0.017 | 0.000917 | MPS |
| SB03 | 2.8 | 10 | 79 | 1 | 7.8 | 1 | 0.008333 | MPS |
| SB02 | 6.6 | 9.1 | 38 | 0.75 | 4.46 | 0.215 | 0.01 | LPS |
Three types of model were developed according to different input variables used for each model:
(i) S-ANN1: this model is developed using twenty three water quality variables as input data sets
(ii) S-ANN2: this model is developed using the six most important water quality variables, namely dissolved oxygen (DO), biochemical oxygen demand (BOD), pH, ammoniacal nitrogen (AN), chloride (Cl) and E. coli, which were determined by forward stepwise DA mode
(iii) S-ANN3: this model is developed using the seven most important water quality variables, namely DO, BOD, pH AN, Cl, E.coli and Coliform, determined by backward stepwise DA mode.
The three output nodes define the HPS, MPS and LPS regions (as determined by HACA). The number of nodes in the hidden layer was varied between 1 to 10 via trial and error procedure. Single hidden layer was used in these models. The network structure for the S-ANN3 model is presented in Fig. 3. Thirty network structures were examined for each model in order to determine the best prediction model. Consequently, the prediction performance for all the models were compared among each other. The performance of each network is determined by the misclassification rate (MR) and coefficient of correlation (R).
 | ||
| Fig. 3 Example of the network structure used in spatial pattern recognition by S-ANN2 model. | ||
3. Results
3.1 Classification of sampling station based on historical water quality data
This section examines the historical values of water quality parameters in order to classify the water quality stations based on their similarity level using HACA. HACA was performed on the water quality data set to evaluate spatial variation among sampling stations. This analysis resulted in the grouping of sampling stations into three clusters/groups (Fig. 4). Fig. 5 shows the 3 regions given by HACA. The clustering procedure generated 3 groups/clusters in a very convincing way, as the stations in these groups have similar characteristics and natural backgrounds.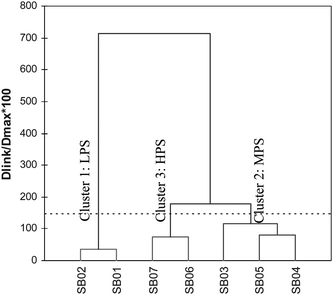 | ||
| Fig. 4 Dendogram showing different clusters of sampling sites located at Langat River Basin based on water quality parameters. | ||
 | ||
| Fig. 5 Classification of regions due to surface river water quality by HACA for Langat River Basin. | ||
Cluster 1 (Stations SB01 and SB02), Cluster 2 (Stations SB03, SB04 and SB05) and Cluster 3 (Stations SB06 and SB07) correspond to LPS from Pangsoon and Ulu Lui, MPS from Cheras and Hulu Langat and HPS from sub-basin Kajang, Putrajaya, Teluk Datok and Teluk Panglima Garang respectively. This result implies that for rapid assessment of water quality, only one station in each cluster is needed to represent a reasonably accurate spatial assessment of the water quality for the whole network. It is evident that the HACA technique is useful in offering reliable classification of surface water of the whole region and can be used to design future spatial sampling strategies in an optimal manner.
3.2 Spatial variations of river water quality
To study the spatial variation among different stream regions, DA was applied to the raw data post grouping of the Langat Basin into three main clusters/groups defined by the cluster analysis (HACA). Groups (HPS, MPS and LPS) were treated as dependent variables, while water quality parameters were treated as independent variables. DA was carried out via standard, forward stepwise and backward stepwise methods. The accuracy of spatial classification using standard, forward stepwise and backward stepwise mode DFA were 90.5% (23 discriminant variables), 88.5% (6 discriminant variables) and 88.9% (7 discriminant variables) respectively (Table 3). The Wilk's Lambda test for standard mode gave a Lambda value of 0.062 and p < 0.0001. The null hypothesis states that the means of vectors of the 3 clusters (HPS, MPS, LPS) are equal. The alternative hypothesis, on the other hand, states that at least one of the means of vectors is different from another. Since the computed p-value is lower than the significance level of alpha = 0.05, one should reject the null hypothesis and accept the alternative hypothesis. The risk of rejecting the null hypothesis while it is true is lower than 0.01%. Thus the 3 clusters are indeed different from one another.| Sampling regions | %Correct | Regions assigned by DA | ||
|---|---|---|---|---|
| HPS | LPS | MPS | ||
| Standard DA mode | ||||
| HPS | 95.65 | 66 | 1 | 2 |
| LPS | 90.63 | 0 | 58 | 6 |
| MPS | 87.50 | 2 | 13 | 105 |
| Total | 90.51 | 68 | 72 | 113 |
| Forward stepwise mode | ||||
| HPS | 91.30 | 63 | 1 | 5 |
| LPS | 92.19 | 0 | 59 | 5 |
| MPS | 84.17 | 3 | 16 | 101 |
| Total | 88.14 | 66 | 76 | 121 |
| Backward stepwise mode | ||||
| HPS | 91.30 | 63 | 1 | 5 |
| LPS | 93.75 | 0 | 60 | 4 |
| MPS | 85.00 | 3 | 15 | 102 |
| Total | 88.93 | 66 | 76 | 111 |
Using forward stepwise discriminant analysis, DO, BOD, pH, AN, Cl and E. coli were found to be the significant variables. This indicates that these parameters have high variation in terms of their spatial distribution. Backward stepwise mode on the other hand included coliform as the 7th parameter to have a high spatial variation. Box and whisker plots of three of these water quality parameters over the eight year period (1995–2002) are shown in Fig. 6. Seven selected water quality parameters which gave high variations (the most significant) by backward stepwise DA were then used for further analysis.
 | ||
| Fig. 6 Box and whisker plots of some parameters separated by spatial DA associated with the water quality data of Langat River. Grey crosses are mean values, top and bottom of whiskers indicate maximum and minimum values, respectively while horizontal lines of the boxes from top to bottom indicate the third quartile, median and first quartile, respectively. | ||
3.3 Predicting the spatial distribution of water quality samples using ANN
In the development of ANN to predict the spatial distribution of water quality samples by regional origin, 30 network structures were examined. The summary of the results obtained, given by misclassification rate (MR) and coefficient of correlation (R) are presented in Table 4, and the example of output and predicted region are presented in Table 5. Generally, all ANN models gave satisfactory results in discriminating water quality samples by regional origin. Seven hidden nodes are considered optimum as a further increase in the complexity of the topology, as reflected by the increase in the number of hidden nodes (8 to 20) result in no significant improvement of the prediction performance (Fig. 7(a) and (b)).| Model | Network | Misclassification Rate | R |
|---|---|---|---|
| a Note: Square brackets [w,x,y,z] indicate ANN structure. w is the number of input nodes, x is the number of hidden nodes, y is the number of hidden layers and z is the number of output nodes. | |||
| S-ANN1 | [23,1,1,3] | 0.024 | 0.898 |
| [23,2,1,3] | 0.012 | 0.951 | |
| [23,3,1,3] | 0.016 | 0.952 | |
| [23,4,1,3] | 0.004 | 0.967 | |
| [23,5,1,3] | 0 | 0.978 | |
| [23,6,1,3] | 0 | 0.986 | |
| [23,7,1,3] | 0 | 0.995 | |
| [23,8,1,3] | 0 | 0.997 | |
| [23,9,1,3] | 0 | 0.998 | |
| [23,10,1,3] | 0 | 0.998 | |
| S-ANN2 | [6,1,1,3] | 0.059 | 0.842 |
| [6,2,1,3] | 0.055 | 0.891 | |
| [6,3,1,3] | 0.028 | 0.925 | |
| [6,4,1,3] | 0.02 | 0.940 | |
| [6,5,1,3] | 0.012 | 0.963 | |
| [6,6,1,3] | 0.012 | 0.976 | |
| [6,7,1,3] | 0 | 0.984 | |
| [6,8,1,3] | 0 | 0.993 | |
| [6,9,1,3] | 0.004 | 0.992 | |
| [6,10,1,3] | 0 | 0.996 | |
| S-ANN3 | [7,1,1,3] | 0.051 | 0.854 |
| [7,2,1,3] | 0.036 | 0.912 | |
| [7,3,1,3] | 0.024 | 0.939 | |
| [7,4,1,3] | 0.016 | 0.951 | |
| [7,5,1,3] | 0.016 | 0.966 | |
| [7,6,1,3] | 0.004 | 0.988 | |
| [7,7,1,3] | 0.004 | 0.990 | |
| [7,8,1,3] | 0.004 | 0.992 | |
| [7,9,1,3] | 0 | 0.995 | |
| [7,10,1,3] | 0 | 0.996 |
| DO | BOD | pH | NH3-N | Cl | E. coli | Coliform | Region | Predicted |
|---|---|---|---|---|---|---|---|---|
| 1.10 | 0.30 | 6.65 | 0.85 | 10913.50 | 1100 | 2400 | HPS | HPS |
| 2.70 | 2.80 | 6.40 | 1.10 | 3650.24 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4100 | HPS | HPS |
| 5.90 | 5.00 | 7.90 | 0.06 | 13800.00 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
197![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
HPS | LPS |
| 5.20 | 3.00 | 6.80 | 0.40 | 7.00 | 5000 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
MPS | MPS |
| 2.53 | 17.00 | 6.03 | 0.40 | 4.00 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
MPS | MPS |
| 4.23 | 13.60 | 6.47 | 1.70 | 10.80 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
LPS | LPS |
| 6.92 | 2.00 | 6.60 | 0.46 | 2.00 | 7000 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
LPS | LPS |
 | ||
| Fig. 7 The performance of the each S-ANN model obtained by (a) R values and (b) misclassification rate. | ||
From the results, S-ANN1 seems to give the best performance. This model achieved zero MR with 5 hidden nodes onwards. Consequently, this S-ANN1 is considered as the reference model to be compared with models S-ANN2 and S-ANN3, both with reduced input variables. Model S-ANN2 achieved zero MR with 7 hidden nodes onwards. By using 7 input variables and 9 to 10 hidden nodes, model S-ANN3 successfully discriminated the water quality samples. Both models, S-ANN2 and S-ANN3, successfully showed these characteristics by using only 6 and 7 water quality parameters, respectively, this without loss of much important information compared to model S-ANN1. Comparatively, model S-ANN3 exhibited better performance than S-ANN2 in discriminating water quality samples. In general, model S-ANN3 successfully discriminated each region with an average of 94% correct classification using 7 input variables, while model S-ANN2 successfully discriminated only an average of 92% correct classification (Table 6).
| Sampling regions | %Correct | Regions assigned by S-ANN | ||
|---|---|---|---|---|
| HPS | LPS | MPS | ||
| S-ANN1 | ||||
| HPS | 97.1 | 67 | 1 | 1 |
| LPS | 100.0 | 0 | 64 | 0 |
| MPS | 97.5 | 0 | 3 | 117 |
| Total | 98.0 | 67 | 68 | 118 |
| S-ANN2 | ||||
| HPS | 94.2 | 65 | 2 | 2 |
| LPS | 90.6 | 0 | 58 | 6 |
| MPS | 90.8 | 4 | 7 | 109 |
| Total | 91.7 | 69 | 67 | 117 |
| S-ANN3 | ||||
| HPS | 94.2 | 65 | 1 | 3 |
| LPS | 93.8 | 0 | 60 | 4 |
| MPS | 95.0 | 0 | 6 | 114 |
| Total | 94.5 | 65 | 67 | 121 |
As mentioned in the methodology, the principal aim of this section is to discriminate water quality sample (datasets/observations) by their geographical origin (region), using supervised pattern recognition. Initially, linear DA was used to assign the regional origin of the water quality data sets. In this case, at least, variables DO, BOD, pH, AN, Cl, E. coli and coliform were necessary to achieve 90.5% (23 variables), 88.14% (6 variables) and 88.93% (7 variables) predictive ability using standard, forward stepwise and backward stepwise mode. The linear classifier was able to correctly predict each data set (observation) with a p-value of less than 0.05. Thus, when including at least 6 water quality variables to describe the analyzed samples, the problem turned out to be linearly separable.
On the contrary, using ANN we could obtain 98% (23 variables), 91.7% (6 variables) and 94.5% (7 variables) predictive ability for the three different models (different number of inputs for S-ANN1, S-ANN2 and S-ANN3). Traditional methods of multivariate analysis, such as DA, however, present a well known and extremely serious drawback: the interpretation of the components and the establishment of relationships with actual events are very labourious and relevant information may be ignored, while the simple use of an ANN model provides no direct insight into the relevant ecological processes.59
Conclusions
In the spatial pattern recognition model, ANN models were developed to predict the three regions (HPS, MPS and LPS) of Langat River Basin obtained by DA. Prediction performance comparison analysis between ANN and DA in discriminating the regional (spatial) areas based on their water quality patterns was also carried out. ANN showed better prediction performance in discriminating the regional area with an excellent percentage of correct classification (98%, 92% and 94%) compared to DA (91%, 88% and 89%). Results obtained for the ANN models show the superior generalization ability of ANN models.It showed that the ability of ANN to discriminate water quality samples using only 6 and 7 input variables was comparable to using all the available water quality parameters (23 variables). The use of ANN allows a reduction of the number of water quality parameters needed to identify the correct regional samples. The results showed that all the S-ANN models are successful in discriminating water quality samples according to the three different regions along the Langat River, better than DA. These S-ANN models are definitely very useful tools in helping decision makers achieve better river basin management
Acknowledgements
The authors acknowledge the financial and technical support for this project provided by the Ministry of Science, Technology and Innovation and Universiti Putra Malaysia under the ScienceFund Project no. 01-01-04-SF0733. The authors wish to thank the Department of Environment, and Department of Irrigation and Drainage, Ministry of Natural Resources and Environment of Malaysia, Institute for Development and Environment (LESTARI), Universiti Kebangsaan Malaysia, Universiti Malaya Consultancy Unit (UPUM) and Chemistry Department of Universiti Malaya, who have provided us with secondary data and valuable advice.References
- P. H. Verburg, A. Veldkamp, L. Willemen, K. P. Overmars, J.-P. Castella, in Landscape level analysis of the spatial and temporal complexity of land-use change, AGU Monograph, ed. R. De Vries and R. Houghton, 2004, (in press) Search PubMed.
- H. S. Abdul Hadi, H. Samad, in Modelling for integrated drainage basin management. Integrated Drainage Basin Management and Modelling, (Environmental Management Programme, Centre of Graduate Studies), ed. J. Jamaluddin, M. N. Abdul Rahim, H. S. Abdul Hadi, and M. Ahmad Fariz, UKM Press, Bangi, 2000, p. 164–190 Search PubMed.
- J. A. Griffith, Water, Air, Soil Pollut., 2002, 138, 181–197 CrossRef CAS.
- S. T. Y. Tong and W. Chen, J. Environ. Manage, 2002, 66, 377–393 Search PubMed.
- O. Buck, D. K. Niyogi and C. R. Townsend, Environ. Pollut., 2004, 130, 287–299 CrossRef CAS.
- A. Baker, Hydrol. Processes, 2003, 17, 2499–2501 CrossRef.
- L. B. Johnson, C. Richards, G. E. Host and J. W. Arthur, Freshwater Biol., 1997, 37, 193–208 CrossRef CAS.
- D. Chapman, in Water Quality Assessment, ed. D. Chapman on behalf of UNESCO, WHO and UNEP, Chapman & Hall, London, 1992 Search PubMed.
- W. Dixon and B. Chiswell, Water Res., 1996, 30, 1935–1948 CrossRef CAS.
- V. Simeonov and J. W. Einax, Anal. Bioanal. Chem., 2002, 374, 898–905 CrossRef CAS.
- D. Brodnjak-Voncina, D. Dobcnik, M. Novic and J. Zupan, Anal. Chim. Acta, 2002, 462, 87–100 CrossRef CAS.
- T. Kowalkowski, R. Zbytniewski, J. Szpejna and B. Buszewski, Water Res., 2006, 40, 744 CrossRef CAS.
- D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. De Jong, P. J. Lewi and J. Smeyers-Verbeke, Handbook of chemometrics and qualimetrics; data handling in science and technology. Parts A and B (Vol. 20A and 20B), Elsevier, Amsterdam, 1997 Search PubMed.
- M. Vega, R. Pardo, E. Barrado and L. Deban, Water Res., 1998, 32, 3581–3592 CrossRef CAS.
- S. Shrestha and F. Kazama, Environmental Modelling Software, 2007, 22, 464–475 Search PubMed.
- B. Helena, Pardo, R. Vega, M. Barrado, E. Fernandez and J. M. L. Fernandez, Water Res., 2000, 34, 807–816 CrossRef CAS.
- K. P. Singh, A. Malik and S. Sinha, Anal. Chim. Acta, 2005, 538, 355–374 CrossRef CAS.
- S. D. Brown, T. B. Blank, S. T. Sum and L. G. Weyer, Anal. Chem., 1994, 66, 315R–359R CAS.
- S. D. Brown, S. T. Sum and F. Despagne, Anal. Chem., 1996, 68, 21R–61R CrossRef.
- W. D. Alberto, D. M. D. Pilar, A. M. Valeria, P. S. Fabiana, H. A. Cecilia and B. M. D. L. Angeles, Water Res., 2001, 35, 2881–2894 CrossRef.
- W. N. Xiang, Landscape Urban Planning, 1996, 34, 1–10 Search PubMed.
- L. B. Johnson and S. H. Gage, Freshwater Biol., 1997, 37, 113–132 CrossRef.
- P. R. Kannel, S. Lee, S. R. Kanel and S. P. Khan, Anal. Chim. Acta, 2007, 582, 390–399 CrossRef CAS.
- M. J. Adams, The principles of multivariate data analysis, in Analytical Methods of Food Authentication, 350, ed. P. R. Ashurst and M. J. Dennis, Blackie Academic & Professional, London, 1998 Search PubMed.
- S. D. Brown, R. K. Skogerboe and B. R. Kowalski, Chemosphere, 1980, 9, 265–276 CrossRef CAS.
- A. Qadir, R. N. Malik and S. Z. Husain, Environmental Monitoring Assessment, 2007, 140(1–3), 43–59 Search PubMed.
- D. Silverman and J. A. Dracup, J. Appl. Meteorol., 2000, 39(1), 57–66 Search PubMed.
- M. Scardi, Ecol. Modell., 2001, 146, 33–45 CrossRef.
- F. Recknagel, J. Bobbin, P. Whigham and H. Wilson, Journal of Hydroinformatics, 2002, 4(2), 125–134 Search PubMed.
- G. J. Bowden, G. C. Dandy and H. R. Maier, J. Hydrol., 2005, 301, 75–92 CrossRef.
- N. Muttil and K.-W. Chau, Engineering Applications of Artificial Intelligence, 2007, 20, 735–744 Search PubMed.
- D. E. Rumelhart, E. Hinton and J. Williams, Parallel Distributed Processing, 1986, 1, 318–362 Search PubMed.
- J. B. Elsner and A. A. Tronis, Bull. Am. Meterol. Soc., 1992, 73(1), 49–60 Search PubMed.
- R. Schalkoff, Pattern Recognition: Statistical, Structural and Neural Approaches, New York, Wiley, 1992 Search PubMed.
- G. F. Hepner, T. Logan, N. Ritter and N. Bryant, Photogrammetric Engineering and Remote Sensing, 1990, 56, 469–473 Search PubMed.
- N. D. Gershon and C. G. Miller, I.E.E.E. Spectrum, 1993, 30, 28–32 CrossRef.
- J. A. Benediktsson, P. H. Swain and O. K. Ersoy, I.E.E.E. Transactions on Geoscience and Remote Sensing, 1990, 28, 540–551 Search PubMed.
- D. R. Peddle, G. M. Foody, A. Zhang, S. E. Franklin and E. F. Ledrew, Canadian Journal of Remote Sensing, 1994, 12, 277–302 Search PubMed.
- Q. Zhang and S. J. Stanley, Water Resource, 1997, 31, 2340–2350 Search PubMed.
- A. Jain and S. K. V. P. Indurthy, Journal of Hydrologic Engineering, 2003, 8, 93–98 Search PubMed.
- E. Clarici, Environmental Modelling Using Neural Networks, PhD Thesis, Imperial College, 1995 Search PubMed.
- H. R. Maier and G. C. Dandy, Water Research, 1996, 32, 1013–1022.
- L. DeSilets, B. Golden, Q. Wang and R. Kumar, Computer and Operations Research, 1992, 19, 227–285 Search PubMed.
- H. Ha and M. K. Stenstrom, Water Res., 2003, 37, 4222–4230 CrossRef CAS.
- A. Astel, S. Tsakovski, P. Barbieri and V. Simeonov, Water Res., 2007, 41(19), 4566–4578 CrossRef CAS.
- Hafizan Juahir, Sharifuddin M. Zain, Mohd. Ekhwan Toriman, M. Nazari Jaafar and W. Klaewtanong, Performance of autoregressive integrated moving average and neural network approaches for forecasting dissolved oxygen at Langat River Malaysia, in Urban Ecosystem Studies In Malaysia: A study of change, N. M. Hashim and R. Rainis, Universal Publishers, USA, 2003, p. 145–165 Search PubMed.
- Mohd. Ekhwan Toriman and Hafizan Juahir, Artificial Neural Network Modelling For Langat River Discharge: Implication For River Restoration, in Competition of Research and Innovation Week UKM, Centre of Research Management, 2003 Search PubMed.
- J. Hafizan, S. M. Zain, M. Ekhwan Toriman and M. B. Mokhtar, Jurnal Kejuruteraan Awam, 2004, 16(2), 42–55 Search PubMed.
- M. Sojka, M. Siepak, A. Ziola and M. Frankowski, Environ. Monit. Assess., 147, pp. 159–170 Search PubMed.
- J.-T. Kuo, Y.-Y. Wang and W.-S. Lung, Water Res., 2006, 40, 1367–1376 CrossRef CAS.
- D. L. Massart and L. Kaufman, The interpretation of analytical data by the use of cluster analysis, Wiley, New York, 1983 Search PubMed.
- J. E. McKenna Jr, Environmental Modelling & Software, 2003, 18(3), 205–220 Search PubMed.
- P. Willet, Similarity and Clustering in Chemical Information Systems, Research Studies Press, Wiley, New York, 1987 Search PubMed.
- M. J. Adams, The principles of multivariate data analysis, in Analytical Methods of Food Authentication, ed. P. R. Ashurst and M. J. Dennis, vol. 350, Blackie Academic & Professional, London, UK, 1998 Search PubMed.
- M. Otto, Multivariate methods, in Analytical Chemistry, R. Kellner, J. M. Mermet, M. Otto and H. M. Widmer, Wiley-VCH, Wenheim, 1998 Search PubMed.
- M. Forina, C. Armanino and V. Raggio, Anal. Chim. Acta, 2002, 454, 13–19 CrossRef CAS.
- K. P. Singh, A. Malik, D. Mohan and S. Sinha, Water Res., 2004, 38, 3980–3992 CrossRef CAS.
- R. A. Johnson and D. W. Wichern. Applied Multivariate Statistical Analysis, 3rd edn, 1992. Prentice-Hall Int., New Jersey Search PubMed.
- C. E. N. Gatts, A. R. C. Ovalle and C. F. Silva, Environmental Modelling & Software, 2005, 20, 883–889 Search PubMed.
Footnote |
| † Part of a themed issue dealing with water and water related issues. |
| This journal is © The Royal Society of Chemistry 2010 |

