Electrochemical chlorine evolution at rutile oxide (110) surfaces†
Received
24th August 2009
, Accepted 7th October 2009
First published on
11th November 2009
Abstract
Based on density functional theory (DFT) calculations we study the electrochemical chlorine evolution reaction on rutile (110) oxide surfaces. First we construct the Pourbaix surface diagram for IrO2 and RuO2, and from this we find the chlorine evolution reaction intermediates and identify the lowest overpotential at which all elementary reaction steps in the chlorine evolution reaction are downhill in free energy. This condition is then used as a measure for catalytic activity. Linear scaling relations between the binding energies of the intermediates and the oxygen binding energies at cus-sites are established for MO2 (M being Ir, Ru, Pt, Ti). The linear relations form the basis for constructing a generalized surface phase diagram where two parameters, the potential and the binding energy of oxygen, are needed to determine the surface composition. We calculate the catalytic activity as function of the oxygen binding energy, giving rise to a Sabatier volcano. By combining the surface phase diagram and the volcano describing the catalytic activity, we find that the reaction mechanism differs depending on catalyst material. The flexibility in reaction path means that the chlorine evolution activity is high for a wide range of oxygen binding energies. We find that the required overpotential for chlorine evolution is lower than the overpotential necessary for oxygen evolution.
Introduction
Chlorine is an essential product for the global chemical industry – approximately 50% of the total turnover of the chemical industry depends on chlorine and caustic soda.1 Chlorine production by chlor-alkali processes is one of the largest current technological applications of electrochemistry.2
The most active anode catalysts are usually based on RuO2, however, RuO2 is barely stable at the high potentials. Therefore RuO2 is mixed with IrO2 and additives such as TiO2 and SnO2, in order to improve the stability. The most commonly used electrocatalyst in industrial chlorine processes is the so-called Dimensionally Stable Anodes (DSA®) which is named according to its improved lifetime compared with earlier used electrocatalysts.3
The equilibrium potential for Cl2 evolution is 1.36 V at room temperature and standard conditions, which is slightly larger than the equilibrium potential for oxygen evolution, which is 1.23 V under the same conditions. This means that under chlorine evolution the simultaneous evolution of oxygen tends to occur as a parasitic side reaction, especially at high current densities. However, depending on the employed catalyst, oxygen evolution usually requires a somewhat larger overpotential than chlorine evolution. Unfortunately, RuO2 is known to be a good catalyst for oxygen evolution as well as for chlorine evolution. This suggests an overlap of the activity volcanoes for the two reactions, and it has in fact been suggested that high catalytic activity for chlorine evolution is fundamentally linked with high oxygen evolution activity.2
Anodic chlorine evolution at oxide electrodes, and especially chlorine evolution on RuO2, has been widely studied experimentally. A variety of different reaction mechanisms have been suggested based on indirect experimental quantities such as Tafel slopes and reaction orders.4 Among the possible reactions are the Volmer–Tafel reaction5
| | | 2* + 2Cl− → 2Cl* + 2e− → 2* + Cl2 + 2e−, | (1) |
the Volmer–Heyvrosky reaction
6| | | * +2Cl− → Cl* + e− + Cl− → * +Cl2 + 2e−, | (2) |
and the Khrishtalik reaction
7,8| | | * +2Cl− → Cl* + e− + Cl− → (Cl*)+ + 2e− + Cl− → * + Cl2 + 2e−. | (3) |
Here, * is an active site, which may be a surface oxygen or a metal atom.
8
Very little is known about the reaction mechanism for chlorine evolution and about the atomic-scale structure of the surface, which depends strongly on catalyst material, electrostatic potential, and electrolyte. Recent developments within density functional theory analysis of electrochemical reactions have opened up the possibilities to study these reactions at the atomic scale.9 In particular, investigations of fuel cell catalysis such as oxygen reduction10–13 and methanol oxidation14–17 have deepened the insight into reaction mechanisms and surface composition under electrocatalytic reaction conditions. In a previous study the oxygen evolution reaction was investigated.18 There it was established that it is possible to describe the trends in the oxygen evolving activity using one single descriptor: the adsorption energy of O-atoms on the surfaces. RuO2 was determined to be the most active rutile (110) surface, which is in good agreement with the experiments. Recently, theoretical studies have addressed heterogeneously catalyzed chlorine production by the so-called Deacon process.19,20 However, in spite of the significant importance of electrochemical chlorine evolution, detailed electronic structure studies of this process have not appeared in the literature.
The aim of the present study is to analyze the surface structure and the activity trends underlying electrochemical chlorine evolution over rutile oxides. We start by analyzing IrO2 and RuO2 and we construct surface phase diagrams of the rutile (110) surfaces. This allows us to derive plausible mechanisms of the electrochemical chlorine evolution based on the reaction intermediates. We determine the lowest potential where Cl evolution is possible. Applying adsorption energy correlations, we can determine a reduced set of key energetic descriptors for the surface reactions involved, and generalize the analysis of IrO2 and RuO2 to a trend study where all the material dependence is included in a single descriptor, in this case the oxygen binding energy.
Methods
Calculation details
All electronic structure calculations have been carried out using density functional theory (DFT), with the RPBE functional for exchange and correlation.21 A periodically repeated 4-layer slab is chosen for the rutile (110) surfaces of RuO2, IrO2, TiO2, and PtO2. A vacuum layer of 16 Å is used to separate the slab from its periodically repeated images. We use a 2![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 surface unit cell and 4
1 surface unit cell and 4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 4
4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 Monkhorst–Pack type k-point sampling for slab calculations.22 The Kohn–Sham equations are solved using a plane wave basis with a cutoff of 350 eV for the eigenstates, and the densities are described using a cutoff corresponding to 500 eV. Vanderbilt ultrasoft pseudopotentials are used to deal with the ion cores.23 A Fermi smearing of 0.1 eV is used, and energies are extrapolated to an electronic temperature of 0 K. The two bottom layers of the slab are fixed in their bulk structure, while the two top layers as well as possible adsorbates on it are relaxed until the sum of the absolute forces is less than 0.05 eV Å−1. All calculations are performed using the Dacapo and ASE simulation package.24
1 Monkhorst–Pack type k-point sampling for slab calculations.22 The Kohn–Sham equations are solved using a plane wave basis with a cutoff of 350 eV for the eigenstates, and the densities are described using a cutoff corresponding to 500 eV. Vanderbilt ultrasoft pseudopotentials are used to deal with the ion cores.23 A Fermi smearing of 0.1 eV is used, and energies are extrapolated to an electronic temperature of 0 K. The two bottom layers of the slab are fixed in their bulk structure, while the two top layers as well as possible adsorbates on it are relaxed until the sum of the absolute forces is less than 0.05 eV Å−1. All calculations are performed using the Dacapo and ASE simulation package.24
The surface of the unit cell contains two bridge and two cus sites, which means that the total coverage at each type site varies between 50% and 100%. We consider all relevant combinations of adsorption site and adsorbates. We find that adsorbates bind stronger at bridge sites than on cus sites and bridge sites are therefore occupied with oxygen for a large range of conditions. We therefore focus on cus sites throughout this paper. Mixed phases where different kinds of adsorbates are mutually present at the cus sites may exist, however, we find that they are in general only stable in very narrow windows of conditions.
We consider the adsorption of Clc, OHc and Oc at a cus site, c, as well as the formation of O2cc and Cl(Oc)2 adsorbed at two cus sites. The adsorption energy of chlorine is calculated using:
| | | ΔE(Clc) = E(Clc) − E(c) − ½E(Cl2). | (4) |
For oxygen the energy is calculated relative to
water| | | ΔE(Oc) = E(Oc) − E(c) − E(H2O) + E(H2) | (5) |
and for ClO
c we apply the combined reference energy states from above
| | | ΔE(ClOc) = E(ClOc) − E(c) − ½E(Cl2) − E(H2O) + E(H2). | (6) |
The adsorption energy of O
2cc is defined with reference to
water and
hydrogen| | | ΔE (O2cc) = E(O2cc) − E(2c) − 2E(H2O) + 2E(H2), | (7) |
and the adsorption energy of Cl(O
c)
2 is defined by
| | | ΔE(Cl(Oc)2) = E(Cl(Oc)2) − E(2c) − 2E(H2O) + 2E(H2). − ½E(Cl2). | (8) |
The changes in the interaction between the liquid electrolyte and the surface upon adsorption of molecules are expected to be small as long as all
hydrogen bonds are saturated. It has previously been shown that the O and OH adsorption energies at the cus site is changed by less than 0.05 eV by the presence of
water at the surface on RuO
2.
18 These interactions are therefore neglected in the present study.
Furthermore, the effect of the local field in the Helmholtz layer is not accounted for. Previously, it has been shown that for metal surfaces the effect of the field is negligible for adsorbates with small dipole moments perpendicular to the surface.25 For RuO2 we find that applying a homogeneous external field up to −0.53 V Å−1, corresponding to a 1.6 V potential drop across a 3 Å thick Helmholtz layer, changes the relative adsorption energies by less than 0.11 eV.
The above simplifications are expected to be independent on the catalyst material, and therefore the resulting trends in catalytic activity should only be weakly affected by them. Variations in the adsorption energy of e.g. oxygen on the (110) surfaces are several eV between e.g. IrO2 and TiO2, while differences in water interaction and field effects are at least an order of magnitude smaller, and therefore vanish on the adsorption energy scale.
Surface phase diagram
There are four parameters determining the surface composition: the potential, the pH, the concentration of Cl−, and the electrode material. Only the latter is directly available in the simulations, and the other three parameters can be included analytically as described below. By applying the computational standard hydrogen electrode,9 it is possible to construct surface Pourbaix diagrams, and identify the most stable structure of the catalyst surface at a range of potentials and pH values.26 At conditions where oxygen and chlorine evolution are negligible, the structure of the catalyst surface is determined by the equilibrium with water, protons and chloride ions. The oxidation of water may lead to the formation of OHc or Oc through| | | H2O(l) + c ⇌ HOc + H+(aq) + e− ⇌ Oc + 2H+(aq) + 2e− | (9) |
Chloride ions may be exchanged with the surface via| | | Cl−(aq) + c ⇌ Clc + e− | (10) |
ClOc may be formed by first having Oc adsorbed on the surface followed by Cl− adsorption on top of Oc. At potentials where evolution of Cl2 or O2 is appreciable, the surface structure is, however, controlled by the steady-state reaction.
At standard conditions (zero pH), H+(aq) + e− is in equilibrium with ½H2(g) at zero potential vs. the standard hydrogen electrode. At finite pH and potential the chemical potential of a proton and an electron is:
| | μ(H+(aq)) + μ(e−) = ½μH2(g) − eUSHE + kBT![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ln(10)pH. ln(10)pH. | (11) |
Similarly, Cl
−(aq) is in equilibrium with ½Cl
2 + e
− under standard conditions at the potential of standard chlorine
electrode,
| | | Cl−(aq) ⇌ ½Cl2 + e− @USHE = 1.36 V. | (12) |
For an arbitrary potential and activity we therefore obtain
| | μ(Cl−(aq)) − μ(e−) = ½μCl2(g) − e(USHE − 1.36 V) + kBT![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) lnaCl−. lnaCl−. | (13) |
Eqns (11) and (13) allow us to calculate the free energies of O
c, OH
c, Cl
c, and ClO
c adsorbed at a surface site in the electrochemical environment, based on calculations of the gas-phase molecules rather than the solvated ions.
The free energy of adsorption for a surface with an adsorbate at USHE = 0 V is given by
| | | ΔG = ΔE + ΔZPE − TΔS + ΔGref, | (14) |
where ΔZPE is the change in zero point energy,
T is the temperature, Δ
S is the change in entropy upon absorption, and Δ
E is the DFT-calculated adsorption energy. The zero-point energy contribution and the entropy for the adsorbed species are obtained from harmonic vibrational analysis and from tables of thermodynamic properties in the case of gas-phase species. The numbers for ΔZPE and −
TΔ
S are listed in the ESI
† (in Table S1). The correction Δ
Gref is 1.36 eV for Cl
c, ClO
c and Cl(O
c)
2 and zero for HO
c and O
c, and is related to the reversible potentials of the chlorine and
hydrogen electrodes, respectively (see ESI for details
†).
To obtain a measure of the activity we apply a simplified estimate: the chlorine evolution reaction is considered possible if and only if all the involved reaction steps are neutral or downhill in free energy. For a given reaction we can determine the lowest potential for which this is the case. Due to the significant challenges in treating reaction barriers for electrochemical processes, we do not include reaction barriers in the present study, and can therefore not directly compare e.g. the relative rates of the Volmer–Tafel and the Volmer–Heyvrosky reactions. Our approach can thus be viewed as a “lower-bound overpotential analysis” of the chlorine evolution activity. Since barriers of surface reactions27 as well as barriers for proton transfer reactions28 are known to often be linearly dependent on the reaction energy, we expect that the trends are conserved even when barriers are included.
Results and discussion
Surface phase diagram for IrO2
Fig. 1 shows the interesting part of the phase diagram of IrO2. At pH = 7 the surface sites are covered by OH and O at most potentials. At low potential, the surface is covered by OH groups (not shown). Increasing the potential oxidizes OH to O first at the bridge sites and then at the cus sites. Eventually formation of OOH becomes thermodynamically favored. When this happens, we expect oxygen evolution to become appreciable,18 and the surface structure is then determined by the kinetics of the steady-state evolution of oxygen. The formation of chlorine adsorbates directly at the cus sites requires pH < −3. Formation of Cl at the bridge sites requires even lower pH.
 |
| | Fig. 1 Surface phase diagram for IrO2 (110) in equilibrium with Cl−, H+ and H2O at 298.15 K and aCl− = 1. The regions where we expect chlorine or oxygen evolution to become significant have been marked. c and b denote cus site and bridge sites, respectively. The adsorbate phases are shown in the insets. Ir atoms are cyan, O atoms are red, H atoms are white and Cl atoms are green. | |
We would expect that for a good catalyst the formation of the Cl intermediate has ΔG ∼ 0 eV near 1.36 V and that there are free sites available for the formation of this intermediate. A mechanism involving Cl adsorbed directly at an Ir cation, does not fulfill any of these requirements. Instead we see from the phase diagram that a ClOc intermediate is thermodynamically favored for U > 1.5 V in the pH range from 0 to 3.
This suggests the following sequence of intermediates on IrO2
| | | Oc + 2Cl−(aq) → ClOc + Cl−(aq) + e− → Oc + Cl2(g) + 2e− | (15) |
as both steps have |Δ
G| = 0.14 eV at
U = 1.36 V, and a significant amount of O
c sites exist at
U > 1.36 V. The reaction is written here as a Volmer–Heyvrosky mechanism. However, as we only consider the stability of the adsorbed intermediate, we cannot compare the relative rates of the Tafel, Heyvrosky and Khrishtalik steps.
Surface phase diagram for RuO2
The phase diagram for RuO2 (110) turns out to be a bit more complicated (see Fig. 2). At pH = 7, the surface is dominated by species formed by the oxidation of water. At low potential, only the bridge sites are covered by OH. When the potential is increased, OH is formed at the cus sites, before OH is oxidized to O. We find that oxygen association at the cus sitesis exothermic by 0.71 eV for the fully O-covered surface. The association barrier is only 0.18 eV, while desorption of O2cc is endothermic by 1.16 eV. O2cc will therefore most likely be present at the surface rather than Oc. Oxygen evolution could happen by further oxidation of the surface| | | H2O + O2cc → O2c + c + H2O → O2c + OHc + H+ + e−. | (17) |
The stability of the O2c + OHc structure relative to H2O and H+ is indicated in Fig. 3. Desorption of O2 from this surface has ΔG = −0.1 eV, however, so when O2c + OHc starts to form, we expect oxygen evolution to become important. Additional barriers could exist, but we will not go further into the details of oxygen evolution.
 |
| | Fig. 2 Surface phase diagram for RuO2 (110) in equilibrium with Cl−, H+ and H2O at 298.15 K and aCl− = 1. The regions where we expect chlorine or oxygen evolution to become significant have been marked. c and b denote cus site and bridge sites, respectively. | |
 |
| | Fig. 3 The adsorption energies of chlorine at cus (black): ΔE(Clc) = 0.59![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) −2.26 eV (■ – vacant neighboring cus-sites, ▲ – Cl neighbor, ● – O neighbor), the adsorption energy of ClO (red) at cus: ΔE(ClOc) = 0.52 ΔE(Oc) −2.26 eV (■ – vacant neighboring cus-sites, ▲ – Cl neighbor, ● – O neighbor), the adsorption energy of ClO (red) at cus: ΔE(ClOc) = 0.52![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 0.62 eV ( ΔE(Oc) + 0.62 eV ( – vacant neighboring cus sites, – vacant neighboring cus sites,  – O neighbor, – O neighbor,  – average adsorption energy of ClO for the fully covered surface vs. average adsorption energy for O for fully covered surface), adsorption energy of Cl atop O at cus (blue): ΔE(Clc) = −0.48 – average adsorption energy of ClO for the fully covered surface vs. average adsorption energy for O for fully covered surface), adsorption energy of Cl atop O at cus (blue): ΔE(Clc) = −0.48![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 0.68 eV ( ΔE(Oc) + 0.68 eV ( – Cl atop O vs. O with vacant neighboring cus sites, – Cl atop O vs. O with vacant neighboring cus sites,  —Cl atop O vs. O with O neighbors, —Cl atop O vs. O with O neighbors,  – Cl atop O vs. O with ClO neighbors, – Cl atop O vs. O with ClO neighbors,  – average adsorption energy of Cl atop O for fully covered surface on vs. average adsorption energy of O for fully covered surface), the adsorption energy of O2ccvs. the average adsorption energy of Oc (yellow): ΔE(O2cc) = 0.94 – average adsorption energy of Cl atop O for fully covered surface on vs. average adsorption energy of O for fully covered surface), the adsorption energy of O2ccvs. the average adsorption energy of Oc (yellow): ΔE(O2cc) = 0.94![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 1.96 eV, and the adsorption energy of Cl(Oc)2vs. the average adsorption energy of Oc (green): ΔE(Cl(Oc)2 = 0.56 ΔE(Oc) + 1.96 eV, and the adsorption energy of Cl(Oc)2vs. the average adsorption energy of Oc (green): ΔE(Cl(Oc)2 = 0.56![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 2.51 eV. The mean absolute error of the fits are below 0.21 eV. ΔE(Oc) + 2.51 eV. The mean absolute error of the fits are below 0.21 eV. | |
On RuO2–chlorine species formed at pH < 1.3, however, oxygen is still the most stable adsorbate near U = 1.36 V. We find that the 2Ob + Oc + OClc intermediate is metastable relative to a 2Ob + Cl(Oc)2 structure. The latter structure forms at U > 1.5 V, and we expect this to be the intermediate on RuO2 (110).
| | | O2cc + 2Cl−(aq) → Cl(Oc)2 + Cl−(aq) + e− → Oc + Cl2(g) + 2e−. | (18) |
Adsorption of oxygen at the cus sites leads to an increase in the work function. This is consistent with negatively charged O
2cc adsorbates. Subsequent formation of Cl(O
c)
2 leads to a decrease in the work function. This is consistent with Cl(O
c)
2 being more positively charged than O
2cc, as has been suggested for the Khrishtalik mechanism.
We note in passing that the formation of O2cc and Cl(Oc)2 depend on the presence of pairs of Ru cus sites at the surface, and it may not be relevant for alloys of e.g. TiO2 and RuO2. Neglecting the formation of O2cc and Cl(Oc)2 and considering the IrO2 reaction path eqn (15), we find that at U = 1.36 V each step has |ΔG| = 0.05–0.12 eV, depending on whether there is Oc or OClc adsorbed at the other cus site in the (2 × 1) unit cell. The trend in the change of the function upon formation of Oc and ClOc is similar to the change of the work function upon formation of O2cc and Cl(Oc)2.
Scaling relations.
As mentioned above, it is possible to construct the surface phase diagram and reaction intermediate as function of pH, potential and the Cl− concentration for a given material. The aim is now to generalize the analysis, not studying a single or a few oxide surfaces but rather determining a descriptor which will be a continuous material variable. The starting point of our analysis is to establish correlations between adsorption energies of intermediates on various (110) rutile oxide surfaces. Such relations can be useful in establishing simplified models describing the surface activity and composition, and can be suitable for subsequent screening purposes.29 In Fig. 3 the adsorption energies of Clc and ClOc as defined above are plotted against the O binding at the cus-site with the same environment at the surface. The plot clearly shows that the Cl and O adsorption energies are linearly correlated. Such linear energy relations between adsorption energies of hydrogenated species (CHx, OH, SH, and NHx) and the adsorption of the corresponding unhydrogenated atoms: (C, O, S, and N) have previously been shown for transition metals30,31 and transition metal compounds including oxides.18,32 The scaling of Cl with respect to O is very similar to the scaling of OH with respect to O. This reflects the fact that Cl has a valency of one like the oxygen atom in OH. ClOc thus also scales as OH (and similar to HOOc). The present results suggest that the oxygen adsorption energy is a general measure (a so-called “descriptor”) for the reactivity of oxides which has also been suggested for the case of cations in oxides by Pankratiev.33
Adsorption of Cl atop Oc is determined by:
| | | ΔE = E(ClOc) − E(Oc) − ½E(Cl2) = ΔE(ClOc) − ΔE(Oc) | (19) |
The linear scaling relations established above makes it possible to analyze the reaction, not only for a specific metal
oxide surface, but for potential metal
oxide catalyst surfaces with continuously varying reactivity as measured by the adsorption energy of oxygen at the cus-site. The obtained reactivity curves will then be continuous in the oxygen adsorption energy, whereas specific oxides (
e.g. RuO
2, IrO
2, PtO
2, and TiO
2) will show up as discrete points. The descriptor approach provides a fast overview of the “phase-space” of materials, but leaves the problem of how to find specific materials with the desired descriptor properties unanswered.
Generalized phase diagram
Since the binding energy of all intermediates at the cus sites scales directly with ΔE(Oc), it is possible to construct a generalized phase diagram showing the most stable phase at potential U as function of the material-dependent descriptor, ΔE(Oc).
We choose the electrolytic conditions such that when increasing the potential the most stable form of chlorine goes directly from Cl− to Cl2, which means that the pH value should be between −1 and 3. HCl(aq) is more stable than Cl− at pH values below ∼−1, whereas HClO(aq) becomes stable at pH values higher than ∼3. We keep the electrolyte pH and Cl− concentration fixed (pH = 0, aCl− = 1) and investigate the surface phase diagram as a function of ΔE(Oc ) and potential. This approach is not a limitation of the method, since other electrolyte conditions can be treated just by changing the free energies accordingly.
This is shown in Fig. 4. In the limit of weak binding, oxygen association becomes exothermic and barrierless, so phases like ClOc and Cl(Oc)2 cannot form. From the linear relations we find that
has |Δ
G| < 0 for Δ
E(O
c) > 2.97 eV. We therefore chose to consider only OH
c and Cl
c for Δ
E(O
c) > 2.97 eV. The free energies of OH
c and Cl
c are within 0.01–0.27 eV depending on the
oxide, and we expect some coexistence in these regions of phase space. The range of Δ
E(O
c) for some
rutile oxides is seen in
Fig. 5. For IrO
2 and RuO
2 the line at lowest Δ
E(O
c) marks the adsorption energy with free neighboring cus sites, and the line at highest Δ
E(O
c) marks the adsorption energy with O
c neighbors as calculated in the (2 × 1) unit
cell. For PtO
2 and TiO
2 the line at weakest binding marks the binding energy at high O
c coverage. The variation in adsorption energy with coverage may be seen as an uncertainty arising from neglecting adsorbate–adsorbate interactions. For the considered oxides Δ
E(O
c) is more affected by changing the
oxide than changing the O
c coverage. The change of the most stable adsorbate when the potential is increased is qualitatively reproduced for RuO
2 and IrO
2.
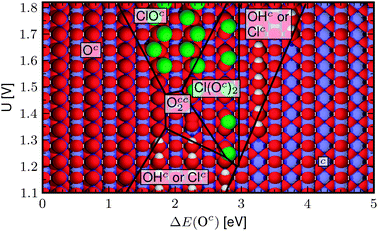 |
| | Fig. 4 The most stable surface at pH = 0 and aCl− = 1 as a function of potential, U, and the surface reactivity descriptor, ΔE(Oc). Metal ions are blue, O atoms red, hydrogen atoms white, and chlorine atoms are green. The regions in the figure are determined by the most stable surface configuration at the given potential. The phase borders are defined by the equilibrium point of the reactions. So for example, the border between the surface with Oc on the surface and the surface with ClOc is defined by: Oc + Cl−(aq) ⇌ ClOc + e−, ΔG(Oc) − ΔG(ClOc) − eUSHE = 0. | |
 |
| | Fig. 5 Sabatier volcanoes (black dotted) for the considered reaction paths involving ClOc, Cl(Oc)2 and Clc (from left to right). The domains of the most stable surface structure as function of potential and oxygen binding energy is marked by gray. To be truly active, the intermediate should form at sites that are stable, as this makes the active site abundant. The solid black line shows the combined Sabatier volcano taking into account the stability of the active sites for a given mechanism. The Sabatier volcano for oxygen evolution18 (dashed blue line) shows OER always requires a higher potential than ClER. The activity of IrO2 and RuO2 are indicated with error bars derived from the variation of the Oc adsorption energy with varying Oc coverage. | |
Chlorine evolution activity.
Firstly, we investigate the mechanism involving ClOc| | | Oc + 2Cl−(aq) → ClOc + Cl−(aq) + e− → Oc + Cl2(g) + 2e−. | (21) |
The potential at which all steps are neutral or downhill is:| | | U = Ueq + |ΔG(ClOc) − ΔG(Oc)|/e, | (22) |
where Ueq is the equilibrium potential for chlorine evolution, in this case 1.36 VSHE. Secondly, we investigate the mechanism involving Cl(Oc)2:| | | O2cc + 2Cl−(aq) → Cl(Oc)2 + Cl−(aq) + e− → Oc + Cl2(g) + 2e−. | (23) |
The potential at which all steps are neutral or downhill is:| | | U = Ueq + |ΔG(Cl(Oc)2) − ΔG(O2cc)|/e. | (24) |
Thirdly we consider a mechanism involving Clc adsorbed directly at the metal cus site.| | | 2Cl−(aq) + c → Cl−(aq) + Clc + e− → Cl2(g) + c + 2e−. | (25) |
This mechanism could be relevant for oxides with weaker adsorption energy at the cus site than RuO2. However, our calculations suggest that this mechanism will be somewhat poisoned by OHc formation at the cus sites. The potential where all steps are neutral or downhill is:| | | U = Ueq + |ΔG(Clc)|/e, | (26) |
RuO2 and PtO2 have |ΔG(Clc)| < 0.05 eV for high and low coverage of Clc, respectively, and could in principle work as good catalysts following this path; however, for RuO2 we find the cus sites to be blocked by O2cc.
Since the different chlorine evolution potentials all are functions of ΔE(Oc), the potentials can be plotted directly on the phase diagram as shown in Fig. 5. This is similar to the Sabatier activity volcano curves known from heterogeneous catalysis.34 To have the surface phase diagram in the same plot as the potential volcano directly assures that the activity volcano and the stable surface configuration agree. In other words, the different activity plots are relevant in different areas of the phase diagram, which are easily obtained by looking at Fig. 5. The thick black line marks the volcanoes, where the mechanism involves one of the most stable surfaces as an intermediate at the potential where all steps are neutral or downhill in free energy. We note that the surface composition during oxygen and chlorine evolution is not determined by equilibrium, but rather by a steady state. However, it seems plausible that the surface composition determined by equilibrium is one of the intermediates during the reaction. Fig. 5 also shows the activity of IrO2 and RuO2 based on Oc adsorption energy, with the error bars corresponding to the variation of the Oc adsorption energy when going from low to high Oc coverage.
If the accuracy of the linear relations are taken into account, the three investigated mechanisms form a single volcano with a broad plateau for ΔE(Oc) from 1.5 eV to 3.5 eV. Deviations from the linear relations could be important in this area. The agreement between the detailed analysis for IrO2 and RuO2 and the linear relations is therefore surprisingly good.
We find RuO2 to be at the top of the volcano, whereas IrO2 binds Cl on top Oc too weakly. TiO2 does not show up on this activity scale. To our knowledge, only a few studies of the relative activity of rutile oxides have been carried out. Kuhn and Mortimer found IrO2 and RuO2 to have similar activities and to be more active than TiO2. Mixtures of TiO2 with Ir and Ru are more active than mixtures of TiO2 with Cr, Co, or Pt.35 Arikado et al. found the overpotential to increase in the order RuO2 < Ti/PtO2 < IrO2.36 Kelly et al. found the specific activity of Ru sites at RuxTi1−xO2 to be 45% more active than the Ir sites at IrxTi1−xO2. 4,37 We note the discrepancy between the relative activity of RuO2, IrO2, and PtO2 could be because different preparation methods may lead to different surface roughness factors and different concentrations of residual chlorine in thermally prepared oxides.4 The high activity of RuO2 and IrO2 relative to TiO2 is in agreement with experiments. The rutile crystal structure of PtO2 is not the most stable structure for PtO2. It is however possible that some PtO2 may be found in the rutile crystal phase if PtO2 is mixed with oxides that do form the rutile crystal phase.
For comparison the potential for oxygen evolution is also shown in Fig. 5. It is seen that the potential for chlorine evolution is lower than the potential for oxygen evolution in spite of the lower equilibrium potential for oxygen evolution. This is the reason why electrochemical chlorine evolution is possible. It is also seen that a good oxygen evolution catalyst is also a good chlorine evolution catalyst. A comparison of the experimental potentials for OER and ClER has suggested that the selectivity of oxides does not depend appreciably on the catalyst material.2 The potential of chlorine evolution changes with the potential of oxygen evolution with a slope of 1. Interestingly, one of the biggest outliers in the comparison above was a Pt/MnO2 catalyst in acid where the potential for oxygen evolution was 0.3 eV higher than the potential of chlorine evolution. MnO2 has an oxygen binding energy around 3.2 eV.38 Based on Fig. 5 we would therefore expect the potential for chlorine evolution to be 0.4 V lower than the potential for oxygen evolution. We note that at other pH values the competition between chlorine and oxygen evolution will change; see Fig. 1 and Fig. 2.
Single-crystal experiments on RuO2 show that the (110) surface is less active for Cl2 evolution than the (101) and the (320) surfaces.8,39 On polycrystalline RuO2,40 mixed RuO2 + TiO2,41 and RuO2 (320)39 the activity depends on pH, whereas the activity of RuO2 (110) is independent on pH. The variation of activity with pH has been explained by the reaction
| | | OHc ⇌ Oc + H+(aq) + e− | (22) |
determining the availability of active O
c sites.
7,39,40,42 This clearly requires O
c and OH
c to be near equilibrium at the reaction conditions for Cl
2 evolution. Since the bridge sites and cus-sites on the (110) surface of
rutile oxides fulfill the same scaling relations between O and OH adsorption as perovskites,
32 it is reasonable to assume the scaling relations are identical for all
rutile oxide surfaces. In this case
Fig. 5 applies for any
rutile oxide surface, but with the oxygen adsorption energy depending on the specific surface facet. It has been argued that the binding energy on the stepped (320) surface is stronger than on the (110) surface.
39 If it is assumed the O
2cc and Cl(O
c)
2 intermediates form at the (320) surface as well,
Fig. 5 shows that as Δ
E(O
c) is decreased from
ca. 2.6 eV, the OH
c–O
2cc equilibrium shifts to higher potential, which leads to increased blocking of the active sites by OH
c at a fixed overpotential. We note the overpotential at constant current is found to be 80 meV lower on the (320) surface than on the (110) surface,
39 and thus within the vertical error bars indicated in
Fig. 5.
Conclusion
Based on DFT calculations, we have established linear scaling relations between Cl, ClO, and O adsorption energies at the cus-sites of rutile oxides. These linear energy relations enable the construction of a generalized surface phase diagram where potential and binding of oxygen are the descriptors determining the surface composition. By applying an electrochemical–thermodynamic approach we can make the first simple theoretical analysis of the electrocatalytic chlorine evolution reaction based on the free energies of the reaction intermediates. A lower-bound to the overpotential required for driving the reaction is thereby determined as function of the oxygen adsorption energy. This approach is an electrochemical analogue to the Sabatier analysis used in heterogeneous catalysis. Combining the surface phase diagram and the Sabatier volcano, one obtains a qualified suggestion for the surface structure during reaction condition. The analysis shows that ClO or Cl(Oc)2 will form spontaneously on the cus-sites of IrO2 and RuO2 at the potential required for chlorine evolution. This indicates that the Cl2 evolution occurs through these intermediates on IrO2 and RuO2. The potential necessary for Cl2 evolution is always smaller than the potential for oxygen evolution for oxides exhibiting certain oxygen adsorption energies. A simple explanation is that the oxide evolution reaction involves three intermediates, and since the bindings of these intermediates to the catalyst are linearly related, there cannot be found a material that binds all of them to the surface with exactly the right binding strength. This is the reason for the high overpotential even at the top of the oxygen evolution volcano. The chlorine evolution reaction, on the other hand, involves only a single intermediate, and a material that optimizes this bond could in principle exist. This difference in overpotential is consistent with experiments2 and rationalizes experimental findings.
Acknowledgements
The authors thank Prof. M. T. M. Koper for useful discussions. The Center for Atomic-scale Materials Design is funded by the Lundbeck Foundation. This work was supported by the Danish Center for Scientific Computing through Grant No. HDW-1103-06, the European Commission (Marie Curie Research Training Network MRTNCT-2006-032474) and The Danish Council for Strategic Research though the HyCycle Center (No. 2104-07-0041).
References
- EuroChlor (representing the chloro-alkali industry), Chlorine Industry Review, 2007–2008.
- S. Trasatti, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 2000, 45, 2377–2385 CrossRef CAS.
- E. J. Kelly, D. E. Heatherly, C. E. Vallet and C. W. White, J. Electrochem. Soc., 1987, 134, 1667–1675 CrossRef CAS.
- S. Trasatti and W. E. O'Grady, Adv. Electrochem. Electrochem. Eng., 1981, 12, 117–261 Search PubMed.
-
S. Trasatti and G. Lodi, Electrodes of Conductive metallic Oxides, Elsevier, 1980, pp. 301–358 Search PubMed.
- L. I. Krishtalik, Electrochim. Acta, 1981, 26, 329 CrossRef CAS.
- T. Hepel, F. Pollak and W. E. J. O'Grady, J. Electrochem. Soc., 1986, 133, 69–75 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. J. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef CAS.
- M. Lischka, C. Mosch and A. Gross, Electrochim. Acta, 2007, 52, 2219–2228 CrossRef CAS.
- A. Panchenko, M. T. M. Koper, T. E. Shubina, S. J. Mitchell and E. J. Roduner, J. Electrochem. Soc., 2004, 151, A2016–A2026 CrossRef CAS.
- A. U. Nilekar and M. Mavrikakis, Surf. Sci., 2008, 602, L89–L94 CrossRef CAS.
- J. Rossmeisl, G. S. Karlberg, T. Jaramillo and J. K. Nørskov, Faraday Discuss., 2008, 140, 337–346 Search PubMed.
- P. Liu, A. Logadottir and J. K. Nørskov, Electrochim. Acta, 2003, 48, 3731 CrossRef CAS.
- D. Cao, G. Q. Lu, A. Wieckowski, S. A. Wasileski and M. J. Neurock, J. Phys. Chem. B, 2005, 109, 11622 CrossRef CAS.
- P. Ferrin, A. U. Nilekar, J. Greeley, M. Mavrikakis and Rossmeisl, Surf. Sci., 2008, 602, 3424–3431 CrossRef CAS.
- M. T. M. Koper, T. E. Shubina and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 686 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- N. López, J. Gómez-Segura, R. P. Martin and J. Pérez-Ramírez, J. Catal., 2008, 255, 29–39 CrossRef CAS.
- D. Crihan, M. Knapp, S. Zweidinger, E. Lundgren, C. J. Weststrate, J. N. Andersen, A. P. Seitsonen and H. Over, Angew. Chem., Int. Ed., 2008, 47, 2131–2134 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892–7895 CrossRef.
- Open-source codes available at http://wiki.fysik.dtu.dk/dacapo and http://wiki.fysik.dtu.dk/ase.
- G. S. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158–5161 RSC.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730 RSC.
- J. K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. S. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. J. H. Jacobsen, J. Catal., 2002, 209, 275 CrossRef CAS.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 Search PubMed.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- E. Fernandez, P. G. Moses, A. Toftelund, H. A. Hansen, J. I. Martinez, F. Abild-Pedersen, J. Kleis, B. Hinnemann, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2008, 47, 4683–4686 CrossRef CAS.
- Y. D. Pankratiev, React. Kinet. Catal. Lett., 1982, 20, 255.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- A. T. Kuhn and C. J. Mortimer, J. Electrochem. Soc., 1973, 120, 231–236 CAS.
- T. Arikado, C. Iwakura and H. Tamura, Electrochim. Acta, 1978, 23, 9–15 CrossRef CAS.
- E. J. Kelly, C. E. Vallet and C. W. White, J. Electrochem. Soc., 1990, 137, 2482–2491 CrossRef CAS.
- J. Rossmeisl, K. Dimitrievski, P. Siegbahn and J. K. Nørskov, J. Phys. Chem. C, 2007, 111, 18821–18823 CrossRef CAS.
- E. Guerrini, V. Consonni and S. Trasatti, J. Solid State Electrochem., 2005, 9, 320–329 CrossRef CAS.
- J. L. Fernández, M. R. Gennero de Chialvo and A. C. Chialvo, Electrochim. Acta, 2002, 47, 1129–1136 CrossRef CAS.
- R. G. Erenburg, L. I. Krishtalik and N. P. Rogozhina, Elektrokhimiya, 1984, 20, 1183 Search PubMed.
- R. G. Erenburg, Elektrokhimiya, 1984, 20, 1602 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details regarding construction of the phase diagrams; Tables S1–S5, and linear relations. See DOI: 10.1039/b917459a |
|
| This journal is © the Owner Societies 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 surface unit cell and 4
1 surface unit cell and 4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 4
4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ×
×![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 Monkhorst–Pack type k-point sampling for slab calculations.22 The Kohn–Sham equations are solved using a plane wave basis with a cutoff of 350 eV for the eigenstates, and the densities are described using a cutoff corresponding to 500 eV. Vanderbilt ultrasoft pseudopotentials are used to deal with the ion cores.23 A Fermi smearing of 0.1 eV is used, and energies are extrapolated to an electronic temperature of 0 K. The two bottom layers of the slab are fixed in their bulk structure, while the two top layers as well as possible adsorbates on it are relaxed until the sum of the absolute forces is less than 0.05 eV Å−1. All calculations are performed using the Dacapo and ASE simulation package.24
1 Monkhorst–Pack type k-point sampling for slab calculations.22 The Kohn–Sham equations are solved using a plane wave basis with a cutoff of 350 eV for the eigenstates, and the densities are described using a cutoff corresponding to 500 eV. Vanderbilt ultrasoft pseudopotentials are used to deal with the ion cores.23 A Fermi smearing of 0.1 eV is used, and energies are extrapolated to an electronic temperature of 0 K. The two bottom layers of the slab are fixed in their bulk structure, while the two top layers as well as possible adsorbates on it are relaxed until the sum of the absolute forces is less than 0.05 eV Å−1. All calculations are performed using the Dacapo and ASE simulation package.24
![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ln(10)pH.
ln(10)pH.![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) lnaCl−.
lnaCl−.


![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) −2.26 eV (■ – vacant neighboring cus-sites, ▲ – Cl neighbor, ● – O neighbor), the adsorption energy of ClO (red) at cus: ΔE(ClOc) = 0.52
ΔE(Oc) −2.26 eV (■ – vacant neighboring cus-sites, ▲ – Cl neighbor, ● – O neighbor), the adsorption energy of ClO (red) at cus: ΔE(ClOc) = 0.52![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 0.62 eV (
ΔE(Oc) + 0.62 eV ( – vacant neighboring cus sites,
– vacant neighboring cus sites,  – O neighbor,
– O neighbor,  – average adsorption energy of ClO for the fully covered surface vs. average adsorption energy for O for fully covered surface), adsorption energy of Cl atop O at cus (blue): ΔE(Clc) = −0.48
– average adsorption energy of ClO for the fully covered surface vs. average adsorption energy for O for fully covered surface), adsorption energy of Cl atop O at cus (blue): ΔE(Clc) = −0.48![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 0.68 eV (
ΔE(Oc) + 0.68 eV ( – Cl atop O vs. O with vacant neighboring cus sites,
– Cl atop O vs. O with vacant neighboring cus sites,  —Cl atop O vs. O with O neighbors,
—Cl atop O vs. O with O neighbors,  – Cl atop O vs. O with ClO neighbors,
– Cl atop O vs. O with ClO neighbors,  – average adsorption energy of Cl atop O for fully covered surface on vs. average adsorption energy of O for fully covered surface), the adsorption energy of O2ccvs. the average adsorption energy of Oc (yellow): ΔE(O2cc) = 0.94
– average adsorption energy of Cl atop O for fully covered surface on vs. average adsorption energy of O for fully covered surface), the adsorption energy of O2ccvs. the average adsorption energy of Oc (yellow): ΔE(O2cc) = 0.94![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 1.96 eV, and the adsorption energy of Cl(Oc)2vs. the average adsorption energy of Oc (green): ΔE(Cl(Oc)2 = 0.56
ΔE(Oc) + 1.96 eV, and the adsorption energy of Cl(Oc)2vs. the average adsorption energy of Oc (green): ΔE(Cl(Oc)2 = 0.56![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ΔE(Oc) + 2.51 eV. The mean absolute error of the fits are below 0.21 eV.
ΔE(Oc) + 2.51 eV. The mean absolute error of the fits are below 0.21 eV.

