Quasi-classical statistico-dynamical description of polyatomic photo-dissociations: state-resolved distributions
Maykel Leonardo
González-Martínez
*ab,
Laurent
Bonnet
*b,
Pascal
Larrégaray
b and
Jean-Claude
Rayez
b
aDepartamento de Física General, Instituto Superior de Tecnologías y Ciencias Aplicadas, Habana 6163, Cuba. E-mail: mleo@instec.cu
bInstitut des Sciences Moléculaires, Université Bordeaux 1, 351 Cours de la Libération, 33405 Talence Cedex, France. E-mail: l.bonnet@ism.u-bordeaux1.fr
First published on 10th November 2009
Abstract
An alternative methodology to investigate indirect polyatomic processes with quasi-classical trajectories is proposed, which effectively avoids any binning or weighting procedure while provides rovibrational resolution. Initial classical states are started in terms of angle-action variables to closely match the quantum experimental conditions and later transformed into Cartesian coordinates, following an algorithm very recently published [J. Chem. Phys. 2009, 130, 114103]. Trajectories are then propagated using the ‘association’ picture, i.e. an inverse dynamics simulation in the spirit of the exit-channel corrected phase space theory of Hamilton and Brumer [J. Chem. Phys. 1985, 82, 595], which is shown to be particularly convenient. Finally, an approximate quasi-classical formula is provided which under general conditions can be used to add possible rotational structures into the vibrationally-resolved quasi-classical distributions. To introduce the method and illustrate its capabilities, correlated translational energy distributions from recent experiments in the photo-dissociation of ketene at 308 nm [J. Chem. Phys. 2006, 124, 014303] are investigated. Quite generally, the overall theoretical algorithm reduces the total number of trajectories to integrate and allows for fully theoretical predictions of experiments on polyatomics.
I. Introduction
The 20th century witnessed both the advent of modern computers and the associated exponential growth in computational power, which continues nowadays. As more can be done in significantly less time, simulation of inherently more complex processes and/or larger systems is attempted. In the field of chemical physics, what started as describing atomic and diatomic molecular processes currently looks after the simulation of, e.g. larger polyatomics, clusters, phenomena at surfaces and biomolecular complexes of interest.However, despite all the effort being devoted to develop approaches which include quantum effects in the dynamics of large molecular systems,1 realistic quantum-mechanical simulations of polyatomic processes remain prohibitively expensive. To date, the only general theoretical alternative is the quasi-classical trajectory method (QCT),2–4 which is based on numerically solving Hamilton’s (or Newton’s) equations of motion. Primarily, this is due to the cumbersome basis sets that need to be handled within quantum calculations in order to avoid crude approximations, but also partially because developing general, i.e. scalable classical trajectory codes is relatively easier.
To allow for comparison with experiments, both the selection of classical initial conditions and the statistical treatment of QCT results should be semiclassical in spirit. In particular, to mimic quantum features using classical (continuous) magnitudes, additional binning or weighting procedures are quite difficult to avoid. As implied, the underlying source of the problem—as with some other drawbacks of QCT—is that classically, vibrations and rotations are not quantised per se. In this regard, important advances have been made in the last few years by replacing the standard/histogram binning (SB) procedure by a Gaussian weighting (GW).5–12 In the latter, the different trajectories are assigned different (Gaussian) statistical weights, larger the closer its final actions to integer values. Despite its many promising capabilities, we have recently pointed out how the convergence of GW could be affected when applied to processes involving polyatomics.11 This is mainly because increasing the number of atoms in a molecule will almost certainly increase the number of modes for which a quantum-mechanical description is required—and Gaussian weights must be assigned. As a result, the overall weight of a given trajectory could be significantly reduced, in particular if several actions vary simultaneously.
At the same time, powerful experimental techniques have been developed during the precedent decades and very precise measurements of state-to-state observables are now possible. Correlated product distributions—where final state and/or translational energy distributions are measured in coincidence with given rovibrational states of the products—are among such. These increasingly sophisticated experiments demand finer statistics on the QCT results for highly resolved, intrinsically quantum features are much more difficult to ‘converge’ using classical mechanics. The ‘brute force’ approach is of course to increase the number of trajectories in the classical ensemble—and as their propagation is easily task-parallelised, i.e. particularly suitable to solve in computer clusters—running millions of such is becoming common.
In this work we report on an alternative QCT algorithm for investigating polyatomic processes which effectively avoids any binning or weighting method while providing both vibrational and rotational resolution. Its main advantage comes from the fact that initial conditions are directly generated at the semiclassical rovibrational states of interest in terms of angle-action variables, which automatically reduces the total number of trajectories to integrate. These are however propagated in Cartesian coordinates, by means of a transformation very recently published.13 In addition, a quasi-classical formula is derived to further incorporate possible rotational structures. To introduce and illustrate the capabilities of our method, we simulate highly-structured empirical correlated product distributions from the dissociation of ketene at 308 nm.14
The paper is organized as follows: the problem, theoretical aspects of the QCT implementation and results of its application are dealt with in section II and later discussed in section III; finally, section IV summarizes the results.
II. Theory and application
IIA: Ketene dissociation at the S0 electronic surface
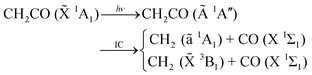
The photo-fragmentation of ketene,is arguably the most intensively investigated polyatomic process in the last two decades, cf.ref. 14–34. At present, it is firmly established that following optical excitation to the Ã
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A′′ state, the molecule either undergoes intersystem crossing to the lowest-lying, triplet, or fast internal conversion to the singlet electronic state. From these, dissociation into methylene and carbon monoxide occurs. Despite the triplet threshold lying ∼3150 cm−1 below the singlet, the fact that it presents a (small) barrier to dissociation—a few hundred inverse centimetres —but mainly, that the interaction which accounts for the change in electronic spin is rather weak, makes the singlet channel statistically dominant from excess energies as low as 100–200 cm−1. Such conditions make this process an effective prototype for a barrierless polyatomic unimolecular reaction on a single potential energy surface (PES). Experimentally, it has the additional advantage of a well-defined total energy and time origin distinctive of photo-dissociations.14
1A′′ state, the molecule either undergoes intersystem crossing to the lowest-lying, triplet, or fast internal conversion to the singlet electronic state. From these, dissociation into methylene and carbon monoxide occurs. Despite the triplet threshold lying ∼3150 cm−1 below the singlet, the fact that it presents a (small) barrier to dissociation—a few hundred inverse centimetres —but mainly, that the interaction which accounts for the change in electronic spin is rather weak, makes the singlet channel statistically dominant from excess energies as low as 100–200 cm−1. Such conditions make this process an effective prototype for a barrierless polyatomic unimolecular reaction on a single potential energy surface (PES). Experimentally, it has the additional advantage of a well-defined total energy and time origin distinctive of photo-dissociations.14
Earlier measurements of energy-dependent rates and overall product distributions were used as benchmarks to test and develop various statistical models including phase space theory (PST) and Rice–Ramsperger–Kassel–Marcus (RRKM) theory, cf.refs. 21–24. It was concluded that under moderate excitations the molecule dissociates statistically, exit-channel effects becoming increasingly important with augmenting energy. The dissociating picture therefore evolves from that of a loose to a tight transition state (TS).31 During the last decade, however, there has been growing interest in the problem of correlated product distributions.14,27,32 In the most recent experiments, Komissarov et al.14 studied the photo-fragmentation of the molecule at 308 nm and measured product translational energy distributions for specific rotational states of CO, i.e. P(Et;jCO). These are the observables we will focus on in the present work.
IIB: Singlet potential energy surface
Extensive trajectory calculations require a reliable numerical representation of the singlet PES. This was generated from the most recently reported high-level ab initio data.29 In this work, Klippenstein, East and Allen used a separation in transitional and conserved modes to determine the quadratic force fields along the reaction path—at the CCSD/[5s4p2d, 4s2p] level of theory—in terms of CIs symmetry internal coordinates. For excess energies of the order of that obtained with a 308 nm laser (Eexc ≈ 2350 cm−1), these force fields should provide all essential information on the couplings between the intra-fragment modes and the dissociation coordinate in the vicinity of the reaction path, as well as the interaction dependence on the mutual orientation of the fragments.† To further assess its quality, in the same work, the authors showed that variational RRKM energy-dependent rates predicted with this PES are in quantitative agreement with the experiment.With S = {Si} the symmetry internal coordinates, Fij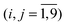 the quadratic force constants and VCC (Fig. 7 in ref. 29) the minimum potential energy along the reaction path as a function of the C–C interatomic distance, S4, the PES may be written as
the quadratic force constants and VCC (Fig. 7 in ref. 29) the minimum potential energy along the reaction path as a function of the C–C interatomic distance, S4, the PES may be written as
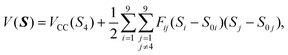 | (1) |
Slightly more elaborate are 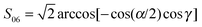 and
and 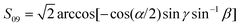 , where—if individual ketene atoms are numbered as they enter in the chemical formula—α = ∠(H1C1H2), β = β1,2 = ∠(H1,2C1C2) and γ (CH2 wagging angle) are all angular internal coordinates defined in Fig. 1 of the same work. The Fij functions were obtained from fittings to values in Table VI in ref. 29.
, where—if individual ketene atoms are numbered as they enter in the chemical formula—α = ∠(H1C1H2), β = β1,2 = ∠(H1,2C1C2) and γ (CH2 wagging angle) are all angular internal coordinates defined in Fig. 1 of the same work. The Fij functions were obtained from fittings to values in Table VI in ref. 29.
Finally, we validated the PES by diagonalising the Hessian matrix and confirming that all local harmonic frequencies previously reported (Table VII in ref. 29) were successfully reproduced.
IIC: Quasi-classical trajectories
We will introduce in what follows a particular implementation of QCT ideas and show its predictive power in the simulation of highly-resolved jCO-correlated translational energy distributions, from the unimolecular dissociation of ketene. Theoretically, it can be assumed that under the experimental conditions reported in ref. 14, these product distributions correspond to a given total energy E = Eexc + Enmodes and angular momenta J, i.e. P(Et;jCO) ≡ P(Et;E,J,jCO). The zero-point energy in the molecule normal modes, Enmodes ≈ 4730 cm−1.In reading the following section, it is important to keep in mind that we use an association rather than a dissociation picture for propagating trajectories. This is based on a method due to Hamilton and Brumer35 which will be introduced in section IIC2, where its many advantages are also discussed.
Discarding all center-of-mass coordinates the phase-space results:
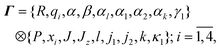 | (2) |
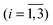 and CO (i = 4); J, Jz, the moduli of the total angular momentum and its z-axis projection in the laboratory frame; l, the modulus of the orbital angular momentum; j1, j2, the moduli of CH2 and CO rotational angular momenta; k, the modulus of the total rotational angular momentum k = j1 + j2; and κ1, the algebraic value of the projection of j1 onto the C2 axis of CH2. Finally, α, β, αl, α1, α2, αk and γ1 are respectively all the angles conjugate to the angular momenta mentioned above. It is apparent that in terms of these variables we can effectively set up, individually, all the vibrational and rotational modes of the fragments.
and CO (i = 4); J, Jz, the moduli of the total angular momentum and its z-axis projection in the laboratory frame; l, the modulus of the orbital angular momentum; j1, j2, the moduli of CH2 and CO rotational angular momenta; k, the modulus of the total rotational angular momentum k = j1 + j2; and κ1, the algebraic value of the projection of j1 onto the C2 axis of CH2. Finally, α, β, αl, α1, α2, αk and γ1 are respectively all the angles conjugate to the angular momenta mentioned above. It is apparent that in terms of these variables we can effectively set up, individually, all the vibrational and rotational modes of the fragments.
Given E, J (fixed to 1) and j2 (≡jCO)—for each set of energetically permitted vibrational states xi, 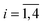 —the total available energy Eavail and maximum allowed values lmax and j1,max are completely determined.§ From all these, Jz, k and κ1 are thus randomly selected from uniform distributions according to Jz ∈ [−J,J], |j1,max − j2| ≤ k ≤ j1,max + j2 and κ1 ∈ [−j1,max,j1,max]. Microcanonical distributions are finally obtained by aleatory selection of all angles and phases from a uniform distribution in [0,2π]. All vector constraints on the set of angular momenta must also be satisfied.
—the total available energy Eavail and maximum allowed values lmax and j1,max are completely determined.§ From all these, Jz, k and κ1 are thus randomly selected from uniform distributions according to Jz ∈ [−J,J], |j1,max − j2| ≤ k ≤ j1,max + j2 and κ1 ∈ [−j1,max,j1,max]. Microcanonical distributions are finally obtained by aleatory selection of all angles and phases from a uniform distribution in [0,2π]. All vector constraints on the set of angular momenta must also be satisfied.
At this point, the Γ vector is transformed to Cartesian coordinates, using the algorithm presented in ref. 13. Here, a slight readjustment is necessary due to the conditions of the experiment, as the total energy of the system—rather than the relative velocity between the fragments—must be fixed. Specifically, the three Cartesian components of P (section IIC3 in ref. 13) should be computed right before the final step (determination of nuclear momenta, second part of section IIC11 in ref. 13) for only at this point it is possible to calculate the energy available to translation, Eavail,t, from which 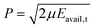 (μ being the system reduced mass). Computationally, an incubation period is needed before using an otherwise acceptable initial state to avoid possible correlations in the numerical generation of pseudo-random numbers.
(μ being the system reduced mass). Computationally, an incubation period is needed before using an otherwise acceptable initial state to avoid possible correlations in the numerical generation of pseudo-random numbers.
Besides its simplicity, the ECCPST offers quite a few practical advantages, e.g. (1) initial conditions are generated where the assumptions for partitioning into product normal modes are best fulfilled—i.e. at the inter-fragment distance for which the interaction between the CH2 and CO is negligible—so the usual dispersion in the ensemble’s total energy will be minimum (of about 2–3 cm−1 in our calculations); (2) all threshold behaviour is expected to be reproduced at its best, since product states are given precise energies in direct correspondence to their quantum counterparts; (3) initial conditions are straightforwardly defined by fixing the centres-of-mass distance between the resulting fragments—which explicitly appears in the transformation from angle-action variables to Cartesian coordinates13—while the TS can be re-defined at convenience during propagation (in this case, by the C–C interatomic distance which was proven best29); (4) since product states statistics is performed on a subset of initial conditions, the extra (non-trivial) work of discretising classical magnitudes at the end of the trajectories is avoided; (5) any binning or weighting to cope with the conceivable non-adiabaticity of vibrations in the course of reaction—which was found to be of about 15–20% after some preliminary calculations—can be avoided; and (6) the PES does not need to be determined within the reactant region. A few other advantages will be discussed in the following sections.
The main drawback, however, is that (possibly) many trajectories are propagated which never actually reach the TS. In fact, we found that approximately only 1 out of 10 trajectories enters the reactants region.¶ The overall propagation time may thus be significantly reduced by applying strategies to quickly identify those trajectories which will ultimately be discarded.
A fixed-step fourth-order Adams–Bashforth–Moulton predictor-corrector method initialised with a fourth-order Runge–Kutta integrator was used for propagation. Trajectories were followed until one of two conditions was fulfilled: (1) the molecule reached the transition state (at the C–C interatomic distance R‡ ≡ RCC, as relevant to the specific excitation energy from Table X in ref. 29); and (2) t = Tmax = 20 ps. The step size Δt = 2 × 10−4 ps was adjusted so that the maximum error in total energy did not exceed ΔE = 20 cm−1, i.e. less than 0.3% of E, with which the mean error was 〈ΔE〉 = 5 cm−1. Under these conditions, the fraction of non-fragmented to fragmented trajectories was consistently smaller than 0.5%. Typically, a single trajectory required between 1 and 3 s of CPU time—according to the specific values of x2 and j2—on an Altix XE210 computer with two Dual-Core Intel® Xeon® 5030 (‘Dempsey’) processors.
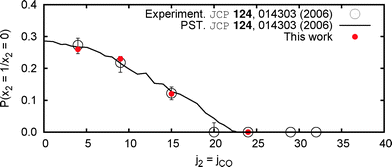 | ||
| Fig. 1 (Colour online) Vibrational branching ratio for singlet CH2 in coincidence with selected CO (x4 = 0,j2) states. Comparison with experimental and previous PST calculations. | ||
In principle, to predict these weights at a given j2 state of interest two contributions need to be taken into account. First, Monte Carlo methods should be applied to find the relative probability that for each scissor state x2 a given set of angle-action variables is finally accepted as a valid initial condition. Here the ECCPST proves again particularly convenient, since this is readily done if track is kept on the percentage of successful trials and the hypervolume in phase space from which each x2 set of initial conditions was randomly selected. The second step is to correct this relative probability for dynamical effects, which in practice would mean to determine the ratio of capture probabilities from each scissor mode. Despite its apparent simplicity, obtaining a reliable approximation for the latter could be difficult for it not only depends on the quality of the PES, but also on the relative accuracy of TS locations and the set of integration parameters. However, it was previously shown that, by cancellation of errors, least-biased values (also referred as PST, depending on the convention employed) are in excellent agreement with the experiment.14 The values reported in Fig. 1 are directly calculated from our initial conditions by the algorithm explained at the top of this paragraph. Their agreement with experimental and previous theoretical values confirms the correctness of our approach. At last, the theoretical distributions are Gaussian-blurred to match the experimental resolution.
Calculated curves for several representative j2 states are compared with measurements in Fig. 2—and have been quoted as ‘λ = 0.0’ (blue), the reason for which will be given in the following section. The reported contributions from adjacent rotational states14 was appropriately taken into account to produce the distributions corresponding to j2 = 4 and 9. Additionally, the zero-point-energy (ZPE) corrected distribution41 has been included in the j2 = 4 panel, which illustrates the general behaviour for all other rotational states. To produce the latter, an ensemble of 2 × 105 initial conditions with continuous actions was started in the products, being the vibrational modes constraint between zero and their maximum energetically allowed values.
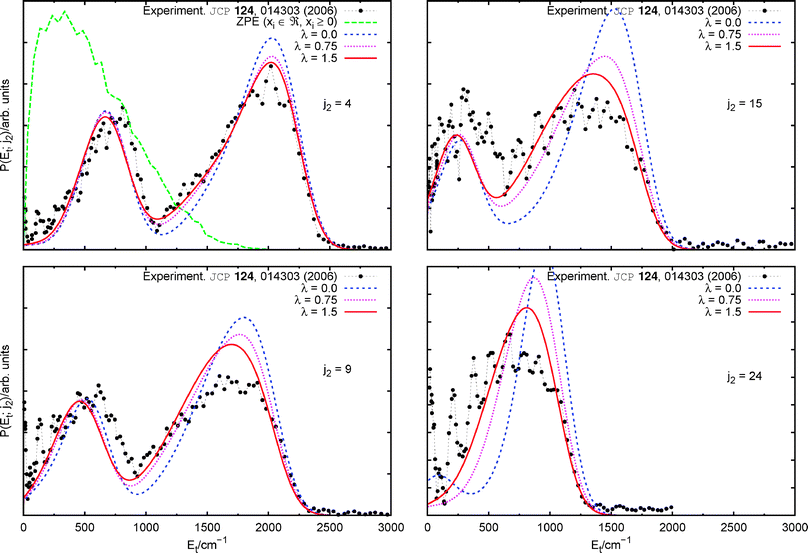 | ||
| Fig. 2 (Colour online) Correlated product translational energy distributions after excitation with a 308 nm laser: QCT results with vibrational resolution. Comparison with the experiment. | ||
However, it is clear that within each vibrational lobe, these theoretical distributions tend to predict larger than observed populations of low CH2 rotational levels. A plausible explanation may be derived from calculations on triatomic complexes. From these, it is known that quadratic representations of PES systematically tend to overestimate the energy transfers from the diatomic rotation to the inter-fragment translational degree of freedom.42 Physically, this is due to the bending mode being unrealistically hindered, i.e. insufficiently damped, in the course of fragmentation. The previous reaction rate calculations on this PES,29 being an observable of ‘global’ character, would very likely not depend as strongly on it as the distributions we intent to reproduce. Nevertheless, only the construction of a new global PES or ab initio dynamics calculations could give a reliable answer to this issue. Both these are beyond the scope of the present work.
On the other hand, several modifications can be attempted in order to bring the rotation-to-translation transfers closer to the empirical observations, under various physical grounds. One possible direction is to slightly change the force constants related with the molecular modes directly responsible for such transfers. The alternative followed here was to rewrite the PES as
| Vλ(S) = xV(S) + (1 − x)V∞(S), | (3) |
Trajectories were propagated on the modified PES of eqn (3) and the theoretical curves corresponding to λ = 0.75 and 1.5 are included in Fig. 2. From these, it is clear that reducing the energy transfer between CH2 rotation and inter-fragment recoil translation invariably leads to the overall experimental trend. The change is more strongly pronounced at higher CO rotational excitations and all λ = 1.5 curves are in very good agreement with the experiment.
IID: ‘Inserting’ the CH2 rotational structure
From Fig. 2 is readily seen that the main qualitative difference between ours (e.g., λ = 1.5) and the experimental results is the rotational structure observed in the latter, which relates to that of CH2 (ã![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1). In this section we show how these features can also be theoretically reproduced by the adequate modification of the PC(Et;E,J,jCO) distributions.
1A1). In this section we show how these features can also be theoretically reproduced by the adequate modification of the PC(Et;E,J,jCO) distributions.
Classically, after removing all center-of-mass coordinates, this is exactly
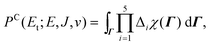 | (4) |
| Γ = {R,q,α,β,αl,αj,P,x,J′,Jz,l,j} | (5) |
Δ1 = δ(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t − Et), t − Et), | (6) |
Δ2 = δ(![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − E), − E), | (7) |
| Δ3 = δ(J′ − J), | (8) |
| Δ4 = δ(x − v), | (9) |
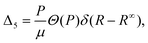 | (10) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t +
t + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) rv, i.e. into its translational and rovibrational components, with
rv, i.e. into its translational and rovibrational components, with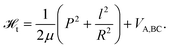 | (11) |
At last, χ(Γ) dΓ is the probability for the system mechanical state to be in the volume dΓ of phase space. The χ(Γ) function can be rewritten as
χ(Γ) = CJJzlj ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) (Γ), (Γ), | (12) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) is effectively independent of R∞ (provided this is large enough) and carries all the information on the full dissociation process: that coming from both the initial state distribution and possible dynamical effects, i.e. the state-to-state transition probabilities.
is effectively independent of R∞ (provided this is large enough) and carries all the information on the full dissociation process: that coming from both the initial state distribution and possible dynamical effects, i.e. the state-to-state transition probabilities.
On recalling some basic δ-function properties, partial integration in eqn (4) can be shown to yield (we simplify notation by discarding the explicit parametric dependence with respect to E and J in what follows)
PC(Et;v) ∝ ∫CJJzljδ(E − Et − Erv) ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) (Et,Jz,l,j;v) dJz dl dj, (Et,Jz,l,j;v) dJz dl dj, | (13) |
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) is the angle/phase average of
is the angle/phase average of ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) . The centrifugal orbital term has been neglected for it depends on R−2 which becomes negligible as R → R∞. Using the mean value theorem, this can be expressed as
. The centrifugal orbital term has been neglected for it depends on R−2 which becomes negligible as R → R∞. Using the mean value theorem, this can be expressed as| PC(Et;v) = ΞC(Et;v)PCLB(Et;v), | (14) |
| PCLB(Et;v) = ∫CJJzljδ(E − Et − Erv) dJz dl dj | (15) |
Eqn (14) may even look deceptively simple, though its derivation here proves useful to disentangle the physical origin of its factors. In a sense, the underlying ideas can be related to the theory of surprisal analysis of Levine and Bernstein,43 if the least-biased plays the role of the prior distribution. Eqn (14) basically states that PC differs by a scaling factor (which in turn depends on Et and v) with respect to the least-biased value PCLB. The factor itself, ΞC, ‘inherits’ from ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) all the dynamical information on the particular process, but it is additionally ‘weighted’ by the density of constrained rotational states.
all the dynamical information on the particular process, but it is additionally ‘weighted’ by the density of constrained rotational states.
In obtaining a quasi-classical analogue to eqn (14) two approximations are made. First, we replace the integrals in eqn (15) by the corresponding quantum sums and second, we postulate that if QCT founding ideas are valid for the process under study, using ΞC in the place of its quantum analogue ΞQ must be a fairly good approximation. We should note that the latter is not only a dynamical statement, but also a subtle assumption on the equivalence between the classical and convoluted-quantum densities of rotational states, which is expected to hold under quite general conditions.|| By means of these approximations one can write
| PQC(Et;v) = ΞC(Et;v)PQLB(Et;v), | (16) |
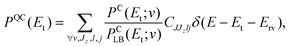 | (17) |
Although our derivation has been made for a triatomic system, it is easy to write the equivalent of eqn (17) for the correlated translational energy distribution in the fragmentation of ketene
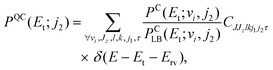 | (18) |
| CJJzlkj1j2τ = Δ(J,l,k)Δ(k,j1,j2)Θ(J − |Jz|) Θ(j1 − |τ|). | (19) |
The ECCPST proves again particularly convenient as the PCLB distribution in eqn (18) can be directly obtained from the ensemble of microcanonical initial conditions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1A1) asymmetric rotor energy levels.
Methylene has different its three principal moments of inertia (i.e. Iaa < Ibb < Icc), being thus an asymmetric rotor (AR). There is no general quantum formula which determines the rotational energy levels for such molecules in terms of the set of (quantum numbers) action variables, j1,κ1, used for computing the corresponding initial conditions.13
1A1) asymmetric rotor energy levels.
Methylene has different its three principal moments of inertia (i.e. Iaa < Ibb < Icc), being thus an asymmetric rotor (AR). There is no general quantum formula which determines the rotational energy levels for such molecules in terms of the set of (quantum numbers) action variables, j1,κ1, used for computing the corresponding initial conditions.13
However, it can be proved that the rigid-rotor Hamiltonian ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) rot becomes block-diagonal in the matrix representation of symmetric rotor (SR) eigenfunctions.44,45 It is also possible to show that for a given angular momentum J, every AR state correlates with one prolate (J,Ka) and one oblate (J,Kc) SR level only. It is thus a very common practice to label the AR levels as JKaKc, the indexes taking the values Ka ∈ {0,1,1,2,2,…,J,J} and Kc ∈ {J,J,…,2,2,1,1,0} with increasing energy of the terms. As it is easily seen, one could alternatively use a single label defined by τ = Ka − Kc, which in turn spans the 2J + 1 values from −J to J. τ rather than κ1 has been used in eqn (18) to stress the fact that this label has no direct correspondence to the κ1 action.
rot becomes block-diagonal in the matrix representation of symmetric rotor (SR) eigenfunctions.44,45 It is also possible to show that for a given angular momentum J, every AR state correlates with one prolate (J,Ka) and one oblate (J,Kc) SR level only. It is thus a very common practice to label the AR levels as JKaKc, the indexes taking the values Ka ∈ {0,1,1,2,2,…,J,J} and Kc ∈ {J,J,…,2,2,1,1,0} with increasing energy of the terms. As it is easily seen, one could alternatively use a single label defined by τ = Ka − Kc, which in turn spans the 2J + 1 values from −J to J. τ rather than κ1 has been used in eqn (18) to stress the fact that this label has no direct correspondence to the κ1 action.
In our calculations, spectroscopic CH2(ã![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1A1) energy levels were used when available and complemented with theoretical AR calculations at higher energies.46,47 The error in theoretical values could be of several inverse centimetres, especially at large values of j1 and τ.
1A1) energy levels were used when available and complemented with theoretical AR calculations at higher energies.46,47 The error in theoretical values could be of several inverse centimetres, especially at large values of j1 and τ.
III. Discussion
Rotational structures are barely visible in the measurements for j2 = 4 and 9, being strongly blurred due to the contribution of adjacent rotational states. Fig. 3 then shows the application of eqn (18) to λ = 1.5 theoretical distributions, corresponding to j2 = 15 and 24, as a test on the capabilities of the method. Within each panel, two theoretical curves correspond to convolutions with different strengths. One of them (darker, red) has been chosen to closely match the experimental resolution14 while the other (blue) shows the typical fine structures which are attainable with our method.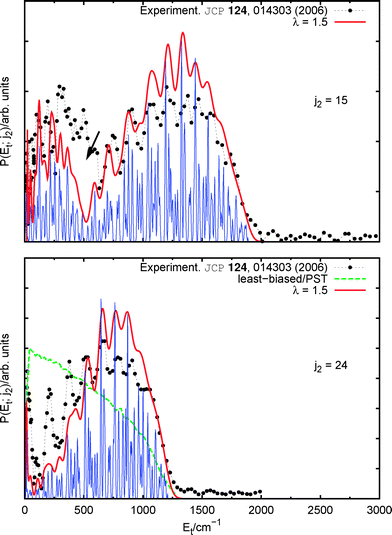 | ||
| Fig. 3 (Colour online) Correlated product translational energy distributions after excitation with a 308 nm laser: QCT results with rovibrational resolution. Comparison with the experiment. | ||
The empirical rotational structure is fairly well reproduced by the QCT calculations, being all theoretical and experimental peaks correctly aligned. The larger disagreement is observed within the upper panel, in the region shown by an arrow. This area corresponds to the matching between the low energy tail of the x2 = 0 state and the high energy component of x2 = 1, being the former the main contribution to it. The discrepancy between our curve and the experiment is thus a secondary effect due to the overestimation of rotation-to-translation transfers already discussed in section IIC5. It cannot be seen in Fig. 2 as the convolution used there artificially ‘populates’ the missing rotational states.
The least-biased distribution corresponding to j2 = 24 is also depicted in Fig. 3, obtained from the whole set of initial conditions. This distribution is directly comparable with the PST calculations shown in Fig. 8 of ref. 14. In fact, application of eqn (18) in order to ‘add’ a rotational structure to this curve would trivially reduce it to the quantum version of the least-biased/PST distribution. At last, by comparing this with the final theoretical curves, it is readily seen how the suppression observed in the low-Et part is correctly described by QCT.
It is important to address one last point referring to the insertion of the rotational structures in section IID. In principle, one might think that a different, simpler approach could be used: To additionally fix all rotational quantum numbers and propagate separate ensembles for each semiclassical state, very much as we have done here for each scissor excitation or can be found elsewhere, e.g.ref. 40. However, with respect to the initial conditions there is a basic difference in the way the vibrational and rotational modes are determined.13 Using the normal-mode approximation, the former are assigned precise energies corresponding to the quantum values. This means that normal mode displacements and conjugate momenta are calculated to exactly match the desired energy in the particular mode. On the other hand, classically, after fixing the angular momentum vector for a particular fragment, there remains an indetermination in the rotational energy due to the vibration–rotation coupling. In other words, there are different inertia tensors due to dissimilar normal-mode displacements which will result in different energies even for the same angular momentum. In the case of ketene, for example, calculations after additionally fixing the values of j1 and κ1 yield broad structures in the correlated translational energy distributions which are several hundred inverse centimetres wide. This would completely blur the rotational structures observed in Fig. 3. The indetermination should be smaller for symmetric tops—where a formula exists that determines the energy in terms of the angular momentum and one of its components—but still would, in general, strongly limit the QCT rotational resolution.
IV. Summary and conclusions
A QCT algorithm has been presented that allows to simulate indirect polyatomic processes involving exit-channel effects up to rovibrational resolution without the use of any binning or weighting procedure. It consists of three stages: (1) initial conditions are started in terms of angle-action variables to individually select the experimental states to be studied, which are later transformed into Cartesian coordinates for trajectory integration; (2) trajectories are propagated using an inverse dynamics simulation in the spirit of the exit-channel corrected phase space theory of Hamilton and Brumer; and (3) finally, an approximate quasi-classical formula is used to accurately incorporate possible rotational structures into the quasi-classical product distributions. Of these, only the second step is linked to the statistical assumptions inherent to the study of indirect processes, being the other two of general applicability.The method was introduced and its capabilities illustrated with the simulation of highly-resolved correlated translational energy distributions from recent experiments in the photo-dissociation of ketene at 308 nm.14 After slightly modifying the PES to deal with an overestimation of the energy transfer among rotational and translational degrees of freedom, calculated distributions with both vibrational and rotational resolution are in good agreement with the experiment.
Acknowledgements
Support from an Inter-University Agreement on International Joint Doctorate Supervision between the Instituto Superior de Tecnologías y Ciencias Aplicadas, Cuba and the Université Bordeaux 1, France, as well as the PNCB/2/4 project of the Departamento de Física General in the Cuban institution, are gratefully acknowledged. We wish to dedicate this work to Prof. Vincenzo Aquilanti, for his outstanding contribution to chemical reaction theory.References
- W. H. Miller, J. Chem. Phys., 2006, 125, 132305 CrossRef.
- R. N. Porter and L. M. Raff, Dynamics of Molecular Collisions, Part B, Plenum, New York, 1976 Search PubMed.
- D. G. Truhlar and J. T. Muckerman, in Atom–Molecule Collision Theory: A Guide for the Experimentalist, Plenum Press, New York, 1979, ch. Reactive Scattering Cross Sections: Quasiclassical and Semiclassical Methods, p. 505 Search PubMed.
- T. D. Sewell and D. L. Thompson, Int. J. Mod. Phys. B, 1997, 11, 1067 CrossRef CAS.
- L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 1997, 277, 183 CrossRef CAS.
- L. Bañares, F. J. Aoiz, P. Honvault, B. Bussery-Honvault and J. M. Launay, J. Chem. Phys., 2003, 118, 565 CrossRef CAS.
- L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 2004, 397, 106 CrossRef CAS.
- T. Xie, J. M. Bowman, J. W. Duff, M. Braunstein and B. Ramachandran, J. Chem. Phys., 2005, 122, 014301 CrossRef.
- M. L. González-Martínez, L. Bonnet, P. Larrégaray and J.-C. Rayez, J. Chem. Phys., 2007, 126, 041102 CrossRef CAS.
- L. Bonnet, J. Chem. Phys., 2008, 128, 044109 CrossRef CAS.
- M. L. González-Martínez, W. Arbelo-González, J. Rubayo-Soneira, L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 2008, 463, 65 CrossRef CAS.
- Z. Sun, D. H. Zhang, C. Xu, S. Zhou, D. Xie, G. Lendvay, S. Y. Lee, S. Y. Lin and H. Guo, J. Am. Chem. Soc., 2008, 130, 14962 CrossRef CAS.
- M. L. González-Martínez, L. Bonnet, P. Larrégaray, J.-C. Rayez and J. Rubayo-Soneira, J. Chem. Phys., 2009, 130, 114103 CrossRef CAS.
- A. V. Komissarov, M. P. Minitti, A. G. Suits and G. E. Hall, J. Chem. Phys., 2006, 124, 014303 CrossRef.
- V. Zabransky and R. W. Carr, Jr., J. Phys. Chem., 1975, 79, 1618 CrossRef CAS.
- D. J. Nesbitt, H. Petek, M. F. Foltz, S. V. Filseth, D. J. Bamford and C. B. Moore, J. Chem. Phys., 1985, 83, 223 CrossRef CAS.
- H. Bitto, I.-C. Chen and C. B. Moore, J. Chem. Phys., 1986, 85, 5101 CrossRef CAS.
- I.-C. Chen, W. H. Green, Jr and C. B. Moore, J. Chem. Phys., 1988, 89, 314 CrossRef CAS.
- W. H. Green, Jr, I.-C. Chen and C. B. Moore, Ber. Bunsen-Ges. Phys. Chem., 1988, 84, 389.
- E. D. Potter, M. Gruebele, L. R. Khundkar and A. H. Zewail, Chem. Phys. Lett., 1989, 164, 463 CrossRef CAS.
- S. J. Klippenstein and R. A. Marcus, J. Chem. Phys., 1989, 91, 2280 CrossRef CAS.
- S. K. Kim, Y. S. Choi, C. D. Pibel, Q.-K. Zheng and C. B. Moore, J. Chem. Phys., 1991, 94, 1954 CrossRef CAS.
- W. H. Green, Jr, A. J. Mahoney, Q.-K. Zheng and C. B. Moore, J. Chem. Phys., 1991, 94, 1961 CrossRef.
- S. J. Klippenstein and R. A. Marcus, J. Chem. Phys., 1990, 93, 2418 CrossRef CAS.
- I. Garcia-Moreno, E. R. Lovejoy and C. B. Moore, J. Chem. Phys., 1994, 100, 8890 CrossRef CAS.
- I. Garcia-Moreno, E. R. Lovejoy and C. B. Moore, J. Chem. Phys., 1994, 100, 8902 CrossRef CAS.
- C. G. Morgan, M. Drabbels and A. M. Wodtke, J. Chem. Phys., 1996, 104, 7460 CrossRef CAS.
- C. G. Morgan, M. Drabbels and A. M. Wodtke, J. Chem. Phys., 1996, 105, 4550 CrossRef CAS.
- S. J. Klippenstein, A. L. L. East and W. D. Allen, J. Chem. Phys., 1996, 105, 118 CrossRef CAS.
- E. A. Wade, H. Clauberg, S. K. Kim, A. Mellinger and C. B. Moore, J. Phys. Chem. A, 1997, 101, 732 CrossRef CAS.
- E. A. Wade, A. Mellinger, M. A. Hall and C. B. Moore, J. Phys. Chem. A, 1997, 101, 6568 CrossRef CAS.
- M. L. Costen, H. Katayanagi and G. E. Hall, J. Phys. Chem. A, 2000, 104, 10247 CrossRef CAS.
- K. M. Forsythe, S. K. Gray, S. J. Klippenstein and G. E. Hall, J. Chem. Phys., 2001, 115, 2134 CrossRef CAS.
- J. Liu, F. Wang, H. Wang, B. Jiang and X. Yang, J. Chem. Phys., 2005, 122, 104309 CrossRef.
- I. Hamilton and P. Brumer, J. Chem. Phys., 1985, 82, 595 CrossRef CAS.
- W. H. Miller, Adv. Chem. Phys., 1974, 25, 69.
- H. Goldstein, Classical Mechanics, Addison-Wesley, MA, 2nd edn, 1980 Search PubMed.
- D. M. Wardlaw and R. A. Marcus, J. Chem. Phys., 1985, 83, 3462 CrossRef.
- M. S. Child, Semiclassical Mechanics with Molecular Applications, Clarendon, Oxford, 1991 Search PubMed.
- F. J. Aoiz, V. Sáez-Rábanos, T. González-Lezana and D. E. Manolopoulos, J. Chem. Phys., 2007, 126, 161101 CrossRef CAS.
- A. J. C. Varandas, Chem. Phys. Lett., 1994, 225, 18 CrossRef CAS.
- P. Larrégaray, L. Bonnet and J.-C. Rayez, Phys. Chem. Chem. Phys., 2002, 4, 1781 RSC.
- R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, Oxford, 1987 Search PubMed.
- R. N. Zare, Angular Momentum, Wiley, New York, 1988 Search PubMed.
- P. R. Bunker and P. Jensen, Fundamentals of Molecular Symmetry, Institute of Physics Publishing, IoP London, 2005 Search PubMed.
- H. Petek, D. J. Nesbitt, D. C. Darwin and C. B. Moore, J. Chem. Phys., 1987, 86, 1172 CrossRef CAS.
- U. Bley and F. Temps, J. Chem. Phys., 1993, 98, 1058 CrossRef CAS.
Footnotes |
| † We discuss the implications of this quadratic approximation to the PES for trajectory calculations in some detail in section IIC5. |
| ‡ Throughout this work all actions will be quoted in ℏ units. |
| § The choice of R will become apparent in sections IIC2 and IIC3. |
| ¶ The indetermination on the exact TS location makes necessary to discard some trajectories even when propagating outwards from the reactants region. In this case, these constitute nearly one half of the total ensemble. |
| || This is not generally true for vibrational states, hence we deal with vibrationally-resolved distributions. |
| This journal is © the Owner Societies 2010 |